Задача
Задача. Предприятие выпускает два вида изделий: А и В, используя для этого сырье трех видов, запасы n-го ограничены. Норма расхода сырья на изготовление единицы каждого вида изделий, а также прибыль, получаемая от реализации изделий каждого вида следующие:
|
Сырье |
Норма расхода сырья на единицу изделия (кг) |
Запасы сырья (кг) |
|
|
1 |
2 |
||
|
1 3 |
6 0 12 |
6 4 6 |
54 32 72 |
|
Прибыль
от
реализации
единицы
изделия в у. |
4 |
2 |
|
Составить план выпуска изделий, дающий наибольшую прибыль предприятия. Составить математическую модель задачи, решить ее графически, составить двойственную задачу, решить ее и провести экономический анализ задачи.
Решение: Составим математическю модель. Пусть будет изготовлено х1 – изделий вида А и х2-изделий вида В. Тогда план производства представляется вектором (х1, х2).
Прибыль
от
реализации
одного
изделия вида А
составляет 4
единицы, а от
реализации х1
изделий – 4х1
единиц.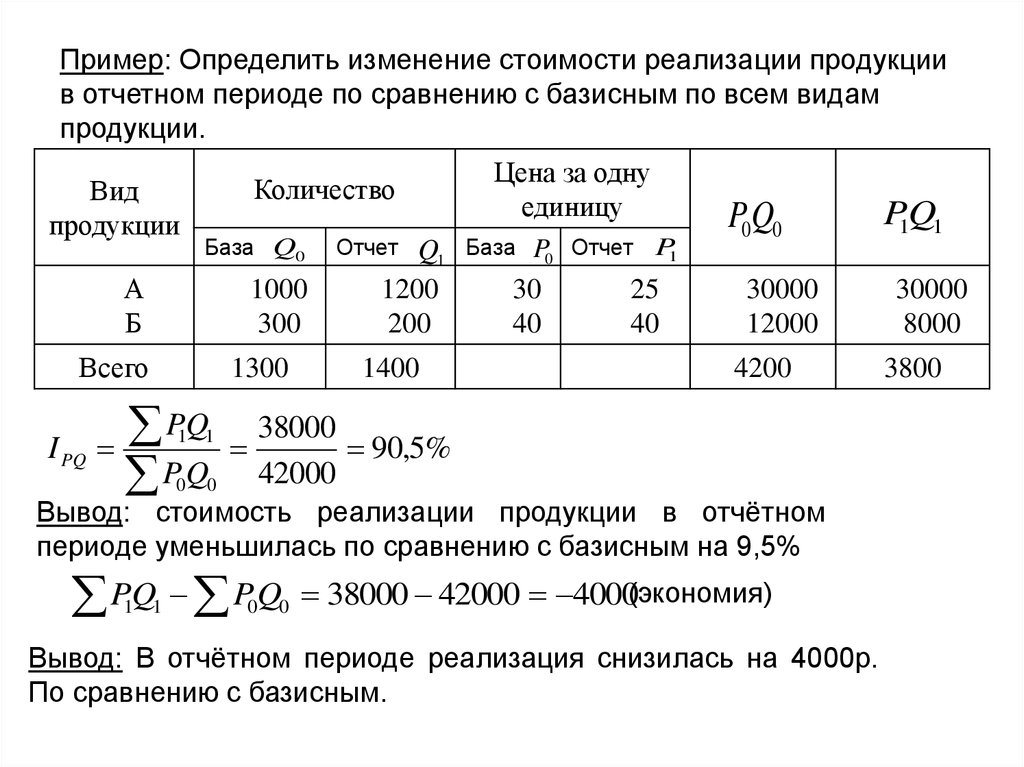
Прибыль от
реализации
одного изделия
вида В
составляет 2
единицы, а от
реализации х2
изделий – 2х2
На
производство
единицы
изделия А
расходуется 6
единиц сырья
первого вида,
а на х1
изделий А
расходуется 6х1
единиц сырья
первого вида.
На производство
единицы
изделия В
расходуется 6
единиц сырья
первого вида,
а на х2
изделий В
расходуется
6х2 единиц
сырья
первого вида.
Запасы сырья
первого вида
составляют 54
единицы ,
следователь 6х1+6х2£54.
Аналогичные
рассуждения
проводятся
по 2 и 3 видам
сырья.
Решим задачу графическим методом. Область допустимых решений задачи -пересечение полуплоскостей, определенных каждым неравенством системы ограничений.
Для
первого
неравенство:
6х1+6х2£54
строим
прямую 6х1+6х2=54.
Взяв
произвольную
точку из
одной из полуплоскостей,
определим,
является ли
данная полуплоскость
множеством
решений
данного
неравенства.
Например:
точка 0 (0;0). 6×0+6×0£54 Þ0< 54, т.е.
полуплоскость,
содержащая
т.
Аналогично строим полуплоскости, определяемые остальными неравенствами.
Х2
12
9 В 3
А 8 D
0 4 Е 9 1 Х1
2
Пересечение
этих
полуплоскостей
образует
область
допустимых
решений, т.
е.
многоугольник
ОАВDЕ. По теореме
об
экстремуме
целевой
функции,
если
оптимальное
решение
существует,
то оно
совпадает с
угловой
точкой
области допустимых
решений. Для
нахождения
оптимального
решения
строим
вектор
,
перпендикулярно
ему проводим линию уровня,
которую
перемещаем
по
направлению
вектора , т.к. задача
решается на max.
Последняя
точка
пересечения
линии уровня
и области
допустимых
решений
является оптимальным
решением
задачи. Если
оптимальное
решение
совпадает с
двумя
угловыми
точками
области
допустимых
решений,
например, х
где
в т.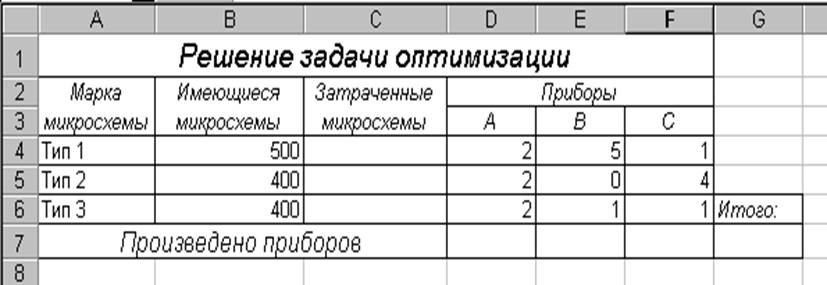
D,
которая
лежит на
пересечении I
и П граничных
прямых
Составим двойственную задачу к исходной. В исходной задаче ограничения заданы неравенствами и на переменные наложено ограничение неотрицательности, то получим симметричную пару задач.
Каждому ограничению исходной задачи соответствует переменная в двойственной. Цель задачи меняется на противоположную. Транспонируется матрица коэффициентов задачи, коэффициенты при переменных в целевой функции заменяются сводными членами системы ограничений исходной задачи.
Исходя
из теорем
двойственности,
найдем
решение
двойственной
задачи.
т.е. >0,
поэтому
соответствующие
им 1 и 2
ограничения
двойственной
задачи
выполняются
как равенства.
Первое и
третье
ограничения
исходной
задачи
выполняются
как строка
равенства Þ
соответствующие
им у
Получили:
8у3=2,
Экономический
анализ. Для
получения
максимальной
прибыли в ед.
необходимо
произвести изделий
вида А и — вида В, при
этом сырье 1 и 3
видов будет
израсходовано
полностью и
каждая
дополнительно
привлеченная
единица
сырья 1 вида
принесет
дополнительно
ед.
прибыли, а
каждая
дополнительно
привлеченная
единица
сырья 3 вида
даст
дополнительно
ед.
3.3: Графические решения — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 67077
Было бы неплохо, если бы мы могли просто производить и продавать бесконечное количество единиц продукта и, таким образом, зарабатывать бесконечную сумму денег? В бизнесе (и в повседневной жизни) мы знаем, что некоторые вещи просто неразумны или невозможны. Вместо этого мы надеемся максимизировать или минимизировать некоторое количество при заданном наборе ограничений.
Чтобы иметь задачу линейного программирования, мы должны иметь:
- Ограничения, представленные в виде неравенств
- Целевая функция , то есть функция, значение которой мы либо хотим получить как можно больше (хотим максимизировать), либо как можно меньше (хотим минимизировать).
Рассмотрим это расширение примера из конца последнего раздела.
Пример \(\PageIndex{1}\)
Компания выпускает базовую и расширенную версии своего продукта. Базовая версия требует 20 минут сборки и 15 минут покраски. Премиум-версия требует 30 минут сборки и 30 минут покраски. Если в компании штатное расписание на 3,900 минут сборки и 3300 минут покраски каждую неделю. Они продают базовые продукты с прибылью в 30 долларов, а продукты премиум-класса с прибылью в 40 долларов. Сколько экземпляров каждой версии нужно произвести, чтобы максимизировать прибыль?
Решение
Пусть \(b-\) количество произведенных базовых продуктов и \(p=\) количество произведенных продуктов премиум-класса.
Наша целевая функция — это то, что мы пытаемся максимизировать или минимизировать. В этом случае мы пытаемся максимизировать прибыль. Общая прибыль \(P\) равна
\[P = 30b + 40p\номер \]
В последнем разделе пример развивал наши ограничения. Вместе они определяют нашу задачу линейного программирования:
Целевая функция: \[P = 30b + 40p\nonumber \]
Ограничения:
\[\begin{array}{*{20}{c}} 20b + 30p \leq 3900 \\ 15b + 30p \leq 3300 \end{array}\nonumber \]
\[b \geq 0, \quad p \geq 0\nonumber \]
В этом разделе мы рассмотрим этот тип задачи графически. Начнем с построения графика ограничений, чтобы определить достижимая область – множество возможных решений. Просто показывая набор решений, где четыре неравенства перекрываются, мы видим четкую область.
Чтобы понять, как связана целевая функция, предположим, что мы рассмотрели все возможные производственные комбинации, дающие прибыль \(P = \$3000\), так что \(3000 = 30b + 40p\).
Этот набор комбинаций образует линию на графике. Делая то же самое для прибыли в 5000 и 6500 долларов, вы получите дополнительные линии. Нанося на график те, которые находятся на вершине нашей допустимой области, мы видим закономерность:
Обратите внимание, что все линии постоянной прибыли параллельны и что в целом прибыль увеличивается по мере продвижения вверх вправо. Обратите также внимание на то, что для прибыли в 5000 долларов некоторые уровни производства находятся внутри допустимой области для этого уровня прибыли, а некоторые — за ее пределами. Это означает, что мы могли бы реально получить прибыль в размере 5000 долларов, производя, например, 167 базовых предметов и не производя предметов премиум-класса, но мы не можем заработать 5000 долларов, производя 125 предметов премиум-класса и не производя базовых предметов, потому что это выходит за рамки наших ограничений.
Решением нашей задачи линейного программирования будет максимально возможная прибыль, которая все еще достижима.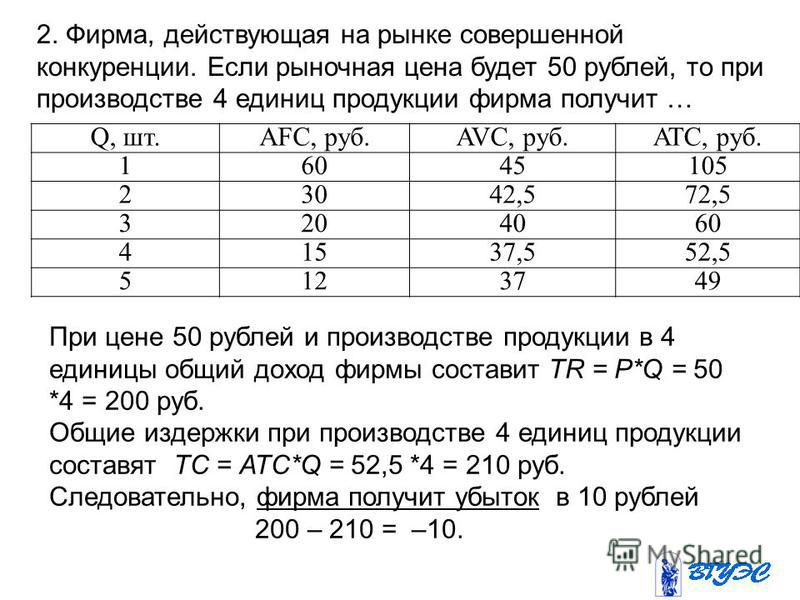
Графически это означает линию, расположенную дальше всего в правом верхнем углу, которая все еще касается допустимой области по крайней мере в точке. Это решение приведено ниже. 40(0) = \$ 5850. \nonumber \]
Обратите внимание, что это немного больше, чем прибыль, которая была бы получена при полном использовании всего персонала в \(b = 120, p = 50\), где прибыль составила бы быть 5600 долларов.
Целевая функция вместе с четырьмя угловыми точками выше образует ограниченную задачу линейного программирования. То есть представьте, что вы смотрите на три столба забора, соединенных ограждением (черная точка и линии соответственно). Если бы вы поместили свою собаку посередине, вы могли бы быть уверены, что она не убежит (при условии, что забор достаточно высок). Если это так, то у вас есть задача ограниченного линейного программирования. Если бы собака могла ходить бесконечно в любом направлении, то проблема была бы неограниченной.
В предыдущем примере видно, что линия максимальной прибыли всегда будет касаться границы допустимой области.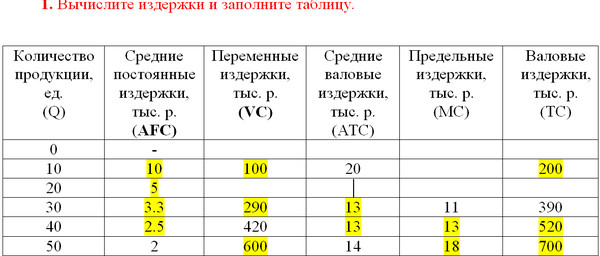
Это наблюдение легло в основу фундаментальной теоремы линейного программирования.
Фундаментальная теорема линейного программирования
- Если существует решение ограниченной задачи линейного программирования, то оно находится в одной из угловых точек.
- Если допустимая область неограничена, то максимальное значение целевой функции не существует.
- Если допустимая область неограничена, а целевая функция имеет только положительных коэффициентов, то минимальное значение существует.
В последнем примере мы решаем проблему несколько интуитивно, «сдвинув» линию прибыли вверх. Обычно мы используем более процедурный подход.
Графическое решение задачи линейного программирования
- Определите переменные для оптимизации. Заданный вопрос является хорошим индикатором того, какими они будут.
- Запишите целевую функцию сначала словами, а затем преобразуйте в математическое уравнение
- Запишите ограничения сначала словами, а затем преобразуйте в математические неравенства
- График неравенств ограничений и затенение допустимой области
- Определите угловые точки, решая системы линейных уравнений, пересечение которых представляет собой угловую точку.
- Проверка всех угловых точек целевой функции. «Выигрышная» точка — это точка, оптимизирующая целевую функцию (наибольшая при максимизации, наименьшая при минимизации)
Упражнение \(\PageIndex{1}\)
Максимизация \(P = 14x + 9y\nonumber \) с учетом ограничений:
\[\begin{align*} x + y &\leq 9 \\ 3x + y &\leq 15 \\ x \geq 0, & \; y \geq 0 \\ \end{align*} \nonumber \]
- Ответ
На графике допустимой области мы видим три угловые точки, представляющие потенциальный интерес: (0, 9), (5, 0) и пересечение двух линий в (3, 6). Затем мы оцениваем целевую функцию в каждой угловой точке.
\(P\) максимизируется, когда \(x = 3, y = 6\).
Точка
\(Р = 14х + 9у\)
(0, 9)
81
(5, 0)
70
(3, 6)
96
Пример \(\PageIndex{2}\)
Предприятие по производству здоровой пищи хочет создать смесь сухофруктов с высоким содержанием калия в виде коробки с 10 фруктовыми батончиками.
Было принято решение использовать курагу, содержащую 407 мг калия на порцию, и сушеные финики, содержащую 271 мг калия на порцию. Компания может закупать фрукты оптом по разумной цене. Курага стоит 9 долларов.0,99/фунт. (около 3 порций) и сушеные финики стоят 7,99 долларов за фунт. (около 4 порций). Компания хотела бы, чтобы коробка батончиков содержала по крайней мере рекомендуемую суточную норму потребления калия около 4700 мг и содержала не менее 1 порции каждого фрукта. Сколько порций каждого сухофрукта должно поместиться в коробку с батончиками, чтобы минимизировать затраты?
Решение
Начнем с определения переменных. Пусть
\(x =\) количество порций кураги
\(y =\) количество порций сушеных фиников
Теперь мы работаем над целевой функцией.
Для абрикосов в одном фунте 3 порции. Это означает, что стоимость одной порции составляет 9,99/3 = 3,33 доллара США. Таким образом, стоимость \(x\) порций составит 3,33\(x\).
Для фиников 4 порции на фунт. Это означает, что стоимость одной порции составляет \(\$ 7,99 / 4=\$ 2,00 .\) Таким образом, стоимость \(y\) порций будет \(2,00 y.\)
Общая стоимость, \(C \), для абрикосов и фиников будет
\[C=3,33 x+2,00 y \nonnumber\]
Обычно у нас были бы ограничения \(x \geq 0\) и \(y \geq 0\), так как нельзя использовать отрицательные порции. Но в этом случае мы дополнительно ограничены. Прописью:
- Должно быть не менее 1 порции каждого фрукта
- Продукт должен содержать не менее \(4700 \mathrm{мг}\) калия
Математически,
- Поскольку должно быть хотя бы 1 порция каждого фрукта, \(x \geq 1\) и \(v \geq 1\)
- В \(x\) порциях абрикосов содержится \(407 x\) мг калия, а в \(y\) порциях фиников — \(271 y\) мг калия. Сумма должна быть больше или равна \(4700 \mathrm{мг}\) калия или \(407 x+271 y \geq 4700\)
Итак, имеем.
Целевая функция:
\[C=3,33 x+2,00 y \nonumber\]
Ограничения:
\[\begin{align*}407 x+271 y \geq 4700 \\ x \geq 1, \ quad y \geq 1\end{align*}\]
Нарисуем ограничения и заштрихуем допустимую область:
Область не ограничена, но мы все равно сможем найти минимум. Мы видим две угловые точки.
В левом верхнем углу находится пересечение линий \(407x + 271y = 4700\) и \(x=1\). Решение пересечения с помощью замены:
\[\begin{align*} 407(1) + 271y &= 4700 \\ y &\ приблизительно 15,8 \\ \end{align*} \nonumber \]
Точка: \((1, 15.8)\ )
Внизу справа находится пересечение линий \(407x + 271y = 4700\) и \(y = 1\).
\[\begin{align*} 407x + 271(1) &= 4700 \\ x &\ приблизительно 10,9 \end{align*} \]
Точка: \((10.9, 1)\)
Проверка целевая функция в каждой из этих угловых точек:
Точка | Стоимость, \(C = 3,33x + 2,00y\)
|
|---|---|
(10.9, 1) | |
(1, 15,8) | \(С = 3,33(1) + 2,00(15,8) = \$34,96\) |
Компания может минимизировать затраты, используя 1 порцию абрикосов и 15,8 порций фиников.
Упражнение \(\PageIndex{2}\)
Компания производит два продукта. Изделие А требует 3 часов производства и 1 часа сборки. Продукт B требует 4 часов производства и 2 часов сборки. Всего доступно 84 часа производства и 32 часа сборки. Определить объем производства, обеспечивающий максимальную прибыль, если прибыль от продукта А составляет 50 долларов, а прибыль от продукта В — 60 долларов.
- Ответить
Пусть \(a\) – количество произведенного продукта A, а \(b\) – количество продукта B.
Наша цель — максимизировать прибыль: \(P = 50a + 60b\).
Из изготовления получаем ограничение:
\[3a + 4b \leq 84\номер\]
Из сборки получаем ограничение:
\[1a + 2b \leq 32\номер \]
У нас есть угловые точки (0, 16), (28, 0). Третий находится на пересечении двух линий. Чтобы найти это, мы могли бы умножить второе уравнение на -2 и добавить:
\[\begin{array}{rc} 3a + 4b &= 84 \\ — 2a — 4b &= — 64 \\ \hline a&= 20 \end{array} \nonumber \]
Третья угловая точка находится в точке (20, 6).
Оценка целевой функции в каждой из этих точек:
Точка
\(П\)
(0, 16)
\(Р = 50(0) + 60(16) = 960\)
(28, 0)
\(Р = 50(28) + 60(0) = 1400\)
(20, 6)
\(Р = 50(20) + 60(6) = 1360\)
Прибыль будет максимальной при производстве 28 единиц продукта A и 0 единиц продукта B.
Пример \(\PageIndex{3}\)
Фабрика производит стулья и столы, каждая из которых требует использования трех операций: резки, сборки и отделки. Первую операцию можно использовать не более 40 часов; второй не более 42 часов; а третий не более 25 часов. Стул требует 1 часа резки, 2 часов сборки и 1 часа отделки; столу требуется 2 часа на резку, 1 час на сборку и 1 час на отделку. Если прибыль составляет 20 долларов за единицу стула и 30 долларов за стол, сколько единиц каждого из них необходимо произвести, чтобы максимизировать прибыль?
Решение
Начнем с определения переменных. Пусть
\(c =\) количество изготовленных стульев
\(t =\) количество изготовленных столов
Прибыль, \(P\), будет \(P = 20c + 30t\).
Для резки \(c\) стульев потребуется \(1c\) часов, а для \(t\) столов потребуется \(2t\) часов. Мы можем использовать максимум 40 часов, поэтому
\[c + 2t \leq 40\nonumber \].
Для сборки \(c\) стульев потребуется \(2c\) часов, а для t столов потребуется \(1t\) часов. Мы можем использовать максимум 42 часа, поэтому
\[2c + t \leq 42\номер \].
Для отделки c стульев потребуется \(1c\) часов, а для \(t\) столов потребуется \(1t\) часов. Мы можем использовать не более 25 часов, поэтому
\[c + t \leq 25\nonumber \].
Поскольку мы не можем создавать отрицательные элементы, \(c \geq 0,\quad t \geq 0\).
Построив ограничения, мы можем увидеть допустимую область.
В этом регионе есть пять угловых точек.
Точка 1 :
В левом нижнем углу, где \(t = 0\) пересекает \(c = 0\). Точка: (0, 0)
Точка 2 :
В левом верхнем углу, где \(c = 0\) пересекает \(c + 2t = 40 \).
С помощью подстановки \(0 + 2t = 40 \), поэтому \(t = 20\).
Точка: \((0, 20)\)
Точка 3 :
В правом нижнем углу, где \(t = 0\) пересекает \(2c + t = 42 \).
С помощью подстановки \(2c + 0 = 42 \), поэтому \(c = 21\).
Точка: \((21, 0)\)
Точка 4 :
Где \(c + 2t = 40\) пересекает \(c + t = 25\).
Мы можем решить это как систему, используя любые известные нам методы. Мы могли бы решить второе уравнение относительно \(c\), получив \(c = 25 — t\), а затем подставить в первое уравнение:
\[\begin{align*} (25 — t) + 2t &= 40 \\ 25 + t &= 40 \\ t &= 15 \end{align*} \nonumber \]
Тогда \(c = 25 – 15 = 10\).
Точка: \((10, 15)\)
Точка 5 :
Где \(2c + t = 42\) пересекает \(c + t = 25\).
Мы можем решить это как систему, используя любые известные нам методы. На этот раз, используя другую технику, мы могли бы умножить нижнее уравнение на -1, а затем добавить его к первому:
\[\begin{array}{rc} 2c + t &= 42 \\ — c — t &= — 25 \\ \hline c = 17 \end{array} \nonumber \]
Затем с помощью \( c + t = 25 \), имеем \(17 + t = 25\), поэтому \(t = 8\).
Точка: \((17, 8)\)
Проверка целевой функции в каждой из этих угловых точек:
Точка | Прибыль, \(P = 20c + 30t\)
|
|---|---|
(0, 0) | \(P = 20(0) + 30(0) = \$0\) |
(0, 20) | \(P = 20(0) + 30(20) = \600$\) |
(21, 0) | \(P = 20(21) + 30(0) = \$420\) |
(10, 15) | \(P = 20(10) + 30(15) = \650$\) |
(17, 8) | \(P = 20(17) + 30(8) = \$580\) |
Прибыль будет максимальной при производстве 10 стульев и 15 столов.
Важные темы этого раздела
Целевая функция
Уравнения ограничений
Допустимая область
Угловые точки
Фундаментальная теорема линейного программирования
Решение задачи линейного программирования с использованием графа
3.3: Graphical Solutions распространяется по недекларированной лицензии, автором, ремиксом и/или куратором является LibreTexts.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Теги
Что такое производство? Типы, примеры и риски
От телефонов до одежды и автомобилей, производство превращает сырье в продукты с помощью машин. Различные стили производства удовлетворяют разные потребности, будь то мелкосерийное производство на заказ или полностью автоматизированные фабрики, работающие круглосуточно. Современное производство стало возможным благодаря достижениям в области технологий, а технологии продолжают трансформировать производственные процессы во всем мире.
Что такое производство?
Производство – это процесс превращения сырья и компонентов в материальные продукты с использованием машин, обычно в больших объемах. Производство позволяет детищу изобретателя завершить путь к тому, чтобы стать любимым гаджетом потребителя. Оптимизированный производственный процесс может означать разницу между успехом и провалом любого продукта.
Что такое производственный бизнес?
Производственный бизнес — это любая компания, которая использует сырье или компоненты для создания готовой продукции. Производственные предприятия производят большую часть продукции, которую мы используем, включая электронные устройства, мебель, медицинское оборудование и самолеты. Эти продукты могут распространяться либо непосредственно среди клиентов, либо через посредников, таких как розничные магазины. Некоторые производители производят компоненты, которые включаются в продукцию других компаний.
Производство и оптовая торговля: Оптовики служат посредниками между производителями и розничными торговцами. Они покупают товары оптом у производителей, затем хранят и перепродают их розничным торговцам и другим предприятиям в меньших количествах по более высокой цене за единицу.
- Ключевые отличия: В то время как производители разрабатывают и производят продукты, оптовики сосредотачиваются на распространении этих продуктов. Использование оптовиков для управления дистрибуцией позволяет производителям привлекать клиентов с меньшими затратами и позволяет им направить свою энергию на проектирование и производство. Оптовики также могут повысить ценность, помогая продавать и поддерживать продукты.
Производство и производство. Термины «производство» и «производство» часто используются взаимозаменяемо. Однако производство – это всего лишь один из видов производства. В то время как производство относится к процессу изготовления продуктов из сырья с помощью машин, производство — это более широкий термин, который может применяться к созданию множества различных продуктов и услуг с использованием ручных, а также автоматизированных процессов.
- Основные отличия: В то время как результатом производства является физическая, осязаемая продукция, термин «производство» может применяться и к менее осязаемой продукции. К ним относятся результаты деятельности предприятий сферы услуг, таких как аналитики фондового рынка, уборщики, стоматологи и авторы.
Ключевые выводы
- Производство — это процесс сборки сырья в продукты с использованием машин, как правило, в больших масштабах.
- Производство генерирует более 11% общего объема производства в США, а промышленные товары составляют основную часть мировой торговли товарами.
- Три ключевых типа производства: изготовление на складе (MTS), изготовление на заказ (MTO) и изготовление на сборке (MTA).
- Производственные системы адаптированы к различным объемам продукции и требованиям клиентов, от систем для мелкосерийной продукции на заказ до полностью автоматизированных заводов с большими объемами.
- Технологии, способные трансформировать производство, включают Интернет вещей (IoT), искусственный интеллект, блокчейн и робототехнику.
Производство Объяснение
Производство направлено на создание такого количества продуктов, которое рынок может купить по самой низкой цене. Это возможно только за счет использования машин и автоматизации.
Производство можно разделить на две широкие категории: дискретное и непрерывное производство. Дискретное производство преобразует сырье и компоненты в изделия, начиная от автомобилей и заканчивая мобильными телефонами и одеждой. Непрерывное производство, напротив, объединяет ингредиенты в соответствии с формулами или рецептами для производства больших количеств товаров, таких как напитки, химикаты и фармацевтические препараты.
Производство включает в себя несколько этапов превращения сырья в готовую продукцию, включая планирование и проектирование продукции, создание прототипов, коммерческое производство, проверку и доставку. Производители часто используют сборочные линии для более быстрого производства товаров с меньшими трудозатратами и требованиями к квалификации. При таком подходе изделия изготавливаются поэтапно по мере их перемещения по последовательным рабочим местам вдоль сборочной линии.
Почему важно производство?
Производство остается чрезвычайно важной частью экономики в США и во всем мире.
По данным Национальной ассоциации производителей, на производителей приходится более 11% от общего объема производства в США, в них занято 12,8 млн человек, а объем производства составил 2,3 трлн долларов в 2018 году. Большинство из этих компаний небольшие: из почти 250 000 фирм в производственном секторе США три четверти имеют менее 20 сотрудников.
Промышленные товары также составляют большую часть мировой торговли. Согласно анализу Всемирной торговой организации, в 2020 году они составили 71% от общего объема товарного экспорта на общую сумму 12,1 трлн долларов. По данным Организации Объединенных Наций по промышленному развитию (ЮНИДО), во всем мире производство является ключом к повышению производительности и экономическому росту, которая утверждает, что существует тесная связь между экономическим ростом, обусловленным производством, и снижением уровня бедности в стране.
История производства
Хотя производственные инновации, такие как печать, появились в Средние века, история современного производства всерьез началась с промышленной революции. В конце 1700-х годов многие ремесленные отрасли претерпели революцию благодаря внедрению машин. Эти отрасли включали текстильное производство, которое было преобразовано тремя машинами: прядильным станком, механическим ткацким станком и хлопкоочистительной машиной.
На протяжении столетий текстильное производство основывалось на преобразовании шерсти, а затем и хлопка в пряжу с использованием прялки с ручным приводом. Прядильщики использовали веретено для создания одной нити, которая затем доставлялась ткачу.
В конце 1700-х годов Джеймс Харгривз изобрел прялку «Дженни», в которой паровой двигатель сочетался с другими инновациями, что позволяло одному оператору прясть восемь веретен одновременно. Последующие улучшения увеличили это число до 80 шпинделей. Между тем, ткацкий станок Эдмунда Картрайта механизировал медленный ручной процесс превращения нити в ткань. Через Атлантику Эли Уитни разработал хлопкоочистительную машину, чтобы ускорить медленный процесс отделения хлопка от его семян.
Появление этих машин превратило текстильное производство из ремесленного производства в фабричное производство, а возросшая производительность сделала одежду более доступной для большего числа людей.
Автоматизация аналогичным образом изменила производство многих других продуктов, а новые методы и технологии продолжали стимулировать дальнейшее развитие. Массовое производство было популяризировано в начале 20-го века Генри Фордом, который применил методы сборочного конвейера для создания автомобилей по низкой цене. Бережливое производство, впервые внедренное Toyota в Японии в XIX веке.70-х годов, направленных на то, чтобы сделать производство быстрее и эффективнее, а также уменьшить количество дефектов. Сегодня робототехника и автоматизация процессов продолжают преобразовывать производство, повышать производительность и снижать производственные затраты.
Типы производства
Производственные стратегии можно разделить на три типа, каждый из которых предназначен для поддержки различных бизнес-требований: изготовление на складе, изготовление на заказ и изготовление на сборку.
Производство на складе (MTS): Производство на складе (MTS) — это широко используемая производственная стратегия, при которой производитель определяет, какое количество продукта производить, основываясь на прогнозах спроса. Затем продукты хранятся в качестве запасов компанией, дистрибьютором или розничным продавцом до тех пор, пока они не будут проданы. Преимущества MTS двояки: клиенты могут получить немедленную доставку продукции, а производители получают выгоду от эффекта масштаба. Точное прогнозирование спроса имеет решающее значение для успеха этого метода. Производство слишком малого количества товаров приводит к неудовлетворенным потребностям клиентов и упущенным возможностям получения дохода, а производство слишком большого количества товаров приводит к избыточным запасам, которые могут остаться непроданными.
Изготовление на заказ (MTO): При изготовлении на заказ (MTO) производитель изготавливает товары только после получения на них заказа. Это означает, что компания не рискует создавать непроданные продукты и может настраивать продукты в соответствии со спецификациями клиентов. MTO обычно используется для трудоемких, дорогостоящих промышленных товаров и в ситуациях, когда складирование продуктов было бы непрактично. Коммерческие самолеты, например, это продукция МТО.
Сборка на заказ (MTA): Метод сборки на заказ (MTA), иногда называемый сборкой на заказ, представляет собой комбинацию MTS и MTO. Производитель создает запас компонентов до получения заказов клиентов, но собирает их в продукты только на основе полученных заказов. Эта стратегия часто используется в ситуациях, когда для изготовления компонентов требуются значительные усилия и затраты, но их можно относительно быстро и легко собрать в конечный продукт. Преимущество MTA заключается в том, что производители могут предложить клиентам более широкий выбор опций, не рискуя окончательной сборкой до тех пор, пока они не получат твердый заказ.
Производственные системы
Производственные системы, как правило, делятся на четыре основных типа: от систем, предназначенных для обработки небольших партий продукции в малых объемах, до полностью автоматизированных заводов, которые могут производить огромные объемы продукции с минимальными затратами.
- Система производства на заказ: В системе производства на заказ продукты изготавливаются на заказ для каждого клиента. Один квалифицированный мастер или небольшая группа рабочих изготавливают отдельные дорогостоящие изделия в основном вручную или на специализированных машинах. Поскольку производство на заказ ориентировано на качество, а не на объем, эта система имеет самые высокие затраты на единицу продукции.
- Система периодического производства: При таком подходе единая производственная линия спроектирована с возможностью производства различных продуктов. Продукция изготавливается партиями на основе заказов клиентов, при этом производственная линия перенастраивается после каждой партии для выпуска следующего набора продуктов. Системы периодического производства обычно обрабатывают небольшие объемы каждого продукта.
- Система непрерывного производства: Предназначен для массового производства единичного изделия. Полуквалифицированные рабочие на каждой станции сборочной линии выполняют последовательные этапы сборки изделия по мере его прохождения. Этот подход идеален для крупносерийного производства, но требует больших первоначальных затрат.
- Гибкая производственная система: Это современный подход к созданию крупносерийной системы, которую можно относительно легко переконфигурировать для производства различных продуктов. Он направлен на автоматизацию каждого этапа производства и включает использование роботов, которые можно перепрограммировать для производства различных продуктов. Поскольку весь процесс спроектирован так, чтобы быть автоматическим и использовать как можно меньше людей, эти системы могут работать 24 часа в сутки и производить огромные объемы продукции при очень низкой удельной стоимости.
Примеры производства
По мере роста предприятий им необходимо адаптировать свои производственные стратегии и технологии, чтобы справляться с возросшей сложностью операций, поддерживать более высокий спрос и извлекать выгоду из новых возможностей получения дохода. Вот два примера:
- Компания Corkcicle начала свою жизнь с разработки инновационного продукта для охлаждения в бутылках, который позволил потребителям охлаждать вино и другие напитки без ведерка со льдом. Благодаря этому успеху компания расширилась, чтобы создать целую линейку охлаждающих продуктов, от коробок для завтрака до спортивных столовых. По мере роста сложности бизнеса Corkcicle внедрила интегрированную систему ERP, которая обеспечила большую прозрачность и контроль над управлением запасами и планированием спроса, а также многоканальной торговлей. Компания также получила дополнительный доход за счет индивидуальных вариантов производства, таких как фирменные логотипы и логотипы команд.
- Компания Saddleback Leather начала свой путь с единственного продукта: изготовленной на заказ кожаной сумки, которую ее основатель разработал для своих школьных учебников. Перенесемся в сегодняшний день, и компания производит десятки изделий из кожи, в том числе портфели, кошельки, кошельки, ремни и украшения, которые продаются непосредственно потребителям на ее веб-сайте. В условиях сильно колеблющегося сезонного спроса управление запасами имеет решающее значение. Чтобы удовлетворить этот спрос без затоваривания, Saddleback внедрила облачное решение для планирования запасов вместе с интегрированной системой ERP, которая поддерживает производство, электронную торговлю и другие функции.
Производственные риски
Производство представляет собой сложный и часто капиталоемкий бизнес, подверженный многим рискам. Факторы, которые могут нарушить производственные операции, варьируются от сбоев в цепочке поставок до ошибок прогнозирования.
- Колебания цен на сырье: Цены на сырье и компоненты могут быстро и непредсказуемо колебаться из-за таких факторов, как изменения глобального спроса и предложения. Даже когда производители сами фиксируют цены на материалы, они могут быть уязвимы к колебаниям стоимости доставки по всему миру.
- Проблемы с цепочкой поставок: Проблемы с цепочкой поставок могут привести к задержкам в получении важных компонентов. Недоступность компонентов может привести к остановке всего производственного процесса.
- Отзыв продукции: Дефекты продукции могут привести к дорогостоящим отзывам, судебным искам и ущербу для репутации. Важно поддерживать строгий и последовательный контроль качества на протяжении всего производственного процесса, включая окончательную проверку перед отправкой продукции.
- Соответствие нормативным требованиям: Строгие местные правила определяют, могут ли многие продукты продаваться на рынках по всему миру. Для производителей жизненно важно проанализировать нормативные требования на своих целевых рынках, прежде чем продавать свою продукцию, иначе они рискуют быть вынужденными заплатить дорогостоящие штрафы.
- Ошибки прогнозирования: Неточное прогнозирование может привести к производству большего количества продуктов, чем может быть продано, или недостаточно для удовлетворения спроса. Производители могут свести риск к минимуму, используя программное обеспечение, учитывающее исторические и сезонные модели продаж, а также внешние факторы.
- Киберриски: Хакеры регулярно атакуют производственные системы программами-вымогателями и другими вредоносными атаками. Сосредоточение внимания на кибербезопасности имеет решающее значение для производственных компаний.
Будущее производства
Технологии продолжают трансформировать производство точно так же, как они трансформируют другие отрасли. Вот четыре наиболее важные технологии, которые, по мнению EY, определят будущее производства:
- Интернет вещей (IoT): Производственные системы все чаще могут подключаться к Интернету и друг к другу, поэтому они могут передавать важную информацию, которая используется для мониторинга и оптимизации производственных процессов. Например, машины могут предоставлять непрерывную информацию о рабочих условиях окружающей среды или выдавать предупреждения, когда заканчиваются запасы определенного компонента.
- Искусственный интеллект (ИИ): Обещание ИИ обеспечить интеллектуальную осведомленность о сложных процессах имеет значительный потенциал в производстве. Приложения включают профилактическое обслуживание: анализируя исторические данные для выявления закономерностей, связанных с отказами, ИИ может прогнозировать необходимость обслуживания, помогая избежать дорогостоящих остановок производства. ИИ также может быть применен к цепочке поставок для анализа огромного количества факторов, которые могут повлиять на доступность сырья.
- Блокчейн: Блокчейн — технология, лежащая в основе таких криптовалют, как биткойн, — обеспечивает неизменную запись действий и транзакций. В производстве блокчейн можно использовать для отслеживания предметов, используемых в производстве, выявления контрафактных компонентов и проверки проверки и других этапов процесса на соответствие нормативным требованиям.
- Робототехника: Робототехника включает в себя множество различных футуристических технологий; их применение в производстве очевидно. Робототехника может использоваться для автоматизации процессов, снижения затрат на рабочую силу и, поскольку они могут работать 24 часа в сутки, могут привести к впечатляющему повышению производительности.
Управляйте своим производственным бизнесом и масштабируйте его с помощью NetSuite
Современным производственным компаниям нужны технологии, которые можно масштабировать вместе с их бизнесом, обеспечивая при этом гибкость для адаптации к изменяющимся условиям бизнеса. Облачное программное обеспечение ERP от NetSuite предоставляет единую платформу для управления сложными бизнес-процессами, такими как планирование, закупки, производство, цепочка поставок, управление данными о продуктах, продажи и поддержка.
Интегрированные приложения NetSuite помогают компаниям сократить время выхода на рынок, повысить качество продукции и повысить эффективность поддержки и обслуживания. Поддержка нескольких дочерних компаний по всему миру помогает оптимизировать глобальные операции и повышает прозрачность на региональном и корпоративном уровне. Предприятия могут повысить производительность за счет автоматизации подверженных ошибкам процессов на основе электронных таблиц, а настраиваемые информационные панели обеспечивают представление в режиме реального времени производительности во всех областях бизнеса.
Заключение
Технологии продолжают трансформировать производство так же, как и другие жизненно важные секторы экономики. Облачные приложения могут помочь производителям повысить эффективность, управлять сложными цепочками поставок и быстрее поставлять продукцию.
Часто задаваемые вопросы по производству
Что означает производство?
Производство – это сборка и преобразование сырья в продукты с использованием машин. Обычно это включает в себя автоматизацию производственного процесса, чтобы производить продукцию в больших масштабах с меньшими затратами.
Что такое производство простыми словами?
Производство использует машины для производства продуктов, которые люди или предприятия могут купить.
Какие существуют 3 типа производства?
Существует три типа производства:
- Производство на складе (MTS): Продукты производятся на основе прогнозов спроса. Затем они хранятся в качестве запасов на складе или в пункте розничной торговли до тех пор, пока покупатель не купит их.