Представить комплексные числа в тригонометрической форме: Комплексные числа онлайн

Тригонометрическая и показательная форма комплексного числа

В данном параграфе больше речь пойдет о тригонометрической форме комплексного числа. Показательная форма в практических заданиях встречается значительно реже. Рекомендую закачать и по возможности распечатать тригонометрические таблицы, методический материал можно найти на странице Математические формулы и таблицы. Без таблиц далеко не уехать.

Любое комплексное число (кроме нуля)   можно записать в тригонометрической форме: , где   – это модуль комплексного числа, а   – аргумент комплексного числа. Не разбегаемся, всё проще, чем кажется.

Изобразим на комплексной плоскости число  . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что  : 

Модулем комплексного числа   называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длинарадиус-вектора, который на чертеже обозначен красным цветом.

Модуль комплексного числа   стандартно обозначают:   или 

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа:  . Данная формула справедлива для любых значений «а» и «бэ».

Аргументом комплексного числа   называется угол   между положительной полуосьюдействительной оси   и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:  .

Аргумент комплексного числа   стандартно обозначают:   или 

Из геометрических соображений получается следующая формула для нахождения аргумента: . Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой. Эти случаи мы тоже разберем.

Но сначала рассмотрим простейшие примеры, когда комплексные числа располагаются на координатных осях.

Пример 7

Представить в тригонометрической форме комплексные числа:  ,  ,  ,  . Выполним чертёж:

На самом деле задание устное. Для наглядности перепишу тригонометрическую форму комплексного числа: 

Запомним намертво, модуль – длина (которая всегда неотрицательна), аргумент – угол.

1) Представим в тригонометрической форме число  . Найдем его модуль и аргумент. Очевидно, что  . Формальный расчет по формуле:  . Очевидно, что   (число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме:  .

Ясно, как день, обратное проверочное действие: 

2) Представим в тригонометрической форме число  . Найдем его модуль и аргумент. Очевидно, что  . Формальный расчет по формуле:  . Очевидно, что   (или 90 градусов). На чертеже угол обозначен красным цветом. Таким образом, число в тригонометрической форме:  .

Используя таблицу значений тригонометрических функций, легко обратно получить алгебраическую форму числа (заодно выполнив проверку):

3) Представим в тригонометрической форме число  . Найдем его модуль и аргумент. Очевидно, что  . Формальный расчет по формуле:  . Очевидно, что   (или 180 градусов). На чертеже угол обозначен синим цветом. Таким образом, число в тригонометрической форме:  .

Проверка: 

4) И четвёртый интересный случай. Представим в тригонометрической форме число  . Найдем его модуль и аргумент. Очевидно, что  . Формальный расчет по формуле:  .

Аргумент можно записать двумя способами: Первый способ:   (270 градусов), и, соответственно:  . Проверка: 

Однако более стандартно следующее правило: Если угол больше 180 градусов, то его записывают со знаком минус и противоположной ориентацией («прокруткой») угла:   (минус 90 градусов), на чертеже угол отмечен зеленым цветом. Легко заметить, что   и   – это один и тот же угол.

Таким образом, запись принимает вид: 

Внимание! Ни в коем случае нельзя использовать четность косинуса, нечетность синуса и проводить дальнейшее «упрощение» записи:

Кстати, полезно вспомнить внешний вид и свойства тригонометрических и обратных тригонометрических функций, справочные материалы находятся в последних параграфах страницы Графики и свойства основных элементарных функций. И комплексные числа усвоятся заметно легче!

В оформлении простейших примеров так и следует записывать: «очевидно, что модуль равен… очевидно, что аргумент равен…».  Это действительно очевидно и легко решается устно.

Перейдем к рассмотрению более распространенных случаев. Как я уже отмечал, с модулем проблем не возникает, всегда следует использовать формулу  . А вот формулы для нахождения аргумента будут разными, это зависит от того, в какой координатной четверти лежит число  . При этом возможны три варианта (их полезно переписать к себе в тетрадь):

1) Если   (1-ая и 4-ая координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле  .

2) Если   (2-ая координатная четверть), то аргумент нужно находить по формуле  .

3) Если   (3-я координатная четверть), то аргумент нужно находить по формуле  .

Пример 8

Представить в тригонометрической форме комплексные числа:  ,  ,  ,  .

Коль скоро есть готовые формулы, то чертеж выполнять не обязательно. Но есть один момент: когда вам предложено задание представить число в тригонометрической форме, точертёж лучше в любом случае выполнить. Дело в том, что решение без чертежа часто бракуют преподаватели, отсутствие чертежа – серьёзное основание для минуса и незачета.

Эх, сто лет от руки ничего не чертил, держите:

Как всегда, грязновато получилось =)

Я представлю в комплексной форме числа   и  , первое и третье числа будут для самостоятельного решения.

Представим в тригонометрической форме число  . Найдем его модуль и аргумент. Поскольку   (случай 2), то   – вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение  , поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:  – число   в тригонометрической форме.

Расскажу о забавном способе проверки. Если вы будете выполнять чертеж на клетчатой бумаге в том масштабе, который у меня (1 ед. = 1 см), то можно взять линейку и измерить модуль в сантиметрах. Если есть транспортир, то можно непосредственно по чертежу измерить и угол.

Перечертите чертеж в тетрадь и измерьте линейкой расстояние от начала координат до числа  . Вы убедитесь, что действительно  . Также транспортиром можете измерить угол и убедиться, что действительно  .

Представим в тригонометрической форме число  . Найдем его модуль и аргумент.

Поскольку   (случай 1), то   (минус 60 градусов).

Таким образом:   – число   в тригонометрической форме.

А вот здесь, как уже отмечалось, минусы не трогаем.

Кроме забавного графического метода проверки, существует и проверка аналитическая, которая уже проводилась в Примере 7. Используем таблицу значений тригонометрических функций, при этом учитываем, что угол   – это в точности табличный угол   (или 300 градусов):  – число   в исходной алгебраической форме.

Числа   и   представьте в тригонометрической форме самостоятельно. Краткое решение и ответ в конце урока.

В конце параграфа кратко о показательной форме комплексного числа.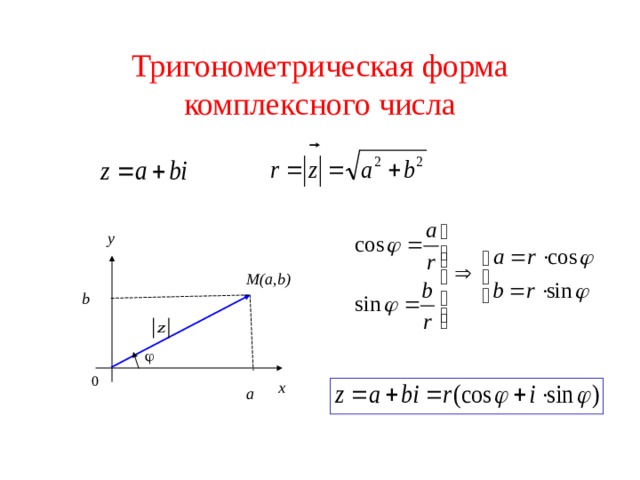

Любое комплексное число (кроме нуля)   можно записать в показательной форме: , где   – это модуль комплексного числа, а   – аргумент комплексного числа.

Что нужно сделать, чтобы представить комплексное число в показательной форме? Почти то же самое: выполнить чертеж, найти модуль и аргумент. И записать число в виде  .

Например, для числа   предыдущего примера у нас найден модуль и аргумент:  ,  . Тогда данное число в показательной форме запишется следующим образом:  .

Число   в показательной форме будет выглядеть так: 

Число   – так: 

 И т.д.

Единственный совет – не трогаем показатель экспоненты, там не нужно переставлять множители, раскрывать скобки и т.п. Комплексное число в показательной форме записывается строго по форме  .

Как сложить комплексные числа в тригонометрической форме?

Как сложить комплексные числа в тригонометрической форме?

z = a + bi = r(cos φ + i sin φ). Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.

Как выполняется сложение комплексных чисел?

Чтобы сложить два комплексных числа в алгебраической форме, надо отдельно сложить действительные части этих чисел, отдельно — коэффициенты при мнимых частях. Комплексные числа также можно складывать, как обычные многочлены, то есть раскрыть скобки и привести подобные слагаемые.

Для чего нужны комплексные числа?

Комплексные числа нужны для описания тех процессов, которые мы не «видим». … Примерно для того же, для чего нужны отрицательные, а так же иррациональные и рациональные — чтобы ловко и умело решать всякие задачи, которые не решаются в простых и умозрительные натуральных числах.

Как выполняется умножение комплексных чисел?

При умножении комплексных чисел, заданных в тригонометрической форме, получено следующее правило: модуль произведения комплексных чисел равен произведению модулей сомножителей, то есть аргумент произведения комплексных чисел равен сумме аргументов сомножителей.

Как выполняется деление комплексных чисел в алгебраической форме?

Деление комплексных чисел в алгебраической форме сначала делимое и делитель умножают на число, комплексно сопряженное делителю, после чего делитель становится действительным числом; в числителе умножают два комплексных числа; полученную дробь почленно делят.

Что называется произведением двух комплексных чисел?

Комплексными числами называются числа следующего вида: z=a+bi, где a и b являются действительными, или вещественными, числами, а i – мнимая единица. … Произведением двух комплексных чисел z1=a+bi и z2=c+di является комплексное число z1z2 = (ac-bd)+i(ad+cb).

Что называется разностью двух комплексных чисел?

Комплексными числами называются числа следующего вида: z=a+bi, где a и b являются действительными, или вещественными, числами, а i – мнимая единица. … Разностью двух комплексных чисел z1=a+bi и z2=c+di является комплексное число z1-z2 = a-c+i(b-d).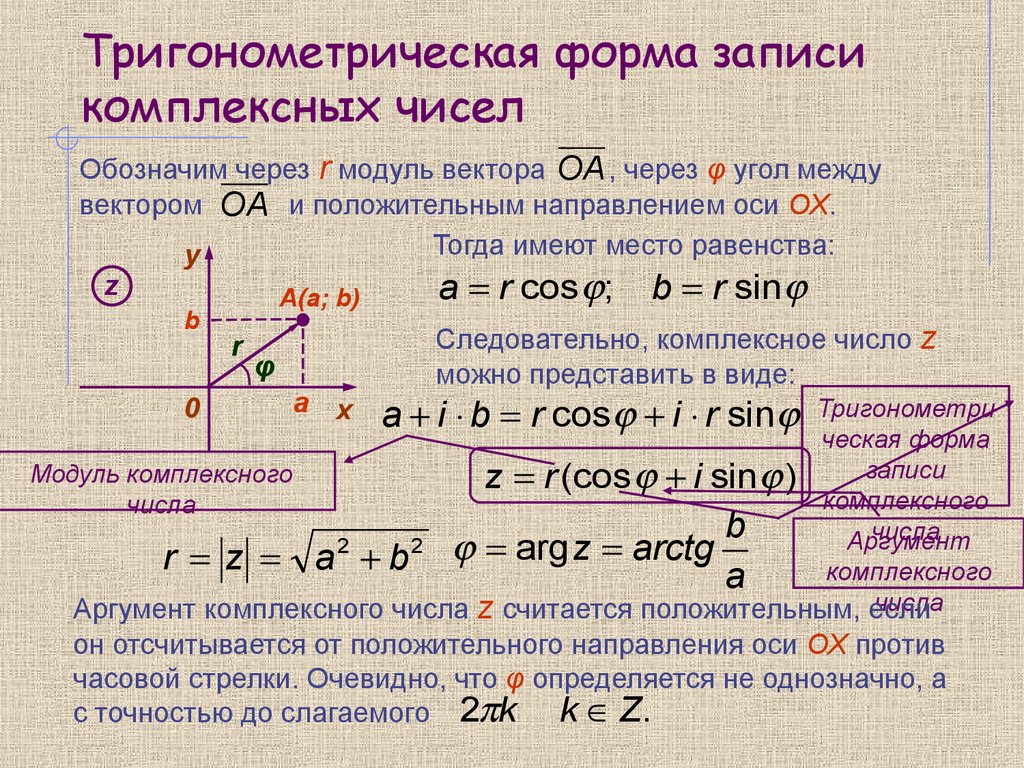

Что называется частным двух комплексных чисел?

Частным двух комплексных чисел z1 и z2≠0 называется комплексное число z , при умножении которого на z2 получается z1: … На практике частное комплексных чисел находят умножением делимого и делителя на число, комплексно-сопряженное делителю. С помощью формулы правило деления комплексных можно записать так: Примеры.

Как умножаются и делятся комплексные числа заданные в тригонометрической форме?

Отсюда вытекает правило умножения комплексных чисел в тригонометрической форме записи. Для того, чтобы перемножить два комплексных числа в тригонометрической форме записи нужно перемножить их модули, а аргументы сложить. Доказательство проводится индукцией по числу сомножителей и предоставляется читателю.

Как вычитать комплексные числа?

Резюме

1. Чтобы сложить комплексные числа в алгебраической форме, сложите действительные компоненты и сложите мнимые компоненты. Вычитание выполняется аналогично.
2. Чтобы перемножить комплексные числа в полярной форме, перемножьте амплитуды (модули) и сложите углы.

Как геометрически изображаются комплексные числа?

Комплексные числа изображаются на так называемой комплексной плоскости. Ось, соответствующая в прямоугольной декартовой системе координат оси абсцисс, называется действительной осью, а оси ординат — мнимой осью (рис. 1).

Чему равно произведение двух сопряженных комплексных чисел?

Произведение двух взаимно сопряженных комплексных чисел есть число действительное. Но i2 = — 1. (а + bi) (а — bi) = а2 + b2.

Какие числа называются сопряженными?

Определение. Два комплексных числа, имеющие одну и ту же действительную часть и взаимно противоположные коэффициенты мнимых частей, называются взаимно) сопряженными. Для любого комплексного числа z существует одно и только одно сопряженное с ним комплексное число, которое обозначается .

Что значит сопряженное выражение?

Неразрывно связанный, соединенный с чем-н., такой, чему непременно сопутствует что-н. другое. Это сопряжено с большими затруднениями.

Что такое модуль комплексного числа?

Длина вектора, изображающего комплексное число, называется модулем комплексного числа. Модуль любого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа a + b·i обозначается |a + b·i|, а также буквой r.

Что называют модулем и аргументом комплексного числа?

Модуль и аргумент комплексного числа Программа предназначена для вычисления модуля и аргумента комплексного числа. Модуль комплексного числа — это длина r вектора изображающего комплексное число z. Угол между вектором, изображающим комплексное число z, и осью Re z называется аргументом комплексного числа z.

Что такое комплексные числа простым языком?

Определение. Ко́мпле́ксные числа — числа вида 𝑎 + 𝑏𝑖 , где 𝑎 и 𝑏— вещественные числа, 𝑖— мнимая единица , то есть число, для которого выполняется равенство: 𝑖² = –1 (ничего не напоминает?..

Как найти модуль Z?

находим модуль |z| = sqrt(x2 + y2) .

Как найти аргумент?

Аргумент заданного комплексного числа z = a + b i можно вычислить, используя следующие формулы: ⁡ φ = a a 2 + b 2 ; sin ⁡

Как найти комплексное число z?

Для комплексного числа z=ρ(cosφ+isinφ)≠0 и целого числа n справедливо zn=ρn(cosφ+isinφ)n=ρn(cosnφ+isinnφ)

Как представить в алгебраической форме комплексное число?

Алгебраическая форма записи комплексного числа выглядит так: z=x+i*y , где x — действительная часть комплексного числа, y — мнимая часть.

В каком случае комплексное число совпадает с действительным числом?

Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число. Комплексное число a + bi при b = 0 считается совпадающим с действительным числом a: a + 0i = a.

Как вычислить мнимую часть комплексного числа?

Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z.

Как найти мнимую часть?

Получение мнимой части числа: Im(z) = b. Модуль числа: |z| = √(a2 + b2) Аргумент числа: arg z = arctg(b / a) Экспонента: ez = ea·cos(b) + i·ea·sin(b)

Чему равно I в комплексных числах?

Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi.

Чему равно значение мнимой единицы?

Подобные утверждения о мистических свойствах мнимых были и у других ученых. Это приводит нас к понятию чисел, по своей природе невозможных и обычно называемых мнимыми или воображаемыми, потому что они существуют только в воображении. Мнимая единица (обозначается буквой i) — это число, квадрат которого равен -1.

Что принято за мнимую единицу?

Мни́мая едини́ца — обычно комплексное число, квадрат которого равен −1 (минус единице). Однако возможны и иные варианты: в конструкции удвоения по Кэли—Диксону или в рамках алгебры по Клиффорду.

Чему равно число J?

Джо́уль (англ. Joule; русское обозначение: Дж; международное: J) — единица измерения работы, энергии и количества теплоты в Международной системе единиц (СИ). Джоуль равен работе, совершаемой при перемещении точки приложения силы, равной одному ньютону, на расстояние одного метра в направлении действия силы.

\circ)] \end{array} $$$

После возведения в степень мы можем изучить корни. \circ$$) : 9\circ}{4}$$$

Как мы видим, этот метод очень похож на тот, который используется с полярной формой комплексных чисел.

5. Комплексные числа и тригонометрия — количественная экономика с Python

Количественная экономика с Python

Комплексные числа и тригонометрия

Томас Дж. Сарджент и Джон Стахурски

• Обзор

• Теорема де Муавра

• Приложения теоремы Муавра

Эта лекция знакомит с элементарной математикой и тригонометрией.

Полезные и интересные сами по себе, эти концепции приносят существенную пользу при изучении динамики, генерируемой линейными разностными уравнениями или линейными дифференциальными уравнениями.

Например, эти инструменты являются ключом к пониманию результатов, достигнутых Полом Самуэльсон (1939) [Sam39] в своей классической статье о взаимодействиях между ускорителем инвестиций и кейнсианской функцией потребления, наша тема в лекции Samuelson Multiplier Accelerator.

В дополнение к созданию основы для работы Самуэльсона и расширению эту лекцию можно читать как отдельное краткое напоминание о ключевых результатах из начальной средней школы тригонометрии.

Итак, приступим.

5.1.1. Комплексные числа

Комплексное число имеет действительную часть 9о\).

Давайте воспользуемся Python для построения тригонометрической формы комплексного числа. \(z = 1 + \sqrt{3} i\).

 # Сокращение полезных значений и функций
π = np.pi
# Установить параметры
г = 2
θ = π/3
х = г * np.cos (θ)
x_range = np.linspace (0, х, 1000)
θ_range = np.linspace (0, θ, 1000)
# Сюжет
рис = plt.figure(figsize=(8, 8))
ax = plt.subplot(111, проекция='полярный')
ax.plot((0, θ), (0, r), marker='o', color='b') # График r
ax.plot(np.zeros(x_range.shape), x_range, color='b') # График x
ax.plot(θ_range, x / np.cos(θ_range), color='b') # График y
ax.plot(θ_range, np.full(θ_range.shape, 0.1), color='r') # График θ
ax.margins(0) # Пусть график начинается в начале координат
ax.  n \cos{(\omega + n\theta)}
\] 90 \cos{(\omega + n\theta)}\). 
 
 С пакетом  sympy  на Python мы можем решить и построить график
динамика \(x_n\) при различных значениях \(n\). 
 
 В этом примере мы устанавливаем начальные значения: - \(r = 0,9\) -
\(\theta = \frac{1}{4}\pi\) - \(x_0 = 4\) -
\(x_1 = r \cdot 2\sqrt{2} = 1,8 \sqrt{2}\). 
 
 Сначала мы численно решим для \(\omega\) и \(p\), используя
  nsolve  в пакете  sympy  на основе вышеуказанного начального
состояние: 
 
 # Установить параметры
г = 0,9
θ = π/4
х0 = 4
х1 = 2 * г * квадрат (2)
# Определить символы для расчета
ω, p = символы ('ω p', действительное = Истина)
# Найдите ω
## Примечание: мы выбираем решение около 0
eq1 = Eq(x1/x0 - r * cos(ω+θ) / cos(ω), 0)
ω = nsolve(eq1, ω, 0)
ω = поплавок (ω)
печать (f'ω = {ω: 1.3f}')
# Находим p
eq2 = Eq(x0 - 2 * p * cos(ω), 0)
p = nsolve(eq2, p, 0)
р = поплавок (р)
печать (f'p = {p: 1.3f}')
 
 ω = 0,000
р = 2.000
 
 Используя приведенный выше код, мы вычисляем, что
\(\omega = 0\) и \(p = 2\).
 Затем мы подставляем найденные значения \(\omega\) и \(p\)
и построить динамику.
 
 # Определить диапазон n
макс_n = 30
n = np.arange(0, max_n+1, 0,01)
# Определить x_n
х = лямбда n: 2 * p * r**n * np.cos (ω + n * θ)
# Сюжет
рис, топор = plt.subplots (figsize = (12, 8))
ax.plot (п, х (п))
ax.set(xlim=(0, max_n), ylim=(-5, 5), xlabel='$n$', ylabel='$x_n$')
# Установить ось X в середине графика
ax.spines['нижний'].set_position('центр')
ax.spines['право'].set_color('нет')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('внизу')
ax.yaxis.set_ticks_position('слева')
ticklab = ax.xaxis.get_ticklabels()[0] # Установить позицию x-метки
транс = тиклаб.get_transform()
ax.xaxis.set_label_coords (31, 0, преобразование = транс)
ticklab = ax.yaxis.get_ticklabels()[0] # Установить положение метки Y
транс = тиклаб.get_transform()
ax.yaxis.set_label_coords (0, 5, преобразование = транс)
топор.сетка()
plt.show()
 9{я\тета} \\
&= (\cos{\omega} + я \sin{\omega})(\cos{\theta} + я \sin{\theta}) \\
&= (\cos{\omega}\cos{\theta} - \sin{\omega}\sin{\theta}) +
я (\ соз {\ омега} \ грех {\ тета} + \ грех {\ омега} \ соз {\ тета})
\конец{выровнено}
\end{split}\]
 Так как и действительная, и мнимая части приведенной выше формулы должны быть
равны, получаем:
 \[\begin{split}
\begin{выровнено}
\cos{(\omega + \theta)} = \cos{\omega}\cos{\theta} - \sin{\omega}\sin{\theta} \\
\sin{(\omega + \theta)} = \cos{\omega}\sin{\theta} + \sin{\omega}\cos{\theta}
\конец{выровнено}
\конец{разделить}\]
 Приведенные выше уравнения также известны как  тождества суммы углов  .
No related posts.