 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)алгебраическая форма комплексного числа онлайн
Вы искали алгебраическая форма комплексного числа онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и алгебраическая форма комплексного числа онлайн калькулятор, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «алгебраическая форма комплексного числа онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как алгебраическая форма комплексного числа онлайн,алгебраическая форма комплексного числа онлайн калькулятор,аргумент комплексного числа онлайн калькулятор,в тригонометрической форме комплексные числа онлайн калькулятор,выполнить действия в алгебраической форме записи,записать в тригонометрической форме комплексное число онлайн,записать комплексное число в тригонометрической форме онлайн,из алгебраической в показательную,из алгебраической в показательную форму онлайн,из показательной в алгебраическую форму онлайн,как перевести комплексное число в алгебраическую форму,калькулятор комплексных чисел онлайн в показательной форме,калькулятор онлайн комплексные числа в показательной форме,комплексное число в тригонометрической форме онлайн,комплексное число перевести в показательную форму,комплексное число представить в показательной форме онлайн,комплексные числа в показательной форме калькулятор онлайн,комплексные числа в показательной форме онлайн калькулятор,комплексные числа в тригонометрической форме калькулятор онлайн,комплексные числа в тригонометрической форме онлайн калькулятор,комплексные числа онлайн калькулятор в показательной форме,комплексные числа онлайн калькулятор в тригонометрической форме,комплексные числа представить в тригонометрической форме онлайн,модуль комплексного числа онлайн калькулятор,найти аргумент комплексного числа онлайн,найти модуль и аргумент комплексного числа онлайн калькулятор,онлайн калькулятор аргумент комплексного числа,онлайн калькулятор комплексные числа в тригонометрической форме,онлайн калькулятор комплексных чисел в показательной форме,онлайн калькулятор модуль комплексного числа,онлайн показательная форма комплексного числа,перевести комплексное число в показательную форму,перевод в алгебраическую форму комплексного числа,перевод в показательную форму комплексного числа,перевод в тригонометрическую форму комплексного числа,перевод из алгебраической формы в показательную,перевод из алгебраической формы в показательную онлайн,перевод из алгебраической формы в тригонометрическую,перевод из комплексной формы в показательную,перевод из показательной в алгебраическую,перевод из показательной формы в алгебраическую,перевод из показательной формы в алгебраическую онлайн,перевод из тригонометрической формы в алгебраическую,перевод комплексного числа в алгебраическую форму,перевод комплексного числа в показательную форму,перевод комплексного числа в тригонометрическую форму,перевод комплексных чисел,перевод комплексных чисел в показательную форму онлайн,перевод комплексных чисел в тригонометрическую форму,показательная форма комплексного числа онлайн,представить в алгебраической форме комплексное число онлайн калькулятор,представить в показательной форме комплексное число онлайн,представить в тригонометрической форме комплексное число онлайн,представить в тригонометрической форме комплексные числа онлайн,представить в тригонометрической форме число онлайн,представить комплексное число в алгебраической форме онлайн калькулятор,представить комплексное число в показательной форме онлайн,представить комплексное число в показательной форме онлайн калькулятор,представить комплексные числа в тригонометрической форме онлайн,представить число в тригонометрической форме онлайн,светотехника калькулятор тоэ,светотехника тоэ калькулятор,тригонометрическая форма записи комплексного числа онлайн,тригонометрическая форма комплексного числа калькулятор онлайн,тригонометрическая форма комплексного числа онлайн,тригонометрическая форма комплексного числа онлайн калькулятор.
Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как алгебраическая форма комплексного числа онлайн,алгебраическая форма комплексного числа онлайн калькулятор,аргумент комплексного числа онлайн калькулятор,в тригонометрической форме комплексные числа онлайн калькулятор,выполнить действия в алгебраической форме записи,записать в тригонометрической форме комплексное число онлайн,записать комплексное число в тригонометрической форме онлайн,из алгебраической в показательную,из алгебраической в показательную форму онлайн,из показательной в алгебраическую форму онлайн,как перевести комплексное число в алгебраическую форму,калькулятор комплексных чисел онлайн в показательной форме,калькулятор онлайн комплексные числа в показательной форме,комплексное число в тригонометрической форме онлайн,комплексное число перевести в показательную форму,комплексное число представить в показательной форме онлайн,комплексные числа в показательной форме калькулятор онлайн,комплексные числа в показательной форме онлайн калькулятор,комплексные числа в тригонометрической форме калькулятор онлайн,комплексные числа в тригонометрической форме онлайн калькулятор,комплексные числа онлайн калькулятор в показательной форме,комплексные числа онлайн калькулятор в тригонометрической форме,комплексные числа представить в тригонометрической форме онлайн,модуль комплексного числа онлайн калькулятор,найти аргумент комплексного числа онлайн,найти модуль и аргумент комплексного числа онлайн калькулятор,онлайн калькулятор аргумент комплексного числа,онлайн калькулятор комплексные числа в тригонометрической форме,онлайн калькулятор комплексных чисел в показательной форме,онлайн калькулятор модуль комплексного числа,онлайн показательная форма комплексного числа,перевести комплексное число в показательную форму,перевод в алгебраическую форму комплексного числа,перевод в показательную форму комплексного числа,перевод в тригонометрическую форму комплексного числа,перевод из алгебраической формы в показательную,перевод из алгебраической формы в показательную онлайн,перевод из алгебраической формы в тригонометрическую,перевод из комплексной формы в показательную,перевод из показательной в алгебраическую,перевод из показательной формы в алгебраическую,перевод из показательной формы в алгебраическую онлайн,перевод из тригонометрической формы в алгебраическую,перевод комплексного числа в алгебраическую форму,перевод комплексного числа в показательную форму,перевод комплексного числа в тригонометрическую форму,перевод комплексных чисел,перевод комплексных чисел в показательную форму онлайн,перевод комплексных чисел в тригонометрическую форму,показательная форма комплексного числа онлайн,представить в алгебраической форме комплексное число онлайн калькулятор,представить в показательной форме комплексное число онлайн,представить в тригонометрической форме комплексное число онлайн,представить в тригонометрической форме комплексные числа онлайн,представить в тригонометрической форме число онлайн,представить комплексное число в алгебраической форме онлайн калькулятор,представить комплексное число в показательной форме онлайн,представить комплексное число в показательной форме онлайн калькулятор,представить комплексные числа в тригонометрической форме онлайн,представить число в тригонометрической форме онлайн,светотехника калькулятор тоэ,светотехника тоэ калькулятор,тригонометрическая форма записи комплексного числа онлайн,тригонометрическая форма комплексного числа калькулятор онлайн,тригонометрическая форма комплексного числа онлайн,тригонометрическая форма комплексного числа онлайн калькулятор.
Где можно решить любую задачу по математике, а так же алгебраическая форма комплексного числа онлайн Онлайн?
Решить задачу алгебраическая форма комплексного числа онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Алгебраическая форма комплексного числа.
 Сложение, вычитание, умножение и деление комплексных чисел
Сложение, вычитание, умножение и деление комплексных чиселСложение комплексных чиcел
Пример 1
Z1=1+4i, Z2= 4-6i;
Z1+Z2=1+4i+4-6i=5-2i;
Вычитание комплексных чисел
Пример 2
Z1=1+4i, z2=4-6i;
Z1-z2= 1+4i-4-6i=-3-2i;
Умножение комплексных чисел
Пример 3
Построим на комплексной плоскости следующие комплексные числа
Z1=1,Z2=-2 , ,,,,,
Изобразим на комплексной плоскости число . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что:
Представить в тригонометрической форме комплексные числа: ,,,. Выполним чертёж:
Представить
в тригонометрической форме комплексные
числа:
,,,.
Деление комплексных чисел
Пример 4
, , а
Пример 5
Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме).
В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение, то есть на:
Пример 6
Даны два комплексных числа ,. Найти их сумму, разность, произведение и частное.
5 + 2i + 2 — 5i = (5 + 2) + (2 — 5)i = 7 — 3i
5 + 2i — (2 — 5i) = (5 — 2) + (2 + 5)i = 3 + 7i
(5 + 2i) · (2 — 5i) = 5·2 — 5·5i + 2·2i — 2·5i 2 = 10 — 25i + 4i + 10 = 20 — 21i
5 + 2i | = | (5 + 2i)(2 + 5i) | = | 5·2 + 5·5i + 2·2i + 2·5i2 | = | 10 + 25i + 4i — 10 | = | 29i | = | 1i |
2 — 5i | (2 — 5i)(2 + 5i) | 2·2 + 5·5 | 4 + 25 | 29 |
Изобразим
на комплексной плоскости число
. Для определённости и простоты объяснений
расположим его в первой координатной
четверти, т.е. считаем, что:
Для определённости и простоты объяснений
расположим его в первой координатной
четверти, т.е. считаем, что:
Пример 7
Представить в тригонометрической форме комплексные числа
1)
Найдем модуль и аргумент заданного комплексного числа:
Тогда
2)
аргумент
Отсюда получаем, что
Пример 8
Запишите в тригонометрической форме числа ,,,.
Решение. Находим модуль, аргумент, а затем выписываем тригонометрическую форму:
Пусть ,. Найдем произведение:
Найдем произведение:
Заметим, что во внутренних скобках стоят формулы косинуса и синуса суммы аргументов. Поэтому
Последняя запись является тригонометрической формой комплексного числа . Значит,
иными словами, при умножении комплексных чисел их модули перемножаются, а аргументы складываются
Аналогично можно доказать, что
иными словами, при делении комплексных чисел их модули делятся один на другой, а аргументы вычитаются.
Несложно проверить, что если , то
Используя правило умножения комплексных чисел в тригонометрической форме, получим формулу для возведения комплексного числа в степень , где— натуральное число.
Пусть . Тогда
то есть
Далее находим
то есть
Продолжая умножения дальше, придем к формуле
Эта
формула называется формулой
Муавра.
Пример 9
Возвести в квадрат комплексное число: z=3+2i
z2=(3+2i)(3+2i)
z2=*(3+2i)2=32+3*2*2i+(2i)2=9+12i-4=5+12i
Пример 10
Вычислить если
По первой формуле Муавра получаем:
Пример 11
Возвести в степень комплексные числа i8, i31, (-i)19
i8 = (i2)4 = (-1)4= 1
i31=i*i30=i*(i2)15=i*(-1)15=i*(-1)=-i
(-i)19=(-1)19*i19=-i*i19=-i*(i2)9=-i*(-1)9=i
Пример 12
Решить уравнение .
Решение. Вычисляем дискриминант
. Вычисляем корни из дискриминанта по формуле квадратных корней из комплексного числа:
.
Вычисляем корни уравнения по формуле корней квадратного уравнения:
или ; .
Ответ: .
Пример 13
разложить трехчлен 2x 2 – 4x – 6 на множители первой степени.
Р е ш е н и е . Во-первых, решим уравнение: 2x 2 – 4x – 6 = 0. Его корни:
x1 = –1 и x2 = 3. Отсюда, 2x 2 – 4x – 6 = 2 ( x + 1 ) ( x – 3 ) .
Пример 14
,
если . Представить результат в тригонометрической
форме и изобразить его на комплексной
плоскости.
Представить результат в тригонометрической
форме и изобразить его на комплексной
плоскости.
Решение: итак, требуется подставить в «страшную» дробь, провести упрощения, и перевести полученное комплексное число в тригонометрическую форму. Плюс чертёж.
Как лучше оформить решение? С «навороченным» алгебраическим выражением выгоднее разбираться поэтапно. Во-первых, меньше рассеивается внимание, и, во-вторых, если таки задание не зачтут, то будет намного проще отыскать ошибку.
1) Сначала упростим числитель. Подставим в него значение , раскроем скобки и поправим причёску:
В ходе преобразований используются совершенно бесхитростные вещи – правило умножения многочленов и уже ставшее банальным равенство . Главное, быть внимательным и не запутаться в знаках.
2) Теперь на очереди знаменатель. Если , то:
Заметьте,
в какой непривычной интерпретации
использована формула
квадрата суммы . Как вариант, здесь можно выполнить
перестановку под формулу .
Результаты, естественно, совпадут.
Как вариант, здесь можно выполнить
перестановку под формулу .
Результаты, естественно, совпадут.
3) И, наконец, всё выражение. Если , то:
Чтобы избавиться от дроби, умножим числитель и знаменатель на сопряженное знаменателю выражение. При этом в целях применения формулы разности квадратов следует предварительно (и уже обязательно!) поставить отрицательную действительную часть на 2-ое место:
На завершающем шаге произошло хорошее сокращение и это просто отличный признак.
Обозначим наше достижение буквой
Представим полученный результат в тригонометрической форме. Вообще говоря, здесь можно обойтись без чертежа, но коль скоро, требуется – несколько рациональнее выполнить его прямо сейчас: Вычислим модуль комплексного числа:
Найдём аргумент. Так как число расположено во 2-й координатной четверти , то:
Угол
элементарно проверяется транспортиром. Вот в чём состоит несомненный плюс
чертежа.
Вот в чём состоит несомненный плюс
чертежа.
Таким образом: – искомое число в тригонометрической форме.
Выполним проверку: ,
.
Ответ:
Операции с числами
Ввод действительных чисел
Командное окно
Окно с названием форматов (numeric format)
Результат с форматом Long E
Ввод комплексных чисел
Обозначение мнимой части
Элементарные математические функции
Элементарные действия с комплексными числами
Арифметические действия с комплексными числами
Функции комплексного аргумента
Комплексные числа от элементарных функций
Комплексные числа от дополнительных функций
Формы комплексного числа с примерами решения
Содержание:
- Тригонометрическая форма комплексного числа
В операциях с комплексными числами особую роль играет комплексное число (0,1), которое обозначается буквой и называется мнимой единицей. Пользуясь формулой (7.2), вычислим
Пользуясь формулой (7.2), вычислим
Итак,
С учетом последнего любое комплексное число можно представить в виде
Таким образом, для комплексного числа получили представление
которое и называется алгебраической формой записи комплексного числа.
Алгебраическая форма записи комплексного числа позволяет производить операции с комплексными числами так же, как они производятся с алгебраическими многочленами.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Например,
Комплексное число называется сопряженным по отношению к комплексному числу Справедливо равенство
Действительно,
Теперь нетрудно проверить, что для частного двух комплексных чисел и справедлива формула
Действительно,
Возможно вам будут полезны данные страницы:
Контрольная производная и ее геометрический смысл |
Комплексные числа: примеры решения |
Тригонометрические комплексные числа |
Алгебраические комплексные числа |
Пример с решением
Пусть
Вычислить:
Проводим вычисления:
Тригонометрическая форма комплексного числа
Рассмотрим на плоскости декартову прямоугольную систему координат Каждому комплексному числу можно сопоставить точку с координатами и наоборот, каждой точке с координатами можно сопоставить комплексное число (рис. 7.1). Таким образом, между точками плоскости и множеством у комплексных чисел устанавливается вза- & имно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости.
7.1). Таким образом, между точками плоскости и множеством у комплексных чисел устанавливается вза- & имно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости.
Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью и обозначается
| Ось абсцисс называется действительной осью, а ось ординат — мнимой осью. |
Пусть произвольное комплексное число, которое на комплексной плоскости изображается точкой Тогда этому комплексному числу можно сопоставить также радиус-вектор Длина вектора называется модулем комплексного числа и обозначается Угол, образованный радиус-вектором с осью Ох, называется аргументом числа и обозначается (см. рис. 7.1).
Аргумент комплексного числа определяется не однозначно, а с точностью до числа, кратного Однако обычно аргумент указывают в промежутке или в промежутке Аргумент комплексного числа не определен. Итак, по определению
Итак, по определению
С учетом формулы (7.5) получим
или
Теперь введем понятие полярной системы координат. Говорят, что на плоскости задана полярная система координат, если на этой плоскости фиксирована некоторая точка называемая полюсом полярной системы координат, и задан выходящий из точки луч, называемый полярной осью.
Если на плоскости задана полярная система координат, то тогда произвольной точке плоскости соответствуют полярные координаты где расстояние от точки до точки а — угол между вектором и полярной осью, отсчитываемый от последней против часовой стрелки (рис. 7.2).
Теперь предположим, что положительная ось прямоугольной системы координат совпадает с полярной осью
(рис. 7.3). Тогда очевидно, что декартовы координаты и полярные координаты связаны формулами
Заметим, что модуль и аргумент комплексного числа являются полярными координатами точки (р (рис. 7.4). Тогда получаем Следовательно, комплексное число можно записать в виде или
Последнее представление называется тригонометрической формой записи комплексного числа.
Аргумент ( комплексного числа определяется из формул
где модуль числа
Пример 1:
Комплексные числа
представить в тригонометрической форме.
Сначала следует найти модуль и аргумент данного комплексного числа, а после этого воспользоваться формулой (7.10):
В тригонометрической форме удобно производить операции умножения и деления комплексных чисел.
Пусть даны два произвольных комплексных числа
Вычислим произведение согласно формуле (7.2):
Мы получили формулу
Из этой формулы следуют равенства
Итак, мы пришли к важному заключению: при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Аналогично можно доказать, что
иными словами, при делении комплексных чисел их модули делятся один на другой а аргументы вычитаются.
Правило умножения комплексных чисел в тригонометрической форме (7.12) распространяется на любое количество множителей. В частности, если имеются множителей и все они равны одному и тому же комплексному числу то получим
В частности, если имеются множителей и все они равны одному и тому же комплексному числу то получим
Эта формула называется формулой Муавра.
Пример 2:
Вычислить если
Комплексное число представим в тригонометрической форме:
По формуле Муавра находим
Вычисляя косинус и синус, окончательно получим
Показательная форма комплексного числа
Рассмотрим комплексное число, представленное в тригонометрической форме
Обозначим
Эта формула называется формулой Эйлера. На основании этой формулы комплексное число можно представить в виде
Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь
Нетрудно заметить, что — периодическая функция периода
Поскольку
следовательно, график функции при представляет собой окружность радиуса 1 с центром в точке Справедливы равенства
Действительно,
С помощью формулы Эйлера (7. 14) можно определить показательную функцию комплексного аргумента. Пусть Тогда
14) можно определить показательную функцию комплексного аргумента. Пусть Тогда
Например,
Из формулы Эйлера (7.14) легко получить
Пример 3:
Комплексное число представить в показательной форме.
Находим модуль и аргумент данного комплексного числа:
Следовательно, показательная форма такова:
Пример 4:
Комплексное число записано в показательной форме Найти его алгебраическую форму.
По формуле Эйлера получаем
основы. Алгебраическая и тригонометрическая форма комплексного числа
Комплексные числа — это числа вида a + bi, где a и b — действительные числа, а i — число особого рода, квадрат которого равен минус единице: i²=−1.
Действия над комплексными числами выполняются по таким же правилам, что и над многочленами, при этом i² заменяют на −1.
Комплексные числа вводятся в связи с тем, что действительных чисел
недостаточно, чтобы решить любое квадратное уравнение с действительными коэффициентами. Простейшее из квадратных уравнений, не имеющих корней среди действительных чисел, есть
Простейшее из квадратных уравнений, не имеющих корней среди действительных чисел, есть
x² + 1 = 0.
Задача такова: нужно расширить систему действительных чисел до такой системы чисел, в которой это уравнение обладало бы корнем.
Решение: x² = — 1, x =√-1,
где √-1 — квадратный корень из минус единицы — мнимая единица, обозначаемая буквой i.
Название «мнимые числа» ввёл в 1637 году французский математик и философ Р. Декарт. А в 1777 году один из крупнейших математиков того времени Л. Эйлер предложил использовать первую букву французского слова «imaginaire» (мнимый) для обозначения числа √-1 «мнимой единицы».
Продвинемся ещё на шаг к алгебрической форме записи комплексных чисел. Квадратное уравнение
имеет корни и
, где i = √-1 — квадратный корень
из минус единицы.
Таким образом, у комплексных чисел есть действительная и мнимая части. В алгебраической записи комплексного числа a + bi есть действительная часть a и мнимая часть bi.
В литературе наиболее часто встречается именно такая обобщённая алгебраическая форма комплексного числа: z = a + bi. Но сейчас мы применим запись z = x + yi только для того, чтобы было более понятно отображение комплексного числа в привычной системе координат с осями x и y.
Отображая на плоскости горизонтальную ось x как ось действительных чисел, а вертикальную ось y как ось мнимых чисел, можно любое комплексное число z = x + yi отобразить как точку P в декартовой системе координат (рисунок ниже).
Поэтому возможна и запись комплексного числа в тригонометрической форме:
,
где —
модуль комплексного числа,
(аргумент комплексного числа) — угол, который радиус-вектор
образует с осью Ox. Теперь мы видим, что более подходящим
является сравнение записи комплексного числа в тригонометрической форме с отображением точки в полярной системе координат.
Теперь мы видим, что более подходящим
является сравнение записи комплексного числа в тригонометрической форме с отображением точки в полярной системе координат.
Обобщим ещё раз понятие модуля и аргумента комплексного числа. Модуль комплексного числа — это расстояние от начала координат до точки, в виде которой отображается комплексного числа или, что то же самое — длина радиус-вектора . Аргумент комплексного числа — это угол, который радиус-вектор образует с осью Ox.
Теперь о том, как перейти от алгебраической формы комплексного числа к тригонометрической. Доказано, что
и
.
Поэтому можем легко найти косинус и синус аргумента комплексного числа:
, .
Пример 1. Найти тригонометрическую форму числа .
Решение. Сначала найдём модуль комплексного числа. Для этого в соответствии с
обобщенной записью числа z = a + bi запишем
данное число как z = 1 + 1i,
где a = 1 и b = 1.
Из этого получаем модуль данного числа — квадратный корень из 1 + 1 = 2, что равно
. Чтобы
определить аргумент числа, учтём, что и
.
То есть, значение угла
равно .
Поэтому получаем тригонометрическую форму данного комплексного числа:
Сначала найдём модуль комплексного числа. Для этого в соответствии с
обобщенной записью числа z = a + bi запишем
данное число как z = 1 + 1i,
где a = 1 и b = 1.
Из этого получаем модуль данного числа — квадратный корень из 1 + 1 = 2, что равно
. Чтобы
определить аргумент числа, учтём, что и
.
То есть, значение угла
равно .
Поэтому получаем тригонометрическую форму данного комплексного числа:
.
Пример 2. Найти тригонометрическую форму комплексного числа 1.
Возможны возражения: 1 — это же обычное, точнее, действительное число. Это так. Но это число можно представить и как комплексное число , то есть, комплексное число, в котором a = 1 и b = 0.
Решение. Модуль данного числа
. Чтобы
определить аргумент числа, найдём и
.
Следовательно, аргумент комплексного числа . Получили тригонометрическую форму данного комплексного числа:
Получили тригонометрическую форму данного комплексного числа:
.
Пройти тест по теме Комплексные числа
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пример 3. Найти тригонометрическую форму комплексного числа .
Решение. Модуль данного числа . Чтобы определить аргумент числа, найдём и . Для нахождения угла с таким косинусом и таким синусом повернём воображаемый циркуль от угла 0 до и ещё на . Получаем . Следовательно, аргумент комплексного числа . Получили тригонометрическую форму данного комплексного числа:
.
Пример 4. Найти тригонометрическую форму комплексного числа .
Решение. Модуль данного числа . Чтобы определить аргумент числа, найдём и . Аргумент, то есть угол, у которого найденный косинус и найденный синус, определяется однозначно: . Получили тригонометрическую форму данного комплексного числа:
.
Пример 5. Найти тригонометрическую форму комплексного числа -3.
Решение. Модуль данного числа . Чтобы определить аргумент числа, найдём и . Аргумент, то есть угол, у которого найденный косинус и найденный синус, определяется однозначно: . Получили тригонометрическую форму данного комплексного числа:
.
Пример 6. Найти тригонометрическую форму комплексного числа .
Решение. Модуль данного числа . Чтобы определить аргумент числа, найдём и . Чтобы найти угол, у которого найденный косинус и найденный синус, отвыкшим от школьных лет и тригонометрии, возможно, придётся чуть побольше попыхтеть, вращая воображаемый циркуль по координатной плоскости. Вот они, шаги вычисления угла: поворачиваем циркуль на , затем на и на Получаем . Получили тригонометрическую форму данного комплексного числа:
.
Пример 7. Найти тригонометрическую форму
комплексного числа .
Найти тригонометрическую форму
комплексного числа .
Решение. Модуль данного числа . Чтобы определить аргумент числа, найдём и . Шаги вычисления угла, то есть аргумента: поворачиваем циркуль на , затем на и на Получаем . Получили тригонометрическую форму данного комплексного числа:
.
Пройти тест по теме Комплексные числа
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
О множествах чисел
Множества и операции над множествами
Комплексные числа (2) — Алгебраическая форма комплексного числа
Скачать 63.63 Kb.
|
С этим файлом связано 3 файл(ов). Среди них: Лекции теория вероятностей 2019.pdf, 12 КРИВЫЕ ВТОРОГО ПОРЯДКА.ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА. (1).docx, Таблица оригинал-изображение.DOC. Показать все связанные файлы Подборка по базе: ВВОД И ФОРМАТИРОВАНИЕ ТЕКСТА_1.docx, Пример решения контрольной работы. Формат HTMLФайл.pdf, Практическая работа 3 (часть 1) Форма для заполнения (1).docx, 1 урок-Натуральные числа и ноль.docx, Отчетная форма.doc, КР 1 натуральные числа 5 класс.docx, Новый документ в формате RTF.rtf, 44.03.01 ФОС_Начальное образование (4 года-очная форма-ФГОС 3++), Балет как высшая форма искусства. Посвящается Алешиной Т.А. дб.d, Новый документ в формате RTF.rtf Формы записи комплексных чисел Алгебраическая форма комплексного числа – это запись комплексного числа z в виде: где и – действительные числа, – мнимая единица, удовлетворяющая соотношению . Комплексное число считается записанным корректно, если записано именно в данном виде. Запись по типу: – ошибка. Правильный вариант: . Чтобы изобразить комплексное число на комплексной плоскости необходимо, в первую очередь, изобразить саму плоскость, представляющую из себя обычную координатную плоскость, но с осями (вместо ) и (вместо ), на первой оси отметить значение , на второй – значение . Пересечение перпендикуляров к этим точкам и есть число . Тригонометрическая форма комплексного числа , не равного нулю, – это запись: Где – модуль комплексного числа, а угол . Аргумент находится следующим образом: Чтобы изобразить комплексное число на комплексной плоскости необходимо из начала координат провести прямую под углом и отложить на ней расстояние . Короче говоря, число на комплексной плоскости задает вектор с координатами , длиной и углом наклона к оси . Показательная форма комплексного числа – выражение: где – модуль комплексного числа, – его аргумент, – экспонента, – мнимая единица. По формуле Эйлера: Сопряженные комплексные числа Комплексны числа и называются сопряженными. в тригонометрической форме: в показательной форме: Геометрический смысл: сопряженное числу есть число, симметричное самому числу относительно оси . Свойства операции сопряжения: ; тогда и только тогда, когда – комплексное число; Действия с комплексными числами ; Равенство комплексных чисел: В алгебраической форме: , если и В тригонометрической форме: , если и Сложение комплексных чисел: В алгебраической форме: (аналогично с вычитанием) В тригонометрической форме: (аналогично с вычитанием) Умножение комплексных чисел: В алгебраической форме: (простое раскрытие скобок) В тригонометрической форме: Деление комплексных чисел: В алгебраической форме: (раскрытие скобок с помощью домножения знаменателя на сопряженное) В тригонометрической форме: Возведение комплексного числа в степень в тригонометрической форме (формула Муавра): в показательной форме: Важно помнить, что аргумент и должен находиться в диапазоне , следовательно, нужно не забыть вычесть нужное количество после домножения. Чтобы извлечь корень из комплексного числа, в первую очередь, нужно представить его в тригонометрической форме. Количество корней есть значение, равное степени корня. То есть, извлекая корень 4-й степени из комплексного числа, мы получаем 4 корня. Как и для возведения в целую степень, будет справедливо: – степень извлекаемого корня, . Вычисляем извлеченные корни поочередно, в каждый из которых подставляем свое значение n. Важно помнить, что аргумент и должен находиться в диапазоне , следовательно, нужно не забыть вычесть нужное количество после всех операций вычисления. Если комплексное число не равно нулю, то корни степени существуют всегда, и их можно изобразить на комплексной плоскости: они будут представлять собой вершины правильного -угольника, который вписан в окружность с центром в начале координат и радиусом . Свойства комплексных чисел Переместительное свойство: ; Сочетательное свойство: ; Распределительное свойство: |
3.
 6: Векторы с алгебраической точки зрения
6: Векторы с алгебраической точки зрения- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7116
- Тед Сандстром и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @Grand Valley State University
Основные вопросы
Следующие вопросы предназначены для того, чтобы направлять наше изучение материала в этом разделе. Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
- Как найти компонентную форму вектора?
- Как найти величину и направление вектора, записанного в компонентной форме?
- Как складывать и вычитать вектора, записанные в компонентной форме, и как найти скалярное произведение вектора, записанного в компонентной форме?
- Чему равно скалярное произведение двух векторов?
- Что скалярное произведение говорит нам об угле между двумя векторами?
- Как найти проекцию одного вектора на другой?
Введение и терминология
Мы видели, что вектор полностью определяется величиной и направлением. Таким образом, два вектора, имеющие одинаковую величину и направление, равны. Это означает, что мы можем расположить наш вектор на плоскости и идентифицировать его по-разному. Например, мы можем поместить кончик вектора \(\textbf{v}\) в начало координат, а хвост завершится в некоторой точке \((v_{1}, v_{2})\), как показано на Рисунок \(\PageIndex{1}\).
Таким образом, два вектора, имеющие одинаковую величину и направление, равны. Это означает, что мы можем расположить наш вектор на плоскости и идентифицировать его по-разному. Например, мы можем поместить кончик вектора \(\textbf{v}\) в начало координат, а хвост завершится в некоторой точке \((v_{1}, v_{2})\), как показано на Рисунок \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\): Вектор в стандартной позиции
Говорят, что вектор с начальной точкой находится в стандартной позиции и представлен \(\textbf{v } = \langle v_{1}, v_{2} \rangle\). Обратите внимание на важное различие в обозначениях между вектором \(\textbf{v} = \langle v_{1}, v_{2} \rangle\) и точкой \((v_{1}, v_{2})\ ). Координаты конечной точки \((v_{1}, v_{2})\) называются компонентами вектора \(\textbf{v}\). Мы называем \(\textbf{v} = \langle v_{1}, v_{2} \rangle\) 9\circ\)) называется углом направления вектора. См. рисунок \(\PageIndex{1}\).
Использование базисных векторов
Существует еще один способ алгебраически записать вектор, если компоненты вектора известны. При этом используются так называемые стандартные базисные векторы для векторов на плоскости. Эти два вектора обозначаются \(\textbf{i}\) и \(\textbf{j}\) и определяются следующим образом и показаны на диаграмме ниже.
\(\textbf{i} = \langle 1, 0 \rangle\) и \(\textbf{j} = \langle 0, 1 \rangle\)
На рис. 3.28 показано, как использовать векторы \(\textbf{i}\) и \(\textbf{j}\) для представления вектора \(\textbf{v} = \langle a, б \угол\).
Рисунок \(\PageIndex{2}\): Использование векторов \(\textbf{i}\) и \(\textbf{j}\)
Диаграмма показывает, что если мы поместим основание вектора \(\textbf{j}\) на вершине вектора \(\textbf{i}\), мы видим, что \[\textbf{v} = \langle a, b \rangle = a\textbf{i } + b\textbf{j}\]
Это часто называют \(\textbf{i}\), \(\textbf{j}\) форма вектора , а действительное число \(a\) называется компонентой \(\textbf{i}\)- вектора \(\textbf{v}\), а действительное число \(b\ ) называется \(\textbf{j}\)- компонент \(\textbf{v}\)
Алгебраические формулы для геометрических свойств вектора
Векторы обладают определенными геометрическими свойствами, такими как длина и угол направления. Используя компонентную форму вектора, мы можем написать алгебраические формулы для этих свойств. Мы будем использовать диаграмму справа, чтобы объяснить эти формулы. 9\circ\), и \[\cos(\theta) = \dfrac{v_{1}}{|\textbf{v}|}\] и \[\sin(\theta) = \dfrac{v_{2 }}{|\textbf{v}|}\]
Используя компонентную форму вектора, мы можем написать алгебраические формулы для этих свойств. Мы будем использовать диаграмму справа, чтобы объяснить эти формулы. 9\circ\), и \[\cos(\theta) = \dfrac{v_{1}}{|\textbf{v}|}\] и \[\sin(\theta) = \dfrac{v_{2 }}{|\textbf{v}|}\]
Упражнение \(\PageIndex{1}\)
- Предположим, что горизонтальный компонент вектора \(\textbf{v}\) равен 7, а вертикальный компонент равен \(-3\). Итак, мы имеем \(\textbf{v} = 7\textbf{i} + (-3)\textbf{j} = 7\textbf{i} — 3\textbf{j}\). Определите величину и угол направления \(\textbf{v}\). 9\circ) \приблизительно -6,840\]
Операции с векторами
В разделе 3.5 мы научились складывать два вектора и умножать вектор на скаляр. В то время описания этих операций носили геометрический характер.
 Теперь мы знаем о компонентной форме вектора. Итак, хороший вопрос: «Можем ли мы использовать компонентную форму векторов для сложения векторов и умножения вектора на скаляр?»
Теперь мы знаем о компонентной форме вектора. Итак, хороший вопрос: «Можем ли мы использовать компонентную форму векторов для сложения векторов и умножения вектора на скаляр?»Чтобы проиллюстрировать эту идею, мы посмотрим на Progress Check 3.25 на стр. 223, где мы добавили два вектора \(\textbf{v}\) и \(\textbf{w}\). Хотя мы не использовали составные формы этих векторов, теперь мы можем видеть, что \[\textbf{v} = \langle 2, 3 \rangle = 2\textbf{i} + 3\textbf{j}\] и \ [\textbf{w} = \langle 4, -1 \rangle = 4\textbf{i} + (-1)\textbf{j}\]
Приведенная выше диаграмма была частью решений для этой проверки хода выполнения, но теперь показывает векторы в координатной плоскости.
Обратите внимание, что \[\textbf{v} + \textbf{w} = 6\textbf{i} + 2\textbf{j}\] \[\textbf{v} + \textbf{w} = (2 + 4)\textbf{i} + (3 + (-1))\textbf{j}\]
На рис. 3.29 показана более общая диаграмма с \[\textbf{v} = \langle a, b \rangle = a \textbf{i} + b\textbf{j}\] и \[\textbf{w} = \langle c, d \rangle = c\textbf{i} + d\textbf{j}\]
в стандарте должность.
 Эта диаграмма показывает, что конечной точкой \(\textbf{v} + \textbf{w}\) в стандартном положении является \((a + c, b + d)\), и поэтому
Эта диаграмма показывает, что конечной точкой \(\textbf{v} + \textbf{w}\) в стандартном положении является \((a + c, b + d)\), и поэтому\[\textbf{v} + \textbf{w} = \langle a + c, b + d \rangle = (a + c)\textbf{i} + (b + d)\textbf{j}\ ]
Это означает, что мы можем сложить два вектора, сложив их горизонтальные и вертикальные компоненты. Следующая проверка прогресса проиллюстрирует нечто подобное для скалярного умножения.
Рисунок \(\PageIndex{3}\): сумма двух векторов
Упражнение \(\PageIndex{2}\)
Пусть \(\textbf{v} = \langle 3, -2 \ угол\). Нарисуйте вектор v в стандартном положении, а затем нарисуйте векторы \(2\textbf{v}\) и \(-2\textbf{v}\) в стандартном положении. Каковы составляющие формы векторов \(2\textbf{v}\) и \(-2\textbf{v}\)?
Как, по-вашему, следует определять скаляр, кратный вектору \(\textbf{a} = \langle a_{1}, a_{2} \rangle\) на скаляр \(c\)? Напишите формальное определение скалярного кратного вектора, основываясь на своей интуиции.

- Ответить
2. Для вектора \(\textbf{a} = \langle a_{1}, a_{2} \rangle\) и скаляра \(c\) мы определяем скалярное кратное \(c\textbf{a }\) равно \[c\textbf{a} = \langle ca_{1}, ca_{2} \rangle.\]
На основании проделанной нами работы мы даем следующие формальные определения.
Определение
Для векторов \(\textbf{v} = \langle v_{1}, v_{2} \rangle = v_{1}\textbf{i} + v_{2}\textbf{j}\) и \(\textbf{w} = \langle w_{1}, w_{2} \rangle = w_{1}\textbf{i} + w_{2}\textbf{j}\) и скалярный \(c\ ), мы делаем следующее определение:
\[\textbf{v} + \textbf{w} = \langle v_{1} + w_{1}, v_{2} + w_{2}\rangle\]
\[\textbf{v} + \textbf{w} = (v_{1} + w_{1})\textbf{i} + (v_{2} + w_{2})\textbf{j}\]
\[\textbf{v} — \textbf{w} = \langle v_{1} — w_{1}, v_{2} — w_{2}\rangle\]
\[\textbf{v} — \ textbf{w} = (v_{1} — w_{1})\textbf{i} + (v_{2} — w_{2})\textbf{j}\]
\[c\textbf{v} = \langle cv_{1}, cv_{2}\rangle\]
\[c\textbf{v} = (cv_{1})\textbf{i} + (cv_{2})\textbf{j}\]Упражнение \(\PageIndex{3}\)
Пусть \(\textbf{u} = \langle 1, -2 \rangle\), \(\textbf{u} = \langle 0, 4 \rangle\ ) и \(\textbf{u} = \langle -5, 7 \rangle\).

- Определить компонентную форму вектора \(2\textbf{u} — 3\textbf{v}\).
- Определите величину и угол направления для \(2\textbf{u} — 3\textbf{v}\).
- Определить компонентную форму вектора u\(\textbf{u} + 2\textbf{v} — 7\textbf{w}\).
- Ответить
Пусть \(\textbf{u} = \langle 1, -2 \rangle\) и \(\textbf{w} = \langle -5, 7 \rangle\).
1. \(2\textbf{u} — 3\textbf{v} = \langle 2, -4 \rangle — \langle 0, 12 \rangle = \langle 2, -16 \rangle\)
9\круг\).3. \(\textbf{u} + 2\textbf{v} — 7\textbf{w} = \langle 1, -2 \rangle + \langle 0, 8 \rangle — \langle -35, 49 \rangle = \langle 36, -43 \rangle\).
Скалярное произведение двух векторов
Поиск оптимальных решений систем является важной задачей прикладной математики. Часто бывает так, что мы не можем найти точное решение, удовлетворяющее определенным ограничениям, поэтому вместо этого мы ищем «лучшее» решение, удовлетворяющее ограничениям.
 Примером этого является подгонка кривой наименьших квадратов к набору данных, как это делают наши калькуляторы при вычислении кривой синусоидальной регрессии. Скалярный продукт полезен в таких ситуациях для поиска «наилучших» решений определенных типов проблем. Хотя мы не увидим этого в этом курсе, наличие наборов перпендикулярных векторов очень важно, поскольку позволяет выполнять быстрые и эффективные вычисления. Скалярное произведение векторов позволяет нам измерить угол между ними и, таким образом, определить, перпендикулярны ли векторы. Скалярное произведение имеет множество применений, например, для нахождения компонент сил, действующих в разных направлениях, в физике и технике. В этом разделе мы вводим и исследуем скалярные произведения.
Примером этого является подгонка кривой наименьших квадратов к набору данных, как это делают наши калькуляторы при вычислении кривой синусоидальной регрессии. Скалярный продукт полезен в таких ситуациях для поиска «наилучших» решений определенных типов проблем. Хотя мы не увидим этого в этом курсе, наличие наборов перпендикулярных векторов очень важно, поскольку позволяет выполнять быстрые и эффективные вычисления. Скалярное произведение векторов позволяет нам измерить угол между ними и, таким образом, определить, перпендикулярны ли векторы. Скалярное произведение имеет множество применений, например, для нахождения компонент сил, действующих в разных направлениях, в физике и технике. В этом разделе мы вводим и исследуем скалярные произведения.Мы видели, как складывать векторы и умножать векторы на скаляры, но мы еще не ввели произведение векторов. В общем, произведение векторов должно давать нам другой вектор, но оказывается, что действительно полезного способа определить такое произведение векторов не существует.
 {2}} = \sqrt{u_{1}u_{1} + u_{2}u_{2}}\]
{2}} = \sqrt{u_{1}u_{1} + u_{2}u_{2}}\]Выражение под вторым квадратным корнем является важным, и мы расширяем его и даем ему специальное имя.
Определение
Пусть \(\textbf{u} = \langle u_{1}, u_{2} \rangle\) и \(\textbf{v} = \langle v_{1}, v_{2} \ rangle\) — векторы на плоскости. Произведение точек из \(\textbf{u}\) и \(\textbf{v}\) является скаляром \[\textbf{u}\cdot \textbf{v} = u_{1}v_{1 } + u_{2}v_{2}.\]
Это число может показаться странным для вычисления, но оказывается, что скалярное произведение двух векторов полезно для определения угла между двумя векторами. Вспомните, что в ходе проверки 3.27 на странице 225 мы использовали закон косинусов для определения суммы двух векторов, а затем использовали закон синусов для определения угла между суммой и одним из этих векторов. Теперь мы увидели, насколько проще вычислить сумму двух векторов, когда векторы находятся в компонентной форме. Скалярное произведение позволит нам определить косинус угла между двумя векторами в компонентной форме.
 Это связано со следующим результатом: 9\circ\)), затем
Это связано со следующим результатом: 9\circ\)), затем\[\textbf{u}\cdot \textbf{v} = |\textbf{u}||\textbf{v}|\cos(\theta)\] или \[\ cos(\theta) = \dfrac{\textbf{u}\cdot \textbf{v}}{|\textbf{u}||\textbf{v}|}\]
Обратите внимание, что если мы записали векторы \(\textbf{v}\) и \(\textbf{w}\) в компонентной форме, то у нас есть формулы для вычисления \(|\textbf{v}|, |\textbf{w}|\), и \(\textbf{v}\cdot \textbf{w}\). Этот результат может показаться удивительным, но он является довольно прямым следствием закона косинусов, как мы сейчас покажем. Пусть \(\theta\) будет углом между \(\textbf{u}\) и \(\textbf{v}\), как показано на рис. 3.30. 9{2} — 2|\textbf{u}||\textbf{v}|\cos(\theta)\]
\[-2(\textbf{u} \cdot \textbf{u}) = -2| \textbf{u}||\textbf{v}|\cos(\theta)\]
\[\textbf{u} \cdot \textbf{u} = |\textbf{u}||\textbf{v} |\cos(\theta)\]Упражнение \(\PageIndex{4}\)
1. Определите угол \(\theta\) между векторами \(\textbf{u} = 3\textbf{i } + \textbf{j}\) и \(\textbf{v} = -5\textbf{i} + 2\textbf{j}\).

2. Определить все векторы, перпендикулярные \(\textbf{u} = \langle 1, 3 \rangle\). Сколько таких векторов? 9\circ\) и поэтому \(\cos(\theta) = 0\). Итак, мы должны иметь \(\textbf{u}\cdot\textbf{v} = 0\), а это означает, что \(a + 3b = 0\). Таким образом, любой вектор \(\textbf{v} = \langle a, b \rangle\), где \(a = -3b\) будет перпендикулярен \(\textbf{v}\), и таких векторов бесконечно много . Один вектор, перпендикулярный \(\textbf{u}\), равен \(\langle -3, 1 \rangle\).
Одной из целей проверки выполнения 3.34 было использование формулы \[\cos(\theta) = \dfrac{\textbf{u}\cdot \textbf{v}}{|\textbf{u}||\textbf{ v}|}\] 9\circ) = 0\), мы видим, что из этой формулы следует, что \(\textbf{u}\) и \(\textbf{v}\) будут перпендикулярны тогда и только тогда, когда \(\textbf{u}\cdot \textbf{v} = 0\) (Это потому, что дробь будет равна \(0\) только тогда, когда числитель равен \(0\) и знаменатель не равен нулю.) Итак, мы имеем:
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно \(0\).

Примечание
Когда два вектора перпендикулярны, мы также говорим, что они ортогональны .
Проекции
Еще одним полезным применением скалярного произведения является нахождение проекции одного вектора на другой. Пример того, где такой расчет полезен, следующий.
Усэйн Болт из Ямайки взволновал мир легкой атлетики в 2008 году своими мировыми рекордами на беговой дорожке. Болт выиграл 100-метровый забег с мировым рекордом 9,69 секунды. С тех пор он улучшил это время, проехав 9,58 секунды при содействии ветра 0,9.метров в секунду в Берлине, 16 августа 2009 года2. Помощь ветра — это мера скорости ветра, которая помогает бегунам двигаться по дорожке. Гораздо легче провести очень быструю гонку, если ветер дует в сторону гонки. Чтобы мировые рекорды не зависели от погодных условий, время записывается как рекордное только в том случае, если ветер, помогающий бегунам, меньше или равен 2 метрам в секунду. Скорость ветра для гонки регистрируется анемометром, установленным рядом с трассой.
 Однако важно отметить, что погода не всегда так сговорчива, как хотелось бы. Ветер не всегда дует точно в направлении гусеницы, поэтому датчик должен учитывать угол, который ветер образует с гусеницей.
Однако важно отметить, что погода не всегда так сговорчива, как хотелось бы. Ветер не всегда дует точно в направлении гусеницы, поэтому датчик должен учитывать угол, который ветер образует с гусеницей.Если ветер дует в направлении вектора \(\textbf{u}\) и путь проходит в направлении вектора \(\textbf{v}\) на рис. 3.31, то только часть общий вектор ветра на самом деле работает, чтобы помочь бегунам.
Рисунок \(\PageIndex{5}\): Проекция \(\textbf{u}\) на \(\textbf{v}\)
Эта часть называется проекцией вектора \(\textbf{u}\) на вектор \(\textbf{v}\) и обозначается \(\textbf{proj}_\textbf{v}\textbf{u}\).
Мы можем найти эту проекцию с помощью небольшой тригонометрии. Для этого пусть \(\theta\) будет углом между \(\textbf{u}\) и \(\textbf{v}\), как показано на рисунке \(\PageIndex{5}\). Используя тригонометрию прямоугольного треугольника, мы видим, что \[|\textbf{proj}_\textbf{v}\textbf{u}| = |\textbf{u}|\cos(\theta) = |\textbf{u}|\dfrac{\textbf{u}\cdot \textbf{v}}{|\textbf{u}||\textbf{ v}|} = \dfrac{\textbf{u}\cdot \textbf{v}}{|\textbf{v}|}\]
Величина, которую мы только что получили, называется скалярной проекцией ( или компонент ) из \(\textbf{u}\) на \(\textbf{v}\) и обозначается как \(\textbf{comp}_\textbf{v}\textbf{u}\ ). {2}}\textbf{v}\] 9{2}}\textbf{v} = \dfrac{\textbf{u}\cdot \textbf{v}}{\textbf{v}\cdot \textbf{v}}\textbf{v}\]
{2}}\textbf{v}\] 9{2}}\textbf{v} = \dfrac{\textbf{u}\cdot \textbf{v}}{\textbf{v}\cdot \textbf{v}}\textbf{v}\]составляющая ветра, которая действует перпендикулярно направлению \(\textbf{v}\) на рисунке \(\PageIndex{5}\), называется проекцией \(\textbf{u}\) , ортогональной \ (\textbf{v}\) и обозначается \(\textbf{proj}_{\perp\textbf{v}}\textbf{u}\), как показано на рис. 3.32. Поскольку \(\textbf{u} = \textbf{proj}_{\perp\textbf{v}}\textbf{u} + \textbf{proj}_{\textbf{v}}\textbf{u}\) , у нас есть
Рисунок \(\PageIndex{6}\): Проекция \(\textbf{u}\) на \(\textbf{v}\)
\[\textbf{proj}_{\perp \textbf{v}}\textbf{u} = \textbf{u} — \textbf{proj}_{\textbf{v}}\textbf{u}\]
Ниже приводится сводка полученных нами результатов. .
Для ненулевых векторов \(\textbf{u}\) и \(\textbf{v}\) проекция вектора \(\textbf{u}\) на вектор \(\textbf {v}\) \(\textbf{proj}_\textbf{v}\textbf{u}\), равно 9{2}}\textbf{v} = \dfrac{\textbf{u}\cdot \textbf{v}}{\textbf{v}\cdot \textbf{v}}\textbf{v}\]
См.
 Рисунок \(\PageIndex{6}\). Проекция \(\textbf{u}\) , ортогональная \(\textbf{v}\), обозначенная \(\textbf{proj}_{\perp\textbf{v}}\textbf{u }\), это
Рисунок \(\PageIndex{6}\). Проекция \(\textbf{u}\) , ортогональная \(\textbf{v}\), обозначенная \(\textbf{proj}_{\perp\textbf{v}}\textbf{u }\), это\[\textbf{proj}_{\perp\textbf{v}}\textbf{u} = \textbf{u} — \textbf{proj}_{\textbf{v}}\ textbf{u}\]
Заметим, что \[\textbf{u} = \textbf{proj}_{\perp\textbf{v}}\textbf{u} + \textbf{proj}_{\textbf{ v}}\textbf{u}\]
Упражнение \(\PageIndex{5}\)
Пусть \(\textbf{u} = \langle 7, 5 \rangle\) и \(\textbf{v} = \langle 10, -2\rangle\ ). Определите \(\textbf{proj}_{\textbf{v}}\textbf{u}\) и \(\textbf{proj}_{\perp\textbf{v}}\textbf{u}\) и убедитесь, что \(\textbf{u} = \textbf{proj}_{\perp\textbf{v}}\textbf{u} + \textbf{proj}_{\textbf{v}}\textbf{u}\ ). Нарисуйте рисунок, показывающий все векторы, участвующие в этом.
- Ответить
Пусть \(\textbf{u} = \langle 7, 5 \rangle\) и \(\textbf{v} = \langle 10, -2\rangle\). Затем 9{2}}\textbf{v}= \langle 7, 5 \rangle — \langle \dfrac{600}{104}, \dfrac{-120}{104} \rangle = \langle \dfrac{128}{104 }, \dfrac{640}{104} \rangle \приблизительно \langle 1,231, 6,154 \rangle\]
Резюме раздела 3.
 6
6В этом разделе мы изучили следующие важные понятия и идеи: v} = \langle v_{1}, v_{2} \rangle\) и \(\textbf{i},\textbf{j}\) форма одного и того же вектора \(\textbf{v} = v_ {1}\textbf{i} + v_{2}\textbf{j} \). Используя это обозначение, мы имеем 9\circ\), и \[\cos(\theta) = \dfrac{v_{1}}{|\textbf{v}|}\] и \[\sin(\theta) = \dfrac{v_{2 }}{|\textbf{v}|}\]
- Горизонтальный, компонентный и вертикальный компоненты вектора \(\textbf{v}\) и дирекционного угла \(\theta\) равны \[v_{1} = |\textbf{v}|\cos(\theta) \] и \[v_{2} = |\textbf{v}|\sin(\theta)\]
- \[\textbf{v} + \textbf{w} = \langle v_{1} + w_{1}, v_{2} + w_{2}\rangle = (v_{1} + w_{1 })\textbf{i} + (v_{2} + w_{2})\textbf{j}\]
- \[\textbf{v} — \textbf{w} = \langle v_{1} — w_{1}, v_{2} — w_{2}\rangle = (v_{1} — w_{1}) \textbf{i} + (v_{2} — w_{2})\textbf{j}\]
- \[c\textbf{v} = \langle cv_{1}, cv_{2}\rangle = (cv_{1})\textbf{i} + (cv_{2})\textbf{j}\]
- Произведение точек из \(\textbf{v}\) и \(\textbf{w}\) равно \(\textbf{u}\cdot \textbf{v} = u_{1}v_{1} + и_{2}в_{2}.
 \) 9{2}}\textbf{w} = \dfrac{\textbf{v}\cdot \textbf{w}}{\textbf{w}\cdot \textbf{w}}\textbf{w}\]
\) 9{2}}\textbf{w} = \dfrac{\textbf{v}\cdot \textbf{w}}{\textbf{w}\cdot \textbf{w}}\textbf{w}\]Проекция \(\textbf{v}\), ортогональная \(\textbf{w}\), обозначается как \(\textbf{proj}_{\perp\textbf{w}}\textbf{v}\) , равно
\]Заметим, что \[\textbf{w} = \textbf{proj}_{\perp\textbf{w}}\textbf{v} + \textbf{proj}_{\textbf{w}}\textbf{v }\] См. рисунок \(\PageIndex{7}\).
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Тед Сандстром и Стивен Шликер
- Лицензия
- СС BY-NC-SA
- Версия лицензии
- 3,0
- Показать страницу TOC
- нет
- Теги
- источник@https://scholarworks.
 gvsu.edu/books/12
gvsu.edu/books/12
- источник@https://scholarworks.
- Найдите число такое, что 3 плюс это число равно 7
- площадь круга равна произведению номер (ок. 3.14159) с произведением радиуса окружности на сама
- Произведение двух дробей – это дробь, у которой знаменатель равен произведению знаменателей двух исходных дробей и чей числитель является произведением числителей двух исходных дроби.
- учитывая любые два числа, мы получаем один и тот же результат независимо от в каком порядке мы их добавляем.
- найти х таких что 3+x = 7 .
- А = r 2
- н/м p/q = np/mq
- для всех номеров n и м , н+м = м+н
- Что означает 2/4?
- Что означает «=»
- Если терм имеет переменную, то он называется «Алгебраическим термом» .
- Если термин представляет собой просто число, то он называется «Постоянный термин» .
- Определите отношение между двумя последовательными фигурами или числами.
- Сформируйте отношение между позицией и фигурой или числом.
- Представлять изменяющееся значение с помощью переменной.
- Запишите правило, используя переменную.
- Определите неизвестную величину в операторе.
- Определите операцию , необходимую для связи известных и неизвестных величин.
- «добавлено» или «сумма» или «увеличено на» или «более чем» — все означает сложение .
- Определите неизвестную величину в операторе.
- Определите операцию , необходимую для связи известных и неизвестных величин.
- «Умножить на», «раз», «из» — все означает умножение .
- Иногда у вас может быть задействовано более одной операции.
- Определите неизвестную величину в операторе.
- Определите операцию , необходимую для связи известные и неизвестные величины.

- «Частное», «деленное на» — все означает деление .
- Иногда у вас может быть задействовано более одной операции.
- Выражение слева от «=» называется левой стороной или LHS.
- Выражение справа от «=» называется Right-Hand Side или RHS.
- Идентифицируем неизвестное и представляем его с помощью переменной.
- Укажите операцию, которая будет использоваться.
- Обратите внимание на такие термины, как «добавлено к», «сумма», «больше чем» или «увеличение». Эти термины указывают на то, что используемой операцией является сложение (+).
- Составьте уравнение.
- Проанализируйте вопрос, чтобы определить известных и неизвестных величин.
- Составьте уравнение , связывающее величины.
- Решите уравнение , чтобы найти значение неизвестного.
- 1.
 Определение неизвестной величины
Определение неизвестной величины - 2. Написание правила для узоров из спичек
- 3. Составление алгебраического выражения для данного утверждения
- 4. Проверить, является ли данное значение решением уравнения
- Определить неизвестную величину и представить ее с помощью переменной
- Определите постоянную или фиксированную величину
- Определите операцию, связывающую известные и неизвестные величины
- Внимательно рассмотрите уравнение для переменной
- Мы должны поставить значение вместо переменной
- Внимательно выполняйте операции с номерами
- Основные примеры алгебраических выражений
- Примеры алгебраических выражений, состоящие из нескольких частей
».0499 против часовой стрелки
Переключите координату и умножьте один слева на:
Для двух векторов \(\textbf{v}\) и \(\textbf{w}\) с \(\textbf{v} = \langle v_{1}, v_{2} \rangle = v_{1 }\textbf{i} + v_{2}\textbf{j}\) и \(\textbf{w} = \langle w_{1}, w_{2} \rangle = w_{1}\textbf{i} + w_{2}\textbf{j}\) и скаляр \(c\):
Рисунок \(\PageIndex{7}\): Проекция \(\textbf{v}\) на \(\textbf{w}\)
Эта страница под названием 3.6: Векторы с алгебраической точки зрения распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Тедом Сандстремом и Стивеном Шликером (ScholarWorks @Grand Valley State University) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Язык алгебры — Определения
Обучение алгебра немного похожа на изучение другого языка. На самом деле алгебра — это просто язык, используемый для создания математических моделей реальных ситуаций и для решать проблемы, которые мы не можем решить, используя только арифметику. Вместо того, чтобы использовать словами, алгебра использует символы, чтобы делать утверждения о вещах. В алгебре мы часто используют буквы для обозначения чисел.
С алгебры использует те же символы, что и арифметика для сложения, вычитания, умножения и деления, вы уже знакомы с основным словарным запасом.
В этом уроке вы выучите несколько важных новых словарных слов и увидите, как переводить с простого английского на «язык» алгебры.
Первый шаг
в обучении «говорить на алгебре» — это изучение определений
наиболее употребительные слова.
Алгебраический Выражения | Переменные | Коэффициенты | Константы | Реальные числа | Рациональный Числа | Иррациональные числа | Идет перевод Слова в выражения
Алгебраический
Выражения
Алгебраическое выражение — это один или несколько алгебраических терминов во фразе.
Он может включать переменные,
константы,
и рабочие символы, такие как знаки плюс и минус. Это всего лишь фраза, а не
все предложение, поэтому оно не включает знак равенства.
Алгебраический
выражение:
3x 2 + 2y + 7xy + 5
В алгебраическое выражение, термины — это элементы, разделенные плюсом или минусом знаки. В этом примере четыре термина: 3x 2 , 2y , 7xy , и 5 . Термины могут состоять из переменных и коэффициентов или констант.
Переменные
В алгебраических выражениях буквы обозначают переменные. Эти буквы на самом деле
номера в маскировке. В этом выражении переменными являются x и y. Мы называем
эти буквы» var iables», потому что
числа, которые они представляют, могут варьироваться это
то есть мы можем заменить буквы в выражении одним или несколькими числами.
Эти буквы на самом деле
номера в маскировке. В этом выражении переменными являются x и y. Мы называем
эти буквы» var iables», потому что
числа, которые они представляют, могут варьироваться это
то есть мы можем заменить буквы в выражении одним или несколькими числами.
Коэффициенты
Коэффициенты — это числовая часть термов с переменными. В 3x 2 + 2y + 7xy + 5 , коэффициент первого члена равен 3. Коэффициент
второго члена равен 2, а коэффициент третьего члена равен 7.
Если срок состоит только переменных, его коэффициент равен 1.
Константы
Константы — это термины в алгебраическом выражении, которые содержат только числа.
То есть это термины без переменных. Мы называем их константами, потому что
их значение никогда не меняется, так как в терме нет переменных, которые могут
изменить его значение. В выражении 7x 2 + 3xy + 8 постоянный член равен «8».
Реальный
Номера
В алгебре мы работаем с набором действительных чисел, которые мы можем смоделировать, используя
числовой ряд.
Действительные числа описывают реальные величины, такие как количества, расстояния, возраст, температура и так далее. Вещественное число может быть целым числом, дробью или десятичный. Они также могут быть как рациональными, так и иррациональными. Числа, которые не «настоящие» называются воображаемыми. Мнимые числа используются математиками для описания чисел, которые не могут быть найдены на числовой прямой. Они более сложный предмет, чем мы будем работать здесь.
Рационал
Номера
Мы называем множество действительных целых чисел и дробей «рациональными числами». Rational происходит от слова « отношение ».
потому что рациональное число всегда можно записать как отношение ,
или частное двух целых чисел.
Примеры
рациональных чисел
Дробь ½ представляет собой отношение 1 к 2.
Так как три может быть выражено как три к одному или отношение 3 к одному, это также Рациональное число.
Число «0,57» также является рациональным числом, так как его можно записать в виде дроби.
Иррациональное
Номера
Некоторые действительные числа нельзя представить как частное двух целых чисел. Мы называем
эти числа «иррациональные числа». Десятичная форма иррационального
number — неповторяющееся и не заканчивающееся десятичное число. Например,
Вы, вероятно, знакомы с числом под названием «пи». Это иррациональное
число настолько важно, что мы даем ему имя и специальный символ!
Пи не может быть
записывается как частное двух целых чисел, и его десятичная форма продолжается вечно
и никогда не повторяется.
Перевод
Words in Algebra Language
Здесь
некоторые утверждения на английском языке. Чуть ниже каждого утверждения находится его перевод
по алгебре.
сумма трех умноженных на число и восемь
3x + 8
Слова » сумма» говорит нам, что нам нужен знак плюс, потому что мы собираемся добавить три раз число до восьми. Слова «трижды» говорят нам о первом срок — это число, умноженное на три.
В этом выражении нам не нужен знак умножения или скобки. Такие фразы, как «число». или «число» говорит нам, что наше выражение имеет неизвестную величину, называется переменной. В алгебре мы используем буквы для обозначения переменных.
произведение числа и того же числа меньше 3
x(x 3)
Слова »
произведение» говорит нам, что мы собираемся умножить число, умноженное на число
меньше 3. В этом случае мы будем использовать круглые скобки для представления умножения. Слова «меньше 3» говорят нам вычесть три из неизвестного числа.
Слова «меньше 3» говорят нам вычесть три из неизвестного числа.
а число, деленное на то же число меньше пяти
Слова «делится by» говорит нам, что мы собираемся разделить число на разность числа и 5. В этом случае мы будем использовать дробь для обозначения деления. Слова «меньше 5» говорит нам, что нам нужен знак минус, потому что мы собираемся вычесть пять.
задняя часть наверх
символов
символ Верхние индексы (показатели), такие как
2 из х 2 ,
используются для обозначения повторяющихся умножений. Например, x 2 является сокращением от xx, и x 3 является сокращением для х.х х ). Символ (греч.
буква «пи») используется для обозначения специального числа
3.14159…
Верхние индексы (показатели), такие как
2 из х 2 ,
используются для обозначения повторяющихся умножений. Например, x 2 является сокращением от xx, и x 3 является сокращением для х.х х ). Символ (греч.
буква «пи») используется для обозначения специального числа
3.14159…Таким образом, алгебра полна таких выражений, как
- 3x 2 + 2x + 4
(а+б)/2
а +с
- у = 2х 3 + 2х + 7
мин = нм
(х+а)(х-а) = х 2 — а 2
А = г 2
Что такое переменные?
Буквы, которые встречаются в алгебраических выражениях, например x в 3x 2 + 2x +4 , называются переменными. Числа, например 3 , 2 а также 4 , в приведенном выше выражении являются константами — их значение постоянно. Но переменные «варьируются», то есть их можно заменить любым числом, чтобы получить
арифметическое выражение (выражение, состоящее только из чисел и операций), которое
затем можно оценить.
Но переменные «варьируются», то есть их можно заменить любым числом, чтобы получить
арифметическое выражение (выражение, состоящее только из чисел и операций), которое
затем можно оценить. Если в выражении 3x 2 + 2х +4 берем х = а также то получаем результат Чтобы увидеть значение выражения для других значений x просто измените значение x и нажмите кнопку «оценить выражение».
Примечание: , если значение, которое вы указываете, равно x слишком велик, вы не сможете увидеть весь ответ, если не используйте клавиши со стрелками.
Примечание: Для некоторых расчетов с десятичными дробями ответ может
быть «слегка выключенным» — это результат того, как компьютер
обрабатывает десятичные дроби. Для простого примера этого возьмите х = 5,3 .
Какая польза от алгебраических выражений и уравнений?
Одно из применений таких выражений состоит в том, чтобы дать краткий способ выразить определенные задачи, формулы и общие математические факты. Рассмотрим следующие три утверждения:
Рассмотрим следующие три утверждения: 
Формула A = r 2 выражает область, А , круга через его радиус r . То есть, зная радиус круга, мы можем использовать формулу, чтобы найти его область. Например, у круга радиусом три фута есть площадь А = 3 2 90 524 = 33 = 9 , поэтому, принимая 3,14 в качестве нашего приближения для нас получить А = 3,149 = 28,26 как площадь круга. Что мы сделали, так это заменили «переменный» r с конкретным число, 3 , и постоянный символ, , с его (приблизительным) числовым значением и оценил выражение как получить соответствующее числовое значение для переменной A , то есть площадь круга..
Но в чем наша проблема, что мы знаем район
и мы хотим найти радиус? Например, если у садовника достаточно
семя для посадки 50 квадрат
футов какого-то цветка, и он хочет посадить его на круглую грядку, тогда как
большую клумбу он должен копать? В этом случае мы можем использовать
та же формула, A = r 2 ,
но на этот раз мы знаем район, А ,
и мы пытаемся найти радиус, r . То есть мы знаем, что A = 50 = r 2 .
Опять же, приближение
на 3.14 мы можем переписать это как 50
= 3,14r 2 .
Делим обе части на 3.14 получаем 15,9236 = г 2 ,
затем извлечение квадратного корня из обеих частей дает 3,99.
= г . Таким образом, с практической точки зрения (садовника)
желаемая клумба должна иметь радиус в четыре фута!
То есть мы знаем, что A = 50 = r 2 .
Опять же, приближение
на 3.14 мы можем переписать это как 50
= 3,14r 2 .
Делим обе части на 3.14 получаем 15,9236 = г 2 ,
затем извлечение квадратного корня из обеих частей дает 3,99.
= г . Таким образом, с практической точки зрения (садовника)
желаемая клумба должна иметь радиус в четыре фута!
Мы можем получить общую формулу для желаемого результата
из формулы А
= г 2 по
разделив обе части уравнения на
, получив А/
= r 2 и затем взяв квадрат
корень обеих сторон, получая общую формулу р
=А/,
для радиуса при заданной площади. . Обратите внимание, что эта формула говорит делать то же самое, что мы делали раньше. То есть,
решаем задачу садовников берем A = 50, раздели на и возьми квадрат
корень. Конечно, вам может быть интересно, как же мы
Знать, что делать? Что ж, это то, чему вы научитесь, изучая
Алгебра средней школы.
Современная алгебраическая система счисления предлагает множество преимуществ
над более ранними обозначениями. Главным из них является то, что он делает
проще манипулировать алгебраическими выражениями и, следовательно, проще
объяснять и применять алгебраические понятия.
История алгебраической нотации
История алгебраических обозначений длинна и разнообразны на протяжении тысячелетий. Наши нынешние обозначения относительно недавняя разработка, насчитывающая всего несколько сотен лет.Использование символов, знаков равенства и надстрочных индексов на самом деле относительно недавнее развитие алгебры. Через большую часть его историческая алгебра была написана с использованием только слов и чисел.
«Современные обозначения» значительно облегчают запись алгебраических идей.
и результаты. Что еще более важно, использование соответствующих обозначений
значительно облегчает выполнение многих необходимых рутинных манипуляций
решать алгебраические задачи.
Без использования современных обозначений было бы, вероятно, крайне сложно написать программу для полиномиального калькулятора.
———————-
Алгебраическая нотация имеет множество применений. Например, мы можем использовать его для записи таких формул, как формула A = r 2 для площадь круга, чтобы дать математические определения, такие как 90 513 (n/p + r/s) = (ns + pr)/sr для сложения дробей , представить общие математические результаты, такие как м+н = n+m , выражающее коммутативность сложения ( тот факт, что результат сложения двух чисел не зависит от порядка в котором мы их добавляем), и для описания многих видов функций. Таким образом, алгебраическая нотация обеспечивает краткий способ выражения многих видов отношения.
Однако еще более важным является тот факт, что запись алгоритма может
использоваться для манипулирования такими выражениями, чтобы мы могли решать различные
проблемы. Большая часть материала школьной алгебры посвящена
с различными способами манипулирования такими выражениями и с различными
виды проблем, которые мы можем решить с помощью таких манипуляций.
Совершенна ли математическая запись?
Поскольку математическая запись совершенствовалась в течение нескольких тысяч лет, мы могли бы ожидать, что к этому времени он будет довольно совершенным. К сожалению, это не совсем так, и ситуаций бывает много. где обозначение потенциально неоднозначно. То есть там В математике много ситуаций, когда данное обозначение может иметь больше чем одно значение. Часто разные значения тесно связаны но различия все же существенны. Эта двусмысленность делает не вызывают затруднений у опытных математиков, так как они, как правило, могут выяснить, что имеется в виду из общего контекста, но это может вызвать некоторые реальные проблемы для студентов.Алгебра | Блог
Алгебра — это раздел математики, в котором для представления неизвестных величин используются буквы или символы. Он включает в себя правила манипулирования этими символами. Использование букв помогает нам составлять уравнения, связанные с неизвестными и известными величинами, и генерировать формулы для вычисления площадей, периметров, объемов, банковских процентов и т. д.
Использование букв помогает нам составлять уравнения, связанные с неизвестными и известными величинами, и генерировать формулы для вычисления площадей, периметров, объемов, банковских процентов и т. д.
Математика — это не только числа; иногда мы сталкиваемся с проблемой, когда невозможно знать все значения, и мы должны использовать переменные для представления этих неизвестных значений. Алгебра научит вас обращаться с этими переменными в уравнениях.
Давайте посмотрим это видео, чтобы понять необходимость алгебры:
Мы видели, что во многих ситуациях существует некоторая величина, значение которой нам неизвестно. Мы можем представить отношение между известными и неизвестными величинами, используя алгебру. Такие величины представляются любой буквой английского алфавита. Пример: x, y, p, q, a, b, c и т. д.
Можете ли вы привести пример из реальной жизни, где вы используете алгебру?
Предположим, вы идете в школу каждый день в 8 утра. Что вы делаете в первую очередь накануне вечером? Вы, вероятно, поставите будильник, рассчитав примерное время, которое вам нужно, чтобы проснуться, почистить зубы, принять душ и позавтракать перед тем, как отправиться на улицу. Вы также учтете время, необходимое для того, чтобы добраться от дома до школы, и соответственно установите будильник. Неосознанно здесь вы использовали алгебру, чтобы установить свой утренний распорядок! Поскольку вы не знали точно, сколько времени требуется для каждого из ваших утренних занятий, вы использовали концепцию переменных, чтобы получить приближение.
Вы также учтете время, необходимое для того, чтобы добраться от дома до школы, и соответственно установите будильник. Неосознанно здесь вы использовали алгебру, чтобы установить свой утренний распорядок! Поскольку вы не знали точно, сколько времени требуется для каждого из ваших утренних занятий, вы использовали концепцию переменных, чтобы получить приближение.
Понятия
Глава «Алгебра» охватывает следующие понятия:
Переменные и константы Алгебраические выражения Алгебраические уравнения
Переменные и константы
В некоторых ситуациях могут быть величины, значение которых может варьироваться. Такие величины представляются любой буквой английского алфавита и называются переменными. Пример: x, y, p, q, a, b, c и т. д. Этот раздел математики, который имеет дело с числами и переменными, называется алгеброй. Примеры переменных из реальной жизни включают в себя: количество людей, посещающих библиотеку в разные дни, пробеги, набранные игроком в разных матчах, и т. д.
д.
Существуют определенные количества, которые не меняют своей стоимости; они остаются фиксированными. Такие фиксированные значения называются константами. Например, такие числа, как 4, 26, 100 и т. д., являются константами.
Алгебраические выражения
Алгебраические термы — это термы с переменными. Они могут принимать разные значения в зависимости от значения переменной. Постоянные члены — это просто числа, имеющие фиксированное значение. Термины в сочетании с математическими операторами составляют алгебраическое выражение.
Алгебраическое выражение — это математическое выражение, содержащее переменные. Алгебраическое выражение можно описать как комбинацию констант и переменных с четырьмя математическими операциями, а именно сложением, вычитанием, умножением и/или делением.
Рассмотрим следующее утверждение:
Это можно записать в математическом выражении так:
Давайте посмотрим еще несколько таких утверждений.
Помните, что числовые значения в выражении всегда фиксированы и постоянны.
Теперь давайте научимся формировать правила для различных шаблонов чисел. Рассмотрим этот шаблон:
Сделаем наблюдение.
Если мы рассмотрим положение каждого числа как «m», то правило будет таким:
Итак, мы можем сформировать правило и для числовых шаблонов. Чтобы сформировать правило для любого заданного геометрического или числового шаблона:
Как написать правильные шаблоны спичек правил? Подсчитайте количество спичек в каждой форме узора. Также обратите внимание на положение фигуры.
Также обратите внимание на положение фигуры.
Теперь определите паттерн и его связь с позицией. Здесь мы видим, что в каждом случае количество использованных спичек равно:
5 × номер позиции + 1
Здесь номер позиции фигуры меняется, поэтому мы представляем ее с помощью переменной n. Правило будет 5n + 1.
Мы можем составить алгебраические выражения для заданных словесных выражений заявления, включающие различные операции. Давайте посмотрим, как:
Сложение
При преобразовании оператора в алгебраическое выражение:
Вычитание
Когда утверждение преобразуется в алгебраическое выражение:
Определите
неизвестную величину.
Определите операцию , необходимую для связи известные и неизвестные величины.
«Минус», «разность», «уменьшение на», «меньше чем» — все означает вычитание .
Умножение
Когда оператор преобразуется в алгебраическое выражение:
Подразделение
Когда оператор преобразуется в алгебраическое выражение:
Математические правила и формулы могут быть записаны в виде алгебраических выражений. Например, площадь прямоугольника рассчитывается как произведение длины и ширины прямоугольника, т. е. площадь = длина × ширина. Мы можем записать эту формулу в виде алгебраического выражения, рассматривая длину и ширину прямоугольника как переменные, а именно «l» и «b» соответственно.
Итак, формула для нахождения площади прямоугольника может быть записана как:
Площадь = l × b = lb
Для любой формы, такой как квадрат, прямоугольник, треугольник или круг, периметр – это расстояние вокруг форма. Периметр можно записать в алгебраической форме как сумму всех сторон.
Алгебраические выражения помогают нам представить любое правило в виде общего выражения.
Теперь давайте научимся составлять алгебраическое выражение для коммутативности целых чисел. Мы знаем, что когда мы складываем два целых числа, порядок их сложения не имеет значения. В общем случае мы можем представить два целых числа как «а» и «б».
Отсюда согласно коммутативному свойству сложения целых чисел имеем
Напомним еще одно важное свойство целых чисел. При умножении трех или более целых чисел мы можем группировать числа и умножать. Как мы группируем числа, на самом деле не имеет значения. Итак, вообще говоря, для любых трех целых чисел ‘a’, ‘b’ и ‘c’ мы можем сформулировать ассоциативное свойство умножения как:
Точно так же мы можем представить распределительное свойство целых чисел (‘a’, «б» и «в») как
Алгебраические уравнения
Алгебраическое уравнение имеет знак «=» с выражениями или константами по обе стороны от него. Например, 5x + 9 = 19. Мы видим, что в этом уравнении также участвуют переменные. Другими словами, задействованы алгебраические термины.
Алгебраическое выражение — это просто комбинация алгебраических терминов. В нем нет знака «=». Например, 4x + 6.
Можем ли мы составить уравнения для данного математического утверждения в словесной форме? Чтобы сформировать уравнение из оператора, мы следуем шагам, приведенным ниже:
Что означает знак «равно» в уравнении? Знак равенства указывает на то, что обе части уравнения равны, т. е. уравнение истинно только в том случае, если выражение в левой части равно выражению в правой части.
е. уравнение истинно только в том случае, если выражение в левой части равно выражению в правой части.
Давайте поймем смысл удовлетворения уравнения или решения уравнения. Например, рассмотрим линейное уравнение 5x + 12 = 27, где x = 3.
Возьмем значение «x» равным 2,9.0032
Таким образом, мы можем заключить, что x = 2 не является решением уравнения 5x + 12 = 27.
Этот метод подстановки различных значений и получения значения, удовлетворяющего уравнению, называется методом проб и ошибок. метод.
Чтобы проверить, является ли заданное значение решением уравнения:
При решении реальных задач мы следуем этой стратегии:
Распространенные ошибки
Ниже приведены темы, в которых учащиеся допускают распространенные ошибки при работе с алгеброй
Идентификация неизвестного количества
В данной ситуации у нас могут быть известные и неизвестные количества. Нам нужно правильно определить неизвестную величину и представить ее буквой или переменной. Пример, рассмотрим утверждение:
Как мы можем выразить это утверждение в математической форме? Здесь мы не знаем, что такое число. Следовательно, это неизвестная величина. Мы представляем это с помощью переменной, скажем, «x». Число 18 — известная величина.
Помните, что числовые значения в выражении всегда фиксированы и постоянны. Вышеприведенное утверждение может быть представлено математически как «x + 18».
Написание правила для узоров из спичек
Как написать правильное правило для составления заданного узора из спичек? Подсчитайте количество спичек в каждой форме узора. Также обратите внимание на положение фигуры.
Теперь определите паттерн и его связь с позицией. Здесь мы видим, что в каждом случае количество используемых спичек равно:
5 × номер позиции + 1
Здесь номер позиции фигуры варьируется, следовательно, мы представляем его с помощью переменной «n». будет 5n + 1.
Составление алгебраического выражения для данного утверждения
Чтобы составить алгебраическое выражение из данного утверждения, мы должны:
Позаботьтесь об операции. Например, рассмотрим утверждение:
Дважды число означает 2, умноженное на число. Добавлено означает добавление или «+». Таким образом, правильным утверждением будет 2p + 12.
Добавлено означает добавление или «+». Таким образом, правильным утверждением будет 2p + 12.
Проверить, является ли заданное значение решением уравнения
Чтобы проверить, является ли заданное значение решением уравнения:
Пример, проверьте, является ли 4 решением уравнения:
Обратите внимание, что и в левой, и в правой части есть переменная «y». Поместите значение «y» в обе стороны и найдите значение.
Заключение
Алгебра — интересная глава со многими приложениями в реальной жизни. Теперь, когда вы узнали об этом все, можете ли вы решить головоломку ниже?
Найдите значение каждого цвета воздушных шаров ниже:
Арпана
Автор
Энтузиаст математики и педагог, Арпана имеет сильное академическое образование и продемонстрировала впечатляющий опыт работы в сфере образования. Арпана умеет разрабатывать и проверять планы уроков, учебные материалы, оценки, видеорассказы и сценарии.
Арпана умеет разрабатывать и проверять планы уроков, учебные материалы, оценки, видеорассказы и сценарии.
рабочих примеров алгебраических выражений — ChiliMath
Не существует единого метода или стратегии перевода математических фраз в алгебраические выражения. Пока вы помните основы, вы должны быть в состоянии справиться с более сложными. Просто убедитесь, что вы можете обосновать собственное алгебраическое выражение и, что более важно, что оно имеет для вас смысл. При необходимости обратитесь за помощью к своим учителям или сотрудничайте со своими одноклассниками, чтобы проверить свои ответы.
Чтобы развить ваши навыки написания алгебраических выражений, мы рассмотрим различные способы отображения каждой операции в виде слова или фразы в задаче. Четыре арифметических действия: сложение, вычитание, умножение и деление.
Ключевые слова для сложения
Ключевые слова для вычитания
Ключевые слова для умножения
Ключевые слова для деления
Пришло время рассмотреть некоторые примеры алгебраических выражений, чтобы попрактиковаться в их написании. Я делю примеры на две категории:
Я делю примеры на две категории:
Основные примеры алгебраических выражений
Пример 1: Напишите алгебраическое выражение для математической фразы «сумма числа и четырех».
Решение: Слово «сумма» сразу дает нам подсказку, которую мы собираемся добавить сюда. Обратите внимание, что мы хотим сложить две величины: одно неизвестное число и число 4. Поскольку нам неизвестно значение числа, мы можем использовать переменную для его представления. Вы можете использовать любые буквы алфавита. В этом случае давайте договоримся использовать y в качестве переменной.
Когда мы складываем переменную y и 4, мы получаем y + 4. Можно также написать ответ как 4 + y, потому что сложение является коммутативным, то есть изменение порядка сложения не меняет сумму.
Окончательный ответ: y+4.
Пример 2: Напишите алгебраическое выражение для математической фразы «10 умножить на число».
Решение: Ключевые слова «увеличено на» подразумевают сложение. Это означает, что к 10 было добавлено неизвестное число. Используя букву k в качестве переменной, мы можем перевести приведенное выше утверждение как 10 + k. Поскольку сложение коммутативно, мы можем переписать его как k + 10. Любой из двух ответов является правильным.
Окончательный ответ: k+10.
Пример 3: Напишите алгебраическое выражение для математической фразы «разность 1 и числа».
Решение: Слово «разность» предполагает, что мы собираемся вычитать. Кроме того, когда вы встречаете это математическое слово (разница), обязательно обратите внимание на порядок. Сначала идет число 1, затем неизвестное число идет вторым. Это означает, что число 1 является уменьшаемым, а неизвестное число — вычитаемым. Если мы решим использовать букву x в качестве нашей переменной, ответ станет 1 − x.
Окончательный ответ: 1 — х.
Пример 4 : Напишите алгебраическое выражение для математической фразы «число меньше 8».
Решение: Будьте очень осторожны при работе с ключевыми словами «меньше чем». Первое количество, которое идет перед ключевыми словами «меньше чем», которое является «числом», является вычитаемым. В то время как количество, которое идет после него, становится уменьшаемым.
Другими словами, мы собираемся вычесть неизвестное число из числа 8. Если мы выберем в качестве переменной букву а, мы получим 8 — а.
Окончательный ответ 8 — а.
Пример 5: Напишите алгебраическое выражение для математической фразы «произведение 5 и числа».
Решение : Чтобы найти произведение двух количеств или величин, нужно их перемножить. Выбрав букву m в качестве нашей переменной, алгебраическое выражение для этой математической фразы будет просто 5 m . Это означает 5 умножить на неизвестное число м .
Это означает 5 умножить на неизвестное число м .
Окончательный ответ: 5м.
Пример 6: Напишите алгебраическое выражение для математической фразы «дважды число».
Решение: Слово «дважды» означает, что мы собираемся что-то удвоить. В этом случае мы хотим удвоить неизвестное значение или количество. Пусть буква d будет неизвестным числом, удвоив его, мы получим алгебраическое выражение 2d.
Окончательный ответ 2d.
Пример 7: Напишите алгебраическое выражение для математической фразы «частное числа и 7».
Решение: Ключевое слово «частное» означает, что мы выполняем операцию деления. Мы разделим неизвестное число на 7. Выбрав букву w в качестве нашей переменной, математическая фраза выше может быть выражена как алгебраическое выражение ниже.
\LARGE{w \over 7}
Пример 8: Напишите алгебраическое выражение для математической фразы «отношение 10 и числа».
Решение: Точно так же слово «отношение» означает деление. Порядок здесь очень важен. Первая величина — это число 10, а вторая величина — это неизвестное число. Это означает, что 10 делится на неизвестное число. Пусть c будет неизвестным числом, алгебраическое выражение для приведенной выше математической фразы можно записать как
\LARGE{10 \over c}
Примеры алгебраических выражений, состоящих из нескольких частей
На этот раз мы рассмотрим еще несколько сложные математические фразы. Алгебраические выражения в этом разделе могут содержать две или более операций. Основные ключевые слова, которые мы выучили ранее, послужат основой, когда мы будем работать над более сложными математическими фразами, чтобы перевести их в алгебраические выражения.
Пример 1 : Напишите алгебраическое выражение для математической фразы «3 больше, чем удвоенное число».
Решение: Чтобы упростить понимание, мы разделим эту фразу на две части. Во-первых, признать, что у нас есть неизвестный номер. Мы можем представить его любыми буквами алфавита. Пусть неизвестное число будет переменной x. Диаграмма ниже должна помочь нам увидеть, что происходит на самом деле.
Во-первых, признать, что у нас есть неизвестный номер. Мы можем представить его любыми буквами алфавита. Пусть неизвестное число будет переменной x. Диаграмма ниже должна помочь нам увидеть, что происходит на самом деле.
Если подумать, существует неизвестное число, представленное переменной x, которая удваивается или умножается на 2. Каким бы ни было произведение, мы добавим к нему 3. Итак, наш окончательный ответ должен выглядеть так, как показано ниже.
Окончательный ответ: 2x+3.
Пример 2: Напишите алгебраическое выражение для математической фразы «разность половины числа и 10».
Решение: Предположим, что переменная y является неизвестным числом. Ключевое слово «разность» подсказывает нам, что мы собираемся выполнить вычитание. Здесь важно обратить внимание на порядок вычитания. После слова «разность» следует ожидать две величины. Первое — уменьшаемое, второе — вычитаемое. Взгляните на диаграмму ниже.
Ссылаясь на диаграмму, мы вычтем первую величину из второй величины. Окончательный ответ для математической фразы должен выглядеть примерно так:
Окончательный ответ для математической фразы должен выглядеть примерно так:
Пример 3: Напишите алгебраическое выражение для математической фразы «на 7 меньше, чем произведение числа и 6».
Решение: Мы знаем, что «меньше чем» предполагает операцию вычитания. Но здесь нам нужно быть немного осторожными, потому что важен порядок вычитания. Предположим, неизвестное число представлено переменной k. Давайте изобразим это на диаграмме, чтобы было понятно.
На самом деле, эту математическую фразу можно переписать как
«произведение числа и 6 минус 7»
«7 меньше» означает «минус 7″ к любой описываемой величине, которая в данном случае является » произведение числа и 6”. Вот окончательная интерпретация математической фразы в алгебраическом выражении:
6k-7
Пример 4: Напишите алгебраическое выражение для математической фразы «среднее число и 4».
Решение: Чтобы начать эту конкретную математическую фразу, мы должны сначала определить термин «среднее значение». Чтобы вычислить среднее или среднее двух или более чисел, сложите все числа, чтобы получить сумму, а затем разделите ее на количество записей или чисел. Если мы позволим m быть переменной для представления неизвестного числа, математическая фраза выше может быть выражена в алгебраических выражениях как,
Чтобы вычислить среднее или среднее двух или более чисел, сложите все числа, чтобы получить сумму, а затем разделите ее на количество записей или чисел. Если мы позволим m быть переменной для представления неизвестного числа, математическая фраза выше может быть выражена в алгебраических выражениях как,
\LARGE{{m + 4} \over 2}
Пример 5: Напишите алгебраическое выражение выражение для математической фразы «частное от 1 и 1 уменьшилось на число».
Решение: Ключевое слово «частное» означает, что мы будем делить. В данном случае мы хотим разделить число 1 на количество 1, уменьшенное на число. Ниже приведено алгебраическое выражение, которое может представлять математическую фразу выше. Пусть а неизвестное число.
Пример 6: Напишите алгебраическое выражение для математической фразы «треть квадрата числа, умноженная на 2».
Решение: Здесь происходит несколько вещей. Во-первых, часть фразы, в которой говорится «треть квадрата числа», можно интерпретировать как «квадрат числа, деленный на 3». Нам нужно будет увеличить неизвестное число на 2, а затем разделить его на 3. Предположим, что неизвестное число равно t, мы получаем
Во-первых, часть фразы, в которой говорится «треть квадрата числа», можно интерпретировать как «квадрат числа, деленный на 3». Нам нужно будет увеличить неизвестное число на 2, а затем разделить его на 3. Предположим, что неизвестное число равно t, мы получаем
Мы еще не закончили. Последний шаг, который нужно сделать, это добавить указанное выше количество на 2, чтобы включить оставшуюся часть фразы «увеличение на 2». Итак, вот окончательное представление данной математической фразы.
Вас также могут заинтересовать:
Алгебраические выражения
Алгебраические задачи на предложения
Алгебраическое представление: значение и примеры
Премьер-министр, вероятно, один из самых занятых людей в Великобритании быть везде одновременно. В случае, когда он не может присутствовать на мероприятии, он пришлет представителя. Человек не премьер-министр, а своего рода заместитель. Это похоже на то, что мы видим в алгебраических выражениях и уравнениях. Используемые переменные представляют собой реальное значение. Мы называем это алгебраическим представлением.
Используемые переменные представляют собой реальное значение. Мы называем это алгебраическим представлением.
Все, что связано с алгеброй, предполагает использование букв для обозначения чего-либо.
В этой статье мы рассмотрим значение алгебраического представления, алгебраическое представление геометрических преобразований, формул и функций, а также некоторые примеры их применения.
Алгебраическое представление означает
Алгебраическое представление предполагает использование переменных, чисел и символов для представления величин в уравнении или выражении.
Алгебраические представления описывают происходящее, не выражая его словами. Алгебраические представления могут применяться к разным вещам. Его можно применять для геометрических преобразований, для построения формул и представления функций.
Некоторые примеры алгебраических представлений , и .
Алгебраическое представление преобразований
Преобразование связано с геометрическим изменением математического объекта. Объект может быть геометрической формой, которая претерпевает трансформацию своего положения или размера. Различными формами преобразований являются перемещение, отражение, вращение, увеличение или их комбинация. Чтобы получить более глубокие знания о преобразованиях, ознакомьтесь с нашей статьей о преобразованиях.
Объект может быть геометрической формой, которая претерпевает трансформацию своего положения или размера. Различными формами преобразований являются перемещение, отражение, вращение, увеличение или их комбинация. Чтобы получить более глубокие знания о преобразованиях, ознакомьтесь с нашей статьей о преобразованиях.
Для алгебраического представления преобразований мы имеем дело с геометрическими фигурами, преобразуемыми по оси и.
Перевод
Перевод связан с движением s вверх, вниз, влево или вправо, или их комбинацией. Форма просто перемещается из одного положения в другое. Размер и форма остаются прежними, но позиция меняется на . Чтобы узнать больше о переводе, ознакомьтесь с нашей статьей о переводах.
Посмотрите на изображение ниже.
График преобразования перевода — StudySmarter Original
На этом изображении мы видим прямоугольник и прямоугольник. Мы будем считать этот последний прямоугольник результирующей фигурой, изображением, применяя перевод к первому прямоугольнику. Обратите внимание, что форма и размер фигуры остаются прежними, но положение отличается.
Обратите внимание, что форма и размер фигуры остаются прежними, но положение отличается.
Итак, как мы можем использовать алгебраическое представление в переводе? Давайте установим некоторые правила. Правила показывают, как изменяются координаты при перемещении фигуры.
Здесь могут происходить четыре различных движения; фигура может перемещаться вверх, вниз, влево и вправо по оси и .
Давайте начнем с пары и представим число единиц, на которое фигура должна переместиться по оси. Если фигура должна двигаться в правильном направлении по -оси, она будет . Если двигаться влево, то будет .
Пусть представляет количество единиц, на которое фигура должна переместиться по оси. Если изображение будет двигаться вверх, это будет . Если двигаться вниз, то будет .
So we have,
Translation | Rules |
Move right units | |
Move left units | |
Move up units | |
Единицы перемещения вниз |
Отражение
Отражение — это отражение фигуры по линии. Линия называется линия отражения или линия симметрии. Отражение также называют зеркальным отражением формы. В этом преобразовании форма позиции изменяется , но ее размер и форма остаются прежними. См. изображение ниже.
Линия называется линия отражения или линия симметрии. Отражение также называют зеркальным отражением формы. В этом преобразовании форма позиции изменяется , но ее размер и форма остаются прежними. См. изображение ниже.
График преобразования отражения — StudySmarter Original
На изображении выше мы можем видеть и. Мы будем считать первый треугольник изображением второго, применяя отражение по оси y.
Существуют правила, которые показывают, как меняются координаты при отражении фигуры. Способ изменения координат зависит от того, движется ли фигура вверх, вниз, влево или вправо. Мы увидим два простых отражения над осями.
Фигура отражается либо по -оси, либо по -оси, и при этом знаки координат меняются. Итак, если у вас есть координаты фигуры, и она отражается по оси -, вы должны умножить -координату на . Если он отражается по оси -, вы должны умножить -ось на .
Отражение | Правила |
Перемещение по оси | Умножьте координату на: |
Перемещение по оси | Умножьте координату на: |
.
 Врождение0
Врождение0Ротация
0. Когда фигура вращается вокруг оси, координаты меняются. И снова в этом преобразовании форма позиции
изменяется , но ее размер и форма остаются прежними. См. график ниже.График, показывающий преобразование вращения — StudySmarter Original
Некоторые правила помогут вам узнать, как будут изменяться координаты. Правила представлены в таблице ниже.
Вращение | Правила | |
по часовой стрелке | Switch координаты и умножение на один на один на один на один на один на один на один на один на один на один на один на один на один на один на один на один на один на один на один на один на: « | |
по часовой стрелке или против часовой стрелки | Умножение оба координируют на | . |
| Прямоугольник | ||
We’ve done the calculations and the co-ordinates of the reflected rectangle составляют:
Теперь построим график.
На графике выше показан прямоугольник и его отражение.
Давайте рассмотрим пример преобразования вращения.
Четырехугольник имеет вершины. Найдите вершины после поворота против часовой стрелки. Постройте график четырехугольника и его повернутого изображения.
Решение
Нам даны координаты четырехугольника. Четырехугольник нужно повернуть против часовой стрелки.
Вспомните, что правило вращения против часовой стрелки состоит в том, что вы меняете координаты и умножаете левую на .
Сделаем расчет в таблице.
| Quadrilateral | ||
We’ve сделал расчеты и вершины для повернутого четырехугольника.
Теперь построим график
На графике показан четырехугольник и его повернутое изображение
Рассмотрим несколько примеров алгебраических представлений в формулах.
Найдите площадь прямоугольника ниже.
Решение
Чтобы найти площадь прямоугольника, нам нужна формула. Формула:
где площадь
длина
ширина
Из рисунка выше
Давайте подставим формулу
Мы можем убрать знак умножения, и это будет означать то же самое .
Мы можем еще больше упростить, умножив каждый член в скобках на значение снаружи, и мы получим:
Площадь прямоугольника:
Возьмем другой пример.
Формула расчета простых процентов . представляет простые проценты. Найдите простые проценты, когда и .
Решение
Вопрос просит нас найти простые проценты. Нам дана формула простых процентов:
Нам также даны значения переменных в формуле.
Теперь нам нужно подставить значения, указанные в формуле.
Обратите внимание, что мы делим значение R на 100. Это потому, что оно в процентах.
Простые проценты .
Давайте рассмотрим несколько примеров алгебраического представления и формулы.
Учитывая , оцените следующее.
Решение
а.
Дана функция, которую мы попросили оценить.

 docx
docx Число называется действительной частью комплексного числа и имеет обозначение . Число называется мнимой частью комплексного числа и имеет обозначение .
Число называется действительной частью комплексного числа и имеет обозначение . Число называется мнимой частью комплексного числа и имеет обозначение . Конец отрезка есть число .
Конец отрезка есть число .
 Теперь мы знаем о компонентной форме вектора. Итак, хороший вопрос: «Можем ли мы использовать компонентную форму векторов для сложения векторов и умножения вектора на скаляр?»
Теперь мы знаем о компонентной форме вектора. Итак, хороший вопрос: «Можем ли мы использовать компонентную форму векторов для сложения векторов и умножения вектора на скаляр?» Эта диаграмма показывает, что конечной точкой \(\textbf{v} + \textbf{w}\) в стандартном положении является \((a + c, b + d)\), и поэтому
Эта диаграмма показывает, что конечной точкой \(\textbf{v} + \textbf{w}\) в стандартном положении является \((a + c, b + d)\), и поэтому

 Примером этого является подгонка кривой наименьших квадратов к набору данных, как это делают наши калькуляторы при вычислении кривой синусоидальной регрессии. Скалярный продукт полезен в таких ситуациях для поиска «наилучших» решений определенных типов проблем. Хотя мы не увидим этого в этом курсе, наличие наборов перпендикулярных векторов очень важно, поскольку позволяет выполнять быстрые и эффективные вычисления. Скалярное произведение векторов позволяет нам измерить угол между ними и, таким образом, определить, перпендикулярны ли векторы. Скалярное произведение имеет множество применений, например, для нахождения компонент сил, действующих в разных направлениях, в физике и технике. В этом разделе мы вводим и исследуем скалярные произведения.
Примером этого является подгонка кривой наименьших квадратов к набору данных, как это делают наши калькуляторы при вычислении кривой синусоидальной регрессии. Скалярный продукт полезен в таких ситуациях для поиска «наилучших» решений определенных типов проблем. Хотя мы не увидим этого в этом курсе, наличие наборов перпендикулярных векторов очень важно, поскольку позволяет выполнять быстрые и эффективные вычисления. Скалярное произведение векторов позволяет нам измерить угол между ними и, таким образом, определить, перпендикулярны ли векторы. Скалярное произведение имеет множество применений, например, для нахождения компонент сил, действующих в разных направлениях, в физике и технике. В этом разделе мы вводим и исследуем скалярные произведения. {2}} = \sqrt{u_{1}u_{1} + u_{2}u_{2}}\]
{2}} = \sqrt{u_{1}u_{1} + u_{2}u_{2}}\] Это связано со следующим результатом: 9\circ\)), затем
Это связано со следующим результатом: 9\circ\)), затем

 Однако важно отметить, что погода не всегда так сговорчива, как хотелось бы. Ветер не всегда дует точно в направлении гусеницы, поэтому датчик должен учитывать угол, который ветер образует с гусеницей.
Однако важно отметить, что погода не всегда так сговорчива, как хотелось бы. Ветер не всегда дует точно в направлении гусеницы, поэтому датчик должен учитывать угол, который ветер образует с гусеницей. {2}}\textbf{v}\] 9{2}}\textbf{v} = \dfrac{\textbf{u}\cdot \textbf{v}}{\textbf{v}\cdot \textbf{v}}\textbf{v}\]
{2}}\textbf{v}\] 9{2}}\textbf{v} = \dfrac{\textbf{u}\cdot \textbf{v}}{\textbf{v}\cdot \textbf{v}}\textbf{v}\] Рисунок \(\PageIndex{6}\). Проекция \(\textbf{u}\) , ортогональная \(\textbf{v}\), обозначенная \(\textbf{proj}_{\perp\textbf{v}}\textbf{u }\), это
Рисунок \(\PageIndex{6}\). Проекция \(\textbf{u}\) , ортогональная \(\textbf{v}\), обозначенная \(\textbf{proj}_{\perp\textbf{v}}\textbf{u }\), это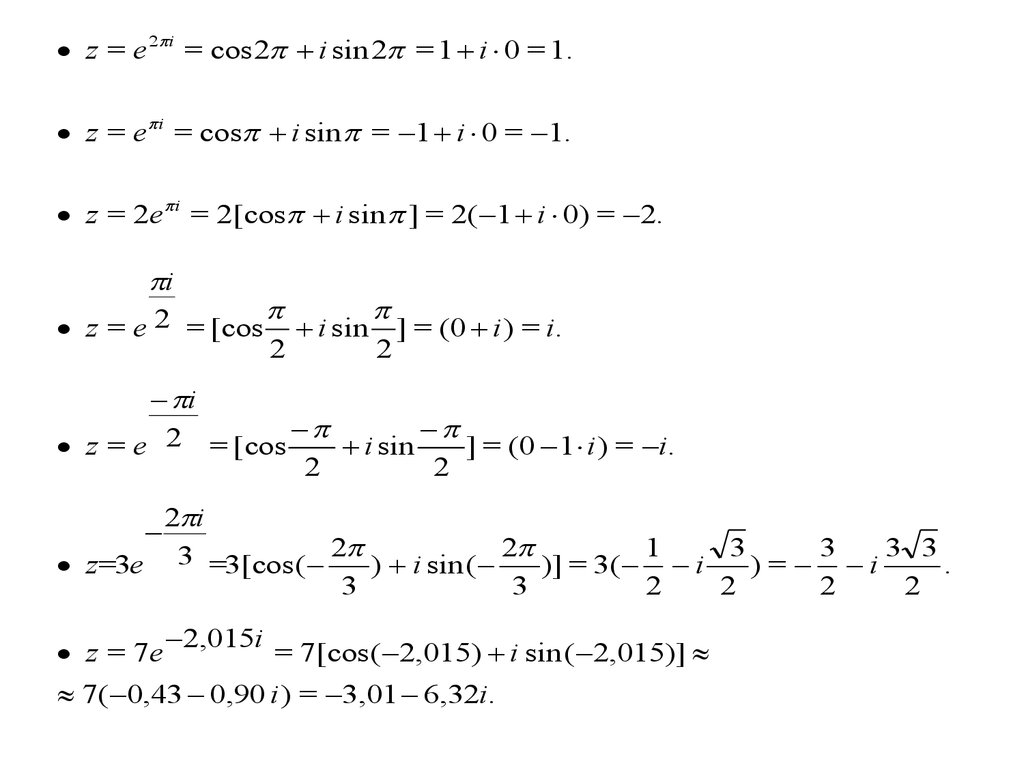 6
6 \) 9{2}}\textbf{w} = \dfrac{\textbf{v}\cdot \textbf{w}}{\textbf{w}\cdot \textbf{w}}\textbf{w}\]
\) 9{2}}\textbf{w} = \dfrac{\textbf{v}\cdot \textbf{w}}{\textbf{w}\cdot \textbf{w}}\textbf{w}\] gvsu.edu/books/12
gvsu.edu/books/12