§ 2. Формы комплексного числа
Существует три формы комплексного числа, так как различные операции над комплексными числами удобнее проводить с различными формами.
1. Алгебраическая форма: z = x + iy.
Пример 1. Найти действительную и мнимую части, модуль, аргумент комплексного числа z = 2 + 3i, сопряженное к нему и изобразить z и на комплексной плоскости.
Р ешение.
Действительная и мнимая части: Rez = x = 2, Imz = y = 3.
Модуль: .
Аргумент:
Сопряженное к z равно , тогда, если z = 2 + 3i, то сопряженное к нему равно .
Комплексному числу z = 2 + 3i соответствует
вектор ,
комплексному числу
соответствует вектор , z и
изображены на рис.
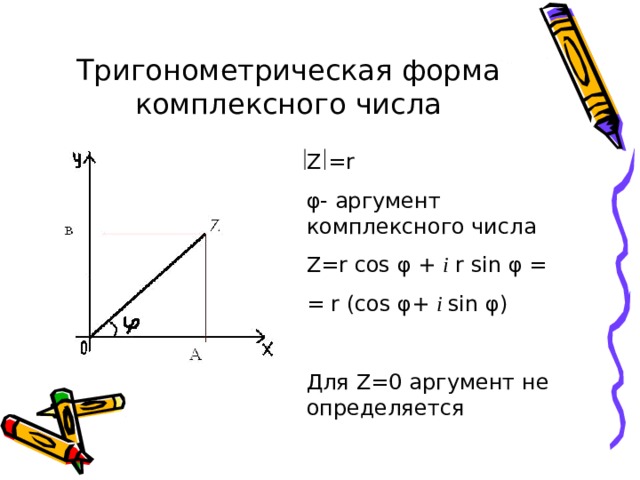
2. Тригонометрическая форма: .
И з рисунка 3 видно, что .
Если подставить данные выражения в алгебраическую форму, то получится комплексное число в тригонометрической форме:
z = x + iy = = .
Пример 2. Представить в алгебраической форме комплексное число . Найти к нему сопряженное.
Решение.
, отсюда .
или, что одно и то же .
3. Показательная форма:
Используя формулу Эйлера:
,
комплексное число можно записать в так называемой показательной форме:
z =
Примеры.
Пример 3. Представить в показательной форме комплексное число . Записать к нему сопряженное, найти модуль.
Решение.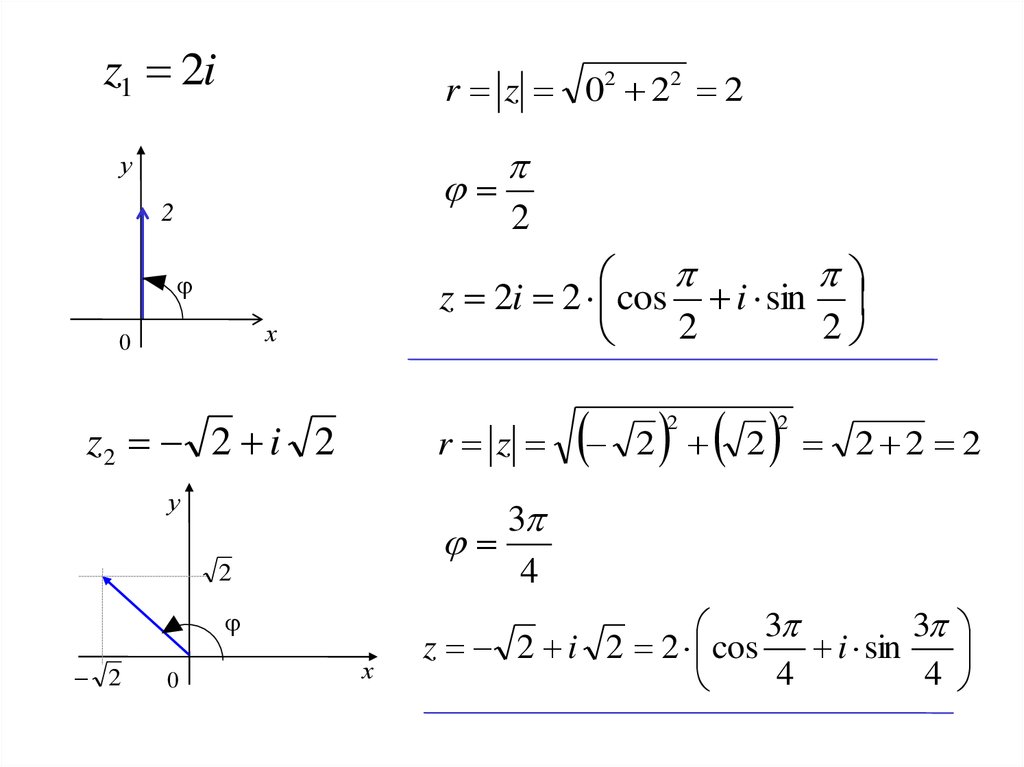
, отсюда , тогда , r = 4.
Пример 4. Дано комплексное число . Записать его в трех формах.
Решение.
Алгебраическая форма комплексного числа: .
, .
Тригонометрическая форма комплексного числа: .
Показательная форма комплексного числа: .
Определение 8. Уравнение определяет на плоскости Гаусса окружность с центром в точке О и радиусом, равным а.
Пояснение: – уравнение окружности.
Определение 9. Уравнение определяет на плоскости Гаусса окружность с центром в точке z0 и радиусом, равным а.
– уравнение окружности с центром в точке и радиусом, равным а.
Замечание.
Неравенство (
)
определяет множество точек верхней
полуплоскости.
Неравенство ( ) определяет множество точек нижней полуплоскости.
Неравенство (x > 0) определяет множество точек правой полуплоскости.
Неравенство (x < 0) определяет множество точек левой полуплоскости.
Пример 5. Изобразить на комплексной плоскости множество точек, задаваемых условиями 1) , 2) , 3) , 4) 5)
Решение.
1) – окружность с центром в точке О и радиусом равным 2 (рис. 4).
2) – окружность с центром в точке i и радиусом равным 1. (рис. 5).
3) часть плоскости за окружностью с центром
в точке О радиусом 2, включая саму
окружность. –
сектор между двумя лучами: В пересечении получается часть плоскости
за окружностью, включая саму окружность,
лежащая внутри сектора раствором в (рис.
6).
4) , т.е. – полоса между осью (Ох) и прямой y = 2, не включая данную прямую (рис. 7).
5) – данная область – кольцо между окружностями , причем последняя не принадлежит области. – сектор между двумя лучами: В пересечении получается область внутри кольца между двумя лучами, не включая внутреннюю окружность (рис. 8).
Тригонометрическая и показательная форма комплексного числа
О чем статья
Аргумент комплексного числа
Рассмотрим аргумент комплексного числа на примере. Пусть вектор изображает комплексное число (рис. 1). Аргументом числа называется любое из значений угла наклона вектора к оси :
, где .
Таким образом, у аргумента комплексного числа появляется бесконечное множество значений. Аргумент не определяется.
Рис. 1
Наименьшее за абсолютной величиной значение (то есть значение с интервалом ) называется главным значением аргумента комплексного числа и обозначается , поэтому .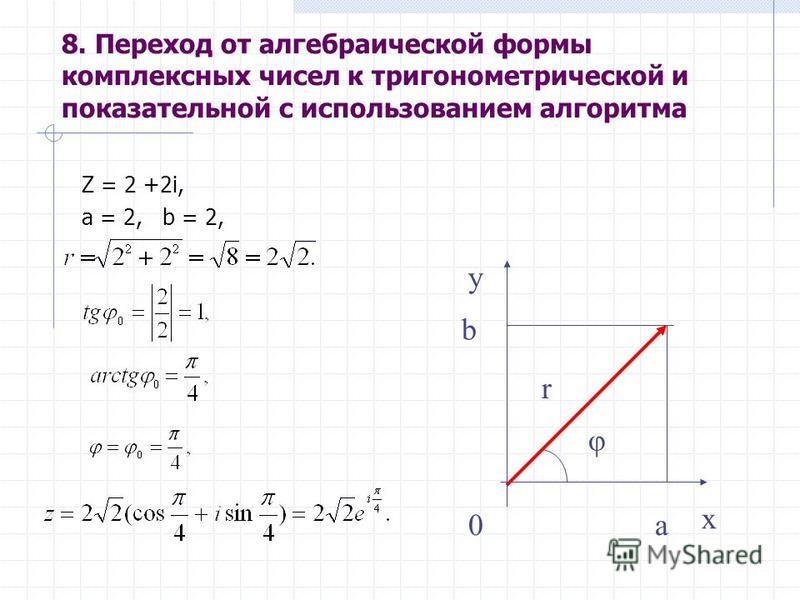
Вычисление аргумента
Вычисление аргумента знать необходимо, но сначала нужно отметить свойство: .
1) Аргумент действительного и чисто мнимого числа: если , тогда .
2) Аргумент любого числа можно находить по формуле:
(1)
В первой формуле, если четверти, во второй формуле, если четверти, а в третьей, если четверти.
Доведём последнюю формулу в случае, если изображается точкой во второй четверти (рис. 2). С . Так как тогда
Рис. 2
Другие случаи расположения числа на плоскости рассматриваются аналогично.
Если не требуется высокой точности, тогда аргумент комплексных чисел можно находить графическим способом. С этой целью стоит построить комплексные числа на миллиметровом листе и измерять соответствующий угол при помощи транспортира. Этот способ иногда используют для грубой проверки вычислений.
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов).
Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Тригонометрическая форма комплексного числа
Пусть известны модуль и аргумент комплексного числа (см. рис. 1).
– полярные координаты точки , которая изображает число ( если – полярная ось).
В случае размещения осей и , показанному на рисунке 1 известны формулы перехода от полярных к прямоугольным координатам точки , . Добавим эти равенства, умножив вторую часть на :
.
Последняя форма записи комплексного числа называется тригонометрической.
Как видим, чтобы найти тригонометрическую форму, достаточно вычислить модуль и аргумент комплексных чисел.
Показательная форма комплексного числа
Показательная форма комплексного числа в практике встречается реже, чем в тригонометрической форме, но всё же иногда встречается и поэтому, о ней необходимо знать хотя бы самое основное.
Пусть . Если число записать в тригонометрической форме , а потом применить формулу Эйлера , где – любое действительное число, получим так званую показательную форму комплексного числа:
.
Такая форма записи чисел позволяет использовать свойства экспоненты и поэтому удобна для разных преобразований.
Умножение, деление и возведение в степень комплексных чисел: если
, тогда
, ;
, где – целое.
Примеры решений
Пример 1
Задача
Записать в тригонометрической форме следующие числа: 1) , 2) , 3) .
Решение
1)
2) .
3) .
Ответ
1) .
2) .
3) .
Пример 2
Задача
Используя тригонометрическую форму, вычислить произведение чисел . Выяснить геометрическое содержание операции множества этих чисел.
Решение
, = ; , = ;
.
С геометрической точки зрения были выполнены следующие преобразования:
1) поворот вектора на угол – результат поворота;
2) сжатие (без изменения направления) вектора в два раза – результат умножения.
При помощи рисунка 3 в данном случае легко проверить, что .
Рис. 3
Ответ
Произведение чисел .
Пример 3
Задача
Записать в показательной форме число .
Решение
, .
Ответ
.
Пример 4
Задача
Используя показательную форму чисел , , . Вычислить приблизительно ( все вычисления выполнять с четырьмя знаками после запятой). Для контроля найти точно значение , выполняя вычисления в алгебраической форме.
Решение
Находим квадраты модулей и аргументы (в градусах) данных чисел: , , ;
,
,
.
Выполняя действия над числами в показательной форме, получаем:
.
К алгебраической форме записи числа переходим при помощи формулы Эйлера:
.
Контроль
Выполняем действия в алгебраической форме:
.
Средняя оценка 5 / 5. Количество оценок: 1
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
7256
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Видео с вопросами: Преобразование комплексных чисел из алгебраической формы в полярную форму
Стенограмма видео
Учитывая, что 𝑍 равно шести корням из двух минус шесть корней из двух 𝑖, запишите 𝑍 в тригонометрической форме.
В этом вопросе нам дано комплексное число 𝑍, записанное в алгебраической форме. Это форма 𝑎 плюс 𝑏𝑖, где 𝑎 и 𝑏 — действительные числа. И нам нужно преобразовать это комплексное число в тригонометрическую форму. Итак, начнем с того, что вспомним, что мы подразумеваем под тригонометрической формой комплексного числа. Это также известно как полярная форма. Это форма 𝑟, умноженная на cos 𝜃 плюс 𝑖 sin 𝜃, где значение 𝑟 — величина 𝑍, а 𝜃 — аргумент 𝑍. Следовательно, чтобы записать 𝑍 в тригонометрической форме, нам нужно найти его величину и аргумент.
Начнем с определения величины 𝑍. Напомним, что мы можем найти величину комплексного числа, записанного в алгебраической форме, извлекая квадратный корень из суммы квадратов его действительной и мнимой частей. Другими словами, величина 𝑎 плюс 𝑏𝑖 для действительных чисел 𝑎 и 𝑏 равна квадратному корню из 𝑎 в квадрате плюс 𝑏 в квадрате. Применяя это к 𝑍, мы получаем, что величина 𝑍 равна квадратному корню из корня из шести в квадрате из двух плюс отрицательный корень из шести в квадрате.
И тогда мы можем вычислить это выражение. Шесть корней из двух в квадрате равно 72. Таким образом, величина 𝑍 равна корню 72 плюс 72, что является квадратным корнем из 144, который, как мы можем вычислить, равен 12. И это значение 𝑟 в тригонометрической форме 𝑍.
Далее нам нужно определить аргумент 𝑍. Мы сделаем это, нарисовав 𝑍 на диаграмме Аргана. Помните, что для отображения 𝑍 на диаграмме Аргана его 𝑥-координата будет реальной частью 𝑍, а 𝑦-координата будет мнимой частью 𝑍. В этом случае его 𝑥-координата будет равна шести корням из двух, а 𝑦-координата будет отрицательным шести корням из двух. А поскольку его 𝑥-координата положительна, а 𝑦-координата отрицательна, 𝑍 лежит в четвертом квадранте диаграммы Аргана. Мы хотим использовать это, чтобы определить аргумент 𝑍. Помните, что аргумент 𝑍 — это угол, который отрезок линии от 𝑍 до начала координат на диаграмме Аргана образует с положительной действительной осью, измеренной против часовой стрелки.
Мы можем определить этот угол, построив следующий прямоугольный треугольник.
И назовем меру этого угла в нашем прямоугольном треугольнике 𝜑. Тогда мы можем видеть, что в этом прямоугольном треугольнике сторона, противоположная углу 𝜑, имеет длину шесть корней два, а сторона, примыкающая к углу 𝜑, также имеет длину шесть корней два. Следовательно, используя тригонометрию прямоугольного треугольника, тангенс 𝜑 равен шести корням из двух над шестью корнями из двух. Затем мы можем оценить это для 𝜑. Во-первых, шесть корней два больше шести корней два равно единице, и мы знаем, что обратный тангенс единицы равен 𝜋 четырем. Итак, 𝜑 равно 𝜋 на четыре. Если мы затем назовем аргумент 𝑍 𝜃, мы увидим, что мера 𝜃 и мера 𝜑 складываются в один полный оборот. Это два 𝜋.
Следовательно, аргумент 𝑍 равен двум 𝜋 минус 𝜋 на четыре, что, как мы можем вычислить, равно семи 𝜋 на четыре. А это значение 𝜃 в тригонометрической форме нашего комплексного числа. И прежде чем мы подставим эти значения в нашу тригонометрическую форму, стоит отметить одну вещь. Мы могли бы также измерить аргумент 𝑍 по часовой стрелке от положительной действительной оси.