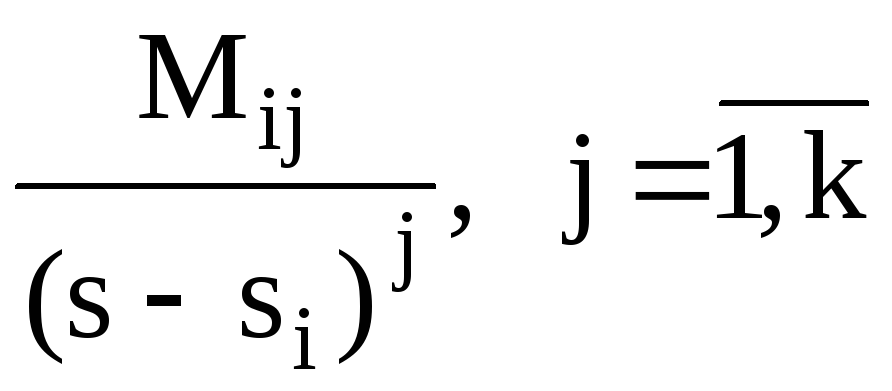Преобразование лапласа калькулятор онлайн: Преобразование Лапласа онлайн

Передаточная функция для системы с замкнутым и разомкнутым контуром Калькулятор

✖Выход системы — это информация, производимая системой на определенном входе.ⓘ Выход системы [Cs]			+10% -10%
✖Ввод системы — это то, что мы вводим или вводим в систему для достижения результата.ⓘ Ввод системы [Rs]			+10% -10%

✖Передаточная функция электронного компонента или компонента системы управления представляет собой математическую функцию, которая теоретически моделирует выход устройства для каждого возможного входа.ⓘ Передаточная функция для системы с замкнутым и разомкнутым контуром [Gs]

⎘ копия

👎

Формула

сбросить

👍

Передаточная функция для системы с замкнутым и разомкнутым контуром Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Выход системы: 20 —> Конверсия не требуется
Ввод системы: 48 —> Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

0.416666666666667 —> Конверсия не требуется

< 10+ Основы системы управления Калькуляторы

Передаточная функция для системы с замкнутым и разомкнутым контуром формула

Функция передачи = Выход системы/Ввод системы
G_s = C_s/R_s

Что такое передаточная функция?

Передаточная функция системы управления определяется как отношение преобразования Лапласа выходной переменной к преобразованию Лапласа входной переменной при условии, что все начальные условия равны нулю. Блок-схема — это визуализация системы управления, которая использует блоки для представления передаточной функции и стрелки, которые представляют различные входные и выходные сигналы. Для любой системы управления существует эталонный вход, известный как возбуждение или причина, который действует через операцию передачи (то есть передаточную функцию), чтобы произвести эффект, приводящий к управляемому выходу или ответу.

Share

Copied!

математика

Операционное исчисление

Преобразование Лапласа.

Рассмотрим функцию действительного переменного , определенную при . Будем также считать, что функция — кусочно-непрерывная, т.е. в любом конечном интервале она имеет конечное число точек разрыва первого рода, и определена на бесконечном интервале , но при .

Будем считать, что функция ограничена условием:

Рассмотрим функцию

где – комплексное число.

Определение. Функция называется изображением Лапласа

функции .

Также функцию называют – изображением или преобразованием Лапласа.

Обозначается

При этом функция называется начальной функцией или оригиналом, а процесс нахождения оригинала по известному изображению называется операционным исчислением.

Теорема. (Теорема единственности) Если две непрерывнные функции и имеют одно и то же – изображение , то они тождественно равны.

Определение. Функцией Хевисайда называется функция

Таблица изображений некоторых функций.

Для большинства функций изображение находится непосредственным интегрированием.

Пример. Найти изображение функции .

Для многих функций изображения посчитаны и приведены в соответствующих таблицах.

№	f(t)	F(p)	№	f(t)	F(p)
1	1		5
2			6
3			7
4			8

Свойства изображений.

Если , то справедливы следующие свойства:

1) Свойство подобия.

Пример.

2) Свойство линейности.

Пример.

3) Смещение изображения.

Пример.

4) Дифференцирование изображения.

Пример.

5) Дифференцирование оригинала.

6) Интегрирование изображения.

(Справедливо при условии, что интеграл сходится)

Пример.

7) Интегрирование оригинала.

Пример.

Теоремы свертки и запаздывания.

Теорема. (теорема запаздывания) Если f(t) = 0 при t < 0, то справедлива формула

где t₀ – некоторая точка.

Пример.

Определение. Выражение называется сверткой функций f₁(t) и f₂(t) и обозначается f₁ f₂.

Теорема. (теорема свертки) Преобразование Лапласа от свертки равно произведению преобразований Лапласа от функций f₁(t

) и f₂(t) .

Теорема. (Интеграл Дюамеля). Если , то верно равенство

Для нахождения изображений различных функций наряду с непосредственным интегрированием применяются приведенные выше теоремы и свойства.

Пример. Найти изображение функции .

;

Восстановление оригинала по данному изображению

Решение задач на отыскание оригиналов по их изображениям вызывает определенные трудности, так как при этом необходимо использование таблиц изображений в «обратном» порядке, что требует в свою очередь некоторой изобретательности. Как правило, данное изображение путем тех или иных алгебраических преобразований приводится к «табличному» изображению или сумме «табличных» изображений. При этом, в случае необходимости, используются: простейшие теоремы операционного исчисления; смещения и запаздывания; известный метод разложения правильной рациональной дроби на сумму простейших дробей.

Примеры

1.

;

.

2.

,

По теореме запаздывания: .

3. .

4.

;

Теорема разложения

Теорема: Если изображение функции представляет собой дробь , знаменатель которой имеет только простые корни , то оригинал имеет следующий вид: .

Операционное исчисление используется как для нахождения значений интегралов, так и для решения дифференциальных и интегральных уравнений.

Пусть дано линейное дифференциальное уравнение с постоянными коэффициентами.

Требуется найти решение этого дифференциального уравнения, удовлетворяющее начальным условиям:

Если функция является решением этого дифференциального уравнения, то оно обращает исходное уравнение в тождество, значит функция, стоящая в левой части уравнения и функция имеет (по теореме единственности) одно и то же изображение Лапласа.

Из теоремы о дифференцировании оригинала {} можно сделать вывод, что

Тогда

Обозначим

Получаем:

Это уравнение называется вспомогательным (изображающим) или операторным уравнением.

Отсюда получаем изображение , а по нему и искомую функцию x(t).

Изображение получаем в виде:

Где

Этот многочлен зависит от начальных условий. Если эти условия нулевые, то многочлен равен нулю, и формула принимает вид:

Рассмотрим применение этого метода на примерах.

Пример. Решить уравнение

Изображение искомой функции будем искать в виде:

Находим оригинал, т.е. искомую функцию:

Контрольная работа №1

(номер варианта определяется по последней цифре номера зачетной книжки)

Задача 1. Найти функции-изображения для данных функций-оригиналов.

1.1. .

1. 2. .

1.3.

1.4.

1.5.

1.6.

1.7.

1.8.

1.9.

1.10.

Задача 2. По данных функций-изображений найти функции-оригиналы.

2.1. ; .

2.2. ;

2.3. ; .

2.4. ; .

2.5. ; .

2.6. ;

2.7. ; .

2.8. ;

2.9. ; .

2.10. ;

Задача 3. Решить дифференциальное уравнение и систему дифференциальных уравнений методом операционного исчисления.

3.1. ;

3.2. ;

3.3. ;

3.4. ;

3.5. ;

3.6. ;

3. 7. ;

3.8. ;

3.9. ;

3.10. ;

7

Калькулятор преобразования Лапласа

Калькулятор преобразования Лапласа с шагами

Калькулятор преобразования Лапласа используется для преобразования функции вещественной переменной в функцию комплексного значения. Этот калькулятор Лапласа обеспечивает пошаговое решение данной функции.

Используя наш интегральный калькулятор Лапласа, вы также можете получить дифференцирование и интегрирование комплекснозначной функции.

Как работает калькулятор преобразования Лапласа?

Выполните следующие шаги, чтобы преобразовать функцию с действительным знаком.

•    Введите функцию в поле ввода.

•    Используйте значок на клавиатуре для ввода математических символов.

•    Нажмите кнопку вычислить , чтобы получить результат.

•    Нажмите кнопку показать еще , чтобы просмотреть решение с пошаговыми инструкциями.

•    Чтобы ввести другой ввод, нажмите кнопку сброса .

Что такое преобразование Лапласа?

Преобразование Лапласа — это метод преобразования заданной функции в некоторую другую функцию s . Это несобственный интеграл от нуля до бесконечности от e до минус st умножить на f от t относительно t . Обозначение преобразования Лапласа представляет собой L-подобный символ, используемый для преобразования одной функции в другую.

\(L\left\{f\left(t\right)\right\}=F\left(s\right)\)

Преобразование Лапласа преобразует заданную вещественную функцию в комплекснозначную функцию путем интегрирования функции. 92F\left(s\right)-s f\left(0\right)−f′\left(0\right)\)

Ссылки

• Преобразования Лапласа введение | дифференциальные уравнения (видео). Сформируйте Академию Хана.
• Таблица преобразований Лапласа | Tutorial.math.lumar.edu (nd)

Калькулятор преобразования Лапласа | Преобразование с помощью калькулятора Лапласа

Введение в Калькулятор преобразования Лапласа

Калькулятор преобразования Лапласа — это онлайн-инструмент, используемый для отображения преобразования функции переменной в комплексную переменную. Калькулятор интеграла Лапласа делает расчет точным и быстрым и изменяет интеграл в дробях. Этот калькулятор представляет собой бесплатный онлайн-инструмент для преобразования простых переменных в сложные.

Что такое калькулятор Лапласа с шагами?

Калькулятор преобразования Лапласа с шагами основан на методе преобразования Лапласа, который используется для решения дифференциальных уравнений, когда для переменной условия заданы нулевыми. Это бесплатный онлайн-инструмент, который быстро преобразует сложные функции для вычисления преобразования Лапласа онлайн.

Формула, используемая Калькулятором преобразования Лапласа

Каждая концепция математики, даже исчисление, работает по определенной формуле для их расчета.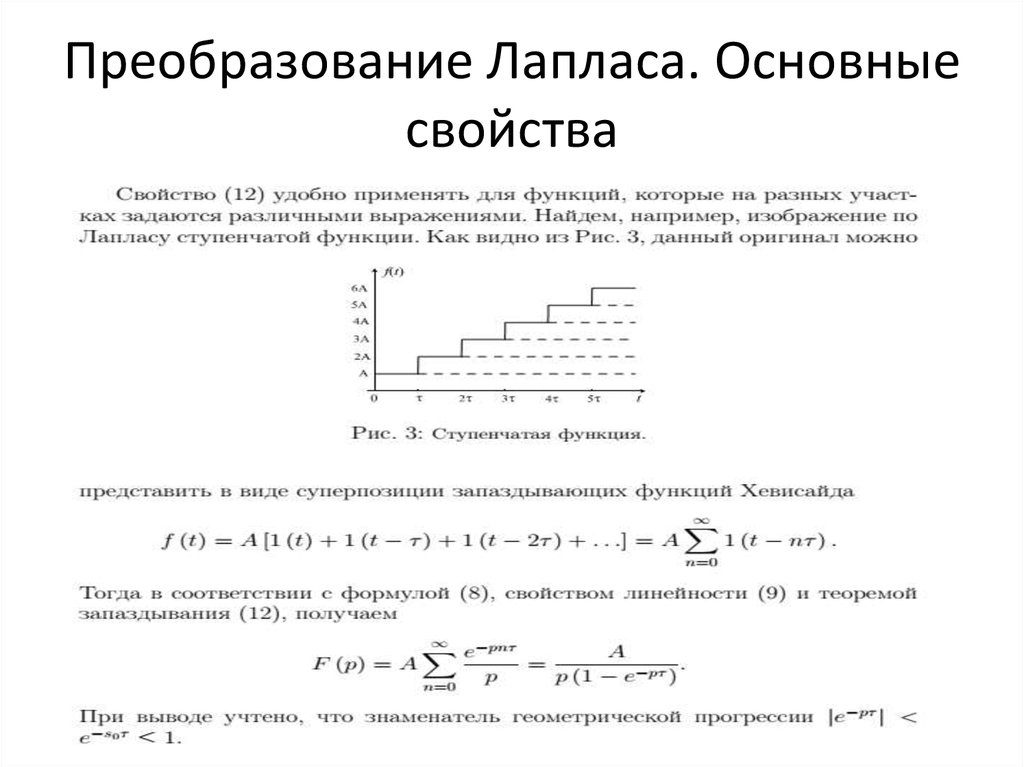 Решение преобразования Лапласа — довольно сложная концепция в изучении исчисления. Но ученый с большим исследованием предоставил нам формулу, которая поможет нам легко понять эту концепцию. Формула, используемая этим калькулятором, выглядит следующим образом: 9{-й} \;.\; дт $$

Где
L(s) = преобразование Лапласа
s = комплексное число t = действительное число >= 0
t’ = первая производная функции f(t)

Как онлайн-калькулятор преобразования Лапласа решает проблемы?

Онлайн-калькулятор Лапласа использует вышеупомянутую формулу для решения задач с пошаговым решением. Давайте разберемся с примерами.

Пример: Расчет преобразования Лапласа 9{-As}}{s} \right] $$ $$ \mathcal L \{ 1 \} \;=\; \frac{1}{s} , \text{для всех s>0} $$

Как работает решатель преобразования Лапласа?

Калькулятор преобразования Лапласа — это простой в использовании инструмент. Он может преобразовать функцию реальной переменной в функцию сложной переменной, выполнив следующие шаги. Ниже приведен способ использования этого калькулятора для получения точных результатов:

Шаг 1: Прежде всего, введите функцию, переменную функции и переменную преобразования в необходимое поле ввода.

Шаг 2: Теперь нажмите кнопку «Рассчитать», чтобы получить интегральное преобразование переменной с пошаговыми вычислениями.

Шаг 3: Результат будет отображаться на экране вашего окна.

Шаг 4: Чтобы рассчитать новую переменную, сначала очистите предыдущую историю и введите новую переменную в поле ввода.

Как найти калькулятор интеграла Лапласа?

Чтобы найти калькулятор кусочного преобразования Лапласа с шагами преобразования простой переменной в сложную, выполните следующие шаги;

Прежде всего, откройте главный экран браузера по умолчанию.

• Введите калькулятор преобразования Лапласа онлайн или калькулятор Лапласа в строку поиска.
• Затем дождитесь результатов поиска.
• Теперь выберите Интегральный калькулятор из предложений Google.
• И вы получите калькулятор уравнения Лапласа.

Открыв это приложение с сайта, щелкните онлайн-калькулятор кусочного преобразования Лапласа для преобразования вашей задачи. Теперь добавьте переменные в необходимые поля, чтобы получить комплексные переменные.

Преимущества калькулятора уравнения Лапласа

Решатель преобразования Лапласа имеет удивительные преимущества для пользователей и студентов. Калькулятор преобразования Лапласа шаг за шагом разрабатывает решение и обеспечивает точное руководство по преобразованию переменных в функцию комплексной переменной. Этот калькулятор Лапласа с шагами бесплатен и доступен в Интернете. Он предоставляет пользователям бесплатные услуги без абонентской платы и обеспечивает точное преобразование переменных. Калькулятор дифференциального уравнения Лапласа с шагами имеет следующие преимущества:

• Решатель Лапласа с шагами позволяет сэкономить время.
• Этот онлайн-калькулятор используется для преобразования обыкновенного дифференциального уравнения (ОДУ) в алгебраическое выражение, потому что решить алгебраическую форму проще, чем обыкновенное дифференциальное уравнение.
• Это надежный инструмент.
• Дает точное преобразование.
• Этот калькулятор быстрее и проще в использовании.
• Дружественный интерфейс для пользователей.

Часто задаваемые вопросы

Почему Лаплас лучше, чем Фурье?

Преобразования Лапласа могут фиксировать переходное поведение систем, например, в системе ODE. Преобразования Фурье фиксируют только стационарное поведение, т. е. ряды Фурье. По мере преобразования Лапласа, чтобы дать вам широкую перспективу мышления в сложных частотных пространствах, что может быть немного неудобно, и работать с использованием алгебраических формул, а не просто чисел.

Что такое преобразование Лапласа числа 1?

Преобразование Лапласа для ввода единичного шага начинается в момент времени t=0, возрастает до постоянного значения 1 и имеет преобразование Лапласа 1/с. Одиночный/единичный импульсный вход, который начинается в момент времени t=0 и возрастает до значения 1, имеет преобразование Лапласа, равное 1.