Окружность. Свойства отрезков пересекающихся хорд, секущих и касательных
Цель: повысить мотивацию к обучению; развивать вычислительные навыки, сообразительность, умение работать в команде.
Ход занятия
Актуализация знаний. Сегодня мы продолжим говорить об окружности. Позвольте напомнить определение окружности: что называется окружностью?
Слайд 2
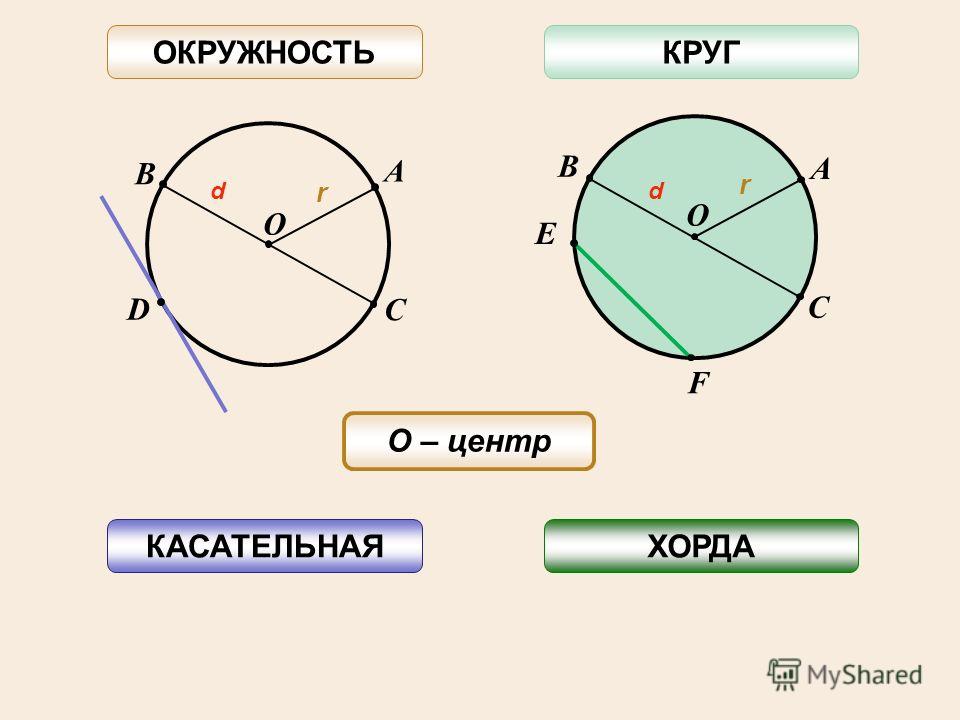
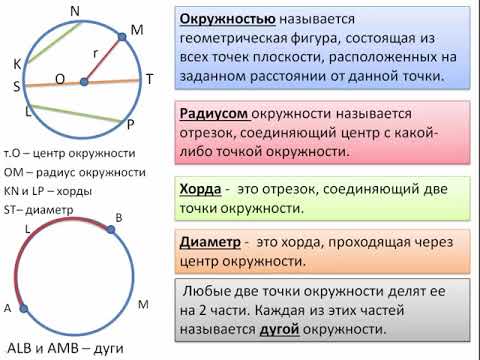
Окружность — это линия, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от одной точки плоскости, называемой центром окружности.
На слайде изображена окружность, отмечен ее
центр — точка О, проведены два отрезка: ОА и СВ.
Отрезок ОА соединяет центр окружности с точкой
на окружности. Он называется РАДИУСОМ (по-латыни
radius — “спица в колесе”). Отрезок СВ соединяет
две точки окружности и проходит через ее центр.
Это диаметр окружности (в переводе с греческого
– “поперечник”).
Также нам понадобится определение хорды окружности — это отрезок, соединяющий две точки окружности (на рисунке – хорда DE).
Давайте выясним вопрос о взаимном расположении прямой и окружности.
Слайд 3
Следующий вопрос и он будет основным: выяснить свойства, которыми обладают пересекающиеся хорды, секущие и касательные.
Слайд 4
Доказывать эти свойства вы будете на уроках математики, а наша задача научиться применять эти свойства при решении задач, так как они находят широкое применение на экзаменах и в форме ЕГЭ, и в форме ГИА.
Задание для команд.
- Изобразить и записать свойство пересекающихся в точке Р хорд КМ и NF.
- Изобразить и записать свойство касательной КМ и секущей КF.
- Изобразить и записать свойство секущих КМ и МF.
Далее продолжим работать в парах над решением простейших задач по применению этих свойств:
Используя данные на рисунке, найдите х.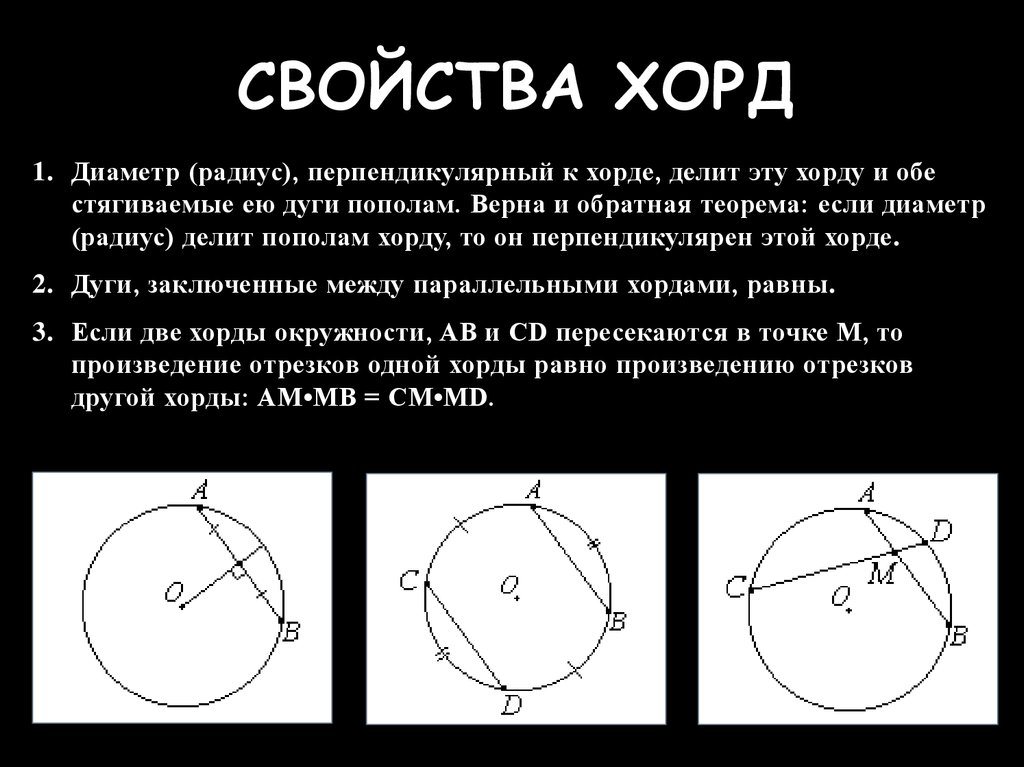 Слайд
5–6
Слайд
5–6
Кто быстрее, правильней. С последующим обсуждением и проверкой решения всех задач. Отвечающие зарабатывают для своей команды поощрительные баллы.
Ну, а теперь приступим к решению более серьезных задач. Вашему вниманию предлагается три блока: пересекающиеся хорды, касательная и секущая, две секущие. Подробным образом разберем решение по одной задачи из каждого блока.
(Разбирается решение с подробной записью №4, №7, №12)
2. Практикум по решению задач
а) Пересекающиеся хорды
1. E – точка пересечения хорд AB и CD. AE=4, AB=10, СE:ED=1:6. Найти CD.
Решение:
2. E – точка пересечения хорд AB и CD. AB=17, CD=18, ED=2CE. Найти AE и BE.
Решение:
3. E – точка пересечения хорд AB и CD. AB=10, CD=11, BE=CE+1. Найти CE.
Решение:
4. E – точка пересечения хорд AB и CD. ED=2AE, CE=DE-1, BE=10.
Найти CD.
E – точка пересечения хорд AB и CD. ED=2AE, CE=DE-1, BE=10.
Найти CD.
Решение:
Ответы:
- 14
- 8;9
- 3
- 11
б) Касательная и секущая
5. Из одной точки проведены к окружности касательная и секущая. Касательная равна 6, секущая – 18. Определить внутренний отрезок секущей.
Решение:
6. Из одной точки проведены к окружности касательная и секущая. Найти касательную, если известно, что она меньше внутреннего отрезка секущей на 4 и больше внешнего отрезка на 4.
Решение:
7. Из одной точки проведены к окружности
касательная и секущая. Найти секущую, если
известно, что внутренний её отрезок относится к
внешнему, как 3:1, а длина касательной равна 12.
Решение:
8. Из одной точки проведены к окружности касательная и секущая. Найти внешний отрезок, секущей, если известно, что внутренний её отрезок 12, а длина касательной 8.
Решение:
9. Касательная и секущая, исходящие из одной точки, соответственно равны 12 и 24. Определить радиус окружности, если секущая удалена от центра на 12.
Решение:
Ответы:
- 16
- 8
- 24
- 4
- 15
в) Две секущие
10. Из одной точки проведены к окружности две
секущие, внутренние отрезки которых
соответственно равны 8 и 16. Внешний отрезок
второй секущей на 1 меньше внешнего отрезка
первой. Найти длину каждой секущей.
Найти длину каждой секущей.
Решение:
11. Из одной точки проведены к окружности две секущие. Внешний отрезок первой секущей относится к своему внутреннему, как 1:3. Внешний отрезок второй секущей на 1 меньше внешнего отрезка первой и относится к своему внутреннему отрезку, как 1:8. Найти длину каждой секущей.
Решение:
12. Через точку А, которая находится вне окружности на расстоянии 7 от её центра, проведен прямая, пересекающая окружность в точках В и С. Найдите длину радиуса окружности, если АВ=3, ВС=5.
Решение:
13. Из точки А проведены к окружности секущая длиной 12 см и касательная, составляющая внутреннего отрезка секущей. Найдите длину касательной.
Решение:
Ответы:
- 10,5; 17,5
- 12;18
- 5
- 6
3.
Считаю, что вы обладаете достаточным запасом знаний, чтобы отправится в небольшое путешествие по лабиринтам вашего интеллекта, посетив следующие станции:
- Соображай-ка!
- Решай-ка!
- Отвечай-ка!
На станции можно находиться не более 6 минут. За каждое верное решение задачи команда получает поощрительные баллы.
Командам вручаются маршрутные листы:
Маршрутный лист
| Станция | Номера задач | Отметка о решении |
| Решай-ка! | №1, №3 | |
| Соображай-ка! | №5, №8 | |
| Отвечай-ка! | №10, №11 |
| Станция | Номера задач | Отметка о решении |
| Соображай-ка! | №5, №8 | |
| Отвечай-ка! | №10, №11 | |
| Решай-ка! | №1, №3 |
| Станция | Номера задач | Отметка о решении |
| Соображай-ка! | №5, №8 | |
| Отвечай-ка! | №10, №11 | |
| Решай-ка! | №1, №3 |
4. Подведение итогов
Подведение итогов
Хотелось бы подвести итоги нашего занятия:
Помимо новых знаний надеюсь, вы лучше познакомились друг с другом, приобрели опыт работы в команде. А как вы думаете, полученные знания находят где-то применение в жизни?
Поэт Г. Лонгфелло был еще и математиком. Наверное, поэтому яркие образы, украшающие математические понятия, которые он использовал в своем романе “Каванг”, позволяют запечатлеть на всю жизнь некоторые теоремы и их применение. Читаем в романе следующую задачу:
“Лилия, на одну пядь поднимавшаяся над поверхностью воды, под порывом свежего ветра коснулась поверхности озера в двух локтях от прежнего места; исходя из этого требовалось определить глубину озера” (1 пядь равна 10 дюймам, 2 локтя – 21 дюйму).
А решается эта задача на основе свойства пересекающихся хорд. Посмотрите на рисунок, и станет ясно, как находится глубина озера.
Решение:
21•21=10•(2х+10)
441=20х+100
20х=341
Х=17,05
Открытая Математика.
 Планиметия. Окружность, отрезок и прямая
Планиметия. Окружность, отрезок и прямаяОкружность, отрезок и прямая
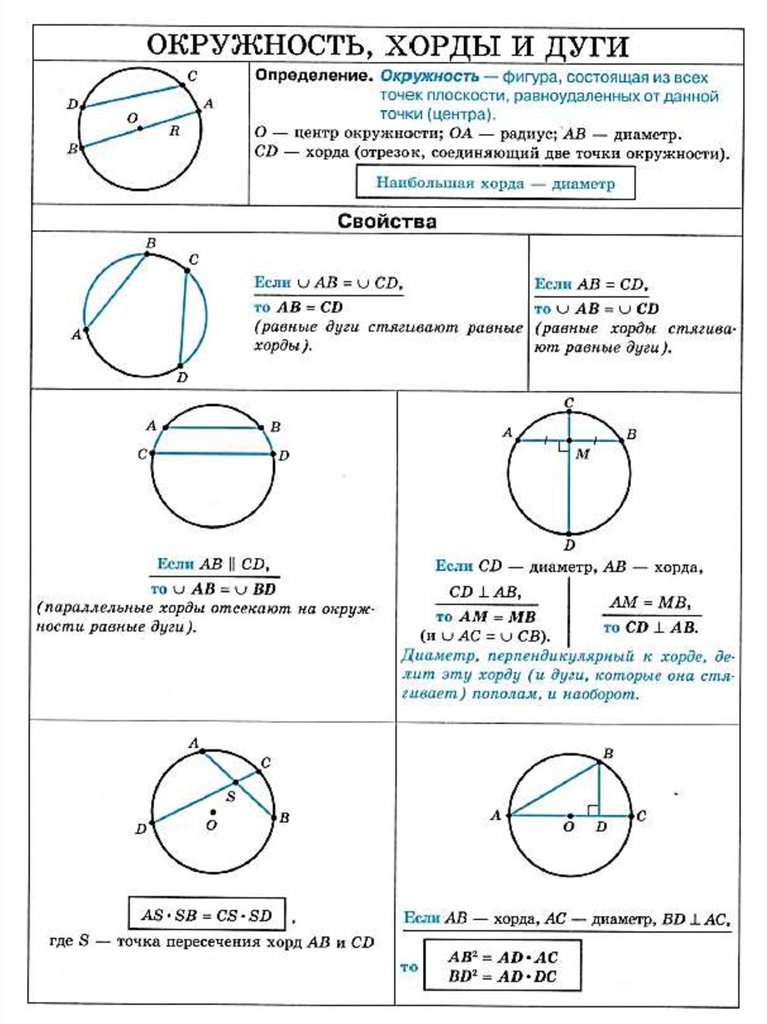
Окружностью называется геометрическая фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки плоскости. Эта точка называется центром окружности. Отрезок, соединяющий любую точку окружности с её центром, а также его длина, называется радиусом окружности.
ОкружностьОкружность разбивает плоскость на две части. Одной из них принадлежат все точки плоскости расстояние от которых до центра окружности меньше или равно её радиуса. Эта часть плоскости называется кругом. Про окружность при этом говорят как о границе круга, а её радиус считается также радиусом круга. О точках плоскости, не принадлежащих кругу, говорят как о точках, лежащих вне окружности. Очевидно, что расстояние до каждой такой точки от центра окружности больше её радиуса.
Определение окружности позволяет проиллюстрировать понятие геометрического места точек.
Геометрическим местом точек (ГМТ) называется совокупность таких и только таких точек плоскости, которые обладают заданным свойством.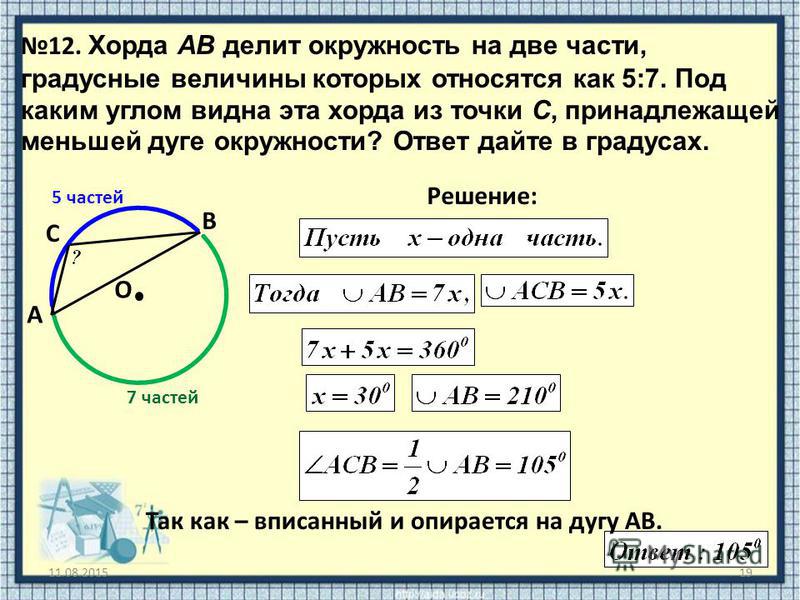
В соответствии с этим определением окружность – это геометрическое место точек плоскости, равноудаленных от заданной точки. Действительно, все точки окружности и только они обладают тем свойством, что лежат на расстоянии радиуса от её центра.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром.
Хорда и диаметрПрямая, имеющая единственную общую точку с окружностью, называется касательной, а их общая точка – точкой касания.
Pадиус, проведённый в точку касания, перпендикулярен касательной.
Пусть ω (O; R) – данная окружность, прямая a касается её в точке P. Пусть радиус OP не перпендикулярен к a. Проведём из точки O перпендикуляр OD к касательной. По определению касательной, все её точки, отличные от точки P, и, в частности, точка D лежат вне окружности.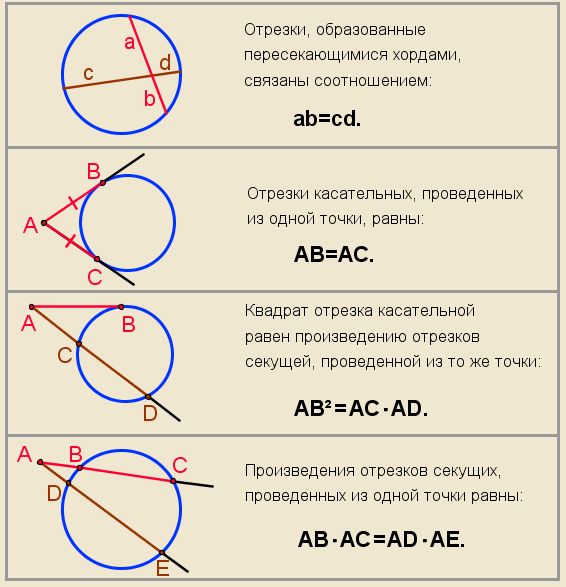 Следовательно, длина перпендикуляра OD больше R – длины наклонной OP. Это противоречит свойству наклонной, и полученное противоречие доказывает утверждение.
Следовательно, длина перпендикуляра OD больше R – длины наклонной OP. Это противоречит свойству наклонной, и полученное противоречие доказывает утверждение.
Говорят, что две окружности касаются, если они имеют единственную общую точку. Эта точка называется точкой касания окружностей.
Проведём через точку касания окружностей касательную к одной из них. Тогда можно доказать, что она будет касательной и к другой окружности, то есть будет общей касательной. Будем говорить, что окружности касаются внешним образом, если их центры лежат в разных полуплоскостях от общей касательной, и внутренним образом, если центры лежат в одной полуплоскости от общей касательной.
Случаи касания окружностейДиаметр окружности, проходящий через середину хорды, не являющейся диаметром, перпендикулярен ей.
Пусть AB – хорда окружности и C – её середина. Треугольник AOB – равнобедренный с основанием AB. Боковые стороны AO и OB равны как радиусы окружности. По свойству медианы равнобедренного треугольника, проведённой к основанию, отрезок OC является высотой. Поэтому диаметр окружности, проведённый через середину хорды, перпендикулярен хорде. Свойство доказано.
Треугольник AOB – равнобедренный с основанием AB. Боковые стороны AO и OB равны как радиусы окружности. По свойству медианы равнобедренного треугольника, проведённой к основанию, отрезок OC является высотой. Поэтому диаметр окружности, проведённый через середину хорды, перпендикулярен хорде. Свойство доказано.
Прямая, проведённая через центры касающихся окружностей, проходит через точку их касания.
Соединим центры окружностей с точкой их касания. Поскольку через точку A касания двух окружностей проходит общая касательная l к этим окружностям, то угол (l, [AO1)) = (l, [AO2)) = 90°. Следовательно, угол O1AO2 – развёрнутый и точки O1, A, O2 лежат на одной прямой a, перпендикулярной к касательной l. Свойство доказано.
Свойство доказано.
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ «Облако знаний».
Хорда окружности: определение и формула
Изображение : Хорда окружностиОкружность представляет собой двумерную замкнутую форму, в которой множество всех точек, зафиксированных на плоскости, равномерно удалены от ее границы. Центром окружности называется неподвижная точка, содержащая равноудаленные от границы или периметра окружности.
В этой статье Edureify приводит определение и теоремы Circle. Но прежде чем перейти к определению хорды окружности, вот некоторые термины, которые важно понимать, связанные с окружностью.0003
- Центр – Средняя точка окружности, равноудаленная от границы окружности от всех точек, является центром окружности.

- Диаметр — диаметр это прямая линия, проходящая через центр круга и касающаяся своим концом границы круга
- Окружность. Окружность — это расстояние вокруг окружности, также известное как периметр. Прочтите статью Edureify об окружности круга, чтобы узнать больше об этом.
- Радиус – Радиус также является прямой линией, проведенной из центра круга, но только с одной стороны. Радиус — одна из самых важных характеристик, необходимых для расчета всего, что связано с кругом.
- Пи – Очень важным и ключевым компонентом кругов, который помогает в вычислении их площади и длины окружности, является число Пи. Значение Пи определяется отношением длины окружности к диаметру.
Хорда окружности
Хорда окружности — это линия, соединяющая любые две точки на окружности окружности. Следует отметить, что диаметр — это самая длинная хорда окружности, проходящая через центр окружности.
На приведенном выше рисунке O — это центр круга. Линия, проходящая через центр круга О, является диаметром круга, самой длинной хордой круга. Линия ниже диаметра является еще одной хордой окружности.
Свойства хорды окружности
Ниже приведены некоторые важные свойства хорды окружности-
- Перпендикулярная линия, проведенная из центра окружности, делит хорду пополам
- Хорды окружности, равноудаленные от центра окружности, равны
- Когда хорда рисуется в окружности, она делит окружность на две части, называемые сегментами — большой сегмент и малый сегмент
- Когда хорда бесконечно продолжается с обоих концов, она становится секущей
Как рассчитать хорду окружности?
Вот две основные формулы для расчета хорды окружности-
- Вычисление длины с использованием перпендикулярного расстояния от центра-
Длина хорды = 2×√(r2- d2)
- Длина хорды с использованием тригнометрии-
Длина хорды = 2×r×sin(c/2)
Пример расчета хорды окружности
Пример 1-
Вычислите хорду окружности, где: r = 7 см, а перпендикулярное расстояние от хорды составляет 4 см
Решение:
r = 7 см и расстояние d = 4 см
Длина хорды ×√(r2- d2)
= 2×√(7×7-4×4)
=2×√(49-16)
=2√33
=2×5,744
= 11,48 см
Следовательно, длина хорды равна 11,48 см
Вот определение и формула для расчета хорды окружности.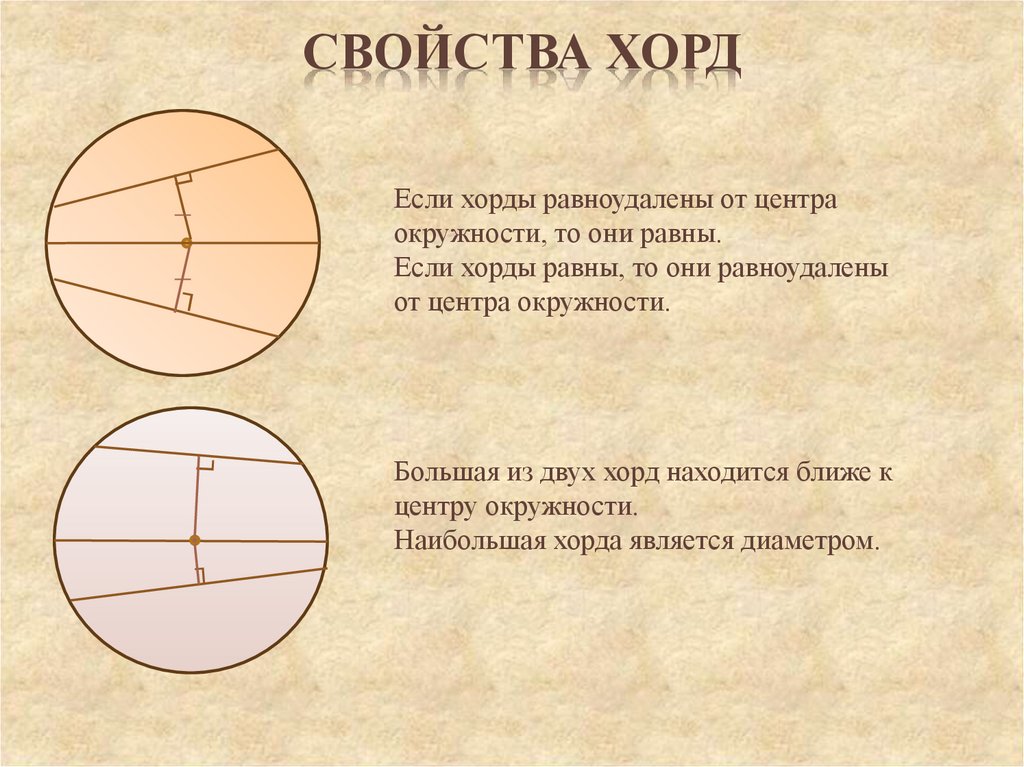
В Edureify есть специальный раздел, посвященный математике. Учащиеся могут изучать и практиковать формулы и многое другое с Edureify, лучшим приложением для обучения искусственному интеллекту.
Некоторые часто задаваемые вопросы о хорде окружности-
В.) Что такое хорда окружности?
Хорда окружности — это линия, соединяющая любые две точки на окружности окружности.
В.) Является ли диаметр хордой окружности?
Да, диаметр — это самая длинная хорда окружности.
В.) По каким формулам вычисляется хорда окружности?
Формулы для расчета хорды окружности-
- Расчет длины по перпендикулярному расстоянию от центра-
Длина хорды = 2×√(r2- d2)
- Длина хорды с использованием тригнометрии-
Длина хорды = 2×r×sin(c/2)
В.) Что такое r в формуле для вычисления хорды окружности?
r обозначает радиус окружности в формуле расчета хорды окружности.
В.) Где я могу узнать больше математических формул?
Воспитывай! В Edureify есть специальный раздел, посвященный математике, который поможет учащимся изучать и практиковать математику.
Дуги и хорды
Дуга — Определение:
Дуга окружности представляет собой часть окружности окружности.
Хорда — Определение:
Хорда окружности — это отрезок прямой линии, обе конечные точки которого лежат на окружности.
Использование дуг окружностей
На плоскости угол, вершина которого является центром окружности, является центральным углом окружности.
Если мера центрального угла ∠APB меньше 180°, то A и B и точки окружности ⊙P, показанные ниже внутри ∠APB, образуют малую дугу окружности. Точки A и B и точки окружности ⊙P во внешности ∠APB образуют большую дугу окружности. Если конечные точки дуги являются конечными точками диаметра, то дуга является полуокружностью.
Именование дуг
Дуги именуются по их конечным точкам. Например, меньшая дуга, связанная с ∠APB выше, называется AB. Большие дуги и полуокружности называются по их концам и точке на дуге.
Например, меньшая дуга, связанная с ∠APB выше, называется AB. Большие дуги и полуокружности называются по их концам и точке на дуге.
Например, главная дуга, связанная с ∠APB выше, называется ACB.
ЭФР внизу полукругом.
Измерение дуг
Мерой малой дуги считается мера ее центрального угла.
Для мгновенного действия на приведенной выше диаграмме
мера дуги GF = m∠GHF = 60°
Мы можем записать меру дуги рядом с дугой. Размер полукруга равен 180°.
Размер большой дуги определяется как разница между 360° и мерой связанной с ней малой дуги.
Например, на приведенной выше диаграмме
мера дуги GEF = 360° — 60° = 300°
Мера всего круга равна 360°.
Постулат сложения дуг
Мера дуги, образованной двумя соседними дугами, равна сумме мер двух дуг.
На диаграмме, показанной выше, мы имеем
Теоремы о хордах окружностей
Теорема 1 :
В одном и том же круге или в конгруэнтных окружностях две малые дуги конгруэнтны тогда и только тогда, когда конгруэнтны их соответствующие хорды.
На диаграмме, показанной выше, мы имеем
Теорема 2 :
Если диаметр окружности перпендикулярен хорде, то диаметр делит хорду и ее дугу пополам.
На схеме, показанной выше, у нас есть
Теорема 3 :
Если одна хорда перпендикулярна биссектрисе другой хорды, то первая хорда является диаметром.
На приведенной выше диаграмме хорда JK является серединным перпендикуляром к хорде ML.
Итак, хорда JK — это диаметр окружности.
Теорема 4 :
В одном и том же круге или в конгруэнтных кругах две хорды конгруэнтны тогда и только тогда, когда они равноудалены от центра.
На схеме, показанной выше, у нас есть
AB ≅ CD, если и только если EF ≅ EG
Нахождение мер дуг
Пример 1 :
Найдите меру дуги MPN дуги ⊙R.
Решение:
Дуга MPN является большой дугой, поэтому
мера дуги MPN = 360° — 80°
мера дуги MPN = 280° конгруэнтные окружности являются конгруэнтными дугами, если они имеют одинаковую меру.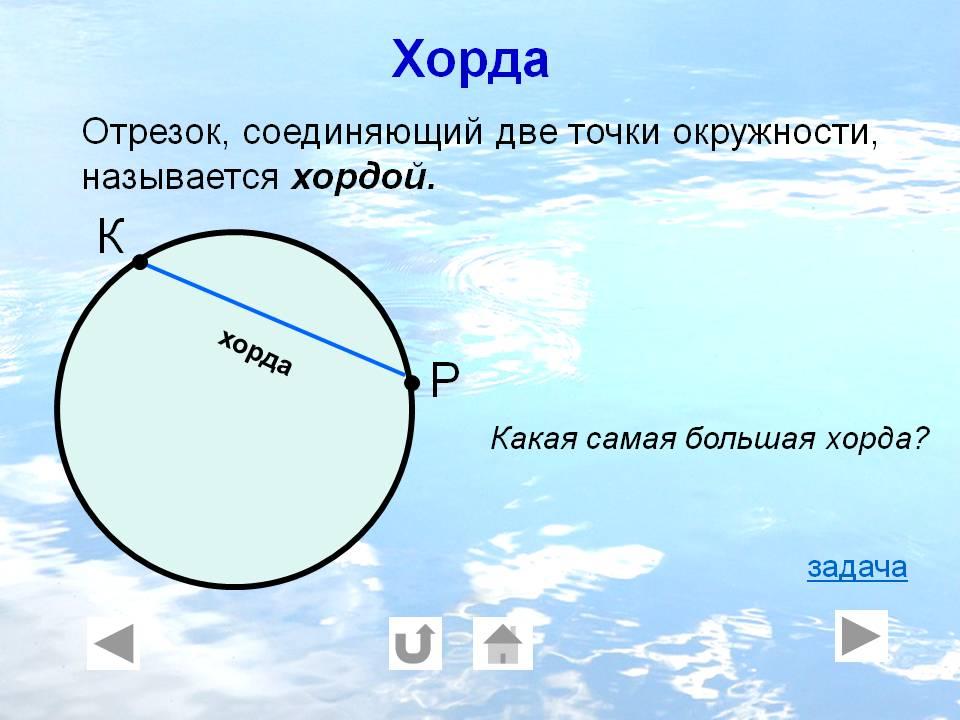 Итак, две малые дуги одной окружности или конгруэнтных окружностей конгруэнтны, если их центральные углы конгруэнтны.
Итак, две малые дуги одной окружности или конгруэнтных окружностей конгруэнтны, если их центральные углы конгруэнтны.
Это было проиллюстрировано в следующих примерах.
Пример 2 :
Найдите размеры синих дуг на диаграмме, показанной ниже. Они конгруэнтны?
Решение :
Дуги AB и DC лежат в одной окружности.
И, m∠arc AB = m∠arc DC = 45°. Итак, у нас есть
дуга AB ≅ дуга DC
Пример 3 :
Найдите размеры синих дуг на диаграмме, показанной ниже. Они конгруэнтны?
Решение:
м∠дуга XY = м∠дуга ZW = 65°, но дуга XY и дуга ZW не являются дугами одной и той же окружности или конгруэнтными окружностями.
Итак, дуга XY и дуга ZW не равны.
Использование свойств хорд
Пример 4:
Молоток для каменной кладки имеет молоток на одном конце и изогнутую отмычку на другом конце. Отмычка работает лучше всего, если мы поворачиваем ее по круговой кривой, которая соответствует форме отмычки.