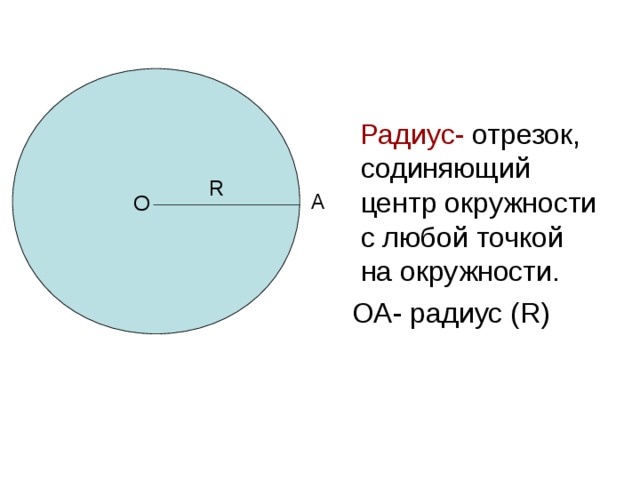
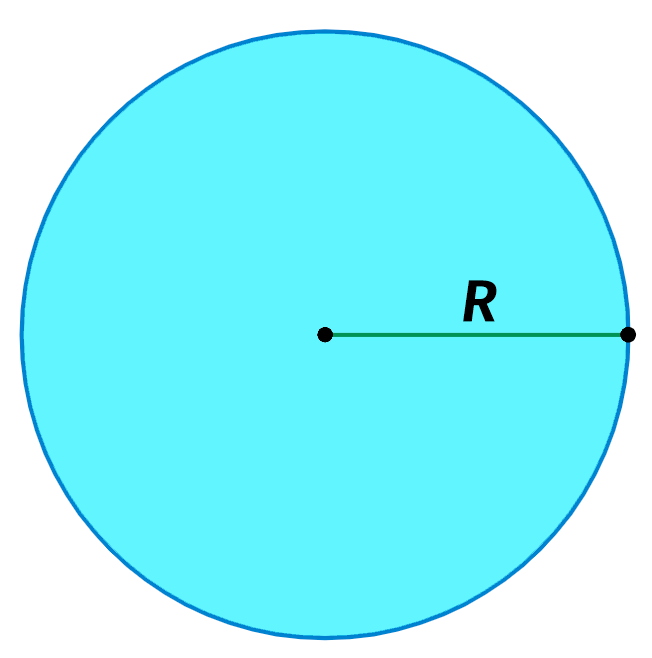
Радиус окружности в: Радиус вписанной окружности в треугольник

alexxlab / / Разное

Радиус вписанной окружности в треугольник

Главная » геометрия

Обновлено

Радиус вписанной в треугольник окружности
рассчитать и выразить через периметр, площадь,
высоту, основание, стороны, диаметр. Формулы
радиуса окружности вписанной в треугольник.

Центр вписанной в треугольник окружности — это одна
из замечательных точек треугольника, она расположена
в точке пересечения биссектрис треугольника, её
иногда называют инцентром.

Центр вписанной окружности правильного треугольника — это
точка, где пересекаются высоты, медианы и биссектрисы.

В любой треугольник можно вписать только одну
окружность, которая находится внутри треугольника.
Центр вписанной окружности равноудален от всех

сторон треугольника. Точка, где окружность пересекается
со стороной треугольника, называется точкой касания.

Все отрезки, которые проведены от точки касания к центру
вписанной окружности имеют одинаковую длину.

Чтобы найти радиус окружности вписанной в треугольник
надо площадь разделить на полупериметр.

Диаметр вписанной окружности в треугольник численно
равен двум радиусам вписанной окружности. Радиус
вписанной окружности можно найти по разным
формулам, все зависит от того, какой треугольник.

Всего различают четыре вида треугольников:

  • Разносторонний / любой
  • Правильный / равносторонний
  • Равнобедренный /  равнобочный
  • Прямоугольный / прямой

Содержание

  1. Радиус вписанной окружности в любой треугольник
  2. Радиус вписанной окружности в правильный треугольник
  3. Радиус вписанной окружности в равнобедренный треугольник
  4. Радиус вписанной окружности в прямоугольный треугольник

Радиус вписанной окружности в любой треугольник

  1. Радиус вписанной окружности в любой треугольник через площадь и полупериметр

    \[ r = \frac{S}{p} \]

    S — площадь; p — полупериметр;

  2. Радиус вписанной окружности в любой треугольник через все стороны и полупериметр

    \[ r = \sqrt\frac{{(p-a)(p-b)(p-c)}}{p} \]

    a, b, c — стороны; p — полупериметр;

  3. Радиус вписанной окружности в любой треугольник через основание, высоту и полупериметр

    \[ r = \frac{\frac{1}{2}a \cdot h}{p} \]

    a — основание, сторона на которую падает высота; h — высота; p — полупериметр;

  4. Радиус вписанной окружности в любой треугольник через диаметр вписанной окружности

    \[ r = \frac{D}{2} \]

    D — диаметр вписанной окружности;

Радиус вписанной окружности в правильный треугольник

  1. Радиус вписанной окружности в правильный треугольник через сторону

    \[ r = \frac{a}{2\sqrt 3} \]

    a — сторона;

  2. Радиус вписанной окружности в правильный треугольник через радиус описанной окружности

    \[ r = \frac{R}{2} \]

    R — радиус описанной окружности;

  3. Радиус вписанной окружности в правильный треугольник через диаметр вписанной окружности

    \[ r = \frac{D}{2} \]

    D — диаметр вписанной окружности;

Радиус вписанной окружности в равнобедренный треугольник

  1. Радиус вписанной окружности в равнобедренный треугольник через боковые стороны и основание

    \[ r = \frac{b}{2} \cdot \sqrt{\frac{2a-b}{2a+b}} \]

    a — боковая сторона; b — основание;

  2. Радиус вписанной окружности в равнобедренный треугольник через высоту и основание

    \[ r = \frac{bh}{b + \sqrt{4h^2+b^2}} \]

    b — основание; h — высота;

  3. Радиус вписанной окружности в равнобедренный треугольник через диаметр вписанной окружности

    \[ r = \frac{D}{2} \]

    D — диаметр вписанной окружности;

Радиус вписанной окружности в прямоугольный треугольник

  1. Радиус вписанной окружности в прямоугольный треугольник через два катета и гипотенузу

    \[ r = \frac{a+b-c}{2} \]

    a, b — катеты; с — гипотенуза.

  2. Радиус вписанной окружности в прямоугольный треугольник через гипотенузу и два катета

    \[ r = \frac{ab}{a+b+c} \]

    c — гипотенуза; a, b — катеты;

  3. Радиус вписанной окружности в прямоугольный треугольник через диаметр вписанной окружности

    \[ r = \frac{D}{2} \]

    D — диаметр вписанной окружности;

Вписанная окружность в треугольник — это окружность,
которая вписана в треугольник и касается всех его сторон.

Радиус вписанной окружности в треугольник — это отрезок,
проведенный от центра вписанной окружности до любой стороны.

Длина радиуса вписанной окружности, диаметра
вписанной окружности а также других величин
измеряется в мм, см, м, км и так далее.

В любом треугольнике все радиусы и диаметры
равны, имеют одинаковую длину.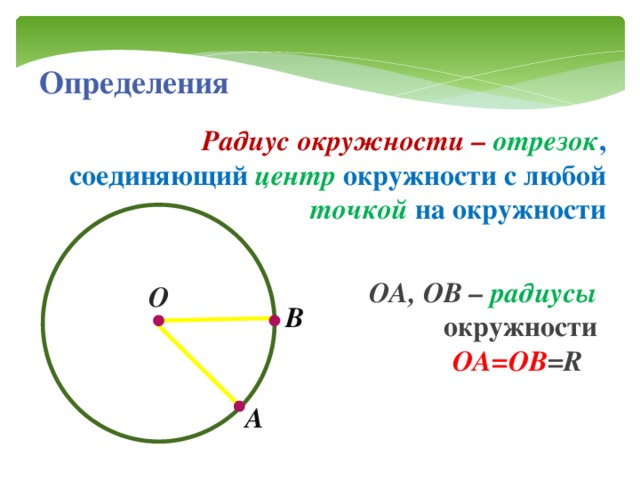

Радиус вписанной окружности в равносторонний треугольник онлайн

С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в равносторонний треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Содержание

  1. Радиус вписанной в равносторонний треугольник окружности, если известна сторона треугольника
  2. Радиус вписанной в равносторонний треугольник окружности, если известна высота треугольника
  3. Радиус вписанной в равносторонний треугольник окружности, если известна площадь треугольника

1. Радиус вписанной в равносторонний треугольник окружности, если известна сторона треугольника

Пусть известна сторона a равностороннего треугольника (Рис. 1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.

Радиус вписанной в равнобедренный треугольник окружности через основание a и боковую сторону b вычисляется из следующей формулы:

Учитывая, что у равностороннего треугольника все стороны равны (\( \small a=b \)), имеем:

\( \small r=\frac{\large a}{\large 2} \cdot \sqrt{\frac{\large 2a-a}{\large 2a+a}} \) \( \small =\frac{\large a}{\large 2} \cdot \sqrt{\frac{\large a}{\large 3a}} \) \( \small =\frac{\large a}{\large 2 \cdot \sqrt{3}} \)

То есть

\( \small r=\frac{\large a}{\large 2 \cdot \sqrt{3}} \)(2)

или, умножив числитель и знаменатель на \( \small \sqrt{3} \):

\( \small r=\frac{\large \sqrt{3}}{\large 6 } \cdot a \)(3)

Пример 1. Известна сторона a=17 равностороннего треугольника. 2}{ 6h}\small =\large \frac{1}{3} \small \cdot h \)

То есть, радиус вписанной в равносторонний треугольник окружности по высоте вычисляется из формулы:

\( \small r = \large \frac{1}{3} \small \cdot h \)(6)

Пример 2. Известна высота \( \small h=39 \) равностороннего треугольника. Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значение \( \small h=39 \) в (6):

Ответ:

3. Радиус вписанной в равносторонний треугольник окружности, если известна площадь треугольника

Пусть известна площадь S равностороннего треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.

Площадь равностороннего треугольника по радиусу вписанной окружности вычисляется из следующей формулы:

\( \small S= 3\cdot \sqrt{3}r^2. 2= \large \frac{S}{3 \cdot \sqrt{3}} \) \( \small = \large \frac{\sqrt{3} \ \cdot \ S }{9} \)

Тогда:

\( \small r= \large \frac{\sqrt[4]{3} }{3} \small \cdot \sqrt{S} \)(7)

Пример 3. Известна площадь равностороннего треугольника: \( \small S=42 . \) Найти радиус окружности вписанной в треугольник.

Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (7). Подставим значение \( \small S=42 \) в (7):

Ответ:

Смотрите также:

  • Окружность, описанная около треугольника
  • Радиус описанной окружности около треугольника онлайн
  • Радиус описанной окружности около равнобедренного треугольника онлайн
  • Радиус описанной окружности около равностороннего треугольника онлайн
  • Радиус описанной окружности около прямоугольного треугольника онлайн
  • Радиус вписанной в треугольник окружности онлайн

 – SVG&колония; Масштабируемая векторная графика

Элемент SVG представляет собой базовую форму SVG, используемую для рисования кругов на основе центральной точки и радиуса.

 html,
тело,
свг {
  высота: 100%;
}
сх

Координата центра окружности по оси X. Тип значения : <длина> | <процент> ; Значение по умолчанию : 0 ; Анимация : да

Координата центра окружности по оси Y. Тип значения : <длина> | <процент> ; Значение по умолчанию : 0 ; Анимация : да

р

Радиус круга. Значение ниже или равное нулю отключает визуализацию круга. Тип значения : <длина> | <процент> ; Значение по умолчанию : 0 ; Анимация : да

длина пути

Общая длина окружности круга в пользовательских единицах. Тип значения : <число> ; Значение по умолчанию : нет ; Анимация : да

Примечание. Начиная с SVG2, cx , cy и r являются Свойствами геометрии , что означает, что эти атрибуты также могут использоваться в качестве свойств CSS для этого элемента.

Глобальные атрибуты

Основные атрибуты

В частности: идентификатор , tabindex

Атрибуты стиля
класс , стиль
Атрибуты условной обработки

В частности: requiredExtensions , systemLanguage

Атрибуты событий

Глобальные атрибуты событий, Графические атрибуты событий

Атрибуты презентации

В частности: Clip-Path , Правила клипа , Color , Color-Interpolation , Цветовой Ренденринг , Cursor , Display , Fill , Fill-opcytiny , заполняем , Фильтр , Mask , Opacity , Pointer-Events , Рендендинг формы , Husm , Husce-Dasharray , -Dashoffset , Stroke-LineCap , холк. -linejoin , Stroke-miterlimit , Stroke-Opacity , Stroke-Width , Transform , Vector-Effect , Видимость

Атрибуты ARIA

Aria-ActiveDescendendend ,

Aria-Atomic , ARIA-AutocOpplite , Aria-Busy , , проверенная Aria , Aria-Colcount , Aria-Colindex , 4, , , , , 4, , , , , 4, , , , , 4, , , . ария-управление , ARIA-Current , ARIA-Describedby , Details Aria , Aria-Disabled , Aria-Detaffect , ARIA-Edrormessage , ARIA-EXPADEDADED , ARIA-FLOWTO , ARIA-EXPADEDED , , ARIA-FLOWTO , , , , 5, , , , 5, , , ARIA-FLOWTO , ARIA-EXPADED. aria-grabbed , aria-haspopup , aria-hidden ,
aria-invalid , aria-keyshortcuts , aria-label , aria-labelledby , aria-level , aria -live , ария-модальный , Aria-Multiline , Aria-MultiSelectable , , ария-ориентированная , Aria-Powns , Aria-Placeholder , Aria-Posinset , ARIA-Pressed , , ARIA-Rechonly , ARIA-PRESSED , , , , , , , , , , , , 4, , , ARIA-PRESSED , , , , ARIA-PRESSED , . ARIA-Relevant , ARIA-Required , ARIA-Roledescription , Aria-Rowcount , Aria-Rowindex , Aria-Rowsspan , , выбранная Aria , 4-SetSize , .
-сортировать , aria-valuemax , aria-valuemin , aria-valuenow , aria-valuetext , роль

Категории Основной элемент формы, графический элемент, элемент формы
Предполагаемый контент. Любое количество следующих элементов, в любом порядке:
Animation Elements Elements Elements
.
Спецификация
Масштабируемая векторная графика (SVG) 2
# CircleElement

Таблицы BCD загружаются только в браузере

с включенным JavaScript. Включите JavaScript для просмотра данных.
  • Другие базовые формы SVG: <эллипс> , <линия> , <полигон> , <полилиния>
     , <прямоугольник>

Последнее изменение: , авторы MDN

Как показать радиус на Картах Google?

Для местных предприятий, которые предлагают доставку на дом — будь то доставка еды, сантехника или ремонт электрики — очень важно установить географические границы в отношении того, куда они будут доставлять свой товар или услугу.

Возьмем ресторан доставки пиццы №1 в Торонто (по версии Tripadvisor), Goodfellas Wood Oven Pizza, , например .

Популярный ресторан обязательно получит заказы со всего города. Но для них нет оперативного смысла доставлять за 20 км на другой конец города.

Так как же они могут установить географические границы?

Например, они могут визуально показать зону доставки на Google Maps . Как? Позвольте мне показать вам:

По умолчанию в Google Maps нет инструментов для рисования и отображения радиуса, поэтому вам придется использовать внешний инструмент, такой как инструмент радиуса FreeMapTools или KML4Earth, и создать свою собственную карту.

Шаг 1. Найдите свое место на Картах Google

Определите место, которое вы хотите обвести кругом на Картах Google.

Я продолжу с примером пиццы Goodfellas Wood Oven Pizza.

Затем запишите широту и долготу местоположения. Для этого просто щелкните правой кнопкой мыши маркер местоположения.

Вы увидите что-то вроде этого.

При щелчке левой кнопкой мыши широта и долгота будут скопированы в буфер обмена. Держите его в стороне ⁠ — мы будем использовать его на следующем шаге.

Шаг 2. Создание файла KML

Теперь перейдите к одному из двух инструментов карты, о которых я упоминал, чтобы создать файл KML (язык разметки замочной скважины). ( Файл KML используется для отображения географических данных ⁠ — мы создадим его на этом шаге и загрузим на Google Maps на следующем)

Я выберу KML4Earth для демонстрации:

  • Введите расстояние по радиусу в км или милях.
  • Затем введите координаты, то есть широту и долготу, которые вы получили на предыдущем шаге.
  • И нажмите «Создать круг».

Инструмент автоматически создаст и загрузит файл KML на ваш компьютер.

Шаг 3: Создайте свою собственную карту

Очевидно, что Google не позволит всем показывать круги на своей универсальной карте. Вам придется создать собственную карту и нарисовать в ней радиус.

Чтобы создать карту:

  1. Перейдите на mymaps.google.com
  2. Нажмите «Создать новую карту»

Шаг 4: Импортируйте файл KML

Ваша новая карта будет выглядеть примерно так:

С левой стороны у вас будет возможность добавить слой. Создайте его и импортируйте файл KML.

Как только вы импортируете файл, карта приблизится к местоположению и отобразит круг (радиус 5 км).

Теперь внесите изменения в карту/круг, если необходимо. Например, вы можете изменить цвет границы, цвет заливки круга, добавить маркеры, добавить метки, отредактировать круг и т. д. из отдельных элементов слоя.

Я поставил маркер на месте ресторана и отредактировал круг, чтобы никто не мог заказать со своей яхты на 500 метров в море 😬.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *