Прилежащие и противолежащие углы: Гипотенуза, прилежащий и противолежащий катеты (статья)

Теорема синусов. Формулы и доказательства

Поможем понять и полюбить математику

Начать учиться

Железнодорожные рельсы параллельны друг другу, а деревья растут под наклоном к земле. Увы, с соотношением сторон в треугольнике все не так просто: чтобы их определить, нужна теорема синусов.

Доказательство теоремы синусов

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

1. На b сокращаем, воспользуемся правилом пропорции и получим:

Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

• Стороны треугольника, если даны два угла и одна сторона.

• Углы треугольника, если даны две стороны и один прилежащий угол.

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

,где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.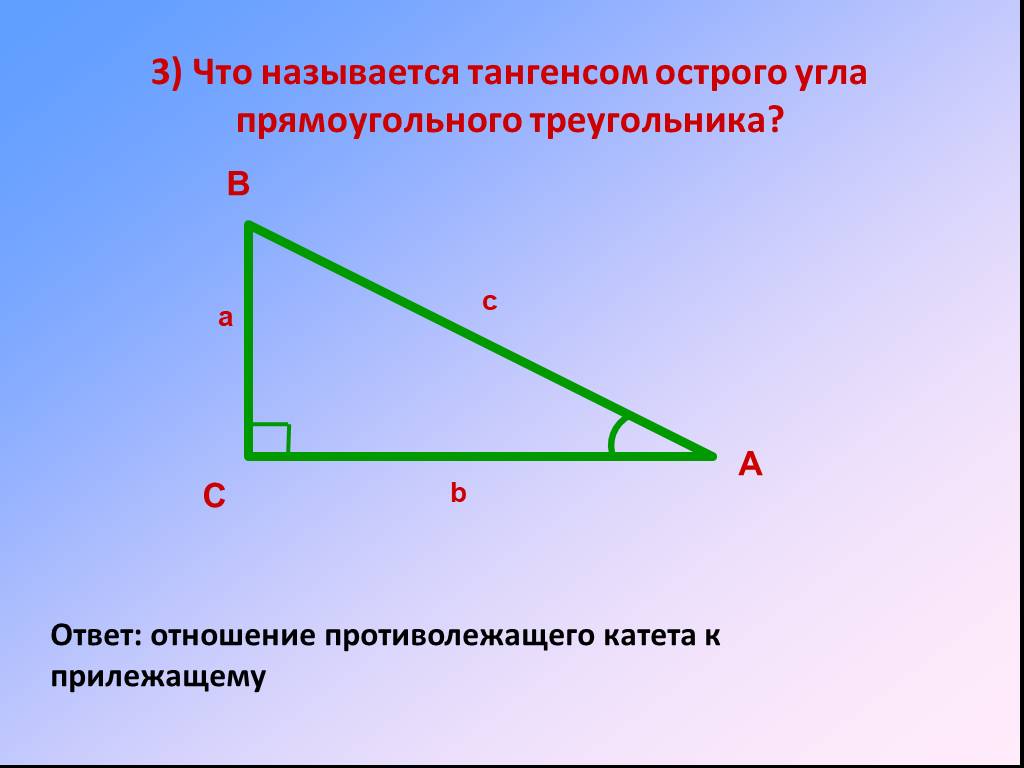

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA₁. В этом случае точка А и точка А₁ лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А₁ = α. Треугольник BA₁C — прямоугольный, в нём ∠ BCA₁ = 90°, так как он опирается на диаметр BA₁.

Чтобы найти катет a в треугольнике BA₁C, нужно умножить гипотенузу BA₁ на синус противолежащего угла.

BA₁ = 2R, где R — радиус окружности

Следовательно:

Для остроугольного треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.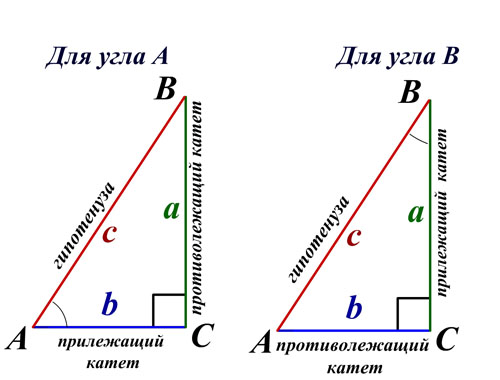

Проведем диаметр окружности BA₁. Точки А и A₁ по разные стороны от прямой ВС. Четырёхугольник ACA₁B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А₁ = 180° — α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° — α) = sinα.

В треугольнике BCA₁ угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° — α) = 2R sinα

Следовательно:

Для тупоугольного треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

3.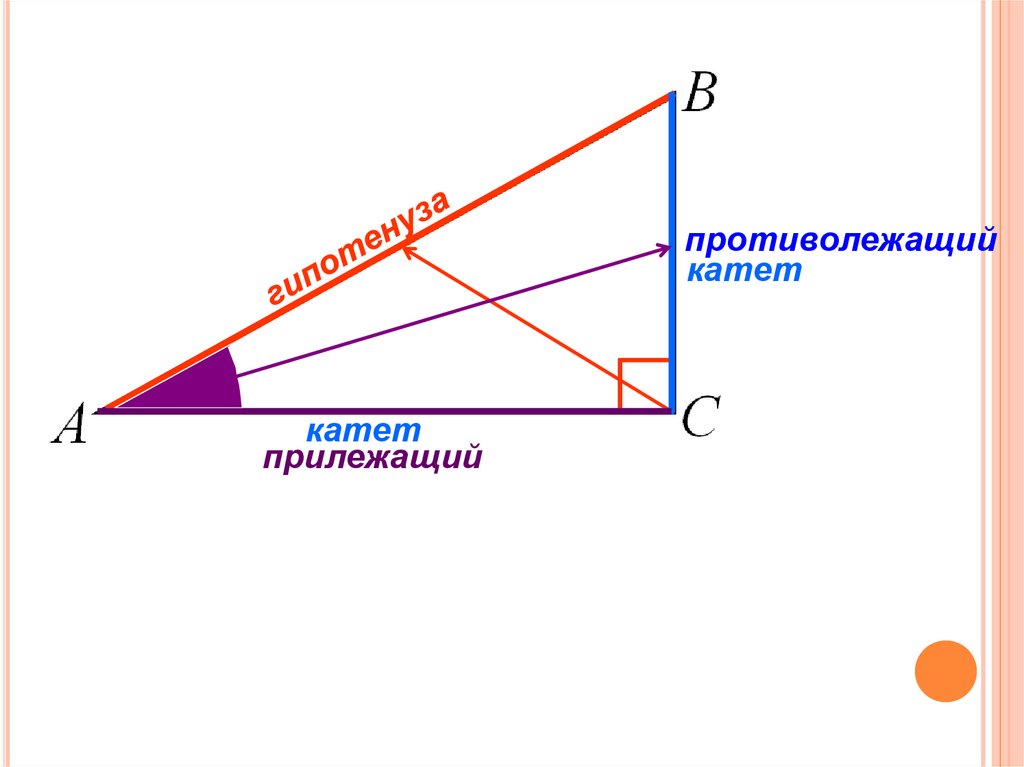 Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Следовательно:

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Как решаем:

• Согласно теореме о сумме углов треугольника:

  ∠A + ∠B + ∠C = 180°

  ∠B = 180° — 45° — 15° = 120°

• Сторону AC найдем по теореме синусов:

Ответ: AC = 12.

Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см соответственно. Найти угол, который расположен напротив данного катета.

Как решаем:

Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Следовательно:

Значит .

Ответ: угол составляет примерно 53,1°.

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

, где R — радиус описанной вокруг треугольника окружности.

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

364. 4K

Разряды и классы чисел

К следующей статье

223.9K

Прямая и обратная пропорциональность

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

8.1.3. Свойство углов и сторон параллелограмма

Задача 1. Один из углов параллелограмма равен 65°. Найти остальные углы параллелограмма.

Решение.

∠C =∠A = 65° как противоположные углы параллелограмма.

∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма.

∠В = 180° — ∠А = 180° — 65° = 115°.

∠D =∠B = 115° как противолежащие углы параллелограмма.

Ответ: ∠А =∠С = 65°; ∠В =∠D = 115°.

Задача 2. Сумма двух углов параллелограмма равна 220°. Найти углы параллелограмма.

 Решение.

Так как у параллелограмма имеется  2 равных острых угла и 2 равных тупых угла, то нам дана сумма двух тупых углов, т.е. ∠В +∠D = 220°. Тогда ∠В =∠D = 220°: 2 = 110°.

∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма, поэтому ∠А = 180° — ∠В = 180° — 110° = 70°. Тогда  ∠C =∠A = 70°.

Ответ: ∠А =∠С = 70°; ∠В =∠D = 110°.

Задача 3. Один из углов параллелограмма в 3 раза больше другого. Найти углы параллелограмма.

Решение.

Пусть ∠А =х. Тогда ∠В = 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне равна 180°, составим уравнение.

х + 3х = 180;

4х = 180;

х = 180 : 4;

х = 45.

Получаем: ∠А =х = 45°, а ∠В = 3х = 3 ∙ 45° = 135°.

Противолежащие углы параллелограмма равны, следовательно,

∠А =∠С = 45°; ∠В =∠D = 135°.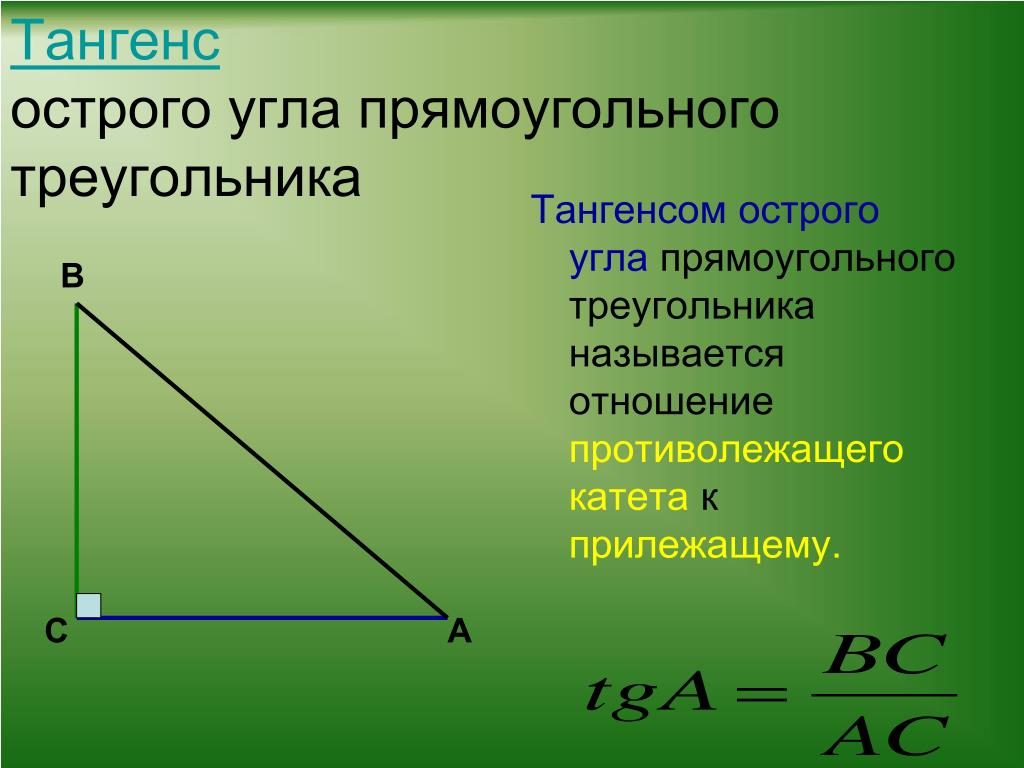

Ответ: ∠А =∠С = 45°; ∠В =∠D = 135°.

Задача 4. Докажите, что если у четырехугольника две стороны параллельны и равны, то этот четырехугольник – параллелограмм.

 Доказательство.

Проведем диагональ BD  и рассмотрим  Δ ADB и Δ CBD.

AD = BC по условию. Сторона BD – общая.  ∠1 = ∠2 как внутренние накрест лежащие при параллельных (по условию) прямых AD и BC и секущей BD. Следовательно, Δ ADB = Δ CBD по двум сторонам и углу между ними (1-й признак равенства треугольников).  В равных треугольниках соответственные углы равны, значит, ∠3 =∠4. А эти углы являются внутренними накрест лежащими при прямых AB и CD и секущей BD. Отсюда следует параллельность прямых AB и CD. Таким образом, в данном четырехугольнике ABCD противолежащие стороны попарно параллельны, следовательно, по определению ABCD – параллелограмм, что и требовалось доказать.

Задача 5. Две стороны параллелограмма относятся как 2 : 5, а периметр равен 3,5 м.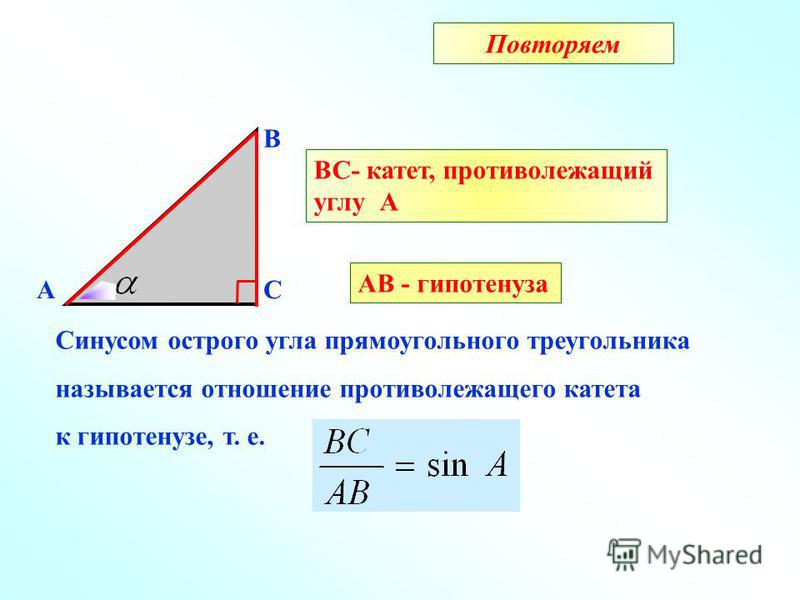 Найти стороны параллелограмма.

Решение.

Периметр параллелограмма P_ABCD= 2 ∙ (AB + AD).

Обозначим одну часть через х. тогда AB = 2x, AD = 5x метров. Зная, что периметр параллелограмма равен 3,5 м, составим уравнение:

2 ∙ (2x + 5x) = 3,5;

2 ∙ 7x = 3,5;

14x = 3,5;

x = 3,5 : 14;

x = 0,25.

Одна часть составляет 0,25 м. Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.

Проверка.

Периметр параллелограмма P_ABCD= 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1,75 = 3,5 (м).

Так как противоположные стороны параллелограмма равны, то CD = AB = 0,25 м; BC = AD = 1,25 м.

Ответ: CD = AB = 0,25 м; BC = AD = 1,25 м.

 

В чем разница между противоположным, смежным и гипотенузой? (Выбери свою сторону) – Все отличия

Геометрия – древний раздел математики.

Все дело в формах и размерах. Геометрия помогает нам понять, как объекты связаны друг с другом. Практическая геометрия помогает нам во многих отношениях, таких как измерение расстояний, вычисление площадей, рисование фигур и т. д.

При работе с практической геометрией и тригонометрией вы сталкиваетесь с множеством различных терминов.

Противоположный, смежный и гипотенуза — три термина, используемые для описания сторон прямоугольного треугольника. Чаще всего они используются в математике и геометрии, но могут быть полезны, если вы изучаете тригонометрию или тригонометрические функции.

Основное различие между этими тремя терминами заключается в том, что противоположная сторона — это сторона, противоположная описываемому углу. Смежной называется сторона, лежащая рядом с описываемым углом. Наконец, гипотенуза треугольника — его самая длинная сторона, и она всегда проходит перпендикулярно двум другим сторонам.

Давайте подробно обсудим эти три термина.

Содержание страницы

Что означает противоположность в прямоугольном треугольнике?

В прямоугольном треугольнике это сторона, лежащая против угла 90 градусов.

Треугольник

Противоположная сторона может быть определена с помощью тригонометрической функции, называемой синусом. Вы можете сделать это, проведя линию от вершины угла к его гипотенузе, а затем измерив, насколько далеко эта линия находится от каждого катета треугольника. Длина этой линии будет определять, какая сторона противоположна или противоположна данному углу.

Что означает термин «прилегающий в прямоугольном треугольнике»?

Смежный означает две вещи. Это может означать «рядом с» или «на той же стороне, что и».

Смежный — это термин, используемый для описания отношения между двумя сторонами прямоугольного треугольника, когда одна из этих сторон примыкает к гипотенузе.

Гипотенуза — это сторона, противоположная прямому углу, а две другие стороны называются катетами.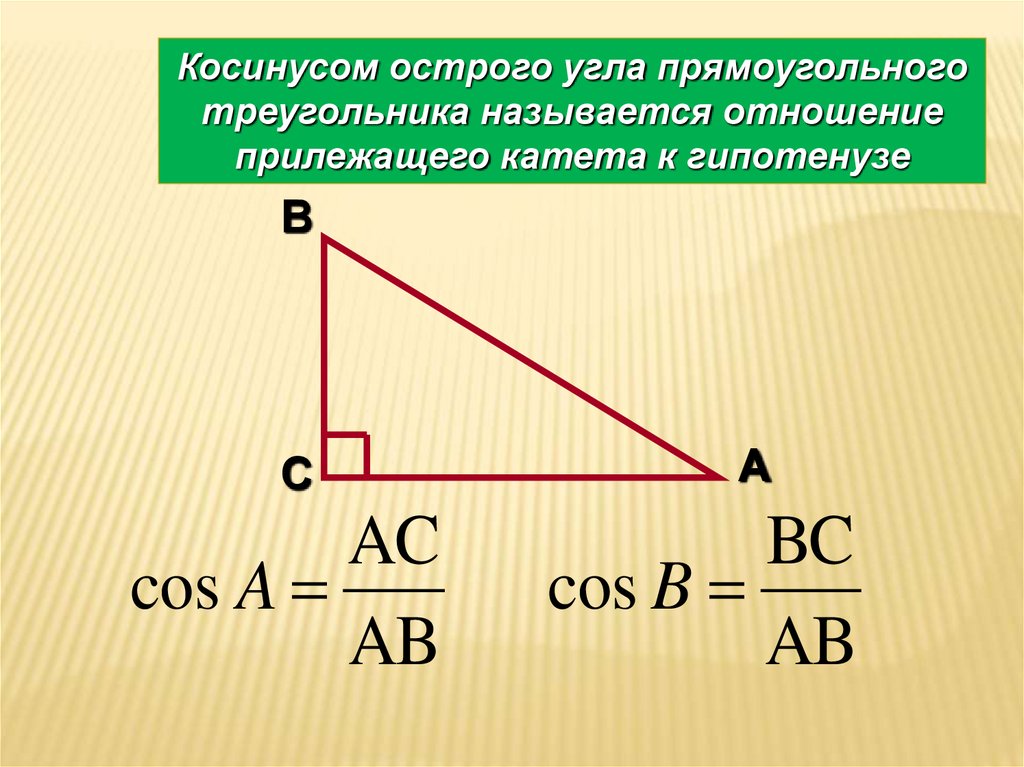 Это стороны, которые примыкают друг к другу.

Что означает гипотенуза в прямоугольном треугольнике?

Обычно гипотенуза прямоугольного треугольника находится напротив прямого угла.

Сторона, противоположная прямому углу, называется гипотенузой.

Гипотенуза служит единицей измерения и также известна как самая длинная сторона прямоугольного треугольника. Гипотенуза всегда длиннее обеих других сторон прямоугольного треугольника.

Слово «гипотенуза» происходит от греческого и означает «длина», что точно описывает роль этой конкретной стороны в прямоугольном треугольнике.

Гипотенуза также известна как «каттер, противолежащий прямому углу», так как она разделяет это качество со своим аналогом, противоположным катетом (тот, который не содержит угла 90 градусов).

Разница между противоположной, смежной и гипотенузой

Различия между тремя сторонами треугольника следующие:

Противоположная

самая длинная сторона треугольника.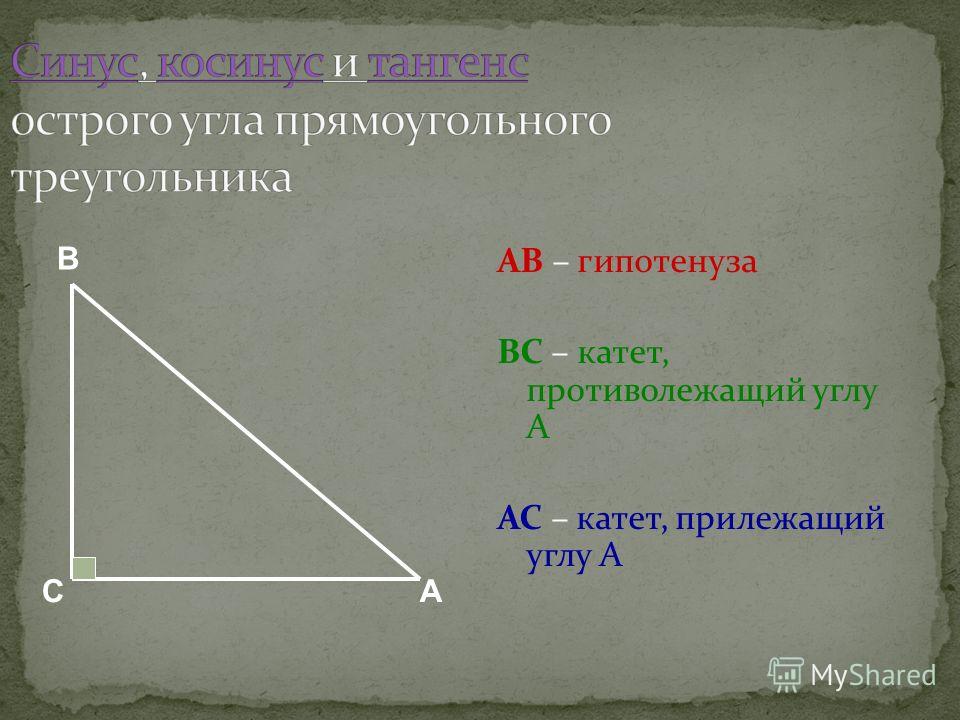 Например, если у вас есть треугольник с 9Угол 0 градусов, его противоположная сторона будет в два раза длиннее, чем прилежащая сторона.

Смежная

Смежная сторона — это та, которая имеет общую вершину (угол) с другой стороной. Например, если есть два прямоугольных треугольника, один из которых имеет угол 90 градусов, их смежные стороны будут равны по длине.

Гипотенуза

У каждого треугольника самая длинная сторона является гипотенузой. Он представляет собой расстояние от одной вершины до другой по воображаемой линии, проходящей через обе вершины (перпендикулярно всем сторонам).

Вот таблица, суммирующая эти различия.

Противоположные	Две стороны не примыкают друг к другу.
Смежный	Две стороны находятся рядом друг с другом.
Гипотенуза	Самая длинная сторона прямоугольного треугольника.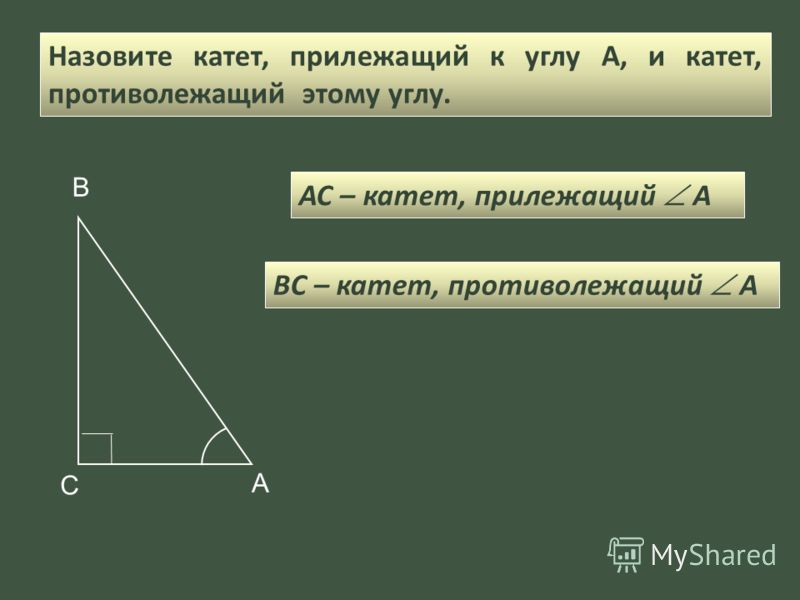

Противоположные, смежные и гипотенузы

Как обозначаются противоположные, гипотенузы и смежные?

Чтобы обозначить противоположную сторону, гипотенузу и смежные стороны прямоугольного треугольника, вы должны знать, с каким прямоугольным треугольником вы имеете дело.

• Если у вас есть равнобедренный прямоугольный треугольник с двумя сторонами одинаковой длины, вы можете обозначить противоположную сторону (которая также является гипотенузой) «a», а затем обозначить смежную сторону «b».
• Если у вас есть равносторонний прямоугольный треугольник — один с тремя равными сторонами — вы можете обозначить гипотенузу «с», а затем обозначить одну из смежных сторон «а», а другую смежную сторону — «б».
• Если у вас есть тупоугольный треугольник (угол между двумя сторонами больше 90 градусов), то вы можете сказать, что одна сторона противоположна другой стороне.

Вот видео, определяющее все эти стороны в треугольнике.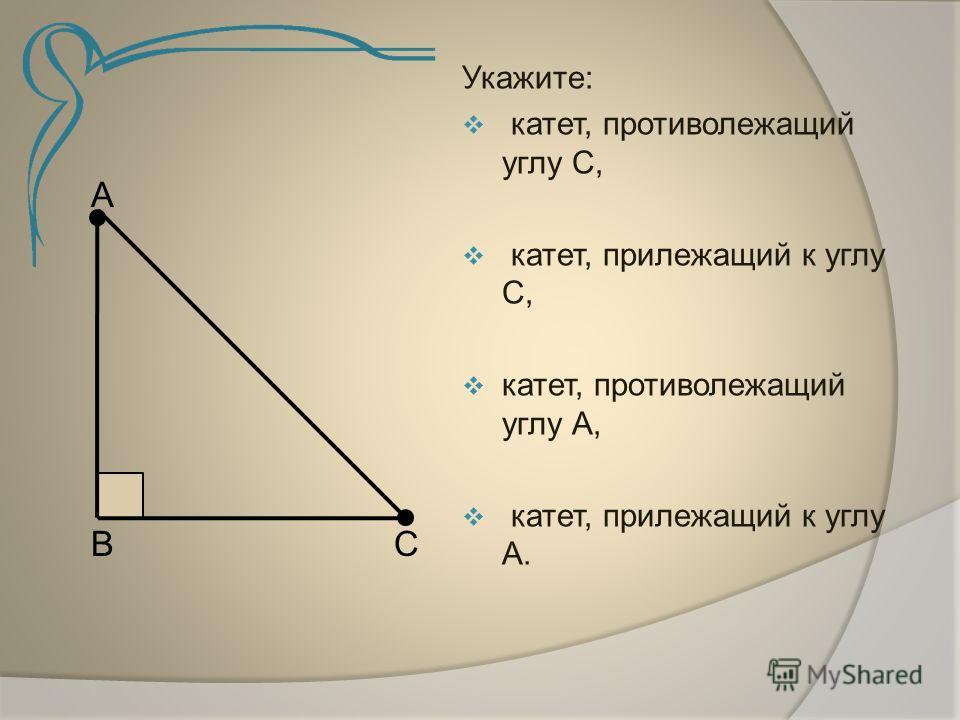

Гипотенуза, смежная и противоположная

Что противоположно гипотенузе?

Гипотенуза — самая длинная сторона прямоугольного треугольника. Противолежащая гипотенузе сторона прямоугольного треугольника.

Всегда ли соседняя сторона самая короткая?

Прилегающая сторона не всегда является самой короткой, но во многих случаях таковой и является. Треугольники имеют смежную сторону, имеющую общую вершину с данным углом. Другими словами, сторона образует прямой угол с данным углом.

Прилегающая сторона всегда короче противоположной стороны, а другая сторона треугольника образует при данном угле угол, равный 90 градусов. Противоположная сторона короче гипотенузы, самой длинной стороны любого прямоугольного треугольника.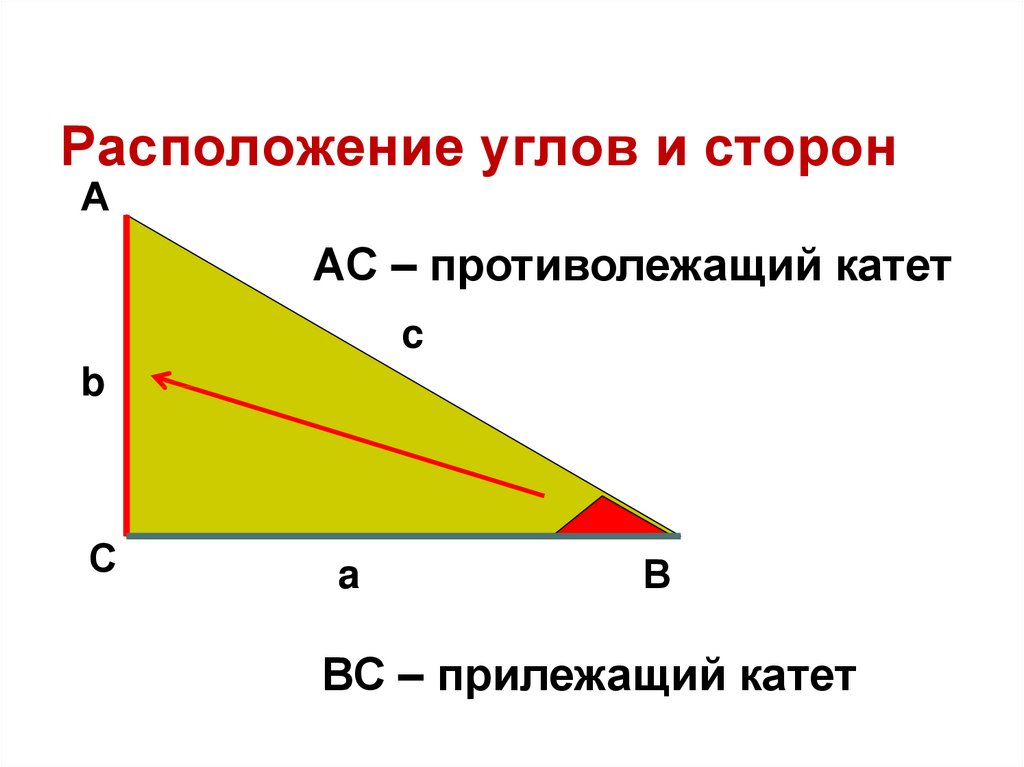

Bottom Line

• Противоположный, смежный и гипотенуза — термины, связанные с прямоугольным треугольником и используемые в геометрических объяснениях математических задач.
• Противоположные стороны — это пара параллельных прямых с концами на одной прямой и общей конечной точкой.
• Смежные стороны — это пара параллельных прямых с концами на одной линии, но не имеющих общего конца.
• Гипотенуза — самая длинная сторона прямоугольного треугольника.

Статьи по теме

• Разница между уравнениями и функциями-1
• Разность фаз магнитных и электрических полей
• Что означает «разница» в математике?

Противоположные углы. Определение, теорема, примеры

При пересечении двух прямых образуются четыре угла. Среди этих углов есть две пары несмежных углов. Они называются противоположными углами, вертикальными углами или вертикально противоположными углами. Эти углы равны по величине. Однако в геометрии термин «противоположные углы» также используется в четырехугольниках. Эти противоположные углы являются углами, которые диагонально противоположны друг другу. Другими словами, это углы, которые соединяются диагоналями. Давайте поймем противоположные углы по отношению к обоим понятиям.

1.	Что такое противоположные углы?
2.	Разница между противоположными углами и смежными углами
3.	Противоположные углы в параллелограмме
4.	Противоположные углы вписанного четырехугольника
5.	Часто задаваемые вопросы о противоположных углах

Что такое противоположные углы?

При пересечении любых двух прямых образуются разные пары углов. Углы, которые прямо противоположны друг другу, называются противоположными углами.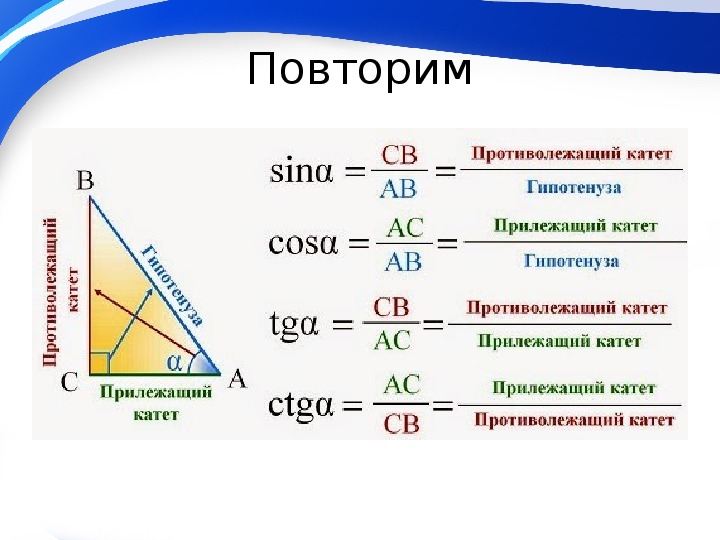 Их также называют вертикальными углами или вертикально противоположными углами, и они равны друг другу. Обратите внимание на следующий рисунок, на котором линии «а» и «b» пересекаются и образуют две пары противоположных углов. Противоположные углы равны ∠1 = ∠3 и ∠2 = ∠4.

Разница между противоположными углами и смежными углами

Пересечение любых двух прямых приводит к возникновению в них смежных и противоположных углов. Однако эти два угла отличаются друг от друга и могут быть легко идентифицированы с помощью их свойств. Обратите внимание на следующий рисунок и таблицу, в которой показана разница между противоположными углами и соседними углами.

Смежные углы	Противоположные углы
Смежные углы имеют общее плечо. Например, на приведенном выше рисунке ∠1 и ∠2 имеют общее плечо АО.	Противоположные углы не имеют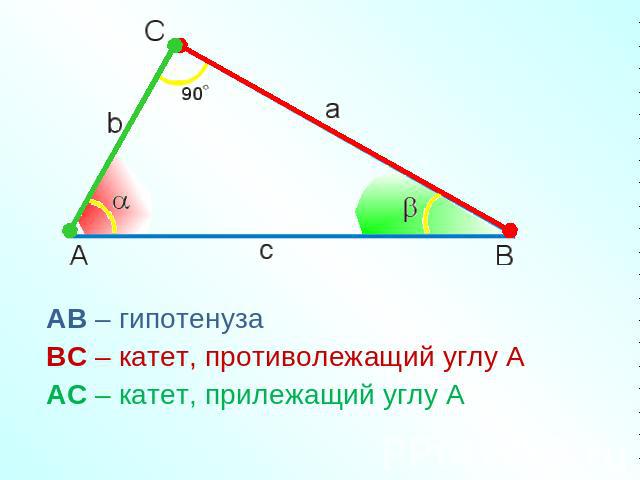 общего плеча. Например, ∠1 и ∠3 не имеют общего плеча.
Смежные углы могут быть или не быть равными по величине.	Противоположные углы всегда равны.
Два смежных угла всегда расположены рядом друг с другом.	Противоположные углы всегда расположены напротив друг друга
На данном рисунке смежные углы равны: ∠1 и ∠2; ∠2 и ∠3; ∠ 3 и ∠ 4; ∠4 и ∠1	На данном рисунке противолежащие углы равны: ∠1 и ∠3; ∠2 и ∠4

Мы поняли понятие противоположных углов относительно пересекающихся прямых. Теперь давайте разберемся с другой концепцией противоположных углов применительно к параллелограмму и вписанному четырехугольнику.

Противоположные углы в параллелограмме

Противоположные углы в четырехугольнике – это те углы, которые расположены по диагонали друг к другу. Другими словами, это углы, которые соединяются диагоналями. Например, в следующем параллелограмме ABCD углы ∠A и ∠C называются противоположными.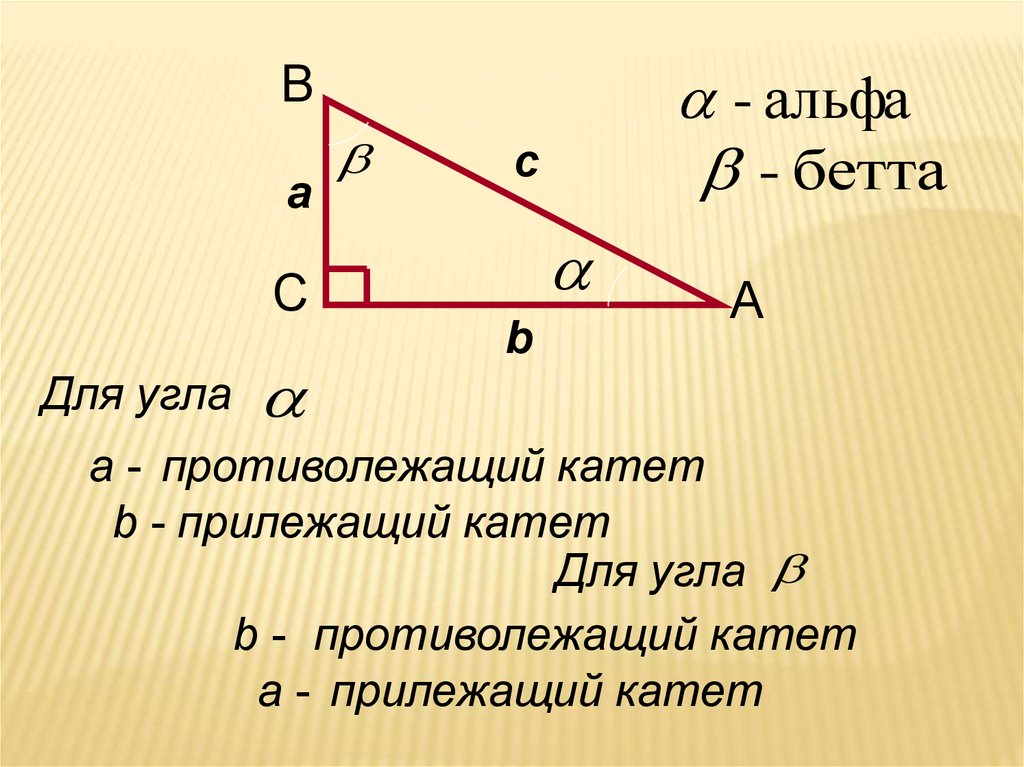 Точно так же ∠B и ∠D являются противоположными углами. Одно из свойств параллелограмма гласит, что противоположные углы равны.

Противоположные углы вписанного четырехугольника

Вписанный в окружность четырехугольник — это четырехугольник, вершины которого лежат на окружности. Он также известен как четырехугольник, вписанный в окружность. Другими словами, это четырехугольник, находящийся внутри круга, и все его вершины касаются круга. Существует множество теорем, связанных с вписанным четырехугольником, и одна из них, касающаяся противоположных углов, гласит, что «Противоположные углы вписанного четырехугольника являются дополнительными, то есть сумма противоположных углов равна 180°». Обратите внимание на следующий рисунок, который показывает, что противоположные углы вписанного четырехугольника являются дополнительными.

Ссылки по теме

Ознакомьтесь со следующими страницами, посвященными противоположным углам.

• Уголки
• Смежные углы
• Четырехугольник

 

Примеры противоположных углов

1. Пример 1: Найдите пары противоположных углов на данном рисунке.

   Решение:

   На данном рисунке две пары противоположных углов.

   ∠a и ∠c, а ∠b и ∠d противоположные углы и они равны между собой, то есть ∠a = ∠c и ∠b = ∠d

2. Пример 2: Напишите верно или неверно следующие утверждения, относящиеся к противоположным углам.

   а.) При пересечении двух прямых противоположные углы всегда дополняют друг друга.

   б.) Противоположные углы всегда лежат рядом друг с другом.

   Решение:

   Используя свойства противоположных углов, мы можем ответить на вопросы.

   а.) Ложные, противоположные углы не всегда могут быть дополнительными, однако они всегда равны.

   б.) Ложь, противоположные углы всегда лежат друг против друга.

перейти к слайдуперейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия.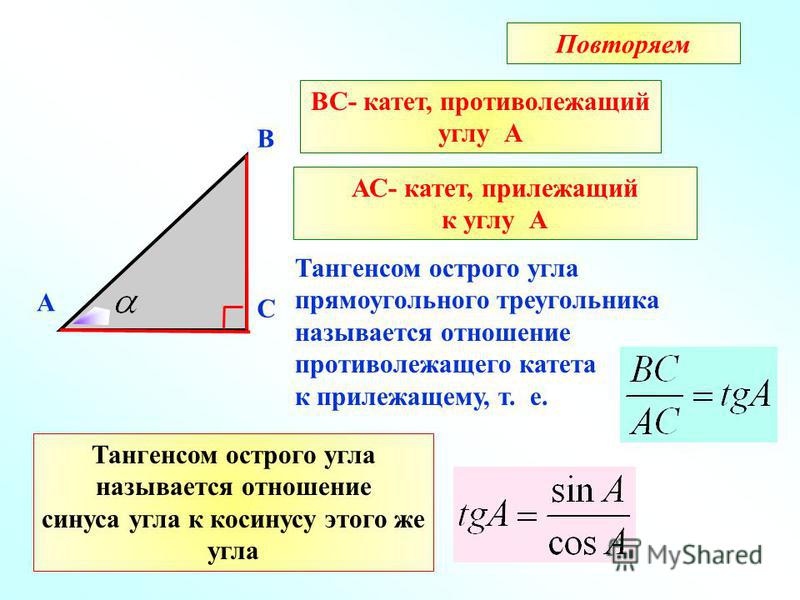 С Cuemath вы будете учиться визуально и будете удивлены результатами.

Забронировать бесплатный пробный урок

Практические вопросы

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о противоположных углах

Как называются противоположные углы?

При пересечении любых двух прямых образуются четыре угла. Углы, которые прямо противоположны друг другу, называются противоположными углами. Их также называют вертикальными углами или вертикально противоположными углами.

В чем разница между смежными углами и противоположными углами?

Смежные углы имеют между собой общее плечо и всегда расположены рядом друг с другом. Противоположные углы образуются при пересечении двух прямых, и они всегда расположены друг напротив друга.

Что такое вертикально противоположные углы?

Противоположные углы также называются вертикально противоположными углами или вертикальными углами. Итак, когда две прямые пересекают друг друга, углы, лежащие друг против друга при вершине, называются вертикально противоположными углами.