алгебра многочлены
задан 5 Мар ’13 19:35
SenjuHashirama
1.8k●1●28●88
100% принятых
изменен 24 Сен ’13 20:08
старыеновыеценные
|
Пусть $%f(x)=a^{4}-6x^{3}+12x^{2}+ax.  $%
Если произвести замену $%t=x-c$%, то условие симметричности графика функции $%f(x)$% относительно прямой $%x=с$% будет равносильно четности функции $%f(t)$%.Подсказка 2: Производная четной функции является нечетной, а производная четной функции — нечетной. ссылка отвечен 5 Мар ’13 20:11 Mather изменен 5 Мар ’13 20:36 |
|
Здесь, возможно, какая-то опечатка в условии. ссылка отвечен 5 Мар ’13 20:47 falcao |
4$%? Так и запись многочлена выглядит естественнее, и ответ получается осмысленный: $%c=-3/2$%, $%a=-9$%.|
Нужно учесть, что значения многочлена в точках $%0$% и $%2c$% — равны. ссылка отвечен 5 Мар ’13 21:21  org/Person»>Anatoliy12.9k●8●47 |
Ваш ответ
Если вы не нашли ответ, задайте вопрос.
5\) Пример 9.4.7.
Если вы когда-либо стояли на конце трамплина, то под вашим весом доска отклонялась , то есть она немного наклонялась вниз к воде внизу. Если бы доска была длиннее , то она прогибалась бы сильнее, а если бы была короче, то меньше.
Если предположить, что один конец доски прочно прикреплен к стене, а другой конец может свободно перемещаться вверх и вниз, то инженеры могут использовать следующее уравнение для моделирования веса, необходимого для отклонения доски заданной длины \(L\ текст{:}\) 93}\) по-прежнему идет к ноль как \(L \to \infty\text{.
}\)
Это имеет смысл, потому что по мере того, как длина доски становится все длиннее и длиннее, потребуется все меньший и меньший вес, чтобы отклонить доску на \(6\) дюймов.
[Однако вес самой доски может вызвать значительный прогиб по мере увеличения длины. Эта функция будет работать для моделирования только досок средней длины, и ее не следует использовать для очень длинных досок.] 92 — 100х + 48\)
Нахождение формулы многочлена.
Если вы знаете корни многочлена, вы можете легко создать список линейных множителей (линий степени \(1\)), которые имеют те же корни. Затем, умножив эти линейные множители вместе, мы создадим полином, который имеет все эти корни.
Пример 9.4.14.
В примере 9.4.12 нам сказали, что многочлен имеет корни \(3\text{,}\) \(\frac{1}{2}\) и \(-4\text{.}\ )
Если бы мы хотели написать формулу для \(f(x)\text{,}\), используя только эту информацию, мы могли бы создать линейные множители:
\начать{собирать*} \влево(х — 3\вправо)\\ (х — \фракция{1}{2})\\ \влево(х + 4\вправо) \конец{собрать*}
Перемножение этих факторов вместе
\begin{уравнение*} \влево(x-3\вправо)(x-\frac{1}{2})\влево(x+4\вправо) \end{уравнение*}
дает многочлен, который имеет все три корня.
Примечание. Этот многочлен равен , а не , как и \(f(x)\) из примера 9.4.12, хотя у него те же корни.
Теперь, помимо создания определенных корней многочлена, вы также можете растягивать или сжимать свою функцию по вертикали, чтобы настроить форму, чтобы она проходила через любую другую точку многочлена, которую вы знаете на многочлене.
Пример 9.4.15.
Предположим, мы знаем, что многочлен \(f(x)\) имеет корни
\начать{выровнять*} х \амп = 5\\ х \amp= -6\\ х \амп = 9 \конец{выравнивание*}
и что он также содержит точку \((4,2)\text{.}\)
Мы можем определить многочлен, обладающий следующими характеристиками, путем создания линейных множителей, имеющих заданные корни:
\начать{выровнять*} х = 5 \ампер\подразумевает (х — 5)\\ х = -6 \амп\ подразумевает (х + 6)\\ х = 9 \amp\ подразумевает (х — 9) \end{выравнивание*}
Перемножив эти множители вместе, мы получим многочлен с данными корнями:
\begin{уравнение*} у = (х-5)(х+6)(х-9) \end{уравнение*}
Однако через точку \((4, 2)\text{,}\) проходит , а не , потому что использование ввода \(x = 4\) дает:
\начать{выровнять*} у \amp= (4-5)(4+6)(4-9)\\ \amp= (-1)(10)(-5)\\ \amp= 50 \конец{выравнивание*}
Чтобы наш полином также проходил через точку \((4,2)\text{,}\) мы будем использовать вертикальное сжатие.
Мы знаем, что это должно быть сжатие, потому что наша функция в настоящее время имеет вывод \(50\), когда вход равен \(4\) — мы хотим, чтобы вывод был только \(2\text{.}\)
Для вертикального сжатия мы включаем постоянный коэффициент \(k\) в нашу функцию:
\begin{уравнение*} у = к (х-5) (х + 6) (х-9) \end{уравнение*}
Обратите внимание, что умножение на константу \(k\) не меняет корней функции.
Чтобы определить значение \(k\), которое будет здесь работать, мы используем точку \((4,2)\text{,}\), подставив \(4\) вместо \(x\text{, }\) и \(2\) для \(y\text{:}\)
\начать{выровнять*} 2 \amp= k(4-5)(4+6)(4-9)\\ 2 \amp= k(50)\\ k \amp= \frac{2}{50}\\ \ампер=0,04 \end{выравнивание*} 94\\ \амп = х (х + 1) (х + 1) (х-6) (х-6) (х-6) (х-6) \конец{выравнивание*}
Поскольку линейный множитель \((x-a)\) соответствует корню \(x = a\text{,}\), то повторение линейного множителя даст нам повторяющийся корень. Повторяющийся корень — это корень полинома, вызванный повторяющимся линейным множителем.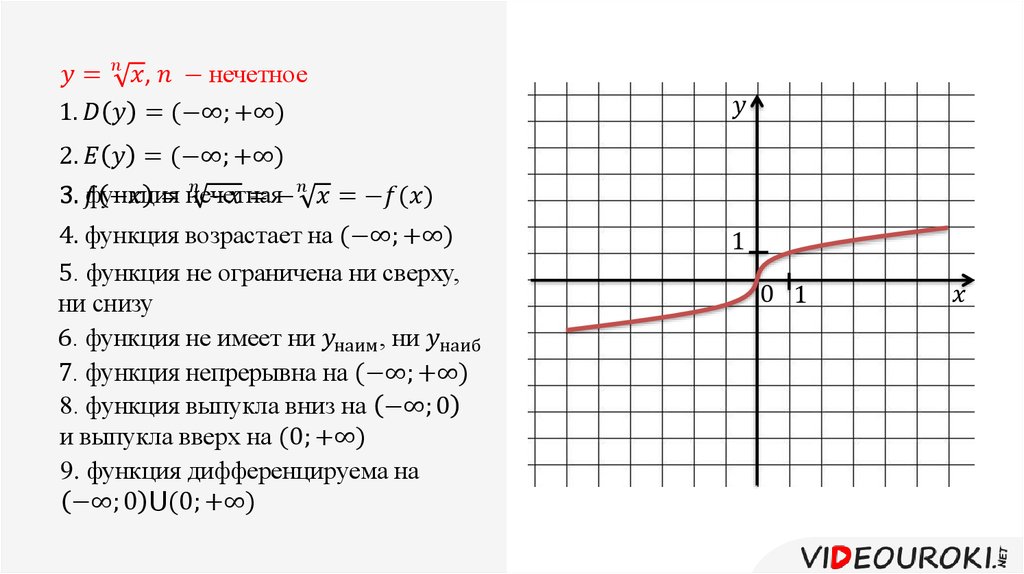
2
\end{уравнение*}
имеет только два корня: \(x = 0\) и \(x = 5\text{.}\)
Мы говорим, что корень \(x = 0\) имеет кратность \(3\text{,}\), а корень \(x = 5\) имеет кратность \(2\text{.}\)
Как повторяющийся корень влияет на график? Мы знаем, что корень появится на графике как \(x\)-отрезок, но будет ли повторение корня в формуле означать, что \(x\)-отрезок также каким-то образом повторяется?
В главе 5 мы научились сдвигать параболу влево или вправо , просто добавляя число к входным данным. Например: 92(х-4)\)
Обратите внимание, что когда кратность корня равна даже , график отскакивает от оси \(x\) при этом значении. Когда кратность корня равна нечетным , график пересекает ось \(x\) при этом значении.
КПП 9.4.20.
Вы, наверное, заметили, что хотя четная кратность корня приводит к тому, что график отскакивает от оси \(x\), иногда график оказывается ниже оси \(x\), а иногда выше оси \(x).
\)-ось.
Чем это вызвано? Как мы можем предсказать, будет ли график находиться выше оси \(x\) или ниже нее?
Причина этого связана с конечным поведением всей функции. То есть график многочлена в конечном итоге будет либо увеличиваться, либо уменьшаться навсегда, когда \(x\) будет далеко от нуля.
Поскольку конечное поведение функции представляет собой тенденцию графика к \(x \rightarrow \infty\) или \(x \to -\infty\text{,}\), мы можем спросить, как определить это, не имея построить график функции. 92 + 12x — 20\) показано ниже.
| \(х\) | \(f(x)\) |
| \(10\) | \(-3400\) |
| \(20\) | \(-9780\) |
| \(30\) | \(-13160\) |
Пока кажется, что функция убывает по мере увеличения \(x\). Однако продолжение таблицы показывает изменение поведения:
| \(40\) | \(-7540\) |
| \(50\) | \(13080\) |
| \(60\) | \(54700\) |
| \(70\) | \(123320\) |
| \(80\) | \(224940\) |
Изначально функция очень быстро уменьшалась, но со временем развернулась и стала увеличиваться (даже быстрее).
3\) 92(х+5)\текст{.}\)
Мы должны использовать то, что мы знаем о корнях и их кратностях, а также о конечном поведении функции.
Сначала нанесите на график точки пересечения \(x\). Помните, что они определяются путем нахождения корней функции.
Далее рассмотрим конечное поведение многочлена. Сделайте это, решив, каким был бы ведущий термин, если бы он был полностью расширен. В крайнем левом и крайнем правом краях графика нарисуйте стрелки, чтобы показать, что график в конечном итоге сделает (увеличит или уменьшит).
Наконец, используйте то, что вы знаете о кратности каждого корня. Начиная со стрелки в крайнем левом углу графика, нарисуйте гладкую кривую, содержащую все точки пересечения \(x\), которые вы нарисовали на первом шаге. Когда вы доберетесь до \(x\)-перехвата, если его кратность
96\text{,}\), поэтому конечное поведение будет увеличиваться как с левой, так и с правой стороны графика.Ответ
График должен выглядеть так:
Обратите внимание, что график пересекает ось \(x\) в точках \(x = -5\) и \(x = 4\text{,}\), и это отскакивает от оси \(x\) в точках \(x = -3\) и \(x = 1\text{.}\)
Упражнения 9.4.3 Упражнения
Графики степенных функций и многочленов
Степень, корни, кратности и конечное поведение
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Алгебраическое упрощение
Формулы для многочленов
14.
15.
16.
17.
18.
Графики многочленов
19.
20.
Дополнительные проблемы
Комбинированная диаграмма в Power BI — Power BI
Редактировать
Твиттер LinkedIn Фейсбук Электронная почта
- Статья
- 4 минуты на чтение
ПРИМЕНЯЕТСЯ К: Рабочий стол Power BI Служба Power BI
В Power BI комбинированная диаграмма представляет собой единую визуализацию, которая сочетает в себе линейную диаграмму и столбчатую диаграмму. Объединение двух диаграмм в одну позволяет быстрее сравнивать данные.
Комбинированные диаграммы могут иметь одну или две оси Y.
Когда использовать комбинированную диаграмму
Комбинированные диаграммы — отличный выбор:
- , когда у вас есть линейная диаграмма и столбчатая диаграмма с одной и той же осью X.
- для сравнения нескольких показателей с разными диапазонами значений.
- , чтобы проиллюстрировать корреляцию между двумя мерами в одной визуализации.
- , чтобы проверить, соответствует ли одна мера цели, определенной другой мерой
- для экономии места на холсте.
Как создать комбинированную диаграмму
Watch Создает комбинированную диаграмму на основе образца «Продажи и маркетинг».
Примечание
В этом видео могут использоваться более ранние версии Power BI Desktop или службы Power BI.
Примечание
Чтобы поделиться своим отчетом с коллегой по Power BI, необходимо, чтобы у вас обоих были отдельные лицензии Power BI Pro или чтобы отчет был сохранен в емкости Premium.
- Рабочий стол Power BI
- Служба Power BI
Чтобы следовать приведенным ниже инструкциям, используйте файл PBIX образца Retail Analysis.
В верхней левой части строки меню выберите Файл > Открыть отчет .
Найдите свою копию PBIX-файла Retail Analysis Sample .
Откройте PBIX-файл Retail Analysis Sample в виде отчета .
Выбрать чтобы добавить новую страницу.
Начните с пустой страницы отчета и создайте столбчатую диаграмму, отображающую продажи и валовую прибыль за этот год по месяцам.
а. На панели Поля выберите Продажи > Продажи за этот год > Значение .
б. Выберите Продажи > Валовая прибыль в этом году и перетащите его в ячейку по оси Y .
в. Выберите Time > FiscalMonth и перетащите его в лунку по оси X .
Визуализация будет аналогична этой.
В правом верхнем углу визуального элемента выберите Дополнительные параметры многоточие (…) и выберите Ось сортировки > FiscalMonth .
Снова щелкните многоточие и выберите Ось сортировки > Сортировка по возрастанию .
Преобразование гистограммы в комбинированную диаграмму. Доступны две комбинированные диаграммы: Строка и столбец с накоплением и Строка и столбец с группировкой . Выбрав столбчатую диаграмму, на панели Visualizations выберите Line и кластеризованную столбчатую диаграмму .
Из области Поля перетащите Продажи > Продажи за прошлый год в корзину Линия оси Y .
Ваша комбинированная диаграмма должна выглядеть примерно так:
Создайте комбинированную диаграмму с двумя осями
В этом задании мы сравним валовую прибыль и продажи.
Создайте новую линейную диаграмму, которая отслеживает Валовая прибыль за прошлый год % по FiscalMonth .
Выберите многоточие для сортировки по FiscalMonth , затем снова выберите многоточие и выберите Ось сортировки > Сортировка по возрастанию .
В январе GM% составлял 35%, достиг пика в 45% в апреле, упал в июле и снова достиг пика в августе. Увидим ли мы аналогичную картину продаж в прошлом и этом году?
Добавьте Продажи за этот год > Значение и Продажи за прошлый год к линейной диаграмме. Масштаб Валовая прибыль в прошлом году % намного меньше, чем масштаб Продажи , что затрудняет сравнение.
Чтобы визуализацию было легче читать и интерпретировать, преобразуйте линейную диаграмму в линейную диаграмму и столбчатую диаграмму с накоплением .
Перетащите Валовая маржа за прошлый год % из столбца по оси Y в строку по оси Y .
Power BI создает две оси, что позволяет по-разному масштабировать наборы данных; левый измеряет продажи в долларах, а правый — процент.
И мы видим ответ на наш вопрос: да, мы видим похожую картину.
Добавьте заголовки к осям
Выберите значок кисти открыть Панель форматирования .
Задайте для оси Y значение на , затем выберите стрелку вниз, чтобы развернуть параметры оси Y .
Установить Ось Y > Значения > Единицы отображения до Миллионы .
Установить Ось Y > Название на На , затем установить Стиль на Показать только заголовок
Установите Вторичная ось Y на На , чтобы отобразить параметры форматирования линейной части комбинированной диаграммы.
Под Вторичная ось Y , установите Заголовок на На .
Теперь на комбинированной диаграмме отображаются две оси с заголовками.
При необходимости измените шрифт, размер и цвет текста и установите другие параметры форматирования для улучшения отображения и удобочитаемости диаграммы.
Отсюда вы можете:
- Добавить комбинированную диаграмму в виде плитки панели мониторинга.
- Сохраните отчет.
- Сделать отчет более доступным для людей с ограниченными возможностями.
Перекрестное выделение и перекрестная фильтрация
При выделении столбца или строки в комбинированной диаграмме происходит перекрестное выделение и перекрестная фильтрация других визуализаций на странице отчета, и наоборот. Используйте визуальные взаимодействия, чтобы изменить это поведение по умолчанию.
Рекомендации и ограничения
В зависимости от размера комбинированной диаграммы метки данных могут отображаться или не отображаться. Если вы не видите метки данных, измените размер комбинированной диаграммы.
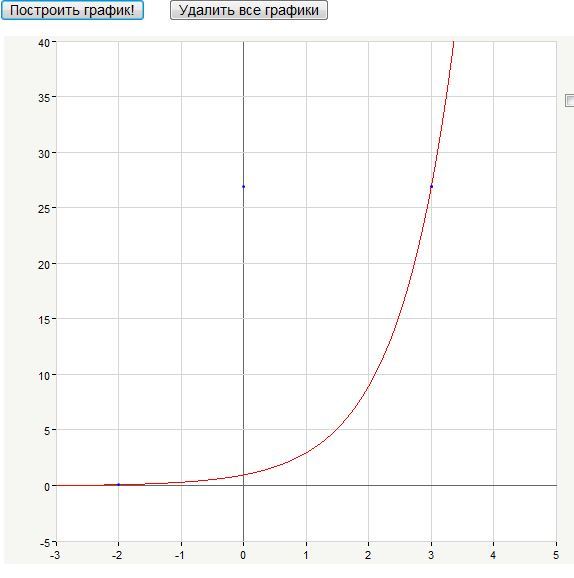96\text{,}\), поэтому конечное поведение будет увеличиваться как с левой, так и с правой стороны графика.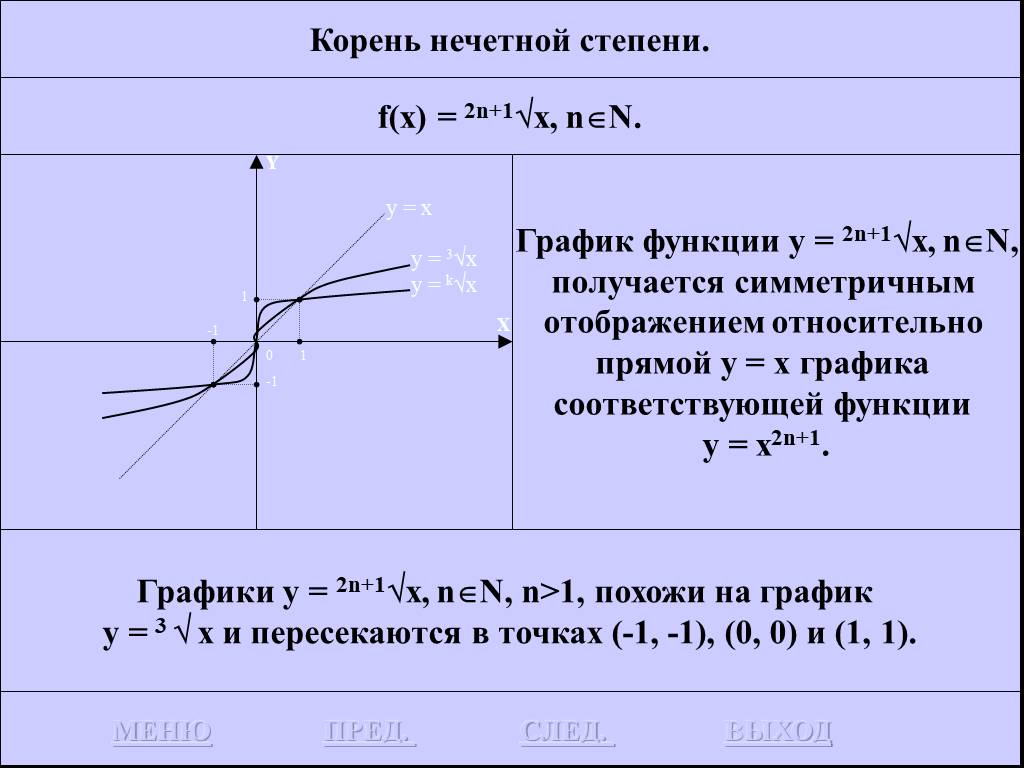
И мы видим ответ на наш вопрос: да, мы видим похожую картину.
