50 примеров действительных чисел | Что это такое и где они находятся?
Набор действительных чисел содержит все рациональные числа и корневые элементы любого положительного целого числа (иррациональные числа). Оно также определяется как расширение рациональных чисел методом фундаментальной последовательности.
Определение, принятое математикой как наукой для набора действительных чисел, требует математических знаний, которые рассматриваются на университетском уровне, в достижениях в области математического анализа, которые первоначально были разработаны Ричардом Дедекиндом и Джорджем Кантором.
Знания Человечества, включая математику и числовые наборы, являются историческими творениями, которые реагируют на экономическую, культурную и научную эволюцию в каждую эпоху, поэтому развитие и знание Действительных чисел стали присутствовать в конце XNUMX-го века, начале XNUMX-го века. век.
Где находятся реальные числа?
Если мы нарисуем все рациональные числа на числовой прямой, останется много пустых мест, которые могут быть заполнены только иррациональными числами.
Примеры:
Геометрическое представление действительных чисел
На основании теоремы Пифагора в Греции за 400 лет до нашей эры появились так называемые несоизмеримые, числа, которые нельзя было измерить имеющимися в то время приборами, ни материальными, ни теоретическими.
Было бы невыполнимой задачей представить все рациональные числа и все иррациональные числа на числовой прямой, чтобы получить так называемую реальную прямую. Действительная строка — это числовая строка, содержащая все действительные числа..
Реальные числа можно использовать в бесчисленных ситуациях, когда необходимо количественно определить, нумеровать, указывать на отсутствие какой-либо величины и показывать числа напротив положительных. Кроме того, это единственный числовой набор, который позволяет адекватно представлять непрерывные явления, такие как длина, время и понятие непрерывной бесконечности.
Примеры действительных чисел
| ситуация | Настоящий номер |
| Отрегулируйте ремешок двадцать шесть миллиметров | 2,6 см |
Каждая секция библиотеки должна быть высотой сорок сантиметров.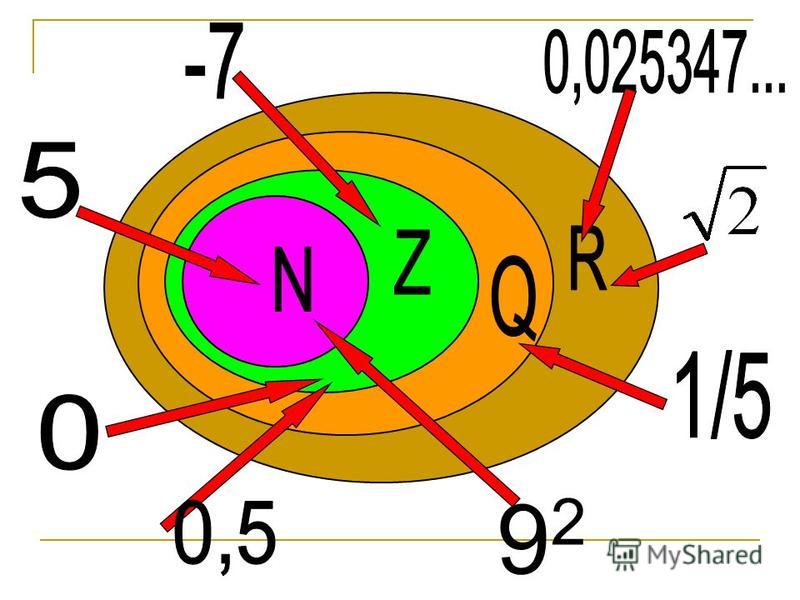 | 0,40 m |
| Расстояние между ними должно быть три миллиметра. | 0,003 m |
| Свободная площадь на складе составляет сорок две тысячи сто тридцать пять квадратных сантиметров. | 4,2135 m2 |
| Длина фасада треугольного углового шкафа 10 см с каждой стороны | 10 см |
| Оптовая цена конфет тридцать центов. | 0,30 $ |
| Я вешу девяносто два килограмма сорок шесть граммов. | 92,046 кг |
| В клубе сорок восемь шахматистов. | 48 |
| Фабрика моего дяди производит девять тысяч шурупов в час. | 9 000 |
| Самая высокая гора в моей стране пять тысяч три метра над уровнем моря | 5 003 |
| Дверь должна быть высотой два метра и пятьдесят сантиметров. | 2,50 m |
| Это отношение длины окружности к ее диаметру. | p |
| Завтра я пришлю тебе три буханки | 3 |
| Мне нужно уменьшить инвентарь на триста тридцать две единицы | -332 |
Чтобы позаботиться о своих коленях, я должен сбросить 15 килограммов. | -15 кг |
| Я потерял одиннадцать песо своих сбережений | — 11 долларов США |
О реальных числах и их операциях
- Сложение двух действительных чисел дает действительное число.
Пример
- Сложение двух действительных чисел коммутативно.
примеров
- Сложение действительных чисел ассоциативно.
Пример
- Для каждого действительного числа существует другое противоположное действительное число, такое, что сумма обоих равна нулю.
примеров
- Сложение действительного числа и нуля — это тоже самое действительное число, нуль — аддитивная нейтраль.
примеров
- Умножение двух действительных чисел дает действительное число.
Пример
- Умножение двух действительных чисел коммутативно.
примеров
- Произведение действительных чисел ассоциативно.

Пример
- При умножении действительных чисел нейтральным элементом является единица.
примеров
- Для каждого отличного от нуля действительного числа существует другое действительное число, называемое мультипликативным обратным, такое, что произведение этих двух действительных чисел равно единице.
примеров
- Распределительное свойство умножения выполняется по отношению к сложению, так что: a ▪ (b + cзнак равноa ▪ b) + (a ▪ c)
Пример
О реальных интервалах
Мы называем реальным интервалом набор действительных чисел, определенный между двумя крайними значениями. a y b принадлежащий множеству действительных чисел, с a < b.
Реальный открытый диапазон
Открытый реальный интервал (a, b) — множество действительных чисел, строго большее, чем a и строго меньше b.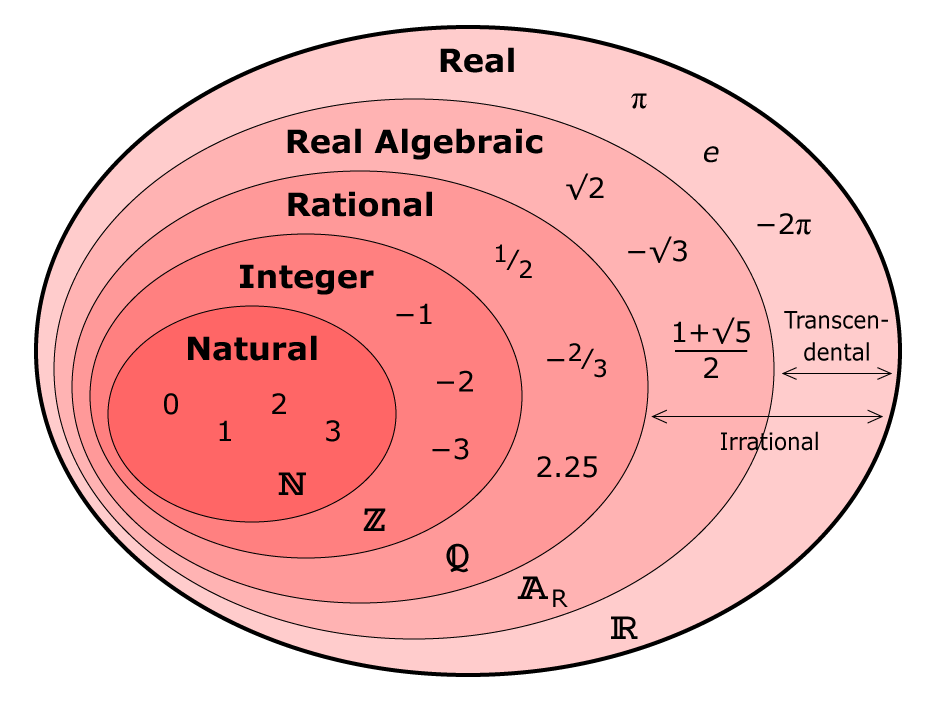
Символически это изображается следующим образом:
Реальный закрытый интервал
Открытый реальный интервал [a, b] — множество действительных чисел, больших или равных a и меньше или равно b.
Символически это изображается следующим образом:
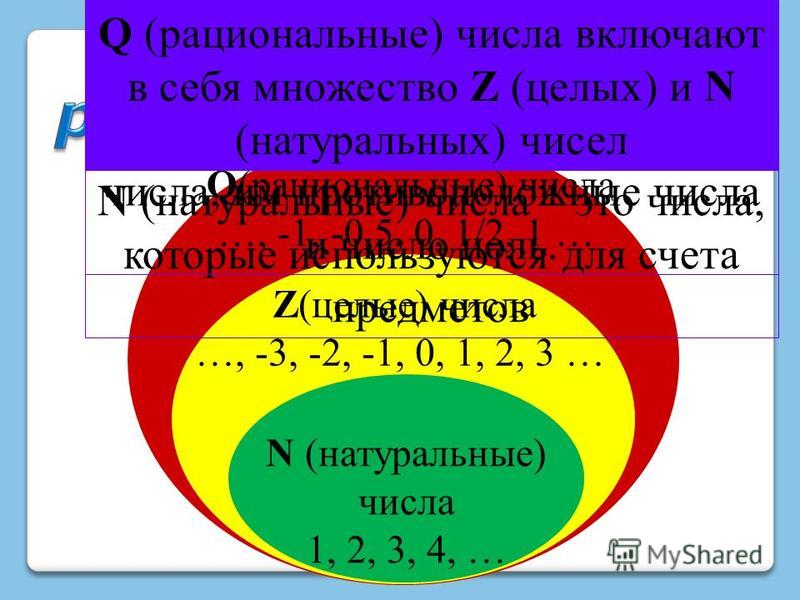
Числовые наборы
Таким образом, разработка реальных чисел означала толчок для развития естественных наук, телекоммуникаций, искусства, экономики и компьютерных наук.
Статья написана профессором со степенью в области математики: Анхелем Мигесом Альваресом.
« 25 примеров диагностики в классе
15 примеров каллиграмм »
3.5. Действительные числа
В математике существуют различные построения теории действительного числа:
— по Дедекинду (построение действительного числа с помощью сечений на множестве рациональных чисел),
— по Вейерштрассу (представление действительного числа как бесконечного десятичного ряда),
— по Кантору (построение действительного числа с помощью фундаментальных последовательностей рациональных чисел)…
Но эти построения
весьма сложны (не случайно в математике
они оформились во второй половине 19
века).
Понятие «действительное число» (как и понятие «бесконечная десятичная дробь»), основные положения теории действительного числа вполне доступны учащимся 7 класса. В настоящее время существует тенденция более раннего изучения действительных чисел, что ускоряет создание цельной системы знаний учащихся о числе, облегчает потребности практики вычислений, позволяет строже изложить некоторые вопросы фундаментальной теории…
Понятие «иррациональное число» появляется в учебниках 8 класса.
Мотивация введения действительных чисел опирается на внутренние потребности математики, а не на практику. Учащиеся убеждаются в необходимости введения новых чисел при решении следующих задач:
— Решить уравнение: х2 = 2.
— Найти отношение длины дуги окружности к ее диаметру.
— Найти сторону квадрата, если его площадь 3 см2.
— Решить графически
уравнение: х2 = 3.
— К множеству каких чисел относятся числа 2, 56565…; 7,23233233…; 0, 123123412345…?
Определение иррационального числа дается через отрицание.
Пример: Алгебра – 8(С.А. Теляковский)
Доказывается, что «среди рациональных чисел нет такого числа, квадрат которого равен 2».
Вводится понятие «действительное число»: «Если к положительным бесконечным десятичным дробям присоединить противоположные им числа и нуль, то получим множество чисел, которые называют действительными числами».
Дается определение иррациональных чисел: «Каждую бесконечную десятичную периодическую дробь можно записать в виде отношения m /n, где m – целое число, n – натуральное число. Бесконечные десятичные непериодические дроби представляют числа, не являющиеся рациональными. Их называют иррациональными числами (приставка «ир» означает отрицание).

Приводятся примеры иррациональных чисел.
Вводятся «действия» над числами. В школьном курсе действия с иррациональными числами сводятся к операциям с их рациональным приближениями по недостатку и по избытку5.
Остановимся более подробно на методике изучения иррациональных чисел.
Рациональные и иррациональные числа
В 5 – 6 классах учащиеся познакомились с обыкновенными дробями. Перед изучением иррациональных чисел целесообразно обобщить эти знания и на новом уровне рассмотреть множество рациональных чисел Q.
В множестве натуральных чисел N операция деления имеет ограниченный характер: если а и в натуральные числа, то не всегда найдется натуральное число х такое, чтобы
ах = в (приведите примеры). Другими словами, в
том случае, когда в не делится нацело на а,
уравнение ах
= в неразрешимо.
Чтобы устранить это несовершенство,
вводятся дроби, записываемые в виде
отношения m/n,
где m,n – натуральные числа. При этом число m называют
числителем, а число n знаменателем
дроби m/n.
Вспомним правила действий с дробями:
Другими словами, в
том случае, когда в не делится нацело на а,
уравнение ах
= в неразрешимо.
Чтобы устранить это несовершенство,
вводятся дроби, записываемые в виде
отношения m/n,
где m,n – натуральные числа. При этом число m называют
числителем, а число n знаменателем
дроби m/n.
Вспомним правила действий с дробями:
(1)
Правило позволяет «сокращать» дробь на общий для числителя множитель. Например,. Как видим, равные дроби могут очень различаться по внешнему виду. (Убедитесь, что дробии- равные дроби.) Натуральное числоn можно считать частным случаем дроби, отождествляя его с .
Построенное
расширение натурального ряда обозначим
через Q+ — этоположительные
рациональные числа (от латинского ratio
— отношение). Умножение в Q+ ассоциативно и коммутативно, уравнения
вида ах = в,
где а и в – любые числа из Q+,
разрешимы (решением будет х =
). Следовательно, (Q+,.)
–коммутативная группа, это –
мультипликативная группа положительных
рациональных чисел (от латинского
multiplication
– умножение). Деление в ней осуществляется
неограниченно.
Следовательно, (Q+,.)
–коммутативная группа, это –
мультипликативная группа положительных
рациональных чисел (от латинского
multiplication
– умножение). Деление в ней осуществляется
неограниченно.
Если ноль и отрицательные числа сначала появились как математические абстракции и лишь впоследствии нашли им содержательное толкование, то дроби были известны с древнейших времен:
— Распределение некоторого общего достояния на индивидуальные доли было повседневной практикой (см., например, в библейской книге Чисел стихи 25 – 46 главы 31).
— Другим видом деятельности, приводившим к дробям, были измерения: если, например, стандарт длины не укладывался между двумя данными точками целое число раз, приходилось прибегать к более мелким его частям6
Присоединяя к
положительным рациональным числам
противоположные им величины и ноль,
получаем все множество рациональных
чисел Q. Оно состоит, таким образом, из нуля,
положительных и отрицательных целых
чисел, положительных и отрицательных
дробей. Сложение, умножение и деление
в Q
выполняются по формуле (1), вычитание
осуществляется по правилу.
Оно состоит, таким образом, из нуля,
положительных и отрицательных целых
чисел, положительных и отрицательных
дробей. Сложение, умножение и деление
в Q
выполняются по формуле (1), вычитание
осуществляется по правилу.
(Выполните действия с рациональными числами: ,, -…. )
В множестве Q
рациональных чисел все четыре
арифметических операции выполняются
беспрепятственно за одним досадным
исключением: нельзя делить на ноль (один
из доводов в пользу того, что 0 –«ненастоящее»
число). Следовательно, в этом множестве
разрешимы уравнения вида
Мы построили поле
рациональных чисел (Q+,.).
Оно расширяет кольцо целых чисел (Z,+,. ),
позволяя неограниченно выполнять
операцию деления (кроме деления на
ноль).
),
позволяя неограниченно выполнять
операцию деления (кроме деления на
ноль).
Поле рациональных чисел бесконечно, но существуют и конечные поля. Таковым будет, например, любое кольцо Zp остатков от деления натуральных чисел на простое число p. Имея перед собой таблицу умножения поля Z5
, легко решить в нем уравнения2х = 1, 3х = 4, 4х= 5. А вот в кольце Z6 эти уравнения не имеют корней.
В поле рациональных чисел разрешимо любое уравнение ах + в = 0,решением будет
х = — . Поле рациональных чисел всюду плотно, так как между любыми двумя рациональными числамиr1и r2можно указать рациональное число (r1+ r2):2 и даже бесконечное множество рациональных чисел.
Наглядное
представление о рациональных числах
дает координатная ось. На некоторой
прямой линии выбирается точка 0 – начало
отсчета, указывается единица масштаба,
направление. Если дано положительное
рациональное число
,то
единица масштаба делится на n
На некоторой
прямой линии выбирается точка 0 – начало
отсчета, указывается единица масштаба,
направление. Если дано положительное
рациональное число
,то
единица масштаба делится на n
-2/3 5/3
——!—.—.—!—.—.—!—.—.—!———>
-1 0 1 2
Построив числовое
множество Q
(поле рациональных чисел), в котором
разрешимо любое линейное алгебраическое
уравнение ах
+ в =о,
естественно перейти к исследованию
квадратных уравнений ах2 + вх + с = 0. В
простейшем случае х2 – 1 = 0, т.е. х2 = 1,
имеет два решения (корня):
х1 =1, х2 = -1. Однако уже следующий напрашивающийся
шаг заводит нас в тупик.
Однако уже следующий напрашивающийся
шаг заводит нас в тупик.
Теорема 1. Уравнение х2 = 2 не имеет решений в поле рациональных чисел.
Теорема 2. Диагональ квадрата несоизмерима с его стороной.
Необходимо самостоятельно познакомиться с доказательствами этих теорем, приводимыми авторами школьных учебников.
Т
Рис. 1.
еоремы 1 и 2 при всем внешнем несходстве представляют собой лишь разные интерпретации одного и того же математического факта: одна на языке алгебры, другая — в геометрических терминах. (В математике это обычное явление.) Обратимся теперь к координатной оси. Если взять на ней точки, соответствующие рациональным числама и в (пусть а < в), то середина отрезка выражается числомс = (а + в): 2. Это тоже рациональное число, так что между любыми двумя рациональными числами лежит еще одно. Деля пополам отрезки и, получим еще два рациональных числа между
 д. Поскольку этот процесс деления
пополам (дихотомия) можно продолжать
неограниченно, приходим к выводу, что
между произвольными рациональными
числами а и в находится
бесконечно много других рациональных
чисел. Представив себе все это, мы могли
бы прийти к заключению, что рациональные
числа заполняют сплошь числовую ось.
Но нет – если от точки 0 отложить
вправо диагональ единичного квадрата,
то согласно теореме 2 другой конец
диагонали не попадет ни в какую
рациональную точку. (См. рис. 1) Аналогично
строится точка.
Вот эти «дыры» на числовой прямой и были
интерпретированы как иррациональные
числа. (В словаре: «иррациональный – не
постигаемый разумом, такой, который не
может быть выражен в логических понятиях».
Повседневный математический смысл
проще: иррациональное число – это число,
не являющееся рациональным.)
д. Поскольку этот процесс деления
пополам (дихотомия) можно продолжать
неограниченно, приходим к выводу, что
между произвольными рациональными
числами а и в находится
бесконечно много других рациональных
чисел. Представив себе все это, мы могли
бы прийти к заключению, что рациональные
числа заполняют сплошь числовую ось.
Но нет – если от точки 0 отложить
вправо диагональ единичного квадрата,
то согласно теореме 2 другой конец
диагонали не попадет ни в какую
рациональную точку. (См. рис. 1) Аналогично
строится точка.
Вот эти «дыры» на числовой прямой и были
интерпретированы как иррациональные
числа. (В словаре: «иррациональный – не
постигаемый разумом, такой, который не
может быть выражен в логических понятиях».
Повседневный математический смысл
проще: иррациональное число – это число,
не являющееся рациональным.) Иррациональных
чисел тоже бесконечно много: если
—
иррациональное, аа – рациональное число, то сумма
а
и произведениеа
(при а)
тоже будет иррациональное число (иначе,
например,оказалось бы рациональным).
Первый конкретный пример иррационального числа – это длина диагонали единичного квадрата, т.е. положительный корень уравнения х2 = 2, обозначаемый через. Рассуждения, проведенные в доказательстве теоремы 1, могут быть дословно повторены и для уравнений х2 = 3, х3 =5, что доказывает иррациональность чисел .
Изобразив действительные числа на координатной прямой, мы получим, что каждой точке координатной прямой соответствует действительное число (прямая без «дырок») и каждому действительному числу отвечает точка на прямой. Координатная прямая, на которой изображено множество действительных чисел, называется числовой прямой, поле действительных чисел стало непрерывным, то есть отношения и алгебраические операции с действительными числами сводятся к одноименным отношениям и операциям с их рациональными приближениями по недостатку и избытку.
После введения
действительных чисел появилась
возможность дать общую запись для
решений любого квадратного уравнения ах2 + вх + с = 0 с
использованием радикала (знака извлечения
корня), а именно х =
или х =.
Если величина D = в2— 4ас (дискриминант) положительна, уравнение имеет два корня, рациональных или иррациональных в зависимости от того, является дискриминант полным квадратом или нет.
Золотым сечением называется деление отрезка длины 1 на две части, большая из которых х является средней пропорциональной величиной между всем отрезком и его меньшей частью 1 – х, то есть принцип золотого сечения (название ввел Леонардо да Винчи в конце 15 века) составлял, в частности, теоретическую основу архитектурных композиций классической древности и эпохи Возрождения. Для нахождения х необходимо решить квадратное уравнение х2 + х – 1 = 0, откуда х = (отрицательный корень отбрасываем). Для нас иррациональность этого числа очевидна, в древности же она была установлена весьма сложным путем, а сам факт её существования произвел удручающее впечатление.
Пример квадратного
уравнения возбудил надежду на то, что
алгебраические уравнения и всех других,
более высоких степеней, окажутся
разрешимыми в радикалах, то есть корни
можно будет выразить с помощью
арифметических операций и извлечения
корней. В середине 16 века итальянские
математики Тарталья, Кардано и Феррари
нашли подобные формулы для кубического
уравнения четвертой степени. (Происходило
это в атмосфере ожесточенной полемики
о приоритете, с публичными состязаниями
в решении соответствующих задач,
проклятиями и покаяниями.) В почти три
последующие столетия существенных
продвижений в этом вопросе не было, и
лишь в 1826 году норвежский математик
Нильс Хенрик Абель (1802 – 1829) доказал,
что для каждого натурального числа n>4
существует алгебраическое уравнение n степени с
целыми коэффициентам, неразрешимыми в
радикалах (например, х5 – 4х – 2 = 0). Окончательное решение
проблемы, занимавшей умы лучших
математиков, принадлежит французу
Эваристу Галуа (1811 – 1832). Он ввел понятие
группы и показал, что каждому алгебраическому
уравнению соответствует некоторая
группа, по свойствам которой и можно
судить, разрешимо или нет уравнение в
радикалах.
В середине 16 века итальянские
математики Тарталья, Кардано и Феррари
нашли подобные формулы для кубического
уравнения четвертой степени. (Происходило
это в атмосфере ожесточенной полемики
о приоритете, с публичными состязаниями
в решении соответствующих задач,
проклятиями и покаяниями.) В почти три
последующие столетия существенных
продвижений в этом вопросе не было, и
лишь в 1826 году норвежский математик
Нильс Хенрик Абель (1802 – 1829) доказал,
что для каждого натурального числа n>4
существует алгебраическое уравнение n степени с
целыми коэффициентам, неразрешимыми в
радикалах (например, х5 – 4х – 2 = 0). Окончательное решение
проблемы, занимавшей умы лучших
математиков, принадлежит французу
Эваристу Галуа (1811 – 1832). Он ввел понятие
группы и показал, что каждому алгебраическому
уравнению соответствует некоторая
группа, по свойствам которой и можно
судить, разрешимо или нет уравнение в
радикалах.
Н. Абель и Э. Галуа
ушли из жизни совсем молодыми (первый
скончался от туберкулеза, второй был
убит на дуэли), их идеи не были должным
образом восприняты современниками, но
впоследствии оказали огромное влияние
на развитие важнейших разделов математики. Имена этих выдающихся ученых носят
многие математические объекты, например,
абелевыми называются коммутативные
группы, а конечные поля – полями Галуа.
Имена этих выдающихся ученых носят
многие математические объекты, например,
абелевыми называются коммутативные
группы, а конечные поля – полями Галуа.
Задания к лекции
Путь построения числового множества в науке отличается от соответствующего пути, принятого в школьной математике. Укажите эти отличия, вскройте их причины.
Проанализируйте методический подход к введению модуля числа, данный в учебниках математики Н.Я. Виленкина. Сравните этот подход с другими, встречающимися в методической и учебной литературе.
3. Познакомьтесь с операциями на множестве Rи разработайте беседу для учащихся 9 класса на тему «Отношения и операции на множестве действительных чисел».
4.Подберите материал и наметьте план беседы для учащихся 9 класса о развитии понятия числа.
Указание1. Большую роль в беседе
следует отвести историческим сведениям
о развитии понятия числа. 2. Постарайтесь
аргументированно обосновать необходимость
расширения числовых множеств, показывая
при этом потребности практики и науки.
2. Постарайтесь
аргументированно обосновать необходимость
расширения числовых множеств, показывая
при этом потребности практики и науки.
5. Сделайте обзор литературы, которая может быть использована а) учителем для проведения элективного курса по изучению комплексных чисел, б) учеником для самостоятельного чтения при изучении комплексных чисел.
Целые и рациональные числа. Действительные числа
ЦЕЛЫЕ и РАЦИОНАЛЬНЫЕ
ЧИСЛА.
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА.
2. Содержание:
СОДЕРЖАНИЕ:1.
2.
3.
4.
5.
Натуральные числа.
Целые числа.
Рациональные числа
Действительные числа
Преобразование выражений с
действительными числами.
3. Знакомьтесь:
ЗНАКОМЬТЕСЬ:Натуральные
числа
Целые
числа
Рациональные
числа
Действительные
числа
N
Z
Q
R
Для счета предметов используются числа , которые
называются натуральными. Для обозначения
множества натуральных чисел употребляется
буква N -первая буква латинского слова Naturalis,
«естественный», «натуральный»
Натуральные числа, числа им противоположные
и число нуль, образуют множество целых чисел,
которое обозначается Z — первой буквой
немецкого слова Zahl — «число».

Натуральные числа
1, 2, 3, 4, 5, 6…
n — натуральное
n∈ N
Сумма и произведение натуральных
чисел есть число натуральное.
6. Целые числа
ЦЕЛЫЕЧИСЛА
Целыми числами называют множество
натуральных чисел, им противоположных и
число нуль.
Z=(1,2,3,4,5,6,7,8…
-1,-2,-3,-4,-5,-6,-7,-8…, 0)
Целые числа замкнуты относительны
суммы, произведения и разности.
Целые числа
…-3;-2;-1;0,1, 2, 3,…
m — целое
m Z
Сумма, произведение и разность
целых чисел есть число целое.
Отрицательные числа ввели
в математический обиход
Михаэль Штифель (1487—1567)
в книге «Полная арифметика» (1544),
и Никола Шюке (1445—1500)его работа была обнаружена в 1848
году.
Числа,
им противоположные
-6
-5
-4
-3
-2
-1
Натуральные числа
1 2 3 4 5 6
Z
Целые
m
Множество чисел, которое можно представить в виде
,
n
называется множеством рациональных чисел и обозначаетсяQ
первой буквой французского слова Quotient
— «отношение».
11. Рациональные числа
РАЦИОНАЛЬНЫЕЧИСЛА
Целые и дробные числа составляют множество
рациональных чисел.
Q=(целые числа, дробные числа)
Рациональные числа замкнуты относительно
суммы, разности, произведения и частного (
исключая деления на нуль)
Рациональное число (лат. ratio —
отношение, деление, дробь) — число,
представляемое обыкновенной дробью , где
числитель m — целое число, а знаменатель n
— натуральное число. Такую дробь следует
понимать как результат деления m на n, даже
если нацело разделить не удаётся. В реальной
жизни рациональные числа используются для
счёта частей некоторых целых, но делимых
объектов, например, тортов или других
продуктов, разрезаемых на несколько частей
Целые числа
Дробные числа
2/7
2
5
7,1
3,2
0,(2)
0,1
1
0
-4
9
58
10
Q
Рациональные
Выполнить действия
Ответы
Вычислите:
.
3,5
ответ
Дроби естественно возникли при решении
задач о разделе имущества, измерении
земельных участков, исчислении времени.

Дробные числа
1
1
23 1
;
;
.
;
8 123
2
67
3
1
1
;
;
;
16 16 4
34 5
; ;
1 1
1
21
;
;
5
100
1
;
3600
Сумма, произведение и частное
дробных чисел есть число дробное.
Десятичные дроби в XV веке
ввел самаркандский ученый
ал — Каши.
Ничего, не зная об открытии ал – Коши,
десятичные дроби открыл второй раз,
приблизительно через 150 лет, после него,
фламандский ученый математик и инженер
Симон Стевин в труде «Децималь» (1585 г).
Множество рациональных чисел
Множество рациональных чисел обозначается и
может быть записано в виде: Q=m:n
Нужно понимать, что численно равные дроби
такие как, например, 3/4 и 9/12 , входят в это
множество как одно число.
Поскольку делением числителя и знаменателя
дроби на их наибольший общий делитель можно
получить единственное несократимое
представление рационального числа, то можно
говорить об их множестве как о множестве
несократимых дробей со взаимно простыми целым
числителем и натуральным знаменателем:
Рациональные числа
r — рациональное
r Q
Сумма, произведение, разность и
частное рациональных чисел есть
число рациональное.

Замените данные рациональные числа
десятичными дробями.
1
2
0,5
1
0,2
5
1
1
0,125
0 ,333…
8
3
1
0,25
4
2
0,4
5
3
0,375
8
2
0 ,666…
3
3
0,75
4
3
0,6
5
5
0,625
8
1
0 ,1666..
6
Чтобы обратить чисто периодическую дробь
в обыкновенную, нужно в числителе обыкновенной
дроби поставить число,
образованное из цифр, стоящих в периоде,
а в знаменателе – написать цифру 9 столько раз,
сколько цифр в периоде.
0,(2)=
2
1 цифра
9
0,(81)=
81
2 цифры
99
9
11
Чтобы обратить смешанную периодическую дробь
в обыкновенную, нужно в числителе обыкновенной дроби
поставить число, равное разности числа, образованного
цифрами, стоящими после запятой до начала второго
периода, и числа, образованного из цифр, стоящих после
запятой до начала первого периода;
а в знаменателе написать цифру 9 столько раз, сколько
цифр в периоде, и со столькими нулями, сколько цифр
между запятой и началом периода.
0,4(6)=
46
1 цифра
1 цифра
46
90
4
42 7
90 15
24. Рациональные числа как бесконечные десятичные дроби
РАЦИОНАЛЬНЫЕ ЧИСЛА КАКБЕСКОНЕЧНЫЕ ДЕСЯТИЧНЫЕ ДРОБИ
Для всех рациональных чисел можно использовать
один и тот же способ записи. Рассмотрим
1. Целое число 5
5,000
2. Обыкновенную дробь
0, 3(18)
3. Десятичную дробь 8,377
8,3(7)
25. Пример. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь.
ПРИМЕР. ЗАПИСАТЬ В ВИДЕ ОБЫКНОВЕННОЙДРОБИ БЕСКОНЕЧНУЮ ДЕСЯТИЧНУЮ
ПЕРИОДИЧЕСКУЮ ДРОБЬ.
Положим, что х=1,(23), т.е. 1,232323…
100х=123,2323…
100х=123,2323…
х=1,2323…
99х=122
х=
Итак: 1,(23)=
122
99
27. Иррациональные числа
ИРРАЦИОНАЛЬНЫЕ ЧИСЛАБесконечная
непериодическая дробь
называется иррациональным
числом.
Например:
Множество иррациональных чисел
обоначается J.
28. Действительные числа
ДЕЙСТВИТЕЛЬНЫЕЧИСЛА
R=(рациональные числа, иррациональные числа)
Действительные числа не обладают свойством
замкнутости — не всякое уравнение имеет корни.

29. Задания для самопроверки
ЗАДАНИЯ ДЛЯ САМОПРОВЕРКИКакие дроби называются десятичными
Действия с обыкновенными и десятичными
дробями
Какие числа называются действительными?
Действия с действительными числами.
Примеры
72
8
8
1) 1, (72) 1
1 1
99
11
11
912 9
903
301
2) 2,9(12) 2
2
2
990
990
495
128 12
116
29
3) 1,12(8) 1
1
1
900
900
225
Какой буквой обозначаются действительные числа. Разряды и классы. Расширенный алгоритм Эвклида
Что такое число? ЧИСЛО — одно из основных понятий математики, зародилось в глубокой древности и постепенно расширялось и обобщалось. В связи со счётом отдельных предметов возникло понятие о целых положительных (натуральных) числах, а затем идея о безграничности натурального ряда чисел: 1, 2, 3, Натуральные числа – это числа, используемые при счёте предметов. 1
История. На раскопках стойбища древних людей нашли волчью кость, на которой 30 тысяч лет тому назад, какой – то древний охотник нанёс пятьдесят пять зарубок. Видно, что, делая эти зарубки, он считал по пальцам. Узор на кости состоял из одиннадцати групп, по пять зарубок в каждой. При этом первые пять групп он отделил от остальных длинной чертой. Также в Сибири и в других местах были найдены, сделанные в ту же далёкую эпоху каменные орудия и украшения, на которых тоже были чёрточки и точки, сгруппированные по 3, по 5 или по 7.Кельты — древний народ, живший в Европе 2500 лет тому назад, являющиеся предками французов и англичан, считали двадцатками (две руки и две ноги давали двадцать пальцев). Следы этого сохранились во французском языке, где слово «восемьдесят» звучит как «четыре раза двадцать». Двадцатками считали и другие народы – предки датчан и голландцев, осетин и грузин. 2
Видно, что, делая эти зарубки, он считал по пальцам. Узор на кости состоял из одиннадцати групп, по пять зарубок в каждой. При этом первые пять групп он отделил от остальных длинной чертой. Также в Сибири и в других местах были найдены, сделанные в ту же далёкую эпоху каменные орудия и украшения, на которых тоже были чёрточки и точки, сгруппированные по 3, по 5 или по 7.Кельты — древний народ, живший в Европе 2500 лет тому назад, являющиеся предками французов и англичан, считали двадцатками (две руки и две ноги давали двадцать пальцев). Следы этого сохранились во французском языке, где слово «восемьдесят» звучит как «четыре раза двадцать». Двадцатками считали и другие народы – предки датчан и голландцев, осетин и грузин. 2
Чётные и нечётные числа. Чётное число целое число, которое делится без остатка на 2: …, 2, 4, 6, 8, … Нечётное число целое число, которое не делится без остатка на 2: …, 1, 3, 5, 7, 9, … Пифагор определяя число как энергию и считал, что через науку о числах раскрывается тайна Вселенной, ибо число заключает в себе тайну вещей. Чётные числа Пифагор считал женскими, а нечётные – мужскими: 2+3=5 5- это символ семьи, брака. Чётные и нечётные числа = женские и мужские числа. 4
Чётные числа Пифагор считал женскими, а нечётные – мужскими: 2+3=5 5- это символ семьи, брака. Чётные и нечётные числа = женские и мужские числа. 4
Простые и составные. Простое число – это натуральное число, имеющее ровно два различных натуральных делителя: единицу и само себя. Последовательность простых чисел начинается так: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, … Составные числа- это числа имеющие 3 и больше делителей. Изучением свойств простых чисел занимается теория чисел. Таким образом, все натуральные числа больше единицы разбиваются на простые и составные. 5
Совершенные и несовершенные числа. Совершенные числа, целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = и 28 = являются совершенными. До сих пор (1976) неизвестно ни одного нечётного Сов. ч. и вопрос о существовании их остаётся открытым.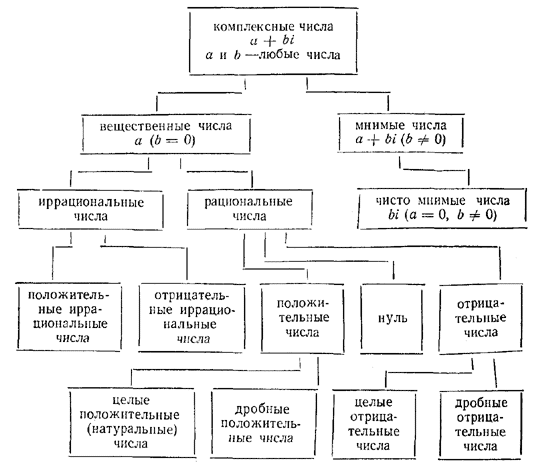 Исследования о Сов. ч. были начаты пифагорейцами, приписывавшими особый мистический смысл числам и их сочетаниям. Несовершенными Пифагор называл числа, сумма правильных делителей, которых меньше его самого. 6
Исследования о Сов. ч. были начаты пифагорейцами, приписывавшими особый мистический смысл числам и их сочетаниям. Несовершенными Пифагор называл числа, сумма правильных делителей, которых меньше его самого. 6
Магические числа. Секреты чисел привлекают людей, заставляют вникать, разбираться, сравнивать свои выводы с реальным соотношением дел. К цифрам в древнем мире относились очень трепетно. Люди, познавшие их, считались великими, их приравнивали к божествам. Самый простой пример – это отсутствие во многих странах самолётов с бортовым номером 13, этажей и номеров в гостиницах с номером «13». 8
Магический ряд 2 – число равновесия и контраста, и поддерживающие устойчивость, смешивающие позитивные и негативные качества. 6 – Символ надёжности. Это идеальное число, которое делится как на чётное число(2), так и на нечётное(3), таким образом, объединяя элементы каждого. 8 – Число материального успеха. Оно означает надёжность, доведённую до совершенства, поскольку представлено двойным квадратом. Разделённое пополам, оно имеет равные части (4 и 4). Если его ещё разделить, то части будут тоже равными (2, 2, 2, 2), показывая четырёхкратное равновесие. 9 – Число всеобщего успеха, самое большое из всех цифр. Как трёхкратное числу 3, девятка превращает неустойчивость в стремление. 10
Разделённое пополам, оно имеет равные части (4 и 4). Если его ещё разделить, то части будут тоже равными (2, 2, 2, 2), показывая четырёхкратное равновесие. 9 – Число всеобщего успеха, самое большое из всех цифр. Как трёхкратное числу 3, девятка превращает неустойчивость в стремление. 10
Найдите на числовой окружности точки с данной абсциссой. Координаты. Свойство координат точек. Центр числовой окружности. От окружности к тригонометру. Найдите на числовой окружности точки. Точки с абсциссой. Тригонометр. На числовой окружности укажите точку. Числовая окружность на координатной плоскости. Числовая окружность. Точки с ординатой. Назвать координату точки. Назвать линию и координату точки.
««Производные» 10 класс алгебра» — Применение производной для исследования функций. Производная равна нулю. Найдите точки. Обобщаем информацию. Характер монотонности функции. Применение производной к исследованию функций. Теоретическая разминка. Закончите формулировки утверждений. Выберите верное утверждение. Теорема. Сравните. Производная положительна. Сравните формулировки теорем. Функция возрастает. Достаточные условия экстремума.
Выберите верное утверждение. Теорема. Сравните. Производная положительна. Сравните формулировки теорем. Функция возрастает. Достаточные условия экстремума.
««Тригонометрические уравнения» 10 класс» — Значения из промежутка. X= tg х. Укажите корни. Верно ли равенство. Серии корней. Уравнение ctg t = a. Определение. Cos 4x. Найти корни уравнения. Уравнение tg t = a. Sin х. Имеет ли смысл выражение. Sin x =1. Не делай никогда того, чего не знаешь. Продолжите фразу. Сделаем выборку корней. Решите уравнение. Ctg x = 1. Тригонометрические уравнения. Уравнение.
«Алгебра «Производные»» — Уравнение касательной. Происхождение терминов. Решить задачу. Производная. Материальная точка. Формулы дифференцирования. Механический смысл производной. Критерии оценок. Функция производная. Касательная к графику функции. Определение производной. Уравнение касательной к графику функции. Алгоритм отыскания производной. Пример нахождения производной. Структура изучения темы. Точка движется прямолинейно.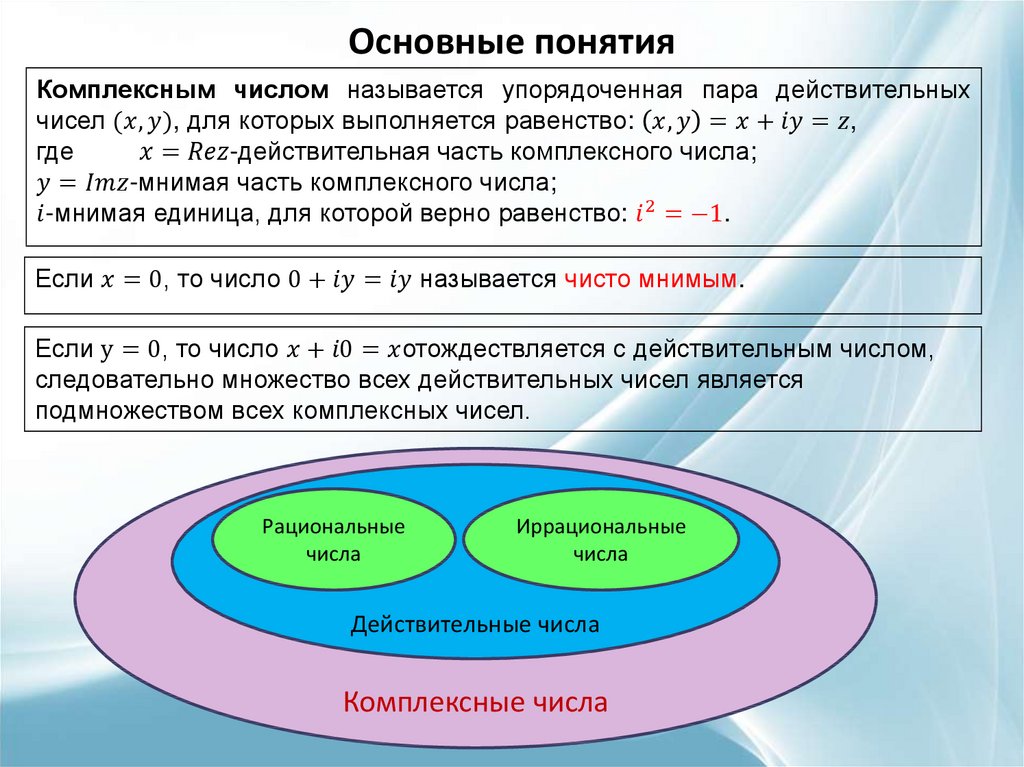
«Кратчайший путь» — Путь в орграфе. Пример двух разных графов. Ориентированные графы. Примеры ориентированных графов. Достижимость. Кратчайший путь из вершины A в вершину D. Описание алгоритма. Преимущества иерархического списка. Взвешенные графы. Путь в графе. Программа “ProGraph”. Смежные вершины и рёбра. Степень вершины. Матрица смежности. Длина пути во взвешенном графе. Пример матрицы смежности. Нахождение кратчайшего пути.
«История тригонометрии» — Якоб Бернулли. Техника оперирования с тригонометрическими функциями. Учение об измерении многогранников. Леонард Эйлер. Развитие тригонометрии с XVI века до нашего времени. Ученику приходится встречаться с тригонометрией трижды. До сих пор тригонометрия формировалась и развивалась. Построение общей системы тригонометрических и примыкающих к ним знаний. Проходит время, и тригонометрия возвращается к школьникам.
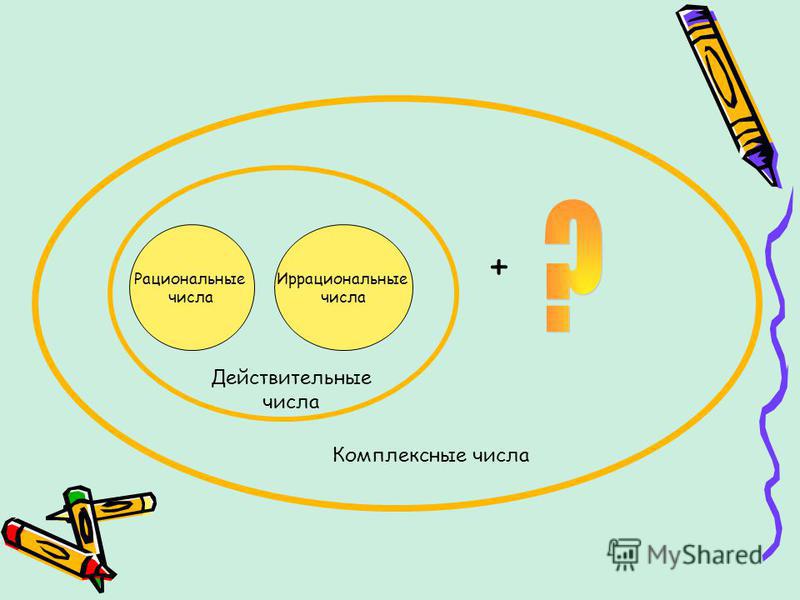
Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.
Определение действительных чисел
Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?
Определение 1
Действительные числа — это рациональные и иррациональные числа. Множество действительных чисел обозначается через R.
Данное определение можно записать иначе с учетом следующего:
- Рациональные числа можно представить в виде конечной десятичной дроби или бесконечной периодической десятичной дроби.
- Иррациональные числа представляют собой бесконечные непериодические десятичные дроби.
Определение 2
Действительные числа — числа, которые можно записать в виде конечной или бесконечной (периодической или непериодической) десятичной дроби.
Действительные числа — это любые рациональные и иррациональные числа. Приведем примеры таких чисел: 0 ; 6 ; 458 ; 1863 ; 0 , 578 ; — 3 8 ; 26 5 ; 0 , 145 (3) ; log 5 12 .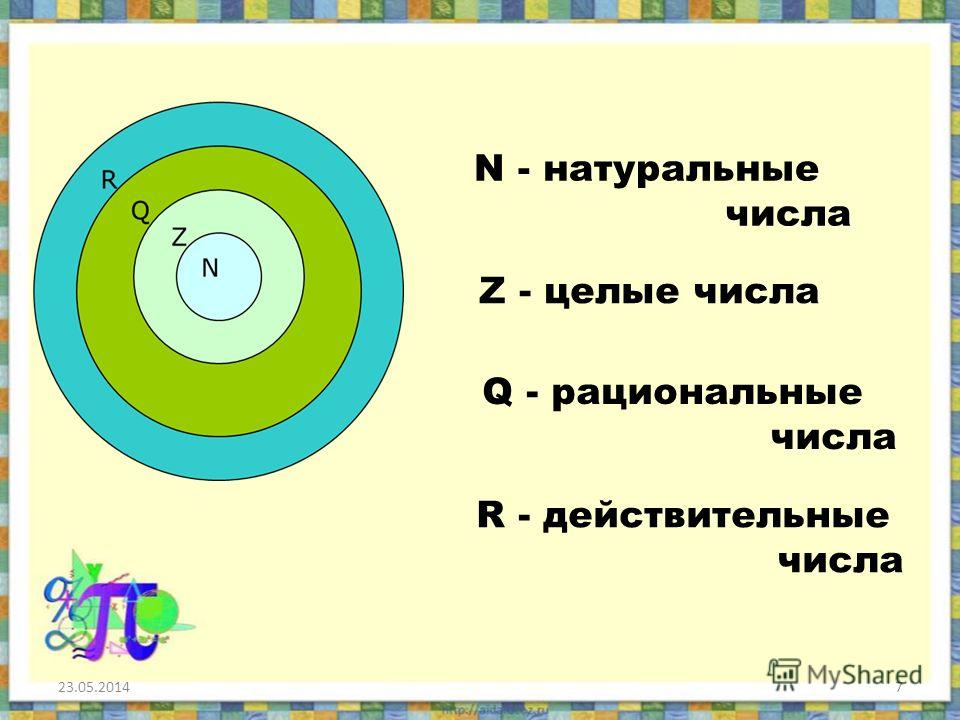
Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.
Еще одно название для действительных чисел — вещественные числа. Эти числа позволяют описывать значение непрерывно меняющейся величины без введения эталонного (единичного) значения этой величины.
Координатная прямая и действительные числа
Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.
Представления действительных чисел
Под определение дейситвительных чисел попадают:
- Натуральные числа.
- Целые числа.
- Десятичные дроби.
- Обыкновенные дроби.
- Смешанные числа.
Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.
Сумма, разность произведение и частное действительных чисел также являются действительными числами.
Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.
Например, значения выражений sin 2 3 π · e — 2 8 5 · 10 log 3 2 и t g 6 7 6 693 — 8 π 3 2 — действительные числа.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Интуитивное представление о числе, по–видимому, так же старо, как и само человечество, хотя с достоверностью проследить все ранние этапы его развития в принципе невозможно. Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе, позволявшим ему различать одного человека и двух людей или двух и многих людей. То, что первобытные люди сначала знали только “один”, “два” и “много”, подтверждается тем, что в некоторых языках, например в греческом, существуют три грамматические формы: единственного числа, двойственного числа и множественного числа. Позднее человек научился делать различия между двумя и тремя деревьями и между тремя и четырьмя людьми. Счет изначально был связан с вполне конкретным набором объектов, и самые первые названия чисел были прилагательными. Например, слово “три” использовалось только в сочетаниях “три дерева” или “три человека”; представление о том, что эти множества имеют между собой нечто общее – понятие троичности – требует высокой степени абстракции. О том, что счет возник раньше появления этого уровня абстракции, свидетельствует тот факт, что слова “один” и “первый”, равно как “два” и “второй”, во многих языках не имеют между собой ничего общего, в то время как лежащие за пределами первобытного счета “один”, “два”, “много”, слова “три” и “третий”, “четыре” и “четвертый” ясно указывают на взаимосвязь между количественными и порядковыми числительными.
Позднее человек научился делать различия между двумя и тремя деревьями и между тремя и четырьмя людьми. Счет изначально был связан с вполне конкретным набором объектов, и самые первые названия чисел были прилагательными. Например, слово “три” использовалось только в сочетаниях “три дерева” или “три человека”; представление о том, что эти множества имеют между собой нечто общее – понятие троичности – требует высокой степени абстракции. О том, что счет возник раньше появления этого уровня абстракции, свидетельствует тот факт, что слова “один” и “первый”, равно как “два” и “второй”, во многих языках не имеют между собой ничего общего, в то время как лежащие за пределами первобытного счета “один”, “два”, “много”, слова “три” и “третий”, “четыре” и “четвертый” ясно указывают на взаимосвязь между количественными и порядковыми числительными.
Названия чисел, выражающие весьма абстрактные идеи, появились, несомненно, позже, чем первые грубые символы для обозначения числа объектов в некоторой совокупности. В глубокой древности примитивные числовые записи делались в виде зарубок на палке, узлов на веревке, выложенных в ряд камешков, причем подразумевалось, что между пересчитываемыми элементами множества и символами числовой записи существует взаимно однозначное соответствие. Но для чтения таких числовых записей названия чисел непосредственно не использовались. Ныне мы с первого взгляда распознаем совокупности из двух, трех и четырех элементов; несколько труднее распознаются на взгляд наборы, состоящие из пяти, шести или семи элементов. А за этой границей установить на глаз их число практически уже невозможно, и нужен анализ либо в форме счета, либо в определенном структурировании элементов. Счет на бирках, по–видимому, был первым приемом, который использовался в подобных случаях: зарубки на бирках располагались определенными группами подобно тому, как при подсчете избирательных бюллетеней их часто группируют пачками по пять или десять штук. Очень широко был распространен счет на пальцах, и вполне возможно, что названия некоторых чисел берут свое начало именно от этого способа подсчета.
В глубокой древности примитивные числовые записи делались в виде зарубок на палке, узлов на веревке, выложенных в ряд камешков, причем подразумевалось, что между пересчитываемыми элементами множества и символами числовой записи существует взаимно однозначное соответствие. Но для чтения таких числовых записей названия чисел непосредственно не использовались. Ныне мы с первого взгляда распознаем совокупности из двух, трех и четырех элементов; несколько труднее распознаются на взгляд наборы, состоящие из пяти, шести или семи элементов. А за этой границей установить на глаз их число практически уже невозможно, и нужен анализ либо в форме счета, либо в определенном структурировании элементов. Счет на бирках, по–видимому, был первым приемом, который использовался в подобных случаях: зарубки на бирках располагались определенными группами подобно тому, как при подсчете избирательных бюллетеней их часто группируют пачками по пять или десять штук. Очень широко был распространен счет на пальцах, и вполне возможно, что названия некоторых чисел берут свое начало именно от этого способа подсчета.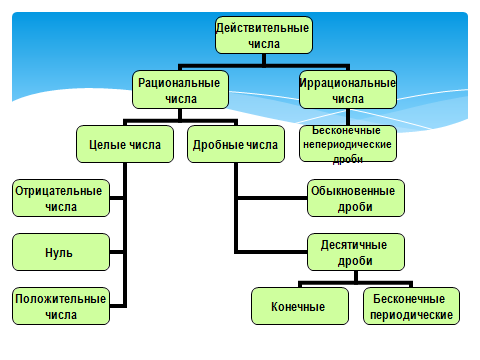
Важная особенность счета заключается в связи названий чисел с определенной схемой счета. Например, слово “двадцать три” – не просто термин, означающий вполне определенную (по числу элементов) группу объектов; это термин составной, означающий “два раза по десять и три”. Здесь отчетливо видна роль числа десять как коллективной единицы или основания; и действительно, многие считают десятками, потому что, как отметил еще Аристотель, у нас по десять пальцев на руках и на ногах. По той же причине использовались основания пять или двадцать. На очень ранних стадиях развития истории человечества за основания системы счисления принимались числа 2, 3 или 4; иногда для некоторых измерений или вычислений использовались основания 12 и 60.
Считать человек начал задолго до того, как он научился писать, поэтому не сохранилось никаких письменных документов, свидетельствовавших о тех словах, которыми в древности обозначали числа. Для кочевых племен характерны устные названия чисел, что же касается письменных, то необходимость в них появилась лишь с переходом к оседлому образу жизни, образованием земледельческих сообществ. Возникла и необходимость в системе записи чисел, и именно тогда было заложено основание для развития математики.
Возникла и необходимость в системе записи чисел, и именно тогда было заложено основание для развития математики.
Основные виды чисел
В отличие от октав, седенионы S не обладают свойством альтернативности, но сохраняют свойство степенной ассоциативности .
Для представления целого положительного числа х в памяти компьютера, оно переводится в двоичную систему счисления. Полученное число в двоичной системе счисления х 2 представляет собой машинную запись соответствующего десятичного числа х 10 . Для записи отрицательных чисел используется т. н. дополнительный код числа, который получается путём прибавления единицы к инвертированному представлению модуля данного отрицательного числа в двоичной системе счисления.
Представление действительных чисел в памяти компьютера (в вычислительной технике для их обозначения используется термин число с плавающей запятой) имеет некоторые ограничения связанные с используемой системой счисления, а также, ограниченностью объёма памяти выделяемого под числа.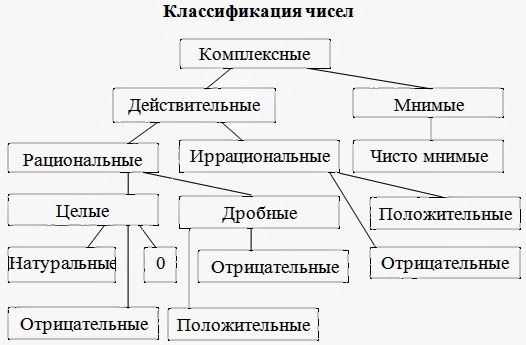 Так, лишь некоторые из действительных чисел могут быть без потерь в точности представлены в памяти компьютера. В наиболее распространённой схеме число с плавающей запятой записывается в виде блока битов часть из которых представляют собой мантиссу числа, часть — степень, а один бит выделяется для представления знака числа (в случае необходимости знаковый бит может отсутствовать).
Так, лишь некоторые из действительных чисел могут быть без потерь в точности представлены в памяти компьютера. В наиболее распространённой схеме число с плавающей запятой записывается в виде блока битов часть из которых представляют собой мантиссу числа, часть — степень, а один бит выделяется для представления знака числа (в случае необходимости знаковый бит может отсутствовать).
Урок алгебры по теме «Действительные числа»
Тип урока: усвоение новых знаний
Планируемые образовательные результаты.
Предметные: знать понятие «действительные числа», систематизировать и развить знания учащихся о различных числовых множествах. Ввести понятия о десятичной периодической и непериодической десятичной дроби, рациональных, иррациональных и действительных числах; установить связи между ними.
Личностные: формирование ответственного отношения к успешной учебной деятельности.
Метапредметные:
- регулятивные – уметь планировать свою деятельность, осуществлять самоконтроль и самооценку, переводить информацию с наглядно – интуитивного уровня на рабочий уровень восприятия, осуществлять прикидку и оценку результата действия;
- коммуникативные – уметь вести диалог, слушать, аргументированно вести свои суждения;
- познавательные – уметь логически мыслить, рассуждать, развивать интерес к предмету посредством применения информационных технологий и экскурсов в историю.

Оборудование: интерактивная доска, презентация «Действительные числа», раздаточный материал.
Учебник: «Алгебра 8 класс», учебник для общеобразовательных учреждений Ш.А Алимов, Ю.А. Колягин и др. М.: Просвещение, 2014г.
Этапы урока
1. Организационный этап.
2. Актуализация знаний учащихся.
3. Обобщение знаний о числовых множествах (проводится с помощью презентации «Действительные числа»)
4. Введение понятия иррационального числа и множества действительных чисел.
5. Решение примеров на запись обыкновенной дроби в виде конечной или бесконечной периодической десятичной дроби.
6. Закрепление изученного. Тест (Приложение 1)
7. Домашнее задание.
8. Рефлексия.
9. Итоги урока.
ХОД УРОКА
1 этап. Организационный
Мотивация учебной деятельности учащихся,
Постановка цели и задач урока (Презентация.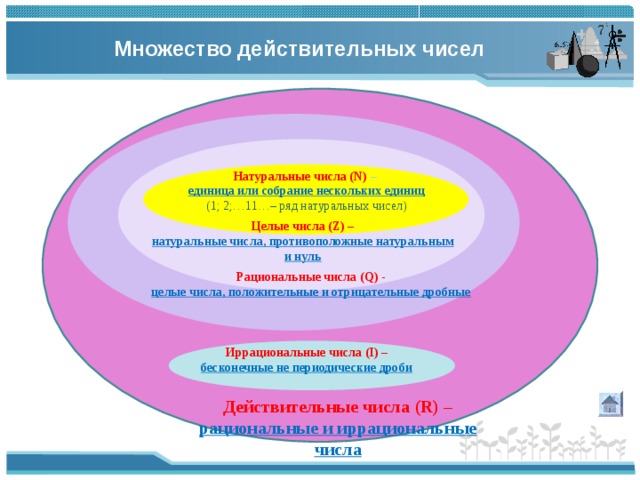 Слайды 1-2)
Слайды 1-2)
2. Актуализация знаний
Определение принадлежности чисел из данной группы тому или иному числовому множеству, известному учащимся. (Слайд 3)
Учитель оценивает выполнение задания, затем следует рассказ учителя о роли числа как формы мысли, отражающей в обобщенном виде свойства и отношения реальных предметов. Подчеркивается, что именно числа дают возможность считать предметы окружающего нас мира, измерять их и измеряя сравнивать.
«Числа существуют в сознании человека, эти «мысленные» создания образуют его знания и умения, являются могучими орудиями с помощью которых он создает все для себя и вокруг себя: материальную среду обитания, культуру и технику».
А. Дородницын
3. Обобщение знаний о числовых множествах
Исторические справки озвучиваются учащимися с помощью слайдов (4-9)
3.1 Натуральные числа (Слайд 4)
Название этих чисел произошло от слова «naturе» (лат.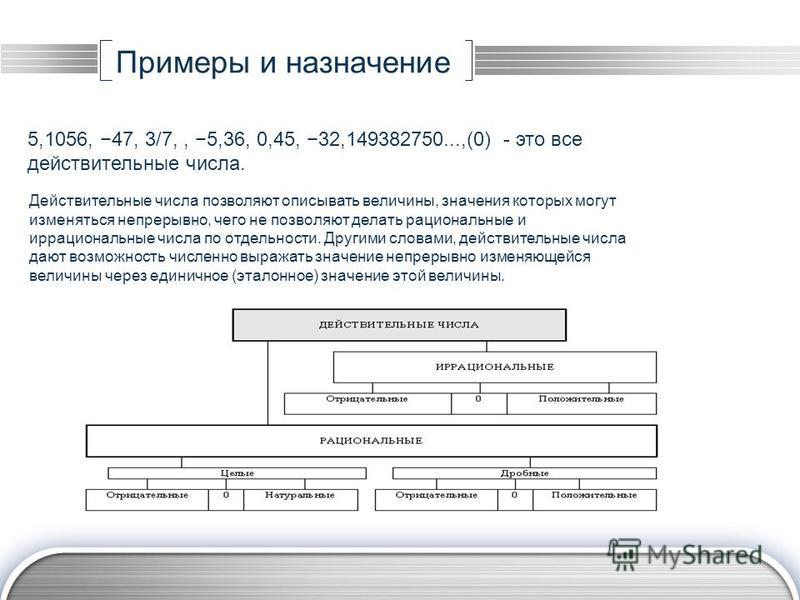 ), то есть, природа.
), то есть, природа.
Натуральные числа возникли много тысяч лет назад. Причиной их появления стала необходимость счета предметов. С помощью чисел человек, например, получил возможность пересчитать добычу охотников и правильно распределить ее между соплеменниками.
На первых стадиях развития человечества для счета использовались только два числа: 1 и 2. Шло время, человек стал привлекать для счета части своего тела: пальцы рук и ног, если таких цифр не хватало, то на помощь призывали родственников, соседей, знакомых.
Знаменитый путешественник Н.Н. Миклухо-Маклай в своей книге «Путешествия» так рассказывает об излюбленном способе счета папуасов Новой Гвинеи: «Загибая пальцы руки, папуас издает определенный звук, например, «бе, бе, бе», досчитав до пяти, он говорит «ибн-бе» – рука, далее продолжает считать до «ибн-али» (две руки), затем идет «самба-бе» – одна нога, «самба-али» – две ноги, а затем при необходимости привлекаются конечности кого-то другого». Так люди начинали учится считать, пользуясь тем, что им дала природа: собственной пятерней. Вот где кроются истоки высказывания «Знаю, как свои пять пальцев».
Вот где кроются истоки высказывания «Знаю, как свои пять пальцев».
Вопрос: Какой способ записи чисел используется нами? Где и когда изобрели эту форму записи?
Учитель: Постепенно росли знания людей, увеличивалась потребность в умении считать и мерить все большими числами. Счет шел уже на сотни и тысячи, а запоминать большие числа трудно или невозможно. Какой выход из положения нашел человек, мы сейчас узнаем.
3.2. Как записывались числа (Слайды 5, 6)
Первым способом записи чисел стали зарубки на палке, именно таким календарем пользовался Робинзон Крузо, попав на необитаемый остров.
Все получалось хорошо, пока числа были небольшими, а сделать тысячи зарубок на палке сложно и неудобно. Представьте себе подобную записную книжку!
Около 5 тысяч лет назад, почти одновременно в разных странах возникли различные формы записи чисел.
В Египте обозначали числа палочками, подковами, спиралями.
Индейцы майя кружочками и черточками.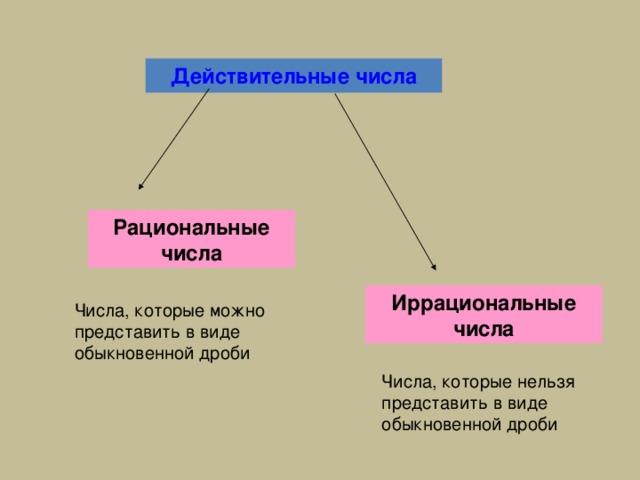
С римским способом записи чисел вы немного знакомы.
Славяне позаимствовали способ записи у греков: они обозначали числа буквами с особыми значками наверху, которые назывались титлы.
Идея бесконечности ряда натуральных чисел еще не возникла.
Самое большое число наши предки называли «колода», что соответствовало 10 в 49 степени «Сего числа несть больше» – писал летописец.
Для обозначения больших чисел был придуман очень интересный способ – одна и та же буква в разном орнаменте.
Учитель: Для обозначения результата вычитания равных натуральных чисел человек изобрел ноль. Однако ремесленникам, торговцам, мореплавателям одних натуральных чисел и нуля было уже мало, поскольку возникали задачи деления земли, наследства и многого другого, да и развивающаяся наука математика нуждалась в разрешении вопроса о не всегда возможном делении натуральных чисел друг на друга.
3.3. Так появились дроби (Слайды 7, 8)
В древности к целым и дробным числам относились по-разному.
«Если ты захочешь делить единицу, математики засмеют тебя и не позволят это сделать» – писал знаменитый ученый и философ Платон. Однако постепенно человек привык к мысли, что дроби – равноправные числа.
Уже в 4 веке до нашей эры Пифагор, создавая теорию музыкальной шкалы, связал музыкальные интервалы с дробями. Долгие годы считалось, что нет ничего сложнее, чем действия с дробями. В средние века деление чисел служило признаком высоко образованного человека.
«Попал в дроби» – эта немецкая поговорка говорит о том, что человек попал в очень сложное положение.
А Лев Николаевич Толстой сделал интересное и меткое арифметическое сравнение, что «человек подобен дроби, числитель которой есть то, что человек представляет собой, а знаменатель, что он думает о себе.
Чем большего мнения о себе человек, тем больше знаменатель, а значит, тем меньше дробь».
Учитель: Мы забежали на много веков вперед. Систематизируя наши знания о числах, нельзя обойтись без рассказа о Пифагоре и его учениках.
3.4. Пифагор и его школа (Слайд 9)
Письменных документов о великом математике не сохранилось. Известно, что в возрасте примерно 40 лет он поселился в одном из греческих городов на юге Италии, Пифагор достиг больших успехов в изучении разных наук, особенно философии математики. Он настолько преуспел в науках, что у него появились ученики и последователи. Была образована философская школа Пифагора, члены которой узнавали друг друга по отличительному знаку – пентаграмме, имеющей форму пятиконечной звезды.
Конечно, выбор символа не был случаен: пифагорейцы считали, что пентаграмма обладает мистическими свойствами и обладает способностью отгонять злых духов. Число лучей воспринималось как число любви, жизни и здоровья. Пифагор первым разделил числа на четные и нечетные, простые и составные. К числам он хотел свести весь мир.
Пифагорейцы изучали свойства дружественных, совершенных. фигурных чисел. Совершенные числа равнялись сумме своих делителей (кроме самого себя), число 6 = 1 + 2 + 3, особенно почиталось, ведь за 6 дней Бог сотворил мир.
Еще важнее считалось число 36 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8, по мнению Пифагора, первые четыре четных и четыре нечетных числа служили основой мира – самая страшная, нерушимая клятва была у пифагорейцев клятва числом 36.
Каждому натуральному числу приписывалось особое, мистическое значение.
«Вещи суть копии чисел, числа – начала вещей», в этом были убеждены последователи Пифагора.
Средневековые математики разделяли эти взгляды: сверхъестественные способности они приписывали дружественным числам.
В одном из трактатов сохранился такой рецепт: «Чтобы добиться взаимности в любви, нужно на чем-либо написать числа 220 и 284, записку с большим числом съесть самому, а меньшее число дать объекту любви»
Автор добавлял, что проверил рецепт на себе.
Изучая свойства различных чисел и их групп, Пифагорейцы заложили основы важного раздела математики – теории чисел.
Учитель: С дробными числами человек познакомился намного раньше, чем с отрицательными. Впервые идея самостоятельных отрицательных чисел возникла у математиков Индии (5-7 век), причем они трактовали эти числа как долг. Окончательно ввел в математику отрицательные числа Рене Декарт, он же определил им место на числовой прямой.
Впервые идея самостоятельных отрицательных чисел возникла у математиков Индии (5-7 век), причем они трактовали эти числа как долг. Окончательно ввел в математику отрицательные числа Рене Декарт, он же определил им место на числовой прямой.
Числа натуральные, целые отрицательные и нуль образовали множество целых чисел Z, к ним добавились дробные числа, и получилось множество рациональных чисел Q («ratio» – отношение) (Слайд 10)
4. Повторяется определение рационального числа.
Действительно, подтвердим примерами корректность определения:
Задание: Представить рациональное число в виде десятичной дроби:
Вопросы учащимся
1. Какие числа вы получили в результате деления?
2. Чем отличаются полученные десятичные дроби? (Введение определения периодической десятичной дроби)
3. Существует ли отличие периодических дробей друг от друга, если «да», то в чем оно выражается?
Вывод: Любое рациональное число представимо в виде конечной или бесконечной периодической десятичной дроби.
Вопрос: Какое число может быть исключено из определения и почему? (Слово «конечная» – так как любая конечная десятичная дробь может быть представлена в виде бесконечной периодической дроби с периодом «0»).
Виды периодических дробей: чисто периодическая и смешанная периодическая, примеры.
Выполнение № 316, уточнить вид дроби.
5. Введение понятия действительного числа. (Слайд № 11)
Вопрос: Существуют ли бесконечные дроби другого вида?
Если «да», то приведите пример. (0,101001000100001000001000000…)
Учащиеся пробуют создать аналогичную дробь.
Учащиеся дополняют круги Эйлера до множества действительных чисел R
Пифагор и его страшная тайна
Открытие иррациональных чисел приписывают пифагорейцам.
Однако, они считали, что иррациональные числа нарушают гармонию мира, поэтому поклялись, держать свое открытие в тайне. Тот, кто нарушит клятву, должен был умереть. Ученик Пифагора Гиппас не сдержал клятву, и боги его покарали, корабль, на котором плыл Гиппас, потерпел кораблекрушение во время бури, ниспосланной богами.
6. Учитель подводит промежуточный итог урока.
Задается домашнее задание: П.21, №317(2,4,6), №318(2,4), №322(2,4,6).
Реферат «История математического открытия» (срок исполнения 1 неделя).
Учитель показывает и рекомендует ряд книг, которые можно использовать для подготовки сообщения (Е.И. Игнатьев «Хрестоматия по истории математики», И.Я. Бурау «Загадки мира чисел», Г.И.Глейзер «История математики в школе для 5-8, 9-10 классов».)
7. Тест (Приложение 1)
Самостоятельная работа учащихся с целью проверки уровня усвоения материала.
Тест состоит из двух вариантов. Каждый из вариантов структурно разбит на два уровня. Первый уровень позволяет проверить, насколько учащийся может повторить новую информацию. Задания второго уровня позволяют проверить, насколько учащийся понял и научился применять новые знания. Задания, включенные в тест, оцениваются в зависимости от их уровня сложности.
8. Рефлексия
Рефлексия
Учащиеся отвечают на вопросы:
1) Понравился ли тебе урок?
2) Что тебе не понравилось?
3) Какой фрагмент урока был самым интересным?
9. Итоги урока
Введены понятия «рациональное число», «действительное число», установлена связь между натуральными, целыми, рациональными и действительными числами. Учащиеся научились обыкновенные дроби представлять в виде бесконечной периодической и, наоборот, бесконечные периодические дроби в виде обыкновенных дробей. Узнали много
интересного из истории развития понятия числа.
(Слайд №12)
Урок заканчивают строки стихотворения В. Брюсова «Числа», посвященного вдохновенным мечтателям, которые с помощью царственных чисел совершают великие открытия.
Мечтатели, сибиллы и пророки!
Дорогами, запретными для мысли,
Проникли – вне сознания – далеко,
Туда, где светят царственные числа.
Вам поклоняюсь, вас желаю, числа!
Свободные, бесплотные, как тени,
Вы радугой связующей повисли
К раздумьям, с вершины вдохновенья!
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 5 из 5 Изучение действительных чисел в курсе алгебры 8 класса связано с введением квадратного корня из числа, который, как известно, может быть числом иррациональным. Содержание учебного материала. 1. Рациональные числа. 2. Иррациональные числа.
1. Изучение действительных чисел начинается с повторения чисел рациональных (от латинского ratio – отношение). В объяснительном тексте учебника повторяются натуральные, целые и рациональные числа. Вводятся обозначения: N – множество натуральных чисел, Z – множество целых чисел, Q – множество рациональных чисел. Используются знаки Î и Ï для записи утверждения, что число является или не является элементом данного числового множества. Основное внимание уделяется числам рациональным, которые состоят из чисел целых и дробных. Далее рассматриваются представления рациональных чисел в виде дроби. Всякое рациональное число (как целое, так и дробное) можно представить в виде обыкновенной дроби , где т – целое число, а п – натуральное число. На ряде примеров (без доказательства) делением числителя на знаменатель учащиеся убеждаются, что каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. При этом конечные десятичные дроби рассматриваются как бесконечные периодические с периодом 0. Верно и обратное утверждение: каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число. Замечание. Существуют правила представления бесконечной десятичной периодической дроби в виде рационального числа. Однако в школе они не рассматриваются. Приведём хитроумный способ такого представления. Например, дробь 0, (17). Пусть 0, (17)=х. Тогда 100х=17,(17). Вычтем из второго равенства первое. 99х=17, х=17/99. 2. Иррациональные числа вводятся посредством операции измерения отрезка. Пусть точка О – начальная точка координатной прямой и отрезок ОЕ – единица измерения.
Рис. 5 Откладывают от точки О единицу измерения – отрезок ОЕ. Он уложился в отрезке ОВ 2 раза. Значит длина отрезка ОВ » 2. Чтобы получить более точный результат, разделим отрезок ОЕ на 10 равных частей. Десятая часть отрезка ОЕ укладывается в остатке СВ 3 раза. Приближённое значение длины отрезка АВ с точностью до 0,1 равно 2,1. Продолжая процесс измерения, мы будем использовать 0,01; 0,001 . . . доли единичного отрезка, получая приближённые значения длины отрезка АВ с точностью до 0,01; 0,001 . . . В процессе десятичного измерения могут представиться два случая: 1) на каком – то шаге не получится остатка; 2) остатки будут получаться на каждом шаге. В первом случае результатом измерения окажется натуральное число или конечная десятичная дробь, во втором случае бесконечная десятичная дробь. Так как всякое натуральное число и конечную десятичную дробь можно представить в виде бесконечной десятичной дроби, то можно считать, что результатом десятичного измерения длины отрезка всегда является бесконечная десятичная дробь. Далее на примерах убеждаемся, что длина отрезка может выражаться бесконечной десятичной периодической дробью либо бесконечной десятичной непериодической дробью. Пример 1. Пусть ОС=7/4 единичного отрезка. При десятичном измерении его длины получим число 1,75. Пример 2.Пусть отрезок ОF = 8/3 единичного отрезка. длины При десятичном измерении его длины получится число 2,666… Пример 3. Пусть стороной квадрата служит отрезок длиной 1. Измерим с помощью этой единицы диагональ квадрата ОК.
Рис. 6
Длина отрезка ОК – сторона квадрата, площадь которого в 2 раза больше площади данного квадрата, равной 1. Следовательно, площадь большого квадрата равна 2. Следовательно, квадрат длины отрезка ОК равен 2. Докажем, что рационального числа, квадрат которого равен 2 не существует. Метод: от противного. Пусть такое рациональное число существует, то есть ( )2=2, где — несократимая дробь. Тогда , т2 – число чётное, значит и т – число чётное. В учебнике содержится ещё один важный вывод: десятичное измерение длин отрезков каждой точке координатной прямой, лежащей справа от начальной точки О, ставит в соответствие положительную бесконечную десятичную дробь. Наоборот, взяв произвольную положительную бесконечную десятичную дробь, мы можем найти на координатной прямой справа от точки О единственную точку А, такую, что длина отрезка Оа выражается этой дробью. Замечание. Рассмотренный материал достаточно трудно усваивается 8-классниками, но, к сожалению, в дальнейшем к изучению числовых систем учащиеся общеобразовательных классов не возвращаются. Литература. 1. Математика: Учебник для 5 кл, общеобразоват. учреждений /Н.Я. Виленкин, В.И. Жохов и др. 2. Математика: Учебник для 6 кл, общеобразоват. учреждений /Н.Я. Виленкин, В.И. Жохов и др. 3. Алгебра: Учебник для 8 кл. сред. шк./ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др; Под ред. С. А. Теляковского.— М.: Просвещение, 2003 г. 2. Сборник нормативных документов. Математика / сост. Э.Д. Днепров, А.Г. Аркадьев. 3. Жохов В.И. и др. Примерное планирование учебного материала и контрольные работы по математике, 5 – 9 классы. 4.Методика и технология обучения математике. Курс лекций: пособие для вузов/под научн. ред.Н.Л. Стефановой. – М.: Дрофа, 2005 г. 5. Методика преподавания математики в средней школе. Частные методики/ Ю.М. Колягин и др.
⇐ Предыдущая12345 Читайте также: Психологические особенности спортивного соревнования Приготовление дезинфицирующих растворов различной концентрации Занятость населения и рынок труда Социальный статус семьи и её типология |
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 520; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
Что такое реальное число? Определение и примеры
Эта запись была опубликована автором Anne Helmenstine (обновлено )
Вещественное число — это любое число, которое может быть представлено на числовой прямой или с использованием бесконечной десятичной дроби. расширение. Число, которое не является действительным, является мнимым.
Реальные числа — это числа, которые люди используют каждый день. Они включают в себя любое число, которое вы можете разместить на числовой прямой, независимо от того, положительное оно или отрицательное. Вот определение действительного числа, взгляд на наборы и свойства действительных чисел, а также конкретные примеры чисел, которые являются действительными и мнимыми.
Вещественное число Определение
Вещественное число — это любое число, которое можно разместить на числовой прямой или выразить в виде бесконечного десятичного представления. Другими словами, действительное число — это любое рациональное или иррациональное число, включая положительные и отрицательные целые числа, целые числа, десятичные дроби, дроби и такие числа, как число пи ( π ) и число Эйлера ( e ).
Другими словами, действительное число — это любое рациональное или иррациональное число, включая положительные и отрицательные целые числа, целые числа, десятичные дроби, дроби и такие числа, как число пи ( π ) и число Эйлера ( e ).
Напротив, мнимое число или комплексное число не является действительным числом . Эти числа содержат число i , где i 2 = -1.
Действительные числа представлены заглавной буквой «R» или двойным перечеркнутым шрифтом ℝ. Действительные числа представляют собой бесконечное множество чисел.
Набор реальных чисел
Набор реальных чисел включает в себя несколько небольших (но все еще бесконечных) подмножества:
| Набор | Определение | Примеры |
|---|---|---|
| ЕВИЧНЫЕ НОМЕРЫ (N) | ||
| ЕВИЧЕСКИЕ НОЯ , начиная с 1. N = {1,2,3,4,…} | 1, 3, 157, 2021 | |
| Целые числа (W) | Нуль и натуральные числа. W = {0,1,2,3,…} | 0, 1, 43, 811 |
| Целые числа (Z) | Целые числа и отрицательные числа всех натуральных чисел. Z = {..,-1,0,1,…} | -44, -2, 0, 28 |
| Рациональные числа (Q) | Числа, которые можно записать в виде дроби целых чисел p/ д, д≠0. , где Q = {p/q}, q≠0 | 1 / 3 , 5 / 4 , 0,8 |
| Действительные числа (P или I) | /q не могут быть выражены в виде целых чисел p. Это непрерывающиеся и неповторяющиеся десятичные дроби.π, e, φ, √2 |
Примеры действительных и мнимых чисел
Хотя знакомые числа, натуральные и целые числа довольно легко распознать как действительные числа, многие люди интересуются конкретными числами. Ноль — действительное число. Пи, число Эйлера и фи — действительные числа. Все дроби и десятичные числа являются действительными числами.
Числа, которые не являются действительными числами, являются либо мнимыми (например, √-1, i , 3 i ), либо комплексными ( a + bi ). Итак, некоторые алгебраические выражения действительны [например, √2, -√3, (1+ √5)/2], а некоторые нет [например, i 2 , (x + 1) 2 = — 9].
Итак, некоторые алгебраические выражения действительны [например, √2, -√3, (1+ √5)/2], а некоторые нет [например, i 2 , (x + 1) 2 = — 9].
Бесконечность (∞) и отрицательная бесконечность (-∞) — это , а не действительных чисел. Они не являются членами математически определенных множеств. В основном это связано с тем, что бесконечность и отрицательная бесконечность могут иметь разные значения. Например, множество целых чисел бесконечно. Как и множество целых чисел. Но эти два набора не одного размера.
Свойства действительных чисел
Четыре основных свойства вещественных чисел — коммутативность, ассоциативность, дистрибутивность и тождественность. Если m, n и r — действительные числа, то:
Переместительное свойство
- Сложение: m + n = n + m. Например, 5 + 23 = 23 + 5.
- Умножение: m × n = n × m. Например, 5 × 2 = 2 × 5.
Ассоциативное свойство
- Дополнение: Общая форма будет m + (n + r) = (m + n) + r.
 Примером аддитивного ассоциативного свойства является 5 + (3 + 2) = (5 + 3) + 2.
Примером аддитивного ассоциативного свойства является 5 + (3 + 2) = (5 + 3) + 2. - Умножение: (mn) r = m (nr). Примером мультипликативного ассоциативного свойства является (2 × 5) 6 = 2 (5 × 6).
Распределительная собственность
- m (n + r) = mn + mr и (m + n) r = mr + nr. Пример распределительного свойства: 2(3 + 5) = 2 x 3 + 2 x 5. Оба выражения равны 16.
Идентификационное свойство
- Для добавления: m + 0 = m. (0 — аддитивная идентичность)
- Для умножения: м × 1 = 1 × m = m. (1 — мультипликативная идентичность)
Ссылки
- Бенгтссон, Ингемар (2017). «Число простейшего SIC-POVM». Основы физики . 47:1031–1041. doi:10.1007/s10701-017-0078-3
- Borwein, J.; Борвейн, П. (1990). Словарь действительных чисел . Пасифик-Гроув, Калифорния: Брукс/Коул.
- Феферман, Соломон (1989).
 T Системы счисления: основы алгебры и анализа . АМС Челси. ISBN 0-8218-2915-7.
T Системы счисления: основы алгебры и анализа . АМС Челси. ISBN 0-8218-2915-7. - Хоуи, Джон М. (2005). Реальный анализ . Спрингер. ISBN 1-85233-314-6.
- Ландау, Эдмунд (2001). Основы анализа . Американское математическое общество. ISBN 0-8218-2693-X.
Вещественные числа: определение, значение и примеры
Вещественные числа — это значения, которые могут быть представлены в виде бесконечного десятичного представления. Действительные числа включают целые числа, натуральные числа и другие, о которых мы поговорим в следующих разделах. Примеры действительных чисел: ¼, пи, 0,2 и 5,9.0007
Вещественные числа классически могут быть представлены в виде длинной бесконечной линии, покрывающей отрицательные и положительные числа.
Типы чисел и символы
Числа, используемые для счета, известны как целые числа и являются частью рациональных чисел. Рациональные числа и целые числа также составляют действительные числа, но их гораздо больше, и их список можно найти ниже.
Натуральные числа с символом (N).
Целые числа с символом (W).
Целые числа с символом (Z).
Рациональные числа с символом (Q).
Иррациональные числа с символом (Q’).
Диаграмма Венна чисел
Типы действительных чисел
Важно знать, что для любого выбранного действительного числа это либо рациональное число, либо иррациональное число, которые являются двумя основными группами действительных чисел.
Рациональные числа
Рациональные числа — это тип действительных чисел, которые можно записать как отношение двух целых чисел. Они выражаются в виде p/q, где p и q — целые числа, не равные 0. Примерами рациональных чисел являются . Множество рациональных чисел всегда обозначается Q.
Примерами рациональных чисел являются . Множество рациональных чисел всегда обозначается Q.
Типы рациональных чисел
Существуют различные типы рациональных чисел, и это
Целые числа, например, -3, 5 и 4.
Дроби в форме p / q, где p и q являются целыми числами, например, ½.
Числа, не содержащие бесконечных десятичных знаков, например, ¼ от 0,25.
Числа с бесконечными десятичными разрядами, например, ⅓ от 0,333….
Иррациональные числа
Иррациональные числа — это тип действительных чисел, которые нельзя записать в виде отношения двух целых чисел. Это числа, которые не могут быть выражены в виде p/q, где p и q — целые числа.
Как упоминалось ранее, действительные числа состоят из двух групп – рациональных и иррациональных чисел, выражается в том, что иррациональные числа можно получить, вычитая группу рациональных чисел (Q) из группы действительных чисел (R). Это оставляет нам группу иррациональных чисел, обозначаемую Q ‘.
Примеры иррациональных чисел
Десятичное значение никогда не заканчивается и не повторяется. Ближайшее к пи дробное значение равно 22/7, поэтому чаще всего мы принимаем число пи равным 22/7.
Свойства действительных чисел
Как и в случае с целыми числами и натуральными числами, множество действительных чисел также обладает свойствами замыкания, коммутативности, ассоциативности и дистрибутивности.
Имущество закрытия
Произведение и сумма двух действительных чисел всегда является действительным числом. Свойство замыкания указано как; для всех a, b ∈ R, a + b ∈ R и ab ∈ R.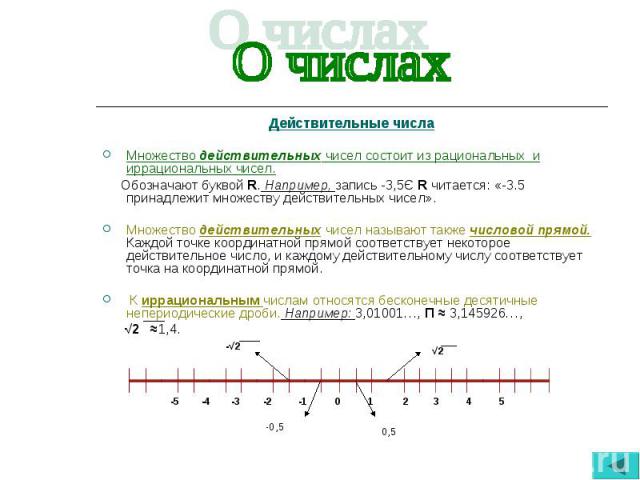
Если a = 13 и b = 23,
, то 13 + 23 = 36
, поэтому 13 × 23 = 299
Где 36 и 299 — действительные числа.
Произведение и сумма двух действительных чисел остаются неизменными даже после изменения порядка чисел. Коммутативное свойство формулируется как; для всех a, b ∈ R, a + b = b + a и a × b = b × a.
Если a = 0,25 и b = 6
, то 0,25 + 6 = 6 + 0,25
6,25 = 6,25
, поэтому 0,25 × 6 = 6 × 0,27
1,90 = 0,9 Произведение любой тройки или 0,90 1,9 номера остаются прежними, даже если группировка номеров изменена.
Ассоциативное свойство указано как; для всех a, b, c ∈ R, a + (b + c) = (a + b) + c и a × (b × c) = (a × b) × c.
Если a = 0,5, b = 2 и c = 0.
Тогда 0,5 + (2 + 0) = (0,5 + 2) + 0
2,5 = 2,5
Итак, 0,5 × (2 × 0) = (0,5 × 2) × 0
Распределительное свойство умножения над сложением выражается как a × (b + c) = (a × b) + ( a × c), а распределительное свойство умножения над вычитанием выражается как a × (b — c) = (a × b) — (a × c).
Если a = 19, b = 8,11 и c = 2.
Тогда 19 × (8,11 + 2) = (19 × 8,11) + (19 × 2)
19 × 10,11 = 154,09 + 38
90,199 192 192.09Итак, 19 × (8,11 — 2) = (19 × 8,11) — (19 × 2)
19 × 6,11 = 154,09 — 38
116,09 = 116,09 может быть выражено как бесконечное десятичное расширение.
Операции с действительными числами
Работа с действительными числами
В этом разделе мы продолжаем рассмотрение свойств действительных чисел и операций с ними. Результат сложения действительных чисел называется суммой Результат сложения. а результат вычитания называется разностью.0016 а , а+0=0+а=а .
Для любого действительного числа a , a+(−a)=(−a)+a=0.
Даны вещественные числа a , b и c , (a+b)+c=a+(b+c).
Даны вещественные числа a и b , a+b=b+a.
Важно отметить, что сложение является коммутативным, а вычитание — нет. Другими словами, порядок, в котором мы добавляем, не имеет значения и даст тот же результат. Однако это не относится к вычитанию.
5+10=10+5 15=15 5−10≠10−5−5≠5
Мы используем эти свойства вместе со свойством двойного отрицательного числа для действительных чисел, чтобы выполнять более сложные последовательные операции. Чтобы упростить задачу, возьмите за правило сначала заменять все последовательные операции сложением или вычитанием, а затем выполнять каждую операцию в порядке слева направо.
Пример 1
Упрощение: −10−(−10)+(−5).
Решение:
Замените последовательные операции и затем выполните их слева направо.
−10−(−10)+(−5)=−10+10−5 Заменить −(−) на дополнение (+). Замените +(−) на вычитание (−).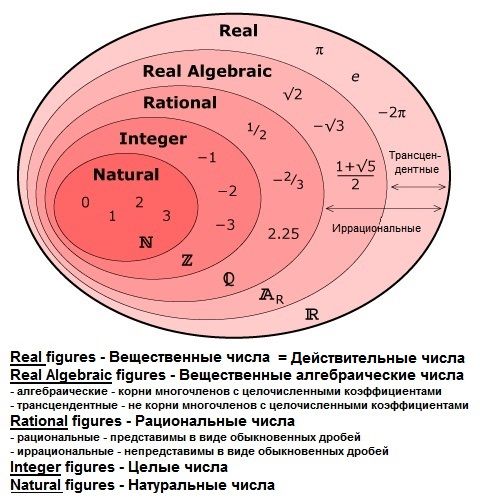 =0−5 =−5
=0−5 =−5
Ответ: −5
Для сложения или вычитания дробей требуется общий знаменательЗнаменатель, который является общим для нескольких дробей.. Предположим, что общий знаменатель c — ненулевое целое число, и мы имеем
ac+bc=a+bc и ac−bc=a−bc
Пример 2
Упростим: 29−115+845.
Решение:
Сначала определите наименьшее общее кратное (НОК) чисел 9, 15 и 45. Наименьшее общее кратное всех знаменателей называется наименьшим общим знаменателем. Наименьшее общее кратное набора знаменателей. (ЖК). Начнем с перечисления кратных каждого заданного знаменателя:
{9,18,27,36,45,54,63,72,81,90,…}кратные 9{15,30,45,60,75, 90,…}Количество 15{45,90,135…}Количество 45
Здесь мы видим, что НОК(9, 15, 45) = 45. Умножьте числитель и знаменатель каждой дроби на значения, которые дают эквивалентные дроби с определенным общим знаменателем.
29−115+845=29⋅55−115⋅33+845=1045−345+845
Получив эквивалентные дроби с общим знаменателем, мы можем произвести операции над числителями и записать результат над общий знаменатель.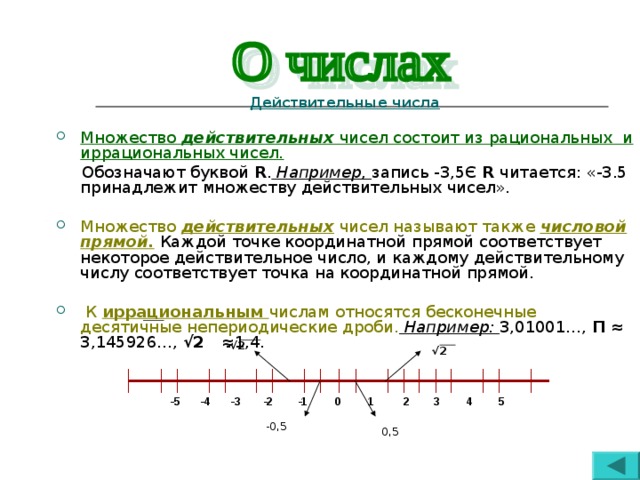
=10−3+845=1545
И затем при необходимости уменьшите, часто бывает очень громоздким. Например, попробуйте составить список кратных чисел 12 и 81. Мы можем упростить процесс нахождения НОК, используя простые множители.
12=22⋅381=34
Наименьшее общее кратное — это произведение каждого простого множителя, возведенного в наивысшую степень. В этом случае
НОК(12,81)=22⋅34=324
Часто возникает необходимость перевести английские предложения, включающие сложение и вычитание, в математические выражения. Ниже приведены некоторые распространенные переводы.
n+2 сумма a числа и 2,2−n разность 2 и a числа.n−2Здесь 2 вычитается из a числа.
Пример 3
Сколько будет 8 вычесть из суммы 3 и 12?
Решение:
Мы знаем, что вычитание некоммутативно; поэтому мы должны позаботиться о том, чтобы вычитать в правильном порядке. Сначала прибавьте 3 и 12, а затем вычтите 8 следующим образом:
Выполните указанные операции.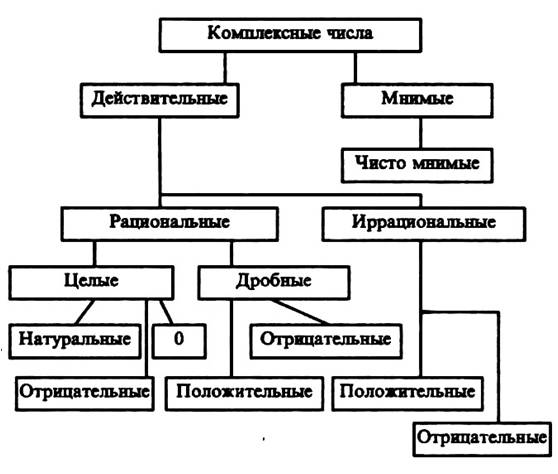
(3+12)−8=(31⋅22+12)−8=(6+12)−8=72−81⋅22=7−162=−92
Ответ: −92
Результат Произведение умножения действительных чисел называется произведением Результат умножения. а результат деления называется частным Результат деления.. Даны любые действительные числа a , b и c , мы имеем следующие свойства умножения:
Для любого действительного числа a , a⋅0=0⋅a=0 .
Для любого действительного числа a , a⋅1=1⋅a=a .
Для любых действительных чисел a , b и c , (a⋅b)⋅c=a⋅(b⋅c).
Для любых действительных чисел a и b , a⋅b=b⋅a.
Важно отметить, что умножение коммутативно, а деление — нет. Другими словами, порядок, в котором мы умножаем, не имеет значения и даст тот же результат. Однако это не относится к делению.
5⋅10=10⋅5 50=50 5÷10≠10÷50,5≠2
Мы будем использовать эти свойства для выполнения последовательных операций, включающих умножение и деление. Напомним, что произведение положительного числа на отрицательное число отрицательно. Кроме того, произведение двух отрицательных чисел положительно.
Напомним, что произведение положительного числа на отрицательное число отрицательно. Кроме того, произведение двух отрицательных чисел положительно.
Пример 4
Умножьте: 5(-3)(-2)(-4).
Решение:
Умножьте два числа за раз следующим образом:
Ответ: −120
Поскольку умножение является коммутативным, порядок умножения не влияет на окончательный ответ. Однако, когда последовательные операции включают умножение и деление, порядок имеет значение; следовательно, мы должны работать операции от слева направо для получения правильного результата.
Пример 5
Упрощение: 10÷(−2)(−5).
Решение:
Сначала выполните деление; иначе результат будет неверным.
Обратите внимание, что порядок умножения и деления влияет на результат. Поэтому важно выполнять операции умножения и деления так, как они появляются слева направо.
Ответ: 25
Произведением двух дробей является дробь, образованная произведением числителей и произведением знаменателей. Другими словами, чтобы умножить дроби, умножьте числители и умножьте знаменатели:
Другими словами, чтобы умножить дроби, умножьте числители и умножьте знаменатели:
ab⋅cd=acbd
Пример 6
Умножьте: −45⋅2512.
Решение:
Умножьте числители и умножьте знаменатели. Сократите, разделив любые общие факторы.
−45⋅2512=−4⋅255⋅12=−41⋅25551⋅123=−53
Ответ: −53
Два действительных числа, произведение которых равно 1, называются обратными. Два действительных числа, произведение которых равно 1.. Поэтому , ab и ba обратны, потому что ab⋅ba=abab=1. Например,
23⋅32=66=1
Поскольку их произведение равно 1, числа 23 и 32 обратны. Некоторые другие взаимные перечислены ниже:
58 и 85 7 и 17 -45 и -54
Это определение важно, потому что делящие фракции требуют, чтобы вы умножали дивиденды на взаимный делитель.
ab ÷ cd = ab cd> dc dc = ab> dc1 = ab> DC
в целом,
AB ÷ CD = ab> DC = ADBC
Пример 7
Упрощайте: 54 ÷ 35om12.
Решение:
Выполните умножение и деление слева направо.
54÷35⋅12=54⋅53⋅12=5⋅5⋅14⋅3⋅2=2524
В алгебре часто предпочтительнее работать с неправильными дробями. В этом случае мы оставляем ответ в виде неправильной дроби.
Ответ: 2524
Попробуйте! Упростить: 12⋅34÷18.
Ответ: 3
(нажмите, чтобы посмотреть видео)
Группировка символов и показателей
В вычислениях, где задействовано более одной операции, группировка символов помогает нам определить, какие операции выполнять в первую очередь. Символы группировки Скобки, квадратные и фигурные скобки, а также дробная черта являются общими символами, используемыми для группировки выражений и математических операций в рамках вычислений. обычно используемые в алгебре:
() скобки [] скобки {} Брекеты фракции
Все вышеперечисленные символы группировки, а также абсолютное значение имеют одинаковый порядок приоритета. Сначала выполните операции внутри самого внутреннего символа группировки или абсолютного значения.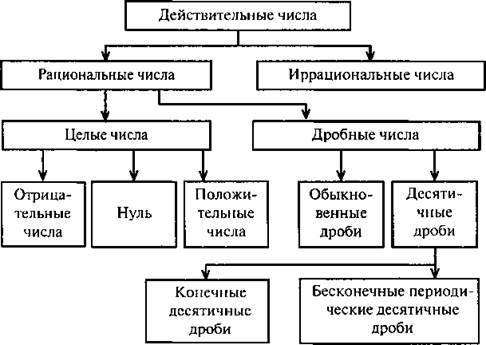
Пример 8
Упрощение: 2−(45−215).
Решение:
Сначала выполните операции в скобках.
2−(45−215)=2−(45⋅33−215)=2−(1215−215)=2−(1015)=21⋅33−23=6−23=43
Ответ: 43
Пример 9
Упрощение: 5−|4−(−3)||−3|−(5−7).
Решение:
Дробная черта группирует числитель и знаменатель. Следовательно, они должны быть упрощены отдельно.
5−|4−(−3)||−3|−(5−7)=5−|4+3||−3|−(−2)=5−|7||−3|+ 2=5−73+2=−25=−25
Ответ: −25
Если число многократно повторяется как множитель, то мы можем записать произведение в более компактной форме, используя экспоненциальную запись. когда фактор a повторяется n раз. Например,
5⋅5⋅5⋅5=54
ОснованиеМножитель a в экспоненциальной записи an. — множитель и положительный целочисленный показатель степени. Положительное целое число n в экспоненциальной записи an, указывающее, сколько раз основание используется в качестве множителя. 4 = 5*5*5*5. В общем, если a — это основание, которое повторяется как множитель n раз, затем
4 = 5*5*5*5. В общем, если a — это основание, которое повторяется как множитель n раз, затем
Когда показатель степени равен 2, мы называем результат квадратом. Результат, когда показатель степени любого действительного числа равен 2, а когда показатель степени равен 3, мы назовите результат кубомРезультат, когда показатель степени любого действительного числа равен 3.. Например,
52=5⋅5=25“5 квадрат”53=5⋅5⋅5=125“5 куб”
Если показатель степени больше 3, то обозначение an читается как « a, возведенное в n-ю степень ». Основанием может быть любое действительное число,
(2,5)2=(2,5)(2,5)=6,25(-23)3=(-23)(-23)(-23)=-827(-2)4=(-2)(-2) (−2)(−2)=16−24=−1⋅2⋅2⋅2⋅2=−16
Обратите внимание, что результат отрицательного основания с четным показателем степени положительный. Результат отрицательного основания с нечетным показателем степени отрицателен. Эти факты часто путают, когда речь идет об отрицательных числах. Внимательно изучите следующие четыре примера:
Скобки указывают, что в качестве основания следует использовать отрицательное число.
Пример 10
Рассчитать:
- (−13)3
- (−13)4
Решение:
Здесь −13 — основание для обеих задач.
Используйте базу как множитель три раза.
(−13)3=(−13)(−13)(−13)=−127
Используйте базу как множитель четыре раза.
(-13)4=(-13)(-13)(-13)(-13)=+181
Ответы:
- −127
- 181
Попробуйте! Упростить:
- −24
- (−2)4
Ответы:
- −16
- 16
(нажмите, чтобы посмотреть видео)
Порядок операций
Когда в расчете необходимо применить несколько операций, мы должны следовать определенному порядку, чтобы обеспечить единственный правильный результат.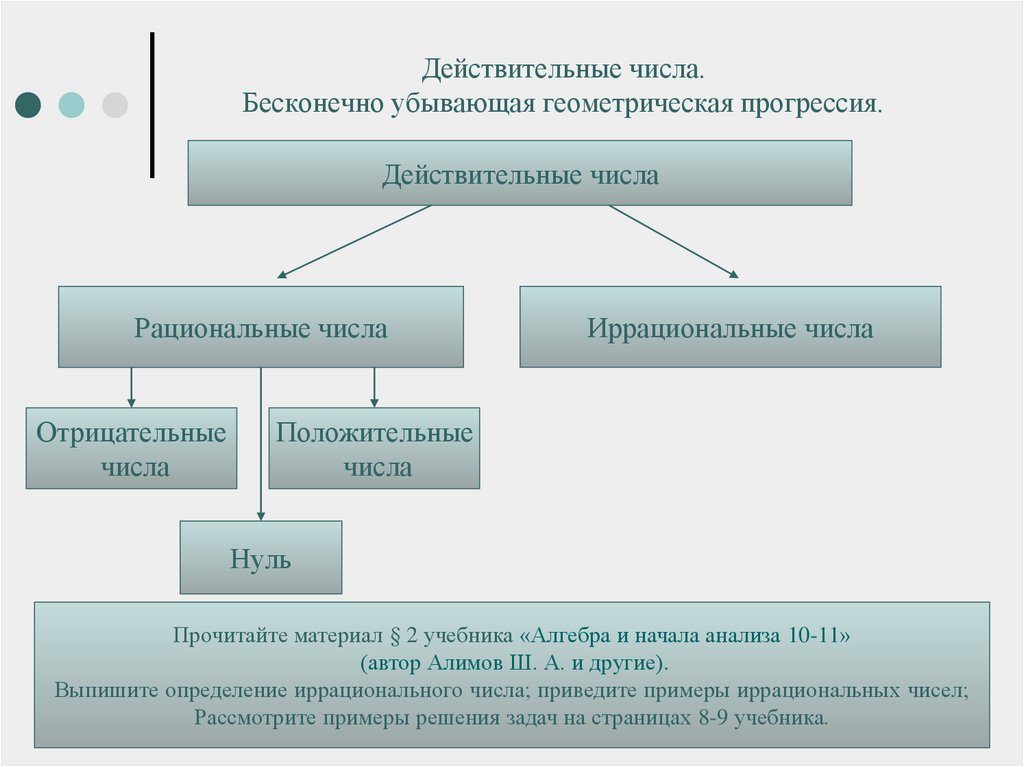
- Сначала выполните все вычисления внутри самых внутренних круглых скобок или символа группировки.
- Вычислить все показателей .
- Применить умножение и деление слева направо.
- Выполнить все оставшиеся операции сложения и вычитания в последнюю очередь слева направо.
Обратите внимание, что умножение и деление должны работать с слева направо . Из-за этого часто бывает разумно выполнить деление перед умножением.
Пример 11
Упрощение: 53−24÷6⋅12+2.
Решение:
Сначала оцените 53, а затем выполните умножение и деление слева направо.
53−24÷6⋅12+2=53−24÷6⋅12+2=125−24÷6⋅12+2=125−4⋅12+2=125−2+2=123+2= 125
Умножение сначала привело бы к неправильному результату.
Ответ: 125
Пример 12
Упрощение: −10−52+(−3)4.
Решение:
Позаботьтесь о том, чтобы правильно определить основание при возведении в квадрат.
−10−52+(−3)4=−10−25+81=−35+81=46
Ответ: 46
Мы с меньшей вероятностью совершим ошибку, если будем выполнять одну операцию за раз. Некоторые проблемы могут включать абсолютное значение, и в этом случае мы присваиваем ему тот же порядок старшинства, что и скобкам.
Пример 13
Упростить: 7−5|−22+(−3)2|.
Решение:
Сначала выполните операции с абсолютным значением.
7−5|−22+(−3)2|=7−5|−4+9|=7−5|5|=7−5⋅5=7−25=−18
Вычитание 7− 5 сначала приведет к неправильным результатам.
Ответ: −18
Попробуйте! Упростить: −62−[−15−(−2)3]−(−2)4.
Ответ: −45
(щелкните, чтобы посмотреть видео)
Ключевые выводы
- Сложение коммутативно, а вычитание — нет. Кроме того, умножение коммутативно, а деление — нет.
- Для сложения или вычитания дробей требуется общий знаменатель; умножение или деление дробей не работает.

- Символы группировки указывают, какие операции выполнять в первую очередь. Мы обычно группируем математические операции со скобками, фигурными скобками, фигурными скобками и дробной чертой. Мы также группируем операции по абсолютным значениям. Все группы имеют одинаковый порядок старшинства: операции внутри самой внутренней группы выполняются первыми.
- При использовании экспоненциального представления an основание a используется как множитель n раз. Круглые скобки указывают, что в качестве основания следует использовать отрицательное число. Например, (−5)2 является положительным, а −52 отрицательным.
- Чтобы обеспечить один правильный результат при применении операций в расчете, соблюдайте порядок операций. Сначала выполните операции в самых внутренних скобках или группах. Затем упростите все показатели. Выполнять операции умножения и деления слева направо. Наконец, выполните операции сложения и вычитания слева направо.

Тематические упражнения
33−(−15)+(−8)
−10−9+(−6)
−23+(−7)−(−10)
−1−(−1)−1
12+13−16
−15+12−110
23-(-14)-16
−32−(−29)−56
34-(-12)-58
−15−32−(−710)
Вычесть 3 из 10.

Вычесть −2 из 16.
Вычесть −56 из 4.
Вычесть −12 из 32.
Вычислите сумму −10 и 25.
Вычислите сумму −30 и −20.
Найдите разницу между 10 и 5.
Найдите разницу между −17 и −3.
10 и 15
6 и 22
0 и 12
−8 и 0
−5 и −25
−12 и −3
13
25
−34
−12
а где а≠0
1а
аб, где а≠0
1аб
−4(−5)÷2
(−15)(−3)÷(−9)
−22÷(−11)(−2)
50÷(−25)(−4)
23(−910)
−58(−1625)
76(−67)
−159(95)
45(−25)÷1625
(−92)(−32)÷2716
85÷52⋅1540
316÷58⋅12
Найдите произведение 12 и 7.

Найдите произведение −23 и 12.
Найдите частное между −36 и 12.
Найдите частное между −34 и 9.
Вычтите 10 из суммы 8 и −5.
Вычтите -2 из суммы -5 и -3.
Джо зарабатывает 18 долларов в час и «полтора часа» за каждый час работы свыше 40 часов. Какова его оплата за 45 часов работы на этой неделе?
Билли купил 12 бутылок воды по 0,75 доллара за бутылку, 5 фунтов различных конфет по 4,50 доллара за фунт и 15 упаковок попкорна для микроволновой печи по 0,50 доллара каждая для своей вечеринки.
 Каков был его общий счет?
Каков был его общий счет?Джеймс и Мэри возвращаются домой из колледжа на День Благодарения. Они ехали вместе, но Мэри проехала вдвое больше, чем Джеймс. Если Мэри проехала 210 миль, то сколько миль заняла вся поездка?
Доска длиной 634 фута должна быть разрезана на 3 части одинаковой длины. Какой длины будет каждый кусок?
Ученица заработала 72, 78, 84 и 90 баллов на первых четырех экзаменах по алгебре. Каков был ее средний балл по тесту? (Напомним, что среднее значение рассчитывается путем сложения всех значений в наборе и деления результата на количество элементов в наборе.)
Самая низкая температура на Земле, -129°F, была зафиксирована в 1983 году на станции Восток в Антарктиде.
 Самая высокая температура на Земле, 136 ° F, была зарегистрирована в 1922 году в Эль-Азизии, Ливия. Рассчитайте диапазон температур на Земле.
Самая высокая температура на Земле, 136 ° F, была зарегистрирована в 1922 году в Эль-Азизии, Ливия. Рассчитайте диапазон температур на Земле.
Часть A. Работа с действительными числами
Выполнение операций. Сократите все дроби до меньших членов.
Формула d=|b−a| дает расстояние между любыми двумя точками на числовой прямой. Определить расстояние между данными числами на числовой прямой.
Определите обратную величину следующего.
Выполните операции.
7-{3-[-6-(10)]}
-(9-12)-[6-(-8-3)]
12{5−(10−3)}
23{−6+(6−9)}
5{2[3(4−32)]}
12{−6[−(12−53)]}
5−|5−(−6)||−5|−|−3|
|9−12|−(−3)|−16|−3(4)
−|−5−(−7)|−(−2)|−2|+|−3|
1−|9−(3−4)|−|−2|+(−8−(−10))
122
(−12)2
−122
−(−12)2
−54
(−5)4
(−12)3
−(−12)3
−(−34)2
−(−52)3
(−1)22
(−1)13
−(−1)12
−(−1)5
−102
−104
Часть B: Группировка символов и показателей
Выполнение операций.
Выполните операции.
5−3(4−32)
8−5(3−32)
(−5)2+3(2−42)
6−2(−52+4⋅7)
5−3[3(2−32)+(−3)2]
10-5[(2-5)2-3]
[52−32]−[2−(5+(−4)2)]
−72−[(2−7)2−(−8)2]
316÷(512−12+23)⋅4
6⋅[(23)2−(12)2]÷(−2)2
3−2⋅5+422−32
(3+(−2)2)⋅4−3−42+1
−52+(−3)2⋅2−382+6(−10)
(-4)2+(-3)3-92-(-12+22)*10
−52−2|−5|
−24+6|24−52|
−(4−|72−82|)
−3(5−2|−6|)
(−3)2−|−2+(−3)3|−42
−52−2|33−24|−(−2)5
5⋅|−5|−(2−|−7|)3
102+2(|−5|3−63)
23 −|12 −(−43)2|
−24|103−12÷15|
Вычислите сумму квадратов первых трех последовательных положительных нечетных целых чисел.

Вычислите сумму квадратов первых трех последовательных положительных четных целых чисел.
Сколько будет 6 вычесть из суммы квадратов 5 и 8?
Сколько 5 вычесть из суммы кубов 2 и 3?
Часть C: Порядок работы
Упрощение.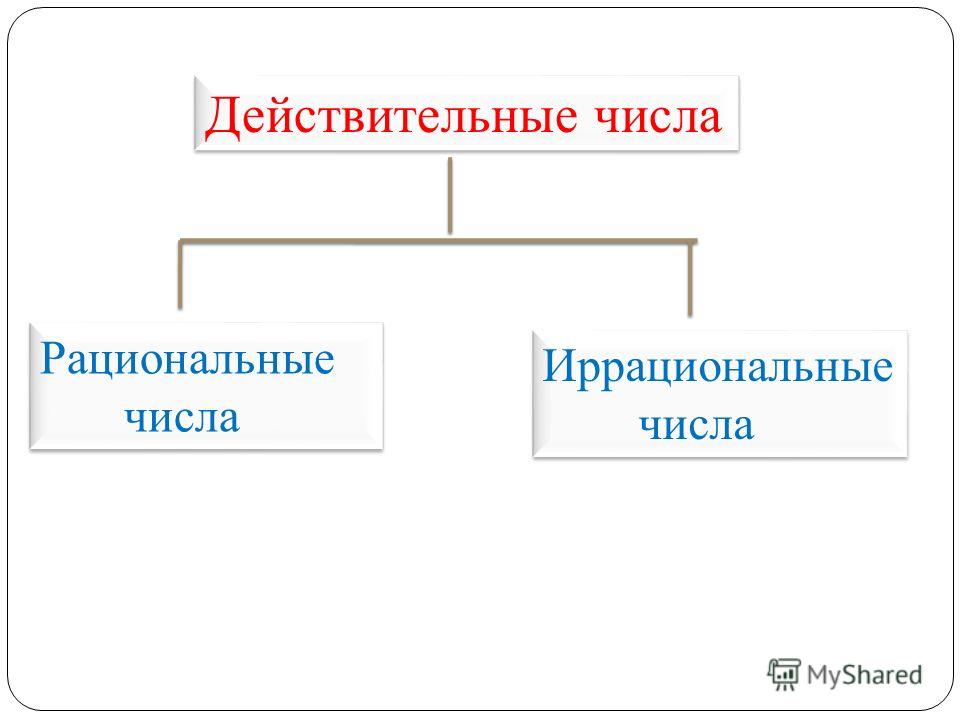
Что такое PEMDAS и чего ему не хватает?
Есть ли у 0 обратная величина? Объяснять.
Объясните, почему нам нужен общий знаменатель, чтобы складывать или вычитать дроби.
Объясните, почему (−10)4 положительно, а −104 отрицательно.

Часть D: Дискуссионная доска
Ответы
40
−20
23
34
58
7
296
15
5
5 шт.

12 шт.
20 шт.
3
−43
1а
ба
10
−4
−35
−1
−12
625
84
−3
−7
$855
315 миль
81 балл
−12
−1
75
−3
0
144
−144
−625
−18
−916
1
−1
−100
20
−17
41
35
97
35
−52
−35
11
−36
150
−1118
35
83
Ответ может отличаться
Ответ может отличаться
20011 — Свойства действительных чисел
Введение: подключение вашего обучения
Вы помните свой первый мобильный телефон? Как насчет вашего первого GPS (глобальная система позиционирования) или вашей первой игровой системы? Думаете ли вы о Droid в вашем кармане или о Nintendo с этими неуклюжими пластиковыми картриджами, из которых вам приходилось выдувать пыль, чтобы заставить игру работать, у вас, вероятно, был подобный опыт с новой технологией. Вы нашли время, чтобы изучить каждую деталь того, как работает ваш новый гаджет. Возможно, вы знаете, как использовать «черепашьи подсказки» в Mario Brothers или загружать приложение на свой планшет, потому что потратили много времени на изучение этих предметов.
Вы нашли время, чтобы изучить каждую деталь того, как работает ваш новый гаджет. Возможно, вы знаете, как использовать «черепашьи подсказки» в Mario Brothers или загружать приложение на свой планшет, потому что потратили много времени на изучение этих предметов.
Математика ничем не отличается. Как только вы вошли в этот мир, вам нужно изучить и открыть для себя характеристики (свойства), благодаря которым работают такие операции, как сложение, вычитание, умножение и деление. На этом уроке вы изучите некоторые свойства действительных чисел.
Сосредоточение вашего обучения
Цели урока
К концу этого урока вы должны уметь:
- Определять основные свойства действительных чисел.
Презентация
Основные свойства действительных чисел
Основные свойства действительных чисел используются для определения порядка упрощения математических выражений. К основным свойствам действительных чисел относятся следующие:
- Свойство замыкания
- Коммутативное свойство
- Ассоциативное свойство
- Распределительная собственность
Внимательно осмотрите каждую собственность.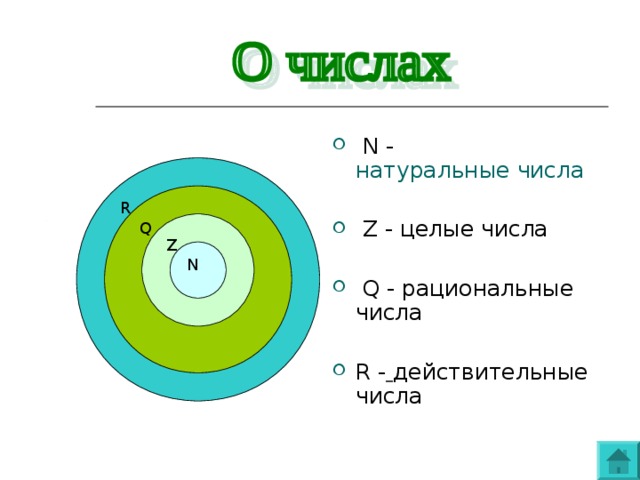
Свойства замыкания
Действительные числа замкнуты при сложении, вычитании и умножении.
That means if a and b are real numbers, then a + b is a unique real number, and a ⋅ b is a уникальный реальный номер.
Например:
3 и 11 — действительные числа.
3 + 11 = 14 и 3 ⋅ 11 = 33 Обратите внимание, что и 14, и 33 — действительные числа.
Каждый раз, когда вы складываете, вычитаете или умножаете два действительных числа, результатом будет действительное число.
Хотя это свойство кажется очевидным, некоторые коллекции не закрываются при определенных операциях.
Вот несколько примеров.
Пример 1
Действительные числа не замыкаются при делении, так как, хотя 5 и 0 являются действительными числами, они не являются действительными числами.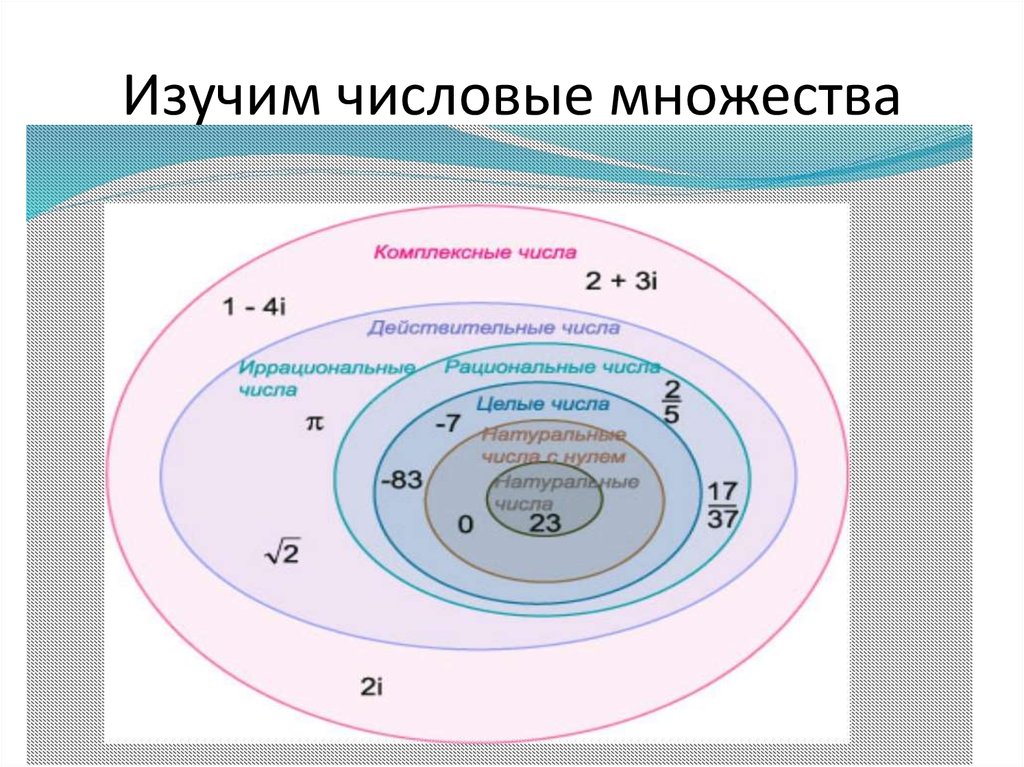 (Вы можете сказать, что это не определено, что означает, что это не имеет значения. Аналогично, это 2, потому что вы можете умножить 3 на 2, чтобы получить 6. Нет числа, на которое можно умножить 0, чтобы получить 5.)
(Вы можете сказать, что это не определено, что означает, что это не имеет значения. Аналогично, это 2, потому что вы можете умножить 3 на 2, чтобы получить 6. Нет числа, на которое можно умножить 0, чтобы получить 5.)
Пример 2
Натуральные числа не замыкаются при вычитании. Хотя 8 — натуральное число, 8 − 8 — нет. (8 − 8 = 0, а 0 не является натуральным числом.)
Посмотрите следующее видео с дополнительным объяснением и примерами свойства замыкания.
Математический видео-инструментарий Имущество закрытия |
Коммутативные свойства
Коммутативные свойства говорят вам, что два числа можно складывать или умножать в любом порядке, не влияя на результат.
Пусть a и b представляют собой действительные числа.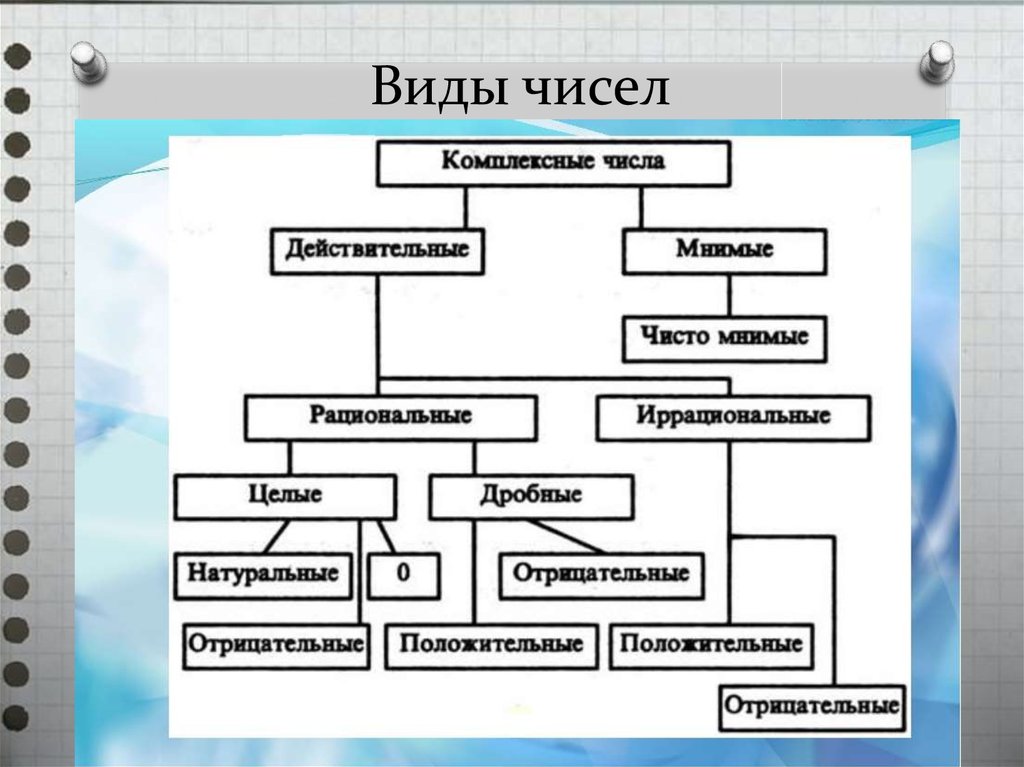
Перестановочное свойство сложения | Переместительное свойство умножения |
а + б = б + а | а ⋅ б = Ь ⋅ а |
Коммутативные свойства: примеры | |
3 + 4 = 4 + 3 | Оба равны 7 |
5 + 7 = 7 + 5 | Оба представляют одну и ту же сумму |
4 ⋅ 8 = 8 ⋅ 4 | Оба равны 32 |
у 7 = 7 у | Оба представляют один и тот же продукт |
5 (3+1) = (3+1) 5 | Оба представляют один и тот же продукт |
(9 + 4) (5 + 2) = (5 + 2) (9+ 4) | Оба представляют один и тот же продукт |
Посмотрите следующие видеоролики с подробным объяснением коммутативных свойств.
Математический видео-инструментарий Коммутативный закон сложения Коммутативный закон умножения |
Практическое упражнение: Коммутативные свойства
Пришло время применить на практике то, что вы узнали. Вам понадобится лист бумаги и карандаш, чтобы выполнить следующее задание . Запишите соответствующую цифру или букву в скобках, чтобы утверждение было верным. Используйте коммутативные свойства. Когда вы закончите, не забудьте проверить свои ответы, чтобы увидеть, насколько хорошо вы справились.
Практическое упражнение
6 + 5 = ( ) + 6
м + 12 = 12 + ( )
9 ⋅ 7 = ( ) ⋅ 9
6 а = а ( )
4 ( к — 5) = ( ) 4
(2) (9 ) а = (9 ) b + 7)(9 a − 1)
Проверить ответы
- 6 + 5 = (5) + 6
- м + 12 = 12 + ( м )
- 9 ⋅ 7 = (7) ⋅ 9
- 6 а = а (6)
- 4( к — 5) = ( к — 5)4
- (9 a — 1)(2 b + 7) = (2 b + 7)(9 a — 1)
Пример
Упростить (переставить в более простую форму): 5 y 6 b 8 ac 4
В соответствии с коммутативным свойством умножения можно получить все числа и переупорядочить цифры вместе и все буквы вместе.
| 5⋅6⋅8⋅4⋅ г ⋅ б ⋅ а ⋅ в | Умножить числа |
| 960 ybac | |
| 960 абси | По соглашению, по возможности пишите все буквы в алфавитном порядке |
Используйте приведенный выше пример для выполнения следующего практического упражнения.
Практика
Упростите каждую из следующих величин.
3 A 7 y D
6 B 8 ACZ 4 ⋅ 5
4 P 6 QR 3 ( A + 16167.9167.9007. Ответы
- 189 ади
- 960 абч
- 72 pqr ( a + b )
Ассоциативные свойства
Ассоциативные свойства говорят о том, что вы можете сгруппировать величины любым способом, не влияя на результат.
(Let A , B и C Представляют реальные числа.)
СООБЩЕНИЯ. Ассоциативное свойство умножения | |
( а + б ) + в = а + ( б + в )75 ( аб ) с = а ( до н.э. ) |
В следующих примерах показано, как можно использовать ассоциативные свойства сложения и умножения.
Ассоциативное свойство сложения | |||
| (2 + 6) + 1 | = | 2 + (6 + 1) | |
| 8 + 1 | = | 2 + 7 | |
| 9 | = | 9 | оба равны 9 |
Ассоциативное свойство умножения | |||
| (2 ⋅ 3) ⋅ 5 | = | 2 ⋅ (3 ⋅ 5) | |
| 6 ⋅ 5 | = | 2 ⋅ 15 | |
| 30 | = | 30 | оба равны 30 |
Посмотрите следующие видео для подробного объяснения ассоциативных свойств.
Математический видео-инструментарий: Ассоциативный закон сложения Ассоциативный закон умножения |
Практическое упражнение: Ассоциативные свойства
Пришло время применить на практике то, что вы узнали об ассоциативных свойствах. Вам нужно будет достать лист бумаги и карандаш, чтобы выполнить следующее задание. Запишите соответствующую цифру или букву в скобках, чтобы сделать утверждение верным. Используйте ассоциативные свойства. Когда вы закончите, не забудьте проверить свои ответы, чтобы увидеть, насколько хорошо вы справились.
Практическое упражнение
(9 + 2) + 5 = 9 + ( )
x + (5 + y ) = ( )+ y
(11 a ) 6 = 11 ( )
Проверить ответы
- (9 + 2) + 5 = 9 + (2 + 35) 9
- х + (5 + у ) = ( х + 5) + у
- (11 a ) 6 = 11 ( a ⋅ 6)
Распределительные свойства
Когда вы впервые познакомились с умножением, вы, скорее всего, поняли, что оно было разработано как описание многократного сложения.
Рассмотрим это: 4 + 4 + 4 = 3 ⋅ 4
Обратите внимание, что здесь три четверки; то есть 4 появляется три раза. Следовательно, 3 умножить на 4. Алгебра — это обобщенная арифметика, и теперь вы можете сделать важное обобщение.
Когда число A добавляется неоднократно, то есть N раз, мы имеем A + A + A + ⋯ + A ( A появляется N Times)
2
2
2
2
2
. , используя умножение как описание многократного сложения, можно заменить a + a + a + ⋯ + a с n ( a ).
Пример 1: x + x + x + x можно записать как 4 x , так как x повторяется 4 раза.
х + х + х + х = 4 х
0016 r , так как r повторно добавлено 2 раза.
r + r = 2 r
Распределительное свойство включает в себя как умножение, так и сложение. Взгляните на объяснение ниже.
Взгляните на объяснение ниже.
Переписать 4( a + b ).
ШАГ 1: Вы продолжаете, читая 4 ( a + b ) как умножение: 4-кратное количество ( a + b ).
ШАГ 2: Теперь вы используете коммутативное свойство сложения, чтобы собрать все a вместе и все b вместе.
ШАГ 3: Теперь вы используете умножение как описание повторяющегося сложения.
- Это указывает нам написать:
4( a + b ) = 4 a + 4 b
- Вы распределили 4 сверх суммы между обоими а и б .
Распределительное имущество
Распределительное имущество | |
A ( B + C ) = A ⋅ B + A ⋅ C | 7 ac C 17 Ховя( б + в ) a = b ⋅ a + c ⋅ a |
Because of the commutative property and the convention of writing the variables in alphabetical order, you can also write the following:
b ⋅ a + c ⋅ a as а ⋅ б + а ⋅ в , так ( b + c ) a = a ⋅ b + a ⋅ c тоже.
Распределительное свойство полезно, когда вы не можете или не хотите выполнять операции внутри круглых скобок.
Примеры
Используйте свойство распределения, чтобы переписать каждую из следующих величин.
2( 5 + 7) =
6 ( х + 3) =
( z + 5) y =
Посмотрите следующие видео для подробного объяснения Распределительного свойства.
Математический видео-инструментарий: Распределительная собственность |
Практическое упражнение: Распределительные свойства
Используйте распределительное свойство, чтобы переписать каждую из следующих величин без круглых скобок. Когда вы выполняете операции с использованием распределительного свойства, его часто называют расширение выражения.
Практическое упражнение
3 (2 + 1)
( x + 6) 7
4 ( A + Y )
(9 + 2) A 9007
9007
(9 + 2) A
7(9 + 2) A 9007
7 (9 + 2) A 9007
(9 + 2) A ( x + 5)
1 ( x + y )
Проверить ответы
- 3 ⋅ 2 + 3 ⋅ 1
- 7 ⋅ х + 7 ⋅ 6
- 4 ⋅ а + 4 ⋅ у
- 9 ⋅ а + 2 ⋅ а
- а ⋅ х + 5 ⋅ а
- 1 ⋅ х + 1 ⋅ г
6 + 3
7 х + 42
4 а + 4 у
9 и + 2 и
топор + 5 а
х + у
Свойства идентичности
Аддитивная идентичность
Число 0 называется аддитивной идентичностью, поскольку при добавлении к любому действительному числу оно сохраняет идентичность этого числа. Ноль — единственная аддитивная идентичность.
Ноль — единственная аддитивная идентичность.
Например: 6 + 0 = 6
Мультипликативное тождество
Число 1 называется мультипликативным тождеством, поскольку при умножении 1 на любое действительное число оно сохраняет тождество этого числа. Единица — единственное мультипликативное тождество.
Например: 6 ⋅ 1 = 6.
Свойства идентичности резюмируются следующим образом.
Аддитивное свойство идентичности | Свойство мультипликативной идентичности |
IF A — это реальное число, затем A + 0 = A и 0 + A = A A A A = A A = A A = A A = A A = и 0 + A = и 0 + A0015 | If a is a real number, then a ⋅ 1 = a and 1 ⋅ a = a |
Посмотрите следующие видеоролики Академии Хана, чтобы получить дополнительные разъяснения и примеры свойства Identity.
Математический видео-инструментарий: Аддитивное свойство идентичности 0 Свойство мультипликативной идентичности 1 |
Свойства инверсии
Аддитивные инверсии
Когда два числа складываются вместе и результатом является аддитивная идентичность 0, числа называются аддитивными инверсиями друг друга.
Пример
Если к −3 прибавить 3, получится 0: 3 + (−3) = 0,
Числа 3 и −3 являются аддитивными инверсиями друг друга.
Чему равна аддитивная величина, обратная −15?
Ответ: 15
Для более подробного объяснения аддитивных инверсий посмотрите следующее видео от Khan Academy.
Обратное свойство сложения |
Мультипликативные обратные числа
Когда два числа умножаются вместе и результатом является мультипликативное тождество 1, числа называются мультипликативными обратными друг другу.
Пример
Когда 6 и умножаются вместе, результат равен 1: то есть 6 ⋅ = 1.
Числа 6 и являются мультипликативными обратными друг другу.
Что является мультипликативным, обратным ?
Ответ:
Обратные свойства таковы.
Обратные свойства
Если a — любое действительное число, то существует уникальное действительное число — a , так что a + (− a ) = 0 и — a + a = 0 |
|
Если a — любое ненулевое действительное число, то существует уникальное действительное число такое, что a ⋅ = 1 и ⋅ a = 1 |
|
Для более подробного объяснения мультипликативных инверсий посмотрите следующее видео от Khan Academy.
Обратное свойство умножения |
Упражнение: аддитивное и мультипликативное обратное преобразование
Выполните следующее упражнение, чтобы попрактиковаться в том, что вы узнали об аддитивных и мультипликативных инверсиях, выбрав ссылку ниже. Практика аддитивных и мультипликативных инверсий После завершения практики вы можете перейти по следующей ссылке, чтобы посмотреть, как вы справились. Проверка аддитивных и мультипликативных обратных ответов |
Подведение итогов обучения
Знаете ли вы, что действительные числа обладают множеством свойств? Теперь вы должны быть знакомы с замыканием, коммутативностью, ассоциативностью, дистрибутивностью, тождественностью и обратными свойствами. Буквальные объяснения были включены, чтобы упростить интерпретацию символических объяснений. Взгляните на следующий веб-сайт для дополнительных объяснений свойств действительных чисел.
Буквальные объяснения были включены, чтобы упростить интерпретацию символических объяснений. Взгляните на следующий веб-сайт для дополнительных объяснений свойств действительных чисел.
Свойства действительных чисел
Оценка вашего обучения
Теперь, когда вы внимательно прочитали урок и попытались ответить на вопросы упражнения, пришло время для проверки знаний. Обратите внимание, что этот является градуированной частью этого модуля, поэтому убедитесь, что вы подготовились перед началом. |
- Выполните обзор арифметики: свойства действительных чисел.
Ресурс:
«Основные свойства действительных чисел: свойства действительных чисел», Эллис В. и Бурзински Д. © 2009 г.получено с http://cnx.org/content/m21894/1.4/, используется в соответствии с авторством Creative Commons http://creativecommons.org/licenses/by/3. 0/. Эта адаптация урока «Свойства действительных чисел» Национального консорциума информационной безопасности и геопространственных технологий (NISGTC) распространяется под лицензией Creative Commons Attribution 3.0 Unported License. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/3.0.
0/. Эта адаптация урока «Свойства действительных чисел» Национального консорциума информационной безопасности и геопространственных технологий (NISGTC) распространяется под лицензией Creative Commons Attribution 3.0 Unported License. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/3.0.
Дополнительные атрибуты
0.3 Вещественные числа – Алгебра среднего уровня
Цели обучения
- Классифицировать вещественное число как натуральное, целое, рациональное или иррациональное число.
- Определите и используйте свойство перестановочности сложения и умножения
- Определение и использование ассоциативного свойства сложения и умножения
- Определение и использование распространяемого свойства
- Определение и использование свойства идентичности сложения и умножения
- Определение и использование свойства, обратного сложению и умножению
- Определение и идентификация констант в алгебраическом выражении
- Вычисление алгебраических выражений для различных значений
Классы чисел, которые мы будем изучать, включают:
Натуральные числа
Наиболее знакомые числа — это натуральные числа (иногда называемые целыми числами или счетными числами): 1, 2, 3 и так далее. Математический символ для множества всех натуральных чисел записывается как \(\mathbb{N}\), а иногда \(\mathbb{N_0}\) или \(\mathbb{N_1}\), когда необходимо указать должен ли набор начинаться с 0 или 1 соответственно.
Математический символ для множества всех натуральных чисел записывается как \(\mathbb{N}\), а иногда \(\mathbb{N_0}\) или \(\mathbb{N_1}\), когда необходимо указать должен ли набор начинаться с 0 или 1 соответственно.
Целые числа
Когда набор отрицательных чисел объединяется с набором натуральных чисел (включая 0), результат определяется как набор целых чисел, \(\mathbb{Z}\)
Рациональные числа
A Рациональное число — это число, которое можно представить в виде дроби с целым числителем и целым положительным знаменателем.
Действительные числа
Действительные числа включают все измеренные числа. Символ для действительных чисел \(\mathbb{R}\). Действительные числа обычно представляются десятичными числами.
Числа, которые мы используем для счета или перечисления предметов, — это натуральных чисел : 1, 2, 3, 4, 5 и так далее. Мы описываем их в системе обозначений как \(\{1, 2, 3, …\}\), где многоточие (…) указывает на то, что числа продолжаются до бесконечности. Натуральные числа, конечно, также называются счетными числами . Всякий раз, когда мы перечисляем членов команды, считаем монеты в коллекции или подсчитываем деревья в роще, мы используем набор натуральных чисел. Набор из целых чисел — это множество натуральных чисел плюс ноль: \(\{0, 1, 2, 3,…\}\).
Натуральные числа, конечно, также называются счетными числами . Всякий раз, когда мы перечисляем членов команды, считаем монеты в коллекции или подсчитываем деревья в роще, мы используем набор натуральных чисел. Набор из целых чисел — это множество натуральных чисел плюс ноль: \(\{0, 1, 2, 3,…\}\).
Набор из целых чисел добавляет к набору целых чисел противоположные натуральные числа: \(\{…-3, -2, -1, 0, 1, 2, 3,…\}\). Полезно отметить, что набор целых чисел состоит из трех различных подмножеств: отрицательных целых чисел, нуля и положительных целых чисел. В этом смысле положительные целые числа — это просто натуральные числа. Другой способ думать об этом состоит в том, что натуральные числа являются подмножеством целых чисел.
\(\begin{array}{lll}{\text{целые отрицательные}}\hfill & {\text{ноль}}\hfill & {\text{целые положительные числа}}\\{\dots ,-3, -2,-1,}\hfill & {0,}\hfill & {1,2,3,\dots }\end{массив}\)
Набор из рациональных чисел записывается как \(\left \{\frac{m}{n}|m\text{ и }{n}\text{ являются целыми числами, а }{n}\ne{ 0 }\right\}\). Обратите внимание на то, что из определения рациональные числа — это дроби (или частные), содержащие целые числа как в числителе, так и в знаменателе, а знаменатель никогда не равен 0. Мы также можем видеть, что каждое натуральное, целое и целое число является рациональным числом с знаменатель 1,
Обратите внимание на то, что из определения рациональные числа — это дроби (или частные), содержащие целые числа как в числителе, так и в знаменателе, а знаменатель никогда не равен 0. Мы также можем видеть, что каждое натуральное, целое и целое число является рациональным числом с знаменатель 1,
Поскольку это дроби, любое рациональное число также может быть представлено в десятичной форме. Любое рациональное число может быть представлено как:
- завершающая десятичная дробь: \(\frac{15}{8}=1,875\) или
- повторяющееся десятичное число: \(\frac{4}{11}=0,36363636\dots =0.\overline{36}\)
Мы используем линию, проведенную над повторяющимся блоком чисел, вместо многократного написания группы.
Пример
Каждое из следующих чисел запишите в виде рационального числа.
- 7
- 0
- \(-8\)
Показать решение
Пример
Запишите каждое из следующих рациональных чисел либо в виде завершающей, либо повторяющейся десятичной дроби.
- \(-\frac{5}{7}\)
- \(\frac{15}{5}\)
- \(\frac{13}{25}\)
Показать решение
Иррациональные числа
В какой-то момент в далеком прошлом кто-то обнаружил, что не все числа являются рациональными числами. Строитель, например, мог обнаружить, что диагональ квадрата с единицей стороны равна не 2 и даже не \(\frac{3}{2}\), а чему-то другому. Или швейник мог заметить, что отношение длины окружности к диаметру рулона ткани чуть больше 3, но все же это не рациональное число. Такие числа называются 9.0016 иррационально
, потому что их нельзя записать в виде дробей. Эти числа составляют набор из иррациональных чисел . Иррациональные числа не могут быть представлены в виде дроби от двух целых чисел. Невозможно описать этот набор чисел одним правилом, кроме как сказать, что число иррационально, если оно не рационально. Итак, мы пишем это, как показано.{ч | h не является рациональным числом}
Пример
Определите, является ли каждое из следующих чисел рациональным или иррациональным. Если оно рационально, определите, является ли оно завершающим или повторяющимся десятичным числом.
Если оно рационально, определите, является ли оно завершающим или повторяющимся десятичным числом.
- \(\sqrt{25}\)
- \(\ гидроразрыва{33}{9}\)
- \(\sqrt{11}\)
- \(\frac{17}{34}\)
- \(0.3033033303333\точки\)
Показать решение
Действительные числа
Для любого числа n мы знаем, что n либо рационально, либо иррационально. Не может быть и того, и другого. Наборы рациональных и иррациональных чисел вместе составляют набор из действительных чисел . Как мы видели с целыми числами, действительные числа можно разделить на три подмножества: отрицательные действительные числа, ноль и положительные действительные числа. Каждое подмножество включает дроби, десятичные числа и иррациональные числа в соответствии с их алгебраическим знаком (+ или -). Ноль не считается ни положительным, ни отрицательным.
Действительные числа можно визуализировать на горизонтальной числовой линии с произвольной точкой, выбранной как 0, с отрицательными числами слева от 0 и положительными числами справа от 0.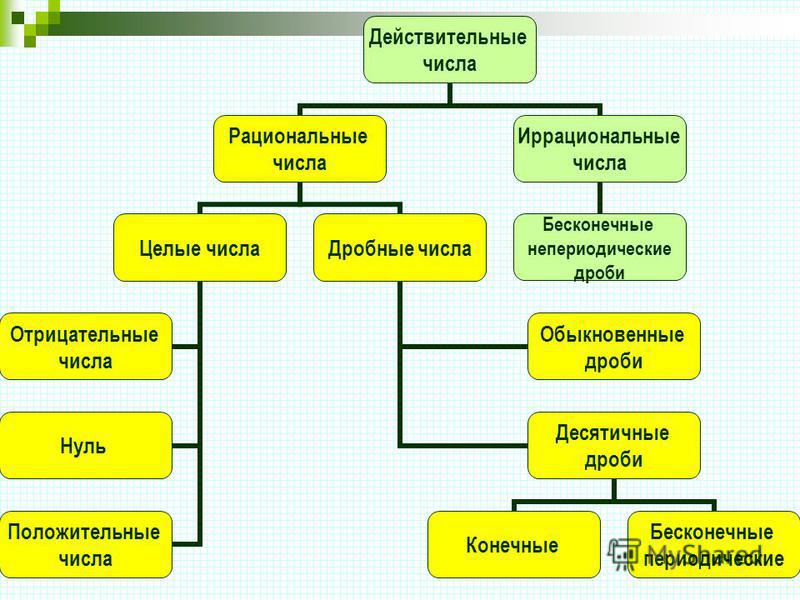 Затем используется фиксированное единичное расстояние для обозначения каждого целого числа (или другое основное значение) по обе стороны от 0. Любое действительное число соответствует уникальной позиции на числовой прямой. Обратное также верно: каждая позиция на числовой строке соответствует ровно одному действительному числу. Это известно как переписка один на один. Мы называем это 9
Затем используется фиксированное единичное расстояние для обозначения каждого целого числа (или другое основное значение) по обе стороны от 0. Любое действительное число соответствует уникальной позиции на числовой прямой. Обратное также верно: каждая позиция на числовой строке соответствует ровно одному действительному числу. Это известно как переписка один на один. Мы называем это 9
Рис. 1. Строка действительных чисел
Пример
Классифицируйте каждое число как положительное или отрицательное, как рациональное, так и иррациональное. Находится ли число слева или справа от 0 на числовой прямой?
- \(-\frac{10}{3}\)
- \(\sqrt{5}\)
- \(-\sqrt{289}\)
- \(-6\пи\)
- \(0,615384615384\точки\)
Показать решение
Наборы чисел как подмножества
Начав с натуральных чисел, мы расширили каждый набор, чтобы сформировать больший набор, а это означает, что между наборами чисел, с которыми мы уже сталкивались, существует отношение подмножества.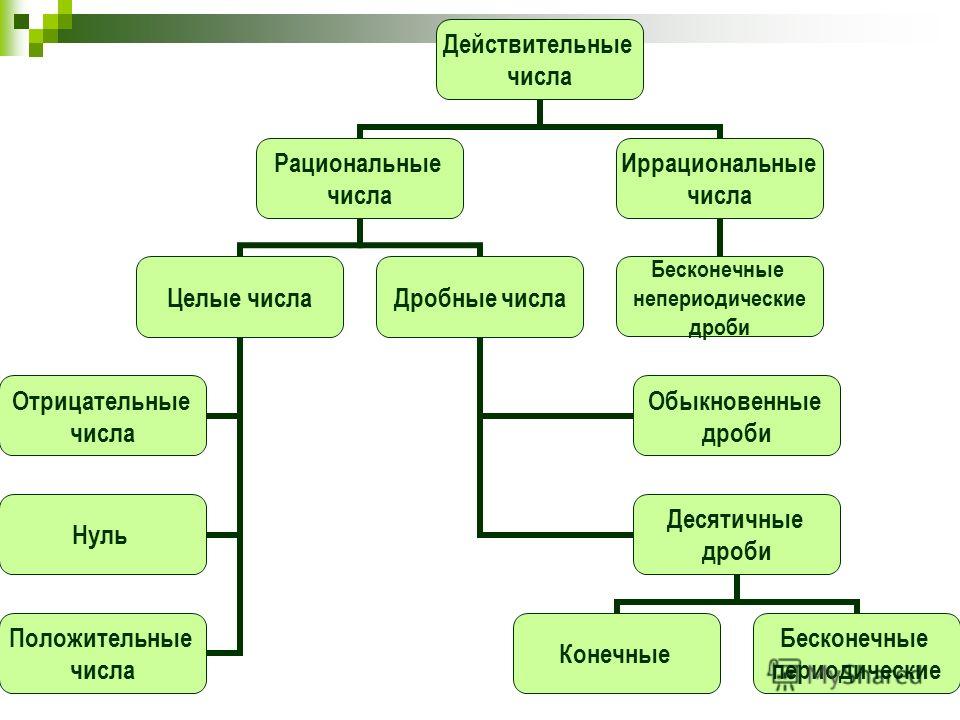 Эти отношения становятся более очевидными, если рассматривать их в виде диаграммы.
Эти отношения становятся более очевидными, если рассматривать их в виде диаграммы.
Рис. 2. Наборы чисел. N : множество натуральных чисел W : множество целых чисел I : множество целых чисел Q : набор рациональных чисел Q´ : набор иррациональных чисел
Общее примечание: наборы чисел
Набор из натуральных чисел включает числа, используемые для счета: \(\{1, 2,3,\точки\}\).
Набор из целых чисел — это набор натуральных чисел плюс ноль: \(\{0,1,2,3,\dots\}\).
Набор из целых чисел добавляет отрицательные натуральные числа к набору целых чисел: \(\{\dots,-3,-2,-1,0,1,2,3,\dots\}\) .
Набор из рациональных чисел включает дроби, записанные в виде \(\{\frac{m}{n}|m\text{ и }n\text{ являются целыми числами, а }n\ne 0\}\).
Набор из иррациональных чисел — это набор нерациональных, неповторяющихся и непрерывных чисел: \(\{h|h\text{ не является рациональным числом}\}\).
Пример
Классифицируйте каждое число как натуральное число ( N ), целое число ( W ), целое число ( I ), рациональное число ( Q ) и/или иррациональное число ( Q’ ).
- \(\sqrt{36}\)
- \(\ гидроразрыва{8}{3}\)
- \(\sqrt{73}\)
- \(-6\)
- \(3.2121121112\точки\)
Показать решение
Использование свойств действительных чисел
Для некоторых действий, которые мы выполняем, порядок одних процессов не имеет значения, но имеет значение порядок других. Например, не имеет значения, надеваем ли мы правый ботинок раньше левого или наоборот. Однако имеет значение, надеваем ли мы сначала обувь или носки. То же самое верно для сложения и умножения.
Коммутативные свойства
Коммутативное свойство сложения гласит, что числа можно складывать в любом порядке, не влияя на сумму.
\(a+b=b+a\)
Мы можем лучше увидеть эту связь, используя действительные числа.
Пример
Покажите, что числа можно складывать в любом порядке без изменения суммы. \(\left(-2\right)+7=5\)
Показать ответ
Точно так же свойство перестановочности умножения утверждает, что числа можно умножать в любом порядке, не затрагивая произведение.
\(a\cdot b=b\cdot a\)
Снова рассмотрим пример с вещественными числами.
Пример
Покажите, что числа можно умножать в любом порядке без изменения произведения.
\(\влево(-11\вправо)\cdot\влево(-4\вправо)=44\)
Показать ответ
Внимание! Важно отметить, что ни вычитание, ни деление не являются коммутативными. Например, \(17 — 5\) не совпадает с \(5 — 17\). Точно так же \(20\div 5\) не совпадает с \(5\div 20\).
Ассоциативные свойства – группировка
Ассоциативное свойство умножения говорит нам, что не имеет значения, как мы группируем числа при умножении. Мы можем переместить символы группировки, чтобы упростить вычисления, а произведение останется прежним.
\(a\left(bc\right)=\left(ab\right)c\)
Рассмотрим этот пример.
Пример
Покажите, что вы можете перегруппировать числа, которые перемножаются вместе и не влияют на произведение.\(\left(3\cdot4\right)\cdot5=60\)
Показать ответ
Ассоциативное свойство сложения говорит нам о том, что числа могут группироваться по-разному, не влияя на сумму.
\(a+\left(b+c\right)=\left(a+b\right)+c\)
Это свойство может быть особенно полезным при работе с отрицательными целыми числами. Рассмотрим этот пример.
Пример
Покажите, что сложение с перегруппировкой не влияет на сумму. \([15+\влево(-9\вправо)]+23=29\)
Показать ответ
Ассоциативны ли вычитание и деление? Просмотрите эти примеры.
Пример
Используйте свойство ассоциативности, чтобы проверить, являются ли вычитание и деление ассоциативными.
1)\(8-\влево(3-15\вправо)\stackrel{?}{=}\влево(8-3\вправо)-15\)
2)\(64\дел\влево( 8\div4\right)\stackrel{?}{=}\left(64\div8\right)\div4\)
Показать ответ
Распределительное свойство
Распределительное свойство утверждает, что произведение множителя, умноженного на сумма — это сумма множителей, умноженных на каждый член суммы.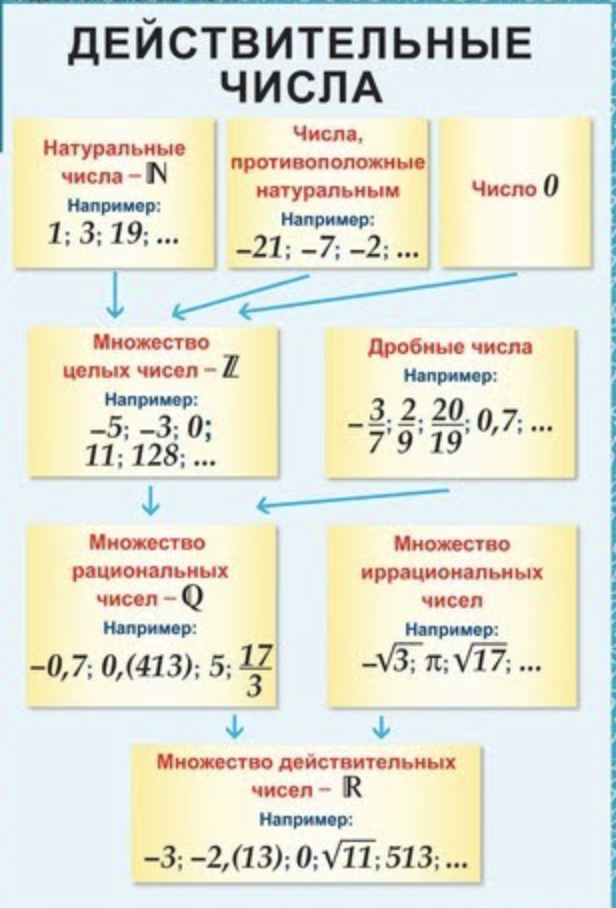
\(a\cdot \left(b+c\right)=a\cdot b+a\cdot c\)
Это свойство сочетает в себе сложение и умножение (и это единственное свойство, которое делает это). Рассмотрим пример.
Пример
Используйте свойство распределения, чтобы показать, что \(4\cdot[12+(-7)]=20\)
Показать ответ
Чтобы быть более точным при описании этого свойства, мы говорим, что умножение распределяется по добавление.
Обратное неверно, как видно из этого примера.
\(\begin{array}{ccc}\hfill 6+\left(3\cdot 5\right)& \stackrel{?}{=}& \left(6+3\right)\cdot \left(6 +5\вправо) \\ \hfill 6+\влево(15\вправо)& \stackrel{?}{=}& \влево(9\вправо)\cdot \влево(11\вправо)\hfill \\ \hfill 21& \ne & \text{ }99\hfill \end{массив}\)
Частный случай дистрибутивного свойства возникает при вычитании суммы членов.
\(a-b=a+\left(-b\right)\)
Например, рассмотрим разность \(12-\left(5+3\right)\). Мы можем переписать разницу между двумя терминами 12 и \(\left(5+3\right)\), превратив выражение вычитания в сложение противоположного. Поэтому вместо вычитания \(\left(5+3\right)\) мы прибавляем обратное.
Поэтому вместо вычитания \(\left(5+3\right)\) мы прибавляем обратное.
\(12+\влево(-1\вправо)\cdot \влево(5+3\вправо)\)
Теперь распределите \(-1\) и упростите результат.
\(\begin{array}{l}12-\left(5+3\right)=12+\left(-1\right)\cdot\left(5+3\right)\\\,\ ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ ,\,\,\,\,\,=12+[\влево(-1\вправо)\cdot5+\влево(-1\вправо)\cdot3]\\\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,=12+\влево(-8\вправо)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=4\end{массив}\)
Пример
Перепишите последний пример, изменив знак каждого члена и добавив результаты.
Показать ответ
Это кажется большим затруднением для простой суммы, но оно иллюстрирует мощный результат, который будет полезен, когда мы введем алгебраические термины.
Свойства идентичности
Свойство идентичности сложения указывает, что существует уникальное число, называемое аддитивной идентичностью (0), которое при добавлении к числу дает исходное число.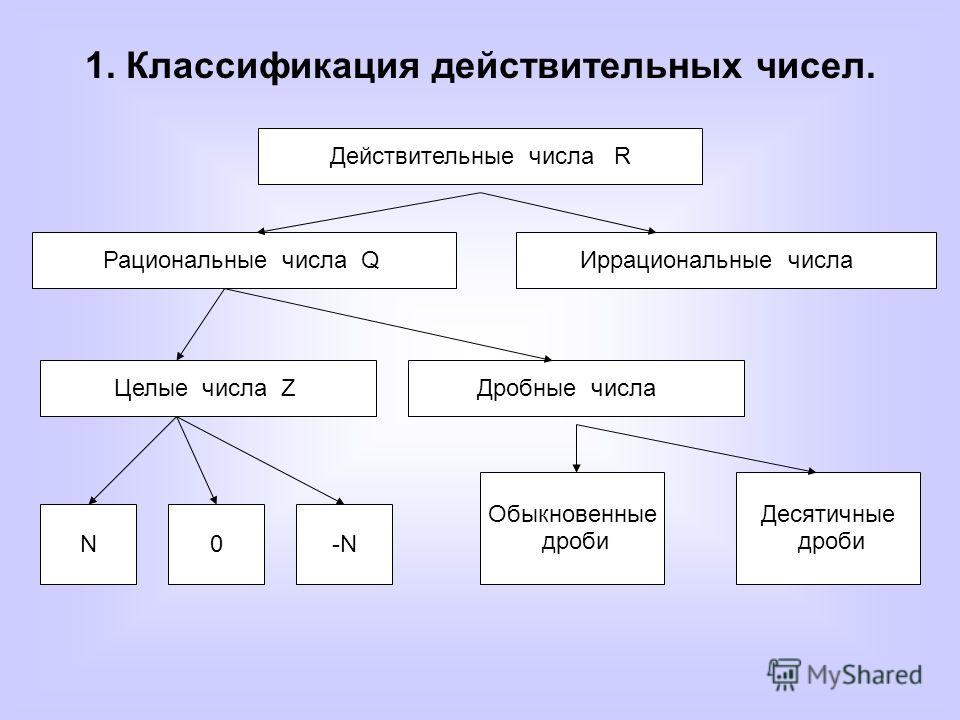
\(a+0=a\)
Свойство тождества умножения утверждает, что существует уникальное число, называемое мультипликативным тождеством (1), которое при умножении на число дает исходное число.
\(a\cdot 1=a\)
Не стоит недооценивать силу и значение этих двух маленьких личностей. Они могут показаться очевидными прямо сейчас, но часто могут быть источником путаницы из-за аббревиатуры в алгебраических выражениях. Каждый член и каждый множитель в каждом выражении можно умножить на 1, но мы редко записываем это. Точно так же мы не записываем, что к каждому члену был добавлен ноль. Позже, упрощая уравнения, старайтесь помнить, что все эти тождества существуют, скрыты под поверхностью и готовы к использованию в любое время. Если вам нужен \(\cdot 1\), вы можете его вставить, а если он вам не нужен, вы можете убрать его, не влияя на результат.
Пример
Показать, что тождественное свойство сложения и умножения истинно для \(-6, 23\)
Показать ответ
Обратные свойства
Обратное свойство сложения утверждает, что для каждого действительного числа a , существует уникальное число, называемое аддитивным обратным (или противоположным), обозначаемое — a , которое при добавлении к исходному числу дает аддитивную идентичность 0.
\(a+\left(- а\справа)=0\)
Например, если \(a=-8\), аддитивное обратное число равно 8, поскольку \(\left(-8\right)+8=0\).
Свойство , обратное умножению , выполняется для всех действительных чисел, кроме 0, поскольку величина, обратная 0, не определена. Свойство гласит, что для каждого действительного числа a существует уникальное число, называемое мультипликативным обратным (или обратным), обозначаемое \(\frac{1}{a}\), которое при умножении на исходное число , приводит к мультипликативному тождеству, 1.
\(a\cdot \frac{1}{a}=1\)
Когда действительное число является рациональным числом \( \frac{m}{n}\), тогда мультипликативная обратная обозначается \( \frac{n}{m}\)
\(\frac{ m}{n} \cdot \frac{1}{\frac{m}{n}} = \frac{m}{n} \cdot 1\cdot\frac{n}{m} = 1\).
Пример
1) Определите добавку, обратную \(a=-8\), и используйте ее для иллюстрации обратного свойства сложения.
2) Напишите обратную величину \(a=-\frac{2}{3}\) и используйте ее, чтобы проиллюстрировать свойство, обратное умножению.
Показать ответ
A Общее примечание: свойства действительных чисел
Следующие свойства действительны для вещественных чисел a , b и c .
\(а+0=а\)
\(а\cточка 1=а\)
\(а+\влево(-а\вправо)=0\)
\(a\cdot \left(\frac{1}{a}\right)=1\)
Пример
Используйте свойства действительных чисел, чтобы переписать и упростить каждое выражение. Укажите, какие свойства применяются. 9{2}}\). В выражении \(x+5\) 5 называется константой , потому что она не меняется, а x называется переменной , потому что она меняется. (При именовании переменной игнорируйте любые показатели степени или радикалы, содержащие эту переменную.) Алгебраическое выражение представляет собой набор констант и переменных, соединенных вместе алгебраическими операциями сложения, вычитания, умножения и деления.
Укажите, какие свойства применяются. 9{2}}\). В выражении \(x+5\) 5 называется константой , потому что она не меняется, а x называется переменной , потому что она меняется. (При именовании переменной игнорируйте любые показатели степени или радикалы, содержащие эту переменную.) Алгебраическое выражение представляет собой набор констант и переменных, соединенных вместе алгебраическими операциями сложения, вычитания, умножения и деления.
Мы уже видели несколько примеров экспоненциальной записи действительных чисел, сокращенного метода записи произведений одного и того же множителя. Когда используются переменные, константы и переменные обрабатываются одинаково. 9{2}}\)
Показать решение
Любая переменная в алгебраическом выражении может принимать или ей присваиваются разные значения. Когда это происходит, значение алгебраического выражения изменяется. Вычислить алгебраическое выражение означает определить значение выражения для заданного значения каждой переменной в выражении. Замените каждую переменную в выражении заданным значением, затем упростите полученное выражение, используя порядок операций. Если алгебраическое выражение содержит более одной переменной, замените каждую переменную ее присвоенным значением и упростите выражение, как и раньше. В следующем примере мы покажем, как подставить различные типы чисел в математическое выражение.
Замените каждую переменную в выражении заданным значением, затем упростите полученное выражение, используя порядок операций. Если алгебраическое выражение содержит более одной переменной, замените каждую переменную ее присвоенным значением и упростите выражение, как и раньше. В следующем примере мы покажем, как подставить различные типы чисел в математическое выражение.
Пример
Вычислите выражение \(2x — 7\) для каждого значения x.
- \(х=0\)
- \(х=1\)
- \(х=\фракция{1}{2}\)
- \(х=-4\)
Показать решение
Теперь мы покажем больше примеров вычисления различных математических выражений для различных значений.
Пример
Оценить каждое выражение для заданных значений.
- \(х+5\) для \(х=-5\)
- \(\frac{t}{2t — 1}\) для \(t=10\) 9{2}}\) для \(m=2,n=3\)
Показать решение
В следующем видео мы представляем больше примеров вычисления различных выражений для заданных значений.
реальных чисел | Что такое реальные числа
следующий → ← предыдущая В системе счисления действительные числа представляют собой смесь рациональных и иррациональных чисел. Как правило, все арифметические операции могут быть выполнены над этими числами, а также могут быть представлены в числовой строке. В то же время ненастоящие числа — это мнимые числа, которые не могут быть представлены в числовой строке. Он широко используется для представления комплексного числа. В этой статье мы рассмотрим вещественные числа, типы и их свойства. Какое реальное число? Действительные числа представляют собой смесь рациональных и иррациональных чисел. Они могут быть как положительными, так и отрицательными числами и обозначаются символом R . Он содержит все натуральные числа, десятичные дроби и дроби. Вещественным числом может быть число, которое можно выразить точкой на числовой прямой. Типы действительных чиселМы знаем, что множество действительных чисел состоит как из рациональных, так и из иррациональных чисел. Это просто указывает на то, что если мы возьмем некоторое число R , это либо рационально, либо иррационально. Существуют следующие типы действительных чисел: .Рациональные числаЛюбое число, указанное в форме p/q или дроби отношения, называется рациональным числом. Числитель определяется как p , а знаменатель представляется как q , где q не равно нулю . Рациональное число может быть целым, целым и натуральным числом. Например: 0,67, 17, 214 и т. д. Иррациональное число Иррациональные числа определяются как действительные числа, которые не могут быть представлены в виде простой дроби. Например, √5, √11, √21 и т. д. Натуральные числаЦелое число больше 0 — натуральное число. Натуральные числа начинаются с 1 и продолжаются до бесконечности, например, 1, 2, 3, 4, 5…….. Для начинающих мы должны использовать натуральные числа, если измеряем что-либо в секундах. Мы не используем десятичную точку в натуральных числах, но можем использовать запятые, когда записываем большие числа, например, 1500 и 156 597 720. Знак минус (-) нельзя использовать с натуральными числами, потому что они не должны быть отрицательными. Целые числа Целое число — это система счисления, содержащая все положительные целые числа от 0 до до бесконечности . Например: 1, 2, 3, 4, 5….. Свойства действительных чиселСуществует четыре основных актива, которые включают коммутативное имущество, ассоциативное имущество, распределительное имущество и свойство идентификации . Коммутативное свойствоВ математических вычислениях коммутативное свойство или коммутативный закон утверждает, что порядок членов не имеет значения при выполнении операции. Это свойство применимо только к методу сложения и умножения, например a + b = b + a, и a b = b a . Но это не относится к форме вычитания и деления, поскольку a — b ≠ b — a и a/b ≠ b/a . Коммутативное свойство дополнения Это свойство указывает, что если мы сложим два целых числа, результат всегда будет одним и тем же числом, даже если изменить положение числа. А + В = В + А Например:
Коммутативное свойство умноженияЭто свойство указывает, что если мы перемножим два целых числа, мы получим один и тот же результат, даже если целое число поменяется местами. Возьмем два целых числа A и B следующим образом; А * В = В * А Например:
Ассоциативное свойство Ассоциативное свойство — это свойство некоторых бинарных операций. В логике высказываний ассоциативность является истинным правилом замены для выражений логического доказательства. В зависимости от ассоциативного свойства мы можем складывать или умножать независимо от того, как сгруппированы числа. Ассоциативное свойство дополненияСвойство сложения ассоциативного следует за ассоциативным свойством. Ассоциативное свойство сложения утверждает, что: (х + у) + г = х + (у + г) Например: Давайте на примере объясним ассоциативное свойство сложения. Мы принимаем значения x, y, z равные 5, 6, 8. Сейчас, (5 + 6) + 8 = 5 + (6 + 8) (11) + 8 = 5 + (14) 19 = 19 L.H.S = R.H.S Ассоциативное свойство для умноженияПравило для ассоциативного свойства умножения выглядит следующим образом: (ху) г = х (у) Например: Давайте на примере объясним ассоциативное свойство умножения. Мы берем значения x, y, z равные 3, 4, 8. Сейчас, (3 * 4) * 8 = 3 * (4 * 8) (12) * 8 = 3 * (32) 96 = 96 L. Распределительная собственностьЭто алгебраическое свойство, используемое для умножения значения на два или более других значения в скобках. Когда множитель умножается на сложение или сумму двух чисел, необходимо умножить каждое из двух чисел на множитель. После этого выполните операцию сложения. Символически это свойство можно описать как: А (В + С) = АВ + АС Например: Давайте рассмотрим пример, объясняющий распределительное свойство. Мы принимаем значения x, y, z равные 2, 5, 7. Сейчас, 2*(5+7) 2*5+2*7 10 + 14 24 Распределительное имущество для пристройкиКогда значение умножается на число, применяется распределительное свойство умножения над сложением. Например: Давайте на примере объясним распределительное свойство сложения. Мы принимаем значения x, y и z как 7, 9 и 3. 7 * (9 + 3) 7*9+ 7*3 63 + 21 84 Распределительное свойство для вычитания Например: Давайте рассмотрим пример, объясняющий распределительное свойство вычитания. Сейчас, = 4 * (8 — 5) = 4*3 = 12 Распределительное имущество подразделенияИспользуя это свойство, мы можем разделить большие числа, разбив их на меньшие множители. Например: Давайте рассмотрим пример, объясняющий распределительное свойство деления. Мы принимаем значение 48/4. Мы можем записать это число 48 как (12 + 36) .Здесь мы можем применить распределительное свойство для деления и разбиения этого числа на мелкие множители, и мы получим: (12/4) + (36/4) = 3 + 9 = 12 Идентификационное свойствоЭто свойство включает аддитивную идентичность и мультипликативную идентичность. Мы можем выполнять различные операции на основе действительных чисел, включая сложение, умножение, вычитание и деление. Что такое аддитивная идентификация? Аддитивная идентичность чисел — это свойство чисел, используемых для выполнения дополнительных операций. |




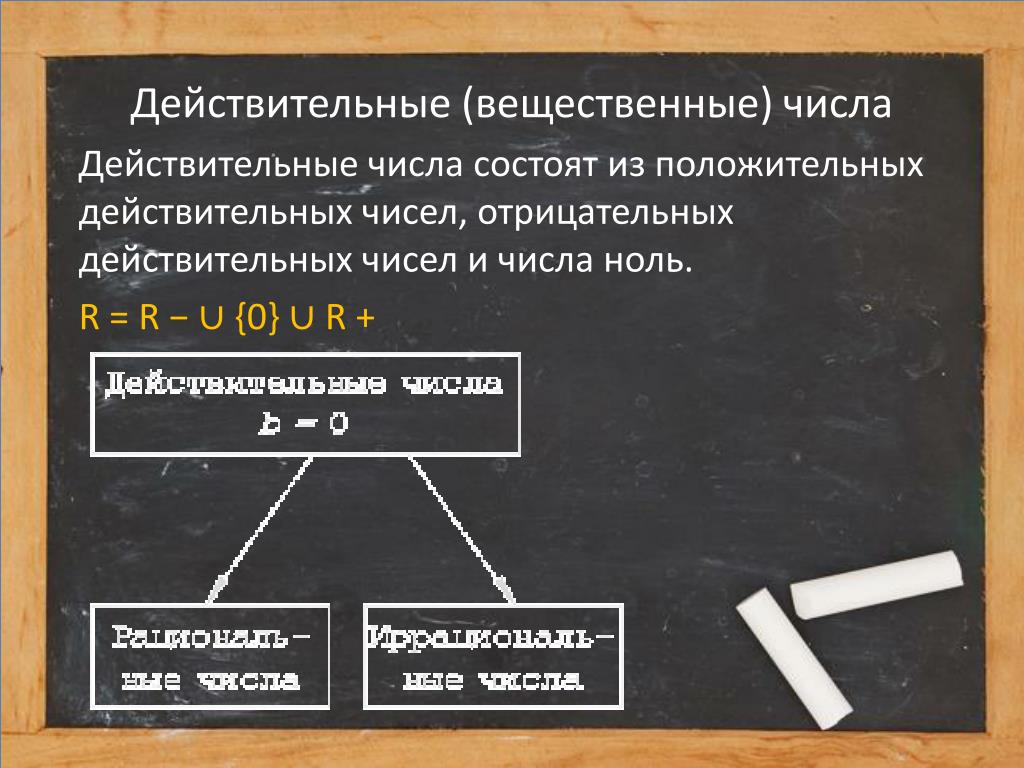
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
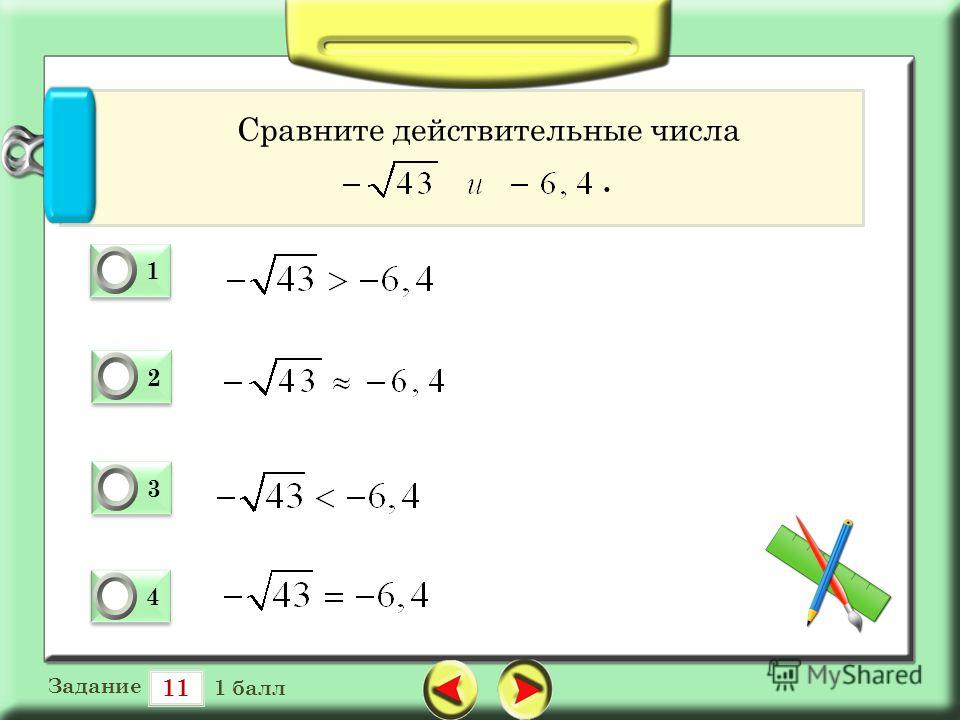
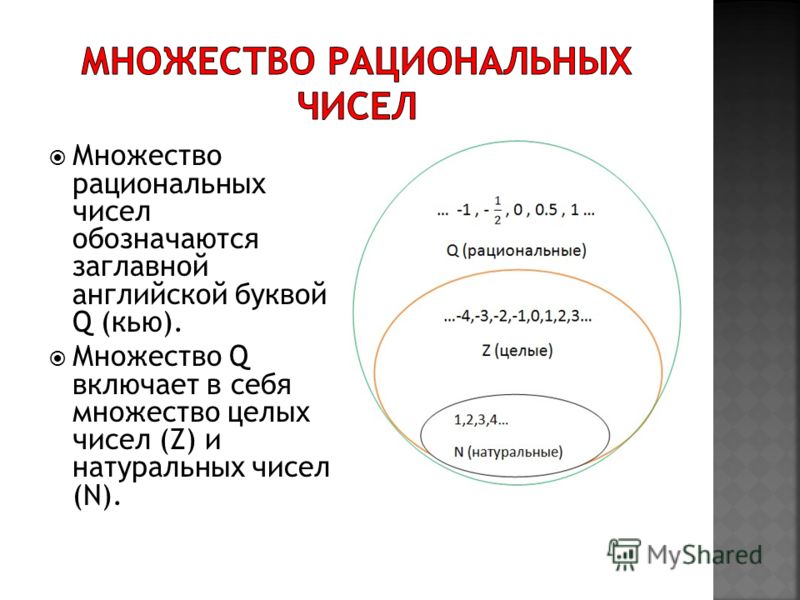 Чтобы измерить отрезок ОВ с помощью единицы измерения ОЕ, поступают следующим образом
Чтобы измерить отрезок ОВ с помощью единицы измерения ОЕ, поступают следующим образом
 Пусть , тогда , то есть п2, а значит и п – число чётное. Тогда дробь сократима на 2, что противоречит нашему предположению. Таким образом, десятичное измерение диагонали квадрата не есть число рациональное, которое всегда бесконечная, десятичная периодическая дробь. При десятичном измерении отрезка ОК получается бесконечная десятичная дробь, которая не является периодической. Бесконечные десятичные непериодические дроби называют иррациональными числами. Далее приводятся примеры иррациональных чисел. Числа рациональные и иррациональные составляют множество действительных чисел. Даются представления о действиях над действительными числами.
Пусть , тогда , то есть п2, а значит и п – число чётное. Тогда дробь сократима на 2, что противоречит нашему предположению. Таким образом, десятичное измерение диагонали квадрата не есть число рациональное, которое всегда бесконечная, десятичная периодическая дробь. При десятичном измерении отрезка ОК получается бесконечная десятичная дробь, которая не является периодической. Бесконечные десятичные непериодические дроби называют иррациональными числами. Далее приводятся примеры иррациональных чисел. Числа рациональные и иррациональные составляют множество действительных чисел. Даются представления о действиях над действительными числами.
 — М., Просвещение, 1977
— М., Просвещение, 1977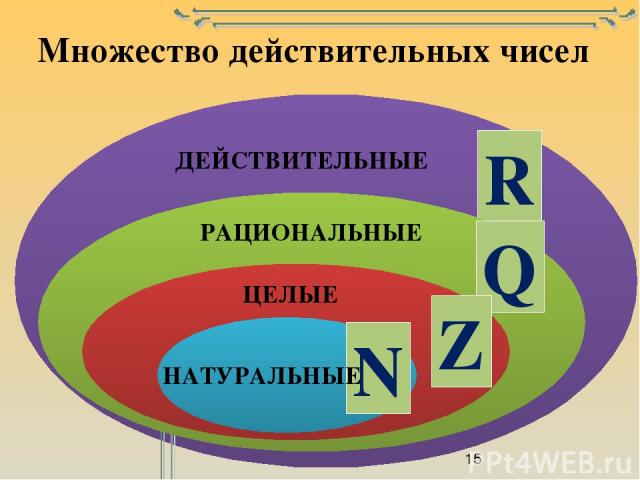 Обратная связь — 161.97.168.212 (0.006 с.)
Обратная связь — 161.97.168.212 (0.006 с.) Примером аддитивного ассоциативного свойства является 5 + (3 + 2) = (5 + 3) + 2.
Примером аддитивного ассоциативного свойства является 5 + (3 + 2) = (5 + 3) + 2. T Системы счисления: основы алгебры и анализа . АМС Челси. ISBN 0-8218-2915-7.
T Системы счисления: основы алгебры и анализа . АМС Челси. ISBN 0-8218-2915-7.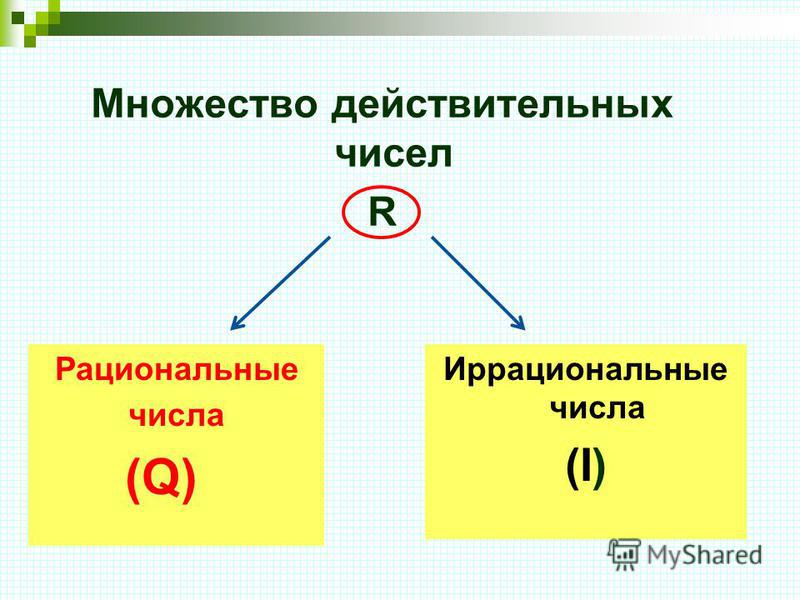

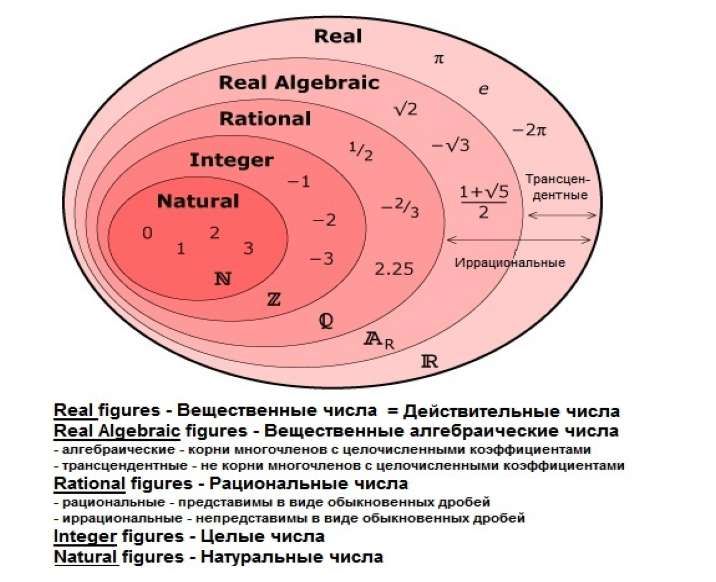
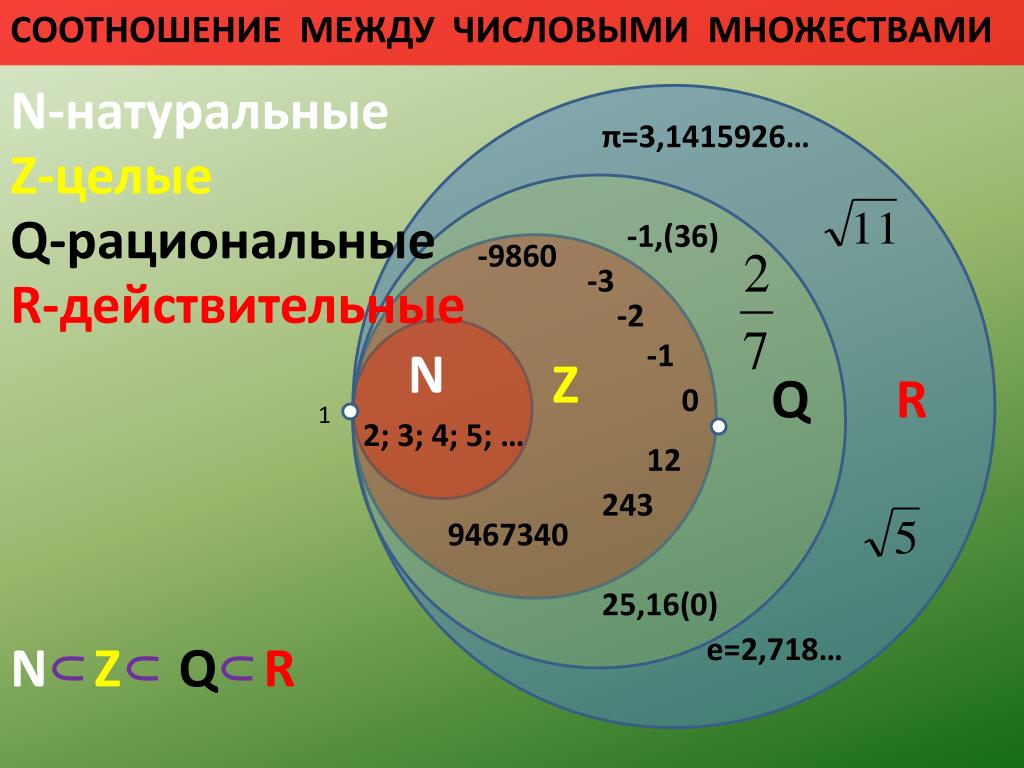
 Каков был его общий счет?
Каков был его общий счет? Самая высокая температура на Земле, 136 ° F, была зарегистрирована в 1922 году в Эль-Азизии, Ливия. Рассчитайте диапазон температур на Земле.
Самая высокая температура на Земле, 136 ° F, была зарегистрирована в 1922 году в Эль-Азизии, Ливия. Рассчитайте диапазон температур на Земле.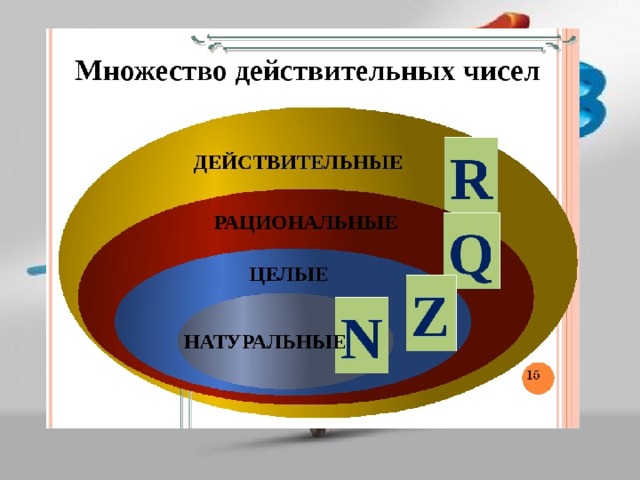



 Некоторые примеры действительных чисел: 3,5, 0,003, 2/3, π, и т. д.
Некоторые примеры действительных чисел: 3,5, 0,003, 2/3, π, и т. д.