Рациональные числа презентация, доклад
РАЦИОНАЛЬНЫЕ ЧИСЛА
6 класс
ПОНЯТИЕ РАЦИОНАЛЬНОГО ЧИСЛА
Рациональные числа — это натуральные, отрицательные и дробные (обыкновенные и конечные десятичные) числа.
От английского «ratio» — отношение,соотношение.
Примеры рациональных чисел:
ИСТОРИЧЕСКАЯ СПРАВКА
“ К созданию понятия отрицательного числа китайские ученые подошли раньше математиков других народов, во II в. до н. э. Положительные количества в китайской математике называли “чжен”, отрицательные – “фу”. Их изображали разными цветами: “ чжен” — красным, “ фу” — черным. Такой способ изображения использовался в Китае до середины ХII столетия, пока Ли Е не предложил более удобное обозначение отрицательных чисел — цифры, которые изображали отрицательные числа перечеркивали черточкой справа налево. Введение отрицательных чисел и правил их сложения и вычитания можно считать одним из самых крупных открытий китайских ученых”
Введение отрицательных чисел и правил их сложения и вычитания можно считать одним из самых крупных открытий китайских ученых”
“ В Европе с сознанием уверенности в справедливости своих вычислений начал оперировать с отрицательными числами французский математик Никола Шюке. В своих трудах в 1484 г. Он рассматривает задачи, приводящие к уравнениям с отрицательными корнями. Шюке заявляет, что “это вычисление, которое иные считают невозможным, правильно”.
Чех Ян Видман уже писал “+” и “ — ” для сложения и вычитания. А чуть позднее немецкий ученый Михель Штофель написал “Полную Арифметику”, которая была напечатана в 1544 году. В ней встречаются такие записи для чисел: 0 – 2; 0 + 2; 0 – 5; 0 + 7. Всеобщее признание отрицательные числа получили в первой половине XIX в., когда была развита строгая теория положительных и отрицательных чисел.
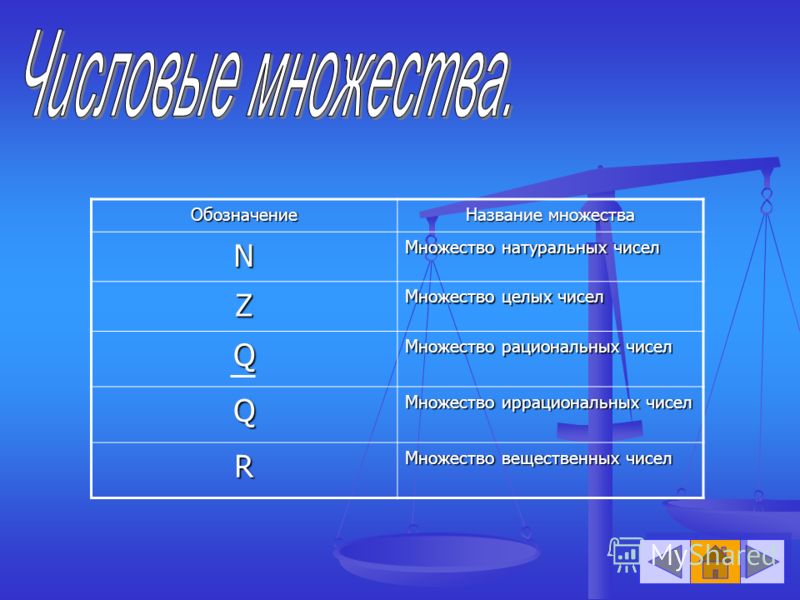
МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ
Множество рациональных чисел обозначаются заглавной английской буквой Q (кью).
Множество Q включает в себя множество целых чисел (Z) и натуральных чисел (N).
РАЦИОНАЛЬНОЕ ЧИСЛО
Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель — натуральным.
a/b, где a ∈ Z ( a принадлежит целым числам ), b∈N ( b принадлежит натуральным числам ).
СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
Сравнение рациональных чисел — это сравнение чисел положительных и отрицательных, целых и дробных (обыкновенные дроби и десятичные дроби).
Из двух рациональных чисел больше то, которому на числовой оси соответствует точка, расположенная правее.
Всякое положительное число больше 0.
Всякое отрицательное число меньше 0.
Из двух отрицательных чисел больше то, модуль которого меньше.
Любое положительное число больше любого отрицательного числа.
ПРОВЕРЬ СЕБЯ.
Даны числа: 3; 2,5; -5,6; 0,25; — 6,89, 0.
Назовите числа противоположные числам.
Найдите модуль каждого из чисел.
Выберите число, модуль которого наибольший; наименьший.
Сравните дроби:
1) 1 и 1 ; 2) 2 и 3 ; 3) 5 и 3 .
5 8 5 4 6 8
СЛОЖЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
Чтобы сложить рациональные числа с одинаковыми знаками, складывают их модули и перед суммой ставят их общий знак.
(+19) + (+23) = 42; (-16) + (-307) = — 323.
Чтобы сложить два рациональных числа с разными знаками и разными модулями, необходимо поставить знак числа с большим модулем и приписать к нему разность между большим и меньшим модулем.
(+107) + (-56) = 51; (-23,6) + 7,5 = -16,1.
Сумма двух противоположных чисел (то есть, с разными знаками и одинаковыми модулями) равна нулю.
(-2,57) + (+2,57) = 0.
При сложении любого рационального числа и нуля получаем само это число.
ЗАКОНЫ СЛОЖЕНИЯ
Законы сложения положительных чисел (переместительный и сочетательный) справедливы и для рациональных чисел. Применяя их, можно по-разному находить сумму нескольких чисел.
Например, сложение нескольких чисел с разными знаками можно выполнять последовательно: сначала найти сумму первых двух слагаемых, к ней прибавить третье слагаемое и т. д. Но иногда удобнее сложение выполнять таким способом: сложить отдельно все положительные числа и отдельно все отрицательные числа, затем полученные два числа сложить по правилу сложения чисел с разными знаками.
(+105) + (-4) + (-8) + (+21) + (-7) = (+126) + (-19) = +107.
ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
Вычитание рациональных чисел зависит от знаков чисел уменьшаемого и вычитаемого.
Чтобы из одного числа вычесть другое, достаточно к уменьшаемому прибавить число, противоположное вычитаемому.
Например: -102 — (-80) = -102 + 80 = -22.
Если уменьшаемое — отрицательное число, а вычитаемое — положительное число, то нужно сложить модули уменьшаемого и вычитаемого и перед полученным результатом поставить знак «-».
Например: -839 — 71 = — (|-839|+|-71|) = — (839+71) = -910.
Если уменьшаемое — положительное число н вычитаемое — положительное число, то нужно найти разность модулей уменьшаемого и вычитаемого и перед полученным результатом поставить знак «-», если модуль уменьшаемого меньше модуля вычитаемого. Если модуль уменьшаемого равен модулю вычитаемого, то разность равна нулю.
Примеры.
0,165 — 0,015 = 0,15 т. к. |0,1б5| > |0,0151
1 307 — 1 307 = 0 т. к. |1 307| = |1 307|
УМНОЖЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ
При умножении двух рациональных чисел умножаются их абсолютные величины (модули чисел) и перед произведением ставится знак, зависящий от знаков множителей.
Знак произведения определяется по таблице знаков.
Таблица знаков
Первый знак Второй знак Знак произведения
+ + +
— — +
+ — —
— + —
Если произведение содержит более двух рациональных чисел, то результат можно определить поэтапно («шаг за шагом»), на каждом этапе вычисляя произведение двух сомножителей. А можно по особому правилу определить знак произведения для всех множителей сразу.
Если в произведении все числа положительные, то модуль их произведения равен произведению модулей всех множителей, а знак произведения — «+».
Если в произведении есть числа положительные и отрицательные, то модуль их произведения равен произведению модулей всех множителей, а знак произведении «+» — при четном количестве отрицательных множителей (минусов) и «-» — при нечетном количестве отрицательных множителей (минусов).
2 — 13 * 7 * 24 = 4 368
2 * (-13) * (-7) * 24 = 4 368, т. к. количество минусов четное;
(-2) * (-13) * (-7) * 24 = -4 368, т. к. количество минусов нечетное.
Если при умножении рациональных чисел одни или несколько множителей равны 0, то все произведение равно 0.
2 * 0,71 * 172 * 0 * (176 — 176) = 0
ДЕЛЕНИЕ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ
Частное от деления двух отрицательных чисел есть число положительное. Модуль частного есть частное модулей делимого и делителя.
Например:
(-81) : (-9) = |-81|:|-9| = 81 : 9 = 9;
(-0,74) : (-0,37) = |-0.74| : |—0,37| = 0,74 : 0,37 = 2
Частное от деления отрицательного числа на положительное число и положительного числа на отрицательное число есть число отрицательное. Модуль частного есть частное модулей делимого и делителя.
Например:
(-180) : 3 = —|—180| : |3| = —(180 : 3) = -60
Рациональные числа, как и другие, па нуль делить нельзя. Если делимое нуль, а делитель — рациональное число, то при любом его значении и знаке частное равно нулю.
Если делимое нуль, а делитель — рациональное число, то при любом его значении и знаке частное равно нулю.
Правила, по которым определяется знак произведения, действительны и для частного. Поэтому знак частного тоже проверяется по таблице знаков.
СТЕПЕНЬ ЧИСЛА
Степень любого числа — это произведение одинаковых сомножителей. Количество сомножителей определяет показатель степени.
Четная степень отрицательного числа — число положительное. Нечетная степень отрицательного числа — число отрицательное. Любая степень числа нуль равна нулю.
Желаю успехов!
Что такое множество
Множество — это набор каких-либо объектов. Объекты, из которых состоит множество, называются элементами этого множества.
Например: множество школьников, множество машин, множество чисел.
В математике множество рассматривается намного шире.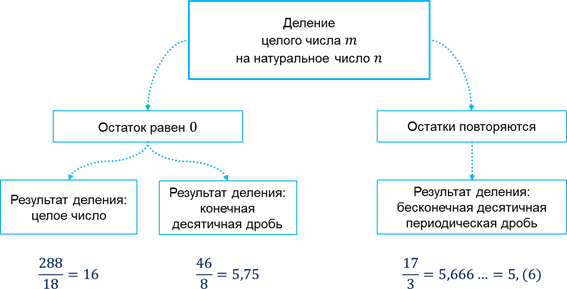 Мы не будем сильно углубляться в эту тему, поскольку она относится к высшей математике и на первых порах может создавать трудности для обучения. Мы рассмотрим только ту часть темы, с которой уже имели дело.
Мы не будем сильно углубляться в эту тему, поскольку она относится к высшей математике и на первых порах может создавать трудности для обучения. Мы рассмотрим только ту часть темы, с которой уже имели дело.
Обозначения
Множество чаще всего обозначают заглавными буквами латинского алфавита, а его элементы — строчными. При этом элементы заключаются в фигурные скобки.
Например, если наших друзей зовут Том, Джон и Лео, то мы можем задать множество друзей, элементами которого будут Том, Джон и Лео.
Обозначим множество наших друзей через заглавную латинскую букву F (friends), затем поставим знак равенства и в фигурных скобках перечислим наших друзей:
F = { Том, Джон, Лео }
Пример 2. Запишем множество делителей числа 6.
Обозначим через любую заглавную латинскую букву данное множество, например, через букву D
D
затем поставим знак равенства и в фигурных скобках перечислим элементы данного множества, то есть перечислим делители числа 6
D = { 1, 2, 3, 6 }
Если какой-то элемент принадлежит заданному множеству, то эта принадлежность указывается с помощью знака принадлежности ∈. К примеру, делитель 2 принадлежит множеству делителей числа 6 (множеству D). Записывается это так:
К примеру, делитель 2 принадлежит множеству делителей числа 6 (множеству D). Записывается это так:
2 ∈ D
Читается как «2 принадлежит множеству делителей числа 6»
Если какой-то элемент не принадлежит заданному множеству, то эта не принадлежность указывается с помощью зачёркнутого знака принадлежности ∉. К примеру, делитель 5 не принадлежит множеству D. Записывается это так:
5 ∉ D
Читается как «5 не принадлежит множеству делителей числа 6»
Кроме того, множество можно записывать прямым перечислением элементов, без заглавных букв. Это может быть удобным, если множество состоит из небольшого количества элементов. Например, зададим множество из одного элемента. Пусть этим элементом будет наш друг Том:
{ Том }
Зададим множество, которое состоит из одного числа 2
{ 2 }
Зададим множество, которое состоит из двух чисел: 2 и 5
{ 2, 5 }
Множество натуральных чисел
Это первое множество с которым мы начали работать. Натуральными числами называют числа 1, 2, 3 и т.д.
Натуральными числами называют числа 1, 2, 3 и т.д.
Натуральные числа появились из-за потребности людей сосчитать те иные объекты. Например, посчитать количество кур, коров, лошадей. Натуральные числа возникают естественным образом при счёте.
В прошлых уроках, когда мы употребляли слово «число», чаще всего подразумевалось именно натуральное число.
В математике множество натуральных чисел обозначается заглавной латинской буквой N.
Например, укажем, что число 1 принадлежит множеству натуральных чисел. Для этого записываем число 1, затем с помощью знака принадлежности ∈ указываем, что единица принадлежит множеству N
1 ∈ N
Читается как: «единица принадлежит множеству натуральных чисел»
Множество целых чисел
Множество целых чисел включает в себя все положительные и отрицательные числа, а также число 0.
Множество целых чисел обозначается заглавной латинской буквой Z.
Укажем, к примеру, что число −5 принадлежит множеству целых чисел:
−5 ∈ Z
Укажем, что 10 принадлежит множеству целых чисел:
10 ∈ Z
Укажем, что 0 принадлежит множеству целых чисел:
0 ∈ Z
В будущем все положительные и отрицательные числа мы будем называть одним словосочетанием — целые числа.
Множество рациональных чисел
Рациональные числа, это те самые обыкновенные дроби, которые мы изучаем по сей день.
Рациональное число — это число, которое может быть представлено в виде дроби , где a — числитель дроби, b — знаменатель.
В роли числителя и знаменателя могут быть любые числа, в том числе и целые (за исключением нуля, поскольку на нуль делить нельзя).
Например, представим, что вместо a стоит число 10, а вместо b — число 2
10 разделить на 2 равно 5. Видим, что число 5 может быть представлено в виде дроби , а значит число 5 входит во множество рациональных чисел.
Легко заметить, что число 5 также относится и ко множеству целых чисел. Стало быть множество целых чисел входит во множество рациональных чисел. А значит, во множество рациональных чисел входят не только обыкновенные дроби, но и целые числа вида −2, −1, 0, 1, 2.
Теперь представим, что вместо a стоит число 12, а вместо b — число 5.
12 разделить на 5 равно 2,4. Видим, что десятичная дробь 2,4 может быть представлена в виде дроби , а значит она входит во множество рациональных чисел. Отсюда делаем вывод, что во множество рациональных чисел входят не только обыкновенные дроби и целые числа, но и десятичные дроби.
Мы вычислили дробь и получили ответ 2,4. Но мы могли бы выделить в этой дроби целую часть:
При выделении целой части в дроби , получается смешанное число . Видим, что смешанное число тоже может быть представлено в виде дроби . Значит во множество рациональных чисел входят и смешанные числа.
В итоге мы приходим к выводу, что множество рациональных чисел содержат в себе:
- целые числа
- обыкновенные дроби
- десятичные дроби
- смешанные числа
Множество рациональных чисел обозначается заглавной латинской буквой Q.
Например укажем, что дробь принадлежит множеству рациональных чисел. Для этого записываем саму дробь , затем с помощью знака принадлежности ∈ указываем, что дробь принадлежит множеству рациональных чисел:
∈ Q
Укажем, что десятичная дробь 4,5 принадлежит множеству рациональных чисел:
4,5 ∈ Q
Укажем, что смешанное число принадлежит множеству рациональных чисел:
∈ Q
Вводный урок по множествам завершён. В будущем мы рассмотрим множества намного лучше, а пока рассмотренного в данном уроке будет достаточно.
В будущем мы рассмотрим множества намного лучше, а пока рассмотренного в данном уроке будет достаточно.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Презентация по теме: Рациональные числа доклад, проект
Тема урока:
РАЦИОНАЛЬНЫЕ ЧИСЛА
Цели урока:
систематизировать знания о
рациональных числах;
формирование навыка работы в парах;
развитие внимания и логического мышления.
Для счета предметов используются числа, которые называются натуральными. Для обозначения множества натуральных чисел употребляется буква N — первая буква латинского слова Naturalis — «естественный», «натуральный»
N — натуральные
1, 2, 3, 4, 5, …
Натуральные числа
Числа,
им противоположные
Целые
Натуральные числа, числа им противоположные и число нуль, образуют множество целых чисел, которое обозначается Z — первой буквой немецкого слова Zahl — «число».
Z — целые
…, -3, -2, -1, 0,
1, 2, 3, …
Целые числа
Дробные числа
Рациональные
Множество чисел, которое можно представить в виде , называется множеством рациональных чисел и обозначается буквой Q — первой буквой французского слова Quotient — «отношение». Есть также версия, что название рациональных чисел связано с латинским словом ratio – разум.
Q — рациональные
…, -3, -2, -1, 0, 1, 2, 3, …
+ дроби
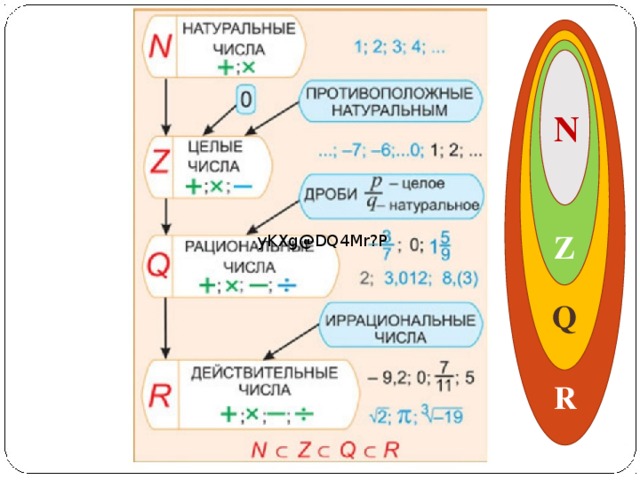
Отношения между множествами натуральных,
целых и рациональных чисел наглядно демонстрирует
геометрическая иллюстрация – круги Эйлера.
N ⊂ Z ⊂ Q
Математический символ ∈ называют знаком принадлежности (элемент принадлежит множеству).
«n — натуральное число»
можно писать n ∈ N
«m — целое число»
можно писать m ∈ Z
«r — рациональное число»
можно писать r ∈ Q
Новые обозначения:
Математический символ ⊂ называют знаком включения (одно множество содержится в другом).
«N — часть множества Z»
можно писать N ⊂ Z,
«Z — часть множества Q»
можно писать Z ⊂ Q
Новые обозначения:
Множества обозначают большими буквами,
элементы множества — маленькими буквами.
«x не принадлежит множеству X»
можно писать x ∉ X
«A не является частью (подмножеством) B»
можно писать A ⊄ B.
Новые обозначения:
N ⊂ Z ⊂ Q
Число 5 — ?
N, Z, Q
Число -7 — ?
Z, Q
Z, Q
Число -6,7 — ?
Q
1. нет
нет
2. да
3. нет
4. да
5. да
6. нет
7. да
8. да
9. да
10. нет
11. нет
12. нет
13. да
14. да
15. нет
Переведите обыкновенные дроби в десятичные:
= 0,375 – конечная десятичная дробь
Если в знаменателе стоят 2, 5, их произведение или произведение комбинацийэтих чисел – всегда КОНЕЧНАЯ ДЕСЯТИЧНАЯ ДРОБЬ!
= 0,272727272727272727… — бесконечная периодическая десятичная дробь
Для краткости написания – ПЕРИОД (круглые скобки)
0,272727272727272727…= 0,(27)
Переведите обыкновенные дроби в десятичные:
0,(2) 2) 2,(21) 3) 1,(1)
4) -3,0(3) 5) -0,1(6) 6) 12,45(7)
Любое рациональное число можно записать в виде бесконечной десятичной периодической дроби?
N ⊂ Z ⊂ Q
5 = 5,000… = 5,(0)
-8,37 = -8,37000… = -8,37(0)
Дроби — ?
Алгоритмы перевода рациональных чисел
в бесконечную десятичную периодическую дробь
= 0,375 = 0,375(0)
= 0,272727… = 0,(27)
Делим числитель
на знаменатель
Любое рациональное число можно записать в виде бесконечной десятичной периодической дроби?
Наоборот, бесконечную периодическую десятичную дробь в обыкновенную?
Пусть х = 0,(2)
10х = 2,(2)
х = 0,(2)
10х = 2,(2)
10х – х = 2,(2) — 0,(2)
9х = 2
Переведем б. п.д. дробь 0,(2)
п.д. дробь 0,(2)
в обыкновенную
Это для
чисто периодической !!!
Пусть х = 0,4(6)
10х = 4,(6)
10х = 4,(6)
100х = 46,(6)
100х – 10х = 46,(6) — 4,(6)
90х = 42
Это для
смешанной периодической !!!
Еще один интересный
вариант перевода …
0,(2)=
2
9
1 цифра
0,(81)=
81
2 цифры
99
Чтобы обратить смешанную периодическую дробь в обыкновенную, нужно в числителе обыкновенной дроби
поставить число, равное разности числа, образованного цифрами, стоящими после запятой до начала второго периода, и числа, образованного из цифр, стоящих после запятой до начала первого периода; а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и со столькими нулями, сколько цифр между запятой и началом периода.
0,4(6)=
4
6
4
1 цифра
9
1 цифра
0
— Знаю (умею, научился), как определить вид числа, его принадлежность к числовым множествам;
— Знаю (умею, научился) правильно пользоваться математической символикой в процессе выполнения заданий;
— Знаю (умею, научился) представлять рациональное число в виде конечной или бесконечной периодической дроби;
— Знаю (умею, научился) представлять бесконечную периодическую дробь в виде обыкновенной дроби;
.
Результаты урока:
Домашнее задание:
1. Дана фраза: «28 — рациональное число». Как можно записать иначе?
а) 28 ∈ N б) 28 ∈ Q в) 28 ∈ Z
2. Вычисли значение дроби − d, если a = 13; b = 36; c = 0,9; d=1,76;
3. Утверждение «−17∈(−17;5]» является:
а) ложным; б) истинным
4. Выясни при каком наименьшем целом значение p число 3p+15p+2 является целым
Выясни при каком наименьшем целом значение p число 3p+15p+2 является целым
5. Вычислить значение выражения:
Разряды и классы чисел — Математика и Английский
Классификация чисел в математике
Хорошо, когда все на своих местах: кастрюли в шкафу, зубная щетка — в ванной. У цифр при записи чисел тоже есть свое место. В этой статье раскроем тему разрядов и классов.
О чем эта статья:
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — Цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
- Единица (1) — самое маленькое число, а самого большого числа не существует. Ноль (0) означает, что предмета нет. Ноль не является натуральным числом.

От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется Однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется Двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются Двузначными, Трехзначными, Четырехзначными или Многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — Позицию.
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют Классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Названия классов многозначных чисел справа налево:
- первый — класс единиц, второй — класс тысяч, третий — класс миллионов, четвертый — класс миллиардов, пятый — класс триллионов, шестой — класс квадриллионов, седьмой — класс квинтиллионов, восьмой — класс секстиллионов.

Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
- 125 911 723 296.
А теперь прочитаем число единиц каждого класса слева направо:
- 125 миллиардов 911 миллионов 723 тысячи 296.
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
- 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу.
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Разрядные единицы обозначают так:
- Единицы — единицами первого разряда (или простыми единицами) и пишут на первом месте справа. Десятки — единицами второго разряда и записывают в числе на втором месте справа. Сотни — единицами третьего разряда и записывают на третьем месте справа. Единицы тысяч — единицами четвертого разряда и записывают на четвертом месте справа. Десятки тысяч — единицами пятого разряда и записывают на пятом месте справа. Сотни тысяч — единицами шестого разряда и записывают в числе на шестом месте справа и так далее.

Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши курсы по математике!
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
55 единиц второго класса и 100 единиц первого класса;
110 единиц второго класса и 5 единиц первого класса;
7 единиц второго класса и 13 единиц первого класса.
Все разрядные единицы, кроме простых единиц, называют Составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
- 10 единиц равны 1 десятку; 10 десятков равны 1 сотне; 10 сотен равны 1 тысяче; 10 тысяч равны 1 десятку тысяч; 10 десятков тысяч равны 1 сотне тысяч; 10 сотен тысяч равны 1 миллиону.

Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
- 11 627 — одиннадцать тысяч шестьсот двадцать семь. 31 502 — тридцать одна тысяча пятьсот два.
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.
С помощью чисел можно сосчитать количество предметов и определить различные величины.
Skysmart. ru
30.08.2019 0:40:54
2019-08-30 00:40:54
Источники:
Https://skysmart. ru/articles/mathematic/razryady-i-klassy-chisel
Рациональные ⚠️ числа: что это значит, как обозначаются, классификация, пример положительных » /> » /> .keyword { color: red; }
Классификация чисел в математике
Рациональные числа в математике — какие так называются
Рациональные числа — числа, которые можно представить в виде обычной дроби вида \(\frac mn\) , где числитель m — это целое число, а знаменатель n — натуральное.
К рациональным относят целые и дробные числа с положительным или отрицательным знаком, а также ноль. Например, 2, 0, -8, \(\frac47, 0,36.\)
Множество рациональных чисел не бесконечно, существуют примеры исключений. Доказательством тому служит множество Иррациональных чисел. К примеру, рациональными не считают:
К примеру, рациональными не считают:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- некоторые корни — например, \(\sqrt2\) ; число Пи, число Эйлера, золотое сечение; непериодические дроби.
Для чего нужны, какой буквой обозначается
Для обозначения Множества рациональных чисел используют букву Q. Это множество можно записать в виде:
Название множества произошло от латинского слова «ratio», которое означает «отношение», «дробь». То есть рациональные числа — это дробные числа. Их применяют при счете целых объектов и их частей — например, если порезать яблоко на несколько долек.
Свойства рациональных чисел
Одно из основных свойств рациональных чисел — их Замкнутость относительно всех арифметических операций.
Это свойство можно объяснить на примере натуральных чисел: 16+14=30. 30 — это натуральное число, как и его слагаемые. Это значит, что множество натуральных чисел замкнуто относительно операции сложения.
30 — это натуральное число, как и его слагаемые. Это значит, что множество натуральных чисел замкнуто относительно операции сложения.
С помощью рациональных чисел можно выполнять любые арифметические операции:
- сложение: 3,5+2=5,5; умножение: \(-\frac45\cdot\frac54=-1\) ; вычитание: 1-7,6=-6,6; деление: \(3:8=\frac38\) .
Таким образом, множество Q замкнуто относительно всех четырех операций.
Список свойств рациональных чисел широк. Его можно сократить до нескольких основных пунктов.
Упорядоченность. Между рациональными числами всегда можно идентифицировать один из видов отношений: «>», « Транзитивность отношения порядка. Для любых трех рациональных чисел a, b, c верно следующее: если a Наличие противоположного числа. У любого рационального числа есть противоположное, при сложении с которым получается 0: a+(-a)=0. Наличие обратного числа. Любое рациональное число имеет обратное ему число, при умножении на которое получается 1: \(\frac ab\cdot\frac ba=1\) .
Классификация рациональных чисел, виды с примерами
Выделяют несколько групп рациональных чисел.
Целые числа. Обыкновенные дроби. Десятичные дроби:
- конечные: после запятой стоит определенное количество цифр — например, 0,6; -4,657; бесконечные периодические: после запятой стоит бесконечное количество цифр, но одна или несколько из них повторяются. Такие повторяющиеся цифры называют Периодом. Их записывают в скобках для краткости: \(0,33333\dots=0,\left(3\right).\)
Какая разница между целыми, натуральными и рациональными числами
Натуральные числа — это все целые числа, начиная с 1. Их множество обозначают буквой N.
1, 14, 47 относятся к натуральным числам.
Это понятие появилось раньше других. Натуральные числа используют для простого счета существующих в окружающем мире предметов. Ноль, отрицательные и дробные числа не входят в множество N. Оно замкнуто относительно операций сложения и умножения.
Целые числа включают в себя натуральные числа, а также ноль и числа, противоположные натуральным — отрицательные. Их множество обозначают буквой Z.
Их множество обозначают буквой Z.
4, 0, -11 относятся к целым числам.
Исторически целые числа возникли как решение проблемы ограниченности натуральных чисел. С развитием математики стало известно о существовании нуля и отрицательных чисел. Однако множество Z не включает в себя дробные числа. Оно замкнуто относительно всех операций, кроме деления.
Множество рациональных чисел, исходя из определения, является наиболее широким из трех. Оно включает в себя все натуральные и целые числа.
Систему отношений между множествами можно представить в виде кругов Эйлера. Схема представлена ниже.
Рациональные числа — числа, которые можно представить в виде обычной дроби вида \(\frac mn\) , где числитель m — это целое число, а знаменатель n — натуральное.
К рациональным относят целые и дробные числа с положительным или отрицательным знаком, а также ноль. Например, 2, 0, -8, \(\frac47, 0,36.\)
Множество рациональных чисел не бесконечно, существуют примеры исключений.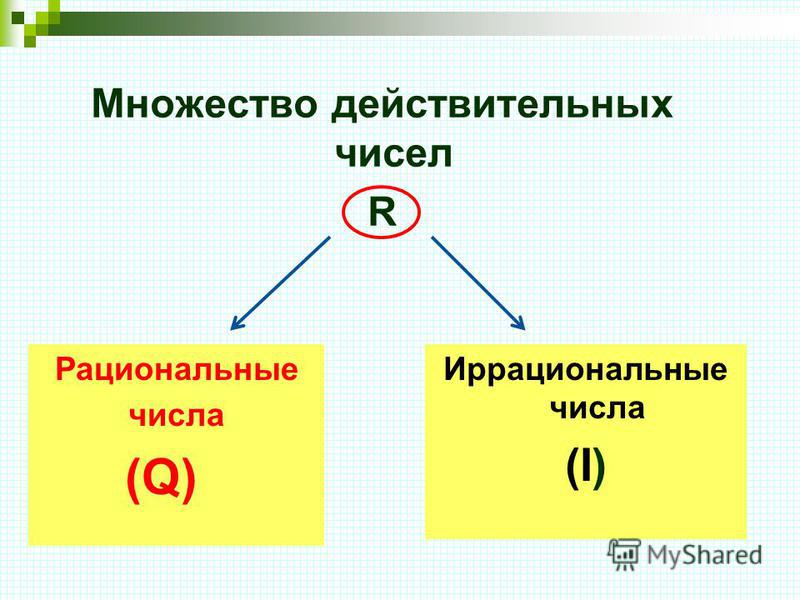 Доказательством тому служит множество Иррациональных чисел. К примеру, рациональными не считают:
Доказательством тому служит множество Иррациональных чисел. К примеру, рациональными не считают:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- некоторые корни — например, \(\sqrt2\) ; число Пи, число Эйлера, золотое сечение; непериодические дроби.
Для чего нужны, какой буквой обозначается
Для обозначения Множества рациональных чисел используют букву Q. Это множество можно записать в виде:
Название множества произошло от латинского слова «ratio», которое означает «отношение», «дробь». То есть рациональные числа — это дробные числа. Их применяют при счете целых объектов и их частей — например, если порезать яблоко на несколько долек.
30 это натуральное число, как и его слагаемые.
Wiki. fenix. help
29.04.2018 14:06:54
2018-04-29 14:06:54
Источники:
Https://wiki. fenix. help/matematika/racionalnye-chisla
fenix. help/matematika/racionalnye-chisla
Множества и классификация чисел: Дискуссионные темы (М) » /> » /> .keyword { color: red; }
Классификация чисел в математике
1. Множество — множество простых чисел (не имеет простых делителей, кроме самого себя).
2. Множество — множество натуральных чисел.
3. Множество — множество целых чисел (это натуральные, ноль, и целые отрицательные).
4. Множество — множество рациональных чисел (это целые числа, либо числа, которые представимы в виде дроби, в числителе и знаменателе которой целые числа. Десятичная запись рациональных либо конечна, либо представима в виде дроби, в которой обязательно есть периодическое повторение).
5. Множество — подмножество действительных чисел, которые представимы в виде радикалов над полем действительных чисел. Сюда включаются все рациональные (Q), а также некоторые иррациональные, например, >>$» />. Более точно — в этом множестве числа, которые можно представить в виде записи с возведением в степень, где в степени будет рациональное число, а любое число которое возводится в степень — рациональное положительное.
6. Множество — подмножество действительных чисел, которые представимы в виде радикалов над полем комплексных чисел. Сюда включаются все рациональные (Q), а также некоторые иррациональные, например, >> + . $» />, которое окажется действительным в итоге. Более точно — в этом множестве числа, которые можно представить в виде записи с возведением в степень, где в степени будет рациональное число, а число которое возводится в степень — рациональное, и может быть отрицательным.
Отличие множества 6 от множества 5. Например, корни уравнения,
Вместе с тем, известно, что кубические уравнения разрешимы в радикалах. Это значит, что эти же корни можно представить в виде записи с числами, мат. операциями, и степенями.
Вопрос. У меня предположение, что части этой записи — будут комплексными числами, т. е. там не обойтись без. Будут корни из отрицательных чисел обязательно. Верно ли предположение?
Если предположение верно, то всегда действительные корни кубических уравнений — принадлежат множеству, но они могут не принадлежать множеству. А вот корни квадратного уравнения всегда принадлежат маломощному множеству.
А вот корни квадратного уравнения всегда принадлежат маломощному множеству.
Вопрос. Всегда ли синус от аргумента (в градусах) представленного в виде рационального числа — принадлежит множеству (или даже ), т. е. всегда ли его можно выразить в радикалах?
Но перейдем к еще более мощному множеству чисел. Действительные корни уравнения 5-й степени, вообще не всегда могут быть выражены в радикалах, т. е. они могут не входить даже в, но есть такое множество, куда они входят —
7. Множество — множество алгебраических чисел, (подмножество действительных чисел) . В это множество входят все возможные действительные корни всех возможных алгебраических уравнений, любых степеней, и с любыми рациональными коэффициентами.
Какие более мощные множества, чем, рассматриваются в математике (не считая самых широких множеств — действительных и комплексных)? Я более мощных не встречал, обычно, если число не входит в то его просто называют трансцендентным. А я бы ввел еще одно множество —
8. Множество — множество чисел, которые могут быть корнями любого математического уравнения (не обязательно алгебраического), с любыми известными функциями (типа синус, дзета-функция, интегральный логарифм и т. д.), которые могут быть разложены представлены в виде ряда или нескольких рядов. Назовем такие числа АНАЛИТИЧЕСКИМИ. Проще говоря — можно задать описание конечных размеров, такое что, по этому описанию можно найти любую цифру после запятой данного числа — до бесконечности.
Множество — множество чисел, которые могут быть корнями любого математического уравнения (не обязательно алгебраического), с любыми известными функциями (типа синус, дзета-функция, интегральный логарифм и т. д.), которые могут быть разложены представлены в виде ряда или нескольких рядов. Назовем такие числа АНАЛИТИЧЕСКИМИ. Проще говоря — можно задать описание конечных размеров, такое что, по этому описанию можно найти любую цифру после запятой данного числа — до бесконечности.
До сих пор все рассматриваемые множества были подмножествами следующего, т. е. подмножество, и т. д. — подмножество. Следующее множество, — отдельное ( в него не входит), но самое мощное.
9. Множество — множество хаотических чисел. (хаотических — мое определение). Это множество всех действительных чисел, которые не входят в. Если число входит в, то никакими математическими описаниями конечных размеров (не важно — рядами, или функциями и т. п.), это число невозможно представить, т. е. если мы зададим описание конечных размеров, то мы не сможем по этому описанию найти любую цифру после запятой данного числа — до бесконечности.
10. Множество — множество ВСЕХ действительных чисел. Это объединение непересекающихся множеств и. Причем множество в множестве — имеет меру нуль. Т. е. в множестве действительных чисел — большинство чисел — хаотические, и меньшинство — аналитические.
11. Множество — множество всех комплексных чисел. Можно было разбить и его на аналогичные подмножества (алгебраические комплексные, аналитические, хаотические и др.) но уже думаю, необязательно.
Правильна моя классификация? Какие еще у математиков есть множества, являющиеся подмножествами трансцендентных, но не являющиеся алгебраическими числами?
7. Множество — множество алгебраических чисел, (подмножество действительных чисел) . В это множество входят все возможные действительные корни всех возможных алгебраических уравнений, любых степеней, и с любыми рациональными коэффициентами.
Но перейдем к еще более мощному множеству чисел. Действительные корни уравнения 5-й степени, вообще не всегда могут быть выражены в радикалах, т. е. они могут не входить даже в, но есть такое множество, куда они входят —
е. они могут не входить даже в, но есть такое множество, куда они входят —
Я более мощных не встречал, обычно, если число не входит в то его просто называют трансцендентным.
Dxdy. ru
17.04.2020 4:58:40
2020-04-17 04:58:40
Источники:
Https://dxdy. ru/topic35655.html
Умножение комплексных чисел — МегаЛекции
Вопрос 1
Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Рациональные числа — это числа вида m/n , где m — целое число, а n — натуральное число.
Множество рациональных чисел принято обозначать буквой Q.
Выполняется соотношение Z⊂Q , поскольку любое число m можно представить в виде m1.
Итак, можно сказать, что
Рациональные числа — это все целые числа, а также положительные и отрицательные обыкновенные дроби.
Действительные числа
Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел. 2 = –1. Число a называется абсциссой, a b – ординатой комплексного числа a+ bi.
2 = –1. Число a называется абсциссой, a b – ординатой комплексного числа a+ bi.
Виды комплексных чисел:
1. Алгебраическая форма комплексного числа
Запись комплексного числа в виде z=a+bi , где a и b — действительные числа, называется алгебраической формой комплексного числа.
Например: z=1-i
2. Тригонометрическая форма комплексного числа
Если — модуль комплексного числа z=a+bi , а — его аргумент, то тригонометрической формой комплексного числа z называется выражение:
3. Показательная форма комплексного числа.
Показательной формой комплексного числа называется выражение:
Геометрический смысл комплексных чисел:
Геометрическая интерпретация комплексных чисел заключается в том, что комплексному числу z = х + yi сопоставляется точка на плоскости с координатами х, у. Именно действительная часть числа мыслится как х-координата, а мнимая — как y-координата. Таким образом устанавливается взаимно однозначное соответствие между комплексными числами и точками «числовой плоскости».
Вопрос 3
Сложение комплексных чисел
Сложить два комплексных числа ,
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:
Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.
Для комплексных чисел справедливо правило первого класса: – от перестановки слагаемых сумма не меняется.
Вычитание комплексных чисел
Пример 2
Найти разности комплексных чисел и , если ,
Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .
Рассчитаем вторую разность:
Здесь действительная часть тоже составная:
Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: .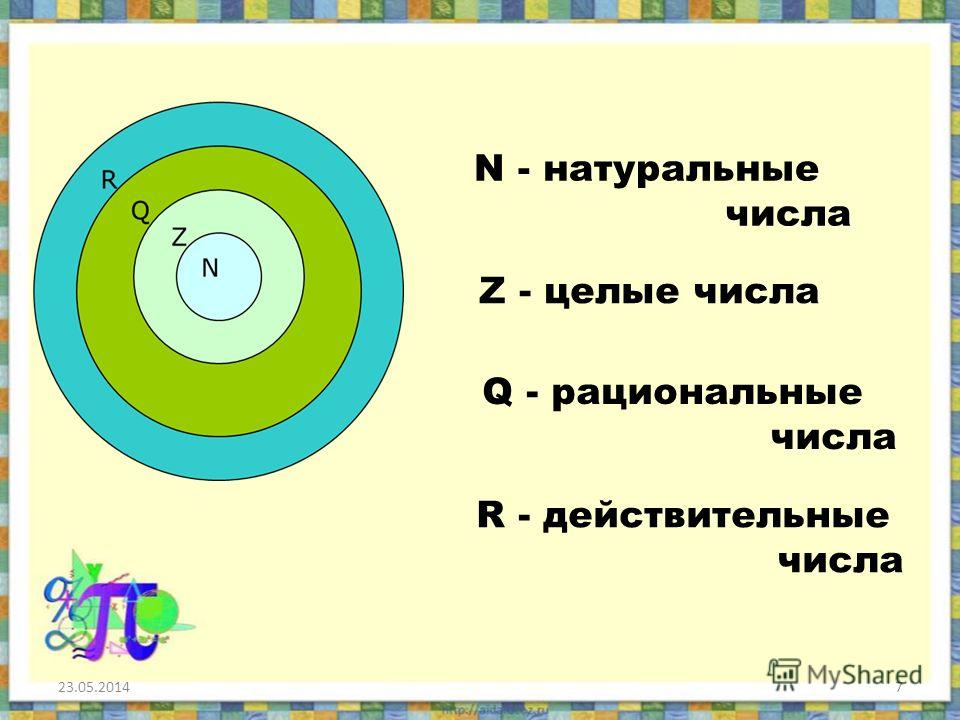 Вот здесь без скобок уже не обойтись.
Вот здесь без скобок уже не обойтись.
Умножение комплексных чисел
Настал момент познакомить вас со знаменитым равенством:
Пример 3
Найти произведение комплексных чисел ,
Очевидно, что произведение следует записать так:
Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что и быть внимательным.
Повторим, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.
Я распишу подробно:
Надеюсь, всем было понятно, что
Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках.
Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .
В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.
Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.
Деление комплексных чисел
Даны комплексные числа , . Найти частное .
Составим частное:
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Вспоминаем бородатую формулу и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть
Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :
Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой (помним, что и не путаемся в знаках!!!).
Распишу подробно:
Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .
В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:
Вопрос 4
Степенью называется выражение вида: , где:
§ — основание степени;
§ — показатель степени.
Степень с натуральным показателем {1, 2, 3,…}
Определяем понятие степени, показатель которой — натуральное число (т.е. целое и положительное).
1. По определению: .
2. Возвести число в квадрат — значит умножить его само на себя:
3. Возвести число в куб — значит умножить его само на себя три раза: .
Возвести число в натуральную степень — значит умножить число само на себя раз:
Степень с целым показателем {0, ±1, ±2,…}
Если показателем степени является целое положительное число:
, n > 0
Возведение в нулевую степень:
, a ≠ 0
Если показателем степени является целое отрицательное число:
,a ≠ 0
Прим: выражение не определено, в случае n ≤ 0. Если n > 0, то
Если n > 0, то
Пример 1.
Воспользуйтесь поиском по сайту:
Принадлежит z. N — натуральные числа Z — целые числа Q
Цели урока:
Оборудование:
- Таблицы “Графики функций”;
- Карточки-задания “Графики функций”;
- Материалы для создания отчётов по мини-проектам (листы формата А2, фломастеры, чертёжные инструменты).
Ход урока.
1.Оргмомент
Приветствие учащихся, приглашение к сотрудничеству, к совместному творчеству.
2.Актуализация опорных знаний
.
Вопросы классу:
1. Что такое функция?
2. С какими функциями мы уже знакомы?
3. Что вы знаете о функциях?
4. Что значит исследовать функцию?
5. По каким параметрам мы исследуем функции?
Самостоятельная работа:
Описать свойства функции, используя её график.
Вариант 1
Вариант 2
(Используются таблицы, на обратной стороне которых записаны правильные ответы другого варианта. Ученики работают по вариантам, 2 ученика работают на обороте “крылышек”, имея мини-таблицы (карточки). Проверка осуществляется следующим образом: открыть ответы на “крыле” доски и ответы на плакате, вызвать ещё одного ученика, который озвучит записи в своей тетради, и сравнить ответы двух учащихся. Ученики в классе меняются тетрадями и выполняют взаимопроверку.)
При проверке результатов работы повторяются следующие вопросы:
- понятие функции;
- возрастание (убывание) функции;
- понятие симметричного множества;
- чётность (нечётность) функции.
3. Постановка проблемы.
Рассмотрим следующее уравнение:
2 – 2х = (х+2) 3 + 3 (*).
Предложите свои идеи решения этой задачи.
(В ходе дискуссии учащиеся приходят к мнению, что уравнение лучше решать графически, но для этого необходимо уметь строить график функции у=х 3)
4.
 Формулирование темы и постановка целей.
Формулирование темы и постановка целей.
Таким образом, нужно знать какая линия является графиком функции у=х 3 .Сегодня на уроке мы рассмотрим функции вида у=х n , n Z.
(Записать на доске и в тетрадях тему урока ).
Вопросы: Как можно назвать эту функцию? (степенная ).
С какими из степенных функций мы уже знакомы? (у=х, у=х 2 ).
Какие функции предстоит изучить? (у=х 3 , у=х 4 , у=х 5 , и т.д. ).
Ранее мы уже встречались с этими функциями при исследовании их на чётность. Какие же из данных функций чётные, а какие – нечётные?
| чётные | нечётные |
| у=х 2 | у=х |
| у=х 4 | у=х 3 |
| у=х 6 | у=х 5 |
| у=х 8 и т.д. | у=х 7 и т.д. |
Вспомните, как используется чётность или нечётность функции при построении её графика? (Нужно построить часть графика при х>0 и достроить при х)
5. Работа в группах.
Каждая группа представляет классу свой проект – график функции и описание её свойств. (I и II группы описывают свойства полностью, а каждая последующая ищет сходство и различия в свойствах.)
Представляется также решение уравнения (*).
Графики функций пересекаются в точке с абсциссой x= –1. Проверка показывает, что x= –1 является корнем уравнения (*).
1. Выясните монотонность функций у=2–2х и у=(х–2) 3 +3.
2. Сколько корней имеет уравнение (*)?
3. Можете ли вы выдвинуть какую-либо гипотезу
относительно решения уравнения f(x)=g(x), где f(x) –
возрастающая, а g(x) – убывающая функции?
6. Итог урока, рефлексия.
Итак, какие же новые знания вы приобрели на
сегодняшнем уроке?. .
.
В дальнейшем мы продолжим рассмотрение свойств данных функций применительно к решению алгебраических и прикладных задач.
В качестве домашнего задания предлагается прочесть соответствующий пункт в учебнике, выполнить построение графиков и исследование свойств тех функций, с которыми не работали в классе.
Из огромного многообразия всевозможных множеств особый интерес представляют так называемые числовые множества , то есть, множества, элементами которых являются числа. Понятно, что для комфортной работы с ними нужно уметь их записывать. С обозначений и принципов записи числовых множеств мы и начнем эту статью. А дальше рассмотрим, как числовые множества изображаются на координатной прямой.
Навигация по странице.
Запись числовых множеств
Начнем с принятых обозначений. Как известно, для обозначения множеств используются заглавные буквы латинского алфавита. Числовые множества, как частный случай множеств, обозначаются также. Например, можно говорить о числовых множествах A
, H
, W
и т. п. Особую важность имеют множества натуральных, целых, рациональных, действительных, комплексных чисел и т.п., для них были приняты свои обозначения:
п. Особую важность имеют множества натуральных, целых, рациональных, действительных, комплексных чисел и т.п., для них были приняты свои обозначения:
- N – множество всех натуральных чисел;
- Z – множество целых чисел;
- Q – множество рациональных чисел;
- J – множество иррациональных чисел;
- R – множество действительных чисел;
- C – множество комплексных чисел.
Отсюда понятно, что не стоит обозначать множество, состоящее, к примеру, из двух чисел 5 и −7 как Q , это обозначение будет вводить в заблуждение, так как буквой Q обычно обозначают множество всех рациональных чисел. Для обозначения указанного числового множества лучше использовать какую-нибудь другую «нейтральную» букву, например, A .
Раз уж мы заговорили про обозначения, то здесь напомним и про обозначение пустого множества, то есть множества, не содержащего элементов. Его обозначают знаком ∅.
Также напомним про обозначение принадлежности и непринадлежности элемента множеству. Для этого используют знаки ∈ — принадлежит и ∉ — не принадлежит. Например, запись 5∈N
означает, что число 5
принадлежит множеству натуральных чисел, а 5,7∉Z
– десятичная дробь 5,7
не принадлежит множеству целых чисел.
Для этого используют знаки ∈ — принадлежит и ∉ — не принадлежит. Например, запись 5∈N
означает, что число 5
принадлежит множеству натуральных чисел, а 5,7∉Z
– десятичная дробь 5,7
не принадлежит множеству целых чисел.
И еще напомним про обозначения, принятые для включения одного множества в другое. Понятно, что все элементы множества N входят в множество Z , таким образом, числовое множество N включено в Z , это обозначается как N⊂Z . Также можно использовать запись Z⊃N , которая означает, что множество всех целых чисел Z включает множество N . Отношения не включено и не включает обозначаются соответственно знаками ⊄ и ⊅. Также используются знаки нестрогого включения вида ⊆ и ⊇, означающие соответственно включено или совпадает и включает или совпадает.
Про обозначения поговорили, переходим к описанию числовых множеств. При этом затронем лишь основные случаи, которые наиболее часто используются на практике.
Начнем с числовых множеств, содержащих конечное и небольшое количество элементов. Числовые множества, состоящие из конечного числа элементов, удобно описывать, перечисляя все их элементы. Все элементы-числа записываются через запятую и заключаются в , что согласуется с общими правилами описания множеств . Например, множество, состоящее из трех чисел 0
, −0,25
и 4/7
можно описать как {0, −0,25, 4/7}
.
Числовые множества, состоящие из конечного числа элементов, удобно описывать, перечисляя все их элементы. Все элементы-числа записываются через запятую и заключаются в , что согласуется с общими правилами описания множеств . Например, множество, состоящее из трех чисел 0
, −0,25
и 4/7
можно описать как {0, −0,25, 4/7}
.
Иногда, когда число элементов числового множества достаточно велико, но элементы подчиняются некоторой закономерности, для описания используют многоточие. Например, множество всех нечетных чисел от 3 до 99 включительно можно записать как {3, 5, 7, …, 99} .
Так мы плавно подошли к описанию числовых множеств, число элементов которых бесконечно. Иногда их можно описать, используя все тоже многоточие. Для примера опишем множество всех натуральных чисел: N={1, 2. 3, …} .
Также пользуются описанием числовых множеств посредством указания свойств его элементов. При этом применяют обозначение {x| свойства}
. Например, запись {n| 8·n+3, n∈N}
задает множество таких натуральных чисел, которые при делении на 8
дают остаток 3
. Это же множество можно описать как {11,19, 27, …}
.
Это же множество можно описать как {11,19, 27, …}
.
В частных случаях числовые множества с бесконечным числом элементов представляют собой известные множества N , Z , R , и т.п. или числовые промежутки. А в основном числовые множества представляются как объединение составляющих их отдельных числовых промежутков и числовых множеств с конечным числом элементов (о которых мы говорили чуть выше).
Покажем пример. Пусть числовое множество составляют числа −10 , −9 , −8,56 , 0 , все числа отрезка [−5, −1,3] и числа открытого числового луча (7, +∞) . В силу определения объединения множеств указанное числовое множество можно записать как {−10, −9, −8,56}∪[−5, −1,3]∪{0}∪(7, +∞) . Такая запись фактически означает множество, содержащее в себе все элементы множеств {−10, −9, −8,56, 0} , [−5, −1,3] и (7, +∞) .
Аналогично, объединяя различные числовые промежутки и множества отдельных чисел, можно описать любое числовое множество (состоящее из действительных чисел). Здесь становится понятно, почему были введены такие виды числовых промежутков как интервал, полуинтервал, отрезок, открытый числовой луч и числовой луч: все они в купе с обозначениями множеств отдельных чисел позволяют описывать любые числовых множества через их объединение.
Обратите внимание, что при записи числового множества составляющие его числа и числовые промежутки упорядочиваются по возрастанию. Это не обязательное, но желательное условие, так как упорядоченное числовое множество проще представить и изобразить на координатной прямой. Также отметим, что в подобных записях не используются числовые промежутки с общими элементами, так как такие записи можно заменить объединением числовых промежутков без общих элементов. Например, объединение числовых множеств с общими элементами [−10, 0] и (−5, 3) есть полуинтервал [−10, 3) . Это же относится и к объединению числовых промежутков с одинаковыми граничными числами, например, объединение (3, 5]∪(5, 7] представляет собой множество (3, 7] , на этом мы отдельно остановимся, когда будем учиться находить пересечение и объединение числовых множеств .
Изображение числовых множеств на координатной прямой
На практике удобно пользоваться геометрическими образами числовых множеств – их изображениями на . Например, при решении неравенств , в которых необходимо учитывать ОДЗ, приходится изображать числовые множества, чтобы найти их пересечение и/или объединение. Так что полезно будет хорошо разобраться со всеми нюансами изображения числовых множеств на координатной прямой.
Например, при решении неравенств , в которых необходимо учитывать ОДЗ, приходится изображать числовые множества, чтобы найти их пересечение и/или объединение. Так что полезно будет хорошо разобраться со всеми нюансами изображения числовых множеств на координатной прямой.
Известно, что между точками координатной прямой и действительными числами существует взаимно однозначное соответствие, что означает, что сама координатная прямая представляет собой геометрическую модель множества всех действительных чисел R
. Таким образом, чтобы изобразить множество всех действительных чисел, надо начертить координатную прямую со штриховкой на всем ее протяжении:
А часто даже не указывают начало отсчета и единичный отрезок:
Теперь поговорим про изображение числовых множеств, представляющих собой некоторое конечное число отдельных чисел. Для примера, изобразим числовое множество {−2, −0,5, 1,2}
. Геометрическим образом данного множества, состоящего из трех чисел −2
, −0,5
и 1,2
будут три точки координатной прямой с соответствующими координатами:
Отметим, что обычно для нужд практики нет необходимости выполнять чертеж точно. Часто достаточно схематического чертежа, что подразумевает необязательное выдерживание масштаба, при этом важно лишь сохранять взаимное расположение точек относительно друг друга: любая точка с меньшей координатой должна быть левее точки с большей координатой. Предыдущий чертеж схематически будет выглядеть так:
Часто достаточно схематического чертежа, что подразумевает необязательное выдерживание масштаба, при этом важно лишь сохранять взаимное расположение точек относительно друг друга: любая точка с меньшей координатой должна быть левее точки с большей координатой. Предыдущий чертеж схематически будет выглядеть так:
Отдельно из всевозможных числовых множеств выделяют числовые промежутки (интервалы, полуинтервалы, лучи и т.д.), что представляют их геометрические образы, мы подробно разобрались в разделе . Здесь не будем повторяться.
И остается остановиться лишь на изображении числовых множеств, представляющих собой объединение нескольких числовых промежутков и множеств, состоящих из отдельных чисел. Здесь нет ничего хитрого: по смыслу объединения в этих случаях на координатной прямой нужно изобразить все составляющие множества данного числового множества. В качестве примера покажем изображение числового множества (−∞, −15)∪{−10}∪[−3,1)∪
{log 2 5, 5}∪(17, +∞)
:
И остановимся еще на достаточно распространенных случаях, когда изображаемое числовое множество представляет собой все множество действительных чисел, за исключением одной или нескольких точек. Такие множества частенько задаются условиями типа x≠5
или x≠−1
, x≠2
, x≠3,7
и т.п. В этих случаях геометрически они представляют собой всю координатную прямую, за исключением соответствующих точек. Иными словами, из координатной прямой нужно «выколоть» эти точки. Их изображают кружочками с пустым центром. Для наглядности изобразим числовое множество, соответствующее условиям (это множество по сути есть ):
Такие множества частенько задаются условиями типа x≠5
или x≠−1
, x≠2
, x≠3,7
и т.п. В этих случаях геометрически они представляют собой всю координатную прямую, за исключением соответствующих точек. Иными словами, из координатной прямой нужно «выколоть» эти точки. Их изображают кружочками с пустым центром. Для наглядности изобразим числовое множество, соответствующее условиям (это множество по сути есть ):
Подведем итог. В идеале информация предыдущих пунктов должна сформировать такой же взгляд на запись и изображение числовых множеств, как и взгляд на отдельные числовые промежутки: запись числового множества сразу должна давать его образ на координатной прямой, а по изображению на координатной прямой мы должны быть готовы с легкостью описать соответствующее числовое множество через объединение отдельных промежутков и множеств, состоящих из отдельных чисел.
Список литературы.
- Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н.
 Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9. - Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 13-е изд., стер. — М.: Мнемозина, 2011. — 222 с.: ил. ISBN 978-5-346-01752-3.
В абстрактной алгебре повсеместно используются символы для упрощения и сокращения текста, а также стандартные обозначения для некоторых групп. Ниже приведён список наиболее часто встречающихся алгебраических обозначений, соответствующие команды в … Википедия
Математические обозначения это символы, используемые для компактной записи математических уравнений и формул. Помимо цифр и букв различных алфавитов (латинского, в том числе в готическом начертании, греческого и еврейского),… … Википедия
Статья содержит список общеупотребительных аббревиатур математических функций, операторов и др. математических терминов. Содержание 1 Аббревиатуры 1.1 Латиница 1.2 Греческий алфавит … Википедия
математических терминов. Содержание 1 Аббревиатуры 1.1 Латиница 1.2 Греческий алфавит … Википедия
Юникод, или Уникод (англ. Unicode) стандарт кодирования символов, позволяющий представить знаки практически всех письменных языков. Стандарт предложен в 1991 году некоммерческой организацией «Консорциум Юникода» (англ. Unicode Consortium,… … Википедия
Список используемых в математике специфических символов можно увидеть в статье Таблица математических символов Математические обозначения («язык математики») сложная графическая система обозначений, служащая для изложения абстрактных… … Википедия
У этого термина существуют и другие значения, см. Плюс минус (значения). ± ∓ Знак плюс минус (±) математический символ, который ставится перед некоторым выражением и означает, что значение этого выражения может быть как положительным, так и … Википедия
Необходимо проверить качество перевода и привести статью в соответствие со стилистическими правилами Википедии. Вы можете помочь … Википедия
Или математические символы знаки, которые символизируют определённые математические действия со своими аргументами. К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения в… … Википедия
К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения в… … Википедия
Знаки операций или математические символы знаки, которые символизируют определённые математические действия со своими аргументами. К самым распространённым относятся: Плюс: + Минус: , − Знак умножения: ×, ∙ Знак деления: :, ∕, ÷ Знак возведения… … Википедия
— Происхождение Q для набора рациональных чисел?
tl;dr
Дедекинд первым использовал букву (R) для обозначения множеств рациональных чисел в 1872 г., затем, начиная с 1895 г., Пеано стал использовать букву r (строчную) для обозначения того же множества (и, с 1889 г., R для множества положительных рациональных чисел). Другие авторы предлагали другие буквы, и только в начале сороковых годов Бурбаки ввел букву Q (не жирный шрифт $\mathbb{Q}$). Возможно, версия для классного жирного шрифта была введена (может быть) в конце пятидесятых или (что более вероятно) в начале шестидесятых, но это уже другой вопрос.
Теперь несколько ссылок.
Дедекинд использовал букву R (верхний регистр) для обозначения набора рациональных чисел в Stetigkeit und irrationale Zahlen (1872), $\S 3$, стр. 16 («die Gerade List ist unendlich viel reicher an Punkt-Individuen, als das Gebiet R der Rationalen Zahlen an Zahl-Individuen», т.е. «прямая линия L есть бесконечно богаче точечными индивидами, чем область R рациональных чисел числовыми индивидами», здесь английский перевод).
О Пеано Википедия «явно» упоминает где-то в Formulaire de mathématiques/Formulaire Mathématique/Formulario Mathematico , где Пеано фактически широко использовал буквы для обозначения наборов ( classe ) чисел. В этом нет никаких сомнений, так как это единственная работа Пеано на эту тему за 1895 год (см. здесь полную библиографию Пеано, работы за 1895 год начинаются на странице 45). Проблема в том, что (см. вики-страницу)
пять изданий Formulario [не являются] изданиями в обычном смысле этого слова.
Каждый из них представляет собой новую разработку, хотя многие материалы повторяются. Более того, название и язык различались: первые три, озаглавленные Formulaire de Mathématiques, и четвертая, озаглавленная Formulaire Mathématique, были написаны на французском языке, а Latino sine flexione, собственное изобретение Пеано, использовалось для пятого издания под названием Formulario Mathematico. . … Уго Кассина перечисляет не менее двадцати отдельно опубликованных статей как части «полного» Formulario!
и, кроме того, Formulario был написан многими сотрудниками Пеано, такими как Джованни Вайлати, Марио Пьери, Алессандро Падоа, Джованни Вакка, Винченцо Виванти, Джино Фано и Чезаре Бурали-Форти, поэтому, когда кто-то пишет «в Formulario, Пеано говорит …» нужно понимать, что на самом деле речь идет о Пеано или об одном из его сотрудников.
Следующие цитаты взяты из Formulario Mathematico , отредактированного в 1908 году, по той причине, что это более ясное и полное изложение предмета. Можно прочитать 1908 Formulario здесь, в то время как различные издания Formulaire de mathématiques находятся на Gallica, например, здесь.
Можно прочитать 1908 Formulario здесь, в то время как различные издания Formulaire de mathématiques находятся на Gallica, например, здесь.
Первый Пеано пишет (конечно, в I.$\S 1$) символ $N_0$ вместе с $0$ и $+$ как «idea primitivo» [sic], т. е. неопределенные примитивные идеи, используемые для определения всех другие символы «Арифметики», смысл которых определяется системой предложений, первый:
$\cdot 0\quad N_0\ \varepsilon\ \text{Cls}$
, что он прочитал «$N_0$ — это класс», и так далее. В II.$\S 5$ находим $N_1=N_0+1$, поэтому $N_1$ — это множество строго положительных натуральных чисел, а в II.$\S 6$ он использует $+N_0$ и $-N_0 $ для положительных и отрицательных чисел и $n$ для объединения (поэтому $n$ означает $\mathbb{Z}$). Тогда в III.$\S 8$ читаем
$\cdot 2 \quad R=N_1/N_1$
и
$R=$ «Обоснование числа». Illo es omni expressione de forma $b/a$, ubi $a$ et $b$ es numero naturale.
..
т. е. $R$ обозначает рациональное число, и это любое выражение для $a/b$, где $a$ и $b$ — натуральные числа; ясно, что Пеано также вводит $r=+R\cup -R\cup \iota 0$ (III.$\S 9 1\cdot 0$). Более того, он добавляет
$\cdot 01\quad r=n/N_1$
$r=$ относительное числовое обоснование
, поэтому $r$ означает $\mathbb{Q}$. Наконец, в III.$\S 12$ мы находим
$5\cdot 0\quad Q=l’`[\text{Cls}` R \cap u\ni(\exists u.\exists R=\eta u)])$
, который Пеано читает
$Q$, lege «количественная реальная положительная оценка» es omni limite supero de aliquo classe $u$ de Reasone, Existente, et tale que exists aliquo ratione maiore de omni $u$
т. е. $Q$, которое читается как «действительные положительные числа», является любой верхней гранью некоторого существующего множества (класса) рациональных чисел $u$, такого, что существует некоторое рациональное число, большее, чем все элементы в $u$; ясно, что в III. $\S 13$ Пеано определяет $q$ как $Q\cup -Q\cup \iota 0$, поэтому $q$ обозначает наш $\mathbb{R}$.
$\S 13$ Пеано определяет $q$ как $Q\cup -Q\cup \iota 0$, поэтому $q$ обозначает наш $\mathbb{R}$.
В Formulaire de mathématiques можно прочитать более или менее то же самое (конечно, по-французски), в частности, в указателе на стр. 56 мы находим «$r$ nombre rationnel».
Во всяком случае, Пеано использовал буквы для набора чисел до 1895 года, см. Arithmetices principia, nova methodo exposita (1889), Signorum Tabula на стр. 13 («$Q$ quantitas, sive numerus realis positivus», т.е. » $Q$ [обозначает] количество, то есть действительное положительное число», а $R$ используется для положительных рациональных чисел, без символа рациональных чисел, положительных или отрицательных).
Подводя итог: да, Пеано использует буквы для обозначения классов чисел, но нет, его употребление отличается (действительно, прямо противоположно) современному; кроме того, заглавные буквы используются для набора только положительных или только отрицательных чисел некоторых типов, а строчные буквы — для положительных или отрицательных чисел ($n$ для $\mathbb{Z}$, $r$ для $\mathbb{Q). }$, $q$ для $\mathbb{R}$ [sic]).
}$, $q$ для $\mathbb{R}$ [sic]).
Кроме того, я не могу найти ни одного независимого от Википедии источника об использовании буквы $Q$ от итальянского «quoziente», и, кроме того, в итальянском языке элементы $Q$ называются «frazioni» (дробями) или «numeri razionali». (рациональные числа, от латинского слова «ratio»), а «quoziente» — результат операции. Выбор букв, сделанный Пеано, прозрачен: $ n $ для «numerus» (целое число, «numero» на итальянском языке), «r» для «(numero) обоснование» (рациональное число, но также и «rapporto» на итальянском языке). , ratio на английском языке), «q» для «quantitas» (итальянское «quantità», английское количество).
Теперь несколько слов о Бурбаки. Да, «они» используют $Q$ для рациональных чисел, и нет, они не используют жирный шрифт $\mathbb{Q}$ (по крайней мере, в статьях 1940-х годов). Раннее появление (возможно, самое раннее напечатанное на бумаге) $Q$ для обозначения набора рациональных чисел находится здесь, на странице 3 в номере 5 (7-10 декабря 1940 г. ) La Tribu , внутреннего информационного бюллетеня Бурбаки. Читаем
) La Tribu , внутреннего информационного бюллетеня Бурбаки. Читаем
$Q$ установлен […] Топология $Q$ […] Завершение $Q$ : номера барабанов
, поэтому нет сомнений, что здесь $Q$ относится к нашему $\mathbb{Q}$. Ясно, что мы находим $Q$ для рациональных чисел в 1942 Алгебре (со страницы 29).
Система счисления: Типы номеров
Ниже приведены подробные сведения о различных типах номеров. Различные типы чисел используются для решения разных ситуаций, поэтому каждый тип числа имеет свое значение.
Натуральные числа- Числа, используемые при счете, называются натуральными числами.
- Множество натуральных чисел обозначается буквой N.
Где N= {1, 2, 3, 4…}
- 1 — наименьшее натуральное число.
- Если в набор натуральных чисел входит ноль, то они называются целыми числами.

- Набор целых чисел обозначается буквой W.
Где W= {0, 1, 2, 3, 4…}
- Все натуральные числа также являются целыми числами.
- Число 0 — первое и наименьшее из всех целых чисел.
- Все натуральные числа, кроме нуля, называются целыми числами.
- Здесь нет последнего или наибольшего целого числа, поскольку они бесконечны.
- Все натуральные числа являются целыми числами. Но все целые числа не являются натуральными числами. Например, 0 — это целое число, но не натуральное.
- Каждое целое число больше предыдущего на 1.
Целые числа
- Когда отрицательные числа всех натуральных чисел включены в набор целых чисел, они называются целыми числами.
- Множество целых чисел обозначается буквой Z. Буква Z взята из немецкого слова zahlen, что означает считать.

Где Z= {…-4, -3, -2, -1, 0, 1, 2, 3, 4…}
- Ноль никогда не может быть положительным или отрицательным целым числом.
- Целые числа можно разделить на два типа:
* Целые положительные числа: Все натуральные числа являются целыми положительными числами.
Пример: I+= {1, 2, 3, 4…}
* Отрицательные целые числа: Все отрицательные числа натуральных чисел являются отрицательными целыми числами.
Пример: I- = {-1, -2, -3, -4…}
Рациональные числа- Числа, которые можно представить в виде p/q, называются рациональными числами.
Здесь p и q целые числа и q не равно 0
- Множество рациональных чисел обозначается буквой Q.
Где Q= {1/2, 1/3, 5/6, 7/2, 5, -2, 0…}
Иррациональные числа
- Числа, которые НЕ МОГУТ быть выражены в форма p/q называется иррациональными числами.

Здесь также p и q целые числа и q не равно 0
- Множество иррациональных чисел обозначается буквой P.
Где P= {√2, √3, √4, √5…}
Факты об иррациональных числах- Сумма рациональных и иррациональных чисел также является иррациональным числом
(Пример: 3+√2, 6+√4)
- Разность рациональных и иррациональных чисел также является иррациональным числом
(Пример: 6-√2, 9-√4)
- Произведение рациональных и иррациональных чисел также является иррациональным числом
(Пример: 2 x √2, 9 x +√4)
- Действительные числа включают как рациональные, так и иррациональные числа. Другими словами, он включает в себя все натуральные числа, целые числа, а также целые числа.
- Действительные числа обозначаются буквой R.
- Примеры действительных чисел: 2, 0, 5, -7, -10, ½, 1/6, 1,14, 1,789.
 …
…
- Числа, которые делятся на 2, называются четными. Они также кратны 2.
- Множество четных чисел обозначается буквой E, где E= {2, 4, 6, 8, 10…}
- Существует бесконечное количество четных чисел
- Числа, которые НЕ делятся на 2, называются нечетными.
- Они НЕ кратны 2.
- Множество нечетных чисел обозначается буквой О, где О= {1, 3, 5, 7, 9…}
- Существует бесконечное количество нечетных чисел
- Числа, которые делятся на 1, и само число называются простыми числами.
- Примеры простых чисел: 2, 3, 5, 7…
- Число 1 не является простым числом.
- Число 2 — единственное четное простое число.
- Существует 25 простых чисел от 1 до 100.
 Из них 15 находятся в диапазоне от 1 до 50, а остальные 10 — в диапазоне от 50 до 100.
Из них 15 находятся в диапазоне от 1 до 50, а остальные 10 — в диапазоне от 50 до 100.
- Два натуральных числа называются взаимно простыми, если их наибольший общий делитель (НОП) равен 1.
- Примеры пар взаимно простых чисел: (7, 9), (15, 16) и т. д.
- Взаимно простые числа всегда пишутся парами между скобками.
- Следует отметить, что пара взаимно простых чисел не обязательно должна быть простой.
- Числа, которые делятся без остатка на числа, отличные от 1 и самого себя, называются составными числами.
- Например, 9 можно разделить без остатка на 3, а также на 1 и 9, поэтому 9 — составное число. Но 7 нельзя разделить без остатка, кроме как на 1 и 7, поэтому НЕ является составным числом. Значит, это простое число.
- Число 1 не может считаться составным числом.
- Последовательные числа — это ряды чисел, в которых каждое число больше предыдущего на 1.

- Например, 6, 7, 8 или 2, 3, 4 или 11, 12, 13, 14… и т. д.
- ← Римская система счисления
- Далее →
— Поделись с друзьями! —
Куллабс
Обзор
Число, которое можно получить, разделив два числа, называется рациональным числом. Числа, которые не являются рациональными и которые не могут быть получены путем деления двух целых чисел, называются иррациональными числами. Наборы системы счисления, т.е. натуральные числа, целые числа, целые числа, рациональные числа и иррациональные числа, определяются под набором системы действительных чисел.- Примечание
- То, что нужно запомнить
- Видео
- Упражнение
- Контрольный опрос
Рациональные и иррациональные числа
Рациональные числа
Рис. Рациональные числа источник: kwizoo.com
Рациональные числа источник: kwizoo.com В общем, число, которое можно получить путем деления двух чисел, называется рациональным числом. Любые числа, которые могут быть выражены в виде \(\frac{a}{b}\), где a и b — целые числа, а b ≠ 0, называются рациональными числами. Множество рациональных чисел обозначается буквой Q. Например, Q = ( \(\frac{1}{2}\), \(\frac{3}{4}\), \(\frac{212}{100}\), \(\frac{20 {12}\) и т.д.. )
Множество рациональных чисел — это множество, включающее в себя множества натуральных чисел (N), целых чисел (W) и целых чисел (Z). Следовательно, множества натуральных чисел, целых чисел и целых чисел являются собственными подмножествами множества рациональных чисел. ∴N < Q, W < Q и Z < Q.
Конечные и неконечные рациональные числа
Когда рациональное число преобразуется в десятичную дробь, полученное десятичное число может быть конечным или неконечным десятичным числом. Прекращение рационального числа как десятичного обычно заканчивается и не повторяется после десятичного числа. Например, \(\frac{1}{2}\) = 0,5, \(\frac{1}{4}\) = 0,25, \(\frac{3}{8}\) = 0,375 и т. д.) примеры окончания десятичной дроби.
Например, \(\frac{1}{2}\) = 0,5, \(\frac{1}{4}\) = 0,25, \(\frac{3}{8}\) = 0,375 и т. д.) примеры окончания десятичной дроби.
Неограниченное рациональное число, поскольку десятичное число продолжает повторяться в шаблоне после десятичного числа. Например, ( \( \frac{1}{3}\) = 0,333333…, \(\frac{1}{15}\) = 0,0666666…. и т. д. являются неконечными рациональными числами как десятичными.
Иррациональные числа
Рис. Иррациональное числоисточник:www.digitmath.com
Числа, которые не являются рациональными и которые не могут быть получены путем деления двух целых чисел, называются иррациональными числами. Если иррациональные числа десятичные, десятичные дроби являются непрерывными, неповторяющимися, которые продолжаются вечно без повторения. Например ( \(\sqrt{5}\) = 2,2360679775,( \(\sqrt{2}\) = 1,41423562 и т. д. являются примерами иррациональных чисел.
Действительная система счисления
Рис. : Действительные числа
: Действительные числа источник: karenbrannon.weebly.com
Наборы системы счисления, т.е. натуральные числа, целые числа, целые числа, рациональные числа и иррациональные числа, определяются под набором действительных чисел система. В следующей таблице показана действительная система счисления: —
Что нужно помнить
- Число, которое можно получить путем деления двух чисел, называется рациональным числом.
- Числа, которые не являются рациональными и которые не могут быть получены путем деления двух целых чисел, называются иррациональными числами .
- Включает в себя все отношения, установившиеся между людьми.
- В обществе может быть более одного сообщества. Сообщество меньше, чем общество.
- Это сеть социальных отношений, которую невозможно увидеть или потрогать.
- общие интересы и общие цели не нужны обществу.

Видео для рациональных и иррациональных чисел
Вопросы и ответы
В общем, число, которое можно получить, разделив два числа, называется рациональным числом. Любые числа, которые могут быть выражены в виде \(\frac{a}{b}\), где a и b — целые числа, а b ≠ 0, называются рациональными числами.
Множество рациональных чисел обозначается буквой ‘Q’.
0=\(\frac{0}{1}\) . Он находится в форме \(\frac{a}{b}\) . Итак, 0 — рациональное число.
-8 =-\(\frac{8}{1}\) . Это в форме \(\frac{a}{b}\) . Итак, -8 — рациональное число.
0. 25= Это завершающее десятичное число. Итак, 0,25 — рациональное число.
25= Это завершающее десятичное число. Итак, 0,25 — рациональное число.
0.16 это повторяющееся десятичное число без конца. Итак, 0,16 — рациональное число.
Рациональное число в середине 2 и 3 = \(\frac{1}{2}\)(2+3)=\(\frac{5}{2}\)
Рациональное число в середине 2 и \(\frac{5}{2}\) = \(\frac{1}{2}\) (2+\(\frac{5}{2}\) = \(\frac{1}{ 2}\) x \(\frac{9}{2}\) =\(\frac{9}{4}\)
Итак, \(\frac{5}{2}\) и \(\ frac{9}{4}\) — любые два рациональных числа от 2 до 3.
Рациональные числа обозначаются ______
← Предыдущий вопрос Следующий вопрос →
1 ответ
+1 голос
Похожие вопросы
Какой буквой обозначается набор целых чисел?
спросил 8 августа 2021 г. по математике — 9 класс по Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- основы систем счисления
Между 2 и 3 имеется _________ рациональных чисел.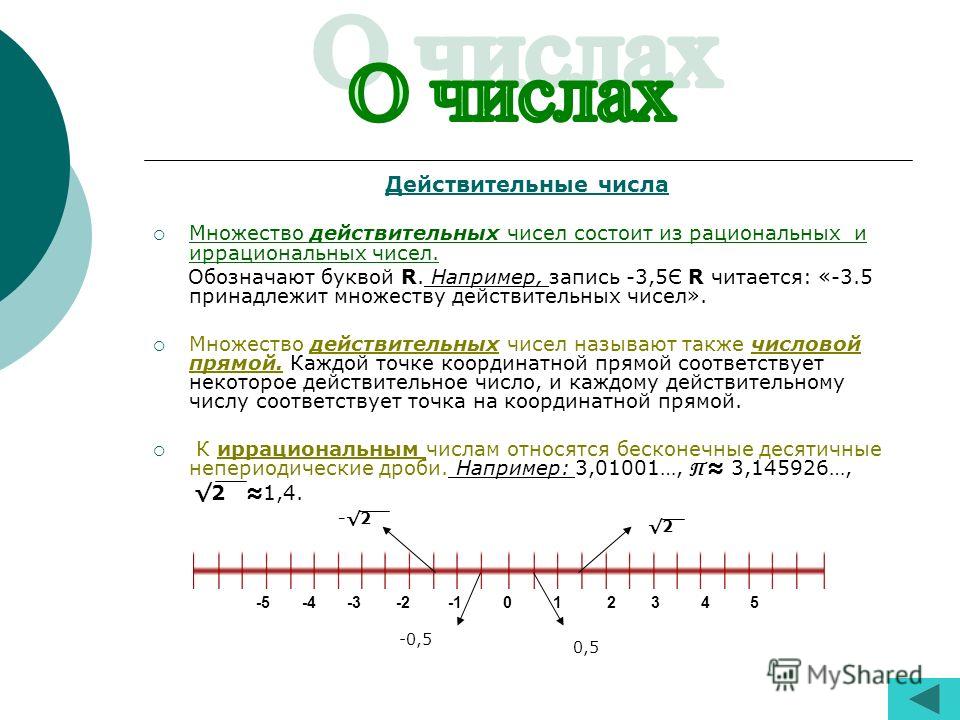
спросил 8 августа 2021 г. по математике — 9 класс по Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- основы систем счисления
Какое из следующих чисел не является рациональным?
спросил 8 августа 2021 г. по математике — 9 класс по Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- основы систем счисления
Ноль — рациональное число.
спросил 8 августа 2021 г. по математике — 9 класспо Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- основы систем счисления
Сколько целых чисел находится между -3 и 3 (включая -3 и 3)?
спросил 8 августа 2021 г. по математике — 9 класс по Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- основы систем счисления
N является подмножеством W, Z и Q. (Допустим общепринятые обозначения)
(Допустим общепринятые обозначения)
спросил 8 августа 2021 г. по математике — 9 класс по Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- основы систем счисления
Найдите неверный вариант (Примите обычные обозначения).
спросил 8 августа 2021 г. по математике — 9 класс по Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- основы систем счисления
Что из перечисленного является натуральным числом?
спросил 8 августа 2021 г. по математике — 9 класс по Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- основы систем счисления
Какой буквой обозначаются действительные числа?
спросил
8 августа 2021 г.
по математике — 9 класс
по
Анзе
(679 тыс. баллов)
баллов)
- математика – 9 класс
- системы счисления
- иррациональные числа
Иррациональные числа обозначаются _______
спросил 8 августа 2021 г. по математике — 9 класс по Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- иррациональные числа
Если мы умножим или разделим два рациональных числа, мы получим a/an __________
спросил 8 августа 2021 г. по математике — 9 класс по Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- , представляющие действительные числа в числовой строке и операции с действительными числами
Сложение или вычитание двух ненулевых рациональных чисел __________
спросил 8 августа 2021 г. по математике — 9 класс по Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- представление действительных чисел на числовой прямой и операции с действительными числами
Десятичное представление рациональных чисел может быть либо конечным, либо неконечным и повторяющимся (повторяющимся).
спросил 8 августа 2021 г. по математике — 9 класспо Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- действительные числа и их десятичные представления
Суммирование или вычитание рациональных и иррациональных чисел всегда представляет собой __________ число.
спросил 8 августа 2021 г. по математике — 9 класс по Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- , представляющие действительные числа в числовой строке и операции с действительными числами
Если мы сложим или вычтем иррациональное число и рациональное число (не ноль), то получим __________ число.
спросил 8 августа 2021 г. по математике — 9 класс по Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- представление действительных чисел на числовой прямой и операции с действительными числами
Если мы сложим или вычтем два иррациональных числа, мы получим __________ число.
спросил 8 августа 2021 г. по математике — 9 класспо Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- представление действительных чисел на числовой прямой и операции с действительными числами
Между двумя числами лежит бесконечное число иррациональных чисел.
спросил 8 августа 2021 г. по математике — 9 класс по Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- действительные числа и их десятичные представления
Сколько действительных чисел находится между 3 и 8 (включая 3 и 8)? 91/4, получаем __________
спросил 8 августа 2021 г. по математике — 9 класс по Анзе (679 тыс. баллов)
- математика – 9 класс
- системы счисления
- законы показателей степени для действительных чисел
Математические слова: рациональные числа
Математические слова: рациональные числа
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рациональное число (определение, примеры, свойства, решение)
Содержание
Определение рационального числа
Слово «Рациональный» происходит от слова «Отношение» . Из самого названия можно предположить, что Рациональное Число имеет что-то родственное Соотношению . Определенно, рациональных числа — это числа, которые могут быть выражены в терминах соотношения целых чисел .
Рациональные числа могут быть определены как числа, которые могут быть выражены в форме \frac{p}{q}, где p и q — целые числа, а q\ne 0. Рациональные числа обозначаются буквой Q.
Следовательно, чтобы число было Рациональным числом , должны быть выполнены два условия:
- Число должно быть выражено в форме \frac{p}{q} где p и q — целые числа и
- Знаменатель q не должен быть равен нулю (0) или q\ne 0.

Примеры рациональных чисел
Все натуральные числа, целые числа и целые числа Числа , потому что все они могут быть выражены в форме \frac {p}{q}, где q\ne 0,
Например, давайте рассмотрим некоторые числа, такие как 2,\, 5,\,15,\, -5,\, -3
Число 2 в приведенном выше примере может быть выражено как \frac{2}{ 1}, здесь p=2, q=1 и q\ne 0.
Аналогично,
5=\frac{5}{1}, p=5, q=1 и q\ne 0
15 =\frac{15}{1}, p=15, q=1 и q\ne 0
-5=\frac{-5}{1}, p=-5, q=1 и q\ne 0
-3=\frac{-3}{1}, p=-3, q=1 и q\ne 0
Число ноль (0) также является рациональным числом, поскольку ноль может быть выражен как
\frac{0}{1}, \frac{0}{2}, \frac{0}{5}, \frac{0}{120} и т. д.
В приведенных выше примерах p и q целых чисел и q\ne 0, что удовлетворяет обоим условиям рационального числа . Следовательно, можно сказать, что 0 также является рациональным числом .
Из приведенного выше обсуждения можно сделать вывод, что все целые числа и дроби могут рассматриваться как рациональные числа .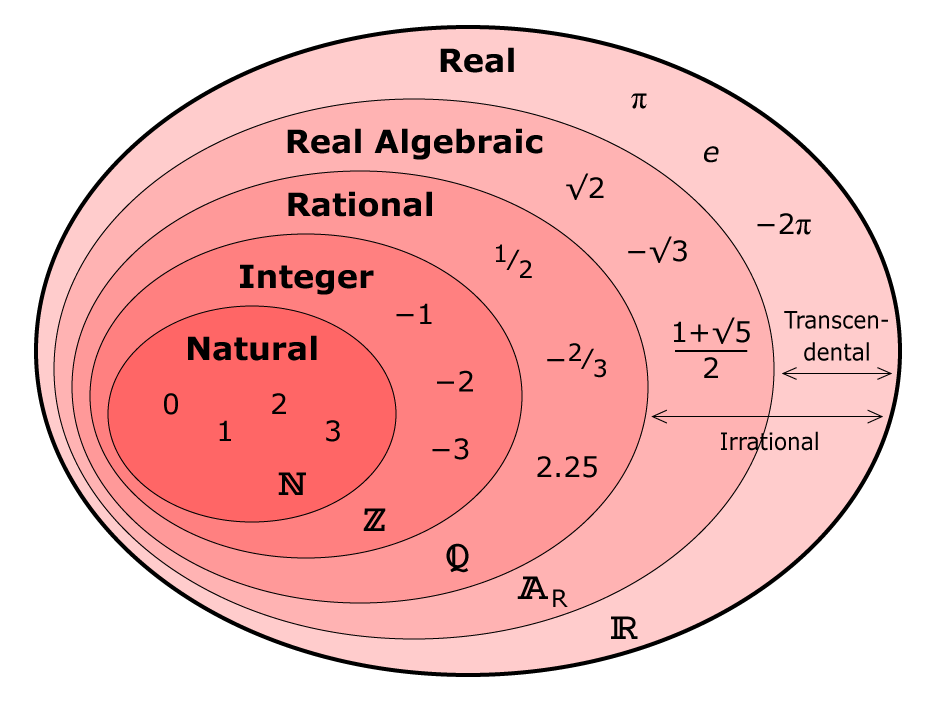 Однако \pi не является рациональным числом , даже если значение pi равно \frac {22}{7}. \pi считается Иррациональное число .
Однако \pi не является рациональным числом , даже если значение pi равно \frac {22}{7}. \pi считается Иррациональное число .
Эквивалентное рациональное число
Чтобы понять концепцию Эквивалентное рациональное число , рассмотрим число как \frac {2}{3}.
Теперь число \frac{2}{3} также можно представить как
\frac{2}{3}=\frac{4}{6}=\frac{6}{9}=\ frac{8}{12}=……… и так далее.
Следовательно, можно сказать, что Рациональные числа не имеют уникального представления и могут быть представлены во многих формах. Эти разные формы Рациональные числа называются Эквивалентными рациональными числами или Дробями.
Однако при представлении такого числа на числовой прямой мы должны рассматривать число, в котором p и q не имеют общего делителя или p и q взаимно просты. В приведенном выше примере числа 2 и 3 не имеют общего делителя в дроби \frac{2}{3}. Следовательно, \frac {2}{3} будет использоваться для представления всех эквивалентных рациональных чисел на числовой строке .
Следовательно, \frac {2}{3} будет использоваться для представления всех эквивалентных рациональных чисел на числовой строке .
Свойства рациональных чисел
Свойство замыкания рациональных чисел
Свойство замыкания рациональных чисел утверждает, что для любых двух рациональных чисел скажем a и b сложение, вычитание и умножение между ними приводит к рациональному числу только . Однако деление не считается свойством замыкания, потому что мы не можем определить деление рационального числа на ноль (0).
- Сложение двух рациональных чисел является рациональным числом
a+b=c
Пример: 1+1=2,\,5+9=14,\, \frac{1}{2}+\frac {1}{2}=1 и т. д.
- Вычитание двух рациональных чисел является рациональным числом
a-b=c
Пример: 1-1=0,\,4-2=2,\, 15-6=9,\,\frac{3}{2}-\frac{1}{2}=1 и т. д.
д.
- Умножение двух рациональных чисел является рациональным числом =c
Пример: 1\times 1=1,\,3\times 2=6, \,12\times 5=60,\, \frac{1}{2} \times \frac{1}{3 }=\frac{1}{6} и т. д.
Коммутативное свойство рациональных чисел
Коммутативное свойство рациональных чисел утверждает, что для любых двух рациональных чисел, скажем, a и b, сложение и умножение между ними являются коммутативными . Однако Коммутативное свойство не применимо к вычитанию и делению между двумя или более рациональными числами .
- Коммутативное свойство сложения двух рациональных чисел
Если a и b два рациональных числа, то
a+b=b+a
- Коммутативное свойство умножения двух рациональных чисел
Если a и b два рациональных числа, то
a\times b=b\times a
Почему коммутативное свойство неприменимо для вычитания между двумя рациональными числами?
Чтобы понять, почему Коммутативное свойство неприменимо для вычитания между двумя или более рациональными числами, давайте рассмотрим два рациональных числа как 9.
 0003
0003a=4 и b=2
Теперь a-b=4-2=2 и b-a=2-4=-2
Здесь a-b\ne=b-a
Следовательно, Коммутативное свойство неприменимо для Вычитание между двумя рациональными числами.
Почему коммутативное свойство неприменимо для деления двух рациональных чисел?
Рассмотрим два рациональных числа a и b, такие что
a=2 и b=5
Теперь \frac {a}{b}=\frac{2}{5}=0,4
и, \frac{b}{a}=\frac{5}{2}=2,5
Здесь \frac{a}{b}\ne\frac{b}{a}
Следовательно, можно сделать вывод, что Коммутативное свойство неприменимо для деления двух рациональных чисел.
Ассоциативное свойство рациональных чисел
Ассоциативное свойство рациональных чисел утверждает, что для любых трех рациональных чисел , скажем a, b и c, сложение и умножение между ними равно Ассоциативное . Однако ассоциативное свойство не применяется для вычитания и деления между двумя рациональными числами .

- Ассоциативное свойство сложения двух рациональных чисел
Если a, b и c равны трем Рациональные числа , то
a+(b+c)=(a+b)+c
4 Ассоциативное свойство умножения двух рациональных чисел
Если a, b и c равны трем Рациональные числа , то
a\times (b\times c)=(a\times b)\times c
Почему ассоциативное свойство неприменимо для вычитания рациональных чисел?
Чтобы понять, почему Ассоциативное свойство неприменимо для вычитания рациональных чисел, давайте рассмотрим три рациональных числа как
a=4, b=3 и c=2
Теперь, a-(b-c)=4-( 3-2)=4-1=3 и (a-b)-c=(4-3)-2=1-2=-1
Здесь a-(b-c)\ne=(a-b)-c
Следовательно, ассоциативное свойство неприменимо для вычитания между рациональными числами.
Почему ассоциативное свойство неприменимо для деления рациональных чисел?
Ассоциативное свойство неприменимо к делению рациональных чисел, поскольку деление рационального числа на ноль (0) не определено.
Распределительное свойство рациональных чисел
Чтобы понять Распределительное свойство рациональных чисел , рассмотрим три рациональных числа a, b и c. Теперь согласно Распределительное свойство ,
a\times (b+c)=(a\times b)+(a\times c)
Доказательство распределительного свойства рациональных чисел
Пусть, a=1, b=2 и c=3
LHS=a\times (b+c)
LHS=1\times (2+3)
LHS=1\times 5
LHS=5
And
RHS=(a\times b)+(a\times c)
RHS=(1\times 2)+(1\times 3)
RHS=2+3
RHS=5
Сверху, LHS=RHS. Отсюда доказано.
Свойство тождественности рациональных чисел
Аддитивное тождество рациональных чисел
Для любого рационального числа нулевой номер (0) называется аддитивной идентичностью , поскольку любое рациональное число, добавленное к нулю, дает одно и то же рациональное число.
Например: 5+0=5,\, 11+0=11,\, \frac{1}{5}+0=\frac{1}{5} и т.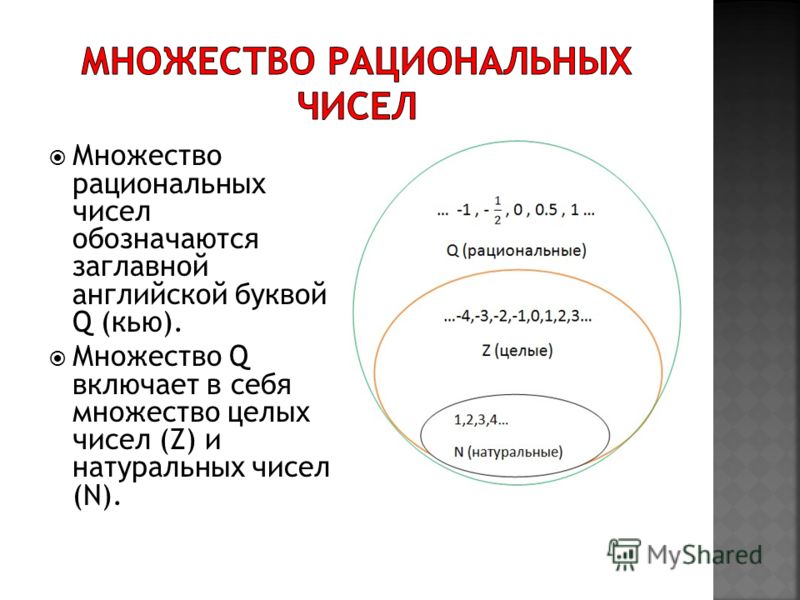

 Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9. Каждый из них представляет собой новую разработку, хотя многие материалы повторяются. Более того, название и язык различались: первые три, озаглавленные Formulaire de Mathématiques, и четвертая, озаглавленная Formulaire Mathématique, были написаны на французском языке, а Latino sine flexione, собственное изобретение Пеано, использовалось для пятого издания под названием Formulario Mathematico. . … Уго Кассина перечисляет не менее двадцати отдельно опубликованных статей как части «полного» Formulario!
Каждый из них представляет собой новую разработку, хотя многие материалы повторяются. Более того, название и язык различались: первые три, озаглавленные Formulaire de Mathématiques, и четвертая, озаглавленная Formulaire Mathématique, были написаны на французском языке, а Latino sine flexione, собственное изобретение Пеано, использовалось для пятого издания под названием Formulario Mathematico. . … Уго Кассина перечисляет не менее двадцати отдельно опубликованных статей как части «полного» Formulario! ..
..


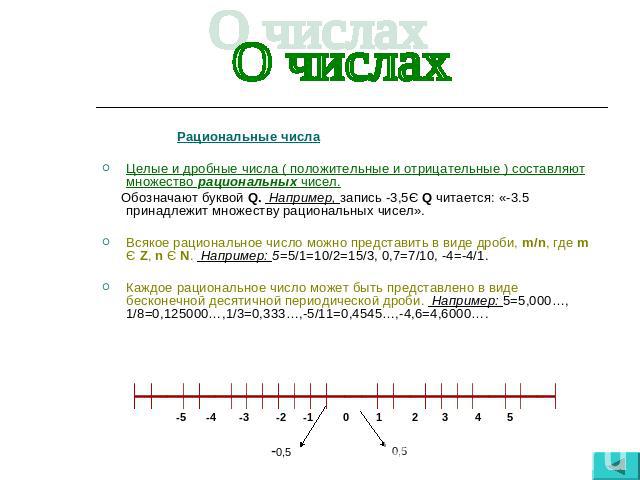 …
… Из них 15 находятся в диапазоне от 1 до 50, а остальные 10 — в диапазоне от 50 до 100.
Из них 15 находятся в диапазоне от 1 до 50, а остальные 10 — в диапазоне от 50 до 100.

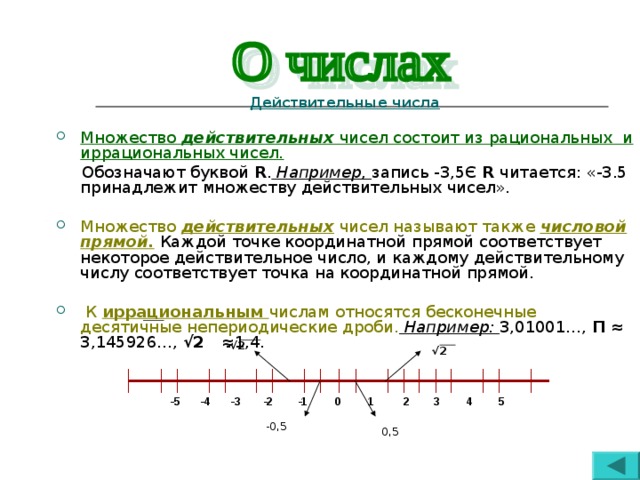 Формально,
рациональные числа — это множество всех
действительные числа, которые можно записать
как отношение целых чисел с ненулевым знаменателем.
Рациональные числа
указано
по символу .
Формально,
рациональные числа — это множество всех
действительные числа, которые можно записать
как отношение целых чисел с ненулевым знаменателем.
Рациональные числа
указано
по символу .

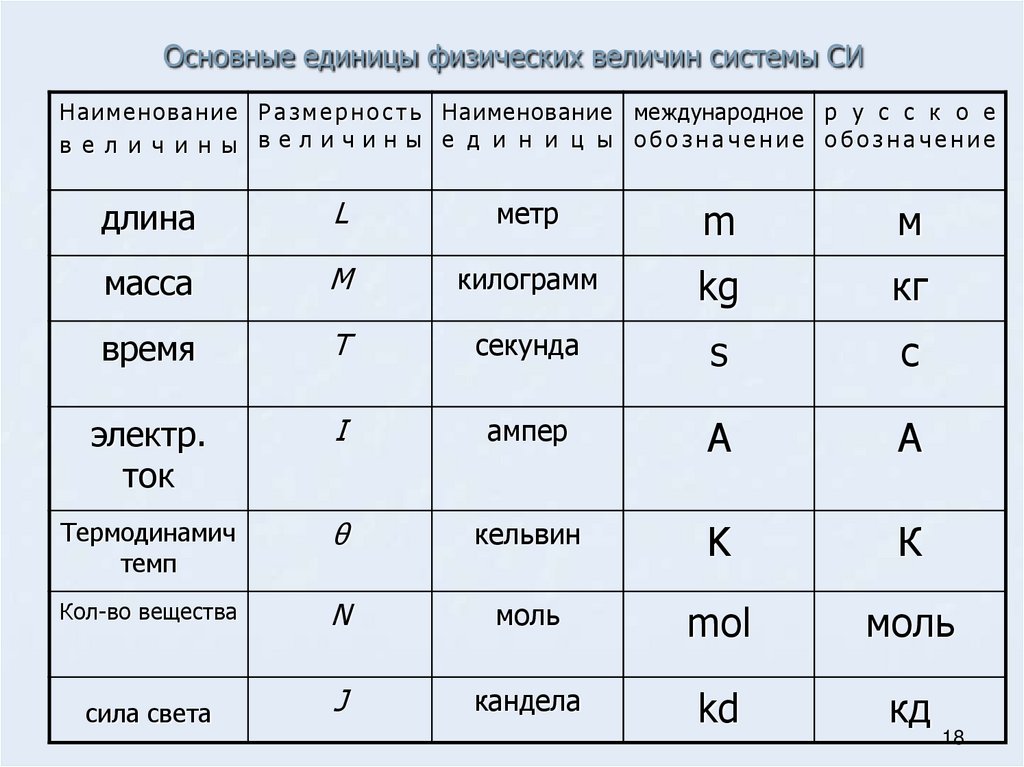 0003
0003