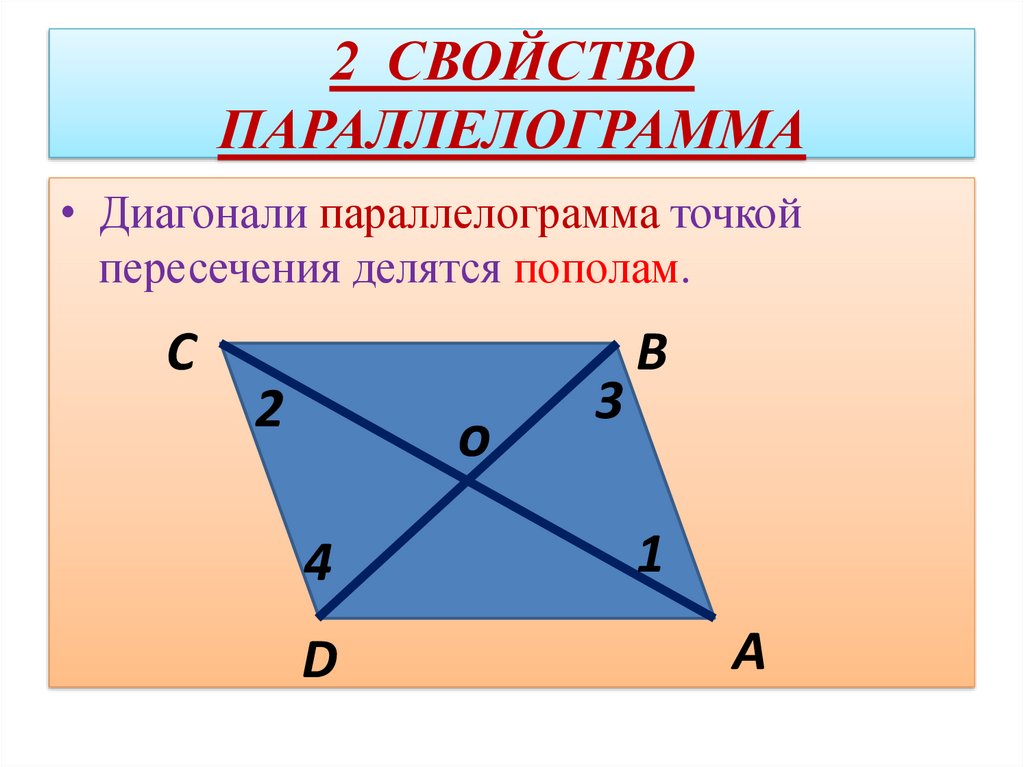
Параллелограмм — Умскул Учебник
На этой странице вы узнаете- Чем отличаются признаки от свойств?
- Сколько крыс у биссектрисы?
- Гибридом чего будет квадрат?
Когда мы видим изображение с множеством деталей, наш мозг автоматически раскладывает их на простые фигуры. Этот процесс занимает доли секунды. Разные геометрические фигуры вызывают у нас разные ощущения, эмоции и ассоциации.А что будет, если мы задержим взгляд на одной из них и разберем подробнее? Давайте сделаем так с параллелограммом.
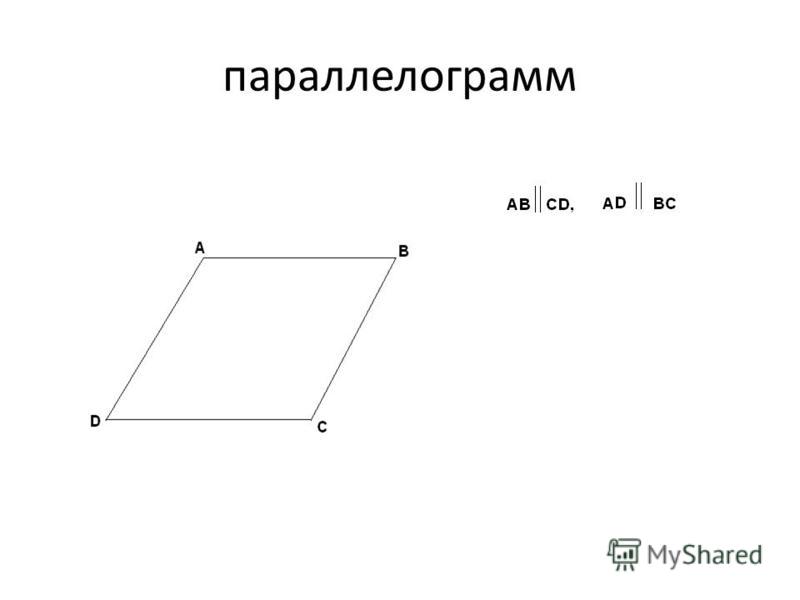
ПараллелограммПараллелограмм – это четырёхугольник, чьи стороны попарно параллельны и равны.
Параллелограмм мы видим достаточно часто.
Признаки параллелограммаУ параллелограмма есть три основных признака. Если для четырехугольника выполняется хотя бы один из признаков, такой четырехугольник можно называть параллелограммом.
Признаки параллелограмма:
- Две противоположные стороны четырехугольника параллельны и равны.

- Противоположные стороны четырехугольника попарно равны.
- Диагонали четырехугольника пересекаются и в точке пересечения делятся пополам.
| Чем отличаются признаки от свойств? Свойства нельзя путать с признаками, хоть они и очень похожи. Свойствами параллелограмма обладает фигура, уже являющаяся параллелограммом, тогда как признаки предназначены для выявления параллелограммов среди четырехугольников. |
Свойства параллелограмма:
- Противолежащие стороны равны.
- Противолежащие стороны параллельны.
- Противолежащие углы равны.
- Сумма всех углов 3600.
- Диагонали пересекаются и точкой пересечения делятся пополам.
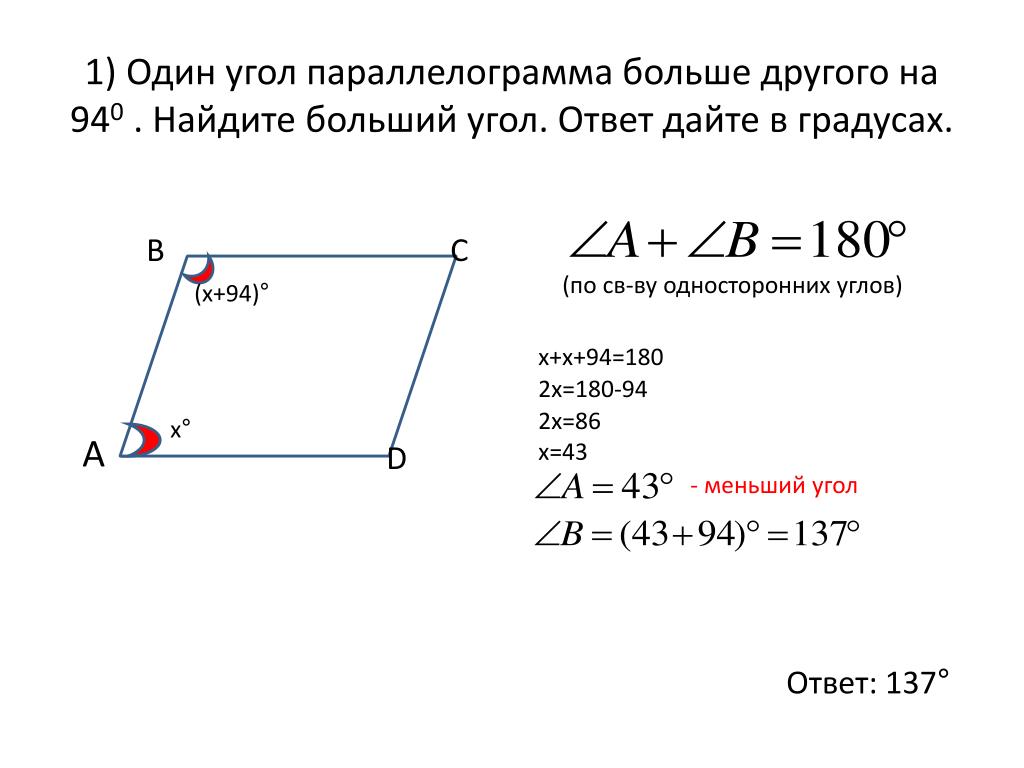
- Сумма углов, прилежащих к любой стороне, равна 1800.

- Сумма квадратов диагоналей равна сумме квадратов всех сторон.
- Диагонали делят параллелограмм на четыре треугольника с одинаковой площадью.
- Каждая диагональ делит параллелограмм на два равных треугольника
Можно ли провести биссектрису в параллелограмме? Да. Биссектриса параллелограмма – это луч, исходящий из вершины угла параллелограмма, делящий этот угол на два равных угла и пересекающий одну из сторон параллелограмма.
| Сколько крыс у биссектрисы? Значение биссектрисы легко запомнить, используя фразу “Биссектриса – это крыса, она бегает по углам и делит угол пополам”. |
Два факта связанные с биссектрисой в параллелограмме:
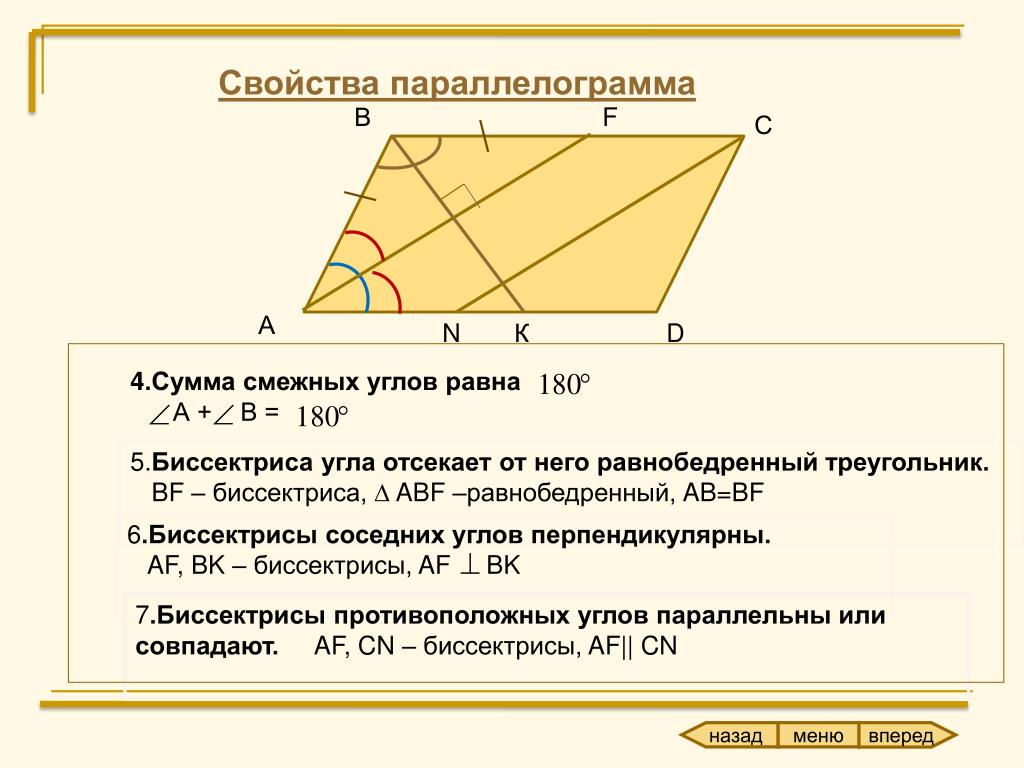
- Биссектриса, проведенная из угла параллелограмма, отсекает от него равнобедренный треугольник.

- Биссектрисы углов, принадлежащих одной стороне параллелограмма, пересекаются под прямым углом.
Есть три формулы площади параллелограмма, которые применяются в зависимости от известных величин
- Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
- Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними.
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.
Как параллелограмм связан с прямоугольником?
Прямоугольник – это параллелограмм, углы которого по 900.
Данную фигуру часто называют частным случаем параллелограмма. Из этого следует, что для прямоугольника применимы те же признаки и свойства, что для параллелограмма, но и имеется ряд собственных.
В жизни прямоугольником можно назвать дверь, картину или фотографию:
Признаки прямоугольника- Параллелограмм, имеющий хотя бы один прямой угол.
- Параллелограмм, все углы которого равны.
- Параллелограмм, диагонали которого равны.
- Четырехугольник, у которого три прямых угла.
- Все углы прямые.
- Диагонали равны.
- Стороны прямоугольника одновременно являются и его высотами.
- Сумма квадратов двух прилежащих сторон равна квадрату диагонали.
Биссектриса делит угол прямоугольника на два угла по 450 и пересекает одну из сторон прямоугольника.
Теперь рассмотрим два способа нахождения площади прямоугольника:
- Площадь прямоугольника равна произведению двух соседних сторон.

- Площадь прямоугольника равна половине произведения квадрата диагонали на синус угла между диагоналями.
Пожалуй, это самая неустойчивая фигура.
Ромб – это параллелограмм, у которого все стороны равны.
Ромб можно увидеть на знаке машины “Митсубиси”, их там целых три.
А также в игровых наградах:
Также является частным случаем параллелограмма и обладает его признаками и свойствами, но имеет и собственные.
Всё о ромбеПризнаки ромба:
- Две смежные стороны параллелограмма равны.
- Диагонали параллелограмма пересекаются под прямым углом.
- Диагональ параллелограмма делит каждый угол пополам.
- Четырехугольник, у которого все стороны равны.
Свойства ромба:
- Все стороны равны.
- Диагонали пересекаются под прямым углом и точкой пересечения делятся пополам.

- Диагонали являются биссектрисами.
- Высоты в ромбе равны.
Как уже отмечено в свойствах ромба, биссектрисой ромба является диагональ.
Как найти площадь ромба?
Для нахождения площади ромба есть три разные формулы:
- Площадь ромба равна произведению стороны и высоты ромба.
- Площадь ромба равна половине произведения его диагоналей.
- Площадь ромба равна произведению квадрата стороны на синус угла ромба.
А вот квадрат, наоборот, достаточно устойчив.
Квадрат – это четырехугольник, у которого все углы и стороны равны.
| Гибридом чего будет квадрат? Если внимательно посмотреть на определение, то можно заметить, что квадрат объединяет в себе и параллелограмм, и прямоугольник, и ромб. |
Квадратом может быть крышка подарочной коробки или окно.
Рассмотрим признаки и свойства данной фигуры.
Всё о квадратеПризнаки квадрата:
- Ромб, у которого хотя бы один угол прямой.
- Ромб, у которого все углы равны.
- Ромб, у которого диагонали равны.
- Четырехугольник, диагонали которого равны и перпендикулярны.
Свойства квадрата:
- Диагональ квадрата равна 2 стороны квадрата.
- Диагонали делят квадрат на четыре равных треугольника.
Биссектрисой квадрата, как и у ромба, является диагональ.
Рассмотрим формулы для нахождения площади квадрата:
- Площадь квадрата равна квадрату его стороны.
- Площадь квадрата равна половине квадрата диагонали.

- Параллелограмм – это четырёхугольник, чьи стороны попарно параллельны и равны.
- Прямоугольник – это параллелограмм, углы которого по 900 и диагонали которого равны.
- Ромб – это параллелограмм, у которого все стороны равны, а также диагонали перпендикулярны друг другу
- Квадрат – это четырехугольник, у которого все углы и стороны равны. Квадрат является гибридом параллелограмма, прямоугольника и ромба.
Задание 1.
Найдите площадь параллелограмма, если его стороны 5 и 8, а угол между ними 300
- 40
- 20
- 10
- 25
Задание 2.
Найдите площадь прямоугольника, если его диагональ 12, а угол между диагоналями 600
- 83
- 6
- 63
- 4
Задание 3.
Найдите площадь ромба, если его диагонали 6 и 10
- 30
- 60
- 15
- 25
Задание 4.
У четырехугольника диагонали пересекаются под углом 300, а его стороны попарно параллельны и равны. Что это за фигура?
- Квадрат
- Ромб
- Прямоугольник
- Параллелограмм
Задание 5.
У четырехугольника две противоположные стороны параллельны и равны и есть один прямой угол. Что это за фигура?
- Квадрат
- Ромб
- Прямоугольник
- Параллелограмм
Ответы: 1. – 2; 2. – 3; 3. – 1; 4. – 4; 5. – 3
| Расчет периметра квадрата, прямоугольника, треугольника, круга (периметры фигур). | ||
| Периметры фигур | ||
Помощь в решении задач по геометрии, учебник онлайн (все калькуляторы по геометрии). | ||
| Калькуляторы по геометрии | ||
| Определения и формулы расчета. | ||
| Периметры фигур. Периметр прямоугольника. | ||
| AO = CO = | d1 |
| 2 | |
| BO = DO = | d2 |
| 2 |
9. Точка пересечения диагоналей называется центром симметрии параллелограмма
10. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
AC2 + BD2 = 2AB2 + 2BC2
11. Биссектрисы противоположных углов параллелограмма всегда параллельны
12. Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)
Четырехугольник ABCD будет параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Четырехугольник имеет две пары параллельных сторон:
AB||CD, BC||AD
AB||CD, AB = CD (или BC||AD, BC = AD)
3. В четырехугольнике противоположные стороны попарно равны:
AB = CD, BC = AD
4. В четырехугольнике противоположные углы попарно равны:
∠DAB = ∠BCD, ∠ABC = ∠CDA
5. В четырехугольнике диагонали точкой пересечения делятся пополам:
AO = OC, BO = OD
6. Сумма углов четырехугольника прилегающих к любой стороне равна 180°:
Сумма углов четырехугольника прилегающих к любой стороне равна 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
7. В четырехугольнике сумма квадратов диагоналей равна сумме квадратов его сторон:
AC2 + BD2 = AB2 + BC2 + CD2 + AD 2
Формулы определения длин сторон параллелограмма:
1. Формула сторон параллелограмма через диагонали и угол между ними:
a = √d12 + d22 – 2d1d2·cosγ2= √d12 + d22 + 2d1d2·cosδ2
b = √d12 + d22 + 2d1d2·cosγ2= √d12 + d22 – 2d1d2·cosδ2
2. Формула сторон параллелограмма через диагонали и другую сторону:
| a = | √2d12 + 2d22 – 4b2 |
| 2 |
| b = | √2d12 + 2d22 – 4a2 |
| 2 |
3.
| a = | hb |
| sin α |
| b = | ha |
| sin α |
4. Формула сторон параллелограмма через площадь и высоту:
| a = | S |
| ha |
| b = | S |
| hb |
Источники
- https://www.webmath.ru/poleznoe/formules13.php
- https://www.calc.ru/Perimetry-Figur-Perimetr-Parallelogramma.html
- https://MicroExcel.ru/perimetr-parallelogramma/
- https://zen.yandex.ru/media/id/5af3fe33dd248465f4efe5b6/chemu-raven-perimetr-parallelogramma-5c117d6c49bb5900a9e7e90f
- https://ru.onlinemschool.com/math/formula/parallelogram/
| Табличка на двери |
В параллелограмме углы прилежащие к одной стороне.
 Параллелограмм и его свойства
Параллелограмм и его свойстваПараллелограмм представляет собой четырехугольник, у которого противоположные стороны попарно параллельны. Это определение уже достаточно, так как остальные свойства параллелограмма следуют из него и доказываются в виде теорем.
Основными свойствами параллелограмма являются:
- параллелограмм — это выпуклый четырехугольник;
- у параллелограмма противоположные стороны попарно равны;
- у параллелограмма противоположные углы попарно равны;
- диагонали параллелограмма точкой пересечения делятся пополам.
Параллелограмм — выпуклый четырехугольник
Докажем сначала теорему о том, что параллелограмм является выпуклым четырехугольником . Многоугольник является выпуклым тогда, когда какая бы его сторона не была продлена до прямой, все остальные стороны многоугольника окажутся по одну сторону от этой прямой.
Пусть дан параллелограмм ABCD, у которого AB противоположная сторона для CD, а BC — противоположная для AD. Тогда из определения параллелограмма следует, что AB || CD, BC || AD.
Тогда из определения параллелограмма следует, что AB || CD, BC || AD.
У параллельных отрезков нет общих точек, они не пересекаются. Это значит, что CD лежит по одну сторону от AB. Поскольку отрезок BC соединяет точку B отрезка AB с точкой C отрезка CD, а отрезок AD соединяет другие точки AB и CD, то отрезки BC и AD также лежат по ту же сторону от прямой AB, где лежит CD. Таким образом, все три стороны — CD, BC, AD — лежат по одну сторону от AB.
Аналогично доказывается, что по отношению к другим сторонам параллелограмма три остальные стороны лежат с одной стороны.
Противоположные стороны и углы равны
Одним из свойств параллелограмма является то, что в параллелограмме противоположные стороны и противоположные углы попарно равны . Например, если дан параллелограмм ABCD, то у него AB = CD, AD = BC, ∠A = ∠C, ∠B = ∠D. Доказывается эта теорема следующим образом.
Параллелограмм является четырехугольником. Значит, у него две диагонали. Так как параллелограмм — это выпуклый четырехугольник, то любая из них делит его на два треугольника.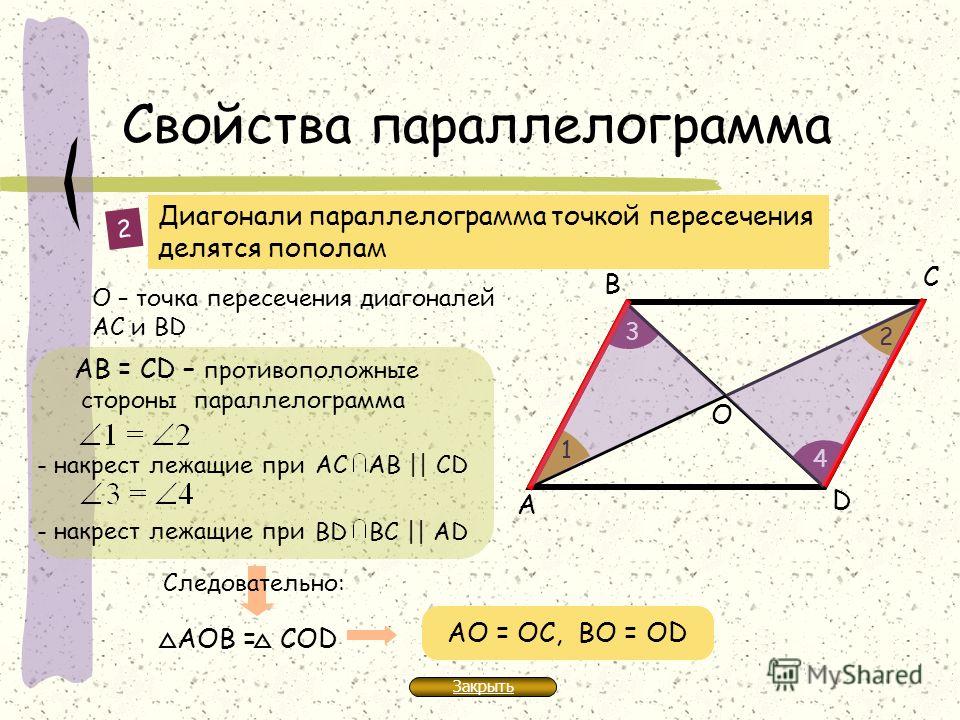 Рассмотрим в параллелограмме ABCD треугольники ABC и ADC, полученные в результате проведения диагонали AC.
Рассмотрим в параллелограмме ABCD треугольники ABC и ADC, полученные в результате проведения диагонали AC.
У этих треугольников одна сторона общая — AC. Угол BCA равен углу CAD, как вертикальные при параллельных BC и AD. Углы BAC и ACD также равны как вертикальные при параллельных AB и CD. Следовательно, ∆ABC = ∆ADC по двум углам и стороне между ними.
В этих треугольниках стороне AB соответствует сторона CD, а стороне BC соответствует AD. Следовательно, AB = CD и BC = AD.
Углу B соответствует угол D, т. е. ∠B = ∠D. Угол A параллелограмма представляет собой сумму двух углов — ∠BAC и ∠CAD. Угол же C равен состоит из ∠BCA и ∠ACD. Так как пары углов равны друг другу, то ∠A = ∠C.
Таким образом, доказано, что в параллелограмме противоположные стороны и углы равны.
Диагонали делятся пополам
Так как параллелограмм — это выпуклый четырехугольник, то у него две две диагонали, и они пересекаются. Пусть дан параллелограмм ABCD, его диагонали AC и BD пересекаются в точке E. Рассмотрим образованные ими треугольники ABE и CDE.
Рассмотрим образованные ими треугольники ABE и CDE.
У этих треугольников стороны AB и CD равны как противоположные стороны параллелограмма. Угол ABE равен углу CDE как накрест лежащие при параллельных прямых AB и CD. По этой же причине ∠BAE = ∠DCE. Значит, ∆ABE = ∆CDE по двум углам и стороне между ними.
Также можно заметить, что углы AEB и CED вертикальные, а следовательно, тоже равны друг другу.
Так как треугольники ABE и CDE равны друг другу, то равны и все их соответствующие элементы. Стороне AE первого треугольника соответствует сторона CE второго, значит, AE = CE. Аналогично BE = DE. Каждая пара равных отрезков составляет диагональ параллелограмма. Таким образом доказано, что диагонали параллелограмма делятся точкой пересечения пополам .
ЧЕТЫРЁХУГОЛЬНИКИ.
§43. ПАРАЛЛЕЛОГРАММ.
1. Определение параллелограмма.
Если пару параллельных прямых пересечём другой парой параллельных прямых, то получим четырёхугольник, у которого противоположные стороны попарно параллельны.
В четырёхугольниках АВDС и ЕFNМ (черт. 224) ВD || АС и АВ || СD;
ЕF || МN и ЕМ || FN.
Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
2. Свойства параллелограмма.
Теорема . Диагональ параллелограмма делит его на два равных треугольника.
Пусть имеется параллелограмм АВDС (черт. 225), в котором АВ || СD и АС || ВD.
Требуется доказать, что диагональ делит его на два равных треугольника.
Проведём в параллелограмме АВDС диагональ СВ. Докажем, что /\ САВ= /\ СDВ.
Сторона СВ общая для этих треугольников; / АВС = / ВСD, как внутренние накрест лежащие углы при параллельных АВ и СD и секущей СВ; / АСВ = / СВD, тоже как внутренние накрест лежащие углы при параллельных АС и ВD и секущей CB (§ 38).
Отсюда /\ САВ = /\ СDВ.
Таким же путём можно доказать, что диагональ AD разделит параллелограмм на два равных треугольника АСD и АВD.
Следствия. 1 . Противоположные углы параллелограмма равны между собой.
/ А = / D, это следует из равенства треугольников САВ и СDВ.
Аналогично и / С = / В.
2. Противоположные стороны параллелограмма равны между собой.
АВ = СD и АС = ВD, так как это стороны равных треугольников и лежат против равных углов.
Теорема 2. Диагонали параллелограмма в точке их пересечения делятся пополам.
Пусть ВС и AD — диагонали параллелограмма AВDС (черт. 226). Докажем, что АО = OD и СО = ОВ.
Для этого сравним какую-нибудь пару противоположно расположенных треугольников, например /\ AОВ и /\ СОD.
В этих треугольниках АВ = СD, как противоположные стороны параллелограмма;
/ 1 = / 2, как углы внутренние накрест лежащие при параллельных АВ и СD и секущей AD;
/ 3 = / 4 по той же причине, так как АВ || СD и СВ — их секущая (§ 38).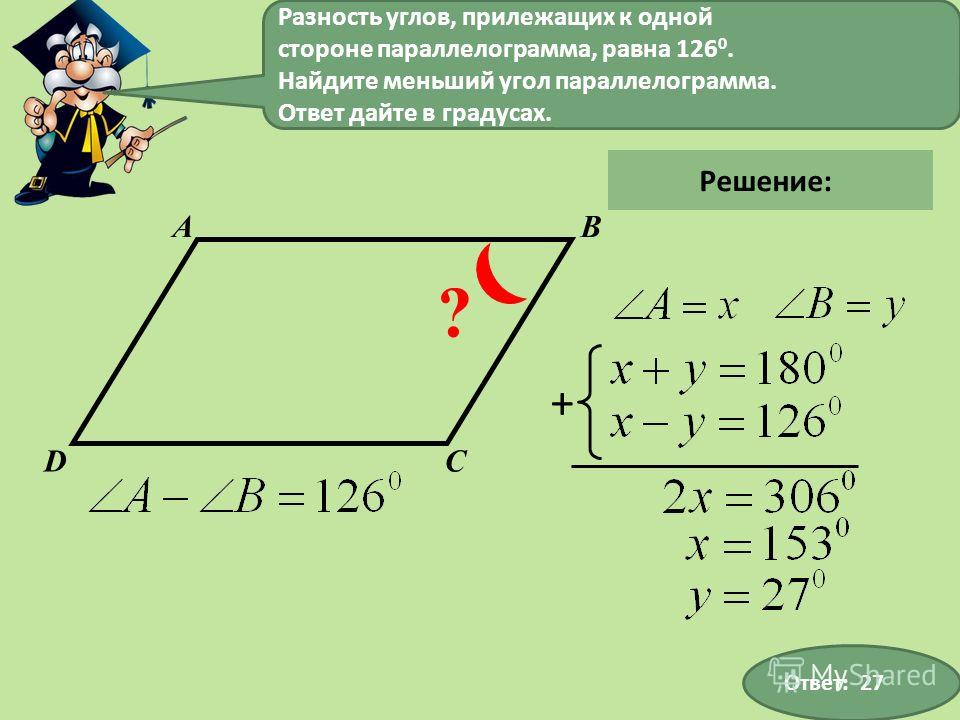
Отсюда следует, что /\ AОВ = /\ СОD. А в равных треугольниках против равных углов лежат равные стороны. Следовательно, АО = OD и СО = ОВ.
Теорема 3. Сумма углов, прилежащих к одной стороне параллелограмма, равна 2 d .
Доказать самостоятельно.
3. Признаки параллелограмма.
Теорема. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
Пусть в четырёхугольнике AВDС (черт. 227) АВ = СD и АС = ВD. Докажем, что при этом условии АВ || СD и АС || ВD, т. е. четырёхугольник АВDC — параллелограмм.
Соединим отрезком какие-нибудь две противоположные вершины этого — четырёхугольника, например С и В. Четырёхугольник АВDС разбился на два равных треугольника: /\ СAВ и /\ СDВ. В самом деле, сторона СВ у них общая, АВ = СD и АС = ВD по условию. Таким образом, три стороны одного треугольника соответственно равны трём сторонам другого, поэтому /\ СAВ = /\ СDВ.
В равных треугольниках против равных сторон лежат равные углы, поэтому
/ 1 = / 2 и / 3 = / 4.
Углы 1-й и 2-й являются внутренними накрест лежащими углами при пересечении прямых АВ и СD прямой СВ. Следовательно, АВ || СD.
Точно так же углы 3-й и 4-й являются внутренними накрест лежащими углами при пересечении прямых СА и ВD прямой СВ, следовательно, СА || ВD (§ 35).
Таким образом, противоположные стороны четырёхугольника АВDС попарно параллельны, следовательно, он параллелограмм, что и требовалось доказать.
Теорема 2. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.
Пусть в четырёхугольнике АВDС АВ = СD и АВ || СD. Докажем, что при этих условиях четырёхугольник АВDС- параллелограмм (черт. 228).
Соединим отрезком СВ вершины С и В. Вследствие параллельности прямых АВ и СD углы 1 и 2, как углы внутренние накрест лежащие, равны (§ 38).
Тогда треугольник САВ равен треугольнику СDВ, так как сторона СВ у них общая,
АВ = СD по условию теоремы и / 1 = / 2 по доказанному. Из равенства этих треугольников вытекает равенство углов 3 и 4, так как они лежат против равных сторон в равных треугольниках.
Но углы 3 и 4 — это внутренние накрест лежащие углы, образованные при пересечении прямых АС и ВD прямой СВ, следовательно, АС || ВD (§ 35), т. е. четырёхугольник
АВDС- параллелограмм.
Упражнения.
1. Доказать, что если диагонали четырёхугольника в точке их взаимного пересечения делятся пополам, то этот четырёхугольник — параллелограмм.
2. Доказать, что четырёхугольник, у которого сумма внутренних углов, прилежащих к каждой из двух соседних сторон, равна 2d , есть параллелограмм.
3. Построить параллелограмм по двум сторонам и углу между ними:
а) используя параллельность противоположных сторон параллелограмма;
б) используя равенство противоположных сторон параллелограмма.
4. Построить параллелограмм по двум смежным сторонам и диагонали.
5. Построить параллелограмм по двум его диагоналям и углу между ними.
6. Построить параллелограмм по его стороне и двум диагоналям.
Параллелограммом называется такой четырехугольник, в котором противоположные стороны попарно параллельны.
Параллелограмм обладает всеми свойствами четырехугольников, но кроме этого имеет и свои отличительные особенности. Зная их, мы можем с легкостью находить как стороны, так и углы параллелограмма.
Свойства параллелограмма
- Сумма углов в любом параллелограмме, как и в любом четырехугольнике, равна 360°.
- Средние линии параллелограмма и его диагонали пересекаются в одной точке и делятся ею пополам. Эту точку принято называть центром симметрии параллелограмма.
- Противоположные стороны у параллелограмма всегда равны.
- Также у этой фигуры всегда равны противоположные углы.
- Сумма углов, которые прилегают к любой из сторон параллелограмма, всегда составляет 180°.

- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон. Это выражается формулой:
- d 1 2 + d 2 2 = 2 (a 2 +b 2), где d 1 и d 2 — диагонали, a и b — смежные стороны.
- Косинус тупого угла всегда меньше нуля.
Как найти углы заданного параллелограмма, применяя эти свойства на практике? И какие еще формулы могут нам в этом помочь? Рассмотрим конкретные задания, в которых требуют: найдите величины углов параллелограмма.
Нахождение углов параллелограмма
Случай 1. Известна мера тупого угла, требуется найти острый угол.
Пример: В параллелограмме ABCD угол A равен 120°. Найдите меру остальных углов.
Решение: Пользуясь свойством № 5, мы можем найти меру угла B, смежного с тем углом, который дан в задании. Он будет равен:
- 180°-120°= 60°
А теперь, пользуясь свойством №4, мы определяем, что два оставшихся угла C и D противоположны тем углам, которые мы уже нашли. Угол C противоположен углу A, угол D — углу B. А следовательно они попарно им равны.
Угол C противоположен углу A, угол D — углу B. А следовательно они попарно им равны.
- Ответ: B = 60°, C = 120°, D=60°
Случай 2. Известны длины сторон и диагонали
В таком случае нам необходимо воспользоваться теоремой косинусов.
Мы можем сначала по формуле вычислить косинус нужного нам угла, а потом по специальной таблице найти, чему равен сам угол.
Для острого угла формула такая:
- cosa = (А² + В² — d²) / (2 * А * В), где
- а — это искомый острый угол,
- А и В — стороны параллелограмма,
- d — меньшая диагональ
Для тупого угла формула немного меняется:
- cosß = (А² + В² — D²) / (2 * А * В), где
- ß — это тупой угол,
- А и В — стороны,
- D — большая диагональ
Пример: необходимо найти острый угол параллелограмма, стороны которого равны 6 см и 3 см, а меньшая диагональ равна 5.2 см
Подставляем значения в формулу для нахождения острого угла:
- cosa = (6 2 + 3 2 — 5.
 2 2) / (2 * 6 * 3) = (36 + 9 — 27.04) / (2 * 18) = 17.96/36 ~ 18/36 ~1/2
2 2) / (2 * 6 * 3) = (36 + 9 — 27.04) / (2 * 18) = 17.96/36 ~ 18/36 ~1/2 - cosa = 1/2. По таблице выясняем, что искомый угол равен 60°.
Параллелограммом называют четырехугольник противолежащие стороны которого попарно параллельны. Также параллелограмм владеет такими свойствами, как противоположные стороны равны, противоположные углы равны, сумма всех углов равна 360 градусов.
Вам понадобится
- Знания по геометрии.
Инструкция
1. Представим дан один из углов параллелограмма и равен A. Обнаружим значения остальных 3. По свойству параллелограмма противоположные углы равны. Значит угол, лежащий наоборот данного равен данному и его значение равно А.
2. Обнаружим оставшиеся два угла. Потому что сумма всех углов в параллелограмме равна 360 градусов, а противоположные углы между собой равны, то получается, что угол, принадлежащий одной стороне с данным, равен (360 — 2А)/2. Ну либо позже реформирования получим 180 — А. Таким образом в параллелограмме два угла равны А, а два других угла равны 180 — А.
Таким образом в параллелограмме два угла равны А, а два других угла равны 180 — А.
Обратите внимание!
Значение одного угла не может превышать 180 градусов. Полученные значения углов дозволено легко проверить. Для этого сложите их и, если сумма равна 360, все посчитано правильно.
Полезный совет
Прямоугольник и ромб являются частным случаем параллелограмма, следственно все свойства и способы вычисления углов применимы и к ним.
Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т.е. лежат на параллельных прямых
Свойства параллелограмма:
Теорема 22. Противоположные стороны параллелограма равны.
Доказательство. В параллелограмме АВСD проведем диагональ АС. Треугольники АСD и АСВ равны, как имеющие общую сторону АС и две пары равных углов. прилежащих к ней: ∠
САВ=∠
АСD, ∠
АСВ=∠
DAC (как накрест лежащие углы при параллельных прямых AD и ВС). Значит, АВ=CD и ВС=AD, как соответственные стороны равных треугольников, ч. т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников:
т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников:
Теорема 23. Противоположные углы параллелограмма равны: ∠
А=∠
С и ∠
В=∠
D.
Равенство первой пары идет из равенства треугольников АВD и CBD, а второй — АВС и ACD.
Теорема 24. Соседние углы параллелограмма, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов.
Это так, потому что они являются внутренними односторонними углами.
Теорема 25. Диагонали параллелограмма делят друг друга в точке их пересечения пополам.
Доказательство. Рассмотрим треугольники ВОС и АОD. По первому свойству AD=ВС ∠
ОАD=∠
ОСВ и ∠
ОDА=∠
ОВС как накрест лежащие при параллельных прямых AD и ВС. Поэтому треугольники ВОС и АОD равны по стороне и прилежащим к ней углам. Значит, ВО=ОD и АО=ОС, как соответственные стороны равных треугольников, ч.т.д.
Признаки параллелограмма
Теорема 26. Если противоположные стороны четырехугольника попарно равны, то он является параллелограммом.
Доказательство. Пусть у четырехугольника АВСD стороны AD и ВС, АВ и CD соответственно равны (рис2). Проведем диагональ АС. Треугольникик АВС и ACD равны по трем сторонам. Тогда углы ВАС и DСА равны и, следовательно, АВ параллельна CD. Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ.
Теорема 27. Если противоположные углы четырехугольника попарно равны, то он является параллелограммом.
Пусть ∠
А=∠
С и ∠
В=∠
D. Т.к. ∠
А+∠
В+∠
С+∠
D=360 о, то ∠
А+∠
В=180 о и стороны AD и ВС параллельны (по признаку параллельности прямых). Также докажем и параллельность сторон АВ и CD и заключим, что АВСD является параллелограммом по определению.
Теорема 28. Если соседние углы четырехугольника, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов, то он является параллелограммом.
Если внутренние односторонные углы в сумме составляют 180 градусов, то прямые праллельны. Значит АВ парал CD и ВС парал AD. Четырехугольник оказывается параллелограммом по определению.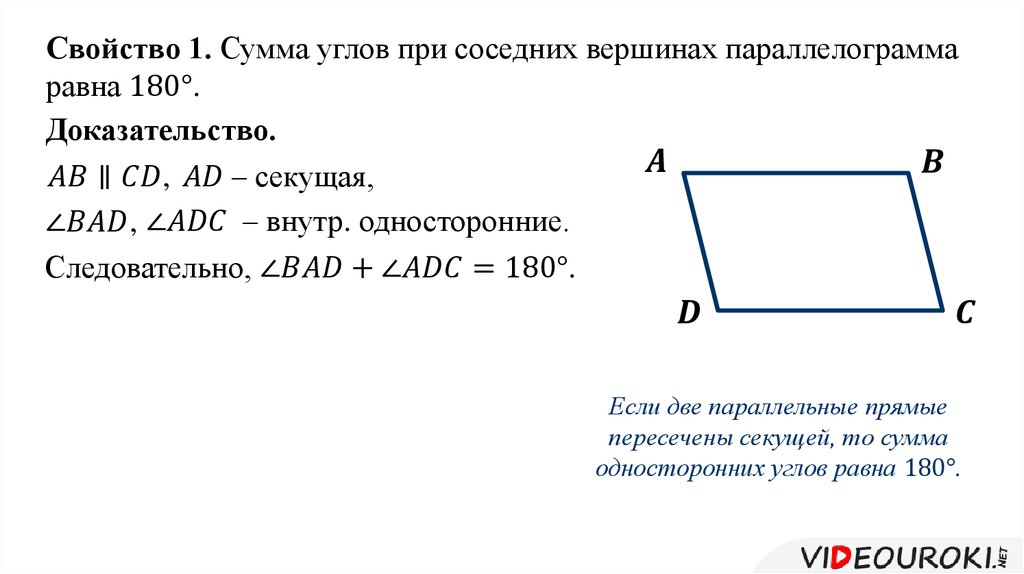
Теорема 29. Если диагонали четырехугольника взаимно делятся в точке пересечения пополам, то четырехугольник — параллелограмм.
Доказательство. Если АО=ОС, ВО=ОD, то треугольники АOD и ВОС равны, как имеющие равны углы (вертикальные) при вершине О, заключенные между парами равных сторон. Из равенства треугольников заключаем, что AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом по признаку 1.
Теорема 30. Если четырехугольник имеет пару равных, параллельных между собой сторон, то он является параллелограммом.
Пусть в четырехугольнике АВСD стороны АВ и CD параллельны и равны. Проведем диагонали АС и ВD. Из параллельности этих прямых следует равенство накрест лежащих углов АВО=СDО и ВАО=ОСD. Треугольники АВО и CDО равны по стороне и прилежащим к ней углам. Поэтому АО=ОС, ВО=ОD, т.е. диагонали точкой пересечения делятся пополам и четырехугольник оказывается параллелограммом по признаку 4.
В геометрии рассматривают частные случаи параллелограмма.
Периметр параллелограмма. Периметр параллелограмма онлайн. Сумма сторон.
- Альфашкола
- Статьи
- Периметр параллелограмма
Периметр параллелограмма
Периметр параллелограмма — это сумма всех его сторон.
\(AB=CD\) \(BC=AD\)
\(P_п=AB+BC+CD+AD =2AB+2BC=2CD+2AD\)
Первая сторона параллелограмма:
Вторая сторона параллелограмма:
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Валерия Сергеевна Архипова
Репетитор по математике
Стаж (лет)
Образование:
МГУ им.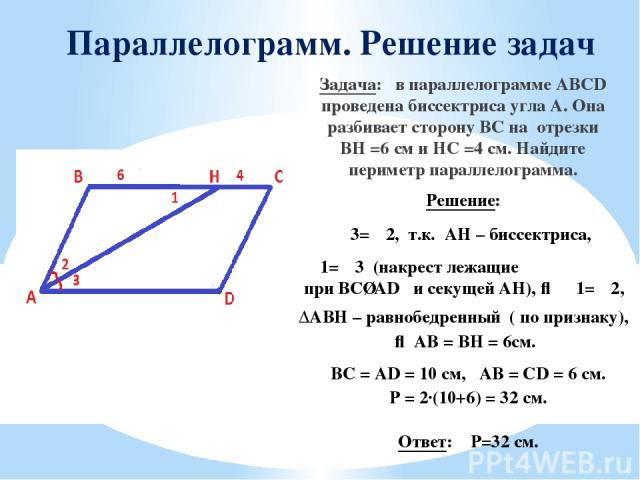 А.Кулешова
А.Кулешова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-8 классов и по физике 5-7 классов. «Числа управляют миром», – говорили пифагорейцы. Но числа дают возможность человеку управлять миром, и в этом нас убеждает весь ход развития науки и техники наших дней. Цель моих занятий — объяснить, а не заучить, поэтому даже после прохождения курса у ученика остаются знания, ведь понимание — ключ к дальнейшему развитию.
Сергей Владимирович Туркенич
Репетитор по математике
Стаж (лет)
Образование:
Гомельский государственный университет им. Ф. Скорины
Ф. Скорины
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по обществознанию для 4-11 классов. Победитель, призёр и лауреат конкурсов педагогического мастерства (в т.ч. МГУ и МПГУ). Магистр права. На наших занятиях всегда интересно! По каждому вопросу привожу примеры и аналогии, что визуализирует материал, упрощает его понимание, прививает интерес к предмету и в итоге даёт положительный результат. Вместе у нас всё получится!
Елена Михайловна Глущенко
Репетитор по математике
Стаж (лет)
Образование:
Стерлитамакский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 6-11 классов.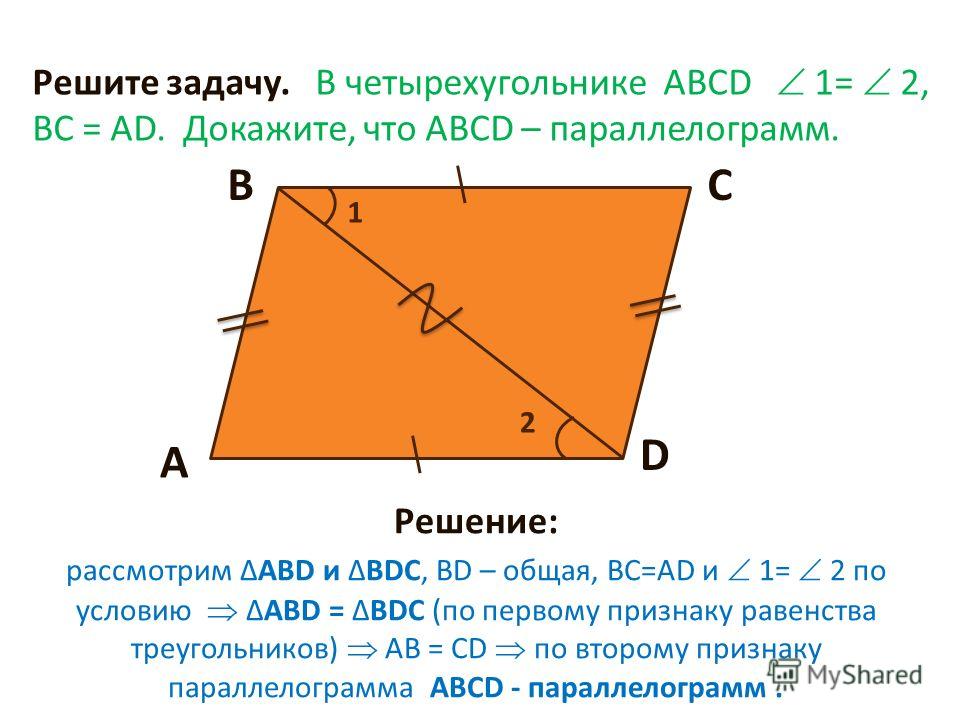 Обществознание и история очень интересные предметы! Здесь можно изучить законы общества, понять свои возможности и выбрать жизненный путь, получить знания из других наук: экономики, философии, политологии, социологии и этики. Использую индивидуальный подход к ученику, стараюсь заинтересовать и расширить кругозор, использую на занятиях презентации, схемы и видео.
Обществознание и история очень интересные предметы! Здесь можно изучить законы общества, понять свои возможности и выбрать жизненный путь, получить знания из других наук: экономики, философии, политологии, социологии и этики. Использую индивидуальный подход к ученику, стараюсь заинтересовать и расширить кругозор, использую на занятиях презентации, схемы и видео.
Похожие статьи
- Площадь прямоугольной пирамиды
- Расстояние между точками на координатной прямой
- ЕГЭ по математике, базовый уровень. Задачи на координатной решетке
- Как по заданным функции, точке и вектору вычислить градиент в точке и производную функции в точке по направлению вектора
- Как написать каноническое и параметрическое уравнение прямой, образованной пересечением плоскостей
- Как легко обмануться, если не знаешь математики
- Подборка логических задач для школьников 3-4 класса
- Как вернуть веру в Деда Мороза и подарить сказку на зимних каникулах
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Как вычислить площадь параллелограмма.
 Параллелограмм и его свойства
Параллелограмм и его свойстваВидеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Примечание . Это часть урока с задачами по геометрии (раздел параллелограмм). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
Теоретический материал
Пояснения к формулам нахождения площади параллелограмма:
- Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
- Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними
Задачи на нахождение площади параллелограмма
Задача .
В параллелограмме меньшая высота и меньшая сторона равны 9 см и корню из 82 соответственно.Большая диагональ 15 см.Найти площадь параллелограмма.
Решение .
Обозначим меньшую высоту параллелограмма ABCD, опущенную из точки B на большее основание AD как BK.
Найдем значение катета прямоугольного треугольника ABK, образованного меньшей высотой, меньшей стороной и частью большего основания. По теореме Пифагора:
AB 2 = BK 2 + AK 2
82 = 9 2 + AK 2
AK 2 = 82 — 81
AK = 1
Продлим верхнее основание параллелограмма BC и опустим на него высоту AN из его нижнего основания. AN = BK как стороны прямоугольника ANBK. У получившегося прямоугольного треугольника ANC найдем катет NC.
AN 2 + NC 2 = AC 2
9 2 + NC 2 = 15 2
NC 2 = 225 — 81
NC 2 = √144
NC = 12
Теперь найдем большее основание BC параллелограмма ABCD.
BC = NC — NB
Учтем, что NB = AK как стороны прямоугольника, тогда
BC = 12 — 1 = 11
Площадь параллелограмма равна произведению основания на высоту к этому основанию.
S = ah
S = BC * BK
S = 11 * 9 = 99
Ответ : 99 см 2 .
Задача
В параллелограмме АВСД на диагональ АС опущен перпендикуляр ВО. Найдите площадь параллелограмма, если АО=8, ОС=6 и ВО=4.
Решение .
Опустим на диагональ АС дополнительно еще один перпендикуляр DK.
Соответственно, треугольники AOB иDKC, COB и AKD попарно равны. Одна из сторон является противолежащей стороной параллелограмма, один из углов — прямой, так как является перпендикуляром к диагонали, а один из оставшихся углов является внутренним накрест лежащим для параллельных сторон параллелограмма и секущей диагонали.
Таким образом, площадь параллелограмма равна площади указанных треугольников. То есть
Sпаралл = 2S AOB +2S BOC
Площадь прямоугольного треугольника равна половине произведения катетов. Откуда
S = 2 (1/2 8 * 4) + 2 (1/2 6 * 4) = 56 см 2
Ответ : 56 см 2 .
При решении задач по данной теме кроме основных свойств параллелограмма и соответственных формул можно запомнить и применять следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними
Рассмотрим задачи, при решении которых используются данные свойства.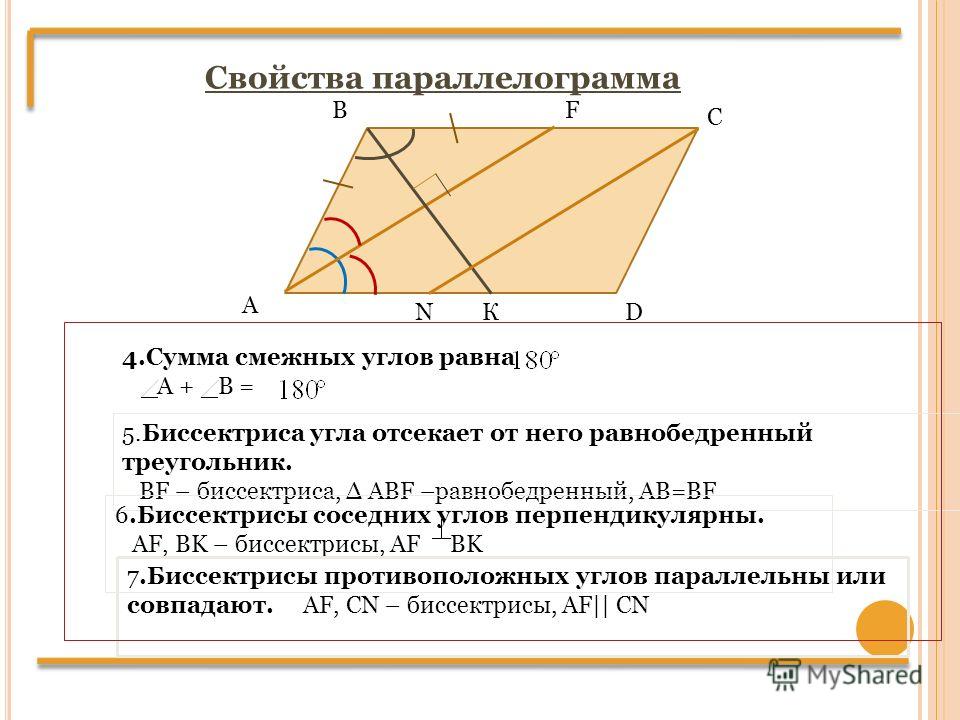
Задача 1.
Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.
Решение.
1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.
2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. АD = АМ + МD = 7 см.
4. Периметр АВСD = 20 см.
Ответ. 20 см.
Задача 2.
В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.
Решение.
1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.
2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD.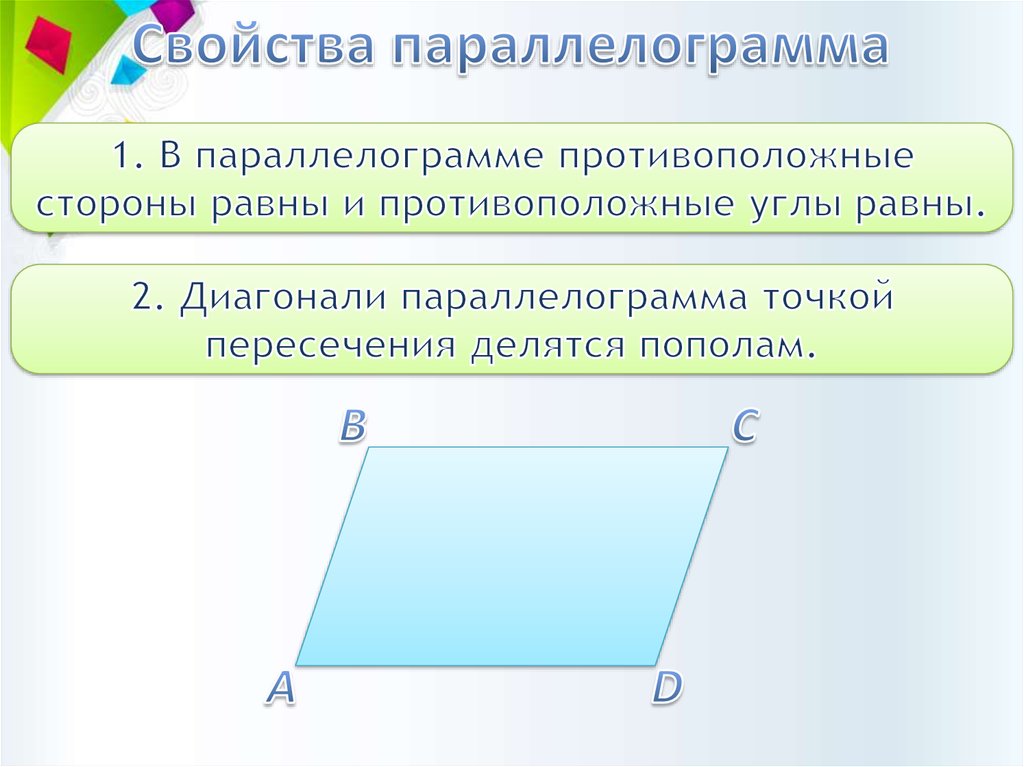 ВЕ = СF. Следовательно, прямая ВС || AD. (*)
ВЕ = СF. Следовательно, прямая ВС || AD. (*)
3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD. Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.
4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)
5. Из условий (*), (**) вытекает – АВСD параллелограмм.
Ответ. Доказано. АВСD – параллелограмм.
Задача 3.
На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О;
Решение.
1. В треугольнике DОМ
2. В прямоугольном треугольнике DНС
(
Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).
Но СD = АВ. Тогда АВ: НD = 2: 1.
3.
4.
Ответ: АВ: НD = 2: 1,
Задача 4.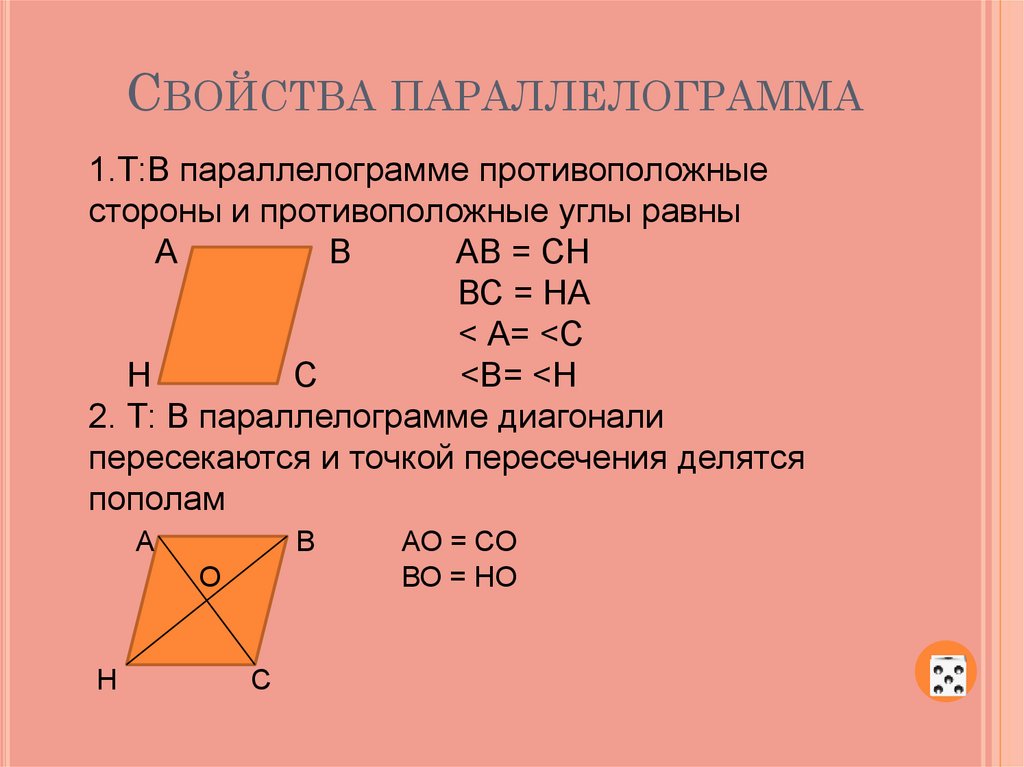
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45 о = OD/sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или
2 · 5√2 · 7√2 = d 1 d 2 ;
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .
d 1 2 + d 2 2 = 296.
3. Составим систему:
{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.
4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;
d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.
d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что
Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или
d 1 · d 2 = 80/(2√2) = 20√2
4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .
2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.
(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.
ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Параллелограмм представляет собой четырехугольную фигуру, у которой противолежащие стороны попарно параллельны и попарно равны. Равны у него также и противоположные углы, а точка пересечения диагоналей параллелограмма делит их пополам, являясь при этом центром симметрии фигуры. Частными случаями параллелограмма являются такие геометрические фигуры как квадрат, прямоугольник и ромб. Площадь параллелограмма может быть найдена различными способами, в зависимости от того, какими исходными данными сопровождается постановка задачи.
Частными случаями параллелограмма являются такие геометрические фигуры как квадрат, прямоугольник и ромб. Площадь параллелограмма может быть найдена различными способами, в зависимости от того, какими исходными данными сопровождается постановка задачи.
Ключевой характеристикой параллелограмма, очень часто используемой при нахождении его площади, является высота. Высотой параллелограмма принято называть перпендикуляр, опущенный из произвольной точки противоположной стороны к отрезку прямой, образующей данную сторону.
- В самом простом случае площадь параллелограмма определяется как произведение его основания на высоту.
S = DC ∙ h
где S — площадь параллелограмма;
a — основание;
h — высота, проведенная к данному основанию.Данную формулу очень легко понять и запомнить, если взглянуть на следующий рисунок.
Как видно из данного изображения, если слева от параллелограмма отрезать воображаемый треугольник и присоединить его справа, то в результате мы получим прямоугольник.
 А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.
А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону. - Площадь параллелограмма может быть также найдена в результате перемножения длин двух смежных оснований и синуса угла между ними:
S = AD∙AB∙sinα
где AD, AB — смежные основания, образующие точку пересечения и угол а между собой;
α — угол между основаниями AD и AB. - Также площадь параллелограмма можно найти разделив пополам произведение длин диагоналей параллелограмма на синус угла между ними.
S = ½∙AC∙BD∙sinβ
где AC, BD — диагонали параллелограмма;
β — угол между диагоналями. - Существует также формула для нахождения площади параллелограмма через радиус вписанной в него окружности. Она записывается следующий образом:
Параллелограммом называют четырехугольник у которого противоположные стороны параллельны между собой. 2)
.
2)
.
Основные признаки параллелограммов:
1. Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом.
2. Четырехугольник с равными противоположными сторонами является параллелограммом.
3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом.
4. Если диагонали четырехугольника в точке пересечения делятся пополам то это параллелограмм.
5. Четырехугольник у которого противоположные углы попарно равны является параллелограммом
Биссектрисы параллелограмма
Биссектрисы противоположных углов в параллелограмме могут быть параллельными или совпадать.
Биссектрисы соседних углов (прилегающие к одной стороне) пересекаются под прямым углом (перпендикулярные).
Высота параллелограмма
Высота параллелограмма
— это отрезок который проведен с угла перпендикулярно к основанию. Из этого следует что из каждого угла можно провести две высоты.
Формула площади параллелограмма
Площадь параллелограмма
равна произведению стороны на высоту проведенную к ней. Формула площади следующая
Вторая формула не менее популярная при вычислениях и определяется так: площадь параллелограмма равна произведению соседних сторон на синус угла между ними
На основе приведенных формул Вы будете знать как вычислить площадь параллелограмма.
Периметр параллелограмма
Формула для вычисления периметру параллелограмма имеет вид
то есть периметр равен удвоенному значению суммы сторон. Задачи на параллелограмм будут рассмотрены в соседних материалах, а пока изучайте формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма достаточно просты и сводятся к знанию теоремы синусов и теоремы Пифагора.
Формула параллелограмма — Что такое формула параллелограмма? Примеры
Параллелограмм – это двумерная фигура. Он имеет четыре стороны, у которых две пары противоположных сторон параллельны. Противоположные стороны параллелограмма равны по длине и противолежащие углы равны по размеру, а сумма смежных углов параллелограмма равна 180 градусам. Прежде чем перейти к формуле параллелограмма, давайте рассмотрим ее свойства.
Противоположные стороны параллелограмма равны по длине и противолежащие углы равны по размеру, а сумма смежных углов параллелограмма равна 180 градусам. Прежде чем перейти к формуле параллелограмма, давайте рассмотрим ее свойства.
Свойства параллелограмма
Ниже перечислены несколько важных свойств параллелограмма:
- Противоположные стороны параллельны и конгруэнтны.
- Внутренние противоположные углы равны.
- Последовательные углы являются дополнительными.
- В случае, если градусная мера любого из углов является прямым, то и все остальные углы будут прямыми.
- Две диагонали делят друг друга пополам.
- Каждая диагональ делит параллелограмм пополам на два равных треугольника
- Сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей, что известно как закон параллелограмма.
Что такое формула параллелограмма?
Рассмотрим параллелограмм ABCD, как показано ниже. Давайте разберемся с формулами параллелограмма.
Давайте разберемся с формулами параллелограмма.
У нас есть,
- AB || компакт-диск, переменный ток || БД
- AB = CD = b
- до н.э. = н.э. = a
- h = высота параллелограмма
- DB = d\(_1\), AC = d\(_2\) — двуугольники параллелограмма
Площадь параллелограмма Формула
Площадь параллелограмма — это область или поверхность, занимаемая двумерной плоскостью. Давайте посмотрим на формулу параллелограмма для вычисления площади.
Формула площади параллелограмма с использованием основания и высоты
- Формула площади параллелограмма = основание × высота
- Площадь параллелограмма ABCD = b × h
Формула площади параллелограмма без высоты
- Если высота параллелограмма не указана, для нахождения площади можно использовать тригонометрию.
- Формула площади параллелограмма = a b sin A = b a sin B
Площадь параллелограмма с использованием диагоналей
Площадь любого параллелограмма также можно рассчитать, используя длины его диагоналей. Предположим, диагонали d\(_1\) и d\(_2\) пересекают друг друга под углом x, тогда площадь параллелограмма определяется как:
Предположим, диагонали d\(_1\) и d\(_2\) пересекают друг друга под углом x, тогда площадь параллелограмма определяется как:
- Площадь формулы параллелограмма = ½ ×\({d_1} × {d_1} sin (x)\)
- Площадь параллелограмма ABCD = ½ × AC × BD sin (x)
Периметр параллелограмма Формула
Периметр параллелограмма – это общее расстояние от границ параллелограмма. Для вычисления периметра параллелограмма необходимо знать его длину и ширину. Пусть стороны параллелограмма равны а и b. Имея в виду свойство параллелограмма, т. Е. Противоположные стороны параллельны и конгруэнтны. Периметр параллелограмма равен:
- Периметр = a + b + c + d (когда a, b, c, d представляют 4 стороны параллелограмма)
- Поскольку сторона AB = CD = b, сторона BC = AD = a
- Периметр параллелограмма = 2 (a+b)
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
С Cuemath вы будете учиться визуально и будете удивлены результатами.
Забронировать бесплатный пробный урок
Пример формулы параллелограмма
Пример 1: Используя формулу параллелограмма, найдите площадь параллелограмма с основанием 6 см и высотой 8 см.
Решение:
Дано:
Основание, b = 6 см
Высота, h = 8 см
Мы знаем, что, используя формулу параллелограмма
Формула площади параллелограмма = b × h квадратных единиц
= 6 × 8 = 48 кв.см
Ответ: Следовательно, площадь параллелограмма = 48 см 2 .
Пример 2: Используя формулу параллелограмма, найдите периметр параллелограмма со сторонами 5 м и 7 м.
Решение:
Дано:
а = 5 м
б = 7 м
Мы это знаем,
Периметр параллелограмма = 2(a + b) единиц
= 2(5 + 7)
= 24 м
Ответ: Таким образом, периметр параллелограмма равен 24 м.
Пример 3: Площадь игровой площадки в форме параллелограмма составляет 25 000 дюймов 2 , одна сторона которой имеет размер 250 дюймов. Найдите соответствующую высоту, используя формулу площади параллелограмма.
Решение:
Площадь детской площадки = 25000 в 2
Сторона детской площадки = 250 в 90 115
Используя формулу Площадь параллелограмма = b × h квадратных единиц
Соответствующая высота = 25000/250 = 100 дюймов
Ответ: Соответствующая высота игровой площадки составляет 100 дюймов.
Часто задаваемые вопросы о формуле параллелограмма
Как вычислить площадь с помощью формулы параллелограмма?
Если даны основание и высота (высота) параллелограмма, то площадь можно выразить как произведение основания и высоты параллелограмма.
А = чч
A = основание × высота (единицы измерения 2 )
Какая формула параллелограмма используется для расчета периметра?
Для вычисления периметра параллелограмма мы используем общую формулу параллелограмма, указанную ниже:
Периметр параллелограмма = 2 (a+b) единицы
Что такое «h» в формуле параллелограмма для площади?
Площадь параллелограмма определяется как A = bh квадратных единиц. Здесь «h» представляет собой высоту (высоту) параллелограмма.
Здесь «h» представляет собой высоту (высоту) параллелограмма.
Что такое «В» в формуле параллелограмма для площади?
Формула площади параллелограмма задается как A = B × H квадратных единиц. Здесь «В» представляет собой основание параллелограмма.
Углы параллелограмма – свойства, теорема и пример
Параллелограмм можно определить как четырехугольник, две стороны которого параллельны друг другу и все четыре угла при вершинах не равны 90 градусам или прямым углам, тогда четырехугольник называется параллелограммом. Противоположные стороны параллелограмма также равны по длине.
Свойства параллелограмма
[Изображение будет загружено в ближайшее время]
Важными свойствами параллелограмма, которые необходимо знать, являются:
Противоположные стороны параллелограмма равны (AB = DC).
Противоположные углы параллелограмма равны (D = B).

Смежные углы в параллелограмме являются дополнительными (A + D = 180°).
Если один угол равен 90 градусов, то и все остальные углы тоже равны 90 градусов.
Диагонали параллелограмма делятся пополам на две равные половины.
Диагональ параллелограмма делит его на два равных треугольника.
[Изображение скоро будет загружено]
Если все стороны параллелограмма равны, то фигура, которую мы имеем, называется ромбом. Свойства параллелограмма применимы и к ромбам. В параллелограмме, где одна пара сторон параллельна, получается форма, которую мы называем трапецией. Параллельные стороны называются основаниями, а непараллельные — катетами. Если стороны конгруэнтны, мы имеем то, что называется равнобедренной трапецией.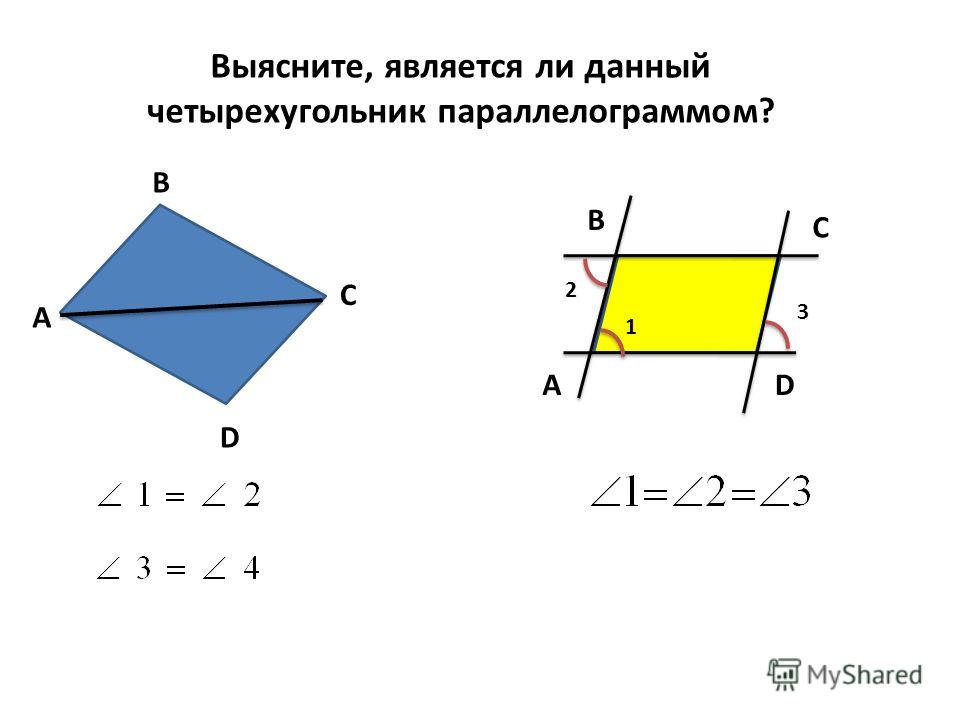
В равнобедренной трапеции диагонали всегда равны. Медиана трапеции параллельна основаниям и составляет половину суммы мер оснований.
[Изображение будет загружено в ближайшее время]
В этой теме мы изучаем угол параллелограмма. Итак, теорема об углах:
Противоположные углы параллелограмма равны является дополнительным
Теорема: Докажите, что противоположные углы параллелограмма равны.
[Изображение будет загружено в ближайшее время]
Дано: Параллелограмм ABCD.
Доказать: ∠B = ∠D и ∠A=∠C
Доказательство:
В параллелограмме ABCD,
AB\CD и AD\BC
Противоположные углы параллелограмма
[Изображение будет Скоро будет загружено]
Рассмотрим треугольник ABC и треугольник ADC,
AC = AC (общая сторона)
Мы знаем, что параллельные внутренние углы равны.
∠1 = ∠4
∠2 = ∠3
По критерию конгруэнтности ASA два треугольника конгруэнтны друг другу.
Следовательно, ∠B = ∠D и ∠A=∠C
Отсюда доказано, что противоположные углы параллелограмма равны.
Пример-
Вопрос: Чтобы доказать, что противоположные углы параллелограмма равны
Решение: Пусть ABCD — параллелограмм, а AC — его диагональ. (1 ) [ Альтернативные ракурсы ]
Точно так же AD∥BC и AC являются секущими.
⇒ ∠DAC=∠BCA —- ( 2 ) [ Альтернативные углы ]
Сложение ( 1 ) и ( 2 ),
⇒ ∠BAC+∠DAC=∠DCA+∠BCA
∠DCBAD= ∠DCBAD=Аналогично можно доказать, что ∠ADC=∠ABC
Таким образом, мы доказали, что противоположные углы параллелограмма равны.
Смежные углы параллелограмма
Теорема: Докажите, что любые последовательные углы параллелограмма являются дополнительными.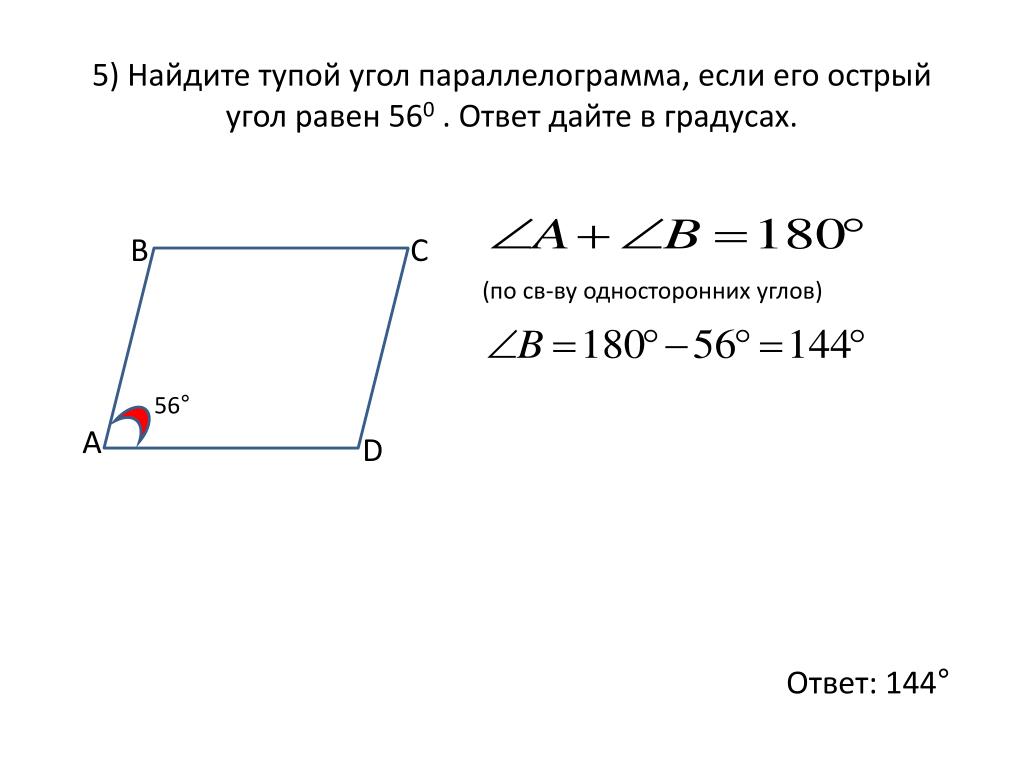
[Изображение скоро будет загружено]
Дано: Параллелограмм ABCD.
Чтобы доказать: ∠A + ∠B = 180 градусов, ∠C + ∠D = 180 градусов
Доказательство:
Углы параллелограмма
AB ∥ CD и AD трансверсальны.
Мы знаем, что внутренние углы на одной стороне являются дополнительными.
Следовательно, ∠A + ∠D = 180°
Аналогично, ∠B + ∠C = 180°, ∠C + ∠D = 180° и ∠A + ∠B = 180°.
Следовательно, сумма любых двух смежных углов параллелограмма равна 180°.
Таким образом, доказано, что любые два смежных или следующих друг за другом угла параллелограмма являются дополнительными.
Из приведенной выше теоремы можно вывести, что если один угол параллелограмма равен 90 градусам, то и все четыре угла равны 90 градусам. Следовательно, он станет прямоугольником.
Если один угол равен 90 градусов, то все четыре угла равны 90 градусов:
Так как смежные стороны являются дополнительными.
Например, ∠A, ∠B — смежные углы, а ∠A = 90°, тогда:
∠A + ∠B = 180°
90° + ∠B = 180°
∠B = 180° – 90°
∠B = 90°
Аналогично D = 90°
Пример 1:
На соседнем рисунке ∠D = 85° и ∠B = (x+25) °, найдите значение x.
[Изображение будет загружено в ближайшее время]
Решение:
Дано,
∠D = 60° и ∠B = (x+20)°
Согласно теореме, противоположные углы параллелограмма равны.
Следовательно,
(x+20)° = 60°
x = 60° -20°
x = 40°
Следовательно, значение x равно 40.
Площадь параллелограмма
3 Площадь равна 9 основание, умноженное на высоту:
Площадь = b × h
(h под прямым углом к b)
Пример:
Параллелограмм имеет основание 8 м и высоту 5 м, какова его площадь?
Площадь = 8 м × 5 м = 18 м2
Периметр параллелограмма
Периметр — это расстояние по краям.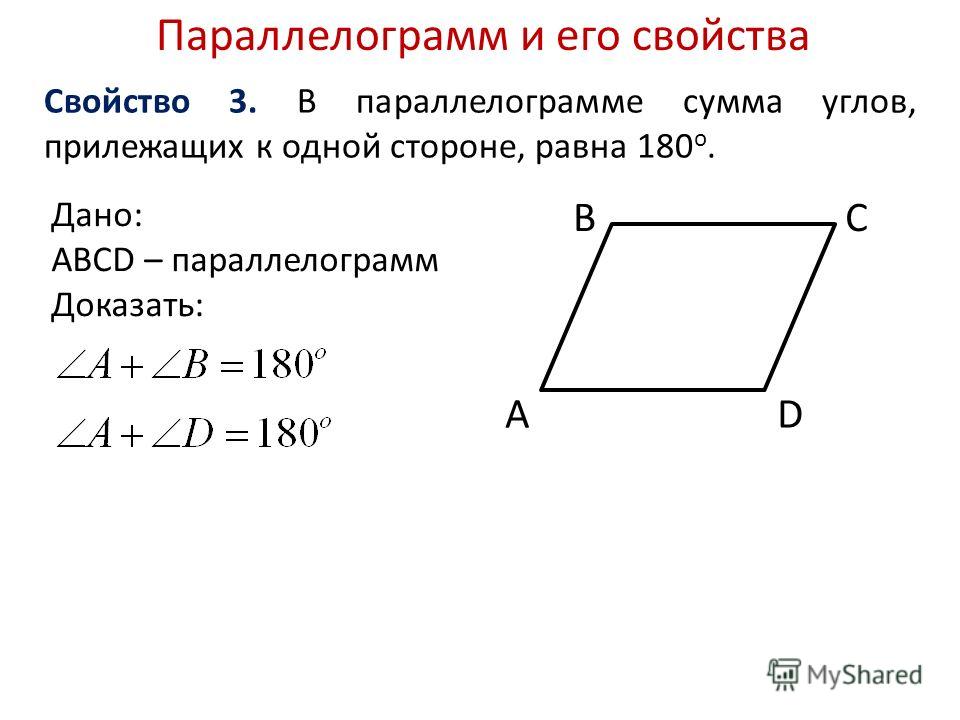
[Изображение будет загружено в ближайшее время]
Периметр равен 2 (длина основания + сторона):
Периметр = 2 (b+s)
Решено Пример:
Параллелограмм имеет основание 10 см и сторону длина 5 см, чему равен его периметр?
Периметр = 2 × (10 см + 5 см) = 2 × 15 см = 30 см
Внутренние углы параллелограмма иногда, всегда или никогда не составляют в сумме 360 градусов?
Геометрия
Наука
- Анатомия и физиология
- астрономия
- Астрофизика
- Биология
- Химия
- науки о Земле
- Наука об окружающей среде
- Органическая химия
- Физика
Математика
- Алгебра
- Исчисление
- Геометрия
- Преалгебра
- Предварительный расчет
- Статистика
- Тригонометрия
Гуманитарные науки
- Английская грамматика
- История США
- Всемирная история
- Сократическая мета
- Избранные ответы
.
 .. и не только
.. и не толькоТемы
Влияние этого вопроса
1967 просмотров по всему миру
Вы можете повторно использовать этот ответ
Лицензия Creative Commons
Решения NCERT для математики класса 8, глава 3
- Решения НЦЭРТ
- Класс 8
- Математика
- понимание четырехугольников
Математика NCERT 8 класс, Глава 3: Понимание четырехугольников — Различные разновидности кривых уже обсуждались на предыдущих занятиях.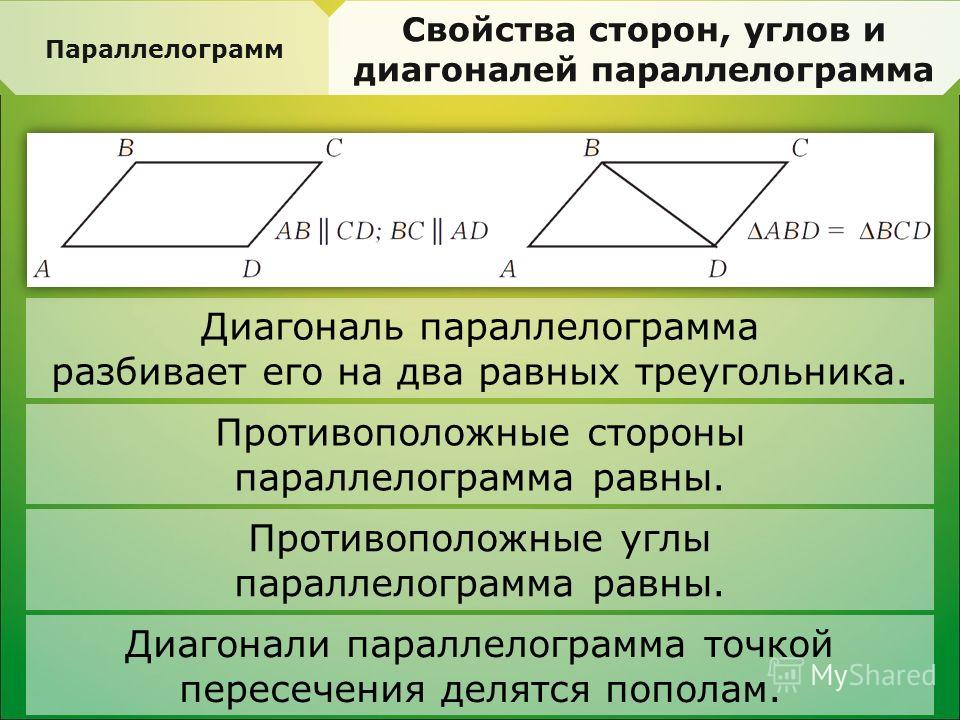 Начиная с многоугольников глава переходит к теме классификация многоугольников .
Начиная с многоугольников глава переходит к теме классификация многоугольников .
- Разница между многоугольными кривыми и неполигональными кривыми поясняется с помощью диаграммы.
- Многоугольники классифицируются по количеству сторон (или вершин ). Классификация поясняется с помощью подходящих цифр в таблице, приведенной в разделе 3.2.1. Студенты должны понимать эту концепцию и помнить данные классификации.
- Диагональ — это отрезок линии , соединяющий две непоследовательные вершины многоугольника .
После этого обсуждаются Выпуклый и вогнутый многоугольник . Прежде чем перейти к свойству суммы углов , учащиеся узнают о правильных и неправильных многоугольниках .
- Правильный многоугольник является одновременно равноугольным и равносторонним.
- Прямоугольник является равноугольным , но не равносторонним.
- Квадрат имеет стороны равные длины и углов равных мер, поэтому он считается правильным многоугольником .
- Говоря о свойстве суммы углов ; Свойство суммы углов утверждает, что сумма мер трех углов треугольника это 180° .
После прохождения вводного раздела учащимся по рассмотренным выше темам необходимо решить задачи упражнения 3.1.
Сумма внешних углов многоугольника — еще одна тема, которая будет обсуждаться в этой главе.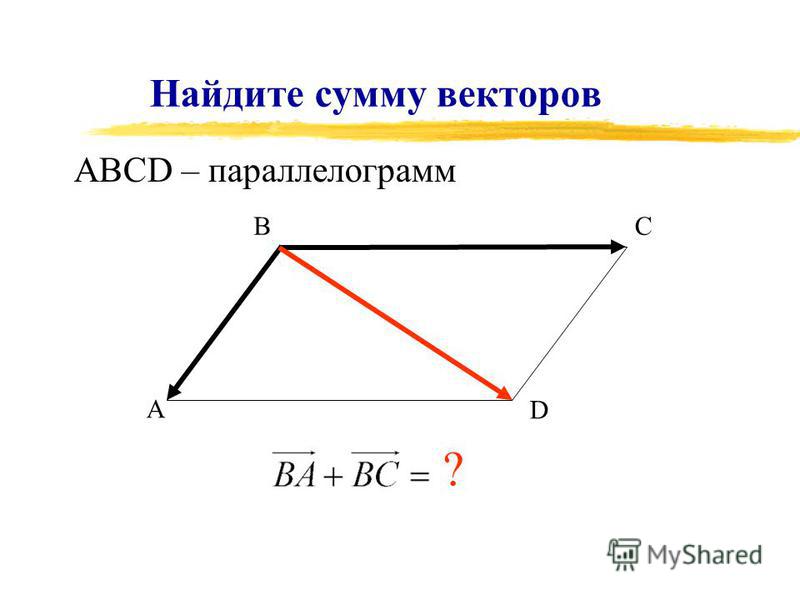
- Сумма мер внешних углов любого многоугольника равна 360° .
Различные виды четырехугольников объясняются как трапеция , параллелограмм и т. д. Следует отметить, что воздушный змей также является особым типом четырехугольника . Также обсуждаются углы параллелограмма и некоторых специальных параллелограммов .
- Противолежащие углы параллелограмма имеют одинаковую величину.
- Краткое примечание о диагонали параллелограмма дано, что вообще диагонали параллелограмма — это , а не из равной длины .
- В этом разделе перечислены некоторые специальные параллелограммы , такие как ромб , квадрат и прямоугольник .

- Свойства всех четырехугольников являются важной частью этой главы. Студенты должны изучить все перечисленные свойства.
Всего в этой главе 4 упражнения.
В конце концов, Тема То, что мы обсуждали до сих пор, дано в этой теме, обсуждаются все важные ключевые моменты главы.
Страница № 41:
Вопрос 1:
Дано здесь какие-то фигуры.
(1) | (2) | (3) |
(4) | (5) | (6) |
(7) | (8) |
Классифицировать
каждого из них на основании следующего.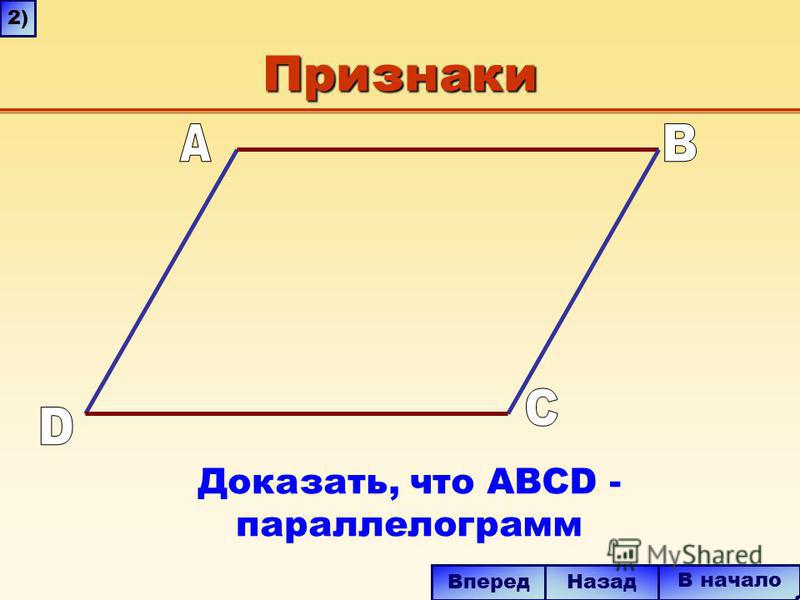
(а) Простая кривая
(б) Простая замкнутая кривая
(в) Многоугольник
(г) Выпуклость многоугольник
(e) Вогнутый многоугольник
Ответ:
(а) 1, 2, 5, 6, 7
(б) 1, 2, 5, 6, 7
(в) 1, 2
(г) 2
(д) 1
Страница № 41:
Вопрос 2:
Сколько диагонали имеет каждый из следующих?
(а) А выпуклый четырехугольник
(б) А правильный шестигранник
(c) A треугольник
Ответ:
(a) Там 2 диагонали в выпуклом четырехугольнике.
(б) Есть в правильном шестиугольнике 9 диагоналей.
(в) А в треугольнике нет ни одной диагонали.
Страница № 41:
Вопрос 3:
Что сумма мер ангелов выпуклого четырехугольника? Будет ли выполняться это свойство, если четырехугольник невыпуклый? (Сделать невыпуклый четырехугольник и попробуйте!)
Ответ:
Сумма
градусная мера углов выпуклого четырехугольника равна 360°, т. выпуклый четырехугольник состоит из двух треугольников.
выпуклый четырехугольник состоит из двух треугольников.
Здесь, ABCD представляет собой выпуклый четырехугольник, составленный из двух треугольников ΔABD и ΔBCD. Следовательно, сумма все внутренние углы этого четырехугольника будут равны сумма всех внутренних углов этих двух треугольников, то есть 180º + 180º = 360º
Да, это свойство верно и для четырехугольника, который не является выпуклым. Это потому, что любой четырехугольник можно разделить на два треугольника.
Здесь опять же, ABCD — вогнутый четырехугольник, составленный из двух треугольников ΔABD и ΔBCD. Таким образом, сумма все внутренние углы этого четырехугольника также будут равны 180º + 180º = 360º
Страница № 41:
Вопрос 4:
Изучить Таблица. (Каждая фигура разделена на треугольники и сумма углы, выведенные из этого.)
Рисунок | ||||
Боковой | 3 | 4 | 5 | 6 |
Сумма углов | 180° | 2 × 180° = (4 − 2) × 180° | 3 × 180° = (5 − 2) × 180° | 4 × 180° = (6 − 2) × 180° |
Что может Вы говорите о сумме углов выпуклого многоугольника с количеством сторон?
(а) 7
(б) 8
(в) 10
(г) п
Ответ:
Из
таблицы можно заметить, что сумма углов выпуклого многоугольника n сторона равна ( n −2) × 180º. Следовательно, сумма углов
выпуклых многоугольников, имеющих указанное выше число сторон, будет таким
следует.
Следовательно, сумма углов
выпуклых многоугольников, имеющих указанное выше число сторон, будет таким
следует.
(а) (7 — 2) × 180º = 900°
(б) (8 − 2) × 180º = 1080°
(в) (10 − 2) × 180º = 1440°
(г) ( n − 2) × 180°
Страница № 42:
Вопрос 5:
Что такое правильный многоугольник?
Укажите имя правильного многоугольника
(i) 3 стороны
(ii) 4 стороны
(iii) 6 стороны
Ответ:
Многоугольник с равными сторонами и равными углами называется правильным многоугольником.
(i) Равносторонний Треугольник
(ii) Квадрат
(iii) Обычный Шестигранник
Страница № 42:
Вопрос 6:
Найдите величину угла x на следующих рисунках.
(а) | (б) |
(с) | (г) |
Ответ:
(a)
Сумма мер всех внутренних углов четырехугольника равна
360º. Therefore, in the given quadrilateral,
Therefore, in the given quadrilateral,
50° + 130° + 120° + x = 360°
300° + x = 360°
x = 60°
(b)
Из рисунка можно сделать вывод, что
90º + a = 180º (Линейная пара)
a = 180º − 90º = 90º
Сумма мер всех внутренних углов четырехугольника равна 360º. Следовательно, в данном четырехугольнике
60° + 70° + х + 90° = 360°
220° + х = 360°
x = 140°
(в)
Из рисунка можно сделать вывод, что
70 + a = 180° (Линейная пара)
3 9
b = 120°
Therefore, in the given pentagon,
120° + 110° + 30° + x + x = 540°
260° + 2 x = 540°
2 x = 280°
x = 140°
(d)
Сумма всех внутренних углов пятиугольника равна 540°.
5 x = 540°
x = 108°
Страница № 42:
Вопрос 7:
(а) найти х + y + z
(б) найти х + y + z + w
Ответ:
(a) x + 90° = 180° (Линейная пара)
х = 90°
z + 30° = 180° (Линейная пара)
z = 150°
y = 90° + 30° (теорема о внешнем угле)
y = 120°
x + y + z = 90° + 120° + 150° = 360°
(б)
Сумма мер всех внутренних углов четырехугольника равна
360º. Следовательно, в данном четырехугольнике
Следовательно, в данном четырехугольнике
a + 60° + 80° + 120° = 360°
а + 260° = 360°
a = 100°
x + 120° = 180° (Линейная пара)
х = 60°
y + 80° = 180° (Линейная пара)
г = 100°
z + 60° = 180° (Линейная пара)
z = 120°
w + 100° = 180° (линейная пара)
ш = 80°
Сумма мер всех внутренних углов = х + у + г + ш
= 60° + 100° + 120° + 80°
= 360°
Страница № 44:
Вопрос 1:
Найти x на следующих рисунках.
(а) | (б) |
Ответ:
Мы знаем
что сумма всех внешних углов любого многоугольника равна 360º.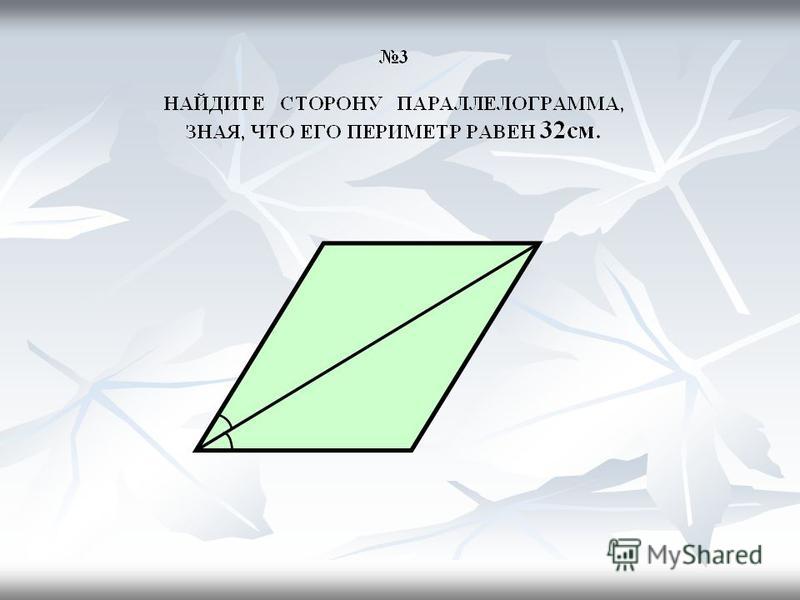
(а) 125° + 125° + x = 360°
250° + х = 360°
х = 110°
(б)
60° + 90° + 70° + x + 90° = 360°
310° + х = 360°
x = 50°
Страница № 44:
Вопрос 2:
Найдите мера каждого внешнего угла правильного многоугольника
(и) 9 стороны
(ii) 15 сторон
Ответ:
(i) Сумма все внешние углы данного многоугольника = 360º
Каждый внешний угол правильного многоугольника имеет одинаковую меру.
Таким образом, мера каждого внешнего угла правильного многоугольника с 9 сторонами
знак равно
(ii) Сумма всех внешних углов данного многоугольника = 360º
Каждый внешний угол правильного многоугольника имеет одинаковую меру.
Таким образом, мера каждого внешнего угла правильного многоугольника с 15 сторонами
знак равно
Страница № 44:
Вопрос 3:
Сколько сторон у правильного многоугольника, если внешний угол равен 24°?
Ответ:
Сумма всех внешних углов данного многоугольника = 360º
Размер каждого внешнего угла = 24º
Таким образом, количество сторон правильного многоугольника
Q.
 No.: 3)
No.: 3)NCERT Решение для 8 класса по математике — понимание четырехугольников 44 , Вопрос 3
Страница № 44:
Вопрос 4:
Как сколько сторон имеет правильный многоугольник, если каждый из его внутренних углов 165°?
Ответ:
Мера каждый внутренний угол = 165°
Мера каждый внешний угол = 180° − 165° = 15°
Сумма все внешние углы любого многоугольника равны 360º.
Таким образом, количество сторон многоугольника
Страница № 44:
Вопрос 5:
а) Возможен ли правильный многоугольник с мерой каждого внешний угол равен 22°?
(б) Банка внутренний угол правильного многоугольника? Почему?
Ответ:
Сумма все внешние углы всех многоугольников равны 360º. Также в обычном многоугольника, все внешние углы имеют одинаковую величину. Следовательно, если 360º является кратным заданному внешнему углу, то данный полигон будет возможен.
(а) Внешний вид угол = 22°
360º не является кратным 22º. Следовательно, такой многоугольник
это невозможно.
Следовательно, такой многоугольник
это невозможно.
(б) Интерьер угол = 22°
Внешний угол = 180° − 22° = 158°
Такой многоугольник невозможен, так как 360° не является идеальным кратным 158°.
Страница № 44:
Вопрос 6:
(a) Какой минимальный внутренний угол возможен для правильного многоугольника?
(b) Каков максимальный внешний угол правильного многоугольника?
Ответ:
Рассмотрим правильный многоугольник с наименьшим возможным числом сторон (т. е. равносторонний треугольник). Внешний угол этого треугольника будет максимальным внешним углом, возможным для любого правильного многоугольника.
Внешний угол равностороннего треугольника
Следовательно, максимально возможная мера внешнего угла любого многоугольника равна 120º. Кроме того, мы знаем, что внешний угол и внутренний угол всегда находятся в линейной паре.
Следовательно, минимальный внутренний угол = 180° − 120° = 60°
Страница № 50:
Вопрос 1:
Учитывая
параллелограмм АВСD. Дополните каждое утверждение вместе с определением
или используемое имущество.
Дополните каждое утверждение вместе с определением
или используемое имущество.
(i) AD = …
(ii) ∠DCB = …
(iii) ОС = …
(iv) м ∠DAB + м ∠CDA = …
Ответ:
(i) В параллелограмм, противоположные стороны равны по длине.
AD = BC
(ii) В параллелограмм, противоположные углы равны.
∠DCB = ∠DAB
(iii) В параллелограмм, диагонали которого делят пополам.
Следовательно, OC = OA
(iv) В a параллелограмм, смежные углы дополняют друг друга.
Следовательно, м ∠DAB + m ∠CDA =180°
Страница № 51:
Вопрос 2:
Рассмотреть следующие параллелограммы. Найдите значения неизвестных х , и , z .
(и) | (ii) |
(iii) | (iv) |
(в) |
Ответ:
(i) х + 100° = 180° (смежные углы дополнительные)
х = 80°
z = x = 80º(Противоположные углы равны)
y = 100° (Противоположные углы равны)
(ii) 50° + y = 180° (Смежные углы дополнительные)
y = 130°
x = y = 130° (Противоположные углы равны)
z = x = 130° (соответствующие углы)
(iii) x = 90° (вертикально противоположные углы)
x + y + 30° = 180° (Свойство суммы углов треугольников)
120° + y = 180°
г = 60°
z = y = 60° (чередующиеся внутренние углы)
(iv) z = 80° (соответствующие углы)
y = 80° (Противоположные углы равны)
x+ y = 180° (Смежные углы дополнительные)
x = 180° − 80° = 100°
(v) y = 112° (Противоположные углы равны)
x+ y + 40° = 180° (свойство суммы углов треугольников)
х + 112° + 40° = 180°
х + 152° = 180°
х = 28°
z = x = 28° (Чередующиеся внутренние углы)
Страница № 51:
Вопрос 3:
Может ли четырехугольник ABCD быть параллелограммом, если
(i) ∠D + ∠B = 180°?
(ii) AB = DC = 8 см, AD = 4 см и BC = 4,4 см?
(iii) ∠А = 70° и ∠С = 65°?
Ответ:
(i) Для ∠D + ∠B
= 180°, четырехугольник ABCD может быть параллелограммом, а может и не быть. Наряду с этим условием должны быть также следующие условия.
выполнено.
Наряду с этим условием должны быть также следующие условия.
выполнено.
Сумма мер смежных углов должна быть 180º.
Противоположные углы также должны быть одинаковой величины.
(ii) № Противоположные стороны AD и BC имеют разную длину.
(iii) № Противолежащие углы А и С имеют разную величину.
Страница № 51:
Вопрос 4:
Розыгрыш грубая фигура четырехугольника, который не является параллелограммом, но имеет ровно два противоположных угла равной величины.
Ответ:
Здесь, четырехугольник ABCD (воздушный змей) имеет два внутренних угла ∠B и ∠D тех же размеров. Тем не менее, четырехугольник ABCD не является параллелограммом, так как меры оставшейся пары противоположных углов, ∠A и ∠C не равны.
Страница № 51:
Вопрос 5:
меры двух смежных углов параллелограмма относятся друг к другу 3:2. Найдите величину каждого из углов параллелограмма.
Ответ:
Пусть
меры двух смежных углов, ∠A
и ∠B параллелограмма
ABCD находятся в соотношении 3:2. Пусть ∠A
= 3 x и ∠B = 2 x
Пусть ∠A
= 3 x и ∠B = 2 x
Мы знаем что сумма мер смежных углов равна 180º для параллелограмм.
∠А + ∠B = 180º
3 x + 2 x = 180º
5 x = 180º
∠А = ∠C = 3 x = 108º (Противоположные углы)
∠B = ∠D = 2 х = 72º (Противоположные углы)
Таким образом, меры углов параллелограмма 108º, 72º, 108º и 72º.
Страница № 51:
Вопрос 6:
Два смежные углы параллелограмма равны. Найди мера каждого из углов параллелограмма.
Ответ:
Сумма смежные углы = 180°
∠A + ∠В = 180º
2∠А = 180º (∠А = ∠В)
∠А = 90º
∠B = ∠А = 90º
∠С = ∠A = 90º (Противоположный углы)
∠D = ∠B = 90º (Противоположный углов)
Таким образом, каждый угол параллелограмма равен 90º.
Страница № 51:
Вопрос 7:
Соседняя фигура НАДЕЖДА является параллелограммом. Найдите угол x , y и z . Укажите свойства, которые вы используете, чтобы найти их.
Укажите свойства, которые вы используете, чтобы найти их.
Ответ:
y = 40 ° (альтернативные внутренние углы)
70 ° = z + 40º (соответствующие углы)
70 ° — 40 ° = Z
70 ° — 40 ° = Z
70 ° — 40 ° = .
x + ( z + 40º) = 180° (Adjacent pair of angles)
x + 70º = 180°
x = 110°
Video Solution for understanding quadrilaterals (Page : 51 , Q.№: 7)
NCERT Решение для 8 класса по математике — понимание четырехугольников 51 , Вопрос 7
Страница № 51:
Вопрос 8:
следующие рисунки GUNS и RUNS являются параллелограммами. Найдите х и и . (Длина указана в см)
(и) | (ii) |
Ответ:
(i) Мы знаем, что длины противоположных сторон
параллелограмм равны между собой.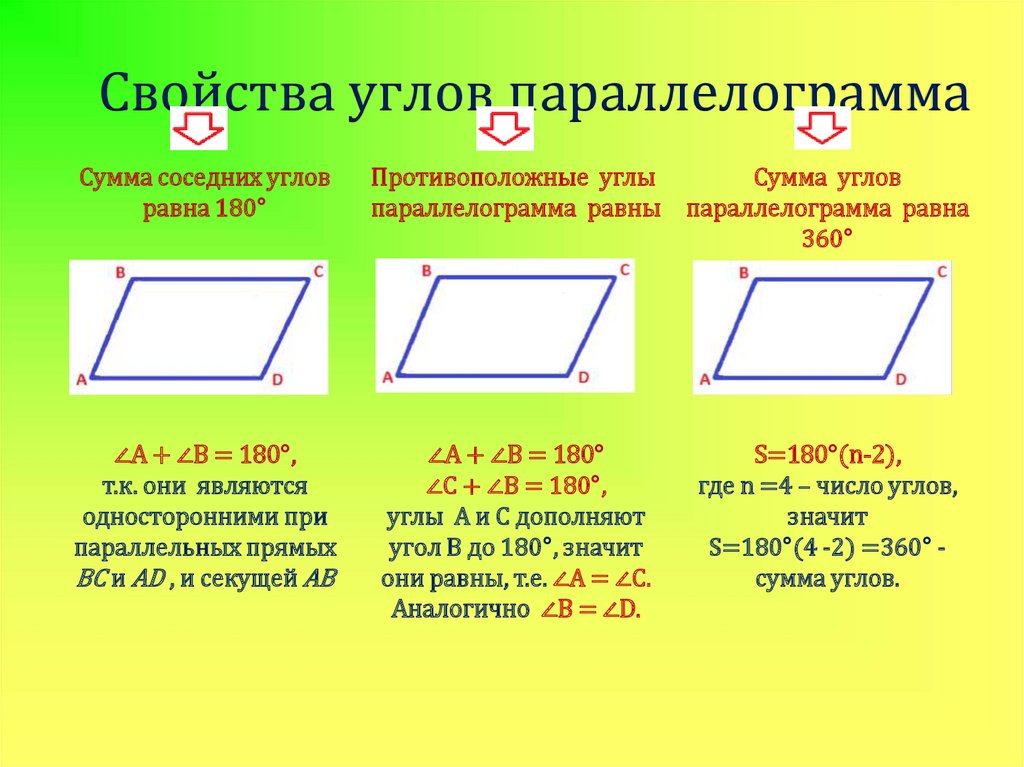
ГУ = серийный номер
3 г — 1 = 26
3 y = 27
г = 9
СГ = НУ
3 х = 18
х = 6
Следовательно, размеры x и y равны 6 см и 9 см. соответственно.
(ii) Мы знаем, что диагонали параллелограмма делят каждую пополам. Другой.
г + 7 = 20
г = 13
х + у = 16
х + 13 = 16
х = 3
Следовательно, размеры x и y равны 3 см и 13 см. соответственно.
Страница № 51:
Вопрос 9:
На приведенном выше рисунке и РИСК, и ПОДСКАЗКА являются параллелограммами. Найдите значение x .
Ответ:
Смежные углы параллелограмма дополнительные.
В параллелограмме РИСК, ∠RKS + ∠ISK = 180°
120° + ∠ISK = 180°
∠ISK = 60°
Также противоположные углы параллелограмма равны.
В параллелограмме CLUE ∠ULC = ∠CEU = 70°
Сумма мер всех внутренних углов треугольника равна 180º.
x + 60° + 70° = 180°
x = 50°
Видео Решение для понимания четырехугольников (Страница: 51, Q.№: 9)
8 NCERT Class Solution for math — понимание четырехугольников 51 , вопрос 9Страница № 52:
Вопрос 10:
Объяснить как эта фигура является трапецией. Какие из двух его сторон параллельны?
Ответ:
Если поперечная прямая пересекает две данные прямые такие, что сумма градусная мера углов по одну сторону от поперечной равна 180º, то данные две прямые будут параллельны друг другу.
Здесь, ∠NML + ∠MLK = 180°
Следовательно, NM||LK
As четырехугольник KLMN имеет пару параллельных прямых, следовательно, является трапеция.
Страница № 52:
Вопрос 11:
Найти m ∠C на следующем рисунке, если
Ответ:
Дано что,
∠Б + ∠C = 180° (Углы на на той же стороне поперечной)
120º + ∠С = 180°
∠С = 60°
Страница № 52:
Вопрос 12:
Найдите
мера ∠P и ∠S,
если на следующем рисунке. (Если вы найдете м ∠R,
есть ли более одного способа найти м ∠P?)
(Если вы найдете м ∠R,
есть ли более одного способа найти м ∠P?)
Ответ:
∠P + ∠Q = 180° (Углы на той же стороне поперечной)
∠P + 130° = 180°
∠P = 50°
∠R + ∠S = 180° (Углы на той же стороне поперечной)
90° + ∠R = 180°
∠Ю = 90°
Да. Там это еще один способ найти меру м ∠P.
м ∠R и м ∠Q. Найдя м ∠S, свойство суммы углов четырехугольника можно применить, чтобы найти м ∠П.
Страница № 55:
Вопрос 1:
Штат будь то Истина или Ложь.
(а) Все прямоугольники это квадраты.
(б) Все ромбы — параллелограммы.
(в) Все квадраты — это ромбы, а также прямоугольники.
(г) Все квадраты не параллелограммы.
(д) Все воздушные змеи — это ромбы.
(е) Все ромбы — воздушные змеи.
(ж) Все параллелограммы это трапеции.
(ч) Все квадраты это трапеции.
Ответ:
(а) Неверно. Все квадраты являются прямоугольниками, но не все прямоугольники являются квадратами.
Все квадраты являются прямоугольниками, но не все прямоугольники являются квадратами.
(б) Верно. Противоположные стороны ромба равны и параллельны друг другу.
(с) Верно. Все квадраты ромбы, так как все стороны квадрата равные длины. Все квадраты также являются прямоугольниками, так как каждый внутренний угол измеряет 90°.
(г) Неверно. Все квадраты параллелограммы, так как противоположные стороны равны и параллельно.
(e) Неверно. У воздушного змея не все стороны одинаковой длины.
(е) Верно. У ромба также есть две различные последовательные пары сторон. равной длины.
(ж) Верно. Все параллелограммы имеют пару параллельных сторон.
(ч) Верно. Все квадраты имеют пару параллельных сторон.
Страница № 55:
Вопрос 2:
Идентифицировать все четырехугольники, у которых
(а) четыре стороны одинаковой длины
(b) четыре прямые углы
Ответ:
(а) Ромб
и Квадрат — четырехугольники, у которых 4 стороны одинаковой длины.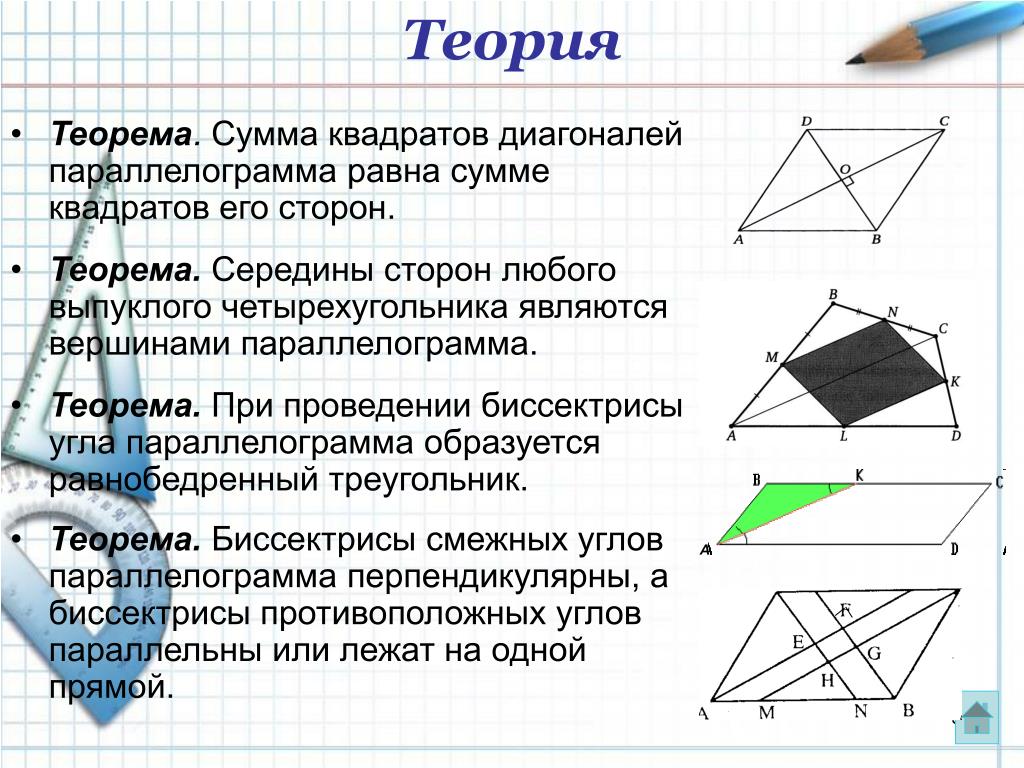
(б) Квадрат а прямоугольник — это четырехугольники, у которых 4 прямых угла.
Страница № 55:
Вопрос 3:
Объяснить как квадрат.
(и) а четырехугольник
(ii) а параллелограмм
(iii) а ромб
(iv) а прямоугольник
Ответ:
(i) A квадрат является четырехугольником, так как у него четыре стороны.
(ii) А квадрат является параллелограммом, так как его противоположные стороны параллельны друг друга.
(iii) А квадрат является ромбом, так как его четыре стороны имеют одинаковую длину.
(iv) А квадрат является прямоугольником, так как каждый внутренний угол равен 90°.
Страница № 55:
Вопрос 4:
Имя четырехугольники, диагонали которых.
(i) делить пополам друг друга
(ii) являются перпендикулярные биссектрисы друг к другу
(iii) равно
Ответ:
(i) Диагонали параллелограмма, ромба, квадрата и прямоугольника
делят друг друга пополам.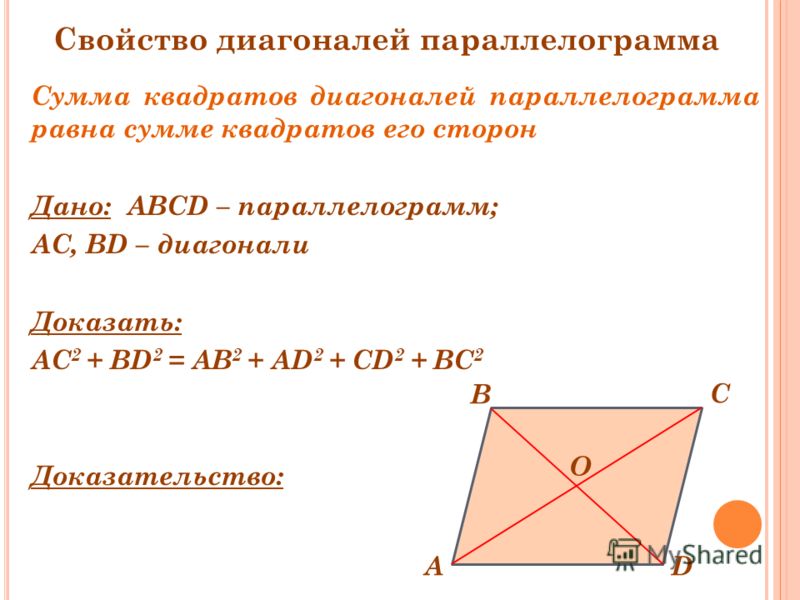
(ii) диагонали ромба и квадрата действуют как серединные перпендикуляры.
(iii) диагонали прямоугольника и квадрата равны.
Страница № 55:
Вопрос 5:
Объяснить почему прямоугольник является выпуклым четырехугольником.
Ответ:
В прямоугольника, есть две диагонали, обе лежат внутри прямоугольника. прямоугольник. Следовательно, это выпуклый четырехугольник.
Страница № 55:
Вопрос 6:
ABC – прямоугольный треугольник, а O – середина стороны, противоположной прямому углу. Объясните, почему O равноудалено от A, B и C. (Штриховые линии нарисованы дополнительно, чтобы помочь вам).
Ответ:
Проведите прямые AD и DC так, чтобы AD||BC, AB||DC
AD = BC, AB = DC
ABCD – прямоугольник, противоположные стороны которого равны и параллельны друг другу и все внутренние углы равны 90 градусов.
Диагонали прямоугольника имеют одинаковую длину и делят друг друга пополам.
Следовательно, AO = OC = BO = OD
Таким образом, O равноудалена от A, B и C.0413
NCERT Решение для 8-го класса по математике — понимание четырехугольников 55 , Вопрос 6
11 Примеры параллелограмма в реальной жизни — StudiousGuy
Параллелограмм — это четырехугольник, состоящий из двух пар сторон, которые взаимно параллельны друг другу и равны по длине. Площадь параллелограмма можно получить, вычислив произведение его основания на высоту, где основанием является одна из параллельных сторон, а высота соответствует высоте, проведенной от одного угла к основанию многоугольника. Периметр, т. е. длина внешней границы параллелограмма, в два раза больше суммы длин его смежных сторон. Простыми словами, параллелограмм — это прямоугольник, который растягивают, удерживая его противоположные углы.
Индекс статьи (щелкните, чтобы перейти)
Свойства параллелограмма 1. Противоположные стороны параллелограмма параллельны и равны по длине.
2. Противоположные углы параллелограмма равны.
3. Сумма смежных углов параллелограмма равна 180°. Следовательно, смежные углы параллелограмма являются дополнительными.
4. Если какой-либо из углов параллелограмма прямой, то остальные углы будут равны 90° каждый. В таком случае результирующая геометрическая фигура называется прямоугольником.
5. Диагонали параллелограмма делят друг друга пополам.
6. Два треугольника, образованные соединением противоположных углов параллелограмма, конгруэнтны друг другу.
7. Сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей. Это соотношение известно как закон параллелограмма.
Примеры параллелограмма1. Плитка
Плитка бывает разных форм и размеров. Наиболее популярными формами, используемыми в промышленности для производства настенной и напольной плитки, являются прямоугольник, квадрат, ромб и параллелограмм. Следовательно, плитка представляет собой прекрасный пример предметов в форме параллелограмма, используемых в повседневной жизни.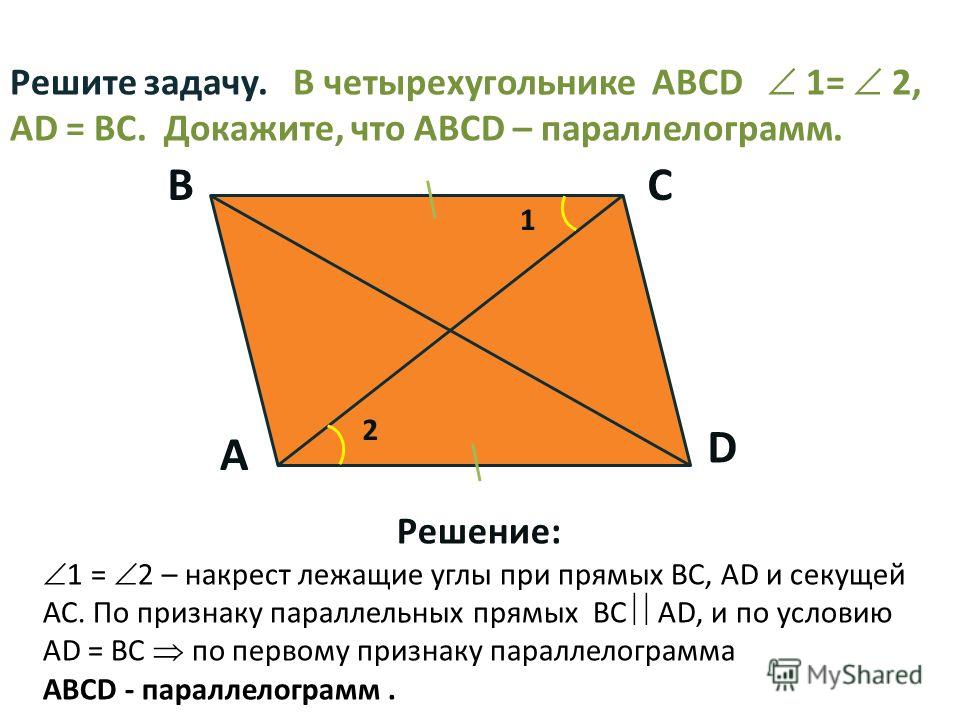
2. Здания
В современном мире архитекторы используют ряд геометрических фигур для строительства зданий с уникальным дизайном. Одной из самых популярных геометрических фигур, используемых строителями при возведении зданий, является параллелограмм. Например, офисное здание дока, расположенное в Гамбурге, Германия, имеет форму параллелограмма.
3. Крыши
Если вы посмотрите сбоку на двускатную крышу, солончаковую или односкатную крышу дома, вы можете легко визуализировать двухмерный геометрический плоский четырехугольник, состоящий из двух пар параллельных и равных стороны. Следовательно, крыши являются ярким примером объектов в форме параллелограмма, присутствующих вокруг нас.
4. Бумага
Бумага для рукоделия, используемая для изготовления артефактов, доступна в различных формах и размерах. Одной из наиболее распространенных форм бумаги для рукоделия является параллелограмм. Следовательно, это еще один пример объектов в форме параллелограмма, присутствующих вокруг нас.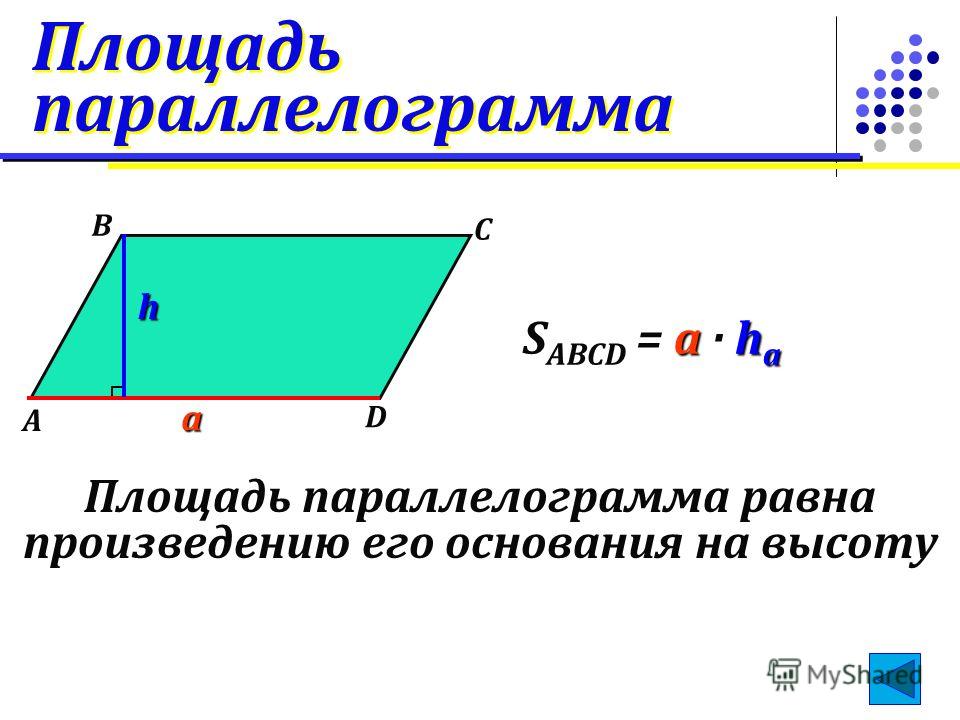
5. Столы
Столы обычно имеют прямоугольную или квадратную форму. Прямоугольный стол состоит из двух пар параллельных сторон, имеющих одинаковую длину. Следовательно, прямоугольник также является параллелограммом. По этой причине прямоугольные столы также являются ярким примером предметов в форме параллелограмма, используемых в повседневной жизни.
6. Ластики
Ряд канцелярских принадлежностей и школьных принадлежностей имеет форму параллелограмма. Например, большинство ластиков, которые мы используем в повседневной жизни, имеют форму параллелограмма.
7. Солнечные панели
Солнечные панели обычно изготавливаются двух популярных геометрических форм, а именно прямоугольника и параллелограмма. Обычно предпочтение отдается солнечным панелям в форме параллелограмма, поскольку их легко прикрепить к боковым сторонам односкатных крыш домов. Следовательно, солнечные панели являются ярким примером объектов в форме параллелограмма, используемых в повседневной жизни.
8. Полосатый стержень
Стержень, раскрашенный широкими косыми цветными полосами, представляет собой прекрасный пример параллелограмма. Если внимательно наблюдать за граничными линиями наклонной полосы, нарисованной на шесте, она образует четырехугольник, очень похожий на вытянутый прямоугольник. Следовательно, это еще один пример формы параллелограмма, встречающейся в повседневной жизни.
9. Ступени лестницы Случай
Если внимательно посмотреть на форму ступеней лестницы, то можно легко представить себе параллелограмм. Следовательно, ступени лестницы представляют собой яркий пример объектов в форме параллелограмма, присутствующих вокруг нас.
10. Рисунок на кардигане
Рисунок на кардигане и свитере, как правило, представляет собой причудливое сочетание различных геометрических фигур. Одной из популярных геометрических фигур, используемых чулочно-носочной и трикотажной промышленностью для проектирования шерстяной одежды, является параллелограмм.
11. Структура грифа гитары
Если вы посмотрите на гриф гитары, вы увидите определенные маркерные точки на ладах под номерами 3, 5, 7, 9, 12, 15, 17. , 19, 21 и 24. Иногда маркерные точки заменяются полосами. Эти стержни обычно имеют форму параллелограмма. Следовательно, форму параллелограмма можно легко определить в реальной жизни, взглянув на маркеры на грифе гитары.
чему равна сумма параллелограмма
Вы просматриваете статью: чему равна сумма параллелограмма на audreysalutes.com
какова сумма параллелограмма
В параллелограмме четыре внутренних угла и сумма внутренних углов параллелограмма параллелограмм всегда равен 360°. Противолежащие углы параллелограмма равны, а смежные углы параллелограмма попарно смежны.
Все ли параллелограммы в сумме дают 180?
Важными свойствами углов параллелограмма являются: … Противоположные углы параллелограмма равны (или конгруэнтны) Смежные углы являются дополнительными углами друг к другу (это означает, что их сумма составляет 180 градусов)
Параллелограмм равен 180?
Следовательно, сумма любых двух смежных углов параллелограмма равна 180°. Следовательно, доказано, что любые два смежных или следующих друг за другом угла параллелограмма являются дополнительными.
Следовательно, доказано, что любые два смежных или следующих друг за другом угла параллелограмма являются дополнительными.
Все ли углы параллелограмма равны 360?
Сумма всех углов треугольника равна 180?
Какие углы в сумме дают 360?
Сумма углов вокруг точки всегда составляет 360 градусов.
Параллелограмм дает в сумме 360?
Объяснение: Параллелограммы имеют углы в 360 градусов, но также имеют совпадающие пары углов на концах диагоналей.
Параллелограмм дает в сумме 180 или 360?
Объяснение: Параллелограммы имеют углы, составляющие 360 градусов, но также имеют совпадающие пары углов на концах диагоналей. Поэтому 2 дополнительных угла должны совпадать с 2 указанными в вопросе.
Что в сумме дают все параллелограммы?
Объяснение: На этот вопрос очень просто ответить, если помнить, что ВСЕ паралеллограммы имеют две пары равных и противоположных углов, и что сумма четырех углов в любом четырехугольнике ДОЛЖНА составлять 360 градусов.
Четырехугольники в сумме дают 180?
Четырехугольники составлены из двух треугольников. … Поскольку мы знаем, что сумма внутренних углов треугольника равна 180°, отсюда следует, что сумма внутренних углов четырехугольника равна 360°.
Все ли углы параллелограмма равны 90 градусов?
Параллелограмм можно определить как четырехугольник, две стороны которого параллельны друг другу, а все четыре угла при вершинах не равны 90 градусам или прямым углам, тогда четырехугольник называется параллелограммом. Если один угол равен 90 градусов, то все остальные углы также равны 90 градусов. …
Параллелограммы в сумме дают 180?
Важными свойствами углов параллелограмма являются: … Противоположные углы параллелограмма равны (или конгруэнтны) Смежные углы являются дополнительными углами друг к другу (это означает, что их сумма составляет 180 градусов)
Что делает 4-сторонний параллелограмм добавить к?
Правильный ответ: На этот вопрос очень просто ответить, если помнить, что ВСЕ паралеллограммы имеют две пары равных и противоположных углов, и что четыре угла в любом четырехугольнике ДОЛЖНЫ составлять в сумме 360 градусов.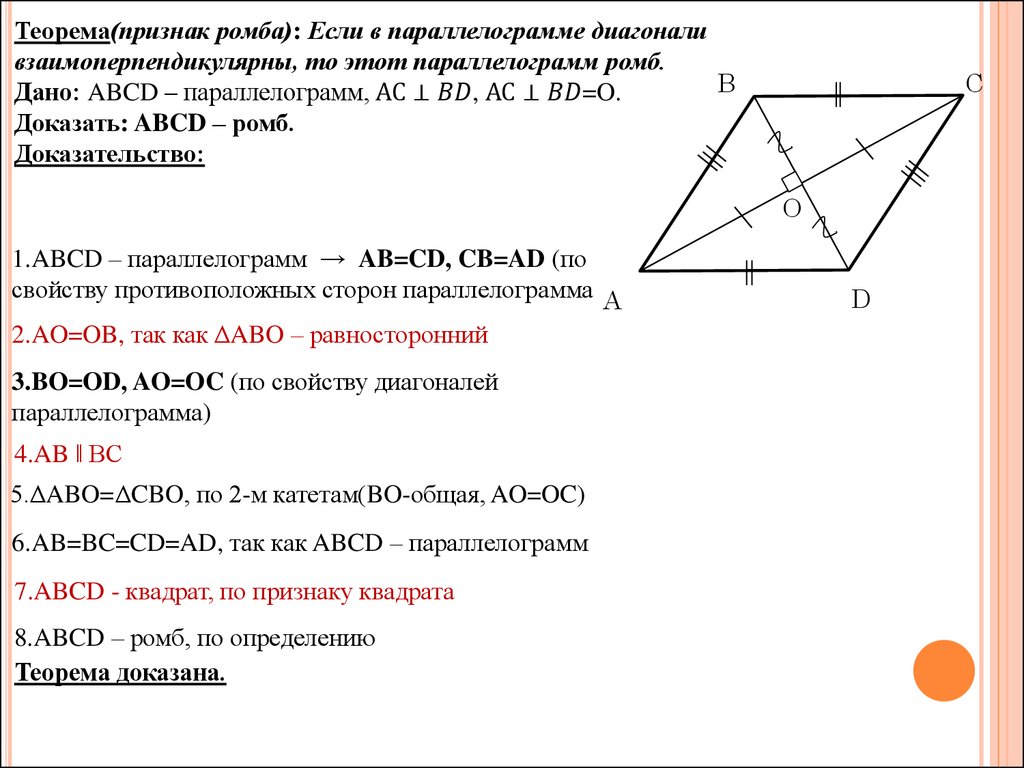
Параллелограммы в сумме дают 180?
Важными свойствами углов параллелограмма являются: … Противоположные углы параллелограмма равны (или конгруэнтны) Смежные углы являются дополнительными углами друг к другу (это означает, что их сумма составляет 180 градусов)
Являются ли все 4 стороны равные параллелограммы?
Параллелограмм – это параллелограмм, у которого противоположные стороны равны (одинаковые) и противоположные углы равны. 4 равные стороны являются квадратами или ромбами, поэтому они параллелограммы, но не все параллелограммы являются квадратами или ромбами. Не обязательно. Противоположные стороны должны быть равны, но не смежные стороны.
Чему равна сумма четырех углов параллелограмма?
В параллелограмме четыре внутренних угла, а сумма внутренних углов параллелограмма всегда равна 360°. Противолежащие углы параллелограмма равны, а смежные углы параллелограмма попарно смежны.
Чему равна сумма четырехстороннего параллелограмма?
Обратите внимание, что каждая фигура имеет четыре прямые стороны и четыре угла.


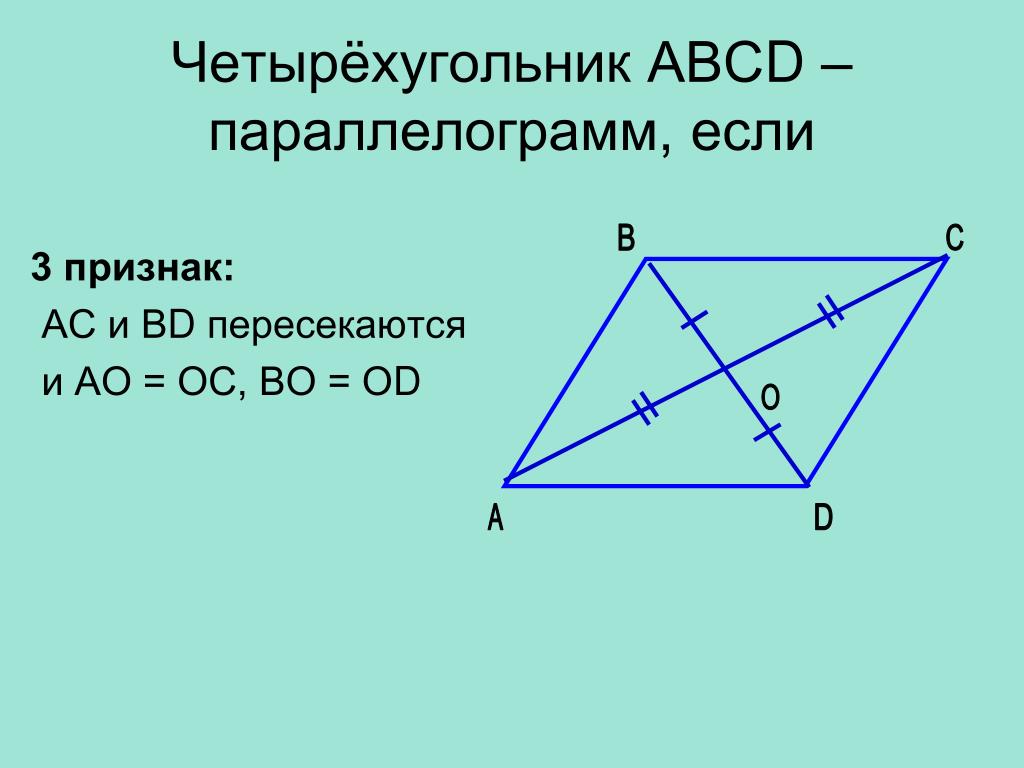
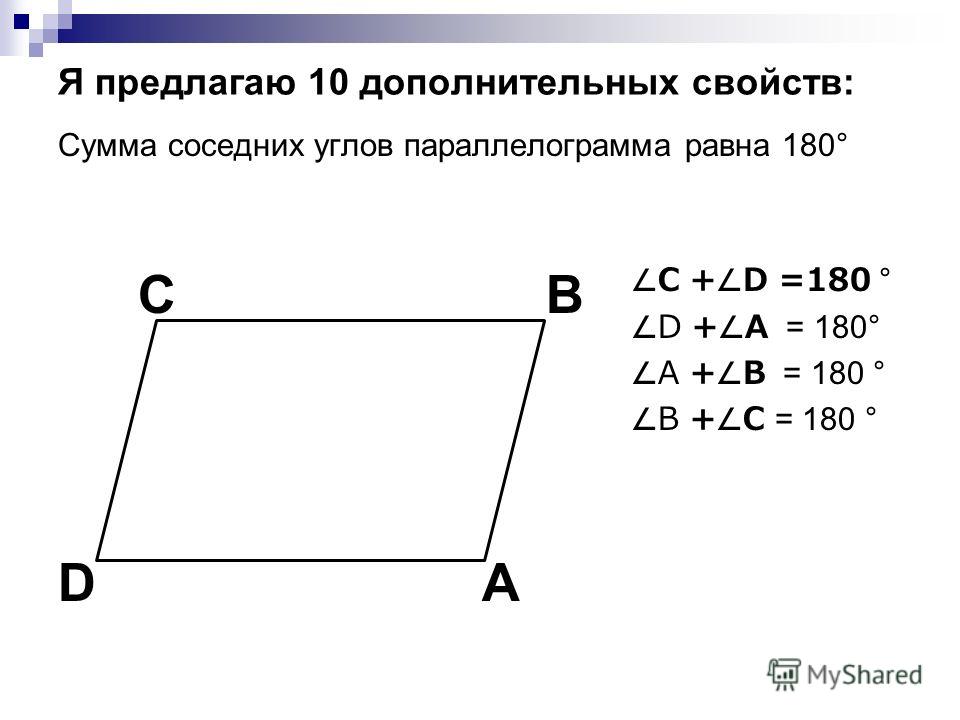
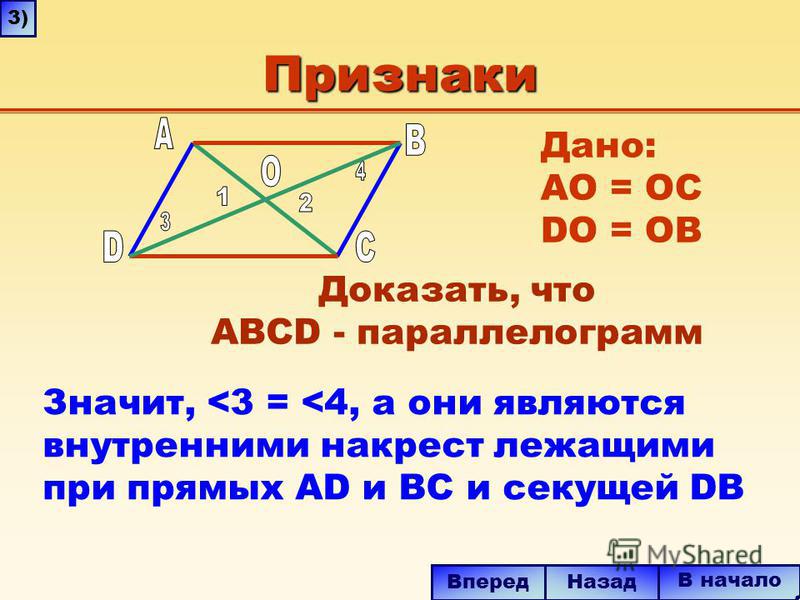
 Квадрат будет иметь все признаки и свойства родительских фигур:параллелограмма, прямоугольника и ромба.
Квадрат будет иметь все признаки и свойства родительских фигур:параллелограмма, прямоугольника и ромба.
 Величина площади параллелограмма выражается числом заключающихся в него квадратных единиц.
Величина площади параллелограмма выражается числом заключающихся в него квадратных единиц. Ее длина, умноженная на два, равна: 2b = P – 2a = 50 см – 2 * 7 см = 36 см.
Ее длина, умноженная на два, равна: 2b = P – 2a = 50 см – 2 * 7 см = 36 см. Противоположные стороны параллелограмма параллельны:
Противоположные стороны параллелограмма параллельны: Как найти сумму длин всех рёбер параллелепипеда
Как найти сумму длин всех рёбер параллелепипеда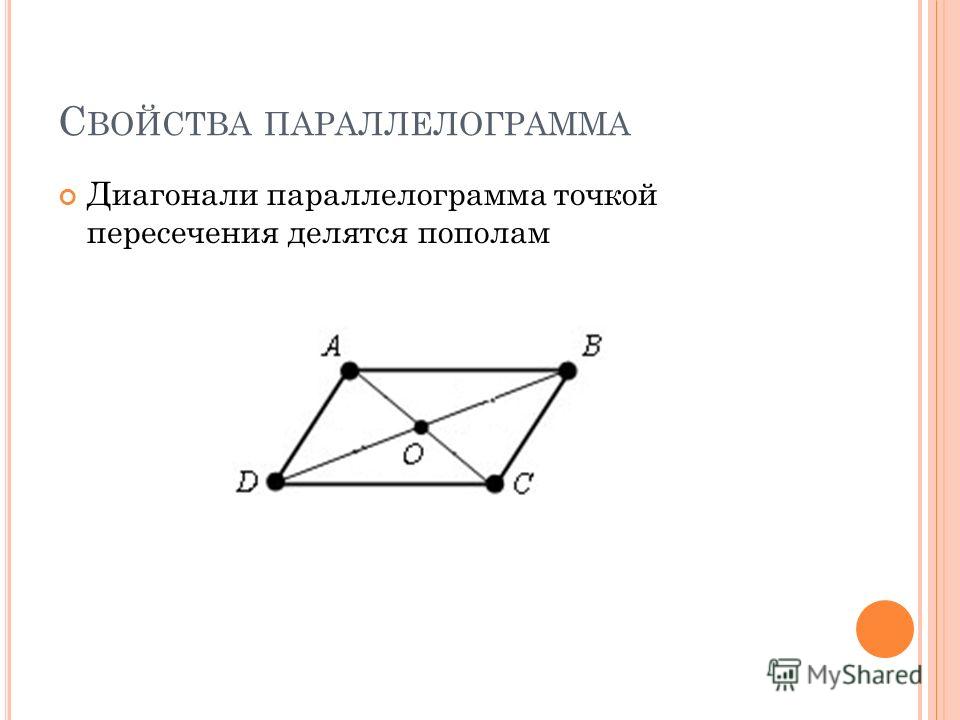
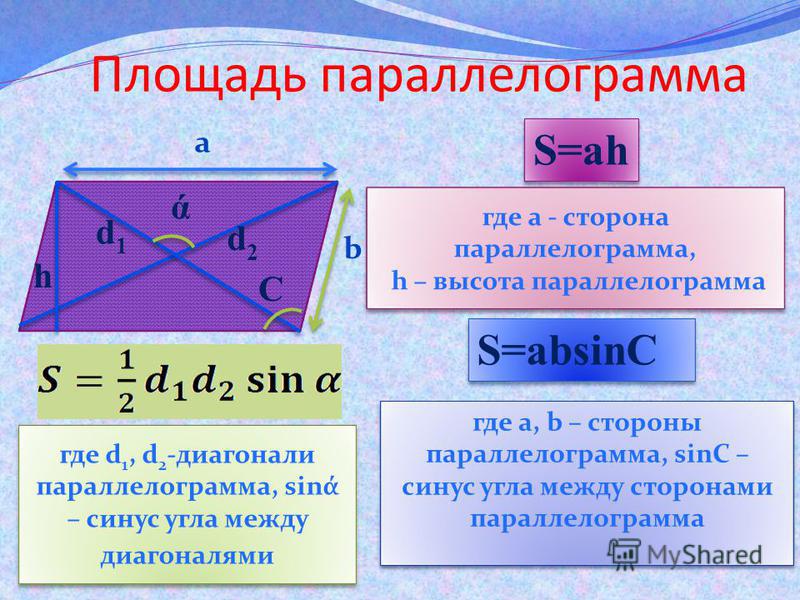
 Получается, что напротив стороны А лежит такая же сторона А. Исходя из определения параллелограмма понятно, что верхняя грань его тоже равна А. Получается, что сумма длин всех сторон данного параллелограмма равна 4А.
Получается, что напротив стороны А лежит такая же сторона А. Исходя из определения параллелограмма понятно, что верхняя грань его тоже равна А. Получается, что сумма длин всех сторон данного параллелограмма равна 4А.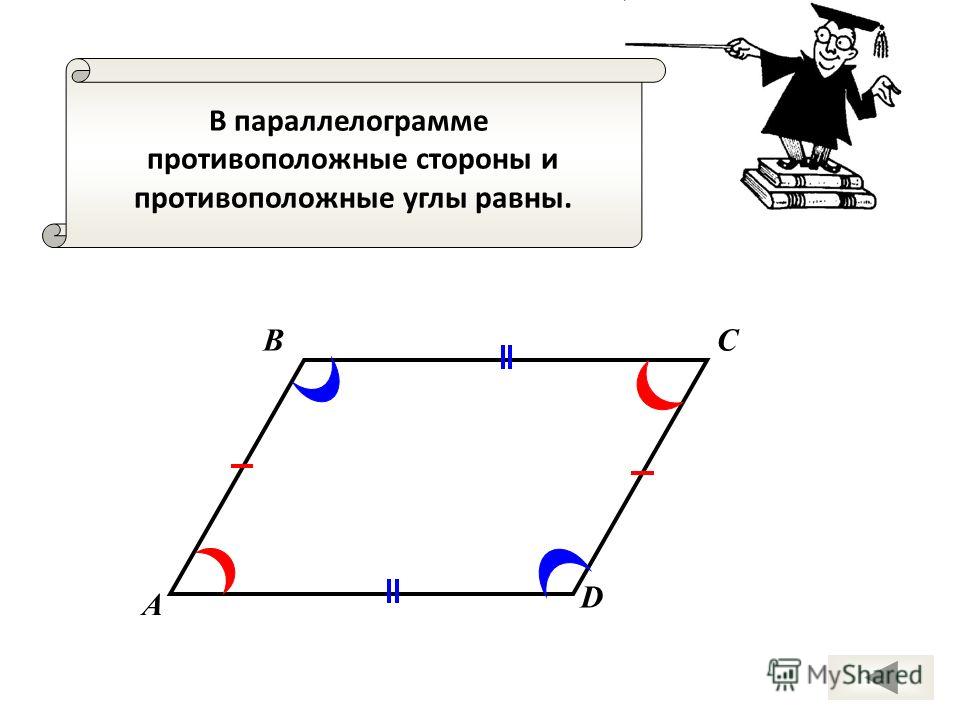
 Таким образом, сумма всех четырех этих сторон равна 4А.
Таким образом, сумма всех четырех этих сторон равна 4А.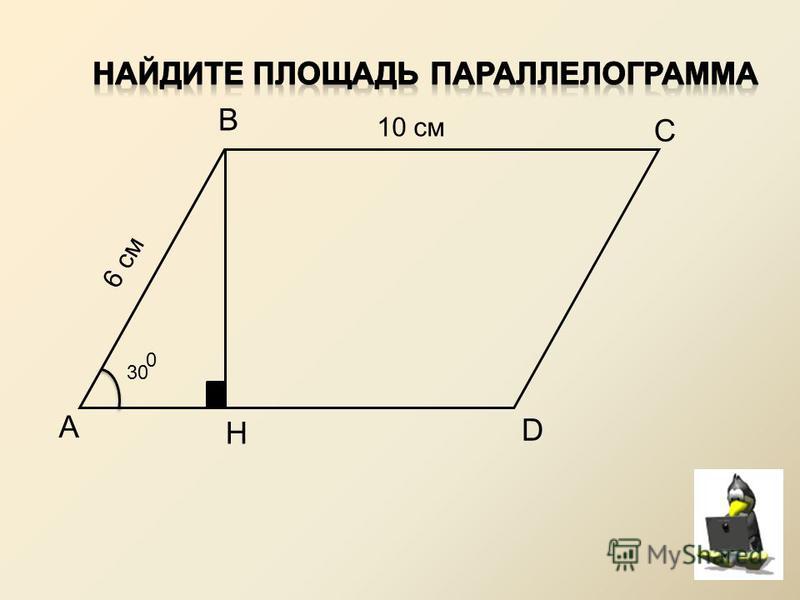
 Противолежащие грани параллелепипеда равны. У прямоугольного параллелепипеда 12 ребер и 8 вершин. Три ребра, выходящие из одной вершины, называют измерениями параллелепипеда или его длиной, высотой и шириной. Таким образом, у прямоугольного параллелепипеда есть четверки равных по длине ребер: 4 высоты, 4 ширины и 4 длины.
Противолежащие грани параллелепипеда равны. У прямоугольного параллелепипеда 12 ребер и 8 вершин. Три ребра, выходящие из одной вершины, называют измерениями параллелепипеда или его длиной, высотой и шириной. Таким образом, у прямоугольного параллелепипеда есть четверки равных по длине ребер: 4 высоты, 4 ширины и 4 длины.
 Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.  Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху. 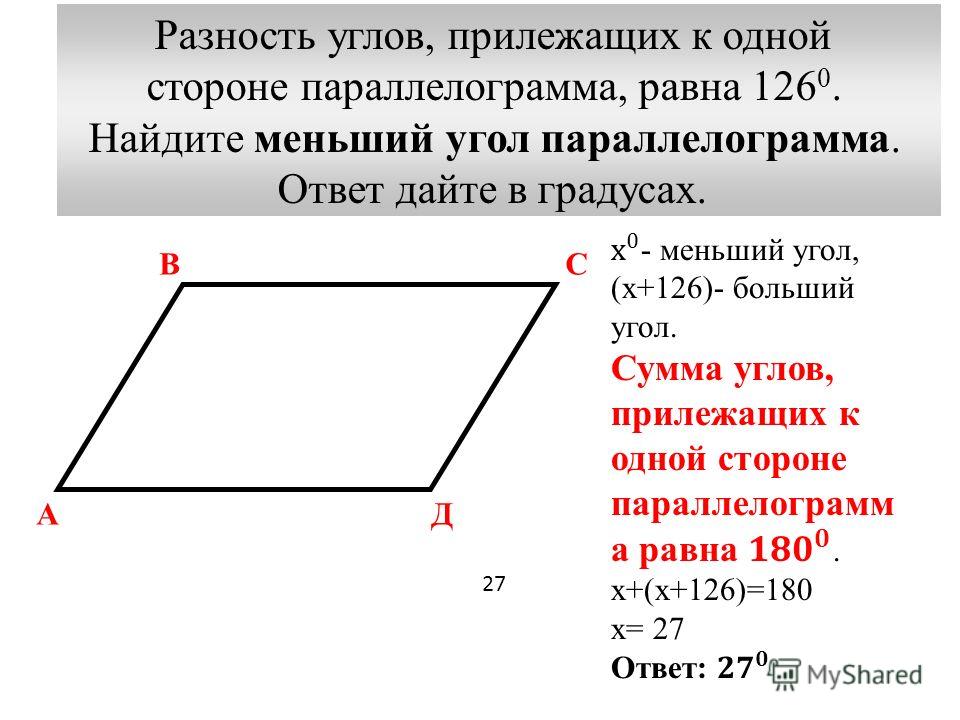 По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования. Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.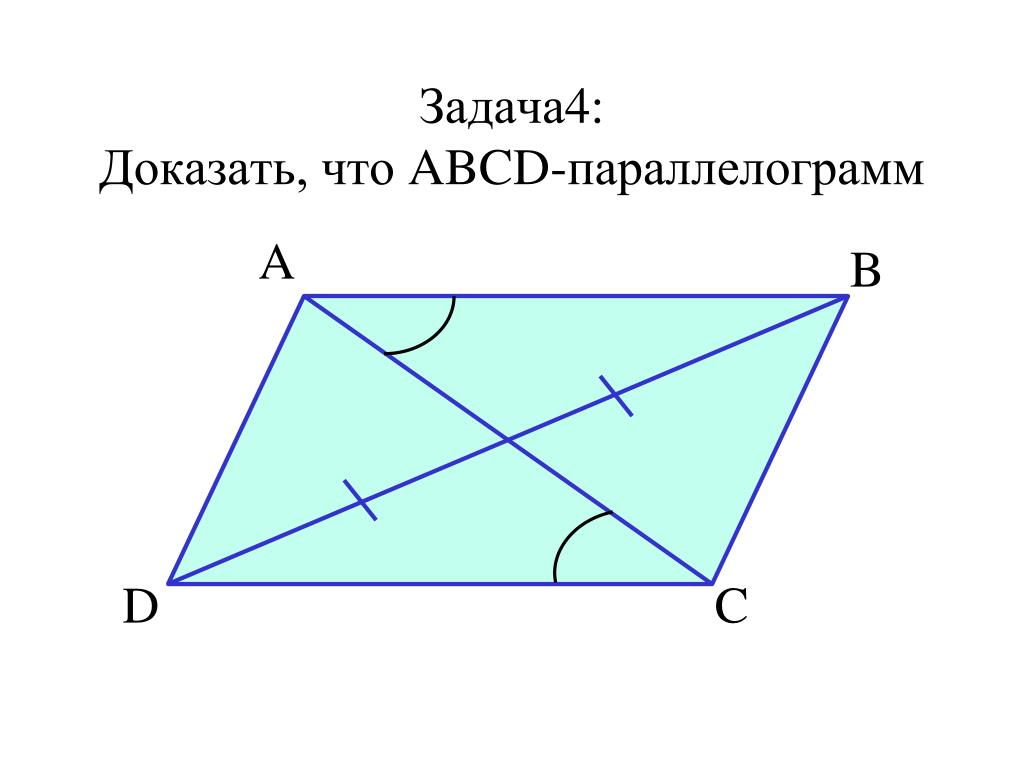 Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
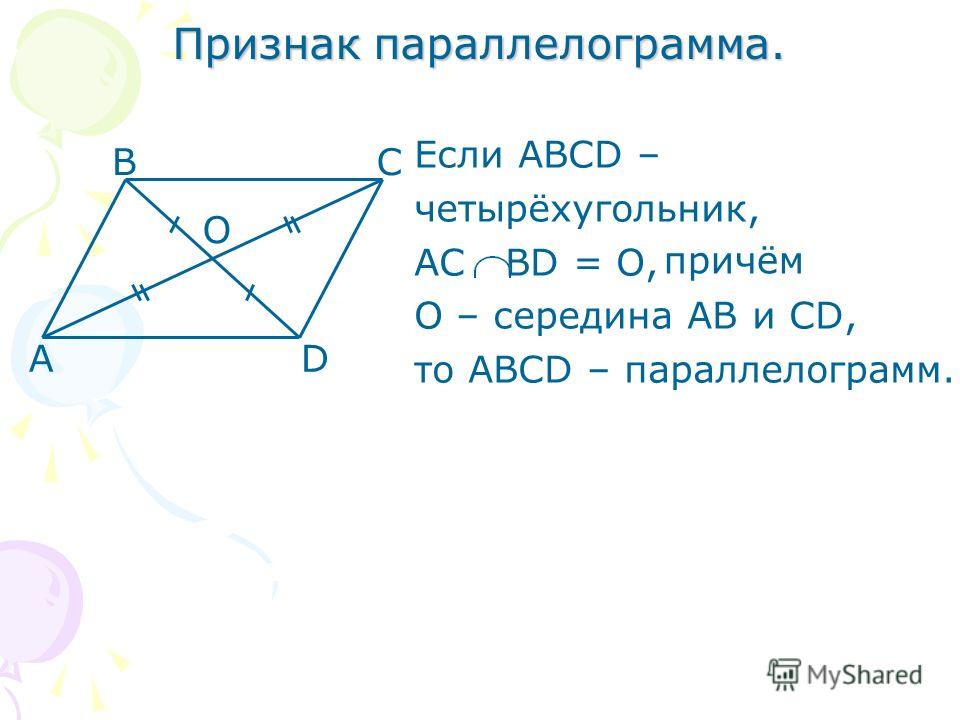
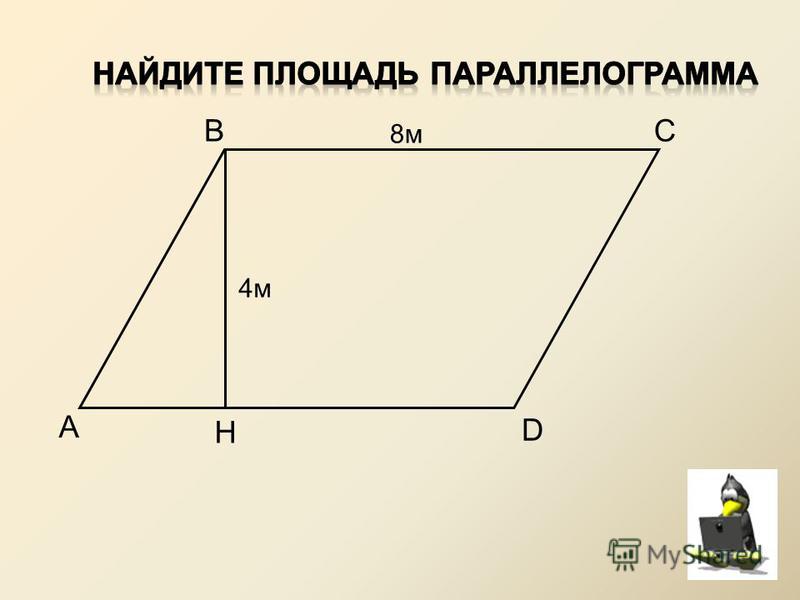 Это не математическое действие.
Это не математическое действие.
 Какой еще туалет?
Какой еще туалет?
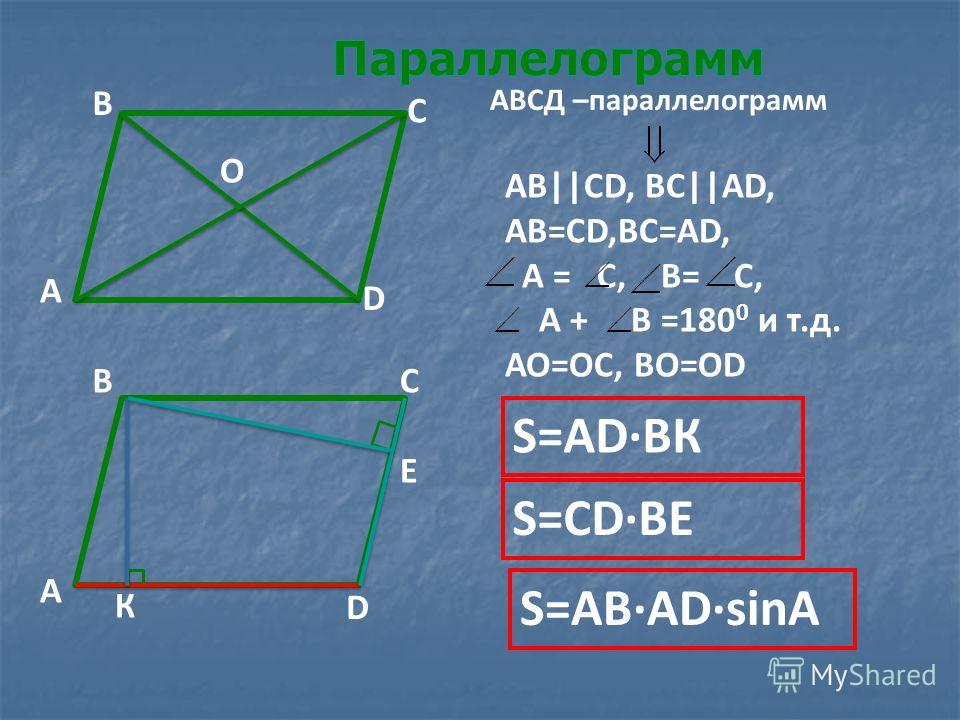 2 2) / (2 * 6 * 3) = (36 + 9 — 27.04) / (2 * 18) = 17.96/36 ~ 18/36 ~1/2
2 2) / (2 * 6 * 3) = (36 + 9 — 27.04) / (2 * 18) = 17.96/36 ~ 18/36 ~1/2 А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.
А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.