Пример решения системы уравнений: Решение систем уравнений — метод как решить систему линейных уравнений

alexxlab / / Разное

Как решить систему уравнений в R (3 примера)

Чтобы решить систему уравнений в R, мы можем использовать встроенную функциюsolve() .

В следующих примерах показано, как использовать эти функции для решения нескольких различных систем уравнений в R.

Пример 1. Решение системы уравнений с двумя переменными

Предположим, у нас есть следующая система уравнений, и мы хотели бы найти значения x и y:

5х + 4у = 35

2х + 6у = 36

В следующем коде показано, как использовать функциюsolve() в R для поиска значений x и y:

#define left-hand side of equations
left_matrix <- matrix(c(5, 2, 4, 6), nrow= 2 )
left_matrix
 [,1] [,2]
[1,] 5 4
[2,] 2 6
#define right-hand side of equations
right_matrix <- matrix(c(35, 36), nrow= 2 )
right_matrix
 [,1]
[1,] 35
[2,] 36
#solve for x and y
solve(left_matrix, right_matrix) 
 [,1]
[1,] 3
[2,] 5

Это говорит нам о том, что значение x равно 3 , а значение y равно 5 .

Пример 2. Решение системы уравнений с тремя переменными

Предположим, у нас есть следующая система уравнений, и мы хотели бы найти значения x, y и z:

4х + 2у + 1з = 34

3x + 5y – 2z = 41

2х + 2у + 4з = 30

В следующем коде показано, как использовать функциюsolve() в R для решения значений x, y и z:

#define left-hand side of equations
left_matrix <- matrix(c(4, 3, 2, 2, 5, 2, 1, -2, 4), nrow= 3 )
left_matrix
 [,1] [,2] [,3]
[1,] 4 2 1
[2,] 3 5 -2
[3,] 2 2 4
#define right-hand side of equations
right_matrix <- matrix(c(34, 41, 30), nrow= 3 )
right_matrix
 [,1]
[1,] 34
[2,] 41
[3,] 30
#solve for x, y, and z
solve(left_matrix, right_matrix) 
 [,1]
[1,] 5
[2,] 6
[3,] 2

Это говорит нам о том, что значение x равно 5 , значение y равно 6 , а значение z равно 2 .

Пример 3. Решение системы уравнений с четырьмя переменными

Предположим, у нас есть следующая система уравнений, и мы хотели бы найти значения w, x, y и z:

6ш + 2х + 2у + 1з = 37

2ш + 1х + 1у + 0з = 14

3ш + 2х + 2у + 4з = 28

2ш + 0х + 5у + 5з = 28

В следующем коде показано, как использовать функциюsolve() в R для поиска значений w, x, y и z:

#define left-hand side of equations
left_matrix <- matrix(c(6, 2, 3, 2, 2, 1, 2, 0, 2, 1, 2, 5, 1, 0, 4, 5), nrow= 4 )
left_matrix
 [,1] [,2] [,3] [,4]
[1,] 6 2 2 1
[2,] 2 1 1 0
[3,] 3 2 2 4
[4,] 2 0 5 5
#define right-hand side of equations
right_matrix <- matrix(c(37, 14, 28, 28), nrow= 4 )
right_matrix
 [,1]
[1,] 37
[2,] 14
[3,] 28
[4,] 28
#solve for w, x, y and z
solve(left_matrix, right_matrix)
 [,1]
[1,] 4
[2,] 3
[3,] 3
[4,] 1

Это говорит нам о том, что значение w равно 4 , x равно 3 , y равно 3 и z равно 1 . 2 -xy-2x+1 = 0\\x-y=1\end{cases} $$

Поскольку второе уравнение этой системы линейно относительно каждой из переменных х и у, то одна из этих переменных,; например у, легко выражается через другую:

у = х — 1.

Подставляя это выражение для

у в первое уравнение системы, получаем:

x2 + 3 (х — 1)2 — х (х — 1) — 2х + 1 = 0,

откуда

3x2 — 7x +4 = 0; x1 = 4/3; x2 = 1

Этим значениям х согласно второму уравнению системы соответствуют следующие значения у: y1 = 1/3; y2 = 0.

Таким образом, данная система уравнений имеет два решения:

x1 = 4/3; y1 = 1/3; и x2 = 1; y2 = 0. 2 =8\end{cases} \;\;\; (1) $$

Характерная особенность этой системы уравнений состоит в том, что она содержит лишь выражения x2, y2 и ху, суммарная степень х и у в которых постоянна и равна 2.

Для решения данной системы выполним следующие преобрaзования. Из первого уравнения системы (1) вычтем второе, умноженное на 2. В результате получим уравнение

2x2 — 3ху + y2 = 0, (2)

правая часть которого равна 0.

Заметим, что х \(\neq\) 0. В противном случае из (2) вытекало бы, что у = 0, а это явно противоречит уравнениям системы (1). Но если х \(\neq\) 0, то уравнение (2) можно почленно разделить на x2, что дает

2- 3 y/x + ( y/

x )2 = 0.

Мы получили квадратное уравнение относительно y/x. Из него следует, что либо y/x = 1, либо y/x = 2.

Рассмотрим эти два случая отдельно.

1) Если y/x = 1, то у = х. Замена у в первом уравнении данной системы на х приводит к следующему результату:

4x2 + 5x2 + 3x2 = 16,

или

12x2 = 16.

Следовательно,

$$ x=\pm\sqrt{\frac{16}{12}} = \pm\sqrt{\frac{4}{3}} = \pm\frac{2}{\sqrt3} $$

Отсюда получаем следующие два решения данной системы:

x1 = 2/√3 , y1=2/√3 ; x2= — 2/√3 , y2= — 2/√3

2) Если y/x = 2, то у = 2х. Заменяя у в первом уравнении данной системы на 2х, получаем:

14x2 — 10x2 + 12x2 = 16,

или

16x2 = 16.

Следовательно, х = ±1. Отсюда, учитывая, что у = 2х

, получаем еще два решения данной системы:

x1 = 1, y1=2; x2= — 1 , y2= — 2

Проверка показывает, что ни одно из полученных четырех решений системы (1) не является «посторонним».

Ответ. Данная система уравнений имеет 4 решения:

1) x1 = 2/√3 , y1=2/√3 ; 2) x2= — 2/√3 , y2= — 2/√3

3) x1 = 1, y1=2; 4) x2= — 1 , y2= — 2

Пример 3. Решить систему уравнений

$$ \begin{cases}x+y = 6\\xy= -7\end{cases} $$

Если только данная система уравнений имеет решение, то по теореме, обратной теореме Виета, это решение должно состоять из корней квадратного уравнения (см. § 52):

x2 — 6x — 7 = 0.

Это уравнение имеет корни x1= -1, x2 = +7. Следовательно, в роли решений данной системы уравнений могут выступать только следующие две пары чисел:

x1 = — 1, y1 = 7 и x2 = 7, y2 = — 1.

Элементарная проверка показывает, что каждая из этих пар чисел является решением нашей системы.

Ответ. Данная система уравнений имеет два решения:

x1 = — 1, y1 = 7 и x2 = 7, y

2 = — 1. 2 = 5 \\ xy= -2 \end{cases} $$

Из второго уравнения получаем x2y2 = 4. Но в таком случае по теореме, обратной теореме Виета, x2 и y2 можно рассматривать как корни квадратного уравнения

z2 — 5z + 4 = 0,

откуда z1 = 4, z2 = 1. Поэтому возможны два случая: 1) x2 = 4, и тогда y2 = 1; 2) x2= 1, и тогда y2 = 4.

Случай 1. Если х = + 2, то у = -1 (согласно второму уравнению исходной системы ху = — 2 ). Если х =- 2, то у = 1.

Случай 2. Если x = 1, то у

= — 2, если же x = — 1, то у = 2.

Мы получили 4 решения данной системы уравнений:

x1 = 2, y1 = — 1 ; x2 = — 2, y2 = 1;

x3 = 1, y3 = — 2 ; x4 = — 1, y4 = 2. 2 + y = 4\\x + y = 2 \end{cases} $$

На одном и том же рисунке начертим две кривые, первая из которых имеет уравнение x2 + у = 4, или у = 4 — x2, а вторая — уравнение х + у = 2, или у

= 2 — х. Очевидно, что искомыми решениями данной системы уравнений будут координаты точек пересечения этих двух кривых.

Как видно из рисунка, рассматриваемые кривые пересекаются в двух точках: А с координатами (- 1,3) и В с координатами (2, 0). Поэтому данная система уравнений имеет два решения: x = — 1, у = 3 и x = 2, у = 0.


Решить систему уравнений в R

  • Читать
  • Обсудить
  • Практика
  • Видео
  • Курсы

    • Улучшить статью

    Сохранить статью

    В этой статье мы обсудим, как решить систему уравнений на языке программирования R.

    Solve() Функция языка R используется для решения уравнения. Здесь уравнение похоже на a*x = b, где b — вектор или матрица, а x — переменная, значение которой будет вычислено.

    Syntax: solve(a, b)

    Parameters:

    • a: coefficients of the equation
    • b: vector or matrix of the equation

    Example 1: Решение системы уравнений из трех уравнений 
      Данных уравнений: 
х + 2у + 3г = 20
2х + 2у + 3з = 100
3x + 2y + 8z = 200

  Матрица A и B для решения с использованием коэффициента уравнения: 
А->
1 2 3
2 2 3
3 2 8
Б->
20
100
200

    для решения этого с использованием двух матриц в R Мы используем следующий код:

    R

    A <- RBIND ( C (1, 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3), 3).

    C (2, 2, 3),

    C (3, 2, 8))

    (3, 2, 8))

    (3, 2, 8))

    B <- c (20, 100, 200)

       

    solve (A, B)

    Output: 

     80 -36 3.99999999999999

    , что означает x=80, y=-36 и z=4, является решением линейных уравнений.

    Пример 2: Решение системного уравнения из трех уравнений

    Чтобы получить решения в виде дробей, мы используем библиотеку MASS на языке R и оборачиваем функцию решения в дроби.

      Приведенные уравнения: 
19x + 32y + 31z = 1110
22x + 28y + 13z = 1406
31x + 12y + 81z = 3040
  Матрицы A и B для решения с использованием коэффициентов уравнения: 
А->
19 32 31
22 28 13
31 12 81
Б->
1110
1406
3040

    Чтобы решить это с помощью двух матриц в R, мы используем следующий код:

    R

    библиотека (MASS)

       

    A <- rbind ( c (19, 32, 31), 

                c (22, 28, 31), 

                c (31, 12, 81))

    B <- c (1110, 1406, 3040)

       

    fractions ( solve (A , Б))

    Output: 

     [1] 159950/2243 -92039/4486  29784/2243

    which means x=159950/2243 , y=-92039/4486 and z=29784/2243 is the solution для приведенного выше линейного уравнения.

    Пример 3: Решение обратной матрицы

    R

    A <- MATRIX ( C (4, 7, 7, 3, 7, 3, 3, 7, 3, 7, 3, 7, 3, 3, 7, 7, 3, 7, 7, 7, 3, 7, 7, 3, ( .

    печать (A)

       

    print ( "Inverse matrix" )

       

    print ( solve (A))

    Вывод: 

     [1] [2]
[1,] 4 3
[2,] 7 6
[1] «Обратная матрица»
          [1] [2]
[1,] 2.000000 -1.000000
[2,] -2,333333 1,333333

    Реальные примеры — решение систем линейных уравнений

    Написание уравнений из систем реального мира

    При написании систем уравнений важно уметь извлекать информацию из задачи. При извлечении информации вам нужно будет выбрать переменные для представления различных частей проблемы истории. Убедитесь, что вы последовательны при настройке этих переменных и знаете, что они представляют. Если у вас есть два или более уравнений, вы можете решить систему уравнений, используя график, замену или исключение.

    Написание уравнений из систем реального мира Пример

    Задача : Предположим, вы начинаете бизнес по сборке и продаже скутеров. Инструменты и оборудование для начала работы стоят 1500 долларов, а материалы для каждого самоката стоят 200 долларов за каждый самокат. Ваши скутеры продаются по 300 долларов. (a) Напишите и решите систему уравнений, представляющую общую стоимость и доход вашего бизнеса. (b) Опишите, что означает решение с точки зрения ситуации. (c) Приведите пример разумного количества самокатов, которые вы могли бы собрать и продать, чтобы получить прибыль, и определите прибыль, которую вы получите от этого количества самокатов.

    (a) Напишите и решите систему уравнений, представляющую общие затраты и доходы вашего бизнеса.
    Let S = Scooter and Let I = Доход
    Стоимость: I = 1500 + 200 S
    Доход: I = 300 S

    . как и я - я знаю, что потратил не менее 1500 долларов на покупку инструментов и оборудования для сборки скутеров. Это деньги, которые не зависят от скутеров, но я потратил их несмотря ни на что. у меня 200 умножается на s  потому что это будет стоить 200 долларов за каждый скутер. Поэтому, если мне нужно 4 самоката, я подключу 4, где s  в уравнении.


    Причина, по которой я создал уравнение дохода в том виде, в каком я его создал, — я знаю, что буду продавать скутеры за 300 долларов. Поэтому, в зависимости от количества самокатов, которые я продам, мне нужно будет умножить это на 300 долларов, чтобы рассчитать свой доход.


    Решение: (Мой выбор метода - Замена )

    (b) Опишите, что означает решение с точки зрения ситуации.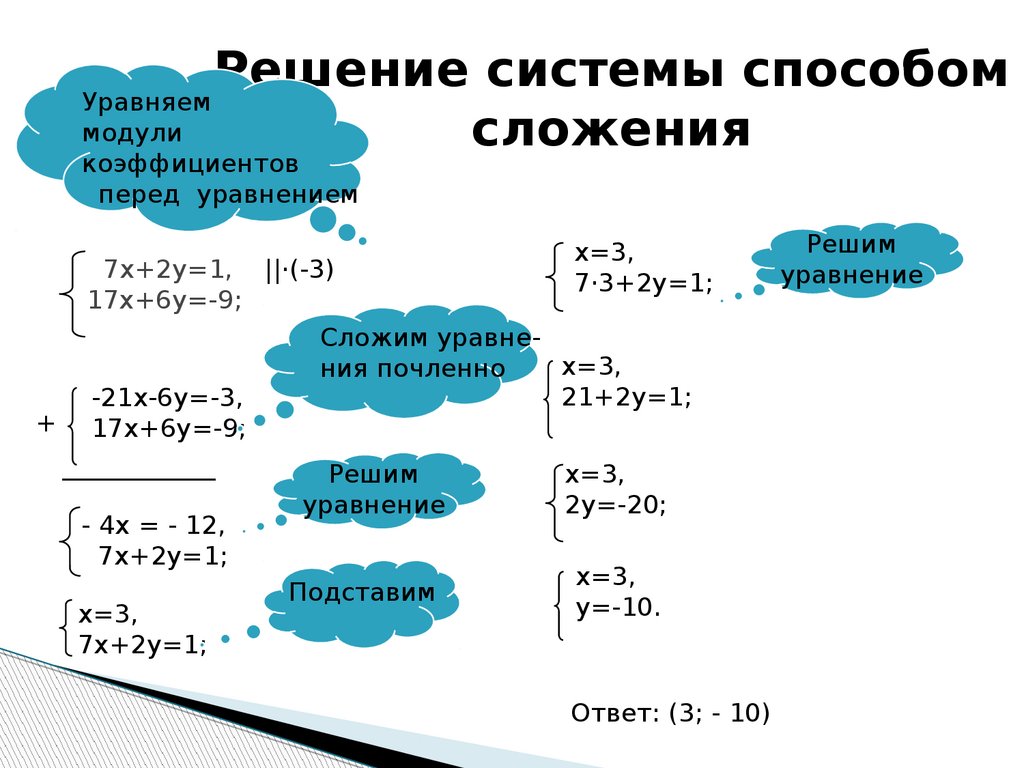
    Решение означает, что как только мы получим прибыль в размере 4500 долларов США за продажу 15 самокатов, мы достигнем безубыточности между затратами и выручкой. Следовательно, любая точка после этой будет прибылью

    (c) Приведите пример разумного количества самокатов, которые вы могли бы собрать и продать, чтобы получить прибыль, и определите прибыль, которую вы получите от этого количества самокатов.

    Номер скутера: 25
    Прибыль: $2000

    Написание уравнений из систем реального мира Дополнительные ресурсы

    Дополнительные видеоролики о том, как писать системы уравнений на основе примеров из реальной жизни.

    Ниже приведен пример, который позволит вам попрактиковаться в решении систем линейных уравнений, возникающих в реальных задачах.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *