Пример с корнем как решить: Решение примеров с корнями

Преобразование ⭐ выражений, содержащих квадратные корни: как решать задачи

Определение арифметического корня и его свойства

Определение 

Арифметический корень из числа а>0, является таким неотрицательным числом, которое в квадрате равно а.

При извлечении квадратного корня из некоего числа в любом случае получается один результат, который больше нуля. Он и будет арифметическим корнем, имеющим ряд характерных свойств. Перечислим их:

1. Корень произведения соответствует произведению корней: . Приведем пример: 
2. Корень из дроби равен корню из числителя и корню из знаменателя: . Приведем пример: 
3. При возведении корня в степень необходимо возвести в данную степень подкоренное значение: . Приведем пример: .

Решение задач по вынесению множителя из квадратного корня

Операция вынесения числа, то есть множителя, из-под знака корня представляет собой извлечение корня из выражения, находящегося под знаком корня. Такое выражение называют подкоренным.

Приведем несколько примеров:

С целью упрощения вынесения чисел и множителей из-под знака квадратного корня следует ознакомиться с таблицей квадратов:

 

Источник: microexcel.ru

Разберем несколько наглядных примеров, с которыми можно встретиться на уроках в классе, а также при решении контрольных и проверочных работ. Вынесем множитель из-под знака корня (с объяснением) в таком выражении:

Заметим, что извлечение квадратного корня в данном случае возможно лишь из числа 25. Выполним действия:

Разберем другое задание для повторения темы, которое следует решать аналогичным методом. Представим, что нужно вынести корень из числа:

В первую очередь стоит разложить выражение, которое записано под знаком корня. Множителями являются числа 9 и 5. Заметим, что извлекается квадратный корень в этом случае лишь из 9. Запишем:

Когда под знаком корня записано выражение, то его можно вынести. Данное утверждение справедливо лишь в том случае, когда под корнем произведение. Приведем примеры:

Все, за исключением первого выражения, являются неверными. В таких случаях целесообразно сначала выполнить действия под знаком корня, а затем переходить к его извлечению. Продолжим вычисления:

Во многих задачах по алгебре и физике можно встретить выражения, для решения которых необходимо вынести из-под знака корня не число, а букву. В таком случае необходимо выполнить тождественные преобразования и преобразовать эту букву в дробь. Роль числителя при этом будет играть степень подкоренного выражения, а знаменателем является непосредственно сам корень:

Данная формула справедлива также при выполнении действий с числами. Приведем несколько типичных примеров:

Решение задач по внесению множителя под знак корня

На следующем этапе стоит потренироваться с внесением чисел под знак корня. Запишем некое выражение с содержанием корня:

Отметим, что после внесения числа под знак корня решение существенно упростилось. Рассмотрим число:

Заметим, что цифру 3 можно внести под корень. Это связано с тем, что данное число является корнем квадратным из числа 9:

С помощью записанных закономерностей получилось значительно расширить возможности при решении разнообразных заданий. Например:

Здесь важно отметить, что внесение под знак арифметического корня допускается лишь в том случае, когда число является положительным.

Разберем еще несколько примеров:

Решение задач по освобождению от иррациональности в знаменателе

При решении задач можно встретить примеры с дробями, в знаменателе которых записан корень или иррациональное число. В таком случае следует выполнить умножение данной дроби на какой-то член или выражение. В результате получится исключить корень. Существует несколько видов выражений, где нужно избавиться от иррациональности в знаменателе дроби. Рассмотрим наиболее распространенные из них.

Когда в знаменателе записан одночлен, следует внимательно изучить такую дробь. При отсутствии корня упростить подобное выражение не составит труда. Однако при наличии в знаменателе квадратного или другого корня необходимо выполнить умножение числителя и знаменателя на какой-нибудь одночлен, что в итоге позволит избавиться от корня. Разберем пример:

Воспользуемся записанным правилом и упростим выражение:

Когда в знаменателе дроби записан двучлен в виде суммы или разности пары одночленов, в один из которых включен корень, недопустимо выполнять умножение дроби на подобный двучлен, так как не получится исключить иррациональность:

Рассмотрим это правило на примере дроби:

Здесь в одночлене a или b имеется корень.

Попробуем упростить выражение:

Заметим, что в составе одночлена 2ab в любом случае имеется корень а или b.

Разберем наглядный пример:

Заметим, что в этом случае отсутствует возможность исключить корень из знаменателя, так как в нем записан одночлен 

При решении подобных задач следует воспользоваться понятием сопряженного двучлена, то есть такого двучлена, который состоит из аналогичных одночленов, но знак между ними противоположный. Таким образом,  является сопряженным для двучлена . Применим данное правило к нашему выражению:

При умножении числителя и знаменателя дроби на сопряженный двучлен одночлены будут возведены в квадрат, что позволяет избавиться от знака корня:

Заметим, что в последнем задании имеется общий множитель в числителе и знаменателе:

4 — 2 = 2

Таким образом, можно сократить дробь:

Разберем другие выражения, при решении которых нужно избавиться от иррациональности. К таким относят обратные выражения. Представим, что требуется определить выражение, которое является обратным для данного и содержит корень. В этом случае следует рационализировать полученную дробь, а затем приступать к ее упрощению. Здесь пригодятся правила, описанные ранее.  Рассмотрим пример:

Запишем для этого выражения обратное. На первом шаге следует выполнить деление единицы на это выражение. В том случае, когда имеется дробь, нужно поменять местами числитель со знаменателем. Важно заметить, что какое-либо выражение достаточно просто записать в виде дроби. При этом в знаменателе будет стоять единица.

Избавимся от корня путем умножения числителя и знаменателя на некое выражение. При этом значение полученной дроби сохранится без изменений. Применительно к этой задаче, следует умножить дробь на сопряженный двучлен:

Упростим выражение с помощью сокращения выражения, записанного в знаменателе:

Задания для самостоятельной работы

Задача 1

Упростить записанное выражение:

Решение

Воспользуемся свойством арифметического квадратного корня и выполним необходимые вычисления:

Ответ: 

Задача 2

Решить пример:

Решение

Вспомним свойства арифметического квадратного корня и выполним преобразования:

Вычислим модули по определению:

Ответ: 

Задача 3

Дано выражение, которое требуется упростить:

Решение

Переведем показатели степеней в вид рациональных чисел.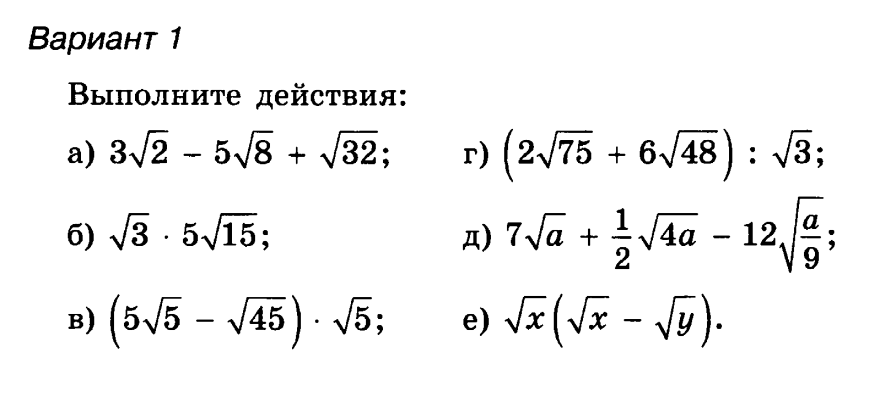 Затем выполним необходимые преобразования:

Ответ: 

Задача 4

Выполнить вычисления:

Решение

Здесь следует исключить иррациональность, которую можно наблюдать в первой дроби. Сделать это можно путем умножения числителя и знаменателя дроби на выражение, которое сопряжено со знаменателем, то есть на . Таким образом:

Заметим, что дробь, которая получилась, может быть преобразована. При этом целесообразно воспользоваться формулами сокращенного умножения:

  

Далее необходимо выполнить вычитание дробей, заранее приведя их к общему знаменателю:

Ответ: 

Задача 5

Дано выражение, которое следует упростить:

Решение

Здесь следует записать выражение, расположенное под знаком корня, как:

В результате получился квадрат суммы, записанный под знаком корня:

Вспомним свойство, которым обладает арифметический квадратный корень:

Применим записанную формулу:

Заметим, что результат данных преобразований является разностью квадратов. 2

9.1: Извлечение квадратных корней — Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

18382

• Анонимный
• LibreTexts
9{2}+b x+c=0\]

, где a , b и c — действительные числа и \(a\neq 0\). Решение такого уравнения называется корнем . Квадратные уравнения могут иметь два действительных решения, одно действительное решение или не иметь действительного решения. Если квадратное выражение на левых факторах, то мы можем решить его факторингом. Ниже приводится обзор шагов, используемых для решения факторингом:

Шаг 1: Выразите квадратное уравнение в стандартной форме. 9{2}\).

После применения свойства квадратного корня у нас остается квадратный корень из отрицательного числа. Следовательно, реального решения этого уравнения нет.

Ответ :

Нет действительного решения

Обратный процесс, чтобы найти уравнения с заданными решениями вида ±k .

Пример \(\PageIndex{5}\)

Найдите уравнение с решениями \(-2 \sqrt{3}\) и \(2 \sqrt{3}\).

Решение 9{2}} & {=25} & {\color{Cerulean}{Применить\: the\:square \:root \:property.}} \\ {x+2} & {=\pm \sqrt{25} } & {\color{Cerulean}{Упрощение. }} \\ {x+2}& {=\pm5} \\ {x}&{=-2\pm5}\end{массив}\)

На этом этапе разделите «плюс или минус» на два уравнения и упростить каждое в отдельности.

\(\ begin {массив} {ll} {x = -2-5} & {\ text {или} x = -2 + 5} \\ {x = -7} & {\ quad \: \: x=3}\end{массив}\)

Ответ

:

Решения: -7 и 3. 9{2}-2=0\)

Ответ

\(15\pm 6\sqrt{3}\)

Пример \(\PageIndex{9}\)

Длина прямоугольника в два раза больше его ширины. Если диагональ равна 2 футам, найдите размеры прямоугольника.

Рисунок \(\PageIndex{1}\)

Решение

Пусть w представляет ширину.

Пусть 2w представляет длину.

Диагональ любого прямоугольника образует два прямоугольных треугольника. Таким образом, применима теорема Пифагора. Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы: 9{2}&=\frac{4}{5}\quad\:\:\quad\color{Cerulean}{Extract\:the\:roots.} \\ w&=\pm\sqrt{\frac{4} {5}}\\w&=\pm\frac{2}{\sqrt{5}} \end{aligned}\)

Здесь мы получаем два решения, \(w=-\frac{2}{\sqrt {5}}\) и \(w=\frac{2}{\sqrt{5}}\). Поскольку задача требовала длины прямоугольника, мы не учитываем отрицательный ответ. Кроме того, мы рационализируем знаменатель и представим наши решения без каких-либо радикалов в знаменателе.

{2}-36=0\) 9{2}−52=0\)

Ответить

1. ±4

3. ±3

5. ±\(\frac{1}{2}\)

7. ±0,5

9. ±\(2\sqrt{3}\)

11. ±\(\frac{3}{4}\)

13. ±\(\sqrt{\frac{1}{2}}\)

15. ±10

17. Нет реального решения

19. ±\(\frac{2}{3}\)

21. ±0,3

23. ±\(\sqrt{7}\)

25. ±\(2\sqrt{2}\)

27. Нет реального решения

29. ±\(\frac{3 \sqrt{3}}{4}\)

31. ±\(6\sqrt{2}\)

33. ±\(3\sqrt{3}\)

35. \(−9, −5\)

37. \(−3, 6\)

39. \(5\)±\(2\sqrt{5}\)

41. ±\(\frac{\sqrt{6}-2}{3}\)

43. ±\(\frac{\sqrt{3}}{2}-2\)

45. ±\(\frac{3 \sqrt{3}-2}{6}\)

47. Нет реального решения

49. ±\(\frac{4 \sqrt{6}}{3}+23\)

Упражнение \(\PageIndex{5}\) извлечение квадратных корней

Найдите квадратное уравнение в стандартной форме со следующими решениями. {2}−49{2}\)

• \((3x−1)(x+4)=2x(x+6)−(x−3)\)

Ответить

1. ±0,33

3. ±5,66

5. ±7,94

7. ±3,61

Упражнение \(\PageIndex{7}\) извлечение квадратных корней

Составьте алгебраическое уравнение и используйте его для решения следующего.

1. Если из 4-кратного квадрата числа вычесть 9, то получится 3. Найдите число.
2. Если из квадрата числа вычесть 20, то получится 4. Найдите число.
3. Если к 3-кратному квадрату числа прибавить 1, то получится 2. Найдите число.
4. Если к удвоенному квадрату числа прибавить 3, то получится 12. Найдите число.
5. Если площадь квадрата 8 квадратных сантиметров, то найдите длину каждой стороны.
6. Если площадь круга 32\(\pi\) квадратных сантиметров, то найдите длину радиуса. 9{2}\).)
7. Длина прямоугольника в 6 раз больше его ширины. Если площадь равна 96 квадратных дюймов, то найдите размеры прямоугольника.
8. Основание треугольника вдвое больше его высоты. Если площадь 16 квадратных сантиметров, то найдите длину его основания.
9. Квадрат имеет площадь 36 квадратных единиц. На какую величину нужно увеличить стороны, чтобы получился квадрат с удвоенной площадью?
10. Круг имеет площадь 25\(\pi\) квадратных единиц. На сколько надо увеличить радиус, чтобы получился круг с удвоенной площадью?
11. Если сторона квадрата равна 1 единице, то найдите длину диагонали.
12. Если сторона квадрата равна 2 единицам, то найдите длину диагонали.
13. Диагональ квадрата равна 5 дюймов. Найдите длину каждой стороны.
14. Диагональ квадрата равна 3 дюймам. Найдите длину каждой стороны.
15. Длина прямоугольника в два раза больше его ширины. Если диагональ равна 10 см, найдите размеры прямоугольника.
16. Длина прямоугольника в два раза больше его ширины. {2}+9{2}+1600\), где t в секундах.
    1. Сколько времени потребуется, чтобы преодолеть половину расстояния до земли?
    2. Сколько времени потребуется, чтобы преодолеть оставшееся расстояние до земли? Округлите до сотых долей секунды.
17. Создайте собственное уравнение, которое можно решить, извлекая корень. Поделитесь им вместе с решением на доске обсуждений.
18. Объясните, почему метод извлечения корней значительно расширяет наши возможности решения квадратных уравнений.
19. Объясните своими словами, как решить путем извлечения корней. 106. Выведите формулу диагонали квадрата через его стороны.

Ответить

1. \(−\sqrt{3}\) или \(\sqrt{3}\)

3. \(−3\sqrt{3}\) или \(3\sqrt{3}\)

5. \(2\sqrt{2}\) см

7. \(3\sqrt{2}\) см

9. Длина: 24 дюйма; ширина: 4 дюйма

11. \(−6+6\sqrt{2}\ок.

2,49\) ед.

13. \(\sqrt{2}\) единиц

15. \(52\sqrt{2}\) дюймов

17. Длина: \(4\sqrt{5}\) футов; ширина: \(2\sqrt{5}\) футов

19. Длина: \(310−−\sqrt{2}\) метров; ширина: \(10−−\sqrt{2}\) метров

21. \(\frac{3}{4}\) секунды

23. а. 2,12 секунды б. 0,88 секунды

25. Ответы могут отличаться

---

Эта страница под заголовком 9.1: Извлечение квадратных корней распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Anonymous.

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Аноним

   Печать CSS

   Плотный

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   3,0

   Программа OER или Publisher

   Издатель, имя которого нельзя называть

   Показать страницу TOC

   нет

2. Теги

   1. корни
   2. квадратный корень

Научитесь решать уравнения, извлекая квадратный корень

Часть 1

В этом видео мы рассмотрим решение уравнений, извлекая квадратный корень.

Например:
Если нам дано уравнение

, мы можем найти x, взяв квадратный корень из обеих частей.

Это оставит нам только x. Однако квадратный корень из 9 — это не просто 3. Он может быть положительным или отрицательным 3. Итак,

Если бы у нас было что-то более сложное, например,

, то сначала нам пришлось бы получить сам по себе. Итак, сначала добавьте 5 к обеим сторонам, чтобы изолировать . Теперь нам осталось. Затем извлеките квадратный корень из обеих сторон



Часть 2

В этом видео мы собираемся более подробно рассмотреть решение уравнений путем извлечения квадратного корня.
Например:
Если нам дано уравнение

, мы можем сначала извлечь квадратный корень из обеих частей.

Это оставит нас с

Затем вычтите 5 с обеих сторон и получите
и
Это приводит нас к окончательному ответу

Если бы у нас было что-то более сложное, например

, то мы сначала должны были бы получить само по себе. Итак, сначала добавьте 3 к обеим сторонам, чтобы изолировать . Теперь нам осталось. Затем извлеките квадратный корень из обеих сторон


Вычтите 2 из обеих сторон

и
Итак


Примеры решения уравнения путем извлечения квадратного корня

Пример 1

Каковы решения ?
Найдите квадратный корень из обеих частей.


Мы можем разбить это на:

Окончательный ответ:

Наши решения:
и

Пример 2

Каковы решения ?
Во-первых, давайте вычтем обе стороны


Затем найдем, извлекая квадратный корень из обеих сторон.




Итак, у нас есть два ответа:

и

Стенограмма видеоурока. Часть 1

Давайте рассмотрим решение уравнений методом извлечения квадратных корней.

Если у нас есть это уравнение:

Чтобы найти значение , мы должны получить квадратный корень.

Сложность здесь заключается в извлечении квадратного корня из .

Потому что он может быть не только положительным, но и отрицательным.

Итак, у нас есть два ответа:

и

Давайте посложнее.

Чтобы решить эту проблему, мы должны сначала уйти сами по себе.

Итак, давайте избавимся, добавив обе части уравнения.

Таким образом, наши решения

{}

Также возможно, что мы получим решение, которое не сработает.

На этом остановимся.

Наши окончательные ответы:

и

Давайте еще один

Мы можем разбить это на:

Я решил написать это, потому что квадратный корень возможен.

Итак, наш ответ

Наши решения:

и

Стенограмма видеоурока.



No related posts.