Примеры двоичная система: Двоичная система счисления

alexxlab / / Разное

Page not found — Сайт skobelevserg!

  • Главная
  • Информатика
  • Практикумы
  • Подготовка к ОГЭ
  • Рабочие программы
  • Используемая литература
  • Об авторах

Unfortunately the page you’re looking doesn’t exist (anymore) or there was an error in the link you followed or typed. This way to the home page.

  • Главная
  • Информатика
    • 5 класс (ФГОС)
      • Информация вокруг нас
      • Компьютер — универсальная машина для работы с информацией
      • Ввод информации в память компьютера
      • Управление компьютером
      • Хранение информации
      • Передача информации
      • Кодирование информации
      • Текстовая информация
      • Представление информации в виде таблиц
      • Наглядные формы представления информации
      • Компьютерная графика
      • Обработка информации
    • 6 класс (ФГОС)
      • Объекты окружающего мира
      • Компьютерные объекты
      • Отношения объектов и их множеств
      • Разновидности объектов и их классификация
      • Системы объектов
      • Персональный компьютер как система
      • Как мы познаем окружающий мир
      • Понятие как форма мышления
      • Информационное моделирование
      • Знаковые информационные модели
      • Табличные информационные объекты
      • Графики и диаграммы
      • Схемы
      • Что такое алгоритм
      • Исполнители вокруг нас
      • Формы записи алгоритмов
      • Типы алгоритмов
      • Управление исполнителем Чертежник
      • Компьютерный практикум
    • 7 класс (ФГОС)
      • Информация и информационные процессы
      • Компьютер универсальное устройство для работы с информацией
      • Обработка графической информации
      • Обработка текстовой информации
      • Технология мультимедиа
    • 8 класс (ФГОС)
      • Математические основы информатики
      • Основы алгоритмизации
      • Начала программирования
    • 9 класс (ФГОС)
      • Моделирование и формализация
      • Алгоритмизация и программирование
      • Обработка числовой информации в электронных таблицах
      • Коммуникационные технологии
    • 10 класс (ФГОС)
      • Информация и информационные процессы
      • Компьютер и его программное обеспечение
      • Представление информации в компьютере
      • Элементы теории множеств и алгебры логики
      • Современные технологии создания и обработки информационных объектов
    • 11 класс (ФГОС)
      • Обработка информации в электронных таблицах
      • Алгоритмы и элементы программирования
      • Информационное моделирование
      • Сетевые информационные технологии
      • Основы социальной информатики
  • Практикумы
    • Google формы
    • Основы работы в Microsoft PowerPoint
    • Создание анимации в презентациях
    • Основы работы в Microsoft Word
    • Основы работы в Microsoft Excel
    • Создание простейшей базы данных
    • Практикум по MS Excel
  • Подготовка к ОГЭ
  • Рабочие программы
  • Используемая литература
  • Об авторах
    • Блоги
    • Сайты

Двоичная система счисления | Презентация к уроку:

Слайд 1

Двоичная система счисления Система счисления. Часть2

Слайд 2

Историческая справка 1703г. – великий немецкий математик Лейбниц ввел в математику двоичную систему счисления. 1936-1938гг. – американский инженер и математик Клод Шеннон предложил использовать двоичную систему счисления для конструирования электрических схем. В двоичной системе счисления для записи чисел используются всего две цифры: 0 и 1, q = 2 .

Слайд 3

Перевод чисел из двоичной системы счисления в десятичную ( N 2  N 10 ) ( через развернутую форму записи числа ) Пример: 1011,01 2 =1*2 3 +0*2 2 +1*2 1 +1*2 0 +0*2 -1 +1*2 -2 =8+2+1+ ¼ =11 ¼ . Таблица степеней числа 2 2 0 2 1 2 2 2 3 2 4 2 5 2 6 2 7 2 8 2 9 2 10 ___________________________________________________________________________________________________________________ 2 4 8 16 32 64 128 256 512 1024 Задание 8: переведите в десятичную систему счисления 10110,011 2 110101,1 2 10101,101 2

Слайд 4

Перевод целых чисел из десятичной системы счисления в двоичную ( N 10  N 2 ) Способ – деление на основание системы счисления 22 10 =10110 2 Задание 9: переведите десятичные числа 27; 35; 54; 66 в двоичную систему счисления

Слайд 5

Арифметические операции с двоичными числами. Рассмотрим правила выполнения арифметических операций над одноразрядными числами. Представим их в виде таблиц. Правило сложения Правило вычитания Правило умножения 0+0=0 0-0=0 0*0=0 0+1=1 1-0=1 0*1=0 1+0=1 1-1=0 1*0=0 1+1=10 0-1=-1 1*1=1 1+1+1=11

Слайд 6

Арифметические операции с двоичными числами. Примеры. 1. 1010+10101=11111 1010 10101 11111 2. 10101-1010=1011 10101 1010 1011 3. 10111*11=1000101 10111 11 10111 10111 1000101

Слайд 7

Упражнения Произведите сложение двоичных чисел: 111+101; 11011+1110 Выполните вычитание двоичных чисел: 111-101; 11011-01110 Умножьте двоичные числа: 111*101; 11011*1110

Слайд 8

Перевод десятичных дробей в двоичную систему счисления ( N 10  N 2 ) (умножением на 2) Пример: 0,5625 10 = N 2 = 0,1001 2 0, 5625 2 1 1250 2 0 2500 2 0 5000 2 1 0000 Задание 10: переведите десятичные дроби в двоичную систему счисления с точностью до 6 знаков после запятой: 0,7 10 0,4622 10 0,5198 10 0,5803 10

Слайд 9

Перевод смешанных чисел из десятичной системы счисления в двоичную Алгоритм перевода: 1) перевести целую часть; 2) перевести дробную часть; 3) сложить полученные результаты. Пример : перевести 17,25 10 в двоичную систему счисления. Решение: 17 10 = 10001 2 0,25 10 = 0,01 2 17,25 10 = 10001,01 2 Задание 11: переведите в двоичную систему счисления числа: 40,5 10 31,75 10 124,25 10

Слайд 10

Упражнения: Переведите в двоичную запись десятичные числа: 17; 48; 193; 513 используя правило деления на 2. 2. Переведите в десятичную запись двоичные числа: 1001; 10111; 1011000; 10111011

Слайд 11

Основной недостаток двоичной системы – ее громоздкость. Более компактной является восьмеричная система счисления с основанием 8. В ней используется восемь символов 0,1,2,3,4,5,6,7, заимствованных из десятичной. Для представления двоичных чисел восьмеричными цифрами разряды двоичного числа объединяют в группы по три (триады), начиная с младшего разряда, а дробную часть, со старшего и каждую триаду преобразуют в восьмеричный эквивалент: 11111101 2 = 011 111 101 =375 =3*8 2 +7*8 1 +5*8 0 =253 Восьмеричная и шестнадцатиричная система счисления.

Слайд 12

Если для образования триад не хватает разрядов, то добавляют незначащие нули. Еще более компактную форму записи двоичных чисел дает шестнадцатиричная система счисления, в которой используется 16 символов: 0,1,2,3,4,5,6,7,8,9,А,В,С, D ,Е, F . Десять символов заимствованы из десятичной системы, а в качестве недостающих использованы буквы латинского алфавита: А-10, В-11, С-12, D -13, Е-14, F -15. Процедура преобразования двоичного числа в шестнадцатиричное довольно проста. Двоичное число разбивается на четверки (тетрады),начиная с младшего разряда, а дробная часть со старшего и каждая тетрада заменяется шестнадцатиничным символом: 10101011111101 =0010 1010 1111 1101 =2А FD 1111000101111011 2 = Восьмеричная и шестнадцатиричная система счисления.

Слайд 13

Таблица двоичных кодов десятичных и шестнадцатеричных 1 2 3 4 5 6 7 8 9 A B C D E F 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

Слайд 14

1111000101111011 2 = F17B 16 Ответ

Слайд 15

1. выполните сложение и проведите проверку 11010101 2 +1110 2 2. выполните вычитание и результат переведите в десятичную СС: 110101110 2 -10111111 2 3.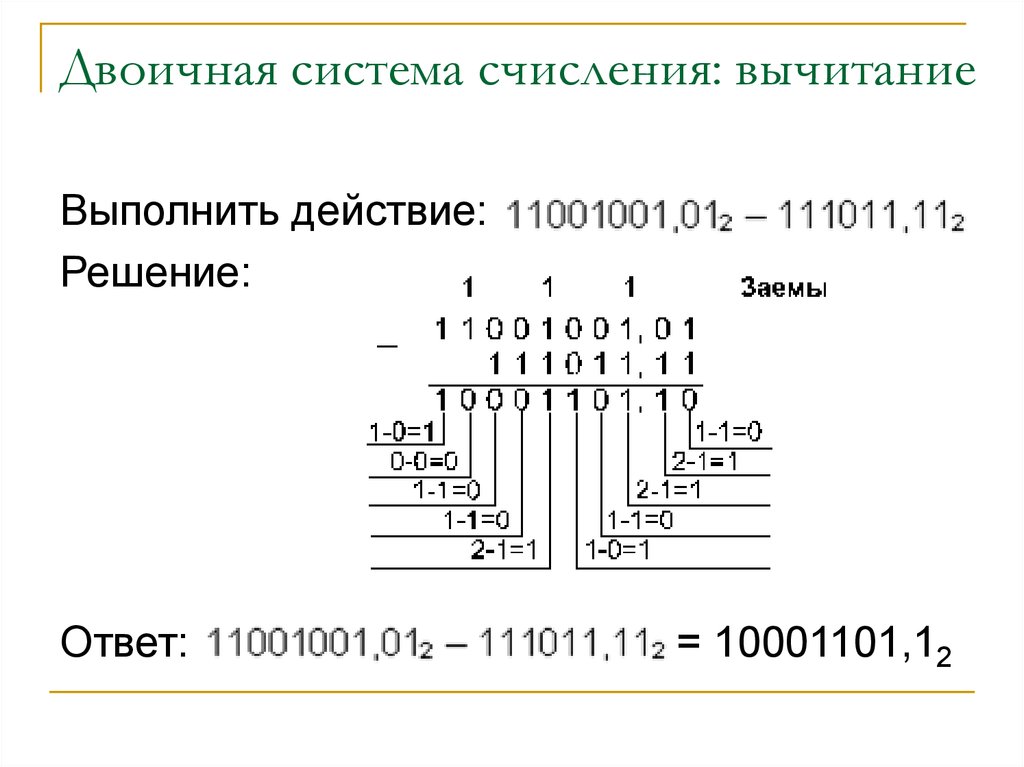 выполните умножение и результат переведите в десятичную СС: 111100 2 *100100 2 4. переведите из 10-ой СС в 2-ичную, 8 –ричную,16- ричную СС числа: 126, 533 5. запишите в развернутом виде (по формуле) числа: 657; 15А12 Самостоятельная работа

Двоичная система счисления

— определение, преобразование, примеры

Двоичная система счисления — это один из четырех типов систем счисления, используемый для определения числа в двоичной системе. Двоичная система счисления представляет число только двумя цифрами, то есть 0 (ноль) и 1 (единица). В слове «двоичный» «би» означает «два». В результате это возвращает линию к представлению числа, используя только числа 0 и 1. Система счисления с основанием 2 используется для представления двоичных чисел. Например, (1101) 2 — двоичное число, где 2 — основание. Каждая цифра в двоичной системе счисления называется «бит».

Эта система счисления широко используется в компьютерах. Все входные данные, поступающие на компьютер, декодируются им в последовательность 0 или 1 перед дальнейшей обработкой, поскольку компьютер может понимать только двоичную информацию, которая представлена ​​числами 0 или 1. Десятичное число просто преобразовать в числовое значение. двоичное число и наоборот. Обозначения для десятичных чисел и двоичных чисел различны. Например, десятичная дробь представлена ​​как (15) 10 , где 10 — основание десятичного числа, а соответствующее двоичное число представлено как (1111) 2 , где 2 — основание двоичного числа.

Binary Number Table

0002 101

999

Decimal Number

Binary Number

Decimal Number

Binary Number

1

001

11

1011

2

010

12

1100

3

011

13

1101

4

100

14

1110

5

5

5

15

1111

6

110

16

10000

7

111

17

10001

8

1000

18

10010

110

9

1001

19

10011

10

1010

20

10100

Binary to Decimal Преобразование

Двоичное число преобразуется в десятичное число путем умножения каждой цифры двоичного числа на степень 1 или 0 до соответствующей степени 2. Предположим, что двоичное число имеет n цифр, B = a n-1 …a 3 a 2 a 1 a 0 . Теперь соответствующее десятичное число задается в виде ) + (а 1 × 2 1 ) + (а 0 × 2 0 ).

Давайте рассмотрим пример, чтобы лучше понять концепцию.

Пример: Преобразование (10011) 2 в десятичное число.

Решение:

Данное двоичное число равно (10011) 2 .

(10011) 2 = (1 х 2 4 ) + (0 х 2 3 ) + (0 х 2 2 ) + (1 х 2 1 ) + (1 х 2 1 ) + (1 х 9 2 ) 0 )

= 16 + 0 + 0 + 2 + 1 = (19)10

Следовательно, двоичное число (10011) 2 выражается как (19) 10 .

Преобразование десятичного числа в двоичное

Десятичное число преобразуется в двоичное путем непрерывного деления заданного десятичного числа на 2 до тех пор, пока мы не получим частное равное 1, и записываем числа снизу вверх.

Давайте рассмотрим пример, чтобы лучше понять концепцию.

Пример: Преобразуйте (28) 10 в двоичное число.

Решение:

 

Следовательно, (28) 10 выражается как (11100) 2 .

Арифметическая операция над двоичными числами

Двоичное сложение

Результат сложения двух двоичных чисел также является двоичным числом. Чтобы получить результат сложения двух двоичных чисел, мы должны сложить разряд двоичных чисел по разряду. Помните таблицу, приведенную ниже, при сложении двух двоичных чисел.

 Binary number 1 

 Binary number 2 

 Addition 

 Carry 

0

0

0

0

0

1

1

0

1

1

0046

0

1

0

1

1

0

1

Binary Subtraction

The result вычитания двух двоичных чисел также является двоичным числом.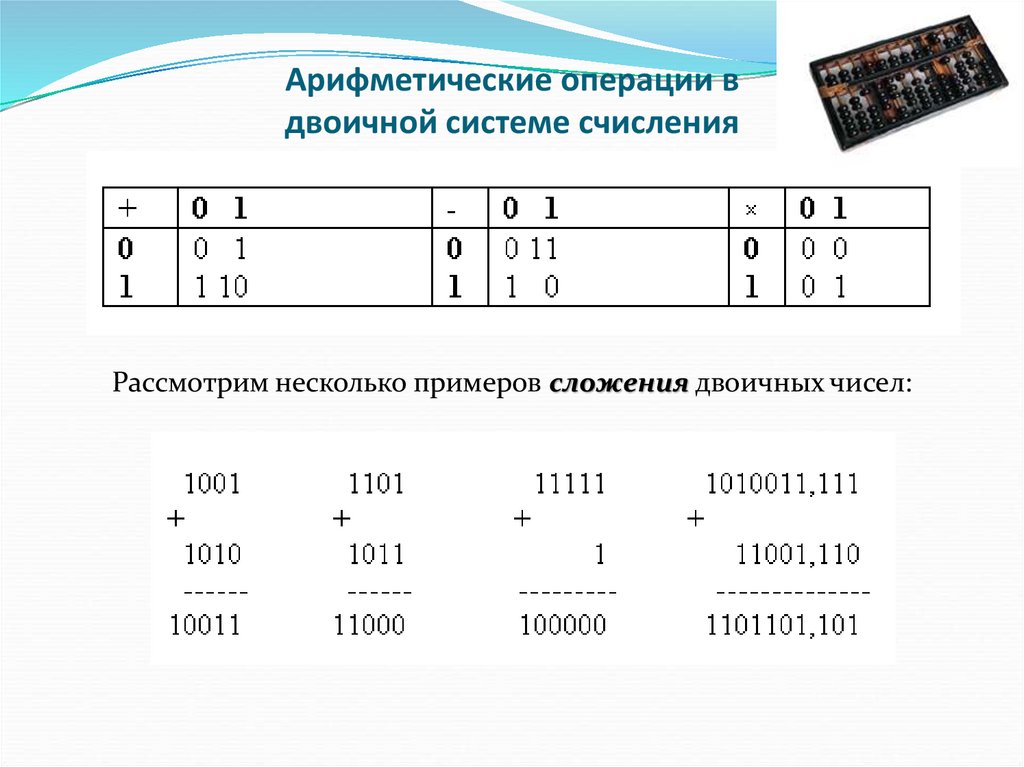 Чтобы получить результат вычитания двух двоичных чисел, мы должны вычесть разряд двоичных чисел за разрядом. Вспомните таблицу, приведенную ниже, при вычитании двух двоичных чисел.

 Binary number 1 

 Binary number 2 

 Subtraction 

 Borrow 

0

0

0

0

0

1

1

1

1

1

0046

0

1

0

1

1

0

0

Binary Multiplication

The multiplication процесс двоичных чисел аналогичен умножению десятичных чисел. Правила умножения любых двух двоичных чисел следующие:

1

0011

 Binary number 1 

 Binary number 2 

 Multiplication 

0

0

0

0

1

0

1

0

0

1

1

1

1

Двоичное деление

Метод деления двоичных чисел аналогичен методу деления десятичных чисел.

Давайте рассмотрим пример, чтобы лучше понять концепцию.

Пример: Разделить (101101) 2 на (110) 2 .

Решение:

 

Дополнение 1 и 2 двоичного числа
  • Дополнение до 1 двоичного числа получается путем инвертирования цифр двоичного числа.

Пример: Определить дополнение до 1 числа (10011) 2 .

Решение:

Данное двоичное число равно (10011)2.

Теперь, чтобы найти его дополнение до 1, мы должны инвертировать цифры данного числа.

Таким образом, дополнение (10011) 2 до 1 равно (01100) 2 .

  • Дополнение до 2 двоичного числа получается путем инвертирования цифр двоичного числа, а затем добавления 1 к младшему значащему биту.

Пример: Определите дополнение до 2 (1011) 2 .

Решение:

Данное двоичное число равно (1011)2.

Чтобы найти дополнение до 2, сначала найдите его дополнение до 1, т. е. (0100) 2 .

Теперь, прибавив 1 к младшему значащему биту, мы получим (0101) 2 .

Следовательно, дополнение до 2 (1011) 2 равно (0101) 2 .

Задачи на основе двоичной системы счисления

Задача 1. Преобразование десятичного числа (98) 10 в двоичное.

Решение:

Чтобы получить двоичное число для 98, мы должны непрерывно разделить его на 2. .

Задача 2. Преобразование двоичного числа (1010101) 2 в десятичное число.

Решение:

Данный двоичный номер составляет (1011101) 2

= (1 × 2 0 ) + (0 × 2 1 ) + (1 × 2 2 ) 1 ) + (1 × 2 2 ) 1 ) + (1 × 2 2 ) + (1 × 2 2 + (0 × 2 3 ) + (1 × 2 4 ) + (0 × 2 5 ) + (1 × 2 6 )

= 1 + 0 + 4 + 0 + 16 + 0 + 64

= (85) 10

Таким образом, двоичное число 1010101 равно 85 в десятичном виде.

Задача 3: Разделить (11110) 2 на (101) 2 .

Решение:

 

Задача 4. Сложите (11011) 2 и (10100) 2 .

Решение:

 

Следовательно, (11011) 2 + (10100) 2 = (101111) 2 .

Задача 5: Вычесть (11010) 2 и (10110) 2 .

Решение:

Следовательно, (11010) 2 – (10110) 2 = (00100)

1 2 .

Задача 6: Умножьте (1110) 2 и (1001) 2 .

Решение:

Таким образом, (1110) 2 × (1001) 2 = (1111110)

1 2 .


Двоичная система счисления Определение и значение

  • Лучшие определения
  • Викторина
  • Примеры

Сохраните это слово!

Метод представления чисел, основанный на 2 и использующий только цифры 0 и 1. Каждая последующая цифра представляет собой степень числа 2. Например, 10011 представляет (1 X 24) + (0 X 23) + ( 0 X 22) + (1 X 21) + (1 X 20), или 16 + 0 + 0 + 2 + 1, или 19.

КОНТРОЛЬ

ВЫ ПРОПУСТИТЕ ИЛИ ЗАПОЛНИТЕ ЭТИ ГРАММАТИЧЕСКИЕ ВОПРОСЫ?

Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!

Вопрос 1 из 7

Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.

Слова рядом с двоичной системой счисления

двоичная цифра, двоичное деление, двоичная форма, двоичная запись, двоичное число, двоичная система счисления, двоичная операция, двоичная оппозиция, двоичный пульсар, двоичная звезда, двоичная система

Научный словарь American Heritage® Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.

Как использовать двоичную систему счисления в предложении

  • Было много положительных отзывов от людей, интересующихся неполовобинарными людьми.

    Проблема трансгендерных знакомств Grindr|Дэвид Левсли|9 января 2015 г.|DAILY BEAST

  • «Наши участники продолжают сталкиваться с рядом проблем», — сказала она.

    Война республиканцев с Кале|Патриция Мерфи|7 января 2015 г.|DAILY BEAST

  • В 2014 году на регулярных рейсах коммерческой авиации не было ни одного случая смерти в системе, выполняющей 68 000 рейсов в день.

    Раздражающие задержки в аэропорту могут помешать вам стать следующей AirAsia 8501|Клайв Ирвинг|6 января 2015 г.|DAILY BEAST

  • Однако количество несогласных беспрецедентно для современной эпохи.

    Демократы случайно спасли Бонера от республиканского переворота|Бен Джейкобс, Джеки Кусинич|6 января 2015 г.|DAILY BEAST

  • Она наполняет своих персонажей — сильных женщин, сопротивляющихся сексистской системе — такой сердечной.

    Оскар 2015: Выбор The Daily Beast, от Скарлетт Йоханссон до «Отрочества»|Марлоу Стерн|6 января 2015 г.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *