Примеры исследование функции с помощью производной и построение графика: Исследование функции и построение графика функции

Алгоритм исследования функции с помощью производной и построения ее графика — Студопедия

Поделись  

Практическое занятие №49

Тема: «Исследование функций и построение их графиков с помощью производной»

Задание №1.Пройдите по ссылке и посмотрите примеры исследования функци и построение графиков с помощью производно (там я объясняю)

Если видео не загружается, посмотрите разобранный пример ниже.

Задание №2.Выполните практическую работу.Решаете только 1 пример из двух предложенных на ваш выбор.

Алгоритм исследования функции с помощью производной и построения ее графика

1. Находим область определения D(f) функции y = f(x).

2. Проверяем функцию на четность.

Если f(-x) = f(x), то функция четная,график функции симметричен относительно оси OY.

Если f(-x) = — f(x),

то функция нечетная,график нечетной функции симметричен относительно начала координат.

В противном случае функция является ни четной, ни нечетной.

3. Если функция периодическая, то находим период функции.

4. Находим точки пересечения графика с осями координат.

Находим нули функции — это точки пересечения графика функции с осью абсцисс (Ox).

Для этого мы решаем уравнение f(x) = 0.

Находим точку пересечения графика функции с осью ординат (Oy). Для этого ищем значение функции при x=0.

5. Промежутки монотонности (возрастания и убывания функции)

Для этого мы следуем привычному алгоритму.

а) Находим производную

б) Приравниваем производную к нулю и находим критические точки функции (  и область определения производной)

Промежутки, на которых производная отрицательна, являются промежутками убывания функции.

Точки, в которых производная меняет знак с плюса на минус, являются точками максимума.

Точки, в которых производная меняет знак с минуса на плюс, являются точками минимума.

7. Найти значения функции в точках экстремума.

8. По данным исследования построить график функции.

 

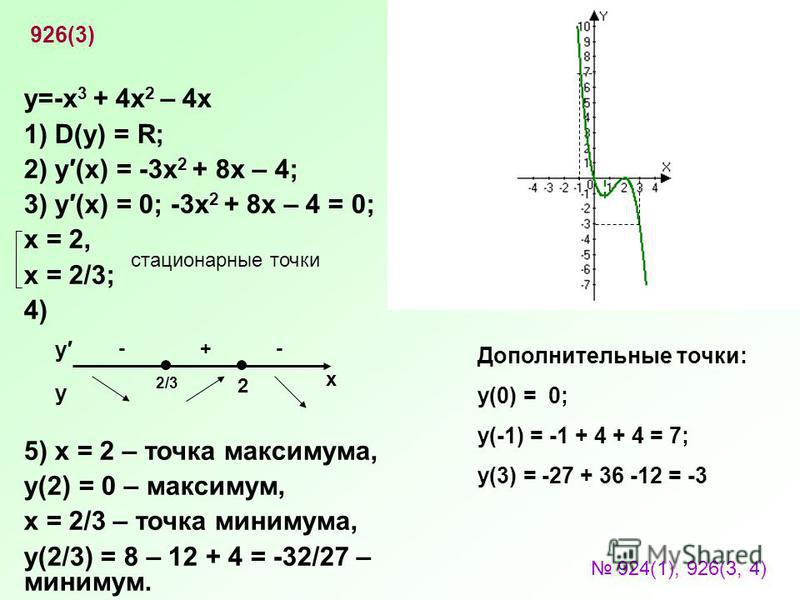
Пример 1. Исследовать функцию и по результатам исследования построить график.

Решение.

1) D(f): R

2) Проверим функцию на чётность/нечётность:

, значит, данная функция не является чётной или нечётной.

3) Функция непериодическая.

4) Нули функции.

С осью Оy:

Чтобы найти точки пересечения с осью Ox (нули функции) требуется решить уравнение f(x) = 0:

5,6) Найдём критические точки:

Отложим их на числовой прямой и определим знаки производной:
1
Следовательно, функция возрастает на и убывает на .
Экстремумы функции

точка максимума, так как при переходе через нее производная меняет знак с «+» на «-»

. точка  минимума, так как при переходе через нее производная меняет знак с «-» на «+».

7).

.

8) Строим график функции.



Применение производной к построению графиков функций

Урок 13. Алгебра 11 класс ФГОС

Данный видеоурок будет посвящён применению производной к построению графиков функций. Мы приведём общую схему исследования свойств функции с помощью её производной. Будем строить график функции, используя результаты исследования.

Конспект урока «Применение производной к построению графиков функций»

Сегодня на уроке мы приведём общую схему исследования свойств функции с помощью её производной. Будем строить график функции, используя результаты исследования.

Прежде чем приступить к рассмотрению новой темы, давайте вспомним, что на предыдущих занятиях мы рассмотрели применение производной к нахождению промежутков возрастания и убывания функций. Выяснили, какие точки называют точками максимума функции и точками минимума функции. Научились находить эти точки и значения функции в них. Сегодня на уроке мы применим эти знания к построению графиков функций.

Давайте начнём с примера. Итак, постройте график функции .

Полученные результаты исследования функции удобно записать в виде следующей таблице.

В первой строке этой таблицы указаны в порядке возрастания критические точки функции и ограниченные ими промежутки. Во второй строке отмечены знаки производной на этих промежутках. В третьей строке записаны выводы о ходе изменения данной функции, в четвёртой строке – о виде критических точек.

При построении графика обычно находят точки пересечения графика с осями координат.

Построим график функции.

Получается, что для построения графика функции сначала исследуют свойства этой функции с помощью её производной.

Давайте приведём схему исследования свойств функции с помощью её производной.

Итак, при исследовании свойств функции надо найти:

1) область определения; производную; стационарные точки;

2) промежутки возрастания и убывания;

3) точки экстремума и значения функции в этих точках.

Результаты исследования удобно записать в виде таблицы, используя которую, строят график функции. Для более точного построения графика обычно находят точки пересечения с осями координат. Также можно найти координаты ещё нескольких точек графика.

Отметим, что для построения графика чётной (нечётной) функции достаточно исследовать свойства и построить её график при , а затем отразить его симметрично относительно оси ординат (начала координат).

Давайте построим график функции .

Полученные результаты исследования запишем в виде таблицы.

Найдём значение функции в точке  – крайней точке рассматриваемого интервала. .

Построим график функции.

Так как рассматриваемая функция является нечётной, то её график при  строим с помощью симметрии относительно начала координат.

Часто встречаются задачи, в которых требуется исследовать функцию не на всей области определения, а на некотором промежутке.

Давайте построим график функции  на отрезке .

Запишем полученные результаты исследования функции в виде таблицы.

Получается, что график функции не пересекает ось абсцисс.

Построим график функции.

Предыдущий урок 12 Экстремумы функции

Следующий урок 14 Наибольшее и наименьшее значения функции

Получите полный комплект видеоуроков, тестов и презентаций Алгебра 11 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

График производной | Исчисление I

Результаты обучения

• График производной функции по графику заданной функции
• Установить связь между производными и непрерывностью
• Опишите три условия, при которых функция не имеет производной

Графики производных функций

Мы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение производной функции, мы можем построить его график. {\prime}(x)=+\infty[ /latex], что соответствует вертикальной касательной к [latex]f(x)[/latex] в точке 0,9{\prime}(x)[/latex] над осью [latex]x[/latex]?

Показать решение

Попробуйте

Производные и непрерывность

Теперь, когда мы можем построить график производной, давайте рассмотрим поведение графиков. Сначала рассмотрим связь между дифференцируемостью и непрерывностью. Мы увидим, что если функция дифференцируема в точке, она должна быть там непрерывной; однако функция, непрерывная в точке, не обязательно должна быть дифференцируемой в этой точке. На самом деле функция может быть непрерывной в точке и не быть дифференцируемой в этой точке по одной из нескольких причин. 9{\prime}(a)=\underset{x\to a}{\lim}\dfrac{f(x)-f(a)}{xa}[/latex]

 

Мы хотим показать, что [ латекс]f(x)[/latex] непрерывен в [latex]a[/latex], показывая, что [latex]\underset{x\to a}{\lim}f(x)=f(a)[/ латекс]. Таким образом,

[латекс]\begin{array}{lllll} \underset{x\to a}{\lim}f(x) & =\underset{x\to a}{\lim}(f(x) -f(a)+f(a)) & & & \\ & =\underset{x\to a}{\lim}(\frac{f(x)-f(a)}{x-a}\cdot ( x-a)+f(a)) & & & \text{Умножить и разделить} \, f(x)-f(a) \, \text{by} \, x-a.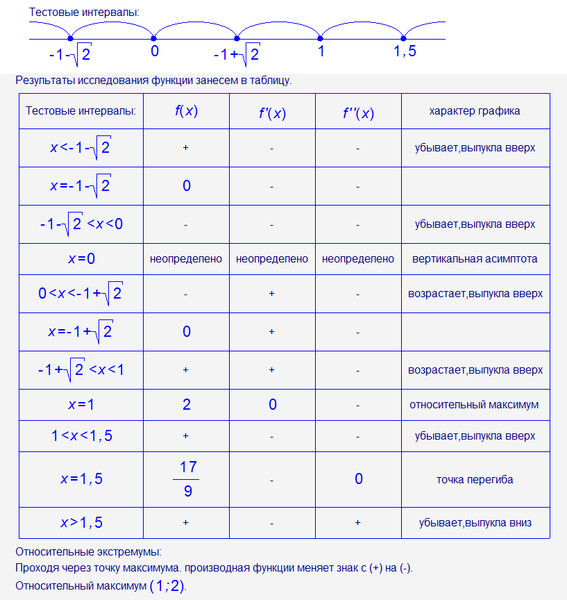 {\prime}(0)[/латекс] не определен. Это наблюдение приводит нас к мысли, что непрерывность не влечет дифференцируемости. Давайте исследовать дальше. Для [латекс]f(x)=|x|[/латекс], 9{\prime}(0)[/latex] не существует. Беглый взгляд на график [latex]f(x)=\sqrt[3]{x}[/latex] проясняет ситуацию. Функция имеет вертикальную касательную в точке 0 (рис. 7).

Рис. 7. Функция [latex]f(x)=\sqrt[3]{x}[/latex] имеет вертикальную касательную в точке [latex]x=0[/latex]. Она непрерывна в 0, но не дифференцируема в 0.

Функция [latex]f(x)=\begin{cases} x \sin\left(\frac{1}{x}\right) & \text{ if } \, x \ne 0 \\ 0 & \text{ if } \, x = 0 \end{cases}[/latex] также имеет производную, которая демонстрирует интересное поведение при 0. Мы видим, что 9{\ prime} (0) = \ underset {x \ to 0} {\ lim} \ dfrac {x \ sin \ left (\ frac {1} {x} \ right) -0} {x-0} = \ underset{x\to 0}{\lim} \sin\left(\dfrac{1}{x}\right)[/latex]

 

Этот предел не существует, в основном потому, что наклоны секущих непрерывно меняют направление по мере приближения к нулю (рис.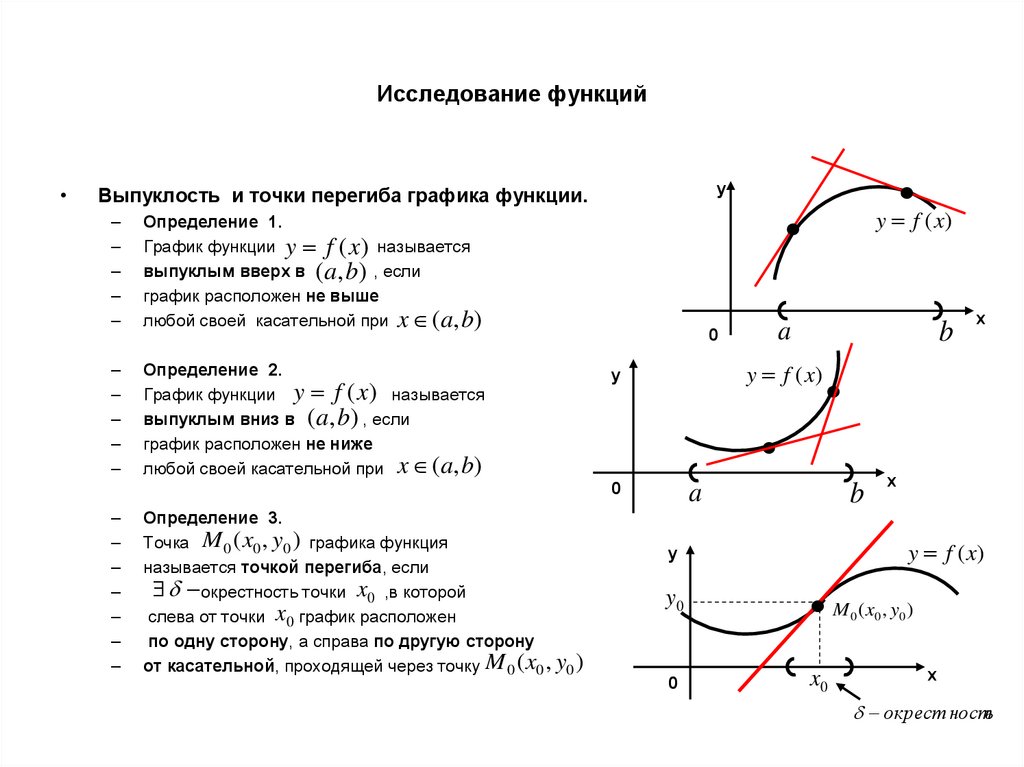 8).

Рис. 8. Функция [latex]f(x)=\begin{cases} x \sin(\frac{1}{x}) & \text{ if } \, x \ne 0 \\ 0 & \ text{ if } \, x = 0 \end{cases}[/latex] не дифференцируем в точке 0,

 

Итого:

1. Заметим, что если функция не непрерывна, она не может быть дифференцируемой, поскольку каждая дифференцируемая функция должна быть непрерывной. Однако, если функция непрерывна, она может не быть дифференцируемой.
2. Мы видели, что [latex]f(x)=|x|[/latex] не может быть дифференцируемым в 0, потому что пределы наклона касательных линий слева и справа не совпадают. Визуально это вылилось в острый угол на графике функции в 0. Отсюда делаем вывод, что для того, чтобы быть дифференцируемой в точке, функция должна быть в этой точке «гладкой».
3. Как мы видели на примере [latex]f(x)=\sqrt[3]{x}[/latex], функция не может быть дифференцируемой в точке, где есть вертикальная касательная.
4. Как мы видели с [латексом]f(x)=\begin{cases} x \sin(\frac{1}{x}) & \text{ if } \, x \ne 0 \\ 0 & \text{ если } \, x = 0 \end{cases}[/latex] функция может не быть дифференцируемой в точке и более сложными способами.

 

Пример. Кусочная непрерывная и дифференцируемая функция 92 + bx + c & \text{, если } \, x

< -10 \\ -\frac{1}{4}x + \frac{5}{2} & \text{, если } \, x \ge - 10 \end{cases}[/latex], где [latex]x[/latex] и [latex]f(x)[/latex] указаны в дюймах. Чтобы вагон двигался по трассе плавно, функция [latex]f(x)[/latex] должна быть непрерывной и дифференцируемой при -10. Найдите значения [latex]b[/latex] и [latex]c[/latex], которые делают [latex]f(x)[/latex] непрерывными и дифференцируемыми.

Рис. 9. Для плавного движения автомобиля по трассе функция должна быть одновременно непрерывной и дифференцируемой. 92 & \text{ if } \, x \ge 3 \end{cases}[/latex] оба непрерывны и дифференцируемы в 3.

Показать решение

Производные и форма графика: значение

Пеший туризм может быть способом соединения исчисления с природой. Идти в гору совершенно иначе, чем спускаться с нее, и в большинстве случаев легче подниматься, чем спускаться. Не говоря уже о том, что некоторые холмы могут быть круче других!

Просто взглянув на холм, вы можете заранее узнать, будет ли на него легко подняться или нет, его форма на самом деле дает вам информацию!

Вместо того, чтобы думать о холме, вы можете представить график. Форма и производные функции могут дать важную информацию о ее поведении, поэтому здесь мы рассмотрим, как связаны производные и форма графика.

Производные и форма графика Значение

Говоря о форме графика, сначала может показаться немного расплывчатым. Какие фигуры присутствуют на графике?

В исчислении форма графика относится к важным содержит различных участков графика:

• Увеличивается или уменьшается?
• Это выше или ниже оси x?
• У него крутой склон?
• Его касательные лежат ниже или выше графика?

Вышеуказанные функции могут применяться к различным участкам или интервалам графика. График может увеличиваться на одном интервале и уменьшаться на другом!

Связь между производными и формой графика

Теперь, когда вы увидели значение формы графика в исчислении, вам может быть интересно узнать, как задействованы производные.

Производные измеряют изменение, , поэтому наличие производной функции является ключом к пониманию того, как изменяется ее график.

Первая производная говорит вам, является ли график увеличением или уменьшением .

Вторая производная говорит вам, изгибается ли график вверх или кривые вниз.

Зная эту информацию, достаточно, чтобы грубо набросать график функции без использования программного обеспечения для построения графиков!

Влияние первой производной на форму графика

Как было сказано ранее, первая производная функции говорит вам, увеличивается или уменьшается функция в определенном интервале. Вот как это работает:

• Функция \(f (x) \) равна , увеличивая на интервале, где ее производная равна .положительный , то есть \(f'(x) > 0\).
• Функция на уменьшается на в интервале, где ее производная отрицательна на , то есть \( f'(x) <0\).

Вы также можете дать графическую интерпретацию приведенным выше утверждениям, то есть

• Функция возрастает на интервале, где наклон линии, касательной к ее графику, положителен.
• Функция убывает на интервале, где наклон линии, касательной к ее графику, отрицательный.

Рисунок 1. Убывающий и возрастающий интервалы функции

Точки, в которых \(f'(x)=0 \), известны как критических точек. В функциях с непрерывными производными критическими точками могут быть точки, в которых функция переключается с возрастающей на убывающую или наоборот. Для получения дополнительной информации по этой теме, пожалуйста, ознакомьтесь с нашей статьей о первом тесте производных!

Влияние второй производной на форму графика первую производную функции, то есть путем дифференцирования функции два раза подряд. Вторая производная функции, если она существует, говорит вам, в какую сторону изгибается функция. Для этой идеи в исчислении есть два специальных слова: 9.

0019 Вогнутая и выпуклая .

Говорят, что функция является вогнутой вниз или просто вогнутой в интервале, где ее вторая производная отрицательна. Прямые, касательные к графику функции внутри интервала, где она вогнута, будут лежать на выше графика на .

Рис. 2. Касательная к функции в интервале, где она выпукла, лежит над графиком

А что, если касательные лежат под графиком?

Говорят, что функция вогнут вверх или выпукло в интервале, где его вторая производная положительна. Прямые, касательные к графику функции внутри интервала, где она выпукла, будут лежать на ниже графика.

Рис. 3. Прямая, касающаяся функции в интервале, где она выпукла, лежит под графиком

Вогнутость графика не зависит от возрастания или убывания! Вы можете иметь, например, вогнутый убывающий интервал или выпуклый убывающий интервал. Возможны все четыре комбинации!

На следующих графиках вы можете увидеть разницу между вогнутыми и выпуклыми функциями с помощью графиков.

Обе указанные ниже функции увеличиваются. Однако обратите внимание, как они изгибаются по-разному.

Рисунок 4. Касательная находится над функцией, поэтому она вогнутая

Рисунок 5. Касательная находится под функцией, поэтому она выпуклая

Теперь обе функции ниже убывающие. Обратите особое внимание на изгиб.

Рис. 6. Касательная находится над функцией, поэтому она вогнутая

Рис. 7. Касательная линия находится под функцией, поэтому она выпуклая

Точки, в которых функция переключается с вогнутой на выпуклую или наоборот, называются точками перегиба. Для получения дополнительной информации по этой теме, пожалуйста, обратитесь к нашей статье о тесте второй производной.

Примеры влияния первой и второй производной на форму графика

Первую производную функции можно использовать для нахождения интервалов возрастания или убывания функции. Вот пример того, как это делается. 92-4>0,\]

, которые можно разложить как

\[(x+2)(x-2)>0.\]

Приведенное выше неравенство утверждает, что произведение двух выражений больше нуля . Это означает, что оба выражения имеют одинаковый знак, поэтому либо

\[ x+2>0 \quad \text{and} \quad x-2>0 \]

, либо

\[ x+2<0 \ quad \text{and} \quad x-2<0.\]

Решение приведенного выше составного неравенства показывает, что \( x>2 \) или \(x<-2\), поэтому функция возрастает в интервале \( (-\infty,-2) \) и в интервале \( (2,\infty)\).

Чтобы найти, где функция убывает, вы можете решить неравенство

\[ f'(x) <0,\]

, но поскольку вы уже решили подобное равенство, оставшийся интервал является убывающим интервалом, поэтому функция убывает на интервале \((-2,2)\).

Чтобы убедиться, что ваш результат имеет смысл, вы должны закончить, взглянув на график данной функции.

Рис. 8. Функция имеет один убывающий интервал и два возрастающих интервала 92-4. \]

Снова используя степенное правило, вы можете найти вторую производную, поэтому

\[ f»(x)=2x.\]

Чтобы найти интервалы, в которых функция вогнута, вы нужно решить неравенство

\[ f»(x) < 0,\]

то есть

\[2x <0,\]

решение которого

\[ x<0.\]

Это означает, что функция вогнута в интервале \( (-\infty,0) \).

Чтобы найти интервалы, на которых функция выпукла, нужно решить неравенство

\[ f»(x) >0, \]

но поскольку вы только что решили подобное неравенство, вы можете просто поменять знак неравенства, поэтому

\[ x>0\]

дает вам интервал, где функция выпуклая, то есть \((0,\infty)\).

Рис. 9. Функция вогнута на одном интервале и выпукла на другом

Производные и форма графика — основные выводы

• Производная функции может сказать, возрастает или убывает функция на интервале.
  • Если \( f'(x) >0\), \( f(x) \) равно , увеличивая .

    No related posts.