Навигация по странице: |
|
Физический смысл производной функции. Задачи на физический смысл производной: примеры решения
Математические задачи находят своё применение во многих науках. К таковым следует отнести не только физику, химию, технику и экономику, но также медицину, экологию и прочие дисциплины. Одним из важных понятий, которое следует освоить, чтобы находить решения важных дилемм, является производная функции. Физический смысл её объяснить совсем не так сложно, как может показаться непосвящённому в суть вопроса. Достаточно лишь найти подходящие примеры тому в реальной жизни и обычных бытовых ситуациях. На самом деле любой автомобилист справляется с подобной задачей каждый день, когда смотрит на спидометр, определяя скорость своей машины в конкретное мгновение фиксированного времени. Ведь именно в этом параметре заключена суть физического смысла производной.
Как найти скорость
Определить скорость движения человека по дороге, зная пройденное расстояние и время в пути, с лёгкостью может любой пятиклассник. Для этого следует первую из заданных величин разделить на вторую. Но не каждый из юных математиков знает о том, что в данный момент находит отношение приращений функции и аргумента. Действительно, если представить движение в виде графика, откладывая по оси ординат путь, а по абсциссе — время, это будет именно так.
Однако скорость пешехода или любого другого объекта, которую мы определяем на большом участке пути, считая движение равномерным, вполне может меняться. В физике известно множество форм движения. Оно может совершаться не только с постоянным ускорением, но замедляться и возрастать произвольным образом. Следует обратить внимание, что в данном случае линией, описывающей перемещение, будет уже не прямая. Графически она может принимать самые сложные конфигурации. Но для любой из точек графика мы всегда можем провести касательную, представленную линейной функцией.
Для уточнения параметра изменения перемещения в зависимости от времени приходится сокращать измеряемые отрезки. Когда же они станут бесконечно малыми, вычисляемая скорость окажется мгновенной. Данный опыт помогает нам дать определение производной. Физический смысл её также логически вытекает из подобных рассуждений.
С точки зрения геометрии
Известно, что чем больше скорость тела, тем круче график зависимости перемещения от времени, а значит, и угол наклона касательной к графику в какой-то определённой точке. Показателем подобных изменений может стать тангенс угла между осью абсцисс и линией касательной. Как раз он определяет значение производной и вычисляется отношением длин противолежащего к прилежащему катету в прямоугольном треугольнике, образованном перпендикуляром, опущенным из некоторой точки на ось абсцисс.
В этом заключается геометрический смысл первой производной. Физический же раскрывается в том, что величина противолежащего катета в нашем случае представляет собой пройденный путь, а прилежащего – время. При этом отношением их является скорость. И снова мы приходим к выводу, что мгновенная скорость, определяемая при стремлении обоих промежутков к бесконечно малому, и является сутью понятия производной, указывая на её физический смысл. Второй производной в данном примере будет ускорение тела, демонстрирующее, в свою очередь, степень изменения скорости.
При этом отношением их является скорость. И снова мы приходим к выводу, что мгновенная скорость, определяемая при стремлении обоих промежутков к бесконечно малому, и является сутью понятия производной, указывая на её физический смысл. Второй производной в данном примере будет ускорение тела, демонстрирующее, в свою очередь, степень изменения скорости.
Примеры нахождения производных в физике
Производная – это показатель скорости изменения любой функции, даже когда речь не идёт о движении в прямом смысле слова. Чтобы наглядно продемонстрировать это, приведём несколько конкретных примеров. Допустим, сила тока, завися от времени, изменяется согласно следующему закону: I = 0,4t2. Требуется найти значение скорости, с которой происходит изменение этого параметра в конце 8-й секунды процесса. Заметим, что сама искомая величина, как можно судить из уравнения, постоянно возрастает.
Для решения требуется найти первую производную, физический смысл которой был рассмотрен ранее. Здесь dI/dt = 0,8t. Далее найдём оную при t=8, получим, что скорость, с которой происходит изменение силы тока, равна 6,4 A/c. Здесь считается, что сила тока измеряется в амперах, а время, соответственно, в секундах.
Здесь dI/dt = 0,8t. Далее найдём оную при t=8, получим, что скорость, с которой происходит изменение силы тока, равна 6,4 A/c. Здесь считается, что сила тока измеряется в амперах, а время, соответственно, в секундах.
Всё изменчиво
Видимый окружающий мир, состоящий из материи, постоянно претерпевает изменения, находясь в движении протекающих в нём разнообразных процессов. Для описания их можно использовать самые разные параметры. Если они объединены зависимостью, то математически записываются в виде функции, наглядно показывающей их изменения. А где есть движение (в каком бы виде оно ни выражалось), там существует и производная, физический смысл которой мы и рассматриваем в настоящий момент.
По этому поводу следующий пример. Допустим, температура тела изменяется по закону T=0,2t2. Следует найти скорость его нагревания в конце 10-й секунды. Решение задачи производится способом, аналогичным описанному в предыдущем случае. То есть мы находим производную и подставляем в неё значение для t = 10, получаем T = 0,4t = 4. Значит, окончательным ответом считается 4 градуса за секунду, то есть процесс нагревания и изменение температуры, измеряемой в градусах, происходит именно с такой скоростью.
Решение задачи производится способом, аналогичным описанному в предыдущем случае. То есть мы находим производную и подставляем в неё значение для t = 10, получаем T = 0,4t = 4. Значит, окончательным ответом считается 4 градуса за секунду, то есть процесс нагревания и изменение температуры, измеряемой в градусах, происходит именно с такой скоростью.
Решение практических задач
Конечно, в реальной жизни всё бывает гораздо сложнее, чем в теоретических задачах. На практике значение величин определяется обычно в ходе эксперимента. При этом используются приборы, которые выдают показания при измерениях с определённой погрешностью. Поэтому при вычислениях приходится иметь дело с приближёнными значениями параметров и прибегать к округлениям неудобных чисел, а также другим упрощениям. Приняв это ко вниманию, снова приступим к задачам на физический смысл производной, учитывая, что они являются лишь некоей математической моделью происходящих в природе сложнейших процессов.
Извержение вулкана
Представим, что происходит извержение вулкана. Насколько он может быть опасен? Для выяснения этого вопроса необходимо рассмотреть множество факторов. Мы постараемся учесть один из них.
Из жерла «огненного чудовища» выбрасываются вертикально вверх камни, имеющие начальную скорость с момента выхода наружу 120 м/с. Необходимо просчитать, какой они могут достигнуть максимальной высоты.
Для нахождения искомого значения составим уравнение зависимости высоты H, измеряемой в метрах, от прочих величин. К таковым относятся начальная скорость и время. Значение ускорения считаем известным и приблизительно равным 10 м/с2.
Частная производная
Рассмотрим теперь физический смысл производной функции немного с другой стороны, ведь само уравнение может содержать не одну, а несколько переменных. К примеру, в предыдущей задаче зависимость высоты подъёма камней, выбрасываемых из жерла вулкана, определялась не только изменением временных характеристик, но и значением начальной скорости.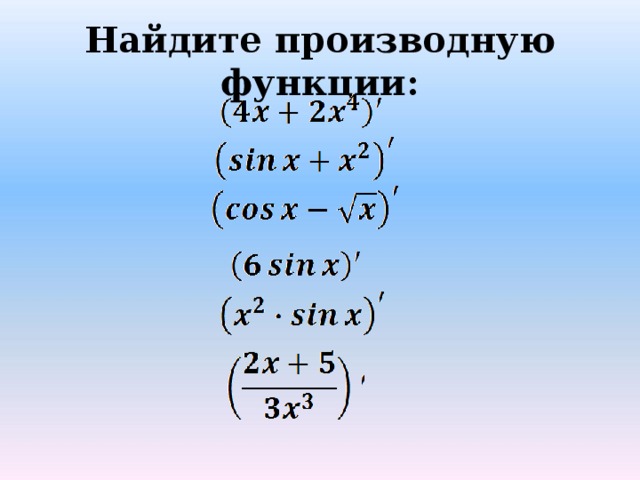 Последняя считалась постоянной, фиксированной величиной. Но в других задачах с совершенно иными условиями всё могло быть иначе. Если величин, от которых зависит сложная функция, несколько, расчёты производятся согласно указанным ниже формулам.
Последняя считалась постоянной, фиксированной величиной. Но в других задачах с совершенно иными условиями всё могло быть иначе. Если величин, от которых зависит сложная функция, несколько, расчёты производятся согласно указанным ниже формулам.
Физический смысл частой производной следует определять, как и в обычном случае. Это скорость изменения функции в некоторой определённой точке при росте параметра переменной. Она вычисляется таким образом, что все остальные составляющие принимаются за постоянные, лишь только один рассматривается как переменная. Далее всё происходит по обычным правилам.
Незаменимый советник по многим вопросам
Понимая физический смысл производной, примеры решения запутанных и сложных проблем, ответ в которых позволяют найти подобные знания, привести несложно. Если у нас есть функция, описывающая расход горючего в зависимости от скорости автомобиля, можем рассчитать, при каких параметрах последней расход бензина будет наименьшим.
В медицине можно предвидеть, каким образом будет реагировать человеческий организм на прописанное врачом лекарство. Приём препарата сказывается на самых разных физиологических показателях. К ним относятся изменения артериального давления, пульса, температуры тела и многого другого. Все они зависят от дозы принимаемого лекарственного средства. Данные расчёты помогают предвидеть ход лечения, как в благоприятных проявлениях, так и в нежелательных случайностях, способных фатальным образом отразиться на изменениях в организме больного.
Приём препарата сказывается на самых разных физиологических показателях. К ним относятся изменения артериального давления, пульса, температуры тела и многого другого. Все они зависят от дозы принимаемого лекарственного средства. Данные расчёты помогают предвидеть ход лечения, как в благоприятных проявлениях, так и в нежелательных случайностях, способных фатальным образом отразиться на изменениях в организме больного.
Несомненно, важным оказывается понимание физического смысла производной в технических вопросах, в частности в электротехнике, электронике, конструировании и строительстве.
Тормозной путь
Рассмотрим очередную задачу. Двигаясь с постоянной скоростью, автомобиль, приближаясь к мосту, за 10 секунд до въезда вынужден был затормозить, так как водитель заметил дорожный знак, запрещающий движение со скоростью более 36 км/час. Не нарушил ли правила шофёр, если тормозной путь его можно описать формулой S = 26t – t2?
Вычислив первую производную, найдём формулу для скорости, получим v = 28 – 2t. Далее подставим в указанное выражение значение t=10.
Далее подставим в указанное выражение значение t=10.
Так как эта величина была выражена в секундах, скорость оказывается равной 8 м/с, а значит, 28,8 км/час. Это даёт возможность понять, что шофёр начал тормозить вовремя и не нарушил правила движения, а значит, и предел указанной на знаке скорости.
Подобное доказывает важность физического смысла производной. Пример решения данной задачи демонстрирует широту использования этого понятия в самых разных сферах жизни. В том числе и в бытовых ситуациях.
Производная в экономике
До XIX столетия экономисты в основном оперировали средними величинами, будь то производительность труда или цена на выпускаемую продукцию. Но с некоторого момента для составления эффективных прогнозов в данной области больше стали необходимы предельные величины. К таковым можно отнести предельную полезность, доход или издержки. Понимание этого дало толчок к созданию совершенно нового инструмента в экономических исследованиях, который существует и развивается вот уже более ста лет.
Для составления подобных расчётов, где главенствуют такие понятия, как минимум и максимум, просто необходимо понимание геометрического и физического смысла производной. Среди создателей теоретической основы указанных дисциплин можно назвать таких видных английских и австрийских экономистов, как У. С. Джевонс, К. Менгер и других. Конечно, предельные величины в экономических выкладках не всегда использовать удобно. А, к примеру, квартальные отчёты не обязательно укладываются в существующую схему, но всё же применение подобной теории во многих случаях бывает полезно и эффективно.
Задания для самостоятельного решения
Понятие производной.
Правила дифференцирования. Таблица производных
Пусть определена в точке и в некоторой ее окрестности.
Пусть точка рассматриваемой окрестности, то приращением аргумента в точке называется величина , приращением функции – величина . Если выразить , то .
Производной функции в точке называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, при условии, что предел существует.
Производную в точке обозначают . По определению
, (1)
или, что то же,
, (2)
при условии, что пределы (1),(2) существуют.
Функция, имеющая производную в точке, называется дифференцируемой в этой точке. Операция нахождения производной называется дифференцированием.
Производная функции в точке – это число. Если функция дифференцируема на некотором множестве X из ее области определения, то также является функцией (ее обозначают также ).
Основные правила дифференцирования
Пусть -дифференцируемые функции. Справедливы формулы:
; (3)
; (4)
; (5)
; (6)
.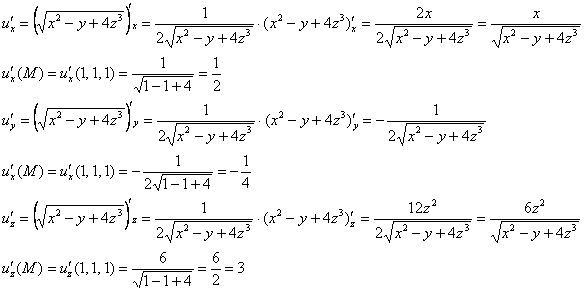 (7)
(7)
Таблица производных основных элементарных функций
1) ,где ,
в частности
а) ,
б) ;
2) где ,
в частности
;
3) где ,
в частности
;
4) ;
5) ;
6) ;
7) ;
8) ;
9) ;
10) ;
11) ;
12) ;
13) ;
14) ;
15) .
Пример 1: Найти производную функции в точке , пользуясь определением, если:
1) , ;
2) .
Решение. 1.Используем определение производной в виде формулы (1):
Поскольку по условию , то
2. По формуле (1) получаем
Далее, применив тригонометрическую формулу , получим:
Так как при имеем и, применив формулу первого замечательного предела, получаем:
Поскольку по условию , то
Пример 2:Вычислить производную функции , пользуясь определением производной.
Решение.Пусть произвольная фиксированная точка из . Пользуясь формулой (1), имеем:
Таким образом, операция дифференцирования ставит в соответствие функции , функцию .
Пример 3.Найти производную функции:
1) ;
2) ; 3) .
Решение. 1. Дифференцируем функцию и используем формулы (4), (5) и таблицу производных, получаем:
2. Дифференцируем функцию по формулам (3), (4), (6) и соответствующим формулам таблицы производных:
3. Дифференцируем функцию по формулам (7), (5), (3) и первой формуле таблицы производных:
Пример 4. Вычислить производную функции, используя правила дифференцирования и таблицу производных:
1) 2) ;
3)
Решение.1. Преобразуем функцию, пользуясь свойствами логарифма:
Полученное выражение дифференцируем по формулам (4), (5), (6) и формулам таблицы производных:
2. Перед дифференцированием преобразуем выражение, пользуясь свойствами логарифма:
Перед дифференцированием преобразуем выражение, пользуясь свойствами логарифма:
Дальше воспользуемся формулами (3), (4), (5) и таблицей производных:
3. Так как непосредственное дифференцирование вызывает значительные трудности, предварительно упростим выражение по формулам тригонометрии:
Полученное выражение дифференцируем по формуле (7) и соответствующим формулам таблицы производных.
Задания для самостоятельного решения
I уровень
1.1.Пользуясь определением, найдите производную функции:
1) 2)
1.2.Найдите производную функции:
1) ; 2) ;
3) ; 4) ;
5) ; 6) ;
7) ; 8) .
1.3. Найдите , если
1) ; 2) ;
3) ; 4) ;
5) ; 6) .
1.4.Вычислите:
1) , если: ;
2) если
;
3) если .
1.5. Вычислите , если
1.6.Вычислите , если .
1.7. Решите уравнение:
1) , где
2) , где .
II уровень
2.1. Найдите производные , предварительно преобразовав выражение:
1) ; 2) ;
3) ; 4) .
2.2. Для функции найдите
2.3.Известно, что . Найдите .
2.4. Решите неравенство , где .
III уровень
3.1. Вычислите , если:
1) ,
2) , .
3.2. Пользуясь определением производной, найдите , где
3.3. Найдите значение производной функции в точке , если .
3.4.Найдите сумму значений производной функции в точках x = 1 и x = 0.
Дата добавления: 2016-07-27; просмотров: 6912; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Вычисление производных степенно-показательных функций. Производная степенно-показательной функции
Содержание
- Таблица производных и правила дифференцирования
- Производные сложных функций
- Производные элементарных функций
- Геометрический и физический смысл производной
- Производная функции с экспонентой
- Понятие производной сложной функции
- Определение и формулы
- Пошаговые примеры – как найти производную
- Примеры решения задач
- Применение дифференциала в приближенных вычислениях
- Производная суммы и разности
- Таблица производных часто встречающихся функций
- Найти производные самостоятельно, а затем посмотреть решения
- Производная функции с корнем
- Логарифмическая производная
- Производная сложной степенной функции
- Правила нахождения производных
- Таблица производных некоторых сложных функций
- Примеры
- Производная произведения
- Продолжаем искать производные вместе
- Синтаксис описания формул
- Производная дроби с переменной произвольной степени в знаменателе
- 1-ый способ
- Производные простых функций
- Вычисление производной
Таблица производных и правила дифференцирования
Основные ссылки – таблица производных, правила дифференцирования и примеры решений (10 шт).
Пример
Задание. Найти производную функции
Решение. Так как производная суммы равна сумме производных, то
Воспользуемся формулами для производных показательной и обратной тригонометрической функций:
Ответ.
Производные сложных функций
Основные ссылки – теоретический материал и примеры решений (10 шт).
Пример
Задание.Найти производную функции
Решение. По правилу дифференцирования сложной функции:
В свою очередь производная также берется по правилу дифференцирования сложной функции:
Ответ.
Производные элементарных функций
Элементарные функции — это все, что перечислено ниже. Производные этих функций надо знать наизусть. Тем более что заучить их совсем несложно — на то они и элементарные.
Итак, производные элементарных функций:
| Название | Функция | Производная |
| Константа | f(x) = C, C ∈ R | 0 (да-да, ноль!) |
| Степень с рациональным показателем | f(x) = x n | n · x n − 1 |
| Синус | f(x) = sin x | cos x |
| Косинус | f(x) = cos x | − sin x (минус синус) |
| Тангенс | f(x) = tg x | 1/cos2 x |
| Котангенс | f(x) = ctg x | − 1/sin2 x |
| Натуральный логарифм | f(x) = ln x | 1/x |
| Произвольный логарифм | f(x) = log a x | 1/(x · ln a) |
| Показательная функция | f(x) = e x | e x (ничего не изменилось) |
Если элементарную функцию умножить на произвольную постоянную, то производная новой функции тоже легко считается:
(C · f)’ = C · f ’.
В общем, константы можно выносить за знак производной. Например:
(2x 3)’ = 2 · (x 3)’ = 2 · 3x 2 = 6x 2.
Очевидно, элементарные функции можно складывать друг с другом, умножать, делить — и многое другое. Так появятся новые функции, уже не особо элементарные, но тоже дифференцируемые по определенным правилам.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:
Производная функции с экспонентой
производная сложной функции примеры, производная показательной функцииТут на самом деле 2 функции: экспонента и степенная функция (с отрицательным показателем -1). Отсюда и поэтапное вычисление этой производной. В заблуждение может ввести натуральный логарифм, но заметьте – натуральный логарифм от 5 все лишь число.
Отсюда и поэтапное вычисление этой производной. В заблуждение может ввести натуральный логарифм, но заметьте – натуральный логарифм от 5 все лишь число.
Понятие производной сложной функции
Пусть y – сложная функция x, т.е. y = f(u), u = g(x), или
Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u = g(x), то сложная функция также дифференцируема в точке x и находится по формуле
Типичная ошибка при решении задач на производные – машинальное перенесение правил дифференцирования простых функций на сложные функции. Будем учиться избегать этой ошибки.
Посмотрите на формулу 9 в таблице производных. Исходная функция является функцией от функции, причём аргумент x является аргументом лишь второй функции, а вторая функция является аргументом первой функции, или, согласно более строгому определению – промежуточным аргументом по независимой переменной x.
А теперь посмотрите на картинку ниже, которая иллюстрирует решение задач на сложные производные по аналогии с простым примером из кулинарии – приготовлении запечёных яблок, фаршированных ягодами.
Итак, “яблоко” – это функция, аргументом которой является промежуточный аргумент, а промежуточный аргумент по независимой переменной x, в свою очередь, является “фаршем” (ягодами). Представим себе, что решая задачи на производные сложной функции, сначала помещаем яблоко с фаршем в особую (физико-математическую) духовку и устанавливаем режим 1. При таком режиме духовка воздействует только на “яблоко”, поскольку нужно, допустим, больше пропечь яблоко, а фарш из ягод оставить более сочным, то есть обрабатывать в другом режиме. Итак, в при режиме 1 обрабатывается яблоко, а фарш остаётся незатронутым, или, ближе к нашим задачам, находим производную функции лишь от промежуточного аргумента, то есть, “яблока”. Затем в духовке устанавливается режим 2, который воздействует только на фарш, иначе говоря, записываем производную функции, являющейся промежуточным аргументом по независимой переменной x. И, в конце концов, записываем произведение производной “яблока” и производной “фарша”. Можно подавать!
И, в конце концов, записываем произведение производной “яблока” и производной “фарша”. Можно подавать!
Пример 1.Найти производную функции
Сначала определим, где здесь “яблоко”, то есть функция по промежуточному аргументу u, а где “фарш”, то есть промежуточный аргумент u по независимой переменной x. Определяем: возведение в степень – это функция по промежуточному аргументу, то есть “яблоко”, а выражение в скобках (разность двух тригонометрических функций) – это промежуточный аргумент, то есть “фарш”.
Тогда
Далее по таблице производных (производная суммы или разности, производные синуса и косинуса) находим:
Требуемая в условии задачи производная (готовое “фаршированое яблоко”):
Нахождение производной сложной логарифмической функции имеет свои особенности, поэтому у нас есть и урок “Производная логарифмической функции”.
Пример 2.Найти производную функции
Неправильное решение:вычислять натуральный логарифм каждого слагаемого в скобках и искать сумму производных:
Правильное решение:опять определяем, где “яблоко”, а где “фарш”. Здесь натуральный логарифм от выражения в скобках – это “яблоко”, то есть функция по промежуточному аргументу u, а выражение в скобках – “фарш”, то есть промежуточный аргумент u по независимой переменной x.
Тогда (применяя формулу 14 из таблицы производных)
Во многих реальных задачах выражение с логарифмом бывает несколько сложнее, поэтому и есть урок “Производная логарифмической функции”.
Пример 3.Найти производную функции
Неправильное решение:
Правильное решение.В очередной раз определяем, где “яблоко”, а где “фарш”. Здесь косинус от выражения в скобках (формула 7 в таблице производных)- это “яблоко”, оно готовится в режиме 1, воздействующем только на него, а выражение в скобках (производная степени – номер 3 в таблице производных) – это “фарш”, он готовится при режиме 2, воздействующей только на него. И как всегда соединяем две производные знаком произведения. Результат:
И как всегда соединяем две производные знаком произведения. Результат:
Производная сложной логарифмической функции – частое задание на контрольных работах, поэтому настоятельно рекомендуем посетить урок “Производная логарифмической функции”.
Первые примеры были на сложные функции, в которых промежуточный аргумент по независимой переменной был простой функцией. Но в практических заданиях нередко требуется найти производную сложной функции, где промежуточный аргумент или сам является сложной функцией или содержит такую функцию. Что делать в таких случаях? Находить производные таких функций по таблицам и правилам дифференцирования. Когда найдена производная промежуточного аргумента, она просто подставляется в нужное место формулы. Ниже – два примера, как это делается.
Кроме того, полезно знать следующее. Если сложная функция может быть представлена в виде цепочки из трёх функций
,
то её производную следует находить как произведение производных каждой из этих функций:
.
Для решения многих ваших домашних заданий может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Пример 4.Найти производную функции
Применяем правило дифференцирования сложной функции, не забывая, что в полученном произведении производных промежуточный аргумент по независимой переменной x не меняется:
Готовим второй сомножитель произведения и применяем правило дифференцирования суммы:
Второе слагаемое – корень, поэтому
Таким образом получили, что промежуточный аргумент, являющийся суммой, в качестве одного из слагаемых содержит сложную функцию: возведение в степень – сложная функция, а то, что возводится в степень – промежуточный аргумент по независимой переменной x.
Поэтому вновь применим правило дифференцирования сложной функции:
Степень первого сомножителя преобразуем в корень, а дифференцируя второй сомножитель, не забываем, что производная константы равна нулю:
Теперь можем найти производную промежуточного аргумента, нужного для вычисления требуемой в условии задачи производной сложной функции y:
Тогда
Пример 5.Найти производную функции
Сначала воспользуемся правилом дифференцирования суммы:
Получили сумму производных двух сложных функций. Находим первую из них:
Здесь возведение синуса в степень – сложная функция, а сам синус – промежуточный аргумент по независимой переменной x. Поэтому воспользуемся правилом дифференцирования сложной функции, попутно вынося множитель за скобки:
Теперь находим второе слагаемое из образующих производную функции y:
Здесь возведение косинуса в степень – сложная функция f[g(x)], а сам косинус – промежуточный аргумент по независимой переменной x. Снова воспользуемся правилом дифференцирования сложной функции:
Снова воспользуемся правилом дифференцирования сложной функции:
Результат – требуемая производная:
Определение и формулы
- Степенно-показательная функция
- – это функция, имеющая вид степенной функции
y = uv,
у которой основание u и показатель степени v являются некоторыми функциями от переменной x:
u = u(x) v = v(x).
Эту функцию также называют показательно-степенной или сложной показательной функцией.
Заметим, что степенно-показательную функцию можно представить в показательном виде:
.
Поэтому ее также называют сложной показательной функцией.
Далее мы покажем, что производная степенно-показательной функции определяется по формуле:
(1) .
Пошаговые примеры – как найти производную
Пример 3. Найти производную функции
.
Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль. Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как производную “икса”. Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
А проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями”.
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций”.
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого – квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на :
Проверить решение задачи на производную можно на калькуляторе производных онлайн.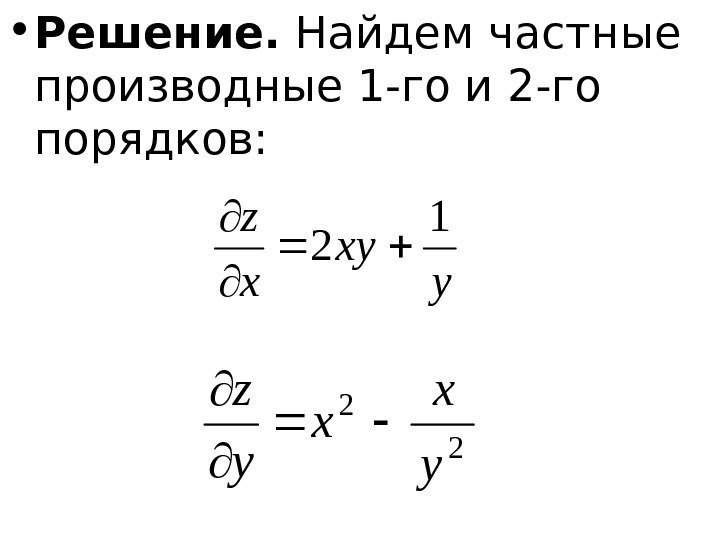
Примеры решения задач
Применение дифференциала в приближенных вычислениях
Основные ссылки – теоретический материал и примеры решений (10 шт).
Задание. Вычислить приближенно , заменяя приращение функции ее дифференциалом.
Решение. Рассмотрим функцию . Необходимо вычислить ее значение в точке . Представим данное значение в виде следующей суммы:
Величины и выбираются так, чтобы в точке можно было бы достаточно легко вычислить значение функции и ее производной, а было бы достаточно малой величиной. С учетом этого, делаем вывод, что , то есть , .
Вычислим значение функции в точке :
Далее продифференцируем рассматриваемую функцию и найдем значение :
Тогда
Итак,
Ответ.
Производная суммы и разности
Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:
Тогда можно найти производную суммы и разности этих функций:
- (f + g)’ = f ’ + g ’
- (f − g)’ = f ’ − g ’
Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)’ = f ’ + g ’ + h ’.
Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g, и тогда останется лишь одна формула — производная суммы.
Задача. Найти производные функций: f(x) = x 2 + sin x; g(x) = x 4 + 2x 2 − 3.
Функция f(x) — это сумма двух элементарных функций, поэтому:
f ’(x) = (x 2 + sin x)’ = (x 2)’ + (sin x)’ = 2x + cos x;
Аналогично рассуждаем для функции g(x). Только там уже три слагаемых (с точки зрения алгебры):
g ’(x) = (x 4 + 2x 2 − 3)’ = (x 4 + 2x 2 + (−3))’ = (x 4)’ + (2x 2)’ + (−3)’ = 4x 3 + 4x + 0 = 4x · (x 2 + 1).
Ответ:
f ’(x) = 2x + cos x;
g ’(x) = 4x · (x 2 + 1).
Таблица производных часто встречающихся функций
В следующей таблице приведены формулы для производных от степенных, показательных (экспоненциальных), логарифмических, тригонометрических и обратных тригонометрических функций. Доказательство большинства их этих формул выходит за рамки школьного курса математики.
| Функция | Формула для производной | Название формулы |
y = c , где c – любое число | y’ = 0 | Производная от постоянной функции |
y = x c , где c – любое число | y’ = c xc – 1 | Производная степенной функции |
| y = e x | y’ = e x | Производная от экспоненты (показательной функции с основанием e) |
y = a x где a – любое положительное число, не равное 1 | y’ = a x ln a | Производная от показательной функции с основанием a |
| y = ln x , x > 0 | , x > 0 | Производная от натурального логарифма |
y = log a x , x > 0 где a – любое положительное число, не равное 1 | , x > 0 | Производная от логарифма по основанию a |
| y = sin x | y’ = cos x | Производная синуса |
| y = cos x | y’ = – sin x | Производная косинуса |
y = tg x , | , , | Производная тангенса |
y = ctg x , | , , | Производная котангенса |
y = arcsin x , | Производная арксинуса | |
y = arccos x , | Производная арккосинуса | |
| y = arctg x | Производная арктангенса | |
| y = arcctg x | Производная арккотангенса |
| Производная от постоянной функции |
Функция: y = c , где c – любое число Формула для производной: y’ = 0 |
| Производная степенной функции |
Функция: y = x c , где c – любое число Формула для производной: y’ = c xc – 1 |
| Производная от экспоненты (показательной функции с основанием e) |
Функция: y = e x Формула для производной: y’ = e x |
| Производная от показательной функции с основанием a |
Функция: y = a x где a – любое положительное число, не равное 1 Формула для производной: y’ = a x ln a |
| Производная от натурального логарифма |
Функция: y = ln x , x > 0 Формула для производной: , x > 0 |
| Производная от логарифма по основанию a |
Функция: y = log a x , x > 0 где a – любое положительное число, не равное 1 Формула для производной: , x > 0 |
| Производная синуса |
Функция: y = sin x Формула для производной: y’ = cos x |
| Производная косинуса |
Функция: y = cos x Формула для производной: y’ = – sin x |
| Производная тангенса |
Функция: y = tg x , где Формула для производной: , |
| Производная котангенса |
Функция: y = ctg x , где Формула для производной: , |
| Производная арксинуса |
Функция: y = arcsin x , Формула для производной: |
| Производная арккосинуса |
Функция: y = arccos x , Формула для производной: |
| Производная арктангенса |
Функция: y = arctg x Формула для производной: |
| Производная арккотангенса |
Функция: y = arcctg x Формула для производной: |
Найти производные самостоятельно, а затем посмотреть решения
Пример 7. Найти производную функции
Найти производную функции
.
Правильное решение и ответ.
Пример 8. Найти производную функции
.
Правильное решение и ответ.
Пример 9. Найти производную функции
, где a и b – константы.
Правильное решение и ответ.
Пример 10. Найти производную функции
.
Правильное решение и ответ.
Пример 11. Найти производную функции
.
Правильное решение и ответ.
Производная функции с корнем
производная сложной функции примеры, производная функции с корнемСтепенная функция плюс осложнение внутри скобки. Пример не дорешан, всего лишь нужно вспомнить из таблицы пару элементарных функций.
Логарифмическая производная
Если производная от логарифмов – это такая сладкая музыка, то возникает вопрос, а нельзя ли в некоторых случаях организовать логарифм искусственно? Можно! И даже нужно.
Пример 11
Найти производную функции
Похожие примеры мы недавно рассмотрели. Что делать? Можно последовательно применить правило дифференцирования частного, а потом правило дифференцирования произведения. Недостаток способа состоит в том, что получится огромная трехэтажная дробь, с которой совсем не хочется иметь дела.
Но в теории и практике есть такая замечательная вещь, как логарифмическая производная. Логарифмы можно организовать искусственно, «навесив» их на обе части:
Примечание: т.к. функция может принимать отрицательные значения, то, вообще говоря, нужно использовать модули: , которые исчезнут в результате дифференцирования. Однако допустимо и текущее оформление, где по умолчанию принимаются во внимание комплексные значения. Но если со всей строгостью, то и в том и в другом случае следует сделать оговорку, что , которые исчезнут в результате дифференцирования. Однако допустимо и текущее оформление, где по умолчанию принимаются во внимание комплексные значения. Но если со всей строгостью, то и в том и в другом случае следует сделать оговорку, что .
Но если со всей строгостью, то и в том и в другом случае следует сделать оговорку, что .
Теперь нужно максимально «развалить» логарифм правой части (формулы перед глазами?). Я распишу этот процесс очень подробно:
Собственно приступаем к дифференцированию.
Заключаем под штрих обе части:
Производная правой части достаточно простая, её я комментировать не буду, поскольку если вы читаете этот текст, то должны уверенно с ней справиться.
Как быть с левой частью?
В левой части у нас сложная функция. Предвижу вопрос: «Почему, там же одна буковка «игрек» под логарифмом?».
Дело в том, что эта «одна буковка игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ (если не очень понятно, обратитесь к статье Производная от функции, заданной неявно). Поэтому логарифм – это внешняя функция, а «игрек» – внутренняя функция. И мы используем правило дифференцирования сложной функции :
В левой части как по мановению волшебной палочки у нас «нарисовалась» производная . Далее по правилу пропорции перекидываем «игрек» из знаменателя левой части наверх правой части:
Далее по правилу пропорции перекидываем «игрек» из знаменателя левой части наверх правой части:
А теперь вспоминаем, о каком таком «игреке»-функции мы рассуждали при дифференцировании? Смотрим на условие:
Окончательный ответ:
Пример 12
Найти производную функции
Это пример для самостоятельного решения. Образец оформления примера данного типа в конце урока.
С помощью логарифмической производной можно было решить любой из примеров № 4-7, другое дело, что там функции проще, и, может быть, использование логарифмической производной не слишком-то и оправдано.
Производная сложной степенной функции
В сложной функции вместо x представлено более сложное выражение. Производная такой функции определяется по формуле:
(yn)‘ = nyn-1 ⋅ y‘
Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.
Таблица производных некоторых сложных функций
Для сложных функций на основании правила дифференцирования сложной функции формула производной простой функции принимает другой вид.
| 1. Производная сложной степенной функции, где u – дифференцируемая функция аргумента x | |
| 2. Производная корня от выражения | |
3. Производная показательной функции Производная показательной функции | |
| 4. Частный случай показательной функции | |
| 5. Производная логарифмической функции с произвольным положительным основанием а | |
| 6. Производная сложной логарифмической функции, где u – дифференцируемая функция аргумента x | |
| 7. Производная синуса | |
| 8. Производная косинуса | |
| 9. Производная тангенса | |
| 10. Производная котангенса | |
| 11. Производная арксинуса | |
| 12. Производная арккосинуса | |
| 13. Производная арктангенса | |
| 14. Производная арккотангенса |
Примеры
Решим примеры. Преобразования, позволяющие применить другие свойства производной, мы применять не будем. В решениях будем использовать только формулу производной от дроби.
По условию даются функции. Нужно найти производные.
Пример 1
Рисунок 2. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 3. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 4. Пример. Автор24 — интернет-биржа студенческих работ
Производная произведения
Математика — наука логичная, поэтому многие считают, что если производная суммы равна сумме производных, то производная произведения strike“>равна произведению производных. А вот фиг вам! Производная произведения считается совсем по другой формуле. А именно:
(f · g) ’ = f ’ · g + f · g ’
Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.
Задача. Найти производные функций: f(x) = x 3 · cos x; g(x) = (x 2 + 7x − 7) · e x .
Функция f(x) представляет собой произведение двух элементарных функций, поэтому все просто:
f ’(x) = (x 3 · cos x)’ = (x 3)’ · cos x + x 3 · (cos x)’ = 3x 2 · cos x + x 3 · (− sin x) = x 2 · (3cos x − x · sin x)
У функции g(x) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:
Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:
g ’(x) = ((x 2 + 7x − 7) · e x )’ = (x 2 + 7x − 7)’ · e x + (x 2 + 7x − 7) · (e x )’ = (2x + 7) · e x + (x 2 + 7x − 7) · e x = e x · (2x + 7 + x 2 + 7x −7) = (x 2 + 9x) · e x = x(x + 9) · e x .
Ответ:
f ’(x) = x 2 · (3cos x − x · sin xg ’(x) = x(x + 9) · e x .
Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию. А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.
Продолжаем искать производные вместе
Пример 12. Найти производную функции
Найти производную функции
.
Решение. Применяя правила вычисления производной алгебраической суммы функций, вынесения постоянного множителя за знак производной и формулу производной степени (в таблице производных – под номером 3), получим
.
Пример 13. Найти производную функции
Решение. Применим правило дифференцирования произведения, а затем найдём производные сомножителей, так же, как в предыдущей задаче, пользуясь формулой 3 из таблицы производных. Тогда получим
Пример 14. Найти производную функции
Решение. Как и в примерах 4 и 6, применим правило дифференцирования частного:
Теперь вычислим производные в числителе и перед нами уже требуемый результат:
Пример 15.Найти производную функции
Шаг1. Применяем правило дифференцирования суммы:
Шаг2. Найдём производную первого слагаемого. Это табличная производная квадратного корня (в таблице производных – номер 5):
Найдём производную первого слагаемого. Это табличная производная квадратного корня (в таблице производных – номер 5):
Шаг3. В частном знаменатель – также корень, только не квадратный. Поэтому преобразуем этот корень в степень:
и далее дифференцируем частное, не забывая, что число 2 в первом слагаемом числителя – это константа, производная которой равна нулю, и, следовательно всё первое слагаемое равно нулю:
Корень из константы, как не трудно догадаться, является также константой, а производная константы, как мы знаем из таблицы производных, равна нулю:
,
а производная, требуемая в условии задачи:
Синтаксис описания формул
В описании функции допускается использование одной переменной (обозначается как x), скобок, числа пи (pi), экспоненты (e), математических операций: + — сложение, – — вычитание, * — умножение, / — деление, ^ — возведение в степень.
Допускаются также следующие функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec— экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, abs — абсолютное значение (модуль), sgn — сигнум (знак), logP — логарифм по основанию P, например log7(x) — логарифм по основанию 7, rootP — корень степени P, например root3(x) — кубический корень.
Производная дроби с переменной произвольной степени в знаменателе
( 1 / xс )’ = – c / xс+1
Пример нахождения производной дроби:
( 1 / x2 )’ = – 2 / x3 .
(впереди ставим минус, показатель степени переменной поднимаем в числитель дроби, а степень переменной в знаменателе увеличиваем на единичку. Немного “ненаучно”, но подходит для быстрого запоминания)
1-ый способ
Применяя формулу:
То есть вначале производная берется как от степенной функции, а потом как от показательной.
Замечание
Порядок следования слагаемых неважен: можно вначале взять производную от показательной функции, а затем как от степенной, так как от перестановки слагаемых сумма не меняется:
Пример
Задание. Найти производную функции
Решение. Применяем формулу. В рассматриваемом случае
В рассматриваемом случае
Тогда имеем:
Ответ.
Производные простых функций
1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0
Пояснение:
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях – скорость его изменения всегда равна нулю.
2. Производная переменной равна единице
x´ = 1
Пояснение:
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение:
В данном случае, при каждом изменении аргумента функции (х) ее значение (y) растет в с раз.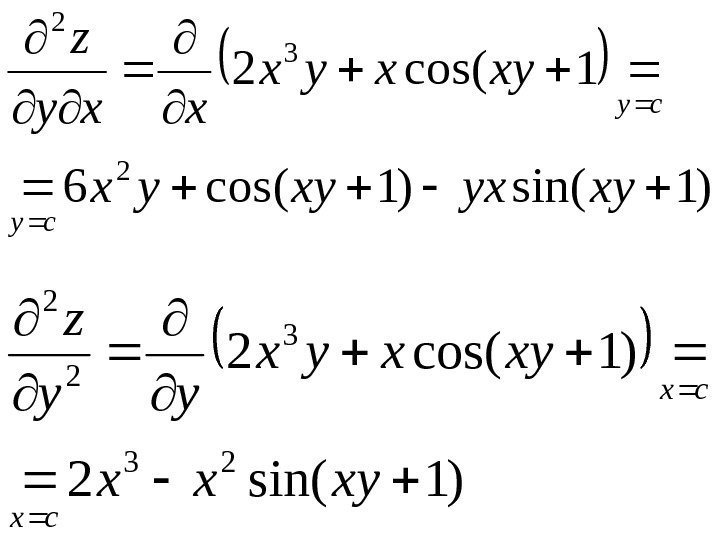 Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с.
Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с.
Откуда следует, что
(cx + b)’ = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|’ = x / |x| при условии, что х ≠ 0
Пояснение:
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x < 0 оно равно (-1), а когда x > 0 – единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных – наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
( xc )’= cxc-1, при условии, что xc и сxc-1,определены а с ≠ 0
Пример:
(x2 )’ = 2x
(x3)’ = 3x2
Для запоминания формулы:
Снесите степень переменной “вниз” как множитель, а потом уменьшите саму степень на единицу. Например, для x2 – двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x3 – тройку “спускаем вниз”, уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x2 . Немного “не научно”, но очень просто запомнить.
6. Производная дроби 1/х
(1/х)’ = – 1 / x2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)’ = (x-1 )’ , тогда можно применить формулу из правила 5 таблицы производных
(x-1 )’ = -1x-2 = – 1 / х2
7. Производная дроби с переменной произвольной степени в знаменателе
Производная дроби с переменной произвольной степени в знаменателе
( 1 / xc )’ = – c / xc+1
Пример:
( 1 / x2 )’ = – 2 / x3
8. Производная корня (производная переменной под квадратным корнем)
( √x )’ = 1 / ( 2√x ) или 1/2 х-1/2
Пример:
( √x )’ = ( х1/2 )’ значит можно применить формулу из правила 5
( х1/2 )’ = 1/2 х-1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
( n√x )’ = 1 / ( n n√xn-1 )
.
Вычисление производной
Вычисление производной — дело нехитрое, достаточно знать несколько простых правил и формулы дифференцирования простых функций; сложнее в этом онлайн калькуляторе было сделать интерпретатор математических выражений и алгоритм упрощения полученного результата, но об этом как-нибудь в другой раз…
Источники
- https://www.
 webmath.ru/primeri_reshenii/derivative.php
webmath.ru/primeri_reshenii/derivative.php - https://www.berdov.com/docs/fluxion/rules/
- https://Zaochnik.ru/blog/proizvodnaya-dlya-chajnikov-opredelenie-kak-najti-primery-reshenij/
- https://zen.yandex.ru/media/maminov/proizvodnaia-slojnoi-funkcii-5bd5cda71ea36b00aa3a19ae
- https://function-x.ru/derivative2.html
- https://1cov-edu.ru/mat_analiz/proizvodnaya/nayti/logarifmicheskaya/stepenno-pokazatelnaya-funktsiya/
- https://function-x.ru/derivative.html
- http://ru.solverbook.com/spravochnik/proizvodnye/proizvodnaya-stepennoj-funkcii/
- https://www.resolventa.ru/spr/matan/derivative_rule.htm
- http://www.mathprofi.ru/slozhnye_proizvodnye_logarifmicheskaja_proizvodnaja.html
- https://MicroExcel.ru/proizvodnaya-stepennoy-funktsii/
- https://spravochnick.ru/matematika/formula_proizvodnoy_ot_drobi_primery/
- https://planetcalc.ru/675/
- https://profmeter.com.ua/communication/learning/course/course17/lesson642/
- https://www.
 webmath.ru/poleznoe/formules_8_17.php
webmath.ru/poleznoe/formules_8_17.php - https://profmeter.com.ua/communication/learning/course/course17/lesson251/
Примеры решения задач к разделу пределы и…
Привет, мой друг, тебе интересно узнать все про ы решения задач к разделу пределы, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое ы решения задач к разделу пределы, производная дифференциальое исчисление , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальное исчисление.
Пример N 1
Вычислить: .
Решение.
Числитель и знаменатель дроби неограниченно возрастают при . В этом случае говорят, что имеет место неопределенность типа . Разделим числитель и знаменатель дроби на старшую степень переменной x , в нашем случае — на x2 :
.
Так как при каждая из дробей .
Ответ: 3
Пример N 2
Вычислить: .
Решение.
Числитель и знаменатель дроби при также стремятся к нулю. В этом случае имеет место неопределенность типа . Умножим числитель и знаменатель дроби на :
Знаменатель дроби при , следовательно .
Ответ: .
Пример N 3
Вычислить: .
Решение.
Воспользуемся тригонометрической формулой и заменим числитель и знаменатель дроби эквивалентными бесконечно малыми и :
Ответ: 0.
Пример N 4
Вычислить: .
Решение.
При выражение , а (x +7) неограниченно возрастает.
В этом случае имеет место неопределенность типа . Об этом говорит сайт https://intellect.icu . Рекомендуется использовать второй замечательный предел или следствие из него:
Так как при , то . Учитывая, что (см. пример N1), окончательно получаем
Учитывая, что (см. пример N1), окончательно получаем
Ответ: .
Пример N 5
Вычислить: .
Решение.
Так как при выражение , имеет место неопределенность типа . Преобразуем функцию так, чтобы использовать второй замечательный предел. Выделим целую часть из дроби (для этого к числителю дроби прибавим и отнимем 3): , тогда
Так как при , то .
Учитывая, что окончательно получим:
Ответ: .
Пример N 6
Исследовать функцию на непрерывность и построить схематически ее график.
Решение.
Данная функция терпит разрыв в точках и , так как при этих значениях знаменатель дроби обращается в нуль. Исследуем характер разрыва в каждой из этих точек.
Для этого найдем
Для точки :
Так как
и , то в точке функция имеет разрыв первого рода или скачок.
Для точки :
Таким образом, для точки и , значит, и при функция также терпит разрыв первого рода или скачок. Для схематического построения графика исследуем поведение функции при
Следовательно, при график функции находится около прямой y = 1 . Найдем точку пересечения графика с осью ОУ:
Найдем точку пересечения графика с осью ОУ:
.
Ответ: Схематический график функции (рис. 8):
Рис. 8
Пример N 7
Найти производную функции .
Решение.
Преобразуем квадратный корень в степень: .
Данная функция — сложная, используем последовательно формулы: производная степенной функции, производная дроби, производная логарифма.
Ответ: .
Пример N 8
Вычислить производную функции .
Решение.
Данная функция относится к виду показательно — степенной функции . Для нахождения ее производной прологарифмируем данную функцию: .
Для нахождения ее производной прологарифмируем данную функцию: .
Дифференцируя левую и правую часть этого равенства, получаем
Ответ: .
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про ы решения задач к разделу пределы Надеюсь, что теперь ты понял что такое ы решения задач к разделу пределы, производная дифференциальое исчисление и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальное исчисление
Из статьи мы узнали кратко, но емко про ы решения задач к разделу пределы
2\right) + \dfrac{d}{dx}(\cos x) = \, …$Правило произведения для производных
\begin{align*}
\dfrac{d}{dx}(fg)& = \left(\dfrac{d}{dx}f \right)g + f\left(\dfrac{d}{dx}g \right)\\[8px]
&= \Big[\text{ (производное 1-го) } \times \text{ (2-го) }\Big] + \Big[\text{ (1-го) } \times \text{ (производного 2-го)}\Big]
\end{align *}
IV.
 2} \\[8px]
2} \\[8px] &=\dfrac{{\Big[\text{(производная числителя) } \times \text{ (знаменатель)}\Big] – \Big[\text{ (числитель) } \times \text{ (производная знаменатель)}}\Big]}{\text{все разделить на [знаменатель в квадрате]}}
\end{align*}
Многие студенты помнят правило частного, думая о числителе как о «привет», демонинаторе как «lo», производная как «d», а затем пение
«lo d-hi минус hi d-lo over lo-lo»
[свернуть]
Чтобы получить доступ к большему количеству проблем и решений, включая AP- создавайте вопросы с несколькими вариантами ответов, бесплатно войдите в свою учетную запись Google, Apple или Facebook или создайте специальный Matheno за 60 секунд. Вы также сможете отметить задачи 9{46}.$
Два конкретных случая, которые вы быстро запомните:
$$\dfrac{d}{dx}\text{(константа)} = 0$$
$$\dfrac{d}{dx}( x) = 1$$
Задача дифференцирования по степенному правилу #1
Дифференцировать $f(x) = 2\pi$.
Щелкните, чтобы просмотреть расчетное решение
$2\pi$ — это просто число: это константа. И производная любой константы равна 0:
\[ \begin{align*}
\dfrac{d}{dx}(2\pi) &= \dfrac{d}{dx}(\text{constant}) \ \[8px]
&= 0 \quad \cmark 9{x+1} \quad \cmark
\end{align*} \]
Обратите внимание, что последние две строки полностью эквивалентны. Любой правильный ответ.
[свернуть]
Чтобы получить доступ к другим проблемам и решениям, включая вопросы с несколькими вариантами ответов в стиле AP, бесплатно войдите в свою учетную запись Google, Apple или Facebook или создайте специальный Matheno за 60 секунд. Вы также сможете отмечать задачи , которые вы хотите обязательно просмотреть перед экзаменами. Просто используйте область входа в систему в нижней части этого экрана. 92 x
\end{align*}} \]
Обратите внимание, что перед производными кофункций: косинуса, косеканса и котангенса стоит знак минус.
Запустить задачу дифференцирования #1
Дифференцировать $f(x) = \sin x – \cos x$.
Нажмите, чтобы просмотреть расчетное решение
Напомним из таблицы, что $\dfrac{d}{dx}(\sin x) = \cos x,$ и $\dfrac{d}{dx}(\cos x) = -\sin x.$
\[ \begin{align*}
\dfrac{d}{dx} \left(\sin x – \cos x \right) &= \dfrac{d}{dx}(\ sin x) – \dfrac{d}{dx}(\cos x) \\[8px] 92 x \quad \cmark
\end{align*} \]
[свернуть]
IV. Правило продукта
\[\bbox[yellow,5px]{
\begin{align*}
\dfrac{d}{dx}(fg)&= \left(\dfrac{d}{dx}f \right )g + f\left(\dfrac{d}{dx}g \right)\\[8px]
&= [{\small\text{(производное первого)} \times\text{(второе) }}]\, + \,[{\small \text{ (1-й) } \times \text{ (производный от 2-го)}}]
\end{align*}}\]
Дифференциация правила продукта Проблема №1
Дифференцировать $f(x) = x\sin x. $
$
Щелкните, чтобы просмотреть решение исчисления
Поскольку функция является произведением двух отдельных функций, $x$ и $\sin x$, мы должны использовать произведение Правило. Напомним, что $\dfrac{d}{dx}x = 1,$ и что $\dfrac{d}{dx}\sin x = \cos x.$
\[ \begin{align*}
\dfrac{d }{dx} \left( x\sin x\right)&= \left(\dfrac{d}{dx}x\right)\sin x + x \left( \dfrac{d}{dx}\sin x \right) \\[8px]
&= (1)\sin x + x \,(\cos x) \\[8px]
&= \sin x + x\cos x \quad \cmark 92} \\[8px]
&=\dfrac{{[{\small \text{(производная числителя) } \times \text{ (знаменатель)}]}\\ \quad – \, [{\ small \text{ (числитель) } \times \text{ (производная знаменателя)}}]}}{{\small \text{все разделить на [знаменатель в квадрате]}}}
\end{align* }}\]
Многие учащиеся запоминают правило частных, представляя числитель как «привет», демонинатор как «ло», производную как «д», а затем напевая
«ло д-при минус привет д-ло». 2 x$$ 92} \quad \cmark
2 x$$ 92} \quad \cmark
\end{align*} \]
[свернуть]
VI. Цепное правило
Цепное правило — большая тема, поэтому у нас есть отдельная страница для задач, требующих цепного правила.
Нужно использовать производную, чтобы найти уравнение касательной (или уравнение нормальной линии)? У нас есть отдельная страница на эту тему здесь.
У вас есть вопрос, предложение или пункт, который вы хотели бы, чтобы мы включили? Пожалуйста, дайте нам знать на нашем форуме!
Хотите получить доступ к всем нашим задачам и решениям исчисления? Войдите бесплатно с помощью своей учетной записи Google, Facebook или Apple или с помощью специальной учетной записи Matheno (которую вы можете создать за 60 секунд). Затем посетите наш главный экран исчисления.
И если у вас есть вопрос по исчислению, с которым вам может понадобиться помощь, зайдите на наш форум и опубликуйте. Будем рады помочь!
По состоянию на сентябрь 2022 года мы используем наш форум для комментариев и обсуждения этой темы, а также для любых математических вопросов. Будем рады вас видеть и помочь! Нажмите, чтобы посетить наш форум: community.matheno.com.
Войти
Вы можете бесплатно войти в систему, чтобы получить доступ ко всем нашим материалам, с помощью своей учетной записи Facebook, Google или Apple ИЛИ с помощью специальной учетной записи Matheno. (У вас нет специальной учетной записи Matheno, но вы хотели бы ее? Создайте ее за 60 секунд здесь.)
Производные: определение, примеры и типы
Один из самых быстрых автомобилей в мире, Venom F5 Hennessey Performance Engineering работает со скоростью максимальная скорость превышает \(300 миль в час\) и может перейти от \(0\) до \(62 мили в час\) всего за \(2,6\) секунды! 1
В этой статье вы изучите методы, которые можно использовать для расчета ускорения, которое достигает Venom F5 при приближении к своей максимальной скорости.
- Назначение дериватов
- Определение производных
- Формула производных
- Правила производных
- Примеры производных
вычислить наклон касательной к кривой
.Но что именно это означает?
Это означает, что вы вычисляете скорость изменения функции в точке. В частности, это может означать расчет скорости и изменения скорости во времени, как вы хотели бы сделать для Venom F5. Однако использование производных гораздо более разнообразно:
Они полезны во всех областях математики , науки и техники .
Производные инструменты имеют решающее значение для бизнеса анализа .
Они необходимы для медицинских приложений.
Определение производной
Теперь, когда вы хорошо понимаете пределы, вы заложили основу для изучения исчисления!
Секущая и касательная
Чтобы по-настоящему начать изучение исчисления, вы должны вернуться к понятиям секанс и тангенс строк кривой.
Два способа расчета наклона секущей к кривой
Вы можете рассчитать наклон секущей к кривой одним из двух способов, как показано на графиках и формулах ниже. Поскольку оба метода дают один и тот же ответ, вы можете выбрать тот метод, который проще всего вычислить.
Вы можете использовать формулу: \( m_{sec} = \frac{f(x)-f(a)}{x-a} \) для вычисления наклона секущей к кривой.
Вы можете использовать формулу: \( m_{sec} = \frac{f(a+h)-f(a)}{h} \) для вычисления наклона секущей к кривой.
Эти формулы для наклона секущей к кривой представлены в виде разностного отношения . Их формальное определение таково:
- Пусть \(f\) будет функцией, которая определена на интервале \(I\), и пусть \(I\) содержит значение \(a\). Если \( x \) находится в \( I \) и \( x \neq a \) , то коэффициент разности равен: \[ Q = \frac{f(x)-f(a)}{x-a } \]
- И, частное разности с приращением \( \bf{ h } \) , которое существует, если \( h \neq 0 \), выбрано так, что \( a+h \) находится в интервале \( I \), есть: \[ Q = \frac{f(a+h) -f(a)}{h} \]
При перемещении второй точки – \( (x, f(x)) \) на верхнем графике выше и \( (a+h, f(a +h)) \) на нижнем графике выше – секущей ближе к первой точке – \( (a, f(a)) \) на обоих графиках выше – вы подходите к касательной линии к кривой в этой первой точке. Это приводит к тому, что вы используете ограничения , чтобы определить касательную к кривой как:
Это приводит к тому, что вы используете ограничения , чтобы определить касательную к кривой как:
- Пусть \( f(x) \) будет функцией, которая определена на открытом интервале, содержащем \( a \). Касательная к \( f(x) \) в точке \( a \) — это линия, проходящая через точку \( (a, f(a)) \) и имеющая наклон:\[ m_{tan} = \lim_{x \to a} \frac{f(x)-f(a)}{x-a} \], если предел существует.
- И, если предел существует, вы также можете определить касательную линию к \( f(x) \) в \( a \) как прямую, проходящую через точку \( (a, f( a)) \) и имеет наклон: \[ m_{tan} = \lim_{h \to 0} \frac{f(a+h)}{h}. \]
Более подробный обзор и примеры см. в статье о касательных линиях.
Производная функции в точке
Использование пределов для нахождения наклона касательной к функции (или кривой) в точке приводит вас прямо к производной . По сути, термин производная — это просто специальное название для этого типа предела, а процесс нахождения (также называемый взятием) производной называется дифференцированием . определение производной функции в точке :
определение производной функции в точке :
- производная функции \( f(x) \) в точке \( a \), которую обозначают ‘(a) \) (читается как «f-простое число a»), и при условии, что \( f(x) \) — функция, определенная на открытом интервале, который содержит \( a \), и что существует предел , определяется как: \[ f'(a) = \lim_{x \to a} \frac{f(x)-f(a)}{x-a}. \]
- И, опять же, если предел существует, вы также можете определить производную \( f(x) \) в \( a \) как: \[ f'(a) = \lim_{h \to 0 } \frac{f(a+h)-f(a)}{h}. \] 9{2}-4x-4}{x-2} \]
- Фактор числителя.\[ f'(2) = \lim_{x \to 2} \frac{(x-2)(3x+2) }{x-2} \]
- Отменить общий множитель.\[ f'(2) = \lim_{x \to 2} (3x+2) \]
- Подставить \( x = 2 \).\ [ f'(2) = \lim_{x \to 2} (3(2)+2) \]
- Вычислить предел.\[ \bf{ f'(2) } = \bf{ 8 } \]
- Применим определение ( здесь \( a = 2 \)).
 \[ f'(2) = \lim_{h \to 0} \frac{f(2+h)-f(2)}{h} \] 9{2}+8h}{h} \]
\[ f'(2) = \lim_{h \to 0} \frac{f(2+h)-f(2)}{h} \] 9{2}+8h}{h} \] - Фактор числителя.\[ f'(2) = \lim_{h \to 0} \frac{h(3h+8)}{h} \]
- Отменить общий множитель.\[ f'(2) = \lim_{h \to 0} (3h+8) \]
- Заменить \( h = 0 \).\[ f'(2) = \lim_{ h \to 0} (3(0)+8) \]
- Оценить предел.\[ \bf{ f'(2) } = \bf{ 8 } \]
Обратите внимание, что при использовании любого метода вы получите точно такой же ответ!
Скорости и темпы изменения
Один из наиболее распространенных способов использования производных — найти скорости и скорости изменения . Если у вас есть функция, которая представляет положение объекта во времени, называемая \( s(t) \), то его средняя скорость определяется разностным коэффициентом:
\[ v_{avg} = \frac{s(t) -с(а)}{т-а}. \]
Поскольку значения \(t\) приближаются к значению \(a\), значение \(v_{avg}\) приближается к тому, что вы называете мгновенной скоростью при \(a\). Мгновенная скорость в \(a\), обозначаемая как \(v(a)\), определяется как:
Мгновенная скорость в \(a\), обозначаемая как \(v(a)\), определяется как:
\[ v(a) = s'(a) = \lim_{t \to a} \frac{s(t)-s(a)}{t-a} .\]
Другими словами, если вы хотите найти среднюю скорость объекта во времени, вы можете сделать это, взяв производную от функции, которая представляет положение объекта во времени.
Средняя скорость в сравнении с мгновенной скоростью
Наклон секущей представляет собой среднюю скорость функции на отрезке \([a, t] \). Наклон касательной — это мгновенная скорость в точке \(а\).
Приведенный выше график поможет вам понять разницу между средней скоростью и мгновенной скоростью . На этом графике наклон секущей (зеленый) представляет собой среднюю скорость объекта за интервал времени \([a, t]\). Наклон касательной (розовый) — это мгновенная скорость объекта в момент времени \( t = a \). Положение объекта в момент времени \(t\) представлено функцией \(y = s(t)\) (синий).
Как видите, наклон касательной к функции и мгновенная скорость связаны. Вы вычисляете оба, находя производную, и оба измеряете мгновенную скорость изменения функции — скорость изменения указанной функции в определенной точке.
мгновенная скорость изменения функции \( f(x) \) при значении \(a\) является ее производной при \(a\) . Другими словами, мгновенная скорость изменения \(f(x)\) в точке \(a\) имеет значение \(f'(a)\).
Используя формулу для \(v(a)\), вы можете рассчитать мгновенную скорость объекта или использовать таблицу значений для оценки скорости движущегося объекта. Вы можете подтвердить эту оценку, используя формулу для \(v_{avg}\).
Допустим, у вас есть груз на пружине, который колеблется вверх и вниз. Его положение в момент времени \(t\) относительно фиксированной горизонтальной линии (или датума) определяется функцией:
\[ s(t) = sin(t). \]
Используя таблицу значений, оцените \(v(0)\). Проверьте эту оценку, используя формулу для \(v(a)\).
Проверьте эту оценку, используя формулу для \(v(a)\).
Решение :
Вы можете оценить мгновенную скорость в момент времени \(t=0\), создав таблицу значений, выбрав значения \(t\), приближающиеся к \(0\), как в таблице ниже.
| \(t\) | \( \frac{sin(t)-sin(0)}{t-0} = \frac{sin(t)}{t} \) |
| \(-0,1\) | \(0,998334166\) |
| \(-0,01\) | \(0,999983333\) |
| \(-0,074 1)99999833\) | |
| \(0.001\) | \(0.999999833\) |
| \(0.01\) | \(0.999983333\) |
| \(0.1\) | \(0.998334166\ ) |
Из этой таблицы видно, что средняя скорость за интервалы времени, приближающиеся к \(t=0\), приближается к скорости \(1\), поэтому кажется, что \(v(0) =1\) является хорошей оценкой.
Вы можете проверить эту оценку по формуле:
\[ v(a) = s'(a) = \lim_{t \to a} \frac{s(t)-s(a)}{t-a} . \]
\]
Используя эту формулу, вы получите:
\[ \begin{align}v(0) = s'(0) &= \lim_{t \to 0} \frac{sin(t)-sin(0) }{t-0} \\&= \lim_{t \to 0} \frac{sin(t)}{t} \\&= 1.\end{align} \]
Следовательно, \( \bf { v(0) } = \bf{ 1 } \).
Формула производной
До сих пор вы рассматривали производную функции в определенной точке. Рассматривая саму производную как функцию, вы можете найти производную функции в каждой точке ее области определения, для которой производная определена (существует предел). Ниже вы формально определяете производная функция .
Производные функции и формула производной
Существует формула, по которой можно найти любую производную любой функции. Он определяется как:
Пусть \(f(x)\) будет функцией. Производная этой функции по \(x\), обозначаемая через \(f'(x)\), представляет собой функцию, область определения которой состоит из значений \(x\) таких, что существует следующий предел:
\ [ f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}. \]
\]
Это называется определение производной .
Конечно, по мере вашего продвижения в изучении исчисления вы обнаружите более эффективные способы вычисления производных функций, которые принимают определенные формы. Они затронуты немного позже в этой статье, а более подробные объяснения и анализы находятся в статье о правилах дифференциации и ее подстатьях.
Использование формулы для определения производной всегда будет работать, хотя поиск производной таким способом может занять больше времени! 9{2}}{h} \]
Подробный анализ и дополнительные примеры см. в статье о производных функциях.
График производной
Поскольку функция и ее производная связаны, можно ожидать, что их графики также связаны, потому что производная дает нам скорость изменения функции. Лучше всего это видно на примере. 9{2}-2x \) и его производная \( f'(x) = 2x-2 \).
Лучше всего это видно на примере. 9{2}-2x \) и его производная \( f'(x) = 2x-2 \).
Решение :
Графики функции (синий) и ее производной (зеленый).
Когда функция (синяя) и ее производная (зеленая) изображены на одной координатной плоскости, вы можете увидеть их взаимосвязь.
- Вы можете видеть, что \( f(x) \) уменьшается для значений \( x < 1 \).
- Следовательно, при тех же значениях \(x\) \( f'(x) < 0 \).
- Вы также можете видеть, что \( f(x) \) увеличивается для значений \( x > 1 \).
- Следовательно, при тех же значениях \(x\) \( f'(x) > 0 \).
- И \(f(x)\) имеет горизонтальную касательную в точке \(x=1 \).
- Здесь \( f'(1)=0 \).
Производные и непрерывность
Теперь, когда вы построили график производной, давайте обсудим поведение этих графиков. Первое, что нужно рассмотреть, это дифференцируемость и непрерывность . Начнем с теоремы:
Начнем с теоремы:
Теорема – Дифференцируемость влечет непрерывность
Пусть \(f(x)\) — функция, в области определения которой есть \(a\). Если \(f(x)\) дифференцируема в \(а\), то она также непрерывна в \(а\).
Обратите внимание, что эта теорема НЕ работает в обратном порядке! Из дифференцируемости следует непрерывность, но из непрерывности не следует дифференцируемость.
Доказательство теоремы: дифференцируемость влечет непрерывность.
Если \(f(x)\) дифференцируема в \(a\), то \(f'(a)\) существует и:
\[ f'(a) = \lim_{x \to a } \frac{f(x)-f(a)}{x-a}. \]
Чтобы доказать это, нам нужно показать, что \(f(x)\) непрерывна в \(a\), показав, что \( \lim_{x \to a} (f(x)) = f(a )\). Итак,
\[ \begin{align}\lim_{x to a} (f(x)) &= \lim_{x \to a}(f(x)-f(a)+f(a)) \\&= \lim_{x \to a} \left( \frac{f(x)-f(a)}{x-a} \times (x-a) + f(a) \right) \\&= \left ( \lim_{x \to a} \frac{f(x)-f(a)}{x-a} \right) \times \left( \lim_{x \to a} (x-a) \right) + \lim_ {x \to a} f(a) \\&= f'(a) \times 0 + f(a) \\&= f(a). \end{align} \]
\end{align} \]
Поскольку \( f( а) \) определено и \( \lim_{x \to a} (f(x)) = f(a) \), можно заключить, что \( f(x) \) непрерывна в \(a\ ).
Непрерывность не означает дифференцируемости.
Давайте посмотрим на функцию абсолютного значения:
\[ f(x) = |x|. \]
График родительской функции абсолютного значения.
Вы знаете, что эта функция везде непрерывна, но везде ли она дифференцируема? Попробуем взять производную в точке, где \( x=0 \).
\[ \begin{align}f'(0) &= \lim_{x \to 0} \frac{f(x)-f(0)}{x-0} \\&= \lim_{x \to 0} \frac{|x|-|0|}{x-0} \\&= \lim_{x \to 0} \frac{|x|}{x}.\end{align} \] 9{+}} \frac{|x|}{x} = 1. \]
Другими словами, по мере приближения к пределу с левой стороны графика предел равен \(-1\), и когда вы приближаетесь к пределу с правой стороны графика, предел равен \(+1\). Чтобы предел существовал, он должен быть непротиворечивым независимо от того, с какой стороны вы приближаетесь к пределу.
Это был только один пример, когда непрерывность не означает дифференцируемости. Краткий обзор ситуаций, когда непрерывная функция не является дифференцируемой, включает:
Краткий обзор ситуаций, когда непрерывная функция не является дифференцируемой, включает:
- Как и в случае с функцией абсолютного значения, если пределы наклона касательных к кривой слева и справа не совпадают, функция не дифференцируема.
- В случае функции абсолютного значения это привело к острому углу графика в точке \(0\). Это приводит нас к выводу, что для того, чтобы функция была дифференцируемой в точке, она должна быть «гладкой» в этой точке.
- Функция не дифференцируема ни в одной точке, где касательная к ней вертикальна.
- Функция может быть не дифференцируема более сложными способами, например, функция, колебания которой становятся все более частыми по мере приближения к некоторому значению.
Типы производных
Поскольку сама производная является функцией, можно найти производную от производной. Наиболее распространенным примером этого является, когда речь идет о позиции , скорости и ускорении :
Производной функции положения является скорость изменения положения или скорость.

Производная функции скорости — это скорость изменения скорости или ускорение.
Когда вы берете производную от производной, новая функция называется второй производной . Вы можете продолжить этот процесс, чтобы найти третью производную , четвертую производную и т. д. Эти типы производных вместе называются производными высшего порядка . Обозначение производных высших порядков функции \( y = f(x) \) может быть выражено в любом из следующих форматов: 9n} \]
Подробный анализ и примеры см. в статье о производных более высокого порядка.
Правила производных
Как упоминалось ранее, можно найти производные функций, используя только определение производной. Однако этот процесс может быть довольно длительным, а иногда и довольно сложным! Этот раздел знакомит вас с правилами поиска производных без необходимости каждый раз использовать определение производной. n \), где \(n\) — натуральное число, являются строительными блоками, из которых каждый многочлен и рациональное число функции построены. Если вы хотите найти их производные, не используя определение производной, вам нужно сначала разработать формулы для дифференцирования этих функций.
n \), где \(n\) — натуральное число, являются строительными блоками, из которых каждый многочлен и рациональное число функции построены. Если вы хотите найти их производные, не используя определение производной, вам нужно сначала разработать формулы для дифференцирования этих функций.
Основные правила производных
Постоянное правило
Начнем с самой простой функции, постоянной функции: \( f(x)=c \). Правило дифференцирования постоянных функций называется постоянным правилом .
Правило констант гласит, что производная любой постоянной функции равна нулю . То есть, поскольку постоянная функция представляет собой горизонтальную линию, наклон (или скорость изменения) постоянной функции равен нулю.
Теорема – постоянное правило
Пусть \(с\) — любая константа. Если \( f(x)=c \), то производная \(f(x)\) может быть записана любым из следующих способов:
\[ f'(c)=0 \]
\ [ y'(c)=0 \]
\[ \frac{d}{dx}(c)=0 \]
Сумма, разность и постоянные множественные правила
Как и при работе с функциями, правила, помогающие находить производные функций, которые вы складываете, вычитаете или умножаете на константу.
Теорема. Правила суммы, разности и постоянного кратного числа
Пусть \(f(x)\) и \(g(x)\) — дифференцируемые функции, а \(с\) — постоянная. Тогда выполняется каждое из следующих утверждений:
Правило суммы – Производная суммы двух функций, \(f(x)\) и \(g(x)\), равна сумме производных \(f(x)\) и \(g(x)\).\[ \frac{d}{dx} (f(x)+g(x)) = \frac{d}{ dx}(f(x)) + \frac{d}{dx}(g(x)) \] или, если у вас есть\[ h(x) = f(x) + g(x), \], то \[ h'(x) = f'(x) + g'(x). \]
Правило разности . Производная разности двух функций \( f(x) \) и \(g(x) \) равна разности производных \( f(x) \ ) и \( g(x) \).\[ \frac{d}{dx} (f(x)-g(x)) = \frac{d}{dx}(f(x))-\frac {d}{dx}(g(x)) \] или, если у вас есть\[ h(x) = f(x) — g(x) \],то\[ h'(x) = f'(x ) — g'(x). \]
Множественное число констант Правило – Производная константы \(c\), умноженная на функцию, равна константе, умноженной на производную функции.
 \[ \frac{d}{dx}( c \cdot f(x)) = c \cdot \frac{d}{dx}(f(x)) \] или, если у вас \[ h(x) = c \cdot f(x) \]тогда \[ h'(x) = c \cdot f'(x). \] 9{n-1} \]
\[ \frac{d}{dx}( c \cdot f(x)) = c \cdot \frac{d}{dx}(f(x)) \] или, если у вас \[ h(x) = c \cdot f(x) \]тогда \[ h'(x) = c \cdot f'(x). \] 9{n-1} \]Подробный анализ и примеры см. в статье The Power Rule.
Правило произведения
Правило произведения утверждает, что производная произведения двух функций равна: быть дифференцируемыми функциями. Тогда
\[ \frac{d}{dx}(f(x)g(x)) = \frac{d}{dx}(f(x))g(x) + f(x) \frac {d}{dx}(g(x)), \] или, если у вас есть
\[ h(x) = f(x)g(x) \]
, затем
\[ h'(x) = f'(x)g(x) + f(x)g'(x). \]
Хотя может показаться заманчивым так думать, правило произведения НЕ следует шаблону правил суммы/разности. Производная продукта НЕ ЯВЛЯЕТСЯ продуктом производных!
Подробный анализ и примеры см. в статье The Product Rule.
Частное правило
Теперь, когда вы рассмотрели производные произведения двух функций, давайте рассмотрим частные функции и разработаем правило частного.
Правило частного гласит, что производная от частного двух функций равна:
Производная функции в числителе, умноженная на функцию в знаменателе минус функция в числителе, умноженная на производную функции в в знаменателе,
Все разделить на функцию в знаменателе в квадрате.

Теорема. Правило частных
Пусть \(f(x)\) и \(g(x)\) — дифференцируемые функции. Затем 92}. \]
Хотя может показаться заманчивым так думать, правило частного НЕ следует шаблону правил суммы/разности. Производная частного НЕ ЯВЛЯЕТСЯ частным производных!
Подробный анализ и примеры см. в статье The Quotient Rule.
Комбинирование правил производных
Продолжая изучение исчисления, вы увидите, что редко можно использовать только одно правило дифференцирования для нахождения производной заданной функции. Используя изученные правила, теперь вы можете находить производные полиномиальных и рациональных функций. 9{2}-4t+70 \]
для \( 0 \leq t \leq 10 \)
, где \( t = \) число прошедших часов \(9pm \) представляет температуру вашего дома в течение ночи .
Найдите мгновенную скорость изменения температуры в полночь.
Решение :
Поскольку полночь наступает \(3\) часа после \(9pm\), вы хотите найти мгновенную скорость изменения или производную уравнения в \(t=3\).
 Другими словами, вам нужно вычислить \(T'(3)\). 9{\circ} F \) в час .
Другими словами, вам нужно вычислить \(T'(3)\). 9{\circ} F \) в час .Как найти производную функции извлечения квадратного корня?
Найдите производную функции извлечения квадратного корня \( f(x)=\sqrt{x} \).
Решение :
- Применить определение производной.\[ f'(x) = \lim_{h \to 0} \left( \frac{f(x+h)-f(x)} {h} \right) \]
- Замена \( f(x)=\sqrt{x} \).\[ f'(x) = \lim_{h \to 0} \left( \frac{\sqrt {x+h}-\sqrt{x}}{h} \right) \]
- Умножьте и разделите на \( \sqrt{x+h}+\sqrt{x} \), чтобы упростить дробь. \[ f'(x) = \lim_{h \to 0} \left( \frac{\sqrt{x+h}-\sqrt{x}}{h} \times \frac{\sqrt{x+h }+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}} \right) \]
- Упростить.\[ f'(x) = \lim_{h \to 0} \left( \frac{h}{h \left( \sqrt{x+h} + \sqrt{x} \right)} \right) \]
- Сократить общий делитель \(h\).\[ f'(x) = \lim_{h \to 0} \left( \frac{1}{\sqrt{x+h }+\sqrt{x}} \right) \]
- Оценить предел.\[ f'(x) = \frac{1}{\sqrt{x}+\sqrt{x}} \]
- Упростить .
 \[ \bf{ f'(x) } = \bf{ \frac{1}{2\sqrt{x}} } \]
\[ \bf{ f'(x) } = \bf{ \frac{1}{2\sqrt{x}} } \]
Теперь давайте посмотрим, как функция квадратного корня и ее производная сравниваются графически.
График функции \( f(x)=\sqrt{x} \) и ее производной \( f'(x) = \frac{1}{2\sqrt{x}}.
Решение :
График функции (синий) и ее производной (зеленый)
Когда функция (синий) и ее производная (зеленый) изображены на одной координатной плоскости, вы можете увидеть их взаимосвязь.
- Во-первых, обратите внимание, что \( f(x) \) увеличивается по всей области определения. Это означает, что наклоны всех касательных линий положительны.
- Следовательно, вы ожидаете, что \(f'(x) > 0 \) для всех значений \(x\) в его области определения.
9{2}-4т+1\) (в метрах). Найдите функцию, описывающую его ускорение в момент времени \(t\). - Следовательно, \( v(t) = 6t-4 \).
Решение :
Чтобы найти функцию ускорения из функции положения, нужно взять первую и вторую производные функции положения.
 {2}+4t-1}{h} \right) \\&= \lim_{h \to 0} \left ( \frac{h(6t+3h-4)}{h} \right) \\&= \lim_{h \to 0} (6t+3h-4) \\s'(t) &= 6t-4 \\\конец{выравнивание} \]
{2}+4t-1}{h} \right) \\&= \lim_{h \to 0} \left ( \frac{h(6t+3h-4)}{h} \right) \\&= \lim_{h \to 0} (6t+3h-4) \\s'(t) &= 6t-4 \\\конец{выравнивание} \]- Вторая производная функции положения — это функция ускорения: \( s»(t) = v'(t) = a(t) \).\[ \begin{align}s»(t ) &= \lim_{h \to 0} \left( \frac{s'(t+h)-s'(t)}{h} \right) \\&= \lim_{h \to 0} \ влево( \frac{6(t+h)-4-(6t-4)}{h} \right) \\&= \lim_{h \to 0} \left( \frac{6t+6h-4- 6t+4}{h} \right) \\&= \lim_{h \to 0} \left( \frac{6h}{h} \right) \\&= \lim_{h \to 0} (6 ) \\s»(t) &= 6\end{align} \] 9049{2}} } \).
Производные – основные выводы
- Целью производной является вычисление наклона касательной к кривой в определенной точке .
- мгновенная скорость изменения функции \(f(x)\) при значении \(a\) является ее производной при \(a\) , \(f’ (а) \) .

- Определение производной: \[ f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]
- Дифференцируемость подразумевает непрерывность, но непрерывность не влечет дифференцируемости.
- Вы можете взять производную от производной
- Это приведет к производным высшего порядка
- Существует несколько правил производных, которые помогут нам найти производные функций быстрее и проще.
Ссылки
- https://www.hennesseyspecialvehicles.com/2021-venom-f5/
Производные / дифференциальное исчисление: определения, правила
Производная — это другое название наклона касательной в точке. Здесь производные в точках А и В равны нулю.
Содержание :
Основы
- Что такое производная?
- Формула: предельное определение производной
- Формула: предельное определение производной
- Примеры ТИ-89
- Обозначение дифференциации
- Таблицы производных (Краткое справочное руководство по общим производным
- Постоянный фактор Правило 905:00
- Правило продукта
- Цепное правило
- Функции с показателями степени (степенное правило ).

- Частное правило
- Правило взаимности: определение, примеры
- Правило суммы
Специальные функции
- Как найти производную простых функций:
- Постоянные функции (например, y = 5, y = 99)
- лн (натуральное бревно)
- Грех 3x
- Тан х
- Производные обратной функции.
- Производная тригонометрической функции.
Дополнительные определения и примеры
- Автоматическое дифференцирование
- Непрерывная производная
- Конвективная производная
- Критические числа
- Производная не существует в точке: 7 примеров
- Левая производная и правая производная
- Отличие по частям
- Направленные производные
- Эпидериваты
- Явное дифференцирование
- Внешняя производная
- Формула Фаа ди Бруно: определение, примеры шагов
- Четвертые производные
- Дробное исчисление
- Пятая производная (треск)
- Тест первой производной
- Дифференциал Gateaux
- Общее правило Лейбница
- Обобщенная производная: обзор, примеры
- Производные высшего порядка
- Производная Хукухара: Определение 905:00
- Неявное дифференцирование
- Lanczos Производная
- Производная Ли
- Линейность дифференцирования
- Местный производный
- Логарифмическая производная
- Смешанная производная (частичная, повторяющаяся)
- N-ая производная
- Численное дифференцирование
- Односторонняя производная
- Параметрическая производная
- Частная производная
- Полярная производная
- Второй производный тест 905:00
- Симметричная производная
- Третьи производные
- Суммарный дифференциал/производная: формула, пример
- Когда функция не дифференцируема?
- Слабые производные
Проще говоря, это мгновенная скорость изменения. Он говорит вам, как быстро меняется соотношение между вашим входом (x) и выходом (y) в любой конкретный момент времени.
Он говорит вам, как быстро меняется соотношение между вашим входом (x) и выходом (y) в любой конкретный момент времени.
Следующая формула дает более точное (т.е. более математическое) определение.
Есть коротких путей, , но когда вы впервые начнете изучать исчисление, вы будете использовать формулу.
Нередко дойдя до конца семестра, вы все еще не знаете точно, что это такое! Это потому, что определение не сразу интуитивно понятно; вы действительно поймете, что это такое, после того, как вы практиковались — и практиковались. Это как знать, что такое амбушюр при игре на кларнете; вам могут сказать, что это размещение языка, но требуется много недель (иногда месяцев) практики, прежде чем вы действительно хорошо поймете, как сделать идеальный анбушер и почему это важно.
Производные можно найти несколькими способами. Нахождение производных с использованием предельного определения производной — это один из способов, но он требует некоторых сильных навыков алгебры. Посмотрите видео с парой быстрых пошаговых примеров:
Посмотрите видео с парой быстрых пошаговых примеров:
Предельное определение производных примеров
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Пример задачи №1: Найдите производную f(x) = √(4x + 1)
Шаг 1: Вставить функцию в формулу. Функция равна √(4x + 1), поэтому:
f'(x) = lim Δx → 0 √( 4( x + Δx ) + 1 – √(4x + 1)) / Δx.
Если это выглядит запутанно, все, что мы сделали, это заменили «x» в формуле на x + Δx в первой части формулы.
Шаг 2: Используйте алгебру для работы с формулой. Здесь вам пригодятся хорошие навыки алгебры, потому что каждая формула уникальна.
- Умножьте верхнее и нижнее число на √( 4( x + Δx) + 1 + √(4x + 1):
f'(x) = lim Δx → 0 √( 4( x + Δx) + 1 – √(4x + 1) ) * √( 4( x + Δx) + 1 + √(4x + 1) / Δx* √( 4( x + Δx) + 1 + √(4x + 1)
, что сводится к:
= lim Δx → 0 4(x + Δx) + 1 – (4x + 1) / Δx(√ (4x + Δx) + 1) + √ 4x + 1 - Распределить 4:
= lim Δx → 0 (4x + 4Δx + 1 – 4x – 1) / (Δx(√ (4x + Δx) + 1) + √ (4x + 1) - Удалить термины.
 В этом случае можно удалить 4x, Δx и 1.
В этом случае можно удалить 4x, Δx и 1.
= lim Δx → 0 4 / ((√ (4x + Δx) + 1) + √ 4x + 1))
Шаг 3: Возьмите предел. Δx выпадет (потому что это незначительное приращение). Опять же, здесь помогут сильные навыки алгебры:
= 4 / ((√ (4x + 1) + √ 4x + 1)
= 4 / 2 √(4x + 1)
= 2 / √(4x + 1)
Вот так
Вернуться к началу
Почему важна производная
По сути, они важны, потому что позволяют извлекать информацию, о которой вы не знали 9.0514 Например, если вы знаете, где находится объект (т. е. у вас есть функция положения), вы можете использовать производную, чтобы найти скорость, ускорение или рывок (скорость изменения ускорения). Как? Производная от…
- …позиция – это скорость.
- …скорость — это ускорение.
- …ускорение резкое.
Вы можете продолжать брать производные (например, четвертую, пятую), извлекая все больше и больше информации из этой простой функции положения. И это работает не только с позицией; Исчисление может работать с любой функцией.
И это работает не только с позицией; Исчисление может работать с любой функцией.
Поиск производных на TI 89 или TI 89 Titanium включает те же шаги. Это потому, что два калькулятора по сути одинаковы, за исключением нескольких наворотов на Титаниуме, таких как дополнительная память. Эти обновления не влияют на то, как вы находите деривативы.
- Производные TI 89/титановые ступени
- Оценка производной по определенному значению,
- Нахождение высших производных (2-я, 3-я…),
Пример задачи: Найдите производную f(x) = 3x.
Шаг 1: Нажмите F3.
Шаг 2: Выберите «1: d(дифференцировать». Используйте клавишу со стрелкой вниз или , введите «1», чтобы выбрать его.
Шаг 3: Нажмите ENTER.
Шаг 4: Введите
Шаг 5: Введите X
Шаг 6: Введите закрывающую скобку
Шаг 7: Нажмите ENTER. Решение (3 в этом примере) находится в правой части экрана.
Решение (3 в этом примере) находится в правой части экрана.
2. Оценка производной по определенному значению
Шаг 1: Выполните шаги с 1 по 4 выше.
- Нажмите кнопку F3
- Выберите «1: d(дифференцировать»
- Нажмите ВВОД
- Введите имя функции с запятой.
- Тип Х
Шаг 2: Закройте круглые скобки «)», затем введите вертикальную черту (называемую символом «с»). На TI-89 вы найдете « | ” с левой стороны. Пока не нажимайте ввод .
Шаг 3: Введите значение, которое вы пытаетесь найти. Например, введите x=3, если вы пытаетесь найти значение производной при x = 3. Нажмите ENTER .
3. Нахождение старших производных (2-я, 3-я…)
Пример задачи: Найдите вторую производную f(x) = 3x 2 на TI 89.
Шаг 1: Выполните шаги с 1 по 4 в первом разделе выше:
- Нажмите кнопку F3 92,x)|x=2
Шаг 3: Нажмите ENTER.

Вот и все! Готово!
Расчетные таблицы: Содержание
- Производные:
- Общие правила
- Степени и многочлены
- Тригонометрические функции
- Экспоненциальные и логарифмические функции
- Обратные тригонометрические функции
- Гиперболические и обратные гиперболические функции
См.: Что такое гиперболическая функция?
Ссылки
Викиучебник Таблицы производных
Посмотрите это 10-минутное введение или прочитайте ниже:
Дробное исчисление за 10 минут.
Посмотрите это видео на YouTube.
Дробное исчисление — это когда вы расширяете определение производной n-го порядка (например, первая производная, вторая производная,…), допуская n , чтобы иметь дробное значение.

Еще в 1695 году Лейбниц (основатель современного исчисления) получил письмо от математика Лопиталя, в котором он спрашивал, что произойдет, если «n» в D n x/Dx n будет равно 1/2. Ответ Лейбница: «Это приведет к парадоксу, из которого будут извлечены однодневные полезные следствия».
Не существует очевидного графического понимания дробного исчисления, и не все основные правила, которые мы вывели для классического исчисления, применимы или становятся очень сложными. Простые идеи, такие как основа цепного правила или правила произведения, больше не являются простыми идеями, когда дело доходит до этого нового вида исчисления, и иногда они просто не работают.
Простой пример исчисления дробей: производная степенной функции
Вычисление производной степенной функции — одна из самых простых задач в исчислении, поэтому, возможно, это хорошее место для начала изучения того, как может вести себя функция половинной производной.
Давайте определим нашу функцию интереса, f(x), как:
Наши знания в области исчисления говорят нам, что первая производная будет
И мы можем повторить это a раза, чтобы получить обобщенный результат
Теперь мы знаем, что факториал эквивалентен гамма-функции,.
 производной, мы должны заменить k = 1 и a = ½.
производной, мы должны заменить k = 1 и a = ½. На приведенном ниже графике эта половинная производная показана фиолетовым цветом, наряду с исходной функцией (синим цветом) и первой производной (красным цветом).
Производная по направлению показывает мгновенную скорость изменения функции в определенном направлении.
Вы можете записать этот тип производной как:
Это обозначение указывает, что вы смотрите на скорость изменения функции f(x,y,z) в определенной точке (x 0 , y 0 , г 0 ). Символ ∇ называется «набла» или «дель».
Эта идея на самом деле является обобщением идеи частной производной. Для частной производной вы берете скорость изменения вдоль одной из кривых координат, сохраняя все остальные координаты постоянными. Для производной по направлению вы должны учитывать все части вашего вектора направления.
Производная по направлению скалярной функции
Производная по направлению скалярной функции (т.
 е. одномерной функции) относительно легко определить. Вдоль вектора v она определяется как:
е. одномерной функции) относительно легко определить. Вдоль вектора v она определяется как:Это скорость изменения функции f в направлении вектора v по отношению ко времени прямо в точке x.
Свойства производной по направлению
У производной по направлению есть одно особенно хорошее свойство; многие свойства обычных производных справедливы и для него.
Например, если наши функции f и g дифференцируемы в точке p:
- Правило сумм выполняется:
- Для любой константы c выполняется правило постоянного множителя:
- Правило произведения (также известное как правило Либница) выполняется:
- И, если g дифференцируема в p и h дифференцируема в g(p), цепное правило также выполняется:
Автоматическое дифференцирование ( autodiff ) использует компьютер для вычисления производных по некоторому заданному значению, используя механическое применение цепного правила.

Это не формула, а значение производной в интересующей точке.
Приложения для автоматического дифференцирования
Autodiff используется в:
- Усвоение данных,
- Оптимизация дизайна,
- Обратные задачи,
- Численные методы,
- Анализ чувствительности.
Может работать с очень сложными функциями; Одним из крупнейших приложений был код из 1,6 миллиона строк (написанный на Fortran 77) для исследований в области гидродинамики.
Преимущества
Преимущества:
- Эффективность и стабильность,
- Ответы достаточно точные,
- Обычно это хороший выбор, если вам нужно вычислить производную в точке.
- Обычно считается, что это лучший выбор, чем другие компьютерные методы дифференциации, такие как метод конечных разностей, символьная дифференциация или ручное кодирование (Gebremedhin, 2014).
Типы автоматической дифференциации
Существует два основных типа автодифференциации:
- Автодифф в прямом режиме,
- Автодиф.
 в обратном режиме.
в обратном режиме.
Прямой режим (также известный как линейный режим тангенса директора ), обычно используется для вычисления производных по направлению. Он включает в себя нахождение производных промежуточных переменных по независимым переменным. Переход от одного оператора к другому осуществляется с помощью цепного правила.
Обратный режим (также известный как обратный , смежный или котангенсный линейный режим ) вычисляет производные зависимых переменных относительно промежуточных значений. Опять же, распространение от одного оператора к другому выполняется в соответствии с цепным правилом.
Эти два режима математически эквивалентны и основаны на одних и тех же принципах, но могут требовать разного количества времени и компьютерной памяти.
Автоматическая дифференциация: ссылки
Bischof, Bucker, Rasch, Slusanschi, and Lang. Автоматическое дифференцирование универсального пакета вычислительной гидродинамики.
 Журнал Fluids Engineering, 2007, том 129.№ 5. стр. 652—658. Резюме получено с http://fluidsengineering.asmedigitalcollection.asme.org/article.aspx?articleid=1431286 31 марта 2019 г. Гебремедхин, А. (2014). Исследования, автоматическая дифференциация. Получено 1 июня 2019 г. с: https://www.cs.purdue.edu/homes/agebreme/research/coloring-derivatives.html
Журнал Fluids Engineering, 2007, том 129.№ 5. стр. 652—658. Резюме получено с http://fluidsengineering.asmedigitalcollection.asme.org/article.aspx?articleid=1431286 31 марта 2019 г. Гебремедхин, А. (2014). Исследования, автоматическая дифференциация. Получено 1 июня 2019 г. с: https://www.cs.purdue.edu/homes/agebreme/research/coloring-derivatives.html
Bücker, Schiller, Hovland et al. Автодиф. Получено с http://www.autodiff.org/?module=Introduction 31 марта 2019 г.
Гроссе, Роджер. CSC32 Лекция 10: Автоматическое дифференцирование. Университет Торонто CS. Получено с https://www.cs.toronto.edu/~rgrosse/courses/csc321_2018/slides/lec10.pdf 30 марта 2019 г..
Курунис, Д. и др. (2017). Символьное дифференцирование во время компиляции с использованием шаблонов выражений C++. Получено 1 июня 2019 г. с: http://arxiv-export-lb.library.cornell.edu/pdf/1705.01729
Wang, Chi-Feng. Автоматическое дифференцирование, объяснение. Как компьютеры рассчитывают производные? Получено с https://towardsdatascience. com/automatic- Differentiation-Explained-b4ba8e60c2ad 31 марта 2019 г. проблемы с оптимизацией.
com/automatic- Differentiation-Explained-b4ba8e60c2ad 31 марта 2019 г. проблемы с оптимизацией.Метод объединяет дельта- и набла-подходы к исчислению вариаций во временных масштабах (Гирейко и др., 2010).
Определение эпидериватов
Эпидериваты обычно делятся на категории:
- Условные эпидеривативы (введены Jahn & Rauh в 1997 г.) или
- Генерализованные контингентные эпидериваты .
Многозначная контингентная производная многозначной функции H в определенной точке представляет собой карту с графиком, равным условному конусу Булигана графа H в выбранной точке (Bigi & Castellani, 2002). Более формально его можно описать с помощью обозначений:
A контингентная эпидеривация из F at ( x , y ) определяется как (Rodriguez-Marin et al., 1997):
00 Однозначное отображение DF (x, y): X → Y, надграфик которого совпадает с контингентным конусом надграфа F в точке (x, y), т. е. epi (DF (x, y) = T (epi(F), (x, y)».
е. epi (DF (x, y) = T (epi(F), (x, y)».Обобщенная контингентная эпипроизводная F AT ( x , Y ) определяется как следующая установленная карта:
D G F ( x , Y ): x → 2 , Y ): x → 2 , Y ): x → 2 99494444444444444444444.
D g F ( x , y ) (x) = Min ({y ∈ Y: (x, y) ∈ T (epi(F), ( x , y )) }).
Производные высшего порядка – это любые производные, кроме первого (второго, третьего, четвертого, …). Производная функции также является функцией, поэтому вы можете продолжать брать производные до тех пор, пока ваша функция не станет f(x) = 0 (в этот момент уже нельзя брать производную).
Повторение производной снова и снова может показаться педантичным упражнением, но производные более высокого порядка имеют множество применений , особенно в физике и технике.

Пример нахождения производных более высокого порядка
Производная — это наклон касательной в точке. Здесь производные в точках А и В равны нулю.
Первая производная функции f(x) = x 4 – 5x 2 + 12x – 13 равна:
f′(x) = 4x 3 – 10x + 12 (найдено по степенному правилу).Но вы можете снова различать эту функцию. Поскольку вы дифференцируете два раза, это называется второй производной. Снова используя правило степени, вы получаете: f′′(x) = 12x 2 – 10
Вы можете пять раз брать производную этой конкретной функции, когда пятая производная равна нулю. Вы не можете взять производную от нуля, поэтому остановитесь на этом.
Высшие производные функции положения
Производные более высокого порядка имеют много теоретических применений, но они также имеют несколько практических применений. Какой именно тип информации вы извлекаете, зависит от того, с какой функции вы начинаете.
 Например, допустим, вы начинаете с функции положения.
Например, допустим, вы начинаете с функции положения.Первая производная функции положения дает вам функцию скорости, которая дает вам скорость объекта.
Вторая производная (функции положения) дает вам ускорение объекта.
Третья производная дает вам рывок — скорость изменения ускорения. Это называется «рывком», потому что именно так ощущается быстрое изменение ускорения. Представьте, что вы едете на спускающемся лифте, который внезапно замедляется: ощущение рывков, которое вы чувствуете, связано с ускорением изменений.
Четвертая производная функции положения дает скорость изменения «рывка». На этом этапе производные более высокого порядка становятся более теоретическими, но у них есть несколько важных применений, особенно для обеспечения безопасности высокоскоростных объектов (таких как американские горки!).
Третья производная является производной второй производной. Другими словами, это скорость изменения или наклон кривой второй производной.

Рывки и рывки
Третья производная функции положения называется рывком , который представляет собой скорость изменения ускорения. Предположим, что s(t) — это функция положения объекта:
- Первая производная s′(t) — это функция скорости объекта,
- Вторая производная, s′′(t), представляет собой его ускорение, 905:00
- s′′′(t) — рывок объекта.
Это называется рывком (или, реже, толчком, креном или всплеском), потому что изменения в ускорении имеют тенденцию ощущаться «рывками», особенно большие. Плавная поездка на лифте кажется именно такой — гладкой. Но прокатившись на Башне Ужаса, башне ускоренного падения в голливудских студиях Disney World, ваш желудок подскажет вам, почему изменения в ускорении также называют «кренами».
Обозначение
Для любой функции f(x), f »’ (x) может быть определен несколькими различными обозначениями, все из которых означают одно и то же (из Stewart, 2009):
Пример
Общие шаги:
- Взять производную функции (используя установленные правила производных) .
 Это называется первой производной.
Это называется первой производной. - Возьмите производную новой функции (т.е. первую производную). Эта новая функция называется второй производной.
- Возьмем производную в третий раз.
Пример : Чему равна третья производная f (x) = x n ?
Решение , многократно используя правило степени:- f′(x) = nx n − 1
- f′′′(x) = n(x n − 1 )′ = n(n − 1) x n − 2
- f′′′(x) = n(n − 1)(x n − 2 )′ = n(n − 1)(n − 2) x n − 3
Четвертые и более высокие производные
Четвертые и более высокие производные менее распространены. Чтобы найти четвертая производная , взять производную еще раз (т.е. взять производную от 3-й производной). По сути, вы можете продолжать и продолжать до бесконечности, беря производные — можно найти сотую, тысячную или миллионную производную. Однако на самом деле (и с типами уравнений, с которыми вы, вероятно, столкнетесь) вы, скорее всего, сможете брать производные только до пятой производной.
 После этого вы, вероятно, получите константу — и хотя вторая, третья и четвертая производные могут дать вам полезную информацию о поведении функции, сотая производная — нет.
После этого вы, вероятно, получите константу — и хотя вторая, третья и четвертая производные могут дать вам полезную информацию о поведении функции, сотая производная — нет.Шестая производная (также называемая pop или pounce ) является результатом шестикратного взятия производной функции (обычно функции положения). Другими словами, это производная от пятой производной.
Производные более высокого порядка, такие как эта, редко встречаются за пределами физики. А когда они случаются, они обычно не имеют большого значения. В физике вы обычно находите приближение, используя ряд Тейлора, а не занимаетесь трудоемким процессом поиска шестых производных. Для простых функций, таких как приведенная ниже, найти шестую производную относительно легко. Но большинство задач реального мира будут включать в себя функции большей сложности, а это значит, что вы все равно захотите аппроксимировать ответ с помощью ряда Тейлора.
Шестая производная: Пример задачи
Пример вопроса: Чему равна шестая производная f(x) = x 6 – 3x 4 + 9 x – 11?
Решение : Воспользуйтесь правилом степени и правилом констант, чтобы взять производные шесть раз:
- f′(x) = 6x 5 – 12x 3 + 9 (первая производная)
- f′′(x) = 30x 4 – 36x 2 (Вторая производная)
- f′′′(x) = 120x 3 – 72x (третья производная)
- f (4) = 360x 2 – 72 (Четвертая производная)
- f (5) = 720x (Пятая производная)
- f (6) = 720 (Шестая производная)
Snap, Crackle, and Pop
Шестая производная называется pop после Snap, Crackle, and Pop of Rice Krispies.
 Дж. Коднер и др. придумали эти имена (см. сноску 17 в Скотте и др.) в ответ на вопрос, заданный в группе новостей USENET sci.physics.
Дж. Коднер и др. придумали эти имена (см. сноску 17 в Скотте и др.) в ответ на вопрос, заданный в группе новостей USENET sci.physics.Связанные статьи
- Пятая производная (треск)
Ссылки
Abramowitz, M. and Stegun, I.A. (Eds.). Справочник по математическим функциям с формулами, графиками и математическими таблицами, 9-е издание. Нью-Йорк: Довер, с. 11, 1972.
Антон, Х. Исчисление: новый горизонт, 6-е изд. Нью-Йорк: Wiley, 1999
Beyer, WH «Производные». Стандартные математические таблицы CRC, 28-е изд. Бока-Ратон, Флорида: CRC Press, стр. 229–232, 1987. 91 291 Биги, Г. и Кастеллани, М. (2002). K-эпипроизводные для многозначных функций и оптимизация. Математические методы исследования операций. 401-412.
Гирейко и др., Условная эпипроизводная и исчисление вариаций во временных масштабах. в области оптимизации — журнал математического программирования и исследования операций. 2010.
Гриванк, А. Принципы и методы алгоритмического дифференцирования. Филадельфия, Пенсильвания: SIAM, 2000.
Филадельфия, Пенсильвания: SIAM, 2000.
Ян, Дж. Раух, Р. Условные эпидеривативы и многозначная оптимизация
Math. Методы Опер. Res., 46 (1997), pp. 193-211
Khan, A. et al. (2015). Многозначная оптимизация: введение в приложения (векторная оптимизация). Спрингер.
Кимеу, Джозеф М., «Дробное исчисление: определения и приложения» (2009). Магистерские диссертации и специализированные проекты. Документ 115. digitalcommons.wku.edu/theses/115 Получено с https://digitalcommons.wku.edu/cgi/viewcontent.cgi?article=1115&context=theses 12 апреля 2018 г.
Kisak, P. (Ed.) ( 2017). Обзор физики рывков: «Значение третьей производной».
ScienceDirect Дробные производные и исчисление. Получено с https://www.sciencedirect.com/topics/physics-and-astronomy/fractional-calculus 8 апреля 2019 г.
Родригес-Марин, Л. и Сама, М. О контингентных эпидеривативах. Дж. Матем. Анальный. заявл. 327 (2007). 745-762.
Скотт, Дж. Некоторые простые хаотические рывковые функции в Am. J. Phys., Vol. 65, № 6, июнь.
J. Phys., Vol. 65, № 6, июнь.
Стюарт, Дж. (2009). Исчисление: концепции и контексты. Cengage Learning.
Стюарт, Джеймс. Исчисление: ранние трансцендентальные. Частные производные: производные по направлениям и вектор градиента. Получено с https://math.libretexts.org/Bookshelves/Calculus/Map%3A_Calculus_-_Early_Transcendentals_(Stewart)/14%3A_Partial_Derivatives/14.6%3A_Directional_Derivatives_and_the_Gradient_Vector 27 июля 2019 г..
TI89 по эксплуатации.
Трольцш Ф. Оптимальное управление и дифференциальные уравнения. Майк Наука/Интерпериодика Паблишинг, 1995.
Вильджоэн, К. и Ван дер Мерве, Л. (1999). Элементарная статистика: расчеты и проценты для бизнеса и экономики. Пирсон Южная Африка.УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Производные / Дифференциальное исчисление: определения, правила» Из CalculusHowTo.com : Исчисление для всех нас! https://www.calculushowto.com/derivatives/————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.
 Ваши первые 30 минут с репетитором Chegg бесплатны!
Ваши первые 30 минут с репетитором Chegg бесплатны!ИсчислениеHowTo.com
Нахождение производной функции в исчислении
Что такое задачи исчисления производных?
Что такое производная функции? 92 и пусть A(x,y) — любая точка на кривой, тогда вы можете взять точку B (x + D x, y + D y), где значения D x и D y чрезвычайно малы. (D означает дельта.) Изучите кривую и концепцию наклона, чтобы найти наклон AB.
Ниже вы увидите, что наклон кривой m представлен выражением 2x. Подставив x, мы можем найти наклон в любой конкретной точке.
Нахождение наклона кривой
Нахождение производной по пределу изменения наклона
Производная функции y= f(x) является пределом функции при D x -> 0 и записывается как:
Lim Dy/ Dx = lim [ f(x + Dx) – f(x) ]/( x + Dx – x )
D x->0 Dx ->0
Чтобы понять концепцию предела и решения предела, когда x приближается к 0, вы можете попрактиковаться в примерах в статье How to Solve Calculus Ограничение проблем.

Приведенный выше метод нахождения производной по определению называется дельта-процессом.
Этот метод можно использовать для нахождения производной следующего:
1. f(x) = 3x + 2
m = 3
2. f(x) = 3×2 – 2x + 1
m = 6x – 2
3. f(x) = -x2 – 5x + 1
m = -2x — 5
Примеры нахождения производной с помощью дельта-процесса
Примеры нахождения производной с помощью степенного правила
Дельта-процесс можно свести к короткой методике, называемой степенным правилом:
Если y = xn , то y’ = nxn-1
Примечание. Существуют другие обозначения для производной функции по x:
y’
f'(x)
DxY
Dy /dx
D f(x)/dx
Примеры нахождения производной по степенному правилу:
1. y = 7×4
y’ = 28×3
2. f(x) = 8/x5
f(x) = 8 x -5
f'(x) = -40 x -6
3. y = 3×2 -6x + px
y’ = 6x -6 + p
4.
 y = √x + 1/√x
y = √x + 1/√xy = x1/2 + x-1/2
y’ = ½ x-1/2 – ½ x-3/2
Примеры нахождения производной Использование правила произведения
Как найти производную с помощью правила произведения
Пусть f(x) и g(x) представляют две функции:
D[ f(x) g(x) ] /dx= f(x) ) d[g(x)]/dx + g(x) d[f(x)]/dx
Или выразить иначе: (f * g )’ = f * g’ + g * f’
Примеры нахождения производной по правилу произведения:
1. f (x) = 3×2 (√x – x )
f'(x) = (3×2)(1/2 x-1/2- 1) + (√x – x )( 6x)
2. f (x) = (4 – x2) ( 1/ х + х)
f'(х) = (4 – х2) (-х-2 + 1) + (1/х + х) (-2х)
3. у = (3х2) (1 – х ) (7×3 – x)
y’ = (3×2) (1 – x) (21×2 – 1) + (7×3 – x) [( 3×2)(-1) + (1 – x)(6x)]
Нахождение производной с использованием правил для производных
Существует несколько правил, которые используются в исчислении для нахождения производной. В этой статье приведены примеры использования правила степени и правила произведения.
 Постоянное правило, частное правило и цепное правило также будут использоваться для решения производных задач.
Постоянное правило, частное правило и цепное правило также будут использоваться для решения производных задач.Большинство задач в исчислении используют основные правила для производных, а не весь дельта-процесс для решения производных. Применение правильного правила к задаче исчисления — это навык, который учащиеся развивают, отрабатывая примеры с использованием всех производных правил. Ознакомьтесь с основными правилами исчисления производных здесь.
Практика в поиске производных
Чтобы попрактиковаться в нескольких примерах поиска производной с использованием степени, произведения, частного и цепных правил, загрузите примеры задач и решений в разделе «Примеры поиска производной с помощью правил исчисления». Эти практические примеры помогут учащимся грамотно использовать и применять каждое правило для нахождения производной.
Как только эти 4 правила будут поняты, изучающий исчисление может перейти к расширению своих знаний, изучая концепцию интеграции.
 Для большей практики как в дифференциации, так и в интеграции, учащиеся могут загрузить приложение Calculus для своего iphone, чтобы помочь с дополнительными примерами и практическими тестами. В статье The Best Iphone Math Apps описывается это приложение Calculus AB Review.
Для большей практики как в дифференциации, так и в интеграции, учащиеся могут загрузить приложение Calculus для своего iphone, чтобы помочь с дополнительными примерами и практическими тестами. В статье The Best Iphone Math Apps описывается это приложение Calculus AB Review.Понимание и применение концепции производных включает решение многих примеров. Когда эти примеры затем применяются к таким проблемам, как проблемы с ускорением, учащиеся могут использовать свои основные навыки решения проблем в практических приложениях. Эта практика о том, как найти производную, поможет студентам, изучающим исчисление, уверенно решать проблемы.
Весь контент, включая изображения, принадлежит автору.
Этот пост является частью серии: Решение предельных и производных задач исчисления
В этой серии показано, как решать несколько типов предельных задач исчисления. Решаются частные случаи пределов и описываются соответствующие графы. В этом руководстве дается понятное решение задач исчисления с пределом и производными.
 См. примеры того, как найти производную, используя производные правила.
См. примеры того, как найти производную, используя производные правила.- Как решить проблемы предела исчисления
- Как решать особые случаи предельных задач исчисления
- Примеры того, как найти производную в исчислении
Производные – что это такое и как их решать?
Прежде чем изучать производные, вам необходимо иметь четкое представление о пределах, наклоне и о том, как их найти.
Зачем нужны производные?
Наклон представляет собой изменение х относительно х на прямая . Она одинакова в каждой точке прямой. Но, конечно, это не так с кривой линии .
Итак, как найти наклон кривой? Он находится путем вычисления наклона секущей, проходящей через две точки кривой.
Выше приведен график функции x 2 . Мы провели секущую, чтобы найти наклон между точкой (1,1) и точкой (2,4),Наклон равен 3.
 Мы нашли его с помощью калькулятора формулы наклона. Этот наклон является средним наклоном между этими точками.
Мы нашли его с помощью калькулятора формулы наклона. Этот наклон является средним наклоном между этими точками.Но что, если мы хотим найти наклон точки в точной точке (1,1), мгновенную скорость изменения? Как мы можем это сделать?
Здесь мы используем производные!! Давайте узнаем больше о производных и о том, как их решать.
Что такое производные?
Производные используются для определения наклона кривой в точной точке. Определение производных будет следующим:
» Производную функции можно интерпретировать как наклон графика функции или, точнее, как наклон касательной в точке. »
При вычислении производных мы находим дифференциал функции. Это означает, что мы находим разницу между двумя точками.
Эти точки расположены так близко друг к другу, что разница между ними почти равна нулю, а секущая линия между ними становится касательной.
Обозначения
Производные обозначаются тремя различными способами.
 Наиболее распространенным способом является обозначение Лабинеса.
Наиболее распространенным способом является обозначение Лабинеса.Mathematician
Notation
Labinez
f(x)
Newton
f'(x)
Lagrange
\ точка f
f
˙
f, с \точкой сверху
Как найти производные?
Надеюсь, теперь ваше замешательство по поводу деривативов и того, почему мы их используем, ясно. Перейдем к расчету производных.
Существует два основных способа решения производных. Один является формальным, а другой — альтернативной формой. Мы изучим оба на общих примерах.
Формальное дифференцированиеЛегко вывести формулу для производных, глядя на график.
Рассмотрим синусоидальную функцию. Мы хотим вычислить наклон между двумя точками на этой кривой. Первая точка — x . Поскольку мы знаем, что y=f(x), мы можем записать точку как (x,f(x)).
Мы хотим вычислить наклон между двумя точками на этой кривой. Первая точка — x . Поскольку мы знаем, что y=f(x), мы можем записать точку как (x,f(x)).Возьмем вторую точку на расстоянии х от х . Точка здесь будет (x+h,f(x+h)), где h — произвольное значение. Это может быть любое число.
Наклон в этой точке:
Поскольку мы хотим вычислить наклон точной точки, мы сблизим две точки так близко друг к другу, что они почти станут одной точкой, а разница между ними будет приближаться к нулю.
Для этой цели мы наложим ограничение на эту функцию. Уравнение становится таким:
Это то, что мы будем называть производной или d по dx (d/dx). Теперь мы можем подставить любое значение вместо x .
Таким образом, это был один из способов вычислить производную или найти наклон в точке. Перейдем ко второй и альтернативной формуле дифференцирования.
Примечание : обычно в вычислениях заменяет h .
Альтернативная форма Дельта означает очень небольшое изменение. Формула уклона с :
Дельта означает очень небольшое изменение. Формула уклона с :Это очень похоже на первую формулу. Но здесь вместо добавления расстояния к x мы возьмем совершенно другую точку (a,f(a)). Посмотрим на его график:
Применяя формулу наклона, уравнение будет:Применяя предел:
Это то же самое, что и формальный способ. Здесь вместо расстояния х мы взяли прямую точку а . Итак, когда x приближается к и расстояние будет почти нулевым. И это именно то, что мы хотим вычислить.
Пример
Найдите производную f(x) = x 2 .
Решение:
Шаг 1: Добавьте расстояние в x 2 . Это расстояние дельты x приблизительно равно нулю. Теперь найдем функцию для (x + ) 2 .

Шаг 2: Применение формулы наклона:
Шаг 3: Примените предел подходов к нулю.
Следовательно, наклон при x 2 = 2x.
Какая производная от x 4 ? Найдите сами и проверьте с помощью калькулятора производных.
Правила дифференциации
Дифференциация упрощается с помощью некоторых правил. Эти правила применяются в определенных ситуациях, чтобы избежать сложных и длительных вычислений. Основные и базовые правила описаны ниже.
Постоянное правилоВероятно, это простейшее производное правило. Если у нас нет переменной в функции, например, y=4, то производная равна 0.
Это правило имеет смысл, если вы попытаетесь визуализировать его.
Поскольку x = 0, следовательно, наклона нет. А график представляет собой прямую вертикальную линию.
 Но давайте посмотрим на это с помощью дифференцирования.
Но давайте посмотрим на это с помощью дифференцирования.
ПримерКакова производная f(x) = 5.
Решение:Шаг 1: Добавьте дельту x.
f(x + Δx) = 3 + Δx = 3 Δx = 0
Шаг 2: Применение формулы.
= 0/Δx
= 0
Степенное правилоСтепенное правило применяется к полиномиальным функциям. Формула:
Пример f(x 2 ) мы решили выучить производные, является идеальным представлением степенного правила. Но для большего понимания см. другой пример:
Пример:
Производная от x 6 . Решите это, используя ограничения, а также правила мощности.
Решение:
Решение с использованием пределов.
Шаг 1: Добавьте дельту x т. е. и расширьте уравнение.
= (x + Δx) 6
f(x + Δx) 6 = (x 6 + 6x 5 ∆x + … + ∆x 6 )
Шаг 2: Примените формулу наклона.

Шаг 3: Применить ограничение.
Решение с использованием степенного правила.
Шаг 1: Запишите функцию.
f(x) = x 6
Шаг 2: Определите компоненты и примените правило степени.
As y n = ny n-1 , (мы сформировали формулу с y , чтобы избежать путаницы.)
Здесь y = x
n = 6
Применение правила;
f’(x 6 ) = (6)x 6-1 = 6x 5
Результаты обоих методов одинаковы. Это доказывает, что правило степеней верно для любых n .
Правило суммы и разностиДве функции сложения или разности также подходят для правила дифференцирования. Правила, применяемые в таких ситуациях:
Для суммы:
f + g = d/dx (f) + d/dx (g)
Для разницы.
f — g = d/dx (f) — d/dx (g)
Пример:
Найдите f’(x) для 2x + 3x 2 .

Решение:
Шаг 1: Применить производную.
= d/dx ( 2x + 3x 2 )
Шаг 2: Примените правило.
= d/dx 2x + d/dx 3x 2
= 2,1x 1-1 + 3,2x 2-1 Применение степенного правила.
= 2 + 6x
Правило произведенияКогда вычисляется производная двух функций при умножении, мы используем правило произведения. Примером такой функции будет 4x 4 (3x + 9).
Формула правила произведения:
Пример:
Какая производная от 4x 4 (3x + 9)?
Решение:
Шаг 1: Применить производную.
= d/dx 4x 4 (3x + 9)
Согласно правилу произведения.
= 4x 4 d/dx (3x + 9) + (3x + 9) d/dx 4x 4
Шаг 2: Найдите d/dx (3x + 9).

d/dx = (3x + 9)
Применить правило сумм.
= d/dx 3x + d/dx 9
= 3 + 0 … (степенное правило для 3x и постоянное правило для 9)
= 3
Шаг 3: Решите для d/dx 4x 4 .
Использование силового правила;
= 4.{(4)x 4-1 }
= 4,4x 3
= 16x 3
Шаг 4: 90
= 4x 4 .3 + (3x +9) 16x 3
= 12x 4 + 48x 4 + 144x 3
= 60x 4 3
= 60x 4 3
9000 = 60x 4 . = x 3 (60x + 144) Частное правилоУ нас есть формула произведения, но есть ли у нас формула деления? Да! И это называется частным правилом. Он в основном выводится из правила произведения для дифференциации.
Частное уравнение выглядит примерно так: f(x)/g(x).
 Чтобы найти ее производную, ее делят на две части: f(x) * 1/g(x). Вы можете видеть, что на самом деле мы должны выполнить правило произведения.
Чтобы найти ее производную, ее делят на две части: f(x) * 1/g(x). Вы можете видеть, что на самом деле мы должны выполнить правило произведения.Все, что нам нужно сделать, это найти производную от 1/g(x). Следуя всем знакомому процессу применения формулы и предела, мы получим:
Обратите внимание, что
— это dg/dx с отрицательным знаком.
Или это можно записать как:
Теперь поместим это значение в формулу произведения, которую мы обсуждали выше:
Принимая LCM.
Это правило частных.
Пример:
Найдите производную от (x — 3)/(x 3 + x).
Решение:
Непосредственно применить правило частных.
Шаг 1: Найдите производную от (x-3).
= d/dx (x-3)
= 1
Шаг 2: Найдите производную от (x 3 -x)
= d/dx 3 (x 39049)
Используя описанные выше правила;
= 3х 2 — 1
Шаг 3: Используйте их в основном уравнении.

После упрощения;
Цепное правилоИ последнее, но не менее важное: у нас есть цепное правило. В нем говорится, что:
Это для простоты. Когда функция имеет много математических операций, ее лучше преобразовать в виде двух функций, например, у нас есть функция:
f(x)= (X 2 + 6) 4
Пусть g = X 2 + 6, тогда
f(g) = (g) 4 где g =X 2 + 6
ИЛИ
f(g(x)) = (g) 2 + 6) 4
Чтобы найти его производную, сначала нужно найти разность f относительно g , а затем g'(x). После этого умножить.
Пример:
Решить d/dx (X 2 + 6) 4
Решение:
х= g(x) 2 + 6
И f(g) = g 4
Итак, производная f(g(x)) = d/dx f(g(x)) =f'(g(x)) .
 g'(х).
g'(х).Применение цепного правила.
Шаг 1: Найдите производную g(x).
d/dx = x 2 + 6 … используя правило степени для x 2 и правило констант для 6
= 2x
Шаг 2: Найдите производную f(g).
= d/dx г 4
= 4г 3
Шаг 3: Ввод формулы и умножение.
= 4(х 2 +6) 3 . 2x
= 8x.(x 2 +6) 3
Неявное дифференцирование
Теперь у вас есть представление о решении производных. Пришло время увидеть, как выполнять неявное дифференцирование.
Неявное уравнение: Уравнение, в котором переменные не могут быть разделены.
Неявное дифференцирование — это простое дифференцирование, за исключением того, что оно выполняется для обеих частей уравнения.

Пример:
Дифференцируйте это неявное уравнение:
x 2 + y 2 = z 2
Где z — константа.
Решение:
Шаг 1: Применить производную.
d/dx (x 2 ) + d/dx(y 2 ) = d/dx(z 2 )
Шаг 2: Решение L.H.S.
= d/dx (x 2 ) + d/dx(y 2 )
= 2x + 2y(d/dx) … применяя цепное правило.
Шаг 3: Решите R.H.S.
Производная постоянных чисел равна 0.
= d/dx (z 2 )
= 0
Шаг 4: подставьте значения в уравнение.
2x + 2y(d/dx) = 0
2y(d/dx) = -2x
y(d/dx) = -x
d/dx = -x/y
Таким образом, при дифференцировании уравнения x 2 + y 2 = z 2 мы получили -x/y как производную.
Резюме
Мы используем производные, чтобы найти наклон кривой.
 Это процесс дифференциации. Это сложный процесс, поэтому мы используем правила дифференцирования.
Это процесс дифференциации. Это сложный процесс, поэтому мы используем правила дифференцирования.Вычисление производных экспоненциальных функций
Показательная функция является одной из самых важных функций в исчислении. На этой странице мы выведем выражение для производной e x и применить его для вычисления производной других экспоненциальных функций.
Наш первый контакт с числом e и экспоненциальной функцией был на странице о непрерывных сложных процентах и числе e. На этой странице мы дали интуитивное определение числа e, а также интуитивное определение экспоненциальной функции.
Мы также вывели альтернативное выражение для показательной функции. Новым выражением экспоненциальной функции был ряд, т. е.3156 бесконечная сумма .
Вы можете спросить, определение предела намного компактнее и проще, чем эта уродливая бесконечная сумма, зачем беспокоиться?
Оказывается, самый простой способ вывести правило взятия производной от e x — использовать это представление бесконечного ряда.
 Почему это? Выражение ряда для e x выглядит как многочлен.
Почему это? Выражение ряда для e x выглядит как многочлен.Мы можем обобщить идею полинома, допустив бесконечное число членов, как в выражении экспоненциальной функции. Бесконечный полином называется силовая серия.
Отличительной чертой степенного ряда является то, что для вычисления его производной вы действуете точно так же, как и для многочлена. То есть вы берете производную почленно. Сделаем это с экспоненциальной функцией.
Производная e
xРассмотрим рядовое выражение экспоненциальной функции
Мы можем вычислить производную левой части, применяя правило для производной суммы. То есть производная суммы равна сумме производных каждого члена
Мы вычисляем производную почленно.
Мы знаем производные от каждого из этих членов. Теперь есть некоторые числа, которые сокращаются
Мы сокращаем некоторые числа, и мы приходим к удивительному результату
Мы получили удивительный результат.
 Выражение для производной такое же, как и для исходной функции. это
Выражение для производной такое же, как и для исходной функции. этоПроизводная от e x равна e x
Производная e x равна e x . Это одно из свойств, которое делает экспоненциальную функцию действительно важной.
Теперь можно на время забыть о выражении ряда для экспоненты. Он нам нужен только здесь, чтобы доказать результат выше. Теперь мы можем применить это для вычисления производной других функций, включающих экспоненту.
Пример 1: f(x) = e xВычислим производную функции
На первый взгляд может быть не очевидно, но это составная функция. Это означает, что нам нужно применить цепное правило. Внешняя функция экспоненциальная. Его производная равна самому себе. Внутренняя функция — это ax:
Производная внешней функции равна исходной функции
Это было просто.
Пример 2: f(x) = e x 2 Может потребоваться еще несколько примеров, чтобы привыкнуть к тому факту, что производная экспоненты — это та же экспонента.
Может потребоваться еще несколько примеров, чтобы привыкнуть к тому факту, что производная экспоненты — это та же экспонента.Рассмотрим теперь другую составную функцию
Для вычисления ее производной снова применим цепное правило. Поскольку внешняя функция экспоненциальная, ее производная равна самой себе
Пример 3: f(x) = e x (1-x 2 )Теперь это выглядит сложнее
Здесь мы имеем продукт, поэтому мы должны использовать правило продукта. Для этого мы выделяем два фактора
И применяем правило продукта
И теперь мы факторизируем e x , чтобы получить окончательный ответ.
Пример 4: f(x) = e cos(x) sin(x)Рассмотрим следующую функцию. Давайте посмотрим, что я имею в виду. Во-первых, мы применяем правило произведения
. Теперь, чтобы вычислить u’, нам нужно применить правило цепочки
.
Пример 5: Экспонента с другим основанием, f(x)=a x Мы подключаем его к правилу произведения 9.0005
Мы подключаем его к правилу произведения 9.0005Теперь давайте рассмотрим экспоненту с основанием, отличным от e.
Как вычислить производную этой функции? Мы используем прием, который регулярно используется при работе с логарифмами. Мы можем записать эту функцию как
Вы можете проверить, что это равенство верно, используя определение логарифма. Теперь воспользуемся свойством логарифмов, которое позволяет нам выводить показатели степени из логарифмического знака 9.0005
Теперь это экспоненциальная функция с основанием e, производную которой мы умеем вычислять.
Но используя уравнение несколькими строками выше, мы можем записать это как
Это показывает одну из причин, по которой естественным выбором основания экспоненциальной функции является число e. Для любого другого основания вы получите это ln(a), засоряющее выражение его производной.
Пример 6: f(x) = a x 2Рассмотрим
Здесь нужно применить цепное правило.

- Производные:

 Есть Приступим. У меня для Вас есть две новости хорошая и очень хорошая. Хорошая новость состоит в следующем чтобы научиться находить производные, совсем необязательно знать и понимать, что такое производная. Более того, определение производной функции, математический, физический, геометрический смысл производной целесообразнее переварить позже, поскольку качественная проработка теории, по моему мнению, требует изучения ряда других тема также некоторого практического опыта. И сейчас наша задача освоить эти самые производные технически. Очень хорошая новость состоит в том, что научиться брать производные не так сложно, существует довольно чёткий алгоритм решения (и объяснения) этого задания, интегралы или пределы, например, освоить труднее.
Есть Приступим. У меня для Вас есть две новости хорошая и очень хорошая. Хорошая новость состоит в следующем чтобы научиться находить производные, совсем необязательно знать и понимать, что такое производная. Более того, определение производной функции, математический, физический, геометрический смысл производной целесообразнее переварить позже, поскольку качественная проработка теории, по моему мнению, требует изучения ряда других тема также некоторого практического опыта. И сейчас наша задача освоить эти самые производные технически. Очень хорошая новость состоит в том, что научиться брать производные не так сложно, существует довольно чёткий алгоритм решения (и объяснения) этого задания, интегралы или пределы, например, освоить труднее.
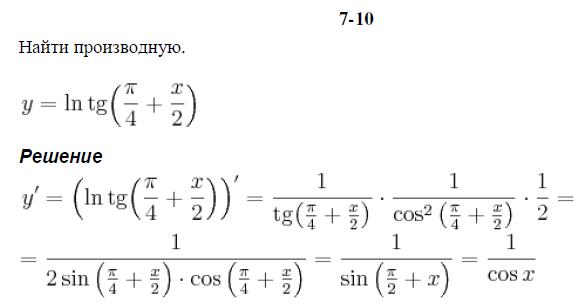 Посмотрите еще раз на таблицу производных – там функции превращаются в другие функции. Единственным исключением является экспоненциальная функция
Посмотрите еще раз на таблицу производных – там функции превращаются в другие функции. Единственным исключением является экспоненциальная функция  Кроме того, это наиболее распространенные формулы, которыми приходится пользоваться практически каждый раз, когда мы сталкиваемся с производными.
Кроме того, это наиболее распространенные формулы, которыми приходится пользоваться практически каждый раз, когда мы сталкиваемся с производными.
 Хотя этого можно и не делать, ошибкой не будет.
Хотя этого можно и не делать, ошибкой не будет.

 В данном случае можно почленно поделить числитель на знаменатель.
В данном случае можно почленно поделить числитель на знаменатель. Примеры решений
Примеры решений

 Все табличные формулы применимы ив том, случае, если икс заменить сложным выражением, в данном случае:
Все табличные формулы применимы ив том, случае, если икс заменить сложным выражением, в данном случае: Разыскиваем в таблице нужную формулу
Разыскиваем в таблице нужную формулу  Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид: Вот характерный пример:
Вот характерный пример:
 Согласно правилу дифференцирования сложной функции
Согласно правилу дифференцирования сложной функции 

 webmath.ru/primeri_reshenii/derivative.php
webmath.ru/primeri_reshenii/derivative.php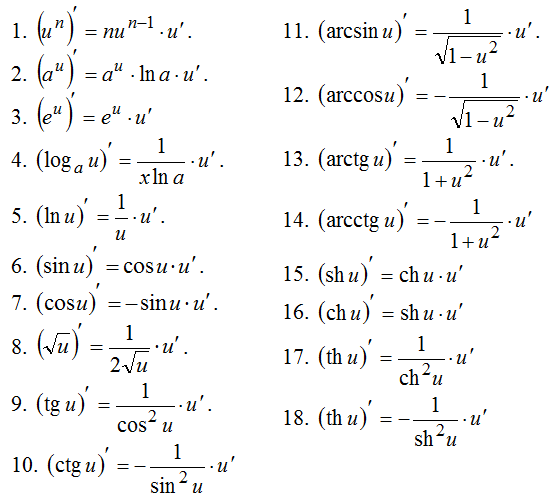 webmath.ru/poleznoe/formules_8_17.php
webmath.ru/poleznoe/formules_8_17.php

 \[ f'(2) = \lim_{h \to 0} \frac{f(2+h)-f(2)}{h} \] 9{2}+8h}{h} \]
\[ f'(2) = \lim_{h \to 0} \frac{f(2+h)-f(2)}{h} \] 9{2}+8h}{h} \]
 \[ \frac{d}{dx}( c \cdot f(x)) = c \cdot \frac{d}{dx}(f(x)) \] или, если у вас \[ h(x) = c \cdot f(x) \]тогда \[ h'(x) = c \cdot f'(x). \] 9{n-1} \]
\[ \frac{d}{dx}( c \cdot f(x)) = c \cdot \frac{d}{dx}(f(x)) \] или, если у вас \[ h(x) = c \cdot f(x) \]тогда \[ h'(x) = c \cdot f'(x). \] 9{n-1} \]
 Другими словами, вам нужно вычислить \(T'(3)\). 9{\circ} F \) в час .
Другими словами, вам нужно вычислить \(T'(3)\). 9{\circ} F \) в час . \[ \bf{ f'(x) } = \bf{ \frac{1}{2\sqrt{x}} } \]
\[ \bf{ f'(x) } = \bf{ \frac{1}{2\sqrt{x}} } \] {2}+4t-1}{h} \right) \\&= \lim_{h \to 0} \left ( \frac{h(6t+3h-4)}{h} \right) \\&= \lim_{h \to 0} (6t+3h-4) \\s'(t) &= 6t-4 \\\конец{выравнивание} \]
{2}+4t-1}{h} \right) \\&= \lim_{h \to 0} \left ( \frac{h(6t+3h-4)}{h} \right) \\&= \lim_{h \to 0} (6t+3h-4) \\s'(t) &= 6t-4 \\\конец{выравнивание} \]

 В этом случае можно удалить 4x, Δx и 1.
В этом случае можно удалить 4x, Δx и 1. 

 производной, мы должны заменить k = 1 и a = ½.
производной, мы должны заменить k = 1 и a = ½.  е. одномерной функции) относительно легко определить. Вдоль вектора v она определяется как:
е. одномерной функции) относительно легко определить. Вдоль вектора v она определяется как:
 в обратном режиме.
в обратном режиме. Журнал Fluids Engineering, 2007, том 129.№ 5. стр. 652—658. Резюме получено с http://fluidsengineering.asmedigitalcollection.asme.org/article.aspx?articleid=1431286 31 марта 2019 г. Гебремедхин, А. (2014). Исследования, автоматическая дифференциация. Получено 1 июня 2019 г. с: https://www.cs.purdue.edu/homes/agebreme/research/coloring-derivatives.html
Журнал Fluids Engineering, 2007, том 129.№ 5. стр. 652—658. Резюме получено с http://fluidsengineering.asmedigitalcollection.asme.org/article.aspx?articleid=1431286 31 марта 2019 г. Гебремедхин, А. (2014). Исследования, автоматическая дифференциация. Получено 1 июня 2019 г. с: https://www.cs.purdue.edu/homes/agebreme/research/coloring-derivatives.html  com/automatic- Differentiation-Explained-b4ba8e60c2ad 31 марта 2019 г. проблемы с оптимизацией.
com/automatic- Differentiation-Explained-b4ba8e60c2ad 31 марта 2019 г. проблемы с оптимизацией. е. epi (DF (x, y) = T (epi(F), (x, y)».
е. epi (DF (x, y) = T (epi(F), (x, y)».
 Например, допустим, вы начинаете с функции положения.
Например, допустим, вы начинаете с функции положения.
 Это называется первой производной.
Это называется первой производной. После этого вы, вероятно, получите константу — и хотя вторая, третья и четвертая производные могут дать вам полезную информацию о поведении функции, сотая производная — нет.
После этого вы, вероятно, получите константу — и хотя вторая, третья и четвертая производные могут дать вам полезную информацию о поведении функции, сотая производная — нет. Дж. Коднер и др. придумали эти имена (см. сноску 17 в Скотте и др.) в ответ на вопрос, заданный в группе новостей USENET sci.physics.
Дж. Коднер и др. придумали эти имена (см. сноску 17 в Скотте и др.) в ответ на вопрос, заданный в группе новостей USENET sci.physics. Филадельфия, Пенсильвания: SIAM, 2000.
Филадельфия, Пенсильвания: SIAM, 2000.  J. Phys., Vol. 65, № 6, июнь.
J. Phys., Vol. 65, № 6, июнь. 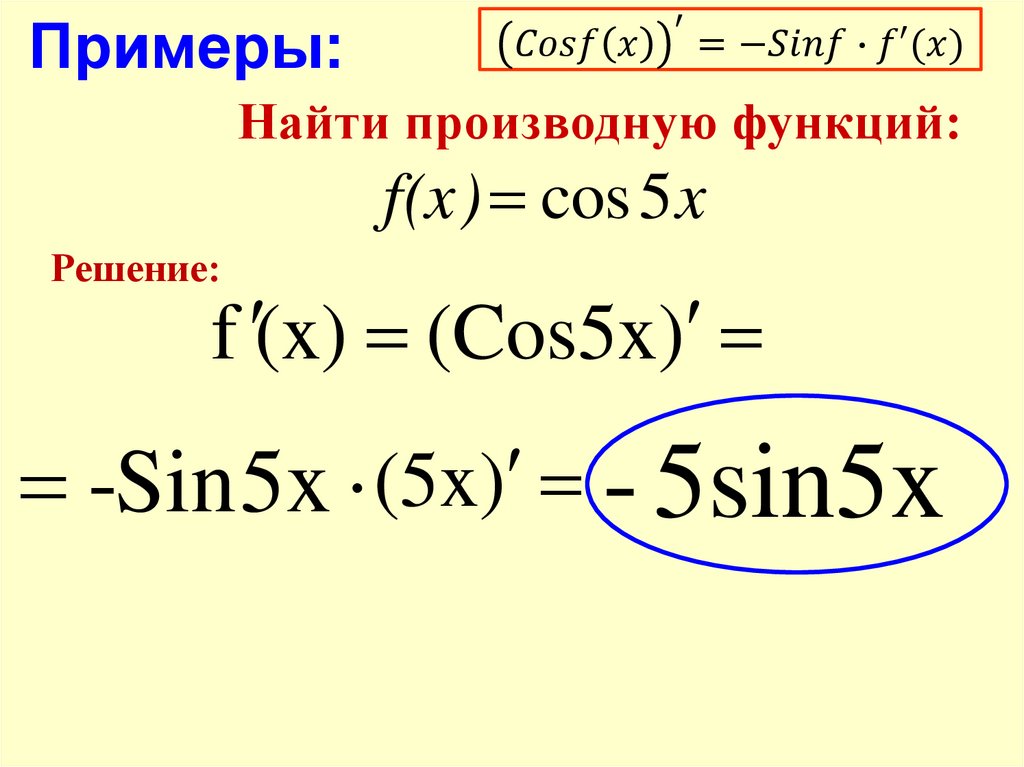 Ваши первые 30 минут с репетитором Chegg бесплатны!
Ваши первые 30 минут с репетитором Chegg бесплатны!
 y = √x + 1/√x
y = √x + 1/√x Постоянное правило, частное правило и цепное правило также будут использоваться для решения производных задач.
Постоянное правило, частное правило и цепное правило также будут использоваться для решения производных задач. Для большей практики как в дифференциации, так и в интеграции, учащиеся могут загрузить приложение Calculus для своего iphone, чтобы помочь с дополнительными примерами и практическими тестами. В статье The Best Iphone Math Apps описывается это приложение Calculus AB Review.
Для большей практики как в дифференциации, так и в интеграции, учащиеся могут загрузить приложение Calculus для своего iphone, чтобы помочь с дополнительными примерами и практическими тестами. В статье The Best Iphone Math Apps описывается это приложение Calculus AB Review. См. примеры того, как найти производную, используя производные правила.
См. примеры того, как найти производную, используя производные правила. Мы нашли его с помощью калькулятора формулы наклона. Этот наклон является средним наклоном между этими точками.
Мы нашли его с помощью калькулятора формулы наклона. Этот наклон является средним наклоном между этими точками. Наиболее распространенным способом является обозначение Лабинеса.
Наиболее распространенным способом является обозначение Лабинеса. Мы хотим вычислить наклон между двумя точками на этой кривой. Первая точка — x . Поскольку мы знаем, что y=f(x), мы можем записать точку как (x,f(x)).
Мы хотим вычислить наклон между двумя точками на этой кривой. Первая точка — x . Поскольку мы знаем, что y=f(x), мы можем записать точку как (x,f(x)). Дельта означает очень небольшое изменение. Формула уклона с :
Дельта означает очень небольшое изменение. Формула уклона с :
 Но давайте посмотрим на это с помощью дифференцирования.
Но давайте посмотрим на это с помощью дифференцирования. 


 Чтобы найти ее производную, ее делят на две части: f(x) * 1/g(x). Вы можете видеть, что на самом деле мы должны выполнить правило произведения.
Чтобы найти ее производную, ее делят на две части: f(x) * 1/g(x). Вы можете видеть, что на самом деле мы должны выполнить правило произведения.
 g'(х).
g'(х).
 Это процесс дифференциации. Это сложный процесс, поэтому мы используем правила дифференцирования.
Это процесс дифференциации. Это сложный процесс, поэтому мы используем правила дифференцирования. Почему это? Выражение ряда для e x выглядит как многочлен.
Почему это? Выражение ряда для e x выглядит как многочлен. Выражение для производной такое же, как и для исходной функции. это
Выражение для производной такое же, как и для исходной функции. это Может потребоваться еще несколько примеров, чтобы привыкнуть к тому факту, что производная экспоненты — это та же экспонента.
Может потребоваться еще несколько примеров, чтобы привыкнуть к тому факту, что производная экспоненты — это та же экспонента. Мы подключаем его к правилу произведения 9.0005
Мы подключаем его к правилу произведения 9.0005