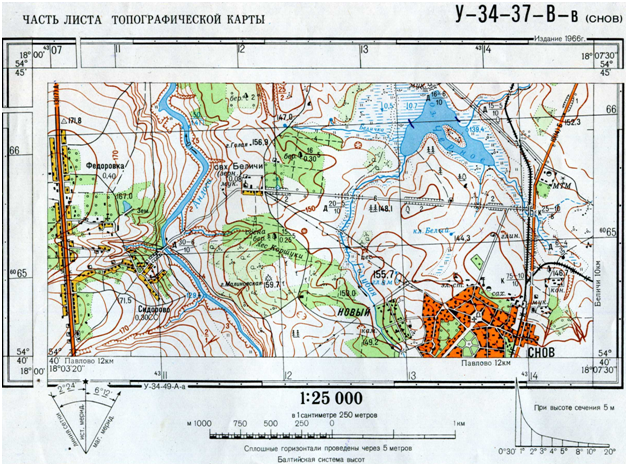
Какие вида масштаба существуют? Приведите пример численного масштаба . Переведите его в именованый масштаб
Масшта́б (нем. Maßstab, букв. «мерная палка»: Maß «мера», Stab «палка») — в общем случае отношение двух линейных размеров. Во многих практических областях применения масштабом называют отношение размера изображения к размеру изображаемого объекта.
То есть, на картах, планах, аэро- или космических снимках это отношение длины отрезка к его действительной длине на местности. Принято, на картах принимать за единицу измерения — 1 сантиметр, а на местности измерять расстояние в метрах.
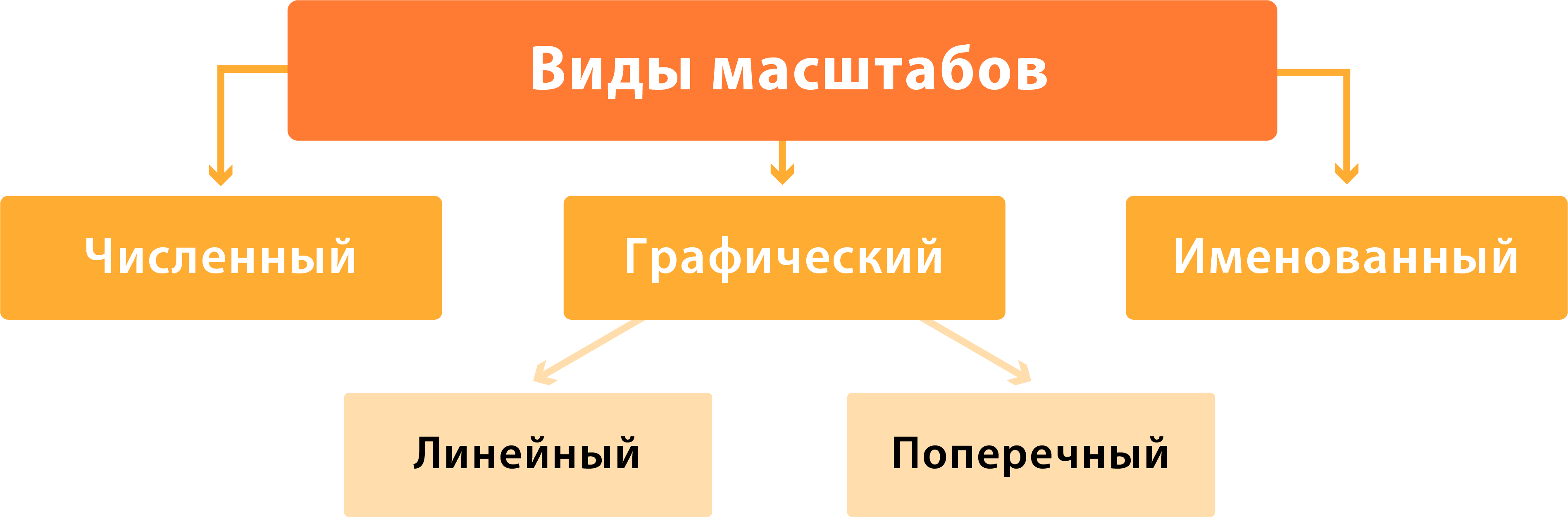
Виды указания масштабов
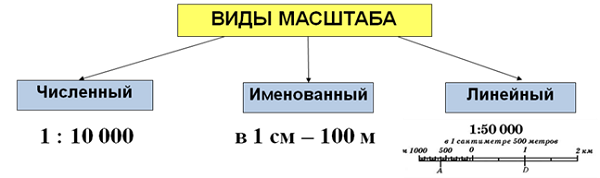
Существует три вида указания масштаба:
- численный;
- именованный;
- линейный.
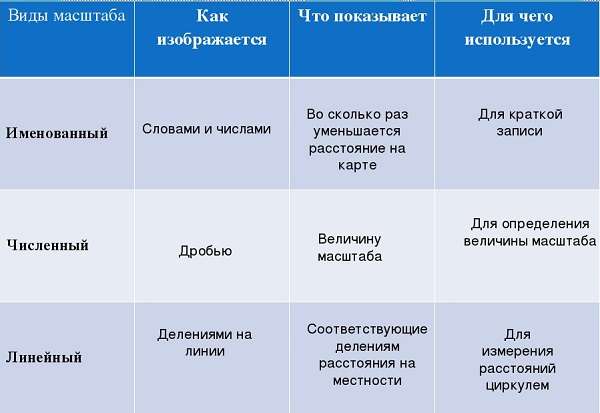
Численный масштаб (самый распространенный и удобный) — масштаб дробного вида, где числитель — единица, а знаменатель — число, показывающее во сколько раз уменьшено данное изображение територии (пример: 1:100 000; 1:15 000). Обе цифры указаны в сантиметрах, что делает невозможным ошибку в переводе, конвертации одних единиц измерения в другие. Но на практике использование такого масштаба не является удобным. Поэтому, при роботе непосредственно на местности, численный масштаб чаще всего переводят в именованный.
Именованный (или словесный) масштаб — словесное указание того, какое расстояние на местности соответствует 1 сантиметру на карте (пример: в 1 см 5 км или 1 см = 500 метров). Такой вид масштаба понятен человеческому уму, но будет сложно производить расчеты и очень легко сделать ошибку.
Существует так же и третий вид указания масштаба. Это линейный масштаб.
Линейный масштаб — вспомогательная мерная линейка на картах для быстрого измерения расстояний, без расчетов.
Масштаб карт всегда одинаков во всех ее точках.
Стандарты топографических карт и планов
В России приняты стандартные численные масштабы:
1:1 000 000
1:500 000
1:200 000
1:100 000
1:50 000
1:25 000
1:10 000.
*Для специальных целей создают также топографические карты в масштабах 1:5 000 и 1:2 000.
Точность масштаба
Предельная возможность измерения и построения отрезков на картах и планах ограничена величиной 0,01 см.
Точность масштаба имеет большое значение, когда в задании нам нужно указать возможную погрешность измерения.
Поэтому, для ее определения следует знаменатель численного масштаба разделить на 10 000 (1 м содержит 10 000 отрезков по 0,01 см). Так, для карты масштаба 1:25 000 точность масштаба равна 2,5 м.
Перевод численного масштаба в именованный
Так как длины линий на местности принято измерять в метрах, а на картах и планах — в сантиметрах, то масштабы удобней всего выражать в словесной форме, например:
в одном сантиметре 100 метров. Это соответствует численному масштабу 1:10 000. Поскольку 1 метр равняется 100 сантиметрам, то число метров на местности, содержащееся в 1 см на карте, легко определяется путем деления знаменателя численного масштаба на 100. Или на 100 000 — для перевода в км.
Примеры:
1:500 000 — в 1 см 5 км.
Задание:
перевести в именованный масштаб.
1:5 000 —
1:12 500 —
1:1000 000 —
1: 200 —
Виды записи масштаба — урок. География, 5 класс.
Масштаб обычно изображают в трёх видах: численном, именованном, линейном.
Численный масштаб записывают как отношение чисел: \(1 : 100\), \(1 : 1000\), \(1 : 100 000\). Первое число — расстояние на карте, а второе — реальное расстояние на местности в тех же единицах измерения. При масштабе \(1 : 1 000 000\) расстояние \(1\) см на карте соответствует \(1 000 000\) см на местности. \(1 000 000\) см — это \(10 000\) метров, или \(10\) километров.
Именованный масштаб показывает, какое расстояние на местности соответствует \(1\) см на плане. Записывается, например: «в \(1\) сантиметре \(100\) километров», или «\(1\) см \(=\) \(100\) км».
Линейный масштаб — это графический масштаб в виде масштабной линейки, разделённой на равные части. Отрезки справа от нуля показывают, какое расстояние на местности соответствует \(1\) сантиметру на плане или карте. Отрезок слева от нуля для большей точности измерений разделён на пять более мелких частей.
Измеряя расстояние между объектами с помощью циркуля-измерителя, можно прикладывать его к линейному масштабу и получать расстояния на местности. С помощью линейного масштаба и циркуля-измерителя определяют длину кривых линий (реки, дороги и др.).
Источники:
Лобжанидзе А. А. География. Планета Земля. 5-6 классы: учеб. для общеобразоват. учреждений с прил. на электрон. носителе. — М.: Просвещение, 2013. — 159 с.
Дронов В. П., Савельева Л. Е. География. Землеведение. 5-6 кл.: учебник — М.: Дрофа, 2015. — 283 с.
https://ru.wikipedia.org
Урок 5: Масштаб — 100urokov.ru
План урока:
Что такое масштаб
Характеристика инструментов для практических заданий
Решение задач по определению величины масштаба
Что такое масштаб
В древние времена люди формировали всевозможные изображения Земли, чтобы передать знания потомкам. Если попытаться рассмотреть отдельные объекты на таких картах, то будет не понятно, насколько они уменьшены.

Старинная географическая карта Источник
Поэтому было введено такое понятие как «масштаб», который обозначает во сколько раз на бумаге уменьшено действительное расстояние. Изображается он в виде соотношения двух чисел. Одно из них свидетельствует о том, в какой степени оно больше чем иное. Масштаб может различаться по числу знаменателя, которое показывает, насколько был уменьшен объект.
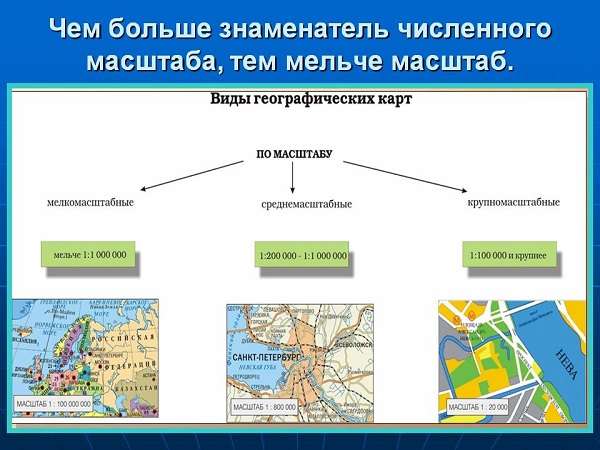
Проведем сравнение карт масштаба 1:25000 и 1:50000. Число масштаба отображает уменьшение предметов на карте в 25000 раз. Масштаб карты равный 1:50000, будет отражать уменьшение в 50000 раз. Если знаменатель будет минимальным, тогда масштаб будет крупнее, то есть объекты будут более подробно показаны. Поэтому карта с численным значением 1:25000 считается более крупной по сравнению с изображением 1:50000.

Предположим, что протяженность между торговым центром и домом 620 м. Показать в реальности этот отрезок, вычертив его на листе, не представляется возможным и придется отразить его с использованием масштаба на плане. Условимся в чертеже протяженность показывать с уменьшением предметов в 10000 раз. Тогда масштаб плана местности представлен в 1 сантиметре 100 метров. Если же план представлен в небольшом масштабе – от 1:10000 до 1:1000000, то его относят к топографической карте.
Существует несколько видов масштаба.

Лучше использовать масштаб, отображенный как прямая линия с выделенными равными частями. Этот масштаб считается линейным. Необходимо принять во внимание, что при отображении линейного масштаба ноль устанавливают, отходя на 1 см от левого конца, а первый сантиметр разбивают на 5 частей. Эти части показывают, какой действительный промежуток подходит одному сантиметру.
Такой масштаб представляют также словами и получаем запись «в 1 см – 100 м». Этот масштаб получил название именованный и можно произвести его перевод в численный. Тогда получим 1:10000 численный масштаб карты.
Часто обозначаются все три типа масштаба.

При увеличении или уменьшении масштаба меняется детальность изображения объектов на карте. На плане местности крупный масштаб, поэтому все объекты изображены очень подробно. Например, рассматривая план любого города, можно разглядеть отдельные улицы и дома. При изображении территории в мелком географическом масштабе можно взять большой участок поверхности, но все объекты будут показаны не так подробно.

При изучении географии придется работать с различными видами карт по масштабу и охвату территории.

Любая группа карт различается по масштабу. Чем больше представленная территория, тем меньше масштаб. С убавлением масштаба сокращаются достоверность отображения предметов и надежность замеров по карте.
Наиболее мелкий масштаб на мировых картах и картах полушарий. Например, на школьных стенных физических картах полушарий масштаб 1:30000000. Представленное значение свидетельствует, что 1 см соответствует 300 км на территории. Такие изображения называются мелкомасштабными.

Источник
Здесь поверхность показана весьма обобщенно и присутствуют заметные искажения очертаний материков, островов, архипелагов – и т.д. Физические карты с таким масштабом малопригодны для измерений, но зато они позволяют одновременно обозревать изображение всей земной поверхности. Поэтому их используют для рассмотрения взаимного расположения материков, омывающих их морей и океанов.
Физические и политические карты материков выполняются с мелким масштабом. Однако здесь изображается больше объектов и со значительными подробностями, чем на мировых картах. По ним легко определять расстояния и географические координаты, хотя они получаются приблизительными. Эти карты используются при изучении природы, населения и размещения государств на материках. Например, материк Австралия на карте воспроизведен в масштабе 1:60000000, который показывает, что 1 см соответствует 600 км.

Источник
Для более подробного изучения отдельных областей материка используют карты, имеющие средний масштаб. Масштаб карт колеблется в промежутке от 1:200000 до 1:1000000. К примеру, карта Еврейской автономной области Дальнего Востока изображена в численном масштабе 1: 1000000.

Карты, которые изображаются в масштабе от 1:10000 до 1:1000000, получили название крупномасштабных или топографических. Здесь очень подробно изображена местность и различные объекты. Часто на них можно увидеть дороги, особенности рельефа, реки, озера, населенные пункты.
Источник
Крупный масштаб мы можем встретить на топографическом плане. Численный масштаб плана может соответствовать значению до 1:10000. Получают план такого масштаба в результате топографической съемки местности. Часто такие планы необходимы при строительстве каких-либо объектов. Тогда изображают подробно весь участок местности с его составляющими.

Масштабы карт и планов будут разные. Следует учитывать, что масштаб плана местности во всех его точках одинаковый, а на карте он будет различаться. Это зависит от того, что план местности не учитывает форму Земли. На географической карте эта кривизна учитывается. Что же тогда означает масштаб на карте? Он считается главным масштабом и сохраняется только в центральной части, а именно в точке пересечения экватора и среднего меридиана. Во всех остальных частях он больше или меньше главного масштаба.
Широко понятие «масштаб» применяется в картографии, строительстве, при проектировании ландшафта. Изготовление всевозможных моделей также осуществляется в масштабе, к примеру, модели летательных аппаратов, автомобилей, зданий и другие. Даже проект вашей квартиры начерчен с использованием масштаба.
Характеристика инструментов для практических заданий
Для определения расстояний по картам с помощью масштаба пользуются различными измерительными приборами. Остановимся более подробно на их характеристике.
- Линейка считается наиболее простым измерительным прибором. Представляет собой узкую пластинку с прямыми сторонами. На любой линейке есть штрихи, проведенные через определенные промежутки. Обозначать они могут сантиметры, миллиметры или дюймы. Для измерения расстояния необходимо приложить линейку к карте и зафиксировать отрезок между точками. Полученный промежуток в сантиметрах перемножить с величиной масштаба карты.

Для вычисления масштаба многие специалисты применяют масштабную либо геодезическую линейку. С помощью такой линейки очень легко можно определить расстояние, однако масштаб линейки должен быть такой же, как и на карте.

Одним из видов линейки считается транспортир. С помощью транспортира и линейки можно определить направление объекта. На уроках математике вы применяли транспортир для определения градусов углов. А по ним уже можно определить направление. На этом мы с вами остановимся в следующем уроке.
- Измерение расстояний можно осуществить с помощью штангенциркуля. Какую конструкцию имеет штангенциркуль, рассмотрим на рисунке.

Также как и у всех других измерительных приборов, у штангенциркуля есть шкала в сантиметрах либо миллиметрах. С целью замера расстояния на карте разметочным штангенциркулем с помощью губок фиксируем длину между объектами. Измеренный промежуток на карте прикладываем к линейному масштабу и получаем реальное расстояние.
Проще всего воспользоваться обычным циркулем и линейкой для работы с картой. Как работать с линейкой мы уже разобрались. Остановимся на циркуле-измерителе.
Для определения протяженности между участками на карте по масштабу, нужно приложить циркуль к ним и зафиксировать отрезок, расстояние которого требуется определить. Затем, зафиксированное расстояние на циркуле, приложим к линейному масштабу карты и получим реальное расстояние.

Можно также воспользоваться численным и именованным масштабом плана. Для этого измеряем циркулем отрезок между объектами и прикладываем его к линейке. Полученное расстояние в сантиметрах умножаем на величину масштаба карты.

Решение задач по определению величины масштаба
Величиной масштаба называется расстояние на местности соответствующее 1 сантиметру на карте.
Остановимся на решении задач по определению величины масштаба на различных картах.

Для определения расстояния от точки А до родника необходимо обратить внимание на условные знаки для топографических планов и представленный масштаб. Величина масштаба данной карты 1:10000, это составляет 100 метров на 1 см. С помощью линейки измеряем расстояние между точками и получаем 8 см. Для перевода данной цифры в метры умножаем 8 см на 100 м. Результат – расстояние от точки А до родника 800 метров. Если необходимо измерить расстояние в километрах, то вспоминаем, что 1 км соответствует 1000 метров. Тогда 800 метров делим на 1000 и получаем 0,8 км.

Во второй задаче дан фрагмент карты с линейным масштабом. Необходимо определить численный и именованный масштаб. По левую сторону от ноля нанесены деления соответствующие метрам, а по правую сторону – километрам. На линии видно, что деление 1 см соответствует 500 метров. Значит, переводим метры в сантиметры – умножаем 500 на 100. Таким образом, получили 50000. Величина численного масштаба – это 1:50000, которая показывает, что 1 см на карте соответствует 500 метров на местности. Именованный масштаб будет в 1 см 500 м.

Для данной задачи известен численный масштаб, запишем его как именованный.
5000/100=50 метров.
Именованный масштаб данной карты в 1 см 50 метров. Длину реки умножаем на число, которое называется величина масштаба, и в данном случае будет составлять 50 метров.
14 см * 50 м = 700 метров
Значит, длина реки составляет 700 метров. Переведем метры в километры: 700/1000 = 0,7 км.
Задача №4
Рассмотрим еще один тип задач, в которых известно протяженность между точками, но не известен масштаб.
Ученик изобразил на бумаге школу и почту. Протяженность между зданиями оказалось равным 7 сантиметров. Каким масштабом пользовался ученик, если на поверхности земли расстояние равно 350 метров?
Для выявления величины масштаба вычислим число метров в 1 сантиметре. 350 метров/7 сантиметров = 50 метров
Значит, 1 сантиметр на плане соответствует 50 метрам. Запишем именованный масштаб в виде численного.
50 * 100 = 5000
Таким образом, численный масштаб данного плана будет соответствовать 1:5000.
Онлайн урок: Масштаб по предмету Математика 6 класс
Различают три вида масштаба:
- численный
- именованный
- графический
Графический, в свою очередь, делится на линейный и поперечный.
Численный масштаб представляют в виде дроби, где числитель — это единица, а знаменатель показывает степень уменьшения размеров изображения объектов относительно их реальных размеров.
Численный масштаб — это дробь, поэтому числитель и знаменатель выражены в одинаковых единицах измерения.
При обозначении численного масштаба не указывают единицы измерения, указывают только числа (1:2 000, 1:200 000, 1:100 и т.п.).
Пример 1
Численный масштаб карты 1:15 000 000, что он показывает?
Данный масштаб показывает, что 1 см на карте соответствует 15 000 000 см в действительности.
Нужно помнить, что чем меньше значение знаменателя в масштабе, тем крупнее масштаб.
Пример 2
Масштаб 1:1 000 крупнее, чем 1:15 000, так как знаменатель первого масштаба равен 1 000, а знаменатель второго масштаба 15 000.
1 000 меньше 15 000, следовательно, масштаб 1:1 000 крупнее.
Чем крупнее масштаб, тем больше можно изобразить объектов действительности, карта (план) получается подробней и содержательней.
При большем масштабе хорошо изображать небольшие по площади территории.
Применяется в топографических картах и планах.
На чертежах могут изображаться как уменьшенные изображения реальных объектов, так и увеличенные, если размеры изображаемого объекта слишком малы.
У меня есть дополнительная информация к этой части урока!
 Закрыть
ЗакрытьЕсли в записи масштаба знаменатель больше числителя, то такой масштаб называют масштабом уменьшения.
Масштаб 1:m, где m > 1
(например, масштаб 1:4, 1:20, 1:100 и т.п.)
Если в записи масштаба знаменатель меньше числителя, то такой масштаб называют масштабом увеличения
Масштаб m:1, где m > 1
(например, масштаб 4:1, 20:1, 100:1 и т.п.)
Масштаб в натуральную величину:
Масштаб 1:1 (числитель и знаменатель равны единице)
При создании изображений в натуральную величину в информации о чертеже указывают масштаб 1:1
Именованный масштаб— это, по сути, словесное обозначение численного масштаба.
Такой масштаб показывает, сколько одному сантиметру на карте (плане) соответствует метров (километров) на местности.
Расстояние на местности, соответствующее 1 сантиметру на карте (плане), называют величиной масштаба.
Пример 3
Дан именованный масштаб: в 1 см — 250 м (в 1 сантиметре 250 метров).
Такой масштаб означает, что 250 м на местности соответствуют 1 см на карте (плане).
Величина этого масштаба равна 250 м.
У меня есть дополнительная информация к этой части урока!
 Закрыть
ЗакрытьНа картах (планах) отмеряют расстояние в сантиметрах, а на местности в метрах или километрах.
Необходимо помнить правила перевода из одной единицы измерения в другую.
1 м = 100 см
1 км = 100 000 см
Рассмотрим правила-помощники для перевода из сантиметров в метры и километры.
Если в значении знаменателя масштаба убрать два последних нуля, то остается число, которое покажет, сколько метров на местности соответствует одному сантиметру на карте (плане), т.е. величину масштаба.
Если в значении знаменателя масштаба убрать пять последних нулей, то остается число, которое покажет, сколько километров на местности соответствует одному сантиметру на карте (плане), т.е. величину масштаба.
Попробуем перевести масштаб из численного в именованный, пользуясь правилами- помощниками

Обратным образом происходит перевод из именованного в численный
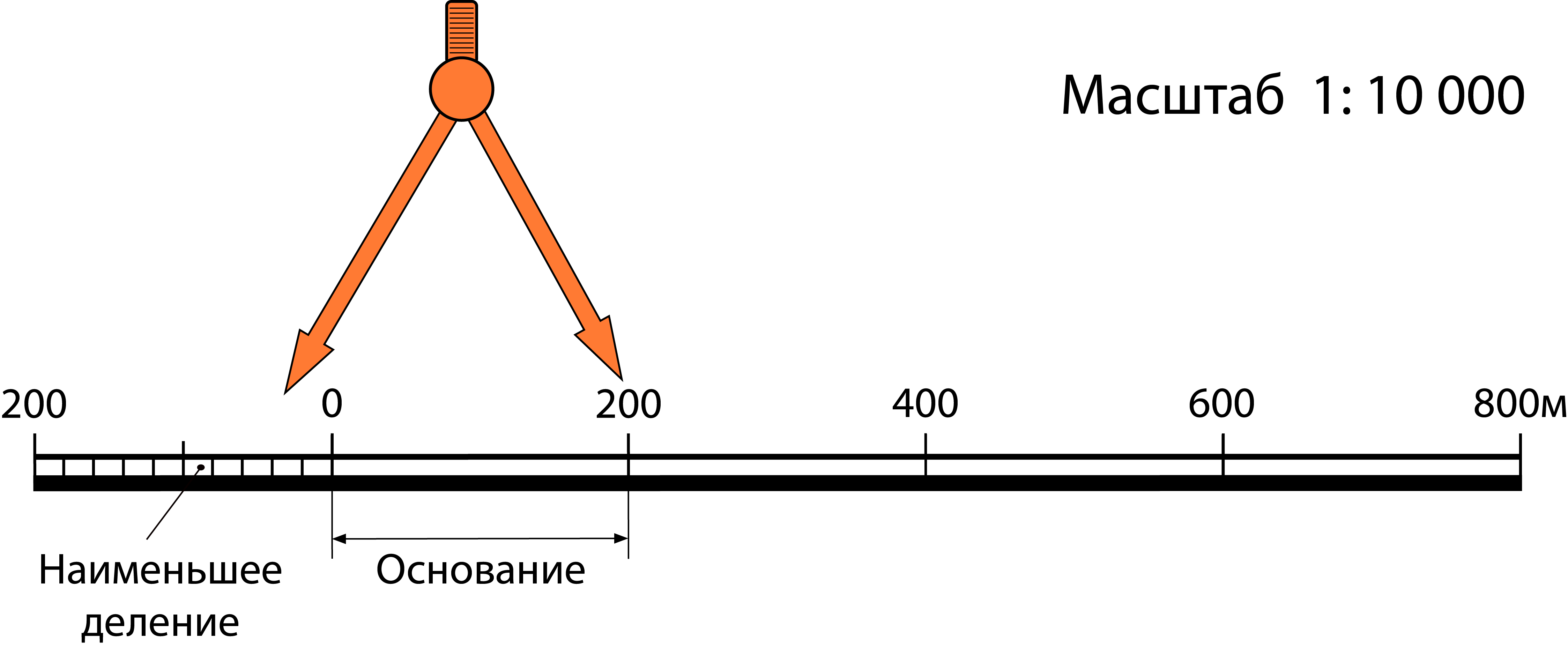
Графический масштаб подразделяют на линейный и поперечный.
Линейный масштаб дает возможность определить расстояние и размеры без расчетов и переводов длин из масштабных в реальные, позволяя тем самым ускорить работу с картой.
Линейный масштаб представляет собой отрезок прямой, разделенный на деления (подобно линейке со шкалой).
Эти деления равной длины, но с разным номинальным значением, называют основанием линейного масштаба.
Каждое деление подписано значениями, указывающими размеры соответствующих им отрезков в действительности.
Основание откладывается по всей длине масштабного отрезка (чаще всего с шагом 2 см).
Крайнее левое от нуля основание делят на более мелкие деления — это наименьшее деление линейного масштаба.
Расстояние в действительности, соответствующее номинальному делению масштаба, называют точностью масштаба (т.е. это отрезок на местности, который соответствует одному минимальному значению масштаба).
У меня есть дополнительная информация к этой части урока!
 Закрыть
ЗакрытьКак правильно пользоваться линейным масштабом
- Приложить к измеряемому отрезку на карте раствор циркуля, сделать замер
- Приложить к линейке масштаба полученный раствор циркуля и по делениям отсчитать значение замера
Отсчет берется по двум значениям: правую ножку циркуля необходимо поставить на деление справа от нуля, левая ножка циркуля может выходить за ноль в левое основание. Таким образом, длина замера будет состоять из двух отсчетов: отсчет целого основания и отсчет наименьших делений линейного масштаба левого основания.
Обратите внимание на рисунок линейного масштаба, представленного выше.
Мы можем увидеть, что раствор циркуля укладывается только в одно правое основание линейного масштаба и в два наименьших деления крайнего левого основания.
Сложив все полученные значения, получаем:
измеряемый отрезок на местности = \(\mathbf{200 м + (2 \cdot 20 м) = 240 м}\)
Поперечный масштаб
Поперечный масштаб это улучшенный вариант линейного масштаба, позволяющий делать максимально точные измерения расстояний и размеров.
Выглядит поперечный масштаб, как сетка, состоящая из горизонтальных линий, пересеченных вертикалями и наклонными линиями (трансверсали).
Используют поперечный масштаб подобно линейному, но измерения откладываются по трем основаниям (горизонталям, вертикалям и трансверсалям).
Для фиксирования длины отрезка на карте также используют циркуль.
Чаще всего поперечный масштаб применяют на специализированных картах.
Этот вид масштаба удобен для определения длинны рек, дорог, горных хребтов и других кривых на карте.
Нередко для удобства на картах приводятся все три вида масштабов: численный, именованный, графический (линейный).
Элементы топографии (литература по туризму)
(Е. Н. Мелихов)
Знание топографии, умение читать карту, уверенно ориентироваться обязательны для туриста. Недостаточное знание топографии приводит к неправильной оценке маршрута, а неумение ориентироваться — к потере времени, срыву похода или к более серьезным последствиям. В этом разделе излагаются основные положения топографии, даются способы ориентирования и практические советы, которые облегчат туристу разработку маршрута похода и его проведение.
КАРТА И ПЛАН
Уменьшенное изображение земной поверхности на бумаге, выполненное условными знаками в определенном масштабе, называется планом или картой. Изображение, на котором дается значительный участок земной поверхности и при этом учитывается кривизна земли, называется картой. Небольшие участки, принимаемые за плоскость, изображаются в виде планов. Отличительный признак карты— сетка географических координат. На планы и топографические карты наносится сетка прямоугольных координат.
В отличие от плана масштаб карты не постоянен на разных ее участках. На крупномасштабных картах эта разница невелика, и карты крупнее 1 : 20 000 не отличаются от планов. Но расстояние, измеренное на мелкомасштабной карте, будет отличаться от действительного.
Масштаб
Масштабом называется отношение длины линии на карте или плане к длине соответствующей линии на местности, выраженное в одинаковых мерах длины. Различают масштабы численные и линейные, которые обычно указываются на нижнем обрезе карты или плана.
Численный масштаб записывается в виде дроби или отношения двух чисел, причем в числителе всегда стоит единица, а в знаменателе — число, показывающее, во сколько раз действительные размеры на местности уменьшены при изображении их на карте. Например: 1/10000 1:10000 и т. д. Здесь число 10 000 показывает, что все расстояния на местности уменьшены в 10 000 раз. Или что 1 см на карте соответствует 10 000 см (100 м) на местности. Чем меньше знаменатель, тем крупнее масштаб карты, тем больше подробностей она содержит. Для разработки маршрута предпочтительнее иметь карты крупного масштаба.
Чтобы определить по карте или плану действительную длину на местности, пользуясь численным масштабом, необходимо измерить расстояние между двумя точками и помножить его на знаменатель численного масштаба.
Пример 1. На карте масштаба 1 : 25 000 измерен отрезок в 3,68 см. Соответствующая ему длина на местности будет:
D = 3,68 смХ25 000 = 92 000 см = 920 м = 0,92 км.
Пример 2. На местности расстояние между двумя пунктами равно 12 240 м. Соответствующая ему длина на карте масштаба 1 : 300 000будет:
Основное достоинство численного масштаба — возможность пользоваться любыми мерами (сантиметрами, дюймами и т. п.) для определения расстояний на картах любых масштабов, в том числе и неметрических, недостаток — необходимость производить вычисления.
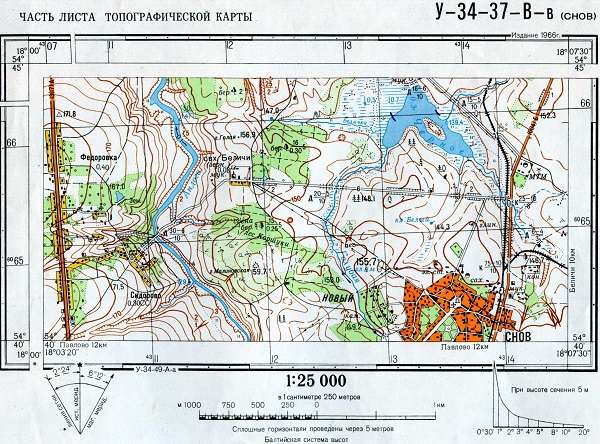
Линейный масштаб. Чтобы избежать вычислений, связанных с пользованием численным масштабом, и получать значения расстояний непосредственно с карты, строят линейный масштаб. Он представляет собой прямую линию, разделенную на отрезки равной длины, называемые основанием линейного масштаба. Основание выбирается с таким расчетом, чтобы ему на местности соответствовало круглое число сотен или тысяч метров. Например, если требуется построить линейный масштаб для карты масштаба 1 : 50 000, то целесообразно за основание принять отрезок 2 см. Тогда каждому такому отрезку на местности будет соответствовать расстояние 1 км. Для измерения линий, меньших длины основания, его делят еще на 5—10 равных частей. В указанном примере 1/10 часть основания соответствует 100 м на местности. Способ пользования линейным масштабом и его оцифровка показаны на рис. 18.
Расстояние можно измерять циркулем или полоской бумаги, на которой черточками отмечают измеряемую длину. Важно представлять себе, с какой точностью можно определять расстояние по карте в зависимости от ее масштаба. Минимальная ошибка, с которой может измеряться длина линии на бумаге циркулем или линейкой, составляет 0,01 см. Длина на местности, соответствующая этому расстоянию, например, на карте масштаба 1 : 10 000 будет 10 м, а на карте 1 : 500 000 — 50 м. Измерить линию на карте с большей точностью нельзя, поэтому расстояния на местности 10 и 50 м, соответствующие 0,01 см на карте, называются предельной точностью масштаба карты. Практически ошибка измерения линий на карте в полевых условиях составляет 0,05 см и более. составляет 0,01 см.
Рис. 18. Линейный масштаб и пользование им
Длина на местности, соответствующая этому расстоянию, например, на карте масштаба 1 : 10 000 будет 10 м, а на карте 1 : 500 000 — 50 м. Измерить линию на карте с большей точностью нельзя, поэтому расстояния на местности 10 и 50 м, соответствующие 0,01 см на карте, называются предельной точностью масштаба карты. Практически ошибка измерения линий на карте в полевых условиях составляет 0,05 см и более.
Переводной линейный масштаб. В практике туризма иногда приходится пользоваться картами неметрических масштабов или фотокопиями карт произвольного масштаба. Чтобы на них можно было производить измерения в метрических мерах, строится переводной линейный масштаб.
Например, после фотографирования карты масштаба 1 : 300 000 масштаб фотокопии получился равным 1 : 387 865. Если построить линейный масштаб с основанием 1 см, то пользоваться им будет неудобно, так как в натуре ему будет соответствовать 3878,65 м. Лучше построить такой линейный масштаб, основанию которого в натуре соответствовало бы круглое число километров или сотен метров, например 5000 м. Длину такого основания можно найти из следующей пропорции:
Определение масштаба карты
В ряде случаев масштаб карты или ее фотокопии может оказаться неизвестным. Для определения масштаба следует измерить расстояние на карте между двумя любыми точками и сравнить его с соответствующим ему расстоянием на местности. Это расстояние может быть определено по другой карте или быть заранее известным (например, расстояние между километровыми столбами).
Пример. На фотокопии расстояние между километровыми столбами получилось 3,65 см. Степень уменьшения размеров будет: 1 км=100 000 см : 3,65 см = 27 400 раз. Масштаб фотокопии 1 : 27400.
Для определения масштаба карты по географической сетке полезно знать, что 1 минута широты равна 1852 м (1 миля).
Пример. Разность широт двух смежных параллелей составляет 30 минут. Расстояние между ними по карте равно 9,26 см. Степень уменьшения размеров будет:
Построение переводного масштаба показано на рис. 19. Пользуются им, как обычным линейным масштабом.
Масштаб карты 1 : 600000.
Измерение кривых и ломаных линий
Для измерения кривых, извилистых и длинных линий удобнее всего пользоваться курвиметром, колесико которого прокатывается вдоль линии, а на циферблате отсчитываются пройденные колесиком сантиметры. При отсутствии курвиметра длину кривой можно измерить с помощью циркуля (с шагом, равным 0,5—1 см), прошагивая им вдоль линии.
Делать шаг циркуля очень малым не рекомендуется, так как при этом снижается точность измерения. Если извилины кривой меньше шага циркуля, то измерить ее таким способом невозможно. Здесь следует рекомендовать прием для измерения ломаных линий (с известным допущением), сущность которого состоит в следующем. Пусть требуется измерить ломаную линию absde. Приложив циркуль к линии ав и не снимая ножки с точки в, ставят вторую ножку в направлении отрезка вс (рис. 20). Ножка из точки в передвигается в точку с, а задняя по ходу ножка становится в направлении линии сд и т. д. Общая длина получится в результате суммирования отдельных отрезков ломаной линии.
При определении длины маршрута по карте следует учитывать два обстоятельства:
1. На картах мельче 1 : 100 000 кривые линии (реки, проселочные дороги и т. п.) наносятся с обобщениями, тем большими, чем мельче масштаб карты. Например, изгибы рек, выражающиеся на картах в 1 мм и мельче, отдельно не показываются и изображаются обобщенно. При этом следует помнить, что 1 мм на карте масштаба 1 : 100 000 составляет в натуре 100 м, а масштаба 1 : 1 000 000 — 1 км. Поэтому длину реки, измеренную на картах масштаба 1 : 200 000— 1 : 300 000, следует увеличить на 20—25%, на картах 1 : 600 000 — на 30 — 50%, а на картах более мелких масштабов фактическая длина может превышать измеренную по карте в 2—3 раза.
2. При определении длины дорог и троп в горных условиях следует учитывать не только степень обобщения карты, но и удлинение маршрута за счет разности высот (спуски, подъемы), поскольку на карте изображаются горизонтальные проекции наклонных линий, а не сами линии. Поэтому карта дает несколько уменьшенное значение расстояний по сравнению с действительной их длиной на местности.
Рис. 20. измерения. Способ ломаных линий
Условные знаки
Местные предметы и рельеф местности изображаются на картах условными знаками. Различают три вида условных знаков:
1. Масштабные — изображающие местные предметы, которые по своим размерам могут быть выражены в масштабе карты: населенные пункты, участки леса, пашни, озера, болота, крупные реки и т. п. Контуры (внешние границы) таких местных предметов показываются на карте сплошными линиями (озера, широкие реки, кварталы населенных пунктов) или точками (контуры леса, луга, болота) в точном соответствии с действительными очертаниями на местности. Площадь внутри контура на карте покрывается краской соответствующего цвета или заполняется дополнительными условными знаками.
2. Внемасштабные — изображающие местные предметы, которые не могут быть выражены в масштабе карты, но имеют важное значение: колодцы в пустыне, зимовки в тайге, предметы, имеющие значения ориентиров *, как-то: радиомачты, фабричные трубы, различного рода башни и т. п. Изображения этих местных предметов на карте делаются увеличенными, поэтому по ним нельзя судить об их действительных размерах. Если основой изображения такого условного знака является квадрат, прямоугольник или окружность, то положению предмета на местности будет соответствовать точка в центре их. Положение других условных знаков определяется вершиной прямого угла в нижней части условного знака или серединой основания у знаков, имеющих форму изображаемого местного предмета, например метеостанция (флюгер), памятник и т. п.
* Выдающиеся местные предметы, хорошо опознаваемые на местности.
С уменьшением масштаба карты некоторые масштабные условные знаки могут превращаться во внемасштабные. Например, на картах мелкого масштаба населенные пункты изображаются уже внемасштабным условным знаком — кружком.
Рис. 21. Условные знаки
Рис. 21. Условные знаки (продолжение)
На картах имеются условные знаки дорог, троп, ручьев, электролиний и других линейных местных предметов, у которых в масштабе выражается только длина. Такие условные знаки занимают промежуточное положение между масштабными и внемасштабными и называются линейными. Их точное положение на карте определяется продольной осью.
3. Пояснительные — к которым относятся все цифры, собственные наименования объектов и подписи, дающие дополнительную характеристику местным предметам. Например, если в контуре леса имеется изображение лиственного дерева, то это показывает, что лес лиственный. Порода, высота, диаметр и густота деревьев указываются записью; «бер25-0,28/5» (береза, высота 25 м, диаметр 0,28 м, расстояние между деревьями 5 м).
Изображение некоторых условных знаков дано на рис. 21.
Рельеф местности
Совокупность неровностей земной поверхности составляет рельеф местности. По характеру рельефа местность делится на равнинную, холмистую и горную. Типовыми формами рельефа являются:
Гора (холм, курган) — куполообразная возвышенность, склоны котооой понижаются во всех направлениях.
Котловина—замкнутая бессточная впадина.
Хребет — вытянутая в каком-либо направлении возвышенность. Линия, разделяющая склоны хребта и проходящая по его наивысшим точкам, называется водоразделом.
Лощина — вытянутое в одном направлении углубление местности. Линия, проходящая по дну и соединяющая наиболее низкие точки лощины, называется водосливом, или тальвегом. Широкие лощины, по дну которых протекает река или ручей, называются долинами.
Седловина — пониженная часть хребта, от которой местность в двух противоположных направлениях повышается и в двух, перпендикулярных им,— понижается. Наиболее низкие седловины в горах, доступные для перехода через хребет или горный массив, называются перевалами.
Способы изображения рельефа на картах
Способ горизонталей. Применяется на топографических картах масштаба 1 : 1 000 000 и крупнее. Сущность его состоит в том, что все неровности местности изображаются замкнутыми кривыми линиями — горизонталями (изогипсами), соединяющими одинаковые по высоте точки местности. Представление о горизонтали можно получить по береговой линии (урезу воды) замкнутого водоема (озера, пруда). Горизонтали, изображающие рельеф дна водоема, называются изобатами.
Горизонтали проводятся через равные по высоте промежутки, называемые высотой сечения. На отечественных топографических картах приняты следующие высоты сечения для равнинно-холмистой местности: 2,5 м — на карте 1:10 000, 5 м — на 1:25 000, 10 м — на 1:50 000, 20 м —на 1:100 000, АО м — на 1:200 000. На картах 1 : 500 000 и 1 : 1 000 000 горизонтали проводятся через 50 м. Высота горизонтали над уровнем моря, выраженная в метрах, называется отметкой. Отметки горизонталей подписываются в разрывах горизонталей, а отметки точек — правее их.
На рис. 22 дано изображение основных форм рельефа и показаны секущие плоскости. Из рисунка видно, что гора и котловина имеют одинаковое начертание, так же как хребет и лощина. Чтобы различать эти формы рельефа и знать, куда понижается местность, на горизонталях в сторону понижения местности ставятся указатели скатов — бергштрихи. Направление понижения местности на карте может быть также определено по расположению водоемов и водотоков, по разности отметок, расположенных на одном скате, и по подписям отметок горизонталей (скат понижается от верха цифры к ее основанию).
Рис. 22. Изображение форм рельефа горизонталями
Чем ближе расположены горизонтали друг к другу, тем круче скат. Максимальная крутизна ската, изображаемая горизонталями, не превышает 40—45°. Более крутые скаты и обрывы изображаются условными знаками.
Для облегчения счета горизонталей каждую пятую основную горизонталь утолщают. Пунктирными горизонталями изображают детали рельефа; их проводят на половине и четверти высоты сечения. Крупным пунктиром изображаются половинные, мелким — вспомогательные горизонтали.
Чтобы судить о крутизне склона местности по топографической карте, можно воспользоваться следующим простым правилом. Расстояние между горизонталями (заложение), равное 1 см (точнее 12 мм), соответствует крутизне 1° на местности.
Во сколько раз заложение будет меньше (или больше), во столько раз крутизна ската будет больше (или меньше) 1°.
На топографических картах для определения крутизны ската строится шкала заложений. На ней последовательно отложены заложения, соответствующие крутизне скатов в 1, 2, 3, 5, 10… и до 45°. Наибольшую крутизну ската определяют так: измеряют циркулем (бумажкой) кратчайшее расстояние между горизонталями и на шкале подбирают соответствующее ему заложение, против которого читают крутизну ската в градусах (рис. 23).
Изображение рельефа способом горизонталей наиболее совершенно, так как позволяет определить крутизну ската, отметки точек, строит* профиль местности и т. п. Недостаток — малая наглядность.
Способы отмывки и гипсометрический применяются вместе с горизонталями на картах более мелких масштабов для лучшей читаемости и большей наглядности изображения рельефа местности.
В основу способа отмывки положен принцип сгущения теней по мере увеличения крутизны ската. Оттенение скатов производится серой или коричневой краской. Горизонтальные поверхности остаются белыми.
Сущность гипсометрического способа заключается в окраске высотных слоев: выше 200 м — коричневой краской (по принципу чем выше, тем темнее»), а ниже 200 м — зеленой краской («чем ниже, тем темнее»). Способ применяется на картах масштаба 1 : 1 500 000 и мельче.
см. также: литература для туристов
Масштаб и его виды, смысл масштаба математический.
Полищук Алина, 2 курс ,3 группаМасштаб — это степень уменьшения длины линий на плане или карте по сравнению с их действительной длиной на местности. Масштаб указывается под южной рамкой листа плана или карты. Различают масштаб трех видов: численный, именованный, линейный. Численный масштаб записывается в виде дроби, в числителе которого единица, а в знаменателе число м, показывающие степень уменьшения: М= 1/м. Например, на карте масштаба 1/100000 или 1: 100 000 длины уменьшены по сравнению с действительностью в 100 000 раз. Очевидно, что чем больше знаменатель масштаба, тем в большее число раз уменьшены длины, тем мельче изображение объектов на карте. Именованный масштаб — это пояснение, указывающее соотношение длин линий на карте и на местности. Например, если численный масштаб 1: 100 000, именованный масштаб выглядит так> в 1см — 1км>, так как 1 см на карте соответствует 100 000 см, т.е. 1 км, на местности. Линейный масштаб служит для измерения по картам длин линий в реальности. Он представляет собой прямую линию, разделенную на равные отрезки, соответствующие десятичным числам расстояний на местности. Отрезки, а называют основанием масштаба. А расстояние на местности, соответствующее основанию, называют величиной линейного масштаба. Для повышения точности определения расстояний крайнее слева основание делят на более мелкие части б, называемые наименьшими делениями линейного масштаба. При работе с планом и картой часто приходиться переводить численный масштаб в именованный или линейный. Для этого необходимо знаменатель численного масштаба перевести в более крупные меры — метры и километры. Например, если численный масштаб плана 1:5000, это значит что в 1 см на плане соответствует на местности 5000 см или 50 метрам.
Задачи:
Из численного в именованный:
1: 100 – в 1 см – 1 м
1: 1000 – в 1 см – 10 м
1: 10 000 – в 1 см – 100 м
1: 100 000 – в 1 см – 1 км
1: 1 000 000 – в 1 см – 10 км
1: 10 000 000 – в 1 см – 100 км
Из именованного в численный:
в 1см — 15 дм – 1:1,500
в 1 см — 150 м – 1:15000
в 1 см — 17 км — 1:1700000
в 1 см — 220 км – 1:22000000
Что такое масштаб в географии, виды, масштабная линейка, как определить именованный, численный, поперечный масштаб карты, способы записи

Что такое масштаб и как его правильно истолковать? Как понять, что такое 1:1000, как измерить расстояние от одного города до другого, как перенести размер в реальный?
В средние века первооткрыватели могли легко ориентироваться на местности. Сегодня мы постараемся научиться читать географический атлас также как они.
Калькулятор масштабов
Что такое масштаб
Попробуем ответить на вопрос человека впервые открывшего карту или строительный чертеж. Что такое масштаб? Несколько заветных цифр в углу карты (плана) позволяют строителям, архитекторам и геодезистам делать точные измерения.

Точность – главная причина, необходимо знать, во сколько раз должен быть увеличен тот или иной объект в графическом исполнении.
Масштаб – дробное соотношение единицы измерения на чертеже к реальным размерам изображенного на плане (карте) объекта.
Что такое масштабная линейка
Масштабная линейка это трехсторонняя линейка, используемая архитекторами и чтения чертежей для преобразования между масштабируемыми и фактическими размерами плана без необходимости прибегать к каким-либо математическим расчетам.
Архитектор использует масштабную линейку при черчении для преобразования размеров планируемого объекта (в меньшую сторону), чтобы создать план здания.
После строитель при чтении плана воспользуется подобной линейкой для перевода размеров (указанных архитектором плана) в реальные для строительства.
В географии линейка используется схожим образом. Картограф измеряет расстояние до объекта и указывает во сколько раз оно уменьшено.
Что показывает масштаб
Показывает во сколько раз уменьшен чертеж или географическая карта по отношению к реальным размером местности или строительного объекта.
Чем меньше изображение объекта на карте, тем мельче ее масштаб, и наоборот: если меньше показатель, то крупнее объект на чертеже.
Виды масштабов
Разобравшись с тем, что такое масштаб, перейдем к видам его использования.
В основном, их три:
- Численный – это дробное соотношение единицы к степени проекционного уменьшения.
- Именованный – расстояние заложенное в один сантиметр на карте (плане).
- Графический – запись измерений длинны в виде отрезков.
В свою очередь графические способы отображения масштабности бывают:
- линейными – когда записывается в виде линейки, разделенной на равные отрезки,
- поперечными – описывается при помощи номограммы (пропорционального деления отрезков линейки).
Также есть два стандартных вида масштабирования:
- уменьшения (1 к 500),
- увеличения (2 к 1).
Масштабы чертежей
При составлении чертежей есть смысл руководствоваться принципом дробления крупного проекта на маленькие.
Если есть цель спроектировать особняк, то архитектор, скорее всего, составит план каждой комнаты, кабинета, зала, гостиной и прочего. А уже потом объединит это в один генеральный план особняка с указанием масштаба.
Способы такой записи регулируются ГОСТом 2.302-68. Архитектору остается только выбрать вариант из предоставленной таблицы:
| Наименование масштаба | Предлагаемый ГОСТом ряд |
| Для уменьшения | 1:100000, 1:50000, 1:25000, 1:5000, 1:20, 1:500, 1:100, 1:10, 1:200, 1:50, 1:1000, 1:2000, 1:10000 |
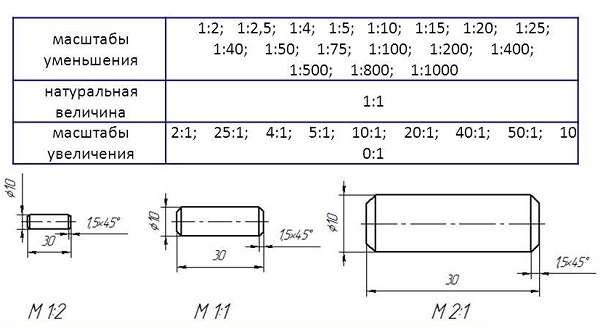
А вот если вы занимаетесь моделированием, то при создании объектов следует прибегать ко второй части таблицы, где самый крупный показатель:
| Наименование масштаба | Предлагаемый ГОСТом ряд |
| Для увеличения | 2:1, 5:1, 20:1, 100:1 |
Что такое масштаб в географии
До восемнадцатого века карты большинства регионов нашей страны выполнялись в виде простых чертежей, без указания размеров и возможности математического расчета расстояния. Так продолжалось до конца XVII века. Петр Первый, заинтересованный географией, при помощи треноги произвел замер реки Дон во время войны с турками.
В дальнейшем карты России стали составлять с учетом достаточно строгих правил, чтобы любой мог прочитать чертеж. Впоследствии такие чертежи стали называть географическими картами – т. е. чертежами, выполненными в соответствии с координатами и масштабным корректированием, а объекты на них стали обозначать специальными символами.
Определение в географии такое: в переводе с немецкого «мерная палочка». Поскольку карта – это чертеж местности, то при ее вычерчивании (либо съемке) расстояние уменьшают в несколько раз.
Другими словами масштабирование в географии показывает кратность уменьшения графического изображения и расстояния на нем относительно снимаемой местности.
Как определить масштаб карты
На политической, административной или карте местности масштабная линейка указывается в углу изображения (обычно в правом нижнем).
Приведем пример расшифровки. На карте указана цифра «1:25000».Это означает, что карта уменьшает размер местности в 25 тысяч раз. При чтении и последующем определении расстояния числовую запись следует перевести в именную «1 к 25 тысячам».
При помощи калькулятора (а лучше в голове) несложно сделать более детальный перевод расстояния: если какое-то расстояние на местности составляло 1000 метров, то на карте он будет в 25 тысяч раз меньше.
Делим 1000 на 25 тысяч и получаем четыре сотых метра или 4 сантиметра. Путем простого деления выясняем, что в 1 сантиметре 250 метров. Произносится это так: в 1 см двести пятьдесят метров.
Решение задач на тему масштаб
Несколько задач, которые встречаются в курсе математики в школе:
- Масштаб карты 1:10000. Найти, сколько в 1 сантиметре метров?
- На плане с масштабированием «один к двадцати тысячам» расстояние между одним автовокзалом и остановкой составляет 4,8 см, а на втором плане 9,6 см. Вычислить масштаб второго плана.
Для начала переведем сантиметры в метры (0.01). Умножаем одну сотую метра на 10000 высчитываем 100 м.
Ответ, который удалось рассчитать: в 1 см на карте содержится сто метров.
Зная масштабное уменьшение, выясняем, что в 1 см 200 метров. Умножаем на количество сантиметров в первом плане получаем 960 метров. Делим на количество сантиметров второго плана и находим 100 метров. В 1 см 100 метров, масштабирование «1 к десяти тысячам».
Заключение
Теперь, руководствуясь статьей, можно в режиме онлайн, узнать расстояние от магазина до дома. Посчитать сколько потребуется пройти по лесу до дороги, когда заблудился. Находить, во сколько раз уменьшен план архитектора при проектировании этажа.
Числовая шкала: Survey Anyplace
Определение числовой шкалы:
Числовая (или числовая) шкала, также известная как числовая рейтинговая шкала (NRS), по сути, представляет собой любую шкалу, которая отображает количественное обозначение атрибута. Этот тип шкалы используется для представления респонденту упорядоченного набора, из которого он может выбрать, например, от 1 до 10 вместе с привязками. Эти якоря можно разместить в конечных точках или в каждой точке шкалы.
Цифровое представление используется для предоставления данных с интервальными свойствами, помимо порядковых.
Выбор лучшего механизма обратной связи или шкалы оценок будет зависеть от того, что вы пытаетесь измерить, и от того, что вы надеетесь узнать из отзывов. В одних ситуациях уместны числовые рейтинги, в то время как устные комментарии дадут гораздо больше полезной информации в других.
Типы числовых шкал
Порядковая шкала
Это связано с ранжированием степени, в которой присутствует определенный атрибут (например, место в классе для учащихся или порядок, в котором участники финишировали в гонке) .Итак, 1-й и 2-й могут быть разделены совсем немного, а 2-й и 3-й — огромным. Также не может быть нулевого ранга.
Шкала интервалов
Каждое число здесь представляет фактическую сумму, а разница между двумя последовательными числами является фиксированной. На этой шкале присутствует ноль, но это не «настоящий» ноль. Например, шкала температуры или шкала интеллекта. Нулевой показатель IQ или температура в ноль градусов не означают, что интеллекта и температуры вообще не существует.
Шкалы коэффициентов
Здесь мы измеряем фактическое количество чего-либо. Например, 4 литра воды означает, что есть 4 литра воды, а 0 литров означает, что воды совсем нет. У нуля есть свое «истинное» значение.
Пример числовой шкалы:
Рулетка является примером числовой шкалы.
Рейтинговые вопросы построены по тому же принципу, хотя здесь шкала присутствует не всегда.
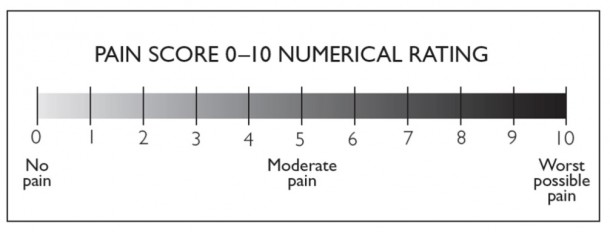
Одним из самых известных примеров является оценка боли, используемая при измерении степени боли, которую испытывает пациент.
Хотите узнать больше?
Загрузить весь список глоссария в виде списка для печати
Номинальная, порядковая, интервальная, масштабная шкала с примерами
Уровни измерения в статистике
Для выполнения статистического анализа данных важно сначала понять переменные и то, что следует измерять с помощью этих переменных. В статистике существуют разные уровни измерения, и данные, измеряемые с их помощью, можно в целом разделить на качественные и количественные данные.
Во-первых, давайте разберемся, что такое переменная. Величина, значение которой изменяется среди населения и может быть измерено, называется переменной.Например, рассмотрим выборку работающих лиц. Переменными для этого набора совокупности могут быть отрасль, местоположение, пол, возраст, навыки, тип работы и т. Д. Значение переменных будет отличаться для каждого сотрудника.
Например, посчитать среднюю почасовую ставку рабочего в США практически невозможно. Таким образом, выборочная аудитория выбирается случайным образом, так что она надлежащим образом представляет большую популяцию. Затем рассчитывается средняя почасовая ставка этой выборочной аудитории.Используя статистические тесты, вы можете сделать вывод о средней почасовой ставке для большей части населения.
Уровень измерения переменной определяет тип статистического теста, который будет использоваться. Математическая природа переменной или, другими словами, способ измерения переменной считается уровнем измерения.
Что такое номинальная, порядковая, интервальная шкала и шкала отношения?
Номинальный, Порядковый, Интервальный и Отношение определяются как четыре основных уровня шкал измерения, которые используются для сбора данных в форме опросов и анкет, каждый из которых представляет собой вопрос с несколькими вариантами ответов.
Каждая шкала представляет собой инкрементный уровень измерения, то есть каждая шкала выполняет функцию предыдущей шкалы, и все шкалы вопросов опроса, такие как Лайкерта, семантическая дифференциация, дихотомия и т. Д., Являются производными этих 4 основных уровней измерения переменных. . Прежде чем мы подробно обсудим все четыре уровня шкал измерения с примерами, давайте кратко рассмотрим, что представляют собой эти шкалы.
Номинальная шкала — это шкала именования, в которой переменные просто «именуются» или помечаются без определенного порядка.В порядковой шкале все переменные расположены в определенном порядке, помимо их именования. Шкала интервалов предлагает метки, порядок, а также определенный интервал между каждой из ее переменных параметров. Масштаб отношения имеет все характеристики интервальной шкалы, в дополнение к этому, он также может содержать значение «ноль» для любой из своих переменных.
Подробнее о номинальном, порядковом, интервальном, соотношении: четыре уровня измерения в исследованиях и статистике.
Номинальная шкала, также называемая категориальной шкалой переменных, определяется как шкала, используемая для обозначения переменных в различных классификациях, и не включает количественное значение или порядок.Эта шкала является самой простой из четырех шкал измерения переменных. Расчеты, выполненные с этими переменными, будут бесполезными, поскольку нет числового значения параметров.
Есть случаи, когда эта шкала используется с целью классификации — числа, связанные с переменными этой шкалы, являются только тегами для категоризации или деления. Расчеты, сделанные на основе этих чисел, будут бесполезными, поскольку они не имеют количественного значения.
Для такого вопроса, как:
Где ты живешь?
- 1- Пригород
- 2- Город
- 3- Город
Номинальная шкала часто используется в исследовательских опросах и анкетах, где значение имеют только метки переменных.
Например, опрос клиентов с вопросом «Какую марку смартфонов вы предпочитаете?» Варианты: «Apple» — 1, «Samsung» — 2, «OnePlus» — 3.
- В этом вопросе опроса для исследователя, проводящего исследование потребителей, имеют значение только названия брендов. Для этих брендов нет необходимости в каком-либо конкретном заказе. Однако, собирая номинальные данные, исследователи проводят анализ на основе связанных ярлыков.
- В приведенном выше примере, когда респондент выбирает Apple в качестве предпочтительного бренда, введенные и связанные данные будут иметь значение «1».Это помогло в количественной оценке и ответе на последний вопрос — сколько респондентов выбрали Apple, сколько выбрали Samsung и сколько выбрали OnePlus — и какой из них самый высокий.
- Это основа количественного исследования, а номинальная шкала — это самая фундаментальная шкала исследования.
Данные и анализ номинального масштаба
Существует два основных способа сбора данных номинальной шкалы:
- Задавая открытый вопрос, ответы на который могут быть закодированы в соответствующий номер ярлыка, выбранный исследователем.
- Другой альтернативой для сбора номинальных данных является включение вопроса с несколькими вариантами ответов, в котором будут помечены ответы.
В обоих случаях анализ собранных данных будет происходить с использованием процентов или режима, то есть наиболее распространенного ответа, полученного на вопрос. Для одного вопроса может быть более одного режима, поскольку в целевой группе могут существовать два общих избранных вопроса.
Примеры номинальной шкалы
- Пол
- Политические предпочтения
- Место жительства
| Ваш пол? | Каковы ваши политические предпочтения? | Где ты живешь? |
|
|
Создать бесплатный аккаунт
Номинальная шкала SPSS
В SPSS вы можете указать уровень измерения как шкалу (числовые данные в интервале или шкале отношений), порядковый или номинальный.Номинальные и порядковые данные могут быть строковыми, буквенно-цифровыми или числовыми.
После импорта данных для любой переменной во входной файл SPSS он принимает их по умолчанию в качестве масштабной переменной, поскольку данные по существу содержат числовые значения. Важно изменить его на номинальный или порядковый или оставить его в виде шкалы в зависимости от переменной, которую представляют данные.
Порядковая шкала: 2 nd Уровень измерения
Порядковая шкалаопределяется как шкала измерения переменных, используемая для простого отображения порядка переменных, а не разницы между каждой из переменных.Эти шкалы обычно используются для отображения нематематических представлений, таких как частота, удовлетворение, счастье, степень боли и т. Д. Довольно просто запомнить реализацию этой шкалы, поскольку «Порядковый номер» звучит так же, как «Порядок», т.е. как раз цель этой шкалы.
Порядковая шкаласохраняет описательные качества наряду с внутренним порядком, но лишена происхождения шкалы, и поэтому расстояние между переменными не может быть вычислено. Описательные качества указывают на свойства маркировки, аналогичные номинальной шкале, в дополнение к которой порядковая шкала также имеет относительное положение переменных.Начало этой шкалы отсутствует, из-за чего нет фиксированного начала или «истинного нуля».
Примеры порядковой шкалы
Статус на рабочем месте, рейтинг команд в турнирах, порядок качества продукции, а также порядок согласия или удовлетворения — некоторые из наиболее распространенных примеров порядковой шкалы. Эти шкалы обычно используются в исследованиях рынка для сбора и оценки относительной обратной связи об удовлетворенности продуктом, изменении восприятия при обновлении продукта и т. Д.
Например, вопрос о шкале семантического дифференциала, такой как:
Насколько вы довольны нашими услугами?
- Очень неудовлетворен — 1
- Неудовлетворительно — 2
- Нейтраль — 3
- Удовлетворены — 4
- Очень доволен — 5
- Здесь порядок переменных имеет первостепенное значение, как и маркировка.Очень неудовлетворенный всегда будет хуже, чем неудовлетворенный, а удовлетворенный будет хуже, чем полностью удовлетворенный.
- Здесь порядковая шкала является ступенью выше номинальной шкалы — порядок имеет отношение к результатам, а также их именование.
- Анализ результатов на основе порядка и имени становится удобным процессом для исследователя.
- Если они намереваются получить больше информации, чем то, что они собрали бы с использованием номинальной шкалы, они могут использовать порядковую шкалу.
Эта шкала не только присваивает значения переменным, но также измеряет ранг или порядок переменных, например:
- Марки
- Удовлетворение
- Счастье
Насколько вы довольны нашими услугами?
- 1- Очень неудовлетворен
- 2- неудовлетворен
- 3-нейронный
- 4- Доволен
- 5- Очень доволен
Порядковые данные и анализ
Данные порядковой шкалы могут быть представлены в табличном или графическом формате, чтобы исследователь мог провести удобный анализ собранных данных.Кроме того, для анализа порядковых данных можно использовать такие методы, как U-критерий Манна-Уитни и H-критерий Краскела-Уоллиса. Эти методы обычно используются для сравнения двух или более порядковых групп.
В U-тесте Манна-Уитни исследователи могут сделать вывод, какая переменная в одной группе больше или меньше другой переменной в случайно выбранной группе. Используя H-тест Краскела-Уоллиса, исследователи могут анализировать, имеют ли две или более порядковые группы одинаковую медианную или нет.
Узнайте о: номинальный vs.Порядковая шкала
Интервальная шкала: 3 rd Уровень измерения
Интервальная шкала определяется как числовая шкала, в которой известен порядок переменных, а также разница между ними. Переменные, у которых есть знакомые, постоянные и вычислимые различия, классифицируются с использованием шкалы интервалов. Легко запомнить и первостепенную роль этой шкалы: «Интервал» указывает на «расстояние между двумя объектами», в достижении которого помогает интервальная шкала.
Эти весы эффективны, так как открывают двери для статистического анализа предоставленных данных. Среднее значение, медиана или мода могут использоваться для расчета центральной тенденции в этой шкале. Единственный недостаток этой шкалы — отсутствие заранее определенной начальной точки или истинного нулевого значения.
Интервальная шкала содержит все свойства порядковой шкалы, кроме того, она предлагает вычисление разницы между переменными. Основная характеристика этого масштаба — равноудаленное расстояние между объектами.
Например, рассмотрим температурную шкалу Цельсия / Фаренгейта —
- 80 градусов всегда выше 50 градусов, и разница между этими двумя температурами такая же, как разница между 70 и 40 градусами.
- Кроме того, значение 0 является произвольным, поскольку отрицательные значения температуры действительно существуют, что делает шкалу температур Цельсия / Фаренгейта классическим примером шкалы интервалов.
- Интервальная шкала часто выбирается в исследовательских случаях, когда разница между переменными является обязательной, чего нельзя достичь с помощью номинальной или порядковой шкалы.Шкала интервалов количественно определяет разницу между двумя переменными, тогда как две другие шкалы способны исключительно связывать качественные значения с переменными.
- Среднее и медианное значения в порядковой шкале можно оценить, в отличие от двух предыдущих шкал.
- В статистике часто используется интервальная шкала, поскольку числовое значение может не только присваиваться переменным, но также может выполняться расчет на основе этих значений.
Даже если интервальные шкалы великолепны, они не вычисляют значение «истинного нуля», поэтому на картинке появляется следующая шкала.
Интервальные данные и анализ
Все методы, применимые к анализу номинальных и порядковых данных, также применимы к интервальным данным. Помимо этих методов, существует несколько методов анализа, таких как описательная статистика, корреляционный регрессионный анализ, который широко используется для анализа интервальных данных.
Описательная статистика — это термин, используемый для анализа числовых данных, который помогает описать, изобразить или суммировать данные значимым образом и помогает в вычислении среднего, медианы и режима.
Примеры интервальной шкалы
- Бывают ситуации, когда пространственные шкалы считаются интервальными шкалами.
- Помимо температурной шкалы, время также является очень распространенным примером шкалы интервалов, поскольку значения уже установлены, постоянны и измеримы.
- Календарные годы и время также подпадают под эту категорию измерительных шкал.
- шкала Лайкерта, Net Promoter Score, Semantic Differential Scale, биполярная матричная таблица и т. Д.являются наиболее часто используемыми примерами интервальной шкалы.
Следующие вопросы относятся к категории интервальной шкалы:
- Каков доход вашей семьи?
- Какая температура в вашем городе?
Создать бесплатный аккаунт
Масштаб передаточного отношения: 4 th Уровень измерения
Ratio Scale определяется как шкала измерения переменных, которая не только определяет порядок переменных, но и делает разницу между переменными известной вместе с информацией о значении истинного нуля.Он рассчитывается, исходя из предположения, что переменные имеют нулевую опцию, разница между двумя переменными одинакова и существует определенный порядок между опциями.
С опцией истинного нуля к переменным можно применять различные методы вывода и описательного анализа. В дополнение к тому факту, что шкала отношений делает все, что могут делать номинальные, порядковые и интервальные шкалы, она также может устанавливать значение абсолютного нуля. Лучшими примерами шкал соотношений являются вес и рост.В маркетинговых исследованиях шкала соотношений используется для расчета доли рынка, годовых продаж, цены предстоящего продукта, количества потребителей и т. Д.
- Шкала коэффициентов
- предоставляет наиболее подробную информацию, поскольку исследователи и статистики могут рассчитать центральную тенденцию, используя статистические методы, такие как среднее значение, медиана, мода, и такие методы, как среднее геометрическое, коэффициент вариации или среднее гармоническое, также могут использоваться в этой шкале. .
- Шкала отношения вмещает характеристики трех других шкал измерения переменных, т.е.е. маркировка переменных, значимость порядка переменных и вычисляемая разница между переменными (которые обычно равноудалены).
- Поскольку существует истинное нулевое значение, шкала отношения не имеет отрицательных значений.
- Чтобы решить, когда использовать шкалу отношений, исследователь должен наблюдать, имеют ли переменные все характеристики шкалы интервалов, а также наличие абсолютного нулевого значения.
- Среднее значение, мода и медиана могут быть рассчитаны с использованием шкалы отношений.
и анализ
На фундаментальном уровне данные шкалы соотношений носят количественный характер, поэтому все методы количественного анализа, такие как SWOT, TURF, кросс-табуляция, объединение и т. Д., Могут использоваться для расчета данных соотношений. В то время как некоторые методы, такие как SWOT и TURF, будут анализировать данные о соотношении таким образом, чтобы исследователи могли создавать дорожные карты по улучшению продуктов или услуг, а кросс-табуляция будет полезна для понимания того, будут ли новые функции полезны для целевого рынка или нет.
Примеры шкалы отношения
Следующие вопросы относятся к категории «Шкала отношения»:
- Какой рост у вашей дочери сейчас?
- Менее 5 футов.
- 5 футов 1 дюйм — 5 футов 5 дюймов
- 5 футов 6 дюймов — 6 футов
- Более 6 футов
- Какой у вас вес в килограммах?
- Менее 50 килограммов
- 51-70 килограмм
- 71-90 килограмм
- 91-110 килограмм
- Более 110 килограммов
Узнайте о: Interval vs.Масштаб отношения
Резюме — Уровни измерения
Четыре шкалы измерения данных — номинальная, порядковая, интервальная и относительная — довольно часто обсуждаются в академическом обучении. Приведенная ниже легко запоминающаяся диаграмма может помочь вам в тесте статистики.
| Предложений | Номинал | Порядковый номер | Интервал | Передаточное число |
| Последовательность переменных установлена | – | Есть | Есть | Есть |
| Режим | Есть | Есть | Есть | Есть |
| Медиана | – | Есть | Есть | Есть |
| Среднее | – | – | Есть | Есть |
| Разницу между переменными можно оценить | – | – | Есть | Есть |
| Сложение и вычитание переменных | – | – | Есть | Есть |
| Умножение и деление переменных | – | – | – | Есть |
| Абсолютный ноль | – | – | – | Есть |
Создать бесплатный аккаунт
.Весы
Шкалы измерений используются для категоризации и / или количественной оценки переменных. В этом уроке описываются четыре шкалы измерения, которые обычно используется в статистическом анализе: номинальный, порядковый, интервальный, и шкалы соотношений.
Примечание: Ваш браузер не поддерживает видео в формате HTML5.Если вы просматриваете эту веб-страницу в другом браузере (например, последняя версия Edge, Chrome, Firefox или Opera), вы можете посмотреть видеоматериал об этом уроке.
Свойства измерительных весов
Каждая шкала измерения удовлетворяет одному или нескольким из следующих свойств: измерение.
- Идентификационный номер . Каждое значение на шкала измерений имеет уникальное значение.
- Звездная величина . Ценности на шкала измерения имеет упорядоченное отношение друг к другу. То есть некоторые значения больше, а некоторые меньше.
- Равные интервалы . Единицы шкалы по шкале: равны друг другу. Это означает, например, что разница между 1 и 2 будут равны разнице между 19 и 20.
- Минимальное нулевое значение .На шкале есть истинная нулевая точка, внизу которых не существует никаких значений.
Номинальная шкала измерения
Номинальная шкала измерения удовлетворяет только свойству идентичности измерение. Значения, присвоенные переменным, представляют собой описательную категорию, но не имеют собственного числового значения по величине.
Пол — это пример переменной, которая измеряется по номинальной шкале. Физическим лицам может быть классифицирован как «мужской» или «женский», но ни одно из значений не представляет собой или менее «гендерный», чем другой. Религия и политическая принадлежность другие примеры переменных, которые обычно измеряются по номинальной шкале.
Порядковая шкала
Порядковая шкала имеет свойство идентичности и величины.Каждое значение на порядковая шкала имеет уникальное значение и имеет упорядоченное отношение к любое другое значение на шкале.
Примером порядковой шкалы в действии могут быть результаты лошади гонка, обозначаемая как «победа», «место» и «шоу». Мы знаем порядок ранжирования, в котором кони финишировали. Победившая лошадь финишировала впереди лошади, размещена, и лошадь, которая разместилась, финишировала впереди лошади, которая показала.Однако по этой порядковой шкале мы не можем сказать, было ли это близким гонки или победившая лошадь выиграла милю.
Интервальная шкала измерения
Интервальная шкала измерения имеет свойства идентичности, величины и равные интервалы.
Прекрасным примером интервальной шкалы является шкала Фаренгейта для измерения температура.Шкала состоит из одинаковых единиц температуры, так что разница между 40 и 50 градусами по Фаренгейту равна разнице от 50 до 60 градусов по Фаренгейту.
С интервальной шкалой вы не только знаете, больше ли разные значения или меньше, вы также знаете , насколько они на больше или меньше. Для Например, предположим, что в понедельник 60 градусов по Фаренгейту и 70 градусов по Фаренгейту. Вторник.Вы знаете не только то, что во вторник было жарче, вы также знаете что было на 10 градусов жарче.
Коэффициент масштабирования
Соотношение шкалы измерения удовлетворяет всем четырем свойствам измерение: идентичность, величина, равные интервалы и минимальное значение ноль.
Вес объекта может быть примером шкалы отношений. Каждое значение на весы имеют уникальное значение, веса могут быть ранжированы, единицы по весу равны друг другу, а весы имеют минимальное значение нуль.
Весы имеют минимальное значение нуля, потому что объекты в состоянии покоя могут быть невесомыми, но не могут иметь отрицательный вес.
Проверьте свое понимание
Проблема 1
Учитывайте шкалу Цельсия для измерения температуры. Какой из нижеуказанных Свойства измерения удовлетворяет шкала Цельсия?
Я.Величина.
II. Равные интервалы.
III. Минимальное значение ноль.
(A) только я
(B) только II
(C) только III
(D) I и II
(E) II и III
Решение
Правильный ответ (D). Шкала Цельсия имеет свойство величины, потому что каждое значение на шкале может быть оценено как большее или меньшее, чем любое другое значение.И у него есть свойство равных интервалов, потому что шкала состоит из равных единицы.
Однако шкала Цельсия не имеет минимального нулевого значения. Вода замерзает на ноль градусов по Цельсию, но температура становится ниже. В Арктике температуры почти всегда ниже нуля.
.Категориальные и числовые типы данных
Первое, что нужно сделать, когда вы начинаете изучать статистику, — это познакомиться с используемыми типами данных, такими как числовые и категориальные переменные. Для разных типов переменных требуются разные типы статистических и визуальных подходов. Поэтому очень важно понимать, как классифицировать данные, с которыми вы работаете.


Прочитав это руководство, вы можете начать изучение соответствующей статистики для выполнения различных тестов.


Более того, вы можете использовать эти знания в качестве ступеньки к карьере в области науки о данных.


Примечание автора: если вам интересно, как сделать науку о данных своим профессиональным путем, ознакомьтесь с нашими статьями: Профиль специалиста по данным, Как пройти стажировку в области науки о данных, 5 основ бизнеса для специалистов по данным и , конечно же, Карьерный путь специалиста по данным: как найти свой путь в лабиринте науки о данных.
Числовые и категориальные типы данных в статистике
Теперь давайте сосредоточимся на классификации данных.Мы можем сделать это двумя основными способами — в зависимости от типа и уровня измерения.
Начнем с типов данных, которые у нас могут быть: числовые и категориальные.
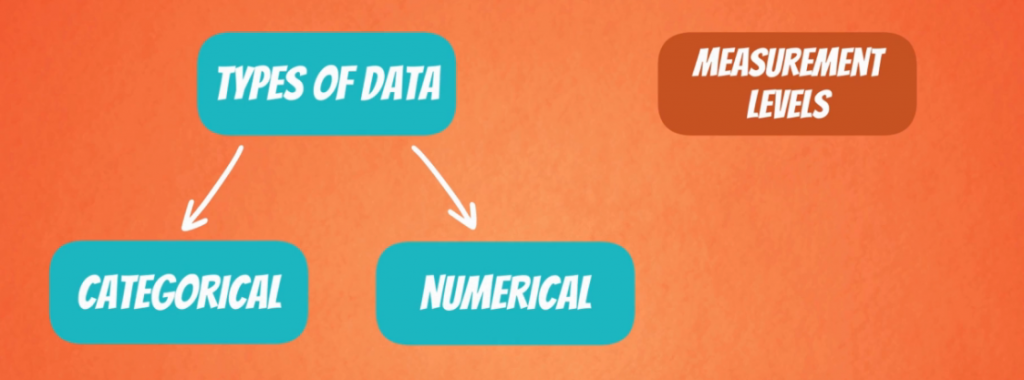

Категориальная переменная
Категориальные данные описывают категории или группы. Одним из примеров могут быть такие марки автомобилей, как Mercedes, BMW и Audi — они показывают разные категории .


Другой пример категориальных переменных — это ответы на вопросы да и нет .Например, если вас спросят:
Вы в настоящее время зачислены в университет?
Или:
У вас есть машина? 

Да и нет — это две группы ответов, которые можно получить.
Это то, что вам следует знать о категориальных переменных.
Числовые переменные
Числовые данные, с другой стороны, как следует из названия, представляют собой числа. Далее он делится на два подмножества: дискретный и непрерывный.
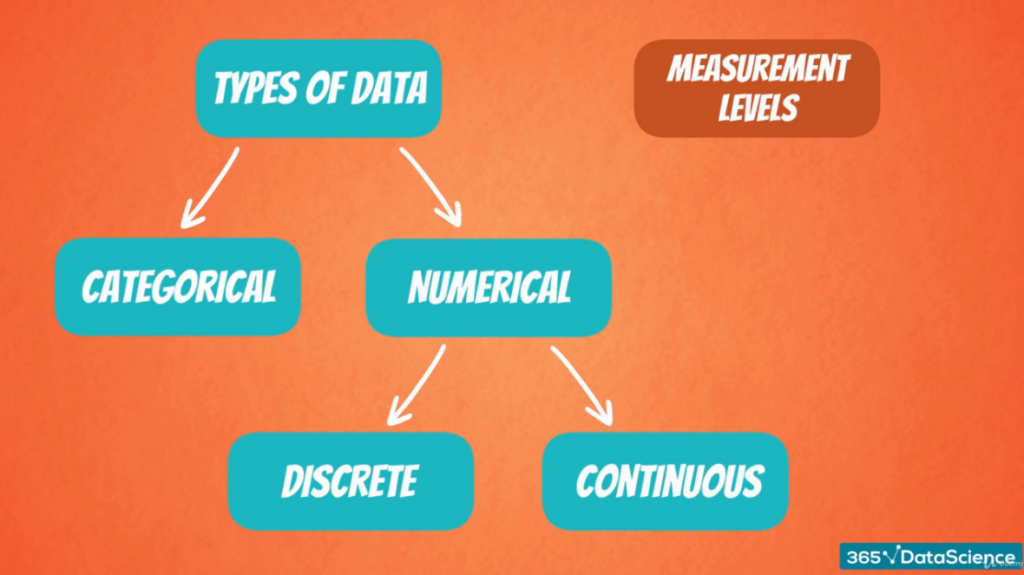

Дискретные данные
Дискретные данные обычно могут быть подсчитаны в конечном объеме.
Примеры
Возьмите количество детей, которых вы хотите иметь. Даже если вы не знаете, сколько именно, вы абсолютно уверены, что значение будет целым числом. Таким образом, число вроде 0, 1, 2 или даже 10.


Другой пример — оценки на экзамене SAT. Вы можете получить 1000, 1560, 1570 или 2400. Что важно для переменной, определяемой как дискретный , так это то, что вы можете представить каждый член набора данных.Мы знаем, что баллы SAT варьируются от 600 до 2400. Более того, 10 баллов разделяют все возможные баллы, которые могут быть получены. Итак, мы можем представить и перебрать все возможные значения в своей голове. Следовательно, числовая переменная дискретна.


Непрерывные данные
Дискретные данные легче понять, если сказать, что они противоположны непрерывным данным. Непрерывные данные бесконечны, их невозможно сосчитать и невозможно вообразить.
Пример в пункте
Например, ваш вес может принимать любое значение в некотором диапазоне.
Давайте углубимся в это.
Допустим, вы попадаете на весы, и на экране отображается 150 фунтов или 68,0389 кг.


Но это всего лишь приближение.
Если вы наберете 0,01 фунта, цифра на шкале вряд ли изменится, но ваш новый вес будет 150,01 фунта или 68,0434 килограмма.


Почему ваш вес является постоянной величиной
Теперь подумайте о потоотделении. Каждая капля пота уменьшает ваш вес на вес этой капли, но, опять же, весы вряд ли уловят это изменение.Процесс похудания и набора веса происходит постоянно. Ваш точный вес является непрерывной переменной — он может принимать бесконечное количество значений независимо от того, сколько цифр стоит после точки.


Подводя итог, ваш вес может варьироваться в непостижимо малых количествах и составляет непрерывно , в то время как количество детей, которые вы хотите иметь, прямо понятно и составляет дискретных .


Дополнительные примеры дискретных данных
Для уверенности — вот еще несколько примеров дискретных и непрерывных данных:
- Оценки в университете дискретные — A, B, C, D, E, F, или от 0 до 100 процентов.
- Количество объектов в целом. Будь то бутылки, стаканы, столы или машины. Они могут принимать только целые числа.
- Деньги можно рассматривать как и то, и другое, но физические деньги, такие как банкноты и монеты, определенно дискретны. Вы не можете заплатить 1,243 доллара. Вы можете заплатить только 1,24 доллара. Это потому, что разница между двумя денежными суммами может составлять максимум 1 цент.


Еще примеры непрерывных данных
Что еще является непрерывным?
Помимо веса, другие измерения также являются непрерывными:

Все они могут варьироваться в бесконечно меньших количествах, непонятных для человека.Время на часах дискретное, а время вообще нет! Это может быть что-нибудь вроде 72,123456 секунды.


При измерении веса, роста, площади, расстояния и времени наша технология ограничивает нас, но в целом они могут принимать любые значения.
Разница между числовыми и категориальными переменными
Итак, это были типы данных. Мы привели примеры как категориальных переменных, так и числовых переменных. Кроме того, мы объяснили разницу между дискретными и непрерывными данными.И снова вас завалили примерами, чтобы вы могли лучше их понять.
Если вы помните, мы упоминали, что существует 2 способа классификации данных. В этом уроке мы рассмотрели только первый. Если вы хотите узнать, как классифицировать данные на основе их уровня измерения, перейдите к следующему руководству.
***
Хотите узнать больше? Вы можете улучшить свои навыки с помощью нашего курса статистики!
Попробовать курс статистики бесплатно
Next Tutorial : Levels of Measures
.