Примеры матрицы четвертого порядка: Матрица 2 и 3 порядка примеры. Определитель матрицы

1.2.4. Примеры решения задач по теме «Определители»

Задача 1.

Вычислить определитель

.

Указание

Воспользуйтесь либо правилом треугольников, либо разложением определителя по 2-й строке или 2-му столбцу, содержащим нулевой элемент.

Решение

1-й способ (правило треугольников).

Вычислим определитель 3-го порядка, используя его определение:

Δ = 2·0·(-1) + (-3)·(-4)·2 + 5·1·1 — 2·0·5 -1·(-4)·2 – (-1)·1·(-3) =

= 0 + 24 + 5 – 0 + 8 – 3 = 34.

2-й способ (разложение по строке).

Применим свойство определителя:

.

Для удобства вычисления выберем 2-ю строку, содержащую нулевой элемент (А22 = 0), поскольку при этом нет необходимости находить А22, так как произведение А22 А22 = 0. Итак,

(напомним, что определитель второго порядка, входящий в алгебраическое дополнение Aij, получается вычеркиванием из исходного определителя I-й строки и J-го столбца).

Тогда Δ = А21 А21 + А23 А23 = 1·2 + (-4)(-8) = 34.

Ответ: Δ = 34.

Задача 2.

Используя свойства определителя, вычислить определитель

.

Указание

Вычитая из 2-й и 3-й строк определителя соответствующие элементы 1-й строки, добьемся того, что в 1-м столбце останется только один ненулевой элемент. Далее можно разложить определитель по 1-му столбцу.

Решение

Поскольку все элементы первого столбца равны 1, вычтем из 2-й и 3-й строк определителя соответствующие элементы 1-й строки (при этом величина определителя не изменится – свойство 6):

.

Заметим, что теперь все элементы 2-й строки кратны двум, а элементы 3-й строки кратны трем. По следствию 2.2 соответствующие множители можно вынести за знак определителя:

.

Вычтем из элементов 3-й строки полученного определителя соответствующие элементы 2-й строки:

И разложим определитель по 1-му столбцу:

Ответ: Δ = 6.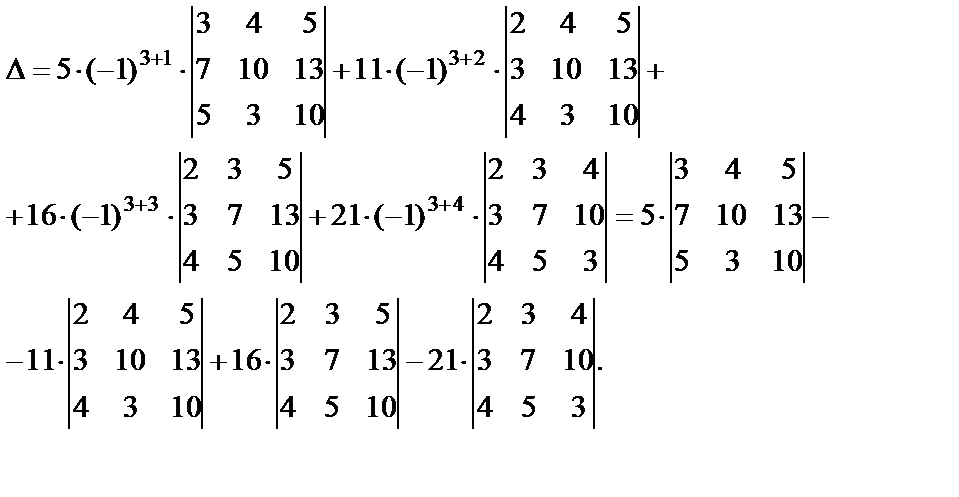

Разумеется, можно было вычислять этот определитель непосредственно (например, по правилу треугольников), но использование свойств определителей позволило существенно сократить и упростить численные расчеты.

Задача 3.

Используя свойства определителей, вычислить определитель

.

Указание

Прибавьте к элементам 2-й строки соответствующие элементы 1-й строки, а из элементов 3-й строки вычтите удвоенные элементы 1-й строки. Затем вынесите за знак определителя все общие множители элементов какой-либо строки или столбца.

Решение

Прибавим к элементам 2-й строки соответствующие элементы 1-й строки, а из элементов 3-й строки вычтем удвоенные элементы 1-й строки:

Вынесем за знак определителя множитель -1 из 2-й строки и 3 – из 3-й:

Теперь из 3-го столбца вынесем множитель -2:

Вычтем из элементов 2-го столбца элементы 3-го столбца и разложим полученный определитель по 3-й строке:

Ответ: Δ = 306.

Задача 4.

Решить уравнение

Указание

Разложив определитель, стоящий в левой части равенства, по первой строке, и приравняв его 40, вы получите квадратное уравнение для Х.

Решение

Разложим определитель, стоящий в левой части равенства, по первой строке. Предварительно найдем соответствующие алгебраические дополнения:

Тогда

И требуется решить квадратное уравнение

.

Ответ:

Задача 5.

Решить неравенство

Указание

Раскройте определитель, стоящий в левой части неравенства, по 1-й строке.

Решение

Раскроем определитель, стоящий в левой части неравенства, по 1-й строке:

3(10 — 12) – X(2X – 9) + 4X – 15 > — 3;

-2X2 + 13X – 18 > 0;

2X2 – 13X + 18 < 0;

2 < X < 4,5.

Ответ: (2; 4,5).

Задача 6.

Используя свойства определителей (не раскрывая определитель), вычислить определитель

Указание

Используйте тригонометрическую формулу cos 2A = cos2A — sin2A и свойство определителя с двумя равными столбцами.

Решение

Из тригонометрии известно, что cos 2A = cos2A — sin2A. Вычтем из элементов

2-го столбца определителя соответствующие элементы 1-го столбца:

У полученного определителя, равного исходному (свойство 6), два столбца одинаковы, поэтому он равен нулю (следствие 2.1).

Ответ: 0.

Задача 7.

Вычислить определитель 4-го порядка

.

Указание

Преобразуйте определитель так, чтобы три из четырех элементов какой-либо строки или столбца стали равными нулю. Для этого воспользуйтесь свойством 6.

Решение

Преобразуем определитель так, чтобы три из четырех элементов какой-либо строки или столбца стали равными нулю. Для этого воспользуемся свойством 6. Его особенно удобно применять, если в определителе существует элемент, равный +1. Выберем в качестве такого элемента А13 = 1 и с его помощью обратим все остальные элементы 3-го столбца в нуль. С этой целью:

А) к элементам 2-й строки прибавим соответствующие элементы 1-й строки;

Б) из элементов 3-й строки вычтем элементы 1-й строки, умноженные на 2;

В) из элементов 4-й строки вычтем элементы 1-й строки

(напомним, что при этом величина определителя не изменится).

Тогда

Разложим полученный определитель по 3-му столбцу:

Вычтем из элементов 1-й строки нового определителя удвоенные элементы 2-й строки:

И разложим этот определитель по 1-й строке:

Ответ: Δ = -9.

Задача 8.

Вычислить определитель 4-го порядка

Указание

Разложите определитель по 1-й строке, а затем полученный определитель 3-го порядка вновь разложите по 1-й строке.

Решение

Разложим определитель по 1-й строке:

Полученный определитель 3-го порядка вновь разложим по 1-й строке:

Ответ: Δ = 24.

Обратите внимание: если в определителе все элементы, стоящие по одну сторону от главной диагонали, равны нулю, то определитель равен произведению элементов, Стоящих на главной диагонали.

Ответ: Δ = 24.

< Предыдущая		Следующая >

Вычислить определители — примеры, решения

Пример 1:

Вычислить определитель:

Решение от преподавателя:

Ответ: 7.

Пример 2:

Решение от преподавателя:

Указанная матрица получается из второй при умножении второй строки на 2 и первого столбца на -1, так что ее определитель равен (-1)*2*(-1)=2.

Пример 3:

Вычислить определители

Решение от преподавателя:

Пример 4:

Вычислить определитель матрицы:

A =

7 5 1 3 -1 4 -6 1 1

Решение от преподавателя:

Запишем матрицу в виде: 

A =

7 5 1 3 -1 4 -6 1 1

Найдем определитель, использовав разложение по 1-му столбцу: 
Минор для (1,1): 
Вычеркиваем из матрицы 1-ю строку и 1-й столбец.  

7	5	1
3	-1	4
-6	1	1

Получаем: 

∆ 1,1 =

Найдем определитель для этого минора. 

∆_1,1 = ((-1)*1-1*4) = -5 
Минор для (2,1): 
Вычеркиваем из матрицы 2-ю строку и 1-й столбец. 

7	5	1
3	-1	4
-6	1	1

Получаем: 

∆ 2,1 =

Найдем определитель для этого минора.  
∆_2,1 = (5*1-1*1) = 4 
Минор для (3,1): 
Вычеркиваем из матрицы 3-ю строку и 1-й столбец. 

7	5	1
3	-1	4
-6	1	1

Получаем: 

∆ 3,1 =

Найдем определитель для этого минора. 
∆_3,1 = (5*4-(-1)*1) = 21 
Определитель: 
∆ = (-1)¹⁺¹7*(-5)+(-1)²⁺¹3*4+(-1)³⁺¹(-6)*21 = 7*(-5)-3*4+(-6)*21 = -173

Пример 5:

Найти определитель матрицы:

Решение от преподавателя:

Найдем определитель, использовав разложение по 1-му столбцу: 
Минор для (1,1): 
Вычеркиваем из матрицы 1-ю строку и 1-й столбец.  

1	-1	1
2	1	1
1	1	2

Получаем: 

Δ1,1 =

Найдем определитель для этого минора. 
∆_1,1 = (1*2-1*1) = 1 
Минор для (2,1): 
Вычеркиваем из матрицы 2-ю строку и 1-й столбец. 

1	-1	1
2	1	1
1	1	2

Получаем: 

Δ2,1 =

Найдем определитель для этого минора.  
∆_2,1 = ((-1)*2-1*1) = -3 
Минор для (3,1): 
Вычеркиваем из матрицы 3-ю строку и 1-й столбец. 

1	-1	1
2	1	1
1	1	2

Получаем: 

Δ3,1 =

Найдем определитель для этого минора. 
∆_3,1 = ((-1)*1-1*1) = -2 
Определитель: 
∆ = (-1)¹⁺¹1*1+(-1)²⁺¹2*(-3)+(-1)³⁺¹1*(-2) = 1*1-2*(-3)+1*(-2) = 5 

Пример 6:

Решение от преподавателя:

Пример 7:

Вычислить определитель методом понижения порядка до второго.

Решение от преподавателя:

Преобразуем определитель, чтобы получить нули в первом столбце за исключением первой строки

Элементы 1-й строки, умноженные на -2, складываем с элементами 2-й строки, и результат записываем во 2-ю строку; элементы 1-й строки, умноженные на -1, складываем с элементами 3-й строки, и результат записываем в 3-ю строку; элементы 1-й строки, умноженные на -2, складываем с элементами 4-й строки, и результат записываем в 4-ю строку; значения элементов 1-й строки не меняем

Преобразуем определитель, чтобы получить нули в третьем столбце за исключением второй строки

Элементы 2-й строки, умноженные -5, складываем с элементами 1-й строки, и результат записываем в 1-ю строку; элементы 2-й строки, умноженные -5, складываем с элементами 3-й строки, и результат записываем в 3-ю строку; значения элементов 2-й строки не меняем

Пример 8:

Решение от преподавателя:

Пример 9:

Вычислить определитель.

Решение от преподавателя:

Пример 10:

Решение от преподавателя:

Верные :2) и 3)

Пример 11:

Вычислить определитель 2-го порядка:

Решение от преподавателя:

Пример 12:

Вычислить определитель матрицы  А,

1. с помощью правила приписывания первых двух столбцов;
2. разложением по любой строке;
3. разложением по любому столбцу;
4. получением двух нулей в какой-либо строке и разложением по элементам этой строки.

Решение от преподавателя:

Пример 13:

Вычислить определитель третьего порядка методом Саррюса:

Решение от преподавателя:

Пример 14:

Вычислить определители:

m = 1, n = 5

Решение от преподавателя:

Пример 15:

Вычислить определитель матрицы:

Решение от преподавателя:

линейная алгебра — произведение тензоров 4-го порядка и обратное вычисление

В настоящее время я работаю над предметом, который включает множество вычислений тензоров 4-го порядка, включая двойное произведение точек и обратное вычисление тензоров четвертого порядка.

Сначала определения, чтобы мы были на одной странице. То, что я называю двойным точечным произведением:

$$ (A:B)_{ijkl} = A_{ijmn}B_{mnkl} $$

и для двойного точечного произведения между тензором четвертого порядка и второго порядка тензор:

$$ (A:s)_{ij} = A_{ijkl}s_{kl}$$

Используя соглашение о суммировании повторяющихся индексов.

То, что я называю тождеством тензоров четвертого порядка, является единственным тензором, таким что:

$$ A:I = I:A = A $$

он определяется как $ I = \delta_{ik}\delta_ {jl} e_{i} \otimes e_{j} \otimes e_{k} \otimes e_{l} $.

То, что я называю инверсией тензора четвертого порядка, является инверсией по отношению к двойному скалярному произведению, то есть инверсией $A$ является единственный тензор $B$, такой что $AB = BA = I$.

Двойной точечный продукт легко вычислить, если не думать об эффективности кода, а просто создать массив и выполнить цикл по четырем индексам. Вычисление обратного — это нечто другое. Каждый тензор, который я использую, имеет второстепенные симметрии $A_{ijkl} = A_{jikl} = A_{ijlk}$, поэтому я решил использовать представление Манделя для тензоров второго и четвертого порядка, упомянутых в Википедии. Тензор четвертого порядка можно представить в виде матрицы $6\times6$ со следующими компонентами:

$$[C] = \begin{bmatrix} C_{1111} & C_{1122} & C_{1133} & \sqrt{2}C_{1123} & \sqrt{2}C_{1131} & \sqrt{2}C_{1112}\\ C_{2211} & C_{2222} & C_{2233} & \sqrt{2}C_{2223} & \sqrt{2}C_{2231} & \sqrt{2}C_{2212}\\ C_{3311} & C_{3322} & C_{3333} & \sqrt{2}C_{3323} & \sqrt{2}C_{3331} & \sqrt{2}C_{3312}\\ \sqrt{2}C_{2311} и \sqrt{2}C_{2322} и \sqrt{2}C_{2333} и 2C_{2323} и 2C_{2331} и 2C_{2312}\\ \sqrt{2}C_{3111} и \sqrt{2}C_{3122} и \sqrt{2}C_{3133} и 2C_{3123} и 2C_{3131} и 2C_{3112}\\ \sqrt{2}C_{1211} и \sqrt{2}C_{1222} и \sqrt{2}C_{1233} и 2C_{1223} &2C_{1231} и 2C_{1212} \end{bmatrix} $$ 9{-1} \qquad \qquad (2) $$

где $\cdot$ — обычное матричное произведение. Но это не работает или, по крайней мере, я чего-то не понимаю. Если я помещу тождественный тензор 4-го порядка, определенный выше, в нотацию Манделя, я получу следующую матрицу:

$$ [I] = \begin{bmatrix} 1&0&0&0&0&0\\ 0&1&0&0&0&0\\ 0&0&1&0&0&0\\ 0&0&0&2&0&0\\ 0&0&0&0&2&0\\ 0&0&0&0&0&2 \end{bmatrix} $$ 9Тензоры {th}$ порядка, обладающие минорными симметриями.

Что мне здесь не хватает?

Большое спасибо за вашу помощь и предстоящие обсуждения 🙂

Квадратная матрица

• Математические сомнения
• Матрицы
• Тип

Матрица, у которой количество строк равно количеству столбцов, называется квадратной матрицей.

Квадратная матрица — это один из типов матриц, элементы которого располагаются по количеству строк и столбцов, но расположение элементов в матрице имеет квадратную форму из-за одинакового количества строк и столбцов. Следовательно, матрица называется квадратной матрицей.

Квадратная матрица в общем виде выражается следующим образом. В этой матрице элементы расположены в $m$ строк и $n$ столбцов, а порядок матрицы равен $m \times n$.

$$ млн = {\начать{bmatrix} e_{11} & e_{12} & e_{13} & \cdots & e_{1n}\\ e_{21} & e_{22} & e_{23} & \cdots & e_{2n}\\ e_{31} & e_{32} & e_{33} & \cdots & e_{3n}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ e_{m1} & e_{m2} & e_{m3} & \cdots & e_{mn} \end{bmatrix}}_{\displaystyle m \times n} $$ 9Квадратная матрица {th}$ порядка.

$m$ или $n$ квадратная матрица со строками.

Пример

$$M = \begin{bmatrix} 7 и -2 и 5 и 4\\ -1 и 0 и 3 и -7\\ 9 и 4 и 2 и 5\\ -5 и 3 и 8 и 4 \end{bmatrix} $$

$M$ — пример матрицы. Он имеет $4$ строк и $4$ столбцов. Матрица $M$ называется квадратной матрицей. Матрица $4\times 4$ также называется тремя разными типами.

1. Квадратная матрица порядка $4$.

2. Квадратная матрица четвертого порядка.

   No related posts.