Примеры метода математической индукции: Метод математической индукции: пример решения с объяснением

Содержание

Метод математической индукции как эффективный метод доказательства

Реферативная работа

«Метод математической индукции как эффективный метод доказательства»

Автор: Тарасова Диана,

8 класс,

Руководитель: Чиркова Мария Юрьевна,

учитель математики

2016-2017 учебный год

Оглавление
Введение		3
1	Обзор литературы	4
2	Основные понятия метода математической индукции	5
3	Применение метода математической индукции	8
Заключение		12
Литература		13
Приложение1		14
Приложение2		15

Введение

В математике часто требуется доказательство сформулированных предложений. Универсальным орудием доказательства является метод математической индукции. Однако в школьной программе с методом математической индукции знакомятся только поверхностно. В то время как подробное знакомство с этим методом полезно учащимся не только из-за расширения их кругозора, но также и потому, что на его принципе основано решение многих задач (включая олимпиадные). Это позволяет говорить об актуальности рассмотренной темы.

Цель работы: наглядно показать практическое значение метода математической индукции как необходимого фактора для решения задач.

Задачи работы:

1. Рассмотреть развитие метода математической индукции в истории

математики.

2. Изучить метод математической индукции.

3. Выявить преимущества и недостатки метода математической индукции.

4. Научится решать задачи различных видов, применяя данный метод.

Методы и методики исследования, используемые в работе:

1. Анализ математической литературы и ресурсов интернета по данной теме.

2. Репродуктивное воспроизведение изученного материала.

3. Познавательно-поисковая деятельность.

4. Анализ и сравнение данных в поиске задач.

5. Постановка гипотез и их проверка.

6. Сравнение и обобщение математических фактов.

7. Решение задач различных видов.

8. Анализ полученных результатов.

1.Обзор литературы.

Осознание метода математической индукции как отдельного важного метода восходит к Блезу Паскалю и Герсониду, хотя отдельные случаи применения встречаются ещё в античные времена у Прокла и Эвклида.

Принципом математической индукции фактически пользовались ещё некоторые древнегреческие учёные. Однако впервые он был ярко выражен Герсонидом в 1321 году. Одна из первых характеристик принципа математической индукции содержится у итальянского математика XVI веке Ф. Мавролико, переводчика Архимеда. В «Трактате об арифметическом треугольнике» Б. Паскаль доказывает закон образования членов этого треугольника методом математической индукции, после чего этот метод начинает постепенно привлекать внимание некоторых учёных, в частности Я.

(2ⁿ)+1 являются простыми после того, как проверил факт на пяти случаях, при n=0, 1, 2, 3. Действительно, это будут числа 3, 5, 17, 257. Однако в 1732 году Эйлер опроверг предположение Ферма, доказав, что число F5=225+1=4 294 967 297 составное, ибо делится на 641.

Почётный член Ан СССР и основатель киевской алгебраической школы, Дмитрий Александрович Граве (1863-1939) предполагал, что для всех простых чисел

p число 2^p^-1-1 не делится на p² на основе того, что факт был проверен для всех простых чисел, меньших тысячи. Предположение отвергли, когда было обнаружено, что число 2¹⁰⁹²— делится на 1093²(1093 — простое число). История математики содержит немало таких казусов.

Всё это позволяет говорить об актуальности применения метода математической индукции к доказательству различных утверждений. В наше время развитие метода продолжается.

2. Основные понятия метода математической индукции.

В основе всякого математического исследования лежит дедуктивный и индуктивный методы обоснования того или иного утверждения. Дедуктивный метод – это рассуждение, исходным моментом которого является общее утверждение, а заключительным моментом – частный результат. А индуктивный метод – это рассуждение, в котором, опираясь на ряд частых результатов, делается некий вывод.

Однако результат, полученный индукцией, вообще говоря, логически обоснованным, доказанным. Известно много случаев, когда утверждения, полученные индукцией, были неверными. Т.е. индукция может привести как к верным, так и к неверным выводам.

Рассмотрим пример. Подставляя квадратный трехчлен P(x)=x²+x+41 вместо x натуральные числа 1, 2, 3, 4, 5. Получим, что:

P(1)=43 ;P(2)=47; P(3)=53; P(4)=61; P(5)=71.

Все значения данного трехчлена являются простыми числами. Подставляя вместо x числа 0, -1, -2, -3, -4, получаем:

P(0)=41; P(-1)=41; P(-2)=43; P(-3)=47;

P(-4)=53.

Значения данного трехчлена при указанных значениях переменной x также являются простыми числами. Возникает гипотеза, что значения трехчлена P(x) является простым числом при любом целом значении x. Но высказанная гипотеза ошибочна, так как, например, P(41)=41²+41+41=1763=41∙43.

Так как при этом методе вывод делается после разбора нескольких примеров, не охватывающих всех возможных случаев, то этот метод называется неполной или несовершенной индукцией.

Метод неполной индукции, как мы видим, не приводит к вполне надежным выводам, но он полезет тем, что позволяет сформулировать гипотезу, которую потом можно доказать точным математическим рассуждением или отвергнуть. Иными словами, неполная индукция в математике не считается законным методом строгого доказательства, но является мощным эвристическим методом открытия новых истин.

Если же вывод делается на основании разбора всех случаев, то этот метод рассуждений называют полной индукцией.

Вот пример подобного рассуждения. Пусть требуется установить, что каждое натуральное четное число n в пределах 10<n<20 представимо в виде суммы двух простых чисел. Для этого возьмём все такие числа и выпишем соответствующие разложения: 10=7+3; 12=7+5; 14=7+7; 16=11+5; 18=13+5; 20=13+7. Эти шесть равенств показывают, что каждое из интересующих нас чисел действительно представляется в виде суммы двух простых слагаемых.

Но не всегда в математике утверждения ограничиваются рассмотрением ситуации с конечным числом частных случаев. Чаще всего они охватывают бесконечное множество частных случаев, когда сделать проверку для всех случаев невозможно. Опираться при этом на неполную индукцию опасно, можно сделать неправильный вывод. Во многих случаях выход заключается в обращении к особому методу рассуждений, который называют методом математической индукции.

В основе этого метода лежит следующий принцип. Некоторое утверждение верно при любом натуральном n если:

1) оно верно при n=1 (базис индукции)

2) затем доказывается, что если верно утверждение n=k (k≥1) следовательно, что верно и при n=k+1.

Действительно, при n=1 утверждение верно при n=2; 3=2+1, поэтому в силу второго 2) утверждение верно и при n=3.

Вообще, любое натуральное число n может быть получено из 1 путем последовательного прибавления к нему единицы n – 1 раз. При каждом таком прибавлении мы получаем натуральное число, для которого рассматриваемое утверждение верно. Поэтому оно верно и для натурального числа n.

Рассмотрим применение данного метода на нескольких примерах. Самым известным является задача о Ханойской башне.

Пример 1.

Ханойская башня представляет собой n дисков, нанизанных в порядке уменьшения их размеров на один из трех колышков. Докажем, что возможно переместить всю башню на один из других колышков, перенося каждый раз только один диск и не помещая больший диск на меньший. Пусть изначально диски нанизаны на первом стержне (Приложение, рис. 1), а переложить мы должны на третий. Если n=2, то мы можем действовать следующим образом: переложить меньший диск на второй стержень, потом больший диск на третий, а затем меньший поверх большего (рис. 2). задача решена для n=2. Для n=3 можно было бы так же подробно описать процедуру перекладывания дисков, но мы попробуем воспользоваться тем, что уже умеем перекладывать башню из двух дисков. Временно забудем про нижний, самый большой диск. Тогда останется башня из двух верхних дисков. Переложим ее на свободный стержень. Теперь переложим третий диск на третий стержень (рис. 3), а потом башню из двух верхних дисков со второго стержня на третий (третий диск не мешает проведению операции, так как он самый большой). Аналогично можно поступить и для четырех дисков: сначала переложить башню из трех дисков на второй стержень, потом самый большой диск на третий, а затем башню из трех дисков на второго стержня на третий.

И так далее. Башню из k дисков можно переложить аналогично: сначала переложить башню из k-1 дисков на второй стержень, k-и диск на третий стержень, а затем башню из k-1 дисков на третий стержень.

Понятно, что таким образом мы можем поступать с башней из любого числа дисков (рис. 4).

В этой задаче мы сначала научились решать задачу для n=2, а потом объяснили, как, умея перекладывать башню из k дисков, переложить башню из k+1 дисков. Сделаем вывод: мы сможем предложить башню из любого числа дисков.

Пример 2.

Доказать, что 1+3+5+…+(2n-1)=n².

Для доказательства применим метод математической индукции.

1) Очевидно, что при n=1 данное равенство справедливо.

2) Предположим, что оно справедливо при n= k, т.е. имеет место

1+3+5…+(2k-1)=k²

3) Докажем, что тогда оно имеет место при n=k+1

К выражению, полученному в пункте 2 прибавим, с левой и правой стороны одно и тоже слагаемое 2k+1. Тогда получим следующее

1+3+5+…+(2k-1)+(2k+1)=k²+(2k+1)=k²+2k+1=(k+1)².

Таким образом, из условия, что это равенство справедливо при n=k вытекает, что оно справедливо и при n=k+1, значит оно справедливо при любом натуральном n, что и требовалось доказать.

3. Применение метода математической индукции.

В данной главе представлены доказательства различных примеров с использованием метода математической индукции.

Пример 1. Доказать, что

(1)

1) Проверим справедливость этого утверждения при n=1, т.е.

это очевидно, 1=1.

2) Предположим, что равенство (1) выполняется при n=k, т.е.

(2)

3) Докажем, что проверяемое равенство (1) при n=k+1, тоже верно, т.е. докажем, что верно равенство

(3)

К каждой части равенства (2) прибавим число (k+1)² . Тогда

Итак, равенство (2) вытекает из равенства (3). Оба условия принципа математической индукции выполняются, значит, равенство (1) справедливо для любого натурального числа n.

Пример 2. Доказать, что

(4)

1) Проверим справедливость этого утверждения при n=1, т. е.

2) Предположим, что равенство (4) выполняется при n=k, т.е.

(5)

3) Докажем, что проверяемое равенство (4) при n=k+1, тоже верно, т.е. докажем, что верно равенство

К каждой части равенства (5) прибавим число. Тогда получаем

Итак, из равенства (5) вытекает равенство при n=k+1. Оба условия принципа математической индукции выполняются, значит, равенство (4) справедливо для любого натурального числа n.

Пример 3. Доказать, что при любом n выражение

1) При n=1 получаем

2) Предположим, что утверждение верно и для n=k, т. е. — верно.

3) Докажем для n=k+1, т.е. Преобразуем данное выражение:

Так как утверждение верно для n=k, то первое слагаемое делиться на 9, как видно второе и третье слагаемое тоже делиться на 9. Поэтому, согласно пунктам 1 и 2 мы доказали, что

Пример 4. Доказать, что для любого n выражение

1) При n=1

2) Пусть верно и для n=k,

3) Докажем для n=k+1

Исходя из пункта 2, следует, что, а 6 делиться на 6. Поэтому выражение — истинно.

Пример 5. Найти сумму

Сначала найдем суммы одного, двух и трех слагаемых. Имеем:

В каждом из этих случаев получается дробь, в числителе которой стоит число слагаемых, а в знаменателе – число, на единицу большее числа слагаемых.

Это позволяет высказать предположение, что при любом натуральном n

Для проверки этой гипотезы воспользуемся методом математической индукции.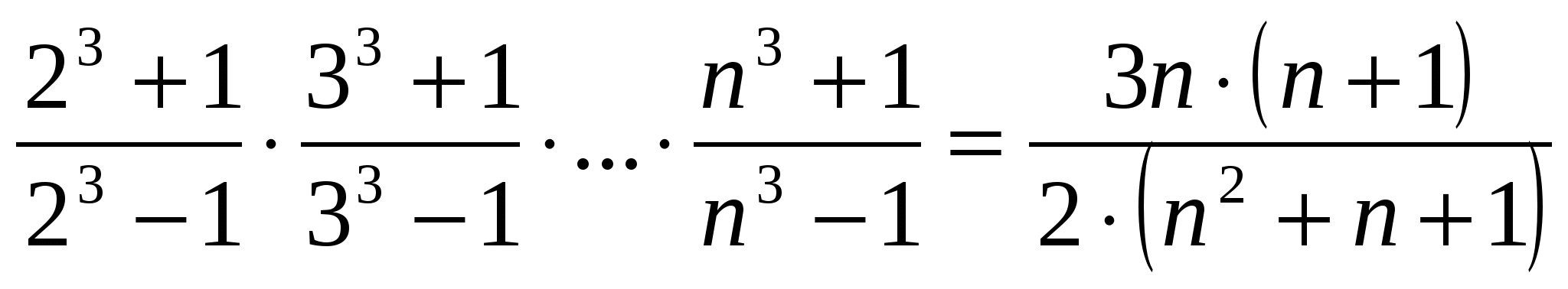

1) При n=1 гипотеза верна, т.к.

2) Предположим, что гипотеза верна при n=k, т.е.

3) Докажем, сто тогда гипотеза должна быть верной и при n=k+1, т.е.

Действительно,

Таким образом, исходя из предположения, что гипотеза верна при n=k, мы доказали, что она верна и для n=k+1. Поэтому формула верна при любом натуральном n.

Пример 6. Вычислите сумму

Сначала найдем суммы одного, двух и трех слагаемых. Имеем:

Это позволяет сделать предположение, что при любом натуральном n

Для проверки этой гипотезы воспользуемся методом математической индукции.

1) При n=1 гипотеза верна, т.к.

2) Предположим, что гипотеза верна при n=k, т.е.

3) Докажем, сто тогда гипотеза должна быть верной и при n=k+1, т.е.

Действительно,

Заключение

В данной работе я рассмотрела понятие индукции, ее виды. Индукция бывает полная и неполная. Метод неполной индукции состоит в переходе к универсальной формулировке после проверки частных формулировок для отдельных, но не всех значений n. Но только применение полной индукции, позволяет говорить об истинности универсальной формулировки, если она справедлива для каждого значения n. Метод математической индукции – метод доказательства, основанный на принципе математической индукции. Он позволяет в поисках общего закона испытывать гипотезы, отбрасывать ложные и утверждать истинные. Достоинством метода математической индукции является его универсальность, так как с помощью этого метода можно решить многие задачи.

В работе представлено широкое применение метода математической индукции в алгебре и арифметике, для доказательства тождеств, решения задач на делимость. Работа над углубленным изучением этого метода, я получила навыки в решении примеров, доказательстве тождеств, которые я считаю, пригодятся мне в дальнейшей учебе.

Обобщив и систематизировав знания по математической индукции, убедилась в необходимости знаний по теме «метод математической индукции». Кроме того эти знания повышают интерес к математике как к науке.

Думаю, моя работа может пригодиться не только школьникам, но и абитуриентам, поступающим в высшие учебные заведения.

Список литературы

1. Говоров В.М., Дыбов П.Т., Мирошин Н.В., Смирнова С.Ф, Сборник конкурсных задач по математике. – М.: Наука, 1983 г.

2. Кутасов А.Д., Пиголкина Т.С., Чехлов В.И., Яковлева Т.Х. пособие по математике для поступающих в вузы. – М.: Наука, 1981 г.

3. Соминский И.С. О математической индукции. – П.: Наука, 1967 г.

4. Журнал «Математика», издательский дом «Первое сентября», №23, 2004 г.

5. Пособие для учителей. Пер. с англ. Тростникова В.Н., Киро С.Н., Киро Н.С. – М.: Просвещение ,1979 г.

6. Энциклопедический словарь юного математика/ Сост. Савин А.П. – М.: Педагогика, 1989 г.

7. Соминский И.С. Метод математической индукции. Популярные оекции по математике, вып. 3 – М.: Наука, 1974 г.

8. Шарыгин И.Ф. Факультативный курс по математике. Решение задач. – М.: просвещение, 1989 г.

9. http://filisof.histiric.ru/

10. http://wikibooks.org

11. http://dic.academic.ru

Приложение 1

Приложение 2

Блез Паскаль (19. 06.1623— 19.08.1662)

Счетная машина Паскаля

Паскаль родился в семье председателя налогового управления и сам неплохо разбирался в математике. В 1641 (по др. сведениям, в 1642) Паскаль сконструировал суммирующую машину. К 1654 закончил ряд работ по арифметике, теории чисел, алгебре и теории вероятностей. Круг математических интересов Паскаля был весьма разнообразен. Паскаль нашел общий алгоритм нахождения признаков делимости любого целого числа на любое другое целое число, сформулировал ряд основных положений элементарной теории вероятностей. В этих работах Паскаль впервые точно определил и применил для доказательства метод математической индукции.

Вместе с Г. Галилеем и С. Стевином Б. Паскаль является основоположником классической гидродинамики: он

установил ее основной закон – т. н. закон Паскаля, принцип действия гидравлического пресса, указал на общность основных законов равновесия жидкостей и газов.

Опыт, проведенный под руководством Паскаля (1648), подтвердил предположение Торричелли о существовании атмосферного давления. Работа Паскаля над проблематикой точных наук в основном относится к 1640-1650 годам.

К тому же Паскаль сыграл огромную роль в формировании французской классической прозы.

Метод математической индукции презентация, доклад

Слайд 1Текст слайда:

Метод
математической индукции

Учитель математики
Баутдинова А.М.

Слайд 2Текст слайда:

В основе всякого математического исследования лежит дедуктивный и индуктивный методы обоснования того или иного утверждения.

Слайд 3Текст слайда:

Дедукция – переход от общих утверждений к частным.

Пример
Все граждане России имеют право на образование.
Петров – гражданин России.
Петров имеет право на образование.

Слайд 4Текст слайда:

Индукция – переход от частных утверждений к общим.

Пример
140 делится на 5.
Все числа, оканчивающиеся нулём, делятся на 5.
140 делится на 5.
Все трёхзначные числа делятся на 5.

Слайд 5Текст слайда:

Рассмотрим пример рассуждения по индукции:

Требуется установить, что
Каждое четное натуральное число в пределах от 4 до 20 можно представить в виде суммы двух простых чисел.

Для этого переберем все интересующие нас числа и выпишем соответствующие суммы:

4 = 2 + 2

6 = 3 + 3

8 = 3 + 5

10 = 3 + 7

12 = 5 + 7

14 = 7 + 7

16 = 3 + 13

18 = 5 + 13

20 = 3 + 17

Эти 9 равенств показывают, что сформулированное общее утверждение верно, оно было доказано перебором всех возможных частных случаев.

Слайд 6Текст слайда:

Это полная индукция, когда общее утверждение доказывается для конечного множества элементов рассмотрением каждого элемента множества по отдельности.

Но ведь чаще общее утверждение относится не к конечному, а к бесконечному множеству, когда рассмотреть каждый элемент множества невозможно.

В таких случаях общее утверждение может быть лишь угаданным, полученным неполной индукцией.
Оно может быть верным, а может быть и неверным.

Слайд 7Текст слайда:

Примеры

1) Рассмотрим суммы первых n нечетных натуральных чисел:

Выдвинем гипотезу, что всегда сумма первых n нечетных натуральных чисел равна n2.

1 = 1

1 + 3 = 4 = 22

1 + 3 + 5 = 9 = 32

1 + 3 + 5 + 7 = 16 = 42

1 + 3 + 5 + 7 + 9 = 25 = 52

Слайд 8Текст слайда:

Проверим ее для шести и семи слагаемых:

Гипотеза подтвердилась.
Но всё равно утверждение остается гипотезой,
пока оно не доказано.

1 + 3 + 5 + 7 + 9 + 11 = 36 = 62

1 + 3 + 5 + 7 + 9 + 11 + 13 = 49 = 72

Докажем его:

1 + 3 + 5 + 7 + … + (2n – l) – это сумма n членов арифметической прогрессии.

Слайд 9Текст слайда:

2) Рассмотрим последовательность yn = n2 + n + 17.

Все полученные числа простые.

y1 = 19

Выпишем первые 7 её членов:

y2 = 23

y3 = 29

y4 = 37

y5 = 47

y6 = 59

y7 = 73

Возникает предположение: вся последовательность состоит из простых чисел.

Проверим это для следующих четырех членов последовательности:

y8 = 89

y9 = 107

y10 = 127

y11 = 149

Эти числа простые. Гипотеза подтвердилась.
И тем не менее она неверна.

Слайд 10Текст слайда:

Есть в последовательности числа, не являющиеся простыми, например:

y16 = 162 + 16 + 17 = 16 · (16 + 1) + 17 = 17(16 + 1) = = 17 · 17 — составное число

Итак, утверждение, полученное неполной индукцией, остается лишь гипотезой, пока оно не доказано точным математическим рассуждением, охватывающим все частные случаи.

Слайд 11Текст слайда:

Во многих случаях выход заключается в обращении к особому методу рассуждений, который называют методом математической индукции.

Слайд 12Текст слайда:

Принцип математической индукции

Утверждение, зависящее от натурального числа n, справедливо для любого n, если выполнены два условия:

1) утверждение верно для n = 1;

2) из справедливости утверждения для n = k, где k – любое натуральное число, вытекает справедливость утверждения и для следующего натурального числа n = k + 1.

Слайд 13Текст слайда:

Пример 1

Доказать, что

1) для n = 1

2) предположим, что равенство (1) выполняется при n = k, т.е., что верно равенство

1 = 1

(1)

(2)

Докажем, что тогда проверяемое равенство (2) верно и при n = k + 1, т. е., что верно равенство

Слайд 14Текст слайда:

Само по себе равенство (3) нас не интересует, нас интересует только один вопрос: вытекает ли оно из равенства (2).

Рассмотрим левую часть равенства (3) и воспользуемся в процессе преобразований равенством (2):

(3)

Слайд 15Текст слайда:

Итак, из равенства (2) вытекает равенство (3). Оба условия принципа математической индукции выполняются, значит, равенство (1) справедливо для любого натурального числа n.

Слайд 16Текст слайда:

Пример 2

Доказать, что

1) для n = 1

2) при n = k верно равенство:

1 = 1

(4)

(5)

при n = k + 1:

или

(6)

Слайд 17Текст слайда:

Заменив сумму кубов в левой части равенства (6) правой частью равенства (5), получим:

Слайд 18Текст слайда:

Итак, из равенства (5) вытекает равенство (6). Оба условия принципа математической индукции выполняются, значит, равенство (4) справедливо для любого натурального числа n.

Слайд 19Текст слайда:

Пример 3

Найти сумму

Решение:

Обозначим заданную сумму символом Sn и найдем ее значение при n = 1, 2, 3, 4:

Получили конечную последовательность

Можно предположить, что

Слайд 20Текст слайда:

Докажем справедливость этой формулы методом математической индукции.

Для n = 1 формула справедлива.

Предположим, что

, и докажем, что тогда

В самом деле,

По принципу математической индукции делаем вывод, что заданная сумма равна

Слайд 21Текст слайда:

Заметим, что в этом примере можно было обойтись без метода математической индукции:

Слайд 22Текст слайда:

Иногда требуется доказать некоторое утверждение не для всех натуральных чисел n, а для n ≥ p.
Тогда на первом шаге проверяют справедливость утверждения не для n = 1, а для n = p, а в остальном схема применения метода математической индукции та же.

Слайд 23Текст слайда:

Пример 4

Доказать, что для n ≥ 2 и x > 0 справедливо неравенство

Решение:

(его называют неравенством Бернулли в честь швейцарского математика Якоба Бернулли (1654-1705))

2) Предположим, что неравенство Бернулли верно для n = k (k ≥ 2):

Докажем, что тогда неравенство Бернулли верно и для n = k + 1,

1) При n = 2 получим верное неравенство:

(поскольку ).

(7)

Слайд 24Текст слайда:

т.е. докажем, что

Умножив обе части неравенства (7) на одно и то же положительное число 1 + x, получим:

Значит, мы доказали, что

По принципу математической индукции делаем вывод, что неравенство Бернулли справедливо для n ≥ 2.

Слайд 25Текст слайда:

«Понимание и умение правильно применять принцип математической индукции, является хорошим критерием логической зрелости, которая совершенно необходима математику».

А.Н. Колмогоров

Метод математической индукции: обзор, приложения

Автор Риту_Кумари
Последнее изменение 19-10-2022

Метод математической индукции: Математическая индукция — это метод математического доказательства, который используется для установления истинности любого данного утверждения для всех натуральных чисел \(n.\). Этот метод также может быть использован для расширения доказательства утверждений для более общих хорошо обоснованных структур, таких как деревья; это обобщение, известное как структурная индукция, используется в логике и информатике.

Справедливость математической индукции логически эквивалентна принципу упорядочения. В математической индукции мы можем доказать истинность любого утверждения для любого натурального числа всего за три шага, и мы можем заключить утверждение в целом.

Типы рассуждений

В математических рассуждениях для получения научных выводов обычно используются два основных процесса рассуждений.

Вычет
Индукция

Процесс вычета

Процесс, используемый для вывода (или вывода) конкретного результата из общего результата, называется дедукцией.

Пример: Все целые числа, чья цифра в разряде единиц равна \(0\) или \(5\), делятся на \(5.\)

Это общее утверждение. Так как \(365\) является целым числом, чья цифра в единичном разряде равна \(5, 365\), то оно делится на \(5.\) Это частное утверждение. Здесь из общего утверждения мы заключили частное утверждение.

Узнайте об алгебраических выражениях здесь

Процесс индукции

Процесс рассуждения от частного результата к общему результату называется индукцией.

Пример: \(44\) делится на \(2.\) Следовательно, все целые числа, оканчивающиеся на \(4\), делятся на \(2. \)

Здесь из конкретного утверждения мы делаем общий вывод. Этот вывод есть не что иное, как предположение или догадка, ибо мы могли бы прийти и к любому другому заключению.

Например, можно сказать, что \(44\) делится на \(2.\). Кроме того, \(44\) состоит из двух цифр. Следовательно, все двузначные числа делятся на \(2\) — ложный вывод. Например, \(53\) — двузначное целое число, но оно не делится на \(2.\) 9.0011

Индукция против дедукции

В процессе индукции мы делаем предварительное предположение. Это предположение может быть точным. Эта истина должна быть доказана надлежащими математическими рассуждениями. В противном случае он объявляется ложным. Это должно быть продемонстрировано с помощью контрпримера, в котором догадка неверна.

Если гипотеза не доказана математически, она остается гипотезой, сколько бы примеров мы ни приводили в ее поддержку. Таким образом, в математической индукции мы сначала приходим к гипотезе, а затем переходим к ее доказательству.

Как доказать гипотезу?

Чтобы доказать гипотезу в форме утверждения, скажем, \(P(n),\) с участием натуральных чисел, мы используем принцип математической индукции.

Давайте узнаем больше о методе индукции принципа в этой статье.

Принцип математической индукции

Из арифметической прогрессии мы знаем, что:

Сумма \(n\) натуральных чисел\( = \frac{{n(n + 1)}}{2}.\) Следовательно ,

Сумма первых \(1\) натуральных чисел\( = 1 = \frac{{1(1 + 1)}}{2}\)
Сумма первых \(2\) натуральных чисел\( = 1 + 2 = 3 = \frac{{2(2 + 1)}}{2}\)
Сумма первых \(3\) натуральных чисел sum\( = 1 + 2 + 3 = 6 = \frac{{3 (3 + 1)}}{2}\)

Мы видели, что данная формула верна для первых трех натуральных чисел, т.е. она будет верна и для первых четырех натуральных чисел.

Мы можем записать это как \(1 + 2 + 3 + 4 + \cdots + n = \frac{{n(n + 1)}}{2}\)

Чтобы проверить утверждение, мы можем подставить любое натуральное число вместо \(n\) и доказать это. Но это не докажет утверждение в целом для \(n.\)

. Чтобы сделать его истинным для всех значений n, мы должны сделать цепную реакцию, которая повлияет на то, верна ли какая-либо формула для некоторого конкретного положительного целого числа. Затем оно должно быть автоматически истинным для следующего положительного целого числа и следующего неопределенного числа.

Такие выводы можно сделать методом математической индукции.

Определение математической индукции

Если \(P(n)\) — утверждение, включающее натуральное число \(n,\), такое, что

Если \(P(1)\) истинно, то есть утверждение истинно для \(n=1\)
Если \(P(k+1)\) истинно всякий раз, когда \(P(k)\) истинно, т. е. истинность \(P(k)\) следует истинность \(P(k+1)\), то \(P(n)\) истинно для всех натуральных чисел \(n.\)

Метод решения математической индукции

Таким образом, чтобы доказать утверждение \(P(n)\) верно для всех натуральных чисел, мы должны следовать рабочему правилу:

Шаг 1: Докажите, что \(P(1)\) верно: т. {{\rm{th}}}}\). Аналогичным образом, чтобы доказать любое утверждение с помощью математической индукции, мы сначала показываем, что оно верно для \(n=1,\), а затем показываем, что оно выполняется для \(n=k + 1\), предполагая, что оно истинно. верно для \(n = k.\). Следовательно, скажем, что утверждение верно и для всех натуральных чисел \(n.\)
Применение математической индукции в реальной жизни
Существует несколько реальных применений математической индукции, и некоторые из них перечислены ниже:
1. Эффект домино
  Эффект домино, также известный как цепная реакция, кумулятивный эффект, возникающий, когда одно из событий запускает цепочку подобных событий.
2. Семейное древо
  Показывает количество потомков в каждом поколении. Чтобы обобщить это, мы используем математическую индукцию. 9{k + 1}} \ge 2k + 2 > (k + 1) + 1\) верно.
  \(∴ P(k+1)\) истинно, когда \(P(k)\) истинно. Следовательно, по принципу математической индукции. \(P(n)\) верно для всех \(n.\)
  Резюме
  Математическая индукция – это метод математического доказательства, используемый для установления истинности утверждения для всех натуральных чисел \(n.\) достоверность математической индукции логически эквивалентна принципу упорядочения. У него есть приложения в реальной жизни, такие как эффект домино и генеалогические деревья. Существует два типа рассуждений, таких как процесс дедукции и процесс индукции. Если \(P(n)\) — утверждение, включающее натуральное число \(n,\), такое, что \(P(1)\) истинно, т. е. утверждение истинно для \(n=1,\) и если \(P(k+1)\) истинно всякий раз, когда \(P(k)\) истинно, то есть истинность \(P(k)\) подразумевает истинность \(P(k+1)\ ), то \(P(n)\) истинно для всех натуральных чисел \(n.\)
  Часто задаваемые вопросы (FAQ)
  Q.1. Что понимается под математической индукцией?
  Ответ: Это метод математического доказательства, который используется для установления истинности любого данного утверждения для всех натуральных чисел \(n. \)
  Вот шаги математической индукции:
  Шаг 1: Докажите, что \(P(1)\) истинно: т. е. \(P(n)\) истинно для \(n=1\)
  Шаг 2 : Предположим, что \(P(k)\) истинно; т. е. \(P(n)\) истинно для \(n=k\)
  Шаг 3 : Докажите, что \(P(k+1)\) также верно; i,e, \(P(n)\) также верно для \(n=k+1.\)
  Следовательно , \(p(n)\) истинно для всех натуральных чисел \(n.\)
  Q.2. Каковы принципы математической индукции?
  Ответ: Если \(P(n)\) — утверждение, включающее натуральное число \(n,\), такое, что
  (i) Если \(P(1)\) истинно, т. е. утверждение истинно для \(n=1\)
  (ii) Если \(P(k+1)\) истинно, всякий раз, когда \(P(k)\) истинно, т. е. истинность \(P(k)\) следует истинность \(P(k+1)\), то \(P(n)\) истинно для всех натуральных чисел \(n.\)
  Q.3. Что такое принцип математической индукции в дискретной математике?
  Ответ: Это метод математического доказательства, который используется для установления истинности любого данного утверждения для всех натуральных чисел \(n. \). основанные структуры, такие как деревья; это обобщение, известное как структурная индукция, используется в математической логике и информатике. Этот метод также используется в дискретной математике для доказательства утверждений.
  Q.4. Чем полезна математическая индукция при анализе задач?
  Ответ: Использование математической индукции сводит данную проблему к математическому утверждению или теореме к простому утверждению, которое можно легко доказать. Каждое утверждение служит шагом к решению более крупного предложения.
  Q.5. Какова цель математической индукции?
  Ответ: Целью математической индукции является предоставление общего доказательства уравнения или утверждений для всех натуральных чисел \(1,2,3,…,\) без выполнения отдельных вычислений. Это делается путем принятия предположений о том, что было доказано в предыдущих расчетах.
  Узнайте о принципе математической индукции здесь
  Мы надеемся, что эта подробная статья о методе математической индукции познакомит вас с этой темой. Если у вас есть какие-либо вопросы, не стесняйтесь размещать их в поле для комментариев. Оставайтесь с нами на embibe.com для получения дополнительной информации.
  Примеры математической индукции
  О «Примерах математической индукции»
  Примеры математической индукции:
  Здесь мы увидим некоторые задачи математической индукции с решениями.
  Дайте определение математической индукции:
  Математическая индукция – это метод или техника доказательства математических результатов или теорем
  Процесс индукции включает следующие этапы.
  Примеры математической индукции
  
  Вопрос 1 :
  По принципу математической индукции докажите, что для n ≥ 1
  1 ² + 3 ² + 5 ² + · · · + (2n − 1) ² = n(2n − 1)(2n + 1)/3
  Решение:
  1 9 (n) = 1 ² + 3 ² + 5 ² + · · · + (2n − 1) ² = n(2n − 1)(2n+1)/3
  10388 Шаг :
  положить n = 1
  p(1) = 1 ² + 3 ² + 5 ² + · · · + (2(1) − 1) ^{3 ( 2 = 9041( 2 = 1) 1) − 1)(2(1)+1)/3}
  1 = 1
  Следовательно, p(1) верно.
  Шаг 2 :
  Предположим, что утверждение верно для n = k 1) ² = k(2k − 1)(2k+1)/3 —(1)
  Нам нужно показать, что P(k + 1) верно. Рассмотрим
  Шаг 3 :
  Предположим, что утверждение верно для n = k + 1
  p(k+1)
  1 ² + 3 · 2 2(к+1) — 1) ² = [(k+1)(2(k+1) − 1)(2(k+1)+1)]/3
  1 ² + 3 ² · · · + (2k +1) ² = [(k+1)(2k + 1) (2k + 3)]/3
  1 ² + 3 ² · · · + (2k-1) ² + (2k+1) ² = [(k+1)(2k + 1) (2k + 3)]/3
  индукция,n ≥ 1
  1 ² + 3 ² + 5 ² + · · · + (2n − 1) ² = n(2n − 1)(2n + 1)/3
  Вопрос 2 :
  Докажите, что сумма первых n ненулевых четных чисел равна n ² + n.
  Решение:
  Пусть p(n) будет утверждением «n ² + n» четно.
  Шаг 1:
  P (n) = N ²+ N
  PUT N = 1
  P (1) = 1 ²+ 1 = 2, что равно
  . 1) верно.
  Ступень 2 :
  Пусть p(m) истинно. Тогда
  p(m) истинно ==> m ² + m четно ==> m ² + m ==> 2λ для некоторого λ ∊ N
  Теперь покажем, что p(m + 1) верно. Для этого нужно показать, что (m+1) ² + (m + 1) — четное натуральное число.
  Сейчас,
  (m+1) ² + (m + 1) = m ² + 2 m + 1 + m + 1
  = m ² + 2 9001 + m1 + 1 2
  = м ² + м + 2м + 2
  = m ² + m + 2(m + 1)
  = 2λ + 2 (m + 1)
  = 2(λ + m + 1)
  Следовательно, p(m + 1) истинно.
  Следовательно, сумма первых n ненулевых четных чисел равна n ² + n.
  Мы надеемся, что после изучения вышеизложенного учащиеся поняли «Примеры математической индукции».
  Помимо всего вышеперечисленного, если вы хотите узнать больше о «Примерах математической индукции».
  No related posts.