Логарифмы примеры решения задач, формулы и онлайн калькуляторы
Содержание:
Логарифмы (Логарифмирование) активно используются в решении задач, так как значительно упрощают обычные алгебраические операции. Использование логарифмов позволяет заменить умножение на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня заменяются соответственно на умножение и деление на показатель степени числа.
Перед изучением примеров решения задач советуем изучить теоретический материал по логарифмам, прочитать определения и все свойства логарифмов.
Логарифм произведения, сумма логарифмов
Теоретический материал по теме — логарифм произведения.
Пример
Задание. Представить $\log _{5} 6$ в виде суммы логарифмов.
Решение. $\log _{5} 6=\log _{5}(2 \cdot 3)=\log _{5} 2+\log _{5} 3$
Слишком сложно?
Примеры решения задач с логарифмами не по зубам? Тебе ответит эксперт через 10 минут!
Задание.
Упростить $\log _{5} 4+\log _{5} 3$
Решение. $\log _{5} 4+\log _{5} 3=\log _{5}(4 \cdot 3)=\log _{5} 12$
Логарифм частного, разность логарифмов
Теоретический материал по теме — логарифм частного.
Пример
Задание. Известно, что $\log _{5} 2=a$, а $\log _{5} 3=b$. Выразить $\log _{5} \frac{2}{3}$ через $a$ и $b$.
Решение. $\log _{5} \frac{2}{3}=\log _{5} 2-\log _{5} 3=a-b$
Пример
Задание. Вычислить значение выражения $\log _{5} 10-\log _{5} 2$
Решение. $\log _{5} 10-\log _{5} 2=\log _{5} \frac{10}{2}=\log _{5} 5=1$
Логарифм степени
Теоретический материал по теме — логарифм степени.
Пример
Задание. Вычислить $\log _{5} 10-\log _{5} 2=\log _{5} \frac{10}{2}=\log _{5} 5=1$
Решение.$\log _{2} \frac{1}{8}+\log _{5} 25=\log _{2} 2^{-3}+\log _{5} 5^{2}=-3 \cdot \log _{2} 2+2 \cdot \log _{5} 5=$
$= -3 + 2 = -1$
Пример
Задание. Второй корень не принадлежит ОДЗ, а значит решение $x=2$ Ответ. $x=2$ Пример Задание. Решить уравнение $\ln (x+1)=\ln (2 x-3)$ Решение. Находим ОДЗ: Решаем уравнение $x+1=2 x-3: x=4 \in$ ОДЗ. Итак, решением исходного логарифмического уравнения
также является это значение. Ответ. $x=4$ Теоретический материал по теме — логарифмические неравенства. Пример Задание. Решить неравенство $\log _{0,5}(x-1)>-1$ Решение. В пересечении с ОДЗ получаем, что $x \in(1 ; 3)$ Ответ. $x \in(1 ; 3)$ Пример Задание. Решить неравенство $\log _{5} 5>\log _{5} x$ Решение. Данное неравенство равносильно системе: Ответ. $x \in(0 ; 5)$ Читать первую тему — формулы и свойства логарифмов,
раздела логарифмы. Как известно, при перемножении выражений со степенями их показатели всегда складываются (ab*ac = ab+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Логарифмом называется выражение следующего вида: logab=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log28. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8. Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений: Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях. В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями: К примеру, дано задание найти ответ уравнения 10х= 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, квадратичная степень! 102=100. А теперь давайте представим данное выражение в виде логарифмического. Получим log10100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число. Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом: Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 34=81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log381 = 4). Для отрицательных степеней правила такие же: 2-5= 1/32 запишем в виде логарифма, получим log2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений. Дано выражение следующего вида: log2(x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три. Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм2x = √9)подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел. При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство. Пусть logab = t, получается at=b. Если возвести обе части в степень m: atn = bn; но так как atn= (aq)nt/q = bn, следовательно logaqbn = (n*t)/t, тогда logaqbn = n/q logab. Теорема доказана. Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся. При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный. Вот примеры десятичных логарифмов: ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Итак, рассмотрим примеры использования основных теорем о логарифмах. Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания. Дано log2(2x-1) = 4. Решение: Ниже даны несколько рекомендаций, следуя которым можно с легкостью решать все уравнения, содержащие выражения, которые стоят под знаком логарифма. библиотека Содержание слайдов Номер слайда 1 Логарифмические уравнения. Основные методы их решения. Номер слайда 2
{2}-x-2=0 \Rightarrow x_{1}=2, x_{2}=-1$$Решение логарифмических неравенств
{-1}$ или $x-1<2 \Rightarrow x<3$Логарифмы: примеры и решения
Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.Разновидности логарифмов
Правила и некоторые ограничения
Как решать логарифмы?
На пересечении в ячейках определены значения чисел, являющиеся ответом (ac=b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!Уравнения и неравенства
Основные теоремы о логарифмах
С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.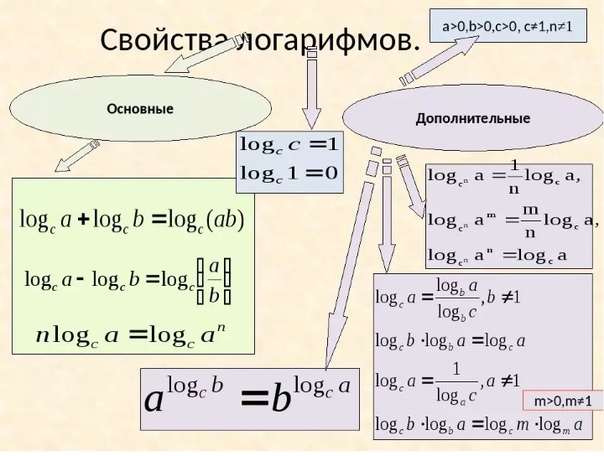
Примеры задач и неравенств
Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.
Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.Как использовать формулы логарифмов: с примерами и решениями
Задания из ЕГЭ
Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».
перепишем выражение, немного его упростив log2(2x-1) = 22, по определению логарифма получим, что 2x-1 = 24, следовательно 2x = 17; x = 8,5.
Презентация «Логарифмические уравнения». — математика, презентации
материалов
.) — английский поэт, прозаик, критик «Ничему тому, что важно знать, научить нельзя, — всё, что может сделать учитель, это указать дорожки» «Кто говорит – тот сеет, кто слушает – тот собирает». Русская народная пословица
Номер слайда 3
Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением. Решение логарифмических уравнений на основании определения логарифма. Определение логарифма: Пример 1: Ответ: 16.
Номер слайда 4
Проверка: Ответ: 4. Пример 3: Ответ: Пример 2:
Номер слайда 5
Пример 4: ОДЗ: Ответ: 2.
2. Метод потенцирования. Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их. где Пример 5: Проверка: Ответ: 1. — верно — не верно
Номер слайда 7
Пример 6: Проверка: верно.
Номер слайда 8
Пример 7: получим Проверка: Ответ: 0. верно
Номер слайда 93.
Метод подстановки. Пример 8: Ответ: ОДЗ: Пусть тогда Значит, или
Номер слайда 10
Пример 9: Ответ: ОДЗ: Приведём логарифмы к одному основанию – 7: Подстановка: Уравнение примет вид: Значит, или
Номер слайда 11
4.
Метод логарифмирования. Пример 10: Ответ: 3; 27. ОДЗ: Пусть тогда Значит, или
Выводы: На основании определения логарифма. Метод потенцирования. Метод постановки. Метод логарифмирования.
Номер слайда 13
Спасибо за внимание! Удачи ! Успехов!
Подборка заданий на свойства логарифмов по егэ.
Логарифмы: примеры и решенияОпределение в математике
Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8.
Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.
Разновидности логарифмов
Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:
- Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
- Десятичный a, где основанием служит число 10.
- Логарифм любого числа b по основанию a>1.
Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.
Правила и некоторые ограничения
В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной.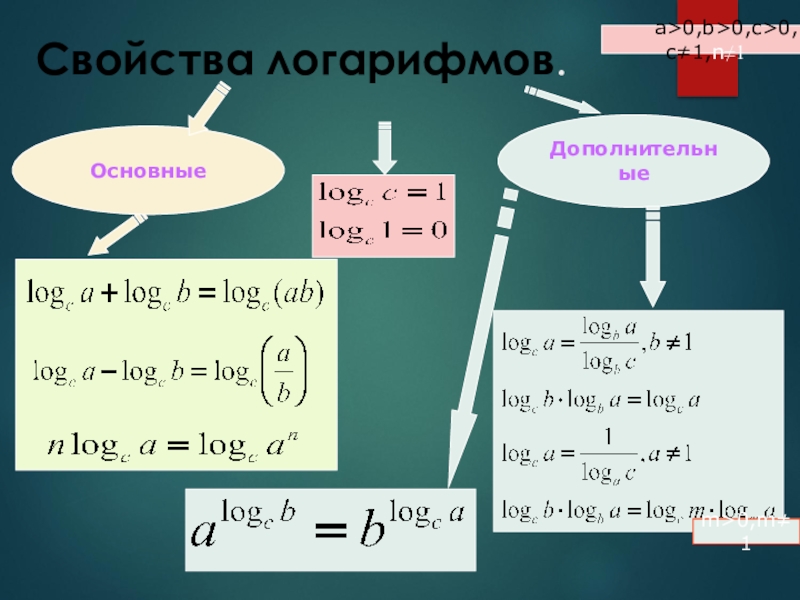
Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:
- основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
- если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.
Как решать логарифмы?
К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.
А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.
Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:
Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!
Уравнения и неравенства
Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства.
Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.
Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.
Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции.
Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.
Основные теоремы о логарифмах
При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.
- Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
- Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2.
Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать. - Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
- Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.
Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.
Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;
но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.
Примеры задач и неравенств
Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике.
Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.
К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.
При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.
Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства.
Давайте на примерах рассмотрим решение логарифмических задач разного типа.
Как использовать формулы логарифмов: с примерами и решениями
Итак, рассмотрим примеры использования основных теорем о логарифмах.
- Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
- log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.
Задания из ЕГЭ
Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания).
Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».
Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.
Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.
- Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
- Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.
Логарифмические выражения, решение примеров. В этой статье мы рассмотрим задачи связанные с решением логарифмов. В заданиях ставится вопрос о нахождении значения выражения. Нужно отметить, что понятие логарифма используется во многих заданиях и понимать его смысл крайне важно.
Что касается ЕГЭ, то логарифм используется при решении уравнений, в прикладных задачах, также в заданиях связанных с исследованием функций.
Приведём примеры для понимания самого смысла логарифма:
Основное логарифмическое тождество:
Свойства логарифмов, которые необходимо всегда помнить:
*Логарифм произведения равен сумме логарифмов сомножителей.
* * *
*Логарифм частного (дроби) равен разности логарифмов сомножителей.
* * *
*Логарифм степени равен произведению показателя степени на логарифм ее основания.
* * *
*Переход к новому основанию
* * *
Ещё свойства:
* * *
Вычисление логарифмов тесно связано с использованием свойств показателей степени.
Перечислим некоторые из них:
Суть данного свойства заключается в том, что при переносе числителя в знаменатель и наоборот, знак показателя степени меняется на противоположный.
Например:
Следствие из данного свойства:
* * *
При возведении степени в степень основание остаётся прежним, а показатели перемножаются.
* * *
Как вы убедились само понятие логарифма несложное. Главное то, что необходима хорошая практика, которая даёт определённый навык. Разумеется знание формул обязательно. Если навык в преобразовании элементарных логарифмов не сформирован, то при решении простых заданий можно легко допустить ошибку.
Практикуйтесь, решайте сначала простейшие примеры из курса математики, затем переходите к более сложным. В будущем обязательно покажу, как решаются «страшненькие» логарифмы, таких на ЕГЭ не будет, но они представляют интерес, не пропустите!
На этом всё! Успеха Вам!
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Что такое логарифм?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Что такое логарифм? Как решать логарифмы? Эти вопросы многих выпускников вводят в ступор. Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно — уравнения с логарифмами.
Это абсолютно не так. Абсолютно! Не верите? Хорошо. Сейчас, за какие-то 10 — 20 минут вы:
1. Поймете, что такое логарифм .
2. Научитесь решать целый класс показательных уравнений. Даже если ничего о них не слышали.
3. Научитесь вычислять простые логарифмы.
Причём для этого вам нужно будет знать только таблицу умножения, да как возводится число в степень…
Чувствую, сомневаетесь вы… Ну ладно, засекайте время! Поехали!
Для начала решите в уме вот такое уравнение:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень.
Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
В этом видеоуроке мы рассмотрим решение довольно серьезного логарифмического уравнения, в котором не просто требуется найти корни, но и отобрать те из них, которые лежат на заданном отрезке.
Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.
Замечание по поводу логарифмический уравнений
Однако из года в год ко мне приходят ученики которые пытаются решать вот такие, прямо скажем, непростые уравнения , но при этом не могут понять: с чего им вообще начинать и как подступиться к логарифмам? Такая проблема может возникнуть даже у сильных, хорошо подготовленных учеников.
В результате многие начинают опасаться этой темы, а то и вовсе считать себя тупыми. Так вот, запомните: если у вас не получается решить такое уравнение, это совершенно не значит, что вы — тупые.
Потому что, например, вот с таким уравнением вы справитесь практически устно:
log 2 x = 4
А если это не так, вы сейчас не читали бы этот текст, поскольку были заняты более простыми и приземленными задачами. Конечно, кто-то сейчас возразит: «А какое отношение это простейшее уравнение имеет к нашей здоровой конструкции?» Отвечаю: любое логарифмическое уравнение, каким бы сложным оно ни было, в итоге сводится вот к таким простейшим, устно решаемым конструкциям.
Разумеется, переходить от сложных логарифмических уравнений к более простым нужно не с помощью подбора или танцев с бубном, а по четким, давно определенным правилам, которые так и называются — правила преобразования логарифмических выражений . Зная их, вы без труда разберетесь даже с самыми навороченными уравнениями в ЕГЭ по математике.
И именно об этих правилах мы будем говорить в сегодняшнем уроке. Поехали!
Решение логарифмического уравнения в задаче C1
Итак, решаем уравнение:
В первую очередь, когда речь заходит о логарифмических уравнениях, вспоминаем основную тактику — если можно выразиться, основное правило решения логарифмических уравнений.
Заключается оно в следующем:
Теорема о канонической форме. Любое логарифмическое уравнение, что бы в него не входило, какие бы логарифмы, по какому бы основанию, и что бы в себе не c одержали, обязательно нужно привести к уравнению вида:
log a f (x ) = log a g (x )
Если мы посмотрим на наше уравнение, то заметим сразу две проблемы:
- Слева у нас стоит сумма двух чисел , одно из которых вообще не является логарифмом.
- Справа стоит вполне себе логарифм, однако в его основании стоит корень. А у логарифма слева — просто 2, т.е. основания логарифмов слева и справа различаются.
Итак, мы составили этакий список проблем, которые отделяют наше уравнение от того канонического уравнения , к которому нужно привести любое логарифмическое уравнение в процессе решения. Таким образом, решение нашего уравнения на данном этапе сводится к тому, чтобы устранить описанные выше две проблемы.
Любое логарифмическое уравнение решается быстро и легко, если свести его к канонической форме.
Сумма логарифмов и логарифм произведения
Давайте действовать по порядку. Сначала разберемся с конструкцией, которая стоит слева. Что мы можем сказать про сумму двух логарифмов? Давайте вспомним замечательную формулу:
log a f (x ) + log a g (x ) = log a f (x ) · g (x )
Но стоить учесть, что в нашем случае первое слагаемо вообще не является логарифмом. Значит, нужно представить единицу в виде логарифма по основанию 2 (именно 2, потому что слева стоит логарифм по основанию 2). Как это сделать? Опять вспоминаем замечательную формулу:
a = log b b a
Здесь нужно понимать: когда мы говорим «Любое основание b », то подразумеваем, что b все-таки не может быть произвольным числом. Если мы вставляем какое-то число в логарифм, на него сразу накладываются определенные ограничения , а именно: основание логарифма должно быть больше 0 и не должно быть равно 1. Иначе логарифм просто не имеет смысла. Запишем это:
0
Давайте посмотрим, что происходит в нашем случае:
1 = log 2 2 1 = log 2 2
Теперь перепишем все наше уравнение с учетом этого факта.
И сразу же применяем другое правило: сумма логарифмов равна логарифму произведения аргументов. В итоге получим:
Мы получили новое уравнение. Как видим, оно уже гораздо ближе к тому каноническому равнению, к которому мы стремимся. Но есть одна проблема, мы записали ее в виде второго пункта: у наших логарифмов, которые стоят слева и справа, разные основания . Переходим к следующему шагу.
Правила вынесения степеней из логарифма
Итак у логарифма, который стоит слева, основание просто 2, а у логарифма, который стоит справа, в основании присутствует корень. Но и это не является проблемой, если вспомнить, что из оснований из аргументов логарифма можно выносить в степень. Давайте запишем одно из этих правил:
log a b n = n · log a b
Переведя на человеческий язык: можно выносить степень из основания логарифма и ставить ее спереди в качестве множителя. Число n «мигрировало» из логарифма наружу и стало коэффициентом спереди.
С тем же успехом мы можем вынести степень из основания логарифма.
Выглядеть это будет так:
Другими словами, если вынести степень из аргумента логарифма, эта степень также пишется в качестве множителя перед логарифмом, но уже не в виде числа, а в виде обратного числа 1/k .
Однако и это еще не все! Мы можем объединить две данные формулы и почить следующую формулу:
Когда степень стоит и в основании, и в аргументе логарифма, мы можем сэкономить время и упростить вычисления, если сразу же вынести степени и из основания, и из аргумента. При этом то, что стояло в аргументе (в нашем случае это коэффициент n ), окажется в числителе. А то, что было степенью у основания, a k , отправится в знаменатель.
И именно эти формулы мы сейчас будем применять для того, чтобы свести наши логарифмы к одному и тому же основанию.
Прежде всего, выберем более-менее красивое основание. Очевидно, что с двойкой в основании намного приятней работать, чем с корнем. Таким образом, давайте попробуем привести второй логарифм к основанию 2.
Давайте выпишем этот логарифм отдельно:
Что мы можем здесь сделать? Вспомним формулу степени с рациональным показателем. Другими словами, мы можем записать в корни в качестве степени с рациональным показателем. А затем выносим степень 1/2 и из аргумента, и из основания логарифма. Сокращаем двойки в коэффициентах в числителе и знаменателе, стоящих перед логарифмом:
Наконец, перепишем исходное уравнение с учетом новых коэффициентов:
log 2 2(9x 2 + 5) = log 2 (8x 4 + 14)
Мы получили каноническое логарифмическое уравнение. И слева, и справа у нас стоит логарифм по одному и тому же основанию 2. Помимо этих логарифмов никаких коэффициентов, никаких слагаемых ни слева, ни справа нет.
Следственно, мы можем избавиться от знака логарифма. Разумеется, с учетом области определения. Но прежде, чем это сделать, давайте вернемся назад и сделаем небольшое уточнение по поводу дробей.
Деление дроби на дробь: дополнительные соображения
Далеко не всем ученикам понятно, откуда берутся и куда деваются множители перед правым логарифмом.
Запишем еще раз:
Давайте разберемся, что такое дробь. Запишем:
А теперь вспоминаем правило деления дробей: чтобы разделить на 1/2 нужно умножить на перевернутую дробь:
Разумеется, для удобства дальнейших вычислений мы можем записать двойку как 2/1 — и именно это мы наблюдаем в качестве второго коэффициента в процессе решения.
Надеюсь, теперь всем понятно, откуда берется второй коэффициент, поэтому переходим непосредственно к решению нашего канонического логарифмического уравнения.
Избавление от знака логарифма
Напоминаю, что сейчас мы можем избавиться от логарифмов и оставить следующее выражение:
2(9x 2 + 5) = 8x 4 + 14
Давайте раскроем скобки слева. Получим:
18x 2 + 10 = 8x 4 + 14
Перенесем все из левой части в правую:
8x 4 + 14 − 18x 2 − 10 = 0
Приведем подобные и получим:
8x 4 − 18x 2 + 4 = 0
Можем разделить обе части этого уравнения на 2, чтобы упростить коэффициенты, и получим:
4x 4 − 9x 2 + 2 = 0
Перед нами обычное биквадратное уравнение , и его корни легко считаются через дискриминант.
Итак, запишем дискриминант:
D = 81 − 4 · 4 · 2 = 81 − 32 = 49
Прекрасно, Дискриминант «красивый», корень из него равен 7. Все, считаем сами иксы. Но в данном случае корни получатся не x , а x 2 , потому что у нас биквадратное уравнение. Итак, наши варианты:
Обратите внимание: мы извлекали корни, поэтому ответов будет два, т.к. квадрат — функция четная . И если мы напишем лишь корень из двух, то второй корень мы просто потеряем.
Теперь расписываем второй корень нашего биквадратного уравнения:
Опять же, мы извлекаем арифметический квадратный корень из обеих частей нашего уравнения и получаем два корня. Однако помните:
Недостаточно просто приравнять аргументы логарифмов в канонической форме. Помните об области определения!
Итого мы получили четыре корня. Все они действительно являются решениями нашего исходного уравнения. Взгляните: в нашем исходном логарифмическом уравнении внутри логарифмов стоит либо 9x
2 + 5 (эта функция всегда положительна), либо 8x
4 + 14 — она тоже всегда положительна.
Следовательно, область определения логарифмов выполняется в любом случае, какой бы корень мы не получили, а это значит, что все четыре корня являются решениями нашего уравнения.
Прекрасно, теперь переходим ко второй части задачи.
Отбор корней логарифмического уравнения на отрезке
Отбираем из наших четырех корней те, которые лежат на отрезке [−1; 8/9]. Возвращаемся к нашим корням, и сейчас будем выполнять их отбор. Для начала предлагаю начертить координатную ось и отметить на ней концы отрезка:
Обе точки будут закрашенные. Т.е. по условию задачи нас интересует заштрихованный отрезок. Теперь давайте разбираться с корнями.
Иррациональные корни
Начнем с иррациональных корней. Заметим, что 8/9
Из этого следует, что корень из двух не попадает в интересующий нас отрезок. Аналогично мы получим и с отрицательным корнем: он меньше, чем −1, т. е. лежит левее интересующего нас отрезка.
Рациональные корни
Остается два корня: x
= 1/2 и x
= −1/2.
Давайте заметим, что левый конец отрезка (−1) — отрицательный, а правый (8/9) — положительный. Следовательно, где-то между этими концами лежит число 0. Корень x
= −1/2 будет находиться между −1 и 0, т.е. попадет в окончательный ответ. Аналогично поступаем с корнем x
= 1/2. Этот корень также лежит на рассматриваемом отрезке.
Убедиться, что число 8/9 больше, чем 1/2, можно очень просто. Давайте вычтем эти числа друг из друга:
Получили дробь 7/18 > 0, а это по определению означает, что 8/9 > 1/2.
Давайте отметим подходящие корни на оси координат:
Окончательным ответом будут два корня: 1/2 и −1/2.
Сравнение иррациональный чисел: универсальный алгоритм
В заключении хотел бы еще раз вернуться к иррациональным числам. На их примере мы сейчас посмотрим, как сравнивать рациональные и иррациональные величины в математике. Для начала по между ними вот такую галочку V
— знак «больше» или «меньше», но мы пока не знаем, в какую сторону он направлен.
Запишем:
Зачем вообще нужны какие-то алгоритмы сравнения? Дело в том, что в данной задаче нам очень повезло: в процессе решения возникло разделяющее число 1, про которое мы точно можем сказать:
Однако далеко не всегда вы с ходу увидите такое число. Поэтому давайте попробуем сравнить наши числа «в лоб», напрямую.
Как это делается? Делаем то же самое, что и с обычными неравенствами:
- Сначала, если бы у нас где-то были отрицательные коэффициенты, то мы умножили бы обе части неравенства на −1. Разумеется, поменяв при этом знак . Вот такая галочка V изменилась бы на такую — Λ.
- Но в нашем случае обе стороны уже положительны, поэтому ничего менять не надо. Что действительно нужно, так это возвести обе части в квадрат , чтобы избавится от радикала.
Если при сравнении иррациональных чисел не удается с ходу подобрать разделяющий элемент, рекомендую выполнять такое сравнение «в лоб» — расписывая как обычное неравенство.
При решении это оформляется вот таким образом:
Теперь это все легко сравнивается. Дело в том, что 64/81
Все, мы получили строгое доказательство, что все числа отмечены на числовой прямой х правильно и именно в той последовательности, в которой они должны быть на самом деле. Вот к такому решению никто не придерется, поэтому запомните: если вы сразу не видите разделяющее число (в нашем случае это 1), то смело выписывайте приведенную выше конструкцию, умножайте, возводите в квадрат — и в итоге вы получите красивое неравенство. Из этого неравенства точно будет понятно, какое число больше, а какое — меньше.
Возвращаясь к нашей задаче, хотелось бы еще раз обратить ваше внимание на то, что мы делали в самом начале при решении нашего уравнения. А именно: мы внимательно посмотрели на наше исходное логарифмическое уравнение и попытались свести его к каноническому логарифмическому уравнению. Где слева и справа стоят только логарифмы — без всяких дополнительных слагаемых, коэффициентов спереди и т.
д. Нам нужны не два логарифма по основанию a
или b
, именно логарифм, равный другому логарифму.
Кроме того, основания логарифмов также должны быть равны. При этом если уравнение составлено грамотно, то с помощью элементарных логарифмических преобразований (сумма логарифмов, преобразование числа в логарифм и т.д.) мы сведем это уравнение именно к каноническому.
Поэтому впредь, когда вы видите логарифмическое равнение, которое не решается сразу «в лоб», не стоит теряться или пробовать подобрать ответ. Достаточно выполнить следующие шаги:
- Привести все свободные элементы к логарифму;
- Затем эти логарифмы сложить;
- В полученной конструкции все логарифмы привести к одному и тому же основанию.
В результате вы получите простое уравнение, которое решается элементарными средствами алгебры из материалов 8—9 класса. В общем, заходите на мой сайт, тренируйтесь решать логарифмы, решайте логарифмические уравнения как я, решайте их лучше меня. А у меня на этом все.
С Вами был Павел Бердов. До новых встреч!
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т. д.
д.Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Логарифмы.
Обобщающее повторение — презентация онлайн Тема урокаОбобщающее повторение по теме «Логарифмы»
(подготовка учащихся к ЕГЭ на уроке математики)
Верещагина Людмила Викторовна.
Учитель математики
МКОУ Отрокская СОШ.
Красноярский край,
Идринский край,
с.Отрок.
2. В кодификаторе элементов содержания ЕГЭ по математике по теме «Логарифмы» указаны элементы:
В КОДИФИКАТОРЕ ЭЛЕМЕНТОВ СОДЕРЖАНИЯ ЕГЭ ПОМАТЕМАТИКЕ ПО ТЕМЕ «ЛОГАРИФМЫ» УКАЗАНЫ
ЭЛЕМЕНТЫ:
Логарифм числа
Логарифм произведения, частного, степени
Десятичный и натуральный логарифмы, число е
Преобразование выражений, включающих операцию
логарифмирования
Логарифмические уравнения
Использование свойств и графиков функций при
решении уравнений
Логарифмические неравенства
Логарифмическая функция, ее график
3. Цели урока:
ЦЕЛИ УРОКА:Обобщение и закрепление изученного материала;
Построение системы знаний о преобразовании
логарифмических выражений, решении логарифмических
уравнений и неравенств;
Формирование компетентности в сфере индивидуальной
самостоятельной познавательной деятельности, критического
мышления, а также навыков работы в команде;
Формирование представлений о математике как части
общечеловеческой культуры, понимания значимости
математики для общественного прогресса.
Развитие познавательных интересов, рефлексивных
способностей, креативных возможностей учащихся.
4. План урока:
ПЛАН УРОКА:Сообщение темы, цели и задач занятия.
Актуализация знаний. Повторение вопросов
теории через выход на практическое
применение.
Практическое применение темы(работа по
методике взаимопроверки индивидуальных
заданий).
Подведение итога урока (табло учета
выполнения индивидуальных заданий)
5. Вопросы к учащимся (двухсторонние карточки):
ВОПРОСЫ К УЧАЩИМСЯ (ДВУХСТОРОННИЕКАРТОЧКИ):
Что называется логарифмом числа в по основанию а?
В чем заключается основное логарифмическое тождество?
Вспомним основные свойства логарифмов, свойства
логарифмической функции, алгоритмы решения
логарифмических уравнений и неравенств, сложные
моменты в решении логарифмических уравнений и
неравенств (учащиеся на карточках отвечают, затем,
перевернув карточку, проверяют правильность и
комментируют).
6. Устный счет (фрагмент). Используются карточки для устного счета. Карточки выдаются на каждого ученика и могут использоваться
УСТНЫЙ СЧЕТ (ФРАГМЕНТ).ИСПОЛЬЗУЮТСЯ КАРТОЧКИ ДЛЯ УСТНОГО СЧЕТА. КАРТОЧКИ ВЫДАЮТСЯ НА
КАЖДОГО УЧЕНИКА И МОГУТ ИСПОЛЬЗОВАТЬСЯ НЕОДНОКРАТНО. ДЛЯ
ЭКОНОМИИ ВРЕМЕНИ ЗАДАНИЕ ВСЛУХ НЕ ЧИТАЕТСЯ, А ПРОГОВАРИВАЕТСЯ
ТОЛЬКО ОТВЕТ. В ЗАВИСИМОСТИ ОТ ПЛАНА УРОКА И УРОВНЯ ПОДГОТОВКИ
УЧАЩИХСЯ ВАРЬИРУЕТСЯ ВРЕМЯ, ОТВОДИМОЕ НА УСТНЫЙ СЧЕТ. ЭТИ ЖЕ
КАРТОЧКИ МОЖНО ИСПОЛЬЗОВАТЬ ДЛЯ НЕБОЛЬШИХ ПРОВЕРОЧНЫХ РАБОТ
2
Log 0,2 0,04
log√51
log51/125
log0,58
3
lg 10
lg1000
lg0,01
lg1
И другие….
Представьте число а в виде логарифма по основанию В
10
а=2, в=3
а=1, в=
а=0, в=1,05
а=3, в=2
Найдите область определения функции
13
Y=log3|x-2|
Y=log4|x|
Y=log6(x-1)2
Y=log2(2x)
7. Примеры индивидуальных заданий для взаимопроверки в парах.
ПРИМЕРЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙДЛЯ ВЗАИМОПРОВЕРКИ В ПАРАХ.
К–1
1.
Упростить, используя понятие логарифма,
свойства логарифмов:
а)
б)
в) log11
г) log105 + log102
д) 2 log72 3 + 3 log72 3
2. Найти значение выражения, используя
понятие логарифма, свойства логарифмов
если
=35.
8. Примеры индивидуальных заданий для взаимопроверки в парах.
ПРИМЕРЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙДЛЯ ВЗАИМОПРОВЕРКИ В ПАРАХ.
К–2
1.
К–3
1. Упростить, используя понятие
логарифма, свойства логарифмов:
Упростить, используя понятие
логарифма, свойства логарифмов:
а)
а)
б)
б)
в)
в)
г) .
+ log21 49
д) log108 + log10125
2. Найти значение выражения, используя
понятие логарифма, свойства
логарифмов
, если
г)
log122 + log1272
д)
2. Найти значение выражения, используя
понятие логарифма, свойства логарифмов
, если
9. Примеры карточек индивидуальных заданий для взаимопроверки в парах
ПРИМЕРЫ КАРТОЧЕК ИНДИВИДУАЛЬНЫХ ЗАДАНИЙДЛЯ ВЗАИМОПРОВЕРКИ В ПАРАХ
К–4
1.
Упростить, используя понятие логарифма, свойства логарифмов:
а)
б)
в)
г ) log215 + log2
д)
2. Найти значение выражения, используя понятие логарифма, свойства
логарифмов
10. Примеры карточек индивидуальных заданий для взаимопроверки в парах
ПРИМЕРЫ КАРТОЧЕК ИНДИВИДУАЛЬНЫХ ЗАДАНИЙДЛЯ ВЗАИМОПРОВЕРКИ В ПАРАХ
К–5
1.
Упростить, используя понятие логарифма, свойства логарифмов:
а)
б)
в)
г)
д) log108 + log10125
2. Найти значение выражения, используя понятие логарифма, свойства логарифмов
11. Подведение итогов урока. (Табло учета выполнения индивидуальных заданий (фрагмент)).
ПОДВЕДЕНИЕ ИТОГОВ УРОКА.(ТАБЛО УЧЕТА ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНЫХ
ЗАДАНИЙ (ФРАГМЕНТ)).
№ Номер
карточки
№1
№2
№3
Вид работы
выполнил
проверил выполнил
1
Бодрина А.
+
+
2
Васютина А.
+
*
*
3
Григорьева С
+
+
*
4
Иванова Д.
+
+
проверил выполнил
проверил
*
И др.
В табло «*» означают, какой вариант задания выполняет обучающийся,
а знак «+» означает, что обучающийся выполнил задание.
12. Алгоритм работы по карточам индивидуальных заданий для взаимопроверки в парах
АЛГОРИТМ РАБОТЫ ПО КАРТОЧАМ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙДЛЯ ВЗАИМОПРОВЕРКИ В ПАРАХ
1. Индивидуальная работа
1. Получите карточку, поставьте точку в листе учета.
2. Выполните задание 1 карточки.
3. Готовы? Сдайте учителю у доски или в группе.
4. Выполните задание 2 карточки.
5. Проверьте себя по листу ответов у учителя.
6. Если все верно, в листе учета замените точку на крестик.
II. Парная работа
1. Найдите партнёра с другой карточкой. Сядьте рядом.
2. Объясните партнёру задание 1 своей карточки. Ответьте на его вопросы.
3. Выслушайте партнера по первой части его карточки. Задайте вопросы.
4. Сделайте соответствующие записи в тетради.
5. Обменяйтесь карточками и выполните второе задание новой для вас, карточки.
6. Сверьте ответы второго задания.
— если они выполнены одинаково, то поблагодарите друг друга за работу
— если есть расхождения, то проверьте задания друг у друга; найдите и исправьте ошибки.
7. В листе учета обведи крестик кружочком против той карточки, которую ты передал партнеру.
8. Проверь в листе учета — против твоей фамилии должен стоять “+” в графе, с номером той карточки,
которую тебе передал партнер.
9. Найдите нового партнера и работайте с ним так, как описано выше с п. 7.
Выдержки из ученических рефератов (приготовленное
домашнее задание к этому уроку)…
Примеры использования неравномерности
логарифмической зависимости
Акустика — интенсивность звука (децибелы).
Отношение сигнал/шум в радиотехнике и электросвязи.
Астрономия — шкала яркости звёзд.
Химия — активность водородных ионов (pH).
Сейсмология — шкала Рихтера.
Теория музыки — нотная шкала, по отношению к
частотам нотных звуков.
История — логарифмическая шкала времени.
Дата рождения:
4 (15) апреля 1707
Место рождения:
Базель, Швейцария
Дата смерти:
7 (18) сентября 1783 (76 лет)
Научная сфера:
Математика, механика, физика, астрономия.
Современное определение показательной,
логарифмической функции — заслуга
Леонарда Эйлера, так же как и их символика.
В России первые таблицы логарифмов
были изданы в 1703 году при участии Л.
Ф. Магницкого.
Таблицы Брадиса (1921) использовались
в учебных заведениях и в инженерных
расчётах, не требующих большой
точности. Они содержали мантиссы
десятичных логарифмов чисел и
тригонометрических функций,
натуральные логарифмы и некоторые
другие полезные расчётные
инструменты.
Определение логарифмов и таблицу их
значений впервые опубликовал в 1614
году шотландский математик Джон
Непер. Логарифмические таблицы,
расширенные и уточнённые другими
математиками, повсеместно
использовались для научных и
инженерных расчётов более трёх
веков
Развитие и образование ни одному человеку не
могут быть даны или сообщены. Всякий, кто
желает к ним приобщиться, должен
достигнуть этого собственной
деятельностью, собственными силами,
собственным напряжением.
А. Дистервег
Домашняя работа на карточках индивидуальных заданий
Спасибо за внимание!
Алгебра и начала анализа в 11-м классе. Тема: «Логарифмы и его свойства»
Цели:
- Методическая: Повышение активно-познавательной деятельности учащихся путем проведения индивидуально-самостоятельной работы и применения опережающих заданий.
- Обучающая: Повторение определения показательной функции, основные свойства степеней. Ввести понятие логарифма и его свойств. Решение упражнений. Систематизировать знания учащихся по теме; способствовать выработке умений и навыков в вычислении логарифмов, в применении их свойств при логарифмировании и потенцировании; рассмотреть более сложные примеры по теме и проверить навыки и умения при самостоятельном решении упражнений.
- Воспитательная: Воспитание аккуратности, собранности. Проверить сформированность качеств знаний: прочность, глубина, оперативность; формировать гуманные отношения на уроке через работу в парах, умение слушать друг друга; добросовестное отношение к учебному труду, ответственность, честность, сопереживание успехам и неудачам товарищей.
- Развивающая: Развивать интеллектуальные способности, мыслительные процессы, речь, память. Развивать любовь и интерес к математике. Установить, могут ли студенты применять знания логарифмов при решении задач; в ходе урока обеспечить развитие у учащихся самостоятельности мышления и в учебной деятельности;
Тип урока: Комбинированный
Форма проведения урока: Индивидуальная и фронтальная. Решение примеров.
Оборудование: Плакаты на тему “ Показательная функция”, “Логарифмы и его свойства”, “гармошка” с заданиями, таблицы. Карточки-задания для индивидуальной самостоятельной работы, лото-задания, учебная литература.
Эпиграф урока:
“Математику уже затем учить надо, что
она ум в порядок приводит” |
Ход урока
1. Организационный моментВступительное слово преподавателя.
Я приветствую вас на сегодняшнем уроке алгебры. Тема урока: “Логарифм и его свойства”. Сегодня мы повторим понятие логарифма числа, свойства логарифма, закрепим умения применять эти понятия при решении уравнений. Эпиграфом урока являются слова М.В. Ломоносова
“Математику уже затем учить надо, что она ум в порядок приводит”. На доске: дата, тема, план, эпиграф урока.
Объявляется цель и задачи урока. Раздаются тетради для самостоятельных работ и учебники.
2. Актуализация опорных знаний, умений студентов
1. Проверка домашнего задания. №472а), №473а).
(Вызвать 2-х учащихся к доске.)
№ 272а)
>2,5; > 2,5; > ; > 1; ;
Х <0.
Ответ: х .
№ 273а).
2х> ; х2 – 3 + 2х > 0; х2 + 2х – 3 > 0.
Решим методом интервалов.
Пусть f (x) = х2 + 2х – 3, где f (x) = 0, т. е. х2 + 2х – 3 = 0.
Д = 22 – 4 * (- 3) = 4 = 12 = 16.
х1 = х2 =
f (0) = 02 + 2 * 0 – 3 < 0.
Ответ: х (-;-3)U(1;+ )
2. Индивидуальная работа по карточкам (10 мин). (Приложение 1)
(Раздать 6 карточек в виде лото-задания.)
Задания:
- Решить показательные уравнения.
- Решить показательные неравенства.
- Задания на свойства показательной функции.
3. Индивидуальная работа у доски.
(Написать свойства степеней.)
4. Выступление у доски.
(Доклад о происхождении степеней. Сведения из истории) Таблички с именами ученых готовить заранее. (Приложение 2)
5. По стенду дать определение показательной функции, свойства показательной функции.
Далее проверить домашнее задание. (Учащиеся комментирует план выполнения работ.)
Ассистенты самостоятельно проверяют индивидуальные работы учащихся, работающих индивидуально.
6. По “гармошке” решить показательные неравенства и уравнения ( задания готовить заранее.)
(Приложение 3)
3. Формирование новых знаний и понятий
Дата, тема и план урока написать заранее. Эпиграф урока на доске.
Преподаватель: Вы знакомы с шестью действиями над числами
| А+В | А-В | А*В | А/В | А |
Эти действия образуют три пары взаимно обратных действий. А для того чтобы решить уравнение а=в , где а>0 и а 1 придумали седьмое действие, которое называется логарифмом.
logа в=с ,где b>0 , а>0, а1, в=а
Преподаватель:
Совершаем небольшой экскурс в историю математики. Ученики слушают сообщение на тему “Изобретение логарифма”. На доске записи, которые предлагаем записать в тетрадь.
Джон Непер – 1614 год – изобретение логарифма
Бригс – 1624 год – создание таблиц логарифмов.
1703 год – перевод таблиц на русский язык
Л. Магницкий – 1716 год – издание семизначных
логарифмических таблиц.
Логарифмическая линейка
Слово логарифм происходит от греческого (число) и (отношение) и переводится, следовательно, как отношение чисел. Выбор изобретателем (1594 г.) логарифмов Дж. Непером такого названия объясняется тем, что логарифмы возникли при сопоставлении двух чисел, одно из которых является членом арифметической прогрессии, а другое — геометрической.
Определение. Логарифмом положительного числа в при положительном основание а, называется показатель степени, в которую нужно возвести основание а, чтобы получить логарифмируемое число в.
Формула (где в>0, а>0 и а1 ) называется основным логарифмическим тождеством.
Пример:
1) log9=2 т.к. 9>0,3>0, 3=1, 3 =9.
2) log3=0,5 т.к. 3>0, 9>0, 9=1, 9 =3
Преподаватель: Также существуют десятичные и натуральные логарифмы.
Log10 x= lg x –это десятичный логарифм.
Logе x=ln x-это натуральный логарифм.
(Таблички с формулами готовить заранее.)
Логарифмы с основанием е ввел С п е й д е л (1619 г.), составивший первые таблицы для функции In x. Название более позднего происхождения натуральный (естественный) объясняется “естественностью” этого логарифма.
Н. Мерка т о р (1620–1687), предложивший это название, обнаружил, что In х – это площадь под гиперболой у = . Он предлагал также название “гиперболический”.
На этом уроке вы познакомитесь со свойствами логарифмов, позволяющими преобразовывать логарифмические выражения, решать логарифмические уравнения и неравенства.
Для этого следует вспомнить свойства степеней.
К доске вызвать учащегося для записи свойств степеней.
Свойство 1. logа x=0
Свойство 2. Logа а=1
Свойство 3. Логарифм произведения положительных чисел равен сумме логарифмов множителей logа xy= logа x+ logв у
Свойство 4. Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя. logа = logах- logа у
Свойство 5. Логарифм степени равен произведению показателя степени на логарифм основания этой степени. logа x=р logа x
Опережающие задание в виде сообщения о возникновение логарифмов.
(Имена ученых-математиков заранее готовится на плакате) (Приложение 4)
4. Применение знаний, навыков, понятий
Работа учащихся у доски.
(Решение примеров №479 а),б), №480 а),б).)
№479 а),б), №480 а),б).- работать самостоятельно.
№ 479
а) log3 = – 4, так как 3 – 4 = ()4 = ;
б) log 16 1 = 0. Так как 160 = 1.
№ 480.
а) log5 0,04 = -2, т. к. 5-2 = = = 0,04;
б) log7 343 = 3, т. к 73 = 343.
№483 а),б) с объяснением
№ 483.
Найдите логарифмы:
№484
а) log3 х = -1; б) log х = -3; х = 3-1; х = =216; х =.
№484 а)б), №486 а)б) с объяснением.
№ 486
Опережающие задание в виде сообщения. Тема “Логарифм и музыка” (Приложение 5)
(Играет музыка )
Преподаватель: Ребята, логарифмы применяются на уроках физики. Закон радиоактивного распада имеет вид m=mе.Формула Циолковского, связывающая скорость ракеты с ее массой v=v ln .
(Все формулы написаны заранее на листе бумаги и прикрепляются на доску с помощью магнитиков.)
№488 – №490 решать устно с места (самостоятельная работа с места по учебнику)
№491 а) Прологарифмируйте по основанию 3 (К доске вызвать учащегося). Решение комментировать.
№ 491а) log3 = log3 = log3 а3b = (log3 а3 + log3 b) = (3log3 а + log3 b) = log3 а + log3 b. б) log3 = log3 = (log3 b – log3 a10) = log3 b – 10 log3 a = log3 b- 2 log3 a.
№492 (а, б) Самостоятельно у доски работает учащийся.
№ 492.
а) lg 100 = lg 100 + lg = 2 + lg (ab3c) = 2 + lg ab3c = 2 + (lg a + 3 lg b + lg c)/
Опережающие задание в виде сообщения. Тема “Звезды, шум и логарифмы” (Приложение 6)
Преподаватель: Более того, коэффициент звукоизоляции стен измеряется также с помощью логарифма, по формуле D=A lg .(Приложение 7)
№495 (а, б) Самостоятельно у доски. (по времени.)
а) lg 8+ lg 125= lg 8*125= lg 1000=3;
б) log2 7- log2= log2 7/= log2 16=4
– Давайте, ребята, послушаем еще одно сообщение, которое явно показывает связь математики и физики (Приложение 8)
5. Обобщение и систематизация знаний учащихся1. Словарная работа
– логарифм;
– показательная функция;
– возрастает;
– степень;
– иррациональный показатель;
– тождество.
– экспонента.
2) Эстафета (МАТЕМАТИЧЕСКОЕ ЛОТО.) (Приложение 9)
(заранее готовить 2 варианта заданий.)
6. Итог урокаПодвести итог урока. Сообщить учащимся оценки, отметить наиболее активных..
7. Домашняя работа№ 479г) -493г) Учить п.37. Готовится к математическому диктанту по пройденной теме.
Практическая тетрадь по теме «Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов. Логарифмические уравнения и их системы. Логарифмические неравенства»
ПРАКТИЧЕСКАЯ ТЕТРАДЬ
по теме «Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов. Логарифмические уравнения и их системы. Логарифмические неравенства.
Пояснительная записка:
Практическая тетрадь «Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов. Логарифмические уравнения и их системы. Логарифмические неравенства.» предназначена в первую очередь для самоконтроля учащихся усвоения ЗУН по вышеуказанным темам. Учителя могут использовать данный материал при подготовке учащихся средней школы к итоговой аттестации по алгебре и началам анализа.
Логарифм числа. Основное логарифмическое тождество.
Свойства логарифмов
Справочные сведения
Логарифмом положительного числа b по основанию а (записывают loga b), где а > 0, a 1, называют показатель степени, в которую нужно возвести число а, чтобы получить число b.
Равенство , где а > 0, a 1, b > 0, называют основным логарифмическим тождеством.
x = logab – корень уравнения ax = b, где а > 0, a 1, b > 0.
Логарифм числа по основанию 10 называется десятичным логарифмом: log10 b = lg b.
Логарифм числа по основанию е называется натуральным логарифмом: logе b = ln b.
Примеры с решениями
Вычислить: 1) 2) 3)
Решение. 1) , так как 34 = 81.
2) Пусть . Тогда по определению логарифма , или , откуда ,.
3) Пусть . Тогда по определению логарифма , откуда , , , .
Найти: 1) 2) 3)
Решение. 1) По определению логарифма (согласно основному логарифмическому тождеству) 2)
3)
3. Вычислить:
1) 2) 3)
Решение.
1)
2)
3)
Дидактический материал
Вычислить:
2) 3)
5) 6)
Ответы: — 4; 4; -3; — 2; 2; 0.
Вычислите десятичные логарифмы:
2) 3) 4) .
Ответы: — 4; — 1; ½; 4.
Вычислите натуральные логарифмы:
2) 3) 4)
Ответы:
Вычислите:
2)
Ответы: — 2; 2.
Найдите значения выражений:
2)
3) 4)
Ответы:
Логарифмические уравнения и их системы
Справочные сведения
Определение. Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим уравнением.
Простейшим логарифмическим уравнением является уравнение
logax = b, (1)
где a и b – данные числа, а х – переменная величина.
Если а > 0 и , то такое уравнение имеет единственный корень x = ab.
Решение более сложных логарифмических уравнений сводится либо к решению алгебраических уравнений, либо к решению уравнений вида (1).
Способы решения логарифмических уравнений
Способ непосредственного применения определения логарифма.
Пример 1. Решим уравнение logx( х3 – 5х + 10 ) = 3.
Решение. По определению логарифма можно написать: х3 – 5х + 10 = х3, откуда: х = 2.
Проверка: log2(23 — 52 + 10) = log28 = 3. Ответ: 2.
Известно, что областью определения логарифмической функции является множество положительных действительных чисел. Поэтому часто при решении логарифмических уравнений вначале определяется
область допустимых значений переменной (ОДЗ). Затем решается данное уравнение и найденные значе-ния переменной проверяются на принадлежность ОДЗ.
Способ приведения уравнения к виду loga f(x) = loga g(x) c последующим применением потенцирования.
Пример 2. Решим уравнение: lg( x + 5) – lg( x2 – 25 ) = 0.
Решение. Найдем ОДЗ. Для этого решим систему неравенств:
Отсюда имеем: .
Преобразуем данное уравнение: lg( x + 5) = lg( x2 – 25 ).
Потенцируя, имеем: х + 5 = х2 – 25 или х2 – х – 30 = 0, откуда х1 = 6, х2 = — 5. Но .
Ответ: 6.
Способ введения новой переменной.
Пример 3. Решим уравнение :
Решение. Пусть log2 х = у, тогда вместо исходного уравнения получим: у2 – у – 2 = 0.
Решив полученное квадратное уравнение, имеем: у1 = 2, у2 = — 1.
Теперь найдем искомые значения х:
log2 х = 2, х1 = 4; log2 х = -1, х2 = .
ОДЗ: х > 0. Оба найденные значения х принадлежат ОДЗ. Ответ: 4; .
Способ почленного логарифмирования.
Пример 4. Решим уравнение:
Решение. Перепишем это уравнение в следующем виде: или
Теперь почленно прологарифмируем это уравнение по основанию 2:
. Применяем свойства логарифмов:
Решаем это уравнение способом введения новой переменной. Получаем:
1) log2 х = 3, х1 = 8; 2) log2 х = -1, х2 = .
Выполняем проверку:
Ответ: 8; .
В практике встречаются логарифмические уравнения, содержащие логарифмы с разными
основаниями. В таких случаях применяется формула перехода к новому основанию:
Пример 5. Решим уравнение:
Решение. ОДЗ:
Используем формулу перехода к новому основанию: тогда данное
уравнение имеет вид: или
Тогда: откуда получаем, что х = 2.
Ответ: 2.
Показательно-логарифмические уравнения.
Чаще всего такие уравнения решаются способом логарифмирования обеих частей уравнения и приведением к логарифмическим уравнениям.
Пример 6. Решим уравнение:
Решение. Перепишем это уравнение в виде: Воспользуемся
основным логарифмическим тождеством , имеем:
Прологарифмируем обе части уравнения по основанию 3: Тогда
откуда: и или х1 = и х2 = 9.
Проверка:
Ответ:
При решении систем логарифмических уравнений в основном применяются те же способы, что и при решении систем алгебраических уравнений ( способы подстановки, алгебраического сложения, введения новых переменных и др.)
Пример 6. Решим систему уравнений:
Решение. Для первого уравнения применяем свойства показательной функции, а второе
уравнение потенцируем:
Введем новые переменные:
получим систему рациональных уравнений:
Решаем систему методом подстановки, получаем: а = 5 и b = 6. Тогда:
или х = 25 и у = 36.
Проверка:
Вывод: пара чисел (25;36) действительно является решением системы.
Ответ: (25;36).
Дидактический материал
Решите логарифмические уравнения:
Решите системы логарифмических уравнений:
Логарифмические неравенства
Справочные сведения
Определение. Неравенство, содержащее переменную под знаком логарифма, называется логарифмическим неравенством.
Всякое значение переменной , при котором данное логарифмическое неравенство обращается в
верное числовое неравенство, называется решением логарифмического неравенства.
Решить логарифмическое неравенство – значит найти все его решения или доказать, что их нет.
Решение логарифмических неравенств в основном сводится к решению неравенств вида
или
Для решения таких неравенств, учитывая область определения логарифмической функции и ее свойства, применяют следующие утверждения:
при а > 1 неравенство равносильно системе неравенств:
(1)
при 0 < а < 1 1 неравенство равносильно системе неравенств:
(2)
Примеры с решениями
Пример 1. Решим неравенство
Решение. Преобразуем правую часть неравенства: Здесь а = , поэтому
используем систему неравенств вида (2): или
Решением последней системы будет промежуток
Ответ:
Пример 2. Решим неравенство
Решение. Используем свойства логарифмов:
В полученном неравенстве а = 10 > 1, поэтому используем систему неравенств вида (1):
отсюда:
Изображая решение каждого неравенства системы по отдельности на координатной прямой, находим общую часть – промежуток Ответ:
Дидактический материал
Решите логарифмические неравенства:
Тест № 1
1. | Вычислите: |
2. | Найти значение выражения: |
3. | Решите уравнение: |
4. | Решите неравенство: |
5. | Решить систему уравнений |
6. | Решите уравнение: |
7. | Найдите произведение корней уравнения |
8. | Решите неравенство: |
9. | Решите неравенство: |
10. | Решить систему уравнений: |
Тест № 2
1. | Вычислите : | |
2. | Используя определение и свойства логарифмов, найдите значение выражения: | |
3. | Решите уравнение: | |
4. | Решить неравенство: | |
5. | Решить систему уравнений | |
6. | Решите уравнение: | |
7. | Найдите произведение корней уравнения: | |
8. | Решите неравенство: | |
9. | Решите неравенство: | |
10. | Решить систему уравнений | |
Тест № 3*
1. | Найти значение выражения: |
2. | Чему равно выражение: |
3. | Решите уравнение: |
4. | Решите уравнение: |
5. | Решить систему неравенств: |
6. | Найдите где х – это корень уравнения |
7. | Вычислите: |
8. | Решите уравнение: |
9. | Решите неравенство: |
10. | Решить систему неравенств: |
Код правильных ответов по теме «Логарифмы»
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Тест № 1 | C | E | D | E | B | C | E | D | C | B |
Тест № 2 | D | E | C | D | A | C | C | E | D | D |
Тест № 3* | C | A | A | E | E | E | A | A | E | E |
— объяснение и примеры
Что такое логарифм? Зачем мы их изучаем? А каковы их правила и законы?
Начнем с того, что логарифм числа «b» может быть определен как степень или экспонента, до которой должно быть возведено другое число «a», чтобы получить результат, равный числу b.
Мы можем символически представить это утверждение как;
журнал a b = n.
Точно так же мы можем определить логарифм числа как обратную его экспоненту.Например, log a b = n может быть представлен экспоненциально как; а н = б.
Таким образом, мы можем сделать вывод, что;
a n = b ⇔ журнал a b = n.
Хотя в школах изучают логарифмы для упрощения вычислений с большими числами, они по-прежнему играют важную роль в нашей повседневной жизни.
Давайте посмотрим на некоторые из этих применений логарифмов:
- Мы используем логарифмы для измерения кислотности и щелочности химических растворов.
- Измерение силы землетрясений производится по шкале Рихтера с использованием логарифмов.
- Уровень шума измеряется в дБ (децибелах) по логарифмической шкале.
- Экспоненциальные процессы, такие как распад соотношения активных изотопов, рост бактерий, распространение эпидемии среди населения и охлаждение мертвого тела, анализируются с использованием логарифмов.
- Логарифм используется для расчета периода выплаты ссуды.
- В математике логарифм используется для различения сложных задач и определения площади под кривыми.
Подобно экспонентам, логарифмы имеют правила и законы, которые работают так же, как правила экспонент. Важно отметить, что законы и правила логарифмов применяются к логарифмам с любым основанием. Однако во всех расчетах должна использоваться одна и та же база.
Мы можем использовать законы и правила логарифмов для выполнения следующих операций:
- Преобразование логарифмических функций в экспоненциальную форму.
- Дополнение
- Вычитание
- Умножение
- Дивизион
- Расширение и уплотнение
- Решение логарифмических уравнений.
Законы логарифмов
Логарифмические выражения могут быть записаны по-разному, но в соответствии с определенными законами, называемыми законами логарифмов. Эти законы могут применяться к любой базе, но при расчетах используется одна и та же база.
Четыре основных закона логарифмов включают:
Закон о правилах производства товаров
Первый закон логарифмов гласит, что сумма двух логарифмов равна произведению логарифмов.Первый закон представлен как;
⟹ журнал A + журнал B = журнал AB
Пример:
- журнал 2 5 + журнал 2 4 = журнал 2 (5 × 4) = журнал 2 20
- журнал 10 6 + журнал 10 3 = журнал 10 (6 x 3) = журнал 10 18
- log x + log y = log (x * y) = log xy
- log 4x + log x = log (4x * x) = log 4x 2
Закон о частных правилах
Вычитание двух логарифмов A и B равно делению логарифмов.
⟹ журнал A — журнал B = журнал (A / B)
Пример:
- журнал 10 6 — журнал 10 3 = журнал 10 (6/3) = журнал 10 2
- журнал 2 4x — журнал 2 x = журнал 2 (4x / x) = журнал 2 4
Закон о верховенстве власти
⟹ log A n = n log A
Пример:
- журнал 10 5 3 = 3 журнал 10 5
- 2 журнал x = журнал x 2
- 5 ln x 2 = ln x (2 * 5) = ln x 10
Изменение закона об основных правилах
⟹ журнал b x = (журнал a x) / (журнал a b)
Пример 4:
- журнал 4 16 = (журнал 16) / (журнал 4).
Правила логарифмов
Логарифмы — очень дисциплинированная область математики. Они всегда применяются в соответствии с определенными правилами и положениями.
При игре с логарифмами необходимо помнить следующие правила:
- Учитывая, что a n = b log a b = n, логарифм числа b определяется только для положительных действительных чисел.
⟹ a> 0 (a ≠ 1), a n > 0.
- Логарифм положительного действительного числа может быть отрицательным, нулевым или положительным.
Примеры
- 3 2 = 9 ⇔ лог 3 9 = 2
- 5 4 = 625 ⇔ лог 5 625 = 4
- 7 0 = 1 ⇔ лог 7 1 = 0
- 2 -3 = 1 / 8 ⇔ лог 2 ( 1 / 8 ) = -3
- 10 -2 = 0,01 ⇔ лог 10 01 = -2
- 2 6 = 64 ⇔ лог 2 64 = 6
- 3 — 4 = 1/3 4 = 1/81 ⇔ лог 3 1/81 = -4
- 10 -2 = 1/100 = 0.01 ⇔ журнал 10 01 = -2
- Логарифмические значения данного числа различны для разных оснований.
Примеры
- бревно 9 81 ≠ лог 3 81
- лог 2 16 ≠ лог 4 16
- Логарифмы с основанием 10 называются десятичными логарифмами. Когда логарифм записывается без основания индекса, мы предполагаем, что основание равно 10.
Примеры
- журнал 21 = журнал 10
- журнал 0.05 = журнал 10 05
- Логарифм по основанию «е» называется натуральным логарифмом. Константа e приблизительно равна 2,7183. Натуральные логарифмы выражаются как ln x, что совпадает с log e .
- Логарифмическое значение отрицательного числа мнимое.
- Логарифм от 1 до любого конечного ненулевого основания равен нулю.
a 0 = 1 ⟹ лог a 1 = 0.
Пример:
7 0 = 1 ⇔ лог 7 1 = 0
- Логарифм любого положительного числа по тому же основанию равен 1.
a 1 = a ⟹ log a a = 1.
Примеры
- журнал 10 10 = 1
- журнал 2 2 = 1
- Учитывая, что x = log a M, затем a log a M = a
Пример 1
Вычислите следующее выражение.
журнал 2 8 + журнал 2 4
Решение
Применяя закон правила продукта, мы получаем;
журнал 2 8 + журнал 2 4 = журнал 2 (8 x 4)
= журнал 2 32
Записываем 32 в экспоненциальной форме, чтобы получить значение его экспоненты.
32 = 2 5
Следовательно, 5 — правильный ответ
Пример 2
Журнал оценки 3 162 — журнал 3 2
Решение
Это выражение вычитания; поэтому мы применяем закон правила частного.
журнал 3 162 — журнал 3 2 = журнал 3 (162/2)
= журнал 3 81
Запишите аргумент в экспоненциальной форме
81 = 3 4
Следовательно, ответ — 4.
Пример 3
Разверните приведенное ниже логарифмическое выражение.
журнал 3 (27x 2 y 5 )
Решение
журнал 3 (27x 2 y 5 ) = журнал 3 27 + журнал 3 x 2 + журнал 3 y 5
= журнал 3 (9) + журнал 3 (3) + 2 журнал 3 x + 5log 3 y
А журнал 3 9 = 3
Получить замену.
= 3 + log 3 (3) + 2log 3 x + 5log 3 y
Пример 4
Вычислить значение журнала √2 64.
Решение
⟹ журнал √2 64 = журнал √2 (2) 6
⟹ журнал √2 64 = 6 журнал √2 (2)
⟹ журнал √2 64 = 6 журнал √2 (√2) 2
⟹ журнал √2 64 = 6 * 2 журнал √2 (√2)
⟹ журнал √2 64 = 12 * 2 (1)
⟹ журнал √2 64 = 12
Пример 5
Решить относительно x, если журнал 0.1 (0,0001) = х
Решение
⟹ лог 0,1 (0,0001) = лог 0,1 (0,1) 4
⟹ log 0,1 (0,0001) = 4log 0,1 0,1
⟹ лог 0,1 (0,0001) = 4 (1)
⟹ лог 0,1 (0,0001) = 4
Следовательно, x = 4.
Пример 6
Найдите заданное значение x, 2log x = 4log3
Решение
2logx = 4log3
Разделите каждую сторону на 2.
⟹ журнал x = (4log3) / 2
⟹ журнал x = 2log3
⟹ журнал x = log3 2
⟹ журнал x = log9
х = 9
Пример 7
Журнал вычислений 2 (5x + 6) = 5
Решение
Перепишите уравнение в экспоненциальной форме
2 5 = 5x + 6
Упростить.
32 = 5x + 6
Вычтем обе части уравнения на 6
32 — 6 = 5x + 6 — 6
26 = 5x
х = 26/5
Пример 8
Решить log x + log (x − 1) = log (3x + 12)
Решение
⇒ журнал [x (x — 1)] = журнал (3x + 12)
Отбросьте логарифмы, чтобы получить;
⇒ [x (x — 1)] = (3x + 12)
Примените свойство распределения для удаления скобок.
⇒ x 2 — x = 3x + 12
⇒ x 2 — x — 3x — 12 = 0
⇒ x 2 — 4x — 12 = 0
⇒ (x − 6) (x + 2) = 0
⇒x = — 2, x = 6
Поскольку аргумент логарифма не может быть отрицательным, то правильный ответ — x = 6.
Пример 9
Вычислить ln 32 — ln (2x) = ln 4x
Решение
ln [32 / (2x)] = ln 4x
Бросьте натуральные бревна.
[32 / (2x)] = 4x
32 / (2x) = 4x.
Перекрестное умножение.
32 = (2x) 4x
32 = 8x 2
Разделите обе стороны на 8, чтобы получить;
х 2 = 4
х = — 2, 2
Поскольку у нас не может быть логарифма отрицательного числа, то правильным ответом остается x = 2.
Практические вопросы- Анализ журнала 4 64 + журнал 4 16
- журнал 3 14−2log 3 5
- Вычислить 2 журнала 3 5 + журнал 3 40-3 журнала 3 10
- Конденсированный журнал 2 4 + лог 2 5
- Развернуть журнал 3 (xy 3 / √z)
- Сократите следующее выражение 5 ln x + 13 ln (x 3 + 5) — 1/2 ln (x + 1)
- Упростить логарифм a 28 — log a 4 как единственный логарифм
- Найдите значение журнала 5 8 + 5 (1/1000)
- Решить относительно x в логарифме 3log 5 2 = 2log 5 X
- Записать log12 + log 5 как единственный логарифм
Логарифмы — Темы в предварительном исчислении
20
Определение
Десятичный логарифм
Натуральные логарифмы
Три закона логарифмов
Доказательство законов логарифмов
Изменение базы
КОГДА МЫ ДАЕМ, например, основание 2 и показатель степени 3, тогда мы можем вычислить 2 3 .
2 3 = 8.
И наоборот, если даны основание 2 и его степень 8 —
2 ? = 8
— тогда какой показатель даст 8?
Эта экспонента называется логарифмом. Мы называем показатель степени 3 логарифмом 8 с основанием 2. Запишем
3 = журнал 2 8.
Мы пишем основание 2 как нижний индекс.
3 — это показатель степени , до которого нужно поднять 2, чтобы получить 8.
Логарифм — это показатель степени.
с
10 4 = 10 000
, затем
журнал 10 10,000 = 4.
«Логарифм 10 000 по основанию 10 равен 4.»
4 — это показатель степени , до которого необходимо поднять 10, чтобы получить 10 000.
«10 4 = 10 000» называется экспоненциальной формой.
«log 10 10,000 = 4″ называется логарифмической формой.
Вот определение:
журнал b x = n означает b n = x .
Основание с этой экспонентой дает x .
Пример 1. Запишите в экспоненциальной форме: log 2 32 = 5.
Ответ . 2 5 = 32,
| Пример 2.Запишите в логарифмической форме: 4 −2 = | . 1 16 | . |
| Ответ. журнал 4 | 1 16 | = −2. |
Задача 1. Какие числа имеют отрицательный логарифм?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
Правильные дроби.
Урок 20 арифметики
Пример 3. Анализ журнала 8 1.
Ответ . 8 до какой степени дает 1? 8 0 = 1.
журнал 8 1 = 0.
Мы можем заметить, что по любому основанию логарифм 1 равен 0.
Пример 4.Журнал оценки 5 5.
Ответ . 5 с каким показателем даст 5? 5 1 = 5. Следовательно,
журнал 5 5 = 1.
В любом основании логарифм самого основания равен 1.
Пример 5. журнал 2 2 м =?
Ответ . 2 увеличенный до какой степени даст 2 м ? м , очевидно.
бревно 2 2 м = м .
Следующее важное формальное правило, действительное для любой базы b :
Это правило воплощает сам смысл логарифма. x — справа — это показатель степени , до которого необходимо поднять основание b , чтобы получить b x .
Правило также показывает, что экспоненциальная функция b x является обратной функцией log b x .Мы увидим это в следующей теме.
| Пример 6. Анализировать журнал 3 | 1 9 | . |
| Ответ. | 1 9 | равно 3 с какой степенью? | 1 9 | = 3 −2 |
| журнал 3 | 1 9 | = | журнал 3 3 −2 = −2. |
Сравните предыдущее правило.
Пример 7. Журнал 2 . 25 =?
Ответ . . 25 = ¼ = 2 2 . Следовательно,
журнал 2 . 25 = журнал 2 2 −2 = −2.
Пример 8. журнал 3 =?
Ответ. = 3 1/5 .(Определение рациональной экспоненты.) Следовательно,
журнал 3 = журнал 3 3 1/5 = 1/5.
Задача 2. Запишите каждое из следующих утверждений в логарифмической форме.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
| a) b n = x | журнал b x = n | б) 2 3 = 8 | журнал 2 8 = 3 | |
| c) 10 2 = 100 | журнал 10 100 = 2 | г) 5 −2 = 1/25. | журнал 5 1/25 = −2. | |
Задача 3. Запишите каждое из следующих утверждений в экспоненциальной форме.
| a) журнал b x = n | b n = x | б) журнал 2 32 = 5 | 2 5 = 32 | |
| c) 2 = журнал 8 64 | 8 2 = 64 | г) лог 6 1/36 = −2 | 6 −2 = 1/36 | |
Проблема 4.Оцените следующее.
| а) журнал 2 16 | = 4 | б) журнал 4 16 | = 2 | |
| c) бревно 5 125 | = 3 | г) бревно 8 1 | = 0 | |
| e) журнал 8 8 | = 1 | f) журнал 10 1 | = 0 | |
Проблема 5.Какой номер n ?
| a) журнал 10 n = 3 | 1000 | b) 5 = журнал 2 n | 32 | |
| c) журнал 2 n = 0 | 1 | d) 1 = журнал 10 n | 10 | |
| e) журнал n | 1 16 | = −2 | 4 | f) журнал n | 1 5 | = -1 | 5 | |
| г) бревно 2 | 1 32 | = n | −5 | ч) журнал 2 | 1 2 | = n | -1 | |
Проблема 6.журнал b b x = х
Проблема 7. Оцените следующее.
| а) журнал 9 | 1 9 | = лог 9 9 -1 = -1 |
| б) бревно 9 | 1 81 | = −2 | в) журнал 2 | 1 4 | = −2 | |||
| г) бревно 2 | 1 8 | = −3 | e) журнал 2 | 1 16 | = -4 | |||
| е) журнал 10 .01 | = −2 | г) журнал 10 .001 | = −3 | |
| h) бревно 6 | = 1/3 | i) журнал b | = 3/4 | |
Десятичный логарифм
Система десятичных логарифмов имеет основу 10.Когда база не указана,
журнал 100 = 2
, то подразумевается система десятичных логарифмов.
Вот степени десяти и их логарифмы:
| Полномочия 10: | 1 1000 | 1 100 | 1 10 | 1 | 10 | 100 | 1000 | 10 000 | ||||||||
| Логарифмы: | −3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | ||||||||
Логарифмы заменяют геометрический ряд арифметическим.
Проблема 8. log 10 n =? № . База 10.
Задача 9. log 58 = 1,7634. Следовательно, 10 1.7634 =?
58. 1,7634 — десятичный логарифм 58. Когда 10 возводится в этот показатель, получается 58.
Задача 10. Журнал (журнал x ) = 1. Какое число x ?
log a = 1, подразумевает a = 10, что является основанием.
Пример 4.
Следовательно, log (log x ) = 1 означает log x = 10. Поскольку 10 является основанием,
x = 10 10 = 10 000 000 000
Натуральные логарифмы
В системе натуральных логарифмов в основе лежит число e . ( e назван в честь швейцарского математика 18 века Леонарда Эйлера.) e — база, используемая в исчислении.Его называют «натуральной» базой из-за определенных технических соображений.
e x имеет простейшую производную. Урок 14 из Подход к исчислению .)
e можно вычислить из следующих рядов, выраженных факториалами:
| и | = 1 + | 1 1! | + | 1 2! | + | 1 3! | + | 1 4! | +.. . |
e — иррациональное число; его десятичное значение примерно
2 . 71828182845904.
Чтобы указать натуральный логарифм числа, мы пишем «ln».
ln x означает журнал e x .
Проблема 11. Какой номер ln e ?
ln e = 1.Логарифм самого основания всегда равен 1. e — основание.
Пример 4.
Задача 12. Запишите в экспоненциальной форме (Пример 1): y = ln x .
e y = x .
е — база.
Три закона логарифмов
1 . log b xy = log b x + log b y
« Логарифм произведения равен сумме
логарифмов каждого множителя. «
| 2 . журнал b | = бревно b x — лог b y |
« Логарифм частного равен логарифму числителя
минус логарифм знаменателя. »
3 . журнал b x n = n журнал b x
« Логарифм x с рациональным показателем равен
показателю степени, умноженному на логарифм.»
Мы докажем эти законы ниже.
| Пример 9. Примените законы логарифмов к логарифму | . abc 2 d 3 | . |
Ответ. Согласно первым двум законам,
| журнал | abc 2 d 3 | = | журнал ( abc 2 ) — журнал d 3 |
| = | журнал a + журнал b + журнал c 2 — журнал d 3 | ||
| = | журнал a + журнал b + 2 журнал c -3 журнала d , | ||
по третьему закону.
Ответ выше показывает полные теоретические шаги. Однако на практике нет необходимости писать строку
| журнал | abc 2 d 3 | = | журнал ( abc 2 ) — журнал d 3 | . |
Студент должен иметь возможность сразу перейти к следующей строке —
| журнал | abc 2 d 3 | = | журнал a + журнал b + журнал c 2 — журнал d 3 |
— если не до самой последней строки
| лог | abc 2 d 3 | = | журнал a + журнал b + 2 журнал c -3 журнала d . |
| Пример 10. Применить законы логарифмов к логарифму | z 5 | . |
| Ответ. | журнал | z 5 | = журнал x + журнал — журнал z 5 |
Теперь = y ½ .(Урок алгебры 29.) Следовательно, согласно третьему закону:
| журнал | z 5 | = журнал x + ½ журнала y — 5 журнала z . |
Пример 11. Используйте законы логарифмов, чтобы переписать ln.
Решение .
| пер. | = | ln (sin x ln x ) ½ |
| = | ½ ln (sin x ln x ), 3-й закон | |
| = | ½ (ln sin x + ln ln x ), 1-й закон. | |
Обратите внимание, что множители sin x ln x являются аргументами функции логарифмирования.
Пример 12. Решите это уравнение для x :
.| журнал 3 2 x + 5 | = | 1 |
| Решение . Согласно 3-му Закону мы можем написать | ||
| (2 x + 5) журнал 3 | = | 1. |
| Теперь журнал 3 — это просто число. Следовательно, при раздаче лога 3, | ||
| 2 x · журнал 3 + 5 журнал 3 | = | 1 |
| 2 x · журнал 3 | = | 1-5 журнал 3 |
| x | = | 1-5 журнала 3 2 журнала 3 |
С помощью этой техники мы можем решить уравнения, в которых неизвестное появляется в экспоненте.
Задача 13. Используйте законы логарифмов, чтобы переписать следующее.
| а) журнал | ab c | = журнал a + журнал b — журнал c | |
| б) журнал | ab 2 c 4 | = журнал a + 2 журнала b — 4 журнала c | |
| c) журнал | z | = 1/3 журнала x + 1/2 журнала y — журнал z | |
d) ln (sin 2 x ln x ) = ln sin 2 x + ln ln x = 2 ln sin x + ln ln x
| д) пер | = ½ ln (cos x · x 1/3 ln x ) |
| = ½ (ln cos x + 1/3 ln x + ln ln x ) | |
| f) ln ( a 2 x — 1 b 5 x + 1 ) | = ln a 2 x — 1 + ln b 5 x + 1 |
| = (2 x — 1) ln a + (5 x + 1) ln b | |
Проблема 14.Решите относительно x .
| пер 2 3 x + 1 | = | 5. |
| (3 x + 1) пер 2 | = | 5 |
| 3 x пер 2 + пер 2 | = | 5 |
| 3 x ln 2 | = | 5 — пер 2 |
| x | = | 5 — пер 2 3 пер 2 |
| Проблема 15.Докажите: −ln x | = ln | 1 x | . |
| −ln x = (−1) ln x | = | пер. | x -1 , | Третий закон |
| = | пер. | 1 x | ||
Доказательство законов логарифмов
Законы логарифмов действительны для любого основания.Мы докажем их для основания e, то есть для y = ln x .
1 . ln ab = ln a + ln b .
Функция y = ln x определена для всех положительных действительных чисел x . Следовательно, существуют действительные числа p и q , такие что
p = ln a и q = ln b .
Это означает
a = e p и b = e q .
Следовательно, по правилам экспонент
ab = e p · e q = e p + q .
И, следовательно,
ln ab = ln e p + q = p + q = ln a + ln b .
Что мы и хотели доказать.
Аналогичным образом доказывается второй закон. Вот 3-й:
3 . ln a n = n ln a .
Существует действительное число p такое, что
p = ln a ;
то есть
a = e p .
И правила экспонент действительны для всех рациональных чисел n (Урок 29 алгебры; иррациональное число — это предел последовательности рациональных чисел). Следовательно,
a n = e pn .
Это означает
ln a n = ln e pn = pn = NP = n ln a .
Это то, что мы хотели доказать.
Изменение базы
Скажем, мы знаем значения логарифмов по основанию 10, но не, например, по основанию 2. Затем мы можем преобразовать логарифм с основанием 10 в единицу с основанием 2 — или с любым другим основанием — понимая, что значения будет пропорциональным.
Каждое значение в базе 2 будет отличаться от значения в базе 10 той же константой k .
Теперь, чтобы найти эту константу, мы знаем, что
Следовательно, положив выше x = 2:
Это означает
Следовательно,
То есть
Зная значения логарифмов по основанию 10, мы можем таким образом вычислить их значения по основанию 2.
В общем, тогда, если мы знаем значения в базе a , то константа пропорциональности при переходе к основанию b — это , обратная его логарифму в базе a .
Задача 16. Напишите правило перехода к основанию 8 от основания e .
Следующая тема: Логарифмические и экспоненциальные функции
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Примеры логарифмов и практические задачи
- Домой
- Математика
- Рабочие листы по математике
Возьмем действительное число x, а b x представляет собой уникальное действительное число. Если мы напишем a = b x , то показатель степени x будет логарифмом a с логарифмической базой b, и мы можем записать a = b x как
журнал b a = x
Запись x = log b a называется Logarithm Notation .
Перед переходом к примеру посмотрите на эти правила логарифмирования и калькулятор логарифмов.
Пример записи логарифма:
(i) 3 = log 4 64 эквивалентно 4 3 = 64
(ii) 1/2 = log 9 3 эквивалентно √9 = 3
Примеры логарифмов
1. Измените логарифм ниже 25 5 = 1/2 на экспоненциальную форму.
журнал 25 5 = 25 1/2 = 5
2.Измените 1/8 = 8 -1 на логарифмическую запись.
Решение:
1/8 = 8 -1 = лог 8 8
3. Оцените значение журнала 4 8
Решение:
x = журнал 4 8
Тогда мы можем сказать
4 x = 8 = 2 3 , извлечение квадратного корня с обеих сторон
2 x = 2 3/2
x = 3/2
4. Найдите значение x из журнала x 100 = 2
решение:
журнал b 1000 = 3
Мы можем записать это как,
б 3 = 1000
b 3 = 10 3
Итак, из приведенного выше уравнения
б = 10
5.Найдите значение для журнала 5 8 + 5 (1/1000)
Решение:
журнал 5 8 + 5 (1/1000) = журнал 5 (8 x 1/1000)
= журнал 5 (1/125)
= журнал 5 (1/5) 3
= журнал 5 (5) -3
= -3log 5 (5)
= -3 х 1
= -3
6. Решить 2log 5 3 X log 9 x + 1 = log 5 3
Решение:
Мы можем переписать приведенное выше уравнение в формате ниже
=> журнал 5 3 2 X журнал 9 x = журнал 5 3 — 1
=> журнал 5 9 X журнал 9 x = журнал 5 3 — журнал 5 5
=> журнал 5 9 X журнал 9 x = журнал 5 (3/5)
Используя изменение основного правила в левой части, мы получаем
=> журнал 5 x = журнал 5 (3/5)
Значение X = 3/5
Практические задачи логарифмирования:
1.Найдите логарифм для следующих уравнений
(i) журнал 5 125
(ii) журнал 2 (2√2)
(iii) журнал 1/3 27
2. Найдите значение x в следующих уравнениях
(i) журнал x 0,001 = -2
(ii) √log 2 x = 3
(iii) 2 журнала 9 x = 1
3. Упростите следующее выражение до одного члена.
(i) журнал 10 2 + журнал 10 10
(ii) 3log 3 2 + 4-8 log 3 3
(iii) журнал 10 5 + журнал 10 20 — журнал 10 24 + журнал 10 25-4
4.Решите следующее уравнение логарифма
(i) 3log 5 2 = 2log 5 x
(ii) xlog 16 8 = -1
(iii) журнал 5 (10 + x) = журнал 5 (3 + 4x)
Логарифмическая функция: определение и примеры — видео и стенограмма урока
Логарифмы:
Логарифм — это показатель степени. Любое экспоненциальное выражение можно переписать в логарифмической форме. Например, если у нас 8 = 23, то основание равно 2, показатель степени равен 3, а результат равен 8.Это можно переписать в логарифмической форме как
3 = журнал2 8.
Обратите внимание, как были переставлены числа. Нижний индекс логарифма — это основание, число в левой части уравнения — это показатель степени, а число рядом с логарифмом — это результат (также называемый аргументом логарифма). Теперь попробуйте переписать некоторые из следующего в логарифмической форме:
упражнение:
Запишите каждое из следующего в логарифмической форме:
1.25 = 52
2. 64 = 43
3. 1 = 50
4. 1/4 = 2-2
Ответы:
1,2 = log5 25
2. 3 = log4 64
3. 0 = log5 1
4.-2 = log2 1/4
Теперь мы также можем начать с выражения в логарифмической форме и переписать его в экспоненциальной форме. Например, выражение 3 = log5 125 можно переписать как 125 = 53.
Здесь 5 — основание, 3 — показатель степени и 125 — результат. Теперь попробуйте следующее:
Упражнений:
Перепишите каждое из следующего в экспоненциальной форме:
1.4 = log2 16
2. 2 = log3 9
3. 1/2 = log9 3
4. 3/2 = log4 8
Ответы:
1. 24 = 16
2. 32 = 9
3. 91/2 = 3
4. 43/2 = 8
Теперь попробуйте решить несколько уравнений. Например, y = log2 8 можно переписать как 2y = 8.
Поскольку 8 = 23, получаем y = 3.
Как упоминалось в начале этого урока, y представляет собой показатель степени, а также логарифм. Следовательно, логарифм — это показатель степени.0 → у = 0,
3. y = log9 27 → 9y = 27 → (32) y = 33 → 32y = 33 → 2y = 3 → y = 3/2
4. y = log4 1/16 → 4y = 1/16 → 4y = 4-2 → y = -2
Графики логарифмических функций
Рассмотрим логарифмическую функцию y = log2 (x).
Мы можем проанализировать его график, изучив его связь с соответствующей экспоненциальной функцией y = 2x.
Обратите внимание, что
Так как 20 = 1
(1, 0) находится на графике y = log2 (x) \ \ [0 = log2 (1)]
и
(0, 1) \ \ находится на графике \ y = 2x
Так как \ 22 = 4
(4, 2) \ \ находится на графике \ y = log2 (x) \ \ [2 = \ log2 (4)]
и
(2, 4) \ находится на графике \ y = 2x
Поскольку \ 23 = 8
(8, 3) \ находится на графике \ y = log2 (x) \ \ [3 = log2 (8)]
и
(3, 8) \ \ находится на графике \ y = 2x
}]
В общем, это верно, (a, b) находится на графике y = 2x тогда и только тогда, когда (b, a) находится на графике y = log2 (x).x путем отражения относительно линии y = x.
Это отношение между функцией и ее обратной в целом.
График y = logb (x) получается из графика y = bx путем отражения относительно линии y = x.
График ниже показывает, что для функций y = 2x и y = log2 (x)
Использование логарифмов в реальном мире — лучшее объяснение
Логарифмы везде. Вы когда-нибудь использовали следующие фразы?
- 6 цифр
- Двузначные цифры
- По порядку величины
- Процентная ставка
Вы описываете числа в терминах степени 10, логарифма.А процентная ставка — это логарифм роста инвестиций.
Удивлены, что логарифмы так распространены? Я тоже. Большинство попыток Math In the Real World ™ указывают на логарифмы в какой-то загадочной формуле или делают вид, что мы геологи увлечены шкалой Рихтера. «Ученые заботятся о бревнах, и вы должны тоже. Кроме того, можете ли вы представить мир без цинка?»
Нет, нет, нет, нет, нет, нет! (Мама миа!)
Math выражает концепции с помощью таких обозначений, как «ln» или «log».Найти «математику в реальном мире» означает столкнуться с идеями в жизни и увидеть, как можно записать с обозначениями. Не ищите буквальных символов! Когда вы в последний раз писали знак деления? Когда вы в последний раз нарезали еду?
Хорошо, хорошо, мы поняли: что такое логарифмы?
Логарифмы находят причину эффекта, т.е. вход для некоторого выхода
Обычный «эффект» — это рост чего-то, например, переход от \ $ 100 до \ $ 150 за 5 лет.Как это случилось? Мы не уверены, но логарифм находит возможную причину: постоянный возврат ln (150/100) / 5 = 8,1% будет учитывать это изменение. Возможно, это не настоящая причина (весь ли рост произошел в последний год?), Но это плавное среднее значение, которое мы можем сравнить с другими изменениями.
Кстати, понятие «причина и следствие» имеет нюансы. Почему 1000 больше 100?
- 100 — это 10, которые выросли за 2 периода времени (10 долларов * 10 долларов)
- 1000 — это 10, которые выросли сами по себе за 3 периода (10 $ * 10 * 10 $)
Мы можем думать о числах как о выходах (1000 — это «1000 выходов») и входах («Во сколько раз нужно вырасти 10, чтобы получить эти выходы?»).Итак,
1000 выходов> 100 выходов
потому что
3 входа> 2 входа
Или другими словами:
журнал (1000)> журнал (100)
Почему это полезно?
Логарифмы помещают числа в удобную для человека шкалу.
Большие числа ломают нам мозг. Миллионы и триллионы «действительно большие», хотя миллион секунд — это 12 дней, а триллион секунд — это 30 000 лет.80 $ = количество молекул во Вселенной
Шкала от 0 до 80 перевела нас от одного объекта к количеству объектов во Вселенной. Не слишком потрепанный.
Умножение логарифмов в виде шагов
Логарифмы описывают изменения в терминах умножения: в приведенных выше примерах каждый шаг в 10 раз больше. С натуральным логарифмом каждый шаг в «e» (2,71828 …) раз больше.
Когда мы имеем дело с серией умножений, логарифмы помогают «подсчитывать» их, точно так же, как сложение подсчитывает для нас, когда добавляются эффекты. 5 $) и 100000 получаем результат из 6 цифр.Говорить о «6» вместо «Сто тысяч» — это суть логарифмов. Это дает приблизительное ощущение масштаба, не вдаваясь в детали.
Бонусный вопрос: как бы вы описали 500 000? Сказать «шестизначный» вводить в заблуждение, потому что шестизначное число часто означает что-то близкое к 100000. Подойдет ли «фигура 6,5»?
Не совсем. В нашей голове 6.5 означает «половину» между 6 и 7 цифрами, но это мышление сумматора. В логарифмах «.5» означает половину умножения, т.е..5 $ означает, что квадратный корень из 9 — 3 равен половине умножения, потому что он 1 к 3 и 3 к 9).
Взяв log (500 000), мы получаем 5,7, добавляем 1 для дополнительной цифры, и мы можем сказать, что «500 000 — это число из 6,7 цифр». Попробуйте здесь:
По порядку величины
Мы, фанаты, любим эту фразу. Это означает примерно «10-кратную разницу», но просто звучит круче, чем «на 1 цифру больше».
В компьютерах, где все считается битами (1 или 0), каждый бит имеет эффект удвоения (не 10x).16 $ ~ 65 536 раз больше памяти, которую можно адресовать.
Процентные ставки
Как определить темпы роста? Страна не намерена расти на 8,56% в год. Вы смотрите на ВВП в один год и на ВВП в следующий, и берете логарифм, чтобы найти неявных темпов роста .
Две мои любимые интерпретации натурального логарифма (ln (x)), то есть натурального логарифма 1,5:
- При 100% росте, сколько времени вам нужно, чтобы достичь 1.5? (.405, меньше половины периода времени)
- Если принять 1 единицу времени, как быстро вам нужно вырасти до 1,5? (40,5% в год, непрерывно начисляется)
Логарифмы — это то, как мы определяем, насколько быстро мы растем.
Шкала измерения: Google PageRank
Google присваивает каждой странице в Интернете оценку (PageRank), которая является приблизительной мерой авторитета / важности. Это логарифмическая шкала, которая в моей голове означает «PageRank подсчитывает количество цифр в вашей оценке».4 $ = 10000).
Грубо говоря, у меня бывает около 7000 посещений в день. Используя свои математические вычисления, я могу предположить, что CNN получает около 7000 * 10 000 = 70 миллионов посещений в день. (Как я это сделал? В голове я думаю, что $ 7k * 10k = 70 * k * k = 70 * M $). У них может быть в несколько раз больше (100M, 200M), но, вероятно, не до 700M.
Google передает много информации с очень приблизительной шкалой (1-10).
Шкала измерения: Рихтер, децибел и т. Д.
Вздох. Мы находимся в типичном примере «логарифмов из реального мира»: шкале Рихтера и децибелах.Идея состоит в том, чтобы поместить события, которые могут сильно различаться (землетрясения), в единую шкалу с небольшим диапазоном (обычно от 1 до 10). Как и в случае с PageRank, каждое увеличение на 1 пункт означает 10-кратное повышение мощности. Самое сильное землетрясение, зарегистрированное людьми, произошло 9,5 балла; Удар на полуострове Юкатан, который, вероятно, привел к вымиранию динозавров, составил 13.
Децибелы аналогичны, но могут быть отрицательными. Звуки могут варьироваться от очень тихих (пиндроп) до очень громких (самолет), и наш мозг может все это обработать. На самом деле звук двигателя самолета в миллионы (миллиарды, триллионы) раз мощнее пиндропа, и неудобно иметь шкалу от 1 до миллиарда.Журналы хранят все в разумном масштабе.
Логарифмические графики
Вы часто будете видеть элементы, нанесенные на «логарифмическую шкалу». В моей голове это означает, что одна сторона считает «количество цифр» или «количество умножений», а не само значение. Опять же, это помогает отображать сильно различающиеся события по единой шкале (от 1 до 10, а не от 1 до миллиардов).
Закон Мура — отличный пример: мы удваиваем количество транзисторов каждые 18 месяцев (изображение любезно предоставлено Википедией).
Отличительной особенностью графиков в логарифмическом масштабе является то, что экспоненциальные изменения (скорости процессора) отображаются в виде прямой линии. Рост в 10 раз в год означает, что вы неуклонно продвигаетесь по «цифровой» шкале.
Вперед и вверх
Если концепция хорошо известна, но не пользуется большой популярностью, это означает, что нам нужно развивать нашу интуицию. Найдите аналогии, которые работают, и не соглашайтесь на помойку из учебника. В голове:
- Логарифмы найдите основную причину эффекта (см. Рост, найдите процентную ставку)
- Они помогают подсчитывать умножения или числа с бонусом в виде частичного подсчета (500k — это 6.0 = 1?)
- Использование логарифмов в реальном мире
- Как мыслить экспонентами и логарифмами
- Что такое дискретное и непрерывное развитие?
- Что на самом деле означает показатель степени?
- Q: Почему е особенное? (2,718 …, а не 2, 3,7 или другое число?)
- По возможности изолируйте экспоненциальные выражения
- Возьмите логарифм обеих сторон
- Используйте свойство экспоненты для логарифмов, чтобы извлечь переменную из экспоненты
- Используйте алгебру, чтобы найти переменную. {{x}})}}} = {ln {{({10})}}} [/ латекс]
Использование свойства экспоненты для журналов, [латекс] \ displaystyle {x} {ln {{({2})}}} = {ln {{({10})}}} [/ latex] Теперь делим на ln (2), [латекс] \ displaystyle {x} = \ frac {{{ln {{({10})}}}}} {{{ln {{({2})}}}}} примерно {2.861} [/ латекс] Обратите внимание, что этот результат совпадает с результатом, который мы получили с помощью изменения базовой формулы.
Пример 2
В первом разделе мы спрогнозировали численность населения (в миллиардах) Индии
t лет после 2008 года с помощью функции f ( t ) 1,14 (1 + 0,0134) t . Если население продолжит следовать этой тенденции, когда оно достигнет 2 миллиардов?Нам нужно найти
t так, чтобы f (t) = 2[латекс] \ displaystyle {2} = {1.{{t}})}}} [/ латекс] Примените свойство экспоненты к правой стороне [латекс] \ displaystyle {ln {{(\ frac {{2}} {{1.14})}}} = {t} {ln {{({1.0134})}}} [/ латекс] Разделите обе стороны на ln (1,0134) [латекс] \ displaystyle {t} = \ frac {{{ln {{(\ frac {{2}} {{1.14}})}}}}} {{{ln {{({1.0134}) }}}}} приблизительно {42.23} {mathtt {{y}}} {mathtt {{e}}} {mathtt {{a}}} {mathtt {{r}}} {mathtt {{s}}} [ / латекс] Если этот рост продолжится, модель предсказывает, что население Индии достигнет 2 миллиардов примерно через 42 года после 2008 года или примерно в 2050 году.
Попробовать 1
Решить 5 (0,93)
x = 10.Помимо решения экспоненциальных уравнений, логарифмические выражения распространены во многих физических ситуациях.
Пример 3
В химии pH — это мера кислотности или основности жидкости. PH связан с концентрацией ионов водорода, [
H + ], измеренной в молях на литр, уравнением p H = –log ([ H + ]).Если концентрация жидкости составляет 0,0001 моль на литр, определите pH.
Определение концентрации ионов водорода в жидкости с pH 7.
Чтобы ответить на первый вопрос, мы вычисляем выражение –log (0,0001). Хотя мы могли бы использовать для этого наши калькуляторы, они нам здесь не нужны, поскольку мы можем использовать обратное свойство журналов:
–log (0,0001) = –log (10
–4 ) = — (- 4) = 4Чтобы ответить на второй вопрос, нам нужно решить уравнение 7 = –log ([
H + ]).Начните с выделения логарифма на одной стороне уравнения, умножив обе части на –1: –7 = log ([ H + ])Переписывание в экспоненциальную форму дает ответ [
H + ] = 10 –7 = 0,0000001 моль на литр.Логарифмы также предоставляют нам механизм для поиска моделей непрерывного роста для экспоненциального роста с учетом двух точек данных.
Пример 4
Население вырастает со 100 до 130 за 2 недели.{{{r} {2}}})}}} [/ латекс]
[латекс] \ displaystyle {ln {{({1.3})}}} = {2} {r} [/ latex] [латекс] \ displaystyle {r} = \ frac {{{ln {{({1.3})}}}} {{2}} приблизительно {0,1312} [/ latex] Это население растет с постоянной скоростью 13,12% в неделю.
В общем, мы можем связать стандартную форму экспоненты с формой непрерывного роста, отметив (используя
k для представления скорости непрерывного роста, чтобы избежать путаницы с использованием r двумя разными способами в одной и той же формуле) :a (1 + r ) x = ae kx
(1 +
r ) x = e kx1 +
r = e kИспользуя это, мы видим, что всегда можно преобразовать из формы непрерывного роста экспоненты в стандартную форму и наоборот.Помните, что скорость непрерывного роста
k представляет собой номинальную скорость роста без учета эффектов непрерывного начисления процентов, а r представляет собой фактическое увеличение в процентах за одну единицу времени (одна неделя, один год и т. Д.).Пример 5
Продажи компании можно смоделировать с помощью функции
S ( t ) = 5000 e 0,12 t , при этом t измеряются в годах. Найдите годовой темп роста.Принимая во внимание, что 1 +
r = e k , тогда r = e 0,12 — 1 = 0,1275, поэтому годовой темп роста составляет 12,75%. Функцию продаж также можно записать в виде S ( t ) = 5000 (1 + 0,1275) t .- Решение экспоненциальных уравнений
Попробовать сейчас Ответы
[латекс] \ displaystyle \ frac {{{ln {{({2})}}}}} {{ln {{({0.
3. Правила регистрации
М. Борна
Поскольку логарифм — это просто показатель степени , который просто записывается в строку, мы ожидаем, что законы логарифма будут работать так же, как правила для показателей степени, и, к счастью, они работают. (7 + x)`
Примечание 2: Этот вопрос — , а не , то же самое, что и `log_7 x`, что означает« логарифм x с основанием «7», что совсем другое.
2. Используя калькулятор, покажите, что
`журнал (20/5) = журнал 20 — журнал 5`.
Ответ
На этот раз я использую числа, чтобы вы убедились, что закон журнала работает.
LHS
`= журнал (20/5)`
`= журнал 4`
`= 0.60206` (с помощью калькулятора)
Сейчас
правая
`= журнал 20 — журнал 5`
`= 1,30103 — 0.5 = 5 журналов x`
Мы выразили его как кратное логарифму, и оно больше не включает показатель степени.
Примечание 1: Каждое из следующих значений равно 1:
журнал 6 6 = журнал 10 10 = журнал x x = журнал a a = 1
Эквивалентные утверждения с использованием обыкновенных степеней следующие:
6 1 = 6
10 1 = 10
x 1 = x
a 1 = a
Примечание 2: Все следующие значения эквивалентны «0»:
журнал 7 1 = журнал 10 1 = журнал e 1 = журнал x 1 = 0
Эквивалентные показатели в экспоненциальной форме:
7 0 = 1
10 0 = 1
e 0 = 1
x 0 = 1
Упражнения
1.3) `
`= 1 / 3log_3 (y) -3 log_3 (2)`
2. Экспресс
2 журнала e 2 + 3 журнала e n
как логарифм одной величины.
Ответ
Применяя законы логарифма, имеем:
2 журнала e 2 + 3 журнала e n
= журнал e 4 + журнал e n 3
= журнал e 4 n 3
Примечание: Логарифм по основанию e — очень важный логарифм.(3 // 4) `
Итак, `x = 3/4`.
Следовательно,
`log_3root (4) 27 = 3/4`
4. Решите относительно y в терминах x :
журнал 2 x + журнал 2 y = 1
Ответ
Используя первый логарифмический закон, мы можем написать:
журнал 2 xy = 1
Тогда xy = 2 1
Так
`y = 2 / x`