Примеры нахождение области определения функции: Как найти область определения функции?

alexxlab / / Разное

что это значит, как найти область определения по графику

Что значит найти область определения функции

В том случае, когда имеется некое значение х из какого-то множества, и для него определено число у, то в алгебре говорят, что на рассматриваемом множества задана функция. При этом х играет роль независимой переменной или аргумента. Число у является зависимой переменной или функцией.

В математике существует функциональная зависимость между переменными у и х, которую можно проследить, если построить график. Данное утверждение принято записывать с помощью букв таким образом:

y = f(x)

Определение 1

Функция представляет собой соответствие между двумя множествами, где каждый элемент одного множества соответствует одному элементу из другого множества.

Определение 2

Область определения функции является множеством, на котором эта функция задана и имеет определенное значение в каждой из его точек.

Предположим, что имеется множество Х, на котором задана некая функция. В том случае, когда эта функция является отображением множества Х в другое множество, рассматриваемое множество Х представляет собой область определения или область задания данной функции.

Представим, что задана некая функция f, являющаяся отображением множества Х в Y. Это можно записать таким образом:

f:X→Y

Тогда множество X представляет собой область определения или область задания функции f. Область определения обозначают таким образом: D(f). Возможны и другие варианты, с помощью которых может обозначаться область определения функции: dom f.

В некоторых случаях можно встретить задачи на определение функции на подмножестве D какого-то множества X. Тогда множество Х называют областью отправления функции f.

В качестве наглядного примера вычисления области определения можно рассмотреть числовые функции, а также несложные понятия меры и функционала.

Определение 3

Числовые функции относятся к следующим классам:

  • вещественнозначные функции вещественного переменного в виде f:ℝ→ R;
  • комплекснозначные функции комплексного переменного вида f:ℂ→ C при ℝ  и ℂ.

Они обозначают множества вещественных и комплексных чисел соответственно.

Рассмотрим тождественное отображение. При этом можно наблюдать совпадение области определения функции f(x)=x и области отправления ℝ или mathbbC.

Попробуем выполнить поиск областей определения, характерных для разных типов функций. Начнем с гармонической функции в виде формулы:

f(x)=1/x

В этом случае областью определения будет называться комплексная плоскость за исключением нуля:

 dom f= C∖{0},

Заметим, что записанное соотношение не позволяет определить значение в виде некого числа для функции в нуле.

Дробно-рациональная функция имеет следующий вид:

f(x)= a0+a1x+…+amxmb0+b1x+…+bnxn

Областью определения дробно-рациональной функции является вещественная прямая, либо комплексная плоскость. Исключение представляет собой конечное количество точек, являющихся корнями следующего уравнения:

b0+b1x+…+bnxn=0.

Данные точки носят название полюсов функции f.

Таким образом, значение функции f(x)=2xx2-4 определено в каждой из точек, в которых знаменатель отличен от нуля. Условие можно записать в виде:

x2-4≠0.

В результате dom f включает в себя множество из всех действительных (или комплексных) чисел, за исключением 2 и -2.

В том случае, когда любая точка из области определения функции представляет собой какое-то множество, к примеру, подмножество рассматриваемого множества, принято говорить, что задана функция множества.

Определение 4

Мера является примером функции, область определения которой представляет собой некую совокупность подмножеств рассматриваемого множества, например, кольцо или полукольцо множеств.

В качестве примера можно называть определенный интеграл. Эта функция является функцией ориентированного промежутка.

Предположим, что имеется некое семейство отображений из множества Х в множество ℝ:

 F={f∣f:X→ R}

В таком случае, допустимо записать следующее соотношение:

F: F→ R.

Данное выражение является функционалом.

Представим, что зафиксирована какая-то произвольная точка:

x0∈ X

Тогда допустимо определить функцию:

F(f)=f(x0).

Рассматриваемая функция принимает в определенной точке f значение, аналогичное тому, которое принимает сама функция f в точке x0x0.

Что указывает на возможное ограничение области определения

Представим, что требуется определить все значения х, которые допустимы в случае некой функции. Наиболее обширным комплексом значений чаще всего является множество действительных чисел, то есть от -∞ до +∞.

С математической точки зрения задачу можно решить в два шага:

  • определение в функции недопустимых операций при неких значениях х;
  • вычисление х таких, которые не приводят к выполнению недопустимых операций.

Существуют действия с принципиальными ограничениями. Именно по их наличию можно определить возможное ограничение области определения функции. Перечислим их:

  1. Деление, дробь. Запрещено выполнять деление на ноль.
  2. Извлечение корня. Запрещено выполнять извлечение корня четной степени из чисел со знаком минуса.
  3. Логарифмы. При logab=c,а>0,a≠1,b>0.
  4. Тригонометрия. Не допустимы значения углов, для которых тангенс и котангенс отсутствуют, ограничения на выражения под знаком арксинуса, арккосинуса.

Область определения показательной и логарифмической функции

Показательная функция имеет следующий вид:

y=ax

Здесь переменная х обозначает показатель степени a > 0 и отличный от 1.

Областью определения показательной функции является множество R.

 Пример 1

Приведем несколько примеров показательной функции, для которых область определения соответствует промежутку от -∞ до +∞:

y=(14)x

y=ex

y=(15)x

y=13x

Логарифмическая функция записана в таком виде:

y=logax

Здесь соблюдается условие, при котором а больше нуля и a ≠ 1.

Областью определения логарифмической функции является множество всех положительных действительных чисел:

D(logax)=(0,+∞).

Предусмотрено несколько вариантов записи области определения логарифмической функции:

  • D(ln)=(0,+∞);
  • D(lg)=(0,+∞).
Пример 2

Приведем примеры логарифмических функций с областью определения, соответствующей множеству (0,+∞):

y=log23x

y=log5x

y=log7x

y = ln x

Примеры нахождения области определения функции

Задача 1

Дано несколько функций, область определения которых следует найти:

y1=x2+2-3x-5

y2=x2-3x+2

y3=2x-73x+21

Решение

В первом случае функцию y1=x2+2-3x-5 допустимо записать, как разность пары функций:

f1x=x2+2;

f2x=3x-5.

Заметим, что функция f1x записана в виде многочлена. По свойству область определения этой функции является множеством всех действительных чисел R.

Функция f2x представляет собой дробно-рациональную функцию. Требуется искать такие значения х, при которых знаменатель принимает нулевое значение:

x-5≠0⇒x≠5

Чтобы найти область определения функции y1, нужно записать следующую систему:

x∈R,x≠5,  ⇒  Dy1:x∈-∞, 5∪5, +∞

Во втором случае, чтобы вычислить область определения функции y2=x2-3x+2, требуется найти решения следующего неравенства:

x2-3x+2≥0

Выполним преобразования путем разложения левой части неравенства на множители. В процессе нужно найти, каковы корни уравнения:

x2-3x+2=0

Согласно теореме Виета:

x1+x2=3

x1·x2=2

Тогда:

x1=1

x2=2.

В результате неравенство будет преобразовано таким образом:

x-1x-2≥0

Можно воспользоваться числовой осью для определения знака неравенства на интервалах, которые получились в итоге. Область определения второй функции соответствует следующим значениям:

Dy2:x∈-∞, 1∪2, +∞

Третья функция y3=2x-73x+21 является дробно-рациональной функцией с числителем в виде многочлена. Область определения многочлена является множеством действительных чисел R. Заметим, что знаменатель содержит знак корня. Область определения знаменателя в таком случае можно вычислить с помощью системы:

3x+21≥0,3x+21≠0,⇒3x+21>0⇒3x>-21⇒x>-7

В результате:

Dy3:x∈-7, +∞.

Ответ: Dy1:x∈-∞, 5∪5, +∞Dy2:x∈-∞, 1∪2, +∞Dy3:x∈-7, +∞.

Задача 2

Дано несколько функций, области определения которых необходимо вычислить:

y1=32x-5-1

y2=-log2x+1

y3=logxx-0,5

Решение

В первом случае представлена функция:

y1=32x-5-1

Найти область ее определения следует путем решения следующего неравенства:

32x-5-1>0⇒32x-5>1⇒32x-5>30

Исходя из того, что основание степени 3>1, запишем следующее неравенство:

2x-5>0⇒2x>5⇒x>2,5

В результате:

Dy1:x∈2,5; +∞.

Во втором случае дана функция:

y2=-log2x+1

В процессе нахождения области определения этой функции необходимо учесть, что выражение, записанное под знаком корня, не должно иметь отрицательное значение. Еще одним условием является положительное значение функции, записанной под логарифмом. Исходя из этого, запишем систему неравенств:

-log2x+1≥0,x>0.

Решение первого неравенства целесообразно выполнить отдельно:

-log2x+1≥0⇒log2x≤1

Исходя из определения логарифма, имеем:

x≤2

Вернемся к начальной системе неравенств:

x≤2,x>0,  ⇒  0<x≤2

В результате область определения второй функции будет записана в таком виде:

Dy2:x∈0, 2

В третьем случае дана логарифмическая функция:

y3=logxx-0,5

Найти область ее определения можно путем решения системы:

x>0,x≠1,x-0,5>0,  ⇒  x>0,x≠1,x>0,5;  ⇒  x≠1,x>0,5;⇒0,5; 1∪1;+∞

Таким образом:

Dy3:x∈0,5; 1∪1; +∞.

Ответ: Dy1:x∈2,5; +∞.;Dy2:x∈0, 2;Dy3:x∈0,5; 1∪1; +∞.

Область определения функции

Остановимся на процедуре нахождения области определе­ния функции.

1. В том случае, когда функция задана в аналитическом виде (посредством формулы)

(3.1)

и никаких ограничений или оговорок более не имеется, область ее определения устанавливается исходя из правил выполнения математических операций, входящих в формулу f в (3.1). Эти ограничения хорошо известны: подкоренное выражение в кор­не четной степени не может быть отрицательным, знаменатель дроби не может быть равным нулю, выражение под знаком ло­гарифма должно быть только

положительным, а также неко­торые другие. Приведем здесь два примера.

Пример 1. у = log2 (x2 — 5x + 6).

Область определения этой функции находится из условия x2 — 5x + 6 > 0.

Поскольку x = 2 и x = 3 — корни квадратно­го трехчлена, стоящего под знаком логарифма, то это условие выполняется на двух полубесконечных интервалах: (-, 2) и (3,). На рис. 3.4 выделена заштрихованная полоса, в которой график функции отсутствует.

Рис. 3.4

Пример 2. у = arcsin .

Область определения этой функции находится из совокуп­ности двух условий: аргумент под знаком arcsin не может быть по модулю больше единицы и знаменатель аргумента не дол­жен равняться нулю, т.е.

Двойное неравенство эквивалентно двум более простым нера­венствам: х + 2 ≥ 1 и х + 2 ≤ -1. Отсюда получаем, что область определения функции состоит из двух полубесконечных проме­жутков: (-, -3] и (-1,). Запретная точках = —

2 сюда не попадает. В отличие от предыдущего примера концы полуин­тервалов входят в область определения функции.

2. Область определения функции задана вместе с функцией f(x).

Пример 3. у = 3x—4­­/3 + 2, 1 ≤ х ≤ 4.

3. Функция имеет определенный прикладной характер, и область ее существования определяется также и реальными значениями входящих параметров (например, задачи с физи­ческим смыслом).

Определение 2. Функция у = f(x) называется четной (сим­метрия относительно оси Оу), если для любых значений аргу­мента из области ее определения выполнено равенство

Определение 3. Функция

у = f(x) называется нечетной (симметрия относительно начала координат О), если выпол­нено условие:

Например, функции у = х2 и у = cos x являются четными, а функции у = x3 и у = sin x— нечетными.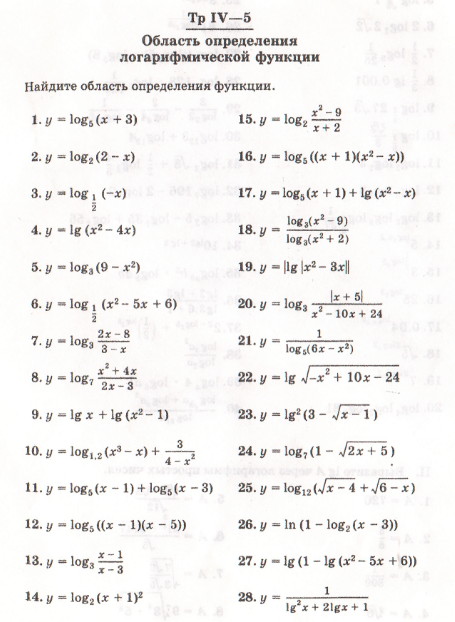

Приведем примеры использования функций в области эко­номики.

1. Кривые спроса и предложения. Точка равнове­сия. Рассмотрим зависимости спроса D (demand) и предложе­ния S (supply) от цены на товар

Р (price). Чем меньше цена, тем больше спрос при постоянной покупательной способности населения. Обычно зависимость D от Р имеет вид ниспадаю­щей кривой (рис. 3.5, а):

(3.2)

где а < 0. В свою очередь предложение растет с увеличением цены на товар, и потому зависимость S от Р имеет следующую характерную форму:

(3.3)

где b ≥ 1 (рис. 3.5, б). В формулах (3.2) и (3.3) с и d — так называемые экзогенные величины; они зависят от внешних причин (благосостояние общества, политическая обстановка и т.п.). Вполне понятно, что переменные, входящие в формулы (3. 2) и (3.3), положительны, поэтому графики функций имеют смысл только в первой координатной четверти.

Рис. 3.5

Для экономики представляет интерес условие равновесия, т.е. когда спрос равен предложению; это условие дается урав­нением

и соответствует точке пересечения кривых D и S — это так называемая точка равновесия (рис. 3.6). Цена Ро, при которой выполнено условие (3.4), называется равновесной.

Рис. 3.6

При увеличении благосостояния населения, что соответ­ствует росту величины с в формуле (3.2), точка равновесия М смещается вправо, так как кривая D поднимается вверх; при этом цена на товар растет при неизменной кривой предло­жения S.

2. Паутинная модель рынка. Рассмотрим простейшую задачу поиска равновесной цены.

Это одна из основных проб­лем рынка, означающая фактически торг между производите­лем и покупателем (рис. 3.7).

Рис. 3.7

Пусть сначала цену P1 называет производитель (в прос­тейшей схеме он же и продавец). Цена P1 на самом деле выше равновесной (естественно, всякий производитель стремится по­лучить максимум выгоды из своего производства). Покупатель оценивает спрос D1 при этой цене и определяет свою цену Р2, при которой этот спрос D1 равен предложению. Цена Р2 ниже равновесной (всякий покупатель стремится купить подешев­ле). В свою очередь производитель оценивает спрос D2, соот­ветствующий цене P2, и определяет свою цену

Р3, при которой спрос равен предложению; эта цена выше равновесной. Процесс торга продолжается и при определенных условиях приводит к устойчивому приближению к равновесной цене, т.е. к «скручи­ванию» спирали. Если рассматривать последовательность чисел, состоящую из называемых в процессе торга цен, то она имеет своим пределом равновесную цену Р0: Pn = P0.

Освоение всех 5 функций Kotlin Scope

Неудивительно, что наша команда Android в Punch Through любит Kotlin и что мы стремимся писать идиоматический Kotlin, по возможности используя преимущества его уникальных языковых возможностей. Некоторые общие вопросы, которые мы получаем от новых членов команды, которые изучают Kotlin, вращаются вокруг его функций области видимости, а именно: позволить , запустить , с , применить , а также . Функции области действия очень похожи в том, как они работают и ведут себя, или так кажется на первый взгляд.

Что такое функции области видимости?

Как следует из названия, функции области видимости изменяют область контекста вашего исполняемого кода — мы используем функцию области видимости, чтобы изменить область видимости объекта как this или it во внешней лямбде.

Основная цель функций области видимости — помочь нам написать более лаконичный и читаемый код. Для нас количество строк кода не является показателем его краткости или удобочитаемости. И хотя использование функций области действия почти всегда увеличивает количество строк кода, оно может помочь уменьшить повторение и ненужную инициализацию переменных.

Очень популярное использование функций области видимости — разворачивание ссылок, допускающих значение NULL, и доступ к их базовым значениям. Мы знаем, что цепочка безопасных вызовов по ссылке, допускающей значение NULL, является одной из ключевых особенностей Kotlin и даже других популярных современных языков программирования, таких как Swift, но длинные цепочечные безопасные вызовы иногда могут показаться неэлегантными при повторном вызове.

Другим популярным примером использования функции области видимости является выполнение настройки объекта после инициализации. Другие варианты использования включают возврат или спасение на раннем этапе выполнения функции, выполнение побочных эффектов, и этот список можно продолжить.

Без лишних слов давайте углубимся в различные функции области действия, которые Kotlin предлагает нам.

‘let’

Краткий обзор:

  • Функция области видимости let изменяет область видимости объекта как it в его лямбда-выражении, если имя параметра не объявлено явно.
  • let возвращает результат вычисления лямбда-выражения.
  • Основное использование командой Punch Through: безопасное развертывание значений, допускающих значение NULL.

Большинство разработчиков впервые столкнутся с функциями области видимости, вероятно, с let . Если мы находимся в классе Activity , this обычно относится к самому указанному классу Activity . Однако, если у нас есть переменная, допускающая значение NULL, которую мы собираемся развернуть, мы могли бы сделать что-то вроде someVariable?.let { … } . В этой лямбде, заключенной в фигурные скобки, someVariable была бы развернута и впоследствии изменена в it .

Некоторые читатели могут спросить: «Можем ли мы вместо этого просто выполнить проверку null и сделать так, чтобы интеллектуальное приведение или вывод типа Kotlin автоматически выводило, что переменная не является null ?»

Что ж, это будет работать, если рассматриваемая ссылка, допускающая значение NULL, представляет собой

val , но в случаях, когда ссылка представляет собой var , смарт-приведение Kotlin будет жаловаться, что не может гарантировать, что эта var останется неизменной на протяжении всего процесса. исполнение , если оператор . Функции области видимости, такие как let , позволяют нам по существу захватить моментальный снимок базовой ссылки и работать с ней, не беспокоясь о том, что она превратится в null из-под нас.

 переменная someVariable: строка? = ноль
если (некоторая переменная != ноль) {
    // Делаем что-то с переменной someVariable, которая по-прежнему может принимать значение null
}
какая-то переменная?.let {
    // Делаем что-то с этим, которое теперь гарантированно не равно нулю
}

Честно говоря, пусть далеко не серебряная пуля, и ручные проверки null иногда встречаются в нашем коде. Мы поговорим об этом подробнее в одном из последующих разделов.

«применить»

Краткий обзор:

  • Функция области действия применить изменяет область видимости объекта как этого в его лямбде.
  • apply возвращает объект, для которого он был вызван.
  • Основное использование командой Punch Through: настройка объекта.

Нашей команде очень нравится функция области apply за ее элегантность при выполнении операций настройки объекта. Например, если мы настраиваем панель действий

AppCompatActivity и не знаем функций области действия, мы бы сделали что-то вроде следующего:

 supportActionBar?.setDisplayShowTitleEnabled(true)
supportActionBar?.setTitle(R.string.title)
supportActionBar?.setDisplayHomeAsUpEnabled(true)

И хотя в приведенном выше коде явно нет ничего плохого, применить позволяет нам писать более элегантный код, а также снижает вероятность ошибок программиста (например, вызов функций для неправильного экземпляра класса).

 supportActionBar?. apply {
    setDisplayShowTitleEnabled (истина)
    setTitle (R.string.title)
    setDisplayHomeAsUpEnabled (истина)
}

Обратите внимание, что нам не нужно было добавлять префикс к вызовам функций внутри лямбда-выражения apply с вместо . Это связано с тем, что apply пересматривает AppCompatActivity ActionBar as this внутри лямбда-выражения, а поскольку выражения Kotlin неявно вызываются на this , нет необходимости ставить перед вызовами функции Intent какой-либо префикс.

Также можно выполнить настройку только что созданного объекта, используя apply .

 valintentFilter = IntentFilter().apply {
    addAction(BluetoothDevice.ACTION_BOND_STATE_CHANGED)
    addAction (BluetoothAdapter. ACTION_STATE_CHANGED)
}

Предостережение: код внутри лямбда-выражения apply будет выполняться первым, прежде чем apply вернет объект, для которого он был вызван. В приведенном выше примере IntentFilter сначала создается, прежде чем он будет настроен в соответствии с нашими спецификациями в лямбда-выражении apply . После завершения лямбда-выражения настроенный IntentFilter возвращается вызовом apply и затем назначается переменная намеренияFilter .

В зависимости от конкретного варианта использования может быть целесообразно рассмотреть возможность выполнения задач настройки отдельно или после назначения переменной, особенно если на этапе после инициализации возникают побочные эффекты кода, на которые опирается другой код.

«также»

Краткий обзор:

  • Функция области видимости и изменяет область видимости объекта как it в его лямбда-выражении, если имя параметра не объявлено явно.
  • также возвращает объект, для которого он вызывается.
  • Основное использование командой Punch Through: выполнить массовую настройку объекта без затенения this.

также — интересная функция прицела. Функционально он почти идентичен , применяя , за исключением того, как он изменяет область действия объекта. применить переопределяет область объекта, для которого он вызывается, как this , в то время как также переопределяет область объекта как это , очень похоже на то, что делает пусть .

Итак, когда мы используем одно вместо другого?

Обычно мы используем и , когда не хотим затенять текущий этим в более широком контексте. Например, если мы находимся в каком-то классе, который либо имеет функцию PerformAddition() — или, что еще хуже, если его суперкласс реализует ее, что скрывает ее — и объект, который мы собираемся настроить, вызывая , применяет или также также имеет функцию PerformAddition() на нем, это может сбить с толку разработчика реализации и других лиц, просматривающих или читающих код, какой именно PerformAddition() вызывается. В таких случаях часто предпочтительнее использовать , а также вместо , применяя .

 абстрактный класс AbstractSuperclass {
    вар данных: Ури? = ноль
}
класс SomeClass : AbstractSuperclass() {
    fun someFunction(): Intent {
        вернуть намерение (Intent.ACTION_SENDTO).также {
            it.data = Uri.parse(CONTACT_EMAIL_URI)
            it.putExtra (Intent.EXTRA_SUBJECT, getString (R.string.support_email_subject))
            it.putExtra (Intent.EXTRA_TEXT, getString (R.string.email_template))
        }
    }
}

В приведенном выше примере AbstractSuperclass имеет свойство data , а Intent также имеет свойство data , которое было автоматически создано из методов Intent Java setData 4 и

3.

При попытке установить данные Intent , использование и устраняет неоднозначность того, какие данные мы устанавливаем, и в результате код становится более читаемым.

Конечно, применяется можно использовать в ситуациях, подобных приведенным выше, но если вы хотите получить доступ к свойству AbstractSuperclass ’ data из лямбда-выражения apply , нужно будет явно добавить префикс data с префиксом this@SomeClass . По нашему мнению, использование и дало бы более чистый фрагмент кода в этом случае, но абсолютно ничто не мешает кому-либо использовать и применить здесь .

«бег»

Кратко:

  • Универсальная версия функции расширения функции области run изменяет область видимости объекта как this в его лямбда-выражении.
  • run возвращает результат вычисления лямбда-выражения.
  • Основное использование командой Punch Through: выполнять многострочные побочные эффекты после оператора elvis ( ?: ) в случае, когда что-то равно null , и возвращаться раньше.

Серия 9Функция области видимости 0004 доступна как в виде отдельной глобальной функции ( kotlin.run {...} ), так и в виде универсальной функции расширения для любого экземпляра класса. Мы сосредоточимся на последнем в этом посте, потому что первый идентичен запуску простой функции.

Наше любимое использование функции области run — выполнение побочных эффектов (например, ведение журнала) в правой части оператора Kotlin elvis ( ?: ), если значение, допускающее значение NULL, присваивается переменной. на самом деле ноль . Если значение, допускающее значение NULL, не равно null , то run не вызывается, и назначение переменной работает должным образом.

 переменная MostRecentLogFilename: Строка? = ноль
личное развлечение
    val имя_файла = имя_самогопоследнего_файла_журнала ?: запустить {
        log("Поделиться нечем")
        возвращаться
    }
    // Выполнение других операций с именем файла, являющимся необнуляемой строкой
    val uri = FileProvider.getUriForFile(
        это,
        "com.punchthrough.testapp.provider",
        getFileStreamPath (имя файла)
    )
    val намерение = намерение (Intent.ACTION_SEND)
        .setType("текст/*")
        .putExtra(Intent.EXTRA_STREAM, uri)
    startActivity(Intent.createChooser(intent, "Поделиться журналом с помощью:"))
}

Обратите внимание, что мы можем вызвать return изнутри run , чтобы вернуться из функции досрочно, если некоторые предпосылки не выполнены, и это то, что делает наше использование run таким мощным. Эта функция похожа на чрезвычайно популярную инструкцию Swift guard и позволяет нам выполнять проверки работоспособности раньше в нашей функции, а не потенциально выполнять кучу одноразовой работы. Это также позволяет нам рассуждать о нашем коде таким образом, что остается очень мало места для ошибок, потому что все неоднозначности (например, значения, допускающие значение NULL) были прояснены в начале функции.

Этот способ комбинирования использования оператора elvis и run также имеет дополнительный бонус — он позволяет переменной, для которой выполняется присваивание, иметь ненулевое значение и избавляет нас от необходимости разворачивать это еще раз в последующем коде.

Можно ли заменить использование run на let ?

Абсолютно. Теперь мы начинаем замечать общую тему, когда функции области действия по существу взаимозаменяемы, но потерпите немного больше, дорогой читатель, когда мы говорим о последней функции области видимости Kotlin, 9. 0003 с .

«с»

Краткий обзор:

  • Функция области видимости с изменяет область видимости объекта как и в его лямбда-выражении.
  • с возвращает результат вычисления лямбда-выражения.
  • Основное использование команды Punch Through: выполнение операций, которые в основном вращаются вокруг центрального объекта.

Основное различие между и и другими функциями прицела заключается в том, что с не вызывается для универсального объекта. Вместо этого объект передается в с в качестве аргумента функции. Кроме того, с на самом деле очень похоже на run . Наши варианты использования между и и запускают , а затем сводятся к выбору того, какой из них имеет грамматический смысл для задачи, и поэтому мы обнаруживаем, что используем с для выполнения операций, которые вращаются вокруг центрального объекта («выполнить эти операции с этот объект»).

 частное значение BroadcastReceiver = объект: BroadcastReceiver() {
    переопределить удовольствие при получении (контекст: контекст, намерение: намерение) {
        с (намерением) {
            если (действие == BluetoothDevice.ACTION_BOND_STATE_CHANGED) {
                val устройство = getParcelableExtra(BluetoothDevice.EXTRA_DEVICE)
                val предыдущееBondState = getIntExtra (BluetoothDevice.EXTRA_PREVIOUS_BOND_STATE, -1)
                val bondState = getIntExtra(BluetoothDevice.EXTRA_BOND_STATE, -1)
                val bondTransition = "${previousBondState.toBondStateDescription()} в " +
                    bondState.toBondStateDescription()
                Timber.w("Состояние связи ${device?.address} изменено | $bondTransition")
            }
        }
    }
    частное развлечение Int. toBondStateDescription() = когда (это) {
        BluetoothDevice.BOND_BONDED -> "СВЯЗАННЫЙ"
        BluetoothDevice.BOND_BONDING -> "СВЯЗЬ"
        BluetoothDevice.BOND_NONE -> "НЕ ПРИВЯЗАН"
        еще -> "ОШИБКА: $это"
    }
}

В приведенном выше примере нам нужно получить много информации из параметра Intent в функции onReceive , и, изменив контекст выполнения на Intent , о котором идет речь, мы могли бы просто использовать getParcelableExtra , getIntExtra , action и т. д. без необходимости добавлять к ним префикс экземпляра Intent .

Предостережения относительно функций области видимости

При всех преимуществах функций области видимости трудно представить, что у них есть недостатки. Однако есть несколько ловушек, с которыми могут столкнуться разработчики, если они переусердствуют с использованием функций области видимости.

Слишком много хороших вещей не обязательно идеальны

Существует тонкий баланс между использованием чего-либо ради использования и использованием этого по назначению. Функции области видимости не являются исключением.

Чрезмерное или ненужное использование функций области может, в свою очередь, затуманить читабельность нашего кода, особенно в случаях apply , с и run , где иногда может быть непонятно, кто получатель ( это ) для заданного вызова функции.

Чрезмерное вложение бизнес-логики во множество функций области действия также устрашающе напоминает печально известный ад обратных вызовов JavaScript. Например, рассмотрим следующий фрагмент кода, который кажется очень громоздким.

 var variableOne: Строка? = ноль
var variableTwo: строка? = ноль
переменная переменнаяТри: Строка? = ноль
variableOne?.let { variableOneUnwrapped ->
variableTwo?.let { variableTwoUnwrapped ->
переменнаяThree?. let { переменнаяThreeUnwrapped ->
результат val = переменнаяOneUnwrapped + variableTwoUnwrapped + variableThreeUnwrapped
}
}
}

В случаях, подобных приведенным выше, намного практичнее и читабельнее записывать эти переменные как экземпляры val и выполнять комбинированные проверки null вручную. В прилагаемой инструкции if все три константы будут не- нулевыми из-за умной системы вывода типов Kotlin.

 val константа1 = переменная1
val константаДва = переменнаяДва
val константаТри = переменнаяТри
if (константаОдин!= null && константаДва != ноль && константаТри != ноль) {
val результат = константаОдин + константаДва + константаТри
}
Функции прицела слишком похожи друг на друга

Когда у вас в ящике для инструментов есть куча отверток примерно одинакового размера, может быть трудно понять, какая из них лучше всего подходит для работы — возможно, все они могут решить такая же проблема, и это проблема сама по себе.

Как мы упоминали в наших примерах на протяжении всего поста, все пять функций обзора технически взаимозаменяемы, и это добавляет путаницы, особенно в командной среде.

В зависимости от культуры вашей команды члены вашей команды уже могут предпочитать делать что-то определенным образом (например, использовать let для распаковки переменных, допускающих значение NULL, по сравнению с использованием run ). Убедитесь, что вы сверились с ними, чтобы избежать байкшеринга и обеспечить согласованность кода!

Наш совет разработчикам, которые работают в одиночку или в командной среде, но которым приходится принимать решения о том, какие функции области видимости и за что делают их команды, быть последовательными . Если вы решите использовать , пусть , чтобы развернуть переменные, допускающие значение NULL, и использовать , применить для выполнения конфигураций объектов, то придерживайтесь этих вариантов использования на протяжении всего проекта. Если есть сомнения, лучше всего начать с того, как команда Punch Through использует каждую функцию масштаба.

Функции осциллографа — это весело!

В этом посте мы рассказали, что такое пять функций области действия Kotlin, что они делают и как мы здесь, в Punch Through, их используем. Мы считаем, что функции области видимости — одна из лучших особенностей Kotlin, и они делают процесс разработки намного более увлекательным. Мы надеемся, что этот пост был полезен для тех из вас, кто пытается понять различия между этими функциями области видимости, и следите за обновлениями, чтобы узнать больше советов и приемов Kotlin!

Все сообщения в нашем блоге написаны инженерами Punch Through — теми же инженерами, которые создают потрясающие продукты для наших клиентов. Нужна помощь в вашем проекте? Узнайте больше о том, как мы можем помочь!

Узнать больше

Область действия переменных Python — изучить на примере

Не все переменные доступны из всех частей нашей программы. Часть программы, где переменная доступна, называется ее «областью » и определяется тем, где объявлена ​​переменная.

В Python есть три разных области видимости переменных:

  • Локальная область
  • Глобальная область
  • Включающая область

Локальная область действия

Переменная, объявленная в функции, имеет ЛОКАЛЬНУЮ область действия. Он доступен с момента объявления до конца функции и существует до тех пор, пока выполняется функция.

 функция myfunc():
    x = 42 # локальная область видимости x
    печать (х)
myfunc() # выводит 42

Локальные переменные удаляются из памяти при завершении вызова функции. Поэтому попытка получить значение локальной переменной вне функции вызывает ошибку.

 функция myfunc():
    x = 42 # локальная область видимости x
моя функция()
print(x) # Триггеры NameError: x не существует

Глобальная область действия

Переменная, объявленная вне всех функций, имеет ГЛОБАЛЬНУЮ область действия. Он доступен во всем файле, а также внутри любого файла, который импортирует этот файл.

 x = 42 # глобальная область x
защита myfunc():
    print(x) # x равно 42 внутри def
моя функция()
print(x) # x is 42 снаружи def

Глобальные переменные часто используются для флаги (логические переменные, которые указывают, истинно ли условие). Например, некоторые программы используют флаг с именем verbose, чтобы сообщить дополнительную информацию об операции.

 подробный = Истина
защита op1():
    если подробно:
        print('Выполняется операция 1')

Изменение глобальных переменных внутри функции

Хотя вы можете получить доступ к глобальным переменным внутри или вне функции, вы не можете изменить их внутри функции.

Вот пример, который пытается переназначить глобальную переменную внутри функции.

 x = 42 # глобальная область x
защита myfunc():
    х = 0
    print(x) # локальный x равен 0
моя функция()
print(x) # global x по-прежнему 42

Здесь значение глобальной переменной x не изменилось. Поскольку Python создал новую локальную переменную с именем x ; который исчезает, когда функция завершается, и не влияет на глобальную переменную.

Чтобы получить доступ к глобальной переменной, а не к локальной, необходимо явно объявить x глобальными, используя ключевое слово global.

 x = 42 # глобальная область x
защита myfunc():
    global x # объявить x глобальным
    х = 0
    print(x) # глобальный x теперь равен 0
моя функция()
print(x) # x is 0

x внутри функции теперь ссылается на x вне функции, поэтому изменение x внутри функции изменяет x снаружи.

Вот еще один пример, который пытается обновить глобальную переменную внутри функции.

 x = 42 # глобальная область x
защита myfunc():
    x = x + 1 # вызывает UnboundLocalError
    печать (х)
моя функция()

Здесь Python предполагает, что x является локальной переменной, что означает, что вы читаете ее перед определением.

Решение снова состоит в том, чтобы объявить x глобальным.

 x = 42 # глобальная область x
защита myfunc():
    глобальный х
    x = x + 1 # глобальный x теперь равен 43
    печать (х)
моя функция()
print(x) # x is 43

Есть еще один способ обновить глобальную переменную из неглобальной области — использовать функцию globals().

Объем

Если переменная объявлена ​​во внешней функции, она не является локальной для вложенных функций. Он позволяет назначать переменные во внешней, но не глобальной области видимости.

Вот пример, который пытается переназначить локальную переменную объемлющей (внешней) функции внутри вложенной (внутренней) функции.

 # объемлющая функция
защита f1():
    х = 42
    # вложенная функция
    защита f2():
        х = 0
        print(x) # х равно 0
    f2()
    print(x) # x по-прежнему 42
    
f1()

Здесь значение существующей переменной x не изменилось. Потому что Python создал новую локальную переменную с именем x , которая затеняет переменную во внешней области.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *