§ Чётные и нечётные функции
Что такое чётная функция
Обратимся к определению чётности функции через формулу.
Запомните!
Функция «у(x)» называется чётной, если
у(−x) = у(x)
для любого «x» из области определения функции.
Другими словами, нужно в формулу функции вместо «x» подставить «−x». Затем сравнить полученный результат с формулой исходной функцией.
Если в итоге «y(−x)» будет равен исходной функции «y(x)», значит, эта функция чётная.
Давайте разбираться на практике.
Разбор примера
Выяснить, является ли функция чётной или нечётной:
у = 2x4
Важно!
При обозначении функции используют разные варианты написания
«у = …» или
«у(x) = …». По сути, это одинаковые обозначения.
Подставим «−x» вместо «x» в исходную функцию «у = 2x4».
Если в итоге мы получим исходную функцию, значит, она чётная.
у(−x) = 2(−x)4 = …
При возведении в чётную степень отрицательного числа всегда получается положительное число.
у(−x) = 2(−x)4 = 2x4
Проверим, выполняется ли условие чётности функции «у(−x) = у(x)».
у(x) = 2x4 у(−x) = 2x4 | у(−x) = у(x) Значит, функция у = 2x4 чётная |
После подстановки «−x» мы получили исходную функцию «у = 2x4». Условие чётности функции «у(−x) = у(x)» выполнено.
Ответ: функция «у = 2x4» чётная.
Что такое нечётная функция
Запомните!
Функция «у(x)» называется нечётной, если
у(−x) = −у(x)
для любого «x» из области определения функции.
Порядок анализа функции на нечётность
:- подставить «−x» в исходную функцию, чтобы получить «у(−x)»;
- вычислить «−у(x)»;
- сравнить «у(−x)» и «−у(x)».
Если они равны,
то функция нечётная.
Если они равны,
то функция нечётная.Разбор примера
Выяснить, является ли функция чётной или нечётной:
у = 3x 5
Подставим «−x» вместо «x» в формулу функции «у(x) = 3x 5».
у(−x) = 3(−x) 5 = …
При возведении в нечётную степень отрицательного числа получается отрицательное число.
у(−x) = 3(−x) 5 = −3x 5
Теперь получим «−у(x)». Для этого умножим левую и правую часть исходной функции «у = 3x 5» на «−1».
у(x) = 3x 5 | · (−1)
−у(x) = −3x 5
Сравним полученные результаты «у(−x)» и «−у(x)».
у(−x) = −3x5 −у(x) = −3x5 | у(−x) = −у(x) Значит, функция у(x) = 3x 5 является нечётной |
Ответ: функция «у(x) = 3x 5» нечётная.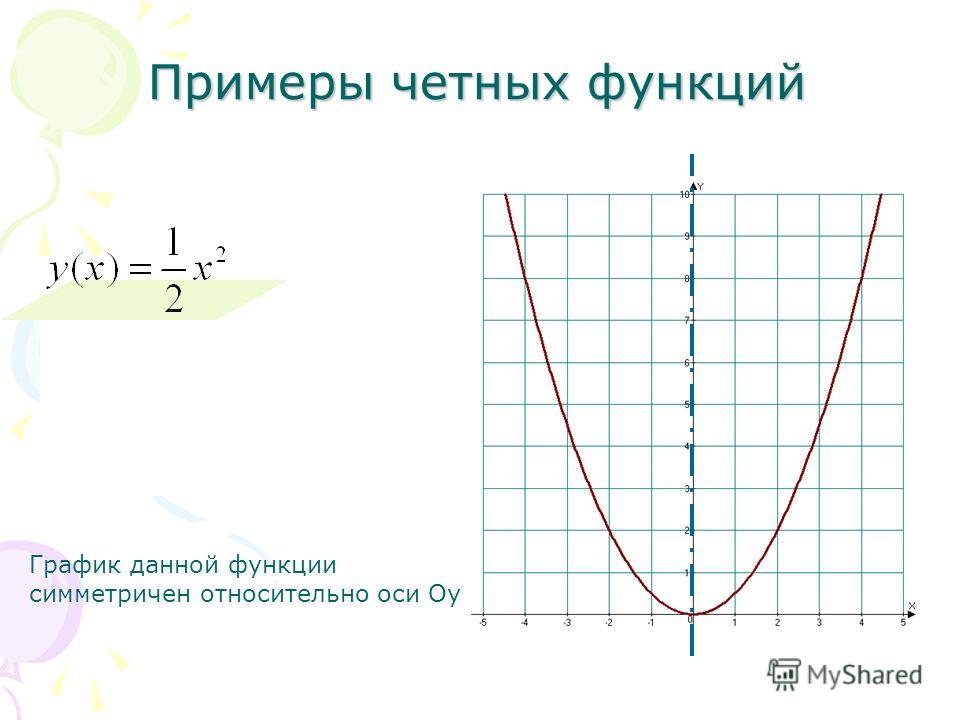
Важно!
Не бывает функций, которые одновременно являются чётными и нечётными.
Поэтому, если при анализе функции вы выяснили, что функция является чётной (или нечётной), нет смысла продолжать ее анализ на чётность/нечётность. Можно сразу записывать ответ.
Функции, которые не являются ни чётными, ни нечётными
Важно!
Не все функции обязательно являются чётными или нечётными. Есть функции, которые не являются ни чётными, ни нечётными.
Разбор примера
Выяснить, является ли функция чётной или нечётной:
у = x 3 − 2
Проверим, является ли функция
«у = x 3 − 2» чётной.
По определению чётной функции
должно выполняться условие
«у(−x) = у(x)».
Подставим «−x» вместо «x» в исходную функцию «у = x 3 − 2».
у(−x) = (−x) 3 − 2 = …
Возведение в нечётную степень отрицательного числа даст отрицательное число.
у(−x) = (−x) 3 − 2 = −x 3 − 2
Сравним исходную функцию «y(x)» и полученную «y(−x)», чтобы проверить, является ли функция «у = x 3 − 2» чётной.
у(x) = x 3 − 2 у(−x) = −x 3 − 2 | у(−x) ≠ у(−x) Функция |
Теперь проверим, является ли функция «у(x) = x 3 − 2» нечётной. По определению нечётной функции должно выполняться условие: «у(−x) = −у(x)».
Функцию «у(−x)» мы рассчитали выше. Осталось вычислить «−у(x)». Для этого умножим левую и правую часть исходной функции «у = x 3 − 2» на «−1».
у(x) = x 3 − 2 | · (−1)
−у(x) = −(x 3 − 2)
Используем
правило раскрытия скобок.
Так как перед скобкой «(x 3 − 2)» стоит знак минуса, все слагаемые
внутри поменяют знак на противоположный.
−у(x) = −x 3 + 2
Сравним «−y(x)» и «−y(x)».
у(−x) = −x 3 − 2 −у(x) = −x 3 + 2 | у(−x) ≠ у(−x) Функция |
Ответ: функция «у(x) = x 3 − 2» не является ни чётной, ни нечётной.
Другие примеры чётных и нечётных функций
Разбор примера
Выяснить, является ли функция чётной или нечётной:
у = x 2 − x + 1
Проверим, является ли функция
«у = x 2 − x + 1» чётной,
то есть должно выполняться условие
«у(−x) = у(x)».
Подставим «−x» вместо «x» в формулу функции.
у(−x) = (−x) 2 − (−x) + 1 = …
При возведении в чётную степень получается положительное число.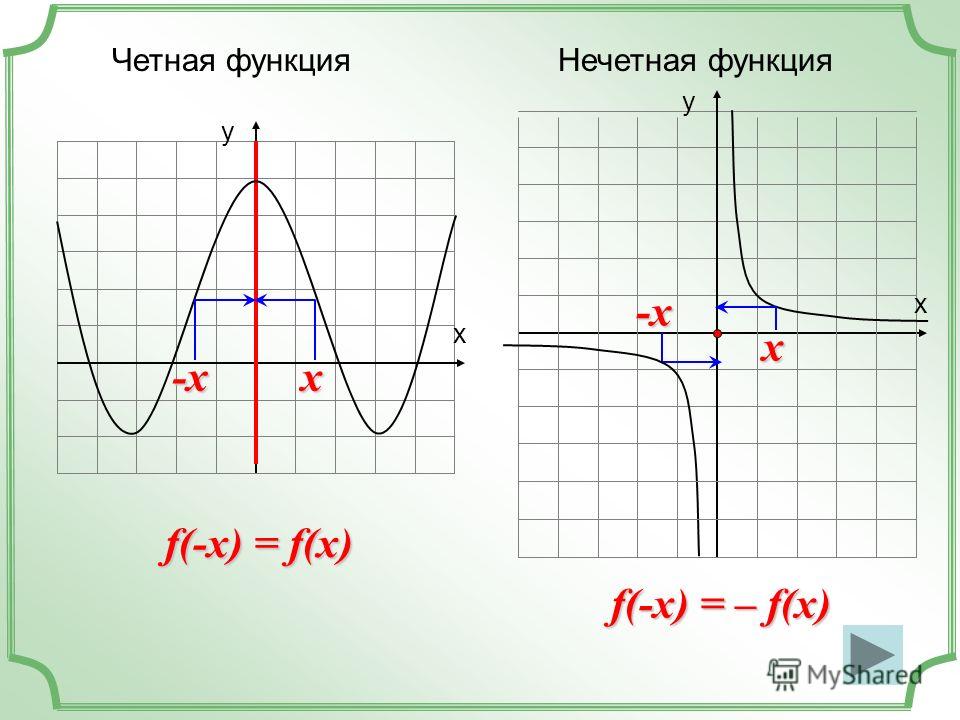
у(−x) = (−x) 2 − (−x) + 1 =
= x 2 − (−x) + 1 = …
Раскроем скобки «− (−x)» по правилу раскрытия скобок: минус на минус даёт плюс.
= x 2 − (−x) + 1 = x 2 + x + 1
Сравним полученную «у(−x)» с исходной функцией «у(x)».
у(x) = x 2 − x + 1 у(−x) = x 2 + x + 1 | у(−x) ≠ у(−x) Функция |
Проверим, является ли функция
«у = x 2 − x + 1»
нечётной функцией.
Для этого должно выполняться условие:
«у(−x) = −у(x)».
Выражение «у(−x)»
мы уже посчитали выше.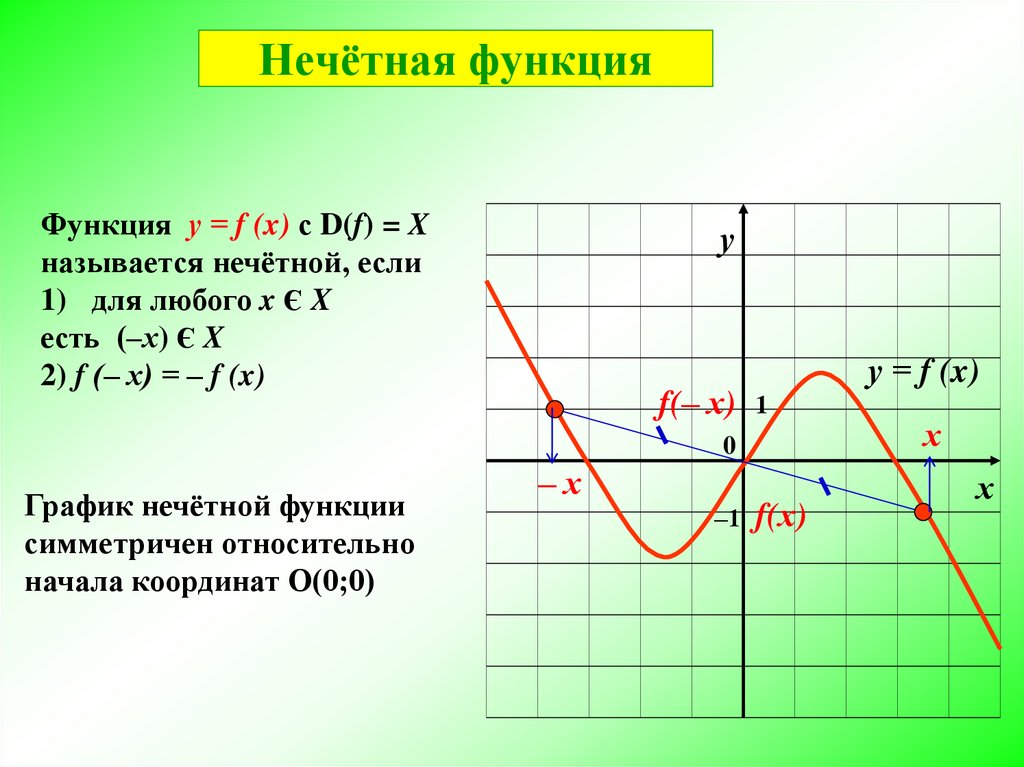
Теперь вычислим «у(−x)».
Умножим левую и правую часть исходной функции на «(−1)».
(−1) · у(x) = (−1) · (x 2 − x + 1)
Используем правило раскрытия скобок. При умножении на «(−1)» все слагаемые внутри скобок поменяют свой знак на противоположный.
−у(x) = −x 2 + x − 1
Сравним полученные «у(−x)» и «−у(x)».
у(−x) = x 2 + x + 1 −у(x) = = −x 2 + x − 1 | у(−x) ≠ у(−x) Функция |
Ответ: функция «у = x 2 − x + 1» не является ни чётной, ни нечётной.
Разбор примера
Исследуйте на чётность функцию:
у = √x − 1 · √x + 1
По определению чётности функции «у(−x) = у(x)».
у(−x) = √(−x) − 1 · √(−x) + 1 =
= √−x − 1 · √−x + 1 = …
Вынесем «(−1)» из каждого корня. После этого каждое слагаемое внутри корней поменяет знак на противоположный.
… = (−1) · √x + 1 · (−1) · √x − 1 =
= (−1) · (−1) √x + 1 · √x − 1 = …
Умножим «(−1)» на «(−1)», используя правило знака: минус на минус дает плюс.
… = √x + 1 · √x − 1 = …
От перемены мест множителей произведение не меняется. Поменяем местами
«√x − 1» и
«√x + 1».
… = √x − 1 · √x + 1
Проверим, выполняется ли условие чётности функции «у(−x) = у(x)».
у(x) = = √x − 1 · √x + 1 у(−x) = = √x − 1 · √x + 1 | у(−x) = у(x) Функция |
Ответ: функция «у = √x − 1 · √x + 1» является чётной.
Разбор примера
Показать, что функция не является чётной и не является нечётной:
у =
| x + 2 |
| x − 3 |
По определению чётности функции «y(−x) = y(x)». Вычислим «y(−x)».
Подставим «−x» в исходную функцию
«у =
| x + 2 |
| x − 3 |
».
у(−x) =
| −x + 2 |
| −x − 3 |
Сравним «у(−x)» и «у(x)».
у(−x) =
у(x) =
| у(−x) ≠ у(x) Значит, функция y =
|
Проверим функцию «y =
| x + 2 |
| x − 3 |
» на нечётность.
По определению нечётности функции «y(−x) = −y(x)». Функцию «y(−x)» мы вычислили ранее. Вычислим «−y(x)».
Для этого умножим левую и правую часть исходной функции на «−1».
у(x) =
| x + 2 |
| x − 3 |
| · (−1)
−у(x) = −
| x + 2 |
| x − 3 |
Сравним «у(−x)» и «−у(x)».
у(−x) =
−у(x) = = −
| у(−x) ≠ −у(x) Значит, функция y =
|
Ответ: функция «y =
| x + 2 |
| x − 3 |
»
не является ни чётной, ни нечётной.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».
Оставить комментарий:
| Отправить |
Четные и нечетные функции
Цели:
- сформировать понятие чётности и нечётности функции, учить умению определять и использовать эти свойства при исследовании функций, построении графиков;
- развивать творческую активность учащихся, логическое мышление, умение сравнивать, обобщать;
- воспитывать трудолюбие, математическую культуру; развивать коммуникативные качества.
Оборудование: мультимедийная установка, интерактивная доска, раздаточный материал.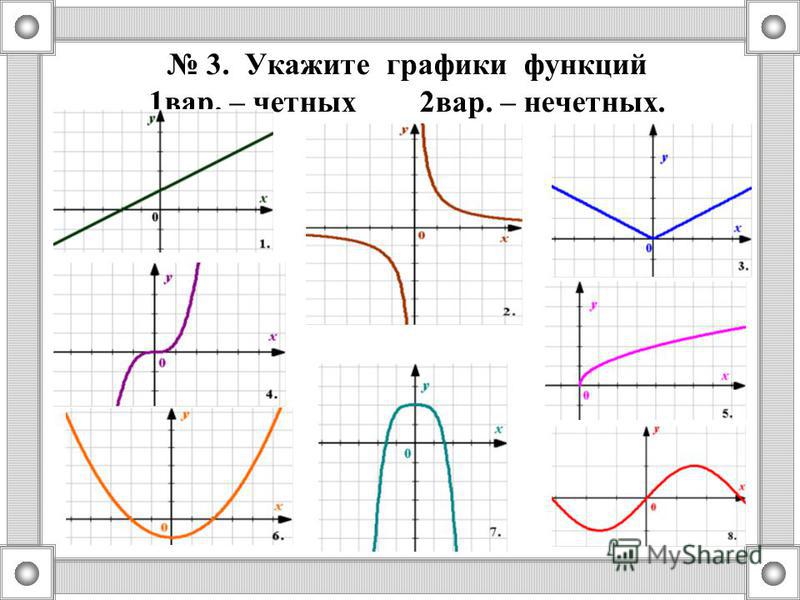
Формы работы: фронтальная и групповая с элементами поисково-исследовательской деятельности.
Информационные источники:
1.Алгебра9класс А.Г Мордкович. Учебник.
2.Алгебра 9класс А.Г Мордкович. Задачник.
3.Алгебра 9 класс. Задания для обучения и развития учащихся. Беленкова Е.Ю. Лебединцева Е.А
ХОД УРОКА
1. Организационный момент
Постановка целей и задач урока.
2. Проверка домашнего задания
№10.17 (Задачник 9кл. А.Г. Мордкович).
а) у = f(х), f(х) =
б) f (–2) = –3; f (0) = –1; f(5) = 69;
в) 1. D(f) = [– 2; + ∞)
2. Е(f) = [– 3; + ∞)
3. f(х) = 0 при х ~ 0,4
4. f(х) >0 при х > 0,4 ; f(х)
< 0 при – 2 < х < 0,4.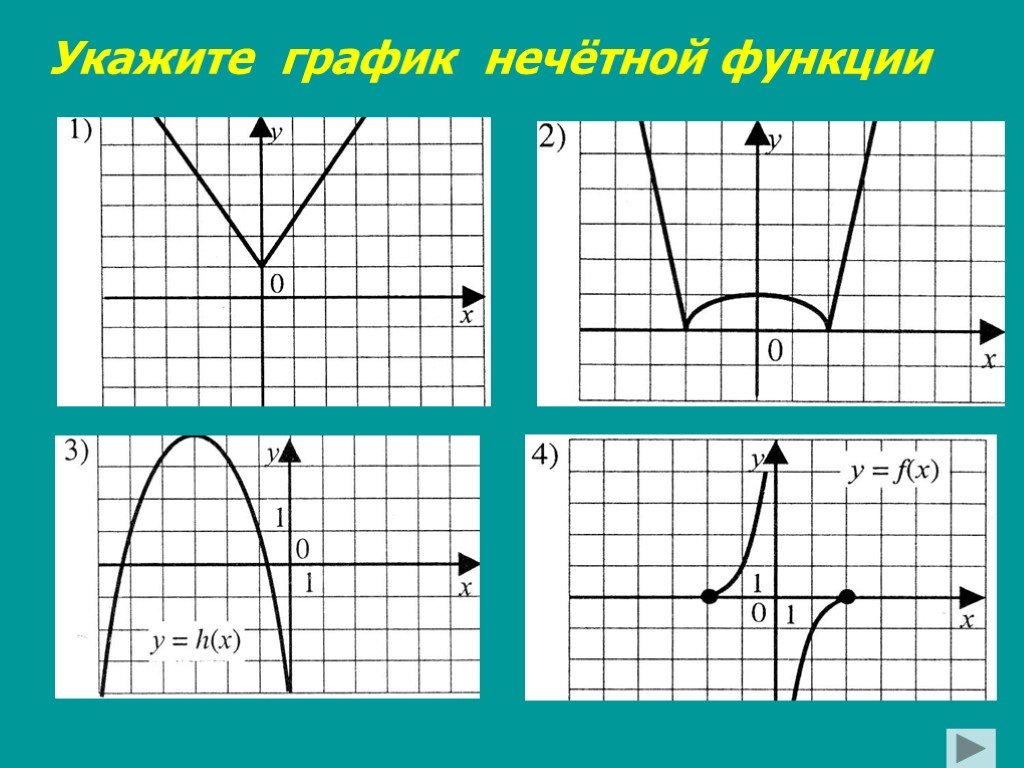
5. Функция возрастает при х € [– 2; + ∞)
6. Функция ограничена снизу.
7. унаим = – 3, унаиб не
существует
8. Функция непрерывна.
(Вы использовали алгоритм исследования функции?) Слайд.
2. Таблицу, которую вам задавалась, проверим по слайду.
| Заполните таблицу | |||||
Функция |
Область определения |
Нули функции |
Промежутки знакопостоянства |
Координаты точек пересечения графика с Оу | |
у > 0 |
у < 0 |
||||
х ≠ –3 |
х = –5, |
х € (–5;3) U |
х € (–∞;–5) U |
( 0;) |
|
х ∞ –5, |
х = –3 |
х € (–5;3) U |
х € (–∞;–5) U |
( 0;) |
|
х ≠ –5, |
нет |
х € (–∞; –5) U |
х € (–5; 2) |
( 0;) |
|
3.
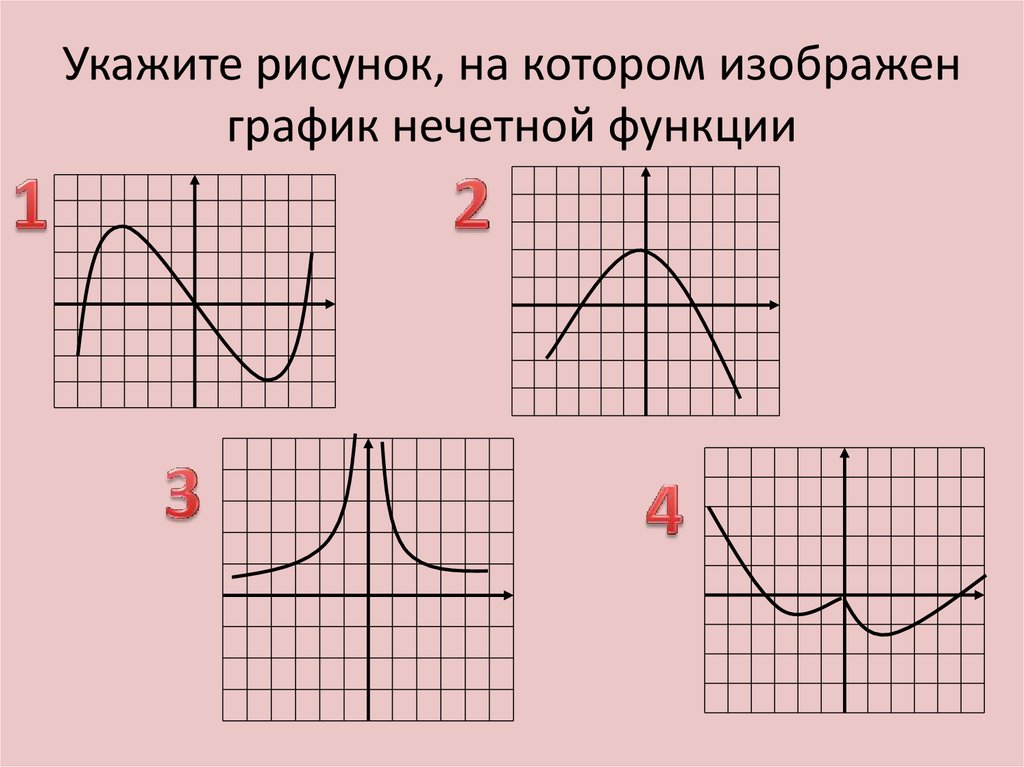Актуализация знаний
– Даны функции.
– Указать область определения для каждой
функции.
– Сравнить значение каждой функции для каждой
пары значения аргумента: 1 и – 1; 2 и – 2.
– Для каких из данных функций в области
определения выполняются равенства f(– х)
= f(х), f(– х) = – f(х)? (полученные
данные занести в таблицу) Слайд
D (f) |
f(1) и f(– 1) | f(2) и f(– 2) | графики | f(– х) = –f(х) | f(– х) = f(х) | |
| 1. f(х) = | R |
2 и 2 |
Г |
|
+ |
|
2. f(х) = х3 |
R |
1 и 1 |
8 и – 8 |
А |
+ |
|
| 3. f(х) = | х | | R |
1 и – 1 |
2 и 2 |
Б |
|
+ |
| 4. f(х) = 2х – 3 | R |
– 1 и – 5 |
1 и – 7 |
Е |
|
|
5. f(х) = |
х ≠ 0 |
6 и – 6 |
3 и – 3 |
В |
+ |
|
| 6. f(х)= | х > –1 | и 0 |
и не опред. |
З |
|
|
4. Новый материал
– Выполняя данную работу, ребята мы выявили ещё
одно свойство функции, незнакомое вам, но не
менее важное, чем остальные – это чётность и
нечетность функции. Запишите тему урока: «Чётные
и нечётные функции», наша задача – научиться
определять чётность и нечётность функции,
выяснить значимость этого свойства в
исследовании функций и построении графиков.
Итак, найдём определения в учебнике и прочитаем
(стр. 110). Слайд
Опр. 1 Функция у = f (х), заданная на множестве Х называется чётной, если для любого значения х Є Х выполняется равенство f(–х)= f(х). Приведите примеры.
Опр. 2 Функция у = f (х), заданная на множестве Х называется нечётной, если для любого значения х Є Х выполняется равенство f(–х)= –f(х). Приведите примеры.
Где мы встречались с терминами «четные» и
«нечётные»?
Какие из данных функций будут чётными, как вы
думаете? Почему? Какие нечётными? Почему?
Для любой функции вида у = хn, где n
– целое число можно утверждать, что функция
нечётна при n – нечётном и функция чётна при n
– чётном.
– Функции вида у = и у = 2х – 3 не являются ни
чётным , ни нечётными, т.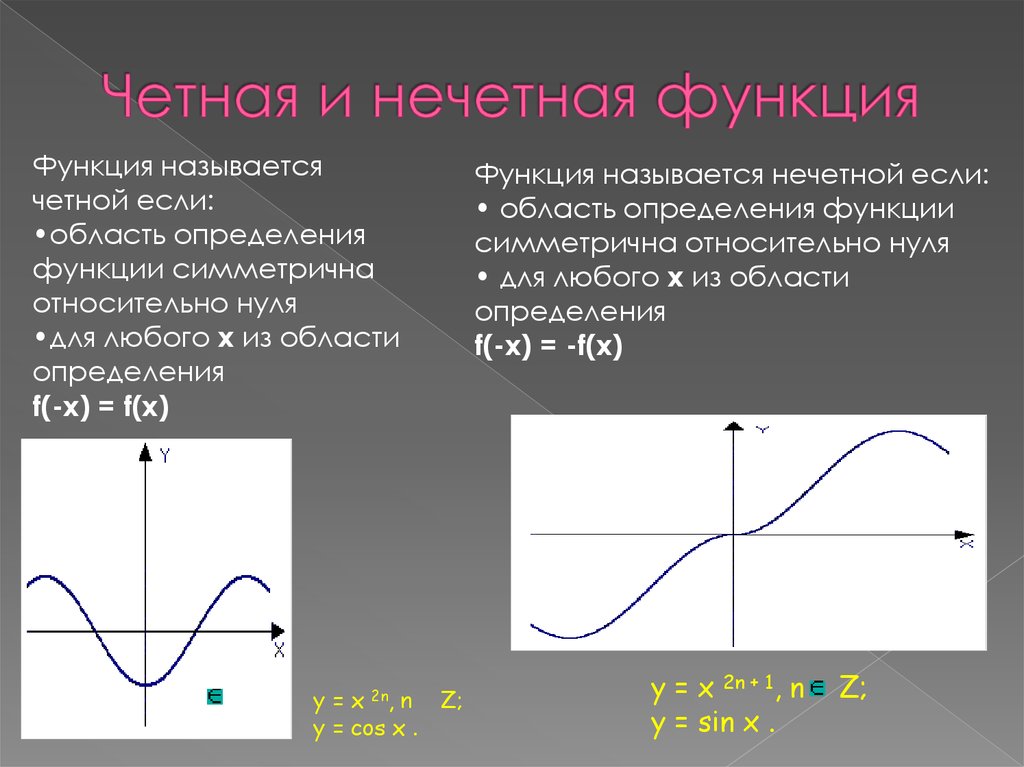
к. не выполняются
равенства f(– х) = – f(х), f(–
х) = f(х)
Изучение вопроса о том, является ли функция чётной или нечётной называют исследованием функции на чётность. Слайд
В определениях 1 и 2 шла речь о значениях функции при х и – х, тем самым предполагается, что функция определена и при значении х, и при – х.
Опр 3. Если числовое множество вместе с каждым своим элементом х содержит и противоположный элемент –х, то множество Х называют симметричным множеством.
Примеры:
(–2;2), [–5;5]; (∞;∞) – симметричные множества, а [0; ∞), (2;–2], [–5;4] – несимметричные.
– У чётных функций область определения –
симметричное множество? У нечётных?
– Если же D(f) – несимметричное множество, то
функция какая?
– Таким образом, если функция у = f(х)
– чётная или нечётная, то её область определения
D(f) – симметричное множество.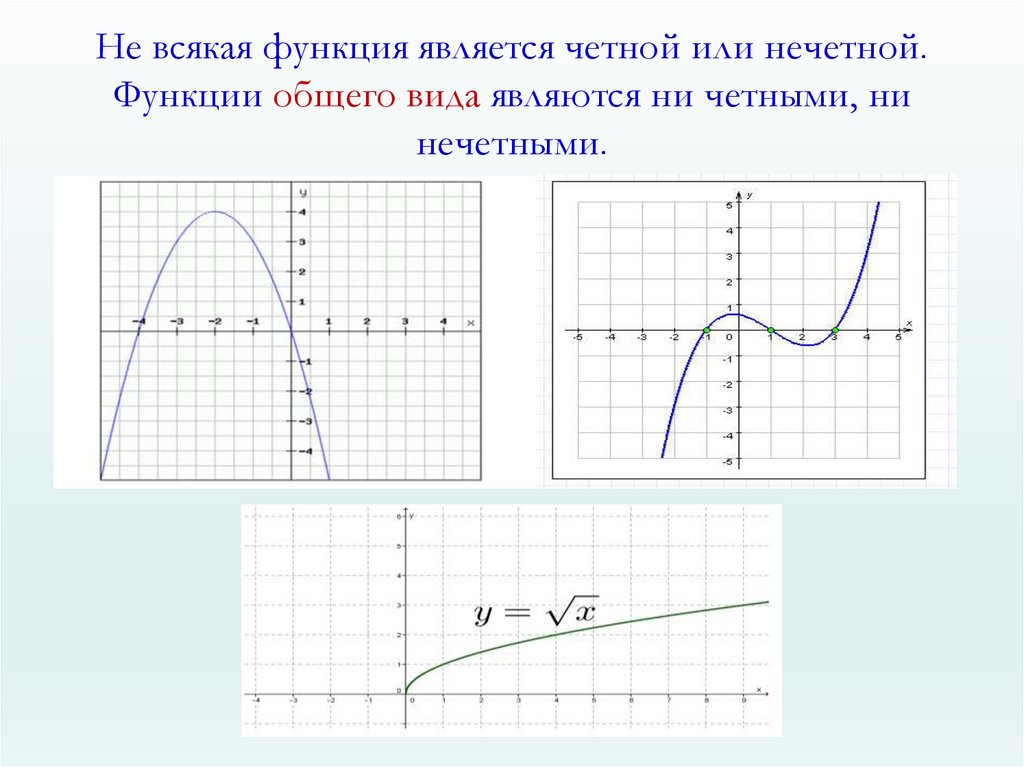
А верно ли
обратное утверждение, если область определения
функции симметричное множество, то она чётна,
либо нечётна?
– Значит наличие симметричного множества
области определения – это необходимое условие,
но недостаточное.
– Так как же исследовать функцию на четность?
Давайте попробуем составить алгоритм.
Слайд
Алгоритм исследования функции на чётность
1. Установить, симметрична ли область определения функции. Если нет, то функция не является ни чётной, ни нечётной. Если да, то перейти к шагу 2 алгоритма.
2. Составить выражение для f(– х).
3. Сравнить f(– х).и f(х):
- если f(– х).= f(х), то функция чётная;
- если f(– х).= – f(х), то функция нечётная;
- если f(– х) ≠ f(х) и f(–
х) ≠ –f(х), то функция не является ни
чётной, ни нечётной.
Примеры:
Исследовать на чётность функцию а) у = х5 +; б) у = ; в) у= .
Решение.
а) h(х) = х5 +,
1) D(h) = (–∞; 0) U (0; +∞), симметричное множество.
2) h (– х) = (–х)5 + – х5 –= – (х5 +),
3) h(– х) = – h (х) => функция h(х) = х5 + нечётная.
б) у = ,
у = f(х), D(f) = (–∞; –9)? (–9; +∞), несимметричное множество, значит функция ни чётная, ни нечётная.
в) f(х) = , у = f (х),
1) D(f) = (–∞; 3] ≠ [3; +∞), симметричное множество.
2)f (– х) == ;
3) f (– х) = f (х) => функция f(х) = чётная.
Итак, по аналитической записи можно определить
четность функции? Но кроме аналитического
способа задания функции есть другие.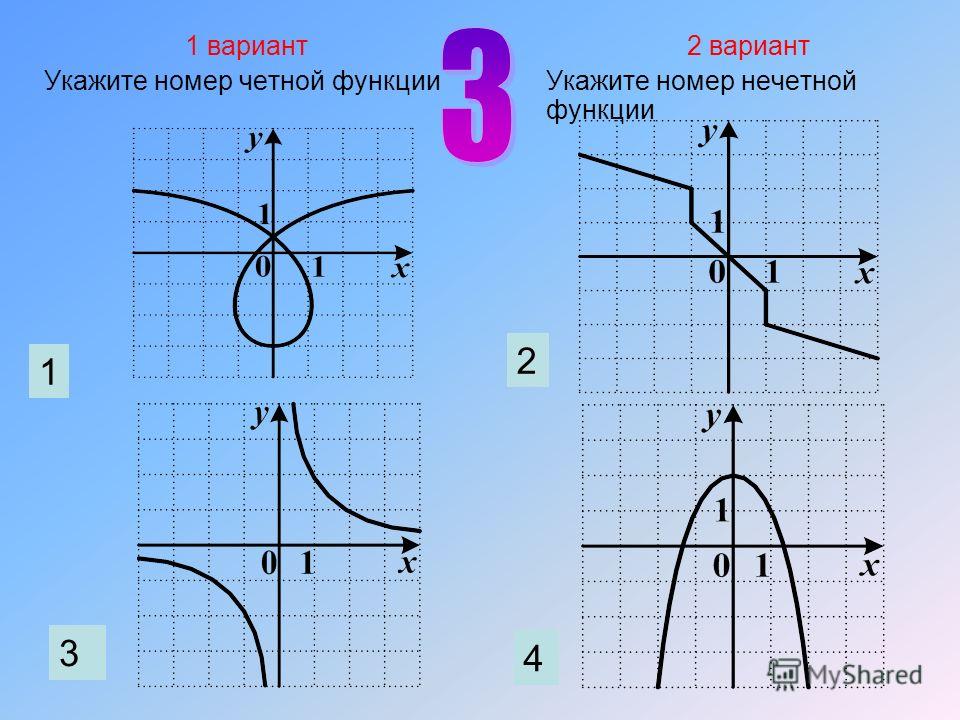
Какие? Можно
ли по графику функции выявить её четность?
Давайте вернёмся к заданию, которое мы выполняли
в начале урока, найдём соответствие между
аналитически заданными функциями и их
графиками (изображёнными на доске), что вы
находите примечательного в расположении
графиков чётных функций? Нечётных?
Слайд.
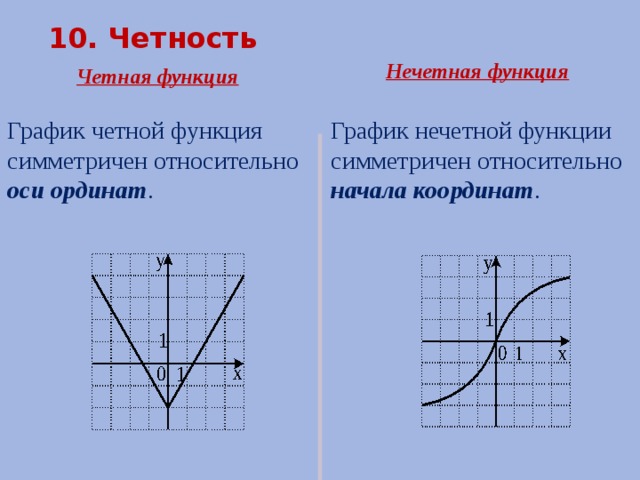
Вывод:
- График чётной функции симметричен относительно оси у.
- График нечётной функции симметричен относительно начала координат.
– Верны ли обратные утверждения?
- Если график функции у = f(х) симметричен относительно оси ординат, то у = f(х) – чётная функция.
- Если график функции у = f(х) симметричен
относительно начала координат, то у = f(х)
– нечётная функция.
Доказательство данных утверждений разобрать дома самостоятельно по учебнику и записать в тетрадь.
– Какова же значимость свойства четности или
нечётности функции? Зачем нужно изучать
свойство чётности функций .В план свойств
функций свойство чётности вы поставили бы на
какое порядковое место
5. Первичное закрепление
Самостоятельная работа
Вариант 1 1. Является ли симметричным заданное множество: а) [–7;7]; б) (∞; –2), (–4; 4]? |
Вариант 2 1. Является ли симметричным заданное множество: а) [–2;2]; б) (∞; 0], (0; 7) ? |
| 2. Исследуйте на чётность функцию: а); б) у = х· (5 – х2).  |
2. Исследуйте на чётность функцию: а) у = х2 · (2х – х3), б) у = |
| 3. На рис. построен график у = f(х),
для всех х, удовлетворяющих условию х?
0. Постройте график функции у = f(х), если у = f(х) – чётная функция.
|
3. На рис. построен график у = f(х),
для всех х, удовлетворяющих условию х ? 0. Постройте график функции у = f(х), если у = f(х) – нечётная функция.
|
Взаимопроверка по слайду.
6. Задание на дом: №11.11, 11.21,11.22;
Доказательство геометрического смысла
свойства чётности.
***(Задание варианта ЕГЭ ).
1. Нечётная функция у = f(х) определена на всей числовой прямой. Для всякого неотрицательного значения переменной х значение этой функции совпадает со значением функции g(х) = х(х + 1)(х + 3)(х – 7). Найдите значение функции h(х) = при х = 3.
7. Подведение итогов
Приложения
Счет, математика и статистика — Набор академических навыков
Нечетные и четные функции
ContentsToggle Главное меню 1 Нечетные функции 1.1 Определение 2 Четные функции 2.1 Определение 3 Свойства 4 Периодические функции 4.1 Определение 5 Рабочие тетради
Нечетные функции
Определение
Функция $f$ является нечетной , если для всех $x$ и $-x$ в области $f$ выполняется следующее уравнение: \[-f(x) = f(-x)\] Геометрически , график нечетной функции обладает вращательной симметрией относительно начала координат, что означает, что его график остается неизменным после поворота на $180^{\circ}$ вокруг начала координат.
92$ и $\cosx$.
Свойства
Некоторые основные свойства нечетных и четных функций:
- Единственная функция, областью определения которой являются все действительные числа, как нечетные, так и четные, — это постоянная функция, тождественно равная нулю, $f(x) =0$.
- Сумма двух четных функций четна, а сумма двух нечетных функций нечетна.
- Разность двух четных функций четна, а разность двух нечетных функций нечетна.
- Произведение двух четных функций четно, а произведение двух нечетных функций четно.
- Произведение четной функции на нечетную является нечетной функцией.
- Частное двух четных функций четно, а частное двух нечетных функций четно.
- Частное четной функции и нечетной функции является нечетной функцией.
- Производная четной функции нечетна, а производная нечетной функции четна.
- Композиция двух четных функций четна, а композиция двух нечетных функций нечетна.
- Композиция четной функции и нечетной функции четна.
Примечание : сумма четной и нечетной функции не является ни четной, ни нечетной, если только одна из функций не равна нулю в данной области.
Периодические функции
Определение
Периодическая функция — это функция, которая повторяется через равные промежутки времени или периодов . Функция $f$ называется периодической с периодом $P$, если: \[f(x+P)=f(x)\] для всех значений $x$ и где $P$ — ненулевая константа.
Периодические функции используются для описания колебаний и волн, а наиболее важными периодическими функциями являются тригонометрические функции. Любая непериодическая функция называется апериодической .
Пример : Функция синуса является периодической с периодом $2\pi$, поскольку $\sin(x+2\pi)=\sin x$ для всех значений $x$. Функция повторяется на интервалах длины $2\pi$, что также хорошо видно на графике.
{2}[/latex] или [latex]f\left(x\right)=|x|[/latex ] приведет к исходному графику. Мы говорим, что эти типы графиков симметричны относительно оси y. Функции, графики которых симметричны относительно оси у, называются 9{3}\text{}[/latex]или[latex]\text{}f\left(x\right)=\frac{1}{x}\text{}[/latex] были отражены поверх и осей, результатом будет исходный график, как показано на рисунке 3-11.
Мы говорим, что эти графы симметричны относительно начала координат. Функция с графиком, симметричным относительно начала координат, называется 9{x}\text{}[/latex] не является ни четным, ни нечетным. Кроме того, единственная функция, которая одновременно является четной и нечетной, — это константная функция [латекс]\текст{}f\left(x\right)=0[/latex].
Функция называется четной функцией , если для каждого ввода [латекс]\текст{}х[/латекс]
[латекс]f\left(x\right)=f\left(-x\right)[ /latex]
График четной функции симметричен относительно оси [latex]y\text{-}[/latex].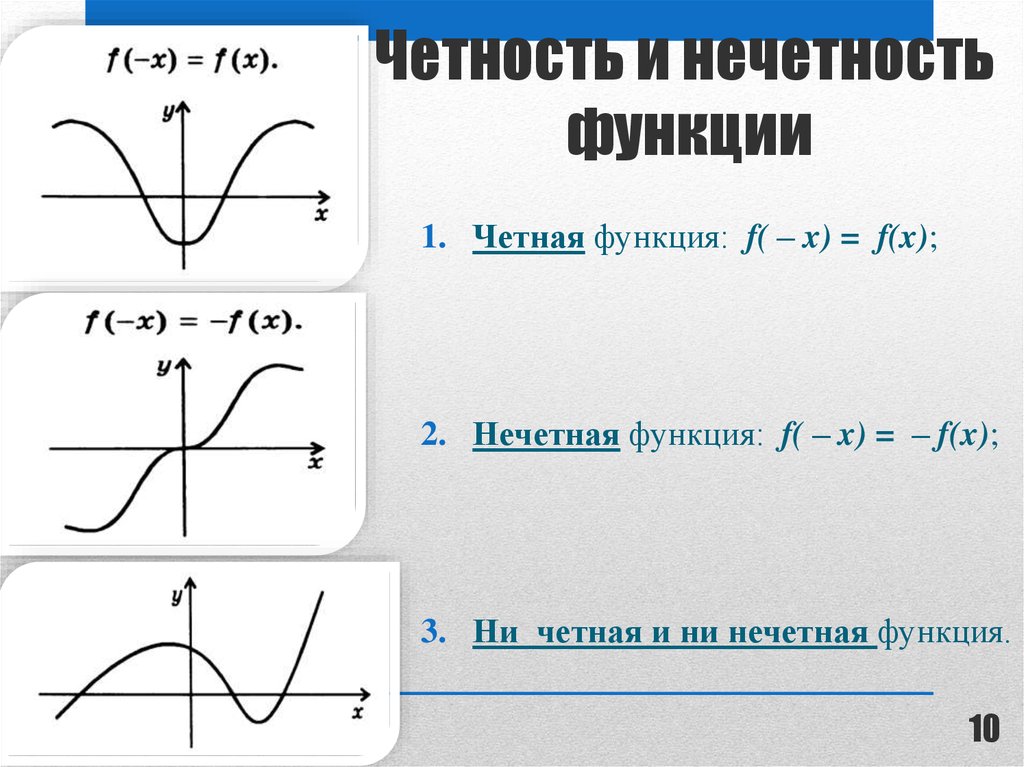
Функция называется нечетной функцией , если для каждого ввода [латекс]\текст{}х[/латекс]
[латекс]f\влево(х\вправо)=-f\влево(-х\вправо)[/латекс]
График нечетной функции симметричен относительно начала координат.
Учитывая формулу функции, определите, является ли функция четной, нечетной или ни одной из них.
- Определите, удовлетворяет ли функция [латекс]\текст{}f\left(x\right)=f\left(-x\right)\text{}[/latex]. Если да, то даже.
- Определите, удовлетворяет ли функция [латекс]\текст{}f\left(x\right)=-f\left(-x\right)\text{}[/latex]. Если это так, то это странно. 9{3}+2x\text{}[/latex] четное, нечетное или ни то, ни другое? Анализ
Рассмотрим график [latex]\text{}f\text{}[/latex] на рис. 3-12. Обратите внимание, что график симметричен относительно начала координат. Каждой точке [латекс]\текст{}\левый(х,у\правый)\текст{}[/латекс] на графике соответствует точка [латекс]\текст{}\левый(-х,-у\ справа)\text{}[/latex] также находится на графике.
