Примеры положительные и отрицательные числа: Сложение Чисел с Разными Знаками

Положительные и отрицательные числа | Образовательная социальная сеть

Слайд 1

П оложительные и отрицательные числа Подготовлено учеником 6в класса Тараненко Сергеем.

Слайд 2

Вступление. Каждый день в повседневной жизни нас окружают различные числа. Мы уже знакомы с таким понятием как натуральные числа. Ну а сегодня мы поговорим об отрицательных числах.

Слайд 3

Примеры отрицательных чисел Отрицательные числа окружают нас каждый день : когда мы смотрим прогноз погоды, измеряем глубину в море или высоту горы. Например когда мы смотрим прогноз погоды мы видим возле городов специальные обозначения, возле которых показана температура

Слайд 4

Примеры отрицательных чисел Еще один пример отрицательных чисел – это зрение человека. — 3,25

Слайд 5

Координатная прямая. Координатная прямая это прямая линия, на которой располагаются все числа: и отрицательные и положительные. Выглядит следующим образом: Здесь показаны только числа от −5 до 5. На самом деле координатная прямая бесконечна. На рисунке представлен лишь её небольшой фрагмент.

Слайд 6

Числа на координатной прямой Числа на координатной прямой отмечают в виде точек. На рисунке жирная чёрная точка является началом отсчёта. Начало отсчёта начинается с нуля. Слева от начала отсчёта отмечают отрицательные числа, а справа — положительные .

Слайд 7

Сравнение отрицательных и положительных чисел Например, сравним два числа: −5 и 3. Минус пять меньше , чем три, несмотря на то, что пятёрка бросается в глаза в первую очередь, как цифра большая, чем три. Связано это с тем, что −5 является отрицательным числом, а 3 — положительным. На координатной прямой можно увидеть, где располагаются числа −5 и 3 Из этого следует : Любое отрицательное число меньше любого положительного числа

Слайд 8

Ноль больше любого отрицательного числа Видно, что 0 лежит правее, а −3 левее. А мы говорили, что «чем правее, тем больше» . И правило говорит, что ноль больше любого отрицательного числа Ноль меньше любого положительного числа Видно, что на координатной прямой 0 располагается левее, а 4 правее. А мы говорили, что «чем левее, тем меньше» . И правило говорит, что ноль меньше любого положительного числа.

Слайд 9

Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой Видно, что −4 лежит левее, а −1 правее. А мы говорили, что «чем левее, тем меньше» . И правило говорит, что из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой.

Слайд 10

Задания для самопроверки

Слайд 11

Задача 1. Решаем устно Карлсон простудился , и вечером его температура с 36.6 повысилась на 2,3. Но утром ему стало легче, и температура снизилась на 1,8. Какой была температура у Карлсона вечером и утром? 1)36,6+2,3=38,9 — вечером 2)38,9-1,8=37,1 — утром

Слайд 12

Задача 2. Решаем устно Сравните : 2 и -5 3 и -720 80 и -75 -45 и 44 15 и -15 65 и -89

Слайд 13

Задача 3 Какие из чисел -5 ; 6 ; 8 ; -10 ; 0 ; -4 ; являются : а ) положительными; б ) Отрицательными? А) 6 ; 8 Б) -5 ; -4 ; -10

Слайд 14

Закрепим материал Правила сравнения отрицательных и положительных чисел : Правило 1. Любое отрицательное число меньше любого положительного числа. Правило 2. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. Правило 3. Ноль больше любого отрицательного числа. Правило 4. Ноль меньше любого положительного числа.

Слайд 15

Узнали что такое отрицательные числа. Научились определять числа на координатной прямой. Научились сравнивать положительные, отрицательные числа и ноль. Узнали где использую отрицательные числа

Сравнить отрицательные числа пример. Сравнение чисел

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Назовите координаты точек, изображенных на координатной прямой Назовите точки, которые лежат левее нуля Назовите точки, которые лежат правее нуля.

Между какими целыми числами на координатной прямой расположено число: -3 0 2,6

Найди соответствие 7 0,1 5 -0,5 -0,1 -5 0,5 -7

«Восстанови равенство» │12│= │0│= │- 6│= 12 6 0

Числа отрицательные новые для вас Лишь совсем недавно изучил ваш класс Сразу же прибавилось вам теперь мороки: Изучить все правила сравнения на уроке.

СРАВНЕНИЕ ЧИСЕЛ

Девиз: Вместе возьмемся, всего добьемся

15 28 13,7 8,6 12,3 о -8 6 — 25 -32.

1 Вывести правило сравнения положительных чисел и нуля. 1. Отметьте точки на координатной прямой: А(3), В(5), D(1), O(0). 2 . Левее или правее находятся точки относительно нуля? 3 . Сравните с помощью координатной прямой числа: 3 * 0 5 * 0 1 * 0 4 . Сформулируйте правило сравнения любого положительного числа и нуля. Приведите свои примеры. Положительное число всегда ……… нуля больше

Вывести правило сравнения отрицательных чисел и нуля. 1. Отметьте на координатной прямой точки: А(-3), В(-5), D (-1), O (0). 2. Левее или правее расположены точки относительно нуля? 3. Сравните с помощью координатной прямой числа: -3 * 0 -5 * 0 0 * -1 4. Сделайте вывод о сравнении любых отрицательных чисел с нулем. Приведите свои примеры. Отрицательное число всегда ………..… нуля. меньше

3. Вывести правило сравнения положительных и отрицательных чисел 1.Отметьте на координатной прямой точки: А(-5), В(2), O(0), С(-2) 2.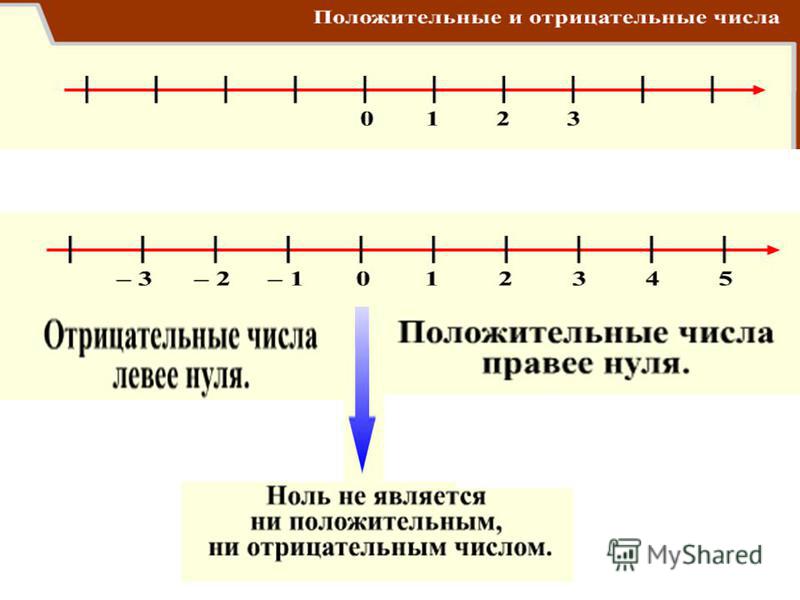 Точки с какой координатой лежит левее точки О(0), какая правее токи О(0)? 3.Выполните сравнение: -5 * 2 -2 * 2 4 . Какое больше из чисел положительное или отрицательное? 5 . Сформулируйте правило сравнения отрицательных и положительных чисел. 6. приведите свои примеры Положительное число всегда ……….. отрицательного. больше

1. Отметьте на координатной прямой точки: А(-3), В(-2). 2. Точка с какой координатой лежит левее? 3. Найдите модули этих чисел. |- 3| = |-2|= 4. Сравните модули. Какой из двух модулей больше? |- 3| * |-2| 5. Сравните числа -3 и -2. Какое число будет меньше? -3 * -2 6. Какое из двух отрицательных чисел будет меньше? 7. Сформулируйте правило сравнения двух отрицательных чисел. Приведите свои примеры. IV. Вывести правило сравнения двух отрицательных чисел. Из двух отрицательных чисел меньше то, модуль которого ………. больше

1.Положительное число всегда больше отрицательного. 2. Из двух отрицательных чисел меньше то, модуль которого больше. 3.Отрицательное число всегда меньше нуля.

4. Положительное число всегда больше нуля.

*** Точка с меньшей координатой лежит на координатном луче левее точки с большей координатой

Положительное число всегда ……….. отрицательного. больше Из двух отрицательных чисел меньше то, модуль которого ………. больше Отрицательное число всегда ………..… нуля. меньше Положительное число всегда ……… нуля. больше

Я хорошо понял, как сравнивают числа и могу научить другого -Я не все понял, у меня были затруднения

Спасибо Вам за урок! Вы- большие молодцы!

В этом уроке мы вспомним, как сравнить положительные числа и рассмотрим сравнение отрицательных чисел.

Начнем с задачи. Днем температура воздуха была +7 градусов, к вечеру понизилась до +2 градусов, ночью стала -2 градуса, а на утро еще понизилась до -7 градусов. Как изменялась температура воздуха?

В задаче речь идет о понижении, т.е. об уменьшении температуры. Значит, в каждом случае конечное значение температуры меньше начального, поэтому 2

Обозначим числа 7, 2, -2, -7 на координатной прямой.

Вспомним, что на координатной прямой большее положительное число расположено правее.

Посмотрим на отрицательные числа, число -2 находится правее, чем -7, т.е. для отрицательных чисел на координатной прямой сохраняется тот же порядок: при движении точки вправо ее координата увеличивается, а при движении точки влево ее координата уменьшается.

Можно сделать вывод: Любое положительное число больше нуля и больше любого отрицательного числа. 1 > 0; 12 > -2,5. Любое отрицательное число меньше нуля и меньше любого положительного числа. -59

Сравнивать рациональные числа (т.е. все и целые, и дробные числа) удобно с помощью модуля.

Положительные числа раполагаются на координатной прямой в порядке возрастания от начала координат, значит чем дальше число от начала координат, тем больше длина отрезка от нуля до числа, т.е. его модуль. Следовательно, из двух положительных чисел больше то, модуль которого больше.

При сравнении двух отрицательных чисел большее будет расположено правее, то есть ближе к началу отсчёта. Значит, его модуль (длина отрезка от нуля до числа) будет меньше. Таким образом, из двух отрицательных чисел больше то, у которого модуль меньше.

Например. Сравним числа -1 и -5. Точка, соответствующая числу -1расположена ближе к началу отсчёта, чем точка, соответствующая числу -5. А значит длина отрезка от 0 до -1 или модуль числа -1 меньше, чем длина отрезка от 0 до -5 или модуль числа -5 , значит, число -1, больше, чем число -5.

Делаем выводы:

При сравнении рациональных чисел обращаем внимание на:

– знаки: отрицательное число всегда меньше положительного и нуля;

– на расположение на координатной прямой: чем правее, тем больше;

– на модули: у положительных чисел модуль больше и число больше, у отрицательных чисел модуль больше, а число меньше.

Литература:

1. Математика.6 класс: поурочные планы к учебнику И.И. Зубаревой, А.Г. Мордковича //автор-составитель Л.А. Топилина. Мнемозина 2009 г.

2. Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. И.И. Зубарева, А.Г. Мордкович.- М.: Мнемозина, 2013 г.

3. Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. /Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2013 г.

4. Справочник по математике —

Репетитор по математике

5. Справочник для учащихся в средней школе

Отрицательные числа: Связь с повседневной жизнью

LearnPracticeDownload

Многие считают математику сложным предметом. Нужно спросить о пользе изучения математики и реальных приложений математики. Математика повсюду, как и значение чисел и их связь с повседневной жизнью. Математика — это все о числах, и числа могут быть сгруппированы в различные типы чисел, такие как целые числа, целые числа, действительные числа, комплексные числа, рациональные, иррациональные числа и многие другие типы.

Все отрицательные числа имеют значение меньше нуля. Отрицательные числа используются со знаком минус или тире (-) рядом с числом. На числовой прямой отрицательные числа — это числа, представленные слева от начала координат (нуля), и их значения меньше нуля.

1.	Применение отрицательных чисел в реальной жизни
2.	Решенные примеры
3.	Практические вопросы
4.	Часто задаваемые вопросы

Применение отрицательных чисел в реальной жизни

Было бы странно отметить, что число меньше нуля. Поскольку мы часто думаем, что ноль ничего не значит. Например, если у вас в коробке осталось 0 штук ручек, у вас нет ручек. Ничего не осталось. В этом случае трудно представить себе меньше, чем ничего. Но в реальной жизни бывают ситуации, когда вы используете числа меньше нуля. Некоторые из их реальных применений приведены ниже. 9{\circ} \mathrm{F}\) по шкале Фаренгейта.

2. Деньги

Отрицательные числа часто используются для обозначения кредита в банковской системе. Отрицательный баланс банка указывает на то, что деньги были перерасходованы. Таким образом, каждый раз, когда кто-то должен деньги, это обозначается отрицательным количеством денег.

3. Лифт/Лифт

Лифт или лифт — это вертикальный транспорт, который перемещает людей или товары между этажами здания. Как правило, в зданиях первый этаж считается нулевым, поэтому переходы на другие этажи ниже первого этажа, такие как подвал или парковка, помечаются отрицательными числами/целыми числами (например, -1, -2, -3.)

4. Уровень моря

Уровень моря (или средний уровень моря; MSL) — средний уровень океанов Земли. Этот уровень поверхностных вод действует как точка отсчета для измерения высот выше или ниже него. Возвышение или понижение географического местоположения — это его высота над или под уровнем моря. Географические местоположения ниже уровня моря представлены с использованием отрицательных чисел (например, -100 футов над уровнем моря)

5. Викторины/игры

Различные виды игр или видов спорта используют отрицательные числа при подсчете очков/баллов или для предоставления штраф.

Неправильный ответ в викторине или проигрыш в игре могут привести к потере очков (такие очки считаются отрицательными числами). Более того, в некоторых видах спорта, таких как гольф, при подсчете очков используются отрицательные числа.

Важные примечания

• Отрицательные числа — это целые числа со знаком минус, которые обычно обозначают низкое значение, отсутствие или уменьшение какого-либо качества или количества.
• Отрицательные числа противоположны положительным числам (+) и отмечаются в левой части числовой строки.

Пример: 1) Ночью температура упала с 5 ºC до -14 ºC. На сколько градусов упала температура?

Падение температуры = от 5 ºC до -15 ºC

5 -15 = 10 ⇒ 10 ºC

Температура упала на 10 ºC

Пример: 2) Найдите предшественник следующих целых чисел:
А) -4
B) 16

A) Предшественник -4 равен -4 -1 = -5
B) Предшественник 16 равен 16 -1 = 15

Связанные темы

• Системы счисления
• Целые числа
• Целые числа

 

 

1. Пример 1. В метеосводке указано, что температура в городе повысилась с -10 до 20 градусов по Цельсию. Что такое повышение температуры?

    

   Решение: Разница между заданной температурой представляет собой повышение температуры и может быть рассчитана как 20 — (-10) = 30

   Повышение температуры составляет 30 градусов по Цельсию.

2. Пример 2. Натан завершил первый раунд викторины с 200 баллами. Во втором раунде он набрал -300 очков, а в третьем — 200 очков. Каков был его общий счет в конце третьего раунда?

   Решение: Счет Натана в первом раунде: 200 очков

   Счет Натана после второго раунда: 200 + (-300) = -100 очков

   Его счет после третьего раунда: -100 + 200 = 100 очков в конце третьего раунда.

3.  

   Пример 3. Найдите предшественник следующих целых чисел:
   . А) -9
   Б) 0
   В) -87
   D) -23

   Решение:  Предшественник означает число, предшествующее данному числу. Итак, если вы хотите найти предшественника данного числа, вычтите 1 из данного числа.

   A) Предшественником -9 является -9 -1 = -10
   B) Предшественник 0 равен 0 -1 = -1
   C) Предшественник -87 равен -87-1 = -88
   D) Предшественник -23 равен -23-1 = -24

перейти к слайдуперейти к слайдуперейти к слайду

 

 

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

 

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду

 

 

Часто задаваемые вопросы об отрицательных числах: как отрицательные числа используются в повседневной жизни

3?

Отрицательные числа обычно используются для описания температуры ниже точки замерзания, кредита/причитающихся денег, высоты над/ниже уровня моря, уровня лифта, когда он ниже уровня земли, в качестве штрафа в викторинах/играх и т.  д.

Почему мы используем отрицательные числа?

Мы используем отрицательные числа, чтобы описать недостаток количества или уменьшение/уменьшение количества. Отрицательные числа обычно используются для описания температуры ниже точки замерзания, кредита денег, высоты ниже уровня моря, уровня лифта, когда он ниже уровня земли, отрицательных результатов на экзаменах, в качестве штрафа в викторинах/играх и т. д.

Как Положительные и отрицательные числа, используемые в реальной жизни?

Отрицательные и положительные числа используются в реальной жизни для описания расстояния от контрольной точки. Например, для лифта уровень земли считается равным 0, а в качестве точки отсчета этажи выше уровня земли обозначаются положительными числами. Этажи ниже уровня земли обозначаются отрицательными числами.

Как целые числа используются в повседневной жизни?

Целые числа обычно используются для описания температуры выше/ниже точки замерзания, дебета/кредита денег, географического уровня выше/ниже уровня моря, уровня лифта, когда он выше/ниже уровня земли, в качестве бонуса и штрафа в викторинах/ игры и т. д.

Является ли 0 действительным числом?

Да, 0 ноль — действительное число. Действительные числа могут быть положительными или отрицательными и включать число 0.

Скачать БЕСПЛАТНЫЕ учебные материалы

Целочисленные рабочие листы

Математические рабочие листы и
наглядная программа

Что такое положительные и отрицательные числа?

Числа — это математические значения или цифры, используемые для измерения или вычисления величин. Он также представлен цифрами 3, 4, 8 и т. д. Некоторые другие примеры чисел: целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д.

Система включает в себя различные типы чисел, например, простые числа, нечетные числа, четные числа, рациональные числа, целые числа и т. д. называется системой счисления. Эти типы чисел могут быть выражены как цифрами, так и словами соответственно.

Например, , такие числа, как 55 и 75, выраженные в виде цифр, также могут быть записаны как пятьдесят пять и семьдесят пять.

Система счисления или Система счисления определяется как элементарная система для выражения чисел и цифр. Это уникальный способ представления чисел в арифметической и алгебраической структуре.

Он используется в различных арифметических значениях, применимых для выполнения различных арифметических операций, таких как сложение, вычитание, умножение и т. д., которые применяются в повседневной жизни для целей вычислений. Значение числа определяется цифрой, ее разрядным значением в числе и основанием системы счисления.

Как правило, числа также известны как цифры, которые представляют собой математические значения, используемые для счета, измерения, маркировки и измерения основных величин.

Числа подразделяются на два типа:

Положительные числа, Отрицательные числа: и далее классифицируются по различным типам, таким как натуральные числа, рациональные числа, целые числа, десятичные числа, целые числа и т. д.

Положительные числа: Положительные числа это числа больше нуля, лежащие справа от числовой прямой. Пример: 0, 1, 2, 3, 4…

Отрицательные числа: Отрицательные числа — это числа, меньшие нуля и лежащие в левой части числовой прямой. Пример:  … -5, -4, -3, -2, -1, 0 

Что такое положительные и отрицательные числа?

Ответ:

Отрицательное положительное иногда отрицательное, иногда положительное, потому что, когда мы складываем две цифры с разными операндами, в результате получается знак старшей цифры. будь то отрицательный или положительный.

Пример: Если мы сложим -8 и 7 , то

    – 8 + 7 = -1

на старшем операнде.

Существует Определенные правила отрицательного положительного

Если мы добавим два положительных числа, то получит положительное число

( +) + ( +) = +

, если мы добавим одно положительное и одно отрицательное число, затем выше операнд будет ответом

( +) + (-) = ± , в какой бы стороне или

, если мы добавим два отрицательных числа, то результат будет в отрицательном

(-) + (-) =-или -5 + (-9)  = -5 -9  = -14

если мы умножим одно положительное и одно отрицательное число, то результат всегда будет отрицательным0003

Если мы делим одно положительное и одно отрицательное число, то результат всегда будет отрицательным

4/( -2) = -2 или (-4)/2 = -2

Вопросы

Вопрос.

No related posts.