Урок 12. Программирование в Mathcad — циклы
Во втором уроке по программированию в Mathcad мы рассмотрим циклы – различные повторяющиеся вычисления. Помимо циклов мы рассмотрим, как можно находить ошибки в программах.
В этом уроке мы изучим три новые команды:
- for – для циклов for.
- while – для циклов while.
- return – как команду для отслеживания ошибок.
Остановка вычислений
Операции Mathcad, которые мы рассматривали ранее, достаточно безвредны – они не заставят Ваш компьютер «зависнуть». Но с циклами это не так. Поэтому для начала следует изучить команды в меню Вычисления –> Элементы управления:
Здесь находятся четыре кнопки:
- Автоматический расчет.
- Остановить все расчеты.
- Рассчитать.
- Отключить область.
Кнопка «Автоматический расчет» обычно включена. Она отключается при нажатии на кнопку «Остановить все расчеты». Зеленый индикатор в левом нижнем углу становится серым. «Остановить все расчеты» служит для прекращения всех расчетов в документе на случай, если что-то пошло не так. При автоматическом расчете вычисления производятся лишь в том случае, когда происходят какие-либо изменения. С помощью кнопки «Рассчитать» можно сделать пересчет всего документа. Кнопка «Отключить область» прекращает вычисления в тех математических областях, которые Вы выбрали.
На рисунке ниже видно, что область серая – значит, она отключена:
Нажмите на нее, затем на кнопку «Отключить область». Тем самым Вы запустите расчет в области. Вычисление займет некоторое время:
Его можно прекратить, нажав на кнопку «Остановить все расчеты», затем отключив область и снова включив автоматический расчет.
Циклы
for
Циклы forприменяются, когда заранее известно число повторений вычислений. Программа ниже формирует вектор из n+1 элементов. Значения начинаются с нуля и имеют шаг 1.
Цикл forначинается со второй строки. Он включает в себя счетчик (здесь – i), который является локальной переменной-диапазоном. Эту строку можно прочитать как: «Для диапазона целых чисел от 0 до nвключительно сделать: …». Затем следуют выполняемые действия – в нашем случае это простое присваивание. Когда цикл завершается, программа выполняет действия на следующей строке – здесь это оператор return.
Составим программу.
Задайте имя программы-функции, вставьте программную структуру (вертикальная линия) и определение цикла forиз меню Математика –> Операторы и символы –> Программирование или с помощью сочетания клавиш [Ctrl+Shift+”]:
Определите имя переменной-счетчика:
Определите диапазон счетчика:
Введите команды тела цикла и оператор return:
Проверим программу:
Как видно, использование дробных или отрицательных чисел – не лучшая идея. Вы можете изменить точку начала, но этого лучше избегать:
Видите нули, которые появились в начале вектора? Причиной появления этих нулей является то, что если не определить некоторые элементы вектора, то им автоматически присвоится значение 0:
Циклы
while
На рисунке ниже – простейший цикл while, который делает то же самое, что и предыдущий цикл for:
До цикла необходимо создать строку, содержащую определение начального значения счетчика. Следующую строку можно прочитать как «Выполнять цикл, пока соблюдается условие i?n». После определения элемента вектора нужно задать команду на увеличение переменной-счетчика, так как в цикле while это не происходит автоматически.
Другой, более «реалистичный», пример цикла while вычисляет экспоненту отрицательного числа, используя разложения в ряд:
Суммирование будем производить с помощью цикла while. Будем проверять, насколько изменяется общая сумма S при каждом увеличении k. Если абсолютное значение этого изменения достаточно мало, цикл завершится. Чтобы начать цикл, необходимо определить первые два элемента вектора:
Кроме того, мы определили начальное значение суммы S и счетчика k. Дальнейшие вычисления производятся в цикле:
Проверка:
С положительными числами программа работает хорошо, но для работы с отрицательными она не предназначена.
Отладка
Одна из простых технологий отладки программ – вывод промежуточных результатов вычислений и их сравнение с тем, какие значения должны быть. Пример на цикле while:
Число элементов вектора верное, но второй элемент неправильный. Похоже, что последние элементы нашего вектора получили правильный индекс, а второй элемент (с индексом 1) – нет. Мы можем проверить, какой индекс получил второй элемент, вставив «returni» в первую строку цикла while. Программа остановит вычисление и вернет значение i:
Вероятно, Вы уже поняли, что ошибка в первой строке. Замените 2 на 1, удалите дополнительную строку return, и Вы получите верный результат.
Можно получить выходное значение итерации цикла, отличной от первой. Для этого требуется применить оператор условия if. В программе ниже выводится элемент вектора после третьей итерации цикла:
После отладки всегда следует удалять дополнительные строки, которые Вы вводите, так как программа всегда прекращает работу после первого оператора return.
Подпрограммы
Примеры программ в этом уроке малы. Настоящие программы могут быть намного больше. В других языках программирования они обычно составляются как основная программа и следующие за ней подпрограммы и процедуры. Эти более малые программы можно составлять сами по себе и затем вызывать их в основной программе. Также могут быть подподпрограммы и так далее.
Ваша собственная программа
Когда Вы начинаете составлять свою собственную программу, может показаться, что Вы находитесь в замкнутом круге: чтобы начать, нужен опыт; чтобы получить опыт, нужно начать.
Начать необходимо, но не следует начинать с набора команд в Mathcad! Для начала следует подготовиться.Прежде всего, нужно решить, что делает Ваша программа. Для больших, сложных программ это, как правило, нетривиальная задача. Какие выходные данные нужны, и какие входные для этого необходимы?
Возможно, самая сложная часть – это представление того, как будет получен желаемый результат. Будьте готовы потратить несколько листов бумаги. Нарисуйте различные структурные диаграммы и детализируйте их. Вы знаете следующие элементы:
- Ввод (input)
- Действие (или определение)
- Вывод (output)
- Одиночное ответвление (if..elseили if..if)
- Многократное ответвление (if..if..if)
- Цикл for
- Цикл while
Решите, какие вспомогательные переменные (например, счетчики) необходимы, и какие имена Вы собираетесь им дать. Постарайтесь предусмотреть, где и что может пойти не так и как это можно проверить.
Только когда Вы поняли, что улучшить программу на бумаге больше нельзя, открывайте Mathcad. Остановите все вычисления, затем вводите код. Возможно, это самая простая часть написания программы.
После написания кода программы сохраните файл. Затем нажмите кнопку «Автоматический расчет», чтобы запустить вычисления. Будьте готовы увидеть неверный результат или ошибку – тогда программу придется отлаживать. Сохраняйте файл каждый раз, когда делаете большие изменения.
После запуска программы ее необходимо проверить. Попробуйте обычные входные значения, а также такие значения, с которыми могут возникнуть проблемы. Программа может дать сообщение об ошибке для неверного входного или выходного значения. В завершение подумайте, как можно улучшить программу.
Резюме
- Отключайте вычисления при написании или редактировании программы (Вычисления –> Остановить все расчеты).
- Цикл for – повторяет вычисления определенное количество раз. Цикл forобязательно включает в себя счетчик и число повторений.
- Цикл while – выполняется, пока соблюдается определенное условие. Начальное значение счетчика следует задавать до цикла. В теле цикла изменение счетчика задается вручную.
- Программы почти всегда требуют отладки. Полезная команда для этого – return, с помощью которой можно вывести промежуточное значение.
- Важно подготовиться к написанию программы, например, составив структурную диаграмму до написания непосредственно кода.
Другие интересные материалы
Урок 11. Программирование в Mathcad
Mathcad содержит встроенную среду программирования, что значительно расширяет возможности вычислительного пакета. Операторы программирования находятся в меню Математика –> Операторы и символы –> Программирование:
Этих операторов не очень много, но и они позволяют построить достаточно сложные алгоритмы. К тому же, уже ознакомившись с базовыми понятиями (операторы, переменные, константы, функции и т.д.), можно использовать Mathcad, если Вы хотите лишь начать изучать программирование.
Команды, которые мы изучим в этом уроке:
- «Программирование» – для создания программной структуры.
- «Локальное назначение» – знак «равно» для программ.
- «Оператор if»– оператор условия.
- «Оператор else»– альтернативный выбор.
- «Оператор return» – выход из программы.
- «Try / On Error» – применяется, если при выполнении программы может возникнуть ошибка.
Эти команды можно сочетать с операторами, переменными и функциями Mathcad. Например, Вы можете использовать структуру функции для ввода входных значений:
«Программирование» и «Локальное определение»
Создадим программу, которая вычисляет разницу между двумя переменными a и b.
На рисунке ниже представлена структурная диаграмма программы:
Здесь всего три элемента: вход, действие и выход. Вместо структурной диаграммы можно использовать другие способы, помогающие созданию программы, например, блок-схемы или псевдокод.
Определите ввод переменных a и b:
Нажмите оператор «Программирование» на панели Математика –> Программирование:
Нажмите [Enter] для создания второй строки:
Переместите курсор в верхний местозаполнитель, затем вставьте оператор «Локальное назначение»:
Заполните местозаполнители слева и справа от оператора:
Переместите курсор в нижний местозаполнитель и вставьте оператор «return»:
Важно! Операторы программирования return, else, if, while и т.д. следует вставлять из меню программирования. Ввод этих команд с клавиатуры не приведет к желаемому результату.
Введите переменную в местозаполнитель:
Всегда тестируйте программы, потому что при некоторых значениях могут получиться бессмысленные результаты. В некоторых случаях это могут быть отрицательные числа, ноль или бесконечность.
У операторов программирования есть свои горячие клавиши. Попробуйте запомнить их:
- «Программирование» – правая квадратная скобка ]
- «Локальное назначение» – левая фигурная скобка {
- «return»– [Ctrl+\]
Создайте предыдущую программу снова, используя горячие клавиши. Теперь это должно занять меньше минуты!
Программе не обязательно задавать входные переменные:
Оператор «return» также не обязателен – программа примет за выходное значение последнее вычисление:
В нашей второй программе (которая более полезна, чем предыдущая) мы вычислим площадь поверхности цилиндра диаметром D и высотой H. Структурная диаграмма этой программы:
Программа и некоторые выходные результаты показаны ниже. Возможно, нужно запретить отрицательные входные значения…
Заметьте, что переменные внутри программы являются локальными. Локальная переменная не определяется вне программы:
Входным значениям можно дать числа с единицами измерения:
Однако если задать единицу измерения только одной переменной, Mathcad скажет, что единицы не совместимы:
Поэтому единицы измерения следует использовать единообразно.
Булева алгебра
В программах часто используются равенства и неравенства. Операторы сравнения находятся в меню Математика –> Операторы и символы –> Операторы –> Сравнение:
Операторы сравнения дают результат 1 при истинном выражении и 0 при ложном:
Операторы сравнения можно сочетать. Пример таких сочетаний с оператором логического И:
Операторы
if и
else
Необходимо создать программу функции, которая принимает следующие значения:
Структурная диаграмма программы представлена ниже. Треугольник означает выбор между двумя или более альтернативными вариантами. Напишем программу, используя операторы if и else.
Введите имя функции и местозаполнитель для первой строки:
Нажмите if в меню программирования или с помощью горячей клавиши }. Появится вторая строка, которая относится к оператору if:
Введите критерий выбора и желаемое значение функции. Обратите внимание на серые линии справа:
Нажмите на внутреннюю серую линию (станет мигающей синей), затем вставьте оператор else. Появится еще одна строка, относящаяся к else:
Введите необходимую функцию под else. Внутренняя серая линия удлинится, что указывает на то, что операторы ifи else связаны между собой. Нажмите на нее, нажмите [Enter], затем вставьте оператор return:
Проверьте программу, построив график функции:
При работе с программой можно добавлять новые строки нажатием клавиши [Enter]. Где появится местозаполнитель, зависит от положения курсора. Выбрана внутренняя серая линия:
Курсор стоит за x2:
Усложним функцию:
На структурной диаграмме показаны различные варианты выбора. Наиболее простой способ создать программу для этой задачи – использовать три различных операторов выбора (в Mathcad нет аналога оператора case).
Здесь важно правильно задать границы независимой переменной. Если Вы введете:
,
то точки 0 и 1 будут исключены, а Mathcad выдаст некорректный результат для этих значений.
Проверим программу для некоторых входных значений:
Для значений, не имеющих смысла, Mathcad выдаст сообщение об ошибке.
Функции в программах
В Mathcad встроено множество функций, которые могут быть полезными в том числе и в программах. Рассмотрим некоторые из них.
Векторы и матрицы
Откройте Функции –> Все функции и откройте раздел Векторы и матрицы. Найдите функции last() и length(). Это функции для определения некоторых свойств вектора:
Функция length() определяет длину вектора, т.е. количество элементов в нем, а функция last() выводит индекс последнего элемента. По умолчанию в Mathcadнумерация элементов вектора начинается с нуля, поэтому у четвертого элемента массива индекс 3.
Теория чисел/комбинаторика
Наибольший общий делитель:
Наименьшее общее кратное:
Остаток от деления x на y:
Кусочно-непрерывные функции
Ступенчатая функция:
Разное
«Разное» содержит функцию time(), которая возвращает системное время момента активации функции.
Строковые функции
Строки в Mathcad заключаются в двойные кавычки:
Строки можно задавать в качестве переменных, но их нельзя использовать в вычислениях. (Строку, содержащую только числа, можно преобразовать в константу.)
Конкатенация строк:
Длина строки (включая пробелы):
Строки могут быть полезны для задания в программах сообщений об ошибках.
Усечение и округление
Наименьшее целое число, большее x:
Наибольшее целое число, меньшее x:
Округление:
Усечение:
Список функций Mathcad огромен. Два совета по ознакомлению с новыми функциями:
- Подведя указатель мыши к имени функции в списке, Вы увидите ее полное название и краткое описание.
- Если Вы вставите функцию в рабочую область, а затем нажмете [F1], Вы получите расширенное описание функции.
Try / On Error
Последняя команда, которую мы изучим в этом уроке, используется для указания, что должно быть сделано, если при выполнении программы возникает ошибка (например, деление на ноль). Если при выполнении программы в блоке tryвозникает ошибка, программа выполняет действия в блоке on error:
Ниже представлена программа с тремя операторами if внутри блока try:
При неверном вводе появится сообщение об ошибке. Таким образом, можно отследить большую часть ошибок, но не все:
Поскольку переменная abc не определена, функция не вычисляется.
Резюме
Мы изучили следующие элементы программирования:
- Входные данные – обычно вводятся как параметры функции.
- Первая строка программы – вводится с помощью ]. Больше линий – с помощью [Enter].
- Оператор локального определения – вводится с помощью {.
- В конструкциях выбора с помощью оператора ifприменяются операторы сравнения.
- If вводится с помощью }. За ifвводится логическое выражение, например x<0. Под оператором записывается алгоритм, который должен быть выполнен, если выражение после if верно.
- После if может следовать оператор else или другой оператор if.
- [Enter] добавляет новую строку в программу. Место появления новой строки зависит от позиции курсора до нажатия на [Enter].
- Вывод переменной осуществляется с помощью оператора return. Переменной может быть одиночная переменная, вектор или матрица, которые могут содержать как числовые значения, так и текст.
- Mathcadсодержит большое число встроенных функций, которые могут быть полезны при написании программ. Список функций с подсказками можно открыть по команде Функции –> Все функции.
- Используйте try / onerror, чтобы указывать на ошибки.
Другие интересные материалы
7. Программирование в Mathcad
Впакете Mathcad существует богатый набор средств для решения различных математических задач, встроено огромное количество функций из различных разделов математики. Однако написать функции для всех практических задач, которые могут стоять перед пользователями пакета, невозможно. Для расширения возможностей разработчики пакета встроили достаточно простой и оригинальный язык программирования. В любом месте документа Mathcad можно вставить код программы на встроенном языке программирования. Это можно сделать при помощи «горячих клавиш» или команд из панели инструментов Programming (Программирование).
Для визуализации панели програм-
мирования необходимо нажать на кнопку  из панели математических инструментов или по-
из панели математических инструментов или по-
дать команду View \Toolbars \Programming. На данной панели имеется десять команд. Щелчок по одной из этих команд создает в текущей
позиции заготовку для соответствующей программной конструкции. При частом использовании команд программирования удобнее запомнить комбинации «горячих клавиш» и команды генерировать при помощи клавиатуры.
Примечание. При составлении программ ключевые слова команд вручную писать нельзя. Заготовку команды можно получить только при помощи щелчка мыши по соответствующей кнопке или при помощи комбинаций клавиш.
Приведем значение «горячих клавиш», использующих при программировании на Mathcadе.
Команда | Горячая клавиша | Команда | Горячая клавиша |
Add Line | ] | ← | { |
if | } | otherwise | CTR+Shift+] |
for | Ctrl+Shift+’ | while | Ctrl+] |
break | Ctrl+Shift+[ | continue | Ctrl+[ |
return | Ctrl+Shift+\ | On error | Ctrl+’ |
Предполагается, что читатель уже знаком с основными идеями программирования, изучив один из стандартных языков про-
118
граммирования: QBasic, Visual Basic, Fortran, Pascal, C++, Java, Ruby или любой другой язык программирования. Данный практикум адресован пользователям, решающим инженерные и научные задачи, для которых программирование не является основным видом деятельности. Для таких пользователей языки программирования C++ и Java противопоказаны, так как ориентированы на профессиональных специалистов. Инженерам, использующим программирование не ежедневно, для решения большинства задач достаточно и одиннадцати команд из панели программирования Mathcad.
Сразу же отметим недостатки программирования в среде Mathcad. Одним из главных недостатков является неразвитость отладчика программ. Ошибки, возникающие при выполнении программ, отображаются, но подробной информации о типе ошибки, значении локальных и глобальных переменных в момент останова программы оперативно получить нельзя. Отлаживать программы уже средней сложности в Mathcad не доставляет особой радости. Поэтому сложные инженерные, научные и экономические задачи удобнее и быстрее, с точки зрения автора, выполнять в рамках визуального алгоритмического языка Visual Basic [3] или последних версий языка Fortran.
Рассмотрим все команды из панели программирования Math-
cad.
1. Add Line – добавить строку в текущую позицию программы. При вводе данной команды появляется или расширяется на одну строку вертикальная линия, объединяющая отдельные операторы в блок с одним входом и одним выходом, который выполняется как один оператор.
Позиция, куда вставится строка, определяется положением курсора. Чтоб вставить новую строку в середину программы, нужно выделить (пробелами) строку перед позицией, куда будет вставлена пустая строка. Удалить лишнюю строку можно с помощью кнопки backspace на клавиатуре.
Для того чтобы начать ввод подпрограммы, необходимо набрать имя программы и в скобках через запятую перечислить формальные параметры подпрограммы, ввести нужное количество раз команду Add Line. Программа выводит последнюю переменную, обрабатываемую программой перед выходом. Вместо
119
имени подпрограммы можно указать имя переменной, куда необходимо вывести результат работы подпрограммы.
2. ← – оператор присваивания значения локальной переменной. При выходе из блока программы значения локальных переменных оказываются недоступны для других участков Mathcad файла.
В Mathcad имеются два оператора присваивания: для глобальных переменных (обозначается двумя символами «:=») и для локальных переменных «←». Глобальные переменные доступны в любом месте программы после объявления данной переменной, а локальные – только в текущем блоке.
Для пояснения действия локального и глобального оператора присваивания рассмотрим пример простейшей программы на
Mathcad.
Напишем программу для решения квадратного уравнения ax2+bx+c=0. В программе при помощи операторов глобального присваивания задаются значения глобальных переменных a, b и c. Для сравнения введем еще локальную переменную k и присвоим ей значение 4. Далее вычисляем значение корней квадратного уравнения при помощи программы, состоящей из одного блока операторов. В программе применяются три оператора локального присваивания и возвращается значения вектора x, состоящего из двух чисел. После выполнения программы выводим значение всех переменных, используемых в программе. При этом значение всех локальных переменных D, x и k, заданных вне блока, программа не видит, поэтому вместо знака = выводится оператор глобального присваивания «:=». В этом случае значение переменной не выводится, а вместо него отображается красный прямоугольный маркер.

Начало программы.
a :=1 b := −4 c := 3 k ← 4 ORIGIN :=1
x1 |
| = | D | ←b2 −4 a c | |||||
|
|
|
|
|
|
|
|
| |
x2 |
|
| x | ← | −b − | D | |||
|
|
|
|
|
|
|
| ||
|
|
| 1 |
|
| 2 a |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| x | ← | −b + | D | |||
|
|
|
|
|
|
| |||
|
|
| 2 |
|
| 2 a |
|
|
|
|
|
| x |
|
|
|
|
| |
D := | x := | k := |
|
|
| ||||
|
|
|
| ||||||
x1 =1 x2 = 3 a =1 b = −4 c = 3.
Конец программы.
3. Оператор if предназначен для организации разветвляющихся вычислительных процессов. Чтобы ввести оператор if в программу, необходимо мышкой щелкнуть по кнопке if из панели программирования или использовать горячую клавишу – }.
При этом в программу вставляется заготовка для оператора if: if .
Общий вид простого оператора if: D if L, L – логическое выражение;
D – оператор, выполняемый в случае, если условие L принимает значение «истина».
Оператор работает следующим образом:
•вычисляется логическое условие L;
•если L – истина, то выполняется оператор D, в ином случае он не выполняется;
•выполнение программы продолжается со следующего,
после if, оператора.
Как мы видим, данный оператор if идентичен аналогичному оператору из других высокоуровневых языков программирования. Единственное отличие заключаются в синтаксисе.
Для формирования сложных условий можно использовать панель инструментов Boolean, содержатся знаки логического равенства, неравенства и логических операций. В частности, «V» означает логическое «или», а «Λ» — логическое «и».
121
Таким образом, чтобы сформулировать условие, что переменная х находится в диапазоне (–3;4), необходимо написать: x > –3 Λ x < 4.
При формулировании сложных логических условий для расстановки приоритетов можно использовать скобки.
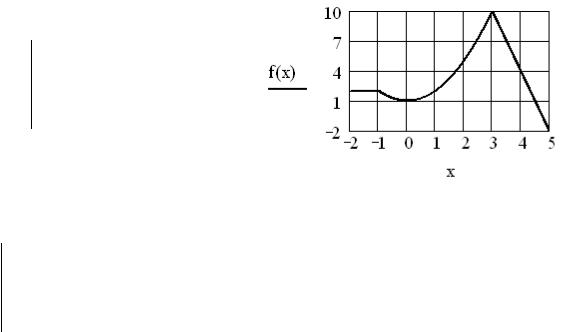
Пример. Построить график следующей функции:
28 −6x, | x (−∞;3) | |
| +1, | x [3;−1] . |
f (x) = x2 | ||
|
| x (1,∞) |
2, |
| |
Решение.
f (x) := 28 −6 x if x > 3
x2 +1 if x ≤ 3 x ≥ −1
2if x < −1
Всложных подпрограммах
часто используется блочный оператор if: if L
D1
Dn
Где D1, …, Dn – действия, выполняемые в случае, если логическое условие L истинно.
Для того чтобы вставить подобную конструкцию, нам необходимо, на панели инструментов Programming, выбрать if , затем установить курсор на место ввода слева от оператора if и n раз нажать на Add Line.
Приведем пример программы с подобным оператором. Усовершенствуем программу для решения квадратного уравнения ax2+bx+c=0.
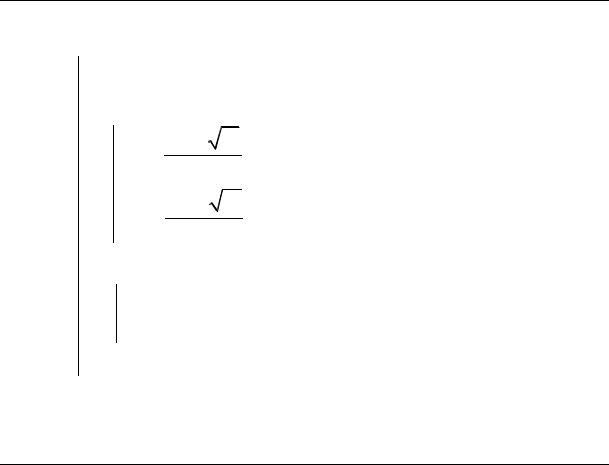
Начало программы.
x1 |
| = | ORIGIN :=1 a :=1 b := −1 c := 4 | |||
|
| D ←b | 2 | −4 | a c | |
x2 |
|
|
| |||
|
|
| if D ≥ 0 |
| ||
x1 ← −b2− a D x2 ← −b2+ a D
if D < 0
x1 ←»действительных корней нет» x2 ←»действительных корней нет»
x
x1 =»действительных корней нет» x2 =»действительных корней нет»
Конец программы.
В данном случае при дискриминанте меньше 0 программа выдает сообщение «действительных корней нет!».
Кроме оператора if, программа Mathcad может содержать и оператор otherwise.
4. Оператор otherwise применяется в случае, когда используется условие с двумя вариантами действия, то есть, если условие истинно, нужно выполнить одно действие (или действия), а если ложно, то другое.
Общий вид такого оператора следующий:
D1 if L
D2 otherwise
В случае если условие L истинно, выполняются действия D1, иначе выполняются действия D2. То есть otherwise аналогичен оператору else в Бейсике, Фортране и других высокоуровневых языках.
Рассмотрим пример программы, использующей операторы if и otherwise. В данном случае проверяются условия, при которых логарифм не существует (x<0 или y<0 или y=1). Если они выпол-
123

нены, выдается сообщение «error», в противном случае вычисля-
ется logyx. |
|
|
|
f _ log(x, y) := |
| «error» | if x ≤ 0 y ≤ 0 y =1 |
| |||
|
| log(x, y) | otherwise |
f _ log(−4,5) =»error» |
| ||
f _ log(8,2) = 3 |
|
|
|
Когда в блоке otherwise несколько строк, нужно установить курсор в место ввода слева от оператора otherwise и нажать Add Line необходимое количество раз.
Вернемся к программе, вычисляющей корни уравнения ax2+bx+c=0, и запишем ее с помощью операторов if и otherwise. Начало программы.
ORIGIN :=1 a :=1 b := 2 c := 2
x1 | = |
| D ←b | 2 | −4 a c |
|
|
| |||
|
|
|
| ||||||||
|
|
|
|
| |||||||
x2 |
|
| if D ≥ 0 |
|
|
| |||||
|
|
|
| x | ← |
| −b − | D | |||
|
|
|
|
| |||||||
|
|
|
|
|
|
| |||||
|
|
|
| 1 |
|
|
| 2 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
| x | ← | −b + | D | ||||
|
|
|
|
|
| ||||||
|
|
|
| 2 |
|
|
| 2 a |
|
|
|
|
|
| otherwise |
|
|
| |||||
|
|
|
| x1 ←»действительных корней нет» | |||||||
|
|
|
| ||||||||
|
|
|
| x2 ←»действительных корней нет» | |||||||
|
|
| x |
|
|
|
|
|
|
| |
x1 = −2 |
| x2 = −1 |
|
|
| ||||||
Конец программы.
5. Оператор for используется для создания циклических вычислительных процессов. В документе Mathcad простейшие циклы могут быть заменены ранжированными векторами. Для более сложных циклов необходимо составлять программу.
Чтобы вставить оператор for в программу, необходимо мышкой щелкнуть по кнопке for из панели программирования или использовать «горячую» клавишу «Ctrl+Shift+’». При этом в программу вставляется заготовка для оператора for:

for
Общий вид оператора выбора for: for i k1..kn
D
Или
for i (k1 k2 k3 … kn)
D
Где i – счетчик цикла. Переменная, которая меняется в диапазоне от k1 до kn. Диапазон изменения счетчика цикла вводится с помощью ранжированной переменной или с помощью вектора.
D –действия, которые выполняются в цикле (тело цикла). Ниже приведен пример, в котором диапазон изменения счетчика цикла n задан с помощью вектора. Вектор вставляется с по-
мощью панели инструментов Matrix.
sum := s ← 0
for n (1 2 5 7 10 11 13 16 17 19)
s ← s + 1n
sum = 2.285.
Данная программа вычисляет сумму
Sum=1+1/2+1/5+1/7+1/10+1/11+1/13+1/16+1/17+1/19.
Если тело цикла оператора for состоит из нескольких строк, то необходимо установить курсор на позицию для ввода тела цикла и соответствующее количество раз нажать на Add Line.
Как и в обычных программах, циклы и условные операторы могут быть вложенными. Mathcad, впрочем, сам следит за вложенностью циклов и сделать ошибку во вложенности просто не позволит.
Пример. Написать функцию FA, создающую матрицу A, состоящую из M строк и N столбцов следующего вида:
125
1 | 2 | 4 | 8 | 16 |
| |
| 0 | 1 | 2 | 4 | 8 |
|
|
| |||||
| 0 | 0 | 1 | 2 | 4 |
|
|
| |||||
| 0 | 0 | 0 | 1 | 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запишем подпрограмму, выводящую эту матрицу с помощью двух вложенных циклов:
FA(M , N ) := |
| for | i 0..M −1 |
| ||||
|
| |||||||
|
|
|
| for | j 0..N −1 |
| ||
|
|
|
|
| Ai , j | ← 1 | if | i = j |
|
|
|
|
| ||||
|
|
|
|
| Ai , j | ← 0 | if | i > j |
|
|
|
|
| Ai , j ← 2 Ai, j−1 | if i < j | ||
|
|
| A |
|
|
|
|
|
1 | 2 | 4 | 8 | 16 |
|
| ||
| 0 | 1 | 2 | 4 | 8 |
|
|
|
FA(4,5) = |
|
|
| |||||
| 0 | 0 | 1 | 2 | 4 |
|
|
|
|
|
|
| |||||
| 0 | 0 | 0 | 1 | 2 |
|
|
|
Обозначим i – | строку матрицы, j – столбец матрицы. | |||||||
Тогда главная диагональ задается уравнением «i=j», элементы матрицы, расположенные выше главной диагонали, уравнением «i<j», а элементы матрицы, расположенные ниже главной диагонали, – усравнением «i<j».
Каждый элемент, расположенный выше главной диагонали, вычисляется как удвоенное произведение элемента, стоящего в этой же строке в предыдущем столбце: Ai j=2* Ai j–1.
Для проверки работы функции подали команду: FA(4,5)=. 6. Оператор цикла while используется тогда, когда цикл дол-
жен выполняться не заданное количество раз, а до тех пор, пока не будет выполнено определенное в цикле условие.
Чтобы вставить оператор while в программу, необходимо мышкой щелкнуть по кнопке while из панели программирования или использовать горячую клавишу – «Ctrl+]». При этом в программу вставляется заготовка для оператора while:
while
Общий вид оператора While: while L
D,
где L – условие, при выполнении которого выполняется цикл (условие цикла). В данном случае, действие D (тело цикла) выполняется до тех пор, пока условие L истинно. Если логическое условие L изначально ложно, то операторы, составляющие тело цикла, не будут выполняться, а управление передается на оператор следующий за оператором while.
Если в теле цикла выполняемых действий должно быть несколько, то необходимо установить курсор на позицию для ввода тела цикла и соответствующее количество раз нажать на Add Line.
Следует заметить, что если условие L истинно всегда, то программа будет работать бесконечно (зациклится). Именно поэтому с циклом while необходимо быть очень осторожным и тщательно проверять условие выхода из цикла, прежде чем выполнять программу.
Если программа все-таки повисла, то чтобы прервать ее выполнение, необходимо нажать клавишу «Esc» и в появившемся окне нажать на кнопку OK.
Приведем пример программы, использующей цикл while.
s ← 0 |
|
|
| ||
n ←1 |
|
|
| ||
| 1 |
|
| ||
while |
|
| > tol | ||
n | |||||
|
|
|
| ||
s ← s + 1n n ← n +1
s
= 2.829.
Вданной программе с указанной точностью (tol) вычисляется сумма s=1+1/2+1/3+1/4+1/5+1/6+1/7…
7. Оператор break обеспечивает экстренный выход из цикла. Программа при этом продолжает выполнять следующую после цикла строку. Данный оператор часто применяется, чтобы избежать «зацикливания» программы.
Вкачестве примера применения оператора break рассмотрим
∞ |
| 12n −1 |
|
|
|
задачу вычисления суммы числового ряда S = ∑ |
|
| . | В | |
n | 3 | ||||
n=1 | + 2n +1 |
|
| ||
приведенной ниже программе, суммирование членов ряда прекращается, когда достигается точность, указанная параметром tol или если число итераций цикла превышает 10000.
f (n) := | 12 n −1 |
| |
n3 + 2 n +1 | |||
| |||
sum(tol) := s ← 0 n ←1
while f (n) > tol s ← s + f (n)
break if n >10000 n ← n +1
s sum(0.000011) =8.726 .
В данном случае оператор break исключается возможность зацикливания программы для расходящегося ряда.
8. Оператор continue возвращает управление в первую строку цикла. Как только этот оператор встречается в программе, выполнение текущей итерации прерывается и выполняется переход на следующую итерацию цикла. Выход из цикла не производится.
Данный оператор, как и оператор break, не содержит параметров.
Пример: Найти сумму N первых членов ряда:
N |
| 1 |
|
S = ∑ |
| . | |
2n | 3 | ||
n=1 | −16 |
|
В программе, при помощи оператора continue, происходит обход слагаемого в котором знаменатель дроби равен нулю.
sum(N ) := |
| s ← 0 | |
| |||
|
| for n 1..N | |
|
|
| a ← 2 n3 −16 |
|
|
| |
|
|
| continue if a = 0 |
|
|
| s ← s + 1 |
|
|
| a |
|
| s | |
sum(100) = −0.024.
9. Оператор return прерывает выполнение программы. В качестве результата работы программы возвращается значение, указанное в позиции для ввода, после оператора return.
При выборе на панели инструментов пункта return вставляется строка.
Пример. Подсчитать с указанной точностью tol сумму ряда:
∞ |
|
| 12n |
|
S = ∑ |
|
| . | |
n | 2 | + 2n +16 | ||
n=1 |
|
|
Если ряд получается расходящийся, программа выдаст сообщение «расходится». Ряд будет считаться расходящимся, если число итераций цикла превысило 1000000 раз.
f 1(n) := | 12n | |||||||
n2 + 2n +16 |
|
|
|
|
| |||
sum1(N ) := |
| s ← 0 | ||||||
| ||||||||
|
| n ←1 | ||||||
|
| while |
| f 1(n) |
| > tol | ||
|
|
|
| |||||
|
|
| s ← s + f 1(n) | |||||
|
|
| ||||||
|
|
| return » ряд расходится» if n >100000 | |||||
|
|
| n ← n +1 | |||||
|
| s | ||||||
129

sum1(0.01) =» ряд расходится».
10. Оператор on error отвечает за обработку ошибок. При выборе данного оператора в программу вставляется заготовка следующего вида:
Общий вид оператора on error: D1 on error D2 .
Если при вычислении выражения D1 произошла ошибка, будет вычислено значение D2.
Данный оператор имеет смысл использовать, если при выполнении программы возможна ошибка в каком-то определенном месте, например деление на ноль.
Приведем пример программы, вычисляющей десятичный логарифм числа xy.
Если логарифм не существует, выдается сообщение об ошибке: «аргумент логарифма <0».
|
|
|
f (x, y) := |
| z ← x y |
| ||
|
| «аргумент логарифма < 0» on error log(z) |
f (0,5) =»аргумент логарифма < 0″; | ||
f (10,1) =1. | ||
Оператор on error можно применять в комплексе встроенной функцией error().
f (x, y) := z ← x y
error(«аргумент логарифма < 0») on error log(z)
В данном случае сообщение об ошибке будет показываться в стандартном для Mathcad виде. При ошибке текст вызова функции выделяется красным цветом, а при подведении мыши к этому вызову внизу отображается запрограммированный в функции error текст.
1 сентября — начало учебного года в НГАСУ (Сибстрин) Уважаемые студенты, преподаватели и сотрудники! В соответствии с рекомендациями МИНОБРНАУКИ РФ с 1 сентября 2020 года, при благоприятной эпидемиологической обстановке в регионе, НГАСУ (Сибстрин) приступает к образовательному процессу в смешанном формате – очное обучение в учебных корпусах университета, и дистанционное обучение для тех студентов, которые не смогут начать год в традиционной форме обучения. В соответствии с требованиями РОСПОТРЕБНАДЗОРА в университете будет соблюдаться строгий масочный режим, входной контроль температуры тела сотрудников и обучающихся, сан.обработка антисептиками. В университет не допускаются лица с признаками инфекционных заболеваний и ОРВИ (повышенная температура, кашель, насморк). Занятия будут проводиться в соответствии с расписанием в аудиториях университета. |
Вниманию студентов очно-заочной (вечерней) формы обучения! Занятия у студентов 1-го курса (группы 111в «Архитектура», и 121 ву «Строительство») по расписанию начнутся с 02.09. 2020 г. в обычном (аудиторном) режиме с обязательным соблюдением мер предотвращения распространения коронавирусной инфекции (масочный режим, дистанция, дезинфекция рук, контроль температуры тела). Организационное собрание состоится 02.09.2020 г в 17 00 аудитория 312 (главный корпус, ул. Ленинградская 113) Занятия у студентов остальных курсов (группы 211в, 311в, 411в 511в, 611в «Архитектура», и 321 ву, 521 ву «Строительство») по расписанию начнутся с 01.09. 2020 г. в обычном (аудиторном) режиме с обязательным соблюдением мер предотвращения распространения коронавирусной инфекции (масочный режим… |
Друзья! Мы приглашаем вас на очередной преакселератор в рамках бизнес-ускорителя А:СТАРТ, который состоится 22 августа Вебинар будет посвящен формированию распределенных команд и кейсами по запуску инновационного стартапа с нуля. Дата: 22 августа (суббота) Время: 14:00 -16:00 Формат: вебинар Необходима регистрация: https://leader-id.ru/event/34824/ Спикер #1: Леонид Кальнеус, организатор IT-комьюнити Google Developer Groups в Новосибирске. Тема: “Работа в распределенных командах” Расскажет: как организовать работу распределенной команды, по каким критериям выбирать сотрудников на “удалёнке” и какие существуют инструменты для управления таким штатом. |
Горожан приглашают принять участие в проектировании сквера «Воинский» Дорогие друзья! Начата разработка проекта благоустройства сквера «Воинский», и все желающие приглашаются принять участие в опросе, который позволит лучше понять запросы и потребности жителей в отношении сквера. Сквер «Воинский» расположен в Октябрьском районе на пересечении улиц Воинская и Никитина. Площадь сквера — около 3,6 га. Сквер граничит со строящимся религиозным объектом — Храмом во имя святого страстотерпца царя Николая. Сквер окружают следующие объекты: Санкт-Петербургский университет технологии управления и экономики, гаражи, частный сектор, малоэтажные жилые дома, зона общественного-делового назначения. В настоящее время сквер представляет собой заброшенную озелененную территорию, огороженную от проезжей части густыми зарослями деревьев и кустарников, главным образом используемую как транзитный короткий путь до магазина для местных жителей. |
1 сентября — начало учебного года в НГАСУ (Сибстрин) Уважаемые студенты, преподаватели и сотрудники! В соответствии с рекомендациями МИНОБРНАУКИ РФ с 1 сентября 2020 года, при благоприятной эпидемиологической обстановке в регионе, НГАСУ (Сибстрин) приступает к образовательному процессу в смешанном формате – очное обучение в учебных корпусах университета, и дистанционное обучение для тех студентов, которые не смогут начать год в традиционной форме обучения. В соответствии с требованиями РОСПОТРЕБНАДЗОРА в университете будет соблюдаться строгий масочный режим, входной контроль температуры тела сотрудников и обучающихся, сан.обработка антисептиками. В университет не допускаются лица с признаками инфекционных заболеваний и ОРВИ (повышенная температура, кашель, насморк). Занятия будут проводиться в соответствии с расписанием в аудиториях университета. |
Вниманию студентов очно-заочной (вечерней) формы обучения! Занятия у студентов 1-го курса (группы 111в «Архитектура», и 121 ву «Строительство») по расписанию начнутся с 02.09. 2020 г. в обычном (аудиторном) режиме с обязательным соблюдением мер предотвращения распространения коронавирусной инфекции (масочный режим, дистанция, дезинфекция рук, контроль температуры тела). Организационное собрание состоится 02.09.2020 г в 17 00 аудитория 312 (главный корпус, ул. Ленинградская 113) Занятия у студентов остальных курсов (группы 211в, 311в, 411в 511в, 611в «Архитектура», и 321 ву, 521 ву «Строительство») по расписанию начнутся с 01.09. 2020 г. в обычном (аудиторном) режиме с обязательным соблюдением мер предотвращения распространения коронавирусной инфекции (масочный режим… |
Друзья! Мы приглашаем вас на очередной преакселератор в рамках бизнес-ускорителя А:СТАРТ, который состоится 22 августа Вебинар будет посвящен формированию распределенных команд и кейсами по запуску инновационного стартапа с нуля. Дата: 22 августа (суббота) Время: 14:00 -16:00 Формат: вебинар Необходима регистрация: https://leader-id.ru/event/34824/ Спикер #1: Леонид Кальнеус, организатор IT-комьюнити Google Developer Groups в Новосибирске. Тема: “Работа в распределенных командах” Расскажет: как организовать работу распределенной команды, по каким критериям выбирать сотрудников на “удалёнке” и какие существуют инструменты для управления таким штатом. |
Горожан приглашают принять участие в проектировании сквера «Воинский» Дорогие друзья! Начата разработка проекта благоустройства сквера «Воинский», и все желающие приглашаются принять участие в опросе, который позволит лучше понять запросы и потребности жителей в отношении сквера. Сквер «Воинский» расположен в Октябрьском районе на пересечении улиц Воинская и Никитина. Площадь сквера — около 3,6 га. Сквер граничит со строящимся религиозным объектом — Храмом во имя святого страстотерпца царя Николая. Сквер окружают следующие объекты: Санкт-Петербургский университет технологии управления и экономики, гаражи, частный сектор, малоэтажные жилые дома, зона общественного-делового назначения. В настоящее время сквер представляет собой заброшенную озелененную территорию, огороженную от проезжей части густыми зарослями деревьев и кустарников, главным образом используемую как транзитный короткий путь до магазина для местных жителей. |
Mathcad Express — бесплатный математический редактор, про который мало кто знает
Прежде всего, приветствую первых посетителей моего блога. Это моя первая статья на Хабре и я надеюсь, что смогу рассказать вам здесь много полезного.РТС Mathcad – это характерный пример математического ПО, предназначенного для осуществления, как численных, так и аналитических расчетов по формулам и визуализации их результатов в виде графиков. На протяжении последних лет Mathcad стал очень популярным, и его, на мой взгляд, по праву можно считать математическим пакетом №1 в мире.
Сначала несколько фактов о Mathcad, конечно, известных большинству читателей, т.к. Mathcad у нас уже не один десяток лет используется в ВУЗовском обучении, научных и инженерных расчетах. Скорее всего, вы использовали «старую» версию Mathcad (последняя – за номером 15), мало изменившуюся еще с прошлого века. В наши дни она вполне успешно сосуществует с более молодым семейством Mathcad, которое носит имя Mathcad Prime. Таким образом, разработчики несколько лет назад полностью переписали код программы, но заботиться о 100%-й совместимости не стали. Поэтому сейчас они благополучно поддерживают оба семейства – и «старый» Mathcad, и «новый» Mathcad Prime. Дальше и в этой статье, и в моем блоге, будем говорить именно о Mathcad Prime.
Сразу скажу, что русскоязычный дистрибутив, полнофункциональную 30-дневную версию Mathcad Prime вы можете скачать с сайта русского реселлера РТС. Если вы уже собрались попробовать ее в работе, мой совет – не торопитесь в Мастере установки согласиться с включением тестового 30-дневного периода. Дело в том, что Mathcad Prime, наряду с мощной полнофункциональной версией (окно которой вы видите сверху) имеет бесплатную ограниченную версию, которая называется Mathcad Express. Особенность Mathcad Express заключается в том, что большинство функций в этой версии выключено и являются недоступными. Тем не менее, в программе Mathcad Express остается довольно богатый функционал, достаточный, по крайней мере, для того, чтобы изучать математику в школе и на 1-м курсе технического ВУЗа.
Формулы можно вводить в документы либо с клавиатуры (если подходящие символы на ней есть), либо при помощи меню Математика. Давайте ради примера посчитаем интеграл от функции cos(x). Для этого выбираем символ интеграла, а потом — в соответствующие местозаполнители вводим (с клавиатуры) пределы интегрирования и подынтегральную функцию cos(x). Остается нажать клавишу «равно», чтобы сразу получить ответ.
Надо хорошо себе представлять, что происходит, когда мы вводим знак равенства. А именно, запускается соответствующий численный алгоритм вычисления интеграла: интервал интегрирования разбивается на некоторое число отрезков, в определенных точках которых вычисляется массив значений подынтегральной функции, который потом пересчитывается в соответствующую аппроксимацию интегральной суммы. Таким образом, большая часть расчетов скрыта и происходит «за кадром», а на экран выводится лишь конечный результат.
Ключевые инструменты Mathcad – это операторы и функции. Например, в наших расчетах мы использовали оператор интегрирования и функцию косинуса. Для выбора нужной встроенной функции удобно использовать меню Функции.
Давайте теперь определим пользовательскую функцию f(t), которая будет зависеть от переменной t. Будем использовать предназначенный для этого в Mathcad оператор присваивания (двоеточие со знаком равно).
Мы определили функцию f(t), как наш интеграл от cos(x) с переменным верхним пределом t. После того, как мы определили функцию f(t), можно посчитать ее значения в точках (для чего достаточно ввести аргумент и нажать клавишу «равно», чтобы вывести в документ ответ). Для ввода константы, например π, используется или меню Символы, или меню Константы.
В качестве аргумента можно использовать не только скалярную, но и векторную переменную. Определить ее можно так:
Тогда и результатом вычисления функции будет соответствующий вектор.
Наконец, одна из важных возможностей Mathcad Express – это возможность построения в документе графиков. Давайте выделим место в документе и вставим в это место XY-график (т.е. декартов график) нашей функции f(x).
Обозначаем на оси абсцисс имя переменной z (чтобы не путать с уже использованными ранее x и t), а на оси ординат – имя функции f(z), функцию, которую, как вы помните, мы определили, как интеграл от косинуса, равный конечно, sin(z). В итоге, получаем график этой функции.
Скажу еще, что в Mathcad Express (возможно, по недосмотру разработчика) остаются доступными матричные операции. Поэтому Mathcad Express — довольно мощный инструмент для решения задач линейной алгебры.
Переходя по документу вверх и вниз, мы можем просматривать свои расчеты, а управлять ими можно при помощи меню Расчет. По умолчанию, включена опция автоматического расчета (по мере ввода формул в документ, эти формулы сразу рассчитываются). Если эту опцию отключить, то для того чтобы рассчитать документ вручную, достаточно нажить кнопку Рассчитать.
Давайте я на этом остановлюсь, полагая, что задача знакомства читателя с Mathcad Express решена, и в следующих статьях блога, когда речь пойдет, собственно, о математике, я смогу использовать расчеты в Mathcad, не углубляясь в его интерфейс.
В заключение, адресую заинтересовавшегося читателя к своему видеокурсу по математическому анализу, который в формате МООС прошел на портале ИНТУИТ в 2014 году. Все лабораторные работы выполнены в Mathcad Prime и скачать их можно здесь. Все эти материалы на сайте Nerepetitor.ru бесплатные, регистрация не требуется.
PS. К своему удивлению столкнувшись с несколькими негативными комментариями, отмечу и несколько недостатков Mathcad (опять-таки, с моей точки зрения):
- имеется только Windows версия
- ресурсоемкий, работает медленнее«прошлых» Mathcad
- интерфейс мог бы быть и более удобным
- нельзя сохранить документ в прошлой версии (напр. из 3-й в формате 2-ю)
- документы из «прошлых» Mathcad не всегда удается импортировать в Prime
7. Программирование в Mathcad
Впакете Mathcad существует богатый набор средств для решения различных математических задач, встроено огромное количество функций из различных разделов математики. Однако написать функции для всех практических задач, которые могут стоять перед пользователями пакета, невозможно. Для расширения возможностей разработчики пакета встроили достаточно простой и оригинальный язык программирования. В любом месте документа Mathcad можно вставить код программы на встроенном языке программирования. Это можно сделать при помощи «горячих клавиш» или команд из панели инструментов Programming (Программирование).
Для визуализации панели програм-
мирования необходимо нажать на кнопку  из панели математических инструментов или по-
из панели математических инструментов или по-
дать команду View \Toolbars \Programming. На данной панели имеется десять команд. Щелчок по одной из этих команд создает в текущей
позиции заготовку для соответствующей программной конструкции. При частом использовании команд программирования удобнее запомнить комбинации «горячих клавиш» и команды генерировать при помощи клавиатуры.
Примечание. При составлении программ ключевые слова команд вручную писать нельзя. Заготовку команды можно получить только при помощи щелчка мыши по соответствующей кнопке или при помощи комбинаций клавиш.
Приведем значение «горячих клавиш», использующих при программировании на Mathcadе.
Команда | Горячая клавиша | Команда | Горячая клавиша |
Add Line | ] | ← | { |
if | } | otherwise | CTR+Shift+] |
for | Ctrl+Shift+’ | while | Ctrl+] |
break | Ctrl+Shift+[ | continue | Ctrl+[ |
return | Ctrl+Shift+\ | On error | Ctrl+’ |
Предполагается, что читатель уже знаком с основными идеями программирования, изучив один из стандартных языков про-
118
граммирования: QBasic, Visual Basic, Fortran, Pascal, C++, Java, Ruby или любой другой язык программирования. Данный практикум адресован пользователям, решающим инженерные и научные задачи, для которых программирование не является основным видом деятельности. Для таких пользователей языки программирования C++ и Java противопоказаны, так как ориентированы на профессиональных специалистов. Инженерам, использующим программирование не ежедневно, для решения большинства задач достаточно и одиннадцати команд из панели программирования Mathcad.
Сразу же отметим недостатки программирования в среде Mathcad. Одним из главных недостатков является неразвитость отладчика программ. Ошибки, возникающие при выполнении программ, отображаются, но подробной информации о типе ошибки, значении локальных и глобальных переменных в момент останова программы оперативно получить нельзя. Отлаживать программы уже средней сложности в Mathcad не доставляет особой радости. Поэтому сложные инженерные, научные и экономические задачи удобнее и быстрее, с точки зрения автора, выполнять в рамках визуального алгоритмического языка Visual Basic [3] или последних версий языка Fortran.
Рассмотрим все команды из панели программирования Math-
cad.
1. Add Line – добавить строку в текущую позицию программы. При вводе данной команды появляется или расширяется на одну строку вертикальная линия, объединяющая отдельные операторы в блок с одним входом и одним выходом, который выполняется как один оператор.
Позиция, куда вставится строка, определяется положением курсора. Чтоб вставить новую строку в середину программы, нужно выделить (пробелами) строку перед позицией, куда будет вставлена пустая строка. Удалить лишнюю строку можно с помощью кнопки backspace на клавиатуре.
Для того чтобы начать ввод подпрограммы, необходимо набрать имя программы и в скобках через запятую перечислить формальные параметры подпрограммы, ввести нужное количество раз команду Add Line. Программа выводит последнюю переменную, обрабатываемую программой перед выходом. Вместо
119
имени подпрограммы можно указать имя переменной, куда необходимо вывести результат работы подпрограммы.
2. ← – оператор присваивания значения локальной переменной. При выходе из блока программы значения локальных переменных оказываются недоступны для других участков Mathcad файла.
В Mathcad имеются два оператора присваивания: для глобальных переменных (обозначается двумя символами «:=») и для локальных переменных «←». Глобальные переменные доступны в любом месте программы после объявления данной переменной, а локальные – только в текущем блоке.
Для пояснения действия локального и глобального оператора присваивания рассмотрим пример простейшей программы на
Mathcad.
Напишем программу для решения квадратного уравнения ax2+bx+c=0. В программе при помощи операторов глобального присваивания задаются значения глобальных переменных a, b и c. Для сравнения введем еще локальную переменную k и присвоим ей значение 4. Далее вычисляем значение корней квадратного уравнения при помощи программы, состоящей из одного блока операторов. В программе применяются три оператора локального присваивания и возвращается значения вектора x, состоящего из двух чисел. После выполнения программы выводим значение всех переменных, используемых в программе. При этом значение всех локальных переменных D, x и k, заданных вне блока, программа не видит, поэтому вместо знака = выводится оператор глобального присваивания «:=». В этом случае значение переменной не выводится, а вместо него отображается красный прямоугольный маркер.

Начало программы.
a :=1 b := −4 c := 3 k ← 4 ORIGIN :=1
x1 |
| = | D | ←b2 −4 a c | |||||
|
|
|
|
|
|
|
|
| |
x2 |
|
| x | ← | −b − | D | |||
|
|
|
|
|
|
|
| ||
|
|
| 1 |
|
| 2 a |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| x | ← | −b + | D | |||
|
|
|
|
|
|
| |||
|
|
| 2 |
|
| 2 a |
|
|
|
|
|
| x |
|
|
|
|
| |
D := | x := | k := |
|
|
| ||||
|
|
|
| ||||||
x1 =1 x2 = 3 a =1 b = −4 c = 3.
Конец программы.
3. Оператор if предназначен для организации разветвляющихся вычислительных процессов. Чтобы ввести оператор if в программу, необходимо мышкой щелкнуть по кнопке if из панели программирования или использовать горячую клавишу – }.
При этом в программу вставляется заготовка для оператора if: if .
Общий вид простого оператора if: D if L, L – логическое выражение;
D – оператор, выполняемый в случае, если условие L принимает значение «истина».
Оператор работает следующим образом:
•вычисляется логическое условие L;
•если L – истина, то выполняется оператор D, в ином случае он не выполняется;
•выполнение программы продолжается со следующего,
после if, оператора.
Как мы видим, данный оператор if идентичен аналогичному оператору из других высокоуровневых языков программирования. Единственное отличие заключаются в синтаксисе.
Для формирования сложных условий можно использовать панель инструментов Boolean, содержатся знаки логического равенства, неравенства и логических операций. В частности, «V» означает логическое «или», а «Λ» — логическое «и».
121
Таким образом, чтобы сформулировать условие, что переменная х находится в диапазоне (–3;4), необходимо написать: x > –3 Λ x < 4.
При формулировании сложных логических условий для расстановки приоритетов можно использовать скобки.
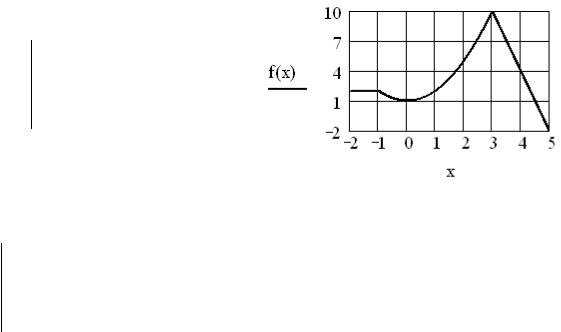
Пример. Построить график следующей функции:
28 −6x, | x (−∞;3) | |
| +1, | x [3;−1] . |
f (x) = x2 | ||
|
| x (1,∞) |
2, |
| |
Решение.
f (x) := 28 −6 x if x > 3
x2 +1 if x ≤ 3 x ≥ −1
2if x < −1
Всложных подпрограммах
часто используется блочный оператор if: if L
D1
Dn
Где D1, …, Dn – действия, выполняемые в случае, если логическое условие L истинно.
Для того чтобы вставить подобную конструкцию, нам необходимо, на панели инструментов Programming, выбрать if , затем установить курсор на место ввода слева от оператора if и n раз нажать на Add Line.
Приведем пример программы с подобным оператором. Усовершенствуем программу для решения квадратного уравнения ax2+bx+c=0.
Начало программы.
x1 |
| = | ORIGIN :=1 a :=1 b := −1 c := 4 | |||
|
| D ←b | 2 | −4 | a c | |
x2 |
|
|
| |||
|
|
| if D ≥ 0 |
| ||
x1 ← −b2− a D x2 ← −b2+ a D
if D < 0
x1 ←»действительных корней нет» x2 ←»действительных корней нет»
x
x1 =»действительных корней нет» x2 =»действительных корней нет»
Конец программы.
В данном случае при дискриминанте меньше 0 программа выдает сообщение «действительных корней нет!».
Кроме оператора if, программа Mathcad может содержать и оператор otherwise.
4. Оператор otherwise применяется в случае, когда используется условие с двумя вариантами действия, то есть, если условие истинно, нужно выполнить одно действие (или действия), а если ложно, то другое.
Общий вид такого оператора следующий:
D1 if L
D2 otherwise
В случае если условие L истинно, выполняются действия D1, иначе выполняются действия D2. То есть otherwise аналогичен оператору else в Бейсике, Фортране и других высокоуровневых языках.
Рассмотрим пример программы, использующей операторы if и otherwise. В данном случае проверяются условия, при которых логарифм не существует (x<0 или y<0 или y=1). Если они выпол-
123

нены, выдается сообщение «error», в противном случае вычисля-
ется logyx. |
|
|
|
f _ log(x, y) := |
| «error» | if x ≤ 0 y ≤ 0 y =1 |
| |||
|
| log(x, y) | otherwise |
f _ log(−4,5) =»error» |
| ||
f _ log(8,2) = 3 |
|
|
|
Когда в блоке otherwise несколько строк, нужно установить курсор в место ввода слева от оператора otherwise и нажать Add Line необходимое количество раз.
Вернемся к программе, вычисляющей корни уравнения ax2+bx+c=0, и запишем ее с помощью операторов if и otherwise. Начало программы.
ORIGIN :=1 a :=1 b := 2 c := 2
x1 | = |
| D ←b | 2 | −4 a c |
|
|
| |||
|
|
|
| ||||||||
|
|
|
|
| |||||||
x2 |
|
| if D ≥ 0 |
|
|
| |||||
|
|
|
| x | ← |
| −b − | D | |||
|
|
|
|
| |||||||
|
|
|
|
|
|
| |||||
|
|
|
| 1 |
|
|
| 2 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
| x | ← | −b + | D | ||||
|
|
|
|
|
| ||||||
|
|
|
| 2 |
|
|
| 2 a |
|
|
|
|
|
| otherwise |
|
|
| |||||
|
|
|
| x1 ←»действительных корней нет» | |||||||
|
|
|
| ||||||||
|
|
|
| x2 ←»действительных корней нет» | |||||||
|
|
| x |
|
|
|
|
|
|
| |
x1 = −2 |
| x2 = −1 |
|
|
| ||||||
Конец программы.
5. Оператор for используется для создания циклических вычислительных процессов. В документе Mathcad простейшие циклы могут быть заменены ранжированными векторами. Для более сложных циклов необходимо составлять программу.
Чтобы вставить оператор for в программу, необходимо мышкой щелкнуть по кнопке for из панели программирования или использовать «горячую» клавишу «Ctrl+Shift+’». При этом в программу вставляется заготовка для оператора for:

for
Общий вид оператора выбора for: for i k1..kn
D
Или
for i (k1 k2 k3 … kn)
D
Где i – счетчик цикла. Переменная, которая меняется в диапазоне от k1 до kn. Диапазон изменения счетчика цикла вводится с помощью ранжированной переменной или с помощью вектора.
D –действия, которые выполняются в цикле (тело цикла). Ниже приведен пример, в котором диапазон изменения счетчика цикла n задан с помощью вектора. Вектор вставляется с по-
мощью панели инструментов Matrix.
sum := s ← 0
for n (1 2 5 7 10 11 13 16 17 19)
s ← s + 1n
sum = 2.285.
Данная программа вычисляет сумму
Sum=1+1/2+1/5+1/7+1/10+1/11+1/13+1/16+1/17+1/19.
Если тело цикла оператора for состоит из нескольких строк, то необходимо установить курсор на позицию для ввода тела цикла и соответствующее количество раз нажать на Add Line.
Как и в обычных программах, циклы и условные операторы могут быть вложенными. Mathcad, впрочем, сам следит за вложенностью циклов и сделать ошибку во вложенности просто не позволит.
Пример. Написать функцию FA, создающую матрицу A, состоящую из M строк и N столбцов следующего вида:
125
1 | 2 | 4 | 8 | 16 |
| |
| 0 | 1 | 2 | 4 | 8 |
|
|
| |||||
| 0 | 0 | 1 | 2 | 4 |
|
|
| |||||
| 0 | 0 | 0 | 1 | 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запишем подпрограмму, выводящую эту матрицу с помощью двух вложенных циклов:
FA(M , N ) := |
| for | i 0..M −1 |
| ||||
|
| |||||||
|
|
|
| for | j 0..N −1 |
| ||
|
|
|
|
| Ai , j | ← 1 | if | i = j |
|
|
|
|
| ||||
|
|
|
|
| Ai , j | ← 0 | if | i > j |
|
|
|
|
| Ai , j ← 2 Ai, j−1 | if i < j | ||
|
|
| A |
|
|
|
|
|
1 | 2 | 4 | 8 | 16 |
|
| ||
| 0 | 1 | 2 | 4 | 8 |
|
|
|
FA(4,5) = |
|
|
| |||||
| 0 | 0 | 1 | 2 | 4 |
|
|
|
|
|
|
| |||||
| 0 | 0 | 0 | 1 | 2 |
|
|
|
Обозначим i – | строку матрицы, j – столбец матрицы. | |||||||
Тогда главная диагональ задается уравнением «i=j», элементы матрицы, расположенные выше главной диагонали, уравнением «i<j», а элементы матрицы, расположенные ниже главной диагонали, – усравнением «i<j».
Каждый элемент, расположенный выше главной диагонали, вычисляется как удвоенное произведение элемента, стоящего в этой же строке в предыдущем столбце: Ai j=2* Ai j–1.
Для проверки работы функции подали команду: FA(4,5)=. 6. Оператор цикла while используется тогда, когда цикл дол-
жен выполняться не заданное количество раз, а до тех пор, пока не будет выполнено определенное в цикле условие.
Чтобы вставить оператор while в программу, необходимо мышкой щелкнуть по кнопке while из панели программирования или использовать горячую клавишу – «Ctrl+]». При этом в программу вставляется заготовка для оператора while:
while
Общий вид оператора While: while L
D,
где L – условие, при выполнении которого выполняется цикл (условие цикла). В данном случае, действие D (тело цикла) выполняется до тех пор, пока условие L истинно. Если логическое условие L изначально ложно, то операторы, составляющие тело цикла, не будут выполняться, а управление передается на оператор следующий за оператором while.
Если в теле цикла выполняемых действий должно быть несколько, то необходимо установить курсор на позицию для ввода тела цикла и соответствующее количество раз нажать на Add Line.
Следует заметить, что если условие L истинно всегда, то программа будет работать бесконечно (зациклится). Именно поэтому с циклом while необходимо быть очень осторожным и тщательно проверять условие выхода из цикла, прежде чем выполнять программу.
Если программа все-таки повисла, то чтобы прервать ее выполнение, необходимо нажать клавишу «Esc» и в появившемся окне нажать на кнопку OK.
Приведем пример программы, использующей цикл while.
s ← 0 |
|
|
| ||
n ←1 |
|
|
| ||
| 1 |
|
| ||
while |
|
| > tol | ||
n | |||||
|
|
|
| ||
s ← s + 1n n ← n +1
s
= 2.829.
Вданной программе с указанной точностью (tol) вычисляется сумма s=1+1/2+1/3+1/4+1/5+1/6+1/7…
7. Оператор break обеспечивает экстренный выход из цикла. Программа при этом продолжает выполнять следующую после цикла строку. Данный оператор часто применяется, чтобы избежать «зацикливания» программы.
Вкачестве примера применения оператора break рассмотрим
∞ |
| 12n −1 |
|
|
|
задачу вычисления суммы числового ряда S = ∑ |
|
| . | В | |
n | 3 | ||||
n=1 | + 2n +1 |
|
| ||
приведенной ниже программе, суммирование членов ряда прекращается, когда достигается точность, указанная параметром tol или если число итераций цикла превышает 10000.
f (n) := | 12 n −1 |
| |
n3 + 2 n +1 | |||
| |||
sum(tol) := s ← 0 n ←1
while f (n) > tol s ← s + f (n)
break if n >10000 n ← n +1
s sum(0.000011) =8.726 .
В данном случае оператор break исключается возможность зацикливания программы для расходящегося ряда.
8. Оператор continue возвращает управление в первую строку цикла. Как только этот оператор встречается в программе, выполнение текущей итерации прерывается и выполняется переход на следующую итерацию цикла. Выход из цикла не производится.
Данный оператор, как и оператор break, не содержит параметров.
Пример: Найти сумму N первых членов ряда:
N |
| 1 |
|
S = ∑ |
| . | |
2n | 3 | ||
n=1 | −16 |
|
В программе, при помощи оператора continue, происходит обход слагаемого в котором знаменатель дроби равен нулю.
sum(N ) := |
| s ← 0 | |
| |||
|
| for n 1..N | |
|
|
| a ← 2 n3 −16 |
|
|
| |
|
|
| continue if a = 0 |
|
|
| s ← s + 1 |
|
|
| a |
|
| s | |
sum(100) = −0.024.
9. Оператор return прерывает выполнение программы. В качестве результата работы программы возвращается значение, указанное в позиции для ввода, после оператора return.
При выборе на панели инструментов пункта return вставляется строка.
Пример. Подсчитать с указанной точностью tol сумму ряда:
∞ |
|
| 12n |
|
S = ∑ |
|
| . | |
n | 2 | + 2n +16 | ||
n=1 |
|
|
Если ряд получается расходящийся, программа выдаст сообщение «расходится». Ряд будет считаться расходящимся, если число итераций цикла превысило 1000000 раз.
f 1(n) := | 12n | |||||||
n2 + 2n +16 |
|
|
|
|
| |||
sum1(N ) := |
| s ← 0 | ||||||
| ||||||||
|
| n ←1 | ||||||
|
| while |
| f 1(n) |
| > tol | ||
|
|
|
| |||||
|
|
| s ← s + f 1(n) | |||||
|
|
| ||||||
|
|
| return » ряд расходится» if n >100000 | |||||
|
|
| n ← n +1 | |||||
|
| s | ||||||
129

sum1(0.01) =» ряд расходится».
10. Оператор on error отвечает за обработку ошибок. При выборе данного оператора в программу вставляется заготовка следующего вида:
Общий вид оператора on error: D1 on error D2 .
Если при вычислении выражения D1 произошла ошибка, будет вычислено значение D2.
Данный оператор имеет смысл использовать, если при выполнении программы возможна ошибка в каком-то определенном месте, например деление на ноль.
Приведем пример программы, вычисляющей десятичный логарифм числа xy.
Если логарифм не существует, выдается сообщение об ошибке: «аргумент логарифма <0».
|
|
|
f (x, y) := |
| z ← x y |
| ||
|
| «аргумент логарифма < 0» on error log(z) |
f (0,5) =»аргумент логарифма < 0″; | ||
f (10,1) =1. | ||
Оператор on error можно применять в комплексе встроенной функцией error().
f (x, y) := z ← x y
error(«аргумент логарифма < 0») on error log(z)
В данном случае сообщение об ошибке будет показываться в стандартном для Mathcad виде. При ошибке текст вызова функции выделяется красным цветом, а при подведении мыши к этому вызову внизу отображается запрограммированный в функции error текст.
ФУНКЦИЯ И ПРИМЕНЕНИЕ ПРОГРАММЫ MATHCAD В ОБУЧЕНИИ МАТЕМАТИКИ
Транскрипция
1. О ФУНКЦИИ И ПРИМЕНЕНИИ ПРОГРАММЫ Matcad MATHCAD В ПРЕПОДАВАНИИ МАТЕМАТИКИ ДЕ ТИНГ ВУ Отделение колледжа Мэта Мороуза, Атланта, Джорджия, 33, США. Представляем Matcad — одну из самых популярных систем компьютерной алгебры (программное обеспечение для матов) в мире.Lke oter CAS, т. Е. Способна выполнять алгебраические операции, операции исчисления и рисовать график или 3 измерения. Мы можем использовать t, чтобы получить числовое, символьное и графическое решение задачи mat. Помимо обычных возможностей, это некая особенность: функция процессора слов лучше работает с CAS. Эта функция позволяет легко создавать текстовый процессор и создавать вокзалы. Следуя текущей тенденции к добавлению программных функций в программное обеспечение, t добавил программные функции к себе, запустил Matcad V7. Улучшение TS делает эту функцию более полной и мощной., Роль программной функции в обучении мат. Несомненно, программное обеспечение и технология коврика — это эффективный способ обучения Mat. Они глубоко влияют на учение о Мате, и можно ожидать, что появление новых технологий проникнет и изменит его структуру. Функции программы — это новая функция программного обеспечения. Естественно, мы хотим знать, полезно ли нам учить Мат? Я полагаю: хотя для большинства проблем мы встречаемся с обучением Мэтту достаточно использовать вычислительные возможности, в некоторых случаях функция программы становится необходимой и очень эффективной.Например, для Numercal Analyss функции программы очень полезны, но для абстрактной алгебры они менее необходимы. В других примерах различных уравнений, когда преподается приблизительный метод для решения другого уравнения, программная функция не обязательна и не учитывает степень и отсутствие решения другого уравнения. Более того, по мере увеличения возможностей программных функций будет обнаружено больше приложений. 3 О презентации Целью презентации является представление программной функции Matcad и проиллюстрирование некоторых применений Matwc на основе моего прошлого опыта в обучении. года.

2. Программные функции Matcad В этой части представлены программные операторы Matcad и структура программы Matcad. Программные операторы программы Matcad Matcad созданы с помощью операторов программы. Matcad как операторы wc доступны с панели инструментов программы. Теперь давайте взглянем на эти операторы .. Оператор «add lne»: для создания программы или добавления строки в программу.Если нажать на панели инструментов программирования, будет создана вертикальная полоса и заполнители .. «»: локальный оператор сопоставления wc defne left старший по rgt старше стрелки. 3. «f»: условный оператор wc можно использовать всякий раз, когда вы хотите, чтобы программный оператор выполнялся только при появлении некоторого условия. «Oterwse»: условный оператор wc может использоваться для обозначения оператора wt «f», когда вы хотите, чтобы Программа для выполнения оператора при условии, что оператор «f» ложен. 5. «for»: оператор цикла wc можно использовать, если вы знаете, сколько раз вы хотите, чтобы оператор программы выполнялся повторно.. «wle»: оператор цикла wc можно использовать, если вы хотите остановить выполнение оператора при возникновении условия, но не знаете точно, когда это произойдет. 7. «break»: оператор управления wc может использоваться, когда вы хотите выйти из цикла. при появлении некоторого условия и wc переводит исполнитель на следующий этап вне цикла. 8. «продолжение»: оператор управления wc может использоваться, когда вы хотите изменить текущий тератон цикла при появлении условия и заставить программу продолжить следующий тератон цикла.9. «return»: оператор управления wc можно использовать в любой программе, когда вы хотите прервать программу и вернуть значение, отличное от значения последнего выражения программы. «On error»: оператор для управления ошибками, который можно использоваться для возврата альтернативного значения, если в выражении добавлена ошибка.

3. Структура программы Matcad Программа — это точная последовательность nstructons, предназначенная для выполнения определенной задачи.Программа Matcad — это последовательность операторов, также созданная операторами программы usng. Но, т. Е. Как спец форма и структура. Теперь мы используем пример для иллюстрации. Пример программы Matcad f (x, y): = u x + y v sn (u) + e u w + u v w Слева s программа Matcad wc определяет функцию n varable. Программа Ts состоит из частей. Имя левой части или переменное имя wc представляет собой вывод последнего оператора программы; Правая часть включает в себя вертикальную панель, представляющую собой тело программы, состоящей из программных операторов. Части бота соединяются тегом defnton sgn «: =».Ts означает, что левая часть определяется правой частью, или программа присваивает результат имени слева. Фактически, программа представляет собой составное выражение, представленное именем слева. Форма и структура программы Matcad позволяют легко распознать и отделить от других частей рабочего стола. Операторы программы просты, так что легко писать программу. Ts очень хорошо подходит для использования в чайных целях. Форма и структура Ts также хороши для обновления программы. Кроме того, форма и структура позволяют взаимодействовать с любыми частями рабочего стола.Программа Altoug Matcad состоит из ts программных операторов, многие функции ts bult-n также могут использоваться в программе. Например, augment, sgn, random varable и так далее. Ts делает программу ts более лаконичной и мощной. Вывод программы Matcad может быть числом, вектором, матрицей и функцией, ts делает приложение wde и flexble. Тем не менее, программная функция Matcad определяется как другие технологии. Например, не все функции ts bult-n можно использовать в программе Matcad, а некоторые из них нельзя использовать полностью, а операторы symbolc не работают в программе.В любом случае, программная функция Matcad — полезный инструмент для изучения Mat.

4 3. Применение функций программы Matcad для обучения различным уравнениям. Altoug Matcad как несколько дополнительных функций (или маршрутов) для решения различных эквивалентов, таких как Odesolve, rkfxed, rkadapt и т. Д. В некоторых случаях нам нужна функция программы ts.Например, когда используются приблизительные методы, решающие разные уравнения, и они отличаются от этих методов, описанных выше, функция программы Matcad становится необходимой и полезной. В частности, сравнение различных методов. В этой части мы рассмотрим их применение на примерах. 3. Приложение к одному другому уравнению В этом разделе мы будем использовать программную функцию Matcad для написания программ, выполняющих метод Эйлера и улучшенный метод Эйлера для дифференциального уравнения первого порядка и сравнивая результаты с точным решением и результатами двух функций. Приведу пример.Рассмотрим пример. Gven: y ‘= + y y + и y () =, x n [,]; Fnd: ts приблизительное решение по gven x x nterval по методу Эйлера и улучшенному методу Эйлера wt step sze =. и ошибки. Создавать программы метода Эйлера и улучшенного метода Эйлера Программа метода Эйлера Программа улучшенного метода Эйлера Eu (f, a, b, c,): = xaybcan for .. n PP xx + + yy + fx, y + augment (x, y) IEu (f, a, b, c,): = xaybcan for .. n PP xx + + yy + fx, y + yy + + fx, y augment (x, y) (+ f (x, y + +)) Примечание: n вышеперечисленных программ. Левая часть вывода программы содержит матрицу значений x и приблизительных значений решения.Правильное определение программы wc использует ввод: ‘f’ функция ODE, ‘конечное значение x; итоговое значение y; точка конца интервала ‘c’; » step sze и выполните приблизительный метод для получения приблизительного раствора. Теперь давайте воспользуемся этими программами, чтобы получить приблизительные решения из приведенного выше примера.

5 В приведенном выше примере Пусть y y f (x, y): = + + a: = b: = c: =: =. xx A: = Eu (f, a, b, c,) B: = IEu (f, a, b, c,) ten, Приближенный раствор, полученный матодом Эйлера: AT = Приблизительный раствор, полученный с помощью улучшенного метода Эйлера: BT = Нетрудно найти точное решение: g (x): = x tan (ln (x)): =., х: = +. Кроме того, найдите решение с помощью функции bult-n Odesolve ‘Gven y’ (x) + y (x) xy (x) + yxy: = Odesolve (x,) y (x) = gx = Теперь мы нарисуем эти решения na pcture.

6 (A) (B) g (x) y (x) x Теперь давайте проанализируем погрешность. мы определяем ошибку метода Эйлера и улучшенного метода Эйлера как ErEu и ErIEu. (A) ErEu: = g x ErIEu: = g x B ErEu T = ErIEu T = ErEu.ErIEu x
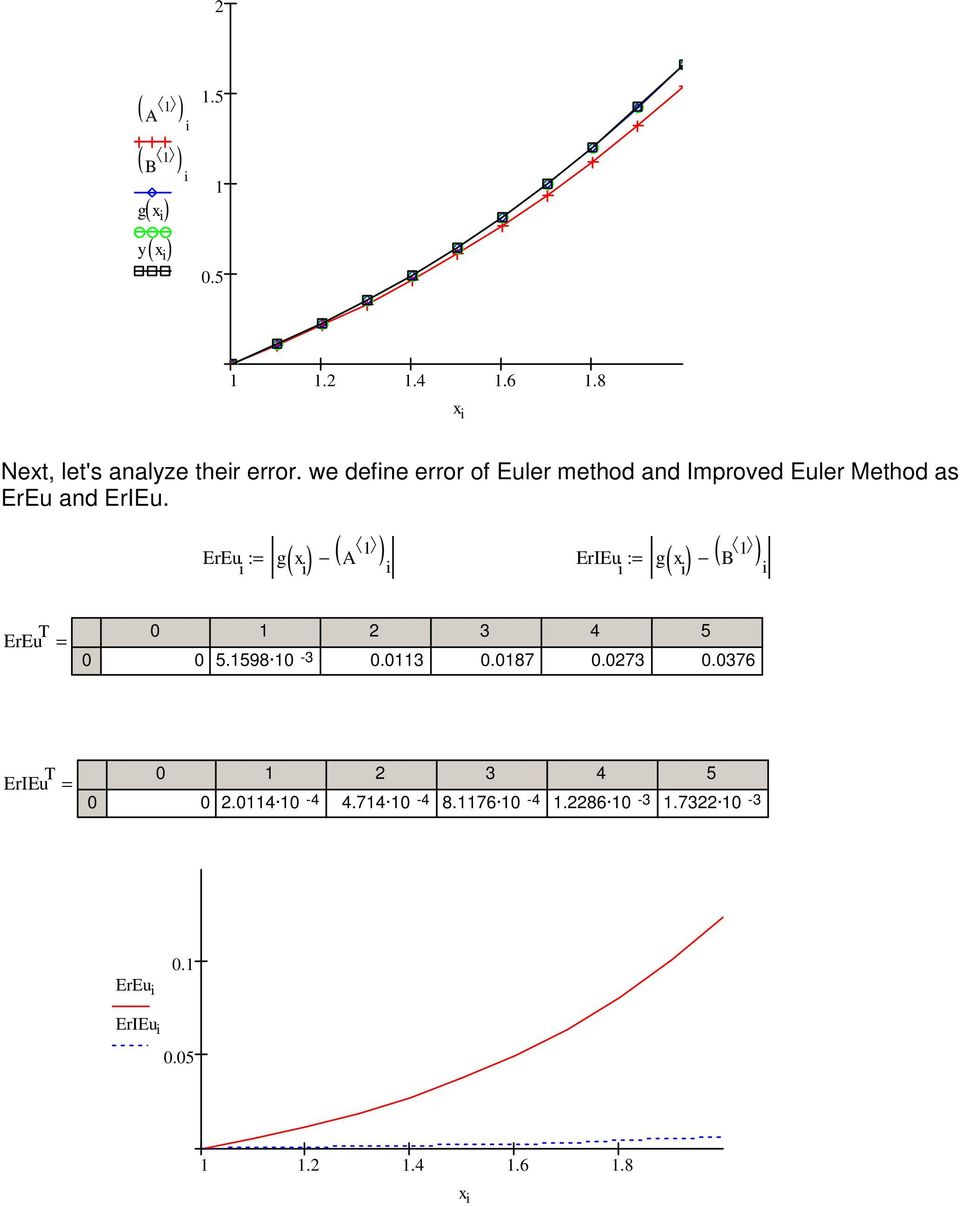
7 3. Приложение к системе различных уравнений В этом разделе мы напишем программу для реализации усовершенствованного метода Эйлера для поиска приближенных решений системы трех различных уравнений и анализа ошибок. Сначала напишите программу IEu (f, f, f3, a, b, c, d, l,): = taubuc u3 dlan для .. n PPPP tt + + (,, u, u3) (,) uu + ft , u, u, u3 + uu + ftu + u3 u3 + f3 t, u, u u3 + (+ f (t, u, u, u)) uu + + ft, uu ,, u3 (+ f (t, u, u, u)) uu + + ft, uu ,, u3 (+ f3 (t, u, u, u)) u3 u3 + + f3 t, uu ,, u3 увеличить (t, u) увеличить (P, u) augment (P, u3) Теперь мы используем программу ts, чтобы найти приближенные решения следующего примера.Gven: u ‘= uu () = u’ = -u- et + u () = tn [,] u3 ‘= — u- et + u3 () = Fnd: ts приблизительное решение с помощью улучшенного метода Эйлера wt step sze = , В примере ts f (t, u, u, u3): = uf (t, u, u, u3): = uet + f3 (t, u, u, u3): = ua: = b: = c: = d: = l: =: =. e t +

8 Пусть A: = IEu (f, f, f3, a, b, c, d, l,) 3 десятка приблизительных растворов, засеянных в матрице. T-значение в столбце s; U-значение в конце столбца; Те 3-й столбец s u-значение; В столбце указано значение u3.A = Его точные решения: g (t): = cos (t) + sn (t) et + g (t): = sn (t) + cos (t) et g3 (t): = sn (t) + cos (t): = .. t: =. g (t) = g t = g3 t = Далее делаем виноград. Первая группа из 3-х приближенных растворов; Найдите один кадр из u и g; 3-й этап, состоящий из u и g; t s график u3 и g3.

9 A A A 3,5 (A) g (t) (A) t.5 (A) g (t) (A 3) g3 (t) t t Теперь давайте проанализируем ошибку.Мы определяем ошибку n u, u, u3 как Eru, Eru, Eru3. g (t) g (t) Eru A: = Eru A: = Eru3 A 3: = g3 (t) Eru T = Eru T = Eru3 T =
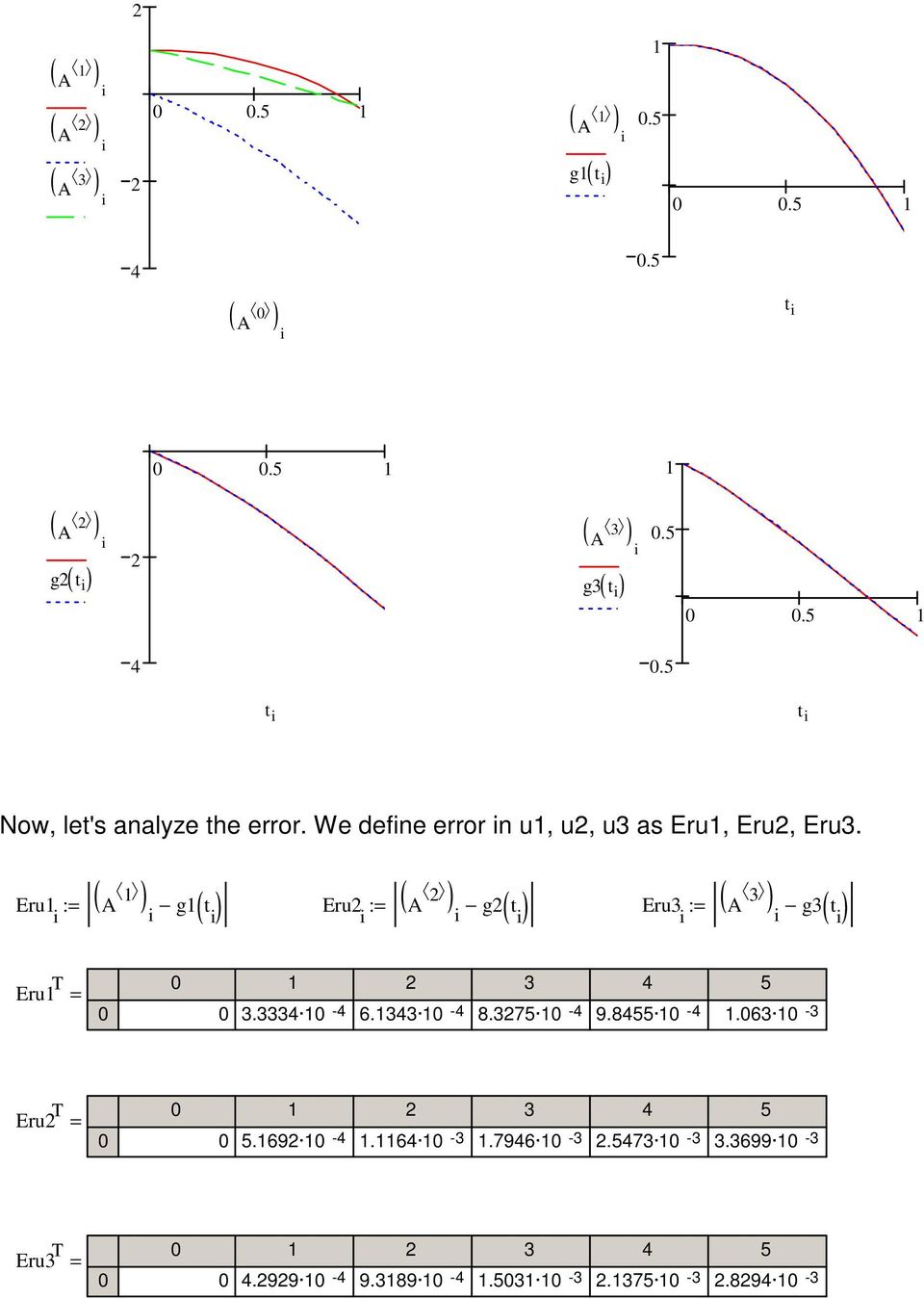
10 Пример следующих ошибок: .8 Eru. Эру Эру т
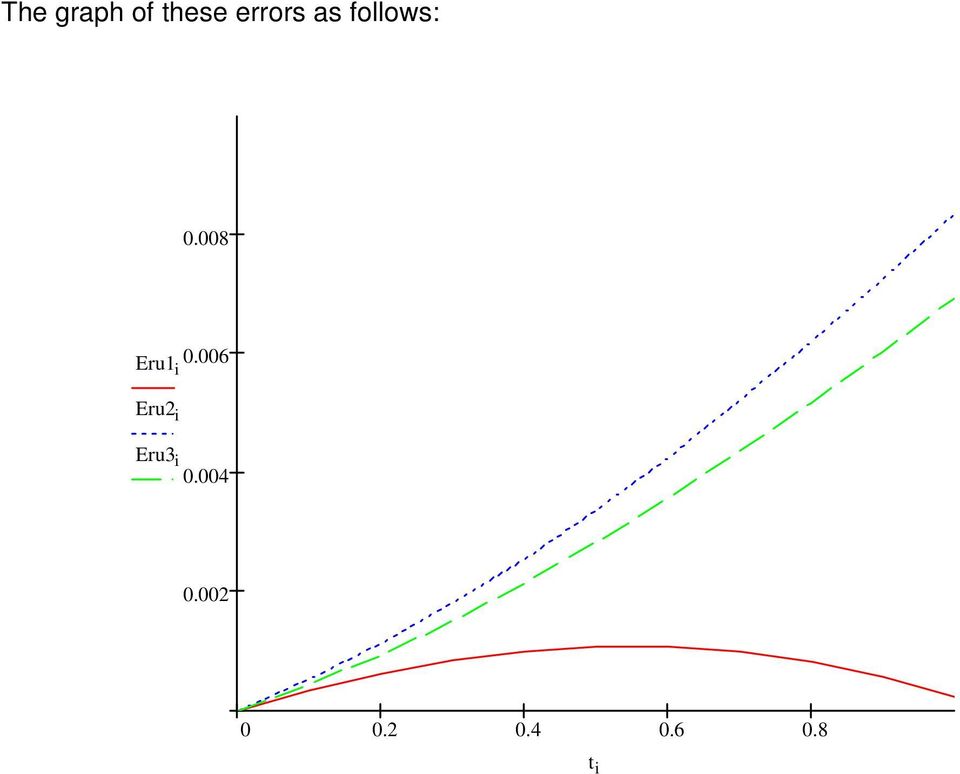
11. Прикладное обучение Numercal Analyss Дополнительная область Numercal Analyss в функциях программы Matcad может демонстрировать все возможности.Snce Numercal Analyss часто требует массовых, повторяющихся и утомительных вычислений, так как функция программы может наилучшим образом удовлетворить эти требования. В этой части мы просто проиллюстрируем примерное решение не-близких эквивалентов и многочлен Ньютона. Применение приближенного решения не-близких экватонов. Метод секущих для поиска приближенного решения не ближайших экватонов. И мы сравним результат с результатом функции bult-n.Программа для метода Секант. ApS (f, a, b, r): = papb wle pppppppppf (p) rpf (p) f (p) f (p) Примечание: ввод: f (x) = — gven equaton a, b-endponts of [a , b] tat скобка te soluton r-desred precision Вывод: Приблизительное решение с требуемой точностью Теперь давайте посмотрим на пример: Fnd приблизительное решение для cos (x) -x = wt точность 5. f (x): = cos (x) xf = f = a: = b: = r: = 5 Используйте график, чтобы найти решение n [,] Te требуемое приближенное решение: x: = ApS (f, a, b, r) x = f (x) x Давайте сравним wtresult от функции bult-n.r: = root (f (x), x ,,) r = Давайте выясним ошибку er: = x r er =

12. Применение многочлена интерполяции Ньютона В этом разделе мы будем использовать программную функцию, чтобы создать программу, которая будет производить коэффициенты многочлена интерполяции Ньютона. Десять операций будем использовать символический оператор для формирования полинома интерполяции Ньютона. Также доказан график полинома Ньютона. Проиллюстрируем это на примере ниже.Пример. Gven: f () =. 75977, f (.3) =. 8, f (.) =. 55, f (.9) =. 888, f (.) =. 33. Постройте интерполяционный многочлен степени по формуле интерполяционного преобразования Ньютона и используйте t для аппроксимации f (). Sol’n: Сначала введите данные: a: = a: =. 3 a: =. а: =. 9 а: =. 3 b: = b: =. 8 b: =. 55 b: =. 888 b: =. 33 3 Во-вторых, используйте программу Followng для определения dvded-dfferences. В программе слежения используйте цикл for для ввода указанного выше набора данных, а десять используйте двойной цикл for для определения dvded-dfferences. Выходные данные программы, матрицы и элементов на диагонали — это дополнительные изменения, необходимые для формулы Ньютона.f: = для f .. x a для f b, .. j .. f f, j, j f, j x x j f = Ten, используйте формулу Ньютона для интерполяции двуд-разности для построения полинома. p (t): = f +, = f, (t a k) k = p (t) smplfy t.337t t t float,

13 Десять, найдите приблизительное значение f () s p = Fnally, Постройте точки данных и многочлен интерполяции Ньютона на графике ниже:: = .. t: =, …. График точек данных и многочлен Ньютона.b p (t) a, t 5. Ссылка [] Р.Л. Берден и Дж. Д. Фарес: »Numercal Analyss» 7t Edton, Brooks / Cole ,. [] Л. Фосетт: «Numercal Metods Usng Matcad», Пренс Холл ,. [3] RKNagle, EBStaff & ADSnde: «Основы различных экватонов», тедтон, Аддтон Уэсли, [} DTWu: «Usng Matcad n Teacng Dfferental Equatons», Электронные материалы ICTMT, 999. Web ste: [5 ] DTWu: «Teacng Numercal Analyss wt Matcad», «Международный журнал компьютерной алгебры и математического образования», том № 3.
![Wu: "Usng Matcad n Teacng Dfferental Equatons", Electronc Proceedngs of ICTMT, 999. Web ste: www.tec.plym.ac.uk/mats/ctmhome/ctmt.tml [5] D.T.Wu: "Teacng Numercal Analyss wt Matcad", "Internatonal Journal of Computer Algebra n Matematcs Educaton" Vol No. Nagle, E.B.Staff & A.D.Snde: "Fundamentals of Dfferental Equatons" t edton, Addton Wesley, [} D.T.](/800/600/https/docplayer.net/docs-images/46/21655598/images/page_13.jpg) ,
,Использование WaterSteamPro в Mathcad
Использование WaterSteamPro в MathcadДля пользователей Mathcad 12
Mathcad Professional — математический пакет, разработанный MathSoft, Inc. Первые версии пакета WaterSteamPro были разработаны в Mathcad и работали только в этой среде. Однако начиная с 5-й версии все функции были переведены на язык C ++, что позволяет использовать пакет WaterSteamPro в других средах.
Чтобы использовать функции для воды и пара в Mathcad в предыдущих версиях, вам следует импортировать рабочий лист Mathcad, содержащий определения функций, в новый. Для этого использовался справочный механизм. Для доступа к функциям из библиотеки OKAWSP6.DLL теперь написана библиотека-заглушка WSPMCAD.DLL, переадресовывающая вызовы из Mathcad в OKAWSP6.DLL. Библиотека WSPMCAD.DLL написана с использованием техники USEREFI, в которую включены функции, написанные на Mathcad C. К сожалению, политика MathSoft предусматривает, что вы можете получить доступ к пользовательским функциям только в версиях Mathcad Professional.Это привело к следующим требованиям к Mathcad:
- Mathcad Professional
- Mathcad 8.0 и выше. В принципе, среда Mathcad 7 Professional будет работать, но определения функций WaterSteamPro в диалоговом окне «Вставить функцию» и встроенное средство Mathcad для работы с размерами недоступны.
- Работа в демо-версии Mathcad (Mathcad Explorer) также возможна, но в протестированной версии Mathcad 8 Explorer (SP2) обнаружен ряд странных ошибок, хотя сами функции работали правильно.
Как уже упоминалось, библиотека WSPMCAD.DLL предоставляет новые возможности новой версии WaterSteamPro в Mathcad Professional. Библиотеку следует хранить в папке USEREFI каталога Mathcad.
Примечание: унифицированные названия функций 5-й версии несовместимы с предыдущими версиями. Поэтому необходимо изменить имена функций в таблицах Mathcad, использующих более ранние версии. Ряд функций для расчета свойств воды / водяного пара на линии насыщения не определен и в 5-й версии (хотя эти функции используются редко).Таблицы, работающие с этими функциями, должны использовать предыдущие версии программы. Другой способ — одновременное применение как новой, так и предыдущей версии WaterSteamPro (успешно протестированной).
Новой возможностью версии программы является то, что вы можете вставлять функции в рабочий лист в стандартном диалоговом окне «Вставить функцию», которое активируется либо с помощью панели инструментов, либо с помощью пункта «Вставить функцию». в меню «Вставить». Чтобы отобразить список функций в «Вставить функцию.»файл WSPMCAD.XML, содержащий определения функций WaterSteamPro, должен находиться в папке DOC \ FUNCDOC каталога Mathcad. Поскольку вы не можете использовать файл WSPMCAD.XML в Mathcad 7 Professional, данная версия Mathcad не допускает определения функций в диалоговое окно «Вставить функцию».
Чтобы установить функции для расчета свойств воды и водяного пара, щелкните имя функции в диалоговом окне «Вставить функцию», показанном ниже. Если список функций отсутствует, переустановите программу или зарегистрируйте файлы вручную, как описано выше.
Все функции пакета WaterSteamPro отображаются в диалоговом окне «Вставить функцию» в разделах, начинающихся со строки «WaterSteamPro» (см. Рис. 7).
Рис. 7. Диалоговое окно «Вставить функцию» с функциями «WaterSteamPro»
Внимание: Настоятельно рекомендуется использовать размеры в функциях WaterSteamPro в Mathcad. Для этого вставьте ссылку на файл «WaterSteamPro.mcd» в активный рабочий лист Mathcad. Как это сделать, описано в руководстве пользователя Mathcad.Описание использования функций измерения дано в «Два способа использования функций WaterSteamPro в Mathcad»
В Mathcad 12 был введен оператор пространства имен. В этом будущем функции WaterSteamPro с размерами работать не будут.
Как вручную решить проблему описано в F.A.Q.
Из-за оператора пространства имен в Mathcad 12 файлы «Watersteampro.mcd» для Mathcad версии ниже 12 и версии 12 и выше отличаются. Итак, для разных версий Mathcad отдельный файл «Watersteampro.mcd «.
В окончательной версии WaterSteamPro 6.0 есть разные файлы «Watersteampro.mcd» для поддержки Mathcad 12 (или более поздней версии) и более старых версий.
Для решения проблемы использования функций измерения WaterSteamPro в релизной версии WaterSteamPro 6.0 использован следующий алгоритм:
- При установке программа установки WaterSteamPro проверяет версию Mathcad. Если версия меньше 12, используется файл «Watersteampro.mcd» для Mathcad 8 и выше.Если версия больше или равна 12, то используется файл «Watersteampro.mcd» для Mathcad 12. Выбранный файл устанавливается в указанную папку с документами.
- Кроме того, файл «Watersteampro.mcd» для версий Mathcad менее 12 установлен в папку «[WATERSTEAMPRO_INSTALL_PATH] \ Samples \ Mathcad \ MC8» и «[MATHCAD_DOCS] \ WaterSteamPro \ MC8» независимо от версии Mathcad. «[WATERSTEAMPRO_INSTALL_PATH]» — это папка, в которой установлен WaterSteamPro, а «[MATHCAD_DOCS]» — это папка, в которой установлены документы Mathcad.
- Аналогичным образом файл «Watersteampro.mcd» для версий Mathcad, равных или более 12, установлен в папку «[WATERSTEAMPRO_INSTALL_PATH] \ Samples \ Mathcad \ MC12» и «[MATHCAD_DOCS] \ WaterSteamPro \ MC12» независимо от версии Mathcad.
Это позволяет использовать файл «Watersteampro.mcd» для установленной версии Mathcad. В случае обновления до другой версии Mathcad необходимо использовать необходимый файл из папки «MC8» или «MC12».
В случае одновременной установки двух и более версий Mathcad (например, Mathcad 11 и Mathcad 12) необходимо сделать ссылку на необходимый файл «Watersteampro».mcd «в папке» MC8 «или» MC12 «. В этом случае сложно работать с одним и тем же документом Mathcad в разных версиях Mathcad.
,Бесплатное ПО | PTC
- Блоги
- События
- партнеры
- Связаться с нами
- Карьера
- информатизации и
- английский
- английский
- 中文 (简体)
- 中文 (繁體)
- Français
