Примеры ранг матрицы: 2.2.4. Примеры решения задач по теме «Ранг матрицы»

Содержание

Ранг матрицы — определение и вычисление с примерами решения

Содержание:

Элементарные преобразования матриц:

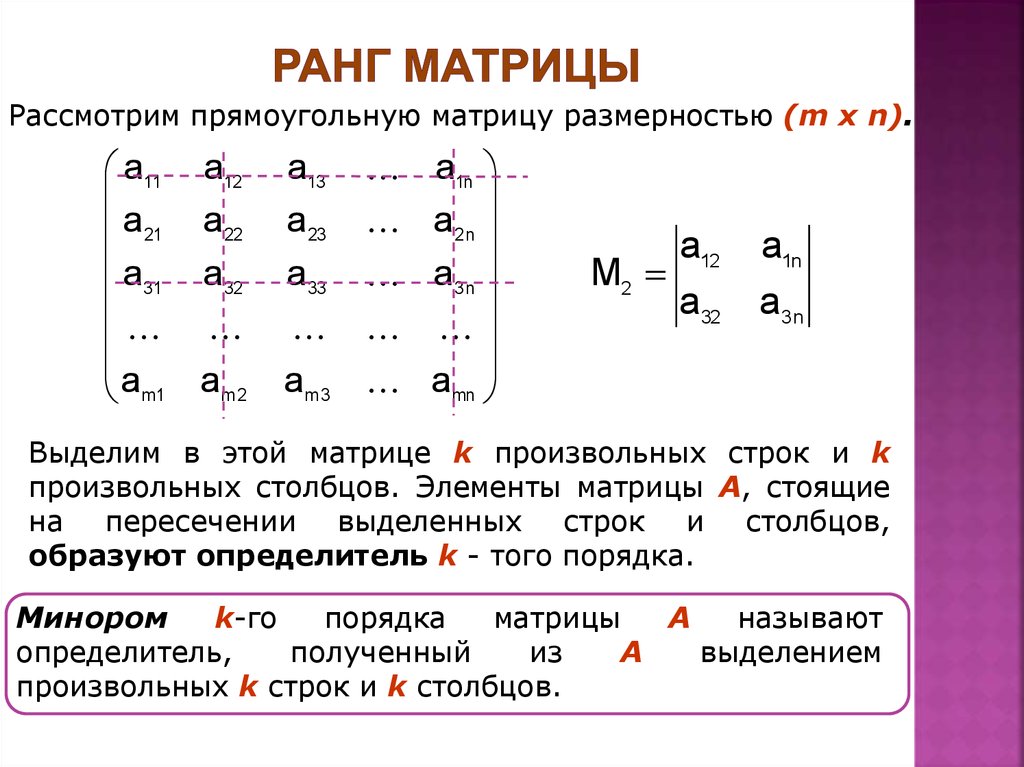
Рассмотрим прямоугольную матрицу:

состоящую из m строк и n столбцов. В п.3.2 отмсчалось, что каждую строку матрицы можно рассматривать как n-мсрный вектор, а каждый столбец — как m-мерный вектор. Тогда матрицу А можно записать в виде:

и, следовательно, данную матрицу можно рассматривать как систему вектор строк или вектор столбцов. Б указанных системах вектор-строк и вектор-столбцов можно выделять линейно независимые (зависимые) векторы. Тогда будем говорить, что строки (столбцы) матрицы линейно независимы (зависимы), если соответствующие им векторы независимы (зависимы).

Определения

Определение: Рангом системы строк (соответственно столбцов) матрицы А называется наибольшее число линейно независимых среди них.

Поскольку легко доказать, что ранг системы строк матрицы равен рангу системы её столбцов, то справедливо следующее

Определение: Рангом матрицы, обозначаемым r(А), называется максимальное число линейно независимых строк (столбцов) матрицы.

При транспонировании матрицы ранг её не изменяется.

Другой метод определения ранга матрицы связан с понятием определителя.

Выделим в матрице А любые k строк и k столбцов. Элементы, стоящие на их пересечении, образуют квадратную матрицу, определитель которой называется минором k-го порядка матрицы А. Ясно, что величина к должна удовлетворять двум условиям: . Полагая последовательно k = 1,2,…,l, где

, составляем при каждом k все миноры k-то порядка матрицы А. Тогда можно сформулировать еще одно определение ранга матрицы.

Определение: Рангом матрицы, обозначаемым r(А), называется порядок самого старшего минора этой матрицы, не равного нулю.

Из определения следует, что если ранг матрицы А равен l, то среди всех её миноров существует хотя бы один минор l-го порядка, отличный от нуля, но все миноры (l+1)-го порядков либо равны нулю, либо не могут быть составлены.

Вычисление ранга матрицы путём перебора всех её миноров весьма трудоёмко. Существует, однако, более простой способ вычисления ранга матрицы, основанный на упрощении структуры матрицы с помощью элементарных преобразований. Элементариыми преобразованиями матрицы называют следующие преобразования:

обмен местами двух строк или двух столбцов матрицы;
умножение всех элементов строки или столбца матрицы на произвольное число , не равное нулю;
прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число;

исключение из матрицы строки или столбца, состоящего из нулей.

Матрицы называются эквивалентными, если от одной из них к другой можно перейти путём конечного числа элементарных преобразований.

Ступенчатой матрицей называется матрица, удовлетворяющая тому свойству, что если в какой-либо из сё строк первый отличный от нуля элемент стоит на l-м месте, то во всех следующих строках на первых l местах стоят нули:

где элементы отличны от нуля, а все элементы, стоящие под ними, равны нулю.

Для вычисления ранга матрицы приводят её с помощью цепочки элементарных преобразований к ступенчатому виду. Тогда ранг матрицы совпадает с числом её ненулевых диагональных элементов.

Теоремы о ранге матриц. Свойства ранга матриц

Относительно ранга матриц можно сформулировать следующие теоремы:

Теорема:

Если матрица имеет минор порядка r, отличный от нуля, для которого все содержащие его миноры порядка(окаймляющие миноры) равны нулю, то ранг этой матрицы равен r.

Вычисление ранга матрицы при помощи метода окаймления нужно вести от низших порядков к высшим. Сначала ищем минор первого порядка (т.е. элемент матрицы) или сразу второго порядка, отличный от нуля. Затем вычисляем окаймляющие его миноры следующего порядка, пока не найдём среди них отличного от нуля и т.д., пока не найдем минор порядка l, отличный от нуля, для которого либо все окаймляющие его миноры порядка l+1 равны нулю, либо такие миноры не могут быть составлены.

Теорема: Элементарные преобразования не меняют ранга матрицы.

Доказательство теоремы следует из определения ранга матрицы и свойств определителей.

Пример:

Найти ранг матрицы:

Решение:

Минор первого порядка в левом верхнем углу равен . Окаймляющий его минор второго порядка:

Вычисляем окаймляющий его минор третьего порядка:

Значит ранг матрицы равен 2.

Пример:

Найти ранг матрицы:

Решение:

При помощи элементарных преобразований приведём данную матрицу к ступенчатому виду. На первом шаге умножим последовательно первую строку на 3, 3, 2 и вычтем из второй, третьей, четвёртой строк соответственно:

В эквивалентной матрице прибавим к третьей строке вторую и вычтем вторую из четвёртой строки:

(поменяем местами третью и четвертую строки)

(поменяем местами третий, четвёртый и пятый столбцы со вторым и опустим строки, состоящие из нулей) Преобразовали матрицу к ступеньчатому виду, у которой на диагонали три ненулевых элемента.

Ранг матрицы равен 3.

Отмстим некоторые свойства ранга матриц.

Ранг суммы двух (или нескольких) матриц не больше суммы их рангов.
Любую матрицу ранга r можно представить в виде суммы r матриц ранга 1, но нельзя представить в виде суммы менее чем r таких матриц.
Любую матрицу С ранга r можно представить в виде произведения , где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
Ранг произведения матриц порядка n удовлетворяет неравенству .

Определение системы m линейных уравнений с n неизвестными

Системой m линейных уравнений с n неизвестными называется система вида:

Числа называются соответственно коэффициентами системы и ее свободными членами. Первый индекс i коэффициента соответствует номеру уравнения, в которое входит этот коэффициент, а второй индекс — номеру неизвестной , при которой стоит этот коэффициент. Индекс свободного члена соответствует номеру уравнения, содержащего .

С помощью знака суммирования систему (5.3.1) можно записать в виде:

Матрица

составленная из коэффициентов системы , называется матрицей

системы. Если к этой матрице добавить столбец свободных членов, то получим расширенную матрицу системы: Обозначив матрицу-столбец неизвестных и матрицу-столбец свободных членов , систему (5. 3.1) можно записать в матричной форме:

где

Используется также табличная форма записи системы (5.3.1):

Отметим, что (5.3.1), (5.3.2), (5.3.3), (5.3.4)- различные виды записи одной и той же системы линейных уравнений.

Решением системы (5.3.1) называется любой упорядоченный набор действительных чисел , который при подстановке в (5.3.1) вместо неизвестных , обращает каждое из уравнений системы в верное равенство.

Система уравнений (5.3.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Две системы уравнений с одинаковыми наборами неизвестных называются равносильными, если они имеют одно и то же множество решений.

Отмстим, что для любой системы (5.3.1) возможны только три случая:

система (5.3.1) имеет единственное решение;
система (5.3.1) имеет бесчисленное множество решений;
система (5.3.1) несовместна.

Множество всех решений системы (5.3.1) называется ее общим решением.

Решить систему (5.3.1) — значит найти ее общее решение.

Пример:

Пусть задана система

Тогда эту систему можно записать в матричном виде:

или в виде таблицы:

Система определенная, так как она имеет единственное решение . Других решений быть не может, так как прямые

на координатной плоскости пересекаются в единственной точке.

Экономические задачи, приводящие к системе линейных уравнений

Предположим, что производственные мощности для изготовления n различных видов продукции установлены в т цехах. Пусть представляет собой суммарную мощность цеха i, и — часть производственного аппарата цеха i, которая необходима для производства единицы продукции вида j. Тогда обозначив через количество выпущенной продукции, получим систему уравнений, показывающих. как можно использовать имеющиеся мощности в полном объёме.

Широкий круг задач экономики приводит к составлению системы уравнений. Так в примере 4.3.2 составлялась система линейных уравнений (4.3.1) балансовой модели для трёх отраслей. В общем случае под балансовой моделью понимается система уравнений, каэ/сдое из которых выражает требование баланса между производимым количеством продукции и совокупной потребностью в этой продукции.

При построении балансовых моделей используется понятие чистой (или технологической) отрасли, т.е. условной отрасли, объединяющей всё производство данного продукта независимо от ведомственной (административной) подчинённости и форм собственности предприятий и фирм. Всё народное хозяйство представляется в виде совокупности п отраслей, каждая из которых рассматривается как производящая и как потребляющая.

Если обозначить через:

— межотраслевые потоки продукции, где i и j — соотвестственно номера отраслей производящих и потребляющих;
— валовой выпуск продукции i-й отрасли; — конечную продукцию i-Й отрасли, ;
— количество продукции i-й отрасли, учитывая только прямые затраты, необходимые для производства единицы продукции j-й отрасли,

то систему уравнений баланса можно записать в виде:

или в матричной форме:

где Х- вектор-столбец валовой продукции; Y- вектор-столбец конечной продукции; А — матрица коэффициентов прямых затрат.

Основу экономико-математической модели межотраслевого баланса составляет технологическая матрица А, содержащая коэффициенты прямых затрат на производство единицы продукции:

Коэффициент!,! прямых затрат являются довольно стабильной величиной во времени.

Переписав матричное уравнение (5.4.2) в виде EX-AX = Y или (E-A)X = Y, (5.4.3) получим стандартную форму записи системы уравнений.

Определение ранга матрицы

Рассмотрим прямоугольную матрицу (4.1). Если в этой матрице выделить произвольно строк и столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу -го порядка. Определитель этой матрицы называется минором -го порядка матрицы

А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен , то это означает, что в матрице А имеется отличный от нуля минор порядка , но всякий минор порядка, большего чем , равен нулю. Ранг матрицы А обозначается через (А).

Очевидно, что выполняется соотношение

Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D -го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен .

Элементарными называются следующие преобразования матрицы:

перестановка двух любых строк (или столбцов),
умножение строки (или столбца) на отличное от нуля число,
прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.

Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: А ~ В.

Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы

равны нулю, например,

При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.

Заказать решение задач по высшей математике

Пример:

Найти методом окаймления миноров ранг матрицы

Решение:

Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор отличный от нуля.

Переходим теперь к минорам 3-го порядка, окаймляющим Их всего два (можно добавить второй столбец или четвертый). Вычисляем их:

Таким образом, асе окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.

Пример:

Найти ранг матрицы и привести ее к каноническому виду.

Решение:

Из второй строки вычтем первую и переставим эти строки:

Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:

из третьей строки вычтем первую; получим матрицу которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:

Вычисление ранга матрицы

Для исследования разрешимости систем линейных уравнений важную роль играет понятие ранга матрицы. Рассмотрим прямоугольную матрицу А

Выделим k произвольных строк и k произвольных столбцов этой матрицы. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы А.

Рангом матрицы А называется наибольший порядок ее миноров, отличных от нуля. Обозначение: rank А,

Базисным минором матрицы называется всякий отличный от нуля ее минор, порядок которого равен рангу матрицы.

Рассмотрим некоторые методы вычисления ранга матрицы.

Метод окаймляющих миноров

Минор порядка k+1, содержащий в себе минор порядка k, называется окаймляющим минором.

Вычисляя ранг матрицы, удобнее переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка, отличный от нуля, а все окаймляющие его миноры порядка k+1 равны нулю, то ранг матрицы равен k.

Как найти ранг матрицы с примерами решения

Содержание:

Примеры с решением
Вычисление ранга матрицы

Пусть дана произвольная матрица размером . Возьмем произвольные строк и столбцов, . Минором порядка называют определитель порядка , составленный из элементов, расположенных на пересечении выбранных строк и столбцов, и обозначают .

Для данной матрицы можно составить миноров первого порядка, миноров второго порядка и т.д., миноров -го порядка.

Определение 8.37. Рангом матрицы называется максимальный порядок минора, отличного от нуля, и обозначается . Очевидно, что .

Определение 8.38. Отличный от нуля минор порядка называется базисным минором матрицы , а строки (столбцы), в которых он расположен, называют базисными строками (столбцами).

Теорема 8.17. (теорема о базисном миноре). Любой столбец (строка) матрицы является линейной комбинацией ее базисных столбцов (строк).

Теорема 8.18. Ранг матрицы равен максимальному числу линейно независимых строк (столбцов) матрицы.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

При элементарных преобразованиях ранг матрицы не меняется. Ранг треугольной матрицы равен числу ненулевых строк этой матрицы.

Для того чтобы найти ранг матрицы, необходимо с помощью элементарных преобразований привести ее к треугольному виду и найти ранг полученной матрицы. Рассмотрим схему таких преобразований подробно. Пусть дана матрица .

Предположим, что отличен от нуля (если , то, переставив строки, этого можно добиться). Разделим первую строку на , после чего на первом месте в первой строке будет стоять 1. Умножая последовательно первую строку на и вычитая, соответственно, из второй, третьей, , образуем в первом столбце все нулевые элементы. . Преобразуем второй столбец, начиная с элемента . Если этот элемент отличен от нуля, то аналогично вышеизложенному получим на его месте единицу, а ниже расположенные элементы превратим в нули.

Если , но ниже его в том же столбце есть элемент, отличный от нуля, то, поменяв местами строки, переставим его на место . Если в столбце не окажется ненулевых элементов, то можно поменять местами столбцы, пока на месте не окажется ненулевой элемент.

Возможно вам будут полезны данные страницы:

Найти определитель матрицы

Нахождение обратной матрицы

Как найти ранг матрицы: пример решения

Жорданова форма матрицы

После второго цикла получим новую эквивалентную матрицу.

Выполняя последовательно несколько циклов подобных эквивалентных преобразований и отбросив нулевые строки, придем окончательно к матрице

Буквой условно обозначены элементы матрицы, которые могут принимать любые числовые значения. Очевидно, что , так как минор, расположенный в первых строках и первых столбцах, равен единице.

Вычисление ранга системы векторов можно свести к вычислению ранга матрицы. Из теоремы 2 следует, что ранг системы векторов равен рангу матрицы, столбцами (строками) которой являются векторы этой системы.

Примеры с решением

Пример 8.18.

Найти ранг системы векторов Составим матрицу из координат векторов и найдем ее ранг.

Ранг данной системы векторов равен трем, т.е. она имеет три линейно независимых вектора.

Вычисление ранга матрицы

Для вычисления ранга матрицы применяют два метода: метод окаймляющих миноров и метод элементарных преобразований. Метод окаймляющих миноров. Минор матрицы называют окаймляющим для минора , если он получается из последнего добавлением одной новой строки и одного нового столбца матрицы . Ясно, что порядок окаймляющего минора на единицу больше, чем порядок минора .

Метод окаймляющих миноров позволяет найти один из базисных миноров матрицы и состоит в следующем.

Выбирается ненулевой минор первого порядка (ненулевой элемент матрицы). К очередному ненулевому минору последовательно добавляются такие строка и столбец, чтобы новый окаймляющий минор оказался ненулевым. Если этого сделать нельзя, то последний ненулевой минор является базисным (что утверждает следующая ниже теорема). Этот процесс рано или поздно закончится из-за ограниченных размеров матрицы.

Теорема 8.10. Если для некоторого минора матрицы все окаймляющие его миноры равны нулю, то он является базисным.

Утверждение теоремы следует из доказательства теоремы 8.7 о базисном миноре. Тем не менее приведем доказательство теоремы 8.10 полностью.

Не ограничивая общности доказательства, предположим, что минор порядка матрицы отличен от нуля, расположен в верхнем левом углу матрицы и все его окаймляющие миноры равны нулю. Рассмотрим минор

полученный добавлением к минору элементов -й строки и -ro столбца матрицы . Он равен нулю при любых значениях и . Если , то , поскольку этот определитель содержит два одинаковых столбца. Если же , то , так как в этом случае является окаймляющим для минора . Итак, . Фиксируем для любое из значений . Раскладывая определитель по последнему столбцу, получаем равенство

в котором через обозначены алгебраические дополнения соответствующих элементов определителя. Отметим, что эти алгебраические дополнения не зависят от номера , т.е. не зависят от того, элементы какого из столбцов матрицы взяты в качестве последнего столбца определителя . Кроме того, . Поэтому из последнего равенства следует, что для всех , где коэффициенты , не зависят от , а это означает, что -я строка матрицы является линейной комбинацией первых ее строк. Вычитая из -й строки матрицы линейную комбинацию первых ее строк с коэффициентами , получаем нулевую строку, не меняя при этом ранга матрицы .

Проделав это для всех , получим матрицу с теми же первыми строками, но нулевыми остальными строками. Ранг полученной матрицы равен рангу исходной матрицы и, очевидно, равен , так как в ней есть неравный нулю минор порядка , а любой минор или большего порядка будет иметь хотя бы одну нулевую строку и, следовательно, будет равен нулю. Это означает, что минор является базисным в исходной матрице .

Пример 8.7.

Найдем ранг матрицы .

На первом шаге выбираем любой ненулевой элемент матрицы, например левый верхний элемент, т. е. 2. Это ненулевой минор первого порядка.

На втором шаге строим окаймляющий минор второго порядка. Добавляем 2-ю строку и 2-й столбец и вычисляем получающийся окаймляющий минор

. Это окаймление не подходит. Меняем 2-й столбец на 3-й. Получаем минор второго порядка . Это окаймление подходит. Третий шаг: добавляем к этому минору 3-ю строку и можно снова попытаться использовать 2-й столбец. Оказывается, что , значит, выбранный минор третьего порядка подходит. Четвертый шаг: добавляем 4-ю строку (других нет) и 4-й столбец и вычисляем определитель четвертого порядка

Выбранный окаймляющий минор не подходит. Меняем 4-й столбец на 5-й: . Итак, ненулевой минор третьего порядка имеет два окаймляющих минора четвертого порядка и оба они равны нулю. Других окаймляющих миноров четвертого порядка нет. Поэтому делаем вывод, что — базисный минор, а ранг матрицы равен трем.

Пример 8.8.

Найдем ранг матрицы методом элементарных преобразований. Для этого достаточно привести матрицу к ступенчатому виду, воспользовавшись, например, алгоритмом из доказательства теоремы 6.3 (см. с. 178). Отметим, что вычисления удобно проводить, если текущий элемент равен единице.

Поэтому операцию 2* алгоритма (перестановка строк) будем выполнять не только для замены нулевого текущего элемента (так было заложено в алгоритме), но также и для того, чтобы в качестве текущего элемента получить единицу или другое небольшое целое число. Отметим также, что можно в любое время умножать ту или иную строку матрицы на ненулевое число, в частности сокращать элементы строки на общий множитель, хотя это и не предусматривается алгоритмом. Эта дополнительная операция позволяет упростить вычисления:

Полученная матрица ступенчатого вида имеет три ненулевые строки, поэтому ранг этой матрицы и, следовательно, матрицы равен трем. Базисным минором в последней матрице является .

Замечание 8.1. Приведенные два метода существенно отличаются друг от друга. При нахождении ранга конкретной матрицы методом окаймляющих миноров может потребоваться большое количество вычислений. Это связано с тем, что метод требует вычисления определителей, порядок которых может возрасти до минимального из размеров матрицы.

Однако в результате будет найден не только ранг матрицы, но и один из ее базисных миноров.

При нахождении ранга матрицы методом элементарных преобразований требуется гораздо меньше вычислений. Причем разница в объемах вычислений возрастает с ростом размеров матрицы и усложнением ее вида. Но этот метод позволяет найти базисный минор лишь для матрицы ступенчатого вида, полученной в результате элементарных преобразований.

Чтобы найти базисный минор исходной матрицы, нужны дополнительные вычисления с учетом уже известного ранга матрицы. В примере 8.8, вычислив наудачу минор третьего порядка, стоящий в тех же строках и столбцах, что и в преобразованной матрице ступенчатого вида, получим

Следовательно, он является одним из базисных миноров матрицы .

способы и примеры Чему равен ранг матрицы a

Любая матрица A порядка m×n можно рассматривать как совокупность m векторов строк или n векторов столбцов .

Рангом матрицы A порядка m×n называется максимальное количество линейно независимых векторов столбцов или векторов строк.

Если ранг матрицы A равен r , то пишется:

Нахождение ранга матрицы

Пусть A произвольная матрица порядка m ×n . Для нахождения ранга матрицы A применим к ней метод исключения Гаусса.

Отметим, что если на каком-то этапе исключения ведущий элемент окажется равным нулю, то меняем местами данную строку со строкой, в котором ведущий элемент отличен от нуля. Если окажется, что нет такой строки, то переходим к следующему столбцу и т.д.

После прямого хода исключения Гаусса получим матрицу, элементы которой под главной диагональю равны нулю. Кроме этого могут оказаться нулевые векторы строки.

Количество ненулевых векторов строк и будет рангом матрицы A .

Рассмотрим все это на простых примерах.

Пример 1.

Умножив первую строку на 4 и прибавив ко второй строке и умножив первую строку на 2 и прибавив к третьей строке имеем:

Вторую строку умножим на -1 и прибавим к третьей строке:

Получили две ненулевые строки и, следовательно ранг матрицы равен 2.

Пример 2.

Найдем ранг следующей матрицы:

Умножим первую строку на -2 и прибавим ко второй строке. Аналогично обнулим элементы третьей и четвертой строки первого столбца:

Обнулим элементы третьей и четвертой строк второго столбца прибавляя соответствующие строки ко второй строке умноженной на число -1.

Для работы с понятием ранга матрицы нам понадобятся сведения из темы «Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений» . В первую очередь это касается термина «минор матрицы» , так как ранг матрицы станем определять именно через миноры.

Рангом матрицы называют максимальный порядок её миноров, среди которых есть хотя бы один, не равный нулю.

Эквивалентные матрицы — матрицы, ранги которых равны между собой.

Поясним подробнее. Допустим, среди миноров второго порядка есть хотя бы один, отличный от нуля. А все миноры, порядок которых выше двух, равны нулю. Вывод: ранг матрицы равен 2. Или, к примеру, среди миноров десятого порядка есть хоть один, не равный нулю. А все миноры, порядок которых выше 10, равны нулю. Вывод: ранг матрицы равен 10.

Обозначается ранг матрицы $A$ так: $\rang A$ или $r(A)$. Ранг нулевой матрицы $O$ полагают равным нулю, $\rang O=0$. Напомню, что для образования минора матрицы требуется вычёркивать строки и столбцы, — однако вычеркнуть строк и столбцов более, чем содержит сама матрица, невозможно. Например, если матрица $F$ имеет размер $5\times 4$ (т.е. содержит 5 строк и 4 столбца), то максимальный порядок её миноров равен четырём. Миноры пятого порядка образовать уже не удастся, так как для них потребуется 5 столбцов (а у нас всего 4). Это означает, что ранг матрицы $F$ не может быть больше четырёх, т.е. $\rang F≤4$.

В более общей форме вышеизложенное означает, что если матрица содержит $m$ строк и $n$ столбцов, то её ранг не может превышать наименьшего из чисел $m$ и $n$, т.е. $\rang A≤\min(m,n)$.

В принципе, из самого определения ранга следует метод его нахождения. Процесс нахождения ранга матрицы по определению можно схематически представить так:

Поясню эту схему более подробно. Начнём рассуждать с самого начала, т.е. с миноров первого порядка некоторой матрицы $A$.

Если все миноры первого порядка (т.е. элементы матрицы $A$) равны нулю, то $\rang A=0$. Если среди миноров первого порядка есть хотя бы один, не равный нулю, то $\rang A≥ 1$. Переходим к проверке миноров второго порядка.
Если все миноры второго порядка равны нулю, то $\rang A=1$. Если среди миноров второго порядка есть хотя бы один, не равный нулю, то $\rang A≥ 2$. Переходим к проверке миноров третьего порядка.
Если все миноры третьего порядка равны нулю, то $\rang A=2$. Если среди миноров третьего порядка есть хотя бы один, не равный нулю, то $\rang A≥ 3$. Переходим к проверке миноров четвёртого порядка.
Если все миноры четвёртого порядка равны нулю, то $\rang A=3$. Если среди миноров четвёртого порядка есть хотя бы один, не равный нулю, то $\rang A≥ 4$. Переходим к проверке миноров пятого порядка и так далее.

Что ждёт нас в конце этой процедуры? Возможно, что среди миноров k-го порядка найдётся хоть один, отличный от нуля, а все миноры (k+1)-го порядка будут равны нулю. Это значит, что k — максимальный порядок миноров, среди которых есть хотя бы один, не равный нулю, т.е. ранг будет равен k. Может быть иная ситуация: среди миноров k-го порядка будет хоть один не равный нулю, а миноры (k+1)-го порядка образовать уже не удастся. В этом случае ранг матрицы также равен k. Короче говоря, порядок последнего составленного ненулевого минора и будет равен рангу матрицы .

Перейдём к примерам, в которых процесс нахождения ранга матрицы по определению будет проиллюстрирован наглядно. Ещё раз подчеркну, что в примерах данной темы мы станем находить ранг матриц, используя лишь определение ранга. Иные методы (вычисление ранга матрицы методом окаймляющих миноров , вычисление ранга матрицы методом элементарных преобразований) рассмотрены в следующих темах.

Кстати, вовсе не обязательно начинать процедуру нахождения ранга с миноров самого малого порядка, как это сделано в примерах №1 и №2. Можно сразу перейти к минорам более высоких порядков (см. пример №3).

Пример №1

Найти ранг матрицы $A=\left(\begin{array}{ccccc} 5 & 0 & -3 & 0 & 2 \\ 7 & 0 & -4 & 0 & 3 \\ 2 & 0 & -1 & 0 & 1 \end{array} \right)$.

Данная матрица имеет размер $3\times 5$, т.е. содержит три строки и пять столбцов. Из чисел 3 и 5 минимальным является 3, посему ранг матрицы $A$ не больше 3, т.е. $\rang A≤ 3$. И это неравенство очевидно, так как миноры четвёртого порядка образовать мы уже не сможем, — для них нужно 4 строки, а у нас всего 3. Перейдём непосредственно к процессу нахождения ранга заданной матрицы.

Среди миноров первого порядка (т.е среди элементов матрицы $A$) есть ненулевые. Например, 5, -3, 2, 7. Вообще, нас не интересует общее количество ненулевых элементов. Есть хотя бы один не равный нулю элемент — и этого достаточно. Так как среди миноров первого порядка есть хотя бы один, отличный от нуля, то делаем вывод, что $\rang A≥ 1$ и переходим к проверке миноров второго порядка.

Начнём исследовать миноры второго порядка. Например, на пересечении строк №1, №2 и столбцов №1, №4 расположены элементы такого минора: $\left|\begin{array}{cc} 5 & 0 \\ 7 & 0 \end{array} \right|$. У этого определителя все элементы второго столбца равны нулю, поэтому и сам определитель равен нулю, т.е. $\left|\begin{array}{cc} 5 & 0 \\ 7 & 0 \end{array} \right|=0$ (см. свойство №3 в теме свойства определителей). Или же можно банально вычислить сей определитель, используя формулу №1 из раздела по вычислению определителей второго и третьего порядков :

$$ \left|\begin{array}{cc} 5 & 0 \\ 7 & 0 \end{array} \right|=5\cdot 0-0\cdot 7=0. $$

Первый проверенный нами минор второго порядка оказался равен нулю. О чём это говорит? О том, что нужно дальше проверять миноры второго порядка. Либо они все окажутся нулевыми (и тогда ранг будет равен 1), либо среди них найдётся хотя бы один минор, отличный от нуля. Попробуем осуществить более удачный выбор, записав минор второго порядка, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №5: $\left|\begin{array}{cc} 5 & 2 \\ 7 & 3 \end{array} \right|$. Найдём значение этого минора второго порядка:

$$ \left|\begin{array}{cc} 5 & 2 \\ 7 & 3 \end{array} \right|=5\cdot 3-2\cdot 7=1. $$

Данный минор не равен нулю. Вывод: среди миноров второго порядка есть хотя бы один, отличный от нуля. Следовательно $\rang A≥ 2$. Нужно переходить к исследованию миноров третьего порядка.

Если для формирования миноров третьего порядка мы станем выбирать столбец №2 или столбец №4, то такие миноры будут равными нулю (ибо они будут содержать нулевой столбец). Остаётся проверить лишь один минор третьего порядка, элементы которого расположены на пересечении столбцов №1, №3, №5 и строк №1, №2, №3. Запишем этот минор и найдём его значение:

$$ \left|\begin{array}{ccc} 5 & -3 & 2 \\ 7 & -4 & 3 \\ 2 & -1 & 1 \end{array} \right|=-20-18-14+16+21+15=0. $$

Итак, все миноры третьего порядка равны нулю. Последний составленный нами ненулевой минор был второго порядка. Вывод: максимальный порядок миноров, среди которых есть хотя бы один, отличный от нуля, равен 2. Следовательно, $\rang A=2$.

Ответ : $\rang A=2$.

Пример №2

Найти ранг матрицы $A=\left(\begin{array} {cccc} -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end{array} \right)$.

Имеем квадратную матрицу четвёртого порядка. Сразу отметим, что ранг данной матрицы не превышает 4, т.е. $\rang A≤ 4$. Приступим к нахождению ранга матрицы.

Среди миноров первого порядка (т. е среди элементов матрицы $A$) есть хотя бы один, не равный нулю, поэтому $\rang A≥ 1$. Переходим к проверке миноров второго порядка. Например, на пересечении строк №2, №3 и столбцов №1 и №2 получим такой минор второго порядка: $\left| \begin{array} {cc} 4 & -2 \\ -5 & 0 \end{array} \right|$. Вычислим его:

$$ \left| \begin{array} {cc} 4 & -2 \\ -5 & 0 \end{array} \right|=0-10=-10. $$

Среди миноров второго порядка есть хотя бы один, не равный нулю, поэтому $\rang A≥ 2$.

Перейдём к минорам третьего порядка. Найдём, к примеру, минор, элементы которого расположены на пересечении строк №1, №3, №4 и столбцов №1, №2, №4:

$$ \left | \begin{array} {cccc} -1 & 3 & -3\\ -5 & 0 & 0\\ 9 & 7 & -7 \end{array} \right|=105-105=0. $$

Так как данный минор третьего порядка оказался равным нулю, то нужно исследовать иной минор третьего порядка. Либо все они окажутся равными нулю (тогда ранг будет равен 2), либо среди них найдётся хоть один, не равный нулю (тогда станем исследовать миноры четвёртого порядка). Рассмотрим минор третьего порядка, элементы которого расположены на пересечении строк №2, №3, №4 и столбцов №2, №3, №4:

$$ \left| \begin{array} {ccc} -2 & 5 & 1\\ 0 & -4 & 0\\ 7 & 8 & -7 \end{array} \right|=-28. $$

Среди миноров третьего порядка есть хотя бы один, отличный от нуля, поэтому $\rang A≥ 3$. Переходим к проверке миноров четвёртого порядка.

Любой минор четвёртого порядка располагается на пересечении четырёх строк и четырёх столбцов матрицы $A$. Иными словами, минор четвёртого порядка — это определитель матрицы $A$, так как данная матрица как раз и содержит 4 строки и 4 столбца. Определитель этой матрицы был вычислен в примере №2 темы «Понижение порядка определителя. Разложение определителя по строке (столбцу)» , поэтому просто возьмём готовый результат:

$$ \left| \begin{array} {cccc} -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0\\ 9 & 7 & 8 & -7 \end{array} \right|=86. $$

Итак, минор четвертого порядка не равен нулю. Миноров пятого порядка образовать мы уже не можем. Вывод: наивысший порядок миноров, среди которых есть хотя бы один отличный от нуля, равен 4. Итог: $\rang A=4$.

Ответ : $\rang A=4$.

Пример №3

Найти ранг матрицы $A=\left(\begin{array} {cccc} -1 & 0 & 2 & -3\\ 4 & -2 & 5 & 1\\ 7 & -4 & 0 & -5 \end{array} \right)$.

Сразу отметим, что данная матрица содержит 3 строки и 4 столбца, поэтому $\rang A≤ 3$. В предыдущих примерах мы начинали процесс нахождения ранга с рассмотрения миноров наименьшего (первого) порядка. Здесь же попробуем сразу проверить миноры максимально возможного порядка. Для матрицы $A$ такими являются миноры третьего порядка. Рассмотрим минор третьего порядка, элементы которого лежат на пересечении строк №1, №2, №3 и столбцов №2, №3, №4:

$$ \left| \begin{array} {ccc} 0 & 2 & -3\\ -2 & 5 & 1\\ -4 & 0 & -5 \end{array} \right|=-8-60-20=-88. $$

Итак, наивысший порядок миноров, среди которых есть хоть один, не равный нулю, равен 3. Поэтому ранг матрицы равен 3, т.е. $\rang A=3$.

Ответ : $\rang A=3$.

Вообще, нахождение ранга матрицы по определению — в общем случае задача довольно-таки трудоёмкая. Например у матрицы сравнительно небольшого размера $5\times 4$ имеется 60 миноров второго порядка. И если даже 59 из них будут равны нулю, то 60й минор может оказаться ненулевым. Тогда придётся исследовать миноры третьего порядка, которых у данной матрицы 40 штук. Обычно стараются использовать менее громоздкие способы, такие как метод окаймляющих миноров или метод эквивалентных преобразований .

Ранее для квадратной матрицы -го порядка было введено понятие минора
элемента. Напомним, что так был назван определитель порядка
, полученный из определителя
вычеркиванием-й строки и-го столбца.

Введем теперь общее понятие минора. Рассмотрим некоторую, не обязательно квадратную матрицу . Выберем какие-нибудьномеров строк
иномеров столбцов
.

Определение . Минором порядка матрицы (соответствующим выбранным строкам и столбцам) называется определитель порядка, образованный элементами, стоящими на пересечении выбранных строк и столбцов, т.е. число

Каждая матрица имеет столько миноров данного порядка , сколькими способами можно выбрать номера строк
и столбцов
.

Определение . В матрице размеров
минор порядканазываетсябазисным , если он отличен от нуля, а все миноры порядка
равны нулю или миноров порядка
у матрицывообще нет.

Ясно, что в матрице может быть несколько разных базисных миноров, но все базисные миноры имеют один и тот же порядок. Действительно, если все миноры порядка
равны нулю, то равны нулю и все миноры порядка
, а, следовательно, и всех бόльших порядков.

Определение . Рангом матрицы называется порядок базисного минора, или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Если все элементы матрицы равны нулю, то ранг такой матрицы, по определению, считают нулем.

Ранг матрицы будем обозначать символом
. Из определения ранга следует, что для матрицыразмеров
справедливо соотношение.

Два способа вычисления ранга матрицы

а) Метод окаймляющих миноров

Пусть в матрице найден минор
-го порядка, отличный от нуля. Рассмотрим лишь те миноры
-го порядка, которые содержат в себе (окаймляют) минор
: если все они равны нулю, то ранг матрицы равен. В противном случае среди окаймляющих миноров найдется ненулевой минор
-го порядка, и вся процедура повторяется.

Пример 9 . Найти ранг матрицы методом окаймляющих миноров.

Выберем минор второго порядка
. Существует только один минор третьего порядка, окаймляющий выбранный минор
. Вычислим его.

Значит, минор
базисный, а ранг матрицы равен его порядку, т.е.

Ясно, что перебирать таким способом миноры в поисках базисного – задача, связанная с большими вычислениями, если размеры матрицы не очень малы. Существует, однако, более простой способ нахождения ранга матрицы – при помощи элементарных преобразований.

б) Метод элементарных преобразований

Определение . Элементарными преобразованиями матрицы называют следующие преобразования:

умножение строки на число, отличное от нуля;

прибавление к одной строке другой строки;

перестановку строк;

такие же преобразования столбцов.

Преобразования 1 и 2 выполняются поэлементно.

Комбинируя преобразования первого и второго вида, мы можем к любой строке прибавить линейную комбинацию остальных строк.

Теорема . Элементарные преобразования не меняют ранга матрицы.

(Без доказательства)

Идея практического метода вычисления ранга матрицы

заключается в том, что с помощью элементарных преобразований данную матрицу приводят к виду

, (5)

в котором «диагональные» элементы
отличны от нуля, а элементы, расположенные ниже «диагональных», равны нулю. Условимся называть матрицутакого вида треугольной (иначе, ее называют диагональной, трапециевидной или лестничной). После приведения матрицык треугольному виду можно сразу записать, что
.

В самом деле,
(т.к. элементарные преобразования не меняют ранга). Но у матрицысуществует отличный от нуля минор порядка:

а любой минор порядка
содержит нулевую строку и поэтому равен нулю.

Сформулируем теперь практическое правило вычисления ранга матрицы с помощью элементарных преобразований: для нахождения ранга матрицыследует с помощью элементарных преобразований привести ее к треугольному виду. Тогда ранг матрицыбудет равен числу ненулевых строк в полученной матрице.

Пример 10. Найти ранг матрицы методом элементарных преобразований

Решение.

Поменяем местами первую и вторую строку (т.к. первый элемент второй строки −1 и с ней будет удобно выполнять преобразования). В результате получим матрицу, эквивалентную данной.

Обозначим -тую строку матрицы –. Нам необходимо привести исходную матрицу к треугольному виду. Первую строку будем считать ведущей, она будет участвовать во всех преобразованиях, но сама остается без изменений.

На первом этапе выполним преобразования, позволяющие получить в первом столбце нули, кроме первого элемента. Для этого из второй строки вычтем первую, умноженную на 2
, к третьей строке прибавим первую
, а из третьей вычтем первую, умноженную на 3
Получаем матрицу, ранг которой совпадает с рангом данной матрицы. Обозначим ее той же буквой:

Так как нам необходимо привести матрицу к виду (5), вычтем из четвертой строки вторую. При этом имеем:

Получена матрица треугольного вида, и можно сделать вывод, что
, т. е. числу ненулевых строк. Коротко решение задачи можно записать следующим образом:

Рассмотрим прямоугольную матрицу. Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r , то это означает, что в матрице А имеется отличный от нуля минор порядка r , но всякий минор порядка, большего чем r , равен нулю. Ранг матрицы А обозначается через r(A). Очевидно, что выполняется соотношение

Вычисление ранга матрицы с помощью миноров

Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т. е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k .

Пример 1. Найти методом окаймления миноров ранг матрицы

Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М 1 = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор M 2 = , отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М 2 . Их всего два (можно добавить второй столбец или четвертый). Вычисляем их: = 0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.

Вычисление ранга матрицы с помощью элементарных преобразований

Элементарными называются следующие преобразования матрицы:

1) перестановка двух любых строк (или столбцов),

2) умножение строки (или столбца) на отличное от нуля число,

3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

Две матрицы называются эквивалентными , если одна из них получается из другой с помощью конечного множества элементарных преобразований.

Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.

Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например,

Пример 2 Найти ранг матрицы

и привести ее к каноническому виду.

Решение. Из второй строки вычтем первую и переставим эти строки:

Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:

;

из третьей строки вычтем первую; получим матрицу

которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:

Строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков всевозможных ненулевых миноров этой матрицы. Ранг нулевой матрицы любого размера ноль. Если все миноры второго порядка равны нулю, то ранг равен единице, и т.д.

Ранг матрицы — размерность образа dim ⁡ (im ⁡ (A)) {\displaystyle \dim(\operatorname {im} (A))} линейного оператора , которому соответствует матрица.

Обычно ранг матрицы A {\displaystyle A} обозначается rang ⁡ A {\displaystyle \operatorname {rang} A} , r ⁡ A {\displaystyle \operatorname {r} A} , rg ⁡ A {\displaystyle \operatorname {rg} A} или rank ⁡ A {\displaystyle \operatorname {rank} A} . Последний вариант свойственен для английского языка, в то время как первые два — для немецкого, французского и ряда других языков.

Энциклопедичный YouTube

1 / 5

Пусть — прямоугольная матрица.

Тогда по определению рангом матрицы A {\displaystyle A} является:

Теорема (о корректности определения рангов). Пусть все миноры матрицы A m × n {\displaystyle A_{m\times n}} порядка k {\displaystyle k} равны нулю ( M k = 0 {\displaystyle M_{k}=0} ). Тогда ∀ M k + 1 = 0 {\displaystyle \forall M_{k+1}=0} , если они существуют.

Связанные определения

Свойства

Теорема (о базисном миноре): Пусть r = rang ⁡ A , M r {\displaystyle r=\operatorname {rang} A,M_{r}} — базисный минор матрицы A {\displaystyle A} , тогда:
Следствия:
Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение для матриц, полученных друг из друга элементарными преобразованиями . Тогда справедливо утверждение: Если A ∼ B {\displaystyle A\sim B} , то их ранги равны.
Теорема Кронекера - Капелли : Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. В частности:
- Количество главных переменных системы равно рангу системы.
- Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
Неравенство Сильвестра : Если A и B матрицы размеров m x n и n x k , то

rang ⁡ A B ≥ rang ⁡ A + rang ⁡ B − n {\displaystyle \operatorname {rang} AB\geq \operatorname {rang} A+\operatorname {rang} B-n}

Это частный случай следующего неравенства.

Неравенство Фробениуса : Если AB, BC, ABC корректно определены, то

rang ⁡ A B C ≥ rang ⁡ A B + rang ⁡ B C − rang ⁡ B {\displaystyle \operatorname {rang} ABC\geq \operatorname {rang} AB+\operatorname {rang} BC-\operatorname {rang} B}

Линейное преобразование и ранг матрицы

Пусть A {\displaystyle A} — матрица размера m × n {\displaystyle m\times n} над полем C {\displaystyle C} (или R {\displaystyle R} ). Пусть T {\displaystyle T} — линейное преобразование, соответствующее A {\displaystyle A} в стандартном базисе; это значит, что T (x) = A x {\displaystyle T(x)=Ax} . Ранг матрицы A {\displaystyle A} — это размерность области значений преобразования T {\displaystyle T} .

Методы

Существует несколько методов нахождения ранга матрицы:

Метод элементарных преобразований

Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.

Метод окаймляющих миноров

Пусть в матрице A {\displaystyle A} найден ненулевой минор k {\displaystyle k} -го порядка M {\displaystyle M} . Рассмотрим все миноры (k + 1) {\displaystyle (k+1)} -го порядка, включающие в себя (окаймляющие) минор M {\displaystyle M} ; если все они равны нулю, то ранг матрицы равен k {\displaystyle k} . В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется.

Ранг матрицы: Решенные примеры задачи

Пример 1.6

Найдите ранг матрицы A =

Решение:

Порядок A — 3 × 3.

ρ ( A ) ≤ 3.

Приведем матрицу A к ступенчатому виду с помощью элементарных преобразований.

Количество ненулевых строк равно 2

∴Ранг A равен 2.

ρ ( A ) = 2.

Примечание

Строка, содержащая хотя бы один ненулевой элемент, называется ненулевой строкой.

Пример 1,7

Найдите ранг матрицы A =

Решение:

Орден A — 3 × 4.

∴ ρ ( A ) ≤3 .

Приведем матрицу A к ступенчатому виду

Количество ненулевых строк равно 3. ∴ ρ( A ) =3.

Пример 1,8

Найдите ранг матрицы A =

Решение:

Орден A — 3 × 4.

∴ ρ ( A ) ≤ 3.

Приведем матрицу A к ступенчатому виду

Число ненулевых строк равно 3.

∴ ρ ( А ) =3.

Проверка непротиворечивости линейных неоднородных уравнений (с двумя и тремя переменными) ранговым методом: Решенные примеры задач

Пример 1.9 y = 8 непротиворечивы и решите их.

Решение:

Матричное уравнение, соответствующее данной системе:

AX=B

Количество ненулевых строк равно 2.

ρ (A )= ρ ([A, B]) = 2 = количество неизвестных.

Данная система совместна и имеет единственное решение.

Теперь данная система преобразуется в

x + Y = 5

Y = 2

∴ (1) ⇒ x + 2 = 5

х = 3

Решение составляет x = 3, Y = 2

Пример 1. 10

Покажите, что уравнения 2 x + y = 5, 4 x +2 y = 10 непротиворечивы и решите их.

Решение:

Уравнение матрицы, соответствующее системе, составляет

ρ ( A ) = ρ A ) = ρ .0008 ([ A , B ]) = 1 < число неизвестных

∴ Данная система непротиворечива и имеет бесконечно много решений.

Теперь данная система преобразована в матричное уравнение.

Let Us Trast Y = K , K ∈ R

⇒ 2 x + K

= 5
x = 1/2 (5 — K
x = 1/2 (5 — k. )
x = 1/2 ( 5 — K ) , Y = K для всех K ∈ R
Таким образом, давая различные значения для K , мы получаем другое решение. Следовательно, система имеет бесконечное число решений.

Пример 1.11
Покажите, что уравнения
Решение:
Матричное уравнение, соответствующее данной системе:

∴Данная система несовместна и не имеет решения.
Пример 1.12
Покажите, что уравнения 2 x + y + z = 5, x + y + z = 4, x — y + z = 4, x — y + z = 4, x — y + z = 4, x — . + 2 z = 1 непротиворечивы и, следовательно, решают их.
Решение:
Матричное уравнение, соответствующее данной системе, имеет вид

Очевидно, последняя эквивалентная матрица имеет ступенчатую форму. Он состоит из трех ненулевых строк.
ρ ( A ) = ρ ( [A , B] ) = 3 = Номер неизвестных.
Данная система совместна и имеет единственное решение.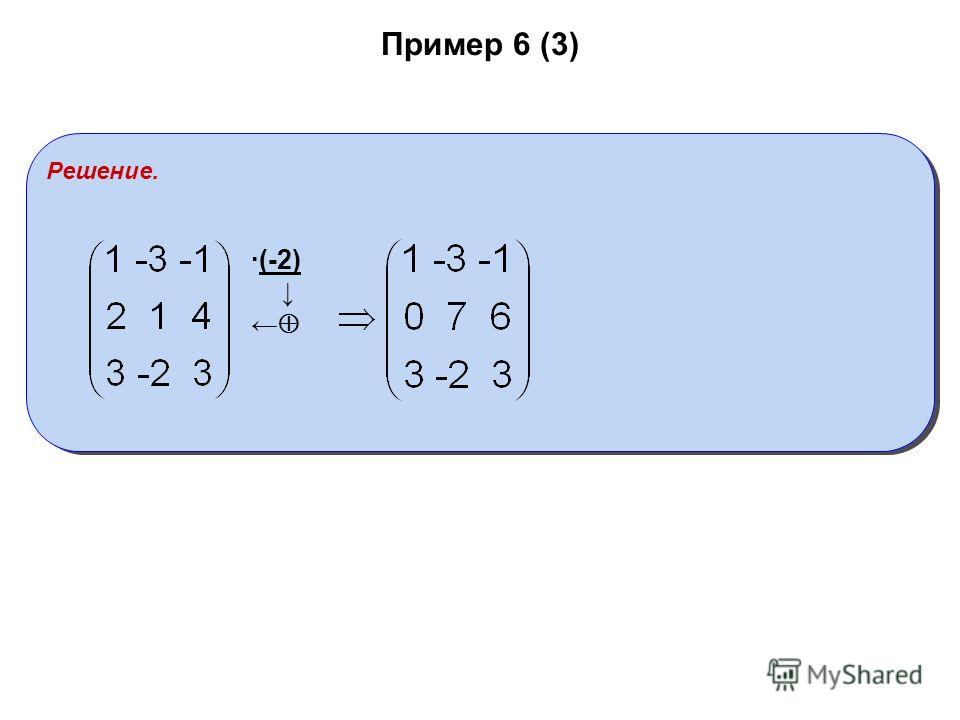
Чтобы найти решение, перепишем приведенную выше ступенчатую форму в матричную.

x + y + z = 4 (1)
y + z = 3 (2)
3z = 3 (3)
(3) ⇒ z = 1
(2) ) ⇒ y = 3 — z = 2
(1) ⇒ x = 4 — y — Z
X = 1
— Z
X = 1
— Z
x = 1 — Z
x = 1 — Z
— y — х = 1, y = 2, z = 1

Пример 1.13
Покажите, что уравнения x + y + z = 6, x +2 y +3 z = 14, x +4 y +7 z = x +4 y +7 z = 30 непротиворечивы и решить их.
Решение:
Матричное уравнение, соответствующее данной системе, имеет вид

Очевидно, что последняя эквивалентная матрица имеет ступенчатую форму. Он имеет две ненулевые строки.
∴ ρ ( [ A , B] ) = 2, ρ ( A ) = 2
ρ ( A ) = ρ ( [ A , B] ) = 2 < Номер неизвестных.
Данная система совместна и имеет бесконечно много решений.
Данная система эквивалентна матричному уравнению — 2 Z ,
(1) ⇒ x = 6 — y — Z = 6 – (9 – (9 нок (9 – (8 – (8 – . z ) − z = z – 2
Давайте возьмем Z = K , K ∈ R , мы получаем x = K — 2, y = 8 — 2 K , таким образом, давая. разные значения для k мы получаем разные решения. Следовательно, данная система имеет бесконечно много решений.

Пример 1.14
Покажите, что уравнения0007 y − 2 z = 13, 7 x — 8 y + 26 z = 5 несовместимы.
Решение:
Матричное уравнение, соответствующее данной системе:

Последняя эквивалентная матрица имеет ступенчатую форму. [ A, B ] имеет 3 ненулевых строки, а [ A ] имеет 2 ненулевые строки.

Система несовместна и не имеет решения.

Пример 1.15
Найти K, , если уравнения x +2 y — 3 z = −2, 3 x — y — 2 z = 1, 2 x + 3 y − 5 z = k непротиворечивы.
Решение:
Матричное уравнение, соответствующее данной системе, имеет вид

.0007 B] ) = ρ ( A )= 2
∴21 + 7 k = 0
7 k .
K = −3
Пример 1.16
Найти K, , если уравнения x + y + z = 7, x +2 Y +3 = 7, 7, x +2 Y +3. z = 18, y + kz = 6 несовместимы.
Решение:
Матричное уравнение, соответствующее данной системе, равно

для уравнений, которые будут противоречивыми
ρ ( [, B] ) гать ρ ( A )
It Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is Is ( A )
. − 2 = 0 . Пример 1.17 + 3z = 10, x + 2 y + az = b имеют
(i) нет решения (ii) единственное решение (iii) бесконечное количество решений.
Решение:
Матричное уравнение, соответствующее данной системе: A , B ]), что возможно только при a − 3 = 0 и b − 10 ≠ 0
Следовательно, для a = 3, b ≠ 10 , система не имеет решения.
Случай (ii) Для единственного решения:
Система имеет единственное решение только тогда, когда ρ ( A ) = ρ ([ A , B ]) = число неизвестных.
т. е. когда ρ ( A ) = ρ ([ A , B ]) = 3
Что возможно только тогда, когда a − 07 b действительное число 9 ≠ 0 и можно наблюдать.
Отсюда для a ≠ 3 и b ∈ R , система имеет единственное решение.
Случай (III) для бесконечного числа решений:
Система обладает бесконечным количеством растворов только при
ρ ( A ) = ρ ([ A ) = ρ ( A ) = ρ ( A ) , B ]) < Номер неизвестных
I, E, когда ρ ( A ) = ρ ([ A , B ]) = 2 <3 (количество неизвестных) что возможно только при a − 3 = 0, b − 10 = 0
Следовательно, для a = 3, b = 10 система имеет бесконечное число решений. Пример 1.18 ) и фиксированное время окончания ( a )
т.е. P = a + bl + cm
Из приведенных ниже данных найдите значения констант a, b и c

Оцените выработку при сверхурочной работе 50 часов и дополнительном машинном времени 15 часов.
Решение:
Мы имеем, P = A + BL + CM
Установки вышеуказанного значения. + 35 б + 9 C
7,100 = A + 40 B + 12 C
Уравнение матрицы, соответствующее данной системе, составляет

∴ Дава

∴ Производственное уравнение составляет P = 5000 + 30 L + 75 M
P на L = 50, M = 15 = 5000 + 30 (50) + 75 (15)
=7625 единиц.
∴Производство = 7625 шт.
Ранг матрицы. Определение
Ранг матрицы равен количеству линейно независимых строк (или столбцов) в ней. Следовательно, он не может превышать количество строк и столбцов. Например, если мы рассмотрим единичную матрицу порядка 3 × 3, все ее строки (или столбцы) линейно независимы, и, следовательно, ее ранг равен 3.
Давайте узнаем больше о ранге матрицы вместе с ее математическим определением и давайте посмотрим, как найти ранг матрицы вместе с примерами.
1. Что такое ранг матрицы?
2. Как найти ранг матрицы?
3. Нахождение ранга матрицы методом минора
4. Ранг матрицы с использованием формы Echelon
5. Ранг матрицы с использованием нормальной формы
6. Ранг столбца и ранг строки матрицы
7. Свойства ранга матрицы
8. Часто задаваемые вопросы о ранге матрицы
Каков ранг матрицы?
Ранг матрицы — это порядок старшего ненулевого минора. Рассмотрим ненулевую матрицу A. Говорят, что действительное число r является рангом матрицы A, если оно удовлетворяет следующим условиям:
каждый минор порядка r + 1 равен нулю.
Существует по крайней мере один минор порядка ‘r’, отличный от нуля.
Ранг матрицы A обозначается через ρ (A). Здесь «ρ» — греческая буква, которую следует читать как «ро». Таким образом, ρ (A) следует читать как «ро A» (или) «ранг A».
Как найти ранг матрицы?
Ранг матрицы можно определить тремя способами. Самый простой из этих способов — «преобразование матрицы в эшелонированную форму».
Второстепенный метод
С использованием эшелонированной формы
Использование обычной формы
Рассмотрим подробно каждый из этих методов.
Нахождение ранга матрицы методом минора
Вот шаги, чтобы найти ранг матрицы A минорным методом.
Найдите определитель матрицы A (если матрица A квадратная). Если det (A) ≠ 0, то ранг A = порядок A.
Если либо det A = 0 (в случае квадратной матрицы), либо A — прямоугольная матрица, то проверьте, существует ли минор максимально возможного порядка, отличный от нуля. Если существует такой ненулевой минор, то ранг A = порядок этого конкретного минора.
Повторите описанный выше шаг, если все миноры порядка, рассмотренного на предыдущем шаге, равны нулю, а затем попытайтесь найти ненулевой минор порядка, который на 1 меньше, чем порядок из предыдущего шага.
Вот пример.
Пример: Найдите ранг матрицы ρ (A), если A = $\left[\begin{array}{lll}
1 и 2 и 3 \\
4 и 5 и 6 \
7 и 8 и 9
\end{массив}\right]$.
Решение:
A — квадратная матрица, поэтому мы можем найти ее определитель.
дет (А) = 1 (45 — 48) — 2 (36 — 42) + 3 (32 — 35)
= -3 + 12 — 9
= 0
Итак, ρ (A) ≠ порядок матрицы. т. е. ρ (A) ≠ 3.
Теперь посмотрим, можно ли найти любой ненулевой минор порядка 2.
$\left|\begin{array}{ll}
1 и 2 \\\
4 и 5
\end{array}\right|$ = 5 — 8 = -3 ≠ 0.
Итак, существует минор порядка 2 (или 2 × 2), отличный от нуля. Итак, ранг A, ρ (A) = 2,
Ранг матрицы с использованием формы Echelon
Что, если в приведенном выше примере первый минор порядка 2 × 2, который мы нашли, был равен нулю? Нам нужно было найти все возможные миноры порядка 2 × 2, пока мы не получим ненулевой минор, чтобы убедиться, что ранг равен 2. Этот процесс может быть утомительным, если порядок матрицы больше. Чтобы упростить процесс нахождения ранга матрицы, мы можем преобразовать ее в эшелонированную форму. Говорят, что матрица «А» находится в форме эшелона, если она находится либо в форме верхнего треугольника, либо в форме нижнего треугольника. Мы можем использовать элементарные преобразования строки/столбца и преобразовать матрицу в форму Echelon.
Преобразование строки (или столбца) может быть одним из следующих:
Замена двух строк местами.
Умножение строки на скаляр.
Умножение строки на скаляр и последующее добавление его к другой строке.
Вот шаги, чтобы найти ранг матрицы.
Преобразуйте матрицу в форму Echelon, используя преобразование строки/столбца.
Тогда ранг матрицы равен количеству ненулевых строк в результирующей матрице.
Ненулевая строка матрицы — это строка, в которой хотя бы один элемент отличен от нуля.
Пример: Найти ранг матрицы A = $\left[\begin{array}{lll}
1 и 2 и 3 \\
4 и 5 и 6 \
7 и 8 и 9
\end{array}\right]$ (та же матрица, что и в предыдущем примере), преобразовав ее в эшелонированную форму.
Решение:
Дана матрица A = $\left[\begin{array}{lll}
1 и 2 и 3 \\
4 и 5 и 6 \
7 и 8 и 9
\end{массив}\right]$.
Применяем R ₂ → R ₂ — 4R ₁ и R ₃ → R ₃ — 7R ₁ , получаем: 90}{lbegin(lbegin) 1
}
1 и 2 и 3 \\
0&-3&-6\
0 и -6 и -12
\end{array}\right]\)
Теперь применим R ₃ → R ₃ — 2R ₂ , получаем:
$\left[\begin{array}{lll}
1 и 2 и 3 \\
0&-3&-6\
0 и 0 и 0
\end{array}\right]$
Теперь он в форме Echelon, поэтому теперь нам нужно подсчитать количество ненулевых строк.
Количество ненулевых строк = 2 = ранг A.
Следовательно, ρ (A) = 2.
Обратите внимание, что мы получили тот же ответ, когда вычисляли ранг с использованием миноров.
Ранг матрицы с использованием нормальной формы
Если прямоугольную матрицу A можно преобразовать в форму $\left[\begin{array}{ll}
I_r&0\\
0 и 0
\end{array}\right]$ с помощью элементарных преобразований строк, то говорят, что A находится в нормальной форме. Здесь I_r — единичная матрица порядка «r», и когда A преобразуется в нормальную форму, ее ранг равен ρ (A) = r. Вот пример. Преобразование в нормальную форму полезно при определении ранга прямоугольной матрицы. Но его можно использовать и для нахождения ранга квадратных матриц.
Пример: Найти ранг матрицы A = $\left[\begin{array}{lll}
1 и 2 и 1 и 2 \\
1 и 3 и 2 и 2 \\
2 и 4 и 3 и 4 \\
3 и 7 и 4 и 6
\end{array}\right]$ (снова та же матрица), приведя ее к нормальной форме.
Решение:
Применить R ₂ → R ₂ — R ₁ , R ₃ → R ₃ — 2R ₁ , и R ₄ → R ₄ — 3R ₁ получаем:
$\left[\begin{array}{lll}
1 и 2 и 1 и 2 \\
0&1&1&0\
0&0&1&0\
0 и 1 и 1 и 0
\end{array}\right]$
Теперь применим, R ₁ → R ₁ — 2R ₂ и R ₄ → R ₄ — R _{2 0
, 0 слева[\begin{массив}{lll}
1 и 0 и -1 и 2 \\
0&1&1&0\
0&0&1&0\
0 и 0 и 0 и 0
\end{array}\right]\)}
Применить R ₁ → R ₁ + R ₃ и R ₂ → R ₂ — R ₃ ,
\begin{массив}{lll}
1&0&0&2\
0&1&0&0\
0&0&1&0\
0 и 0 и 0 и 0
\end{array}\right]\)
Теперь применим C ₄ → C ₄ — 2C ₁ ,
$\left[\begin{array}{lll}
1&0&0&0&0\
0&1&0&0\
0&0&1&0\
0 и 0 и 0 и 0
\end{array}\right]$
То же, что и $\left[\begin{array}{ll}
I_3&0\\
0 и 0
\end{массив}\right]$.
Следовательно, ранг A равен ρ (A) = 3,
Ранг столбца и ранг строки матрицы
Когда мы вычислили ранг матрицы, используя ступенчатую форму и нормальную форму, мы увидели, что ранг матрицы равен количеству ненулевых строк в приведенной форме матрицы. На самом деле это известно как «ранг строки матрицы», поскольку мы подсчитываем количество ненулевых «строк». Точно так же ранг столбца — это количество ненулевых столбцов, или, другими словами, это количество линейно независимых столбцов. Например, в приведенном выше примере (из предыдущего раздела)
Ранг строки = количество ненулевых строк = 3
Ранг столбца = количество ненулевых столбцов = 3
Из этого очень ясно, что здесь «ранг строки = ранг столбца». На самом деле это верно для любой матрицы.
Свойства ранга матрицы
Если A невырожденная матрица порядка n, то ее ранг равен n. т. е. р (А) = п.
Если A находится в форме Echelon, то ранг A = количеству ненулевых строк A.
Если A находится в нормальной форме, то ранг A = порядок единичной матрицы в ней.
Если A — сингулярная матрица порядка n, то ρ (A) < n.
Если A — прямоугольная матрица порядка m x n, то ρ (A) ≤ минимума {m, n}.
Ранг единичной матрицы порядка n равен самому n.
Ранг нулевой матрицы равен 0.
Важные примечания о ранге матрицы:
При преобразовании матрицы в ступенчатую или нормальную форму мы можем использовать преобразование строк или столбцов. Мы также можем использовать сочетание преобразований строк и столбцов.
Чтобы найти ранг матрицы, приведя ее к ступенчатой или нормальной форме, мы можем подсчитать количество ненулевых строк или ненулевых столбцов.
Ранг столбца = ранг строки для любой матрицы.
Ранг квадратной матрицы порядка n всегда меньше или равен n.
☛ Похожие темы:
Калькулятор определителя
Калькулятор собственных значений
Калькулятор сложения матриц
Калькулятор умножения матриц
Часто задаваемые вопросы о ранге матрицы
Что такое определение ранга матрицы?
Ранг матрицы — это количество линейно независимых строк или столбцов в ней. Ранг матрицы A обозначается ρ (A), что читается как «ро матрицы A». Например, ранг нулевой матрицы равен 0, так как в ней нет линейно независимых строк.
Как найти ранг матрицы?
Чтобы найти ранг матрицы, мы можем использовать один из следующих методов:
Найти ненулевой минор старшего порядка, и его порядок даст ранг.
Преобразуйте матрицу в эшелонированную форму, используя операции со строками и столбцами. Тогда количество ненулевых строк в ней даст ранг матрицы.
Преобразование матрицы в нормальную форму $\left[\begin{array}{ll}
I_r&0\\
0 и 0
\end{array}\right]$, где I_r — единичная матрица порядка ‘r’. Тогда ранг матрицы = r.
Каков ранг матрицы порядка 3 × 3?
Ранг матрицы порядка 3 × 3 равен 3, если ее определитель НЕ равен 0. Если ее определитель равен 0, то преобразовать ее в ступенчатую форму с помощью преобразования строки/столбца, тогда количество ненулевых строк/столбцов присвоил бы звание.
Каков ранг матрицы порядка 2 × 2?
Если определитель матрицы 2 × 2 НЕ равен 0, то ее ранг равен 2. Если ее определитель равен 0, то ее ранг равен либо 1, либо 0. Точный ранг можно найти, приведя ее к ступенчатой или нормальной форме. форма.
Как найти ранг матрицы с помощью определителя?
Чтобы найти ранг матрицы порядка n, сначала вычислите ее определитель (в случае квадратной матрицы). Если НЕ 0, то его ранг = n. Если он равен 0, то посмотреть, существует ли ненулевой минор порядка n — 1. Если такой минор существует, то ранг матрицы = n — 1. Если все миноры порядка n — 1 нули, то мы должны повторить процесс для миноров порядка n — 2, и так далее, пока мы не сможем найти ранг.
Каков ранг нулевой матрицы?
Нулевая матрица представляет собой квадратную матрицу, в которой все элементы равны 0. Определитель нулевой матрицы и любого ее минора сам равен 0. Следовательно, не существует минора нулевой матрицы, отличного от нуля. Следовательно, ранг нулевой матрицы равен 0.
Как быстро найти ранг матрицы?
Если определитель матрицы не равен нулю, то ранг матрицы равен порядку матрицы. Это можно использовать как ярлык. Но этот ярлык не работает, когда определитель равен 0. В этом случае мы должны использовать либо минорную форму, форму эшелона, либо нормальную форму, чтобы найти ранг, как процессы объясняются на этой странице.
Каковы применения ранга матрицы?
Ранг матрицы в основном используется для определения количества решений системы уравнений. Если система имеет «n» уравнений с «n» переменными, то сначала мы находим ранг расширенной матрицы и ранг матрицы коэффициентов.
Если ранг (расширенная матрица) ≠ ранг (матрица коэффициентов), то система не имеет решения (несовместна).
Если ранг (расширенная матрица) = ранг (матрица коэффициентов) = количество переменных, то система имеет единственное решение (непротиворечивое).
Если ранг (расширенная матрица) = ранг (матрица коэффициентов) < количества переменных, то система имеет бесконечное число решений (непротиворечивых).
О чем говорит нам ранг матрицы?
Ранг матрицы определяет количество линейно независимых строк (или столбцов). Чем больше ранг матрицы, тем больше линейно независимых строк, а также тем больше информативность.
Может ли ранг матрицы быть больше количества строк или столбцов?
Нет, ранг матрицы всегда меньше или равен количеству строк и количеству столбцов.
Какая связь между рангом матрицы и собственными значениями?
Существует очень тесная связь между рангом матрицы и собственными значениями. Ранг матрицы точно равен количеству ненулевых собственных значений.
Ранг матрицы
Марко Табога, доктор философии
Ранг столбца a матрица линейный размер пространство, охваченное его столбцами.
Ранг строки матрицы — это размерность пространства, натянутого на ее строки.
Поскольку мы можем доказать, что ранг строки и ранг столбца всегда равны, мы просто говорят о ранге матрицы.
СОДЕРЖАНИЕ
Ранг столбца
Рейн строи
Рейн -рейтинг равен равенству ROW
Определение ранга
Максимум
Рейн
Максимум Рейн
111111111111111111111119 гг.1060
Полный ранг
Решенные упражнения
Упражнение 1
Упражнение 2
9190 2 ранг 0
Начнем с определения.
Определение Позволять быть матрица. Ранг столбца это здесь обозначает -й столбец , обозначает линейный пролет, а обозначает измерение.
Помните, что размерность линейное пространство — это количество элементы одного из его базы, то есть количество линейно независимые векторы, порождающие пространство. Итак, ранг столбца a матрица — это количество линейно независимых векторов, порождающих одинаковые пространство, порожденное столбцами матрицы.
Пример Рассмотрим матрицу а также линейное пространство охватываемый двумя столбцычто есть пространство всех векторов, которое можно записать как линейные комбинации а также . Любой вектор можно написать как где а также два скаляра. Обратите внимание, что два столбца а также линейно зависимы потому что, любой вектор можно записать как кратное : В качестве следствие, является основа для . Оно имеет элемент. Следовательно, размерность и ранг столбца равны .
Ранг строки
Определение ранга строки аналогично определению ранга столбца.
Определение Позволять быть матрица. Ранг строки это здесь обозначает -й ряд , обозначает линейный пролет, а обозначает размерность.
Другими словами, ранг строки матрицы — это размерность линейного пространства порождается его строками.
Ранг столбца равен рангу строки
Важным результатом является то, что ранг столбца матрицы всегда равен ее ранг строки.
Предложение Позволять быть матрица. Тогда
Доказательство
Пусть Затем, существует основа из векторы-столбцы, которые охватывают одно и то же пространство, натянутое столбцами . Обозначим через в матрица, полученная из векторов базиса: Каждый столбец может быть выражена как линейная комбинация . Коэффициенты линейных комбинаций можно собрать в матрица такой это как мы показали в лекции о Матрица умножение и линейные комбинации. В той же лекции мы также показано, что строки произведения являются линейными комбинациями строк , с коэффициентами, взятыми из . Таким образом, размах рядов не больше размаха рядов (поскольку линейные комбинации строк могут быть записаны как линейные комбинации строк ). Там находятся ряды в . Если они линейно независимы, то их промежуток имеет размерность . В противном случае он имеет размерность меньше . Как следствие, ранг строки меньше или равно (его ранг столбца). Совершенно аналогичным образом доказывается, что столбец ранг меньше или равен рангу строки: пусть Затем, существует основа из векторы-строки, которые охватывают одно и то же пространство, натянутое строками . Обозначим через в матрица, полученная из векторов базиса: Каждый ряд может быть выражена как линейная комбинация . Коэффициенты линейных комбинаций можно собрать в матрица такой что столбцы продукта являются линейными комбинациями столбцов , с коэффициентами, взятыми из . Таким образом, размах колонн не больше размаха столбцов (поскольку линейные комбинации столбцов могут быть записаны как линейные комбинации столбцов ). Там находятся столбцы в . Если они линейно независимы, то их промежуток имеет размерность . В противном случае он имеет размерность меньше . Как следствие, ранг столбца меньше или равно (его рядовой ранг). Таким образом, мы доказали что и поэтому,
Определение ранга
Доказав, что ранг столбца и строки совпадают, теперь мы готовы предоставить определение ранга.
Определение Позволять быть матрица. Ранг , обозначается , определяется как
Другими словами, ранг матрицы — это размерность линейной оболочки матрицы. его столбцов, что совпадает с размерностью линейного пролета его ряды.
Максимальный ранг
Справедливо следующее предложение.
Предложение Позволять быть матрица. Тогда
Доказательство
У нас есть два возможных случая. Во-первых случае, что есть, число строк меньше или равно числу столбцов. Столбцы представляют собой векторы, имеющие записи. Таким образом, размер пространства, занимаемого столбцами, меньше или равно . В других слова, но так что Во-вторых случае, что есть, число столбцов меньше или равно числу строк. Строки представляют собой векторы, имеющие записи. Таким образом, размер пространства, охваченного строками, меньше или равно . В других слова, но так чтоТаким образом, в обоих случаи,
Полный ранг
Учитывая предыдущие результаты, теперь мы можем дать определение матрицы полного ранга.
Определение Позволять быть матрица. затем называется полноранговым тогда и только тогда если
Очевидно, что если является квадратной матрицей, т. е. если , то он полноранговый тогда и только тогда если в другими словами, если является квадратным и полноранговым, то его столбцы (строки) охватывают пространство всех -размерный векторы: любые -размерный вектор можно записать как линейную комбинацию столбцов (строк) .
No related posts.