Примеры распределение бернулли: Математическое Бюро. Страница 404

Схема Бернулли. Примеры решения задач

5 июля 2011

Не будем долго размышлять о высоком — начнем сразу с определения.

Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P(A) = p. Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно k раз.

Задачи, которые решаются по схеме Бернулли, чрезвычайно разнообразны: от простеньких (типа «найдите вероятность, что стрелок попадет 1 раз из 10») до весьма суровых (например, задачи на проценты или игральные карты). В реальности эта схема часто применяется для решения задач, связанных с контролем качества продукции и надежности различных механизмов, все характеристики которых должны быть известны до начала работы.

Вернемся к определению. Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода:

1. A — появление события A с вероятностью p;
2. «не А» — событие А не появилось, что происходит с вероятностью q = 1 − p.

Важнейшее условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы опытов мы ни проводили, нас интересует одно и то же событие A, которое возникает с одной и той же вероятностью p.

Между прочим, далеко не все задачи в теории вероятностей сводятся к постоянным условиям. Об этом вам расскажет любой грамотный репетитор по высшей математике. Даже такое нехитрое дело, как вынимание разноцветных шаров из ящика, не является опытом с постоянными условиями. Вынули очередной шар — соотношение цветов в ящике изменилось. Следовательно, изменились и вероятности.

Если же условия постоянны, можно точно определить вероятность того, что событие A произойдет ровно k раз из n возможных. Сформулируем этот факт в виде теоремы:

Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:

где C_n^k — число сочетаний, q = 1 − p.

Эта формула так и называется: формула Бернулли. Интересно заметить, что задачи, приведенные ниже, вполне решаются без использования этой формулы. Например, можно применить формулы сложения вероятностей. Однако объем вычислений будет просто нереальным.

Задача. Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно k будут без брака. Решить задачу для k = 0, 1, 10.

По условию, нас интересует событие A выпуска изделий без брака, которое случается каждый раз с вероятностью p = 1 − 0,2 = 0,8. Нужно определить вероятность того, что это событие произойдет k раз. Событию A противопоставляется событие «не A», т.е. выпуск бракованного изделия.

Таким образом, имеем: n = 10; p = 0,8; q = 0,2.

Итак, находим вероятность того, что в партии все детали бракованные (k = 0), что только одна деталь без брака (k = 1), и что бракованных деталей нет вообще (k = 10):

Задача. Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что:

1. герб выпадет три раза;
2. герб выпадет один раз;
3. герб выпадет не менее двух раз.

Итак, нас интересует событие A, когда выпадает герб. Вероятность этого события равна p = 0,5. Событию A противопоставляется событие «не A», когда выпадает решка, что случается с вероятностью q = 1 − 0,5 = 0,5. Нужно определить вероятность того, что герб выпадет k раз.

Таким образом, имеем: n = 6; p = 0,5; q = 0,5.

Определим вероятность того, что герб выпал три раза, т.е. k = 3:

Теперь определим вероятность того, что герб выпал только один раз, т.е. k = 1:

Осталось определить, с какой вероятностью герб выпадет не менее двух раз. Основная загвоздка — во фразе «не менее». Получается, что нас устроит любое k, кроме 0 и 1, т.е. надо найти значение суммы X = P₆(2) + P₆(3) + … + P₆(6).

Заметим, что эта сумма также равна (1 − P₆(0) − P₆(1)), т. {17}} \approx 0,41\end{array}\]

Очевидно, P₂₀(3) > P₂₀(2), т.е. вероятность получить три телевизора со скрытыми дефектами больше вероятности получить только два таких телевизора. Причем, разница неслабая.

Небольшое замечание по поводу факториалов. Многие испытывают смутное ощущение дискомфорта, когда видят запись «0!» (читается «ноль факториал»). Так вот, 0! = 1 по определению.

P. S. А самая большая вероятность в последней задаче — это получить четыре телевизора со скрытыми дефектами. Подсчитайте сами — и убедитесь.

Смотрите также:

1. Локальная теорема Муавра — Лапласа
2. Формула полной вероятности
3. Тест к уроку «Сложение и вычитание дробей» (легкий)
4. Сводный тест по задачам B12 (2 вариант)
5. Как решать задачи про летающие камни?
6. Задача C1: тригонометрические уравнения и формула двойного угла

Испытания Бернулли: схема, биномиальное распределение, примеры

п.1. Схема Бернулли

Схема Бернулли – это последовательность независимых испытаний, в каждом из которых возможны только два исхода – «успех» и «неудача».

7}}\)0,00780,05470,16410,27340,27340,16410,05470,0078

Распределение является симметричным, т.к. p = q
Максимальная вероятность 27,34% при k* = 3 и k* = 4
Минимальные вероятности 0,78% при k = 0 – выпали все решки, и k = 7 – выпали все орлы.

20. Закон распределения Бернулли, его определение, свойства и примеры.

Дискретная случайная величина X имеет биномиальное распределение (или распределена по биномиальному закону), если она принимает значения 0, 1, 2, …, n, с соответствующими вероятностями:

, где,,.

Математическое ожидание и дисперсия случайной величины X, имеющей биномиальное распределение, находятся по формулам:

.

Из формулы Бернулли следует, что случайная величина – число наступлений событиявнезависимых испытаниях () – распределена по биномиальному закону.

21. Биномиальный закон распределения, его определение, свойства и примеры.

Пусть производится n независимых испытаний, в каждом из которых событиеAможет появиться или не появиться. Вероятность наступления события во всех испытаниях постоянна и равнаp(следовательно, вероятность непоявленияq = 1 — p).

Рассмотрим случайную величину X– число появлений событияAв этих испытаниях. Случайная величинаXпринимает значения0,1,2,…nс вероятностями, вычисленными по формуле Бернулли:, гдеk = 0,1,2,…n.

Определение:Биномиальнымназывают раcпределение вероятностей, определяемое формулой Бернулли.

Пример. По мишени производится три выстрела, причем вероятность попадания при каждом выстреле равна 0,8.

Рассматривается случайная величинаX– число попаданий в мишень. Найти ее ряд распределения.

Решение: Случайная величинаXпринимает значения0,1,2,3 с вероятностями, вычисленными по формуле Бернулли, гдеn = 3, p = 0,8(вероятность попадания),q = 1 — 0,8 = = 0,2(вероятность непопадания).

Тогда

,

Таким образом, ряд распределения имеет следующий вид:

0	1	2	3
0,008	0,096	0,384	0,512

Пользоваться формулой Бернулли при больших значениях nдостаточно трудно, поэтому для подсчета соответствующих вероятностей используют локальную теорему Лапласа, которая позволяет приближенно найти вероятность появления события ровноkраз вnиспытаниях, если число испытаний достаточно велико.

22.Закон распределения Пуассона, его определение, свойства и примеры.

Определение. Будем говорить, что случайная величинаε распределена по закону Пуассона с параметромλ , если она принимает значения из множества { 0,1,…,n, …} с вероятностямиP{ε=m} = (λ^m/m!)*e^—λ.

Теорема. Если случайная величинаε распределена по закону Пуассона с параметромλ , то и математическое ожидание, и дисперсия этой случайной величины равны параметру

λ.

Свойства распределения Пуассона:

1. .

Действительно:

2. .

3. если , то из биномиального распределения следует закон распределения Пуассона.

ПРИМЕР 1.Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут: а) три негодных изделия; б) не более трёх повреждённых изделия.

Решение: по условию n=5000, p=0,0002. Найдём .

а) k = 3. Искомая вероятность по формуле Пуассона приближённо равна

.

 б) Пусть случайная величина Х – число изделий, повреждённых в пути, то есть . Очевидно, что данная случайная величина распределена по биномиальному закону. Следовательно, искомую вероятность можно вычислить по формуле

.

 Но, так как , то по свойству 3^о можем воспользоваться законом распределения Пуассона, то есть, можем записать:

.

 Замечание.По формуле Пуассона можно вычислить вероятность того, что число событий, происшедших за время равно, если события образуют пуассоновский поток, причём– интенсивность потока, то есть среднее число событий, которые появляются в единицу времени:

.

 ПРИМЕР 2. В течение часа коммутатор получает в среднем 60 вызовов. Какова вероятность того, что за время 30 сек, в течении которых телефонистка отлучилась, не будет ни одного вызова?

Решение: Найдём, прежде всего, – среднее число вызовов за 1 секунду:

.

 Тогда, при , получим:

 

23.* Геометрическое распределение, его определение, свойства и примеры.

Пусть проводятся независимые испытания, каждое испытание может иметь два исхода: удача с вероятностью p и неудача с вероятностью q = 1 — p. Введем в рассмотрение случайную величину X — число испытаний до первого появления удачи. Эта случайная величина может принимать значения 1, 2, 3, 4 и так далее до бесконечности. Когда говорят, что случайная величина X имеет значение k, то это означает, что первые k — 1 испытание закончились неудачей, а k-ое испытание стало удачным. Вероятность того, что в серии независимых испытаний будет вначале k — 1 неудач, а в k-ое испытание — удача, равна . Таким образом мы получили закон распределения случайной величины X: значению k случайной величины соответствует вероятность. Этот закон распределения и называется геометрическим распределением. Название происходит из того, что величинапредставляет собой геометрическую прогрессию, с первым членом p и знаменателем q. Изучим теперь свойства этого распределения. С ростом k вероятности убывают. Используя формулу для суммы членов геометрической прогрессии, можем записать:, то есть условие, что сумма всех вероятностей в законе распределения равна единице, выполнено. Вычислим теперь математическое ожидание и дисперсию. По определению математического ожидания имеем:. Для вычисления суммы воспользуемся следующим приемом — заменимнаи вынесем производную за знак суммы, в итоге получим:. Оставшаяся сумма представляет собой сумму членов геометрической прогрессии и равна. Вычисляя производную, запишем:. Аналогично можно получить выражение для:. Заменяя сумму на ее значение, вычисляем:. Таким образом, имеем выражение для дисперсии:. Если вероятность удачи равна единице, то математическое ожидание числа испытаний до первой удачи равно 1, а дисперсия — 0. Если, наоборот, вероятность удачи равна нулю, то математическое ожидание — бесконечность (то есть нужно произвести бесконечное число испытаний до появления удачи). Пример 30.1Вероятность попадания в мишень из винтовки равна 0,8. Найти математическое ожидание и дисперсию случайной величины — количества выстрелов до первого попадания.Математическое ожидание, дисперсия. Полученные результаты означают, что при вероятности попадания 0,8 попадание будет в среднем с 1—2 выстрела.

24.Равномерный закон распределения, его определение, свойства и примеры. Законы распределения НСВ Плотности распределения НСВ называют также законами распределения. Часто встречаются законы равномерного, нормального и показательного распределений.

Определение.1. Закон распределения НСВ называется равномерным, если ее плотность распределения задается в виде:

1. Зная плотность распределения, и используя формулу ,

можно найти функцию распределения:

2. Если НСВ имеет равномерное распределение, то ее числовые характеристики могут быть найдены по формулам:

.

3. Вероятность попадания равномерно-распределенной НСВ в интервалможно определить по формуле:

.

Пример 1. Автобусы подходят к остановке с интервалом в 5 минут. Считая, что НСВ — время ожидания автобуса — распределена равномерно, найти среднее время ожидания (математическое ожидание), среднее квадратическое отклонение. Какова вероятность того, случайно подошедший на остановку пассажир будет ожидать автобус не более 4 минут, но и не менее 2 минут.

Решение:

;

.

Независимые повторные испытания и формула Бернулли

• Формула Бернулли: теория
• Формула Бернулли: примеры решения задач

На этом уроке будем находить вероятность наступления события в независимых испытаниях при повторении испытаний. Испытания называются независимыми, если вероятность того или иного исхода каждого испытания не зависит от того, какие исходы имели другие испытания. Независимые испытания могут проводиться как в одинаковых условиях, так и в различных. В первом случае вероятность появления некоторого события во всех испытаниях одна и та же, во втором случае она меняется от испытания к испытанию.

Примеры независимых повторных испытаний:

• выйдет из строя один из узлов прибора или два, три узла, причём выход из строя каждого узла не зависит от другого узла, а вероятность выхода из строя одного узла постоянна во всех испытаниях;
• произведённая в некоторых постоянных технологических условиях деталь, или три, четыре, пять деталей, окажутся нестандартными, причём одна деталь может оказаться нестандартной независимо от любой другой детали и вероятность того, что деталь окажется нестандатной, постоянна во всех испытаниях;
• из нескольких выстрелов по мишени один, три или четыре выстрела попадают в цель независимо от исходов других выстрелов и вероятность попадания в цель постоянна во всех испытаниях;
• при опускании монеты автомат сработает правильно один, два или другое число раз независимо от того, какой результат имели другие опускания монеты, и вероятность того, что автомат сработает правильно, постоянна во всех испытаниях.

Эти события можно описать одной схемой. Каждое событие наступает в каждом испытании с одной и той же вероятностью, которая не изменяется, если становятся известными результаты предыдущих испытаний. Такие испытания называются независимыми, а схема называется схемой Бернулли. Предполагается, что такие испытания могут быть повторены как угодно большое количество раз.

Если вероятность p наступления события A в каждом испытании постоянна, то вероятность того, что в n независимых испытаниях событие A наступит m раз, находится по формуле Бернулли:

(где q = 1 – p — вероятность того, что событие не наступит)

или

Поставим задачу – найти вероятность того, что событие такого типа в n независимых испытаниях наступит m раз.

---

Пример 1. Найти вероятность того, что среди взятых случайно пяти деталей две стандартные, если вероятность того, что каждая деталь окажется стандартной, равна 0,9.

Решение. Вероятность события А, состоящего в том, что взятая случайно деталь стандартна, есть p=0,9, а вероятность того, что она нестандартна, есть q=1–p=0,1. Обозначенное в условии задачи событие (обозначим его через В) наступит, если, например, первые две детали окажутся стандартными, а следующие три – нестандартными. Но событие В также наступит, если первая и третья детали окажутся стандартными, а остальные – нестандартными, или если вторая и пятая детали будут стандартными, а остальные – нестандартными. Имеются и другие возможности наступления события В. Любая из них характеризуется тем, что из пяти взятых деталей две, занимающие любые места из пяти, окажутся стандартными. Следовательно, общее число различных возможностей наступления события В равно числу возможностей размещения на пяти местах двух стандартных деталей, т. е. равно числу сочетаний из пяти элементов по два, а .

Вероятность каждой возможности по теореме умножения вероятностей равна произведению пяти множителей, из которых два, соответствующие появлению стандартных деталей, равны 0,9, а остальные три, соответствующие появлению нестандартных деталей, равны 0,1, т.е. эта вероятность составляет . Так как указанные десять возможностей являются несовместимыми событиями, по теореме сложения вероятность события В, которую обозначим

---

Пример 2. Вероятность того, что станок в течение часа потребует внимания рабочего, равна 0,6. Предполагая, что неполадки на станках независимы, найти вероятность того, что в течение часа внимания рабочего потребует какой-либо один станок из четырёх обслуживаемых им.

Решение. Используя формулу Бернулли при n=4, m=1, p=0,6 и q=1–p=0,4, получим

                 

Статистика — не Ваша специализация? Закажите статистическую обработку данных

Пример 3. Для нормальной работы автобазы на линии должно быть не менее восьми автомашин, а их имеется десять. Вероятность невыхода каждой автомашины на линию равна 0,1. Найти вероятность нормальной работы автобазы в ближайший день.

Решение. Автобаза будет работать нормально (событие F), если на линию выйдут или восемь (событие А), или девять (событие В), или все десять автомашин событие (событие C). По теореме сложения вероятностей,

.

Каждое слагаемое находим по формуле Бернулли. Здесь n=10, m=8;&nbsp9; 10, а p=1-0,1=0,9, так как p должно означать вероятность выхода автомашины на линию; тогда q=0,1. В результате получим

Пример 4. Пусть вероятность того, что покупателю необходима мужская обувь 41-го размера, равна 0,25. Найти вероятность того, что из шести покупателей по крайней мере двум необходима обувь 41-го размера.

Решение. Обозначенное в условии задачи событие (обозначим его через С) состоит в том, что из шести покупателей двум, трём, четырём, пяти или шести необходима обувь 41-го размера. Применив теорему сложения вероятностей, а затем формулу Бернулли, получим ответ. Однако задача решается проще, если сначала искать вероятность не требуемого в условии задачи, а противоположного ему события . Оно состоит в том, что менее чем двум покупателям необходима обувь 41-го размера, то есть или ни одному покупателю (событие А), или только одному (событие В). Таким образом,

.

По формуле Бернулли при n=6, p=0,25, q=0,75 и m=0; 1 получим

(при подсчёте следует иметь в виду, что ). Тогда вероятность события С найдётся как вероятность события, противоположного найденному:

.

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

Пройти тест по теме Теория вероятностей и математическая статистика

К началу страницы

Основные понятия теории вероятностей, непосредственное вычисление вероятностей

Действия над вероятностями

Различные задачи на сложение и умножение вероятностей

Формула полной вероятности и формула Байеса

Распределение вероятностей дискретной случайной величины

Распределение вероятностей непрерывной случайной величины

Математическое ожидание и дисперсия случайной величины

Биномиальное распределение дискретной случайной величины

Распределение Пуассона дискретной случайной величины

Равномерное распределение непрерывной случайной величины

Нормальное распределение непрерывной случайной величины

Биномиальное распределение с примерами решения

Содержание:

1. Схема Бернулли и биномиальное распределение
2. Примеры с решением

В этой статье я дам определения и опишем необходимые нам в последующем основные свойства наиболее известных дискретных вероятностных распределений (как одномерных, гак и многомерных), а также проиллюстрируем их использование в вероятностных и статистических задачах.

Замечательным фактом является то, что существует несколько распределений большой общности, встречающихся в самых разнообразных задачах теории вероятностей и математической статистики.

Прежде всего это биномиальное распределение, распределение Пуассона и нормальное распределение — с первого мы и начнем.

Схема Бернулли и биномиальное распределение

Говорят, что случайная величина имеет распределение Бернулли с параметром если она принимает лишь два значения, обозначаемые обычно О и 1, и при этом

В терминах плотности это можно записать в виде

В символьных обозначениях сказанное выражается кратко так: и называется бернуллиевской моделью. Фундаментальная роль этой модели в теории вероятностей и математической статистике ясна: она является подходящей математической моделью для любого эксперимента с двумя исходами («успех»-*не-успех»), т. е. простейшего статистического эксперимента. Среднее и дисперсия такой случайной величины есть (символ от английского expectation (математическое ожидание = среднее значение), от dispersion (дисперсия)).

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Если все случайные величины последовательности (конечной или бесконечной) независимы и имеют одно и то же распределение то мы имеем последовательность испытаний Бернулли (или, кратко, бернуллиевскую последовательность), называемую так по имени Якоба Бернулли (1654-1705) — выдающегося швейцарского математика, впервые изучавшего такую схему (его основополагающие труды в области теории вероятностей изложены в посмертно изданном сочинении «Искусство предположений» (1713)).

Пусть бернуллневская последовательность с параметром Тогда сумма имеет биномиальное распределение с параметрами что кратко записывается в виде:

Эта случайная величина принимает, очевидно, лишь значения 0,1 и при этом

Термин «биномиальное распределение» связан с тем, что вероятности (3) являются членами известного «бинома Ньютона»:

Таким образом, биномиальная модель описывает распределение числа «успехов» в испытаниях Бернулли с неизменной вероятностью «успеха»

Здесь

Полезно знать также следующее свойство биномиального распределения: если случайные величины независимы и

то

Это свойство биномиального распределения называется воспроизводимостью по параметру

Если параметр нам неизвестен (а так на практике чаще всего и бывает!), то мы имеем биномиальную статистическую модель

(при бернуллиевскую статистическую модель

Возможно вам будут полезны данные страницы:

Таблица производных полная: для студентов

Ранг матрицы: примеры решения

Биномиальный закон распределения

Отрицательное биномиальное распределение

Примеры с решением

Пример 1.

Рассмотрим ситуацию, если в данном эксперименте реализуется схема выбора с возвращением, и если условия эксперимента обеспечивают независимость извлечения каждого очередного шара от результатов предыдущих извлечений (практически это достигается тщательным перемешиванием содержимого урны перед каждым очередным извлечением), то мы имеем бернуллиевскую модель где под «успехом» понимается извлечение белого шара, для которой надо оценить параметр по результатам испытаний. В данном случае наблюдаемая случайная величина есть число белых шаров в выборке из шаров, которая имеет биномиальное распределение

Пример 2.

Рассмотрим подробно описанный эпизод с преподобным Галиани. Здесь мы имеем эксперимент, состоящий в пятикратном бросании трех игральных костей. Интересующая нас величина, характеризующая один опыт, — число выпавших шестерок на трех костях. Обозначим ее В свою очередь, она равна сумме трех бернуллиевских величин где если на кости выпала шестерка, и 0 — в противном случае

Если исходить из того, что кости одинаковы (это обычно не подвергается сомнению, хотя, на самом деле, — это тоже гипотеза), то случайные величины имеют одно и то же распределение Бернулли и они, по условию опыта, независимы. Тем самым их сумма имеет распределение и над этой случайной величиной произведено пять независимых испытаний, т.е. мы имеем случайную выборку из распределения Таким образом, мы построили биномиальную модель для описания нашего эксперимента, и в рамках этой модели требуется проверить гипотезу симметричности костей (т.е. гипотезу о том, что каждая грань выпадает с одинаковой вероятностью 1/6). Как можно формализовать рассуждения преподобного? Общее число выпавших шестерок имеет биномиальное распределение и по формуле (3)

Следовательно, при справедливости гипотезы вероятность наблюдаемого события, т.е. равна что ничтожно мало (!). Наверное, любой разумный человек на месте преподобного усомнился бы в истинности гипотезы в данном случае (при таком наблюдаемом исходе эксперимента)

Замечание.

Обратим внимание на следующее. В данном случае, если отбросить несущественные для математики эмоциональные нюансы (пари), а оставить лишь физическую суть эксперимента (в его ходе было брошено 3×5 15 костей), то можно сразу говорить о случайной выборке объема из распределения Бернулли для которой исследуется случайная величина общее число выпавших шестерок. Конечно, снова

Распределения вероятностей

Случайная переменная — это величина, которая может принимать любое из набора взаимоисключающих значений с определенной вероятностью.

Распределение вероятности показывает вероятности всех возможных значений случайной переменной. Это теоретическое распределение, которое выражено математически и имеет среднее и дисперсию — аналоги среднего и дисперсии в эмпирическом распределении.

Каждое распределение вероятности определяется некоторыми параметрами, параметры служат обобщающими величинами (например среднее, дисперсия), характеризующими данное распределение (т.e. их знание позволит подробно описать распределение).

С помощью соответствующей статистики можно произвести оценку этих параметров в выборке В зависимости от того, является ли случайная переменная дискретной или непрерывной, распределение вероятности может быть либо дискретным, либо непрерывным.

Дискретные распределения

Моделируют вероятность наступления дискретных событий, например, выпадение герба или решки (распределение Бернулли), число выпадений герба или решки при многократном бросании монеты (биномиальное распределение), выпадения определенного числа очков при бросании игральной кости (полиномиальное или мультиномиальное распределение).

Примеры дискретных величин самые разнообразные: число телефонных звонков за день, количество перевезенных пассажиров, количество дефектов в партии продукции, количество распавшихся атомов за определенный промежуток, число квантов света, попавших на сетчатку глаза и множество других в физике, технике, биологии, медицине, экономике, транспорте, телефонии.

Основные дискретные распределения:

Биномиальное распределение

Геометрическое распределение

Гипергеометрическое распределение

Полиномиальное (мультиномиальное) распределение

Распределение Пуассона

Распределения Кокса

Распределение	Вероятность	Параметры
Равномерное дискретное	, k=1, 2,. ..,N	N=1, 2,…
Бернулли
Биномиальное распределение
Распределение Пуассона
Геометрическое распределение
Отрицательно-биномиальное

Непрерывные распределения

Моделируют вероятность наступления непрерывных событий, например, длительность телефонного звонка, момент наступления телефонного звонка, уровень шума в сети, расход электроэнергии за день, местоположение дефектов в микросхеме, количество осадков за месяц, биржевые данные, расстояние, пройденное молекулой газа до следующего столкновения и т. д.

Задавая распределение, вы строите вероятностную модель и затем оцениваете вероятности наступления более сложных событий, например, вероятность того, что количество прерванных звонков в сети превысит норму, вероятность того, что производственный процесс выйдет за допустимые пределы, количество бракованных деталей будет критическим, вероятность возникновения взрыва при ядерной реакции и т. д.

Основные непрерывные распределения:

Равномерное распределение

Нормальное распределение

Многомерное нормальное распределение

Логнормальное распределение

Экспоненциальное распределение

Гамма распределение

Распределение Эрланга

Распределение Стьюдента

Распределение Фишера

Распределение	Плотность	Параметры
Равномерное на [a,b]
Нормальное (гауссовское)
Гамма
Бета
Экспоненциальное
Двусторонне-экспоненциальное
Хи-квадрат
Стьюдента
F
Коши

Связанные определения:
Cимметричное распределение
Двумерная функция распределения
Логнормальное распределение
Плотность распределения вероятностей
Полимодальное распределение
Распределение при выполнении нулевой гипотезы
Унимодальное распределение
Условная функция распределения
Функция распределения
Эмпирическая функция распределения

В начало

Содержание портала

Распределение Бернулли: определение и примеры

Что такое распределение Бернулли?

Распределение Бернулли — это дискретное распределение вероятностей для испытания Бернулли — случайного эксперимента, который имеет только два результата (обычно называемых «Успехом» или «Неудачей»). Например, вероятность выпадения орла («успех») при подбрасывании монеты равна 0,5. Вероятность «неудачи» равна 1 – P (1 минус вероятность успеха, которая также равна 0,5 при подбрасывании монеты). Это частный случай биномиального распределения для n = 1. Другими словами, это биномиальное распределение с одним испытанием (например, с одним подбрасыванием монеты).

Посмотрите видео с определением и тем, как найти PDF, дисперсию, математическое ожидание и вероятности:

Вероятность распределения Бернулли и PDF

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Вероятность ошибки отмечена на оси X как 0, а успех отмечен как 1. В следующем распределении Бернулли вероятность успеха (1) равна 0,4, а вероятность ошибки (0) равна 0,6:

Функция плотности вероятности (PDF) для этого распределения равна p ^x (1 – p) ^{1 – x} , что также может быть записано как:

Ожидаемое значение случайной величины X для Распределение Бернулли:
E[X] = p.
Например, если p = 0,04, то E[X] = 0,04.

Дисперсия случайной величины Бернулли:
Var[X] = p(1 – p).

A Опыт Бернулли — один из самых простых экспериментов, которые вы можете провести. Это эксперимент, в котором вы можете получить один из двух возможных результатов. Например, «Да» и «Нет» или «Орел» и «Решка». Несколько примеров:

• Подбрасывание монеты : запишите, сколько монет выпало орлом и сколько выпало решкой.
• Рождений : сколько мальчиков рождается и сколько девочек рождается каждый день.
• Бросание костей : вероятность того, что при броске двух кубиков выпадет двойная шестерка.

Подбрасывание монеты как игра вероятности и случая существует с римских времен. Испытания Бернулли обычно формулируются в терминах успеха и неудачи . Успех не означает успех в обычном смысле — это просто относится к результату, который вы хотите отслеживать. Например, вы можете узнать, сколько мальчиков рождается каждый день, поэтому вы называете рождение мальчика «успехом», а рождение девочки — «неудачей». В примере с броском кубиков бросок двойной шестерки будет вашим «успехом», а все остальные броски будут считаться «неудачей».

Независимость

Важной частью каждого испытания Бернулли является то, что каждое действие должно быть независимым. Это означает, что вероятности должны оставаться неизменными на протяжении всех испытаний; каждое событие должно быть совершенно отдельным и не иметь ничего общего с предыдущим событием.

Выигрыш в лотерею со скретч-оффом является независимым событием. Ваши шансы на выигрыш по одному билету такие же, как и по любому другому билету. С другой стороны, розыгрыш лотерейных номеров является зависимым событием. Лотерейные номера выпадают из шара (номера не заменяются), поэтому вероятность того, что будут выбраны следующие номера, зависит от того, сколько шаров осталось; когда есть сто шаров, вероятность того, что будет выбрано любое число, составляет 1/100, но когда осталось только десять шаров, вероятность возрастает до 1/10. Хотя эти вероятности можно найти, это не испытание Бернулли, потому что события (выбор чисел) связаны друг с другом.

Процесс Бернулли приводит к нескольким распределениям вероятностей:

• Биномиальное распределение,
• Геометрическое распределение,
• Отрицательное биномиальное распределение.

Распределение Бернулли тесно связано с биномиальным распределением. Пока каждое отдельное испытание Бернулли является независимым, количество успехов в серии следов Бернулли имеет биномиальное распределение. Распределение Бернулли можно также определить как биномиальное распределение с n = 1,9.0009

Использование распределения Бернулли в эпидемиологии

В экспериментах и ​​клинических испытаниях распределение Бернулли иногда используется для моделирования отдельного человека, переживающего такое событие, как смерть, заболевание или воздействие болезни. Модель является отличным индикатором вероятности того, что у человека есть рассматриваемое событие.

• 1 = «событие» (P = p)
• 0 = «не событие» (P = 1 – p)

Распределения Бернулли используются в логистической регрессии для моделирования возникновения заболеваний.

Ссылки

Evans, M.; Гастингс, Н.; и Пикок, Б. «Распределение Бернулли». Ч. 4 в Статистических распределениях, 3-е изд. Нью-Йорк: Wiley, стр. 31-33, 2000.
WSU. Получено 15 февраля 2016 г. с: www.stat.washington.edu/peter/341/Hypergeometric%20and%20binomial.pdf

ЦИФРОВАТЬ ЭТО КАК:
Stephanie Glen . «Распределение Бернулли: определение и примеры» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/probability-distribution/bernoulli-distribution/

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .

Распределение Бернулли — определение, формула, график, примеры

Распределение Бернулли — это тип дискретного распределения вероятностей, при котором каждый проводимый эксперимент задает вопрос, на который можно ответить только да или нет. Другими словами, случайная величина может быть равна 1 с вероятностью p или 0 с вероятностью (1 — p). Такой эксперимент называется испытанием Бернулли. Пройденный или непройденный экзамен может быть смоделирован с помощью распределения Бернулли.

Если у нас есть биномиальное распределение, где n = 1, то оно становится распределением Бернулли. Поскольку это распределение очень легко понять, оно используется в качестве основы для получения более сложных распределений. Распределение Бернулли можно использовать для описания событий, которые могут иметь только два исхода, то есть успех или неудачу. В этой статье мы узнаем о формуле, pmf, CDF и других аспектах распределения Бернулли.

1.	Что такое распределение Бернулли?
2.	Формула распределения Бернулли
3.	Среднее значение и дисперсия распределения Бернулли
4.	График распределения Бернулли
5.	Распределение Бернулли и биномиальное распределение
6.	Применение распределения Бернулли
7.	Часто задаваемые вопросы о распределении Бернулли

Что такое распределение Бернулли?

Распределение Бернулли — это особый тип распределения, который используется для моделирования реальных примеров и может использоваться во многих различных типах приложений. Случайный эксперимент, результат которого может быть только 1 или 0, известен как испытание Бернулли. Такой эксперимент используется в распределении Бернулли.

Распределение Бернулли Определение

Дискретное распределение вероятностей, в котором случайная величина может иметь только 2 возможных результата, называется распределением Бернулли. Если в испытании Бернулли случайная величина принимает значение 1, это означает, что это успех. Вероятность успеха определяется p. Точно так же, если значение случайной переменной равно 0, это указывает на сбой. Вероятность отказа равна q или 1 — p. Распределение Бернулли можно использовать для получения биномиального распределения, геометрического распределения и отрицательного биномиального распределения.

Пример распределения Бернулли

Предположим, есть эксперимент, в котором вы подбрасываете правильную монету. Если в результате броска выпадет орел, вы выиграете. Это означает, что вероятность выпадения орла равна p = 1/2. Если X — случайная величина, следующая распределению Бернулли, мы получаем P(X = 1) = p = 1/2.

Формула распределения Бернулли

Биномиальная случайная величина X также известна как индикаторная переменная. Это связано с тем, что если событие завершается успехом, то X = 1, а если результатом является неудача, то X = 0. X можно записать как X \(\sim\) Бернулли (p), где p — параметр. Формулы для распределения Бернулли задаются функцией массы вероятности (pmf) и кумулятивной функцией распределения (CDF).

Функция массы вероятности для распределения Бернулли

Мы вычисляем функцию массы вероятности для распределения Бернулли. Вероятность того, что дискретная случайная величина будет в точности равна некоторому значению, определяется функцией массы вероятности. Формула для pmf, f, связанная со случайной величиной Бернулли по возможным исходам ‘x’, задается следующим образом:

PMF = f(x, p) = \(\left\{\begin{matrix} p & if \ : x = 1\\ q = 1 — p & if \: x = 0 \end{matrix}\right.\) 9Мы также можем выразить эту формулу как Функция распределения Бернулли

Кумулятивная функция распределения случайной величины Бернулли X при оценке в точке x определяется как вероятность того, что X примет значение, меньшее или равное x. Формула задается следующим образом:

CDF = F(x, p) = \(\left\{\begin{matrix} 0 & if \: x < 0\\ 1 - p & if \: 0 \leq x < 1\\ 1 & x\geq 1 \end{matrix}\right.\)

Среднее значение и дисперсия распределения Бернулли

Среднее арифметическое большого числа независимых реализаций случайной величины X дает нам ожидаемое значение или среднее значение. Ожидаемое значение также можно рассматривать как средневзвешенное значение. Ниже приведены доказательство и формула для среднего распределения Бернулли.

Среднее значение распределения Бернулли Доказательство:

Мы знаем, что для X,

P(X = 1) = p

P(X = 0) = q

Е[Х] = Р(Х = 1) . 1 + Р(Х = 0) . 0

Е[Х] = р . 1 + кв. 0

E[X] = p

Таким образом, среднее или ожидаемое значение распределения Бернулли определяется как E[X] = p.

Дисперсия распределения Бернулли Доказательство:

Дисперсия может быть определена как разность среднего X ² и квадрата среднего X. Математически это утверждение можно записать следующим образом:

Var[ Х] = Е[Х ² ] — (Е[Х]) 9{2}\: P(X=x)\)

E[X ² ] = 1 ² . р + 0 ² . q = p

Подставив это значение в Var[X] = E[X ² ] — (E[X]) ² , мы получим

Var[X] = p — p ²

= p (1 — р)

= р . q

Следовательно, дисперсия распределения Бернулли равна Var[X] = p(1 — p) = p . д

График распределения Бернулли

График распределения Бернулли помогает получить наглядное представление о функции плотности вероятности случайной величины Бернулли.

График показывает, что вероятность успеха равна p, когда X = 1, и вероятность неудачи X равна (1 — p) или q, если X = 0.

Распределение Бернулли и биномиальное распределение

Распределение Бернулли является частным случаем биномиального распределения, когда количество испытаний = 1. Разница между распределением Бернулли и биномиальным распределением приведена ниже:

Распределение Бернулли	Биномиальное распределение
Распределение Бернулли используется, когда мы хотим смоделировать результат одного испытания события.	Если мы хотим смоделировать результат нескольких испытаний события, используется биномиальное распределение.
Представляется как X \(\sim\) Бернулли (p). Здесь р — вероятность успеха.	Обозначается как X \(\sim\) Binomial (n, p). Где n — количество испытаний.
Среднее, E[X] = p	Среднее, E[X] = np
Дисперсия, Var[X] = p(1-p)	Дисперсия, Var[X]= np(1-p)
Пример: Предположим, что вероятность сдачи экзамена составляет 80%, а провала — 20%. Затем распределение Бернулли можно использовать для моделирования сдачи или провала такого экзамена.	Пример: Предположим, что вероятность сдачи экзамена составляет 80%, а провала — 20%. Затем, если мы хотим найти вероятность того, что студент сдаст ровно 4 экзамена из 5, мы используем биномиальное распределение.

Приложения распределения Бернулли

Распределение Бернулли является простым распределением и, следовательно, широко используется во многих отраслях. Ниже приведены некоторые приложения распределения Бернулли.

• В медицине распределения Бернулли используются для моделирования событий, происходящих с одним пациентом. Этими событиями могут быть болезнь, смерть и так далее.
• Логистическая регрессия использует распределение Бернулли для моделирования возникновения определенных событий, таких как конкретный результат броска костей.
Распределение Бернулли
• также используется в качестве основы для получения нескольких других вероятностных распределений, которые находят применение в машиностроении, аэрокосмической и медицинской промышленности.

Статьи по теме:

• Формула биномиального распределения
• Вероятность и статистика
• Суммарная частота

Важные примечания о распределении Бернулли

• Распределение Бернулли — это дискретное распределение вероятностей, в котором случайная величина Бернулли может иметь только 0 или 1 в качестве результата.
• p — вероятность успеха, 1 — p — вероятность неудачи.
• Среднее значение распределения Бернулли равно E[X] = p, а дисперсия Var[X] = p(1-p).
• Распределение Бернулли является частным случаем биномиального распределения, когда проводится только одно испытание.

Часто задаваемые вопросы о распределении Бернулли

Что такое распределение Бернулли в статистике?

Распределение Бернулли — это дискретное распределение вероятностей, в котором результатом испытания Бернулли будет только 0 (неудача) или 1 (успех).

Что означает p в распределении Бернулли?

p — параметр в распределении Бернулли. Распределение Бернулли можно записать как X \(\sim\) Бернулли (p), где X — случайная величина Бернулли. p представляет вероятность успеха.

Является ли распределение Бернулли нормальным распределением?

Распределение Бернулли не является нормальным распределением. Однако, если мы провели испытание Бернулли несколько раз и записали количество успехов, мы можем оценить эту вероятность, используя нормальное распределение.

Каковы две основные характеристики распределения Бернулли?

Две ключевые характеристики распределения Бернулли:

• Случайная величина Бернулли может иметь только 2 результата: 0 и 1.
• Сумма всех значений вероятности должна быть равна 1.

Как найти среднее значение распределения Бернулли?

Среднее значение распределения Бернулли определяется по формуле E[X] = p. Таким образом, мы также можем сказать, что параметр p также является средним.

Как найти дисперсию распределения Бернулли?

Чтобы найти формулу дисперсии распределения Бернулли, мы используем E[X ² ] — (E[X]) ² и применяем свойства. Таким образом, Var[x] = p(1-p) распределения Бернулли.

В чем разница между биномиальным распределением и распределением Бернулли?

Распределение Бернулли — это случай биномиального распределения, когда было проведено только одно испытание. Биномиальное распределение задается X \(\sim\) Binomial (n, p). Когда n = 1, оно становится распределением Бернулли.

Распределение Бернулли | Brilliant Math & Science Wiki

Огнен Вукадин, Скотт Ли, Кристофер Уильямс, а также

способствовал

Содержимое

• Определение
• Основные свойства
• Примеры

Распределение Бернулли — это распределение вероятностей случайной величины XXX, имеющей функцию плотности вероятности

Pr(X=x)={px=11−px=0 \text{Pr}(X=x) = \begin{ случаи} р && х = 1 \\ 1-р&&х=0\ \end{cases}Pr(X=x)={p1−p​​x=1x=0​

для 0

Интуитивно он описывает один эксперимент с двумя исходами: успех («1») с вероятностью p,p,p и неудача («0») с вероятностью 1-p.1-p.1-p. Он описывает одно испытание эксперимента Бернулли. 9{1-x}P(x)=px(1−p)1−x.

Распределение Бернулли можно представить графически следующим образом:

Здесь р=0,3р=0,3р=0,3.

Честная монета подбрасывается один раз. Результат эксперимента моделируется распределением Бернулли с p=0,5p=0,5p=0,5.

ожидаемое значение распределения Бернулли равно

E(X)=0×(1−p)+1×p=p. E(X) = 0\times (1-p) + 1\times p = p. E(X)=0×(1−p)+1×p=p. 92 = р(1-р). Var(X)=E(X2)−E(X)2=12×p+02×(1−p)−p2=p−p2=p(1−p).

Режим , значение распределения Бернулли с наибольшей вероятностью возникновения равно 111, если p>0,5p>0,5p>0,5, и 000, если p<0,5p<0,5p<0,5. Если p=0,5p=0,5p=0,5, успех и неудача равновероятны, и как 000, так и 111 являются модами. Это интуитивно понятно: поскольку есть только два исхода с дополнительными вероятностями, p>0,5p>0,5p>0,5 означает, что вероятность успеха выше, чем вероятность неудачи.

Основные свойства распределения Бернулли можно рассчитать, взяв n=1n=1n=1 в биномиальном распределении.

Используя такие свойства, как линейность ожидания и правила расчета дисперсии, распределение Бернулли используется при расчете свойств распределений на основе эксперимента Бернулли, таких как биномиальное распределение.

Распределение Бернулли моделирует следующие ситуации:

• Новорожденный ребенок мужского или женского пола. (Здесь вероятность того, что ребенок будет мальчиком, примерно равна 0,5.)
• Вы либо сдадите экзамен, либо провалите его.

• Теннисист либо выигрывает, либо проигрывает матч.

• Дротик, брошенный в круглую мишень для дротиков, приземляется случайным образом по своей площади (пример). Дротик либо приземлится ближе к центру, чем к краю, либо нет (во втором случае он либо ближе к краю, либо на равном расстоянии от центра и края). В этом случае р=0,25р=0,25р=0,25.

Целое число n∈{1,…,999999}n\in \{1,\ldots, 999999 \}n∈{1,…,999999} выбирается случайным образом. Мы рассматриваем три переменные: X1, X2, X_1, X_2, X1, X2 и X3X_3X3. X1X_1X1 принимает значение 111, если сумма цифр nnn делится на 999 и на 000 в противном случае; X2X_2X2 принимает значение 111, если nnn может быть выражено как сумма четырех квадратов целых чисел, и 000 в противном случае; X3X_3X3 принимает значения 0,10,10,1 и 222 соответственно, если nnn оставляет остаток 0,10,10,1 и 222 при делении на 333.

• Сумма цифр натурального числа nnn делится на 999 тогда и только тогда, когда 999 делится на nnn. Вероятность того, что случайно выбранное целое число из {1,…,999999}\{1,\ldots, 999999 \}{1,…,999999} будет делиться на 999, равна 19.\frac{1}{9},91 . Таким образом, X1X_1X1 – случайная величина, распределенная по Бернулли, с p=19p=\frac{1}{9}p=91​.

• Каждое натуральное число может быть представлено в виде суммы четырех квадратов, поэтому переменная X2X_2X2​ не является случайной величиной и не имеет распределения Бернулли. В определении распределения Бернулли ограничение 0

• Переменная X3X_3X3 моделирует эксперимент с более чем двумя исходами и, следовательно, не является распределением Бернулли.

Предположим, у нас есть a + ba + ba + b независимых испытаний Бернулли (p) (p) (p). Пусть NaN_aNa будет количеством успехов в первом aaa этих испытаний, а NbN_bNb будет количеством успехов в последнем bbb этих испытаний. Используя свойства распределения Бернулли, мы можем сказать следующее:

• NaN_aNa​ ~ Биномиальное (a, p) (a, p) (a, p), потому что у нас есть aaa независимых испытаний Бернулли (p) (p) (p). Нас не волнуют последние испытания ббб.
• NbN_bNb​ ~ Биномиальное (b, p) (b, p) (b, p), потому что у нас есть bbb независимые испытания Бернулли (p) (p) (p). Нас не волнуют первые ААА испытания.
• Na+NbN_a + N_bNa​+Nb​ ~ Биномиальное (a+b,p)(a + b, p)(a+b,p), потому что все испытания Бернулли независимы, и мы можем рассматривать их как i. i.d.
• NaN_a Na​ и NbN_bNb​ являются независимыми, поскольку две группы испытаний (первые испытания aaa и последние испытания bbb) независимы.

Цитировать как: Распределение Бернулли. Brilliant.org . Извлекаются из https://brilliant.org/wiki/bernoulli-distribution/

Распределение Бернулли – объяснение и примеры

Определение распределения Бернулли:

вероятность случайной величины только с двумя исходами».

В этом разделе мы обсудим распределение Бернулли со следующих аспектов:

1. Что такое распределение Бернулли?
2. Когда использовать распределение Бернулли?
3. Формула распределения Бернулли.
4. Практические вопросы.
5. Ключ ответа.

1. Что такое распределение Бернулли?

Распределение Бернулли — это дискретное распределение вероятностей, которое описывает вероятность случайной величины только с двумя исходами.

В случайном процессе, называемом испытанием Бернулли, случайная величина может принимать один результат, называемый успехом, с вероятностью p, или другой результат, называемый неудачей, с вероятностью q = 1-p.

Успешный исход обозначается как 1, а неудачный результат обозначается как 0.

Распределение Бернулли — это частный случай биномиального распределения, когда проводится одно испытание, а биномиальное распределение представляет собой сумму повторных испытаний Бернулли.

Распределение Бернулли названо в честь швейцарского математика Якоба Бернулли .

– Пример 1

Подбрасывание монеты может привести только к двум возможным исходам (орел или решка). Один из этих исходов (орел) мы называем успехом, а другой (решка) — неудачей.

Вероятность успеха (p) или решка равна 0,5 для честной монеты. Вероятность отказа (q) или хвоста = 1-р = 1-0,5 = 0,5.

Если мы обозначим голову как 1, а хвост как 0, мы можем построить это распределение Бернулли следующим образом:

У нас есть два исхода:

• Решка или 0 с вероятностью 0,5.
• Голова или 1 с вероятностью 0,5 тоже.

Это пример функции массы вероятности , где у нас есть вероятность для каждого исхода.

– Пример 2

У нас есть нечестная монета, где вероятность успеха (p) или решка равна 0,8, а вероятность неудачи (q) или решка = 1-p = 1-0,8 = 0,2.

Если мы обозначим голову как 1, а хвост как 0, мы можем построить это распределение Бернулли следующим образом:

У нас два исхода:

• Решка или 0 с вероятностью 0,2.
• Голова или 1 с вероятностью 0,8.

– Пример 3

Распространенность определенного заболевания среди населения в целом составляет 10%.

Если мы случайным образом выберем человека из этой популяции, у нас может быть только два возможных исхода (больной или здоровый человек). Один из этих исходов (больной человек) мы называем успехом, а другой (здоровый человек) — неудачей.

Вероятность успеха (р) или заболевания человека составляет 10% или 0,1. Итак, вероятность отказа (q) или здорового человека = 1-р = 1-0,1 = 0,9.

Если мы обозначим больного человека как 1, а здорового человека как 0, мы можем построить это распределение Бернулли следующим образом:

Мы имеем два исхода:

• Здоровый человек или 0 с вероятностью 0,9 .
• Заболевший или 1 с вероятностью 0,1.

– Пример 4

В приведенном выше примере заболеваемость составляет 10%, если Нас интересуют здоровые люди и мы называем здорового человека успешным, а больного — неудачником.

Вероятность успеха (р) или здорового человека составляет 90% или 0,9. Итак, вероятность отказа (q) или заболевшего человека = 1-р = 1-0,9 = 0,1.

Если мы обозначим здорового человека как 1, а больного человека как 0, мы можем построить это распределение Бернулли следующим образом:

У нас есть два результата:

• Здоровый человек или 1 с вероятностью 0,9.
• Заболевший или 0 с вероятностью 0,1.

2. Когда использовать распределение Бернулли?

Для случайной величины, описываемой распределением Бернулли:

1. Случайная величина может принимать только один из двух возможных исходов. Мы называем один из этих результатов успехом, а другой — неудачей.
2. Вероятность успеха, обозначаемая p, одинакова в каждом испытании Бернулли.
3. Испытания независимы, т. е. результат одного испытания не влияет на исход других испытаний.

Мы можем определить распределение Бернулли по результатам различных испытаний Бернулли.

– Пример 1

Вы подбрасываете монету. Случайная величина равна 1, если выпадет орел, и 0, если выпадет решка.

Вы подбросили монету 100 раз и получили следующие результаты:

0 1 0 1 1 0 1 1 1 0 1 0 1 1 0 1 0 0 0 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 1 1 0 1 0 0 0 1 0 1 1 1 0 1 1 1 0 0 0 0 1 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 0 0 1 0 0 1.

Какое распределение Бернулли для этой монеты?

Вы можете использовать эти данные для оценки функции массы вероятности (или распределения вероятности) подбрасывания этой монеты.

1. Мы строим таблицу частот для каждого исхода.

Outcome	frequency
0	53
1	47

2. Добавьте еще один столбец для вероятности каждого исхода.

Вероятность = частота/общее количество данных = частота/100.

Outcome	frequency	probability
0	53	0.53
1	47	0,47

Вероятности >= 0 и в сумме дают 1.

Это правильная монета, где вероятность выпадения орла почти равна вероятности выпадения решки = 0,5.

Мы не получаем ровно 50 орлов и 50 решек из-за случайности в процессе, но мы получаем хорошее приближение к вероятности честной монеты = 0,5.

3. Используйте таблицу, чтобы построить распределение Бернулли для этой монеты:

У нас есть два исхода:

• Голова или 1 с вероятностью 0,47.
• Хвост или 0 с вероятностью 0,53.

— Пример 2

Вы провели скрининг 50 особей из определенной популяции на наличие гипертонии и получите следующие результаты:

99136

ID	Condition
.	нормотензивный
2	normotensive
3	normotensive
4	normotensive
5	normotensive
6	нормотензивный
7	нормотензивный
8	normotensive
9	normotensive
10	normotensive
11	hypertensive
12	нормотензивный
13	нормотензивный
14	normotensive
15	normotensive
16	normotensive
17	normotensive
18	нормотензивный
19	нормотензивный
20	hypertensive
21	normotensive
22	normotensive
23	normotensive
24	гипертоническая
25	нормотензивная
26	normotensive
27	normotensive
28	normotensive
29	normotensive
30	нормотензивный
31	гипертонический
32	normotensive
33	normotensive
34	normotensive
35	normotensive
36	нормотензивный
37	нормотензивный
38	normotensive
39	normotensive
40	normotensive
41	normotensive
42	нормотензивный
43	нормотензивный
44	normotensive
45	normotensive
46	normotensive
47	normotensive
48	нормотензивный
49	нормотензивный
50	нормотензивное

Каково расчетное распределение Бернулли для гипертензии в этой популяции?

1. Мы строим таблицу частот для каждого исхода.

Outcome	frequency
hypertensive	4
normotensive	46

2. Добавьте еще один столбец для вероятности каждого исхода. Поскольку нас интересует гипертония, мы обозначаем гипертоников как 1, а людей с нормальным давлением как 0.

Вероятность = частота/общее количество данных = частота/50.

outcome	frequency	probability
1	4	0.08
0	46	0,92

. Вероятности.

Имеем два исхода:

• Гипертоник или 1 с вероятностью 0,08.
• Нормотензивный человек или 0 с вероятностью 0,92.

– Пример 3

Вы проверили образец из 100 таблеток с двух машин по производству таблеток на одном заводе. We denote 1 for rejected tablets and 0 for accepted tablets and get the following results:

49999969999999999999999999999999999999999999999999999999999999999999999НИ0009.

9.

9

6.

1. Мы строим таблицу частот для каждого исхода.

Tablet	machine1	machine2
1	0	0
2	0	0
3	0	0
4	0	1
5	0	0
6	0	0
7	0	1
8	0	0
9	0	0
10	0	0
11	1	1
12	0	0
13	0	0
14	0	1
15	0	0
16	0	0
17	0	0
18	0	1
19	0	0
20	1	0
21	0	0
22	0	0
23	0	0
24	1	0
25	0	0
26	0	1
27	0	0
28	0	0
29	0	0
30	0	0
31	1	0
0	0
33	0	0
34	0	0
35	0	0
36	0	0
37	0	0
38	0	0
39	0	1
40	0	0
41	0	0
42	0	0
43	0	0
44	0	0
45	0	0
46	0	0
47	0	0
48	0	0
49	0	0
50	0	0
51	0	0
52	0	0
53	0	0
54	0	0
55	0	0
56	0	0
57	0	0
58	0	0
59	0	0
60	0	0
61	0	0
62	0	0
63	0	0
64	0	0
65	0	0
66	0	0
67	0	0
68	0	0
69	0	0
70	0	0
71	0	0
72	0	0
73	0	0
74	0	0
75	0	0
76	0	0
77	0	0
78	0	0
79	0	0
80	0	0
81	0	0
82	0	0
83	0	0
84	0	0
85	0	0
86	0	0
87	1	0
88	0	0
89	0	1
90	0	1
91	0	0
92	0	0
93	0	1
94	0	0
95	0	1
96	0	0
97	0	0
98	0	0
99	0	0
100	0	0 9000
0909

Outcome	frequency_machine1	frequency_machine2
0	95	89
1	5	11

2. Добавьте еще один столбец для вероятности каждого исхода.

Вероятность = частота/общее количество данных = частота/100.

Outcome	frequency_machine1	frequency_machine2	probability_machine1	probability_machine2
0	95	89	0,95	0,89
1	5	11	0,05	0,11
. примерно в два раза больше вероятности с первой машины (0,05 или 5%). 3. По таблице построить распределение Бернулли для этих машин: Мы видим, что вероятность брака (исход = 1) с первого автомата составляет 0,05 или 5%, а вероятность брака со второго машина составляет 0,11 или 11%. 90 = р. Таким образом, эту функцию массы вероятности можно переписать как: f(k,p)={■(p&”if ” [email protected]&”if ” k=0)┤ 5. Практические вопросы 1. На следующем графике показано распределение диабета по Бернулли в определенной популяции, где мы обозначили диабетика как 1, а здорового человека как 0: Какова распространенность диабета в этой популяции? 2. На следующем графике показано бернуллиевское распределение выживших после определенной пандемии в некоторой популяции, где мы обозначаем выживших как 1, а умерших как 0:9.0009 Если мы знаем, что это население составляет около 1 миллиона человек. Сколько человек пережило эту пандемию? 3. На следующем графике показано бернуллиевское распределение выживаемости от определенной пандемии в 2 популяциях, популяции 1 и популяции 2, где мы обозначаем выжившего человека как 1, а умершего человека как 0: Какая популяция была более восприимчива к этому пандемия? 4. В следующей таблице частоты показано количество пациентов с гипертонической болезнью в выборке из 100 человек, случайно выбранных из определенного населения. We denote hypertensive persons as 1 and normotensive persons as 0. outcome frequency 0 94 1 6 Каково расчетное распределение Бернулли для гипертензии в этой популяции? 5. В следующей таблице частоты показано количество не сдавших определенный экзамен учащихся из 2 школ, школы 1 и школы 2. We are interested in failed students, so we denote failed students as 1 and succeeded students as 0. outcome school1 school2 0 65 86 1 5 14 What is the estimated Bernoulli distribution for failure in the 2 schools? 6. Ключ ответа 1. Имеем два исхода: Здоровый человек или 0 с вероятностью 0,85. Диабетик или 1 с вероятностью 0,15. Распространенность диабета в этой популяции = вероятность диабета человека = 0,15 или 15%. 2. Имеем два исхода: Мертвец или 0 с вероятностью 0,2. Выживший или 1 с вероятностью 0,8. На 1 миллион человек число выживших = 1 000 000 X 0,8 = 800 000 человек. 3. Имеем два исхода: Погибший или 0. Выживший или 1 с вероятностью. Мы видим, что у популяции 2 вероятность умереть выше (0,25), чем у популяции 1 (0,15), поэтому популяция 2 более восприимчива. 4. Добавляем еще один столбец для вероятности каждого исхода. Вероятность = частота/общее количество данных = частота/100. исход частота probability 0 94 0.94 1 6 0.06 The probabilities are >= 0 и в сумме 1. Используйте таблицу, чтобы построить распределение Бернулли для гипертонии: Таким образом, это распределение Бернулли может быть записано как: f(k,p)={■(0.06&”if ” [email protected]&”if ” k=0)┤ 5. Заметим, что в школе1 учится 70 учеников, а в школе2 – 100 учеников. Добавьте еще один столбец для вероятности каждого исхода. Для школы 1 вероятность = частота/общее количество данных = частота/70. Для школы 2 вероятность = частота/общее количество данных = частота/100. исход школа1 school2 probability_school1 probability_school2 0 65 86 0.93 0.86 1 5 14 0,07 0,14 Мы видим, что вероятность неудачи для учеников от школы1 или 70176

Мы видим, что вероятность неудачи для учеников 1 или 70176

. 14%).

Используйте таблицу, чтобы построить распределение Бернулли для 2 школ:

Для школы 1 распределение Бернулли можно записать как:

f(k,p)={■(0.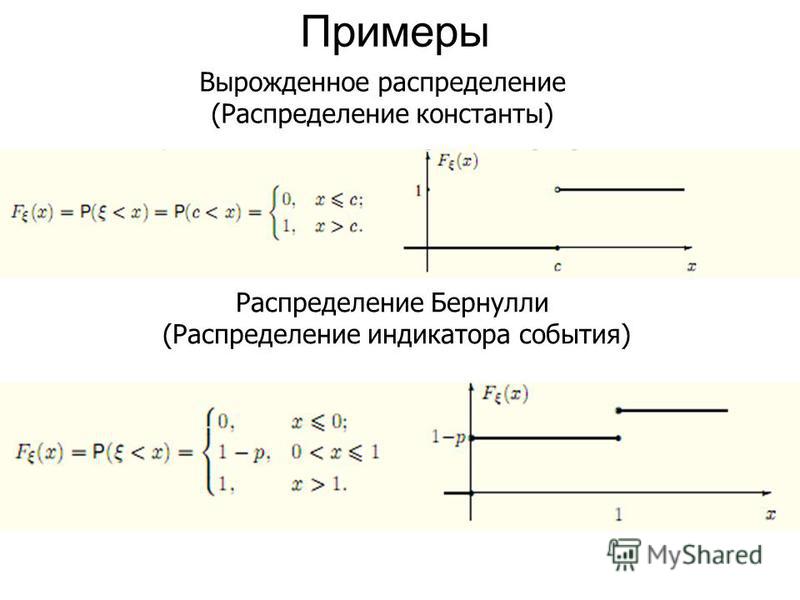 07&”if ” [ email protected]&”if ” k=0)┤

, а для school2 распределение Бернулли может быть записано как:

f(k,p)={■(0.14&”if ” [email protected]& ”if ” k=0)┤

Предыдущий урок | Главная страница | Следующий урок

Распределение Бернулли на примере Python

В этом посте вы узнаете о концепциях распределения Бернулли , а также о реальных примерах и примерах кода Python . Как специалист по данным, очень важно понимать статистические концепции, связанные с различными вероятностными распределениями , чтобы лучше понять распределение данных. В этом посте будут рассмотрены следующие темы:

• Введение в распределение Бернулли
• Реальные примеры распределения Бернулли
• Примеры кода Python для дистрибутива Бернулли

Содержание

Введение в распределение Бернулли

Распределение Бернулли — это дискретное распределение вероятностей , представляющее дискретные вероятности случайной величины, которая может принимать только одно из двух возможных значений, таких как 1 или 0, да или нет, истина или ложь и т. д. Вероятность того, что случайная величина примет значение 1, равна p, а значение 0 равно (1-p). В распределении Бернулли количество испытаний равно только 1. Одно испытание, представляющее распределение Бернулли, также называется 9.0007 Суд над Бернулли. Распределение Бернулли также считается частным случаем биномиального распределения с n = 1, где n представляет количество испытаний.

Вот пример диаграммы, представляющей распределение Бернулли со значением вероятности p = 0,7 для k = 1

Рис. 1. Распределение Бернулли с p = 0,7 для k = 1 быть одним из возможных значений, таких как успех или неудача. Исход процесса Бернулли называется Бернуллиевская случайная величина . Интересующий результат называется успехом. Таким образом, в испытании Бернулли при подбрасывании монеты интересующим исходом является решка. Таким образом, успех связан с появлением головы после подбрасывания монеты. Вероятность успеха равна p, а вероятность неудачи равна 1 – p. При подбрасывании монеты вероятность выпадения орла (или успеха) равна 0,5. Таким образом, вероятность получить решку равна 1 – 0,5 = 0,5.

Поскольку распределение Бернулли является дискретным распределением вероятностей, вероятности различных значений случайной величины можно определить, используя следующие Функция массы вероятности (PMF):

Рис. 2. Функция массы вероятности распределения Бернулли

Ожидаемое значение случайной величины Бернулли равно p , которое также называется параметром распределения Бернулли. Дисперсия значений случайной величины Бернулли составляет p(1-p).

Распределение Бернулли Реальные примеры

Вот несколько реальных примеров распределения Бернулли. Помните, что все, что нам нужно искать, это случайный эксперимент, который может иметь только два возможных результата: успех или неудачу. Интересующий результат обозначается как успех. Важно определить, в чем заключается ваш эксперимент и что означает успех, если эксперимент будет проведен.

• Подбрасывание монеты только с двумя возможными исходами – орел или решка. Успех = 1, если монета выпадает орлом. X = {орел, решка}
• При бросании кубика выпало 6 или нет. Success = 1 for die = 6
• Голосовал ли человек за определенную политическую партию или воздержался от голосования. Успех = 1, если проголосовал за политическую партию
• Получил ли студент более 80 баллов или нет. Успех = 1, если баллов > 80
• Из мешка, состоящего из красного, зеленого и черного шаров, когда вынимается шар, независимо от того, имеет ли вынутый шар красный цвет или нет. Успех = 1, если цвет вынутого шара красный.
• Является ли результат собеседования рекомендацией для следующего раунда собеседования или нет. Успех = 1, если результатом собеседования является рекомендация к следующему этапу собеседования.

Примеры кода Python для распределения Бернулли

Вот код Python, представляющий распределение Бернулли и использование функции массы вероятности для создания гистограммы. Обратите внимание на следующее в приведенном ниже коде:

• Класс Бернулли Python Scipy используется для вычисления значений функции массы вероятности
• Пример распределения Бернулли с параметром p = 0,7
• Результат эксперимента может принимать значения 0, 1. Значения случайной величины Бернулли могут принимать значения 0 или 1.
• Использование функции pmf для определения вероятности разные значения случайной величины

 импортировать matplotlib.pyplot как plt
из scipy.stats импорт Бернулли
#
# Экземпляр распределения Бернулли с параметром p = 0,7
#
бд = Бернулли (0,7)
#
# Результат эксперимента может принимать значения 0, 1
#
Х = [0, 1]
#
# Создать гистограмму; Обратите внимание на использование функции «pmf».
# для определения вероятности различных значений
# случайная переменная
#
plt.figure(figsize=(7,7))
plt.xlim(-1, 2)
plt.bar(X, bd.pmf(X), color='оранжевый')
plt.title('Распределение Бернулли (p=0,7)', fontsize='15')
plt. xlabel('Значения случайной переменной X (0, 1)', fontsize='15')
plt.ylabel('Вероятность', fontsize='15')
plt.show()
 

Приведенный выше код при выполнении приводит к графику, показанному на рис. 1.

Выводы

В этом посте вы узнали о некоторых из следующих фактов, касающихся распределения Бернулли :

• Распределение Бернулли

  7 дискретно распределение вероятностей

  , представляющее вероятности получения различных / дискретных значений случайной величины. Случайная величина может принимать только два возможных значения, таких как успех или неудача. Случайная величина также называется Случайная величина Бернулли.
• Распределение Бернулли представляет вероятности двух возможных исходов одного случайного эксперимента
• Одиночный случайный эксперимент называется испытанием Бернулли.
• Среднее или ожидаемое значение распределения Бернулли равно p, а дисперсия равна p(1-p) включая науку о данных и машинное обучение/глубокое обучение. Я также увлекаюсь различными технологиями, включая языки программирования, такие как Java/JEE, Javascript, Python, R, Julia и т. д., а также такие технологии, как блокчейн, мобильные вычисления, облачные технологии, безопасность приложений, платформы облачных вычислений, большие данные, и т. д. Чтобы быть в курсе последних обновлений и блогов, следите за нами в Twitter. Я хотел бы связаться с вами на Linkedin.

  Ознакомьтесь с моей последней книгой, озаглавленной «Основы мышления: создание успешных продуктов с использованием первых принципов». Недавно я работал в области аналитики данных, включая науку о данных и машинное обучение/глубокое обучение. Я также увлекаюсь различными технологиями, включая языки программирования, такие как Java/JEE, Javascript, Python, R, Julia и т. д., а также такие технологии, как блокчейн, мобильные вычисления, облачные технологии, безопасность приложений, платформы облачных вычислений, большие данные, и т. д. Чтобы быть в курсе последних обновлений и блогов, следите за нами в Twitter. Я хотел бы связаться с вами на Linkedin. Ознакомьтесь с моей последней книгой под названием «Мышление на основе первых принципов: создание успешных продуктов с использованием мышления на основе первых принципов».0009

  Что такое распределение Бернулли? Объяснение распределения Бернулли!

  Предоставил: Шайлендра Сингх
  Профиль LinkedIn: https://www.linkedin.com/in/shailendra-singh-a817802/

  Важным навыком для людей, работающих в области науки о данных, является хорошее понимание фундаментальных концепций. описательной статистики и теории вероятностей. Сюда входят ключевые понятия распределения вероятностей , статистической значимости, проверки гипотез и регрессии. На практике простой анализ с помощью R или scikit-learn в python, без толкового понимания распределений вероятностей, часто заканчивается ошибками и неверными результатами.

  Существует множество распределений вероятностей, но в этой статье мы будем говорить о простейшем распределении вероятностей, называемом распределением Бернулли. Он считается строительным блоком для других более сложных дискретных распределений. Прежде чем перейти к объяснению распределения Бернулли, нам сначала нужно понять некоторые основные понятия, используемые в распределениях вероятностей. Давайте начнем.

  Случайные величины

  В статистике и теории вероятности случайная величина, случайная величина или стохастическая величина описываются как переменные, значения которых зависят от результатов эксперимента (т. е. случайного процесса). Случайные величины бывают двух типов: дискретные и непрерывные. В этом тексте мы рассмотрим тип распределения дискретных случайных величин.

  Чтобы понять случайные величины на простом примере, предположим, что мы выполняем случайный эксперимент по броску игральной кости. Возможный результат, который мы можем получить в этом эксперименте, может быть любым числом от 1 до 6. Если X обозначает случайную величину, которая представляет результат такого случайного процесса, выборочное пространство этого эксперимента состоит из результатов {1, 2, 3 , · · ·, 6}.

  Таким образом, X=1, если результат броска костей равен 1, X=2, если результат броска костей равен 2, и так далее до X=6, если результат броска костей равен 6. 

  Применив математический подход к упрощению и обобщению задачи, мы можем представить одно случайное событие бросания игральной кости, как показано в одной рамке на рисунке ниже. Расширение случайного события до n испытаний, показанных в виде отдельных прямоугольников на рисунке ниже, будет представлять результат n таких случайных событий.

  Распределение вероятностей

  Понимая случайные величины, мы можем определить распределение вероятностей как список всех возможных исходов случайной величины вместе с соответствующими значениями вероятностей.

  Принимая во внимание наш предыдущий пример броска костей, мы можем представить распределение вероятности 6-гранной кости, как показано ниже.

  Outcome	1	2	3	4	5	6
  Probability	1/6	1/6	1/6	1/6	1/6	1/6

  Таблица 1: Распределение вероятностей

  Мы можем представить пример броска игральной кости графически, как показано ниже:

  Мы можем сказать следующее в отношении таблицы распределения вероятностей, показанной выше: в наборе {1,2,3,4,5,6}. Переменная результата всегда будет иметь дискретное значение (от 1 до 6).

• Это -одномерное -распределение, поскольку существует только одна случайная величина, т. е. результат броска костей.

Следовательно, распределение, показанное в таблице выше, можно назвать дискретным одномерным распределением вероятностей.  

Читайте также: Что такое усиление градиента?

Функции вероятности

Если представить вероятность в машинном обучении графически, она будет выглядеть так: раз для X={x1, x2,..xn}, чтобы получить n результатов.

Дискретное распределение вероятностей: (Функция массы вероятности)

Когда мы используем функцию вероятности (которая описана выше) для описания дискретного распределения, мы называем эту функцию функцией массы вероятности (ФМП).

Под дискретным распределением мы подразумеваем, что случайная величина основного распределения может принимать только конечное число различных значений (или можно сказать, что пространство результатов конечно).

Чтобы определить дискретное распределение, мы можем просто перечислить вероятность того, что случайная величина примет каждое из возможных значений. Это перечисление известно как функция массы вероятности, так как оно делит единицу массы (общую вероятность) и возвращает вероятность различных значений, которые может принимать случайная величина.

Как правило, мы можем представить функцию массы вероятности, как показано ниже.


f(x) = P(X = x), например Принимая бросок игральной кости как случайную величину, мы можем записать вероятность того, что игральная кость выпадет на числе 2, как f(2) = P(X=2) = 1/6 .

Функция массы вероятности должна подчиняться правилам вероятности, поэтому-

1. 0<=f(x)<=1
2. ∑f(xi) = f(x1) + f(x2) + … = 1

Некоторыми примерами дискретных событий могут быть броски игральной кости или подбрасывание монеты. Подсчет событий является дискретными функциями. Поскольку промежуточных значений нет, их можно назвать дискретными распределениями. Например, мы можем получить только орел или решку при подбрасывании монеты и число между (1-6) при броске костей. Точно так же при подсчете количества книг, выдаваемых библиотекой в ​​час, вы можете насчитать около 10 или 11 книг, но ничего между ними.

В примере с броском костей бросок костей является случайной величиной. Вероятность того, что на кубике выпадет число 2, можно записать как P(X=2) = 1/6. Где (заглавная буква) X обозначает случайную величину, а 2 — значение результата.

Перед определением распределения Бернулли давайте разберемся с некоторыми основными терминами:

Событие Бернулли: результаты (их можно рассматривать как Успех или Неудача, Да или Нет, Орел или Решка). Событие происходит с вероятностью p и 1-p соответственно.

Испытание Бернулли: Испытание Бернулли — это реализация события Бернулли. Это один из простейших экспериментов, которые можно провести в теории вероятностей и статистике. Это эксперимент, в котором возможны два исхода (успех и неудача).

Примеры испытаний Бернулли:

• Подбрасывание монеты: Запишите, сколько подбрасываний монеты привело к выпадению орла и сколько подбрасываний монеты привело к выпадению решки. Мы можем рассматривать результат выпадения орла как успех, а не выпадение орла, т. е. выпадение решки, как неудачу.
• Футбол: Сколько ударов по воротам привело к забитому голу и сколько ударов было пропущено. Мы можем назвать забитый гол «успехом», а промах — неудачей.
• Бросание костей: Вероятность того, что при броске двух игральных костей выпадет двойная шестерка. Двойной бросок шести кубиков можно считать успешным, а все остальное можно считать неудачным.

Процесс Бернулли: Последовательность испытаний Бернулли называется процессом Бернулли. Среди других выводов, которые можно сделать, для n испытаний вероятность n успехов равна pⁿ.

Что такое распределение Бернулли?

Распределение Бернулли — одно из самых простых для понимания распределений из-за его простоты. Он часто используется в качестве отправной точки для получения более сложных распределений.

Распределение Бернулли — это дискретное распределение только с двумя возможными значениями случайной величины. Распределение имеет только два возможных исхода и одно испытание, которое называется испытанием Бернулли. Два возможных исхода в распределении Бернулли помечены n=0 и n=1, в которых n=1 (успех) происходит с вероятностью 9.0007 p и n=0 (отказ) происходит с вероятностью 1-p, и, поскольку это значение вероятности, поэтому 0<=p<=1.

Функция массы вероятности (PMF) распределения Бернулли определяется как:

Если эксперимент имеет только два возможных исхода, «успех» и «неудача», и если p — вероятность успеха, то-


Другой распространенный способ записать это —

Примечание: Успех здесь относится к результату, который мы хотим отслеживать. Например, в примере с броском кубиков двойная шестерка на обеих костях будет считаться успехом, все остальные броски будут провалом.

Читайте также: Линейная регрессия в машинном обучении

Простым примером может быть один подбрасывание предвзятой/непредвзятой монеты. В случае подбрасывания беспристрастной или честной монеты значение p будет равно 0,5, что дает 50% вероятность каждого исхода. Однако мы должны отметить, что вероятности успеха и неудачи не обязательно должны быть одинаковыми все время, как распределение Бернулли в случае подбрасывания монеты со смещением , где вероятность выпадения орла (успех) равна 0,6, а вероятность выпадения решки (неудача) равна 0,4. . Код Python и график для этого примера приведены ниже.

В приведенном выше распределении Бернулли вероятность успеха (1) справа равна 0,4, а вероятность неудачи (0) слева равна 0,6:

Код Python для построения распределения Бернулли в случае загруженной монеты —

Импорт Numpy As NP

Импорт MATPLOTLIB.PYPLOT AS PLT

%MATPLOTLIB INLINE

Проблс = NP. ARRARE (0,6, 0.4]

Прош = NP.ARRARE (0,6, 0,4]

. , 1]

plt.bar(face, probs)

plt.title(Biased coin Bernoulli Distribution’, fontsize=12)

plt.ylabel(‘Probability’, fontsize=12)

plt .xlabel(Исход предвзятой монеты’, fontsize=12)

axes = plt.gca()

axes.set_ylim([0,1])

7 4

Свойства распределения Бернулли
• Возможны только два исхода: 1 или 0, т. е. успех или неудача в каждом испытании.
• Значения вероятности взаимоисключающих событий, охватывающих все возможные исходы, должны быть в сумме равны единице.
• Если вероятность успеха равна p, то вероятность неудачи определяется как 1-p. Значения вероятности должны оставаться одинаковыми в каждом последующем испытании. Каждое событие должно быть совершенно отдельным и не иметь ничего общего с предыдущим событием. т. е. на вероятности не влияют результаты других испытаний, что означает, что испытания независимы.
• Ожидаемое значение случайной величины X из распределения Бернулли может быть представлено как:

E[X] = 1*(p) +0*(1-p) = p, например, если 0,6, тогда E[X] = 0,6

• Среднее случайной величины Бернулли (X) равно

E[X] = 1(p) +0(1-p) = p

• Дисперсия случайной величины Бернулли равна 

V[X] = E[X²]-[E(X)]² = 1²p+0²(1-p)-p²=p(1-p)

Распределение Бернулли является строительным блоком для других более сложных дискретных распределений. Распределения нескольких типов переменных могут быть определены на основе последовательностей независимых испытаний Бернулли. Такие дистрибутивы перечислены в таблице ниже.

Discrete Distribution	Definition
Binomial Distribution	Models the total number of successes in ‘n’ independent and repeated Bernoulli trials
Geometric Distribution	Models the total number of неудач до первого успеха в «n» независимых повторных испытаниях Бернулли
Отрицательное биномиальное распределение	Моделирует общее количество неудач до x-го успеха в «n» независимых повторных испытаниях Бернулли

Применение результатов Бернулли

В реальной жизни бывают ситуации, требующие отмечать, происходит определенное событие или нет. Такие события записываются как успех или неудача. Например. Некоторые из примеров, которые объясняют сценарии бинарных исходов, включают расчет вероятности:

• Успех лечения
• Опрашиваемый — женщина
• Результат студента (сдал/не сдал) на экзамене /не передается)

Распределение Бернулли находит применение в вышеуказанных случаях, а также в ряде других ситуаций, сходных с вышеуказанными случаями.

Распределение Бернулли с использованием Python

Мы можем сгенерировать распределенную Бернулли дискретную случайную величину, используя метод bernoulli.rvs() из модуля scipy.stats в python. Функция примет вероятность успеха (p) в качестве параметра формы. Параметр размера определяет количество повторений испытаний. Для воспроизводимости мы можем включить аргумент random_state, присвоенный числу.

Код Python для построения построения распределения Бернулли в случае загруженной монеты-

из Scipy.

No related posts.