Расчет прямоугольной трапеции онлайн. Площадь трапеции: формулы и методика вычислений
Главная > Двери > Расчет прямоугольной трапеции онлайн. Площадь трапеции: формулы и методика вычислений
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту:
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.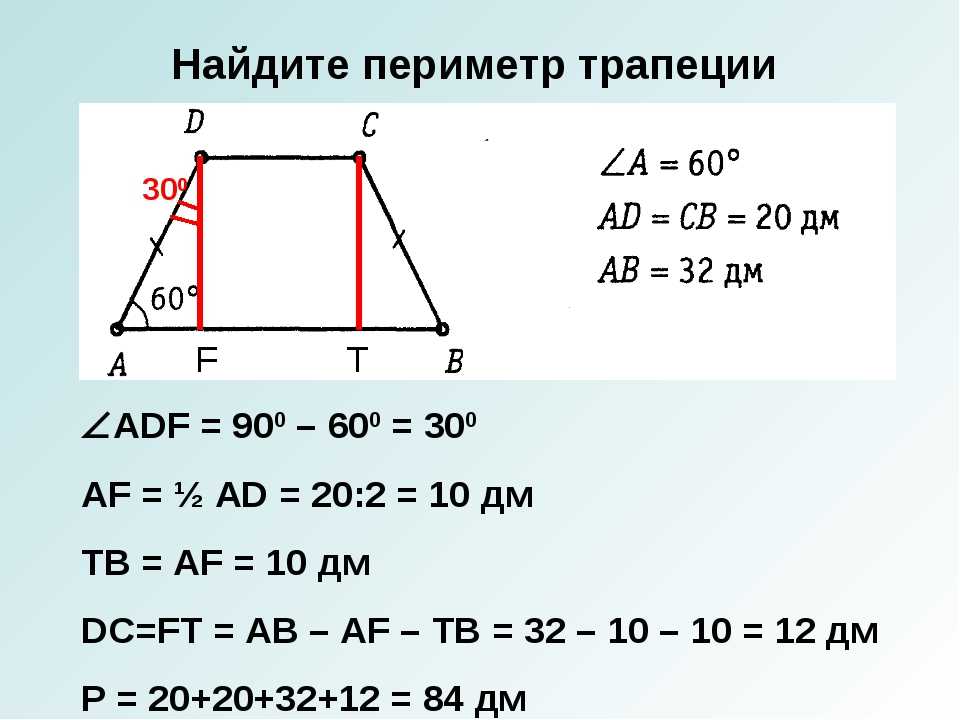
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα:
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x.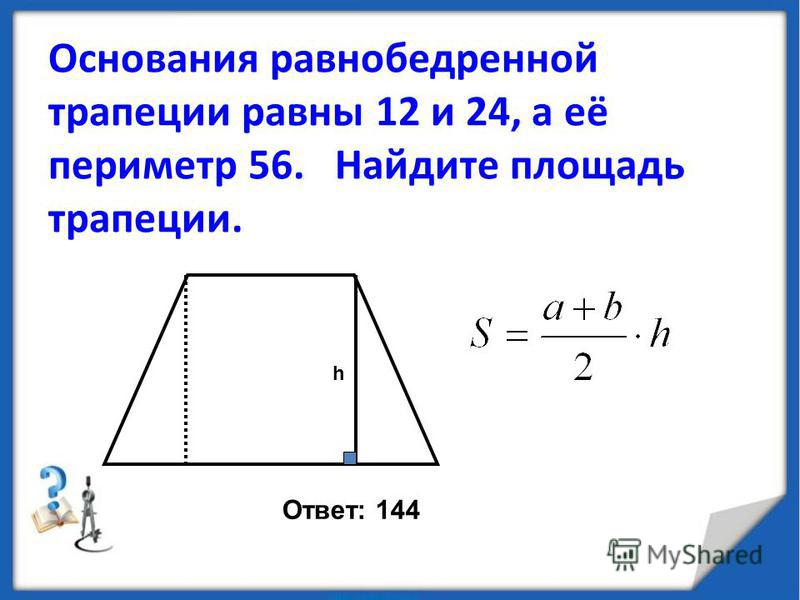 Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение:
Постройте трапецию АМРС.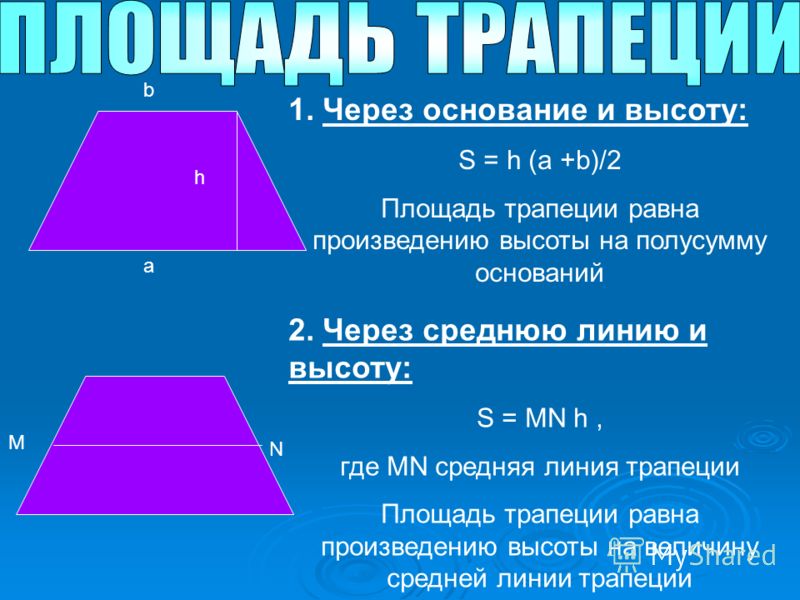
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны.
Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.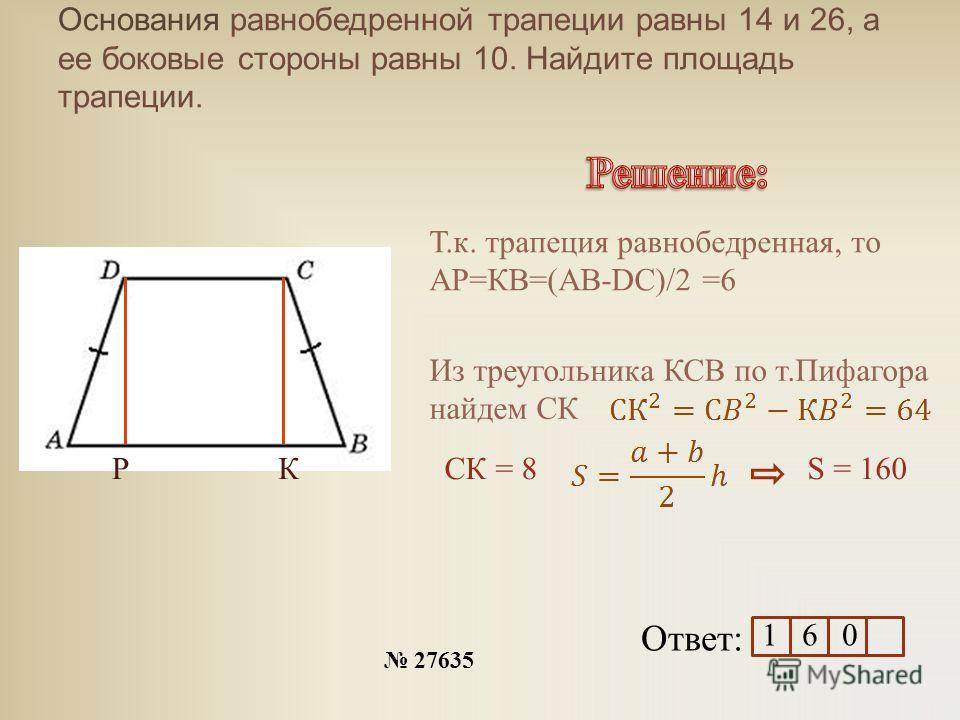
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника .
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы.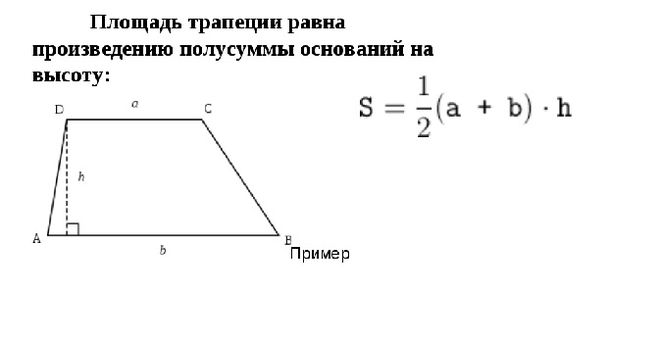 Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике : Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см.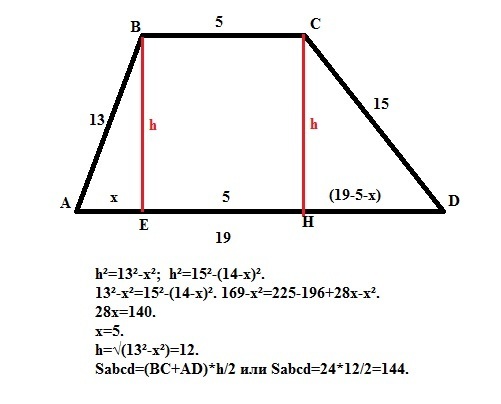 Найдите расстояние до нее от середины противоположной боковой стороны.
Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве , подготовка к ЕГЭ в Строгино .
Трапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет.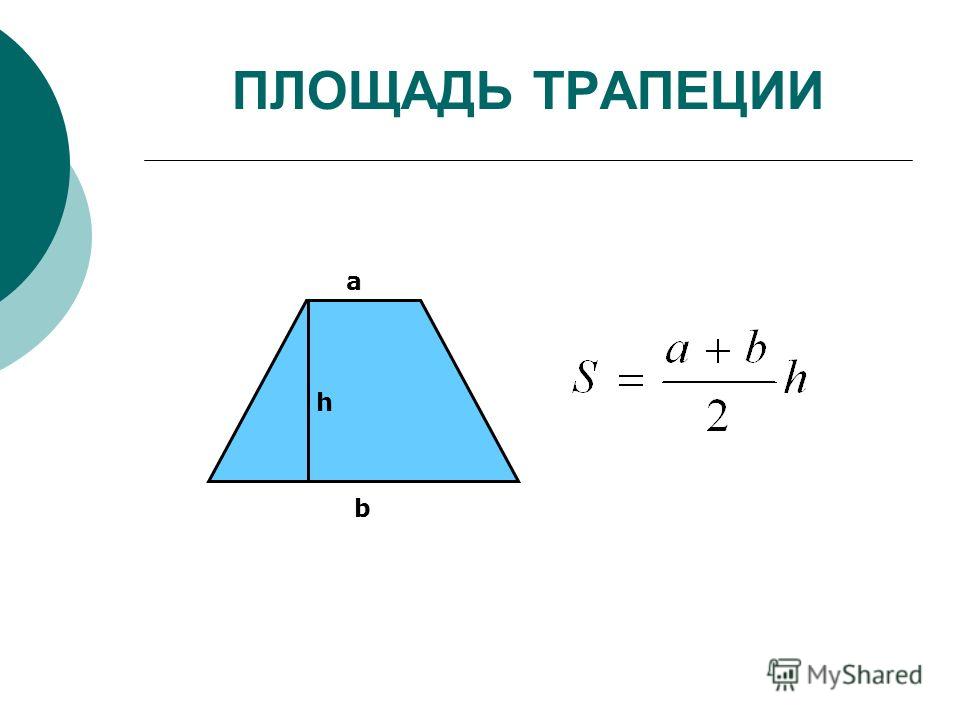 Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.
Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.
Геометрия трапеции
Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
- высота — расстояние между параллельными основаниями фигуры;
- средняя линия — отрезок, соединяющий середины боковых сторон.
Данная геометрическая фигура широко распространена в реальной жизни.
Трапеция в реальности
В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:
- дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
- ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
- мода — форма одежды, обуви и аксессуаров;
- архитектура — окна, стены, основания зданий;
- производство — различные изделия и детали.

При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.
Периметр трапеции
Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
P = a + b + c + d,
где a и c – основания фигуры, b и d – ее боковые стороны.
Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.
Примеры из реальной жизни
Платок
Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза.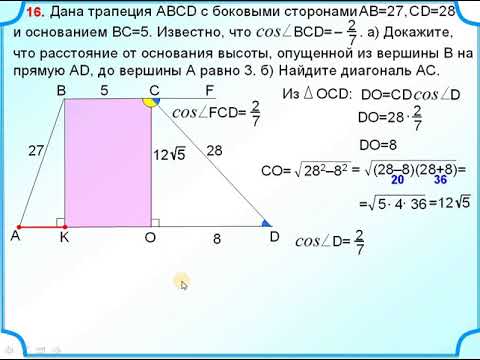 Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.
Откосы
К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.
Заключение
Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
Этот калькулятор рассчитал 2192 задачи на тему «Площадь трапеции»
ПЛОЩАДЬ ТРАПЕЦИИ
Выберете формулу вычисления площади трапеции, которую Вы планируете применить для решения поставленной перед Вами задачи:
Общая теория для вычисления площади трапеции.
Трапеция — это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих попарно эти четыре точки, у которой две противоположные стороны параллельны (лежат на параллельных прямых), а две другие не параллельны.
Точки называются вершинами трапеции и обозначаются заглавными латинскими буквами.
Отрезки называются сторонами трапеции и обозначаются парой заглавных латинских букв соответственно вершинам, которые отрезки соединяют.
Две параллельные стороны трапеции называются основаниями трапеции .
Две не параллельные стороны трапеции называются боковыми сторонами трапеции .
Рисунок №1: Трапеция ABCD
На рисунке №1 представлена трапеция ABCD с вершинами A,B ,C, D и сторонами AB, BC, CD, DA.
AB ǁ DC — основания трапеции ABCD.
AD, BC — боковые стороны трапеции ABCD.
Угол, образованный лучами AB и AD, называется углом при вершине A. Обозначается он как ÐA или ÐBAD, или ÐDAB.
Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB или ÐABC, или ÐCBA.
Угол, образованный лучами CB и CD, называется углом при вершине C. Обозначается он как ÐC или ÐDCB, или ÐBCD.
Угол, образованный лучами AD и CD, называется углом при вершине D. Обозначается он как ÐD или ÐADC, или ÐCDA.
Рисунок №2: Трапеция ABCD
На рисунке №2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме. То есть,.
Рисунок №3: Равнобедренная трапеция ABCD
На Рисунке №3, AD=BC.
Трапеция называется равнобедренной (равнобокой) , если ее боковые стороны равны.
Рисунок №4: Прямоугольная трапеция ABCD
На Рисунке №4 угол D — прямой (равен 90 о).
Трапеция называется прямоугольной, если угол при боковой стороне прямой.
Площадью S плоской фигуры, к которым относится и трапеция, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.
Площадь обладает несколькими свойствами:
1. Она не может быть отрицательной.
2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.
3. Если две фигуры равны, то и площади их равны.
4. Площадь квадрата, который построен на единичном отрезке, равна единице.
За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
При решении задач часто используются следующие формулы вычисления площади трапеции:
1. Площадь трапеции равна полусумме ее оснований умноженной на высоту:
2. Площадь трапеции равна произведению ее средней линии на высоту:
3. При известных длинах оснований и боковых сторон трапеции её площадь можно вычислить по формуле:
4. Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле:
Пример 1: Вычислить площадь трапеции с основаниями a=7, b=3 и высотой h=15.
Решение:
Ответ:
Пример 2: Найти сторону основания трапеции с площадью S=35 см 2 , высотой h=7см и вторым основанием b = 2 см.
Решение:
Для нахождения стороны основания трапеции воспользуемся формулой вычисления площади:
Выразим из данной формулы сторону основания трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 3: Найти высоту трапеции с площадью S=17 см 2 и основаниями a=30 см, b = 4 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 4: Вычислить площадь трапеции с высотой h=24 и средней линией m=5.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 5: Найти высоту трапеции с площадью S = 48 см 2 и средней линией m=6 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы высоту трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 6: Найти среднюю линию трапеции с площадью S = 56 и высотой h=4.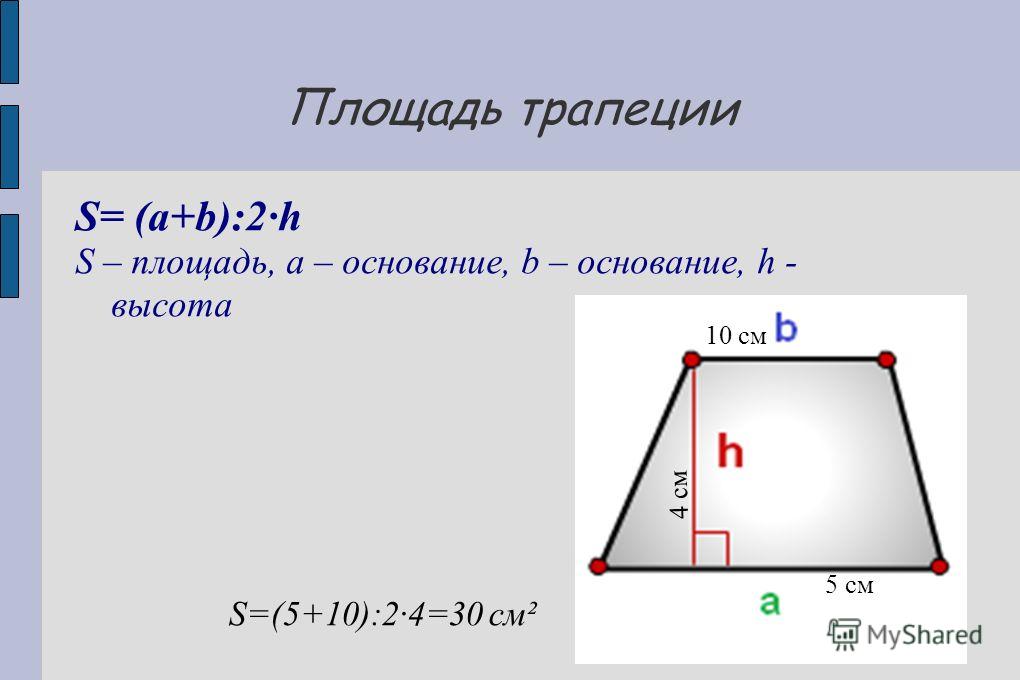
Решение:
Для нахождения средней линии трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы среднюю линию трапеции:
Таким образом, имеем следующее.
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см. найдем площадь фигуры:
найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.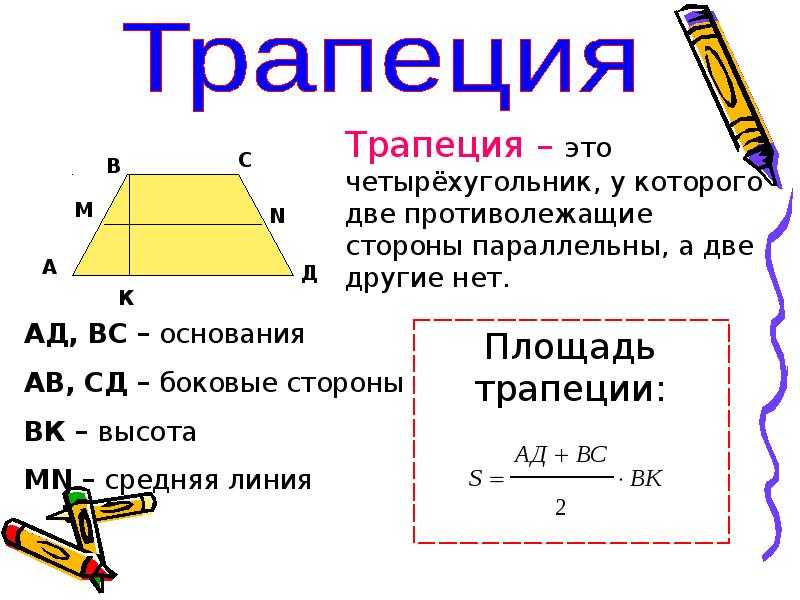
Рассчитать трапецию онлайн. Площадь трапеции
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними. В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).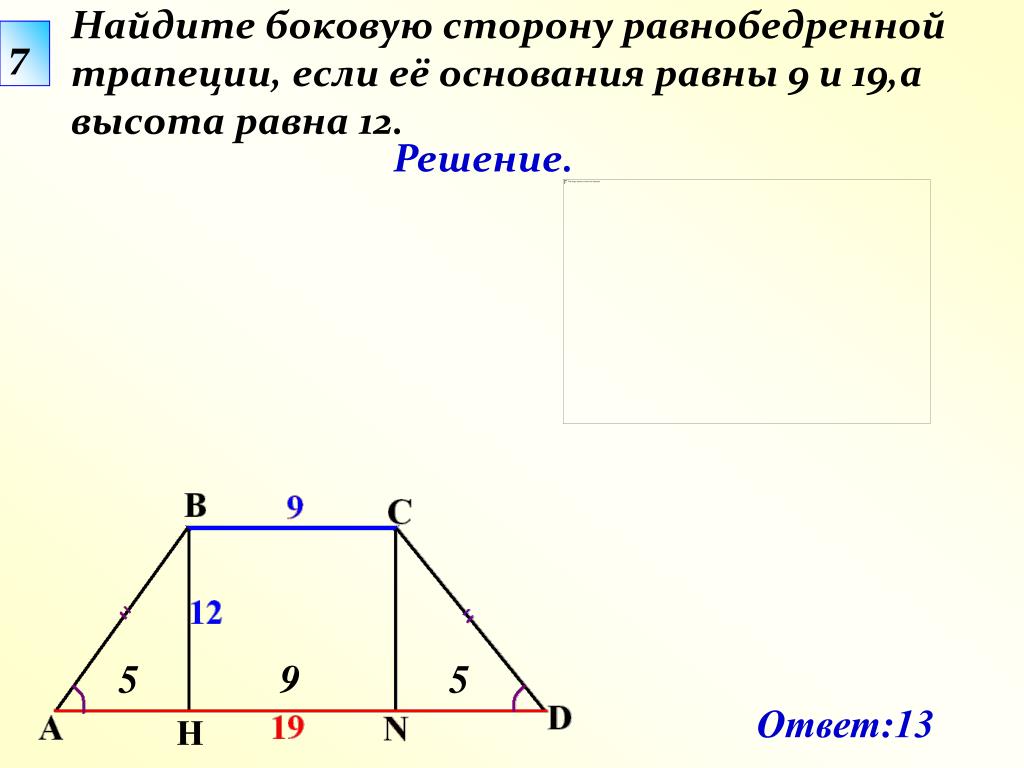
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Этот калькулятор рассчитал 2192 задачи на тему «Площадь трапеции»
ПЛОЩАДЬ ТРАПЕЦИИ
Выберете формулу вычисления площади трапеции, которую Вы планируете применить для решения поставленной перед Вами задачи:
Общая теория для вычисления площади трапеции.
Трапеция — это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих попарно эти четыре точки, у которой две противоположные стороны параллельны (лежат на параллельных прямых), а две другие не параллельны.
Точки называются вершинами трапеции и обозначаются заглавными латинскими буквами.
Отрезки называются сторонами трапеции и обозначаются парой заглавных латинских букв соответственно вершинам, которые отрезки соединяют.
Две параллельные стороны трапеции называются основаниями трапеции .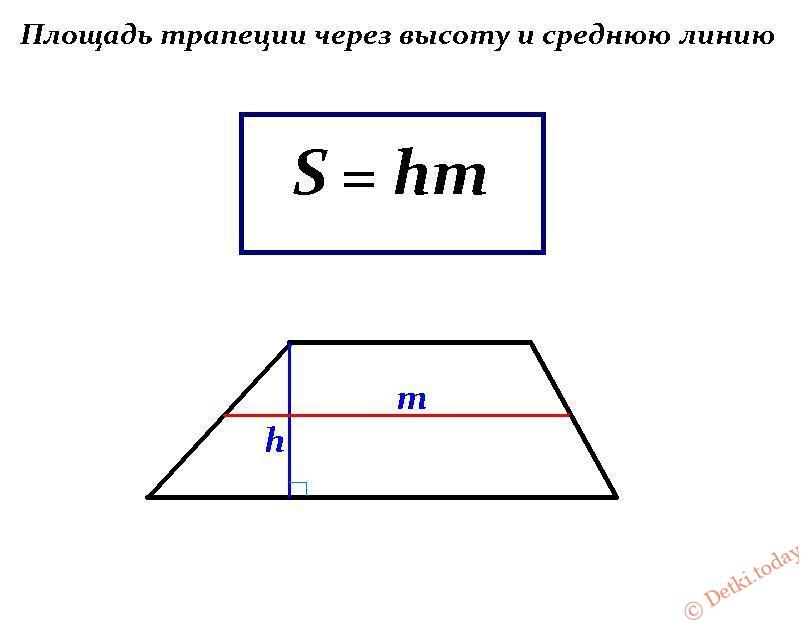
Две не параллельные стороны трапеции называются боковыми сторонами трапеции .
Рисунок №1: Трапеция ABCD
На рисунке №1 представлена трапеция ABCD с вершинами A,B ,C, D и сторонами AB, BC, CD, DA.
AB ǁ DC — основания трапеции ABCD.
AD, BC — боковые стороны трапеции ABCD.
Угол, образованный лучами AB и AD, называется углом при вершине A. Обозначается он как ÐA или ÐBAD, или ÐDAB.
Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB или ÐABC, или ÐCBA.
Угол, образованный лучами CB и CD, называется углом при вершине C. Обозначается он как ÐC или ÐDCB, или ÐBCD.
Угол, образованный лучами AD и CD, называется углом при вершине D. Обозначается он как ÐD или ÐADC, или ÐCDA.
Рисунок №2: Трапеция ABCD
На рисунке №2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме. То есть,.
То есть,.
Рисунок №3: Равнобедренная трапеция ABCD
На Рисунке №3, AD=BC.
Трапеция называется равнобедренной (равнобокой) , если ее боковые стороны равны.
Рисунок №4: Прямоугольная трапеция ABCD
На Рисунке №4 угол D — прямой (равен 90 о).
Трапеция называется прямоугольной, если угол при боковой стороне прямой.
Площадью S плоской фигуры, к которым относится и трапеция, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.
Площадь обладает несколькими свойствами:
1. Она не может быть отрицательной.
2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.
3. Если две фигуры равны, то и площади их равны.
Если две фигуры равны, то и площади их равны.
4. Площадь квадрата, который построен на единичном отрезке, равна единице.
За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
При решении задач часто используются следующие формулы вычисления площади трапеции:
1. Площадь трапеции равна полусумме ее оснований умноженной на высоту:
2. Площадь трапеции равна произведению ее средней линии на высоту:
3. При известных длинах оснований и боковых сторон трапеции её площадь можно вычислить по формуле:
4. Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле:
Пример 1: Вычислить площадь трапеции с основаниями a=7, b=3 и высотой h=15.
Решение:
Ответ:
Пример 2: Найти сторону основания трапеции с площадью S=35 см 2 , высотой h=7см и вторым основанием b = 2 см.
Решение:
Для нахождения стороны основания трапеции воспользуемся формулой вычисления площади:
Выразим из данной формулы сторону основания трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 3: Найти высоту трапеции с площадью S=17 см 2 и основаниями a=30 см, b = 4 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 4: Вычислить площадь трапеции с высотой h=24 и средней линией m=5.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 5: Найти высоту трапеции с площадью S = 48 см 2 и средней линией m=6 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы высоту трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 6: Найти среднюю линию трапеции с площадью S = 56 и высотой h=4.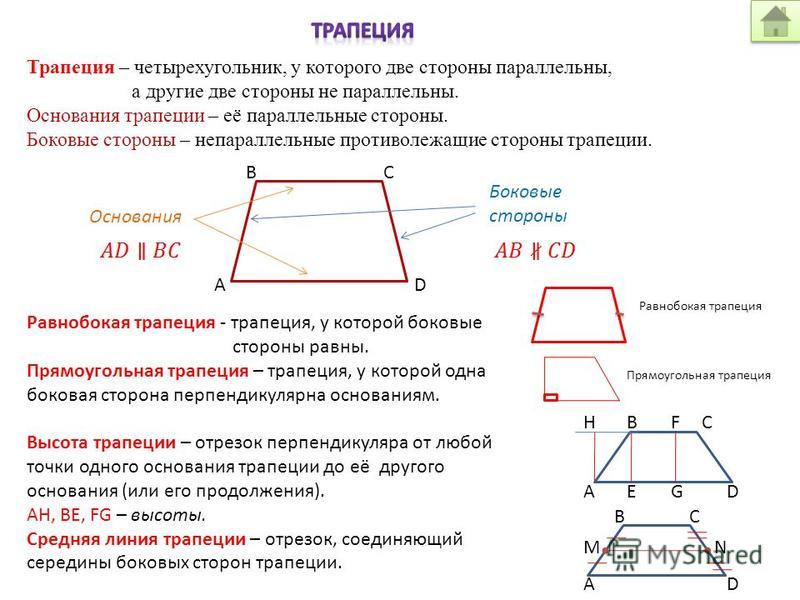
Решение:
Для нахождения средней линии трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы среднюю линию трапеции:
Таким образом, имеем следующее.
Трапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет. Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.
Геометрия трапеции
Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
- высота — расстояние между параллельными основаниями фигуры;
- средняя линия — отрезок, соединяющий середины боковых сторон.

Данная геометрическая фигура широко распространена в реальной жизни.
Трапеция в реальности
В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:
- дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
- ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
- мода — форма одежды, обуви и аксессуаров;
- архитектура — окна, стены, основания зданий;
- производство — различные изделия и детали.
При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.
Периметр трапеции
Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
P = a + b + c + d,
где a и c – основания фигуры, b и d – ее боковые стороны.
Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.
Примеры из реальной жизни
Платок
Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.
Откосы
К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок.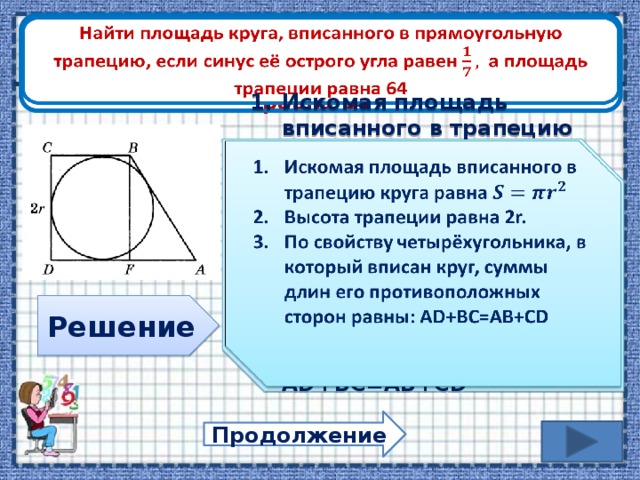 Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.
Заключение
Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см. найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Стороны трапеций найти онлайн, правила, формулы, примеры
Трапеция — это выпуклый четырехугольник с двумя параллельными основами и двумя непараллельными
боковыми сторонами.
Иногда фигура определяется как четырёхугольник, у которого пара противолежащих сторон параллельна,
поэтому параллелограмм и прямоугольник являются частными случаями трапеции. Также это
четырехугольник, у которого одна пара противоположных сторон параллельна, а остальные стороны не
равны между собой.
Параллельные стороны называются основами, а остальные боковыми.
Вычисление стороны необходимо для нахождения периметра, площади трапеции, ее диагоналей и других значимых параметров.
- Длина основания через среднию линию и другое известное основание
- Нижнее основание через верхнее основание, высоту и углы при нижнем основании
- Верхнее основание через нижнее основание, высоту и углы при нижнем основании
- Нижнее основание через боковые стороны, верхнее основание и углы при нижнем основании
- Верхнее основание через боковые стороны, нижнее основание и углы при нижнем основании
- Боковую сторону через высоту и угол при нижнем основании
Длина основания через среднюю линию и известное основание
Средняя линия — отрезок, соединяющий середины боковых сторон фигуры.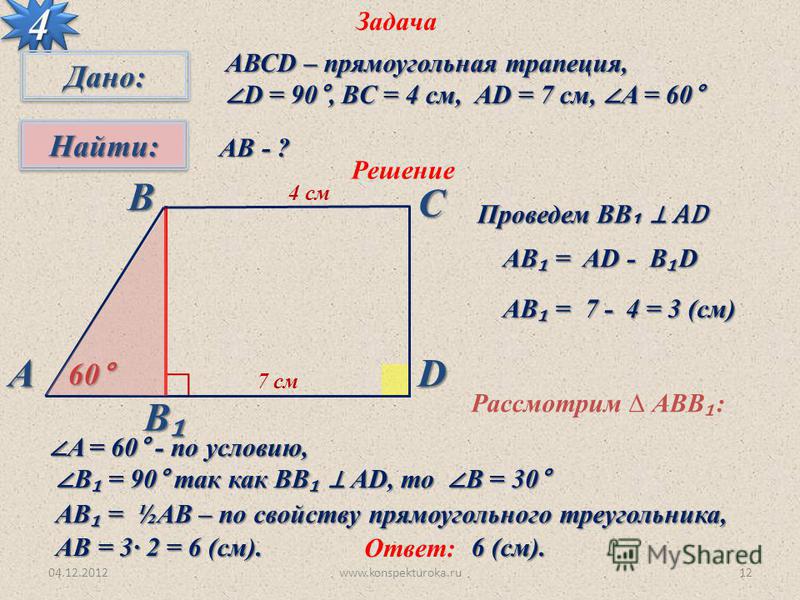 Через её значение
вычисляется одна из основ. Нужно умножить ее на два и вычесть известную:
Через её значение
вычисляется одна из основ. Нужно умножить ее на два и вычесть известную:
a = 2m – b
Средняя линия (m):
ммсмдмм
Изв. основание (b):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Например, средняя линия MN равна 6, а основание а – 9. Соответственно, значения, подставленные в формулу, показывают, что b = 2*6 – 9 = 3.
Нижнее основание через верхнее основание, высоту и углы при нижнем основании
Высота h или BK – перпендикуляр, проведенный от одной основы к другой. Высота проводится в любой их точке, но удобнее всего это делать из вершины углов при меньшей основе. Чтобы найти нижнее основание, надо к верхнему прибавить произведение высоты на сумму котангенсов углов при нижнем:
a = b + h*(ctga + ctgb)
Верх. основание (b):
основание (b):
ммсмдмм
Высота (h):
ммсмдмм
Угол (α):
градусырадианыctg
Угол (β):
градусырадианыctg
Цифр после запятой:
012345678910Результат в: ммсмдмм
Дано верхнее основание 10, высота 6 и углы 30 и 45. По формуле а = 10 + 6*(3+1) = 10 + 63 + 6 = 16+63. Для равнобедренного четырёхугольника выведены две формулы. В первой (a = 2S/h – b) основа выражена с помощью формулы площади. Пример: Площадь равнобедренной трапеции ABCD = 18, высота = 6, а AD = 5. Найти BC. BC = 2*18/6 – 5 = 6 – 5 = 1
Второе выражение сформулировано следующим образом: (a = b + 2h*ctga). Высота АН в трапеции ADEF = 10, DE = 4, а DAF = 45 градусам. Найти AF: AF = 4 + 10*2*1 = 24
Верхнее основание через нижнее основание, высоту и углы при нижнем основании
Чтобы найти верхнюю основу, надо из нижней вычесть произведение высоты на сумму котангенсов углов при ней:
b = a – h*(ctg α + ctg β)
Ниж. основание (a):
основание (a):
ммсмдмм
Высота (h):
ммсмдмм
Угол (α):
градусырадианыctg
Угол (β):
градусырадианыctg
Цифр после запятой:
012345678910Результат в: ммсмдмм
Дана трапеция с нижним основанием 15, высотой 8 и углами в 45 градусов. По формуле а = 15 + 8*(1+1) = 15 + 16 = 31
Формулы для равнобедренного четырёхугольника: b = 2S/h – a и b = a – 2h*ctga.
- Площадь трапеции KLMN = 44, KL=MN, высота равна 8, KN = 5. Найти LM: LM = 44*2/8 – 5 = 6
- Высота трапеции DEFG = 15, DG= 5, а EDG = 45 градусам. Найти EF: EF = 5 + 15*2*1 = 35
Нижнее основание через боковые стороны, верхнее основание и углы при нижнем основании
Для нахождения основы а нужно к основе b прибавить произведение одной и другой стороны и косинусов углов при них
a = b + c * cos α + d * cos β
Верх.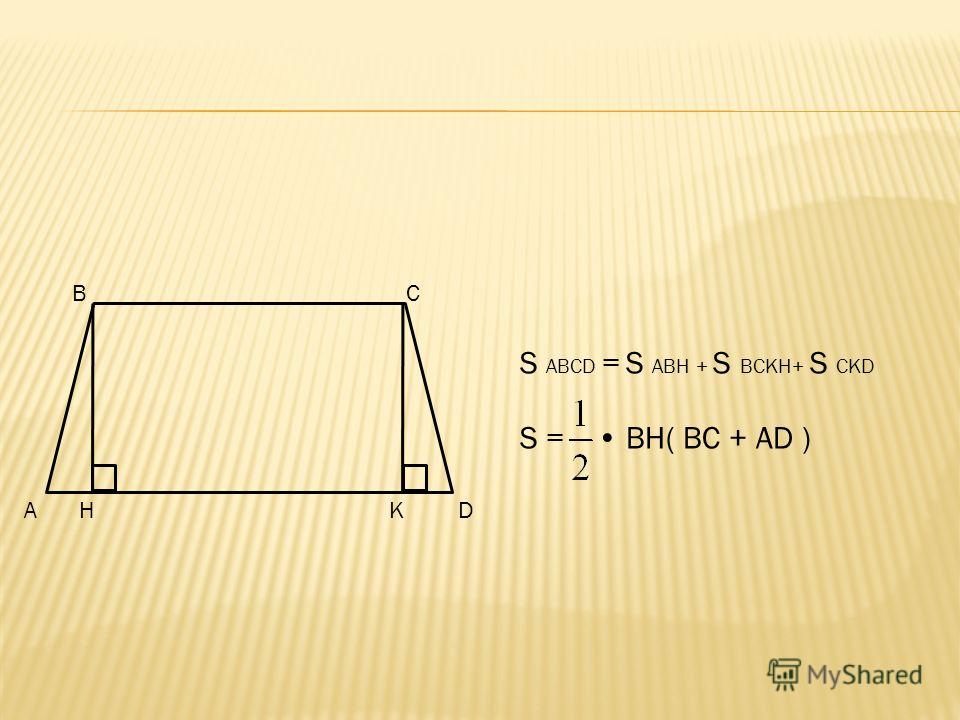 2)/b и a = b +
2c*cosa.
2)/b и a = b +
2c*cosa.
- трапеции ABCD AB = CD = 8, диагональ AC = 12, а BC = 4. Вычислить AD: AD = (12*12 – 8*8)/4 = (144 – 64)/4 = 20
- В трапеции KLMN KL = MN = 4, LM = 7, а LKN равен 30 градусам. Вычислить KN: KN = 7 + 4*2*3/2 = 7 + 43
Верхнее основание через боковые стороны, нижнее основание и углы при нем
Для нахождения основы b нужно из основы а вычесть произведение одной и другой боковой стороны и углов при них
b = a – c * cos α – d * cos β
Ниж. основание (a):
ммсмдмм
Сторона (c):
ммсмдмм
Сторона (d):
ммсмдмм
Угол (α):
градусырадианыcos
Угол (β):
градусырадианыcos
Цифр после запятой:
012345678910Результат в: ммсмдмм
Дана трапеция с нижним основанием 27, боковыми сторонами 20 и 14 и углами в 30 и 60 градусов. 2)/a и b = a — 2c*cosa.
2)/a и b = a — 2c*cosa.
- В трапеции DEFG DE и FG = 11, диагональ АС = 13, а EF = 12. Вычислить DG: DG = (13*13 – 11*11)/12= (169 – 121)/12 = 4
- Боковые стороны трапеции BCDE BC и DE = 25, BE = 10, а CBE равен 60 градусам. Вычислить CD: CD = 25 – 10*2*1/2 = 15
Боковая сторона через высоту и угол при нижнем основании
Чтобы найти боковую сторону, надо разделить высоту на синус угла при ней
d = h / sin α
Высота (h):
ммсмдмм
Угол (α):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: ммсмдмм
Дана трапеция с высотой 12 и углами в 30 и 60 градусов. Найти боковые стороны: c = 12/0,5 = 24, d = 12/3/2 = 243
Для прямоугольного типа формулы несколько отличаются.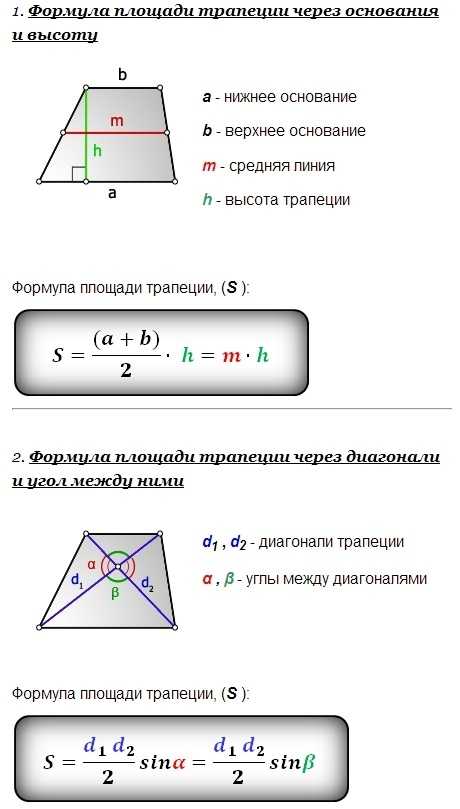 2 – 16*6 =
100 – 96 = 4
2 – 16*6 =
100 – 96 = 4
Виды трапеций
Существуют следующие виды трапеций:
- Равнобедренная трапеция — фигура, у которой боковые стороны и углы при основании равны.
Диагонали также равны. Треугольники, образованные диагоналями и основой, являются
равнобедренными.
 Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб.
Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб. - Прямоугольная трапеция — фигура, у которой одна из боковых сторон перпендикулярна основам и равна высоте. Два угла будут равны 90 градусам, и они всегда принадлежат смежным вершинам, а другие всегда острый и тупой, их сумма всегда будет равна 180 градусам. Каждая диагональ образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, другая прямоугольный треугольник.
- Разносторонняя трапеция — фигура, боковые стороны которой не равны и углы при основании не
являются прямыми.
 2.
2. - Треугольники ABO и DCO, образованные отрезками диагоналей и боковыми сторонами, имеют одинаковую площадь.
- В трапецию можно вписать окружность, если сумма оснований равняется сумме её боковых сторон.
- Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
- Отрезок, соединяющий середины диагоналей, равняется половине разности основ и лежит на средней линии.
- высота — расстояние между параллельными основаниями фигуры;
- средняя линия — отрезок, соединяющий середины боковых сторон.
- дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
- ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
- мода — форма одежды, обуви и аксессуаров;
- архитектура — окна, стены, основания зданий;
- производство — различные изделия и детали.

- Средняя линия трапеции равна полусумме оснований и параллельна им.
- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
- Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
- высота, то есть отрезок, перпендикулярный обоим основаниям;
- средняя линия, которая имеет своими концами середины боковых сторон.
- Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
- У прямоугольной трапеции два угла обязательно прямые
- Оба прямых угла прямоугольной трапеции обязательно принадлежат смежным вершинам
- Оба прямых угла в прямоугольной трапеции обязательно прилежат к одной и той же боковой стороне
- Диагонали прямоугольной трапеции образуют с одной из боковых сторон прямоугольный треугольник
- Длина боковой стороны трапеции, перпендикулярной основаниям равна ее высоте
- У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям
- У прямоугольной трапеции два угла прямые, а два других – острый и тупой
- Что такое трапеция?
- Формула периметра трапеции и углы трапеции
- Как вычислить площадь трапеции
- Как найти высоту трапеции
- Пример: с помощью калькулятора трапеции
- FAQ
Прямоугольник
Мы уже упоминали об этом в начале этого раздела – это трапеция, имеющая две пары противоположных сторон, параллельных друг другу .
Равнобедренная трапеция
Трапеция, у которой катетов имеют одинаковую длину (аналогично тому, как мы определяем равнобедренные треугольники).
Правая трапеция
Трапеция, у которой одна сторона перпендикулярна основаниям . Во-первых, обратите внимание, что здесь требуется, чтобы только одна из сторон удовлетворяла этому условию — другая может быть, а может и нет. Во-вторых, обратите внимание, что если катет перпендикулярен одному из оснований, то он автоматически перпендикулярен и другому, поскольку они параллельны.

- Сумма длин оснований:
а + b. - Разделите дважды площадь на результат шага 1:
2A/(a + b). - Вот оно! Вы нашли высоту трапеции.
- Основание
- Основание b
- Высота
- Сторона c
- Сторона d
- Периметр
- A представляет площадь трапеции,
- A представляет верхнюю параллельную или верхнюю основу трапеции,
- B представляет собой основание трапеции, а
- h относится к высоте трапеции.
- Выберите параметр, для которого вы хотите решить трапецию, т. е. площадь, периметр и т. д.
- Выберите параметры. Например, если вы выбираете область на первом этапе, вы можете выбрать один из двух наборов параметров:
- Основание a, основание b, высота
- Сторона c, сторона d, высота, периметр
- Введите значения в поле соответствующие поля ввода.
- Вы можете использовать любую единицу измерения. см, дюймы, футы, метры, ярды и т. д.
- Нажмите Рассчитать , чтобы получить требуемое значение трапеции.
- Измерьте и запишите основание a , основание b и высоту h трапеции.
- Запишите формулу площади трапеции.
- Подставьте значения в формулу и рассчитайте площадь.
- Всего отзывов 1
- Общий рейтинг 5/5
- Звезды
- Во-первых, нам нужна длина двух оснований (параллельных сторон).
Они находятся путем вычисления расстояния между конечными точками отрезков линий.
(См. Расстояние между двумя точками). Делая это, мы видим, что
г. до н.э. = 22 г. и н.э. = 47 г.
г. - Тогда нам нужна высота. Это перпендикулярное расстояние между основаниями. Как описано в
Трапеция (координатная геометрия) есть несколько способов сделать это
в зависимости от того, повернута трапеция или нет. Делая это, мы видим, что
высота = 21
- Наконец, мы вычисляем площадь как высоту, умноженную на среднюю ширину (средняя длина основания): Что согласуется с расчетной цифрой выше.
- Периметр равен сумме длин четырех сторон.
Таким образом, они находятся путем вычисления расстояния между конечными точками отрезков линий.
 (См. Расстояние между двумя точками). Делая это, мы видим, что
(См. Расстояние между двумя точками). Делая это, мы видим, чтодо нашей эры = 22 AD = 47 AB = 22 CD = 28
- Наконец, мы складываем их, чтобы получить периметр
22 + 22 + 28 + 47 = 119
Что согласуется с расчетной цифрой выше. - Расстояние между двумя точками (с учетом их координат)
- Перпендикулярное расстояние от точки до линии
- Нажмите «скрыть детали» и «повернуть», затем перетащите вершины трапеции вокруг, чтобы создать произвольный размер.
- По координатам угловых точек вычислите площадь и периметр трапеции.

Как найти площадь трапеции: формулы и примеры
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.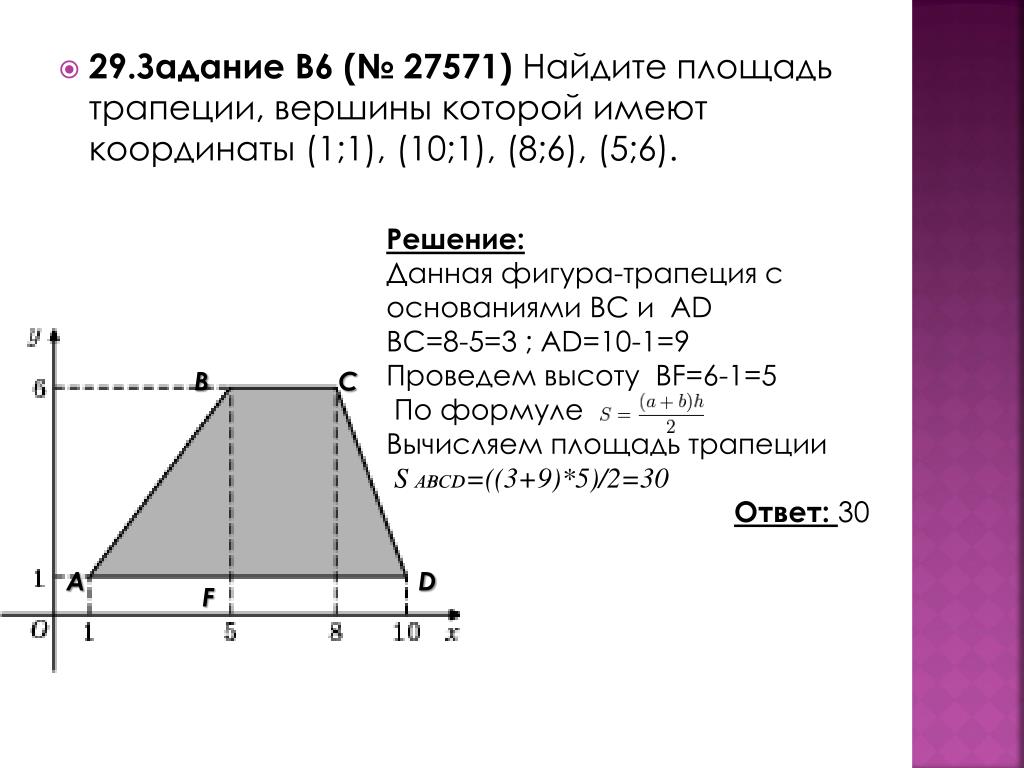
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.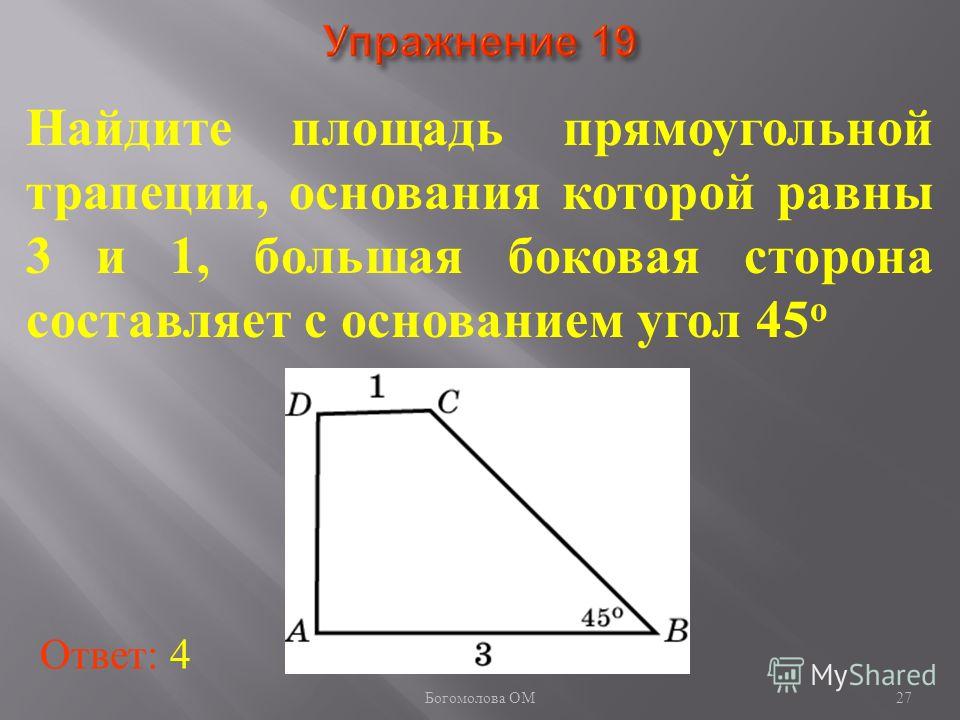
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h.
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h. Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d1и d2, которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d1d2 *sinα.
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c2 – ( ( 1/2(b – a)) * ((b – a)2 + c2 – d2) )2.
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r2/sinα. Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 300: S = 8r2.
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d1 и d2, а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h2.
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка [a; b] на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок [a; b]), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок [a; b]), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫baf(x)dx = F(x)│ba = F(b) – F(a). В этой формуле F – первообразная нашей функции на выбранном отрезке [a; b]. И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ2 = АР2 + РХ2). И высчитать его площадь: SAPX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см2.
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что SAMPC = SAPX = 54 см2.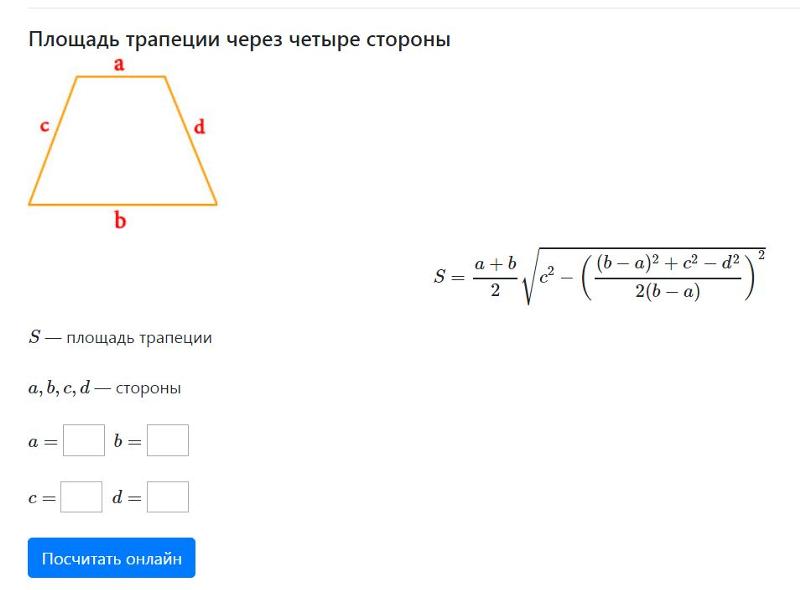
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h1 для треугольника ТМЕ и высоту h2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h1 = 1/5(b + х) * h2. Преобразуем и получим: h1/ h2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h1/ h2 = (х – а)/( b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х2 – а2) = (b2 – х2) ↔ 6х2 = b2 + 5а2 ↔ х = √(5а2 + b2)/6.
Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х2 – а2) = (b2 – х2) ↔ 6х2 = b2 + 5а2 ↔ х = √(5а2 + b2)/6.
Таким образом, ОЕ = х = √(5а2 + b2)/6.
Также советуем посмотреть вам наше новое видео по теме нахождения площади фигур, в том числе и трапеции:
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.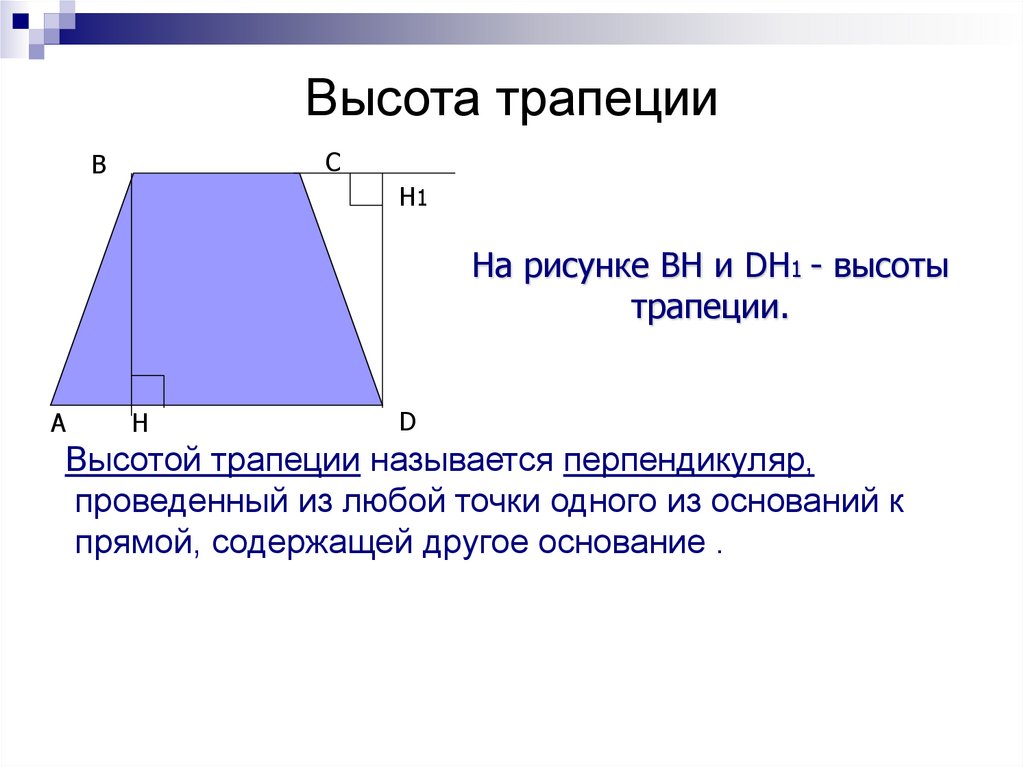
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Площадь трапеции по двум сторонам. Калькулятор периметра трапеции
Этот калькулятор рассчитал 2192 задачи на тему «Площадь трапеции»
ПЛОЩАДЬ ТРАПЕЦИИ
Выберете формулу вычисления площади трапеции, которую Вы планируете применить для решения поставленной перед Вами задачи:
Общая теория для вычисления площади трапеции.
Трапеция — это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих попарно эти четыре точки, у которой две противоположные стороны параллельны (лежат на параллельных прямых), а две другие не параллельны.
Точки называются вершинами трапеции и обозначаются заглавными латинскими буквами.
Отрезки называются сторонами трапеции и обозначаются парой заглавных латинских букв соответственно вершинам, которые отрезки соединяют.
Две параллельные стороны трапеции называются основаниями трапеции .
Две не параллельные стороны трапеции называются боковыми сторонами трапеции .
Рисунок №1: Трапеция ABCD
На рисунке №1 представлена трапеция ABCD с вершинами A,B ,C, D и сторонами AB, BC, CD, DA.
AB ǁ DC — основания трапеции ABCD.
AD, BC — боковые стороны трапеции ABCD.
Угол, образованный лучами AB и AD, называется углом при вершине A. Обозначается он как ÐA или ÐBAD, или ÐDAB.
Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB или ÐABC, или ÐCBA.
Угол, образованный лучами CB и CD, называется углом при вершине C. Обозначается он как ÐC или ÐDCB, или ÐBCD.
Угол, образованный лучами AD и CD, называется углом при вершине D. Обозначается он как ÐD или ÐADC, или ÐCDA.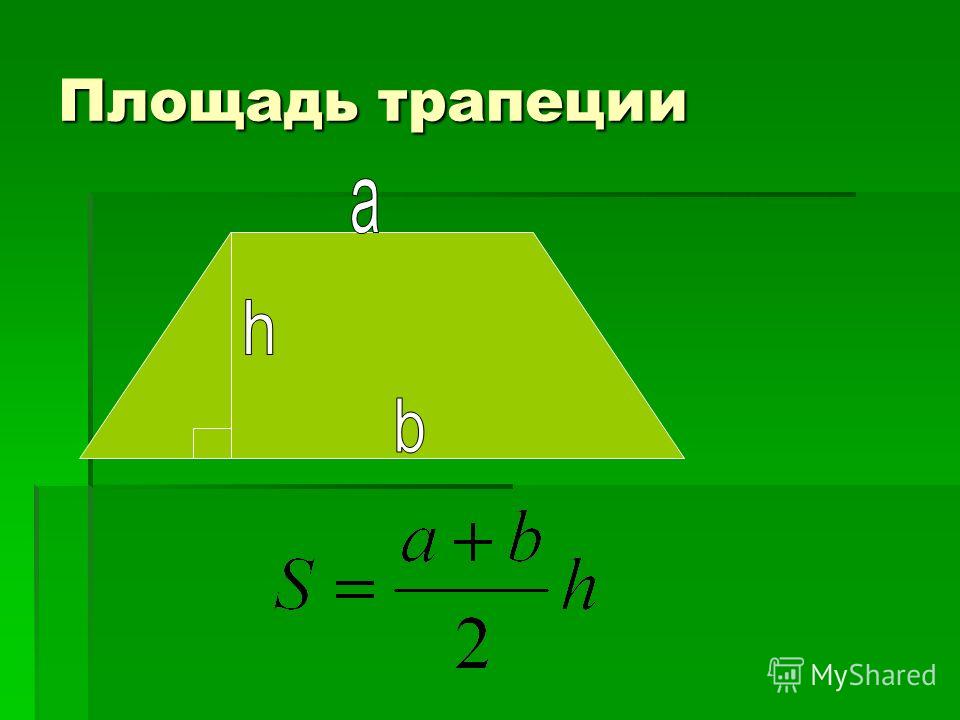
Рисунок №2: Трапеция ABCD
На рисунке №2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме. То есть,.
Рисунок №3: Равнобедренная трапеция ABCD
На Рисунке №3, AD=BC.
Трапеция называется равнобедренной (равнобокой) , если ее боковые стороны равны.
Рисунок №4: Прямоугольная трапеция ABCD
На Рисунке №4 угол D — прямой (равен 90 о).
Трапеция называется прямоугольной, если угол при боковой стороне прямой.
Площадью S плоской фигуры, к которым относится и трапеция, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.
Площадь обладает несколькими свойствами:
1. Она не может быть отрицательной.
2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.
3. Если две фигуры равны, то и площади их равны.
4. Площадь квадрата, который построен на единичном отрезке, равна единице.
За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
При решении задач часто используются следующие формулы вычисления площади трапеции:
1. Площадь трапеции равна полусумме ее оснований умноженной на высоту:
2. Площадь трапеции равна произведению ее средней линии на высоту:
3. При известных длинах оснований и боковых сторон трапеции её площадь можно вычислить по формуле:
4. Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле:
Пример 1: Вычислить площадь трапеции с основаниями a=7, b=3 и высотой h=15.
Решение:
Ответ:
Пример 2: Найти сторону основания трапеции с площадью S=35 см 2 , высотой h=7см и вторым основанием b = 2 см.
Решение:
Для нахождения стороны основания трапеции воспользуемся формулой вычисления площади:
Выразим из данной формулы сторону основания трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 3: Найти высоту трапеции с площадью S=17 см 2 и основаниями a=30 см, b = 4 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 4: Вычислить площадь трапеции с высотой h=24 и средней линией m=5.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 5: Найти высоту трапеции с площадью S = 48 см 2 и средней линией m=6 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы высоту трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 6: Найти среднюю линию трапеции с площадью S = 56 и высотой h=4.
Решение:
Для нахождения средней линии трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы среднюю линию трапеции:
Таким образом, имеем следующее.
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.
Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху.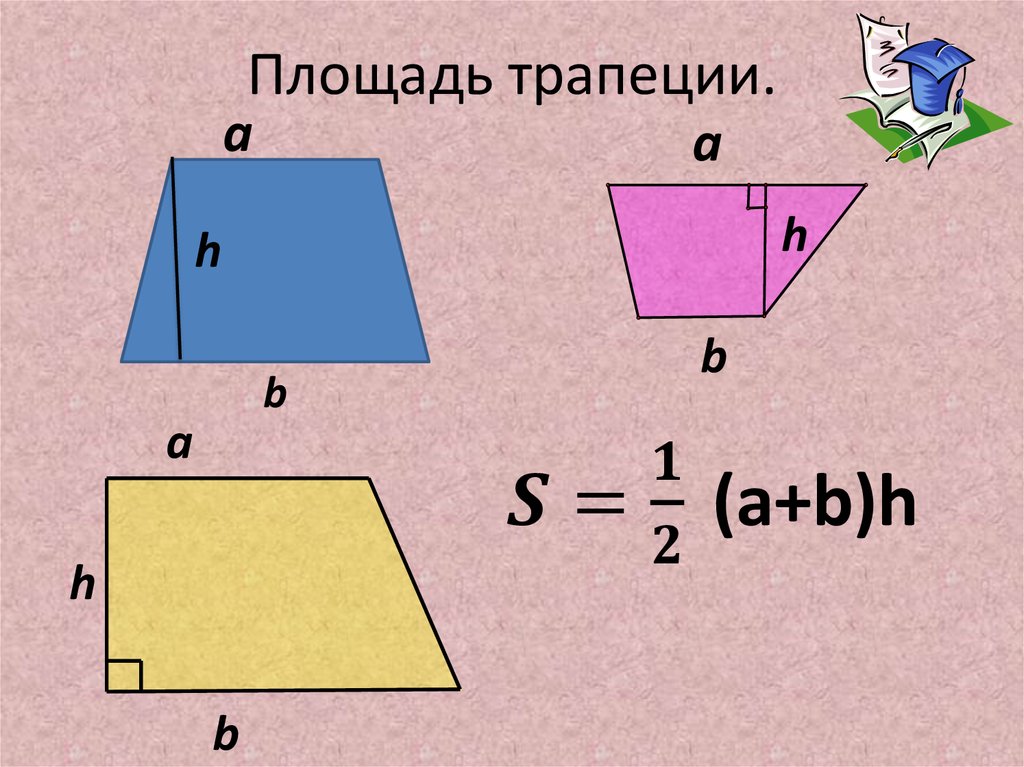 Но никто не запрещает изображать её и наоборот. Вот эскизы:
Но никто не запрещает изображать её и наоборот. Вот эскизы:
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии.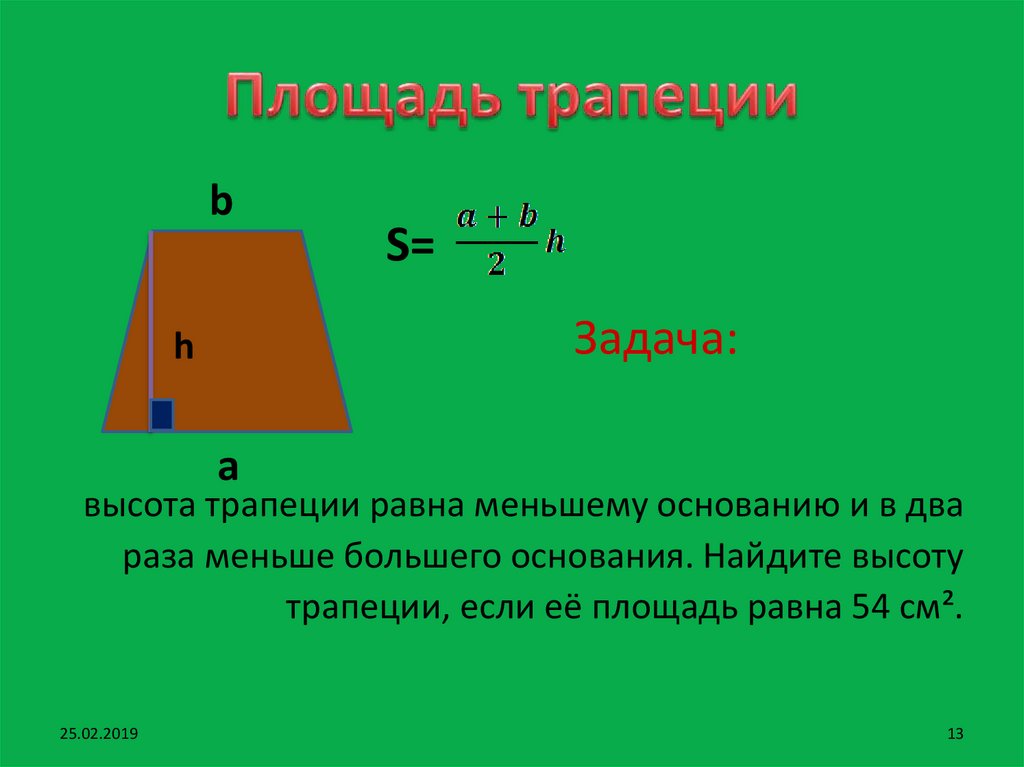 Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что треугольника равна половине параллельного ей основания, то есть:
Хорошо, разобрались. Теперь о площади трапеции.
Площадь трапеции формула:
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.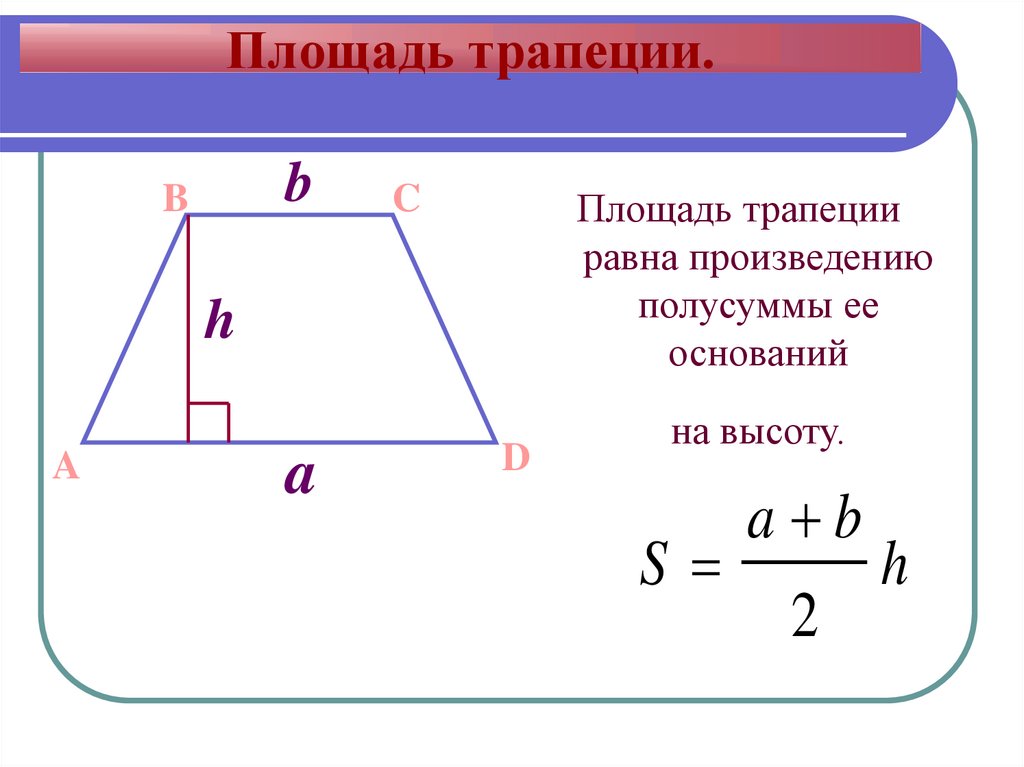
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
С уважением, Александр.
Трапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет. Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.
Геометрия трапеции
Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
«трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
Данная геометрическая фигура широко распространена в реальной жизни.
Трапеция в реальности
В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:
При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.
Периметр трапеции
Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
P = a + b + c + d,
где a и c – основания фигуры, b и d – ее боковые стороны.
Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.
Примеры из реальной жизни
Платок
Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.
Откосы
К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.
Заключение
Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях.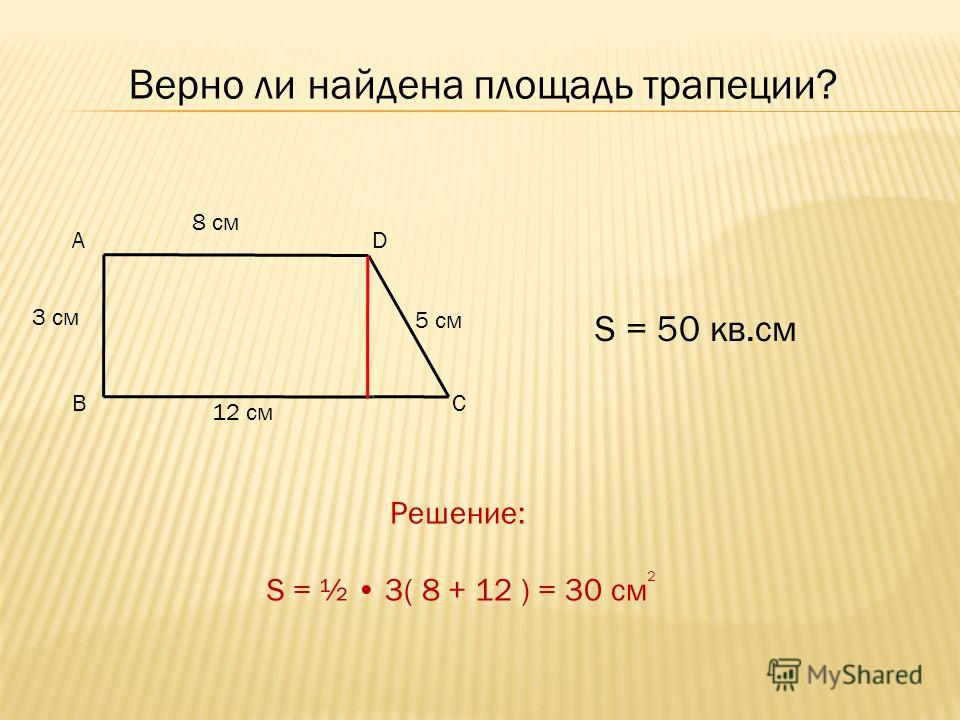 Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
Как найти площадь трапеции .
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
В виде формулы это записывается в виде выражения:
где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
А известны вам будут только длины оснований и боковых сторон.
В этом случае площадь трапеции может быть найдена по формуле:
S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2
где S-площадь, a,b-основания, c,d-боковые стороны трапеции.
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
Многоликая трапеция… Она может быть произвольной, равнобедренной или прямоугольной. И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.
Несколько слов о трапеции и ее элементах
Любой четырехугольник, у которого две стороны параллельны, можно назвать трапецией. В общем случае они не равны и называются основаниями.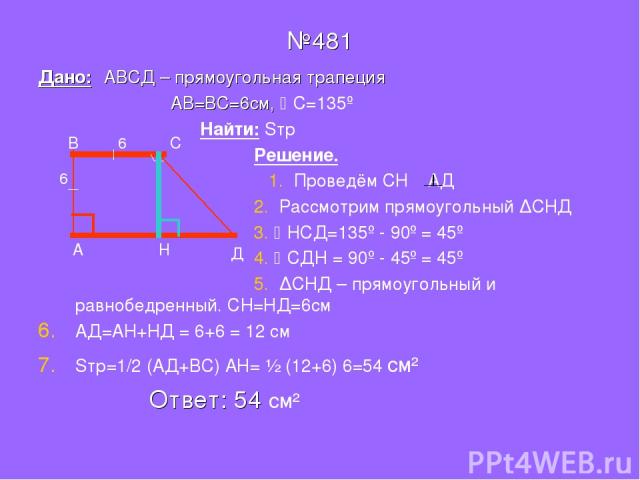 Большее из них — нижнее, а другое — верхнее.
Большее из них — нижнее, а другое — верхнее.
Две другие стороны оказываются боковыми. У произвольной трапеции они имеют различную длину. Если же они равны, то фигура становится равнобедренной.
Если вдруг угол между любой боковой стороной и основанием окажется равным 90 градусам, то трапеция является прямоугольной.
Все эти особенности могут помочь в решении задачи о том, как найти площадь трапеции.
Среди элементов фигуры, которые могут оказаться незаменимыми в решении задач, можно выделить такие:
По какой формуле вычислить площадь, если известны основания и высота?
Это выражение дается основным, потому что чаще всего можно узнать эти величины, даже когда они не даны явно. Итак, чтобы понять, как найти площадь трапеции, потребуется сложить оба основания и разделить их на два. Получившееся значение потом еще умножить на значение высоты.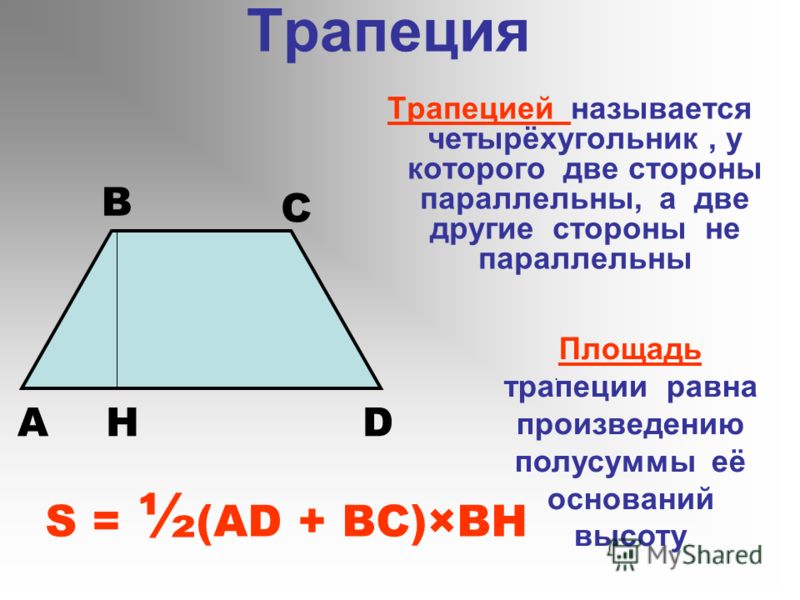
Если обозначить основания буквами а 1 и а 2 , высоту — н, то формула для площади будет выглядеть так:
S = ((а 1 + а 2)/2)*н.
Формула, по которой вычисляется площадь, если даны ее высота и средняя линия
Если посмотреть внимательно на предыдущую формулу, то легко заметить, что в ней явно присутствует значение средней линии. А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:
S = l * н.
Возможность найти площадь по диагоналям
Этот способ поможет, если известен угол, образованный ими. Предположим, что диагонали обозначены буквами д 1 и д 2 , а углы между ними — α и β. Тогда формула того, как найти площадь трапеции, будет записана следующим образом:
S = ((д 1 * д 2)/2) * sin α.
В этом выражении можно легко заменить α на β. Результат не изменится.
Как узнать площадь, если известны все стороны фигуры?
Бывают и такие ситуации, когда в этой фигуре известны именно стороны.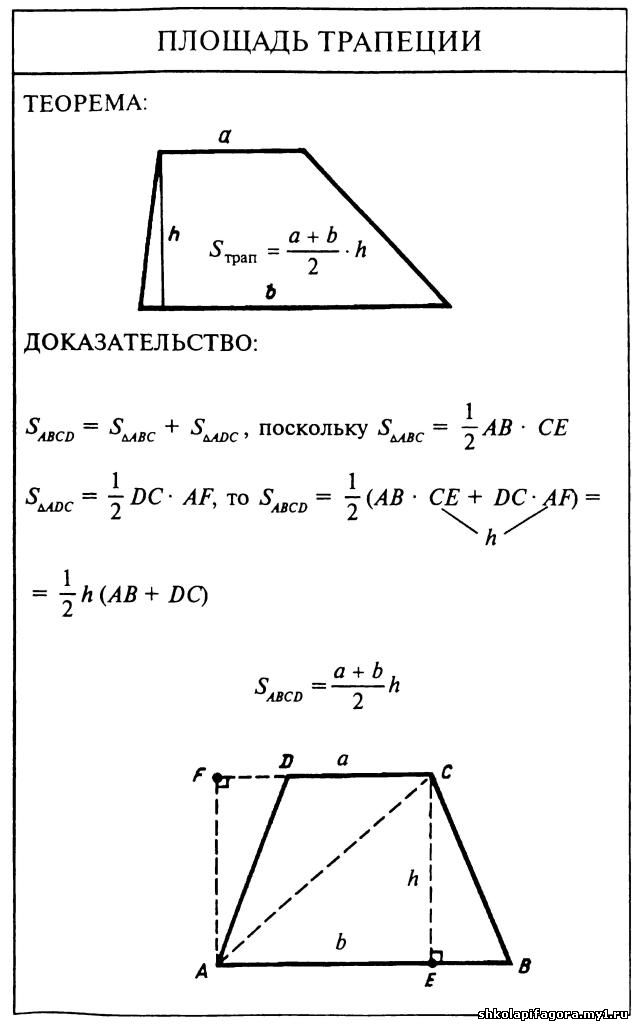 Эта формула получается громоздкой и ее сложно запомнить. Но возможно. Пусть боковые стороны имеют обозначение: в 1 и в 2 , основание а 1 больше, чем а 2 . Тогда формула площади примет такой вид:
Эта формула получается громоздкой и ее сложно запомнить. Но возможно. Пусть боковые стороны имеют обозначение: в 1 и в 2 , основание а 1 больше, чем а 2 . Тогда формула площади примет такой вид:
S = ((а 1 + а 2) / 2) * √ {в 1 2 — [(а 1 — а 2) 2 + в 1 2 — в 2 2) / (2 * (а 1 — а 2))] 2 }.
Способы вычисления площади равнобедренной трапеции
Первый связан с тем, что в нее можно вписать окружность. И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой:
S = (4 * r 2) / sin γ.
Последняя общая формула, которая основана на знании всех сторон фигуры, существенно упростится за счет того, что боковые стороны имеют одинаковое значение:
S = ((а 1 + а 2) / 2) * √ {в 2 — [(а 1 — а 2) 2 / (2 * (а 1 — а 2))] 2 }.
Методы вычисления площади прямоугольной трапеции
Понятно, что подойдет любой из перечисленных для произвольной фигуры. Но иногда полезно знать об одной особенности такой трапеции. Она заключается в том, что разность квадратов длин диагоналей равна разности, составленной из квадратов оснований.
Она заключается в том, что разность квадратов длин диагоналей равна разности, составленной из квадратов оснований.
Часто формулы для трапеции забываются, в то время как выражения для площадей прямоугольника и треугольника помнятся. Тогда можно применить простой способ. Разделить трапецию на две фигуры, если она прямоугольная, или три. Одна точно будет прямоугольником, а вторая, или две оставшиеся, треугольниками. После вычисления площадей этих фигур останется их только сложить.
Это достаточно простой способ того, как найти площадь прямоугольной трапеции.
Как быть, если известны координаты вершин трапеции?
В этом случае потребуется воспользоваться выражением, которое позволяет определить расстояние между точками. Его можно применить три раза: для того, чтобы узнать оба основания и одну высоту. А потом просто применить первую формулу, которая описана немного выше.
Для иллюстрации такого метода можно привести такой пример. Даны вершины с координатами А(5; 7), В(8; 7), С(10; 1), Д(1; 1). Нужно узнать площадь фигуры.
Нужно узнать площадь фигуры.
До того как найти площадь трапеции, по координатам нужно вычислить длины оснований. Потребуется такая формула:
длина отрезка = √{(разность первых координат точек) 2 + (разность вторых координат точек) 2 }.
Верхнее основание обозначено АВ, значит, его длина будет равна √{(8-5) 2 + (7-7) 2 } = √9 = 3. Нижнее — СД = √ {(10-1) 2 + (1-1) 2 } = √81 = 9.
Теперь нужно провести высоту из вершины на основание. Пусть ее начало будет в точке А. Конец отрезка окажется на нижнем основании в точке с координатами (5; 1), пусть это будет точка Н. Длина отрезка АН получится равной √{(5-5) 2 + (7-1) 2 } = √36 = 6.
Осталось только подставить получавшиеся значения в формулу площади трапеции:
S = ((3 + 9) / 2) * 6 = 36.
Задача решена без единиц измерения, потому что не указан масштаб координатной сетки. Он может быть как миллиметр, так и метр.
Примеры задач
№ 1. Условие. Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.
Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.
Решение. Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).
Теперь нужно воспользоваться подходящей формулой для площади:
S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (дм 2). Задача решена.
Ответ: площадь трапеции равна 4,5 дм 2 .
№ 2. Условие. В трапеции АВСД основаниями являются отрезки АД и ВС. Точка Е — середина стороны СД. Из нее проведен перпендикуляр к прямой АВ, конец этого отрезка обозначен буквой Н. Известно, что длины АВ и ЕН равны соответственно 5 и 4 см. Нужно вычислить площадь трапеции.
Решение. Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх. Так ЕН окажется внутри фигуры.
Чтобы отчетливо увидеть ход решения задачи, потребуется выполнить дополнительное построение. А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой — накрест лежащий.
А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой — накрест лежащий.
Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.
Таким образом, площадь трапеции равна 5 * 4 = 20 см 2 .
Ответ: S = 20 см 2 .
№ 3. Условие. Элементы равнобедренной трапеции имеют такие значения: нижнее основание — 14 см, верхнее — 4 см, острый угол — 45º. Нужно вычислить ее площадь.
Решение. Пусть меньшее основание имеет обозначение ВС. Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.
S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2).
Ответ: Искомая площадь равна 45 см 2 .
№ 4. Условие. Имеется произвольная трапеция АВСД. На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.
Решение. Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т; вторую через Е и точкой пересечения с АД будет М.
Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н 1 , большей АОЕД — н 2 .
Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:
(х + а 2) * н 1 = 1/5 (х + а 1) * н 2
н 1 /н 2 = (х + а 1) / (5(х + а 2)).
Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:
н 1 /н 2 = (х — а 2) / (а 1 — х).
В двух последних записях в левой части стоят равные величины, значит, можно написать, что (х + а 1) / (5(х + а 2)) равно (х — а 2) / (а 1 — х).
Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.
В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь квадратный корень.
Ответ : х = √ {(а 1 2 + 5 а 2 2) / 6}.
Прямоугольная трапеция
См. также: трапеция и ее свойства.
Прямоугольная трапеция — это трапеция, у которой хотя бы один из углов прямой (классическое определение)
Примечание. На самом деле, у прямоугольной трапеции, как минимум, два прямых угла (см. ниже — свойства)
ниже — свойства)
Другие определения:
Формулы для прямоугольной трапеции
Обозначения формул даны на чертеже выше.
Соответственно:
a и b — основания трапеции
с — боковая сторона прямоугольной трапеции, перпендикулярная основаниям
d — боковая сторона трапеции, не являющаяся перпендикулярной основаниям
α — острый угол при большем основании трапеции
m — средняя линия трапеции
Интерпретация формул:
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна высоте трапеции (Формула 1)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна произведению синуса острого угла при большем основании на длину второй боковой стороны. (Треугольник CKD — прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)
(Треугольник CKD — прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)
Боковая сторона, перпендикулярная основаниям, равна произведению разности оснований на тангенс острого угла при большем основании. (Треугольник CKD — прямоугольный. Поскольку трапеция — прямоугольная, то длина KD — это и есть разность оснований, а h/KD=tgα по определению тангенса, а c=h, откуда с/KD=tgα) (Формула 3)
Боковая сторона, которая не перпендикулярна основаниям, равна частному разности оснований к косинусу острого угла при большем основании или частному высоты трапеции и синуса острого угла при большем основании. (разность оснований равна KD. В прямоугольном треугольнике CKD по определению косинуса cos α = KD / d, откуда и проистекает искомая формула) (Формула 4)
Боковая сторона прямоугольной трапеции, которая не перпендикулярна основаниям, равна корню квадратному из разности квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее — следствие из теоремы Пифагора — из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)
(Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее — следствие из теоремы Пифагора — из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна корню квадратному из суммы квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, прямоугольный, далее — следствие из теоремы Пифагора — находим сумму квадратов катетов и извлекаем из полученного выражения квадратный корень) (Формула 6)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна частному от деления двойной площади трапеции на сумму ее оснований. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 7)
Боковая сторона прямоугольной трапеции, которая не перпендикулярна основаниям, равна частному от деления двойной площади трапеции на произведение суммы ее оснований и синуса острого угла при основании. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 8)
(Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 8)
Так как прямоугольная трапеция — это частный случай трапеции, то остальные формулы и свойства можно посмотреть в разделе «Трапеция».
Свойства прямоугольной трапеции
Задача
В прямоугольной трапеции большая боковая сторона равна сумме оснований, высота равна 12 см. Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Решение.
Обозначим трапецию как ABCD. Обозначим длины оснований трапеции как a (большее основание AD) и b (меньшее основание BC). Пусть прямым углом будет ∠A.
Площадь прямоугольника, стороны которого равны основаниям трапеции, будет равна
S = ab
Из вершины C верхнего основания трапеции ABCD опустим на нижнее основание высоту CK. Высота трапеции известна по условию задачи. Тогда, по теореме Пифагора
CK2 + KD2 = CD2
Поскольку большая боковая сторона трапеции по условию равна сумме оснований, то CD = a + b
Поскольку трапеция прямоугольная, то высота, проведенная из верхнего основания трапеции разбивает нижнее основание на два отрезка AD = AK + KD. Величина первого отрезка равна меньшему основанию трапеции, так как высота образовала прямоугольник ABCK, то есть BC = AK = b, следовательно, KD будет равен разности длин оснований прямоугольной трапеции KD = a — b.
то есть
122 + (a — b)2 = (a + b)2
откуда
144 + a2 — 2ab + b2 = a2 + 2ab + b2
144 = 4ab
Поскольку площадь прямоугольника S = ab (см. выше), то
144 = 4S
S = 144 / 4 = 36
Ответ: 36 см2 .
0
Калькулятор трапеций: найдите A и P
Создано Maciej Kowalski, кандидатом наук
Отзыв Стивена Вудинга
Последнее обновление: 25 августа 2022 г.
Содержание: Также уделим время описанию некоторых специальных типов четырехугольников: равнобедренной трапеции и прямоугольной трапеции. И не волнуйтесь; мы не оставляем камня на камне — мы даже упоминаем срединный угол и углы трапеции в калькуляторе.
Также уделим время описанию некоторых специальных типов четырехугольников: равнобедренной трапеции и прямоугольной трапеции. И не волнуйтесь; мы не оставляем камня на камне — мы даже упоминаем срединный угол и углы трапеции в калькуляторе.Похоже, есть что обсудить, так что давайте приступим, не так ли?
Что такое трапеция?
Трапеция — это четырехугольник (форма с четырьмя сторонами), по крайней мере одна пара противоположных сторон которого параллельна друг другу. Обратите внимание, что мы сказали « по крайней мере одна пара сторон» — если фигура имеет две такие пары, это просто прямоугольник. И не заблуждайтесь – каждый прямоугольник является трапецией . Обратное, конечно, неверно.
Две параллельные стороны обычно называются основаниями . Обычно мы рисуем трапеции так, как мы это делали выше, что может объяснить, почему мы часто различаем их, говоря снизу и сверху снизу . Две другие непараллельные стороны называются катетами (аналогично двум сторонам прямоугольного треугольника).
Две другие непараллельные стороны называются катетами (аналогично двум сторонам прямоугольного треугольника).
Здесь мы хотели бы упомянуть несколько частных случаев трапеций.
Имея в виду эти особые случаи, зоркий глаз может заметить, что прямоугольника удовлетворяют условиям 2 и 3 . В самом деле, если бы кто-то не знал, что такое прямоугольник, мы могли бы просто сказать, что это равнобедренная трапеция, которая также является прямоугольной трапецией. Довольно причудливое определение по сравнению с обычным, но оно заставляет нас звучать изощренно, не так ли?
Прежде чем мы перейдем к следующему разделу, упомянем еще два отрезка, которые есть у всех трапеций.
Высота трапеции — это расстояние между основаниями, т. е. длина линии, соединяющей два , которая перпендикулярна обоим. На самом деле, это значение имеет решающее значение, когда мы обсуждаем, как вычислить площадь трапеции, и, следовательно, получает отдельный выделенный раздел.
Медиана трапеции — линия, соединяющая середины катетов. Другими словами, имея в виду рисунок выше, это линия, разрезающая трапецию горизонтально пополам . Она всегда параллельна основаниям, и при обозначениях, как на рисунке, имеем
Она всегда параллельна основаниям, и при обозначениях, как на рисунке, имеем медиана = (a + b)/2 . Если вам интересно название, обязательно ознакомьтесь с калькулятором медианы Omni (примечание: он не касается трапеций).
Хорошо, мы достаточно хорошо изучили нашу форму ; мы даже видели одну формулу трапеции! Давайте сделаем еще один шаг и попробуем еще лучше понять тему. Мы начнем этот углубленный анализ с формулы периметра трапеции и ее внутренних углов .
Формула периметра трапеции и углы трапеции
Периметр многоугольника равен сумме длин его сторон . Для героя сегодняшней статьи история ничем не отличается. С обозначениями, как на рисунке в первом разделе (и в калькуляторе трапеций), мы выводим формулу периметра трапеции:
P = a + b + c + d
Довольно просто, не так ли? ?
Далее, поговорим об углах . Как и в любом другом четырехугольнике, сумма углов трапеции равна 9. 0107 360 градусов (или
0107 360 градусов (или 2π радиан). Однако условие быть трапецией (т.е. иметь пару параллельных сторон) навязывает дополнительные свойства отдельным. Точнее, пара углов вдоль одного из катетов являются дополнительными углами. Это означает, что их сумма должна равняться 180 градусов (или π радиан), что в обозначениях из рисунка в первом разделе переводится как:
α + 𝛾 = β + δ = 180°
Обратите внимание, что наш инструмент также упоминает углы в нижнем наборе переменных полей. Таким образом, он также может служить калькулятором угла трапеции всякий раз, когда мы ищем эти числа. И действительно, они часто пригодятся – они играют существенную роль , когда мы учимся находить высоту трапеции, а та, в свою очередь, появляется при изучении того, как вычислить площадь трапеции. Однако начнем с последнего вопроса.
Как вычислить площадь трапеции
Давайте еще раз вернемся к картинке из первого раздела, чтобы вам не приходилось прокручивать всю статью всякий раз, когда вы захотите вспомнить обозначения.
Площадь трапеции по формуле выглядит следующим образом:
A = (a + b) × h/2
Обратите внимание, что, как мы уже упоминали пару раз, крайне важно знать, как найти высоту трапеции, чтобы вычислить ее площадь. Кроме того, ноги никогда не появляются в уравнении. Конечно, они определяют форму нашего четырехугольника, но их длины используются только в формуле периметра трапеции, которую мы обсуждали в предыдущем разделе.
Наконец, давайте проясним, что по порядку операций не имеет значения, в какой момент мы делим на 2 в приведенной выше области формулы трапеции. Мы можем либо сначала вычислить (a + b) × h , а затем разделить все это на 2 , либо сначала найти h/2 , а уже потом умножить на (a + b) . На самом деле зоркий глаз заметит, что (a + b) / 2 равно медиане , которую мы упоминали в первом разделе. Другими словами, в качестве альтернативы мы можем использовать формулу
Другими словами, в качестве альтернативы мы можем использовать формулу A = медиана × h , чтобы найти A .
Хорошо, мы научились вычислять площадь трапеции, и все кажется простым, если нам дают все данные на табличке. А если нет? Базы достаточно просты, но как насчет h ? Что ж, пора посмотреть , как найти высоту трапеции.
Как найти высоту трапеции
Важным фактом, который мы используем, чтобы найти высоту трапеции, является то, что это отрезок, перпендикулярный основаниям . Это дает нам прямой угол в обеих конечных точках, что позволяет нам использовать прямоугольные треугольники. И первое, что приходит на ум, когда мы слышим словосочетание прямоугольный треугольник — это, конечно же, теорема Пифагора.
Проведем линию из одной из верхних вершин , которая падает на нижнее основание a под углом 90 градусов. (Обратите внимание, как для тупых трапеций, подобных той, что на правом рисунке, над высотой
(Обратите внимание, как для тупых трапеций, подобных той, что на правом рисунке, над высотой h выходит за пределы формы, то есть на строку, содержащую a , а не a . Тем не менее, то, что мы опишем ниже, остается в силе для таких четырехугольников.) Длина этой линии равна высоте нашей трапеции, так что именно то, что мы ищем. Обратите внимание, как мы нарисовали линию , она образует прямоугольный треугольник с одной из сторон c или d (в зависимости от того, какую вершину мы выбрали).
Если у нас есть длина катета трапеции и мы можем вычислить другую сторону прямоугольного треугольника (т. е. e или f на картинке выше), то мы знаем, как найти высоту трапеции — используем теорему Пифагора . Однако есть и другой способ расчета.
Если вы немного разбираетесь в тригонометрии, вы сможете найти высоту , используя внутренний угол трапеции . Если быть точным, глядя на углы трапеций в нашем калькуляторе (т.е. на обозначения на картинке), мы можем использовать определение тригонометрических функций, чтобы написать:
Если быть точным, глядя на углы трапеций в нашем калькуляторе (т.е. на обозначения на картинке), мы можем использовать определение тригонометрических функций, чтобы написать:
h = c × sin(α) = d × sin(δ)
, где sin — функция синуса. На самом деле может случиться, что угол равен 30 , 45 или 60 градусов, и в этом случае мы можем просто использовать свойства специальных прямоугольных треугольников с такими внутренними углами.
Наконец, отметим, что весь этот поиск h очень прост в особом случае – когда у нас есть правильная трапеция . Тогда высота нашей трапеции — это просто катет, лежащий рядом с прямым углом. Обратите внимание, что в этом случае приведенная выше тригонометрическая формула все еще работает, поскольку sin(90°) = 1 .
Уф, это было много теории . Самое время воспользоваться этими формулами трапеций и посмотреть как вычислить площадь и периметр трапеции на практике .
Пример: с помощью калькулятора трапеций
Давайте проверим как найти площадь и периметр трапеции со сторонами и углами, обозначенными как в калькуляторе трапеций, и следующими данными:
a = 8 в , b = 5 в , d = 3 в , α = 90° , δ = 45° .
Вроде бы ничего особенного, но посмотрим, что здесь можно сделать . Во-первых, однако, давайте заметим, что наш калькулятор трапеций может легко справиться с нашей задачей даже с таким небольшим количеством информации. Действительно, если мы введем вышеуказанные числа в наш инструмент (обратите внимание, как мы можем переключаться на другие единицы, щелкая по ним и выбирая подходящую из списка), заполнит все остальные поля . Например, в качестве калькулятора угла трапеции он будет использовать тождества, упомянутые во втором разделе, для вычисления β и 𝛾 . Также обратите внимание, что мы можем дополнительно зайти в расширенный режим и посмотреть длину медианы.
Также обратите внимание, что мы можем дополнительно зайти в расширенный режим и посмотреть длину медианы.
Если инструмент может это сделать, сможем и мы! Давайте посмотрим, как вычислить площадь и периметр трапеции вручную.
Прежде всего обратите внимание, что мы имеем дело с прямой трапецией , так как α = 90° (на самом деле у нас тоже β = 90° ). Это означает, что сторона c перпендикулярна основаниям и, следовательно, равна высоте c = h . Однако мы не знаем c , так что нам придется найти еще .
Для этого нарисуйте высоту нашей трапеции , которая идет от вершины между b и d . Вместе с d и частью a , образует прямоугольный треугольник . Более того, нам известен один из его углов – δ = 45° . Значит, это один из частных случаев — это половина квадрата. Следовательно,
Следовательно, ч равно нижней стороне треугольника, а d является, по сути, диагональю квадрата, а значит:
ч = d/√2 = 3 в/√2 = 1,5√2 in ≈ 2,1213 in
(последнее равенство получаем рационализацией знаменателя).
Теперь у нас есть все необходимое чтобы найти А . Вспомните из специального раздела, как рассчитать площадь трапеции, и используйте информацию, чтобы получить
A = (a + b) × h/2 = (8 дюймов + 5 дюймов) × 1,5√2 дюйма / 2 = 9,75 √2 дюйма² ≈ 13,789 дюйма² 90 108 .
Мы также собрали все данные, чтобы найти P , поскольку c = h = 1,5√2 в . По формуле периметра трапеции из второго сечения получаем
P = a + b + c + d = 8 дюймов + 5 дюймов + 1,5√2 дюймов + 3 дюймов = 16 + 1,5√2 дюймов ≈ 18,12 дюймов .
Не так уж и плохо, не так ли? Стороны и углы, которые мы получили в начале, казались довольно случайным набором, но нам удалось найти им хорошее применение. Если вы чувствуете, что изголодались по геометрии и формулам , обязательно ознакомьтесь с другими калькуляторами 2D-форм на веб-сайте Omni — у нас есть все!
Если вы чувствуете, что изголодались по геометрии и формулам , обязательно ознакомьтесь с другими калькуляторами 2D-форм на веб-сайте Omni — у нас есть все!
Часто задаваемые вопросы
Как найти высоту трапеции, зная площадь и основания?
Для определения высоты h по площади А и основаниям а и b :
Какова высота трапеции с площадью 10 и сторонами 2 и 3?
Высота имеет длину 4. Действительно, формула для высоты гласит: h = 2A/(a+b) .
Подстановка значений a = 2 , b = 3 и A = 10 , получаем h = 2 × 10 /(2 + 3) = 4 .
Является ли трапеция параллелограммом?
№ . У параллелограмма две пары параллельных сторон, а у трапеции должна быть только одна пара параллельных сторон. Следовательно, общая трапеция не является параллелограммом.
У параллелограмма две пары параллельных сторон, а у трапеции должна быть только одна пара параллельных сторон. Следовательно, общая трапеция не является параллелограммом.
Является ли параллелограмм трапецией?
Да , каждый параллелограмм является трапецией. То же самое верно для каждого ромба, каждого прямоугольника и каждого квадрата. Однако воздушный змей (дельтовидная) не является трапецией.
У каждой трапеции 2 пары противоположных параллельных сторон?
Нет , у трапеции должна быть хотя бы одна пара параллельных сторон, а это значит, что она может иметь ровно одну такую пару и при этом быть совершенно правильной трапецией. Если у него две пары параллельных сторон, то это, по сути, параллелограмм.
Сколько осей симметрии у трапеции?
Обычная трапеция имеет ноль линий симметрии. Однако есть частный случай 9.0023 равнобедренные трапеции: у них есть одна линия симметрии, которая проходит через середины их оснований.
Maciej Kowalski, кандидат PhD
A (основание)
B (основание)
H (высота)
Область (A)
Периметр
Периметр (P)
. похожие калькуляторы 2d геометрии 📏
ПлощадьПлощадь прямоугольникаПлощадь полумесяца… Еще 18
Калькулятор площади трапеции [Простой в использовании + Руководство по результатам]
a(основание)
b(основание)
h(высота)
Вернуться на страницу калькуляторов
Трапеция – интересная четырехсторонняя геометрическая фигура. У него две параллельные стороны, а оставшиеся две стороны могут быть любой длины и под любым углом. Некоторые возможные формы трапеций показаны ниже, чтобы прояснить концепцию. Обратите внимание, что параллельные линии отмечены стрелками.
В реальной жизни есть много предметов трапециевидной формы, которые вы могли не замечать. См. несколько примеров ниже. Вы удивлены?
Теперь, когда вы разобрались с формой трапеции, давайте обсудим параметры, которые вам нужно знать, чтобы найти ее площадь. Чтобы найти площадь трапеции, необходимо знать три важные длины: длины двух параллельных сторон «а» и «b» и высоту. Высота - это перпендикулярное расстояние между двумя параллельными сторонами. Под перпендикулярным расстоянием мы подразумеваем длину линии, которая соединяет параллельные стороны «a» и «b» и составляет ровно 90 градусов к ним.
Площадь трапеции, A , определяется как:
Эта формула получена из понятия площади треугольника. Возможно, вы уже знаете, как вычислить площадь треугольника, но мы кратко рассмотрим его на случай, если вы забыли или не знаете. Два параметра, которые вам нужно знать, чтобы найти площадь треугольника, — это высота треугольника и основание треугольника. Высота треугольника определяется как расстояние по перпендикуляру от одного угла треугольника до уровня основания. Какую бы сторону треугольника вы ни выбрали в качестве «основания», измерьте высоту, считая угол, точно противоположный основанию. См. диаграммы ниже для большей ясности концепции высоты-базы.
Высота треугольника определяется как расстояние по перпендикуляру от одного угла треугольника до уровня основания. Какую бы сторону треугольника вы ни выбрали в качестве «основания», измерьте высоту, считая угол, точно противоположный основанию. См. диаграммы ниже для большей ясности концепции высоты-базы.
Не запутайтесь, если форма треугольника отличается от той, которую вы обычно ожидаете. Помните о концепции основания и высоты и маркируйте соответственно.
Площадь треугольника определяется как:
Теперь, как это знание поможет нам вычислить формулу площади трапеции? Посмотрим.
Посмотрите внимательно, и вы заметите, что трапецию можно разрезать по диагонали, чтобы образовались два треугольника:
Если мы найдем площади этих двух треугольников, а затем сложим их, мы получим площадь всей трапеции! Основание верхнего треугольника равно длине «а», а основание нижнего треугольника равно длине «b». Высота обоих треугольников одинакова.
Площадь верхнего треугольника равна:
Площадь нижнего треугольника равна:
Следовательно, площадь трапеции будет:
{2}\) в качестве общего множителя получаем:
Надеюсь, теперь вы полностью понимаете концепцию формулы площади трапеции. Давайте сделаем несколько примеров.
Пример 1:Найдите площадь трапеции, приведенная ниже:
Решение:Из рисунка мы можем увидеть, что:
9002 A = 4 CMИз рисунка мы можем увидеть, что 9003 9002 A = 4 CM
. 9 см
h = 5 см
Пусть площадь трапеции представлена переменной 'A'
А = ?
Примените формулу площади трапеции:
Пример 2:Чему равно расстояние по перпендикуляру между двумя параллельными сторонами?
Решение:Заданы следующие параметры:
Параллельная сторона 1 = a= 16 см
Параллельная сторона 2 = b= 12 см
Площадь трапеции = A = 98 см 2
Нам нужно найти расстояние по перпендикуляру между двумя параллельными сторонами. Как мы упоминали ранее в статье, это высота трапеции.
Как мы упоминали ранее в статье, это высота трапеции.
ч = ?
Вспомните формулу площади трапеции и найдите «h».
Теперь подставляем известные значения и находим высоту:
Пример 3:Площадь приведенной ниже трапеции равна 100 см 2 . Найдите неизвестную длину параллельной стороны а.
Решение:Одна сторона этой трапеции образует угол 90 градусов с обеими параллельными сторонами. Это означает, что высота трапеции и длина этой стороны одинаковы. Нам дается следующая информация:
Площадь трапеции = A = 100 см 2
Высота = h = 10 см
Параллельная сторона 2 = b = 11 см
Параллельная сторона 1 = a = ?
Чтобы найти «а», мы преобразуем формулу площади трапеции, чтобы найти «а»:
Теперь подставьте известные значения, чтобы получить окончательный ответ:
Заключительные мысли! Мы попытались охватить почти все, что нужно знать о площади трапеции, от ее вывода до решения различных задач. Геометрия — очень важный раздел математики, и изучение всех форм, существующих в реальном мире, имеет решающее значение, особенно если вы думаете однажды стать инженером! Изучив теорию, вы можете воспользоваться нашим калькулятором площади трапеции, чтобы быстро получить ответы на свои вопросы и сэкономить время!
Геометрия — очень важный раздел математики, и изучение всех форм, существующих в реальном мире, имеет решающее значение, особенно если вы думаете однажды стать инженером! Изучив теорию, вы можете воспользоваться нашим калькулятором площади трапеции, чтобы быстро получить ответы на свои вопросы и сэкономить время!
Калькулятор площади трапеции - пошаговый расчет
Введите информацию
Решите для Выберите optionAreaBase aBase bHeightSide cSide dPerimeter
Дано
Результат
Заполните форму калькулятора и нажмите кнопку «Рассчитать», чтобы получить результат здесь
Получить Индивидуальный калькулятор Для вашего веб-сайта
Получить сейчас
ИЛИ
Получить Калькулятор площади трапеции Для вашего веб-сайта
Получить сейчас
Содержание
| 1 | Что такое трапеция? |
| 2 | Формула площади трапеции |
| 3 | Как найти площадь трапеции? |
| 4 | Часто задаваемые вопросы |
Калькулятор площади трапеции! Онлайн-инструмент для расчета площади трапеции. Кроме того, его можно использовать для расчета:
Кроме того, его можно использовать для расчета:
Вы можете выбрать основание или стороны трапеции в качестве параметра, чтобы найти ее площадь.
В этом разделе мы объясним, как использовать калькулятор площади трапеции, определение трапеции, формулу площади трапеции, и как вычислить площадь трапеции без использования калькулятора.
Что такое трапеция?
Трапеция – это четырехсторонняя плоская форма с одной парой противоположных параллельных сторон. Создается впечатление, что вершина треугольника была срезана параллельно основанию.
Обычно самая длинная сторона трапеции направлена вниз, а ребра имеют две наклонные стороны. Обычно верхняя часть короче нижней.
Внутренние углы трапеции в совокупности составляют 360°. Углы на одной стороне катета также называются смежными и всегда составляют 180°.
α + β = 180°
γ + δ = 180°
Формула площади трапеции
Формула площади трапеции выводится из формулы площади треугольника. Можно сказать так:
A = (A + B) × H / 2
Где:
Примечание. Если трапеция с одинаковой длиной сторон имеет a = b, , это будет прямоугольник. Вы можете рассчитать площадь прямоугольника, используя наш калькулятор площади прямоугольника.
Формула периметра трапеции
Периметр трапеции можно рассчитать с помощью следующего уравнения:
P = a + b + c + d
Периметр трапеции также можно рассчитать с помощью приведенного выше калькулятора.
Как пользоваться калькулятором площади трапеции?
Прежде чем вычислять площадь или периметр трапеции, вы должны знать, как использовать этот калькулятор для этой цели.
Чтобы использовать этот калькулятор, выполните следующие действия:
Как найти площадь трапеции?
Вопрос «Какова площадь трапеции» задавался очень много раз. Мы ответим на этот вопрос и объясним его подробно в этом разделе. Вы всегда можете использовать наш калькулятор трапеций выше, однако вы должны быть в состоянии вычислить площадь трапеции самостоятельно.
Чтобы рассчитать площадь трапеции, выполните следующие действия:
Пример:
Найдите площадь трапеции, имеющей высоту 8 см, длину верха 4 см и длины основания 6 см?
Шаг 1: Измерьте и запишите основание a , основание b и высота h трапеции.
a = 4 см, b = 6 см, h = 8 см
Шаг 2: Запишите формулу площади трапеции.
A = (a + b) × h / 2
Шаг 3: Подставьте значения в формулу и рассчитайте площадь.
A = (4 см + 6 см) × 8 / 2
A = 10 см × 4
A = 40 см
Итак, трапеция с высотой 8 см, верхней стороной 4 см и нижней стороной 6 см площадь 40 см.
Часто задаваемые вопросы
Является ли площадь трапеции квадратной?
Нет, площадь трапеции не равна квадрату. В уравнении площади трапеции мы складываем верхнюю и нижнюю стороны трапеции. Поэтому площадь трапеции не возводится в квадрат.
В уравнении площади трапеции мы складываем верхнюю и нижнюю стороны трапеции. Поэтому площадь трапеции не возводится в квадрат.
A = (a + b) × h / 2
Приводится в одной единице измерения, такой как сантиметр, дюйм и т. д.
Как выглядит трапеция?
Трапеция имеет четыре стороны. Две стороны параллельны друг другу. Трапеция выглядит как треугольник с плоским верхним углом. См. изображение трапеции ниже:
Является ли прямоугольник трапецией?
Согласно всеобъемлющему определению трапеции, прямоугольник является трапецией вместе с ромбами и квадратами. Таким образом, включительно мы можем сказать, что прямоугольник является трапецией.
Каждая ли трапеция является ромбом?
Нет. Каждая трапеция не является ромбом. У ромба две пары параллельных сторон, а у трапеции одна пара параллельных сторон. Если у трапеции обе стороны параллельны, то это ромб.
Другие языки
Рейтинги пользователей
Спасибо! Для вашего рассмотрения
Ваш отзыв скоро появится.
Отправить свой отзыв Закрыть
Отзывы
Пожалуйста, заполните 1 строку
Обратная связь
Отправьте нам свой отзыв!
Нужна помощь? Вы можете связаться с нами в любое время.
КАЛЬКУЛЯТОР ТРАПЕЦИЙ
КАЛЬКУЛЯТОР ТРАПЕЦИЙ  Прямые BC и AD параллельны и называются основаниями. Линии AB и DC являются непараллельными сторонами и называются ответвлениями. Линии AC (или q ) и BD (или p ) называются диагоналями Линия, перпендикулярная линиям AD и BC, называется высотой или высотой. Прямая, параллельная линиям AD и BC, проходит через середины линий AB и DC. и называется медиана или средний сегмент . Длина медианы = (Линия AD + Линия BC) ÷ 2 Трапеции имеют 2 пары смежных углов (A и B) и (B и C), которые являются дополнительными (добавить 180°).
|
| Геометрия | Формы | Контакты и конфиденциальность | Геометрические калькуляторы | Немецкий: Geometriechner, Formen |
| 1DЛиния, дуга окружности, парабола, спираль, кривая Коха
2D Правильные многоугольники: Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, многоугольник, десятиугольник, десятиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольника Другие многоугольники: Круглые формы: Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron Archimedean Solids: Catalan Solids: Solid Johnson Solid: Круглые формы: | Anzeige Вычисления на прямой трапеции (или правильной трапеции). Формулы: Длины сторон, диагонали и периметр имеет одну и ту же единицу измерения (например, метр), площадь имеет эту единицу в квадрате (например, квадратный метр). Поделиться: © Jumk.de Веб-проекты | Онлайн калькуляторы Anzeige |
Площадь и периметр трапеции. (Координатная геометрия)
Площадь и периметр трапеции. (Координатная геометрия) - открытый справочник по математикеОткрытый справочник по математике
Главная Контакт О Тематический указатель
Площадь и периметр трапеции можно вычислить, если знать
координат его
вершины.
Попробуйте это Перетащите любую вершину трапеции ниже. Она останется трапецией, а площадь и периметр рассчитаны. Вы также можете перетащить исходную точку в (0,0) или переместить сам прямоугольник.
Район
Площадь трапеции вычисляется путем умножения средней ширины на высоту. См. Определение трапеции (координатная геометрия), чтобы увидеть, как длины сторон и высота найдены. (Обратите внимание, что срединная длина такая же, как и средняя ширина.)
Как формула:
где
b1, b2 — длины двух оснований (BC и AD)
a — высота трапеции
На рисунке выше перетащите любую вершину трапеции и обратите внимание, как рассчитывается площадь.
Периметр
Периметр трапеции - это просто сумма всех четырех сторон.
Поскольку они не имеют отношения друг к другу, для этого нет формулы.
Просто найдите четыре длины сторон и сложите их. Длину каждой стороны находят с помощью методов, описанных в
Расстояние между двумя точками (с учетом их координат)
которые используются для нахождения расстояния между конечными точками каждой стороны.

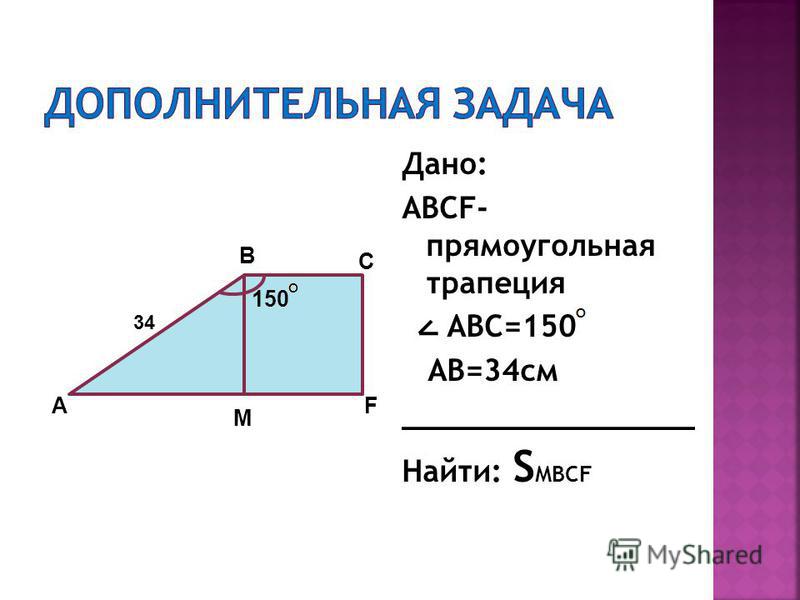

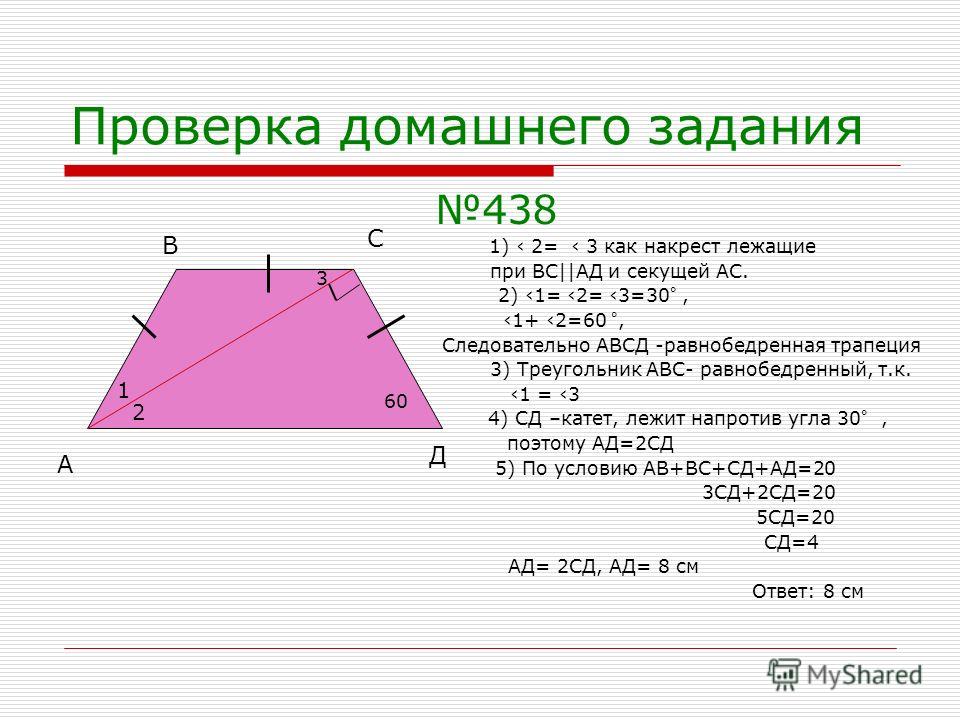
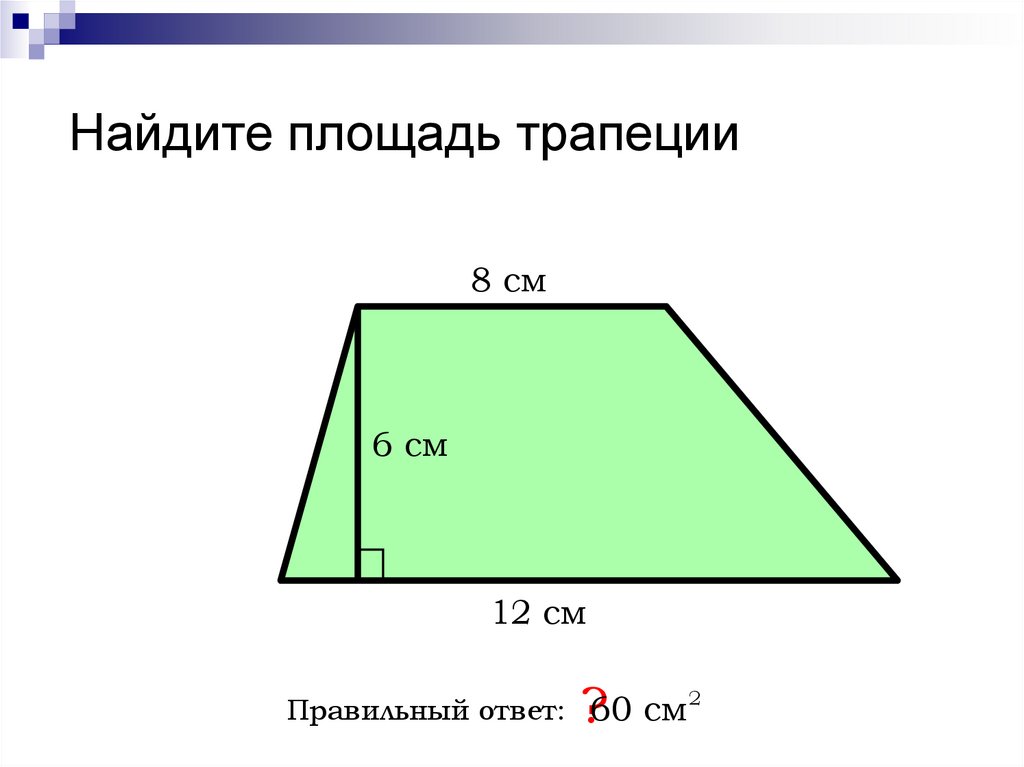 Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб.
Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб. 2.
2.