Сложные интегралы
Данная статья завершает тему неопределенных интегралов, и в неё включены интегралы, которые я считаю достаточно сложными. Урок создан по неоднократным просьбам посетителей, которые высказывали пожелания, чтобы на сайте были разобраны и более трудные примеры.
Предполагается, что читатель сего текста хорошо подготовлен и умеет применять основные приемы интегрирования. Чайникам и людям, которые не очень уверенно разбираются в интегралах, следует обратиться к самому первому уроку – Неопределенный интеграл. Примеры решений, где можно освоить тему практически с нуля. Более опытные студенты могут ознакомиться с приемами и методами интегрирования, которые в моих статьях еще не встречались.
Какие интегралы будут рассмотрены?
Сначала
мы рассмотрим интегралы с корнями, для
решения которых последовательно
используется замена
переменной и интегрирование
по частям.
То есть, в одном примере комбинируются
сразу два приёма. И даже больше.
Затем мы познакомимся с интересным и оригинальным методом сведения интеграла к самому себе. Данным способом решается не так уж мало интегралов.
Третьим номером программы пойдут интегралы от дробей, которые пролетели мимо кассы в предыдущих статьях.
В-четвертых, будут разобраны дополнительные интегралы от тригонометрических функций. В частности, существуют методы, которые позволяют избежать трудоемкой универсальной тригонометрической подстановки.
И в заключении рассмотрим интеграл от корня, под которым находится дробь, в числителе и знаменателе дроби – линейные функции.
Конечно, название урока не совсем точно, будут и не сказать, что сильно сложные интегралы. Тем не менее, крепких орешков предостаточно. Запланировано довольно много примеров, поэтому поехали.
Пример 1
Найти неопределенный интеграл
Подынтегральная
функция представляет собой арктангенс,
под которым находится кубический корень.
Первая же мысль, которая приходит в
голову – избавиться бы от этого корня.
После такой замены у нас получится вполне симпатичная вещь:
Осталось выяснить, во что превратится . Навешиваем дифференциалы на обе части нашей замены:
И само собой раскрываем дифференциалы:
На чистовике решение кратко записывается примерно так:
Проведем замену:
В результате замены получен знакомый тип интеграла, который интегрируется по частям:
(1) Выносим за скобки. К оставшемуся интегралу применяем прием, который рассмотрен в первых примерах урока статьи Интегрирование некоторых дробей.
(2) В подынтегральной функции почленно делим числитель на знаменатель.
(3) Используем свойство линейности неопределенного интеграла. В последнем интеграле сразу подводим функцию под знак дифференциала.
(4)
Берём оставшиеся интегралы.
Обратите
внимание, что в логарифме можно
использовать скобки, а не модуль, так
как
.
(5) Проводим обратную замену, выразив из прямой замены «тэ»:
Студенты-мазохисты могут продифференцировать ответ и получить исходную подынтегральную функцию, как только что это сделал я. Нет-нет, я-то в правильном смысле выполнил проверку =)
Как видите, в ходе решения пришлось использовать даже больше двух приемов решения, таким образом, для расправы с подобными интегралами нужны уверенные навыки интегрирования и не самый маленький опыт.
На практике, конечно же, чаще встречается квадратный корень, вот три примера для самостоятельного решения:
Пример 2
Найти неопределенный интеграл
Пример 3
Найти неопределенный интеграл
Пример 4
Найти неопределенный интеграл
Данные
примеры однотипны, поэтому полное
решение в конце статьи будет только для
Примера 2, в Примерах 3-4 – одни ответы.
Какую замену применять в начале решений,
думаю, очевидно.
Почему я подобрал
однотипные примеры? Часто встречаются
в своем амплуа. Чаще, пожалуй, только
что-нибудь вроде
.
Но не всегда, когда под арктангенсом, синусом, косинусом, экспонентой и др. функциями находится корень из линейной функции, приходится применять сразу несколько методов. В ряде случаев удается «легко отделаться», то есть сразу после замены получается простой интеграл, который элементарно берётся. Самым легким из предложенных выше заданий является Пример 4, в нём после замены получается относительно несложный интеграл.
Презентация к уроку «Вычисление неопределенных интегралов»
Г ПОУ СПО « Печорский промышленно-экономический техникум»
Вычисление неопределенных интегралов
Преподаватель: Тарасенко Е. В.
Эталон ответа к тесту:
Вариант 1
- 1. Функцию, восстанавливаемую по заданной ее производной или дифференциалу, называют первообразной .
- 2. Множество первообразных называют неопределенным интегралом и обозначают
- 3. Теорема. Если F(x) является первообразной функции на некотором промежутке, то множество всех первообразных этой функции имеет вид F(x)+C .
- 4. Чтобы проверить, правильно ли найден неопределенный интеграл, необходимо продифференцировать полученную функцию, если при этом получается подынтегральная функция , то интеграл найден верно.
- 5. Интегрирование — операция обратная дифференцированию .
Эталон ответа к тесту:
Вариант 2
Свойства неопределенного интеграла
№
Производная неопределенного интеграла равна подынтегральной функции
Постоянный множитель подынтегрального выражения можно вынести за знак интеграла
1
Формула
2
Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций
3
Дифференциал неопределенного интеграла равен подынтегральному выражению
4
Неопределенный интеграл от дифференциала (производной) некоторой функции равен сумме этой функции и произвольной постоянной С
5
Эталон ответа к тесту:
Вариант № 3
Методы интегрирования
Метод непосредственного интегрирования
Метод подстановки (замены переменной)
Метод интегрирования по частям
Метод основан на применении основных свойств неопределенных интегралов и сведении их к табличным.
При этом подынтегральную функцию предварительно преобразуют.
Метод основан на применении формулы
Метод основан на применении формулы интегрирования по частям:
При этом новой переменной заменяют такую часть функции, при дифференцировании которой получается оставшаяся часть подынтегрального выражения.
Примеры интегрирования методом подстановки
Примеры непосредственного интегрирования
Пример №1
Пример №4
Пример №5
Пример №2
Пример №6
Пример №3
Пример №7
Пример №2
Пример №2
Пример №1
Постоянный множитель можно вынести за знак интеграла
Интеграл суммы выражений равен сумме интегралов этих выражений
Пример №3
Пример №4
Определяем, к какому табличному интегралу приводится данный интеграл
Определяем, какую часть подынтегральной функции нужно заменить и записываем замену
Находим дифференциалы обеих частей, выражаем старый дифференциал через новый
Производим замену в интеграле и
вычисляем его, используя таблицу
Производим обратную замену, то есть
возвращаемся к старой переменной
Пример №5
Пример №6
Пример №7
Алгоритм вычисления интегралов методом непосредственного интегрирования
- Преобразуем подынтегральную функцию и представляем интеграл в виде суммы или разности интегралов.
2. Выносим постоянные множители за знаки интегралов.
3. Сводим полученные интегралы к табличным интегралам.
4. Вычисляем и записываем ответ.
Алгоритм вычисления интегралов методом замены переменной
- Определяем, к какому табличному интегралу приводится данный интеграл.
2. Определяем, какую часть подынтегральной функции нужно заменить и записываем замену.
3. Вычисляем дифференциал новой переменной, выражаем старый дифференциал через новый.
- Производим замену и вычисляем полученный интеграл с помощью таблицы интегралов.
5. Возвращаемся к старой переменной и записываем ответ.
Найти неопределенный интеграл
Проверить решение
Проверить решение
Следует отметить, что для функции вида f(kx+b) можно применять упрощенную формулу
Применение интегралов к решению профессионально-направленных задач
Задача: В результате значительной потери крови содержание железа в крови уменьшилось на 210 мг.
Решение:
Постоянную С определяем, используя начальные условия:
Интеграл вычисляем методом замены переменной:
Закон восстановления недостатка железа имеет вид:
Объяснение урока: Неопределенные интегралы: правило степени
В этом объяснении мы научимся находить неопределенные интегралы полиномы и общие степенные функции с использованием степенное правило интеграции.
Напомним, что первообразная производная, также известная как обратная производная или примитивная, функции 𝑓 есть другая функция 𝐹, производная равна исходной функции 𝑓.
Определение: первообразная функции
Для любой функции 𝑓, определенной на подмножестве
𝑈⊆ℝ и дифференцируемая функция
𝐹∶𝑈→ℝ, если у нас есть
𝐹′(𝑥)=𝑓(𝑥),
то мы говорим, что 𝐹(𝑥) является первообразной
𝑓(𝑥).
Первообразная функции эквивалентна неопределенному интегралу, которые мы определяем следующим образом.
Определение: неопределенный интеграл
Неопределенный интеграл от 𝑓(𝑥) относительно 𝑥 можно записать в терминах первообразной 𝐹(𝑥) как 𝑓(𝑥)𝑥=𝐹(𝑥)+,dC где C также называют константой интегрирования.
Первообразные 𝑓 всегда существуют, когда 𝑓 непрерывно, и существует бесконечно много первообразных для 𝑓, получается добавлением произвольной константы C к 𝐹. Эта константа, также известная как константа интегрирования, равна очень важно, так как оно дает семейство первообразных, параметризованных C. Другими словами, 𝐹(𝑥)+C есть самая общая функция, имеющая производную 𝑓(𝑥), для всех C∈ℝ. Например, производная от 𝑥 определяется выражением (𝑥)′=1.
Таким образом, мы можем сказать, что 𝑥 является первообразной 1, но
𝑥+C — наиболее общая первообразная 1, что означает
что 𝑥+1, 𝑥+7,
𝑥+√2, 𝑥+𝜋 и т.
д.
все также первообразные 1. Это то, что мы называем неопределенным интегралом и
выражается как
1𝑥=𝑥+.dC
Точно так же производная от 𝑥 равна 𝑥=2𝑥, откуда следует, что неопределенный интеграл от 2𝑥 равен 2𝑥𝑥=𝑥+.dC
Напомним, что производная удовлетворяет свойству (𝑎𝐹(𝑥))′=𝑎𝐹′(𝑥).
Это означает, что мы всегда можем вынести постоянное кратное за пределы производной. Таким образом, 𝑎𝐹(𝑥) является первообразной 𝑎𝑓(𝑥) или 𝑎𝐹(𝑥)+C является общей первообразной 𝑎𝑓(𝑥) для всех C∈ℝ, что совпадает с неопределенным интеграл. Другими словами, если производная умножается на константу, первообразная также умножается на ту же константу и наоборот. Этот следует следующее свойство неопределенных интегралов: (𝑎𝑓(𝑥))𝑥=𝑎𝑓(𝑥)𝑥.dd
Используя неопределенный интеграл от 2𝑥, как написано выше, мы
можно убрать множитель 2, используя это свойство, и разделить обе части
выражение на 2, чтобы получить
2𝑥𝑥=2𝑥𝑥=𝑥+𝑥𝑥=𝑥2+,ddCdC
где мы отмечаем, что мы оставили константу C неизменной с тех пор, как это
является произвольным, а C2 — просто еще одна константа.
В
этого объяснителя нас будет особенно интересовать определение неопределенного
интегралы вида
𝑥𝑥d
используя степенное правило интегрирования. Мы можем определить это правило непосредственно из
степенное правило дифференцирования. Предполагать
𝐹(𝑥)=𝑥, для
𝑝∈ℝ. Производную этой функции можно найти
по степенному правилу дифференцирования следующим образом:
(𝑥)=𝑝𝑥.
Будет полезно переписать это как 1𝑝(𝑥)=1𝑝𝑝𝑥𝑥𝑝=𝑥, где мы разделили на константу 𝑝≠0, как константу кратное функции не влияет ни на производную, ни на первообразную. Но что если мы хотим работать в обратном направлении? (т. е. учитывая 𝑥, мы хотим определить первообразную). Это означает, что мы хотим найти наиболее общее функция, которая дифференцирует, чтобы дать 𝑥.
Мы уже показали, что производная 𝑥𝑝 это 𝑥, для 𝑝≠0. Если мы допустим 𝑝=𝑛+1, то мы имеем 𝑥𝑛+1=𝑥,𝑛≠−1.
Таким образом, 𝑥𝑛+1 является первообразной
𝑥 при условии 𝑛≠−1.
Мы можем выразить
это с точки зрения неопределенного интеграла в следующем определении.
Правило: Степенное правило для интегрирования
Степенное правило для интегрирования позволяет определить неопределенный интеграл от 𝑥 при условии 𝑛≠−1 следующим образом: 𝑥𝑥=𝑥𝑛+1+.dC
Например, используя это степенное правило, мы можем определить неопределенный интеграл от 𝑥 следующим образом: 𝑥𝑥=𝑥2+1+=𝑥3+,dCC в чем можно убедиться непосредственно, продифференцировав правую часть, чтобы получить подынтегральная функция 𝑥.
В первом примере определим неопределенный интеграл функции с участием положительной целочисленной степени 𝑥 с использованием мощности правило вместе со свойством, которое позволяет нам брать константу, кратную вне интеграл.
Пример 1. Степенное правило интегрирования
Определить −𝑥𝑥d.
Ответ
В этом примере мы определим неопределенный интеграл положительного
целочисленная степень 𝑥, в частности функция
−𝑥.
Для определения интеграла воспользуемся следующим свойство неопределенных интегралов: (𝑎𝑓(𝑥))𝑥=𝑎𝑓(𝑥)𝑥.dd
Мы также будем использовать правило степени: 𝑥𝑥=𝑥𝑛+1+,𝑛≠−1.dC
Мы можем использовать это свойство, чтобы убрать множитель (−1) вне интеграла и определить неопределенный интеграл от 𝑥 по степенному правилу: −𝑥𝑥=−𝑥𝑥=−𝑥9+1+=−𝑥10+.ddCC
Теперь рассмотрим пример, в котором будем определять неопределенный интеграл функции, включающей отрицательную целую степень 𝑥 используя степенное правило вместе со свойством, которое позволяет нам взять постоянное кратное вне интеграла.
Пример 2. Поиск интегрирования функции с помощью степенного правила интегрирования с отрицательным показателем степени
Определить −27𝑥𝑥d.
Ответ
В этом примере мы определим неопределенный интеграл отрицательного
целочисленная степень 𝑥, в частности функция
−27𝑥.
Для определения интеграла воспользуемся следующим свойство неопределенных интегралов: (𝑎𝑓(𝑥))𝑥=𝑎𝑓(𝑥)𝑥.dd
Мы также будем использовать правило мощности: 𝑥𝑥=𝑥𝑛+1+,𝑛≠−1.dC
Мы можем использовать это свойство, чтобы взять коэффициент −27 вне интеграла и определить неопределенный интеграл от 𝑥 по степенному правилу: −27𝑥𝑥=−27𝑥𝑥=−27𝑥−9+1+=−27𝑥−8+=2𝑥56+=128𝑥+.
Этот результат верен для всех 𝑥≠0, так как мы требуем подынтегральная функция и интеграл должны быть непрерывными и корректно определенными.
Мы можем использовать правило степеней для определения неопределенного интеграла любой степени
𝑥, а не только целые числа, при условии, что мощность не равна
−1. В следующем примере мы определим неопределенный
интеграл от функции, включающей положительную дробную степень
𝑥, переписав радикал в терминах степени
𝑥 и используя степенное правило вместе со свойством, позволяющим
нам взять постоянное кратное вне интеграла.
Пример 3. Нахождение общей первообразной функции с использованием степенного правила Интеграция с дробными показателями
Определить 7√𝑥𝑥d.
Ответ
В этом примере мы определим неопределенный интеграл положительного дробная степень 𝑥, в частности функция 7√𝑥.
Сначала перепишем подынтегральную функцию, заметив, что √𝑥=𝑥, как 7√𝑥=7𝑥=7𝑥.
Для определения интеграла воспользуемся следующим свойство неопределенных интегралов: (𝑎𝑓(𝑥))𝑥=𝑎𝑓(𝑥)𝑥.dd
Мы также будем использовать правило мощности: 𝑥𝑥=𝑥𝑛+1+,𝑛≠−1.dC
Мы можем использовать это свойство, чтобы взять множитель 7 вне интеграла и определить неопределенный интеграл от 𝑥, используя правило власти. После этого мы можем переписать окончательный ответ обратно в условия квадратного корня: 7√𝑥𝑥=7𝑥𝑥=7𝑥𝑥=7𝑥+1+=7𝑥+=72𝑥5+=145𝑥+=145√𝑥+.
Этот результат верен для всех 𝑥≥0, так как мы требуем
подынтегральная функция и интеграл должны быть непрерывными и корректно определенными, а квадрат
корень определен только для неотрицательных чисел.
Теперь рассмотрим пример, где мы определим неопределенный интеграл функции, включающей отрицательную дробную степень 𝑥 переписав радикал в терминах степени 𝑥 и с помощью степенного правила вместе со свойством, позволяющим взять константу кратное вне интеграла.
Пример 4. Нахождение интегрирования функции с помощью степенного правила с корнями
Определить 6√𝑥𝑥d.
Ответ
В этом примере мы определим неопределенный интеграл отрицательного дробная степень 𝑥, в частности функция 6√𝑥.
Сначала перепишем подынтегральную функцию, заметив, что √𝑥=𝑥, как 6√𝑥=6𝑥=6𝑥.
Для определения интеграла воспользуемся следующим свойство неопределенных интегралов: (𝑎𝑓(𝑥))𝑥=𝑎𝑓(𝑥)𝑥.dd
Мы также будем использовать правило степени: 𝑥𝑥=𝑥𝑛+1+,𝑛≠−1.dC
Мы можем использовать это свойство, чтобы вынести множитель 6 за пределы интеграла
и определить неопределенный интеграл от
𝑥 по силовому правилу:
6√𝑥𝑥=6𝑥𝑥=6𝑥𝑥=6𝑥+1+=6𝑥+=68𝑥7+=487𝑥+.
dddCCCC
Этот результат верен для всех 𝑥>0, так как мы требуем подынтегральная функция и интеграл должны быть непрерывными и корректно определенными, а 8-й корень определен только для неотрицательных чисел.
Напомним, что производная является линейной операцией, так как удовлетворяет условию (𝐹(𝑥)+𝐺(𝑥))′=𝐹′(𝑥)+𝐺′(𝑥).
Отсюда следует аналогичное правило для неопределенных интегралов: (𝑓(𝑥)+𝑔(𝑥))𝑥=𝑓(𝑥)𝑥+𝑔(𝑥)𝑥.ddd
Следовательно, чтобы определить неопределенный интеграл от суммы функций, мы просто находим неопределенный интеграл каждой части в отдельности и складываем результаты вместе, не забывая +C в конце. Обычно мы получаем несколько константы для каждой части из процесса интегрирования, но мы можем комбинировать их в одну константу. Мы также можем объединить это свойство с тем, что позволяет брать константы вне интеграла.
Свойство: свойство линейности интегрирования
Для любых непрерывных функций 𝑓 и 𝑔 определены
на подмножестве 𝑈⊆ℝ имеем линейность
имущество
(𝑎𝑓(𝑥)+𝑏𝑔(𝑥))𝑥=𝑎𝑓(𝑥)𝑥+𝑏𝑔(𝑥)𝑥, ддд
для 𝑎,𝑏∈ℝ.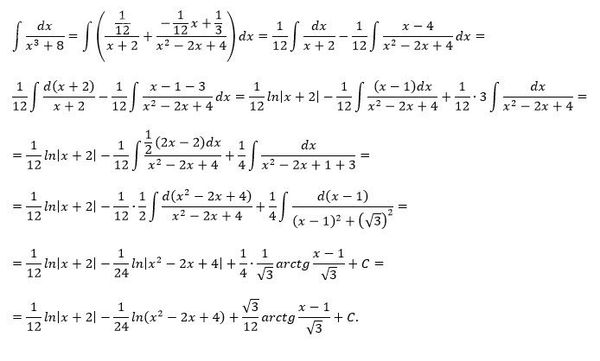
Степенное правило интегрирования вместе с этим свойством линейности позволяют нам определить неопределенный интеграл, включающий суммы различных степеней 𝑥 включая полиномиальные, обратные и радикальные функции. Например, мы можем определить неопределенный интеграл линейной функции 6𝑥+8 следующим образом: (6𝑥+8)𝑥=6𝑥𝑥+8𝑥=6𝑥𝑥+81𝑥=6𝑥1+1+8𝑥+=6𝑥2+8𝑥+=3𝑥+8𝑥+.dddddCCC
В следующем примере мы определим неопределенный интеграл многочлена функция, использующая свойства линейности и правило степени для интегралов.
Пример 5. Нахождение интегрирования полиномиальной функции с помощью степенного правила
Определить 25𝑥−65𝑥+36𝑥d.
Ответ
В этом примере мы определим неопределенный интеграл многочлена функция 25𝑥−65𝑥+36.
Для определения интеграла воспользуемся следующим свойства неопределенных интегралов: (𝑓(𝑥)+𝑔(𝑥))𝑥=𝑓(𝑥)𝑥+𝑔(𝑥)𝑥,(𝑎𝑓(𝑥))𝑥=𝑎𝑓(𝑥)𝑥.ddddd
Мы также будем использовать правило мощности:
𝑥𝑥=𝑥𝑛+1+,𝑛≠−1.
dC
Используя первое свойство, данный интеграл можно разбить на три части. Затем мы можем использовать второе свойство, чтобы взять соответствующие факторы за пределы интеграл и определить неопределенный интеграл от различных членов используя правило мощности: 25𝑥 — 65𝑥+36𝑥 = 25𝑥𝑥+ -65𝑥𝑥+36𝑥 = 25𝑥𝑥 — 65𝑥𝑥+361𝑥 = 25𝑥2+1 — 65𝑥1+1+36𝑥0+ 1=25𝑥3−65𝑥2+36𝑥=253𝑥−652𝑥+36𝑥+.ddddddddC
Обратите внимание, что мы получили бы постоянную интегрирования для каждой части из процесс интегрирования, но мы можем объединить их в одну константу, C.
Теперь рассмотрим пример, где мы определим неопределенный интеграл полиномиальной функции путем распределения двух скобок с помощью свойства линейности и степенное правило для интегралов.
Пример 6. Нахождение интегрирования многочлена, включающего умножение двух скобок и применение правила мощности
Определить (𝑥+4)𝑥−4𝑥+16𝑥d.
Ответ
В этом примере мы определим неопределенный интеграл от полиномиальная функция (𝑥+4)𝑥−4𝑥+16.
Сначала упростим подынтегральную функцию, расставив скобки: (𝑥+4)𝑥−4𝑥+16=𝑥−4𝑥+16𝑥+4𝑥−16𝑥+64=𝑥+64.
Для определения интеграла воспользуемся следующим свойства неопределенных интегралов: (𝑓(𝑥)+𝑔(𝑥))𝑥=𝑓(𝑥)𝑥+𝑔(𝑥)𝑥,(𝑎𝑓(𝑥))𝑥=𝑎𝑓(𝑥)𝑥.ddddd
Мы также будем использовать правило мощности: 𝑥𝑥=𝑥𝑛+1+,𝑛≠−1.dC
Используя первое свойство, данный интеграл можно разбить на две части. Затем мы можем использовать второе свойство, чтобы взять соответствующие факторы за пределы интеграл и определить неопределенный интеграл от различных членов используя правило мощности: (𝑥+4)𝑥−4𝑥+16𝑥=𝑥+64𝑥=𝑥𝑥+64𝑥=𝑥𝑥+641𝑥=𩝑3+1+64𝑥+=𝑥4+64. ddddddCC
Обратите внимание, что мы получили бы постоянную интегрирования для каждой части из
процесс интегрирования, но мы можем объединить их в одну константу,
С.
В следующем примере мы определим неопределенный интеграл рационального функция с использованием факторизации, свойств линейности и степени правило для интегралов.
Пример 7. Нахождение интегрирования рациональной функции с помощью факторизации разности двух квадратов
Определить 𝑥−225𝑥−15𝑥d.
Ответ
В этом примере мы определим неопределенный интеграл рационального функция 𝑥−225𝑥−15.
Сначала упростим подынтегральную функцию, заметив, что числитель равен разность двух квадратов и может быть записана как 𝑥−225=(𝑥+15)(𝑥−15); таким образом, подынтегральная функция становится 𝑥−225𝑥−15=(𝑥+15)(𝑥−15)(𝑥−15)=𝑥+15, за 𝑥≠15. Для определения интеграла будем использовать следующие свойства неопределенных интегралов: (𝑓(𝑥)+𝑔(𝑥))𝑥=𝑓(𝑥)𝑥+𝑔(𝑥)𝑥,(𝑎𝑓(𝑥))𝑥=𝑎𝑓(𝑥)𝑥.dddd
Мы также используйте правило мощности: 𝑥𝑥=𝑥𝑛+1+,𝑛≠−1.dC
Используя первое свойство, мы можем разделить данный интеграл на две части.
Затем мы можем использовать второе свойство, чтобы взять соответствующие факторы за пределы
интеграл и определить неопределенный интеграл от различных членов
используя правило мощности:
𝑥 -225𝑥 — 15𝑥 = (𝑥+15) 𝑥 = 𝑥𝑥+15𝑥 = 𝑥𝑥+151𝑥 = 𝑥1+1+15𝑥+= 𝑥2+15𝑥+.ddddddcc
Примечание мы получили бы постоянную интегрирования для каждой части из процесс интегрирования, но мы можем объединить их в одну константу, С.
Этот результат верен для всех 𝑥≠15, так как мы требуем подынтегральная функция и интеграл должны быть непрерывными и корректно определенными.
Теперь рассмотрим пример, где мы определяем неопределенный интеграл рациональной функции с отрицательными степенями 𝑥 с помощью свойства линейности и степенное правило для интегралов.
Пример 8. Поиск интегрирования функции с помощью степенного правила интегрирования с отрицательным показателем степени
Определить −8+89𝑥+75𝑥𝑥d.
Ответ
В этом примере мы определим неопределенный интеграл рационального функция −8+89𝑥+75𝑥.
Сначала перепишем подынтегральную функцию в виде степени 𝑥: −8+89𝑥+75𝑥=−8+89𝑥+75𝑥.
Для определения интеграла воспользуемся следующим свойства неопределенных интегралов: (𝑓(𝑥)+𝑔(𝑥))𝑥=𝑓(𝑥)𝑥+𝑔(𝑥)𝑥,(𝑎𝑓(𝑥))𝑥=𝑎𝑓(𝑥)𝑥.dddd
Мы также используйте правило мощности: 𝑥𝑥=𝑥𝑛+1+,𝑛≠−1.dC
Используя первое свойство, мы можем разбить данный интеграл на три части. Затем мы можем использовать второе свойство, чтобы взять соответствующие факторы за пределы интеграл и определить неопределенный интеграл от различных членов используя правило мощности: −8+89𝑥+75𝑥𝑥=−8+89𝑥+75𝑥𝑥=−8𝑥+89𝑥𝑥+75𝑥𝑥=−81+89便𝑥𝑥𝑥+75 𝑥−2+1+75𝑥−6+1+=−8𝑥+89𝑥−1+75𝑥−5+=−8𝑥−89𝑥−725𝑥+𝐶. ddddddddCC
Обратите внимание, что мы получили бы постоянную интегрирования для каждой части из
процесс интегрирования, но мы можем объединить их в одну константу,
С.
Этот результат верен для всех 𝑥≠0, так как мы требуем подынтегральная функция и интеграл должны быть непрерывными и корректно определенными.
В следующем примере мы определим неопределенный интеграл функции с корнями и отрицательными показателями, используя свойства линейности и правило степени для интегралов.
Пример 9. Поиск интегрирования функции с помощью степенного правила интегрирования с корнями и отрицательными показателями
Определить −√𝑥+8+9𝑥𝑥д.
Ответ
В этом примере мы определим неопределенный интеграл от функция −√𝑥+8+9𝑥.
Давайте сначала перепишем подынтегральную функцию как степени 𝑥 используя √𝑥=𝑥: −√𝑥+8+9𝑥=8−𝑥+9𝑥, для 𝑥>0. Для определения интеграла будем использовать следующие свойства неопределенных интегралов: (𝑓(𝑥)+𝑔(𝑥))𝑥=𝑓(𝑥)𝑥+𝑔(𝑥)𝑥,(𝑎𝑓(𝑥))𝑥=𝑎𝑓(𝑥)𝑥.dddd
Мы также используйте правило мощности:
𝑥𝑥=𝑥𝑛+1+,𝑛≠−1.
dC
Используя первое свойство, мы можем разбить данный интеграл на три части. Затем мы можем использовать второе свойство, чтобы взять соответствующие факторы за пределы интеграл и определить неопределенный интеграл от различных членов используя правило мощности: −√𝑥+8+9𝑥𝑥=8−𝑥+9𝑥𝑥=8𝑥+−𝑥𝑥+9𝑥𝑥=81𝑥−𝑥𝑥+9𝑥=81𝑥−𝑥𝑥+9𝑥−1 +9𝑥−2+1+=8𝑥−𝑥+9𝑥−1+=8𝑥−23𝑥−9𝑥+=8𝑥−23√𝑥−9𝑥+. ddddddddCCCC
Обратите внимание, что мы получили бы постоянную интегрирования для каждой части из процесс интегрирования, но мы можем объединить их в одну константу, С.
Этот результат верен для всех 𝑥>0, так как мы требуем подынтегральная функция и интеграл должны быть непрерывными и корректно определенными, а квадратный корень равен определяется только для неотрицательных чисел.
В последнем примере мы определим неопределенный интеграл функции
с участием дробных показателей с помощью факторизации, свойств
линейность и правило степени для интегралов.
Пример 10. Нахождение интегрирования функции с помощью факторизации
Определить 36𝑥−49√𝑥(6𝑥+7)𝑥d.
Ответ
В этом примере мы определим неопределенный интеграл от функция 36𝑥−49√𝑥(6𝑥+7).
Заметим, что числитель под интегралом можно записать как разность два квадрата, как 36𝑥−49=(6𝑥)−7=(6𝑥+7)(6𝑥−7). Используя это, мы можем упростить подынтегрально и перепишем оставшиеся члены как степени 𝑥, используя √𝑥=𝑥: 36𝑥−49√𝑥(6𝑥+7)=(6𝑥+7)(6𝑥−7)√𝑥(6𝑥+7)=6𝑥−7√𝑥=(6𝑥−7)𝑥=6𝑥−7𝑥, для 𝑥>0. Для определения интеграла будем использовать следующие свойства неопределенных интегралов: (𝑓(𝑥)+𝑔(𝑥))𝑥=𝑓(𝑥)𝑥+𝑔(𝑥)𝑥,(𝑎𝑓(𝑥))𝑥=𝑎𝑓(𝑥)𝑥.ddddd
Мы также будем использовать правило мощности: 𝑥𝑥=𝑥𝑛+1+,𝑛≠−1.dC
Используя первое свойство, данный интеграл можно разбить на две части. Затем мы можем использовать второе свойство, чтобы взять соответствующие факторы за пределы
интеграл и определить неопределенный интеграл от различных членов
используя правило мощности:
36𝑥−49√𝑥(6𝑥+7)𝑥=6𝑥−7𝑥𝑥=6𝑥𝑥+−7𝑥𝑥=6𝑥𝑥−7𝑥𝑥=6𝑥𝑥=6𝑥𝑥+1 =6𝑥+7𝑥+=68𝑥15+78𝑥7+=16𝑥5−8𝑥+.
ddddddCCCC
Обратите внимание, что мы получили бы постоянную интегрирования для каждой части из процесс интегрирования, но мы можем объединить их в одну константу, C.
Этот результат верен для всех 𝑥>0, так как мы требуем подынтегральная функция и интеграл должны быть непрерывными и корректно определенными, а 8-й корень определен только для неотрицательных чисел.
Давайте закончим рассмотрением ключевых моментов, которые мы рассмотрели в этом объяснитель.
Ключевые моменты
Для определения неопределенных интегралов функций, включающих различные степени 𝑥, включая полиномиальные, обратные и радикальные функции, мы используем следующие:
- Свойство линейности интегралов: (𝑎𝑓(𝑥)+𝑏𝑔(𝑥))𝑥=𝑎𝑓(𝑥)𝑥+𝑏𝑔(𝑥)𝑥, ддд для 𝑎,𝑏∈ℝ.
- Правило мощности для интеграции: 𝑥𝑥=𝑥𝑛+1+,𝑛≠−1.dC
Неопределенный интеграл: значение и расчет
Вы замечали, как члены одной семьи похожи друг на друга? То же верно и для семейств функций! Функции одной формы очень похожи друг на друга, как члены одной семьи.
Неопределенные интегралы здесь ничем не отличаются. Они представляют собой семейство первообразных функции, поэтому они очень похожи друг на друга.
В этой статье вы узнаете, что такое неопределенный интеграл, его определение, формулу и свойства. Вы также увидите примеры вычисления неопределенных интегралов.
Определение неопределенного интеграла
Как вы знаете из статьи о первообразных, процесс нахождения первообразной функции называется интегрированием . Помните, что если вам дана функция \(f(x)\), то первообразной \(f(x)\) является любая функция \(F(x)\), которая удовлетворяет условию:
\[ F'(x) = f(x). \]
Итак, при чем тут неопределенный интеграл?
Ну, он используется для ссылки на все семейство первообразных функции, тогда как первообразная — это лишь одна из бесконечных возможностей.
Имея это в виду, вы определяете неопределенный интеграл как:
Если \( F(x) \) является первообразной функции \( f(x) \), то семейство первообразных f(x) \) называется неопределенным интегралом .
Обозначение для этого неопределенного интеграла:
\[ \int f(x) ~\mathrm{d}x = F(x) + C, \]
, где \(C\) — любая константа.
Обратите внимание, что:
\( \int \) называется интегральным символом ,
\( f(x) \) называется ) называется переменной интегрирования ,
\( \mathrm{d}x \) называется дифференциалом ,
\( F(x) \) является первообразной , а
\( C \) называется константой интегрирования (или константой интегрирования).
Обратите внимание, что термины «неопределенный интеграл» и «первообразная» иногда используются взаимозаменяемо, а в некоторых текстах первообразная также называется «примитивной функцией».
Учитывая терминологию, представленную вам в этом определении, действие по нахождению первообразных функции, \( f \), обычно упоминается как:
- интегрирование \( \mathbf{f} \) o r
- нахождение интеграла от \( \mathbf{f} \). {2}+C \), где \(C \) — любая константа (при условии, что это действительное число).
Формула неопределенного интеграла
Как и в случае с первообразными вообще, неопределенные интегралы не имеют единственной формулы для их решения. Существует множество правил и свойств, которые вы научитесь использовать для решения неопределенных интегралов — они основаны на уже изученных вами правилах дифференцирования. Причина этого обсуждается в статье об основной теореме исчисления.
При этом суть нахождения неопределенного интеграла функции состоит в обратном выполнении уже известных вам правил дифференцирования.
Свойства неопределенного интеграла
Поскольку неопределенный интеграл — это просто семейство первообразных, их свойства одинаковы. Но, повторяю, неопределенный интеграл линейный; т. е. вы можете интегрировать «почленно» для сумм, разностей и постоянных множителей. Эти свойства линейности резюмируются приведенными ниже правилами.
Свойство суммы/разности :
\[ \int (f(x) \pm g(x)) ~\mathrm{d}x = \int f(x) ~\mathrm{d}x \pm \int г(х) ~\mathrm{d}х \]
Постоянное кратное свойство :
\[ \int kf(x) ~\mathrm{d}x = k \int f(x) ~\mathrm{d}x \]
Доказательства свойств Неопределенный интеграл
- В общем, если \(F\) является первообразной \(f\) и \(G\) является первообразной \(g\), то\[ \frac{d}{ dx} (F(x) \pm G(x)) = F'(x) \pm G'(x) = f(x) \pm g(x). \]Это означает, что \( F(x) \pm G(x) \) является первообразной \( f(x) \pm g(x) \), так что \[ \int (f(x) \pm g(x)) ~\mathrm{d}x = F(x) \pm G(x) + C. \]
- Теперь попробуйте найти первообразную \(kf(x)\), где \(k\) — любая константа. Поскольку вы знаете, что \[ \frac{d}{dx} (kf(x)) = k \frac{d}{dx}F(x) = kf'(x) \]для любой константы \( k \) , можно заключить, что \[ \int kf(x) ~\mathrm{d}x = kF(x) + C. \]
Правила нахождения неопределенных интегралов
По большей части правила нахождения неопределенного интеграла интеграл функции являются обратными (или обратными) правилам нахождения производных.
Ниже приведен список правил для общих неопределенных интегралов.
T Правило константы Если вы рассматриваете функцию \( F(x) = 3 \) и записываете ее производную как \( f(x) \), это означает, что \( f(x) = \frac{dF}{dx} \). Вы уже знаете, что можете найти производную этой функции, применяя константное правило для производных: \( \frac{d}{dx}(k) = 0 \).
Теперь предположим, что вы хотите обратить этот процесс вспять, и спросите себя: какая функция (функции) могла бы иметь производную \(f(x) = 0 \)? Очевидно, \( F(x) = 3 \) — один ответ. Вы говорите, что \(F(x) = 3\) является первообразной \(f(x) = 0\).Однако существуют и другие функции, производная которых равна \( f(x) = 0 \), включая, помимо прочего, \( F(x) = 5 \), \( F(x) = -4 \ ) и \( F(x) = 200 \). Это потому, что когда вы берете производную, константа исчезает.
Следовательно, если вам дана первообразная \(f(x)\), все остальные можно найти, добавив другую константу. Другими словами, если \(F(x)\) является первообразной \(f(x)\), то \(F(x) + C\) также является первообразной \(f(x)\) для любой константы \( C \). Эта группа или семейство первообразных представлена неопределенным интегралом. 9{x}}{\ln a} + C, ~\ a \neq 1\end{align} \]
Правило синусов
\[ \begin{align}\text{Производное правило: } &\frac{d}{dx}(\sin(x)) = \cos(x) \\\text{Неопределенное интегральное правило: } &\int \cos(x) ~\mathrm{d}x = \sin (x) + C\end{align} \]
Правило косинуса
\[ \begin{align}\text{Производное правило: } &\frac{d}{dx}(\cos( x)) = -\sin(x) \\\text{Неопределенное интегральное правило: } &\int \sin(x) ~\mathrm{d}x = -\cos(x) + C\end{align} \ ] 9{2}(x) ~\mathrm{d}x = \tan(x) + C\end{align} \]
Правило косеканса
\[ \begin{align}\text{Производная Правило: } &\frac{d}{dx}(\csc(x)) = -\csc(x)\cot(x) \\\text{Неопределенное интегральное правило: } &\int \csc(x)\ cot(x) ~\mathrm{d}x = -\csc(x) + C\end{align} \]
Секущее правило
\[ \begin{align}\text{Производное правило : } &\frac{d}{dx}(\sec(x)) = \sec(x)\tan(x) \\\text{Неопределенное интегральное правило: } &\int \sec(x)\tan( х) ~\mathrm{d}x = \sec(x) + C\end{align} \] 9{rd} \) правило из списка выше:
\[ \int \frac{1}{x} ~\mathrm{d}x = \ln|x| + C \Rightarrow \int \frac{\mathrm{d}x}{x} = \ln|x| + C \]
Неопределенные интегралы: ошибки, которых следует избегать
Вы заметили, что в приведенном выше списке нет правил произведения, частного или цепных правил для интегралов?
Что это значит?
Это означает, что, как и в случае с производными, правила, применимые к сложению и вычитанию, не применяются в той же мере к умножению и делению.
Другими словами, так же, как и с производными:- Интеграл произведения (или частного) двух функций не равен произведению (или частному) интеграла функций .\[ \begin{align}\int f(x) \cdot g (x) ~\mathrm{d}x &\neq \int f(x) ~\mathrm{d}x \cdot \int g(x) ~\mathrm{d}x \\\int \frac{f( x)}{g(x)} ~\mathrm{d}x &\neq \frac{\int f(x) ~\mathrm{d}x}{\int g(x) ~\mathrm{d}x }\end{align} \]
Вместо:
правила произведения и частного для производных приводят к интегрированию по частям, и
цепное правило для производных приводит к интегрированию путем замены.
Хотя интегрирование по частям выводится непосредственно из правила произведения для производных, оно применяется как к произведению, так и к частному интегралов. Это связано с тем, что для любых двух функций \(f\) и \(g\) можно записать частное двух функций в виде произведения:
\[ \frac{f}{g} = f \cdot \ дробь{1}{г}. \]
Другими словами, вы можете думать о частном правиле для деривативов как о замаскированном правиле произведения; то же верно и для интегрирования по частям.
9{2}} ~\mathrm{d}x \]и используйте правило произведения для выполнения интегрирования по частям.
Вычисление неопределенного интеграла
Когда дело доходит до вычисления неопределенного интеграла, точные шаги будут зависеть от самого интеграла. Однако есть несколько очень простых шагов, которые вам нужно будет запомнить для вычисления всех неопределенных интегралов.
Основные шаги для вычисления неопределенного интеграла
Определите, какие свойства и правила применяются.
Если вам нужно использовать более одного свойства или правила, определите порядок их использования.
Используйте выбранные вами правила.
Добавьте константу интегрирования.
Проверьте свой результат, доказав, что \( F'(x) = f(x) \).
Примеры неопределенных интегралов
В следующих примерах оцените каждый из неопределенных интегралов. Этот первый пример относительно прост.
Оценка 9{2} + 2x + 5 \right) ~\mathrm{d}x \]
Ответ :
Определите, какие свойства и правила применяются.
Если вам нужно использовать более одного свойства или правила, определите порядок их использования.
Применение правила суммы/разности для интегралов.
Применение правила постоянного кратного для интегралов.
Применение правила степени для интегралов.
- 9{2}}{x} + \frac{4\sqrt[3]{x}}{x} \right) ~\mathrm{d}x. \]
Теперь вы можете вычислить интеграл почленно, используя правило суммы/разности и правило степени.
Если вам нужно использовать более одного свойства или правила, определите порядок их использования.
Применение правила суммы/разности.
Применение правила мощности.
Используйте выбранные вами правила.
- 9{2}} ~\checkmark\end{align} \]
Этот пример показывает, что упрощение тригонометрических функций под интегралом может значительно упростить задачу.
Вычислить
\[ \int \tan(x) \cos(x) ~\mathrm{d}x \]
Ответ :
Определите, какие свойства и правила применяются.
Если вам нужно использовать более одного свойства или правила, определите порядок их использования.
Используйте выбранные вами правила.
Добавьте константу интегрирования.
\[ \int \sin(x) ~\mathrm{d}x = -\cos(x) + C \]
Проверьте свой результат, доказав, что \( F'(x) = f(x ) \).\[ \begin{align}f(x) &= \tan(x) \cos(x) = \frac{\sin(x)}{\cancel{\cos(x)}} \cancel {\ cos (x)} = \ sin (x) \\ F (x) & = — \ cos (x) + C \\~ \\ F ‘(x) & = — (- \ sin (x)) \\&= \sin(x) ~\checkmark\end{align} \]
Неопределенный интеграл – ключевые выводы
- Если \( F(x) \) является первообразной функции \( f( x) \), то семейство первообразных \( f(x) \) называется неопределенный интеграл . Это записывается как: \[ \int f(x) ~\mathrm{d}x = F(x) + C, \]где \(C\) — любая константа.
- В общем, если \(F\) является первообразной \(f\) и \(G\) является первообразной \(g\), то\[ \frac{d}{ dx} (F(x) \pm G(x)) = F'(x) \pm G'(x) = f(x) \pm g(x).
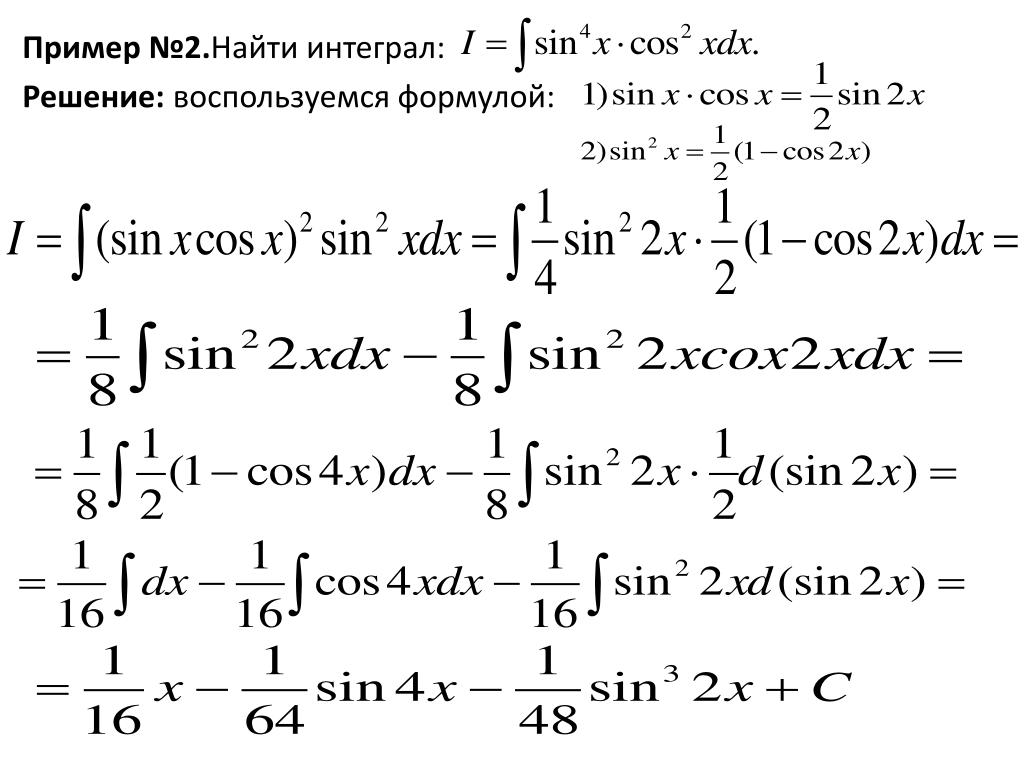{2}+C \), где \(C \) — любая константа (при условии, что это действительное число).
\]Это означает, что \( F(x) \pm G(x) \) является первообразной \( f(x) \pm g(x) \), так что \[ \int (f(x) \pm g(x)) ~\mathrm{d}x = F(x) \pm G(x) + C. \]
Теперь предположим, что вы хотите обратить этот процесс вспять, и спросите себя: какая функция (функции) могла бы иметь производную \(f(x) = 0 \)? Очевидно, \( F(x) = 3 \) — один ответ. Вы говорите, что \(F(x) = 3\) является первообразной \(f(x) = 0\).
Другими словами, так же, как и с производными:
9{2}} ~\mathrm{d}x \]
