Примеры решения производных с ответами
Алгоритм решения производных
Теорема
Производная функции есть предел отношения приращения этой функции к приращению её аргумента при стремлении последнего к нулю, при условии существования данного предела.
Для вычисления производных вам потребуется таблица производных. Кроме того, существуют формулы для нахождения сложных производных.
Процесс нахождения производный называется дифференцированием.
– производная суммы (разницы).
– производная произведения.
– производная частного.
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Примеры решений производных
Пример 1
Задача
Найти производную функции
Решение
Заданная функция является сложной и её производная равна произведению производной от косинуса на производную от его аргумента:
Ответ
Пример 2
Задание
Найти производную функции
Решение
Обозначим , где . 3·cos(x)+6·x·cos(x)-6·cos(x)+6·sin(x).
3·cos(x)+6·x·cos(x)-6·cos(x)+6·sin(x).
Пример 5
Задача
Найти производную функции .
Решение
В этом примере квадратный корень извлекается из суммы . Поэтому сначала вычисляем производную от квадратного корня, а затем умножаем ее на производную от подкоренного выражения:
.
Ответ
.
Пример 6
Задача
Найти производную функции .
Решение
Применяя правила дифференцирования дробей, получаем:
.
Применяя правила дифференцирования котангенса, получаем:
.
Учитывая, что и , после упрощения получим:
.
Ответ
.
Пример 7
Задача
Найти производную функции .
Решение
Применяя правила дифференцирования дробей, получаем:
.
Ответ
.
Пример 8
Задача
Найти производную функции .
Решение
Применяя правила дифференцирования дробей, получаем:
.
Ответ
.
Пример 9
Задача
Найти производную функции .
Решение
Дифференцирование можно произвести в два этапа: вначале продифференцировать степень функции арксинус, а затем произвести дифференцирование самого арксинуса, перемножив результаты:
.
Ответ
.
Пример 10
Задача
Найти производную функции .
Решение
По правилам дифференцирования показательной функции с основанием , производная этой функции равна произведению самой функции на производную функции, являющейся показателем степени:
.
Ответ
.
Средняя оценка 2. 4 / 5. Количество оценок: 94
4 / 5. Количество оценок: 94
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
108536
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
Примеры решения производных
admin Оставить комментарий
- Примеры решения производных
- Производная суммы функций
- Производная произведения функций
- Производная отношения функций
- Производная сложной функций
- Производная функции заданной параметрически
Пример. Производная суммы функций.
Дано: сумма функций .
Найти:
Вычислить производную суммы функций
Решение:
Исходя из того, что производная алгебраической суммы (разности) функций, имеющих производную, равна такой же сумме (разности) производных этих функций: используя формулы производных (ссылка), вычислим производную, заданной в условии задачи суммы функций:
Ответ: производная суммы функций равна
Пример. Производная произведения функций.
Производная произведения функций.
Дано: произведение функций .
Найти:
Вычислить производную произведения функций
Решение:
Исходя из того, что производная двух функций, имеющих производную, вычисляется по формуле: найдем производную, заданного в условии задачи произведения функций:
Ответ: производная произведения функций равна
Пример. Производная отношения функций.
Дано: отношение функций .
Найти:
Вычислить производную отношения функций
Решение:
Исходя из того, что производная отношения двух функций, имеющих производную, вычисляется по формуле: определим производную, заданного в условии задачи отношения функций:
Ответ: производная отношения функций равна
Пример. Производная сложной функций.
Дано: сложная функция .
Найти:
Вычислить производную сложной функции
Решение:
Исходя из того, что функция имеет производную в точке а функция имеет производную в точке причем сложная функция будет иметь производную в точке и в нашем случае получаем следующее а Тогда а значит
Ответ: производная сложной функции равна
Пример. Производная функции заданной параметрически.
Дано: функция заданная параметрически .
Найти:
Вычислить производную функции заданной параметрически.
Решение:
Исходя из того, что производная функции, заданной параметрически, то есть в виде соотношения где изменяется в пределах некоторого множества, определяется по формуле вычислим производную, заданной в задаче функции:
Производная параметрически заданной функции будет тоже функция, заданная параметрически:
Ответ: производная параметрически заданной функции равна
Примеры и решения – mathsathome.
 com
comВидео-урок «Как пользоваться цепным правилом»
Цепное правило с тригонометрическими функциями
Что такое цепное правило?
Цепное правило используется для вычисления производной сложной функции. Формула цепного правила гласит, что dy / dx = dy / du × du / dx 3 9. Другими словами, дифференцируйте внешнюю функцию, сохраняя внутреннюю функцию неизменной, а затем умножайте ее на производную внутренней функции.
Цепное правило: Обозначение Лейбница
Цепное правило: Обозначение функций
Цепное правило используется, когда функция находится внутри другой функции.
Цепное правило определяется как, где u является функцией 𝑥 ( u = g(x) ), а y является функцией u ( y = f(u) ).
В качестве альтернативы цепное правило можно записать в функциональном обозначении как F'(𝑥) = f'(g(𝑥)).g'(𝑥), где F(𝑥) = f(g(𝑥)). g(𝑥) — внутренняя функция, а f(𝑥) — внешняя функция.
Другими словами, цепное правило требует найти производную внешней функции, сохраняя внутреннюю функцию неизменной, а затем умножив ее на производную внутренней функции.
Для использования цепного правила необходимы следующие правила:
- Функция должна быть составной функцией двух или более функций
- Такие функции сами должны быть дифференцируемыми
Как сделать цепное правило
выполнить цепное правило:
Например, дифференцировайте (4𝑥 – 3)
5 с помощью цепного правилаВ этом примере мы будем использовать цепное правило шаг за шагом. Ниже мы будем использовать метод формулы цепного правила.
Мы определяем 4𝑥 – 3 как внутреннюю функцию, а ( ) 5 как внешнюю функцию.
Шаг 1. Дифференцируйте внешнюю функцию, оставив внутреннюю функцию неизменной
Внешняя функция — это ( ) 5 . Мы дифференцируем это так же, как 𝑥 5 .
𝑥 5 дифференцируется в 5𝑥 4 , поэтому мы пишем ( ) 5 , дифференцированное как 5( ) 4 .
Мы сохраняем внутреннюю функцию 4𝑥-3 прежней, поэтому пишем 5(4𝑥 – 3) 4 .
Однако, поскольку у нас в скобках 4𝑥 – 3, а не только 𝑥, мы должны также включить шаг 2.
Шаг 2. Умножьте это на производную от внутренней функции
Из шага 1 у нас уже есть 5(4𝑥 – 3) 4 и теперь мы должны умножить это на производную от внутренней функции.
Внутренняя функция — это функция, заключенная в скобки. Это 4𝑥 – 3.
. Продифференцируем 4𝑥 – 3, чтобы получить 4. Таким образом, мы должны умножить результат 5(4𝑥 – 3) 4 на 4.
. Мы придем к ответу f'(𝑥) = 20(4𝑥 – 3) 4 .
Теперь мы будем использовать формулу цепного правила, чтобы дифференцировать эту функцию. Ответ будет таким же.
Формула цепного правила утверждает, что F'(𝑥) = f'(g(𝑥).g'(𝑥), где g(𝑥) — внутренняя функция, а f(𝑥) — внешняя функция.
Следовательно для F(𝑥) = (4𝑥 – 3) 5 , g(𝑥) = 4𝑥 – 3 и f(𝑥) = 𝑥 5 . f'(g(𝑥)) означает подстановку g(𝑥) вместо 𝑥 в f'(𝑥).
Следовательно, f'(g(𝑥)) = 5(4𝑥 – 3) 4 .
g'(𝑥) = 4.
Следовательно, F'(𝑥) = f'(g(𝑥).g'(𝑥) становится F'(𝑥) = 5(4𝑥 – 3) 4 × 4
Это упрощает до F'(𝑥) = 20(4𝑥 – 3) 4 .
Цепное правило с тригонометрией
Цепное правило используется для дифференцирования тригонометрических функций, содержащих другую функцию. сохраняя внутреннюю функцию неизменной, а затем умножая ее на производную от внутренней функции.0023
сохраняя внутреннюю функцию неизменной, а затем умножая ее на производную от внутренней функции.0023
Здесь могут быть полезны следующие правила дифференцирования тригонометрических функций от sin(𝑥), cos(𝑥) и tan(𝑥):
Например, дифференцировать cos(2𝑥) с помощью цепного правила ) можно записать как внутреннюю функцию 2𝑥 и внешнюю функцию cos().
Шаг 1. Дифференцируем внешнюю функцию, сохраняя внутреннюю функцию такой же ).
Шаг 2. Умножьте это на производную внутренней функции
Внутренняя функция равна 2𝑥, а ее производная равна 2.
Мы умножаем -sin(2𝑥) на 2, чтобы получить f'(x) = -2sin (2𝑥).
Цепное правило можно применять к тригонометрическим функциям, возведенным в степень.
Например, продифференцируйте sin
4 (2𝑥), используя цепное правилоШаг 1. Сначала запишите sin 4 (2𝑥) как [sin(2𝑥 9.0) 1 4 90
Шаг 2. Уменьшите степень и вычтите единицу из степени, сохранив тригонометрическую функцию той же.
Мы опускаем 4 перед скобками, степень становится равной 3, и мы сохраняем sin(2𝑥) внутри скобок, что дает нам 4[ sin(2𝑥) ] 3 .
Шаг 3. Умножить на производную sin(2𝑥). Здесь мы используем цепное правило, поэтому sin(𝑥) — это внешняя функция, которая дифференцируется в cos(𝑥).
Мы оставляем 2𝑥 внутри, чтобы получить cos(2𝑥). Затем мы умножаем это на производную от 2𝑥, которая равна 2.
sin(2𝑥) дифференцировано равно 2cos(2𝑥).
Итак, мы умножаем 4[sin(2𝑥)] 3 на 2cos(2𝑥).
f'(𝑥) = 8sin 3 (2𝑥)cos(2𝑥)
Цепное правило с бревнами
Цепное правило гласит, что для y = ln(u), dy / d𝑥 = 1 / u × du / . Другими словами, дифференцируйте внутреннюю функцию, а затем разделите ее на внутреннюю функцию. Например, если y = ln(𝑥 2 + 3 𝑥 ), dy / d𝑥 = (2𝑥 + 3)/( 𝑥 2 90 15 + 3 9001).
Другими словами, дифференцируйте внутреннюю функцию, а затем разделите ее на внутреннюю функцию. Например, если y = ln(𝑥 2 + 3 𝑥 ), dy / d𝑥 = (2𝑥 + 3)/( 𝑥 2 90 15 + 3 9001).
Производная от y = ln(u) равна 1 / u × дю / d𝑥 .
u — это функция внутри функции ln. Для y = ln(𝑥 2 + 3𝑥), u = 𝑥 2 + 3𝑥.
Следовательно, du / d𝑥 = 2𝑥 + 3.
Производная dy / d𝑥 =.
Мы можем записать это как .
Цепное правило позволяет различать функции журнала. Производная y = ln ( f(𝑥) ) может быть записана как:
или .
Чтобы дифференцировать log любого основания, если y = log a f(𝑥), то .
Например, продифференцируем y = log 5 (2𝑥 + 1):
Здесь f(𝑥) = 2𝑥 + 1 и, следовательно, f'(𝑥) = 2.
Подставляя их в формулу, получаем :
Правило цепи с экспоненциальными функциями
Производная y = E 𝑥 — DY / D𝑥 = E 𝑥 и, следовательно f ( 𝑥 ) is dy / d𝑥 = f'(𝑥 3
). e f ( 𝑥 ) . Просто продифференцируйте мощность e и умножьте ее на исходную функцию.
Например, дифференцировать e 5𝑥+3 .
В этом примере f(𝑥) = 5𝑥 + 3 и, следовательно, f'(𝑥) = 5.
Чтобы найти производную от y = e 5𝑥+3 , просто умножаем на 5.
Получаем dy / d𝑥 = 5 e 5𝑥+3 .
Применение цепного правила с тремя функциями
Цепное правило можно применять к композиции из трех функций. Если y(𝑥) = h(g(f(x))), то y'(𝑥) = f'( 𝑥 ) . g'(f( 𝑥 )) . h'(g(f( 𝑥))). Однако проще применить цепное правило дважды, чтобы различать три функции.
g'(f( 𝑥 )) . h'(g(f( 𝑥))). Однако проще применить цепное правило дважды, чтобы различать три функции.
Например, дифференцировать f(𝑥) = грех 2 (5𝑥).
Здесь у нас есть композиция из 3-х функций.
- Самая внутренняя функция — 5𝑥.
- Действие на 5𝑥 есть функция sin
- Наконец, функция sin возводится в степень 2
Мы записываем sin 2 (5𝑥) как [sin(5𝑥)] 2 .
Мы дифференцируем, используя цепное правило, так что мы дифференцируем внешнюю функцию, оставляя внутреннюю функцию неизменной, а затем умножаем на производную внутренней функции.
Дифференцируя внешнюю квадратичную функцию, сохраняя внутреннюю функцию неизменной, мы получаем 2[sin(5𝑥)]. Сила 2 уменьшилась, мы вычли 1 из мощности и оставили грех (5𝑥) внутри прежним.
Теперь нам нужно умножить это значение на производную внутренней функции sin(5𝑥). Это требует повторного использования цепного правила.
Мы дифференцируем внешнюю функцию sin, чтобы получить cos, и сохраняем внутреннюю функцию 5𝑥 такой же. Получаем cos(5𝑥). Нам нужно умножить это на производную внутренней функции 5𝑥. Мы находим, что производная от sin(5𝑥) равна 5cos(5𝑥).
Теперь мы умножаем предыдущий результат 2[ sin(5𝑥) ] на 5cos(5𝑥), чтобы получить окончательную производную 10sin(5𝑥)cos(5𝑥).
Примеры правил цепи с решениями
Вот несколько примеров использования правила цепи для дифференциации различных функций:
| Функция | Расчет | . ) 3 | 3 × (5𝑥 + 1) 2 × 5 | f'(𝑥) = 15(5𝑥 + 1) 2 |
| F (𝑥) = SIN (5𝑥) | COS (5𝑥) × 5 | F ‘(𝑥) = 5COS (5𝑥) | ||
| F (𝑥 𝑥) = COS) = COS) = COS (𝑥) = COS) = COS) = COS) = COS) = COS) = COS) = COS) = COS) = COS (5𝑥) | ||||
| F (𝑥 5𝑥) = COS (5𝑥) | ||||
| F (𝑥 5𝑥). | -SIN (10𝑥) × 10 | F ‘(𝑥) = -10sin (10𝑥) | ||
| F (𝑥) = -3TAN (2𝑥) | -3SEC 2 (2𝑥) × 2 | -3SEC 2 (2𝑥) × 2.|||
| f(𝑥) = 10e 4𝑥 | 10e 4𝑥 × 4 | f'(𝑥) = 40e 4𝑥 | ||
| F (𝑥) = LN (𝑥 3 ) | 1 /(𝑥 3 ) × 3𝑥 2 = (3𝑥 2 ) /(𝑥 3 ) | ) /(𝑥 3 ) ) /(𝑥 3 ) ) /(𝑥 3 ) ) /( 3 ) 𝑥) = 3 / 𝑥
Когда использовать цепное правило
Цепное правило используется для дифференцирования любой сложной функции вида y = f(g(𝑥)). Это функция, которая имеет внутреннюю функцию с внешней функцией, примененной к ней. Например, у = (3 𝑥 + 2) 5 состоит из функций g( 𝑥) = 3 𝑥 + 2 и f( 𝑥 ) = 𝑥 5 .
Вот несколько примеров того, когда и когда не следует использовать цепное правило:
| Пример | Должен ли я использовать цепное правило? | Почему? |
| y = (3𝑥+2) 5 | Да | Внутренняя функция 3𝑥+2, а внешняя функция 𝑥 5 . |
| y = 𝑥 5 | Нет | Есть только одна функция 𝑥 5 . Его можно дифференцировать напрямую. |
| y = (𝑥+3) sin(𝑥) | Нет | Это произведение двух функций. Используйте правило произведения. |
| y = sin(2𝑥+1) | Да | Внутренняя функция 2𝑥+1, а внешняя функция sin(𝑥) |
| y = 1 (9001+5) +5) | Нет | Это дробь с функцией числителя и знаменателя. Используйте правило отношения. |
| y = ln(𝑥 4 -𝑥) | Да | Внутренняя функция 𝑥 4 -𝑥. Внешняя функция — это ln(𝑥). |
| y = e 2𝑥 | Да | Внутренняя функция равна 2𝑥, а внешняя функция равна e 𝑥 . |
Доказательство цепного правила
Чтобы доказать цепное правило, рассмотрим dy / dx как предел  Это может быть написано в виде ограничений Δ Y / ΔU × Δ U / Δ . Оценивая эти пределы как 𝑥 и u, стремящиеся к нулю, мы получаем цепное правило как dy / d 𝑥 = dy / DU × DY / D 𝑥 339..
Это может быть написано в виде ограничений Δ Y / ΔU × Δ U / Δ . Оценивая эти пределы как 𝑥 и u, стремящиеся к нулю, мы получаем цепное правило как dy / d 𝑥 = dy / DU × DY / D 𝑥 339..
Чтобы доказать цепное правило:
- Запишите dy / d𝑥 как предел Δy / 9001 как Δ07s стремящийся к нулю
- Запишите предел Δy / Δ𝑥 как Δy / Δu × Δu / Δ𝑥 .
 Δu — это просто число, так что это можно сделать.
Δu — это просто число, так что это можно сделать. - Разделите предел на 2 предела: Δy / Δu и Δu / Δ𝑥 .
- Поскольку Δ𝑥 стремится к 0, то же самое происходит и с Δu.
- Оцените оба предела, чтобы получить dy / d𝑥 = dy / du × du / d𝑥 .
Решения дифференциальных уравнений: примеры
Было бы неплохо иметь решение всех ваших задач? Или, по крайней мере, ваши математические проблемы? Как насчет задач с дифференциальными уравнениями? К сожалению, вы даже не можете найти решения всех видов дифференциальных уравнений. Однако здесь можно найти как минимум несколько видов решения дифференциальных уравнений .
Проверка решений дифференциальных уравнений
Начнем с того, как проверить, является ли функция решением дифференциального уравнения. Предположим, вам дано дифференциальное уравнение
\[ y’ = f(x,y),\]
, и кто-то говорит вам, что функция \(y(x)\) является решением уравнения. Как вы видите, правы ли они?
Как вы видите, правы ли они?
Чтобы убедиться, что \(y(x)\) является решением дифференциального уравнения \(y’=f(x,y)\), вычислить \(y'(x) — f(x, y(x ))\) и посмотрите, получите ли вы \(0\). Если да, то \(y(x)\) является решением. 92 — 4x — 4 }\right) \\ &= 0.\end{align}\]
Следовательно, \(y(x)\) является решением дифференциального уравнения.
Что делать, если вы хотите получить представление о том, как выглядит решение, не решая дифференциального уравнения?
Графики решений дифференциальных уравнений
Есть два основных метода, которые можно использовать, чтобы получить представление о том, как выглядит решение дифференциального уравнения и как оно ведет себя, не решая его.
Если вам нужна численная аппроксимация, вы можете использовать метод Эйлера.
Поля направлений, также называемые полями наклона, используют тот факт, что производная представляет собой наклон, для построения «поля» уклонов, которое позволяет предсказать поведение решений.

В статьях по этим темам будет много примеров построения графиков решений. Если вы действительно можете решить дифференциальное уравнение, вы можете построить график общего решения. Если назвать это «общим решением», это будет звучать как единственное решение, но на самом деле это семейство функций. Поведение решения зависит от того, где начинается решение (также называемое начальным условием). Дополнительные сведения по этой теме см. в разделе Общие решения дифференциальных уравнений.
Решения линейных дифференциальных уравнений первого порядка
Линейное дифференциальное уравнение первого порядка всегда можно записать в виде
\[ \frac{\mathrm{d}y}{\mathrm{d}x} + P( x)y=Q(x),\]
, где \(P(x)\) и \(Q(x)\) — функции.
Частный случай этого — когда \(P(x)\) и \(Q(x)\) являются константами, поэтому линейное уравнение первого порядка можно записать как
\[ \frac{\mathrm{d }y}{\mathrm{d}x}+ay=b.\]
Затем
\[y=Ae^{-ax}+\frac{b}{a},\]
— решение линейного дифференциального уравнения первого порядка с постоянными коэффициентами.
При решении линейных дифференциальных уравнений первого порядка используется интегрирующий коэффициент, и в статьях «Линейные дифференциальные уравнения» и «Неоднородные линейные уравнения» есть множество примеров.
Экспоненциальные решения дифференциального уравнения
Решения линейных дифференциальных уравнений первого порядка с постоянными коэффициентами — это почти единственный класс дифференциальных уравнений, для которых гарантировано экспоненциальное решение. Однако это не означает, что другие дифференциальные уравнения не могут иметь в своих решениях экспоненциальные функции. Давайте посмотрим на пример. 92 — 6r + 8 = 0.\]
Это делит на \( (r-2)(r-4) = 0\), которое имеет решения \(r=2\) и \(r=4\) , который оказался в показателях решения! Такие вещи, как характеристические многочлены и линейные дифференциальные уравнения второго порядка, — это некоторые из вещей, о которых вы узнаете, если будете посещать занятия по дифференциальным уравнениям.
Равновесные решения дифференциальных уравнений
Некоторые дифференциальные уравнения имеют равновесное решение.
Равновесный раствор \(y(x)\) дифференциального уравнения первого порядка — это такое, которое удовлетворяет условию \(y'(x)\equiv 0\).
Другими словами, равновесное решение дифференциального уравнения первого порядка — это постоянное решение ! Равновесные решения иногда называют стационарными решениями .Одним из известных дифференциальных уравнений, имеющих не одно, а два равновесных решения, является логистическое уравнение,
\[P’ = r\left( 1- \frac{P}{k}\right)P.\]
92 + 12x } }.\]Итак, теперь у вас есть два равновесных решения и общее решение! Как узнать, какой из них правильный? Ну, технически они все верны. Они составляют набор функций, которые решают дифференциальное уравнение. Если бы вам были даны начальные значения, вы могли бы либо выбрать одно из равновесных решений, либо найти \(B\) в общем решении, чтобы получить конкретное решение.
Чтобы увидеть пример дифференциального уравнения, которое может иметь одно, ни одного или бесконечное множество решений в зависимости от начального значения, см.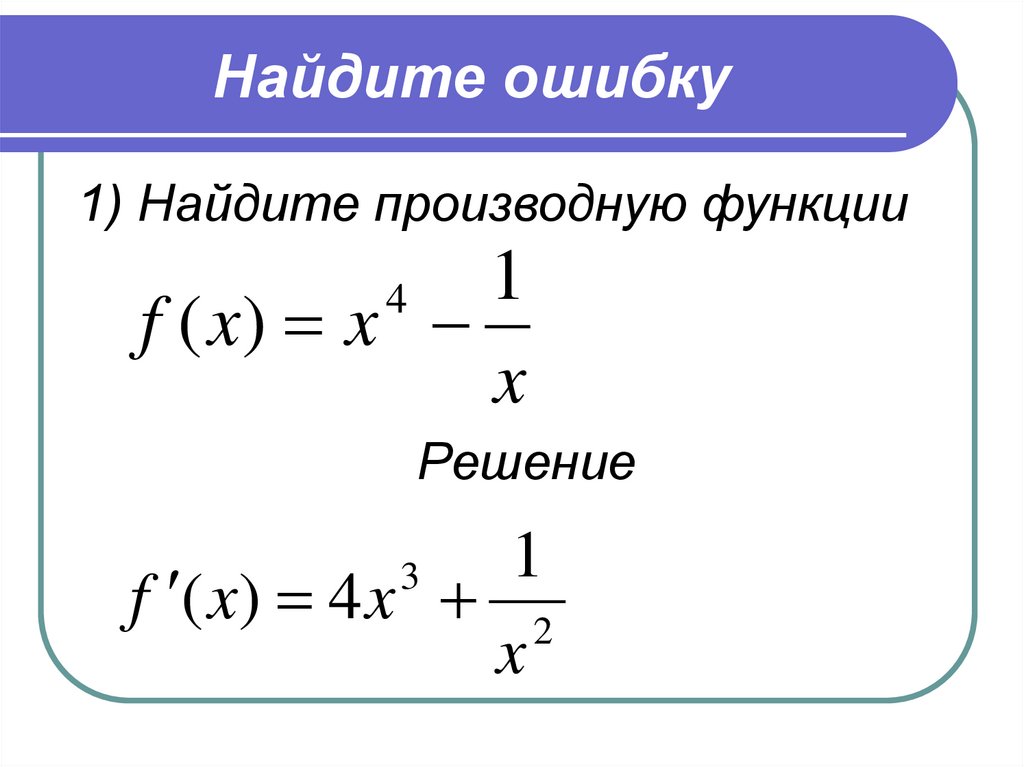
Решение
Во-первых, давайте определимся, что это за переменные. Конечно, одним из них будет время, а другим — температура, но вам нужно выяснить, какая из них является независимой переменной, а какая — зависимой. Поскольку температура пиццы зависит от времени, это означает, что время является независимой переменной, а температура — зависимой переменной. Задав каждому из них переменную, пусть
- \(t\) — время с момента выхода из духовки; и
- \(y(t)\) — температура с момента выхода из духовки.
Теперь нужно выяснить, какое уравнение моделирует эту ситуацию. Закон охлаждения Ньютона вам в помощь! Помните, что для охлаждения объекта (в данном случае ваша пицца охлаждается до комнатной температуры) скорость изменения температуры определяется как константа, умноженная на разницу между текущей температурой и комнатной температурой.
\[y'(t) = k(y(t) — 70),\]
где \(k\) — постоянная охлаждения.
Вам все еще нужно начальное значение, чтобы завершить это как дифференциальное уравнение.
Каково начальное значение? Это температура на выходе из духовки, поэтому \(y(0) = 375\). Итак, чтобы завершить дифференциальное уравнение как задачу с начальным значением,
\[\begin{align} &y'(t) = k(y(t) — 70) \\ &y(0)=375 \end{align}\ ]
где \(k\) — постоянная охлаждения. 9\circ\) перед едой. Как долго вам придется ждать?
Решение
В предыдущем примере вы видели, как составить это дифференциальное уравнение и найти равновесное решение, и вы обнаружили, что
\[\begin{align} &y'(t) = k(y( t) — 70) \\ &y(0)=375 \end{align}\]
где \(k\) — постоянная охлаждения. Давайте опираться на эту информацию.
Это хорошее разделимое уравнение, и запись его в разделимой форме даст вам
\[ \frac{1}{y-70}y’ = k.\]
Тогда интегрирование обеих частей по \(t\) дает
\[ \ln |y-70| = kt+C. \]
\]
Вы можете либо использовать информацию, приведенную в задаче, чтобы сначала найти \(k\) и \(C\), либо найти явное решение, а затем найти константы. В любом случае вы получите один и тот же ответ.
Если вы подставите начальное условие \(y(0) = 375\), вы получите
\[ \ln |375-70| = k\cdot 0 + C,\]
поэтому \( C = \ln 305\). 9\circ\), но вы его не использовали. Переводя это в переменные, \(y(5) = 350\). Подставив его вместе с \(C\) в уравнение, вы получите
\[ \ln |350-70| = 5k+\ln 305 .\]
Другими словами,
\[ \begin{align} 5k &= \ln |350-70| — \ln 305 \\ &= \ln 280 — \ln 305 \\ &= \ln \frac{280}{305}, \end{align}\]
, поэтому
\[k= \frac{1 }{5} \ln \frac{280}{305} .\]
Тогда, сложив все вместе, мы получим решение задачи с начальным значением: 9\круг\). Поэтому вместо того, чтобы искать явное решение, просто подключите температуру и определите время. Это означает
\[ \ln |300-70| = \frac{1}{5}\ln \frac{280}{305} t+\ln 305 \]
, поэтому
\[ \ln 230 — \ln 305 = \frac{1}{5}\ln \frac{280}{305} t \]
, что означает
\[ t = 5\frac{ \ln \frac{230}{305}}{ \ln \frac{280}{305} } \приблизительно 16.

 ‘(𝑥) = -6 sec 2 (2𝑥)
‘(𝑥) = -6 sec 2 (2𝑥) Δu — это просто число, так что это можно сделать.
Δu — это просто число, так что это можно сделать.