принцип, теорема и примеры решения задач
Задание. Решить СЛАУ методом Гаусса.
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент равнялся 1 (это мы делаем для упрощения вычислений):
Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей — три первых:
Все элементы третьей строки делим на два (или, что тоже самое, умножаем на ):
Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
От третьей строки отнимаем вторую, умноженную на 3:
Умножив третью строку на , получаем:
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент , для этого от второй строки отнимем третью:
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:
Полученной матрице соответствует система
или
Ответ.
метод Гаусса. Вычисление матрицы методом Гаусса: примеры
Линейная алгебра, которая преподается в вузах на разных специальностях, объединяет немало сложных тем. Одни из них связаны с матрицами, а также с решением систем линейных уравнений методами Гаусса и Гаусса – Жордана. Не всем студентам удается понять эти темы, алгоритмы решения разных задач. Давайте вместе разберемся в матрицах и методах Гаусса и Гаусса – Жордана.
Основные понятия
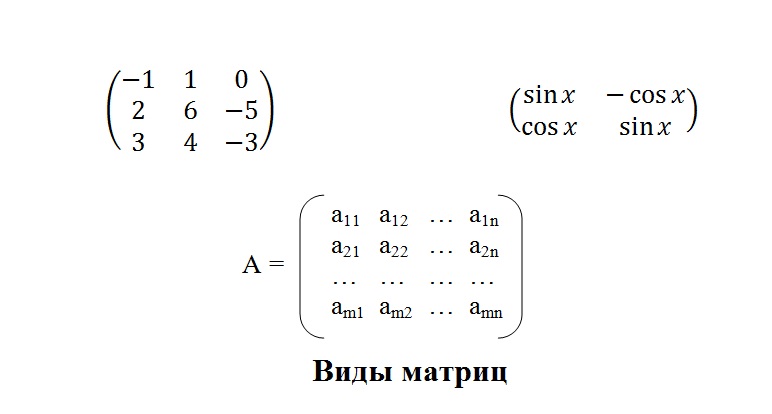
Под матрицей в линейной алгебре понимается прямоугольный массив элементов (таблица). Ниже представлены наборы элементов, заключенные в круглые скобки. Это и есть матрицы. Из приведенного примера видно, что элементами в прямоугольных массивах являются не только числа. Матрица может состоять из математических функций, алгебраических символов.
Для того чтобы разобраться с некоторыми понятиями, составим матрицу A из элементов aij. Индексы являются не просто буквами: i – это номер строки в таблице, а j – это номер столбца, в области пересечения которых располагается элемент aij. Итак, мы видим, что у нас получилась матрица из таких элементов, как a11, a21, a12, a22 и т. д. Буквой n мы обозначили число столбцов, а буквой m – число строк. Символ m × n обозначает размерность матрицы. Это то понятие, которое определяет число строк и столбцов в прямоугольном массиве элементов.
Необязательно в матрице должно быть несколько столбцов и строк. При размерности 1 × n массив элементов является однострочным, а при размерности m × 1 – одностолбцовым. При равенстве числа строчек и числа столбцов матрицу именуют квадратной. У каждой квадратной матрицы есть определитель (det A). Под этим термином понимается число, которое ставится в соответствие матрице A.
Еще несколько важных понятий, которые нужно запомнить для успешного решения матриц, – это главная и побочная диагонали. Под главной диагональю матрицы понимается та диагональ, которая идет вниз в правый угол таблицы из левого угла сверху. Побочная диагональ идет в правый угол вверх из левого угла снизу.
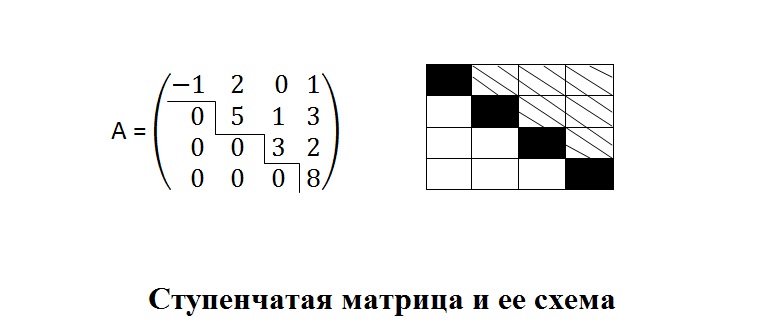
Ступенчатый вид матрицы
Взгляните на картинку, которая представлена ниже. На ней вы увидите матрицу и схему. Разберемся сначала с матрицей. В линейной алгебре матрица подобного вида называется ступенчатой. Ей присуще одно свойство: если aij является в i-й строке первым ненулевым элементом, то все другие элементы из матрицы, стоящие ниже и левее aij, являются нулевыми (т. е. все те элементы, которым можно дать буквенное обозначение akl, где k>i, а l<j).
Теперь рассмотрим схему. Она отражает ступенчатую форму матрицы. В схеме представлено 3 вида клеток. Каждый вид обозначает определенные элементы:
- пустые клетки – нулевые элементы матрицы;
- заштрихованные клетки – произвольные элементы, которые могут быть как нулевыми, так и ненулевыми;
- черные квадратики – ненулевые элементы, которые называются угловыми элементами, «ступеньками» (в представленной рядом матрице такими элементами являются цифры –1, 5, 3, 8).
При решении матриц иногда получается такой результат, когда «длина» ступеньки оказывается больше 1. Такое допускается. Важна лишь «высота» ступенек. В матрице ступенчатого вида этот параметр должен быть всегда равным единице.
Приведение матрицы к ступенчатой форме
Любая прямоугольная матрица может быть преобразована до ступенчатого вида. Делается это благодаря элементарным преобразованиям. Они включают в себя:
- перестановку строк местами;
- прибавление к одной строке другой строки, при необходимости умноженной на какое-либо число (можно также производить операцию вычитания).
Рассмотрим элементарные преобразования в решении конкретной задачи. На рисунке ниже представлена матрица A, которую требуется привести к ступенчатому виду.

Для того чтобы решить задачу, будем следовать алгоритму:
- Удобно выполнять преобразования над такой матрицей, у которой первый элемент в верхнем углу с левой стороны (т. е. «ведущий» элемент) равен 1 или –1. В нашем случае первый элемент в верхней строке равен 2, поэтому поменяем первую и вторую строчки местами.
- Выполним операции вычитания, затронув строки № 2, 3 и 4. Мы должны получить в первом столбце под «ведущим» элементом нули. Для достижения такого результата: из элементов строчки № 2 последовательно вычтем элементы строчки № 1, умноженные на 2; из элементов строчки № 3 последовательно вычтем элементы строчки № 1, умноженные на 4; из элементов строчки № 4 последовательно вычтем элементы строчки № 1.
- Далее будем работать с укороченной матрицей (без столбца № 1 и без строки № 1). Новый «ведущий» элемент, стоящий на пересечении второго столбца и второй строки, равен –1. Переставлять строки не требуется, поэтому переписываем без изменений первый столбец и первую и вторую строки. Выполним операции вычитания, чтобы во втором столбце под «ведущим» элементом получить нули: из элементов третьей строчки последовательно вычтем элементы второй строчки, умноженные на 3; из элементов четвертой строчки последовательно вычтем элементы второй строчки, умноженные на 2.
- Осталось изменить последнюю строку. Из ее элементов вычтем последовательно элементы третьей строки. Таким образом мы получили ступенчатую матрицу.

Приведение матриц к ступенчатой форме используется в решении систем линейных уравнений (СЛУ) методом Гаусса. Перед рассмотрением этого метода давайте разберемся в терминах, имеющих отношение к СЛУ.
Матрицы и системы линейных уравнений
Матрицы применяются в разных науках. С использованием таблиц из чисел можно, например, решать линейные уравнения, объединенные в систему, методом Гаусса. Для начала давайте познакомимся с несколькими терминами и их определениями, а также посмотрим, как из системы, объединяющей несколько линейных уравнений, составляется матрица.
СЛУ – несколько объединенных алгебраических уравнений, в которых присутствуют неизвестные в первой степени и отсутствуют члены, представляющие собой произведение неизвестных.
Решение СЛУ – найденные значения неизвестных, при подстановке которых уравнения в системе становятся тождествами.
Совместная СЛУ – такая система уравнений, у которой есть хотя бы одно решение.
Несовместная СЛУ – система уравнений, которая не имеет решений.
Как же составляется матрица на основе системы, объединяющей линейные уравнения? Существуют такие понятия, как основная и расширенная матрицы системы. Для того чтобы получить основную матрицу системы, необходимо вынести в таблицу все коэффициенты при неизвестных. Расширенная матрица получается путем присоединения к основной матрице столбца свободных членов (в него входят известные элементы, к которым в системе приравнивается каждое уравнение). Понять весь этот процесс можно, изучив картинку ниже.
Первое, что мы видим на картинке, – это систему, включающую в себя линейные уравнения. Ее элементы: aij – числовые коэффициенты, xj – неизвестные величины, bi – свободные члены (где i = 1, 2, …, m, а j = 1, 2, …, n). Второй элемент на картинке – основная матрица из коэффициентов. Из каждого уравнения коэффициенты записываются в строку. В итоге получается в матрице столько строк, сколько уравнений входит в систему. Количество столбцов равно наибольшему количеству коэффициентов в каком-либо уравнении. Третий элемент на картинке – расширенная матрица со столбцом свободных членов.

Общая информация о методе Гаусса
В линейной алгебре методом Гаусса называется классический способ решения СЛУ. Он носит имя Карла Фридриха Гаусса, жившего в XVIII–XIX вв. Это один из величайших математиков всех времен. Суть метода Гаусса заключается в выполнении элементарных преобразований над системой линейных алгебраических уравнений. С помощью преобразований СЛУ приводится к равносильной системе треугольной (ступенчатой) формы, из которой можно найти все переменные.
Стоит отметить, что Карл Фридрих Гаусс не является первооткрывателем классического способа решения системы линейных уравнений. Метод был придуман намного раньше. Первое его описание встречается в энциклопедии знаний древнекитайских математиков, носящей название «Математика в 9 книгах».
Пример решения СЛУ методом Гаусса
Рассмотрим на конкретном примере решение систем методом Гаусса. Будем работать с СЛУ, представленной на картинке.
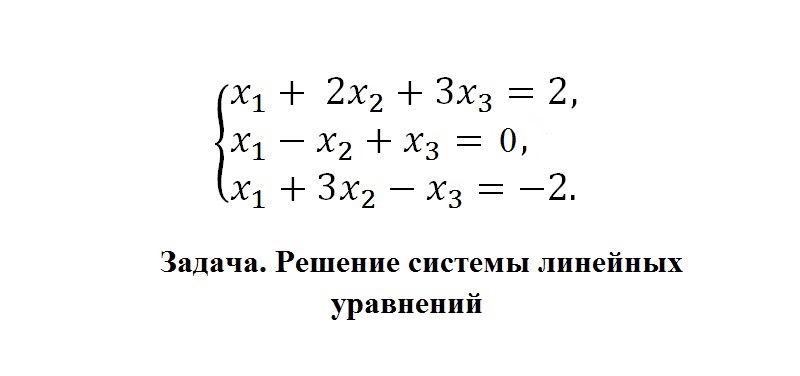
Алгоритм решения:
- Прямым ходом метода Гаусса приведем систему к ступенчатой форме, но для начала составим расширенную матрицу из числовых коэффициентов и свободных членов.
- Чтобы решить матрицу методом Гаусса (т. е. привести ее к ступенчатому виду), из элементов второй и третьей строчек последовательно вычтем элементы первой строчки. Получим в первом столбе под «ведущим» элементом нули. Далее поменяем вторую и третью строчки местами для удобства. К элементам последней строки прибавим последовательно элементы второй строчки, умноженные на 3.
- В результате вычисления матрицы методом Гаусса мы получили ступенчатый массив элементов. На его основе составим новую систему линейных уравнений. Обратным ходом метода Гаусса находим значения неизвестных членов. Из последнего линейного уравнения видно, что x3 равен 1. Подставляем это значение во вторую строчку системы. Получится уравнение x2 – 4 = –4. Отсюда следует, что x2 равен 0. Подставляем x2 и x3 в первое уравнение системы: x1 + 0 +3 = 2. Неизвестный член равен –1.
Ответ: используя матрицу, метод Гаусса, мы нашли значения неизвестных; x1 = –1, x2 = 0, x3 = 1.

Метод Гаусса – Жордана
В линейной алгебре есть еще такое понятие, как метод Гаусса – Жордана. Он считается модификацией метода Гаусса и применяется при нахождении обратной матрицы, вычислении неизвестных членов квадратных систем алгебраических линейных уравнений. Метод Гаусса – Жордана удобен тем, что он в один этап позволяет решить СЛУ (без применения прямого и обратного ходов).
Начнем с термина «обратная матрица». Допустим, у нас есть матрица A. Обратной для нее будет матрица A-1, при этом обязательно выполняется условие: A × A-1 = A-1 × A = E, т. е. произведение этих матриц равно единичной матрице (у единичной матрицы элементы главной диагонали являются единицами, а остальные элементы равны нулю).
Важный нюанс: в линейной алгебре есть теорема существования обратной матрицы. Достаточное и необходимое условие существования матрицы A-1 – невырожденность матрицы A. При невырожденности det A (определитель) не равен нулю.
Основные шаги, на которых основывается метод Гаусса – Жордана:
- Взгляните на первую строку конкретной матрицы. Метод Гаусса – Жордана можно начинать применять, если первое значение не равно нулю. Если же на первом месте стоит 0, то поменяйте строки местами так, чтобы первый элемент имел отличное от нуля значение (желательно, чтобы число было ближе к единице).
- Разделите все элементы первой строки на первое число. У вас получится строка, которая начинается с единицы.
- Из второй строки вычтите первую строку, умноженную на первый элемент второй строки, т. е. в итоге у вас получится строка, которая начинается с нуля. Аналогичные действия выполните с остальными строчками. Для того чтобы по диагонали получались единицы, делите каждую строку на ее первый ненулевой элемент.
- В итоге вы получите верхнюю треугольную матрицу методом Гаусса — Жордана. В ней главная диагональ представлена единицами. Нижний угол заполнен нулями, а верхний угол – разнообразными значениями.
- Из предпоследней строки вычтите последнюю строчку, умноженную на необходимый коэффициент. У вас должна получиться строка с нулями и единицей. Для остальных строк повторите аналогичное действие. После всех преобразований получится единичная матрица.
Пример нахождения обратной матрицы методом Гаусса – Жордана
Для вычисления обратной матрицы нужно записать расширенную матрицу A|E и выполнить необходимые преобразования. Рассмотрим простой пример. На рисунке ниже представлена матрица A.

Решение:
- Для начала найдем определитель матрицы методом Гаусса (det A). Если этот параметр не окажется равным нулю, то матрица будет считаться невырожденной. Это позволит нам сделать вывод о том, что у A точно есть A-1. Для вычисления определителя преобразуем матрицу до ступенчатой формы элементарными преобразованиями. Подсчитаем число K, равное числу перестановок строк. Строки мы меняли местами всего 1 раз. Вычислим определитель. Его значение будет равно произведению элементов главной диагонали, умноженному на (–1)K. Результат вычисления: det A = 2.
- Составим расширенную матрицу, добавив к исходной матрице единичную матрицу. Полученный массив элементов будем использовать для нахождения обратной матрицы методом Гаусса – Жордана.
- Первый элемент в первой строке равен единице. Нас это устраивает, т. к. не нужно переставлять строки и делить данную строку на какое-нибудь число. Начинаем работать со второй и третьей строками. Чтобы первый элемент во второй строке превратился в 0, отнимем от второй строки первую строчку, умноженную на 3. Из третьей строчки вычтем первую (умножения не требуется).
- В получившейся матрице второй элемент второй строчки равен –4, а второй элемент третьей строчки равен –1. Поменяем строки местами для удобства. Из третьей строчки вычтем вторую строчку, умноженную на 4. Вторую строчку разделим на –1, а третью – на 2. Получим верхнюю треугольную матрицу.
- Из второй строчки отнимем последнюю строчку, умноженную на 4, из первой строчки – последнюю строчку, умноженную на 5. Далее вычтем из первой строчки вторую строчку, умноженную на 2. С левой стороны мы получили единичную матрицу. Справа находится обратная матрица.

Пример решения СЛУ методом Гаусса – Жордана
На рисунке представлена система линейных уравнений. Требуется найти значения неизвестных переменных, используя матрицу, метод Гаусса – Жордана.

Решение:
- Составим расширенную матрицу. Для этого вынесем в таблицу коэффициенты и свободные члены.
- Решим матрицу методом Гаусса – Жордана. Из строки № 2 вычтем строку № 1. Из строки № 3 вычтем строку № 1, предварительно умноженную на 2.
- Поменяем местами строки № 2 и 3.
- От строки № 3 отнимем строку № 2, умноженную на 2. Разделим полученную третью строку на –1.
- От строки № 2 отнимем строку № 3.
- От строки № 1 отнимем строку № 2, умноженную на –1. Сбоку у нас получился столбик, состоящий из цифр 0, 1 и –1. Из этого делаем вывод, что x1 = 0, x2 = 1 и x3 = –1.

При желании можно проверить правильность решения, подставив вычисленные значения в уравнения:
- 0 – 1 = –1, первое тождество из системы является верным;
- 0 + 1 + (–1) = 0, второе тождество из системы является верным;
- 0 – 1 + (–1) = –2, третье тождество из системы является верным.
Вывод: используя метод Гаусса – Жордана, мы нашли правильное решение квадратной системы, объединяющей линейные алгебраические уравнения.
Онлайн-калькуляторы
Жизнь современной молодежи, обучающейся в вузах и изучающей линейную алгебру, значительно упростилась. Еще несколько лет назад находить решения систем методом Гаусса и Гаусса – Жордана приходилось самостоятельно. Одни студенты успешно справлялись с задачами, а другие путались в решении, делали ошибки, просили у однокурсников помощи. Сегодня можно при выполнении домашнего задания пользоваться онлайн-калькуляторами. Для решения систем линейных уравнений, поиска обратных матриц написаны программы, которые демонстрируют не только правильные ответы, но и показывают ход решения той или иной задачи.
В интернете есть немало ресурсов со встроенными онлайн-калькуляторами. Матрицы методом Гаусса, системы уравнений решаются этими программами за несколько секунд. Студентам требуется только указывать необходимые параметры (например, количество уравнений, количество переменных).
Решение матриц методом Гаусса, с примерами
Метод Гаусса используется для решения систем линейных уравнений и для нахождения обратной матрицы. Начнем с нахождения обратной матрицы.
Алгоритм нахождения обратной матрицы методом Гаусса
1. Пусть задана квадратная матрица
припишем к столбцам матрицы справа столбцы единичной матрицы того же порядка. Получим матрицу
2. С помощью элементарных преобразований строк приведем матрицу к матрице, в левой части которой будет стоять единичная матрица:
3. Полученная таким образом матрица, стоящая в правой части матрицы , и будет обратной матрицей к матрице
Алгоритм применения метода Гаусса для решения СЛУ
Пусть задана система линейных уравнений
Записывается матрица – расширенная матрица этой системы:
Над строками матрицы производятся элементарные преобразования: разрешается изменять порядок строк, умножать строки на любые отличные от нуля числа и прибавлять к любой строке матрицы любую другую её строку, умноженное на произвольное число. В результате таких элементарных преобразований основная матрица системы должна быть приведена к нижнему треугольному виду
Эта матрица эквивалентна системе линейных уравнений
Из этой системы последовательно снизу вверх выражаются все неизвестные переменные.
Метод Гаусса
Определение и описание метода Гаусса
Метод преобразований Гаусса (также известный как преобразование методом последовательного исключения неизвестных переменных из уравнения или матрицы) для решения систем линейных уравнений представляет собой классический методом решения системы алгебраических уравнений (СЛАУ). Также этот классический метод используют для решения таких задач как получение обратных матриц и определения ранговости матрицы.
Преобразование с помощью метода Гаусса заключается в совершении небольших (элементарных) последовательных изменениях системы линейных алгебраических уравнений, приводящих к исключению переменных из неё сверху вниз с образованием новой треугольной системы уравнений, являющейся равносильной исходной.
Определение 1
Эта часть решения носит название прямого хода решения Гаусса, так как весь процесс осуществляется сверху вниз.
После приведения исходной системы уравнений к треугольной осуществляется нахождение всех переменных системы снизу вверх (то есть первые найденные переменные занимают находятся именно на последних строчках системы или матрицы). Эта часть решения известна также как обратный ход решения методом Гаусса. Заключается его алгоритм в следующем: сначала вычисляется переменные, находящиеся ближе всего к низу системы уравнений или матрицы, затем полученные значения подставляются выше и таким образом находится ещё одна переменная и так далее.
Готовые работы на аналогичную тему
Описание алгоритма метода Гаусса
Последовательность действий для общего решения системы уравнения методом Гаусса заключается в поочередном применении прямого и обратного хода к матрице на основе СЛАУ. Пусть исходная система уравнений имеет следующий вид:
$\begin{cases} a_{11} \cdot x_1 +…+ a_{1n} \cdot x_n = b_1 \\ … \\ a_{m1} \cdot x_1 + a_{mn} \cdot x_n = b_m \end{cases}$
Чтобы решить СЛАУ методом Гаусса, необходимо записать исходную систему уравнений в виде матрицы:
$A = \begin{pmatrix} a_{11} & … & a_{1n} \\ \vdots & … & \vdots \\ a_{m1} & … & a_{mn} \end{pmatrix}$, $b=\begin{pmatrix} b_1 \\ \vdots \\ b_m \end{pmatrix}$
Матрица $A$ называется основной матрицей и представляет собой записанные по порядку коэффициенты при переменных, а $b$ называется столбцом её свободных членов. Матрица $A$, записанная через черту со столбцом свободных членов называется расширенной матрицей:
$A = \begin{array}{ccc|c} a_{11} & … & a_{1n} & b_1 \\ \vdots & … & \vdots & …\\ a_{m1} & … & a_{mn} & b_m \end{array}$
Теперь необходимо с помощью элементарных преобразований над системой уравнений (или над матрицей, так как это удобнее) привести её к следующему виду:
$\begin{cases} α_{1j_{1}} \cdot x_{j_{1}} + α_{1j_{2}} \cdot x_{j_{2}}…+ α_{1j_{r}} \cdot x_{j_{r}} +… α_{1j_{n}} \cdot x_{j_{n}} = β_1 \\ α_{2j_{2}} \cdot x_{j_{2}}…+ α_{2j_{r}} \cdot x_{j_{r}} +… α_{2j_{n}} \cdot x_{j_{n}} = β_2 \\ …\\ α_{rj_{r}} \cdot x_{j_{r}} +… α_{rj_{n}} \cdot x_{j_{n}} = β_r \\ 0 = β_(r+1) \\ … \\ 0 = β_m \end{cases}$ (1)
Матрица, полученная из коэффициентов преобразованной системы уравнения (1) называется ступенчатой, вот так обычно выглядят ступенчатые матрицы:
$A = \begin{array}{ccc|c} a_{11} & a_{12} & a_{13} & b_1 \\ 0 & a_{22} & a_{23} & b_2\\ 0 & 0 & a_{33} & b_3 \end{array}$
Для этих матриц характерен следующий набор свойств:
- Все её нулевые строки стоят после ненулевых
- Если некоторая строка матрицы с номером $k$ ненулевая, то в предыдущей строчке этой же матрицы нулей меньше, чем в этой, обладающей номером $k$.
После получения ступенчатой матрицы необходимо подставить полученные переменные в оставшиеся уравнения (начиная с конца) и получить оставшиеся значения переменных.
Основные правила и разрешаемые преобразования при использовании метода Гаусса
При упрощении матрицы или системы уравнений этим методом нужно использовать только элементарные преобразования.
Таким преобразованиями считаются операции, которые возможно применять к матрице или системе уравнений без изменения её смысла:
- перестановка нескольких строк местами,
- прибавление или вычитание из одной строчки матрицы другой строчки из неё же,
- умножение или деление строчки на константу, не равную нулю,
- строчку, состоящую из одних нулей, полученную в процессе вычисления и упрощения системы, нужно удалить,
- Также нужно удалить лишние пропорциональные строчки, выбрав для системы единственную из них с более подходящими и удобными для дальнейших вычислений коэффициентами.
Все элементарные преобразования являются обратимыми.
Разбор трёх основных случаев, возникающих при решении линейных уравнений используя метод простых преобразований Гаусса
Различают три возникающих случая при использовании метода Гаусса для решения систем:
- Когда система несовместная, то есть у неё нет каких-либо решений
- У системы уравнений есть решение, причём единственное, а количество ненулевых строк и столбцов в матрице равно между собой.
- Система имеет некое количество или множество возможных решений, а количество строк в ней меньше чем количество столбцов.
Исход решения с несовместной системой
Для этого варианта при решении матричного уравнения методом Гаусса характерно получение какой-то строчки с невозможностью выполнения равенства. Поэтому при возникновении хотя бы одного неправильного равенства полученная и исходная системы не имеют решений вне зависимости от остальных уравнений, которые они содержат. Пример несовместной матрицы:
$\begin{array}{ccc|c} 2 & -1 & 3 & 0 \\ 1 & 0 & 2 & 0\\ 0 & 0 & 0 & 1 \end{array}$
В последней строчке возникло невыполняемое равенство: $0 \cdot x_{31} + 0 \cdot x_{32} + 0 \cdot x_{33} = 1$.
Система уравнений, у которой есть только одно решение
Данные системы после приведения к ступенчатой матрице и удаления строчек с нулями имеют одинаковое количество строк и столбцов в основной матрице. Вот простейший пример такой системы:
$\begin{cases} x_1 — x_2 = -5 \\ 2 \cdot x_1 + x_2 = -7 \end{cases}$
Запишем её в виде матрицы:
$\begin{array}{cc|c} 1 & -1 & -5 \\ 2 & 1 & -7 \end{array}$
Чтобы привести первую ячейку второй строчки к нулю, домножим верхнюю строку на $-2$ и вычтем её из нижней строчки матрицы, а верхнюю строчку оставим в исходном виде, в итоге имеем следующее:
$\begin{array}{cc|c} 1 & -1 & -5 \\ 0 & 3 & 10 \end{array}$
Этот пример можно записать в виде системы:
$\begin{cases} x_1 — x_2 = -5 \\ 3 \cdot x_2 = 10 \end{cases}$
Из нижнего уравнения выходит следующее значение $x$: $x_2 = 3 \frac{1}{3}$. Подставим это значение в верхнее уравнение: $x_1 – 3 \frac{1}{3}$, получаем $x_1 = 1 \frac{2}{3}$.
Система, обладающая множеством возможных вариантов решений
Для этой системы характерно меньшее количество значащих строк, чем количество столбцов в ней (учитываются строки основной матрицы).
Переменные в такой системе делятся на два вида: базисные и свободные. При преобразовании такой системы содержащиеся в ней основные переменные необходимо оставить в левой области до знака “=”, а остальные переменные перенести в правую часть равенства.
У такой системы есть только некое общее решение.
Разберём следующую систему уравнений:
$\begin{cases} 2y_1 + 3y_2 + x_4 = 1 \\ 5y_3 — 4y_4 = 1 \end{cases}$
Запишем её в виде матрицы:
$\begin{array}{cccc|c} 2 & 3 & 0 & 1 & 1 \\ 0 & 0 & 5 & 4 & 1 \\ \end{array}$
Наша задача найти общее решение системы. Для этой матрицы базисными переменными будут $y_1$ и $y_3$ (для $y_1$ — так как он стоит на первом месте, а в случае $y_3$ — располагается после нулей).
В качестве базисных переменных выбираем именно те, которые первые в строке не равны нулю.
Оставшиеся переменные называются свободными, через них нам необходимо выразить базисные.
Используя так называемый обратный ход, разбираем систему снизу вверх, для этого сначала выражаем $y_3$ из нижней строчки системы:
$5y_3 – 4y_4 = 1$
$5y_3 = 4y_4 + 1$
$y_3 = \frac{4/5}y_4 + \frac{1}{5}$.
Теперь в верхнее уравнение системы $2y_1 + 3y_2 + y_4 = 1$ подставляем выраженное $y_3$: $2y_1 + 3y_2 — (\frac{4}{5}y_4 + \frac{1}{5}) + y_4 = 1$
Выражаем $y_1$ через свободные переменные $y_2$ и $y_4$:
$2y_1 + 3y_2 — \frac{4}{5}y_4 — \frac{1}{5} + y_4 = 1$
$2y_1 = 1 – 3y_2 + \frac{4}{5}y_4 + \frac{1}{5} – y_4$
$2y_1 = -3y_2 — \frac{1}{5}y_4 + \frac{6}{5}$
$y_1 = -1.5x_2 – 0.1y_4 + 0.6$
Решение готово.
Пример 1
Решить слау методом Гаусса. Примеры. Пример решения системы линейных уравнений заданных матрицей 3 на 3 используя метод Гаусса
$\begin{cases} 4x_1 + 2x_2 – x_3 = 1 \\ 5x_1 + 3x_2 — 2x^3 = 2\\ 3x_1 + 2x_2 – 3x_3 = 0 \end{cases}$
Запишем нашу систему в виде расширенной матрицы:
$\begin{array}{ccc|c} 4 & 2 & -1 & 1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end{array}$
Теперь для удобства и практичности нужно преобразовать матрицу так, чтобы в верхнем углу крайнего столбца была $1$.
Для этого к 1-ой строчке нужно прибавляем строчку из середины, умноженную на $-1$, а саму среднюю строчку записываем как есть, выходит:
$\begin{array}{ccc|c} -1 & -1 & 1 & -1 \\ 5 & 3 & -2 & 2 \\ 3 & 2 & -3 & 0\\ \end{array}$
Далее к средней строчке прибавим верхнюю, умноженную на $5$, а последнюю строчку преобразуем, умножив первую строчку на 3 и сложив с последней, получаем:
$\begin{array}{ccc|c} -1 & -1 & 1 & -1 \\ 0 & -2 & 3 & -3 \\ 0 & -1 & 0 & -3\\ \end{array}$
Домножим верхнюю и последнюю строчки на $-1$, а также поменяем местами последнюю и среднюю строки:
$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & -2 & 3 & -3\\ \end{array}$
Далее сложим последнюю строчку с удвоенной средней:
$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 3 & 3\\ \end{array}$
И разделим последнюю строчку на $3$:
$\begin{array}{ccc|c} 1 & 1 & -1 & 1 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 1\\ \end{array}$
Получаем следующую систему уравнений, равносильную исходной:
$\begin{cases} x_1 + x_2 – x_3 = 1\\ x_2 = 3 \\ x_3 = 1 \end{cases}$
Из верхнего уравнения выражаем $x_1$:
$x1 = 1 + x_3 – x_2 = 1 + 1 – 3 = -1$.
Пример 2
Пример решения системы, заданной с помощью матрицы 4 на 4 методом Гаусса
$\begin{array}{cccc|c} 2 & 5 & 4 & 1 & 20 \\ 1 & 3 & 2 & 1 & 11 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end{array}$.
В начале меняем местами верхнюю исследующую за ней строчки, чтобы получить в левом верхнем углу $1$:
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 2 & 5 & 4 & 1 & 20 \\ 2 & 10 & 9 & 7 & 40\\ 3 & 8 & 9 & 2 & 37 \\ \end{array}$.
Теперь умножим верхнюю строчку на $-2$ и прибавим ко 2-ой и к 3-ьей. К 4-ой прибавляем 1-ую строку, домноженную на $-3$:
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 4 & 5 & 5 & 18\\ 0 & -1 & 3 & -1 & 4 \\ \end{array}$
Теперь к строке с номером 3 прибавляем строку 2, умноженную на $4$, а к строке 4 прибавляем строку 2, умноженную на $-1$.
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & -1 & 0 & -1 & -2 \\ 0 & 0 & 5 & 1 & 10\\ 0 & 0 & 3 & 0 & 6 \\ \end{array}$
Домножаем строку 2 на $-1$, а строку 4 делим на $3$ и ставим на место строки 3.
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 5 & 1 & 10 \\ \end{array}$
Теперь прибавляем к последней строке предпоследнюю, домноженную на $-5$.
$\begin{array}{cccc|c} 1 & 3 & 2 & 1 & 11 \\ 0 & 1 & 0 & 1 & 2 \\ 0 & 0 & 1 & 0 & 2\\ 0 & 0 & 0 & 1 & 0 \\ \end{array}$
Решаем полученную систему уравнений:
$\begin{cases} m = 0 \\ g = 2\\ y + m = 2\ \ x + 3y + 2g + m = 11\end{cases}$
$y=2$, $x = 0$.
Метод Гаусса (последовательного исключения неизвестных). Примеры решений для чайников
Продолжаем рассматривать системы линейных уравнений. Этот урок является третьим по теме. Если вы смутно представляете, что такое система линейных уравнений вообще, чувствуете себя чайником, то рекомендую начать с азов на странице Как решить систему линейных уравнений? Далее полезно изучить урок Правило Крамера. Матричный метод.
Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто! Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.
Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА.Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.
Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:
1) Иметь единственное решение. 2) Иметь бесконечно много решений. 3) Не иметь решений (быть несовместной).
Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решениялюбой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случаеприведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статьяНесовместные системы и системы с общим решением. Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.
Вернемся
к простейшей системе с урока Как
решить систему линейных уравнений? 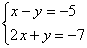 и
решим ее методом Гаусса.
и
решим ее методом Гаусса.
На
первом этапе нужно записать расширенную
матрицу системы: 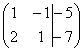 .
По какому принципу записаны коэффициенты,
думаю, всем видно. Вертикальная черта
внутри матрицы не несёт никакого
математического смысла – это просто
отчеркивание для удобства оформления.
.
По какому принципу записаны коэффициенты,
думаю, всем видно. Вертикальная черта
внутри матрицы не несёт никакого
математического смысла – это просто
отчеркивание для удобства оформления.
Справка: рекомендую
запомнить термины линейной
алгебры. Матрица
системы –
это матрица, составленная только из
коэффициентов при неизвестных, в данном
примере матрица системы: 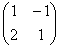 . Расширенная
матрица системы –
это та же матрица системы плюс столбец
свободных членов, в данном случае:
. Расширенная
матрица системы –
это та же матрица системы плюс столбец
свободных членов, в данном случае: 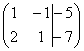 .
Любую из матриц можно для краткости
называть просто матрицей.
.
Любую из матриц можно для краткости
называть просто матрицей.
После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами.
Например, в рассматриваемой матрице
можно безболезненно переставить первую
и вторую строки: 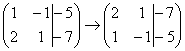
2)
Если в матрице есть (или появились)
пропорциональные (как частный случай
– одинаковые) строки, то следует удалить из
матрицы все эти строки кроме одной.
Рассмотрим, например матрицу 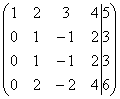 .
В данной матрице последние три строки
пропорциональны, поэтому достаточно
оставить только одну из них:
.
В данной матрице последние три строки
пропорциональны, поэтому достаточно
оставить только одну из них: 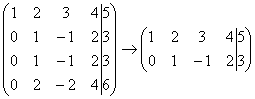 .
.
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следуетудалить. Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули.
4)
Строку матрицы можно умножить
(разделить) на
любое число, отличное
от нуля.
Рассмотрим, например, матрицу 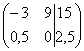 .
Здесь целесообразно первую строку
разделить на –3, а вторую строку –
умножить на 2:
.
Здесь целесообразно первую строку
разделить на –3, а вторую строку –
умножить на 2: 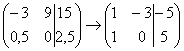 .
Данное действие очень полезно, поскольку
упрощает дальнейшие преобразования
матрицы.
.
Данное действие очень полезно, поскольку
упрощает дальнейшие преобразования
матрицы.
5)
Это преобразование вызывает наибольшие
затруднения, но на самом деле ничего
сложного тоже нет. К строке матрицы
можно прибавить
другую строку, умноженную на число,
отличное от нуля. Рассмотрим нашу матрицу
из практического примера: 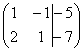 .
Сначала я распишу преобразование очень
подробно. Умножаем первую строку на
–2:
.
Сначала я распишу преобразование очень
подробно. Умножаем первую строку на
–2: 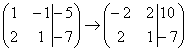 ,
и ко
второй строке прибавляем первую строку
умноженную на –2:
,
и ко
второй строке прибавляем первую строку
умноженную на –2: 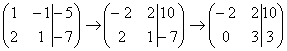 .
Теперь первую строку можно разделить
«обратно» на –2:
.
Теперь первую строку можно разделить
«обратно» на –2: 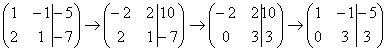 .
Как видите, строка, которую ПРИБАВЛЯЛИ – не
изменилась. Всегда меняется
строка, К КОТОРОЙ ПРИБАВЛЯЮТ.
.
Как видите, строка, которую ПРИБАВЛЯЛИ – не
изменилась. Всегда меняется
строка, К КОТОРОЙ ПРИБАВЛЯЮТ.
На
практике так подробно, конечно, не
расписывают, а пишут короче: 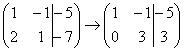 Еще
раз: ко второй строке прибавили
первую строку, умноженную на –2.
Умножают строку обычно устно или на
черновике, при этом мысленный ход
расчётов примерно такой:
Еще
раз: ко второй строке прибавили
первую строку, умноженную на –2.
Умножают строку обычно устно или на
черновике, при этом мысленный ход
расчётов примерно такой:
«Переписываю
матрицу и переписываю первую строку: 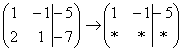 »
»
«Сначала
первый столбец. Внизу мне нужно получить
ноль. Поэтому единицу вверху умножаю
на –2: 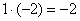 ,
и ко второй строке прибавляю первую: 2
+ (–2) = 0. Записываю результат во вторую
строку:
,
и ко второй строке прибавляю первую: 2
+ (–2) = 0. Записываю результат во вторую
строку: 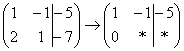 »
»
«Теперь
второй столбец. Вверху –1 умножаю на
–2: 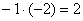 .
Ко второй строке прибавляю первую: 1 + 2
= 3. Записываю результат во вторую
строку:
.
Ко второй строке прибавляю первую: 1 + 2
= 3. Записываю результат во вторую
строку: 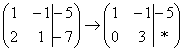 »
»
«И
третий столбец. Вверху –5 умножаю на
–2:  .
Ко второй строке прибавляю первую: –7
+ 10 = 3. Записываю результат во вторую
строку:
.
Ко второй строке прибавляю первую: –7
+ 10 = 3. Записываю результат во вторую
строку: 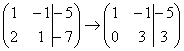 »
»
Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.
Элементарные преобразования не меняют решение системы уравнений
!
ВНИМАНИЕ:
рассмотренные манипуляции нельзя
использовать,
если Вам предложено задание, где матрицы
даны «сами по себе». Например, при
«классических» действиях
с матрицами что-то
переставлять внутри матриц ни в коем
случае нельзя! Вернемся к нашей
системе 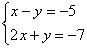 .
Она практически разобрана по косточкам.
.
Она практически разобрана по косточкам.
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
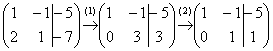
(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.
(2) Делим вторую строку на 3.
Цель
элементарных преобразований – привести
матрицу к ступенчатому виду: 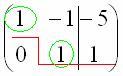 .
В оформлении задания прямо так и
отчеркивают простым карандашом
«лестницу», а также обводят кружочками
числа, которые располагаются на
«ступеньках». Сам термин «ступенчатый
вид» не вполне теоретический, в научной
и учебной литературе он часто
называется трапециевидный
вид или треугольный
вид.
.
В оформлении задания прямо так и
отчеркивают простым карандашом
«лестницу», а также обводят кружочками
числа, которые располагаются на
«ступеньках». Сам термин «ступенчатый
вид» не вполне теоретический, в научной
и учебной литературе он часто
называется трапециевидный
вид или треугольный
вид.
В
результате элементарных преобразований
получена эквивалентная исходной
система уравнений: 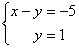
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.
В
нижнем уравнении у нас уже готовый
результат:  .
.
Рассмотрим
первое уравнение системы 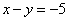 и
подставим в него уже известное значение
«игрек»:
и
подставим в него уже известное значение
«игрек»: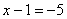
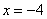
Ответ: 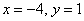
Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.
Пример 1
Решить
методом Гаусса систему уравнений: 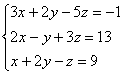
Запишем
расширенную матрицу системы: 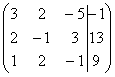
Сейчас
я сразу нарисую результат, к которому
мы придём в ходе решения: 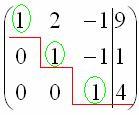 И
повторюсь, наша цель – с помощью
элементарных преобразований привести
матрицу к ступенчатому виду. С чего
начать действия?
И
повторюсь, наша цель – с помощью
элементарных преобразований привести
матрицу к ступенчатому виду. С чего
начать действия?
Сначала
смотрим на левое верхнее число: 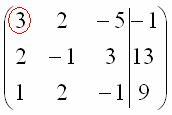 Почти
всегда здесь должна находиться единица.
Вообще говоря, устроит и –1 (а иногда и
другие числа), но как-то так традиционно
сложилось, что туда обычно помещают
единицу. Как организовать единицу?
Смотрим на первый столбец – готовая
единица у нас есть! Преобразование
первое: меняем местами первую и третью
строки:
Почти
всегда здесь должна находиться единица.
Вообще говоря, устроит и –1 (а иногда и
другие числа), но как-то так традиционно
сложилось, что туда обычно помещают
единицу. Как организовать единицу?
Смотрим на первый столбец – готовая
единица у нас есть! Преобразование
первое: меняем местами первую и третью
строки: 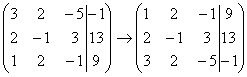
Теперь первая строка у нас останется неизменной до конца решения. Уже легче.
Единица
в левом верхнем углу организована.
Теперь нужно получить нули вот на этих
местах: 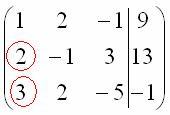
Нули
получаем как раз с помощью «трудного»
преобразования. Сначала разбираемся
со второй строкой (2, –1, 3, 13). Что нужно
сделать, чтобы на первой позиции получить
ноль? Нужно ко
второй строке прибавить первую строку,
умноженную на –2.
Мысленно или на черновике умножаем
первую строку на –2: (–2, –4, 2, –18). И
последовательно проводим (опять же
мысленно или на черновике) сложение, ко
второй строке прибавляем первую строку,
уже умноженную на –2: 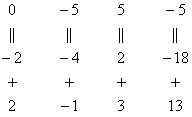
Результат
записываем во вторую строку: 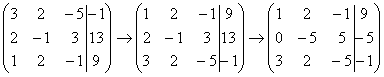
Аналогично
разбираемся с третьей строкой (3, 2, –5,
–1). Чтобы получить на первой позиции
ноль, нужно к
третьей строке прибавить первую строку,
умноженную на –3.
Мысленно или на черновике умножаем
первую строку на –3: (–3, –6, 3, –27). И к
третьей строке прибавляем первую строку,
умноженную на –3: 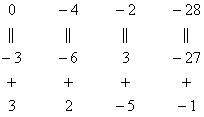
Результат
записываем в третью строку: 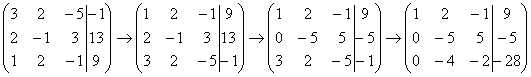
На
практике эти действия обычно выполняются
устно и записываются в один шаг: 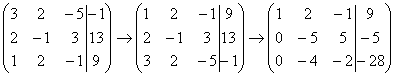
Не
нужно считать всё сразу и одновременно.
Порядок вычислений и «вписывания»
результатов последователен и
обычно такой: сначала переписываем
первую строку, и пыхтим себе потихонечку
– ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО: 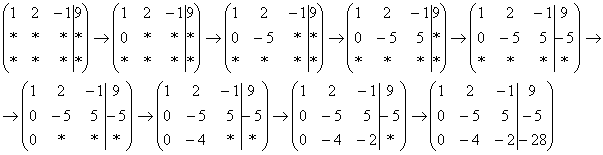 А
мысленный ход самих расчётов я уже
рассмотрел выше.
А
мысленный ход самих расчётов я уже
рассмотрел выше.
Далее
нужно получить единицу на следующей
«ступеньке»: 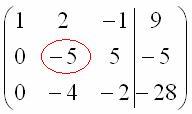
В
данном примере это сделать легко, вторую
строку делим на –5 (поскольку там все
числа делятся на 5 без остатка). Заодно
делим третью строку на –2, ведь чем
меньше числа, тем проще решение: 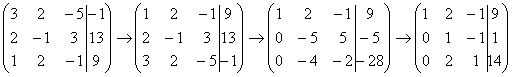
На
заключительном этапе элементарных
преобразований нужно получить еще один
ноль здесь: 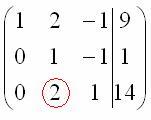
Для
этого к
третьей строке прибавляем вторую строку,
умноженную на –2: 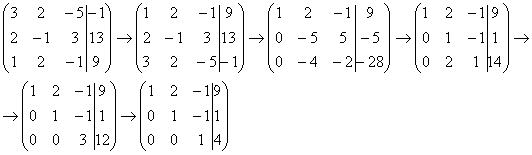 Попробуйте
разобрать это действие самостоятельно
– мысленно умножьте вторую строку на
–2 и проведите сложение.
Попробуйте
разобрать это действие самостоятельно
– мысленно умножьте вторую строку на
–2 и проведите сложение.
Последнее выполненное действие – причёска результата, делим третью строку на 3.
В
результате элементарных преобразований
получена эквивалентная исходной система
линейных уравнений: 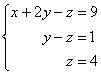 Круто.
Круто.
Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.
В
третьем уравнении у нас уже готовый
результат: 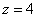
Смотрим
на второе уравнение: 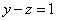 .
Значение «зет» уже известно, таким
образом:
.
Значение «зет» уже известно, таким
образом: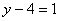
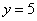
И,
наконец, первое уравнение: 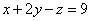 .
«Игрек» и «зет» известны, дело за
малым:
.
«Игрек» и «зет» известны, дело за
малым: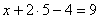
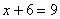
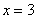
Ответ: 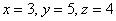
Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.
Пример 2
Решить
систему линейных уравнений методом
Гаусса 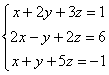
Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.
Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса. Но вот ответы обязательно должны получиться одинаковыми!
Пример 3
Решить
систему линейных уравнений методом
Гаусса 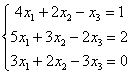
Запишем
расширенную матрицу системы и с помощью
элементарных преобразований приведем
ее к ступенчатому виду: 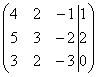
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
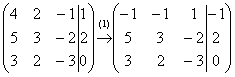
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).
Дальше
алгоритм работает уже по накатанной
колее: 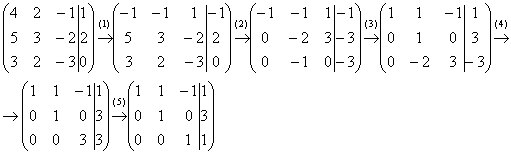
(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 3.
Скверным
признаком, который свидетельствует об
ошибке в вычислениях (реже – об опечатке),
является «плохая» нижняя строка. То
есть, если бы у нас внизу получилось
что-нибудь вроде 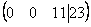 ,
и, соответственно,
,
и, соответственно, 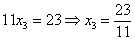 ,
то с большой долей вероятности можно
утверждать, что допущена ошибка в ходе
элементарных преобразований.
,
то с большой долей вероятности можно
утверждать, что допущена ошибка в ходе
элементарных преобразований.
Заряжаем
обратный ход, в оформлении примеров
часто не переписывают саму систему, а
уравнения «берут прямо из приведенной
матрицы». Обратный ход, напоминаю,
работает, снизу вверх. Да тут подарок
получился: 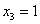
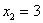
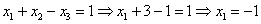
Ответ: 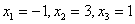 .
.
Пример 4
Решить
систему линейных уравнений методом
Гаусса 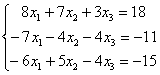
Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.
В
последней части рассмотрим некоторые
особенности алгоритма Гаусса.
Первая
особенность состоит в том, что иногда
в уравнениях системы отсутствуют
некоторые переменные, например: 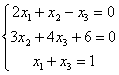 Как
правильно записать расширенную матрицу
системы? Об этом моменте я уже рассказывал
на уроке Правило
Крамера. Матричный метод.
В расширенной матрице системы на месте
отсутствующих переменных ставим
нули:
Как
правильно записать расширенную матрицу
системы? Об этом моменте я уже рассказывал
на уроке Правило
Крамера. Матричный метод.
В расширенной матрице системы на месте
отсутствующих переменных ставим
нули: 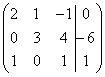 Кстати,
это довольно легкий пример, поскольку
в первом столбце уже есть один ноль, и
предстоит выполнить меньше элементарных
преобразований.
Кстати,
это довольно легкий пример, поскольку
в первом столбце уже есть один ноль, и
предстоит выполнить меньше элементарных
преобразований.
Вторая
особенность состоит вот в чём. Во всех
рассмотренных примерах на «ступеньки»
мы помещали либо –1, либо +1. Могут ли там
быть другие числа? В ряде случаев могут.
Рассмотрим систему: 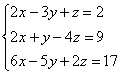 .
.
Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.
Или
еще такой условный пример: 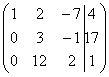 .
Здесь тройка на второй «ступеньке» тоже
нас устраивает, поскольку 12 (место, где
нам нужно получить ноль) делится на 3
без остатка. Необходимо провести
следующее преобразование: к третьей
строке прибавить вторую строку, умноженную
на –4, в результате чего и будет получен
нужный нам ноль.
.
Здесь тройка на второй «ступеньке» тоже
нас устраивает, поскольку 12 (место, где
нам нужно получить ноль) делится на 3
без остатка. Необходимо провести
следующее преобразование: к третьей
строке прибавить вторую строку, умноженную
на –4, в результате чего и будет получен
нужный нам ноль.
Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 десять систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.
Дождливая осенняя погода за окном…. Поэтому для всех желающих более сложный пример для самостоятельного решения:
Пример 5
Решить
методом Гаусса систему 4-х линейных
уравнений с четырьмя неизвестными. 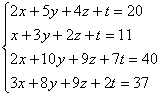
Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.
Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением. Там же можно закрепить рассмотренный алгоритм метода Гаусса.
Желаю успехов!
Решения и ответы:
Пример
2: Решение: Запишем
расширенную матрицу системы и с помощью
элементарных преобразований приведем
ее к ступенчатому виду. 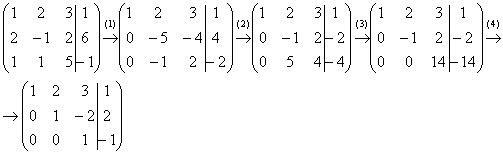 Выполненные
элементарные преобразования: (1)
Ко второй строке прибавили первую
строку, умноженную на –2. К третьей
строке прибавили первую строку, умноженную
на –1. Внимание! Здесь
может возникнуть соблазн из третьей
строки вычесть первую, крайне не
рекомендую вычитать – сильно повышается
риск ошибки. Только складываем! (2)
У второй строки сменили знак (умножили
на –1). Вторую и третью строки поменяли
местами. Обратите
внимание,
что на «ступеньках» нас устраивает не
только единица, но еще и –1, что даже
удобнее. (3)
К третьей строке прибавили вторую
строку, умноженную на 5. (4)
У второй строки сменили знак (умножили
на –1). Третью строку разделили на 14.
Выполненные
элементарные преобразования: (1)
Ко второй строке прибавили первую
строку, умноженную на –2. К третьей
строке прибавили первую строку, умноженную
на –1. Внимание! Здесь
может возникнуть соблазн из третьей
строки вычесть первую, крайне не
рекомендую вычитать – сильно повышается
риск ошибки. Только складываем! (2)
У второй строки сменили знак (умножили
на –1). Вторую и третью строки поменяли
местами. Обратите
внимание,
что на «ступеньках» нас устраивает не
только единица, но еще и –1, что даже
удобнее. (3)
К третьей строке прибавили вторую
строку, умноженную на 5. (4)
У второй строки сменили знак (умножили
на –1). Третью строку разделили на 14.
Обратный
ход: 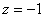
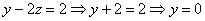
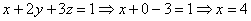
Ответ: 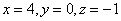 .
.
Пример
4: Решение: Запишем
расширенную матрицу системы и с помощью
элементарных преобразований приведем
ее к ступенчатому виду: 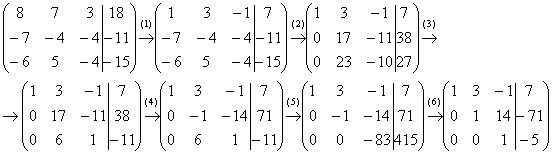
Выполненные преобразования: (1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке». (2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.
Со второй «ступенькой» всё хуже, «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы (3) К третьей строке прибавили вторую, умноженную на –1. (4) Ко второй строке прибавили третью, умноженную на –3. Нужная вещь на второй ступеньке получена. (5) К третьей строке прибавили вторую, умноженную на 6. (6) Вторую строку умножили на –1, третью строку разделили на -83.
Обратный
ход: 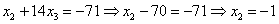
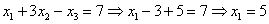
Ответ: 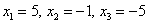
Пример
5: Решение: Запишем
матрицу системы и с помощью элементарных
преобразований приведем ее к ступенчатому
виду: 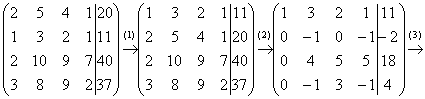
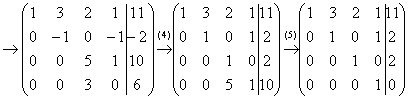
Выполненные преобразования: (1) Первую и вторую строки поменяли местами. (2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –2. К четвертой строке прибавили первую строку, умноженную на –3. (3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1. (4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки. (5) К четвертой строке прибавили третью строку, умноженную на –5.
Обратный
ход: 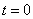
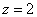
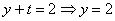
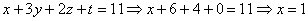
Ответ: 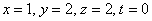
\
Лекция 8. МЕТОД ГАУССА РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ — Студопедия
- Матричное представление метода Гаусса
- Метод Гаусса с частичным выбором главного элемента
- Метод Гаусса с полным выбором главного элемента
- Матричное представление метода Гаусса
Для получения матричного представления метода Гаусса рассмотрим пример. Пусть необходимо решить СЛАУ вида 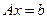 :
:
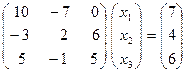 ,
,
где 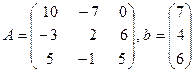 . На первом шаге метода Гаусса производятся исключения в первом столбце матрицы СЛАУ при помощи первого уравнения, т.е. путем элементарных эквивалентных преобразований системы в первом столбце матрицы ниже элемента главной диагонали (ниже 10) делаются нули, а это означает, что переменная
. На первом шаге метода Гаусса производятся исключения в первом столбце матрицы СЛАУ при помощи первого уравнения, т.е. путем элементарных эквивалентных преобразований системы в первом столбце матрицы ниже элемента главной диагонали (ниже 10) делаются нули, а это означает, что переменная 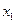 исключается из всех уравнений системы, кроме первого. Это достигается следующим образом: для получения 0 на месте (2,1) нужно первое уравнение (первую строку матрицы и элемент
исключается из всех уравнений системы, кроме первого. Это достигается следующим образом: для получения 0 на месте (2,1) нужно первое уравнение (первую строку матрицы и элемент 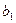 ) умножить на 0.3 и сложить со вторым уравнением; для получения 0 на месте (3,1) нужно первое уравнение умножить на -0.5 и сложить с третьим уравнением. В итоге получена эквивалентная СЛАУ
) умножить на 0.3 и сложить со вторым уравнением; для получения 0 на месте (3,1) нужно первое уравнение умножить на -0.5 и сложить с третьим уравнением. В итоге получена эквивалентная СЛАУ 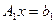 . Величины 0.3 и -0.5 называются множителями. Запишем их рядом с уравнениями СЛАУ
. Величины 0.3 и -0.5 называются множителями. Запишем их рядом с уравнениями СЛАУ 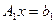 , для которых они использовались:
, для которых они использовались:
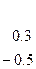
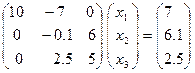 ,
,
где 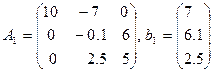 . Элемент, стоящий на месте (2,2) в полученной матрице
. Элемент, стоящий на месте (2,2) в полученной матрице 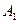 , имеет значение, малое по сравнению с другими элементами второго столбца матрицы
, имеет значение, малое по сравнению с другими элементами второго столбца матрицы 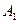 . Ниже мы остановимся подробно на отрицательных последствиях такого явления для решения СЛАУ, а сейчас просто поменяем местами второе и третье уравнения последней системы, что выведет на место (2,2) элемент 2.5. Получим СЛАУ
. Ниже мы остановимся подробно на отрицательных последствиях такого явления для решения СЛАУ, а сейчас просто поменяем местами второе и третье уравнения последней системы, что выведет на место (2,2) элемент 2.5. Получим СЛАУ 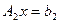 :
:
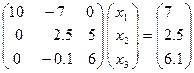 .
.
Здесь 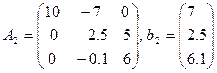 .
.
На втором шаге метода Гаусса исключим при помощи второго уравнения 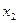 из третьего, обнулив элемент (3,2) второго столбца. Это достигается путем умножения второго уравнения на 0.04 и сложения с третьим. В итоге получаем эквивалентную СЛАУ
из третьего, обнулив элемент (3,2) второго столбца. Это достигается путем умножения второго уравнения на 0.04 и сложения с третьим. В итоге получаем эквивалентную СЛАУ 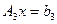 :
:
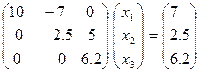 ,
,
где 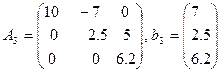 . Заметим, что проводить исключение во втором столбце (обнуление элемента (3,2)) при помощи первого уравнения было нецелесообразно, т.к. это могло сделать ненулевым элемент (3,1) и «испортить» результат, полученный на предыдущем шаге метода Гаусса (обнуление элементов первого столбца матрицы СЛАУ).
. Заметим, что проводить исключение во втором столбце (обнуление элемента (3,2)) при помощи первого уравнения было нецелесообразно, т.к. это могло сделать ненулевым элемент (3,1) и «испортить» результат, полученный на предыдущем шаге метода Гаусса (обнуление элементов первого столбца матрицы СЛАУ).
Система 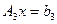 — это результат прямого хода метода Гаусса, результат проведенных исключений. В итоге прямого хода получается СЛАУ с верхней треугольной матрицей. Теперь решение треугольной системы осуществляется путем обратной подстановки (снизу вверх). Так последнее уравнение СЛАУ
— это результат прямого хода метода Гаусса, результат проведенных исключений. В итоге прямого хода получается СЛАУ с верхней треугольной матрицей. Теперь решение треугольной системы осуществляется путем обратной подстановки (снизу вверх). Так последнее уравнение СЛАУ 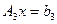 имеет вид:
имеет вид: 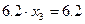 , откуда
, откуда 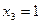 . Это полученное значение может быть подставлено в предпоследнее уравнение:
. Это полученное значение может быть подставлено в предпоследнее уравнение:
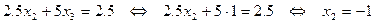 .
.
Подставляя полученные 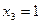 и
и 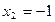 в первое уравнение
в первое уравнение 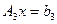 , получим
, получим 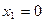 .
.
Решение рассмотренного примера может быть записано в матричном виде. Обозначим
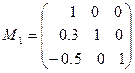 .
.
Заметим, что матрица 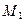 отличается от единичной только первым столбцом, куда записаны множители, использованные при проведении исключений в первом столбце в прямом ходе метода Гаусса.
отличается от единичной только первым столбцом, куда записаны множители, использованные при проведении исключений в первом столбце в прямом ходе метода Гаусса.
Непосредственно проверяем, что
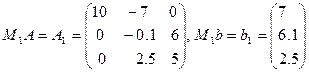 .
.
Обозначим
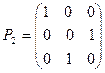 , тогда
, тогда 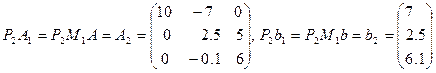 .
.
Матрица 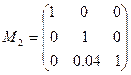 отличается от единичной только вторым столбцом, куда записан множитель, использованный при проведении исключения во втором столбце в прямом ходе метода Гаусса. С использованием
отличается от единичной только вторым столбцом, куда записан множитель, использованный при проведении исключения во втором столбце в прямом ходе метода Гаусса. С использованием 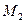 получаем:
получаем:
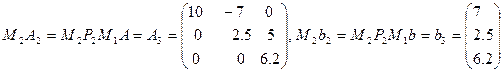 .
.
Таким образом, из исходной СЛАУ 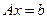 мы пришли к эквивалентной СЛАУ:
мы пришли к эквивалентной СЛАУ:
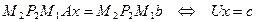 ,
,
матрица которой 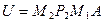 является верхней треугольной, а вектор правой части
является верхней треугольной, а вектор правой части 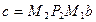 .
.
Аналогичные соотношения справедливы и в общем случае для СЛАУ 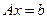 с матрицей размера
с матрицей размера 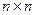 . Обозначим
. Обозначим 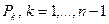 , матрицу, полученную из единичной матрицы той же перестановкой строк, какая применялась к строкам матрицы СЛАУ на
, матрицу, полученную из единичной матрицы той же перестановкой строк, какая применялась к строкам матрицы СЛАУ на 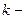 ом шаге исключения (исключения в
ом шаге исключения (исключения в 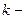 ом столбце). Таким образом,
ом столбце). Таким образом, 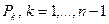 , — это матрицы перестановок (матрица
, — это матрицы перестановок (матрица 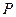 называется матрицей перестановок, если в каждом ее столбце и в каждой ее строке в точности один элемент равен 1, а все остальные равны 0). Умножение произвольной матрицы
называется матрицей перестановок, если в каждом ее столбце и в каждой ее строке в точности один элемент равен 1, а все остальные равны 0). Умножение произвольной матрицы 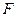 на матрицу перестановок слева поменяет местами в матрице
на матрицу перестановок слева поменяет местами в матрице 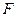 строки с соответствующими номерами, а умножение на матрицу перестановок справа поменяет в
строки с соответствующими номерами, а умножение на матрицу перестановок справа поменяет в 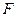 столбцы с теми же номерами.
столбцы с теми же номерами.
Пусть 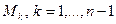 , обозначает матрицу, полученную из единичной матрицы записью в поддиагональные позиции
, обозначает матрицу, полученную из единичной матрицы записью в поддиагональные позиции 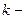 го столбца множителей, используемых на
го столбца множителей, используемых на 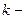 ом шаге исключения. Матрицы
ом шаге исключения. Матрицы 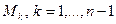 , называются матрицами исключения, являются нижними треугольными. Элементы
, называются матрицами исключения, являются нижними треугольными. Элементы 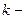 го столбца
го столбца 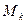 вычисляются в соответствии с формулой
вычисляются в соответствии с формулой
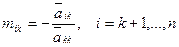 ,
,
где 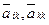 — соответствующие элементы матрицы СЛАУ после
— соответствующие элементы матрицы СЛАУ после 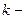 1 шага метода Гаусса (после исключения, проведенного в
1 шага метода Гаусса (после исключения, проведенного в 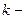 1 столбце).
1 столбце).
В принятых обозначениях матричный вид прямого хода метода Гаусса следующий:
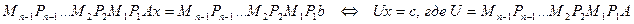 .
.
Матрица итоговой СЛАУ 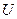 — верхняя треугольная. Полученная СЛАУ легко решается путем обратной подстановки. Если предположить, что перестановки в ходе исключений не делались, то
— верхняя треугольная. Полученная СЛАУ легко решается путем обратной подстановки. Если предположить, что перестановки в ходе исключений не делались, то
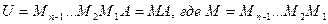 .
.
Матрица 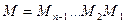 как произведение нижних треугольных матриц является нижней треугольной. Исключения, проводимые на каждом шаге метода Гаусса, требуют пересчета элементов матрицы СЛАУ и вектора правой части. Для
как произведение нижних треугольных матриц является нижней треугольной. Исключения, проводимые на каждом шаге метода Гаусса, требуют пересчета элементов матрицы СЛАУ и вектора правой части. Для 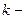 го шага исключения пересчет происходит в соответствии с формулой:
го шага исключения пересчет происходит в соответствии с формулой:
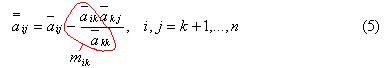
Здесь 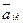 — элементы матрицы СЛАУ после
— элементы матрицы СЛАУ после 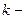 1 го шага исключения,
1 го шага исключения, 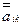 — элементы матрицы СЛАУ после
— элементы матрицы СЛАУ после 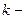 го шага исключения. В матричном виде эти действия просто эквивалентны умножению на матрицу исключения. Поскольку
го шага исключения. В матричном виде эти действия просто эквивалентны умножению на матрицу исключения. Поскольку 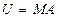 , при этом матрица
, при этом матрица 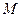 невырожденная, а значит, обратимая, обратная к ней – нижняя треугольная, то
невырожденная, а значит, обратимая, обратная к ней – нижняя треугольная, то 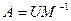 , а это есть ничто иное, как треугольное разложение матрицы
, а это есть ничто иное, как треугольное разложение матрицы 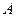 .
.
Диагональные элементы матрицы 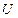 называются ведущими, или главными;
называются ведущими, или главными; 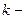 ый ведущий элемент – это коэффициент при
ый ведущий элемент – это коэффициент при 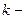 ом неизвестном в
ом неизвестном в 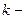 ом уравнении на
ом уравнении на 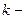 ом шаге исключения Гаусса (исключений в
ом шаге исключения Гаусса (исключений в 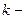 ом столбце матрицы). В предыдущем примере ведущими элементами были 10, 2.5 и 6.2.
ом столбце матрицы). В предыдущем примере ведущими элементами были 10, 2.5 и 6.2.
При вычислении множителей, а также в ходе обратной подстановки происходит деление на ведущие элементы, поэтому ведущие элементы обязательно должны быть отличны от 0. Более того, как показывает следующий пример, ведущие элементы не должны быть малыми по сравнению с другими элементами матрицы.
Пример. Решить СЛАУ 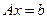 :
:
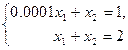 .
.
Точное решение этой системы: 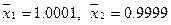 . Здесь
. Здесь 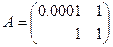 , вектор
, вектор  . Первый шаг метода Гаусса – исключения в первом столбце матрицы СЛАУ
. Первый шаг метода Гаусса – исключения в первом столбце матрицы СЛАУ 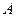 за счет матрицы исключения, имеющей вид:
за счет матрицы исключения, имеющей вид: 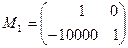 . Тогда исходна система за счет исключений преобразуется к эквивалентному виду:
. Тогда исходна система за счет исключений преобразуется к эквивалентному виду:
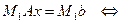
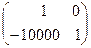
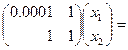
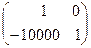
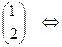
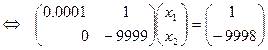 . (10)
. (10)
Для решения полученной СЛАУ с верхней треугольной матрицей применяем обратный ход метода Гаусса. Второе уравнение СЛАУ имеет вид: 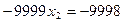 , откуда
, откуда 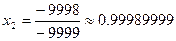 . Предположим, что в нашей вычислительной системе количество разрядов в мантиссе равно
. Предположим, что в нашей вычислительной системе количество разрядов в мантиссе равно 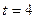 , тогда
, тогда 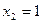 . Если полученное значение
. Если полученное значение 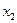 сравнить с точным значением
сравнить с точным значением 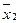 решения данной СЛАУ, то качественно очевидно, что
решения данной СЛАУ, то качественно очевидно, что 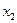 хорошо приближает
хорошо приближает 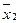 . Продолжим обратный ход метода Гаусса подставляя в первое уравнение СЛАУ
. Продолжим обратный ход метода Гаусса подставляя в первое уравнение СЛАУ 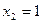 :
: 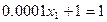 , откуда
, откуда 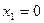 , что «абсольтно не похоже» на точное значение
, что «абсольтно не похоже» на точное значение 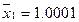 решения данной СЛАУ.
решения данной СЛАУ.
Что произошло, где была допущена катастрофическая ошибка? Здесь не было накопления ошибок округления, вызываемого выполнением большого количества аоифметических операций. Матрица исходной СЛАУ 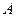 далека от вырожденной:
далека от вырожденной: 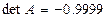 . Полученный результат имеет только одно объяснение: при проводимом исключение ведущий элемент 0.0001 имел значение, малое по сравнению с другими элементами матрицы, что привело в процессе исключения к колосальному росту коэффициентов второго уравнения:
. Полученный результат имеет только одно объяснение: при проводимом исключение ведущий элемент 0.0001 имел значение, малое по сравнению с другими элементами матрицы, что привело в процессе исключения к колосальному росту коэффициентов второго уравнения: 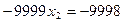 . Эти коэффициенты в 104 раз стали превосходить коэффициенты исходной задачи. Ошибка округления, произошедшая при вычислении
. Эти коэффициенты в 104 раз стали превосходить коэффициенты исходной задачи. Ошибка округления, произошедшая при вычислении 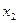 и равная
и равная 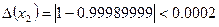 , является малой и приемлемой по отношению к большим коэффициентам уравнения
, является малой и приемлемой по отношению к большим коэффициентам уравнения 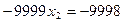 , но совершенно неприемлемой с точки зрения уровня элементов исходной матрицы (ведь там есть элемент 0.0001, который меньше, чем абсолютная погрешность
, но совершенно неприемлемой с точки зрения уровня элементов исходной матрицы (ведь там есть элемент 0.0001, который меньше, чем абсолютная погрешность 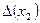 ). Таким образом необходимо при проведении процесса исключения обеспечивать следующее условие: модули значений ведущих элементов не должны быть малыми по сравнению с модулями других элементов матрицы СЛАУ.
). Таким образом необходимо при проведении процесса исключения обеспечивать следующее условие: модули значений ведущих элементов не должны быть малыми по сравнению с модулями других элементов матрицы СЛАУ.
- Метод Гаусса с частичным выбором главного элемента
Для обеспечения устойчивости процесса исключения Гаусса необходимо позаботиться о том, чтобы ведущие элементы имели значения, сравнимые со значениями остальных элементов матрицы СЛАУ. Это можно обеспечить различными способами. Рассмотрим один из них, который называется частичным выбором главного элемента.
Частичный выбор главного элемента может осуществляться по столбцу или по строке. Начнем с выбора по столбцу.
Рассматривается СЛАУ 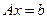 :
:
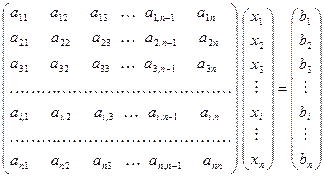 . (20)
. (20)
Перед проведением исключений в первом столбце выберем в этом столбце максимальный по модулю элемент. Пусть этот элемент 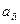 . Выведем этот элемент на место ведущего (на место (1,1)) для первого шага метода Гаусса. Для этого в СЛАУ (20) поменяем местами первое и
. Выведем этот элемент на место ведущего (на место (1,1)) для первого шага метода Гаусса. Для этого в СЛАУ (20) поменяем местами первое и 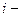 ое уравнения. Получим СЛАУ:
ое уравнения. Получим СЛАУ:
 (30)
(30)
Теперь проведем исключение в первом столбце матрицы СЛАУ (30). В результате исключения СЛАУ (30) примет вид:
 (40)
(40)
В (40) выделены те коэффициенты, которые изменяются (подвергаются пересчету в соответствии с формулой (5)) в процессе исключения. Обозначим полученную систему 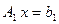 :
:
 .
.
Перед проведением исключений второго шага метода Гаусса выберем максимальный по модулю элемент второго столбца матрицы СЛАУ (40), исключая при выборе элемент стоящий в первой строке (область выбора обозначена в предыдущей формуле). Пусть этот элемент 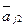 . Выводим его на место ведущего элемента для второго шага исключений – на место (2,2) путем перестановки второго и
. Выводим его на место ведущего элемента для второго шага исключений – на место (2,2) путем перестановки второго и 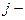 го уравнений (элемент
го уравнений (элемент 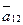 не участвовал при выборе максимального по модулю элемента в силу того, что перестановка первой строки на место второй, в том случае, если бы
не участвовал при выборе максимального по модулю элемента в силу того, что перестановка первой строки на место второй, в том случае, если бы 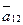 оказался максимальным по модулю, привела бы к порче структуры матрицы, полученной на первом шаге исключения: нулевой элемент первого столбца, стоящий во второй строке, стал бы ненулевым за счет того, что на место (2,1) попал бы элемент
оказался максимальным по модулю, привела бы к порче структуры матрицы, полученной на первом шаге исключения: нулевой элемент первого столбца, стоящий во второй строке, стал бы ненулевым за счет того, что на место (2,1) попал бы элемент 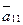 ). В результате получим СЛАУ:
). В результате получим СЛАУ:
 (50)
(50)
Теперь проведем исключение во втором столбце матрицы СЛАУ (50). В результате исключения СЛАУ (50) примет вид:

Перед проведением третьего шага исключения Гаусса (обнуления элементов третьего столбца матрицы СЛАУ ниже главной диагонали) выберем максимальный по модулю элемент третьего столбца среди элементов, исключающих элементы первой и второй строк. Выведем этот элемент на позицию (3,3) – позицию ведущего элемента для третьего шага. И т.д.
Частичный выбор главного элемента можно проводить по строке. В этом случае перед проведением исключений в 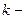 ом столбце матрицы СЛАУ, которую обозначим
ом столбце матрицы СЛАУ, которую обозначим 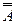 , надо выбрать максимальный по модулю элемент
, надо выбрать максимальный по модулю элемент 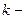 ой строки
ой строки 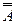 среди элементов
среди элементов 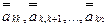 (пусть это элемент
(пусть это элемент 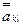 ), вывести его на главную диагональ путем перестановки
), вывести его на главную диагональ путем перестановки 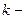 го и
го и 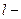 го столбцов, и произвести исключение, как описано выше. Необходимо учитывать и помнить, что перестановка столбцов в матрице СЛАУ повлечет за собой соответствующее изменение порядка неизвестных в векторе
го столбцов, и произвести исключение, как описано выше. Необходимо учитывать и помнить, что перестановка столбцов в матрице СЛАУ повлечет за собой соответствующее изменение порядка неизвестных в векторе 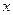 .
.
Частичный выбор главного элемента обеспечит сравнимость ведущих элементов на всех шагах исключения Гаусса с остальными элементами соответствующих столбцов (строк) матрицы СЛАУ, т.е. обеспечит устойчивость исключений Гаусса.
- Метод Гаусса с полным выбором главного элемента
Выбор главного элемента, предваряющий исключение на очередном шаге метода Гаусса, можно проводить, учитывая большее количество элементов матрицы СЛАУ. Так перед исключением в первом столбце выберем максимальный по модулю элемент во всей матрице системы 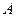 . Пусть этот элемент —
. Пусть этот элемент — 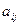 . Для того, чтобы вывести этот элемент на место (1,1), переставим в
. Для того, чтобы вывести этот элемент на место (1,1), переставим в 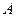 первую и
первую и 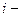 ую строки (соответственно в векторе
ую строки (соответственно в векторе 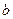 — первый и
— первый и 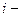 ый элементы), первый и
ый элементы), первый и 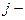 ый столбец, после чего проведем исключения в первом столбце.
ый столбец, после чего проведем исключения в первом столбце.
Перед исключением в 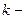 ом столбце выберем максимальный по модулю элемент в матрице СЛАУ
ом столбце выберем максимальный по модулю элемент в матрице СЛАУ 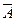 среди ее элементов
среди ее элементов 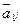 , где
, где 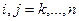 . И т.д.
. И т.д.
Очевидно, что полный выбор главного элемента обеспечит сравнимость ведущих элементов на всех шагах исключения Гаусса с остальными элементами всей матрицы СЛАУ, т.е. обеспечит устойчивость исключений Гаусса, причем, как вытекает из стратегии поиска главного элемента, погрешность метода Гаусса с полным выбором главного элемента будет меньше, чем при частичном выборе.
описание алгоритма решения системы линейных уравнений, примеры, решения.
Метод Гаусса прекрасно подходит для решения систем линейных алгебраических уравнений (СЛАУ). Он обладает рядом преимуществ по сравнению с другими методами:
во-первых, нет необходимости предварительно исследовать систему уравнений на совместность;
во-вторых, методом Гаусса можно решать не только СЛАУ, в которых число уравнений совпадает с количеством неизвестных переменных и основная матрица системы невырожденная, но и системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равен нулю;
в-третьих, метод Гаусса приводит к результату при сравнительно небольшом количестве вычислительных операций.
Краткий обзор статьи.
Сначала дадим необходимые определения и введем обозначения.
Далее опишем алгоритм метода Гаусса для простейшего случая, то есть, для систем линейных алгебраических уравнений, количество уравнений в которых совпадает с количеством неизвестных переменных и определитель основной матрицы системы не равен нулю. При решении таких систем уравнений наиболее отчетливо видна суть метода Гаусса, которая заключается в последовательном исключении неизвестных переменных. Поэтому метод Гаусса также называют методом последовательного исключения неизвестных. Покажем подробные решения нескольких примеров.
В заключении рассмотрим решение методом Гаусса систем линейных алгебраических уравнений, основная матрица которых либо прямоугольная, либо вырожденная. Решение таких систем имеет некоторые особенности, которые мы подробно разберем на примерах.
Навигация по странице.
Основные определения и обозначения.
Решение систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных и основная матрица системы невырожденная, методом Гаусса.
Решение систем линейных алгебраических уравнений, в которых число уравнений не совпадает с числом неизвестных или основная матрица системы вырожденная, методом Гаусса.
Основные определения и обозначения.
Рассмотрим
систему из p линейных
уравнений с n неизвестными
(p может
быть равно n): 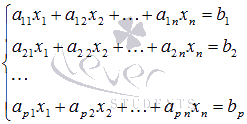 где
где 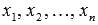 —
неизвестные переменные,
—
неизвестные переменные, 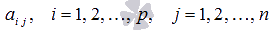 —
числа (действительные или комплексные),
—
числа (действительные или комплексные), 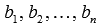 —
свободные члены.
—
свободные члены.
Если  ,
то система линейных алгебраических
уравнений называетсяоднородной,
в противном случае – неоднородной.
,
то система линейных алгебраических
уравнений называетсяоднородной,
в противном случае – неоднородной.
Совокупность
значения неизвестных переменных 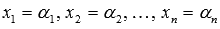 ,
при которых все уравнения системы
обращаются в тождества, называется решением
СЛАУ.
,
при которых все уравнения системы
обращаются в тождества, называется решением
СЛАУ.
Если существует хотя бы одно решение системы линейных алгебраических уравнений, то она называется совместной, в противном случае – несовместной.
Если СЛАУ имеет единственное решение, то она называется определенной. Если решений больше одного, то система называется неопределенной.
Говорят,
что система записана в координатной
форме,
если она имеет вид 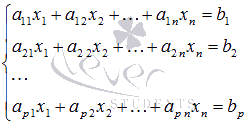 .
.
Эта
система в матричной
форме записи
имеет вид 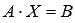 ,
где
,
где 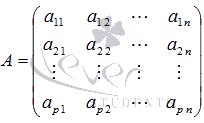 —
основная матрица СЛАУ,
—
основная матрица СЛАУ, 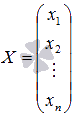 —
матрица столбец неизвестных переменных,
—
матрица столбец неизвестных переменных, 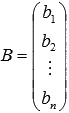 —
матрица свободных членов.
—
матрица свободных членов.
Если
к матрице А добавить
в качестве (n+1)-ого столбца
матрицу-столбец свободных членов, то
получим так называемую расширенную
матрицу системы
линейных уравнений. Обычно расширенную
матрицу обозначают буквой Т,
а столбец свободных членов отделяют
вертикальной линией от остальных
столбцов, то есть, 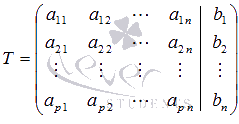
Квадратная матрица А называется вырожденной, если ее определитель равен нулю. Если , то матрица А называется невырожденной.
Следует оговорить следующий момент.
Если
с системой линейных алгебраических
уравнений 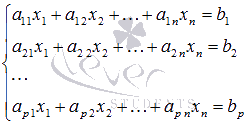 произвести
следующие действия
произвести
следующие действия
поменять местами два уравнения,
умножить обе части какого-либо уравнения на произвольное и отличное от нуля действительное (или комплексное) число k,
к обеим частям какого-либо уравнения прибавить соответствующие части другого уравнения, умноженные на произвольное число k,
то получится эквивалентная система, которая имеет такие же решения (или также как и исходная не имеет решений).
Для расширенной матрицы системы линейных алгебраических уравнений эти действия будут означать проведение элементарных преобразований со строками:
перестановку двух строк местами,
умножение всех элементов какой-либо строки матрицы T на отличное от нуля число k,
прибавление к элементам какой-либо строки матрицы соответствующих элементов другой строки, умноженных на произвольное число k.
Теперь можно переходить к описанию метода Гаусса.
ИСКЛЮЧЕНИЕ ПО ГАУССУ: РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ: ПРИМЕРЫ И РЕШАЕМЫЕ ЗАДАЧИ: ВЫСШАЯ ШКОЛА
Содержимое этой страницы:
Введение
Система уравнений (линейная) — это группа (линейных) уравнений с различные неизвестные факторы. Вообще говоря, неизвестные факторы появляются в различных уравнениях.
Уравнение с различными неизвестными факторами связывает их друг с другом.
Решение системы состоит в нахождении значения неизвестных факторов способом, который проверяет все уравнений, составляющих систему.
Если существует одно решение (одно значение для каждого неизвестного фактора), мы будем говорить, что система Consistent Independent System (CIS) .
Если есть различные решения (система имеет бесконечно много решений), мы говорим, что система является Согласованная зависимая система (CDS). .
Если решения нет, а это произойдет, если есть два или несколько уравнений, которые нельзя проверить одновременно, мы говорим, что это несогласованная система (IS) .Например, следующая система уравнений
$$ \ begin {case} \ begin {array} {lcl} y & = & 0 \\ 2x + y & = & 0 \\ 2x + y & = & 2 \ end {array} \ end {cases} $ $
несовместимо, потому что мы получаем решение x = 0 из второго уравнения, а из третьего — x = 1 .
В этом разделе мы собираемся решать системы, используя метод исключения Гаусса , который заключается в простом выполнении элементарных операций в строке или столбце расширенной матрицы, чтобы получить свой эшелон из или его сокращенный эшелон форма (Гаусс-Иордан).
Метод разрешения
Применяем метод исключения Гаусса-Джордана : получаем сокращенного эшелона строки формы из расширенной матрицы систему уравнений, выполняя элементарные операции в строках (или столбцах).
Получив матрицу, мы применяем теорему Руше-Капелли , чтобы определить тип системы и получить решение (я):
Пусть A · X = B будет системой m линейных уравнений с n неизвестным факторы, m и n натуральные числа (не ноль):
AX = B соответствует тогда и только тогда, когда
$$ ранг (A) = ранг (A | B) $$
AX = B — это непротиворечивый независимый тогда и только тогда, когда,
$$ ранг (A) = n = ранг (A | B) $$
Примечание: Элементарные операции в строках или столбцах позволяют получить системы, эквивалентные исходной, но с формой, упрощающей получение решений (если они есть).Также есть более быстрые инструменты для выработки решений в СНГ, такие как правило Крамера.
Система 1
Показать решение
Расширенная матрица системы
того же размера, что и система (2×3). Вертикальная линия, отделяющая коэффициенты матрицы от вектора независимых членов.
Выполняем элементарные операции в строках, чтобы получить сокращенную форму эшелона строк:Умножаем первую строку на 1/5 а вторую на 1/3
Добавляем вторую строку с первой
Вторую строку умножаем на 5/7
Складываем первую строку со второй, умноженной на -2/5
Эта последняя эквивалентная матрица представлена в сокращенной форме эшелона строк. и это позволяет нам быстро увидеть рейтинг матрица коэффициентов и дополненная.
Считаем ранги:
По теореме Руше-Капелли система непротиворечива Независимая. Полученная матрица представляет собой систему
, который является решением исходной системы.
Система 2
Показать решение
Расширенная матрица системы
Проводим элементарные операции в строках для получения приведенных форма эшелона строки:
Вторую строку умножаем на 1/2
Добавляем первую строку со второй
Умножаем первую строку на 1/3
Эта последняя эквивалентная матрица находится в форме сокращенного эшелона строк и имеет нулевую строку, что означает, что строки в исходной системе линейно зависимы. (любой из них может быть получен путем умножения другого на скаляр, не равный нулю).
Рассчитываем ранги
По теореме Руше-Капелли система непротиворечива. Кроме того, это зависит, поскольку ранг (1) ниже, чем количество неизвестных факторов (2).
Полученная матрица представляет собой систему
Решения
Система 3
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить сокращенный рядный эшелон формыМы меняем порядок строк (так у нас уже будет 1 в первой строке без необходимости умножать)
Складываем вторую строку с первой, умноженной на 5 :
Вторую строку умножаем на -1/15
Эта последняя матрица имеет эшелонированную форму (не сокращена).
Мы можем непосредственно заметить, что система несовместима, потому что у нас следующее равенство (вторая строка):
$$ 0x + 0y = 1 $$, это невозможное равенство.
Рассчитываем ранги матрицы коэффициентов и дополненной:
По теореме Руше-Капелли система несовместна (решения нет). Полученная матрица представляет собой систему
Система непоследовательна, потому что мы имеем невозможное равенство
$$ 0 = 1 $$
Система 4
Показать решение
Расширенная матрица системы
(размер 3х4).
Выполняем элементарные операции в строках, чтобы получить сокращенный рядный эшелон формыУмножаем первую строку на 1/5
Складываем вторую и третью строки, умножив первую на -2
Вторую и третью строки умножаем на 5
Складываем вторую строку с третьей, умноженной на -1
Умножаем вторую строку на -1/10 и третью на 1/11
Мы складываем первую строку со второй, умноженной на -2/5 , а третью со второй, умноженной на -1
Третью строку умножаем на -11/5
Эта последняя эквивалентная матрица находится в сокращенной форме эшелона строк (мы знаем ее, потому что это единичная матрица).Имея единичную матрицу, мы знаем, что это согласованная независимая система, и можем получить единственное решение.
Рассчитываем ранги
По теореме Руше-Капелли система непротиворечива Независимая. Полученная матрица представляет собой систему
, который является решением системы.
Система 5
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить сокращенный рядный эшелон формыМы вычитаем первую строку из второй и добавляем третью строку с первой.
Умножаем первую строку на 1/2 , а вторую на 1/3
Мы складываем первую строку со второй, умноженной на 1/2 , и третью строку со второй, умноженной на -2
Третью строку умножаем на 1/3
Складываем первую строку с третьей, умноженной на -3/2
Эта последняя матрица представляет собой эшелонированную матрицу с сокращенной строкой (мы знаем это, потому что у нас есть единичная матрица).
Рассчитываем ранги
По теореме Руше-Капелли система непротиворечива Независимая. Полученная матрица представляет собой систему
Система 6
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить сокращенный рядный эшелон формыУмножаем вторую строку на -1/3 а третью на 1/4
Складываем вторую и третью строки, умножив первую на -1
Умножаем вторую строку на -3/4 а третью на -1
Третью строку складываем со второй, умноженной на -1
Эта последняя матрица имеет эшелонированную форму (но не сокращена) и мы не продолжаем выполнять операции по строкам, потому что можем видим, что последняя строка делает систему непоследовательной.Эта строка сообщает нам:
$$ 0x + 0y + 0z = -1 $$И все это невозможное равенство.
Фактически у нас есть ранги
По теореме Руше-Капелли система несовместна.
Система 7
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить сокращенный рядный эшелон формыУмножаем первую и вторую строки на 1/3 и на 1/6 соответственно
Вторую строку вычитаем из третьей
Добавляем первую строку со второй
Третью строку умножаем на 3
Эта последняя матрица находится в сокращенном эшелоне строк формы , поэтому мы можем легко вычислить ранги:
Рассчитываем ранги
По теореме Руше-Капелли система непротиворечива.Но он не является независимым, потому что количество неизвестных факторов (3) отличается от ранга. Полученная матрица представляет собой систему
Решения
Система 8
Показать решение
Расширенная матрица системы
Примечание: , прежде чем мы начнем, мы должны прокомментировать, что процедура будет таким же, как и раньше.Но у нас есть корни в матрице, а это значит, что операции над строками будут длинными и утомительно. Эта задача не очень интересна в дидактическом смысле, помимо расчетов.
Проводим элементарные операции в строках, чтобы получить пониженный рядный эшелон формы
Мы складываем вторую строку с первой, умноженной на -√5 и, с третий, умноженный на -2/5
Умножаем вторую строку на 1 / √5 и третью на 5/17
Складываем первую строку с третьей и из второй вычитаем третью
Переписываем матрицу
Вторую строку умножаем на (√5 / 5-5) -1
Складываем первую строку со второй, умноженной на -5
В этой последней матрице (почти) в строке уменьшено форма эшелона (надо поменять второй и третий ряды так что это правда).Из последней матрицы получаем решения:
Система 9
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить сокращенный рядный эшелон формыСкладываем третью и четвертую строки, умножив первую на 3 и -2 соответственно
Складываем первую, вторую и третью строки, а четвертую умножаем на 2 , -3 и 5 соответственно
Четвертую строку умножаем на -1 и меняем на вторую
Умножаем третью и четвертую строки на 1/34 и -1/22 соответственно
Вычитаем третью строку из четвертой
Четвертую умножаем на -187/42
Добавляем в первую строку третью умноженную на -13 и вторую на 8
К первой строке прибавляем четвертую, умноженную на 5/34 , ко второй прибавляем первую, умноженную на 5/17 и к третьему добавляем первое, умноженное на -3/34
По теореме Руше-Капелли система является непротиворечивой Независимой и решением является
Система 10
Показать решение
Расширенная матрица системы
Примечание: Эта система была включена в цель отметить, что теория матрицы применима к комплексным числам.Единственное отличие от предыдущих систем в том, что теперь нам нужно действовать путем умножения и деления комплексные числа.
Выполняем элементарные операции в строках для получения приведенной формы эшелона строк
Умножаем вторую строку на 1/2 и меняем ее на первую
Добавляем вторую строку, первую, умноженную на — (1 + i)
Вторую строку умножаем на
Добавляем первую строку ко второй умноженной на -i / 2
Эта последняя матрица имеет сокращенную форму, потому что это единичная матрица.
По теореме Руше-Капелли система является непротиворечивой Независимой и решением является
Matesfacil.com
компании J. Llopis под лицензией
творческий
Международная лицензия Commons Attribution-NonCommercial 4.0.
,
Систем линейных уравнений: исключение Гаусса
Системы
линейных уравнений:
Решение методом исключения Гаусса (стр.
6 из 7)
Разделы: Определения, Решение по графику, Подстановка, Исключение / добавление, исключение по Гауссу.

Решение трех переменных, линейные системы с тремя уравнениями сложнее, по крайней мере, на начальном этапе, чем решение систем с двумя переменными, поскольку требуемые вычисления более грязный.Вам нужно будет очень аккуратно работать, и вам следует планируйте использовать много бумаги для заметок. Метод решения этих систем является расширением метода сложения двух переменных, поэтому сделайте конечно ты знаешь это метод хорошо и можно использовать его последовательно правильно.
Хотя метод решения основан на добавлении / исключении, попытка выполнить фактическое добавление имеет тенденцию становится очень запутанным, поэтому существует систематизированный метод решения трех или более переменных системы.Этот метод называется «исключение Гаусса» (с уравнения заканчиваются тем, что называется «строковой формой»).
Начнем с простого, и работаем над более сложными примерами.
- Решите следующие проблемы система уравнений.
Достаточно легко увидеть как действовать в этом случае. Я просто подставлю обратно значение z -value из третьего уравнения во второе, решите результат для л , г. а затем подключите z и y в первое уравнение и решите результат для x .
10 л 3 (3) = 11
10 y 9 = 11
10 y = 20
y = 2
5x +
4 (2) (3) = 0
5 x + 8 3 = 0
5 x + 5 = 0
5 x = 5
x = 1
Тогда решение ( х , y , z ) = (1, 2, 3).
Причина, по которой эта система была легко решить, что система была «треугольной»; это относится к уравнениям, имеющим форму треугольника, из-за нижних уравнений содержащий только более поздние переменные.
Дело в том, что в этом формат, система проста в решении. А гауссовское исключение — это метод, который мы будем использовать для преобразования систем в эту верхнетреугольную форму, используя операции со строками, которые мы узнали, когда применяли метод сложения.
- Решите следующие проблемы система уравнений с использованием исключения Гаусса.
Уравнение не решается для переменной, поэтому мне нужно будет выполнить умножение и сложение чтобы упростить эту систему. Чтобы отслеживать свою работу, напишу вниз на каждом шагу, когда я иду. Но я буду делать свои вычисления на бумаге для заметок. Вот как я это сделал:
Первое, что нужно сделать состоит в том, чтобы избавиться от ведущих x -термов в два ряда.А пока я просто посмотрю, какие строки будут легко расчистить; Я могу поменять строки позже, чтобы перевести систему в «верхний треугольной «формы. Нет правила, согласно которому я должен использовать x — срок из первой строки, и в этом случае, думаю, будет проще используйте термин x из третьей строки, так как его коэффициент просто «1». Поэтому я умножу третью строку на 3, и добавьте его в первую строку.Я делаю вычисления на бумаге для заметок:
… а потом записываю результатов:
(Когда мы решали системы с двумя переменными, мы могли умножить строку, переписав систему в сторону, а затем добавить. Для этого нет места в трехвариантная система, поэтому нам и нужна бумажка.)
Предупреждение: поскольку я не на самом деле ничего не делаю с третьей строкой, я скопировал ее без изменений, в новую матрицу уравнений. Я б / у третий ряд, но я на самом деле не менял Это. Не путайте «использование» с «изменением».
Чтобы получить меньшие числа для коэффициентов умножу первую строку пополам:
Теперь умножу третий ряд на 5 и добавьте это ко второму строка.Работаю на бумаге для заметок:
… а потом записываю результаты: Авторские права Элизабет Стапель 2003-2011 Все права защищены
Я ничего не делал с первым рядом, поэтому я скопировал его без изменений. Я работал с третий ряд, но я работал только на вторая строка, поэтому вторая строка обновляется, а третья строка копируется более без изменений.
Хорошо, теперь x — столбец удаляется, за исключением ведущего члена в третьей строке. Так что дальше Приходится работать над колонкой и .
Предупреждение: Начиная с третьего уравнение имеет член x , Я больше не могу использовать его ни в одном из двух других уравнений (или я отменить мой прогресс). Я могу работать с на уравнении, но не на с Это.
Если я добавлю дважды первое во вторую строку, это даст мне ведущую 1 во втором ряду. Я не буду избавились от лидирующего y -терм во втором ряду, но я его преобразовал (не вмешиваясь дробями) в более простую форму. (Вы должны сохранить обратите внимание на такого рода упрощения.) Сначала я делаю царапину работа:
… а потом записываю результатов:
Теперь могу использовать второй ряд, чтобы убрать и -семестр в первом ряду. Вторую строку умножу на 7 и добавить. Сначала я царапаю работа:
… а потом записываю результатов:
я могу сказать что z сейчас, но, чтобы быть внимательным, я разделю первую строку на 43.Затем я переставляю ряды, чтобы придать им верхнетреугольную форму:
Теперь я могу начать процесс обратного решения:
Тогда решение ( х , y , z ) = ( 2, 3, 1 ) .
Примечание: нет ничего священного о шагах, которые я использовал при решении указанной выше системы; там ничего не было особенно о том, как я решил эту систему. Вы могли бы работать в другом упорядочить или упростить разные строки, и все равно придумать правильный ответ. Эти системы достаточно сложны, поэтому вряд ли один правильный способ вычисления ответа. Так что не беспокойтесь о том, «как она знала, что делать дальше? », потому что здесь нет правила.я просто делал все, что пришло мне в голову; Я делал то, что казалось самым простым пришла в голову первая. Не волнуйтесь, если бы вы использовали совершенно другой шаги. Если каждый шаг на этом пути верен, вы получите тот же ответ.
В приведенном выше примере я мог пошли дальше в своих вычислениях и более тщательно проработали строковые операции, очищая все термины и кроме этого во втором ряду и во всех терминах z кроме того, что в первой строке.Вот что будет тогда процесс посмотрели так:
Так я могу просто читать от значений x , л , г. и z , и мне не нужно возиться с обратной заменой. Это более полное метод решения называется «методом исключения Гаусса-Жордана» (с уравнения, попадающие в так называемый «пониженный ряд-эшелон» образуют «).Многие тексты доходят только до исключения Гаусса, но я всегда было легче продолжать и делать Гаусс-Джордан.
Обратите внимание, что я выполнил две строковые операции сразу на этом последнем шаге перед переключением строк. Пока я не работая с и работая на в том же ряду на том же этапе, это хорошо. В этом случае я работал с первой строкой и рабочая по второй и третий ряды.
<< Предыдущая Вверх | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Вернуться к указателю Далее >>
Цитируйте эту статью как: | Стапель, Елизавета.
«Системы линейных уравнений, решаемые методом исключения Гаусса». Purplemath |
Систем линейных уравнений: исключение Гаусса
Системы линейных уравнений: исключение ГауссаРешать нелинейные системы уравнений довольно сложно, а линейные системы довольно легко изучать. Существуют численные методы, которые помогают аппроксимировать нелинейные системы линейными в надежде, что решения линейных систем достаточно близки к решениям нелинейных систем. Мы не будем здесь это обсуждать.Вместо этого мы сосредоточим наше внимание на линейных системах.
Для простоты мы ограничимся тремя, максимум четырьмя неизвестными. Читатель, интересующийся случаем большего количества неизвестных, может легко развить следующие идеи.
Определение. Уравнение
a x + b y + c z + d w = h
где a , b , c , d и h — известные числа, а x , y , z и w — неизвестные числа. называется линейным уравнением .Если h = 0, линейное уравнение называется однородным . Линейная система представляет собой набор линейных уравнений, а однородная линейная система представляет собой набор однородных линейных уравнений.
Например,
и
линейные системы, а
является нелинейной системой (поскольку y 2 ). Система
является однородной линейной системой.
Матричное представление линейной системы
Матрицы помогают переписать линейную систему в очень простой форме.Затем для решения систем можно использовать алгебраические свойства матриц. Сначала рассмотрим линейную систему
Установите матрицы
Используя матричное умножение, мы можем переписать линейную систему выше как матричное уравнение
Как видите, это намного лучше, чем уравнения. Но иногда стоит решить систему напрямую, минуя матричную форму. Матрица A называется матричным коэффициентом линейной системы.Матрица C называется неоднородным членом . когда , линейная система однородна. Матрица X — это неизвестная матрица. Его записи являются неизвестными линейной системы. Расширенная матрица , связанная с системой, является матрицей [ A | C ], где
В общем, если линейная система имеет n уравнений с m неизвестными, то матричный коэффициент будет матрицей nxm, а расширенная матрица — матрицей nx (m + 1).Теперь обратим наше внимание на решения системы.
Определение. Две линейные системы с n неизвестными считаются эквивалентом тогда и только тогда, когда они имеют одинаковый набор решений.
Это определение важно, поскольку идея решения системы состоит в том, чтобы найти эквивалентную систему, которую легко решить. Вы можете спросить, как мы придумаем такую систему? Легко, мы делаем это с помощью элементарных операций . В самом деле, ясно, что если мы поменяем местами два уравнения, новая система все равно будет эквивалентна старой.Если мы умножим уравнение на ненулевое число, мы получим новую систему, по-прежнему эквивалентную старой. И, наконец, заменяя одно уравнение суммой двух уравнений, мы снова получаем эквивалентную систему. Эти операции называются элементарными операциями в системах. Посмотрим, как это работает в конкретном случае.
Пример. Рассмотрим линейную систему
Идея состоит в том, чтобы сохранить первое уравнение и поработать над двумя последними. Поступая так, мы попытаемся убить одного из неизвестных и решить два других.Например, если мы сохраним первое и второе уравнение и вычтем первое из последнего, мы получим эквивалентную систему
Затем мы сохраняем первое и последнее уравнение и вычитаем первое из второго. Получаем эквивалентную систему
Теперь мы сосредоточимся на втором и третьем уравнениях. Повторяем ту же процедуру. Попробуйте убить одного из двух неизвестных ( y или z ). Действительно, мы сохраняем первое и второе уравнение и добавляем второе к третьему после умножения его на 3.Мы получили
Это, очевидно, означает z = -2. Из второго уравнения мы получаем y = -2, и, наконец, из первого уравнения мы получаем x = 4. Следовательно, линейная система имеет одно решение.
Переход от последнего уравнения к первому при решении неизвестных называется обратным решением .
Имейте в виду, что линейные системы, для которых матричный коэффициент является верхнетреугольным, легко решить. Это особенно верно, если матрица имеет эшелонированную форму.Таким образом, фокус состоит в том, чтобы выполнить элементарные операции по преобразованию исходной линейной системы в другую, для которой матрица коэффициентов имеет эшелонированную форму.
Используя наши знания о матрицах, можем ли мы в любом случае переписать то, что мы сделали выше, в матричной форме, которая упростит нашу нотацию (или представление)? Действительно, рассмотрим расширенную матрицу
Проделаем с этой матрицей элементарные операции со строками. Действительно, если мы сохраним первую и вторую строки и вычтем первую из последней, мы получим
Затем мы сохраняем первую и последнюю строки и вычитаем первую из второй.Мы получили
Затем мы сохраняем первую и вторую строки и добавляем вторую к третьей, умножив ее на 3, чтобы получить
Это треугольная матрица, не имеющая эшелонированной формы. Линейная система, для которой эта матрица является расширенной:
Как видите, мы получили ту же систему, что и раньше. Фактически мы следовали тем же элементарным операциям, что и выше. На каждом этапе новая матрица была в точности расширенной матрицей, связанной с новой системой.Это показывает, что вместо того, чтобы писать системы снова и снова, легко поиграться с элементарными операциями со строками, и как только мы получим треугольную матрицу, напишем связанную линейную систему, а затем решим ее. Это известно как Исключение по Гауссу . Подведем итоги процедуры:
Исключение по Гауссу. Рассмотрим линейную систему.
- 1.
- Построить расширенную матрицу для системы;
- 2.
- Используйте операции элементарной строки, чтобы преобразовать расширенную матрицу в треугольную;
- 3.
- Запишите новую линейную систему, для которой треугольная матрица является связанной с ней расширенной матрицей;
- 4.
- Решите новую систему. Возможно, вам потребуется присвоить некоторые параметрические значения некоторым неизвестным, а затем применить метод обратной подстановки для решения новой системы.
Пример. Решите следующую систему методом исключения Гаусса
Расширенная матрица
Мы используем элементарные операции со строками, чтобы преобразовать эту матрицу в треугольную.Мы сохраняем первую строку и используем ее для получения всех нулей в любом месте первого столбца. У нас есть
Далее мы сохраняем первую и вторую строки и стараемся, чтобы во втором столбце были нули. Мы получили
Далее сохраняем первые три ряда. Добавляем последний к третьему, чтобы получить
Это треугольная матрица. Связанная с ним система
Очевидно, что v = 1. Установите z = s и w = t , тогда мы имеем
Из первого уравнения следует Используя алгебраические манипуляции, получаем
x = — — с — т .
Собрав все вместе, у нас есть
Пример. Используйте метод исключения Гаусса для решения линейной системы
Соответствующая расширенная матрица
Сохраняем первую строку и вычитаем первую строку, умноженную на 2, из второй строки. Мы получили
Это треугольная матрица. Связанная система
Очевидно, второе уравнение означает, что эта система не имеет решения.Следовательно, у этой линейной системы нет решения.
Определение. Линейная система называется непоследовательной или переопределенной , если она не имеет решения. Другими словами, набор решений пуст. В противном случае линейная система называется согласованной .
Следуя приведенному выше примеру, мы видим, что если мы выполним элементарные операции со строками над расширенной матрицей системы и получим матрицу, одна из строк которой равна , где , тогда система несовместима.
[Назад] [Следующий] [Геометрия] [Алгебра] [Тригонометрия] [Исчисление] [Дифференциальные уравнения] [Матричная алгебра]S.O.S MATH: Домашняя страница
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Автор : М.А.Хамси
Авторское право 1999-2020 MathMedics, LLC. Все права защищены.Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователей онлайн за последний час ,
Систем линейных уравнений: Примеры
Системы линейных уравнений: примеры (стр. 7 из 7)
Разделы: Определения, Решение по графику, Подстановка, Исключение / добавление по Гауссу устранение.

Хотя системы математического класса обычно имеют целочисленные решения, иногда (особенно для задач со словами) вы увидите решения, включающие дроби.
- Решите следующие проблемы система уравнений методом исключения Гаусса:
Думаю, воспользуюсь первым ряд, чтобы убрать x -термов со второго и третьего рядов:
Технически я должен сейчас первую строку разделите на 2, чтобы получить ведущую 1, но это даст мне дроби, и я бы хотел избежать этого до тех пор, пока насколько возможно.Вместо этого я перейду к использованию второй строки, чтобы очистить из у -триместра из третьего ряда:
я могу разделить третий ряд по 4:
Чтобы быть технически правильным, Теперь я разделю второй ряд на 5 и первый ряд на 2:
(Вы можете проверить с вашим инструктором относительно того, насколько он будет внимательным правильная форма.Вы «должны» показать все единицы для ведущих коэффициентов или допустимо избегать дробей?)
Обратное решение, получаю:
Тогда решение ( х , y , z ) = ( 3 / 10 , 2 / 5 , 0) .
Предупреждение: пока я не показал свою царапину поработав над этой последней проблемой, я должен был сделать скретч. Пожалуйста, используйте бумага для заметок и выписывать; не пытайтесь делать это в своем глава; существует слишком много возможностей для ошибок. (Я хочу знаете, сколько ошибок я сделал при написании этого урока? Даже не получить меня завел!)
Вот еще пример:
- Решите следующие проблемы система:
думаю воспользуюсь вторым ряд для работы на терминах x в первом и третьем рядах.Я смогу убрать третий ряд, и я смогу произвести 1 x как ведущий термин в Первый ряд. Это позволит мне завершить работу по очистке x — столбец, и я смогу это сделать, не имея дела с дробями:
(Многие инструкторы научит вас всегда делить на одну из строк, чтобы получить ведущий коэффициент 1, но я бы предпочел сделать один или два дополнительных шага и использовать дополнение, чтобы получить ведущий 1.Это просто личное предпочтение, но я уверен, что вы видите преимущество как можно дольше избегать дробей. Это действительно может сократить по ошибкам вычислений.)
Сейчас воспользуюсь этим красивым ведущий x дюймов первую строку, чтобы убрать ведущий член во второй строке. Пока Я на нем, еще третий ряд делю на 6, чтобы получить меньшие числа:
Хм… Второй и третьи ряды такие же. Я могу использовать второй ряд, чтобы убрать третий строка целиком: Авторские права Элизабет Стапель 2003-2011 Все права защищены
Вспоминая регистр с двумя переменными, получая строку вида «0 = 0 «(что верно, но бесполезно) означает, что это зависимая система, и решение будет содержать переменные.Если вы попадете в линейную алгебру много, вы узнаете, что ответ выше означает, что решение представляет собой линию в трехмерном пространстве, а не отдельную точку. Для Теперь все, что вам нужно знать, это как написать решение. Чтобы найти решение, мне нужно решить два оставшихся уравнения для x и л дюйм условия z :
х z = 2
x = z 2
л 3 z = 4
y = 3 z 4
( х , y , z ) = ( t 2, 3 т 4, т )
Помните, что ваша книга может используйте переменную, отличную от « t «, и что т — это просто стоит на z .Эта форма решения просто говорит, что z — это какое бы значение вы ни выбрали, тогда x будет на два меньше и y это на четыре меньше, чем в три раза больше, чем z .
- Решите следующие проблемы система уравнений:
Вы должны получить к настоящему времени все повесить, поэтому я просто покажу шаги, которые я использовал:
Как только я получу ерунду строка (например, «0 = 1 «), я знаю что это несовместимая система, и я могу уйти.
Помните разницу между два особых случая: тривиальная строка (например, «0 = 0 «) означает, что вы иметь зависимую систему с решением, содержащим переменные; бессмысленный строка (например, «0 = 1 «) означает, что вы иметь несовместимую систему без какого-либо решения. Не путайте эти; это (Предупреждение!) общие вопросы с подвохом на тестах.
В зависимости от курса, теперь вы можете перейти к использованию матриц для решения систем уравнений.Если вы это сделаете, методы, которые вы будете изучать для матриц, скорее всего, будут быть очень похожим на то, что вы видели на этом уроке.
<< Предыдущая Вверх | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Вернуться к индексу
Цитируйте эту статью как: | Стапель, Елизавета.«Системы линейных уравнений: примеры». Пурпурная математика .
Доступна по номеру |
