Тригонометрические уравнения и неравенства
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И МОЛОДЁЖНОЙ ПОЛИТИКИ ЧУВАШСКОЙ РЕСПУБЛИКИ
Государственное автономное профессиональное
образовательное учреждение Чувашской Республики
«Чебоксарский техникум транспортных и строительных технологии»
(ГАПОУ «Чебоксарский техникум ТрансСтройТех» Минобразования Чувашии)
«Тригонометрические уравнения и неравенства»
Методические рекомендации по выполнению внеаудиторных самостоятельных работ
Дмитриева М.В., Сорокина А.А Тригонометрические уравнения и неравенства: методические рекомендации по выполнению внеаудиторных самостоятельных работ для студентов 1 курса НПО и СПО. – Чебоксары: ГАПОУ «ЧТТСТ» Минобразования Чувашии, 2017.- 17 с.
Перепелкина Зинаида Юрьевна, методист, ГАПОУ «Чебоксарский техникум транспортных и строительных технологий» Минобразования Чувашии.
Григорьева Евгения Дмитриевна, преподаватель математики, ГАПОУ «Чебоксарский техникум технологии питания и коммерции» Минобразования Чувашии.
В пособии представлены рекомендации для оказания методической помощи студентам, обучающимся по профессиям в выполнении самостоятельной внеаудиторной работы при изучении тригонометрических уравнений и неравенств в дисциплине: «Математика».
Материалы пособия рекомендуются преподавателям и студентам профессионального образования.
В настоящее время основной задачей современного образования является переориентация на приоритет развивающей функции обучения. Это означает, что на первый план выходит задача интеллектуального развития личности, т.е. развитие учебно-познавательной деятельности. Пожалуй, ни один общеобразовательный предмет не может конкурировать с возможностями математики в воспитании мыслящей личности. Уже несколько десятилетий тригонометрия, как отдельная дисциплина образовательного курса математики не существует, она плавно растеклась не только в геометрию и алгебру основной школы, но и в алгебру и начала анализа.
Тригонометрические уравнения и неравенства занимают одно из центральных мест в курсе математики в системе СПО, как по содержанию учебного материала, так и по способам учебно-познавательной деятельности. Которые могут и должны быть сформированы при их изучении и применены к решению большого числа задач теоретического и прикладного характера. Тригонометрические уравнения и неравенства одни из самых сложных тем в курсе математики, которые могут возникать при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях. Следует заметить, что решение тригонометрических уравнений и неравенств создаёт предпосылки для систематизации знаний обучающихся, связанных со всем учебным материалом по тригонометрии (например, свойства тригонометрических функций, приёмы преобразования тригонометрических выражений и т.д.), так же даёт возможность установить действенные связи с изученным материалом по алгебре (уравнения, равносильность уравнений, неравенства, тождественные преобразования алгебраических выражений и т.д.). Иначе говоря, рассмотрение приёмов решения тригонометрических уравнений и неравенств, предполагает своего рода перенос этих умений на новое содержание.
Методические рекомендации предназначены для оказания методической помощи студентам 1 курса СПО и НПО при изучении модуля занятий по теме «Тригонометрические уравнения и неравенства».
Общие указания по выполнению самостоятельных работ по математике для студентов 1 курсов НПО и СПО по теме «Тригонометрические уравнения и неравенства»
При выполнении и оформлении самостоятельных работ следует руководствоваться следующими правилами:
1. Представляемые самостоятельные работы должны быть правильно и грамотно оформлены.
2. Задания самостоятельных работ следует решать в порядке их расположения в тексте самостоятельных работ.
3. Решения всех задач и пояснения к ним должны быть достаточно подробными. При необходимости следует делать соответствующие ссылки на вопросы теории, с указанием формул, используемых при решении данной задачи.
4. Чертежи и графики должны быть выполнены аккуратно, четко.
2. Основные формулы тригонометрии
Ниже приводятся формулы, наиболее важные при решении математических задач по разделу «Тригонометрия».
- Формулы половинного аргумента
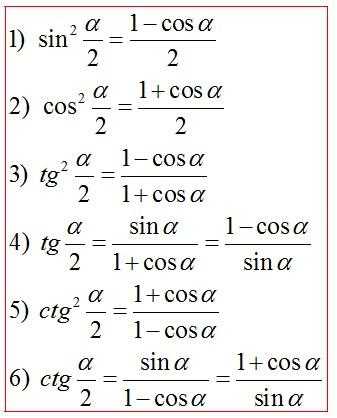
- Универсальная подстановка через тангенс половинного аргумента

3. Обратные тригонометрические функции
Арксинус (y = arcsin x) – это функция, обратная к синусу (x = sin y), имеющая область определения и множество значений 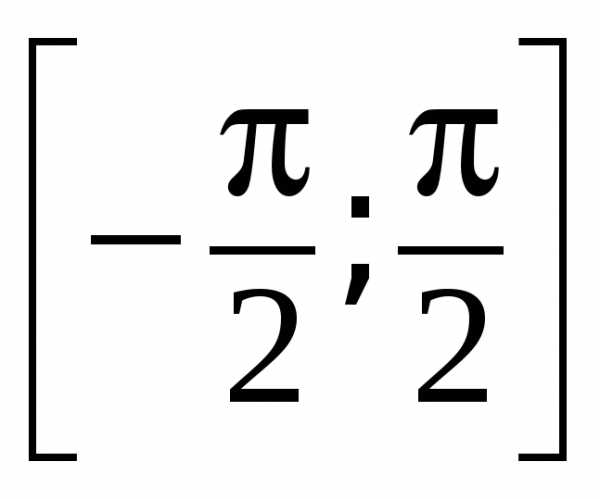 .
.
Арккосинус (y = arccos x) – это функция, обратная к косинусу (x = cos y), имеющая область определения и множество значений  .
.
Арктангенс (y = arctg x) – это функция, обратная к тангенсу (x = tg y), имеющая область определения и множество значений  .
.
Арккотангенс (y = arcctg x) – это функция, обратная к котангенсу (x = ctg y), имеющая область определения и множество значений  .
.
4. Тригонометрические уравнения.
Тригонометрические уравнения — уравнения, содержащие неизвестное под знаком тригонометрической функции.
Уравнения вида , , , , называются простейшими тригонометрическими уравнениями. Рассмотрим схему их решения.
Уравнение
Общий вид решения уравнения , где определяется формулой:
(целые числа), при уравнение не имеет решений.
Частные случаи
Пример 1. Найти решения уравнения 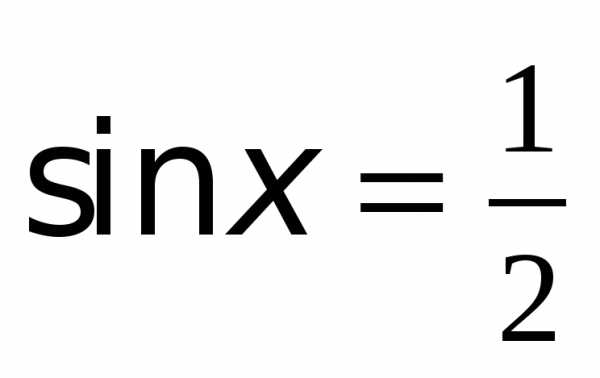 .
.
Применяя формулу общего вида решения уравнения , получим:
.
Ответ: .
Уравнение
Общий вид решения уравнения , где определяется формулой:
, при уравнение не имеет решений.
Частные случаи
Пример 2. Найти решения уравнения 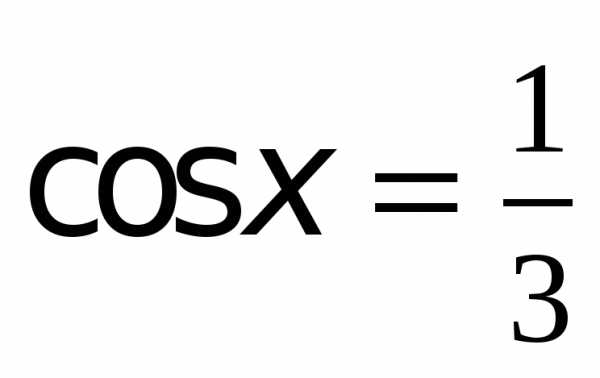 .
.
Применяя формулу общего вида решения уравнения , получим:
.
Ответ: .
Уравнение
Общий вид решения уравнения определяется формулой: .
Пример 3. Найти решения уравнения 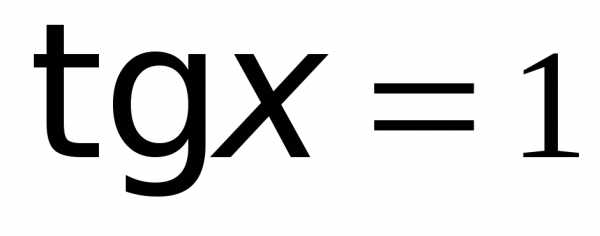 .
.
Применяя формулу общего вида решения уравнения , получим:
,
.
Ответ: .
Уравнение
Общий вид решения уравнения определяется формулой:.
Пример 4. Найти решения уравнения 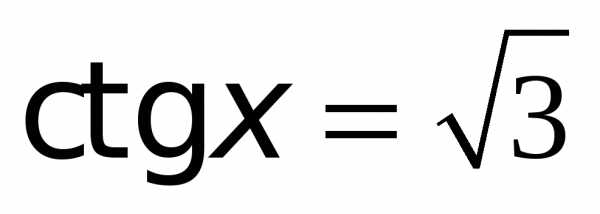 .
.
Применяя формулу общего вида решения уравнения , получим:
,
.
Ответ: .
Рассмотрим уравнения, которые являются алгебраическими, относительно какой — либо тригонометрической функции, а так же уравнения, которые требуют преобразования тригонометрических выражений.
Пример 5. Найти решения уравнения .
Сделаем замену .
.
Найдем корни уравнения:  ,
, 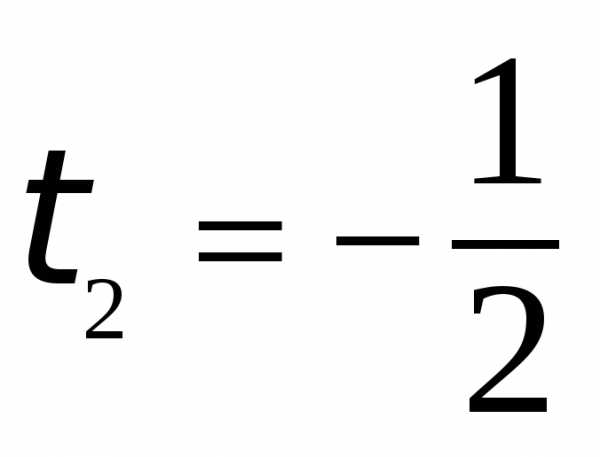
Делаем обратную замену: 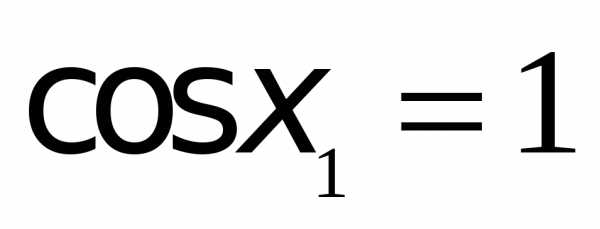 ,
,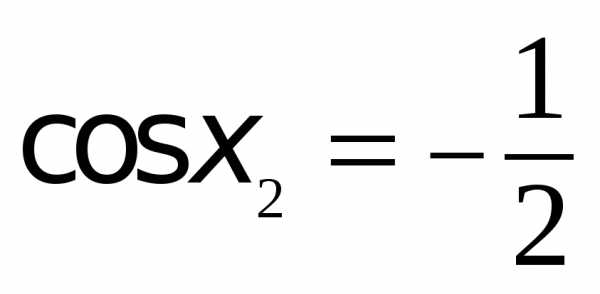 .
.
,
.
Ответ: , .
Пример 6. Найти решения уравнения .
Применяя формулы двойного угла, получим: .
.
.
или  .
.
,
.
Ответ: , .
При решении уравнений, содержащих тригонометрическую функцию, удобно использовать общий план решения любого тригонометрического уравнения:
Выражаем все входящие в уравнении тригонометрические функции через одну какую-либо функцию и один и тот же аргумент.
Определяем значение этой функции, пользуясь общим алгоритмом решения уравнений.
Находим по полученным значениям функции соответствующие значения аргумента.
Записываем ответ, пользуясь формулами общего вида решения простейших тригонометрических уравнений.
Проверяем найденные решения (в случае нарушения равносильности уравнений) и объединяем решения (если это возможно).
5. Самостоятельная работа №1
Вариант 1.
Решите уравнения:
Вариант 2.
Решите уравнения:

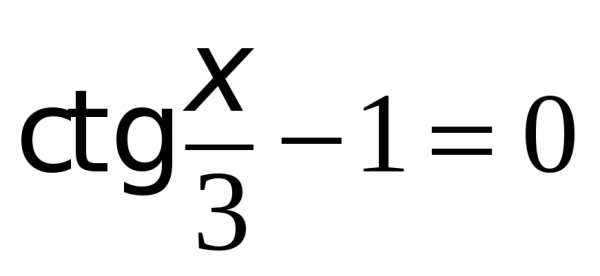
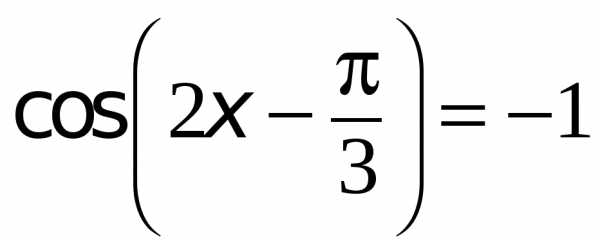
Тригонометрические неравенства
Тригонометрическими неравенствами называются неравенства, которые содержат переменную под знаком тригонометрической функции.
Решение тригонометрических неравенств зачастую сводится к решению простейших тригонометрических неравенств вида:
Решаются простейшие тригонометрические неравенства графически или с помощью единичной тригонометрической окружности.
По определению, синус угла есть ордината точки
есть ордината точки  единичного круга (рис. 1), а косинусом – абсцисса этой точки. Этот факт используется при решении простейших тригонометрических неравенств с косинусом и синусом с помощью единичного круга.
единичного круга (рис. 1), а косинусом – абсцисса этой точки. Этот факт используется при решении простейших тригонометрических неравенств с косинусом и синусом с помощью единичного круга.
Рис. 1
Рассмотрим схему решения тригонометрических неравенств с помощью единичного круга.
Неравенства

Рис. 2
Неравенства

Рис. 3
Неравенства
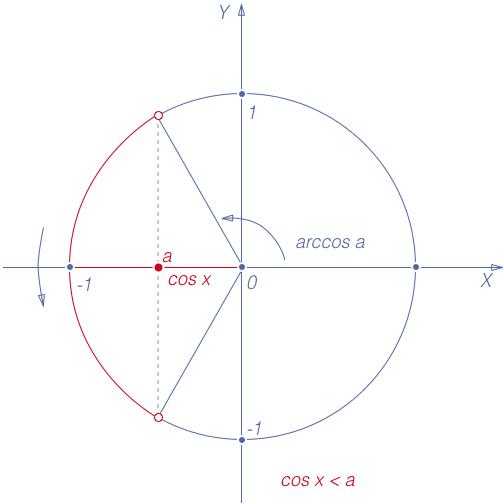
Рис. 4
Неравенства
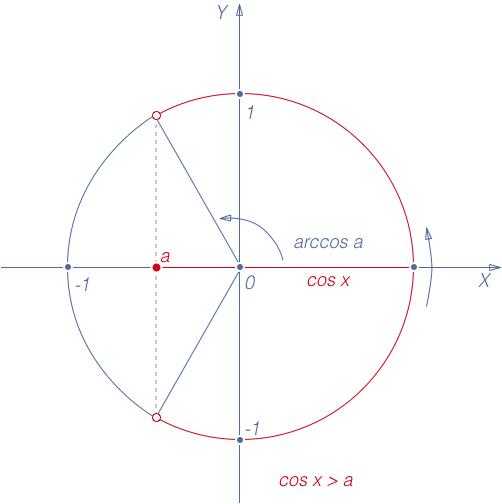
Рис. 5
Неравенства 
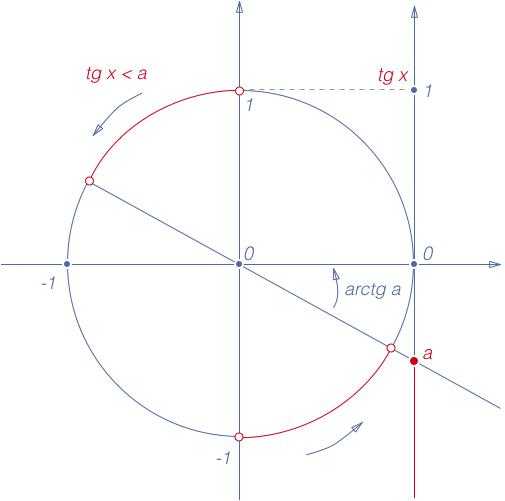
Рис. 6
Неравенства 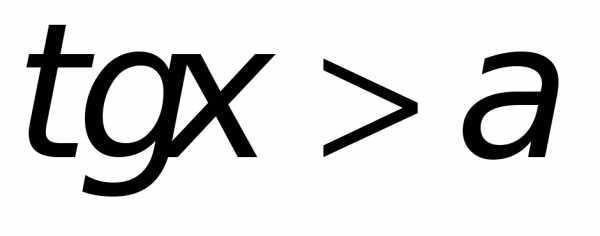
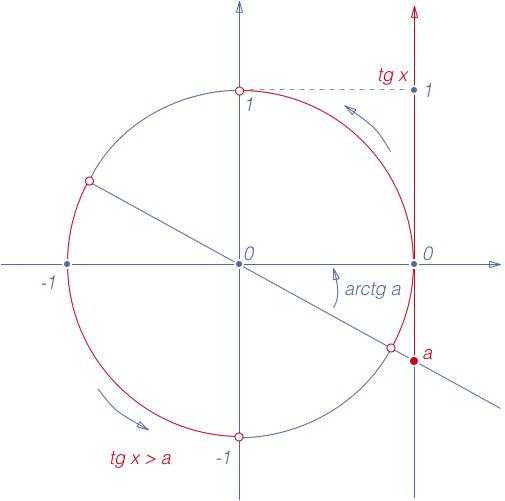
Рис. 7
Неравенства 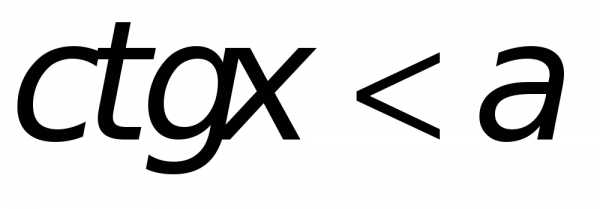
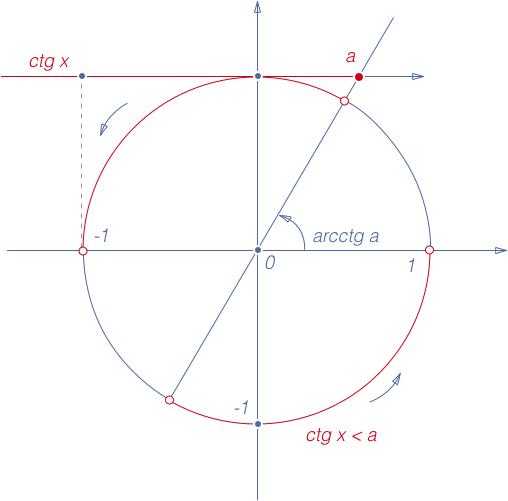
Рис. 8
Неравенства 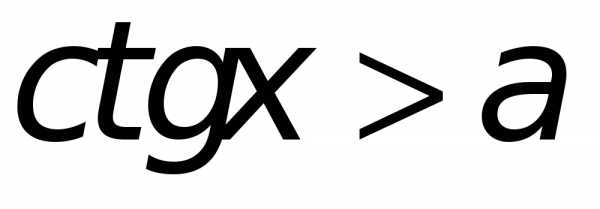

Рис. 9
Самостоятельная работа №2
Вариант 1. Решите неравенства:
|
Вариант 2. Решите неравенства:
|
ЗАКЛЮЧЕНИЕ
В методической разработке были рассмотрены способы решения тригонометрических уравнений и неравенств, как простейших, так и более сложного уровня и приведены варианты внеаудиторных самостоятельных работ, а так же рассмотрены основные теоретические сведения: определение и свойства тригонометрических и обратных тригонометрических функций; выражение тригонометрических функций через другие тригонометрических функции, что очень важно для преобразования тригонометрических выражений, в особенности содержащих обратные тригонометрические функции. Кроме основных тригонометрических формул, хорошо известных из школьного курса, приведены формулы упрощающие выражения, содержащие обратные тригонометрические функции. Ввиду того, что решения тригонометрических уравнений и неравенств можно записать несколькими способами, и вид этих решений не позволяет сразу установить, являются ли эти решения одинаковыми или различными, рассмотрена общая схема решения тригонометрических уравнений и неравенств.
Следует отметить, что выполнение внеаудиторных самостоятельных работ способствует систематизации и закрепления полученных теоретических знаний и практических умений обучающихся, углубления и расширения теоретических знаний, развития познавательных способностей и активности обучающихся: творческой инициативы, самостоятельности, ответственности, организованности и формирование самостоятельности мышления, способностей к саморазвитию, совершенствованию и самоорганизации.
Можно сделать вывод о том, что умение и навыки решать тригонометрические уравнения и неравенства в курсе алгебры и начала анализа являются очень важными, развитие которых требует значительных усилий со стороны преподавателя математики. Тригонометрические уравнения и неравенства занимают достойное место в процессе обучения математики и развитии личности в целом.
ЛИТЕРАТУРА
Алимов, А. Ш. Алгебра и начала математического анализа. 10-11 классы. Учебник / А. Ш. Алимов, Ю.М. Колягин и др. 18-е изд. — М.: Просвещение, 2012. — 464 с.
Гельфанд, И. М. Тригонометрия / И. М. Гельфанд, С. М. Львовский, А. Л. Тоом 5-е изд., стереотип. – М.: МЦНМО, 2014. – 200 с.
Макарычев, Ю.Н. Тригонометрические неравенства и их преобразование / Под ред. С.А. Теляковского. 21-е изд. – М.: Просвещение, 2014. – 271 с.
Медынский, М. М. Полный курс элементарной математики в задачах и упражнениях. Книга 7 / М. М. Медынский — М.: Эдитус, 2015. – 553 с.
Шапкина, Н. Е. Пособие по математике для 10-11 классов подготовительных курсов. Тригонометрия / Н. Е. Шапкина, И. Е. Могилевский — М.: Физический ф-т МГУ, 2014. – 89 с
xn--j1ahfl.xn--p1ai
27)Простейшие тригонометрические уравнения.
Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций.
Уравнения вида sin x = a; cos x = a; tg x = a; ctg x = a, где x — переменная, aR, называются простейшими тригонометрическими уравнениями.



28) Решение иррациональных неравенств и уравнений.
Уравнения.
Уравнение А(х)=В(х), в котором хотя бы одно из выражений А(х), В(х) иррационально, называется иррациональным. Понятие корня уравнения и его решения для иррациональных уравнений определяют так же, как и для рациональных.
Все корни четной степени, входящие в уравнение, являются арифметическими.
Другими словами, если подкоренное выражение отрицательно, то корень лишен смысла, если подкоренное выражение равно нулю, то корень так же равен нулю; если подкоренное выражение положительно, то и значение корня положительно.
Все корни нечетной степени, входящие в уравнение, определены при любых действительных значениях подкоренного выражения.
Неравенства.
Основным методом решения иррациональных неравенств является метод сведения исходного неравенства к равносильной системе рациональных неравенств или совокупности таких систем. Чтобы избежать ошибок при решении иррациональных неравенств, следует рассматривать только те значения переменной, при которых все входящие в неравенство функции определены, т.е. найти ОДЗ этого неравенства, а затем обоснованно осуществлять равносильный переход на всей ОДЗ или ее частях.
29)Решение логарифмических неравенств Решение логарифмических неравенств, сводится к решению: простейших неравенств вида логарифмичекое неравенства. В каждом из этих случаев нужно различать, каким числом является а, так как от этого зависит характер монотонности логарифмической функции. Если показательные неравенства, то функция возрастает, а если показательные неравенства, — убывает. Поэтому приходится рассматривать различные простейшие неравенства. или неравенств вида показательные неравенства показательные неравенства; показательные неравенства;
30) Решение показательных неравенств При решении показательных неравенств вида показательные неравенства следует помнить, что показательная функция показательная функциявозрастает при показательные неравенства и убывает при показательные неравенства . Значит, в случае, когда показательные неравенства, от неравенства показательные неравенства следует переходить к неравенству того же смысла показательные неравенства. В случае же, когда показательные неравенства, от неравенства показательные неравенства следует переходить к неравенству противоположного смысла показательные неравенства.
31.Теорема синусов— теорема, устанавливающая зависим
ость между сторонами треугольника и противолежащими им углами.
Стороны треугольника пропорциональны синусам противолежащих углов:
Теорема косинусов -Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними: Теорема Пифагора —теорема, устанавливающая соотношение между сторонами прямоугольного треугольника.
32. Геометрические фигуры на плоскости:
треугольник,окружность,четырехугольник,многоугольник,точка,прямая. Треугольник-это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Виды треугольников по углам: Остроугольный треугольник — это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º). Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).
Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).
studfiles.net
Примеры решения простейших тригонометрических неравенств
Часть 2.
Начало здесь.
Если вы беретесь за изучение темы «Простейшие тригонометрические неравенства», то должны прежде знать, где находятся оси тангенса и котангенса и уметь решать простейшие тригонометрические
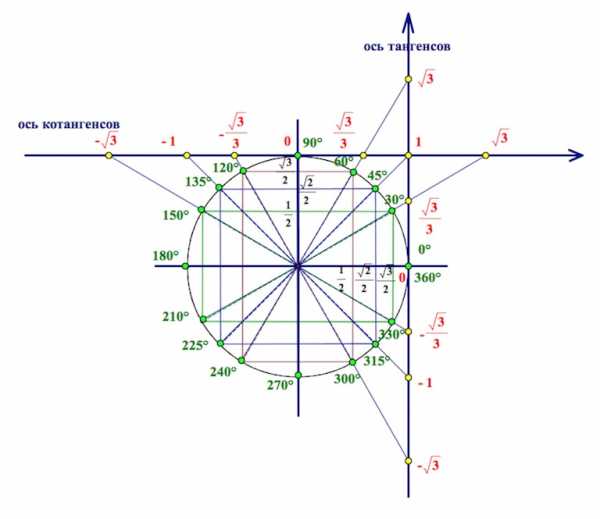
Кстати, для сдающих ЕГЭ по математике, – умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.
Примеры решения простейших тригонометрических неравенств
Пример 1.
Решить неравенство:
Решение:
Отмечаем на оси тангенсов 1. Указываем все значения тангенса, меньшие 1 – ниже 1.
Далее, отмечаем все точки тригонометрического круга, значение тангенса в которых будет меньше 1. Для этого мы мысленно соединяем каждую точку оси тангенсов ниже 1 с началом координат; тогда каждая проведенная прямая пересечет дважды тригонометрический круг. Вот эти-то точки круга нас и интересуют! Они выстраиваются в две дуги (точнее в две серии дуг). Значения тангенса в них – меньше 1.

Заметим, кстати, что дуга повторяет дугу равно через пол круга, то есть через (период функции – это ).
Все подходящие значения можно записать в виде следующего двойного неравенства:
или так
Пример 2.
Решить неравенство:
Решение:
Отмечаем на оси тангенсов . Указываем все значения тангенса, большие или равные – выше (включая саму точку).
«Транслируем» отмеченные точки оси тангенсов на тригонометрический круг.
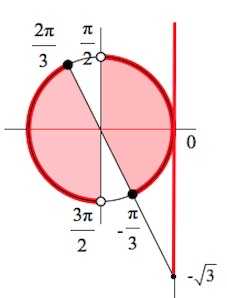
Все подходящие значения можно записать в виде следующего двойного неравенства:
или такого (разницы – никакой):
Пример 3.
Решить неравенство:
Решение:
Отмечаем на оси котангенсов . Указываем все значения котангенса, большие или равные – правее (включая саму точку).
«Транслируем» отмеченные точки оси котангенсов на тригонометрический круг:
Все подходящие значения можно записать в виде следующего двойного неравенства:
Вы обратили внимание, решая тригонометрическое неравенство с тангенсом, – мы не включаем в ответ точки (значение тангенса в этих точках не определено)?
А, решая тригонометрическое неравенство с котангенсом, – мы не включаем в ответ точки (значение котангенса в этих точках не определено).
Пример 4.
Решить неравенство:
Решение:
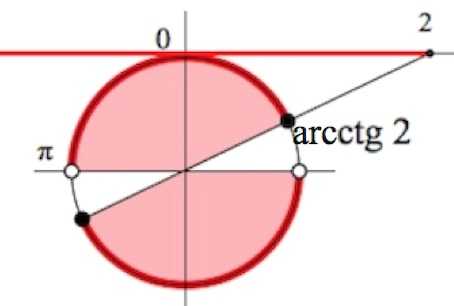
Проверьте себя
Помните, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. (См., например, задание 2).
1. Решить неравенство:
Ответ: + показать
2. Решить неравенство:
Ответ: + показать
3. Решить неравенство:
Ответ: + показать
Если у вас есть вопросы, – пожалуйста, – пишите в комментариях!
egemaximum.ru
Тригонометрические неравенства и их решения
Решение тригонометрических неравенств
Решение тригонометрических неравенств зачастую сводится к решению простейших тригонометрических неравенств вида:
Решаются простейшие тригонометрические неравенства графически или с помощью единичной тригонометрической окружности.
По определению, синусом угла есть ординатой точки единичного круга (рис. 1), а косинусом – абсцисса этой точки. Этот факт используется при решении простейших тригонометрических неравенств с косинусом и синусом с помощью единичного круга.
Рис. 1
Примеры решения тригонометрических неравенств
Тригонометрические неравенства со сложным аргументом
Тригонометрические неравенства со сложным аргументом можно свести к простейшим тригонометрическим неравенствам с помощью замены. После его решения делается обратная замена и выражается исходная неизвестная.
Двойные тригонометрические неравенства
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Решение тригонометрических уравнений и неравенств. 10-й класс
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (5 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Урок-игра: “Соревнование по тяжелой атлетике”
Цели урока:
Образовательные:
- повторение, обобщение и систематизация теоретических знаний методов решения тригонометрических уравнений;
- отработка способов решения тригонометрических уравнений;
- развитие графической культуры;
- расширение представления учащихся о решении тригонометрических уравнений в нестандартных ситуациях.
Развивающие:
- развитие мышления, математической речи, внимания, памяти.
Воспитательные:
- воспитание чувства ответственности, культуры общения, общей культуры.
Оборудование: проектор, презентация, карточки.
“Предмет математики настолько серьезен, что полезно
не упускать случая делать его немного занимательным”.
Паскаль
Ход урок
I. Организационный этап. Постановка цели и задач.
Сегодня мы проводим необычный урок. Урок-соревнование командное по тяжелой атлетике по теме “Решение тригонометрических уравнений и неравенств”.
Цель соревнования: повторить, обобщить и систематизировать материал темы; повторить чтение графиков, расширить представление о решении тригонометрических уравнений в нестандартных ситуациях.
В наших соревнованиях принимают участие четыре команды. В каждой команде есть капитан.
Итак, капитаны представьте свои команды: sinx, cosx, tgx, ctgx.
За правильностью хода наших соревнований будет наблюдать жюри.
Наши соревнования будут проходить в несколько этапов. На каждом этапе на помост будут вызываться атлеты определенной категории:
— легкий вес;
— средний вес;
— тяжелый вес;
— супертяжелый вес.
Каждый этап будет оцениваться определенным количеством баллов, которые затем будут переводиться в кг умножением на 10. В результате победителем будет та команда, которая возьмет самый тяжелый вес. Все результаты будут заноситься в таблицу.
II. Актуализация опорных знаний. “Разминка”.
Итак, начинаем I этап подготовительный. “Разминка”. На этом этапе принимает участие вся команда. Все должны разогреть свои мышцы, привести в порядок свои мысли. “Разминка” будет проходить по кругу (sinx —> cosxtgx ctgx). И состоит она из трех групп заданий.
1 группа.
Проговорить формулу нахождения корней следующих уравнений:
sinx=а, cosx=a, tgx=a, ctgx=a.
2 группа.
Вычислить:
3 группа.
Решите уравнения.
sinx= 0 sinx=1 sinx= -1 cosx=0 cosx=1 cosx= -1 tgx=0 tgx=1 tgx= -1 ctgx=0 ctgx=1 ctgx= -1
Жюри сразу же подводит итог “Разминки” и результат заносится в таблицу.
Итак, команды разогрелись. Мы повторили ключевые моменты для решения тригонометрических уравнений и неравенств. Теперь смело можем переходить на следующий этап, “Кто смелее?”.
III. Основной этап.
Конкурс “Кто смелее?”
На помост вызываются тяжелоатлеты легкого веса. Вам будут предложены, три набора карточек: “зеленые”, “желтые”, “красные”. На каждой карточке записано по одному уравнению разного уровня сложности. Каждой команде предоставляется право выбора, из какой группы взять карточку. По одному представителю выходят к доске, тянут карточку, выбранного цвета и решают. Соответственно, если вы решите уравнение по зеленой карточке, то возьмете вес 40 кг (4б*10), по желтой 60 кг, красной – 80 кг.
Каждая команда имеет право на вторую и 3-ю попытку взятия веса (т.е. по две подсказке) если, конечно это будет необходимо.
Команды следят за ходом решения. Кто первый готов, тот и отчитывается первый. Жюри сразу же подводит итог.
Итак, мы повторили решение простейших тригонометрических уравнений, можем смело переходить на следующий этап соревнований. “Кто сообразительнее?”
Конкурс. “Кто сообразительнее”.
Правильному применению методов можно научиться только применяя их на разнообразных примерах. Г.Цейтен
Соревнуются тяжелоатлеты среднего веса.
Как часто первое наше затруднение при решении тригонометрических уравнений заключается в том, что мы не видим приема решения таких уравнений.
Назовите типы тригонометрических уравнений.
- Простейшие тригонометрические уравнения.
- Тригонометрические уравнения, сводящиеся к квадратным уравнениям.
- Однородные тригонометрические уравнения первой и второй степени.
- Тригонометрические нестандартные уравнения.
Назовите основные методы решения тригонометрических уравнений:
- Метод разложения на множители.
- Метод введения новой переменной.
- Решение тригонометрических уравнений как однородное.
Перед вами записано 10 уравнений:
| 1 | 2sin2x +5cosx=4 |
| 2 | sinx+sin5x=0 |
| 3 | 2sin(x/4)cos3x – cos3x=0 |
| 4 | 6sinxcosx=5cos2x |
| 5 | sin x+cosx=0 |
| 6 | cosx=sin2xcosx |
| 7 | 2cos2x — cosx – 1=0 |
| 8 | cos2x +9sinx + 4 =0 |
| 9 | sin2x + 9cos2x =5sin2x |
| 10 | 3sin22x + 0,5sin4x=4cos22x |
Тяжелоатлеты среднего веса берут листок с таблицей ответов, следующего типа:
| Уравнения, сводящиеся к квадратным | Уравнения, решаемые разложением на множители | Однородные уравнения первой и второй степени |
Ваша задача: глядя на уравнение, не решая его, определить метод решения, и номер этого тригонометрического уравнения, написать в соответствующий столбец заготовленной таблицы. Как только команды будут готовы, оригинал они сдают, а копию оставляют себе. А затем также по кругу идет проверка (отвечают тяжелоатлеты среднего веса). За каждое верно поставленное уравнение 30 кг (3б*10).
Жюри подводит итог.
Итак, мы повторили основные методы решения тригонометрических уравнений и теперь можем смело приступать к самому тяжелому решению таких уравнений. Т.е. мы переходим на следующий этап соревнований. “Кто больше?”
Конкурс. “Кто больше?”
Каждая команда получает карточку с заданием. Около каждого задания проставлены баллы (*10) в соответствии с уровнем сложности. Атлет тяжелого веса распределяет задания между членами команды (можно с помощью капитана) и каждый приступает к решению на отдельном листочке (подписанном: фамилия и название команды). На все решение дается 7 мин. Как только время истечет, все листочки сдаются. Жюри подводит итог. Какая команда больше решит и правильно, та и возьмет больший вес на данном этапе.
По истечении времени команды сдают листы и жюри подводит итог.
Итак, вы применили все свои знания о методах решения тригонометрических уравнений непосредственно в ходе решения.
Но кроме вышеперечисленных приемов решения есть еще один — графический.
Переходим к следующему этапу “Кто быстрее?”.
Конкурс. “Кто быстрее”.
На помост вызываются тяжелоатлеты супер тяжелого веса. Вам предложено решить одно уравнение:
Поможет в решении данного уравнения вам следующая таблица графиков:
Оформляете решение на листочках (т.е. строите графики). Кто первый решит, поднимает руку и т.д. Кто решит быстрее всех и правильно, тот возьмет вес 100 кг (10б * 10), второй – 80 кг; третий – 50 кг; четвертый 30 кг.
По окончании жюри подводят итог.
Итак, мы закончили соревнование атлетов. Вы видите как они прекрасно выступили. Но чтобы достичь таких высоких результатов спортсмены долгое время проводят на тренировках. Вот сейчас и послушаем отчет тренировок. Переходим к следующему этапу “Тренировка” (дом. задание).
Конкурс. “Тренировка”.
Капитаны каждой команды представляет решение физической задачи с применением решения тригонометрических уравнений. Наибольший вес, который может взять капитан равен 100 кг.
Капитаны по очереди представляют задачи.
Пример: Амплитуда колебаний 10 см, а частота 0,5Гц. Написать уравнение х=х(t) и построить его график. Найти фазу и смещение через 1,5 с. Определите, через сколько времени смещение будет 7,1 см?
По окончании жюри подводят итог.
IV. Рефлексия.
| Моё настроение | Своей работой на уроке я | Материал урока мне был | |||||
| не доволен | доволен | бесполезен | полезен | скучен | интересен | ||
V. Домашняя работа. 18.23 (б), 18.33 (б), 18.3 (б).
27.02.2016
xn--i1abbnckbmcl9fb.xn--p1ai
Простейшие тригонометрические уравнения и неравенства. Подведение итогов
Здравствуйте!
Сегодня мы подводим итоги раздела, посвященного решению простейших тригонометрических уравнений и неравенств.
Давайте повторим определения и свойства обратных тригонометрических функций: арксинуса, арккосинуса, арктангенса и арккотангенса:
Запомнить, как строится на тригонометрическом круге множество решений простейшего уравнения, поможет интерактивная модель. Обратите внимание на особые случаи, когда решение уравнения можно записать, используя значения табличных углов.
Посмотрите разбор решения нескольких типов простых тригонометрических уравнений, включая простой случай сведения к квадратному, в этом плейлисте:
С помощью интерактивной модели можно увидеть, как множество решений простейшего тригонометрического неравенства изменяется в динамике на круге и на графике соответствующей функции.
Повторяем задачи к разделу. Напомним, что тренажеры с пошаговым решением и задачи для самостоятельной работы ждут подписчиков в Библиотеке.
Начать тренировку
Мы научились решать простейшие тригонометрические уравнения и неравенства. Но задача №13 варианта КИМ ЕГЭ содержит, как правило, более сложное уравнение. И для этих уравнений существуют свои методы и приемы решений. Какие? Об этом мы узнаем на следующей неделе.
Следите за обновлениями на сайте и подписывайтесь на наш канал в Ютьюбе и группу Вконтакте!
repetitor.1c.ru
Решение простейших тригонометрических неравенств: примеры и алгоритмы
Неравенства, содержащие тригонометрические функции, при решении сводятся к простейшим неравенствам вида cos(t)>a, sint(t)=a и подобным. И уже простейшие неравенства решаются. Рассмотрим на различных примерах способы решения простейших тригонометрических неравенств.
Пример 1. Решить неравенство sin(t) > = -1/2.
Рисуем единичную окружность. Так как sin(t) по определению — это координата y, отмечаем на оси Оу точку у =-1/2. Проводим через неё прямую, параллельную оси Ох. В местах пересечения прямой с графиком единичной окружности отмечаем точки Pt1 и Pt2. Соединяем двум отрезками начало координат с точками Pt1 и Pt2.
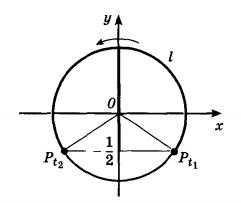
Решением данного неравенства будут все точки единичной окружности расположенные выше данных точек. Другими словами решением будет являться дуга l.. Теперь необходимо указать условия, при которых произвольная точка будет принадлежать дуге l.
Pt1 лежит в правой полуокружности, её ордината равна -1/2, тогда t1=arcsin(-1/2) = — pi/6. Для описания точки Pt1 можно записать следующую формулу:
t2 = pi – arcsin(-1/2) = 7*pi/6. В итоге получаем для t следующее неравенство:
— pi/6
Мы сохраняем знаки неравенств. А так как функция синус функция периодичная, значит решения будут повторяться через каждые 2*pi. Это условие добавляем к полученному неравенству для t и записываем ответ.
Ответ: -pi/6+2*pi*n < = t < = 7*pi/6 + 2*pi*n, при любом целом n.
Пример 2. Решить неравенство cos(t) <1/2.
Нарисуем единичную окружность. Так как согласно определению cos(t) это координата х, отмечаем на грфике на оси Ох точку x = 1/2.
Проводим через эту точку прямую, параллельную оси Оу. В местах пересечения прямой с графиком единичной окружности отмечаем точки Pt1 и Pt2. Соединяем двум отрезками начало координат с точками Pt1 и Pt2.

Решениями будут все точки единичной окружности, которые принадлежать дуге l.. Найдем точки t1 и t2.
t1 = arccos(1/2) = pi/3.
t2 = 2*pi — arccos(1/2) = 2*pi-pi/3 = 5*pi/6.
Получили неравенство для t: pi/3<t<5*pi/6.
Так как косинус — это функция периодичная, то решения будут повторяться через каждые 2*pi. Это условие добавляем к полученному неравенству для t и записываем ответ.
Ответ: pi/3+2*pi*n <t<5*pi/6+2*pi*n, для любого целого n.
Пример 3. Решить неравенство tg(t) < = 1.
Период тангенса равняется pi. Найдем решения, которые принадлежат промежутку (-pi/2;pi/2) правая полуокружность. Далее воспользовавшись периодичностью тангенса, запишем все решения данного неравенства. Нарисуем единичную окружность и отметим на ней линию тангенсов.
Если t будет являться решение неравенства, то ордината точки Т = tg(t) должна быть меньше или равна 1. Множество таких точек будет составлять луч АТ. Множество точек Pt, которые будут соответствовать точкам этого луча – дуга l. Причем, точка P(-pi/2) не принадлежит этой дуге.

Найдем условие, при котором некоторая точка Pt будет принадлежать дуге l.
t1 = arctg(1) = pi/4.
Получаем неравенство –pi/2 <t< = pi/4.
Учитывая период тангенса записываем ответ.
Ответ: -pi/2+pi*n<t< =pi/4+pi*n, для любого целого n.
Нужна помощь в учебе?
Предыдущая тема: Решение простейших тригонометрических уравнений: графики и примеры
Следующая тема:   Примеры решения тригонометрических уравнений и систем уравнений
Все неприличные комментарии будут удаляться.
www.nado5.ru