Примеры с решением пределов: Примеры пределов с решениями

alexxlab / / Разное

Методические рекомендации по решению задач на тему «пределы функции» для студентов | Методическая разработка по теме:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ЖУКОВСКИЙ АВИАЦИОННЫЙ ТЕХНИКУМ ИМЕНИ В.А. КАЗАКОВА»

        

Рассмотрено на заседании

предметной (цикловой) комиссии «Общеобразовательных, естественно-научных и гуманитарных дисциплин»

УТВЕРЖДАЮ

Зам. директора по учебной части

                                 / М.А.Фофанова /

Методические рекомендации по решению задач на тему «пределы функции» для студентов специальности

 160108 «Производство летательных аппаратов»        

Разработал преподаватель                                                Шарова Ж.В.

Жуковский, 2013 г.

Содержание

1. Пояснительная записка        

2. Принцип построения программы        

3. Методические рекомендации        

4. Тематическое планирование        

5. Примерная разработка занятия по теме «Пределы функции и их вычисление»        

7. Заключение        

  1. Пояснительная записка

Необходимостью в наши дни становится непрерывное образование, что требует полноценной  подготовки. Всё больше специальностей связаны с непосредственным применением математики (физика, химия, биология, экономика, информатика и др.) и ее подразделов, в частности, математический анализ.

Предел функции является одним из базовых понятий математического анализа. Важно дать студентам представление об основных определениях и свойствах пределов, а также методах решения задач, связанных с вычислением пределов функций. Успешное усвоение данной темы позволит упростить в дальнейшем  изучение дифференциального и интегрального исчислений.

На занятиях можно повторить теорию по данному вопросу, рассмотреть основные термины и понятия пределов, отработать навыки решения типовых задач. Предлагаемые задачи должны различаться по уровню сложности: от простейших упражнений на применение формул до достаточно сложных расчетов.

 Каждое занятие предполагает: изучение теоретических основ, решение задач с преподавателем, самостоятельная работа, домашнее задание.

  1. Принцип построения программы

         Содержание программы составляют специально подобранные задачи для развития математического мышления.

 Цели курса: 

  • формирование у студентов интереса к математике;
  • выявление и развитие математических способностей;
  • овладение конкретными математическими знаниями, необходимыми для применения в практике математического анализа;
  • интеллектуальное развитие студентов;
  • формирование понимания основ математического анализа.

Задачи:

  • дать необходимые знания о сущности пределов;
  • сформировать умение производить вычисление пределов;
  • научить вычислять пределы функции с различными видами неопределенностей.

Ожидаемые результаты.

В результате обучения студенты должны:

  • понимать смысл термина «предел»;
  • понимать смысл терминов «бесконечно малые» и «бесконечно большие величины»;
  • знать виды неопределенностей;
  • знать свойства предела;
  • уметь преобразовывать алгебраические выражения для упрощения вычисления пределов;
  • уметь использовать в своих вычислениях «первый и второй замечательные пределы».
  1. Методические рекомендации

При объяснении студентам теоретического вопроса, необходимо доступно изложить определение предела на примере числовой последовательности.

 Обязательным является повторение различных способов преобразования алгебраических дробей для упрощения выражений. Вспомнить такие способы, как вынесение общего множителя за скобку, приведение дроби к общему знаменателю, разложение квадратного трехчлена на множители, домножение на сопряженное значение. Необходимо уделить большое внимание повторению формул сокращенного умножения.

Важно предоставить студентам возможность овладеть  способами преобразования выражений для решения пределов сложных функций, прежде чем перейти к изучению «первого» и «второго замечательного пределов». Устный счет является обязательной составляющей каждого занятия, так как приучает к рационализации вычислений и  аналитической оценке результатов, что имеет значение для более рационального вычисления не только пределов, но и других поставленных задач математического анализа.

 При закреплении материала, совершенствовании знаний, умений и навыков целесообразно практиковать самостоятельную работу студентов.

 Домашние задания в разумных пределах являются обязательными для более успешного освоения материала.

  1. Тематическое планирование

№

Наименование разделов, тем, занятий

Кол-во занятий

1

Бесконечная числовая последовательность. Предел числовой последовательности.

2

2

Вычисление предела функции.

2

3

Вычисление предела функции. Упражнения.

2

4

Первый замечательный предел.

2

5

Второй замечательный предел.

2

6

Подготовка к контрольной работе. Решение задач.

2

7

Контрольная работа «Вычисление пределов функции»

2

  1. Примерная разработка занятия по теме «Пределы функции и их вычисление»

Цели и задачи урока:

Понять термин «предел», изучить его свойства и приобрести навыки его вычисления.

Объяснение нового материала:

На примере числовой последовательности с общим членом  () объяснить определение предела.

Предел числовой последовательности ()- объект, к которому члены последовательности приближаются с ростом номера.

Перейти к пределу функции.

Объяснить значение бесконечно малой величины и бесконечно большой и изложить свойства предела:

  • предел отношения конечной величины к бесконечно малой величине равен бесконечно большой величине;
  • предел отношения конечной величины к бесконечно большой равен бесконечно малой величине;
  • предел суммы функций равен сумме пределов;
  • предел произведения функций равен произведению пределов;
  • предел степени с натуральным показателем равен степени предела с таким же показателем;
  • постоянный множитель перед функцией можно вынести перед пределом.

Рассказать про основные виды неопределенностей, которые наиболее часто встречаются в поставленных задачах: ( и показать примеры вычисления пределов простых и сложных функций.

Для раскрытия неопределённостей типа используется следующий алгоритм:

  1. Выявление старшей степени переменной;
  2. Деление на эту переменную как числителя, так и знаменателя.

Для раскрытия неопределённостей типа существует следующий алгоритм:

  1. Разложение на множители числителя и знаменателя;
  2. Сокращение дроби.

В дальнейшем предоставить студентам возможность решать самостоятельно под контролем учителя.

Примеры:

1.

2.

3.

4. (один из видов неопределенности, поэтому необходимо преобразование выражения для вычисления данного предела)

5.

6.  (для того, чтобы вычислить данный предел необходимо квадратный трехчлен числителя и знаменателя разложить на множители)

7.

8.

9. 

Для решения данного примера, необходимо избавиться от иррациональности в знаменателе, домножив числитель и знаменатель на сопряженное знаменателя.

 

10.

В этом случае, числитель домножаем на сопряженное, для того чтобы использовать формулу «разность квадратов» , соответственно на это же выражение домножаем знаменатель и таким образом вычисляем предел.

11.

12.

Постановка домашнего задания:

  1. Повторить определение предела и его свойства.
  2. Решить примеры:

1.

2.

3.

4.

5.

6.

7.

8.

Первый замечательный предел

1.

2.

3.

4.

5.

Второй замечательный предел

1.

2.

6. Закрепление материала.

Примеры для самостоятельного решения.

1.

2.

3.  

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

7. Заключение

Решение задач по теме «Пределы функции» позволяет освоить и закрепить практические навыки работы с различными видами пределов для выражений и функций. По данной теме рассматриваются вычисления пределов для выражений рациональных дробей, тригонометрических и степенных функций. Такой подход позволяет студентам упорядочить базовые знания о пределах, понять свойства замечательных пределов. Опыт, полученный при работе над темой «Пределы функции», послужит в дальнейшем одним из базовых элементов в изучении дифференциального и интегрального исчисления.

Примеры решения задач. Математический анализ

Задача 1.

Теоретическое введение

Функцией переменной величины , называется величина такая, что каждому значению , принадлежащей некоторой области , соответствует единственное значение величины .

Обозначение: .

– область определения функции, – аргумент.

– область изменения функции, – значение;

Функция может быть задана аналитически, таблично, графически.

Основными элементарными функциями являются:

    1. степенные (, где – произвольное число)
  • показательные (, , )
  • логарифмические (,, )
  • тригонометрические
    (, , , )
  • обратные тригонометрические
    (,,, )

Композиция (суперпозиция) двух функций и есть функция, в которой аргументом одной из данных функции, является значение другой функции.


Обозначение: и .

Сложная функция есть композиция двух и более функций.

Элементарная функция есть функция, полученная из основных элементарных функций с помощью арифметических действии и композиции.

Целью математического анализа является изучение различных функций, их свойств, и операций связанных с функциями.

Функция называется четной, если для всех своих аргументов.

Функция называется нечетной, если для всех своих аргументов.

Число называется пределом функции при , стремящемся к и обознается , если при неограниченном приближении к , неограниченно приближается .

Свойства пределов:

  • Передел суммы двух функций равен сумме пределов этих функций, если они существуют:
  • Предел произведения функции равен произведению пределов, если они существуют:
  • Предел частного двух функций равен частному пределов, если они существуют, и предел знаменателя не равен нулю: , при .

Обычно , например:

Однако, иногда значение не входит в область определения функции .
В этом случае имеются различные методы вычисления пределов:

Выделение общего множителя

Выделение главной части

Использование замечательных пределов

Первый замечательный предел:

Второй замечательный предел:

Задача 2.

Теоретическое введение

Производная или от данной функции есть предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю: или

Механический смысл производной – скорость изменения функции.

Геометрический смысл производной – тангенс угла наклона касательной к графику функции:

Правила дифференцирования:

  • Производная постоянной величины равна 0.
  • Производная суммы равна сумме производных.
  • Производная произведения:
  • Производная частного:

Производная сложной функции:

Производная от сложной функции по независимому аргументу равна производной от по промежуточному аргументу , умноженной на его производною по независимой переменной .

Примеры:

  • ;
  • ;
  • ;

Задача 4.

Найти неопределенные интегралы:

а) ;

Решение: введем переменную . Тогда ; . Сделаем замену:

.

б) ;

Решение: используем метод интегрирования по частям:

.

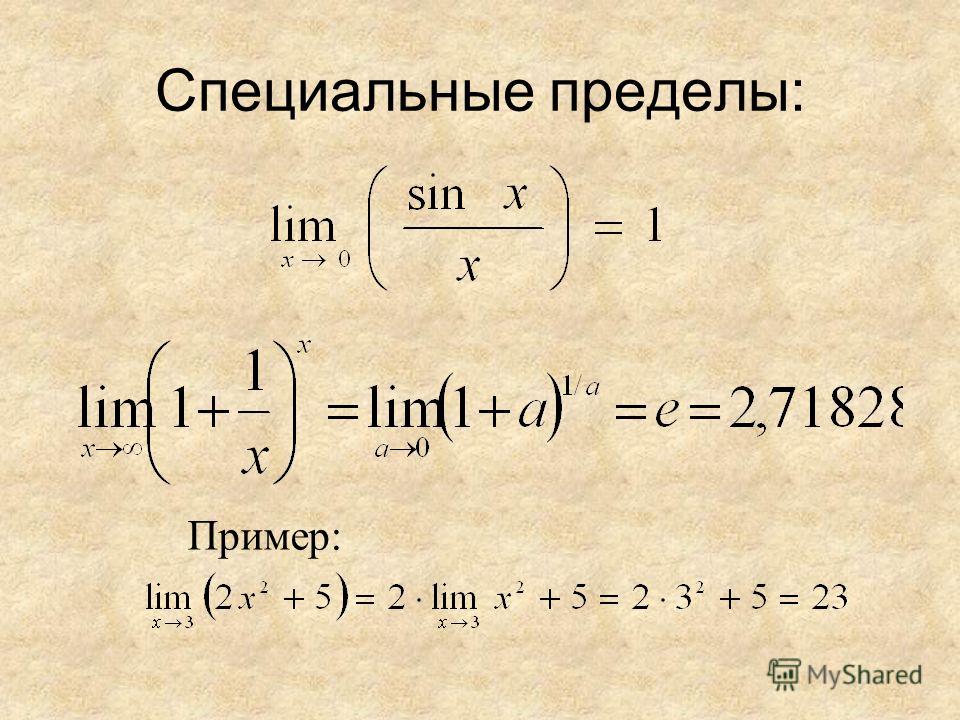
Обозначим: .
Тогда .

Задача 5.

Вычислить площадь фигуры, ограниченной линиями:

и .

Решение:

Найдем точки пересечения графиков данных функций. Для этого приравняем функции и решим уравнение

Итак, точки пересечения и .

Площадь фигуры найдем, используя формулу

.

В нашем случае

Ответ: площадь равна (квадратных единиц).

Законы пределов объясняются примерами с цветовой кодировкой


Краткий обзор

  • Законы пределов представляют собой простые формулы, которые помогают нам точно оценить пределы.
  • Внизу страницы есть краткий список Законов Предела.

Предельные законы

Для следующих уравнений $$a$$ и $$k$$ — константы, а $$n$$ — целое число. Кроме того, предположим, что $$\displaystyle\lim\limits_{x\to a} f(x)$$ и $$\displaystyle\lim\limits_{x\to a} g(x)$$ существуют.

(1) Постоянный закон: $$\displaystyle\lim\limits_{x\to a} k = k$$

Этот закон имеет дело с постоянными функциями (горизонтальными линиями). Поскольку $$y$$ равно , всегда равно $$k$$, не имеет значения, к чему приближается $$x$$.

Пример 1

$$\displaystyle\lim\limits_{x\to6} 8 = 8$$

(2) Закон тождества: $$\displaystyle\lim\limits_{x\to a} x = a$$

Этот закон имеет дело с функцией $$y=x$$. Поскольку $$y$$ и $$x$$ равны, какое бы значение $$x$$ ни приближалось, $$y$$ должно будет приблизиться к тому же значению.

Пример 2

$$\displaystyle\lim\limits_{x\to 4} x = 4$$

(3) большой закон сложения: $$\displaystyle\lim\limits_{x\to a} f(x) + g(x) = \displaystyle\lim\limits_{x\to a} f(x) + \displaystyle \lim\limits_{x\to a} г(х)$$

Это просто означает, что когда мы берем предел сложения, мы можем просто взять предел каждого члена по отдельности, а затем добавить результаты.

Пример 3

$$\displaystyle\lim\limits_{x\to -7} (x + 5)$$

Решение:

$$ \начать{выравнивать*} \ displaystyle \ lim_ {x \ to -7} (\ blue {x} + \ red {5}) & = \ blue {\ lim_ {x \ to -7} x} + \ red {\ lim_ {x \ to -7} 5} && \mbox{Закон сложения}\\ & = \blue{-7} + \red{5} && \blue{Identity\hspace{2mm}Law}\hspace{2mm}and\hspace{2mm}\red{Constant\hspace{2mm}Law}\\ & = -2 \конец{выравнивание*} $$

(4) Закон вычитания: $$\displaystyle\lim\limits_{x\to a} f(x) — g(x) = \displaystyle\lim\limits_{x\to a} f(x) — \displaystyle\ lim\limits_{x\to a} g(x)$$

По существу то же самое, что и закон сложения, но для вычитания. Работайте с каждым термином отдельно, затем вычтите результаты.

Пример 4

$$\displaystyle\lim\limits_{x\to\frac 1 2} (x-9)=$$

Решение:

$$ \\ \начать{выравнивать*} \lim_{x\to\frac 1 2}(\blue{x}-\red{9}) & = \blue{\lim_{x\to\frac 1 2}x} — \red{\lim_{x \to\frac 1 2} 9} && \mbox{Закон вычитания}\\ % & = \blue{\frac 1 2} — \red{9} && \blue{Identity}\hspace{2mm}and\hspace{2mm}\red{Constant}\hspace{2mm}Законы\\ % & = \frac 1 2 — \frac{18} 2\\[6pt] % & = -\frac{17} 2 \конец{выравнивание*} \\ $$

(5) Закон постоянного коэффициента: $$\displaystyle\lim\limits_{x\to a} k\cdot f(x) = k\displaystyle\lim\limits_{x\to a} f(x)$$

Если ваша функция имеет коэффициент, вы можете сначала взять предел функции, а затем умножить на коэффициент.

Пример 5

$$\displaystyle\lim\limits_{x\to 3} (8x)$$

Решение:

$$ \начать{выравнивать*} \lim_{x\to 3} (8x) & = 8\,\lim_{x\to 3} x && \mbox{Закон постоянных коэффициентов}\\ & = 8 (3) && \mbox{Закон тождества}\\ & = 24 \конец{выравнивание*} $$

С помощью первых 5 предельных законов мы теперь можем найти пределы любой линейной функции, которая имеет вид $$y = mx+b$$.

Пример 6

$$\displaystyle\lim\limits_{x\to -2} (4x — 3)$$

Решение:

$$ \начать{выравнивать*} \displaystyle\lim_{x\to -2} (4\blue{x} — \red{3}) & \displaystyle\lim_{x\to-2} (4\blue{x}) — \lim_{x \to-2} \red{3} && \mbox{Закон вычитания}\\ & = 4\,\blue{\lim_{x\to-2} x} — \red{\displaystyle\lim_{x\to-2} 3}&& \mbox{Закон постоянных коэффициентов}\\ & = 4 (\blue{-2}) — \red{3}&& \blue{Identity}\hspace{2mm}and\hspace{2mm}\red{Constant}\hspace{2mm}Законы\\ & = -8 — 3\\ & =-11 \конец{выравнивание*} $$ 92 & = \displaystyle\lim_{x\to 5} (\blue{x}\cdot \red{x})\\ & = \left(\blue{\lim_{x\to 5} x}\right)\left(\red{\lim_{x\to5} x}\right)&& \mbox{Закон умножения}\\ & = (\blue{5})(\red{5}) && \mbox{Закон идентичности}\\ & = 25 \конец{выравнивание*} $$

Первые 6 предельных законов позволяют нам найти пределы любой полиномиальной функции, хотя предельный закон 7 делает его немного более эффективным. 93 + 5(\red{-2}) && \mbox{Закон Тождества}\\ & = 4(-8) — 10\\ & = -32 — 10\\ & = -42 \конец{выравнивание*} $$

(8) Закон деления: $$\displaystyle\lim\limits_{x\to a} \frac{f(x)}{g(x)} = \frac{\displaystyle\lim\limits_{x\to a} е (х) {\ displaystyle \ lim \ limits_ {x \ to a} g (x)} $ $ при условии $ $ \ displaystyle \ lim \ limits_ {x \ to a} г (х) \ neq 0 $ $

Закон деления говорит нам, что мы можем просто найти предел числителя и знаменателя по отдельности, пока мы не получим ноль в знаменателе.

Пример 10

$$\displaystyle\lim\limits_{x\to 12}\frac{2x}{x-4}$$

Решение:

$$ \начать{выравнивать*} \displaystyle\lim_{x\to 12}\frac{2\blue x}{\red x-4} & = \frac{\displaystyle\lim\limits_{x\to 12} (2 \blue x)}{ \displaystyle\lim\limits_{x\to 12} (\red x-4)} && \mbox{Закон деления}\\[6pt] & = \frac{2\,\displaystyle\lim\limits_{x\to12} \blue x}{\displaystyle\lim\limits_{x\to12}(\red x- 4)} && \mbox{Закон постоянных коэффициентов }\\[6pt] & = \ frac {2 \, \ blue {\ displaystyle \ lim \ limits_ {x \ to12} x}} {\ red {\ displaystyle \ lim \ limits_ {x \ to12} x} — \ displaystyle \ lim \ limits_ { x\to12} 4} && \mbox{Закон вычитания}\\[6pt] & = \frac{2(\blue{12})}{\red{12} -4} && \mbox{Тождество и постоянные законы}\\[6pt] & = \frac{24} 8\\[6pt] & = 3 \конец{выравнивание*} $$

С помощью первых восьми предельных законов мы теперь можем найти пределы любой рациональной функции.

(9) Корневой закон: $$\displaystyle\lim\limits_{x\to a} \sqrt[n]{f(x)} = \sqrt[n] L$$ при $$L>0$$, когда $ $n$$ четно.

Для корневых функций мы можем сначала найти предел внутренней функции, а затем применить корень. Мы должны быть осторожны, чтобы не получить квадратный корень из отрицательного числа!

Пример 11

$$\displaystyle\lim\limits_{x\to -2} \sqrt{x+18}$$

Решение:

$$ \начать{выравнивать*} \ displaystyle \ lim_ {x \ to -2} \ sqrt {\ blue x + \ red {18}} & = \ sqrt {\ displaystyle \ lim_ {x \ to -2} (\ blue x + \ red {18})} && \mbox{Корневой закон}\\ & = \ sqrt {\ blue {\ displaystyle \ lim_ {x \ to -2} x} + \ red {\ displaystyle \ lim_ {x \ to -2} 18}} && \ mbox {Закон сложения} \\ & = \sqrt{\blue{-2}+\red{18}} && \mbox{Тождество и постоянные законы}\\ & = \sqrt{16}\\ & = 4 \конец{выравнивание*} $$

(10) Закон о составе

Предположим, что $$\lim\limits_{x\to a} g(x) = M$$, где $$M$$ — константа. {\ cos (\ pi x)} $ $ 9{-1}\\ & = \frac 1 e \конец{выравнивание*} $$

(11) Закон о неравенстве

Предположим, что $$f(x) \geq g(x)$$ для всех $$x$$ вблизи $$x = a$$. Тогда $$\lim\limits_{x\to a} f(x) \geq \lim\limits_{x\to a} g(x)$$

Список предельных законов

  • Постоянный закон $$\lim\limits_{x\to a} k = k$$

  • Закон тождества $$\lim\limits_{x\to a} x = a$$

  • Закон сложения $$\lim\limits_{x\to a} f(x) + g(x) = \lim\limits_{x\to a} f(x) + \lim\limits_{x\to a } г(х)$$

  • Закон вычитания $$\lim\limits_{x\to a} f(x) — g(x) = \lim\limits_{x\to a} f(x) — \lim\limits_{x\to a} g( х)$$

  • Закон о постоянных коэффициентах $$\lim\limits_{x\to a} k\cdot f(x) = k\lim\limits_{x\to a} f(x)$$

  • Закон умножения $$\lim\limits_{x\to a} f(x)\cdot g(x) = \left(\lim\limits_{x\to a} f(x)\right)\left( \lim\limits_{x\to a} g(x)\right)$$ 9n$$ при условии $$\lim\limits_{x\to a} f(x)\neq 0$$, если $$n

  • Закон деления $$\lim\limits_{x\to a} \frac{f(x)}{g(x)} = \frac{\lim\limits_{x\to a}f(x)}{ \lim\limits_{x\to a} g(x)}$$ при условии $$\lim\limits_{x\to a} g(x)\neq 0$$

  • Корневой закон $$\lim\limits_{x\to a} \sqrt[n]{f(x)} = \sqrt[n] L$$ при условии $$L>0$$, когда $$n$$ даже.

  • Закон композиции Предположим, что $$\lim\limits_{x\to a} g(x) = M$$, где $$M$$ — константа. Кроме того, предположим, что $$f$$ непрерывна в $$M$$. Тогда $$\lim\limits_{x\to a} f\left(g(x)\right) = f\left(\lim\limits_{x\to a} g(x)\right) = f(M )$$.

  • Закон неравенства Предположим, что $$f(x)\geq g(x)$$ для всех $$x$$ вблизи $$x=a$$. Тогда $$\displaystyle\lim\limits_{x\to a} f(x) \geq \lim\limits_{x\to a} g(x)$$


Реклама

Infinity и DNE в пределах | Penji

Лучший способ понять, почему мы используем бесконечность, а не не существует (сокращенно DNE), даже если технически это одно и то же, – это сначала определить, что означает бесконечность.

Бесконечность не является реальным числом. Это математическое понятие, предназначенное для представления действительно большого значения, которое на самом деле не может быть достигнуто. С точки зрения решений пределов это означает, что уравнение, для которого вы берете предел, будет двигаться в этом направлении навсегда. 92) будет подниматься все выше и выше. Вы можете представить, как он уходит со страницы и продолжается вверх. Другими словами, предел, когда x приближается к нулю для g(x), равен бесконечности, потому что он продолжает расти без остановки.

Таким образом, хотя бесконечность технически бессмысленна/просто математическая конструкция, ее можно использовать для описания результата ограничений, когда функция продолжает работать вечно (что обычно происходит, когда у вас есть вертикальная асимптота).

Чтобы было ясно, предела на самом деле не существует, так как мы не можем присвоить ему номер (он продолжается вечно), так что вы могли бы сказать:

И это было бы технически правильно, но более полезно (и интуитивно понятно, если вы посмотрите на график) сказать, что оно стремится к бесконечности. Аналогично, если бы у вас было:  

Предел, когда x приближается к нулю, был бы отрицательной бесконечностью, поскольку график идет вниз навсегда, когда вы приближаетесь к нулю с любой стороны:

Как правило, , когда вы берете предел и знаменатель равен нулю, предел уйдет в бесконечность или в отрицательную бесконечность (в зависимости от знака функции).

Так когда же вы сказали, что предела не существует?

Когда односторонние пределы не равны друг другу.

Во-первых, односторонний предел — это когда вы приближаетесь к значению с одной стороны. Вы указываете, с какой стороны вы идете, с плюсом или минусом относительно того, к чему приближается x. Если вы подходите справа, вы используете +, слева вы используете -.

Например:

При приближении к x = 5 справа (обозначено пунктирной линией) f(x) = 2. Это односторонний предел, идущий справа.

Когда вы приближаетесь к x = 5 слева, f(x) снова = 2.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *