ЦИТ Батайск — Объявления
В городе Батайске проводится профилактическое мероприятие «Безопасные осенние дороги» В период с 25 октября по 15 ноября в городе Батайске будет
проводится областное профилактическое мероприятие «Безопасные осенние
дороги», направленное на снижение детского дорожно-транспортного
травматизма, привитие детям навыков безопасного поведения на дороге.
С начала текущего года на территории города Батайска
зарегистрировано 2 дорожно-транспортных происшествия с участием
несовершеннолетних пешеходов. Уважаемые родители! Рассказывайте своим детям, где и как нужно правильно переходить
через проезжую часть дороги, как нужно безопасно вести себя на дорогах и
улицах города. Будьте примером для своих детей и не нарушайте правила
дорожного движения в их присутствии.
Помните, что дети ведут себя так, какдетям о правилах дорожного движения. Обучая несовершеннолетнего
безопасному поведению на дороге, необходимо разъяснять опасность
использования мобильного телефона, наушников при переходе проезжей
части дороги. В темное время суток необходимо использовать свет
возвращающие элементы. Уважаемые водители! Будьте внимательны и осторожны при проезде пешеходных переходов,
особенно в районе образовательных организаций и мест массового
пребывания людей. Помните, что от Вашей дисциплинированности,
выдержки, умения прогнозировать развитие дорожной ситуации, чтрогого
соблюдения правил дорожного движения зависит жизнь и здоровье всех
участников дорожного движения.
Мы в социальных сетях:
Госавтоинспекция города Батайска обращается к жителям города
На территории города Батайска с 28 сентября по 07 октября 2022
года проводятся профилактическое мероприятие «Декадник безопасности
дорожного движения».
Целью проведения профилактического мероприятия является –
профилактическая работа по выявлению нарушений ПДД, являющихся
основными причинами совершения ДТП, повышение дорожно-транспортной
дисциплины на территории города Батайска.
Основными задачами мероприятия:
— пресечение и профилактика нарушений ПДД РФ, являющихся
основными причинами совершения ДТП;
— проведение разъяснительной работы с участниками дорожного
движения о необходимости соблюдения ПДД РФ;
— профилактика детского дорожно-транспортного травматизма;
— профилактика аварийности с участием грузового автотранспорта.
Уважаемые водители! Будьте внимательны на дорогах, снижайте скорость
при подъезде к нерегулируемым пешеходным переходам и уступайте дорогу
пешеходам, вступившим на пешеходный переход. Соблюдайте скоростной
режим, правила проезда перекрестков.
Уважаемые пешеходы! Будьте особенно внимательными при переходе
проезжей части, в темное время суток необходимо использовать
световозвращающие элементы, чтобы дать водителю обнаружить себя
заблаговременно. При переходе проезжей части дороги по нерегулируемому
пешеходному переходу, убедитесь, что приближающийся автомобиль Вас
пропускает, и лишь после этого начинайте переход дороги.
ОГИБДД ОМВД России по городу Батайску убедительно просит всех
соблюдать установленные правила поведения на дорогах, проявлять культуру
и взаимовежливость. Помните, автомобиль – источник повышенной
опасности. Пренебрежение правилами может привести к непоправимым
последствиям.
Уважаемые родители!
Образовательный культурно – просветительский портал Отечество.
ру (http://ote4estvo.ru) формирует уникальный раздел «Семья Победы» с целью воспитания исторической грамотности и чувства патриотизма у подрастающего поколения, формирования чувства сопричастности с происходившими историческими событиями в годы Великой Отечественной войны 1941–1945 гг. В раздел для публикации принимаются истории из семейных архивов о воинских и трудовых подвигах народа.
Все истории будут опубликованы на сайте в разделе –( http://www.ote4estvo.ru/semya-pobedy/).
Мы приглашаем всех заинтересованных принять участие в формировании раздела. Для публикации материала, Вам нужно:
1. Зарегистрироваться http://www.ote4estvo.ru/index.php?do=new_register
2. Добавить публикацию http://www.ote4estvo.ru/addnews.html
3. Так же свои работы Вы можете прислать на почту [email protected].
Уважаемые родители!
Информируем Вас
об уникальной интернет-платформе СПАСИБОЗАВСЕ.
РФ, направленной на патриотическое воспитание граждан Российской Федерации, преемственность поколений, вовлечение молодежи в эти процессы.
Данный проект реализуется посредством интервьюирования или размещения на интернет-портале уже отснятых видео интервью ветеранов ВОВ и других локальных конфликтов современной Российской истории, героев гражданского общества, волонтеров и других достойных граждан России.
Пояснительная записка по проекту СПАСИБОЗАВСЕ.РФ
Последние новости
Ребята студии робототехники «Robotaim» получили первые награды
30.11 2022
В нашем учебно-методическом центре «Авангард» продолжается обучение.
30.11 2022
Уважаемые родители, у нас открыт набор по направлению «Подготовка к школе»
30.11 2022
Решение задач на Паскале Pascal
Решение задач на Паскале Pascal
gif» valign=»center»>.:Pascal:.
Главная страница | Примеры задач | Способы оплаты | Скачать Pascal | Партнерам |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
gif» bgcolor=»#f9f9f9″>
Задача очков | Блог о вероятности и статистике
Есть две известные задачи на вероятность, которые возникли у французского профессионального игрока Шевалье де Мере (1607-1684). Проблемы были решены совместно Блезом Паскалем (1623-1662) и Пьером де Ферма (1601-1665) в серии писем.
Идеи, обсуждавшиеся в этих письмах, часто считались началом теории вероятностей. В предыдущем посте мы обсуждаем одну из задач, поставленных Шевалье де Мере перед Паскалем (проблема с костями). В этом посте мы обсуждаем вторую проблему — проблему очков.
____________________________________________________________________________
Вот описание известной задачи на точки. Два игрока играют в азартную игру с соглашением, что каждый игрок делает равные ставки и что первый игрок, выигравший определенное количество раундов (или очков), получит все ставки. Предположим, что игра прервана до того, как кто-либо из игроков выиграл. Как игроки справедливо делят ставки?
Понятно, что игрок, который ближе к победе, должен получить большую долю ставок. Поскольку игрок, набравший больше очков, ближе к победе, игрок с большим количеством очков должен получить большую долю ставок. Как количественно определить дифференциал?
Чтобы описать проблему более подробно, предположим, что два игрока, A и B, разыгрывают серию очков в игре, так что игрок A выигрывает каждое очко с вероятностью, а игрок B выигрывает каждое очко с вероятностью .
Первый игрок, набравший очки, выигрывает игру. Предположим, что игра остановлена по какой-то причине. На момент остановки игрок А выиграл очки, а игрок В выиграл очки с помощью и . Как они делят ставки? Обратите внимание, что в банке участвуют оба игрока поровну.
При решении проблемы идея Паскаля состоит в том, что доля ставок, получаемая игроком, должна быть пропорциональна его/ее вероятности выиграть, если игра продолжится в момент остановки. Давайте рассмотрим эту идею на примерах.
____________________________________________________________________________
Взгляд на проблему через примеры
Следующие примеры основаны на следующем правиле. Допустим, два игрока (А и В) разыгрывают серию очков с одинаковой вероятностью выиграть очко в каждом раунде. Каждый игрок ставит 32 очка. Первый игрок, набравший четыре очка, забирает все ставки.
Пример 1 (подход Ферма)
Предположим, что игрок А выиграл 2 очка, а игрок В выиграл одно очко непосредственно перед окончанием игры.
Как справедливо разделить ставки?
При анализе мы предполагаем, что игра продолжается. Тогда игроку А нужно еще 2 очка, чтобы выиграть, а игроку Б нужно еще 3 очка, чтобы выиграть. Мы хотели бы рассчитать вероятность того, что игрок А выиграет 2 очка до того, как игрок Б наберет 3 очка. Рассмотрим следующие 2 + 3 – 1 = 4 раунда (при условии, что одно очко за раунд). Если игрок А набирает не менее 2 очков в следующих 4 раундах, игрок А выигрывает игру. Дополнением к этой вероятности будет вероятность того, что игрок B выиграет игру.
Пусть S (успех) — это событие, когда игрок A выигрывает очко, а F (неудача) — это событие, когда игрок A теряет очко (т. е. игрок B выигрывает очко). Выпишем все исходы игры в 4 очка (это был подход Ферма). Таких исходов 16.
Игрок А выигрывает В одиннадцати исходах (со звездочкой). Обратите внимание, что в результатах со звездочкой есть как минимум 2 S. Таким образом, вероятность выигрыша игрока А равна 11/16 = 0,6875. На момент остановки игры шанс игрока А на победу составляет 68,75% (если игра продолжится).
Доля игрока А составляет 0,6875 х 64 = 44,9.0003
Пример демонстрирует подход Ферма. По сути, он преобразовал первоначальную проблему очков в эквивалентную задачу, т. Е. Нахождение вероятности того, что игрок А выиграет игру, если игра будет продолжаться. Затем он использовал комбинаторные методы, чтобы подсчитать количество случаев, в которых игрок А выигрывает. В этом примере дополнительные четыре очка, которые нужно сыграть, являются фиктивными ходами (ходы не обязательно делать), но они полезны для поиска решения. Единственным недостатком подхода Ферма является то, что он использовал счет. Что делать, если количество задействованных точек велико?
Пример 2 (подход Паскаля)
Специфика примера такая же, как и в примере 1. Перечисление всех возможных случаев в примере 1 упрощает поиск решения. Но если количество точек велико, то управление подсчетом может стать затруднительным. Нам нужен алгоритм, которым легко пользоваться и который легко реализовать на компьютере.
Паскаль, по сути, думал так же, как и Ферма, то есть основывал решение на вероятности выигрыша, если игра продолжалась. Паскаль также понял, что исходная проблема с очками эквивалентна проблеме разыгрывания дополнительной серии очков. В этом примере дополнительные 2 + 3 – 1 = 4 очка. Как и в примере 1, находим вероятность того, что игрок А выиграет 2 или более очков в этой серии из 4 очков. Способ Паскаля найти эту вероятность был основан на том, что сейчас известно как треугольник Паскаля и биномиальное распределение. Мы будем использовать следующие современные обозначения:
Обратите внимание, что вышеприведенная вероятность 0,6875 — это вероятность иметь по крайней мере 2 успеха в 4 испытаниях (с вероятностью успеха 0,5 в каждом испытании). Любой, кто хорошо разбирается в биномиальном распределении, может выполнить расчет (или использовать программное обеспечение). Конечно же, эта математическая конструкция пришла от Паскаля! Для современников Паскаля и Ферма это понятие определенно не было обыденным.
Пример 3
Предположим, что игрок A выиграл 1 очко, а игрок B не выиграл ни одного очка на момент окончания игры. Как справедливо разделить призовые деньги?
Исходя из обсуждения Примера 1 и Примера 2, игроку А необходимо набрать как минимум 3 очка, чтобы выиграть игру, а игроку В необходимо набрать 4 или более очков, чтобы выиграть игру. Расширенная серия очков будет иметь 3 + 4 – 1 = 6 очков. Затем игроку А необходимо набрать не менее 3 очков из 6 (не менее 3 успехов из 6 попыток). Ниже приведена вероятность того, что игрок А выиграет расширенную серию розыгрышей.
При общей сумме ставок 64 доля игрока А составит 64 x 42/64 = 42. Доля игрока Б составит 22.
____________________________________________________________________________
Общее обсуждение
Теперь мы обсудим идеи, поднятые в примерах. Как указано выше, два игрока, A и B, вносят равные взносы в ставки, а затем играют серию очков, пока один из них не выиграет очки.
Вероятность того, что игрок А выиграет раунд (одно очко в каждом раунде), равна, а вероятность того, что игрок Б выиграет очко, равна . Предположим, что игра по какой-то причине остановлена до того, как кто-либо из игроков выиграл. На момент остановки игрок А выиграл очки, а игрок В выиграл очки с помощью и . Пусть и . Ключом к решению проблемы очков является рассмотрение расширенной игры очков.
Вот великое открытие Паскаля и Ферма. Они смотрели вперед, а не назад. Они не основывали решение на количестве уже набранных очков. Вместо этого они сосредоточились на расширенной серии очков, чтобы определить долю выигрыша. Эта дополнительная игра очков является «фиктивной», но она помогает прояснить процесс. По сути, они превратили первоначальную проблему очков в проблему этой дополнительной игры очков.
Исходная проблема такова: какова справедливая доля игрока А, если игра остановлена досрочно, когда игрок А выиграл очки, а игрок В выиграл очки? Эквивалентная проблема: какова вероятность того, что игрок А наберет по крайней мере очки из следующих очков, где и (при условии, что игра не остановилась).
Назовем эту вероятность. Рассмотрим настройку этой вероятности. Каждое очко похоже на испытание Бернулли — либо успех (игрок А выигрывает), либо неудача (игрок Б выигрывает). Есть испытания. Вероятность успеха в каждом испытании. Мы хотим найти вероятность того, что будут как минимум успехи. То, что описывается, является биномиальным распределением. Искомая вероятность:
где , а это количество очков, выигранных игроком А, и количество очков, выигранных игроком Б на момент окончания игры.
Вероятность — это вероятность того, что игрок А выиграет игру, если игра продолжится в момент ее завершения. Эта вероятность представляет собой долю ставок, которая будет присуждена игроку А. Конечно, доля, которая должна быть присуждена игроку Б, будет равна . Количество можно получить из заданных параметров и с помощью любого программного обеспечения, имеющего функцию для биномиального распределения.
Проблема очков кажется легко решаемой, поскольку ответ так доступен.
Любой, кто понимает биномиальное распределение, может понять. Также легко вычислить вероятности для биномиального распределения с помощью калькулятора или программного обеспечения. Следует иметь в виду, что решение выглядит доступным сейчас благодаря инструментам и концепциям, которые пришли из путей, проложенных Паскалем и Ферма (и благодаря имеющимся у нас вычислительным инструментам). Инструменты и концепции, такие как треугольник Паскаля и биномиальное распределение, были неизвестны людям во времена Паскаля и Ферма.
_____________________________________________________________________________
Работа в обратном направлении
Для нас расчет легко выполняется с помощью калькулятора или программного обеспечения. Паскаль не вычислял напрямую, а вместо этого выполнял вычисления в обратном направлении, используя следующую формулу.
Формулу можно вывести математически. Но делать это не обязательно. Количество — это вероятность того, что игрок А наберет очки раньше, чем игрок Б наберет очки.
Мы можем вывести приведенную выше формулу, обусловив результат первой точки. Величина рассчитывается в Примере 1 и Примере 2. Это среднее значение двух подобных вероятностей с меньшими параметрами.
Основываясь на рекурсивной формуле в , Паскаль построил ответ в обратном порядке, подобно тому, как пишется компьютерная программа. По сути, этот рекурсивный подход позволяет решать не только один сценарий, но и все сценарии в игре по очкам.
Пример 4
Теперь вернемся к задачам из примеров 1 и 2. Напомним, что игра ведется на 4 очка, т. е. первый игрок, выигравший 4 очка, забирает все ставки из 64 (32 игрок). Каждый игрок получает очко с вероятностью 0,5. Теперь мы покажем, как разделить ставки, когда игра останавливается во всех возможных точках остановки.
На следующей диаграмме (Рисунок 1) показана таблица доли, присужденной игроку А. Таблица пуста, за исключением верхней строки и крайнего правого столбца (цифры выделены красным).
Число 64, указанное в последнем столбце, будет суммой, присужденной игроку А, потому что игрок А набрал 4 очка. Цифра 0 вверху означает, что игрок Б выиграл 4 игры. Таким образом, игрок А ничего не получает. Обратите внимание, что нижняя строка, выделенная оранжевым цветом, показывает количество очков, которые были выиграны игроком А. Нижняя строка, выделенная синим цветом, показывает оставшиеся очки, которые игроку А необходимо набрать, чтобы выиграть все ставки (это фиктивные очки). . Точно так же столбцы, выделенные оранжевым и синим цветом слева, показывают ту же информацию для игрока B.
Рисунок 1 – Доля ставок, присужденная игроку А
Теперь мы можем использовать рекурсивную формулу для заполнения таблицы. В основном каждая ячейка представляет собой среднее число над ней и число справа. Параметр in — это число в синей строке. Параметр in — это число в синем столбце. Ниже показаны результаты.
Рисунок 2 – Доля ставок, присужденная игроку А
Например, когда игрок А набрал 2 очка, а игрок В — 1 очко, доля игрока А составляет 44 (среднее значение 32 и 56), то есть тот же ответ, что и в Примере 1 и Примере 2.
Когда игрок А имеет выиграл 2 очка, а игрок B — 2 очка, оба игрока находятся в равных конкурентных позициях. Тогда каждый игрок получает по 32. Когда игрок А набрал 2 очка, а игрок Б — 3 очка, доля игрока А составляет 16 (среднее 0 и 32).
По сути, формула заключается в использовании меньших шагов, а не всей расширенной игры очков. Эту идею меньших шагов предпочитал Паскаль. В тот момент, когда игроку А нужно больше очков, чтобы выиграть, а игроку Б нужно больше очков, идея состоит в том, чтобы разыграть еще одно очко. Предположим, что игроки знают награды двух игроков после еще одного раунда. Затем они должны разделить разницу между будущими наградами. Подсчет должен начинаться с точки, где каждому игроку для победы нужно еще одно очко (ячейка с цифрой 32 на рис. 2). В этой ячейке мы знаем награды после одного дополнительного раунда. Взяв среднее значение 0 и 64, мы получим 32. Из этой ячейки мы двигаемся вниз и двигаемся влево по таблице. Продолжайте повторять процесс, пока вся таблица не будет заполнена.
Существует способ настройки подхода к таблице для работы с неравной вероятностью выигрыша очка. Допустим, вероятность того, что игрок А выиграет очко, равна 0,6. Тогда вероятность того, что игрок Б выиграет очко, равна 0,4. Значением данной ячейки в таблице будет средневзвешенное значение ячейки справа (вес 0,6) и ячейки над ней (вес 0,4). Когда мы знаем результаты еще одного раунда, мы присваиваем 0,6 результату выигрыша игрока А и 0,4 результату выигрыша игрока Б. В следующей таблице показаны результаты.
Рисунок 3 – Доля ставок, присужденная игроку А (с весом 0,6)
Прямая формула или табличный подход с использованием рекурсивной формулы могут быть легко запрограммированы на компьютере. Для Паскаля табличный подход является очень привлекательным вариантом, поскольку расчет может быть построен на более низких значениях параметров. В приведенной выше конфигурации просто заполните правый столбец (все ставки идут игроку А) и верхнюю строку (игрок А ничего не получает).
Затем остальные ячейки получаются средневзвешенным, как описано в формуле.
Приведем еще один пример.
Пример 5
Предположим, что игрок B — казино, а игрок A — посетитель казино, играющий на 12 очков. Преимущество дома составляет 2%, поэтому вероятность того, что игрок А выиграет раунд, равна 0,48. Если игрок А желает уйти после того, как игрок А наберет 9 очков, а казино наберет 6 очков, какова доля ставок, которая должна быть присуждена игроку А?
Играя на 12 очков, игроку А нужно еще 3 очка, чтобы выиграть, а заведению нужно еще 6 очков, чтобы выиграть. Итак, нам нужно проанализировать расширенную игру 3 + 6 — 1 = 8 очков. Чтобы игрок А выиграл расширенную игру, ему нужно набрать как минимум 3 очка.
Ответ можно получить, вычислив каждый член в сумме (от до ). Другой способ — использовать функцию БИНОМРАСП в Excel следующим образом:
- = 1-БИНОМРАСП(2, 8, 0,48, ИСТИНА) = 1-0,172368083 = 0,827631917
Основываясь на методе справедливого распределения, обсуждаемом в этом сообщении в блоге, игрок А заслуживает 82,76% ставок.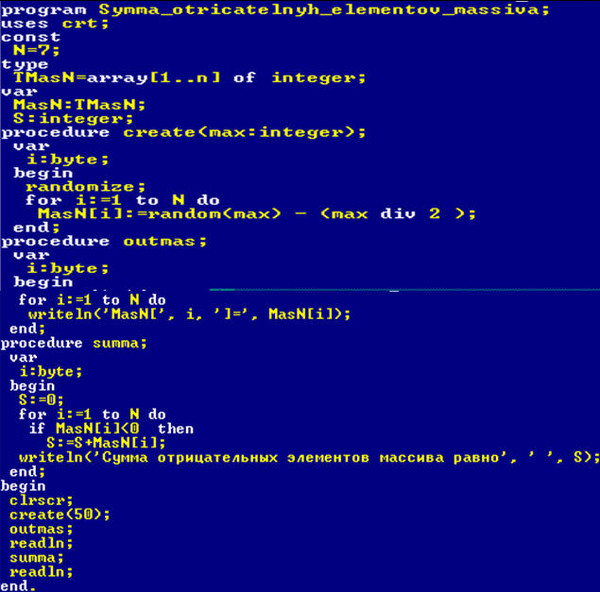
____________________________________________________________________________
Примечания
В переписке Паскаль и Ферма нашли убедительное и последовательное решение проблемы точек. Прежние решения проблемы точек не были удовлетворительными (для всех заинтересованных сторон) и иногда непоследовательны. Разделение ставок только на основе количества выигранных очков может привести к экстремальным результатам. Например, если игрок А выиграл 1 очко, а игрок Б не выиграл ни одного очка, то игрок А получит все ставки. Для игры, описанной на рис. 2, по тому же сценарию игрок А получает 42 из 64 (42/64 = 0,65625), что далеко не 100%.
Более подробную информацию об истории проблемы точек см. в «Истории математики» Виктора Дж. Каца.
_____________________________________________________________________________
Нравится:
Нравится Загрузка…
6.9 Треугольник Паскаля и биномиальное разложение – промежуточная алгебра
Перейти к содержимому
Chapter
Треугольник Паскаля (1653 г.