Примеры задач по комбинаторике с решением: Задачи по комбинаторике. Примеры решений

Решение задач по комбинаторике

Муниципальный координатор по работе с детьми с повышенной учебной мотивацией в области математики.

МБОУ «Лицей №6 имени М.А. Булатова»

 

 

 

 

 

 

 

 

 

Дистанционная лекция

 

 

Решение задач по комбинаторике.

 

 

 

Учитель

МБОУ «СОШ№10 им. Е.И. Зеленко» г. Курска

                                                                                Коротковская О.С.

 

 

 

 

 

 

Курск – 2020

Вступление.

Так что же такое комбинаторика? И какими задачами она занимается? Комбинаторика и слово комбинация очень похожи и имеют прямое отношение друг к другу. В комбинаторике изучают различные комбинации элементов множества и отношения на этих множествах.

Впервые термин «комбинаторика» ввел Лейбниц, который в 1666 году опубликовал большой труд «Рассуждения о комбинаторном искусстве».

Комбинаторика – раздел математики, который занимается решением комбинаторных задач.

Комбинаторные задачи – это задачи, в которых необходимо составить комбинации каких-либо элементов из заданного набора по определённым условиям и (или) подсчитать количество получившихся комбинаций.

В комбинаторике существует несколько способов решения комбинаторных задач. Сейчас мы их подробно рассмотрим.

Способ 1. Перебор всех возможных вариантов.

Рассмотрим сущность способа 1 на конкретном примере.

Пример 1. Из группы теннисистов, в которую входят четыре человека – Антонов, Григорьев, Сергеев и Федоров, тренер выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары?

Решение. 1. Составим сначала все пары, в которые входит Антонов (для краткости будем писать первые буквы фамилий). Получим три пары: АГ, АС, АФ.

2. Выпишем теперь пары, в которые входит Григорьев, но не входит Антонов. Таких пар две: ГС, ГФ.

3. Составим пары, в которые входит Сергеев, но не входят Антонов и Григорьев. Такая пара только одна: СФ.

4. Делаем вывод, что других вариантов составления пар нет, так как все пары, в которые входит Федоров, уже составлены.

5. Итак, мы получили 6 пар: АГ, АС, АФ, ГС, ГФ, СФ. Значит, всего существует 6 вариантов выбора тренером пары теннисистов из данной группы.

Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.

Примечание. В данном примере нам не важен порядок выбора пары: Антонов и Григорьев или Григорьев и Антонов,

Рассмотрим пример задачи, где порядок выбора пары важен.

Пример 2. Три друга – Антон, Борис и Виктор – приобрели два билета на футбольный матч на 1-е и 2-е места первого ряда стадиона. Сколько у друзей есть вариантов занять эти два места на стадионе?

Решение. 1. Если на матч пойдут Антон и Борис, то они могут занять места двумя способами: 1-е место – Антон, 2-е – Борис, или наоборот. Аналогично Антон и Виктор, Борис и Виктор.

2. Таким образом, мы получили 6 вариантов: АБ, БА, АВ, ВА, БВ, ВБ.

            Рассмотрим пример на применение этого же способа на примере задачи с цифрами.

Пример 3. Сколько различных трехзначных чисел можно записать с помощью цифр 1, 2, 3 при условии, что цифры в числе могут повторяться?

Решение. Перебор вариантов можно организовать следующим образом. Выписать все числа, начинающиеся с цифры 1 в порядке их возрастания; затем – начинающиеся с цифры 2; после чего – начинающиеся с цифры 3. Таких комбинаций получим 27. При переборе легко было упустить какую-нибудь из них.

Способ 2. Подсчет вариантов с помощью графов.

Эффективным приемом, организующим подсчет, является построение графов. Так называют геометрические фигуры, состоящие из точек (их называют вершинами) и соединяющих их отрезков (называемых ребрами графа).

Пример 4. Сколько двузначных чисел можно составить, используя         цифры 1, 4 и 7?

Решение. 1. Для того чтобы не пропустить и не повторить ни одно из чисел, будем выписывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4 и, наконец, с цифры 7: 11, 14, 17, 41, 44, 47, 71, 74, 77.

2. Таким образом, из трех данных цифр можно составить всего 9 различных двузначных чисел.

Рассмотрим два вида графов:

1)                  Граф-дерево (называют за внешнее сходство с деревом).

С помощью дерева проиллюстрируем проведенный перебор вариантов в примере 1.

 

 

 

 

 

 

Графы, позволяют в наглядной форме представить идею комбинирования и процесс подсчета комбинаторных объектов. Для подведения учащихся к следующим комбинаторным методам целесообразно рассмотреть задачу, в которой количество всевозможных комбинаций из данных элементов велико и процесс их подсчета затруднителен.

На первом месте в двузначном числе может стоять одна из цифр 1, 4 или 7; на втором – (при условии, что цифры могут повторяться) также любая из трех цифр. Таким образом из рисунка видно, что из трех цифр 1, 4, 7 можно составить 9 различных чисел.

Таким образом, с помощью графа-дерева подсчет вариантов гораздо легче производить. Также вычерчивать дерево вариантов полезно, когда требуется записать все существующие комбинации элементов.

2)                  Полный граф. Используется для решения задач, в которых все элементы множества взаимосвязаны.

Пример 5. При встрече каждый из друзей пожал другому руку (каждый пожал каждому). Сколько рукопожатий было сделано, если друзей было четверо?

Четырех друзей поместим в вершины графа и проведем все возможные ребра. В данном случае отрезки-ребра обозначают рукопожатия каждой пары друзей.

Из рисунка видно, что граф имеет 6 ребер, значит, и рукопожатий было сделано 6.

Способ 3. Перебор с помощью таблицы вариантов

.

Ее можно использовать, когда составляемые комбинации состоят из двух элементов. Рассмотрим сущность способа на конкретной задаче.

Пример 6. Записать всевозможные двузначные числа, используя при этом цифры 0, 1, 2 и 3. Подсчитать их количество N.

Решение. Для подсчета образующих чисел составим таблицу 1:

                                   Таблица 1                                             Таблица 2

1-я цифра	2-я цифра
	0	1	2	3
1
2
3

 

1-я цифра	2-я цифра
	0	1	2	3
1	10	11	12	13
2	20	21	22	23
3	30	31	32	33

 

Решением задачи будет таблица 2. всего вариантов чисел будет N=3·4=12

Способ 4. Использование правил суммы и произведения

Сущность способа рассмотрим на примере задачи 7.

Задача про «Суеверного председателя».

«Опять восьмерка!» — горестно воскликнул председатель клуба велосипедистов, взглянув на прогнутое колесо своего велосипеда. «А все почему? Да потому, что у меня членский билет № 888 – целых три восьмерки. И теперь не проходит и месяца, чтобы то на одном, то на другом колесе не появилась восьмерка. Надо менять номер билета! А чтобы меня не обвинили в суеверии, проведу ка я перерегистрацию всех членов клуба и буду выдавать только билеты с номерами, в которые не входит ни одна восьмерка. Не знаю только, хватит ли на всех номеров – ведь у нас в клубе почти 600 членов. Неужели придется сначала выписать все номера от 000 до 999, а затем вычеркивать из них все номера с восьмерками?»

Чтобы помочь председателю, нам нужно решить такую комбинаторную задачу (учащимся можно предложить ее сформулировать):

Задача 7. Сколько существует трехзначных номеров, не содержащих цифры 8?

Решение. 1) Сначала найдем количество однозначных номеров, отличных от 8. Ясно, что таких номеров девять: 0,1,2,3,4,5,6,7,9. 2) Найдем все двузначные номера, не содержащие восьмерок. Их можно составить так: взять любой из найденных однозначных номеров и написать после него любую из девяти допустимых цифр. В результате из каждого однозначного номера получится 9 двузначных, т. е. всего получится 9·9 = 9

2 двузначных номеров.

3) Итак, существует 9² = 81 двузначный номер без цифры 8. Но к каждому из этих номеров можно приписать справа любую из цифр 0,1,2,3,4,5,6,7,9 и получить трехзначный номер, не содержащий цифру 8. 4) При этом получаются все трехзначные номера с требуемым свойством. В результате мы нашли 9²·9 = 9³ = 729 трехзначных номеров без восьмерок.

Примечание. Если бы председатель клуба был еще суевернее и отказался и от цифры 0, поскольку она походит на вытянутое колесо, то он смог бы составить лишь 8³ = 512 трехзначных номеров и их уже не хватило бы на всех членов клуба.

Пример 8. На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?

Решение: 1) По условию задачи яблоко можно выбрать пятью способами, апельсин – четырьмя. 2) Так как в задаче речь идет о выборе «либо яблоко, либо апельсин», то его, согласно правилу суммы, можно осуществить 5+4=9 способами.

Пример 9. Сколько трехзначных чисел можно составить, используя цифры   7, 4 и 5?

Решение: 1) В данной задаче рассматриваются трехзначные числа, так как цифры в записи этих чисел могут повторяться, то цифру сотен, цифру десятков и цифру единиц можно выбрать тремя способами каждую.

2)Поскольку запись трехзначного числа представляет собой упорядоченный набор из трех элементов, то, согласно правилу произведения, его выбор можно осуществить 27 способами, так как 3∙3∙3=27.

Правило умножения приводит к важному понятию факториала. Давайте на примере разберем это понятие.
            Пример 10. Сколько существует комбинаций из шести букв: А, Б, В, Г, Д, Е. Буквы не повторяются.
           Решение: На первое место мы можем поставить шесть букв, на второе место — уже пять, так как буквы не повторяются, на третье — соответственно четыре, на четвертое — три, на пятое — две, и на шестое — букву.
Используем правило умножения: 6*5*4*3*2*1=720.
Ответ: 720 способов расстановки букв без повторения.

Произведение подряд идущих первых n натуральных чисел обозначают n! (n факториал): n!=1∗2∗…∗(n−1)∗n, n факториал – состоящий из n множителей.

Заметим важное свойство факториала: n!=(n−1)!∗n. Данное свойство значительно упрощает решение задач, где присутствует факториал. Например, для вычисления задач вот такого типа: . Совсем необязательно вычислять все факториалы. Можно все переписать вот в таком виде: . Сократив нашу дробь, получим гораздо более простое выражение: 4∗9∗10=360.

Способ 5. Решение комбинаторных задач с использованием формул

            Кроме основных правил, способов перебора и графов пользуются основными понятиями комбинаторики, которые сопровождаются формулами для подсчета числа отдельных видов комбинаций, встречающиеся наиболее часто. При решении задач на комбинаторные соединения помогает таблица «Общая модель комбинаторной задачи и ее модификации», которая представлена ниже.

Размещения с повторениями	Размещения без повторений	Перестановки с повторениями	Перестановки без повторений	Сочетания с повторениями	Сочетания без повторений
Характер выборки: 1.с повторениями 2. упорядоченная, 3.m — любое	Характер выборки: 1.без повторений 2.упорядоченная, 3.m<n	Характер выборки: 1.с повторением данного состава (m1, m2, …,mn)? 2.упорядоченная	Характер выборки: 1.без повторений 2.упорядоченная 3.m=n	Характер выборки: 1.с повторениями, 2.неупорядоченная.	Характер выборки: 1.без повторений, 2.упорядоченная, 3.m≤n

 

Рассмотрим способы рассуждений при решении некоторых комбинаторных задач на использование формул.

Пример 11. В классе 30 учащихся. Сколькими способами можно выбрать из класса команду из 4 учащихся для участия в олимпиаде по истории, литературе, русскому и английскому языкам?

Анализ задачи. Поиск плана решения. Для начала определим, о каком множестве идет речь. В задаче говорится о 30 учащихся,  значит мы имеем дело с одним множеством Х= {1, 2, 3,…,30}, т. е. n(Х)=30. Так как рассматривается одно множество — значит задача простая.

Рассматривается выборка: выбрать команду из 4 учащихся для участия в олимпиаде. Можно сделать вывод, что m=4. Искомые команды будут отличаться между собой или учащимися, или их порядком, который указывает, на какую олимпиаду пойдет ученик. Поэтому искомое число равно числу размещений из 30 по 4 и поэтому используем формулу для размещения без повторений:

Решение:                               

Это значит, что существует 657 720 способов выбора команды.

Анализ решения. При решении данной задачи мы использовали формулу для размещения без повторений, так как характер выборки:

1.       Без повторений;

2.      Упорядоченная;

3.      m<n.

Пример 12. Сколько восьмизначных чисел кратных пяти можно составить из цифр 1,2,3,4,5,6,7,8 при условии, что числа не должны повторяться.

Анализ задачи. Поиск плана решения. В задаче речь идет о множестве цифр: Х={1, 2, 3, 4, 5, 6, 7, 8}, т. е. n(Х)=8. Для того, чтобы число, составленное из заданных цифр, делилось на 5, необходимо и достаточно, чтобы цифра 5 стояла на последнем месте. Остальные семь цифр могут стоять на оставшихся местах, причем в любом порядке. Следовательно, искомое число восьмизначных чисел, кратных пяти, равно числу перестановок из семи элементов, т.е.:

Решение:                            7! = 7 · 6 · 5 · 4 ·  3 · 2 · 1 = 5040.

Анализ решения. При решении данной задачи мы использовали формулу для нахождения числа перестановок без повторений, так как задача имеет следующий характер выборки:

1.      Без повторений;

2.      Упорядоченная;

3.       m=n.

Пример 13. Требуется составить расписание отправления поездов на различные дни недели. При этом необходимо, чтобы: 3 дня отправлялись по 2 поезда в день, 2 дня — по 1 поезду в день, 2 дня — по 3 поезда в день. Сколько можно составить различных расписаний?

            Анализ задачи. Поиск плана решения. Для того, чтобы определить количество различных расписаний отправления поездов, обозначим количество поездов, отправляемых в день цифрами 1, 2, 3, — это три группы одинаковых элементов, из которых должна быть составлена выборка. При этом в расписании на неделю число 1 повторяется 2 раза, число 2 повторяется 3 раза и число 3 повторяется 2 раза. Число различных расписаний равно числу перестановок с повторением.

            Решение:                          P(2,3,2)= 7!/(2!*3!*2!)=210.

            Анализ решения. Для решения данной задачи мы использовали формулу числа перестановок с повторением, так как задача имеет следующий характер выборки:

1.       С повторением данного состава;

2.      Упорядоченная.

Пример 14. В чемпионате страны по футболу (высшая лига) участвуют 18 команд, причем каждые две команды встречаются между собой 2 раза. Сколько матчей играется в течение сезона?

Анализ задачи. Поиск плана решения. В данной задаче необходимо определить сколько матчей состоится. В первом круге состоится столько матчей, сколько существует двухэлементных подмножеств у множества, содержащего 18 элементов, так как каждая команда должна встретиться между собой 2 раза, а команд всего 18, т.е. их число равно С²₁₈.

Решение:                                  

Анализ решения. При решении данной задачи использовалась формула числа сочетаний без повторении, так как задача имеет следующий характер выборки:

1.      Без повторений;

2.      Упорядоченная;

3.      m≤n.

Пример 15. Из группы, состоящей из 7 мужчин и 4 женщин, надо выбрать 6 человек так, чтобы среди них было не менее 2 женщин. Сколькими способами можно это сделать?

Анализ задачи. Поиск плана решения. В данной задаче речь идет о двух множествах: мужчины и женщины, т. е. задача сложная. Поэтому при решении мы будем пользоваться не только одной формулой.

Из условия задачи можно сделать вывод, что можно выбрать двух, трех или четырех женщин (не менее 2). Поскольку нас интересует лишь состав элементов в комбинации, а не порядок элементов, то используем формулу для числа сочетаний.

Таким образом, двух женщин можно выбрать C ²₄ способами. После этого надо выбрать 4 мужчин, что можно сделать C ⁴₇ способами. По правилу произведения получаем C ^{2₄C 4}₇ способов. Аналогично, выбирая 3 женщин и 3 мужчин, получают C ^{3₄C 3}₇ способов, а  выбирая 4 женщин и 2 мужчин,  получают C ^{4₄C 2}₇ способов.

         По правилу суммы всего

C ^{2₄C 4}₇ + C ^{3₄C 3}₇ + C ^{4₄C 2}₇=371 способ.

                        Анализ решения. При решении данной задачи использовалась формула числа сочетаний без повторений, так как задача имеет следующий характер выборки:

1.      Без повторений;

2.      Упорядоченная;

3.      m≤n.

Помимо данной формулы использовались также правила умножения и суммы.

Пример 16. На книжной полке стоят 10 книг по математике и 10 по логике. Доказать, что наибольшее количество вариантов комплекта, содержащего 10 книг, возможно в том случае, когда число книг по каждому предмету равно 5.

Анализ задачи. Поиск плана решения. 1) Для того, чтобы доказать, что наибольшее количества вариантов комплекта, содержащего  10 книг, возможно в том случае, когда число книг по каждому предмету равно 5, необходимо найти число вариантов комплекта, содержащего 5 книг по каждому из предметов. Для этого пронумеруем все книги. Получим, что номера 1 — 5 – книги по математике, 6 — 10 – книги по логике. 2) Отобрать 5 книг по математике мы можем  способами (число сочетаний без повторений, так как выборка без повторений, упорядоченная, m≤n). При каждом варианте отбора, книги по логике мы можем отобрать также способами. Значит, всего вариантов отбора будет . Но отсчет книг можно вести и в обратном порядке, значит число вариантов возрастет вдвое. Это и будет число вариантов комплекта из 5 книг по каждому предмету. 3) Докажем теперь, что наибольшее кол-во вариантов будет в том случае, когда книг по каждому предмету — 5. Действительно, если бы количество книг по одному из предметов было больше 5, то по другому стало бы меньше 5 (т.к. кол-во книг комплекта — 10). Рассмотрим частный случай, когда комплект составляется из 6 книг по одному из предметов. Общее число вариантов тогда будет , а это меньше, чем в предыдущем случае. При дальнейшем увеличении числа книг по одному предмету в комплекте общее число вариантов будет уменьшаться, следовательно наибольшее число вариантов комплекта содержащего 10 книг, возможно в том случае, когда число книг по каждому предмету равно 5. Что и требовалось доказать.

Самостоятельная работа

1.       Сколькими способами можно выбрать 5 кандидатов на пост губернотора из состава совета депутатов, на котором присутствуют 30 человек?

2.      Сколько наборов из 7 плиток шоколада можно составить, если в продаже имеются 4 сорта шоколада.

3.      В компьютерный класс свободного доступа куплены 3 новых системных блока. В классе также есть свободные 4 клавиатуры, 5 “мышек” и 6 мониторов (все клавиатуры, “мышки” и мониторы отличаются друг от друга). Сколькими способами можно укомплектовать все три компьютера (к каждому подключают одну клавиатуру, одну “мышку” и один монитор)?

4.      На заводе работают 8 токарей. Сколькими способами можно поручить трем из них изготовление трех различных видов деталей (по одному виду на каждого).

5.      Сколькими способами можно построить в одну шеренгу игроков двух футбольных команд, так чтобы при этом два футболиста одной команды не стояли рядом?

 

 

Примеры комбинаторных задач | Презентация к уроку по алгебре (9 класс) на тему:

Слайд 1

Примеры комбинаторных задач Тема урока : 14. 12.2014 Логинова Н.В. учитель математики МБОУ «СОШ № 16» г. Ижевска 9 класс 1 урок

Слайд 2

14.12.2014 2 Такие задачи получили название комбинаторных задач , а раздел математики, в котором рассматриваются эти задачи, называют комбинаторикой. В науке и на практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций . Логинова Н.В. МБОУ «СОШ №16»

Слайд 3

14.12.2014 3 Раздел математики, в котором изучают комбинаторные задачи, называется комбинаторикой Логинова Н.В. МБОУ «СОШ №16»

Слайд 4

14.12.2014 4 — раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций , подчинённых тем или иным условиям, можно составить из заданных объектов. м б о и н а о р и к а к Логинова Н.В. МБОУ «СОШ №16»

Слайд 5

14.12.2014 5 Термин «комбинаторика» был введён в математический обиход немецким философом, математиком Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».

Слайд 6

14.12.2014 6 Познакомимся с некоторыми приемами решения комбинаторных задач решение методом перебора; решение с помощью дерева возможных вариантов; решение с помощью комбинаторного правила умножения; решение с помощью таблиц; решение с помощью графов. Логинова Н.В. МБОУ «СОШ №16»

Слайд 7

14.12.2014 7 №715 У Ирины 5 подруг: Вера, Зоя, Марина, Полина и Светлана. Она решила двух из них пригласить в кино. Укажите все возможные варианты выбора подруг. Сколько таких вариантов? Замечание . При решении для краткости будем писать первые буквы имен. Логинова Н.В. МБОУ «СОШ №16»

Слайд 8

14.12.2014 8 Составим сначала все пары, в которые входит Вера. ВЗ, ВМ, ВП, ВС Выпишем теперь пары, в которые входит Зоя, но не входит Вера. Далее составим пары, в которые входит Марина, но не входят Вера и Зоя. Еще одна пара ЗМ, ЗП, ЗС МП, МС ПС Всего существует 4+3+2+1=10 Решение Ответ:10 вариантов В ера З оя М арина П олина С вета Получим 4 пары . Таких пар три . Их две . Далее составим пары, в которые входит Полина. Логинова Н.В. МБОУ «СОШ №16»

Слайд 9

14.12.2014 9 Рассмотрим еще одну задачу. На цветочной клумбе сидели ш мель, ж ук, б абочка и м уха. Два насекомых улетели. Какие пары насекомых могли улететь? Укажите все возможные варианты. Сколько таких вариантов? Способ рассуждений , которым мы воспользовались при решении задачи, называют перебором возможных вариантов . ш ж б м

Слайд 10

14.12.2014 10 Решение Всего 3+2+1=6 Ответ:6 вариантов ш ш ш ж ж б б б ж м м м Логинова Н.В. МБОУ «СОШ №16»

Слайд 11

14.12.2014 11 Таким образом, из трёх данных цифр можно составить всего 9 различных двузначных чисел. Ответ: 9 чисел. Приемы решения комбинаторных задач метод перебора 11;14;17; (начали с 1) Решение: Для того, чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания: Сколько двузначных чисел можно составить, используя цифры 1; 4; 7? 41;44;47; (начали с 4) 71;74;77; (начали с 7)

Слайд 12

14. 12.2014 12 Приемы решения комбинаторных задач дерево возможных вариантов Решим аналогичную задачу о составлении трехзначных чисел из цифр 1;4;7, так чтобы цифры не повторялись . Для её решения построим схему — дерево возможных вариантов . число 1 4 7 4 4 7 7 1 1 7 7 1 1 4 4 Ответ: числа 147;174;417;471;714;741 6 чисел (вариантов)

Слайд 13

14.12.2014 13 Заметим, что ответ на вопрос, можно получить, не выписывая сами числа. Будем рассуждать так. Первую цифру можно выбрать тремя способами . Так как после выбора первой цифры останутся две, то вторую цифру можно выбрать двумя способами. Остается приписать одну цифру . Следовательно, общее число искомых трехзначных чисел равно произведению Логинова Н.В. МБОУ «СОШ №16»

Слайд 14

14.12.2014 14 «Если объект А можно выбрать m способами, а другой объект В можно выбрать k способами, то объект « А и В » можно выбрать m ∙ k способами». Мы нашли ответ на вопрос, используя так называемое комбинаторное правило умножения Логинова Н. В. МБОУ «СОШ №16»

Слайд 15

14.12.2014 15 У Куклы Светы 3 юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций одежды имеется у Светы? Решение. 3·5 = 15 комбинаторное правило умножения

Слайд 16

14.12.2014 16 Решите задачу, используя дерево возможных вариантов В класс пришли четыре новых ученика М иша, К атя, В ася, Л иза. С помощью дерева возможных вариантов покажи, все возможные варианты расположения четырех учеников за одной партой. Сколько вариантов выбора будет? Л В К М Логинова Н.В. МБОУ «СОШ №16»

Слайд 17

14.12.2014 17 Ответ: 12 вариантов Решение М В К Л

Слайд 18

14.12.2014 18 С помощью дерева возможных вариантов решите задачу №714 . Котлеты Гуляш Рассольник Борщ Обед Пельмени Сосиски Котлеты Гуляш Пельмени Сосиски Логинова Н.В. МБОУ «СОШ №16»

Слайд 19

14.12.2014 19 У Миши 4 ручки разного цвета и 3 блокнота разного размера. Сколько различных наборов из ручки и блокнота сможет составить Миша? Реши задачу, составив таблицу.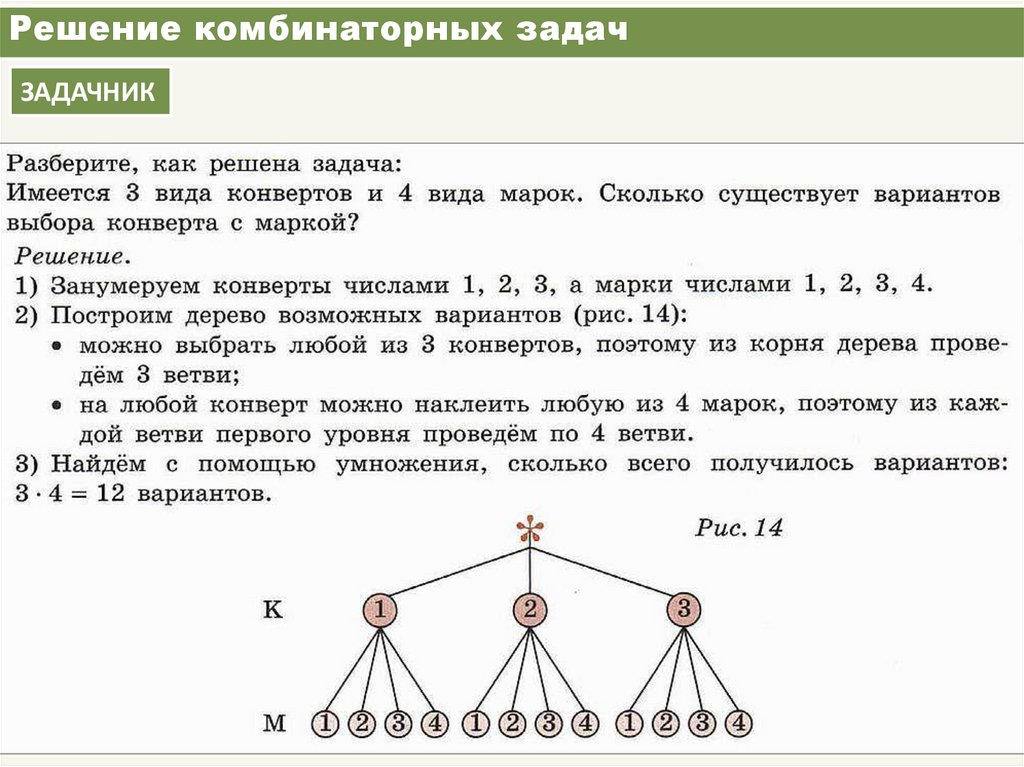 Приемы решения комбинаторных задач задачи, решаемые с помощью таблиц м с б с з ч к Логинова Н.В. МБОУ «СОШ №16»

Слайд 20

14.12.2014 20 12 различных наборов м с б з ч к с

Слайд 21

14.12.2014 21 Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9? Приемы решения комбинаторных задач задачи, решаемые с помощью таблиц Ответ:15 чисел (5·3) 1 2 4 5 9 0 2 4 1 0 1 4 1 2 2 0 2 2 2 4 4 0 4 2 4 4 5 0 5 2 5 4 9 0 9 2 9 4

Слайд 22

м б 14.12.2014 22 о и н а о р и к а к ГРАФ – совокупность объектов со связями между ними. Объекты представляются как вершины , или узлы графа , а связи – как дуги , или ребра . вершины ребра Логинова Н.В. МБОУ «СОШ №16»

Слайд 23

14.12.2014 23 Пятеро друзей встретились после каникул и обменялись рукопожатиями. Каждый, здороваясь, пожал руку. Сколько всего было сделано рукопожатий? Ответ: 10 рукопожатий Логинова Н.В. МБОУ «СОШ №16»

Слайд 24

14.12.2014 24 Сколько различных завтраков, состоящих из 1 напитка и 1 вида выпечки, можно составить из ч ая, к офе, б улочки, п еченья и в афель? Решите задачу, используя граф ч к б п в Логинова Н. В. МБОУ «СОШ №16»

Слайд 25

14.12.2014 25 6 завтраков напитки выпечка ч к б п в Приемы решения комбинаторных задач графы Логинова Н.В. МБОУ «СОШ №16»

Слайд 26

14.12.2014 26 ч к б б п п в в Эту же задачу можно решить, используя дерево возможных вариантов Логинова Н.В. МБОУ «СОШ №16»

Слайд 27

14.12.2014 27 Напитки Выпечка ч ч ч ч к к к к п п п б б б в в в Решение задачи с помощью таблицы Логинова Н.В. МБОУ «СОШ №16»

Слайд 28

14.12.2014 28 Шесть семей уехали отдыхать в разные города. Приехав к месту отдыха, они поговорили друг с другом по телефону. Сколько звонков было сделано? Решите задачу, используя граф Логинова Н.В. МБОУ «СОШ №16»

Слайд 29

14.12.2014 29 Закончи построение графа, соответствующего данной задаче. Логинова Н.В. МБОУ «СОШ №16»

Слайд 30

14.12.2014 30 Приемы решения комбинаторных задач графы Ответ :15 звонков Логинова Н.В. МБОУ «СОШ №16»

Слайд 31

14.12.2014 31 1 2 3 4 5 6 1 2 3 4 5 6 – – – – – – – – – – – – – – – – – – – – – Ответ :15 звонков Приемы решения комбинаторных задач задачи, решаемые с помощью таблиц

Слайд 32

Домашнее задание: п. 30 № 716 (перебор), 720 (дерево), 723 (граф), 725 (таблица), 727 (умножение). 14.12.2014 Логинова Н.В. МБОУ «СОШ №16»

Слайд 33

14.12.2014 33 В магазине продают воздушные шары: красные, желтые, зеленые, синие. Какие наборы можно составить из двух разных шаров? Сколько наборов у тебя получилось? Задачи, решаемые методом организованного перебора Приемы решения комбинаторных задач дополнительные задачи Задача 1

Слайд 34

14.12.2014 34 Задача 1 5 наборов

Слайд 35

14.12.2014 35 Приемы решения комбинаторных задач Задача 2 В парке 4 пруда. Было решено засыпать песком дорожки между ними так, чтобы можно было пройти от одного пруда к другому кратчайшим путем, т.е. не нужно было идти в обход. Задание: покажи, какие дорожки надо сделать. Графы

Слайд 36

14.12.2014 36 Решение

Слайд 37

14.12.2014 37 В танцевальном кружке занимаются пять девочек: Женя, Маша, Катя, Юля и Даша и пять мальчиков: Олег, Вова, Стас, Андрей и Иван. Сколько различных танцевальных пар можно составить? Заполни таблицу. Приемы решения комбинаторных задач Задачи, решаемые с помощью таблиц Логинова Н.В. МБОУ «СОШ №16»

Слайд 38

14.12.2014 38 Ответ : 25 пар Женя Маша Катя Юля Даша Олег Вова Стас Андрей Иван Олег Олег Олег Олег Олег Вова Вова Вова Вова Вова Стас Стас Стас Стас Стас Андрей Андрей Андрей Андрей Андрей Иван Иван Иван Иван Иван Женя Женя Женя Женя Женя Маша Маша Маша Маша Маша Катя Катя Катя Катя Катя Юля Юля Юля Юля Юля Даша Даша Даша Даша Даша

Слайд 39

14.12.2014 39 Задачи, решаемые с помощью таблиц На завтрак Миша может выбрать: плюшку, бутерброд, пряник, или кекс, а запить он может: кофе, соком, кефиром. Сколько возможных вариантов завтрака? Ответ:12 (4·3=12)

Слайд 40

14.12.2014 40 Существует много видов комбинаторных задач, это лишь некоторые из них. Спасибо за внимание! Логинова Н.В. МБОУ «СОШ №16»

задач на комбинации слов | Superprof

 

Упражнение 1

Сколько различных комбинаций руководителей может быть для заполнения должностей президента, вице-президента и казначея футбольного клуба, зная, что есть 12 подходящих кандидатов?

Лучшие репетиторы по математике

Поехали

Упражнение 2

Сколькими способами можно расположить буквы в слове «микро», если оно всегда должно начинаться с гласной?

Упражнение 3

Сколько комбинаций можно составить из семи цветов радуги в группы по три цвета в каждой?

Упражнение 4

Сколько различных пятизначных чисел можно составить, используя только нечетные цифры? Сколько из этих чисел больше 70 000?

Упражнение 5

Сколько игр состоится в лиге, состоящей из четырех команд? (Каждая команда играет друг с другом дважды, по одному разу в соответствующем «домашнем» месте каждой команды)

Упражнение 6

10 человек обмениваются приветствиями на деловой встрече. Сколько приветствий будет обменено, если все поздороваются друг с другом один раз?

Упражнение 7

Сколько пятизначных чисел можно составить из цифр 1, 2 и 3? Сколько из этих чисел четные?

Упражнение 8

Сколько лотерейных билетов нужно купить, чтобы составить все возможные комбинации из шести чисел, каждое из которых может быть от 1 до 49?

Упражнение 9

Сколькими способами можно расположить 11 игроков в футбольной команде, учитывая, что вратарь не может занимать другую позицию, кроме как в воротах?

Упражнение 10

Сколько групп можно составить из слова «дом», если каждая группа состоит из 3 букв?

Упражнение 11

У Сары есть 8 уникальных цветных карандашей. Она хочет выбрать из своей коллекции три цветных карандаша и подарить их младшей сестре. Сколько различных комбинаций цветных карандашей может составить Сара из 8 карандашей?

Упражнение 12

У Алисы 6 шоколадок. Все конфеты разного вкуса. Она хочет подарить две свои шоколадки подруге. Сколько различных комбинаций шоколадных конфет может составить Алиса из шести шоколадных конфет?

 

Решение упражнения 1

Сколько различных комбинаций руководителей может быть для заполнения должностей президента, вице-президента и казначея футбольного клуба, зная, что есть 12 подходящих кандидатов?

Порядок элементов имеет значение.

Элементы не могут повторяться.

 

Решение упражнения 2

Сколькими способами можно расположить буквы в слове «микро», если оно всегда должно начинаться с гласной?

Слова будут начинаться с i или o , за которыми следуют оставшиеся 4 буквы, взятые из 4 на 4.

Порядок элементов имеет значение.

Элементы не могут повторяться.

 

Решение упражнения 3

Сколько комбинаций из семи цветов радуги можно разбить на группы по три цвета в каждой?

Порядок элементов не имеет значения.

Элементы не могут повторяться.

 

Решение упражнения 4

Сколько различных пятизначных чисел можно составить, используя только нечетные цифры? Сколько из этих чисел больше 70 000?

Порядок элементов имеет значение.

Элементы не могут повторяться.

n = 5      k = 5

Нечетные числа больше 70000 должны начинаться с 7 или 9. Следовательно:

 

Решение упражнения, состоящего из 5 игр

5 90 из четырех команд? (Каждая команда играет друг с другом дважды, по одному разу в соответствующем «домашнем» месте каждой команды)

Порядок элементов имеет значение.

Элементы не могут повторяться.

 

Решение упражнения 6

10 человек обмениваются приветствиями на деловой встрече. Сколько приветствий будет обменено, если все поздороваются друг с другом один раз?

Порядок элементов не имеет значения.

Элементы не могут повторяться.

 

Решение упражнения 7

Сколько пятизначных чисел можно составить из цифр 1, 2 и 3? Сколько из этих чисел четные?

Порядок элементов имеет значение.

Элементы повторяются.

Если число четное, оно может заканчиваться только на 2.

 

Решение упражнения 8 от 1 до 49?

Порядок элементов не имеет значения.

Элементы не могут повторяться.

 

Решение упражнения 9

Сколькими способами можно расположить 11 игроков в футбольной команде, учитывая, что вратарь не может занимать другое положение, кроме как в воротах?

Таким образом, есть 10 игроков, которые могут занимать 10 разных позиций.

Порядок элементов имеет значение.

Элементы не могут повторяться.

Решение упражнения 10

Слово дом имеет 5 алфавитов. Если каждое новое слово должно иметь 3 алфавита, то мы должны использовать следующую формулу:

, где

заменяют значения в этом примере в вышеуказанной формуле:

Решение упражнений 11

Количество карандашей, у Сара = 8

. ее младшая сестра = 3

Воспользуемся формулой биномиальных коэффициентов для определения количества комбинаций:

, где

После подстановки получим количество комбинаций:

Следовательно, Сара может составить 56 комбинаций из 8 цветных карандашей, учитывая тот факт, что она может выбирать 3 за раз. Решение упражнения 12 где

После подстановки получим количество комбинаций:

Следовательно, Алиса может составить 15 комбинаций из 6 шоколадок, учитывая тот факт, что она может выбрать 2. Задать вопрос

спросил 8 лет, 10 месяцев назад

Изменено 8 лет, 10 месяцев назад

Просмотрено 654 раза

$\begingroup$

Рассмотрим квадрат.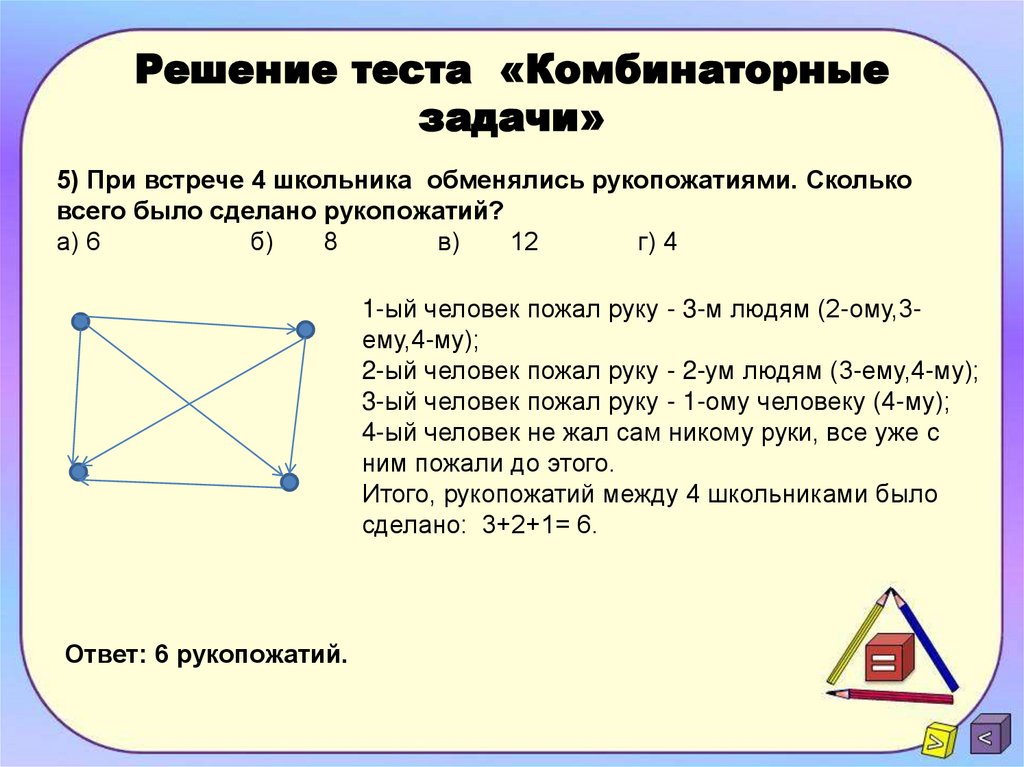 Есть 16 способов покрасить его стороны в два цвета. Для удобства будем изображать один цвет пустой стороной, а другой — линией, проведенной от центра квадратов к середине стороны.

Вот 16 возможных квадратов:

Задача состоит в том, чтобы посчитать способы сложить их вместе в квадрат 4×4, чтобы:

1. Каждый квадрат используется один раз .
2. Запрещено вращать или отражать квадраты.
3. Каждая исходящая линия должна соединяться с другой линией.
   • Конечно, это означает, что ни одна линия не может касаться границы квадрата.

Вот пример правильного решения:

Я знаю из написанной мной простой программы обратного отсчета, что число допустимых решений равно 652. Но можно ли это доказать математически? 9{272}$, но я понятия не имею, как получить фактическое число.

Редактировать: Вот пример решения сложной задачи:

• ко. комбинаторика

$\endgroup$

16

$\begingroup$

Задача 4×4 аналогична маркировке 16 внутренних 24 ребер черными с некоторыми ограничения: верхние 3 ребра должны иметь хотя бы одно черное ребро, а верхние 7 ребер имеют не более 68 допустимых раскрасок. Я не вижу быстрого способа получить 652, но показываю верхняя граница в полмиллиона следует из приведенных выше наблюдений. 9{150}$. Другой анализ углы дают $\binom{225}{128}$; их умножение дает улучшенная верхняя граница, которая все еще слаба. Возможно, можно улучшить эти границы ниже гугола, но я пока не понимаю, как это сделать.

$\endgroup$

4

$\begingroup$

Это предполагает другой подход к ограничению количества конфигураций.