Приведение матрицы к ступенчатому виду онлайн с подробным решением: Приведение матрицы к ступенчатому виду онлайн

Вычислить определитель матрицы системы методом гаусса онлайн. Вычисление определителя

Здесь вы сможете бесплатно решить систему линейных уравнений методом Гаусса онлайн больших размеров в комплексных числах с очень подробным решением. Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.

Размер матрицы: 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 X 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101

О методе

При решении системы линейных уравнений онлайн методом Гаусса выполняются следующие шаги.

1. Записываем расширенную матрицу.
2. Фактически решение разделяют на прямой и обратный ход метода Гаусса. Прямым ходом метода Гаусса называется приведение матрицы к ступенчатому виду. Обратным ходом метода Гаусса называется приведение матрицы к специальному ступенчатому виду. Но на практике удобнее сразу занулять то, что находится и сверху и снизу рассматриваемого элемента. Наш калькулятор использует именно этот подход.
3. Важно отметить, что при решении методом Гаусса, наличие в матрице хотя бы одной нулевой строки с НЕнулевой правой частью (столбец свободных членов) говорит о несовместности системы. Решение линейной системы в таком случае не существует.

Чтобы лучше всего понять принцип работы алгоритма Гаусса онлайн введите любой пример, выберите «очень подробное решение» и посмотрите его решение онлайн.

В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы . Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей , он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!

Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.

На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .

Определитель четвертого порядка тоже не антиквариат, и к нему мы подойдём в конце урока.

Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!

(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см.

следующий урок Свойства определителя и понижение его порядка)

Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!

Обозначения : Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .

1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.

2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.

Начнем с определителя «два» на «два» :

ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.

Сразу рассмотрим пример:

Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 — нормальные.

Начнем с двух простых способов

Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:

Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:

Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:

Пример:

Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

Теперь рассмотрим шесть нормальных способов для вычисления определителя

Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.

Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу .
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.

Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.

В следующем примере будем раскрывать определитель по первой строке .
Для этого нам понадобится матрица знаков: . Легко заметить, что знаки расположены в шахматном порядке.

Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.

Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:

И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?

Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ .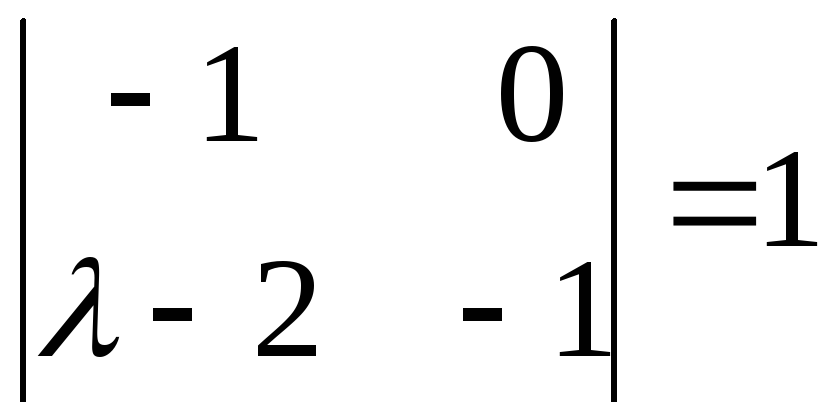 Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.

Коль скоро выбран способ разложения определителя по первой строке

, очевидно, что всё вращается вокруг неё:

Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)

Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:

1) Из матрицы знаков выписываем соответствующий знак:

2) Затем записываем сам элемент:

3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:

Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).

Переходим ко второму элементу строки.

4) Из матрицы знаков выписываем соответствующий знак:

5) Затем записываем второй элемент:

6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:

Ну и третий элемент первой строки. Никакой оригинальности:

7) Из матрицы знаков выписываем соответствующий знак:

8) Записываем третий элемент:

9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:

Оставшиеся четыре числа записываем в маленький определитель.

Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!

Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.

Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:

В следующем примере я раскрыл определитель по четвертому столбцу :

А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.

Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя .

БУДЬТЕ ВНИМАТЕЛЬНЫ!

Содержание

Введение…………………………………………………………………………………………….. 2

1. Постановка задачи………………………………………………………………………….. 3

2. Математические и алгоритмические основы решения задачи……………… 5

2.1 Определитель матрицы………………………………………………………………….. 5

2.2 Метод Гаусса для решения систем линейных уравнений…………………… 6

2.3 Метод Гаусса для вычисления определителя……………………………………. 8

3. Функциональные модели и блок-схемы решения задачи…………………….. 9

4. Программная реализация решения задачи………………………………………. 11

5. Пример выполнения программы…………………………………………………….. 16

Заключение……. ………………………………………………………………………………… 18

Список использованных источников и литературы……………………………… 19

Введение

Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задачи, в которых необходимо решить систему алгебраических уравнений.

Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной.

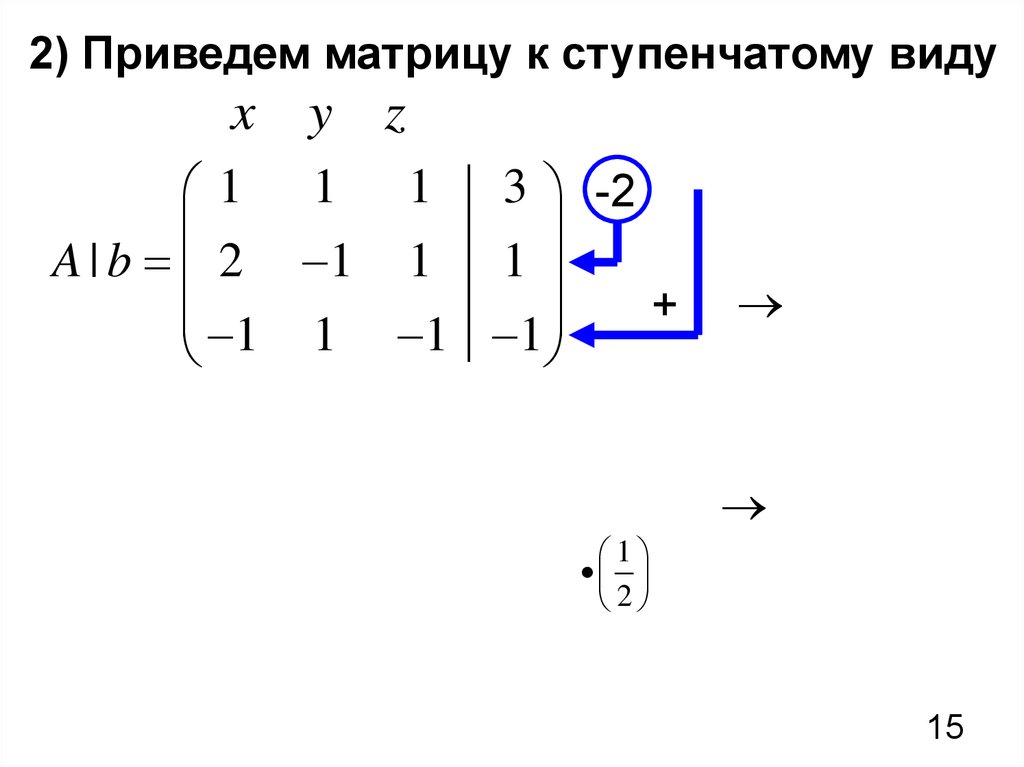
При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.

Помимо аналитического решения СЛАУ, метод Гаусса также применяется для нахождения матрицы, обратной к данной, определения ранга матрицы и нахождения определителя.

Целью данной курсовой работы является реализация вычисления определителя методом исключения Гаусса.

1. Постановка задачи

Вычисление определителя матрицы заключается в выполнении над матрицей алгоритма Гаусса для решения систем линейных алгебраических уравнений. В результате выполнения алгоритма получаем диагональную матрицу, её определитель равен произведению элементов, стоящих на диагонали.

. ~. . .

Вычислить определитель матрицы методом A исключения Гаусса.

.

Приведем матрицу к диагональному виду методом Гаусса.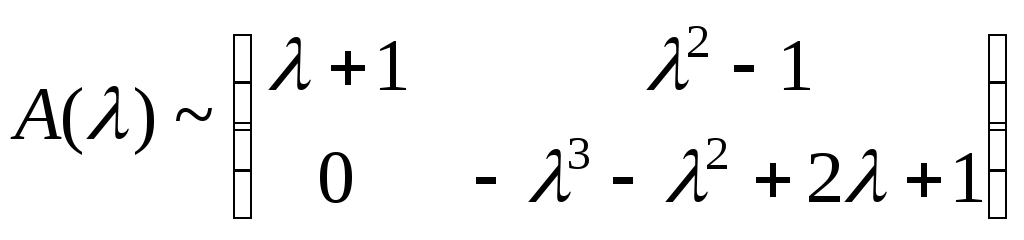

~.

Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:

.

Знак определяется количеством обменов строк, следовательно определитель матрицы

.

2. Математические и алгоритмические основы решения задачи

2.1 Определитель матрицы

Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка n, нужно уже знать, что такое определитель матрицы порядка n-1. Отметим также, что определитель существует только у квадратных матриц.

Определитель квадратной матрицы A будем обозначать

или det A.

Определение. Определителем квадратной матрицы

второго порядка называется число

.

Определителем

квадратной матрицы порядка n,

, называется число — определитель матрицы порядка n-1, полученной из матрицы A вычеркиванием первой строки и столбца с номером k.

2.2 Метод Гаусса для решения систем линейных уравнений

Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.

Воспользуемся идеями метода Гаусса решения систем линейных уравнений.

Дана система:

a11 x1 + a12 x2 + … + a1n xn = b1

a21 x1 + a22 x2 + … + a2n xn = b2

an1 x1 + an2 x2 + … + ann xn = bn

Выполним следующий алгоритм.

На первом шаге найдём в первом столбце наибольший по модулю элемент, поставим уравнение с этим элементом на первую строчку (обменяв две соответствующие строки матрицы A и два соответствующих элемента вектора B), а затем будем отнимать это уравнение от всех остальных, чтобы в первом столбце все элементы (кроме первого) обратились в ноль. Например, при прибавлении ко второй строке будем домножать первую строку на -a21/a11, при добавлении к третьей — на -a31/a11, и т.д.

На втором шаге найдём во втором столбце, начиная со второго элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на вторую строчку, и будем отнимать это уравнение от всех остальных (в том числе и от первого), чтобы во втором столбце все элементы (кроме второго) обратились в ноль. Понятно, что эта операция никак не изменит первый столбец — ведь от каждой строки мы будем отнимать вторую строку, домноженную на некоторый коэффициент, а во второй строке в первом столбце стоит ноль.

Т.е. на i-ом шаге найдём в i-ом столбце, начиная с i-го элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на i-ю строчку, и будем отнимать это уравнение от всех остальных. Понятно, что это никак не повлияет на все предыдущие столбцы (с первого по (i-1)-ый).

В конце концов, мы приведём систему к так называемому диагональному виду:

Т.е. мы нашли решение системы.

Замечание 1. На каждой итерации найдётся хотя бы один ненулевой элемент, иначе система бы имела нулевой определитель, что противоречит условию.

Замечание 2. Требование, что на каждом шаге мы выбираем наибольший по модулю элемент, очень важно в смысле численной устойчивости метода. Если выбирать произвольный ненулевой элемент, то это может привести к гигантской погрешности, когда получившееся решение будет отличаться в разы от правильного.

2.3 Метод Гаусса для вычисления определителя

Будем выполнять те же самые действия, что и при решении системы линейных уравнений, исключив только деление текущей строки на a[i][i] (точнее, само деление можно выполнять, но подразумевая, что число выносится за знак определителя). Тогда все операции, которые мы будем производить с матрицей, не будут изменять величину определителя матрицы, за исключением, быть может, знака (мы только обмениваем местами две строки, что меняет знак на противоположный, или прибавляем одну строку к другой, что не меняет величину определителя).

Но матрица, к которой мы приходим после выполнения алгоритма Гаусса, является диагональной, и определитель её равен произведению элементов, стоящих на диагонали. Знак, как уже говорилось, будет определяться количеством обменов строк (если их нечётное, то знак определителя следует изменить на противоположный). Таким образом, мы можем с помощью алгоритма Гаусса вычислять определитель матрицы за O(N3).

Осталось только заметить, что если в какой-то момент мы не найдём в текущем столбце ненулевого элемента, то алгоритм следует остановить и вернуть 0.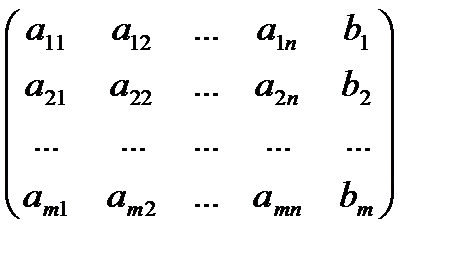

3. Функциональные модели и блок-схемы решения задачи

Блок-схема решения задачи представлена на рисунке 1.

Рисунок 1 – Блок-схема решения задачи для функции DETERMINATE

4 Программная реализация решения задачи

;ФУНКЦИЯ, ВЫЧИСЛЯЮЩАЯ ОПРЕДЕЛИТЕЛЬ

(DEFUN DETERMINANT (MATRIX SIZE)

;ОБЪЯВЛЕНИЕ ПЕРЕМЕННЫХ

;ОПРЕДЕЛИТЕЛЬ

(DECLARE (SPECIAL DET))

;ВСПОМОГАТЕЛЬНЫЕ МАССИВЫ И ПЕРЕМЕННЫЕ

(DECLARE (SPECIAL PAR))

(DECLARE (SPECIAL R))

(DECLARE (SPECIAL T_))

(DECLARE (SPECIAL I))

(DECLARE (SPECIAL II))

;*********************

(SETQ R (MAKE-ARRAY SIZE:ELEMENT-TYPE «FLOAT:INITIAL-ELEMENT 0))

((>= J (- SIZE 1)))

;ИСКЛЮЧАЕМ ДЕЛЕНИЕ НА 0

(IF (= (AREF MATRIX J J) 0)

(SETQ II (+ J 1))

;ИЩЕМ СТРОКУ В КОТОРОЙ J-Й ЭЛЕМЕНТ НЕ 0

((OR (/= (AREF MATRIX II J) 0) (= II (- SIZE 1))))

(SETQ II (+ II 1))

;ЕСЛИ НЕТ ТАКОЙ СТРОКИ ОПРЕДЕЛИТЕЛЬ РАВЕН 0

(IF (AND (= (AREF MATRIX II J) 0) (= II (- SIZE 1))) (SETQ T_ 0))

Вычислим определитель методом Гаусса.

Суть метода состоит в следующем: определитель приводится к треугольному виду с помощью элементарных преобразований, и тогда он равен произведению элементов, стоящих на главной диагонали.

Идея метода состоит в следующем: пусть дан определитель третьего порядка

элементдолжен быть равен
, для этого первую строку разделим на.

Получим определитель вида
(2)

Обнулим элементы, стоящие в первом столбце, кроме первого. Для этого из второй строки вычтем первую, умноженную на
, далее из третьей строки вычтем первую, умноженную на. Получим определитель вида
.

Обозначим его элементы буквой с, тогда

(3)

Теперь надо обнулить элемент . Элемент
должен быть равен
, для этого вторую строку разделим на
. Получим определитель вида
.

.

Обозначим его элементы буквой t, тогда

(4)

Вот мы привели определитель к треугольному виду, теперь он равен
.

Разберем теперь это на конкретном примере.

Пример 4: Вычислить определительметодом Гаусса.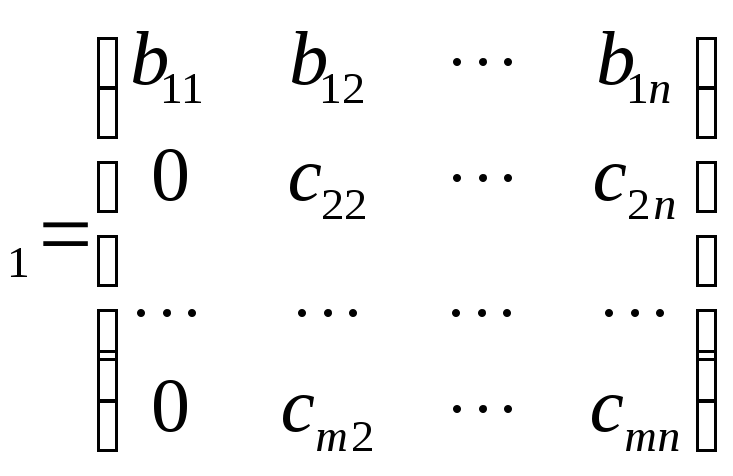

Решение: Поменяем местами первую и третью строки (при замене двух столбцов (строк) определитель меняет знак на противоположный).

Получили

Из второй строки вычтем первую, умноженную на 2, далее из третьей строки вычтем первую, умноженную на 3. Получили

Получили —

§2.Матрицы Виды матриц

Определение 7: Если в матрицеmстрок иnстолбцов, то она называетсяразмерностью mnи пишут
.

Определение 8: Если
, то матрица называется квадратной.

Определение 9: Матрица, состоящая лишь из одной строки (столбца) называется матрицей-строкой (столбцом).

Определение 10: Матрица, состоящая из нулей, называется нулевой матрицей.

Определение 11: Диагональной матрицей называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали равны нулю.

Определение 12: Единичной матрицей называется диагональная матрица, у которой все элементы, стоящие на главной диагонали равны единице.

Определение 13: Треугольной называется квадратная матрица, у которой элементы, расположенные по одну сторону от главной диагонали равны нулю.

Действиянад матрицами.

Определение 14: Две матрицы считаются равными, если они имеют одинаковое число строк и столбцов и равные соответствующие элементы.

Пример 5:

Матрицы А и В равны, т.е.

Определение 15: Суммой (разностью) матриц А и В называется такая матрица С, у которой каждый элемент равен
.

Пример 6: Найти матрицу
, если

Решение:

Cвойства сложения

А+В=В+А(переместительное)

2 0 А+О=А, где О-нулевая матрица

3 0 А+(В+С)=(А+В)+С (дистрибутивное)

4 0 А+(-А)=О, где – А противоположная матрица

(т.е. элементы имеют противоположные знаки)

Определение 16: Произведением матрицы А на число
называется матрица, полученная из данной умножением всех ее элементов на число.

Пример 7:

Умножение матиц

Это действие распространяется на так называемые согласованные матрицы.

Определение 17: Матрица А называетсясогласованной с матрицей В, если число столбцов у матрицы А равно числу строк у матрицы В.

Пример 8:
и
— согласованные

и
— несогласованные

и
несогласованные

Определение 18: Произведением двух матриц А и В называется такая матрица С, каждый элемент которой равен сумме произведений элементовiстроки матрицы А на соответствующие элементыj-го столбца матрицы В.

Если матрица А имеет размерность
, а матрица В
, то
.

Пример 9: Умножить матрицы

Echelon Transform

Матрица имеет форму эшелона строк (ссылка) когда он удовлетворяет следующим условиям.

• Первый ненулевой элемент в каждой строке, называемый ведущая запись , равна 1.
• Каждая ведущая запись находится в столбце справа от ведущая запись в предыдущей строке.
• Строки со всеми нулевыми элементами, если таковые имеются, находятся ниже строк, имеющих ненулевой элемент.

Матрица представлена ​​в виде сокращенной ступенчатой ​​формы строки (rref) когда он удовлетворяет следующим условиям.

• Матрица имеет эшелонированную форму (т. е. удовлетворяет условию три условия, перечисленные выше).
• Первая запись в каждой строке является единственной ненулевой записью в его столбец.

Матрица в форме эшелона называется -ступенчатой ​​матрицей . Матрица A и матрица B являются примерами ступенчатых матриц.

1 2 3 4 0 0 1 3 0 0 0 1 0 0 0 0		1 2 0 0 0 0 1 0 0 0 0 1 0 0 0 0
А		Б

Матрица A имеет форму эшелона строк, а матрица B находится в форме редуцированного эшелонированного ряда.

Как преобразовать матрицу в ее ступенчатую форму

Любую матрицу можно преобразовать в ступенчатую форму, используя серию элементарные операции со строками. Вот как.

1. Поворот матрицы
   1. Найдите опорную точку , первую ненулевую запись в первый столбец матрицы.
   2. Поменять местами строки, переместив основную строку в первую строку.
   3. Умножить каждый элемент в сводной строке на величину, обратную точка опоры, поэтому точка опоры равна 1.
   4. Добавить несколько строк сводной таблицы в каждую из нижних строк, поэтому каждый элемент в сводном столбце нижнего строки равны 0,
2. Чтобы получить матрицу в виде эшелона строк, повторите поворот
   1. Повторите процедуру, начиная с шага 1 выше, игнорируя предыдущий сводные ряды.
   2. Продолжайте, пока не закончатся опорные точки. обработанный.
3. Чтобы получить матрицу , уменьшенную строковую форму эшелона, обработайте ненулевой записи над каждым сводом.
   1. Определите последнюю строку, имеющую опорную точку, равную 1, и пусть это будет сводная строка.
   2. Добавить несколько строк сводной таблицы в каждую из верхних строк, пока каждый элемент над опорной точкой не будет равен 0,
   .
   3. Перемещаясь вверх по матрице, повторите этот процесс для каждой строки.

Преобразование матрицы в ее эшелонированные формы: пример

Чтобы проиллюстрировать процесс преобразования, давайте трансформируем Матрицу A в рядной эшелон форме и к форме редуцированного эшелонированного ряда.

0 1 2 1 2 1 2 7 8	⇒	1 2 1 0 1 2 2 7 8	⇒	1 2 1 0 1 2 0 3 6
А		А 1		А 2

⇒	1 2 1 0 1 2 0 0 0	⇒	1 0 -3 0 1 2 0 0 0
	А №		А rref

Для преобразования матрицы A в ее ступенчатые формы мы реализовали следующую серию элементарных операций над строками.

1. Мы нашли первую ненулевую запись в первом столбце матрицы в строке 2; поэтому мы поменяли местами ряды 1 и 2, в результате чего в матрице A ₁ .

2. Работа с матрицей А ₁ , мы умножили каждый элемент строки 1 на -2 и добавили результат к Ряд 3. Получилось А ₂ .

3. Работа с матрицей А ₂ , мы умножили каждый элемент строки 2 на -3 и добавили результат к Ряд 3. Получилось A _ref . Заметить, что Номер _ref находится в форме эшелонированной строки, потому что он удовлетворяет следующим требованиям: (a) первая ненулевая запись каждого строка равна 1, (b) первая ненулевая запись находится справа от первой ненулевой элемент в предыдущей строке и (c) строки, полностью состоящие из нули находятся внизу матрицы.

4. И, наконец, работа с матрицей A _ref , мы умножили вторую строку на -2 и добавили ее к первый ряд. Это произвело A _rref . Обратите внимание, что A _rref в уменьшено эшелонированную форму строки, так как она удовлетворяет требованиям к форма эшелона строки плюс каждая ведущая ненулевая запись является единственной ненулевой запись в своей колонке.

Примечание: Эшелонная матрица строк, полученная в результате ряда элементарные операции со строками не обязательно уникальны. Другой набор строк операции могут привести к другой ступенчатой ​​матрице строк. Однако, уменьшенная -строчная эшелонированная матрица уникальна; каждая матрица имеет только один уменьшенная ступенчатая матрица строк.

Проверьте свое понимание

Задача 1

Рассмотрим матрицу X , как показано ниже.

X   =

0 1 1 2 0 5

Какая из следующих матриц является редуцированной эшелонированной формой строк матрица Х  ?

0 1 1 0 0 0	1 0 0 1 0 0	1 0 0 1 0 1	1 0 0 0 0 1
А	Б	С	Д

(А) Матрица А
(В) Матрица В
(С) Матрица С
(D) Матрица D
(E) Ничего из вышеперечисленного

Решение

Правильный ответ (В).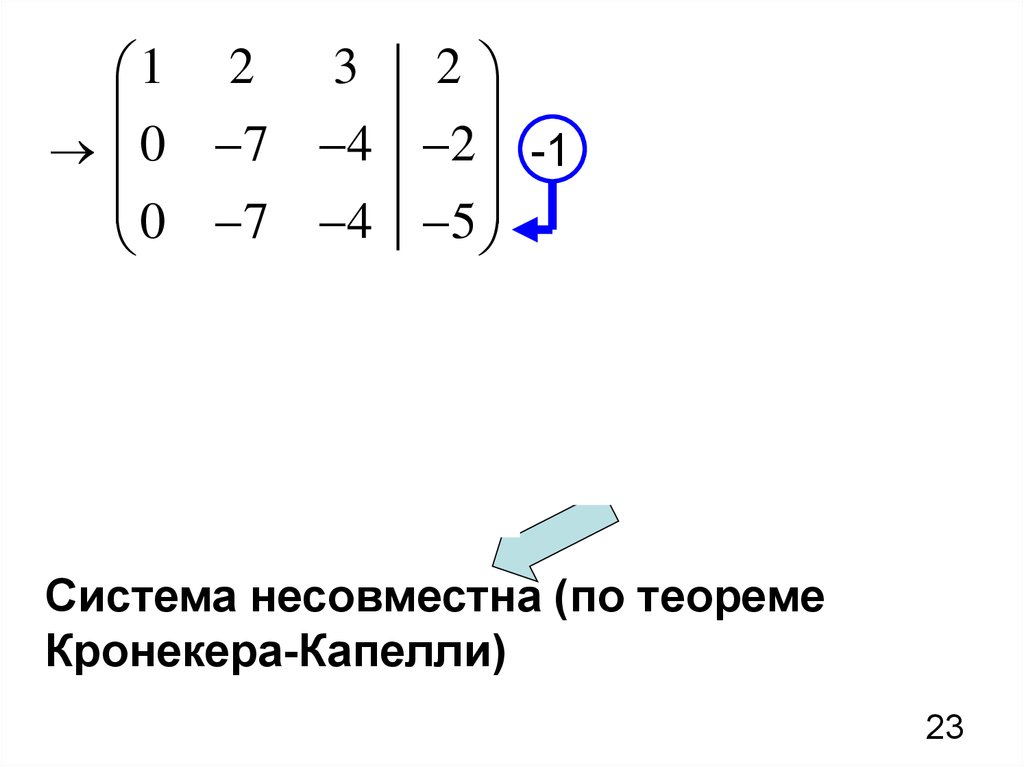 Элементарные операции со строками, используемые для изменения Показана матрица X в ее уменьшенной эшелонированной форме строк. ниже.

0 1 1 2 0 5	⇒	1 2 0 1 0 5	⇒	1 2 0 1 0 0	⇒	1 0 0 1 0 0
Х		Х 1		Х 2		Х rref

Чтобы преобразовать X в его сокращенную эшелонированную форму, мы берем следующие шаги:

1. Поменяйте местами ряды 1 и 2, получив X ₁ .
2. В Х ₁ , умножьте 2-й ряд на -5 и прибавьте его к 3-му ряду, получив Х ₂ .
3. В Х ₂ , умножьте 2-й ряд на -2 и прибавьте его к 1-му ряду, получив X _rref .

Примечание: Матрица A не имеет сокращенной ступенчатой ​​формы, потому что ведущая запись в строке 2 находится слева от ведущей записи в Ряд 3; он должен быть справа. Матрица С не находится в форме редуцированного эшелона строк, потому что столбец 2 имеет больше чем одна ненулевая запись. И, наконец, матрица D не в сокращенной эшелонированной форме строки, потому что следует строка 2 со всеми нулями по строке с ненулевым элементом; все нулевые строки должны следовать за ненулевыми строками.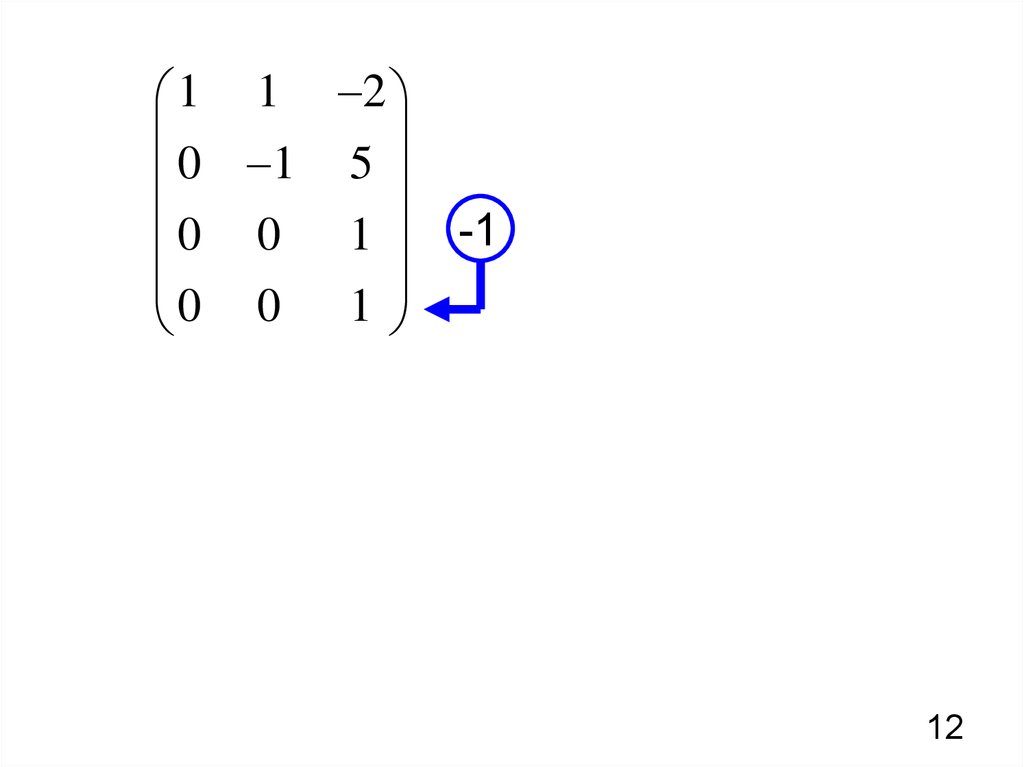

Последний урок Следующий урок

RREF Калькулятор с шагами | Калькулятор формы эшелона с уменьшенным рядом

Калькулятор RREF с шагами | Калькулятор формы эшелона уменьшенного ряда

Калькулятор RREF с шагами

Размер матрицы: x

Показать шаги:

Знание того, как найти Сокращенную форму эшелона строк (RREF) матрицы, очень помогает в решении систем линейных уравнений. По этой причине мы даем вам в руки эти Калькулятор RREF с шагами , который позволяет быстро и легко привести матрицу к форме эшелонирования строк.

Чтобы использовать этот калькулятор, вы должны выполнить следующие простые шаги:

1. Введите размеры матрицы, которую вы хотите уменьшить.
2. Введите матрицу в предназначенные для этого поля.
3. Нажмите кнопку «Рассчитать RREF», при этом автоматически появится окно с подробным пошаговым решением.

Ниже вы найдете краткое изложение наиболее важных теоретических концепций, связанных с как сделать сокращенную форму эшелонирования строк .

Содержание

• 1 Калькулятор RREF с шагами
• 2 Что такое эшелонированная форма (RREF) матрицы?
• 3 Как найти сокращенную форму эшелона строк
• 4 Примеры и решения формы сокращенного эшелона строк
  • 4.1 Пример 01: найти сокращенную форму эшелона строк этой матрицы 2×2
  • 4.2 Пример 02: найти сокращенную форму эшелона строк этой матрицы 3×3

Что такое сокращенная ступенчатая форма (RREF) матрицы?

Сокращенная эшелонированная форма строк матрицы A — это другая матрица H, которая удовлетворяет следующим свойствам:

• Она имеет строки, полностью состоящие из нулей (пустые строки), они сгруппированы в нижней части матрицы.
• Опорная точка (первый ненулевой элемент) каждой непустой строки равна 1.
• Опорная точка каждой ненулевой строки находится справа от предыдущей строки.
• Все элементы, которые появляются в том же столбце, что и сводная строка строки, равны нулю.

Вот пример сокращенной эшелонированной формы строки матрицы:

Каждая матрица имеет одну эшелонированную форму строки, независимо от того, как вы выполняете операции над строками.

Важность матриц в сокращенной ступенчатой ​​форме строк вытекает из следующей теоремы:

Каждая матрица может быть преобразована в уменьшенную ступенчатую форму строк с помощью последовательности операций с элементарными строками.

Сокращенная форма эшелона строк полезна, поскольку она обеспечивает стандартную форму для записи матриц и систем линейных уравнений, что упрощает их решение. Например, если матрица находится в форме эшелона с уменьшенными строками, вы можете легко найти решения соответствующей системы линейных уравнений, считывая значения переменных из матрицы.

Как найти сокращенную форму эшелона строк

Для выполнения этого процесса необходимо выполнить ряд элементарных преобразований строк, а именно:

• Тип I: Поменять местами две строки.
• Тип II: умножить все элементы строки на ненулевой скаляр.
• Тип III: добавьте к одной строке другую, умноженную на скаляр.

1. Мы можем начать с получения опорной точки 1 в первой строке. Если в первом столбце есть какой-то элемент, отличный от нуля, мы получим этот пивот в позиции (1,1). Если все элементы в первом столбце равны нулю, переходим ко второму (позиция (1,2)) и так далее. В зависимости от случая есть несколько способов получить эту опорную точку 1 (конечно, мы можем получить ее в любой строке, а затем обменять, чтобы перейти к первой).
2. В каждой из оставшихся строк элемент, расположенный ниже опорной точки, становится равным 0 путем прибавления первого, умноженного на удобный скаляр (преобразование типа III).

   No related posts.