4.3.7 Приведение кривой второго порядка к каноническому виду
Уравнение второго порядка вида
определяет на плоскости кривую. Группа членов называется квадратичной формой, – линейной формой. Если в квадратичной форме содержатся только квадраты переменных, то такой ее вид называется каноническим, а векторы ортонормированного базиса, в котором квадратичная форма имеет канонический вид, называются главными осями квадратичной формы.
Матрица называется матрицей квадратичной формы. Здесь . Чтобы матрицу привести к диагональному виду, необходимо за базис взять собственные векторы этой матрицы, тогда , где и – собственные числа матрицы .
В базисе из собственных векторов матрицы квадратичная форма будет иметь канонический вид: .
Эта операция соответствует повороту осей координат. Затем производится сдвиг начала координат, избавляясь тем самым от линейной формы.
Канонический вид кривой второго порядка: , причем:
А) если – эллипс, в частности, при это окружность;
Б) если имеем гиперболу;
Дополняя до полного квадрата, будем иметь: .Пример 14. Дано уравнение кривой
в системе координат , где и .
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.
Решение. Приводим квадратичную форму к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы . Находим собственные числа и собственные векторы этой матрицы:
Характеристическое уравнение:
; . Вид квадратичной формы: .
Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать , однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы . .
Собственный вектор, отвечающий числу при : .
В качестве единичного собственного вектора принимаем вектор , где – длина вектора .
Координаты второго собственного вектора, соответствующего второму собственному числу , находим из системы
.
; .
Итак, имеем новый ортонормированный базис .
По формулам (5) пункта 4.3.3. переходим к новому базису:
или
; . (*)
Вносим выражения и в исходное уравнение и, после преобразований, получаем: .
Выделяем полные квадраты: .
Проводим параллельный перенос осей координат в новое начало: , .
Если внести эти соотношения в (*) и разрешить эти равенства относительно и , то получим: , . В системе координат данное уравнение имеет вид: .
Для построения кривой строим в старой системе координат новую: ось задается в старой системе координат уравнением , а ось уравнением . Начало новой системы координат является точкой пересечения этих прямых.
Для упрощения восприятия разобьем процесс построения графика на 2 этапа:
1. Переход к системе координат с осями , заданными в старой системе координат уравнениями и Соответственно.
2. Построение в полученной системе координат графика функции.
Окончательный вариант графика выглядит следующим образом
Аналогично можно упростить, то есть привести к каноническому виду, поверхность второго порядка.
Для самостоятельной работы.
1. Оператор в пространстве действует по закону .
А) Доказать, что вектор является собственным вектором оператора . Найти его собственное число.
Б) Привести матрицу оператора к диагональному виду путем перехода к новому базису. Найти этот базис и соответствующую ему матрицу.
Ответ: ; ; .
2. Доказать, что матрица к диагональному виду не приводится.
3. Даны уравнения кривых:
А) ;
Б) ;
В) .
Определить тип кривых; кривую а) построить.
Ответ: а) эллипс; б) парабола; в) гипербола.
| < Предыдущая | Следующая > |
|---|
13. Приведение к каноническому виду уравнений кривых и поверхностей 2-го порядка:
(См. 12)
Пример:
=1>0, след. прав ориентации
14.Каноническое уравнение кривых и поверхностей II порядка (см.
Реферат)Ax2+Bxy+Cy2+Dx+Ey+F=0 – алгебраическое уравнение кривой 2 порядка относительно переменных x и y.
Эллипс ; если a=b, окружность.
Гипербола
Парабола
Если D=E=F каноническое уравнение.
Конус
Цилиндр эллиптический
Гиперболический цилиндр
Параболический цилиндр
Однополостной гиперболоид
Двуполостной гиперболоид
Гиперболический параболоид
Эллипсоид
Эллиптический параболоид
15.Дифференцильные уравнения (основные понятия, примеры)
Дифференциальным уравнением называется
уравнение, связывающее между собой
независимую переменную х, искомую
функцию у(х) и производные этой функции
по х различных порядков.
Порядок старшей производной называется порядком уравнения.
Дифференциальное уравнение называется линейным, если левая часть этого уравнения – многочлен первой степени относительно неизвестной функции у и ее производных
Функции , определенные и непрерывные в определенном интервале, называются коэффициентами уравнения; f(x) – свободный член.
Пример: — линейное.
Линейное уравнение называют однородным, если f(x) тождественно равно нулю, в противоположном случае – неоднородным.
Всякая функция , которая при подстановке в ДУ превращает его в тождество, называется решением этого уравнения.
Общим решением ДУ называется такое решение , которое содержит столько постоянных , каков порядок уравнения.
16.Ду I порядка. Задача Коши.
— общее решение ДУ I порядка.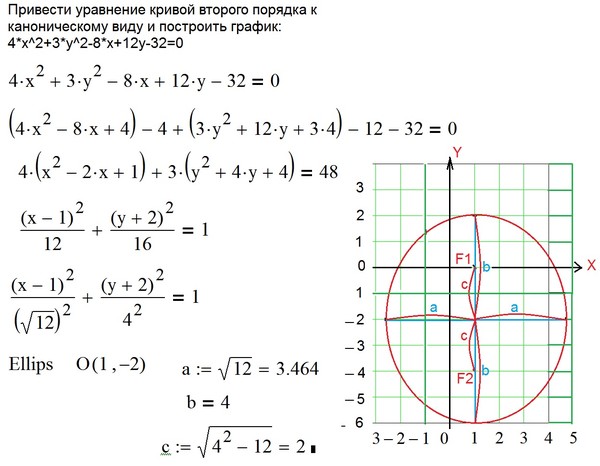
Геометрически общее решение ДУ I порядка – семейство интегральных кривых, соответствующих различным значениям постоянных.
Найти решение , удовлетворяющее условию
Геометрически надо найти интегральную кривую ДУ , проходящую через точку
Уравнение имеет бесконечное число решений, но если выбр.начальн.услов., то решение существует и только единственное.
17.Уравнение, с разделяющимися переменными.
ДУ I порядка называется уравнением с разделяющимися переменными, если оно имеет вид
Пример:
, где
18. Однородные уравнения I порядка.
Функция называется однородной в степени n, если
если и — однородные функции одного и того же порядка
Обозначим y=xz
уравнение с разделяющимися переменными.
19.Линейные уравнения первого порядка.
Уравнение вида , где и функции f(x) и p(х) – непрерывные функции на (a,b), называется дифференциальным линейным уравнением первого порядка.
Если f(x) тождественно =0, следовательно, уравнение называется однородным.
Методы решения линейного уравнения:
1)метод Бернулли:
ищем решение в виде произведения функции y=u(x)v(x)
Подберем v(x)
— общее решение
Общее решение линейного неоднородного уравнения = решению соответствующего однородного уравнения и частного решения неоднородного уравнения.
2) Метод Лагранжа:
— общее решение однородного уравнения
Пусть с=с(х) – функция
— неоднородное уравнение
20.
Уравнение Бернулли:
, где — любое число
Если =1, =0- линейное уравнение
Если 0, 1, то:
,
— линейное уравнение от z(x)
21.Уравнение Рикатти:
, где p, q, z- функции от х.
Пусть — частное решение, т.е.
, ,
(линейное уравнение от u(x)
22.Дифференциальные уравнения второго порядка:
— общее решение
— частное решение. ,
Если в уравнении функции и ее частные производные непрерывны в некой области D, то любой точки этой области существует единственное решение , удовлетворяющее начальному условию.
1). Пусть ,
, +с,
2) Пусть ,
,
3) Пусть , ,
, , ,
,
23.Общие свойства решений линейных
однородных дифференциальных уравнений II порядка.
(1) где и — непрерывные функции.
и — частные решения.
2 решения и называются линейно независимыми, если только тривиальные линейные комбинации этих функций =0 и линейно зависимыми, когда хотя бы 1 из них можно выразить через другой.
( — линейная комбинация)
и — независимы
если
Пример: ( — независ.)
Функции и дифференцируемы и непрерывны на (a;b)линейно зависимы, если определитель Вронского на этом интервале тождественно = 0, и линейно независимы, если вронскиан 0.
Определитель Вронского от непрерывных и дифференцируемых функций — определитель n-ого порядка, в первой строке которого находятся функции, во второй – первые производные и т..
Если функции и являются линейно независимым решением
уравнения (1), то общее решение этого
уравнения есть линейная комбинация
этих решений.
()
Доказательство:
, ч.т.д.
Чтобы найти общее решение ДУ вида (1) достаточно знать 2 частных линейно независимых решения этого уравнения и , тогда
Характеристические кривые для уравнения Трикоми второго порядка
спросил
Изменено 3 года, 10 месяцев назад
Просмотрено 686 раз
$\begingroup$
Рассмотрим уравнение Трикоми $$yu_{xx} + u_{yy} = 0$$ Найдите обыкновенные дифференциальные уравнения, описывающие реальный характеристика кривых и решить эти ОДУ, чтобы получить уравнения для характеристики кривые. Нарисуйте характеристические кривые там, где они есть.
{3/2}=C$. Как получить ОДУ для характеристик? 9{-1/2}$ дает ожидаемое выражение характеристических кривых, вдоль которых $\xi$ или $\eta$ постоянны.
Дополнительная литература: с. 162-163 из
Р. Курант, Д. Гильберт: Методы математической физики том. II: «Уравнения в частных производных». Wiley-VCH, 1962. doi: 10.1002/9783527617234
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.дифференциальных уравнений в частных производных — Другое УЧП второго порядка в канонической форме
спросил
92}{2}+A\psi\phi+B$ для некоторых констант A и B.Мой вопрос: разрешено ли это? Могу ли я рассматривать $\phi$ как константу в первой части этого вычисления? Заранее спасибо.
- уравнения в частных производных
$\endgroup$
0
$\begingroup$
$$u_{\phi\psi}=\frac{1}{\phi-\psi} u_\psi$$ Да замените $z=u_{\psi}$: $$(\фи-\psi)z_{\phi}=z$$ $$(\фи-\psi)z_{\phi}-z=0$$ $$\left ( \dfrac {z}{\phi-\psi} \right)’=0$$ $$ \dfrac {z}{\phi-\psi}=C(\psi)$$ Обратите внимание, что $C$ — это не константа, а функция от $\psi$: $$ {u}_{\psi}=C(\psi)(\phi-\psi)$$ Интегрирование по частям дает: $$ {u}{(\psi,\phi)}=g(\psi)(\phi-\psi)+\int g(\psi)d\psi+f(\phi)$$ 9{-1}$.
{3/2}=C$. Как получить ОДУ для характеристик? 9{-1/2}$ дает ожидаемое выражение характеристических кривых, вдоль которых $\xi$ или $\eta$ постоянны.
