Признак делимости | это… Что такое Признак делимости?
При́знак дели́мости — правило, позволяющее сравнительно быстро определить, является ли число кратным заранее заданному без необходимости выполнять фактическое деление. Как правило, основано на действиях с частью цифр из записи числа в позиционной системе счисления (обычно десятичной).
Существуют несколько простых правил, позволяющих найти малые делители числа в десятичной системе счисления:
Содержание
|
такжеПризнак делимости на 2
Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной.
Признак делимости на 3
Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3 (так как все числа вида 10n при делении на 3 дают в остатке единицу).
Признак делимости на 4
Число делится на 4 тогда и только тогда, когда число из двух последних его цифр (оно может быть двузначным, однозначным или нулём) делится на 4.
Признак делимости на 5
Число делится на 5 тогда и только тогда, когда последняя цифра делится на 5 (то есть равна 0 или 5).Признак делимости на 6
Число делится на 6 тогда и только тогда, когда оно делится и на 2, и на 3.
Признак делимости на 7
Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7 (например, 364 делится на 7, так как 36 — (2 × 4) = 28 делится на 7).
Либо использовать модификацию признака деления на 1001=10³+1, которое само делится на 7:
Для того, чтобы натуральное число делилось на 7 необходимо и достаточно, чтобы алгебраическая сумма чисел, образующих нечётные группы по три цифры (начиная с единиц) взятых со знаком «+» и чётных со знаком «-» делилась на семь.
Ещё один признак — берём первую цифру, умножаем на 3, прибавляем следующую (здесь можно взять остаток от деления на 7 от получившегося числа). И далее — сначала: умножаем на 3, прибавляем следующую… Для 364: 3 * 3 + 6 = 15. Остаток — 1. Далее 1 * 3 + 4 = 7.
Признак делимости на 8
Число делится на 8 тогда и только тогда, когда три его последние цифры — нули или образуют число, которое делится на 8.
Признак делимости на 9
Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
Признак делимости на 10
Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.
Признак делимости на 11
Число делится на 11 тогда и только тогда, когда сумма цифр с чередующимися знаками равна 0 или делится на 11 (то есть 182 919 делится на 11, так как 1 — 8 + 2 — 9 + 1 — 9 = −22 делится на 11) — следствие факта, что все числа вида 10n при делении на 11 дают в остатке (-1)n.
Признак делимости на 12
Число делится на 12 тогда и только тогда, когда оно делится на 3 и на 4.
Признак делимости на 13
Число делится на 13 тогда и только тогда, когда число его десятков, сложенное с учетверённым числом единиц, кратно 13 (например, 845 делится на 13, так как 84 + (4 × 5) = 104 делится на 13).
Признак делимости на 14
Число делится на 14 тогда и только тогда, когда оно делится на 2 и на 7.
Признак делимости на 15
Число делится на 15 тогда и только тогда, когда оно делится на 3 и на 5.
Признак делимости на 17
Число делится на 17 тогда и только тогда, когда число его десятков, сложенное с увеличенным в 12 раз числом единиц, кратно 17 (например, 29053→2905+36=2941→294+12=306→30+72=102→10+24=34. Поскольку 34 делится на 17, то и 29053 делится на 17). Признак не всегда удобен, но имеет определенное значение в математике. Есть способ немного проще — число делится на 17 тогда и только тогда, когда разность между числом его десятков и упятерённым числом единиц кратна 17 (например, 32952→3295-10=3285→328-25=303→30-15=15; поскольку 15 не делится на 17, то и 32952 не делится на 17)
Признак делимости на 19
Число делится на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19 (например, 646 делится на 19, так как 64 + (6 × 2) = 76 делится на 19).
Признак делимости на 23
Число делится на 23 тогда и только тогда, когда число его сотен, сложенное с утроенным числом десятков и единиц, кратно 23 (например, 28842 делится на 23, так как 288 + (3 * 42) = 414; продолжаем: 4 + (3 * 14) = 46 — очевидно, делится на 23).
Признак делимости на 25
Число делится на 25 тогда и только тогда, когда две его последние цифры делятся на 25 (то есть образуют 00, 25, 50 или 75).
Признак делимости на 99
Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) и найдем сумму этих групп, считая их двузначными числами. Эта сумма делится на 99 тогда и только тогда, когда само число делится на 99.
Признак делимости на 101
Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) и найдем сумму этих групп с переменными знаками, считая их двузначными числами. Эта сумма делится на 101 тогда и только тогда, когда само число делится на 101.
Признак делимости на 2
nЧисло делится на n-ю степень двойки тогда и только тогда, когда число, образованное его последними n цифрами, делится на ту же степень.
Признак делимости на 5
nЧисло делится на n-ю степень пятёрки тогда и только тогда, когда число, образованное его последними n цифрами, делится на ту же степень.
Признак делимости на 10
n − 1Разобьем число на группы по n цифр справа налево (в самой левой группе может быть от 1 до n цифр) и найдем сумму этих групп, считая их n-значными числами. Эта сумма делится на 10n − 1 тогда и только тогда, когда само число делится на 10n − 1.
Признак делимости на 10
nЧисло делится на n-ю степень десятки тогда и только тогда, когда n его последних цифр — нули.
Признак делимости на 10
n + 1Разобьем число на группы по n цифр справа налево (в самой левой группе может быть от 1 до n цифр) и найдем сумму этих групп с переменными знаками, считая их n-числами.
Эта сумма делится на 10n + 1 тогда и только тогда, когда само число делится на 10n + 1.
См. также
- Признак Паскаля — универсальный признак делимости, позволяющий для любых целых a и b определить, делится ли a на b. Точнее, он позволяет вывести почти все из выше приведённых признаков.
Ссылки
- Воробьев Н. Н. Признаки делимости. — 4-е изд. — М.: Наука, 1988. — Т. 38. — 94 с. — (Популярные лекции по математике). — ISBN 5-02-013731-6
Признаки делимости чисел | Материал по математике (5 класс):
Конспект урока по математике в 5 классе
ТЕМА: ПРИЗНАКИ ДЕЛИМОСТИ НА 2, 5, 10.
Вид урока: урок изучения нового материала.
Цель урока: Вывести признаки делимости чисел на 2, 5, 10
Задачи урока: 1) образовательная: научить определять делится ли число на 2, 5, 10, не выполняя вычислений
2) воспитательная: воспитывать познавательный процесс
3) развивающая: развивать умение анализировать и систематизировать знания, полученные опытным путем.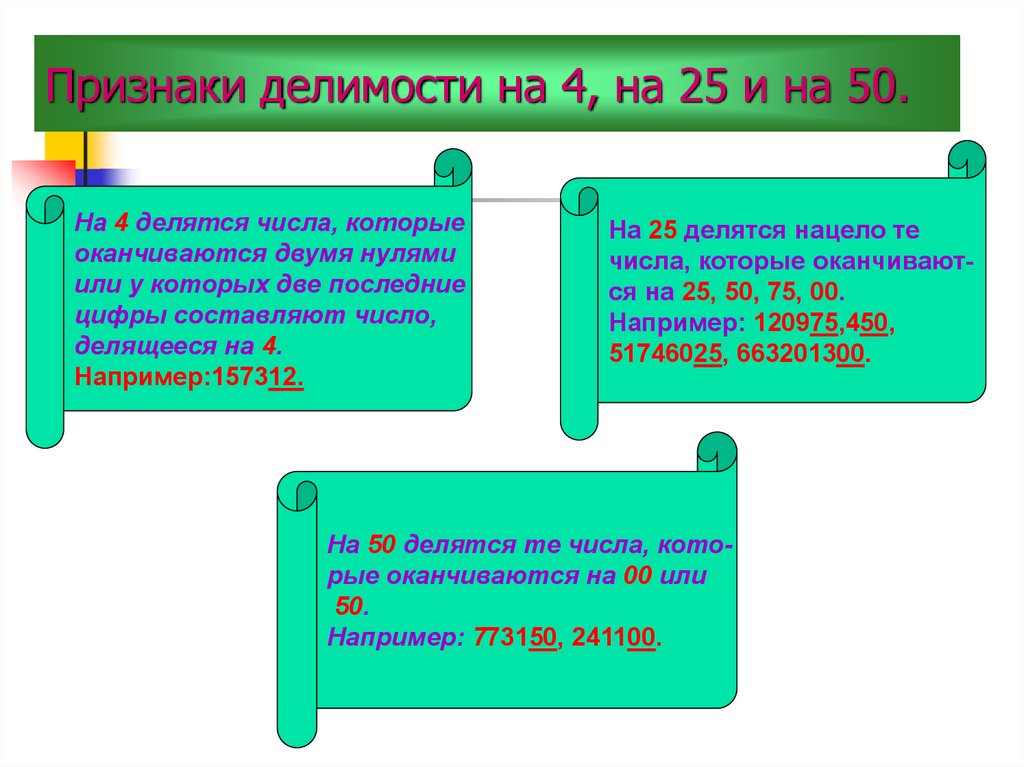
План урока:
- Организационный момент (1 минута)
- Актуализация опорных знаний (4 минуты)
- Постановка проблемы (2 минуты)
- «Открытие» детьми нового знания (18 минут)
- Физкультминутка (3 минуты)
- Первичное закрепление изученного (10 минут)
- Подведение итогов урока (5 минут)
- Постановка домашнего задания (2 минуты)
ХОД УРОКА
1) Организационный момент (1 минута)
Здравствуйте, садитесь. Сегодня на уроке мы с вами познакомимся с признаками делимости чисел на 2, 5, 10. На уроке у каждого из вас будет возможность заработать оценку. Для этого нужно поднять руку и ответить на поставленный вопрос.
2) Актуализация опорных знаний (4 минуты)
Итак, приступим к уроку. В тетрадях пишем число, классная работа, тема урока: «Признаки делимости на 2, 5, 10». (слайд 1)
Первое задание: Найдите лишнее (слайд 2)
Второе задание: Продолжите цепочку (слайд 3)
3) Постановка проблемы (2 минуты)
Скажите, как можно быстро определить, делится число на 10 или нет? (отвечают: оно оканчивается на 0).
Конечно, с этим признаком вы знакомы еще с начальной школы. А как же определить, делится ли число на 2, 5, 10? (слайд 4).
4) «Открытие» детьми нового знания (18 минут)
Попробуем проанализировать числа, которые делятся на 2. (слайд 5)
(дети пытаются выяснить закономерность).
Запишем признак делимости на 2 (слайд 6).
Выполните задание (слайд 7). Итак, что нужно знать, чтобы определить делится ли число на 2? (отвечают: последняя цифра — четная).
Молодцы! С признаком делимости справились.
Далее попробуем выявить признак делимости на 5 (слайд 8).
Попытайтесь сформулировать признак самостоятельно (пытаются сформулировать признак).
Проверим! (слайд 9). (Записывают признак в тетрадь)
Пожалуйста, выполните задание (слайд 10)
Далее задача 1, работаем в тетради. (слайд 11) (Работают самостоятельно).
Попробуйте ответить на вопрос (слайд 12) (отвечают: делится на 10 и оканчивается на 0).
Итак: еще раз повторим признак делимости на 5: (число оканчивается на 5 или на 0) (повторяют признак делимости на 5).
Итак, мы рассмотрели признаки делимости по последней цифре числа.
Следующая группа признаков делимости похожа на первую.
Далее выясним признак делимости на 4. (слайд 13)
Сделайте вывод (слайд 14)
Подсказка (посмотрите на две последние цифры числа)
Аналогично выясните признак делимости на 25 (слайд 15)
Вывод (слайд 16)
Выполните задание устно (слайд 17)
Молодцы! Справились с заданием!
5) Физкультминутка (3 минуты)
6) Первичное закрепление изученного (10 минут)
А теперь проверим, как вы усвоили материал
В тетрадях пишем ТЕСТ. Записываем только ответ.
(слайды 20 – 24 на каждый слайд 1,5 минуты)
Проверим: (слайд 25).
Поставьте себе оценку сами.
7) Подведение итогов урока (5 минут)
Итак, что нового на уроке вы сегодня узнали, чему научились?
Сформулируйте признак делимости на 2, 5, 10, 4, 25. (отвечают)
Хорошо, справились с вопросами.
Оценки за урок.
8) Постановка домашнего задания (2 минуты)
Правила делимости – Делимость и простые числа – Mathigon
Существует несколько различных правил, которые позволяют удивительно легко проверить, делится ли одно число на другое.
В этом разделе мы рассмотрим некоторые из них…
Делимость на 2 и 5
Каждое число делится на 1. Чтобы определить, делится ли число на 2, нам просто нужно проверить, является ли оно четным: любое число оканчивающееся на 0, 2, 4, 6 или 8 делится на 2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
. проверьте, чтобы его последняя цифра была 0 или 5:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
.
Причина. 5 так просто связано с нашей системой счисления. Основание нашей системы счисления равно 10, а это означает, что каждая цифра в числе стоит в 10 раз больше, чем следующая справа. Если мы возьмем число 6382 в качестве примера,
| 6 | 3 | 8 | 2 |
| =6000 | =300 | =80 | =2 |
Now we can separate the last digit of a number from all its other digits:
| abc d | = | abc × 10 | + | d |
| 638 2 | = | 638 × 10 | + | 2 |
Both 2 and 5 are factors of 10, so they will abc × 10 , no независимо от того, каковы значения a , b и c .
Поэтому нам нужно проверить только последнюю цифру: если d делится на 2, то оно также делится на 2. Если d делится на 5, то все число делится на 5.
Самым простым является правило делимости на 10: нам просто нужно проверить, является ли .
Делимость на 4 и 8
К сожалению, 4 не делит 10, поэтому мы не можем просто посмотреть на последнее число, но 4 действительно делит 100, поэтому нам просто нужно немного изменить наше правило выше. Теперь мы пишем ab cd = ab × 100 + cd . Мы знаем, что 4 всегда будет делить ab × 100 , поэтому нам нужно посмотреть на последние цифры, чтобы проверить, делится ли число на 4.
. получить еще сложнее, потому что 100 не делится на 8. Вместо этого мы должны подойти и посмотреть на последние цифры числа.
Например, 120 делится на 8, поэтому 271 120 также делится на 8.
Делимость на 3 и 9
Правило делимости на 3 несколько сложнее. 3 не делит 10, а также не делит 100, 1000 или любую большую степень 10. Просто посмотреть на последние несколько цифр числа не получится.
Вместо этого нам нужно использовать сумму цифр числа, которая является просто суммой всех его отдельных цифр. Например, сумма цифр ${13×n+123} равна ${digitSumString(123+13×n)} = ${digitSum(123+13×n)}, а сумма цифр 3524 равна .
1
2
4
5
7
8
10
11
13
14
16
17
19
20
22
23
25
26
28
29
31
32
34
35
37
38
40
Здесь мы выделили все числа, которые составляют множество трех. Вы можете видеть, что их сумма цифр всегда равна .
Таким образом, чтобы определить, делится ли какое-либо число на 3, вам просто нужно вычислить сумму его цифр и проверить, делится ли результат также на 3.
Далее, давайте посмотрим на кратные 9: числа, делящиеся на 9, имеют сумму цифр, которая делится на 9. Например, сумма цифр 4752 равна , поэтому 4752 делится на 9.
— и, как и раньше, это связано с нашей системой счисления с основанием 10. Как мы видели, написание числа 6 3 8 4 действительно означает
6 × 1000 + 3 × 100 + + 8 7 × 10 9013
Каждое из этих произведений можно разделить на две части:
6 × 999 + 6 + 3 × 99 + 3 + 8 × 9 + 8 + 4 .
Конечно, 9 , 99 , 999 и т. д. всегда делятся на 3 (или на 9). Остается только проверить, что то, что осталось, тоже делится на 3 (или 9).):
6 + 3 + 8 + 4
Это просто сумма цифр! Таким образом, если сумма цифр кратна 3, а мы знаем, что все остальное кратно 3, то результат также должен быть кратен 3.
мы уже сделали всю тяжелую работу. Помните, что 6 = 2 × 3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Чтобы проверить, делится ли число на 6, мы просто должны проверить, что оно делится на 2 и делится на 3. Обратите внимание, что это работает для 6, но, конечно, не для any Номер , который является произведением двух других. Подробнее об этом позже…
Правила делимости от 2 до 25 с примерами вопросов
Правила делимости позволяют проверить делимость числа и упростить вычисления при делении больших чисел.
Когда вы готовитесь к конкурсным экзаменам, таким как банковские, железнодорожные и другие государственные экзамены, время имеет решающее значение и ограничено.
В таком случае хорошее знание этих правил делимости может помочь ответить на вопросы, не тратя лишнего времени. С помощью правила делимости вы можете быстро проверить, какое число делится на число, не выполняя деление.
В сегодняшнем уроке вы узнаете, как проверить делимость чисел и посмотреть, делятся ли они на 2, 3, 4, 5, 7, 11, 13 и другие числа.
Итак, давайте начнем с правил, позволяющих найти делимость на любое число от 2 до 25.
Содержание страницы
Правило делимости на 2
Если число имеет 2, 4, 6, 8 или 0 в качестве единицы измерения, то число делится на 2. Следовательно, чтобы проверить делимость на 2, вам нужно чтобы проверить только цифру разряда единицы и перейти к делимому.
Примечание : Все четные числа делятся на 2.
Примеры,
- 214339 не делится на 2, потому что не имеет 2,4,6,8 или 0 в разряде единиц .
- 569958 делится на 2, потому что в разряде единиц стоит 8.
Вы можете проверить: Математические формулы для 10-го класса
Упражнение с правилом делимости для 2
Q1. Какое из следующих чисел делится на 2?
- 3160
- 2499
- 24393
- 100001
Q2. У Раджеша 262 книги. Может ли он сделать комплекты из 2 книг в каждом, не оставив ни одной книги? Сколько всего наборов будет?
Q3. Рина использует 2 белые бусины, чтобы сделать один разноцветный браслет. Если белых бусинок 3863, сможет ли она использовать их все, не оставив ни одной бусинки?
Q4. Заполните пропуски, чтобы утверждение было верным. Сколько чисел от 10 до 100, которые делятся на 2?
Q6. Если число не делится на 2, что нужно прибавить к этому числу, чтобы оно делилось на 2?
Q7. Если число не делится на 2, что нужно вычесть из этого числа, чтобы оно делилось на 2?
Q8.
Какова наименьшая разница между двумя числами, которые делятся на 2?
Q9. Проверьте, верны ли эти утверждения:
- Если два числа делятся на 2, то их сумма также будет делиться на 2.
- Если два числа не делятся на 2, то их сумма не делится на 2.
Дополнительные правила делимости:
| Правила делимости на 3 и 9 | Правила делимости на 1, 6 и 8 | |||
| Правила делимости 5, 10, и 15 | Правила делимости 6, 12 и 14 | |||
| Правила дивизии 7, 1 | и 13Правила делимости 17, 18, 1 | 8. | Правило делимости от 20 и выше чисел |
Часто задаваемые вопросы (FAQ)
Как узнать правила делимости?
Лучший способ изучить правила делимости — это попрактиковаться. Вы можете начать с одного правила, а затем выбрать случайные числа, чтобы попрактиковаться в проверке их делимости.
Так вы можете узнать все правила делимости от 2 до 20.
Какое правило делимости самое простое?
Если вы потренируетесь, то обнаружите, что все правила делимости даются легко. Но правило делимости на 2 и 10 самое простое.
Сколько правил делимости мне нужно выучить?
Все правила важны, и вам могут понадобиться все они. Но помнить о правилах делимости от 2 до 20 — хорошая идея.
Какое значение имеют правила делимости?
Правила делимости важны и полезны, так как вы можете быстро решать задачи без деления числа. Например, при нахождении множителей большого числа вы знаете, какое число использовать, если знаете правило делимости.
Надеюсь, это поможет! Всегда помните, что практика делает человека совершенным. Следовательно, чтобы запомнить эти правила и правильно использовать их на экзаменах, вам потребуется много практиковаться. Вы можете сделать это, решая вопросы из образцов работ, конкурсных экзаменационных книг или проверяя делимость случайных чисел.