Онлайн калькулятор: Кубическое уравнение
УчебаМатематикаАлгебра
Решение кубического уравнения по формуле Виета. Создан по запросу пользователя.
Сегодня выполняем запрос пользователя Решение кубического уравнения.
Канонический вид кубического уравнения:
Решать кубическое уравнение мы будем по формуле Виета.
Формула Виета — способ решения кубического уравнения вида
Соответственно, чтобы привести к этому виду оригинальное уравнение первым шагом все введенные коэффициенты делятся на коэффициент а:
Калькулятор ниже, а описание формулы Виета — под ним
Кубическое уравнение
коэффициент а
коэффициент b
коэффициент c
коэффициент d
Детали
Точность вычисления
Знаков после запятой: 2
Кстати сказать, на других сайтах почему-то для решения кубических уравнений используют формулу Кардано, однако я согласен с Википедией в том, что формула Виета более удобна для практического применения.
Так что почему везде формула Кардано — непонятно, разве что лень людям Гиперболические функции и Обратные гиперболические функции реализовывать. Ну мне не лень было.
Итак, формула Виета (из Википедии)
Обратите внимание, что по представлению формулы Виета а — второй коэффициент, а коэффициент перед x³ всегда считается равным 1. Калькулятор позволяет ввести а как коэффициент перед х³, но сразу же на него и делит уравнение, чтобы получить 1
Вычисляем:
Вычисляем:
Если S > 0, то вычисляем:
и имеем три действительных корня:
Если S < 0, то заменяем тригонометрические функции гиперболическими. Здесь возможны три случая в зависимости от Q
Q > 0:
(действительный корень)
(пара комплексных корней)
Q < 0:
(действительный корень)
(пара комплексных корней)
Q = 0:
(действительный корень)
(пара комплексных корней)
Если S = 0, то уравнение вырождено и имеет меньше 3 различных решений (второй корень кратности 2):
По этим формулам калькулятор и работает.
Решает вроде правильно, хотя решения с мнимой частью не проверял. Если что, пишите.
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Уравнение прямой по двум точкам
- • Решение квадратного уравнения
- • Уравнения прямой, проходящей через две точки в трехмерном пространстве
- • Решение уравнения 4-й степени
- • Решение системы двух уравнений первой степени с двумя неизвестными
- • Раздел: Алгебра ( 46 калькуляторов )
#математика #уравнение Алгебра кубическое уравнение Математика уравнение формула Виета
PLANETCALC, Кубическое уравнение
Timur2022-06-28 08:32:23
Формула решения уравнения 4 степени / Хабр
Существует несколько методов нахождения корней полиномиального уравнения 4-ой степени.
Однако они не очень удобны при решении уравнений с коэффициентами, которые представляют собой выражения с параметрами.
Инстаграм
1.
3 заменяется наПолучается выражение
В общем описанные в п.2 преобразования не являются тождественными. Но если считать интересными только значения x, которые являются корнями исходного уравнения, то данные преобразования можно считать квазитождественными. И тогда y представляется выражением, соответствующим корням исходного уравнения.
3. Для кубического уравнения операция в п.2 производится еще один раз. В итоге получается система из 3 уравнений по x, которая имеет три ненулевых решения, соответствующих корням исходного уравнения. Из коэффициентов x формируем матрицу
Вычисляем значения, обеспечивающие равенство определителя нулю.
5. В уравнении по y имеются два параметра P и Q. Вычислим их так, чтобы нулю равнялись коэффициенты при второй и первой степени y.
Любое P
, где
6. В итоге имеем уравнение c тремя кратными корнями для y
7.
Остается решить квадратное уравнение с известными y, P, Q
Одно из решений будет решением исходного уравнения.
3. Параметры решения вспомогательного кубического уравнения
Для конкретных значений коэффициентов все выглядит не таким страшным образом.
Отметим, что для формулы решения уравнения 4-ой степени требуется только один корень R вспомогательного кубического уравнения.
Для конкретных коэффициентов вспомогательного уравнения имеем
При использовании формулы решения уравнения 4-ой степени необходимо ссылаться — «Метод ftvmetrics».
Интересные задачи присылайте в Direct Инстаграмм.
Кубическая формула
Кубическая формула(Решить любое полиномиальное уравнение 3-й степени)
Я размещаю это в Интернете, потому что некоторые студенты могут
найти это интересно. Его можно было бы легко упомянуть в
многие математические курсы бакалавриата, хотя это не кажется
появляться в большинстве учебников, используемых для этих курсов.
Ни один из этих материалов не был обнаружен мной. —
ЕС
Вы должны знать, что решение ax 2 +bx+c=0 равно
Аналогичная формула существует для многочленов степени три: решение ax 3 +bx 2 +cx+d=0 есть
(Подобная формула была впервые опубликована Кардано в 1545 году.) Или, короче,
куда
Но я , а не рекомендую вам запомнить эти формулы.
Помимо того, что это слишком сложно,
другие причины, по которым мы не учим этой формуле
студентам-счетчикам. Одна из причин в том, что
мы пытаемся не учить их сложным
числа.
Комплексные числа (т. е. рассматривающие точки
на плоскости как цифры) это более продвинутая тема,
лучше оставить для более продвинутого курса. Но тогда
только числа, которые нам разрешено использовать в исчислении
— действительные числа (т. е. точки на прямой).
Это накладывает на нас некоторые ограничения — например,
мы не можем извлечь квадратный корень из отрицательного
количество. Теперь формула Кардана имеет недостаток
что это может привести к использованию таких квадратных корней
на промежуточных этапах вычислений, даже если те
числа не появляются в задаче или ее ответе.
Например, рассмотрим кубическое уравнение
х 3 -15х-4=0. (Этот пример был
упоминается Бомбелли в его книге в 1572 г.)
Эта проблема имеет реальную
коэффициенты, и имеет три действительных корня
за его ответы. (Подсказка: один из корней
маленькое положительное целое число; Теперь ты можешь найти все
три корня?)
Но если мы применим к этому примеру формулу Кардано,
мы используем a=1, b=0, c=-15, d=-4 и находим, что
нам нужно извлечь квадратный корень из -109в
полученный расчет.
Существует также аналогичная формула для многочленов от степень 4, но гораздо хуже записывается; я не буду хоть здесь попробуй.
нет аналогичных формул для многочленов степени
5. Я не просто имею в виду, что никто не нашел формулы
пока что; Я имею в виду, что в 1826 году Абель доказал, что не может быть
быть такой формулой. Проблема в том, что функции
не делайте достаточно того, что вам нужно для
решение всех уравнений 5-й степени. (Представьте себе калькулятор
что не хватает нескольких кнопок; есть некоторые виды
расчеты, которые вы не можете сделать на нем.) Вам нужно по крайней мере
еще одна функция. Одна из таких функций, например,
обратная функция f(x)=x 5 +х. (Есть
другие функции, которые также будут работать, и некоторые из них
более интересны математикам для различных
причинам, но мне нравится этот, потому что его можно описать
в довольно элементарных терминах.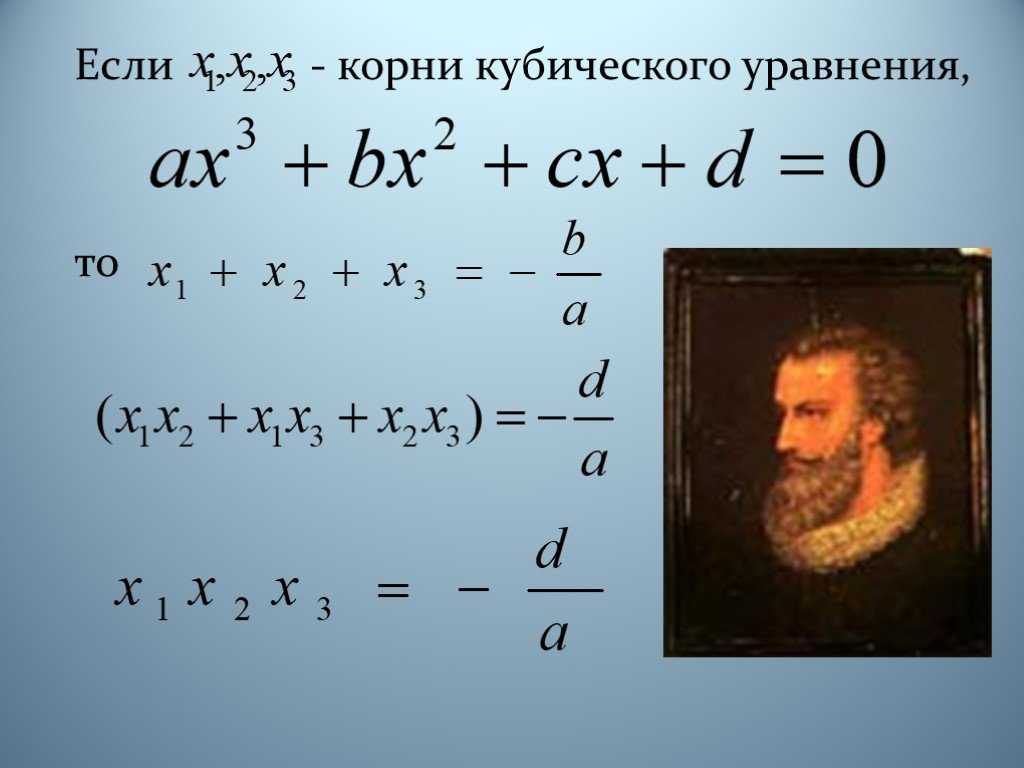
Формула кубического уравнения — GeeksforGeeks
Алгебра — это дисциплина математики, которая имеет дело с символами и правилами их использования. Эти символы (в настоящее время обозначаемые латинскими и греческими буквами) представляют величины без установленных значений, известные как переменные во вводной алгебре. В математике уравнения выражают отношения между переменными так же, как предложения описывают отношения между конкретными словами.
Что такое уравнение?
Уравнения — это математические утверждения, состоящие из двух алгебраических уравнений, стоящих по разные стороны от знака «равно (=)». Он изображает связь равенства между выражением, записанным в левой части, и выражением, записанным в правой части.
LHS = RHS (левая сторона = правая сторона) появляется в каждом математическом уравнении. Уравнения можно использовать для вычисления значения неизвестной переменной, представляющей неизвестную величину.
Кубическое уравнение, часто называемое кубическим многочленом, представляет собой многочлен третьей степени. Кубические уравнения имеют по крайней мере один действительный корень и до трех действительных корней. Корни кубического уравнения также могут быть мнимыми, но по крайней мере один из них должен быть действительным.
Стандартная форма кубического уравнения с переменной x: коэффициенты, а d – константа.
Формула кубического уравнения также может быть использована для расчета кривой кубического уравнения. Использование формулы кубического уравнения для представления кубического уравнения очень полезно при нахождении корней кубического уравнения. Многочлен степени n будет иметь n нулей или корней.
Пример: Найдите кубическое уравнение относительно x для значений a, b, c и d, равных 2, –3, –4, 7 соответственно.
Примеры задачИмеем a = 2, b = –3, c = –4 и d = 7
Общая форма кубического уравнения: x 3 + bx 2 + cx + d = 0,
Итак, требуемое уравнение: + 7
= 2х 3 – 3х 2 – 4х + 7
, –5, 0, 2 соответственно.
Решение:
Имеем a = 6, b = –5, c = 0 и d = 2
Общая форма кубического уравнения: ax 3 + bx 2 + cx + d = 0,
Итак, искомое уравнение:
P(x) = 6x 3 + (– 5)x 2 + 0x + 2
= 6x 3 – 5x 2 + 2
Вопрос 2. Найдите кубическое уравнение относительно y для значений a, b, c и d как 2 , –3, 1, 5 соответственно.
Решение:
Имеем a = 2, b = –3, c = 1 и d = 5
Общая форма кубического уравнения: ax 3 + bx 2 + cx + d = 0,
Итак, искомое уравнение:
P(x) = 2y 3 + (– 3)y 2 + 1y + 5
= 2y 3 – 3y 2 + y + 5
Вопрос 3.
Найдите кубическое уравнение относительно z для значений a, b, c и d как 9, 0, 1, 0 соответственно.
Решение:
Имеем a = 9, b = 0, c = 1 и d = 0
Общая форма кубического уравнения: ax 3 + bx 2 + cx + d = 0.
Итак, требуемое уравнение:
P(x) = 9z 3 + 0x 2 + 1z + 0
= 9z 3 + z
Вопрос 4. Найдите кубическое уравнение относительно x для значений a, b, c и d, равных 6, 0, 0, 9 соответственно.
Решение:
У нас есть, a = 6, b = 0, c = 0 и d = 9
Общая форма кубического уравнения, ax 3 + bx 2 + cx + d = 0.
Итак, требуемое уравнение: + 9
Вопрос 5. Найдите кубическое уравнение относительно y для значений a, b, c и d как –3, –4, 0, 0 соответственно.
Решение:
Имеем a = –3, b = –4, c = 0 и d = 0
Общая форма кубического уравнения: ax 3 + bx 2 + cx + d = 0,
Итак, требуемое уравнение: –3y 3 – 4y 2
Вопрос 6.