Шпаргалка: признаки равенства треугольников, 7 класс. 3 признака: по двум сторонам и углу, по стороне и двум углам, по трем сторонам
31 октября, 2022
1 мин
I признак (по двум сторонам и углу между ними).
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
- II признак (по стороне и прилежащим углам).
Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
- III признак (по трём сторонам).
Если три стороны одного треугольника равны трём сторонам другого треугольника, то такие треугольники равны.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Редакция Без Сменки
Честно.
Понятно. С душой.
44 подписчиков
+ Подписаться
Редакция Без Сменки
10 июня, 2022
1 мин
Био 🦠
Строение кожи
Начнём с лайфхака: как отличить потовую железу от сальной? На рисунке они могут быть схожи. …
Редакция Без Сменки
30 июня, 2022
1 мин
Рус 📖
РАЗБОР НАПРАВЛЕНИЯ «РАЗГОВОР С СОБОЙ»
Данная тематика связана с вопросами, которые человек задает сам себе, об опасности внутреннего.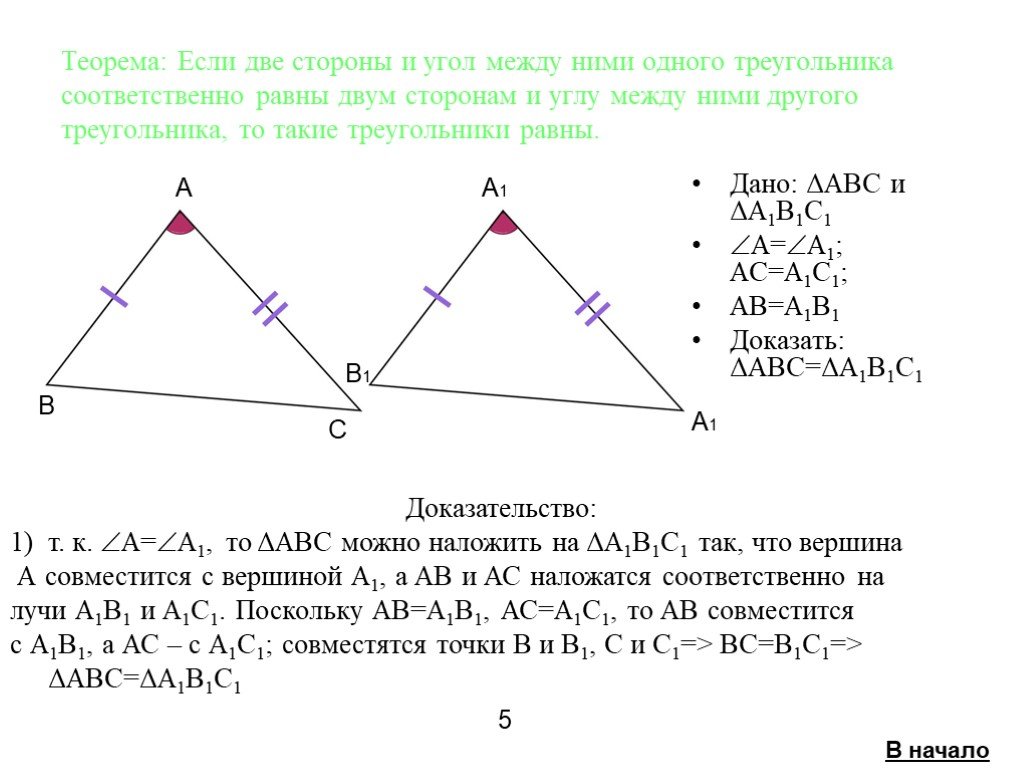
..
Редакция Без Сменки
27 мая, 2022
1 мин
Гео 🌍
Экзогенные процессы
Выветривание — разрушающее воздействие на горные породы и минералы многих факторов внешней среды,…
Подпишитесь на еженедельную рассылку полезных материалов про ЕГЭ, высшее образование и вузы и получите скидку на курсы Вебиума
Признаки равенства двух треугольников: по сторонам, углам
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Признаки равенства треугольников
В данной публикации мы рассмотрим признаки равенства треугольников, а также разберем пример решения задачи разными способами для закрепления изложенного материала.
- Признаки равенства треугольников
- 1 признак
- 2 признак
- 3 признак
- Пример задачи
Признаки равенства треугольников
Два треугольника равны между собой, если выполняется одно из условий, представленных ниже.
1 признак
Две стороны и угол между ними первого треугольника соответственно равны двум сторонам и углу между ними второго треугольника.
2 признак
Сторона и два прилежащих к ней угла первого треугольника соответсвенно равны стороне и двум прилежащим к ней углам второго треугольника.
3 признак
Три стороны первого треугольника соответственно равны трем сторонам второго треугольника.
Примечание: равенство прямоугольных треугольников, наряду с вышеперечисленными, доказывается и по другим признакам.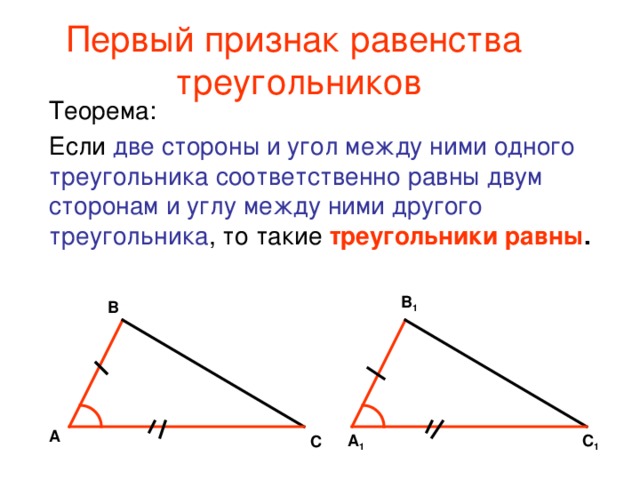
Пример задачи
Диагонали AC и BD параллелограмма ABCD пересекаются в точке E. Докажите, что △AED = △BEC.
Решение 1
Т.к. это параллелограмм, его противоположные стороны равны, т.е. AD=BC.
Диагональ AC, также, является секущей, которая пересекает две параллельные прямые, на которых лежат стороны AD и BC. Как известно, внутренние накрест лежащие углы попарно равны, следовательно, ∠СAD = ∠ACB. Аналогичным образом, равны углы ∠BDA и ∠DBC.
Значит, рассматриваемые нами треугольники △AED и △BEC равны по второму признаку равенства (по стороне и 2 прилежащим к ней углам).
Примечание: таким же способом можно доказать, что △AEB = △CED.
Решение 2
Диагонали параллелограмма в точке пересечения делятся пополам, т.е.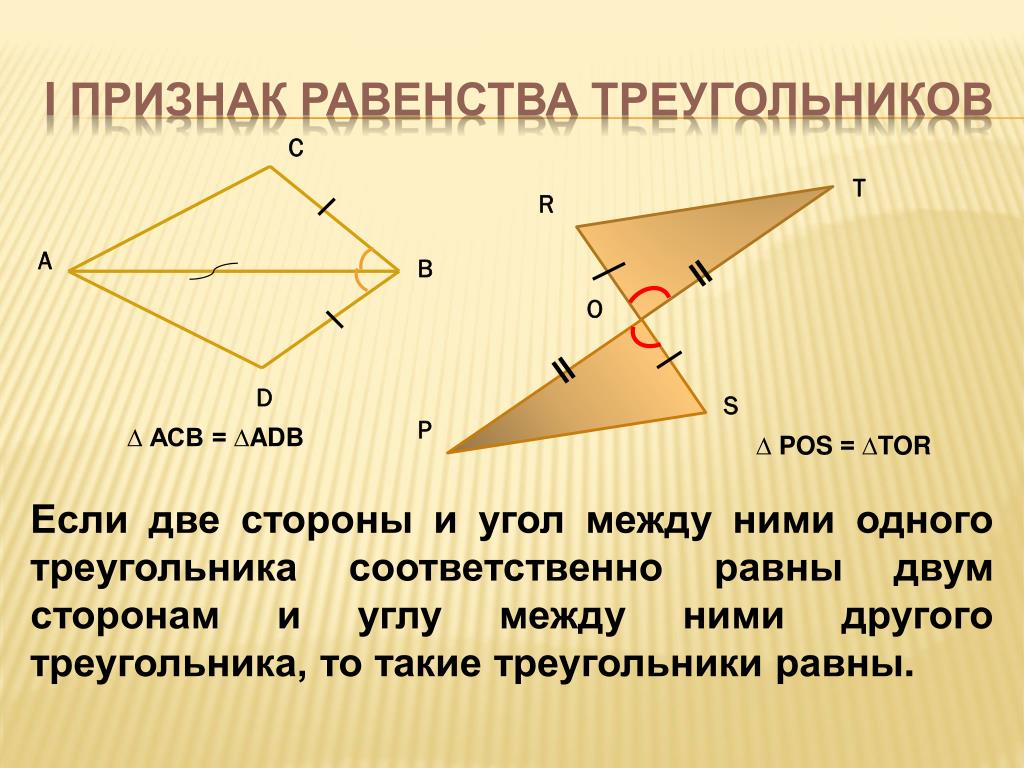
Таким образом, △AED и △BEC равны согласно третьему признаку равенства (по трем сторонам).
Примечание: Аналогичным образом можно доказать равенство △AEB и △CED.
Решение 3
Разбирая решения 1 и 2 мы уже выяснили, что накрест лежащие углы равны, а диагонали параллелограмма в точке пересечения делятся на две одинаковые части.
С учетом этого, доказать равенство треугольников △AED и △BEC (или △AEB и △CED) можно, сославшись на первый признак (по двум сторонам и углу между ними).
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Включен угол треугольника (определение и примеры)
, написанный
Malcolm McKinsey
Проверка по фактам
Paul Mazzola
В комплекте Угол.
угол между двумя отрезками или лучами. Для любого треугольника каждый из трех его внутренних углов заключен между двумя сторонами. Нарисуйте или вообразите равносторонний треугольник:△NAP\triangle NAP△NAP:Чтобы найти углы между ними, начните со сторон:
NA and AP include ∠A\angle A∠A between them
AP and PN include ∠P\angle P∠P between them
PN и NA Включите ♂ N \ Angle Nomats между ними
.0017 [вставить тупоугольный △JET со стороной JE = 13 метров, ET = 7 м, TJ = 9 м, ∠J ≈ 30,8°, ∠E ≈ 41,2°, ∠T ≈ 108,0°]
Is ∠E\ угол E∠E включенный угол для сторон JE и TJ ?
№; ∠J\угол J∠J — их внутренний угол. ∠E\угол E∠E – угол между сторонами JE и ET .
Геометрия позволяет начать с простейших измерений земли (« геометрия» означает « земная мера» ) и построена на более сложных понятиях.
Тригонометрия тесно связана с геометрией, поэтому «включенный угол» находит место в обеих математических областях.
Включенные углы в геометрии
Большинство Студенты-математики считают, что геометрию немного легче понять, чем тригонометрию. Итак, давайте сначала рассмотрим вложенные углы в геометрии. В формальных доказательствах каждый раз, когда вы видите угол, зажатый между другими элементами, вы используете включенный угол:
Конгруэнтность
Изобразите два равнобедренных треугольника. Первый равнобедренный треугольник имеет катет 14 дециметров длины и основание 12 дециметров . Прилежащий угол равен 67° . Посмотрите на второй рисунок. Он имеет такие же измерения.
Два равнобедренных треугольника конгруэнтны ?
Благодаря теореме о стороне, углу и стороне, которая утверждает, что два треугольника конгруэнтны, если две их стороны и угол между ними конгруэнтны. Вы математически знаете, что эти два равнобедренных треугольника конгруэнтны.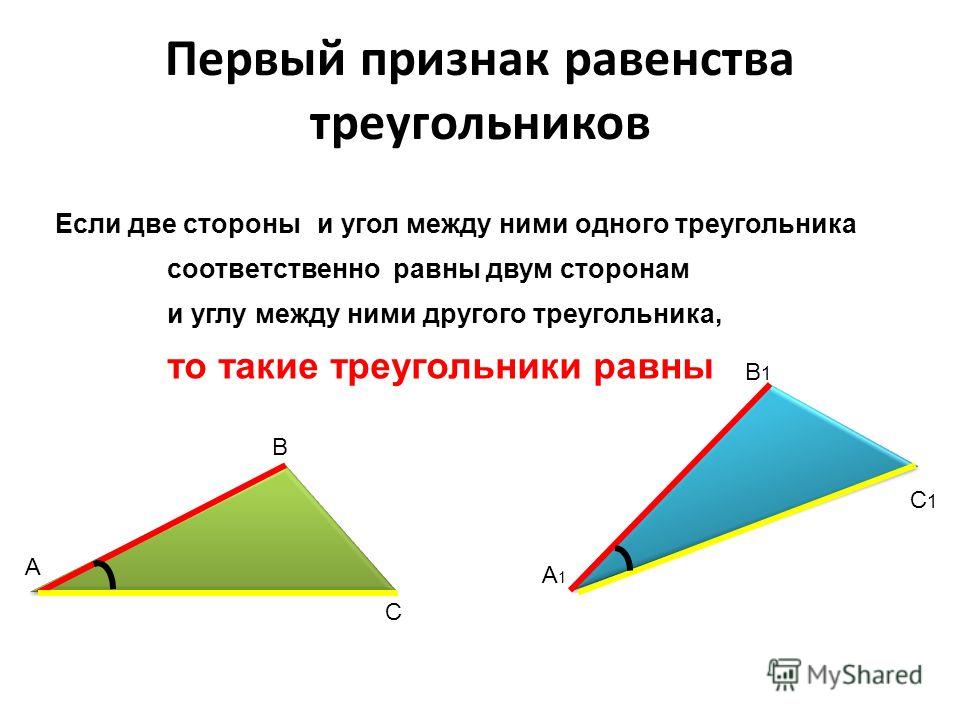
Подобие
Та же концепция применима к подобию треугольников: теорема (или постулат) о подобия стороне и угла говорит нам, что два треугольника подобны, если две соответствующие стороны пропорциональны, а угол между ними конгруэнтен. Вот новый тупоугольный треугольник △CAR\треугольник CAR△CAR, который можно сравнить с △JET\треугольником JET△JET выше.
[вставить тупой разносторонний △CAR со стороной CA = 39 метров, AR = 21 м, RC = 27 м и все углы = △JET]
Notice that side AR = 21 m and RC = 27 m , while our original △JET\triangle JET△JET had ET = 7 m , TJ = 9 м .
Угол между ними, ∠R\угол R∠R в △CAR\треугольнике CAR△CAR и ∠T\угол T∠T в △JET\треугольник JET△JET, оба равны ≈ 108,0° . Эти два треугольника подобны?
У нашего нового △CAR\треугольника CAR△CAR стороны в три раза длиннее, чем у △JET\треугольника JET△JET , но между соответствующими сторонами такой же угол.
Треугольники подобны, но не конгруэнтны, благодаря постулату (или теореме) подобия.
Углы, включенные в тригонометрию
Тригонометрия позволяет находить свойства треугольников, например площадь, используя только отношения между сторонами и углами. В то время как геометрия предлагает формулу для площади, A=12bhA=\frac{1}{2}bhA=21bh, тригонометрия предлагает другую формулу, где A = площадь треугольника, a и b – длины сторон, а C – их угол между ними:
Здесь вы умножаете длины двух сторон на синус прилежащего к ним угла, а затем берете половину этого (поскольку треугольник — это половина прямоугольника).
Предположим, у вас есть государственный парк треугольной формы, известный своими стадами диких зоидов, бродящих по широким открытым пространствам:
[вставьте тупоугольный разносторонний треугольник WYD с ∠Y = 105°; сторона WY = 25 км и сторона YD = 15 км].0025 a и сторона YD будет нашей стороной b .
Нам нужно только найти синус ∠Y\угол Y∠Y, 105° , чтобы найти площадь.
Подставьте то, что вы знаете:
Если 181 квадратный километр кажется большим, помните, что мы рисовали государственный парк, полный широких открытых пространств, куда вы можете пойти, чтобы поймать зоида .
Итоги урока
После изучения этого урока вы теперь можете определить угол между любыми двумя сторонами любого треугольника, использовать углы между ними в геометрических доказательствах подобия и конгруэнтности и применить формулу тригонометрии для нахождения площади треугольника. треугольник, A=12absin(C)A=\frac{1}{2}ab\sin\left(C\right)A=21absin(C), где a и b — стороны треугольника, а C — угол между ними.
MathScene — Векторы — Урок 4
MathScene — Векторы — Урок 42008 Расмус Эф и Джанн Сак |
Урок 4
Скалярное произведение и перпендикулярные векторы
Как
можно ли найти угол между двумя векторами? Правило косинусов выглядит многообещающе, поскольку мы
С его помощью можно найти угол между двумя сторонами треугольника.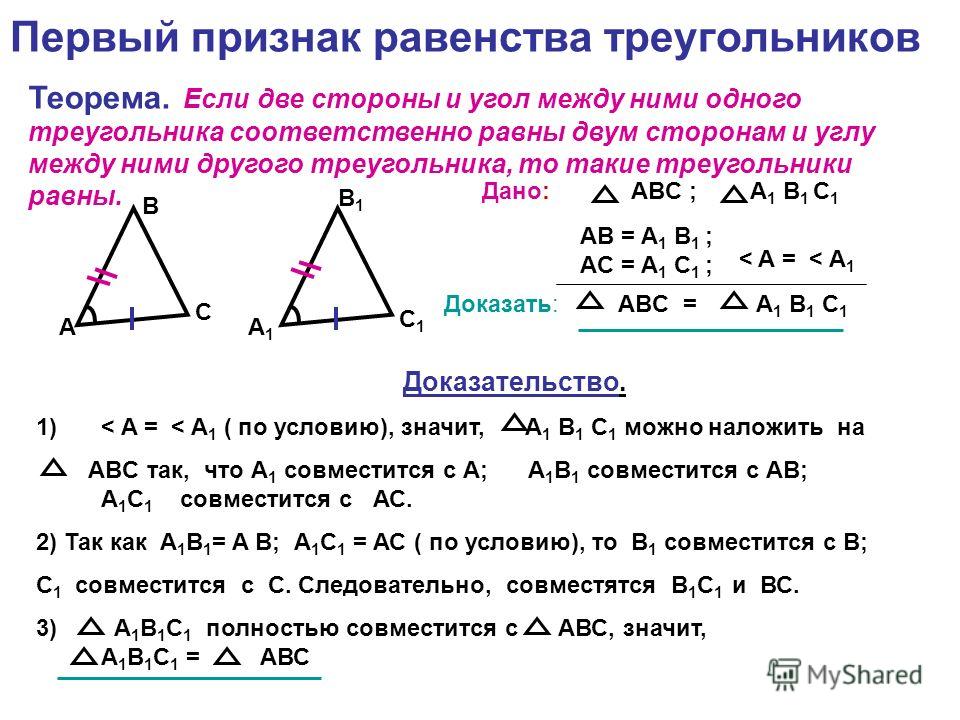
В этом примере легко найти векторы, считая квадраты, но мы будет использовать общую форму для любого вектора:
Правило косинуса выглядит следующим образом:
в 2 = а 2 + б 2 − 2∙b∙a∙cos C
стороны треугольника имеют длины ||, || и | − |. Если обозначить треугольник так, что сторона a = ||, б = || и с = | − | и обозначим угол C как v, мы получим:
| — | 2 = || 2 + || 2 — 2∙||∙ ||∙cos v
Теперь мы можем использовать формулу расстояния, чтобы найти длину векторов. Мы можем опустите квадратный корень, поскольку мы возводим в квадрат длины.
(х а — х б ) 2 + (y a − y b ) 2 = x a 2 + у а 2 + х б 2 + у б 2 − 2∙||∙ ||∙cos v
Если мы упростим левую часть, умножив скобки, получится:
.
х а 2 − 2x a x b + x b 2 + у а 2 — 2г а г б + г б 2
Подставляя это в формулу, мы видим, что все члены в квадрате сокращаются, и мы остаются с уравнением
− 2x a x b − 2y a y b = — 2∙||∙ ||∙cos v
Разделив на −2, мы получим следующую важную формулу:
х а х б + у а у б = ||∙ ||∙cos v |
Каждая часть этого уравнения называется скалярным произведением двух векторов. В другом слов:
скалярное произведение и знак равно
x a x b + y a y b и
скалярное произведение и знак равно
||||кос
v
Символ скалярного произведения — это точка, похожая на символ, иногда используемый для
умножение.
Очень важно различать их. Точка написана
между двумя векторами всегда скалярное произведение. На самом деле его часто называют
Скалярное произведение. Используя это обозначение, мы можем написать:
∙
= х а х б + y a y b и
∙
= ||∙
||∙cos
v
Пример 1
Напишите скалярное произведение векторов и в следующую схему двумя разными способами.
Мы может считывать координаты векторов прямо с диаграммы. Мы также можем см. длину вектора но нам нужно вычислить длину вектора .
Использование координат для нахождения скалярного произведения:
∙ = 3∙4 + 3∙0 = 12 | Координаты x перемножаются, y координаты перемножаются, а затем два результата складываются все вместе . |
Используя другое определение скалярного произведения с длинами векторов и косинусом, мы получить:
|| =
|| = 4
Теперь мы ответим на поставленный нами вопрос и посмотрим, как мы можем найти
угол между двумя векторами.
Для этого мы используем обе формы скалярного произведения.
х а х б + у а у б = ||∙ ||∙cos v
Разделив на
||||
получаем следующую формулу:
Если мы используем формулу расстояния, чтобы найти длины, это будет:
Пример 2
Найдите углы между векторами
≈ 0,8575
в ≈ потому что −1 0,8575 ≈ 31
Пример 3
Найдите вектор такой же длины, как и перпендикулярно к .
Мы называем этот вектор и напишите формулу скалярного произведения и .
х а х б + у а у б = ||∙ ||∙cos 90
Но cos 90 = 0, поэтому мы получаем следующий результат:
.
Икс + 2г = 0
Мы также знаем, что || 2 = х 2 + у 2 = 5.
Решая эти два уравнения вместе, мы получаем , x + 2y = 0 и x 2 + у 2 = 5.
х = -2у и х 2 = 5 — у 2
х 2 = 4г 2 = 5 — г 2
5 лет 2 = 5
у 2 = 1
у = 1
Если y = 1, то x = −2, а если y = −1, то x = 2.
Это означает, что у нас есть две возможности
На диаграмме мы видим эти два результата.
Обобщая приведенные выше результаты, мы видим, что мы можем найти два вектора, которые перпендикулярны друг другу и имеют одинаковую длину путем переключения вокруг x и координаты y и изменение знака по одной из координат.
Вектор перпендикулярно и |
Это связано с тем, что угол между перпендикулярными векторами равен 90, а cos 90 = 0
Если
вектор
является
перпендикулярно вектору
затем
их скалярное произведение равно нулю. |
х а х б + у а у б = 0Верно и обратное этому правилу.
Если скалярное произведение двух векторов равно нулю, то они перпендикулярны друг с другом. |
Пример 4
Треугольник ABC имеет вершины A = (3, 4), B = (17, 12) и C = (5, 16). Найди углы треугольника.
Сначала мы находим векторы, представляющие стороны.
Нам больше не нужно выполнять какую-либо работу, так как векторы и находятся явно перпендикулярны и равны по длине. Следовательно, треугольник является прямым равнобедренный треугольник с углами A = 90, B = 45 и C = 45.
Пример 5
Треугольник ABC имеет вершины A = (3, 3), B = (21, 7) и C = (4, 14).
а) Найдите угол A
Сначала найдите векторы и .