Признак подобия треугольников по трем сторонам: Признаки подобия треугольников — урок. Геометрия, 8 класс.

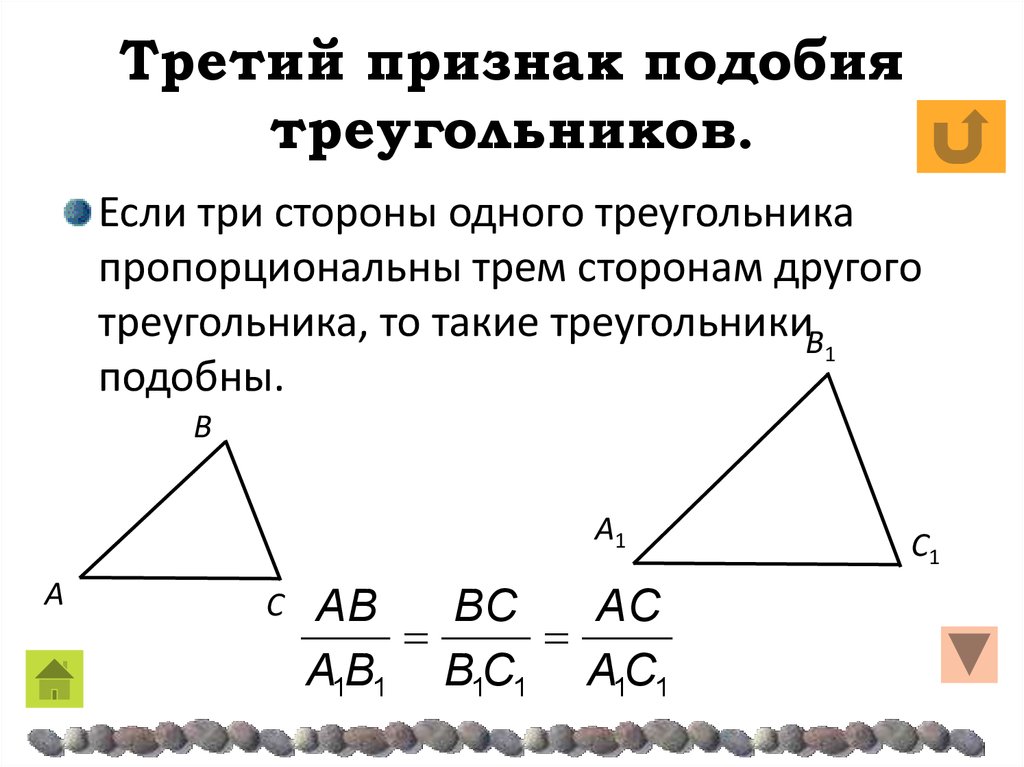
4)Третий признак подобия треугольников.

Если три стороны одного треугольника пропорциональны трем сторонам другого, то эти треугольники подобны.

Дано: треугольники АВС и А₁В₁С_1, у которых АВ : А₁В₁ = АС : А₁С₁ = ВС : В₁С₁. Учитывая второй признак подобия треугольников, достаточно доказать, что угол А равен углу А₁.

рассмотрим треугольник АВС₂, у которого угол 1 (угол С₂АВ) равен углу А₁ и угол 2 (угол С₂ВА) равен углу В₁.Треугольники А₁В₁С₁ и АВС₂ подобны по первому признаку, следовательно, АВ : А₁В₁ = АС₂ : А₁С₁ = ВС₂ : В₁С₁. Сравнивая эти равенства с данными, получим: ВС = ВС₂, АС = АС₂; треугольники АВС и АВС₂ равны по трем сторонам, поэтому угол А равен углу 1 и угол 1 равен углу А

1, следовательно, А равен углу А₁, ч. т. д.

5)Средняя линия треугольника. Теорема о средней линии треугольника.

Средняя линия треугольника – отрезок, соединяющий середины его противоположных сторон.

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Доказательство через подобие треугольников.

6)Доказать свойство медиан треугольника.

1)Три медианы делят треугольник на 6 равновеликих. Доказательство проводится с помощью проведения высот.

2)Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины. Доказательство с помощью проведения средней линии (с. 147).

7)Докажите, что высота прямоугольного треугольника, опущенная из прямого угла делит его на два подобных треугольника, каждый из которых подобен исходному.

Дано: прямоугольный АВС, ВН – высота.

1.ВНС подобен АВС, т. к. угол АНВ = АВС, угол С – общий.

2.АВН подобен АВС, т. к. угол АВН = АВС, угол А – общий.

3.Угол С = 90 – угол А = 90 – НВС угол А равен углу НВС

Угол А = 90 – угол С = 90 – угол АВН угол С равен углу АВН

Из этого следует, что АНВ подобен ВНС, .

8)Пропорциональные отрезки в прямоугольном треугольнике.

1.Высота прямоугольного треугольника есть среднее геометрическое проекций катетов на гипотенузу.

2.Катет прямоугольного треугольника есть среднее геометрическое между гипотенузой и своей проекцией на гипотенузу.

9)Соотношения между сторонами и углами в прямоугольном треугольнике (синус, косинус, тангенс острого угла в прямоугольном треугольнике). Основное тригонометрическое тождество. Значения синуса, косинуса и тангенса для углов 30°, 45°, 60°.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.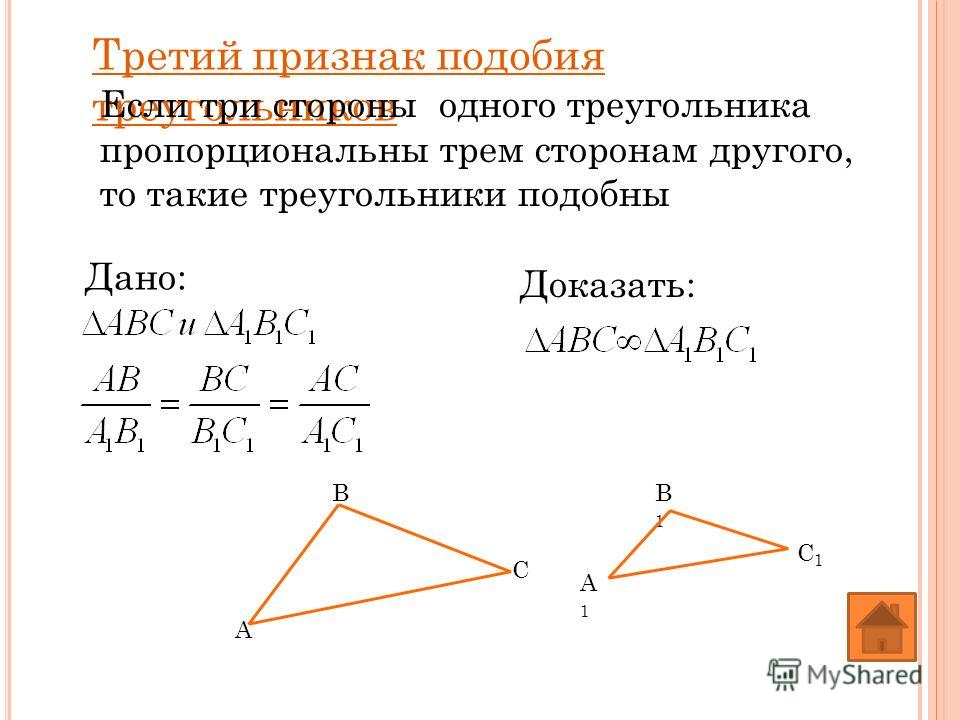

Основное тригонометрическое тождество: sin² A + cos² A = 1.

α	30	45	60
sin α
cos α
tg α		1

10)Докажите, что отрезок, соединяющий середины боковых сторон трапеции (средняя линия трапеции), параллелен основаниям и равен полусумме оснований.

Параллельность доказывается по теореме Фалеса, далее проводится диагональ и рассматриваются средние линии образующихся треугольников.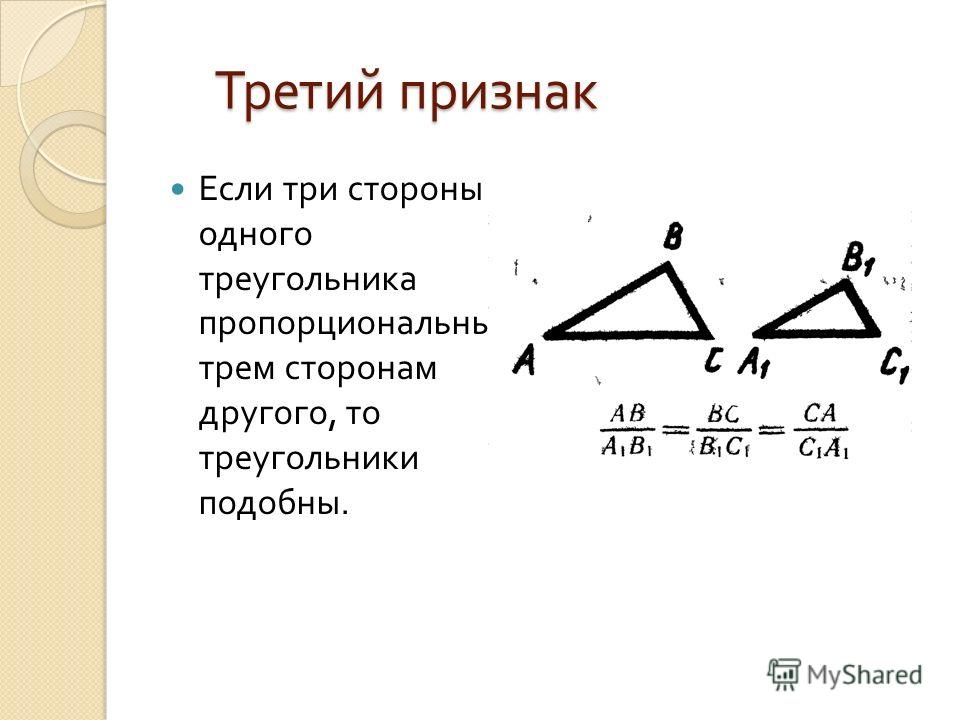

11)Свойство биссектрисы треугольника.

Биссектриса угла треугольника делит его противоположную сторону на отрезки, пропорциональные прилежащим сторонам. Доказательство проводится с помощью теоремы о треугольниках, имеющих равные углы и проведения общей высоты.

Окружность.

1. Взаимное расположение прямой и окружности. Свойство и признак касательной.

Прямая и окружность могут либо иметь две общие точки, либо иметь одну общую точку, либо не иметь общих точек.

Касательная – прямая, имеющая с окружностью одну общую точку, которая называется точкой касания.

Свойство касательной: касательная окружности перпендикулярна к ее радиусу, опущенному в точку касания. Следствие: отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, соединяющей эту точку с центром окружности.

Признак касательной: если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к нему, то она является касательной.

2. Вписанный угол. Теорема о вписанном угле. Следствия.

Вписанный угол – угол, вершина которого лежит на окружности, а обе стороны пересекают эту окружность.

Теорема: вписанный угол измеряется половиной дуги, на которую он опирается. Теорема имеет три случая: 1) сторона вписанного угла является диаметром; 2)диаметр является биссектрисой вписанного угла; 3) диаметр не является ни стороной, ни биссектрисой вписанного угла. Доказательство:

1.Дополнительное построение – центральный угол; далее доказательство проводится через внешний угол равнобедренного треугольника.

2.Доказательство по доказанному (извините за тавтологию).

3.Доказательство с помощью вычитания углов.

Следствия: вписанный угол, опирающийся на полуокружность – прямой; вписанные углы, опирающиеся на одну и ту же дугу, равны.

3. Теорема об отрезках пересекающихся хорд.

Если две секущие пересекаются в окружности, то угол между ними равен полусумме дуг, заключенных между ними.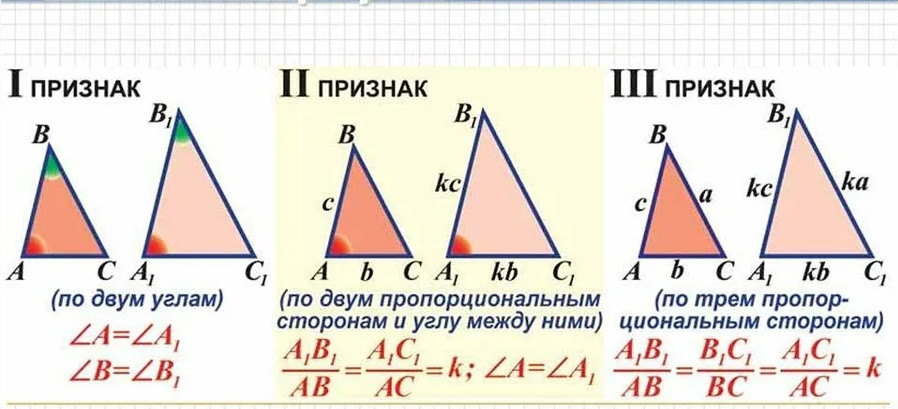 Доказательство: соединяем концы двух хорд, получаем 2 вписанных угла.

4. Свойство биссектрисы угла (теорема, следствие)

Теорема: любая точка биссектрисы неразвернутого угла равноудалена от его сторон. Обратно: если точка равноудалена от сторон угла, то она лежит на его биссектрисе. Доказывается с помощью построение прямоугольных треугольников.

Следствие: биссектрисы треугольника пересекаются в одной точке. Доказательство: проводим биссектрисы и высоты, далее по доказанной теореме.

5. Теорема о серединном перпендикуляре к отрезку.

Серединный перпендикуляр к отрезку – прямая, проходящая через отрезок под прямым углом и делящая его пополам.

Любая точка серединного перпендикуляра равноудалена от концов отрезка. Обратно: если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре.

Следствие: серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство: проводим серединные перпендикуляры к сторонам треугольника и отрезки, соединяющие точку их пересечения с вершинами, далее – по теореме.

6. Теорема о пересечении высот треугольника.

Высоты треугольника (или их продолжения) пересекаются в одной точке. Доказательство: через вершины треугольника проводятся вершины, параллельные основаниям, доказывается, что высоты маленького треугольника – серединные перпендикуляры к сторонам другого, и , следовательно, пересекаются в одной точке.

7. Четыре замечательных точки треугольника.

Подобие треугольников. Часть 2

Автор: Ольга Л., онлайн репетитор по математике

●

18.02.2012

●

Раздел: Математика

Второй признак подобия треугольников

Второй признак подобия треугольников (по двум сторонам и углу между ними): Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, заключенные между этими сторонами, равны, то треугольники подобны (рис. 1). 

Пусть даны треугольники Δ ABC, Δ A₁B₁C₁, в которых углы < A = < A₁ и  АВ/А₁В₁ =  АС/А₁С₁.
Необходимо доказать, что Δ ABC ~ Δ A₁B₁C₁.

Доказательство.

1) Достроим Δ A

1B₂C₁ такой, что < A₁C₁B₂ = < C,
< C₁A₁B₂ = < A = < C₁A₁B₁.

Тогда Δ ABC ~ Δ A₁B₂C₁ по двум углам, следовательно, по определению подобных треугольников, АВ/А₁В₂ = АС/А₁С₁.

2) По условию АВ/А₁В₁ = АС/А₁С₁, из пункта 1
АС/А₁С₁ = АВ/А₁В₂.
Объединив эти равенства, имеем:

АВ/А₁В₁ = АС/А₁С₁ = АВ/А₁В₂, следовательно,  A₁B₁ = A₁B₂.

3) Δ A₁B₂C₁ = Δ A₁B₁C₁ по двум сторонам и углу между ними:

A₁C₁ – общая, A₁B₁ = A₁B₂ из пункта 2,
< C₁A₁B₂ = < C₁A₁B₁ по построению.
Следовательно, по определению равных треугольников, < A₁C₁B₂ = < A₁C₁B₁.

4) Имеем: < A = < C₁A₁B₁ по условию, < C = < A₁C₁B₂ = < A₁C₁B₁ из доказанного,
следовательно, Δ ABC ~ Δ A₁B₁C₁ по двум углам.

Второй признак подобия треугольников позволяет доказать факт, который значительно облегчает решение некоторых задач.

Если AA₁ и CC₁ – высоты треугольника ABC, то треугольник A₁BC₁ подобен треугольнику ABC (рис.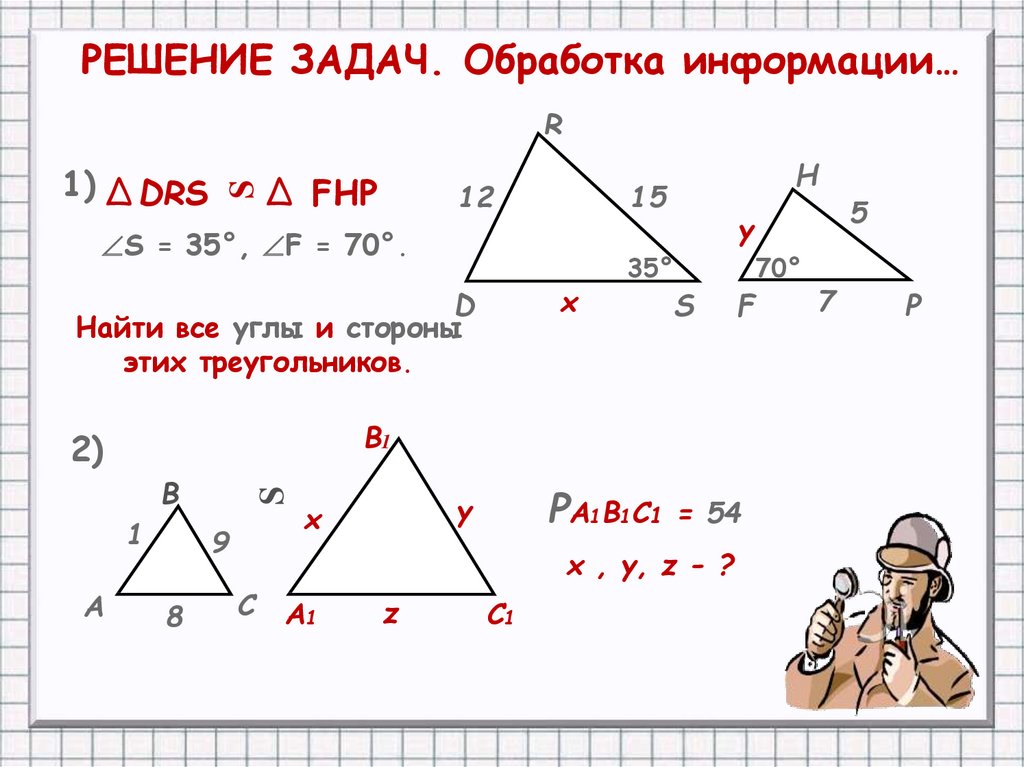 2).

Следует обратить внимание на порядок вершин подобных треугольников ABC и A₁BC₁: вершины одного из них обходятся по часовой стрелке, а второго – против часовой стрелки.

При решении задач второй признак подобия, как правило, используется в сочетании с первым признаком.

Например,  сначала доказывается подобие треугольников с использованием первого признака. Далее делается вывод о пропорциональности сторон. Затем, используя полученную пропорциональность сторон, доказывается подобие другой пары треугольников, опираясь уже на второй признак.

Третий признак подобия треугольников

Третий признак подобия треугольников довольно редко используется в решении задач, а доказательство его аналогично доказательству второго признака, поэтому приводить его не будем.

Третий признак подобия треугольников (по трем сторонам): Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники подобны.

Средние пропорциональные отрезки в прямоугольном треугольнике.

Средним пропорциональным или средним геометрическим двух положительных чисел a и b называется число √(ab).

При проведении высоты к гипотенузе прямоугольного треугольника (рис. 3) образуется три подобных треугольника, в результате чего образованные в треугольнике отрезки связаны некоторыми соотношениями. Итак, имеем:

1. Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное проекций катетов на гипотенузу.

2. Катет прямоугольного треугольника есть среднее пропорциональное гипотенузы и проекции этого катета на гипотенузу.

Кроме того, проекции катетов прямоугольного треугольника на гипотенузу пропорциональны квадратам соответствующих катетов.

Подведем итоги.

В прямоугольном треугольнике выполняются следующие соотношения (рис. 3):

 

а² = b² + c²

h_a² = c_a · b_a

c² = c_a · a

b² = (a · b_a)

h_a = (c · b)/a.

 

 

 Остались вопросы? Не знаете, как решать задачи на подобие треугольников?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Задать вопрос

Использование свойств треугольников для решения задач

Результаты обучения

• Зная величины двух углов треугольника, найдите третий
• Используйте свойства подобных треугольников, чтобы найти неизвестные длины треугольников

Что вы уже знаете о треугольниках? Треугольник имеет три стороны и три угла. Треугольники называются по их вершинам. Треугольник ниже называется [латекс]\Delta ABC[/латекс], читайте «треугольник [латекс]\текст{ABC}[/латекс]». Мы помечаем каждую сторону строчной буквой, чтобы она соответствовала прописной букве противоположной вершины. 9\circ [/латекс]. Найдите величину третьего угла.

Решение

Шаг 1. Прочтите проблему. Нарисуйте рисунок и подпишите его с помощью данной информации.
Шаг 2. Определите , что вы ищете.	Мера третьего угла треугольника.
Шаг 3. Имя. Выберите переменную для ее представления.	Пусть [latex]x=[/latex]мера угла.
Шаг 4. Перевести. Напишите соответствующую формулу и подставьте.	[латекс]м\угол А+м\угол В+м\угол С=180[/латекс]
Шаг 5. Решите уравнение.	[латекс]55+82+x=180[/латекс] [латекс]137+x=180[/латекс] [латекс]x=43[/латекс]
Шаг 6.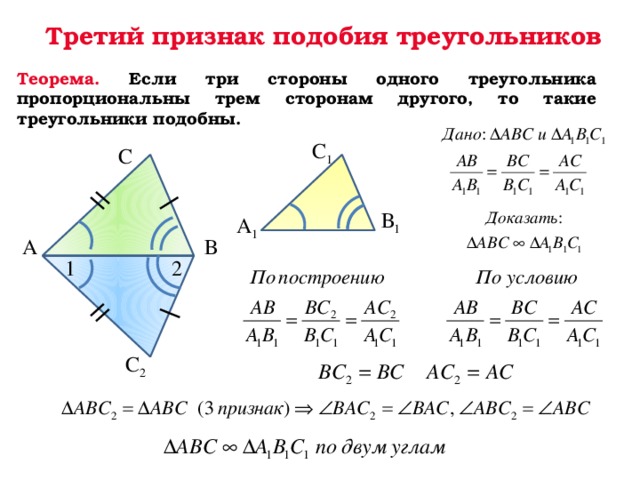 Проверка: [латекс] 55+82+43\stackrel{?}{=}180[/латекс] [латекс]180=180\галочка[/латекс]
Шаг 7. Ответьте на вопрос.	Третий угол равен [латекс]43°[/латекс]

 

попробуйте

В следующем видео мы покажем пример того, как найти величину неизвестного угла в треугольнике. В этом примере у нас есть два треугольника с общей стороной и два неизвестных внутренних угла.

Прямоугольные треугольники

Некоторые треугольники имеют специальные названия. Сначала рассмотрим прямоугольный треугольник. Прямоугольный треугольник имеет один [латекс]9\circ [/latex] больше, чем мера наименьшего угла. Найдите меры всех трех углов.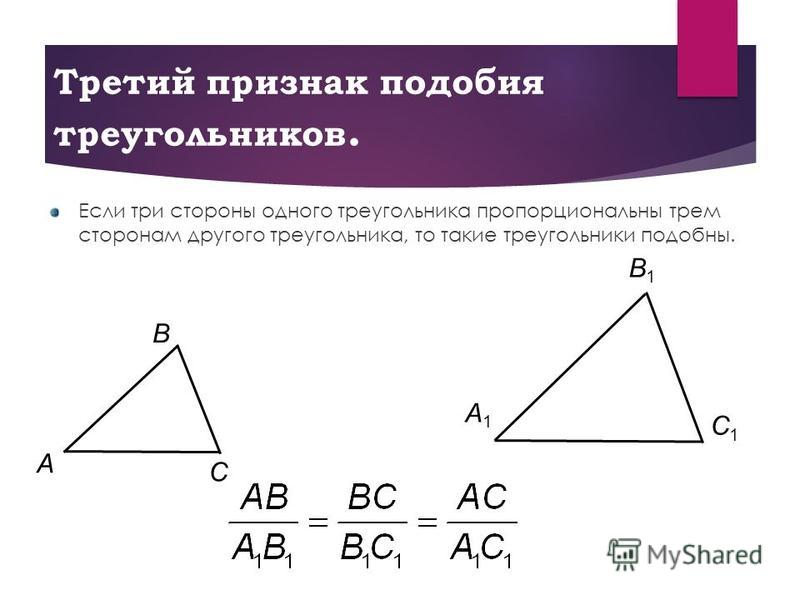

Показать раствор

 

попробуй

Подобные треугольники

Когда мы используем карту для планирования поездки, эскиз для сборки книжного шкафа или выкройку для пошива платья, мы работаем с похожими фигурами. В геометрии, если две фигуры имеют одинаковую форму, но разные размеры, мы говорим, что они похожи. Один является масштабной моделью другого. Соответствующие стороны двух фигур имеют одинаковое отношение, и все их соответствующие углы имеют одинаковые размеры.

Два треугольника ниже похожи. Каждая сторона [латекс]\Delta ABC[/латекс] в четыре раза длиннее соответствующей стороны [латекс]\Дельта XYZ[/латекс], а их соответствующие углы имеют равные размеры.

[латекс]\Delta ABC[/латекс] и [латекс]\Delta XYZ[/латекс] — подобные треугольники. Их соответствующие стороны имеют одинаковое отношение и соответствующие углы имеют одинаковую меру.

Свойства подобных треугольников

Если два треугольника подобны, то их соответствующие меры углов равны, и их соответствующие длины сторон находятся в одном и том же отношении.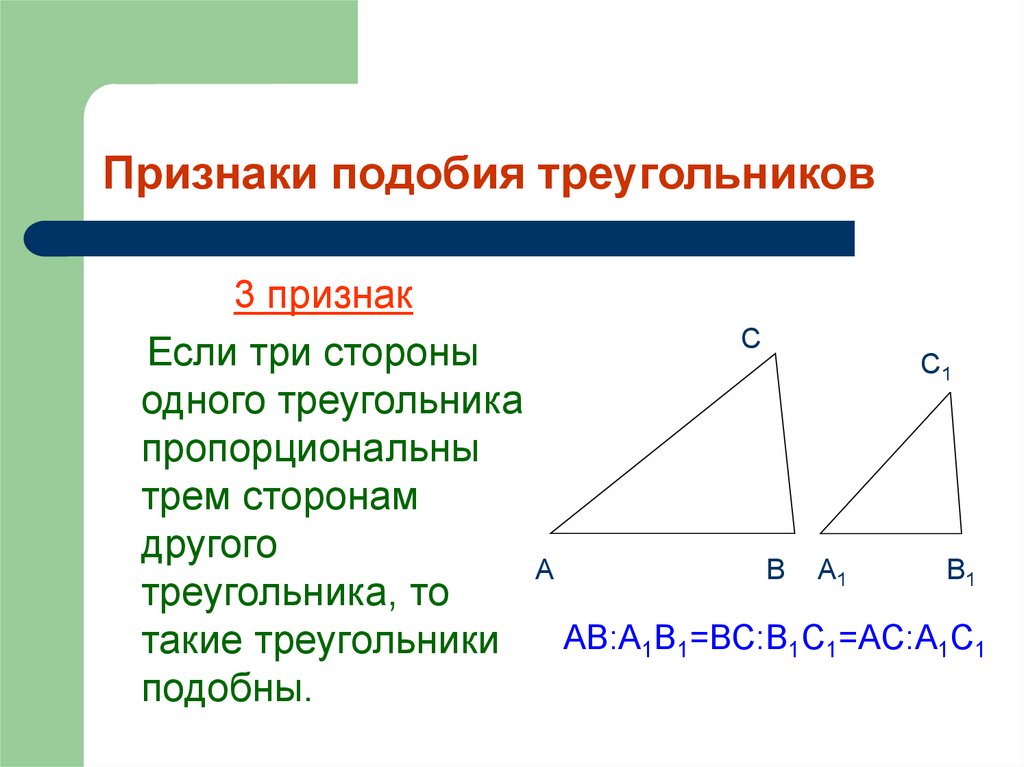

Длину стороны треугольника можно определить по ее концам, двум вершинам треугольника. Например, в [latex]\Delta ABC\text{:}[/latex]

[latex]\begin{array}{c}\text{длина }a\text{также может быть записана}BC\hfill \\ \text{длина}b\text{ также может быть записана }AC\hfill \\ \text{длина }c\text{ также может быть записана }AB\hfill \end{массив}[/latex]

Мы будем часто использовать это обозначение при решении подобных треугольников, потому что это поможет нам сопоставить соответствующие длины сторон.

пример

[латекс]\Delta ABC[/латекс] и [латекс]\Дельта XYZ[/латекс] — подобные треугольники. Показаны длины двух сторон каждого треугольника. Найдите длины третьих сторон каждого треугольника.

Показать раствор

 

попробуйте

В видео ниже мы показываем пример того, как найти недостающие стороны двух подобных треугольников. Обратите внимание, что меры сторон в этом примере — целые числа, и мы используем перекрестное произведение для решения полученных пропорций.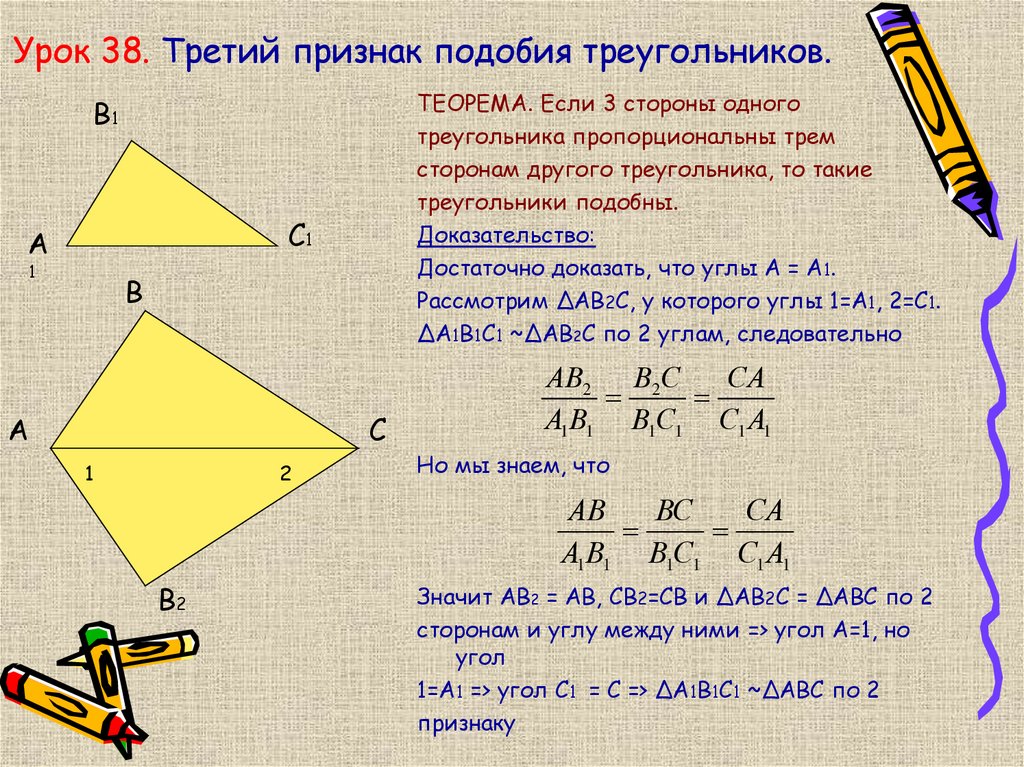

Доказательство (или опровержение) сходства треугольников

Доказательство (или опровержение) того, что треугольники подобны https://schooltutoring.com/help/wp-content/uploads/sites/2/2018/07/kvefr0506s.jpg 660 440 Преподавательский состав Преподавательский состав https://secure.gravatar.com/avatar/d96b825901af08f4b20fdfa2d056868f?s=96&d=mm&r=g 10 июля 2018 г. 10 июля 2018 г.

Определение:

Подобные треугольники имеют равные соответствующие углы и пропорциональные стороны.

Существует три основных метода доказательства подобия треугольников.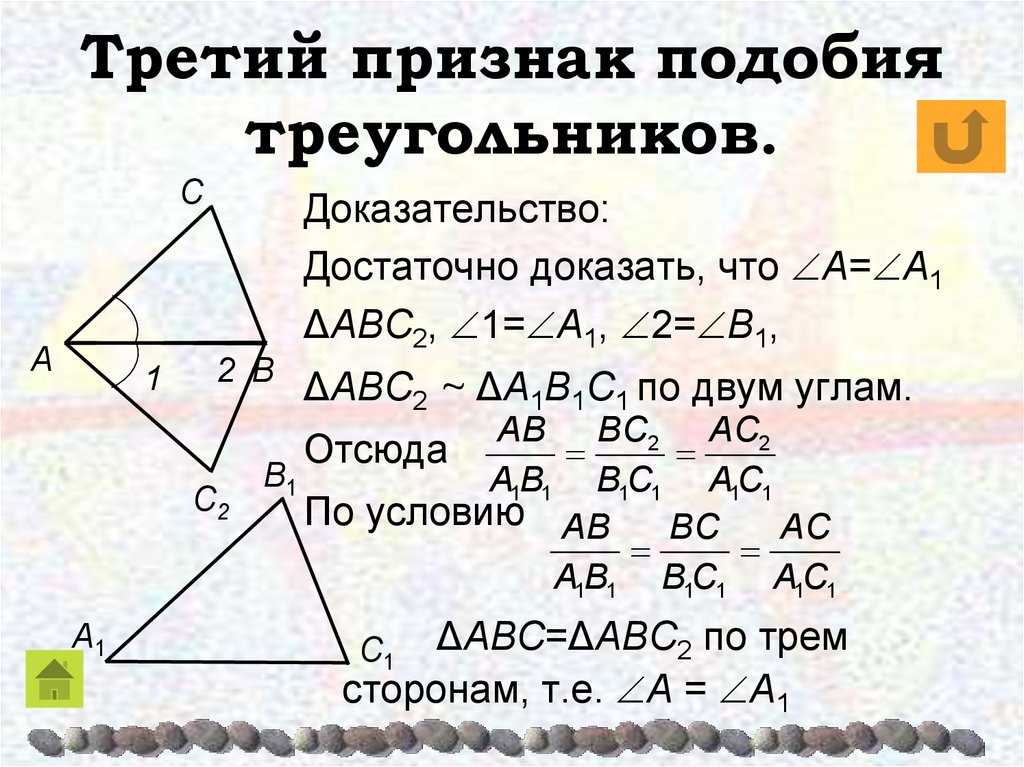 Информация, представленная в вопросе, определяет, какой подход следует предпринять. Ниже приведены подробности о каждом.

Сторона-сторона-сторона Подобие:

Используйте этот метод, когда известны длины всех трех сторон обоих треугольников. Цель состоит в том, чтобы показать, что отношение между каждой парой соответствующих сторон равно. Это достигается путем создания и оценки дробей из пар соответствующих сторон. При выполнении этих расчетов необходимо учитывать две важные вещи:

1. Важно, чтобы сравнивались только соответствующие стороны. (т. е. в прямоугольном треугольнике две гипотенузы будут сравниваться в дроби)    
2. Все значения в числителе должны быть из одного треугольника; точно так же все значения в знаменателе должны быть из одного треугольника.

Если все отношения одинаковы, это означает, что стороны пропорциональны, что является определением подобного треугольника.

 

Пример: Следующие треугольники аналогичны

3/9 = 1/3

4 /12 = 1 /3

5/15 = 1 /3

Угловой Англ.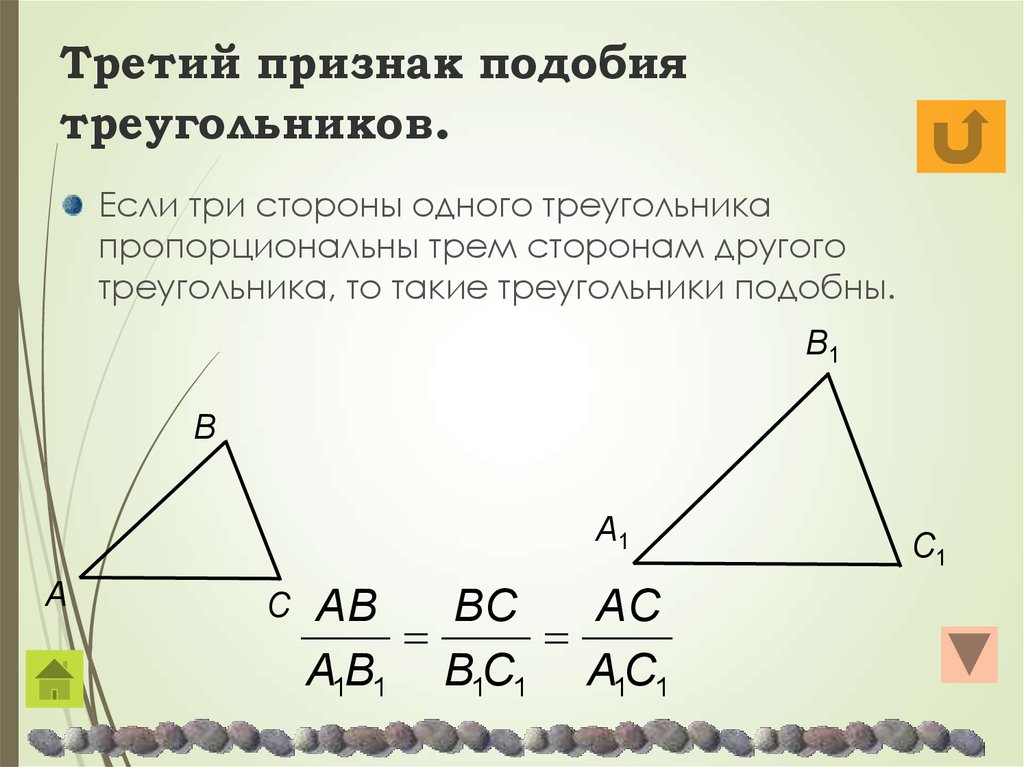

Используйте этот метод, если дано:

1. Все углы в обоих треугольниках
2. Информация, позволяющая решать углы
3. Информация, позволяющая доказать, что углы одного треугольника равны углам другого треугольника. (Это будет в том случае, если в задаче не указаны числа)

Цель состоит в том, чтобы показать, что в каждом треугольнике два угла равны. Поскольку сумма внутренних углов треугольника всегда равна 180 градусам, знание того, что два угла равны, означает, что мы знаем, что и третий угол должен быть таким же. Обратите внимание, что некоторые школы требуют, чтобы это рассуждение также было включено в доказательство. Это означает, что если два угла в треугольнике совпадают с двумя углами в другом треугольнике (соответствующие равные углы), то треугольники подобны.

 

Пример: Следующие треугольники подобны, поскольку известно, что два угла в каждом треугольнике одинаковы.

Сходство стороны-угла-стороны:

Используйте этот метод, когда в каждом треугольнике представлен «угловой бутерброд».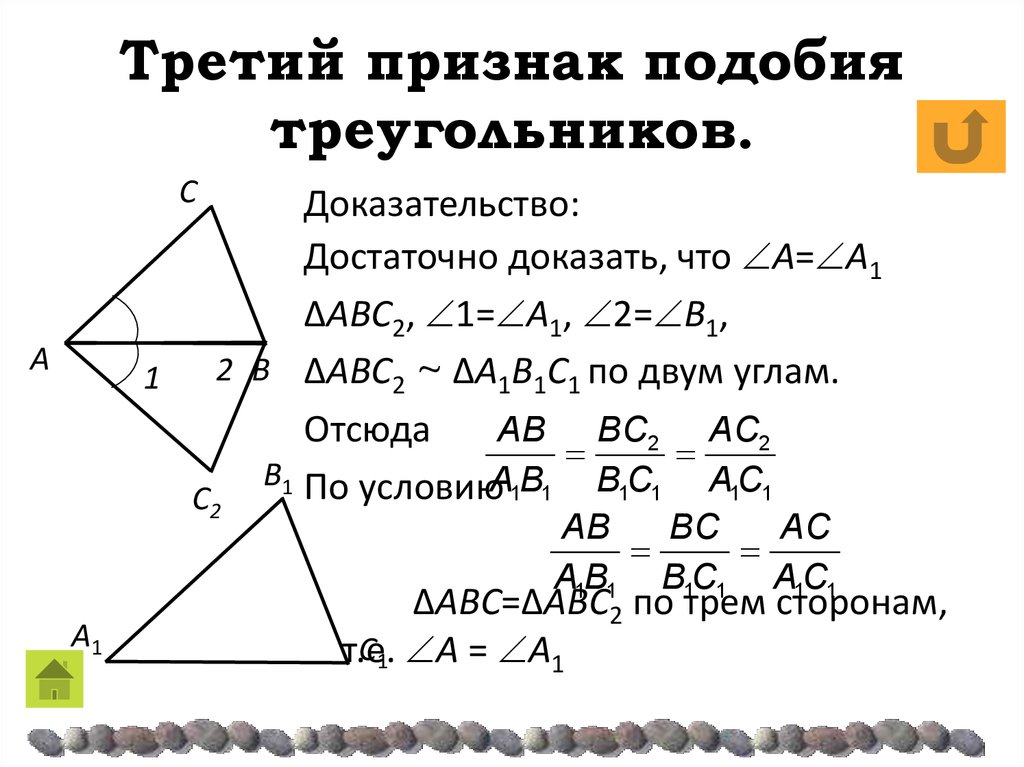 Этот термин относится к ситуации, когда определены угол, а также две окружающие его стороны. Если углы друг от друга «углового бутерброда» одинаковы, проверьте, равны ли соотношения между двумя парами соответствующих сторон (как описано выше в разделе о сходстве сторон). Как только это окажется правдой, информации будет достаточно, чтобы сделать вывод, что это подобные треугольники.

Пример: Следующие треугольники подобны, так как углы равны и

3/7 = .43

3/7 = .43

90 то треугольники не подобны! Объяснение почему является приемлемым опровержением.

Заинтересованы в услугах репетитора по математике? Узнайте больше о том, как мы помогаем тысячам студентов каждый учебный год.

SchoolTutoring Academy – ведущая компания, предоставляющая образовательные услуги для школьников и учащихся колледжей. Мы предлагаем программы репетиторства для учащихся K-12, классов AP и колледжей. Чтобы узнать больше о том, как мы помогаем родителям и учащимся в Эскондидо, Калифорния, посетите: Репетиторство в Эскондидо, Калифорния.