Процедура сравнения двух двузначных чисел начинается с: Сравнение двузначных чисел

Сравнение двузначных чисел | Методическая разработка по математике (1 класс) на тему:

Урок математики в 1 в классеТема урока:Сравнение двузначных чиселЦель урока:-учить сравнивать двузначные числа с опорой на их десятичный состав, формировать умение решать задачи с помощью схемы, совершенствовать умение выполнять сложение и вычитание чисел;-развивать  логико-математическую речь, внимание, аналитическое мышление;-воспитывать  интерес к предмету, дисциплинированность.Формирование универсиальных  учебных  действий:1. Регулятивные УУД: — формулировать тему и цель с помощью учителя;-учиться высказывать свое предположение на основе работы материала учебника;-определять успешность выполнения задания в диалоге с учителем.2. Познавательные УУД:-извлекать информацию из текстов, представлять информацию в виде схемы, графической модели, наблюдать и делать выводы3.Коммуникативные УУД:-слушать и понимать речь своих товарищей, строить речевое высказывание в соответствии с поставленными задачами, умение работать в группе, в парах, вести диалог 4. Личностные УУД: Формирование положительной  учебной мотивации, навыков самооценки, понимание  смысла учебной деятельностиТехнология:Технология  проблемного  диалога.

                                                                                                 Ход урока:

Технология проведения	Деятельность учителя	Деятельность ученика
I этап. Организационный момент. Цель–активизация учащихся.	— Вот звенит для нас звонок – начинается урок. Ровно встали, подтянулись и друг другу улыбнулись. -Тихо сели. Настраиваемся на урок. На каждом уроке, путешествуя по стране математики, мы раскрываем новые тайны. Готовы ли вы сегодня к новым открытиям? А что мы должны взять с собой ?   И так –в путь!	— Да. Знания,умения,навыки,…
11 этап Актуализация знаний Цель- выяснить степень усвоения обучающимися предыдущего материала. Устный счет   III этап. Изучение нового материала. Постановка проблемы. Открытие нового: Цель – Познакомить учащихся с числами  0 и10,  развитие умения находить ответы на проблемные вопросы.	Ц и ф р о г р а д Устный счет 3 плюс2 5 увеличить на3 Покажите сумму чисел 6 и 2 8 уменьшить на4 Покажите разность чисел 7 и 2 Покажите число 1 5.Покажите следующее число.(16) Покажите число1 3.Покажите следующее число.(14) Как получаем следующее число? Покажите число1 4. Покажите предыдущее  число.(13) Покажите число1 6. Покажите предыдущее  число.(15) Как получаем предыдущее  число? Числовой ряд 1,2,3,4,5,6,7,….20 На какие две  группы можно разделить числа? 1,3,…               2,4, …. Какие числа называются четными? 1,2,….              10,11,… Какие числа называются однозн.,двузначн.? Состав чиел. Прочитайте числа   56,14,52,12,16,54 Назовите состав чисел 5 дес.6 ед.,… На какие группы можно разделить данные числа? З а д а ч к и н о Слайды Решить задачи Придумать условие задачи  и вопрос  А у вас есть предположения, как обозначить пустое множество, пустоту? — Откуда вы знаете про это число? — Давайте сравним число 0 с другими изученными числами. — Что обозначает число 0? — А как мы его будем обозначать? — Где будет стоять число 0 в числовом ряду? Как его отметить на числовом отрезке? Почему? ______________________________________________ — Есть ли у него «соседи» ? Сценка. Ребята, а как можно получить число 10, зная числовой отрезок ? о о о о о о о о о + о Почему так думаете? ____________________________________________ — Значит, тема урока — … — Чему мы научимся на этом уроке? Чем ещё будем заниматься7 А теперь немножко отдохнем. Ф и з м и н у т  к  а: — Сели поудобнее, — Закрыли глаза. — Открываем. ( На доске цифры от 1 до 9 вперемешку с 01,02,03) 1.Глазами  найдите числа в порядке возрастания. 2.Посмотрите внимательно на цифры и найдите лишние. Докажите, почему они лишние. Где вы их видели? А как вы думаете почему не 10, 20, 30, а наоборот?	Сложение Вычитание Когда к  числу прибавляем 1, получаем следующее число. Когда из числа вычитаем 1, получаем предыдущее число.   Четные, нечетные. Однозначные, двузначные 5 дес.6 ед.,  1 дес.4 ед., … 2 гр.-по цифре, указ.кол-во десятков 14,12,16          56,52,54 3гр.- по цифре, указ.кол-во единиц 12,52             14,54         16,56 —   — Пустоту, пустое множество, ничего. — Цифрой 0. Дети высказывают свои мысли: — Число 0 будет стоять в начале отрезка, числового ряда, потому что он меньше всех остальных чисел. Ответы детей. Вывод: 0 — обозначает  пустое множество. Число 0 обозначают на письме цифрой 0. Начало числового отрезка надо обозначать цифрой 0.          9+1=10 Когда к  числу прибавляем 1, получаем следующее число. Числа 0 и и10. Научимся писать цифру 0 и число 10. Будем сравнивать числа, решать задачи. Варианты ответов детей. 01, 02, 03 – нет таких чисел. Это номера экстренных вызовов. — Чтобы легче запоминалось, чтобы они выделялись. Вывод: Оказывается и тут наша цифра играет важную роль.
III этап. Изучение нового материала. Постановка проблемы. Открытие нового Цель – Познакомить учащихся с новыми способами сравнения двузначных чисел Постановка целей и задач урока. Физминутка Открытие нового. Физминутка 1V этап. Закрепление изученного. Цель – научиться сравнивать двузначные числа, опираясь на новые знания	В с п о м и н а й-к а! Работа в тетради: Минутка чистописания 29   29  29 Дайте характеристику числу На доске запись 3…6         8…15         34. .54 7…2        19…4          72..76 -Как вы думаете, какое задание я вам приготовила? -На какие знания опирались, когда сравнивали числа? Способы сравнения: 1-можно сравнивать парами (предметы) 2-меньше то число, которое при счете было названо раньше, больше то число,-….позже 3—меньше то число, которое находится ближе к началу числового луча, больше то число,…-дальше от начала…  А как вы здесь докажете? 34… 54. Ведь линейка у нас только до 20.(высказывания детей). Постановка целей и задач урока. — Кто догадался, над какой темой мы будем работать? (сравнение двузначных чисел). — А каких именно? (Больше 20). — Значит, чему мы будем учиться? (сравнивать двузначные числа, опираясь на новые знания). Тема нашего урока «Сравнение двухзначных чисел». Наша задача – найти новый способ сравнения.  Физминутка С р а в н и в а й-к а! Открытие нового. — Кто попытается доказать, почему 34 — А может нам поможет графическая модель? (строят графическую модель: один у доски, остальные на партах). 34 = 3 д. 4 ед. 34 = 54 = 5 д. 4 ед. 54 = — Для чего мы построили графическую модель? Что мы видим с помощью графической модели? (десятки и единицы). 3 д..  34 Вывод: чем меньше десятков в числе, тем меньше двузначное число Чем больше десятков, тем больше двузначное число А как сравнивать числа 72…76 ? 72=7 дес.+2 ед. 76=7 дес.+6 ед. 72 Вывод: если число десятков  в числах одинаково ,то больше то число, в котором больше единиц- Какие знания понадобились, чтобы сравнить двузначные числа? (знания десятичного состава числа) Вывод: опираясь на знания десятичного состава числа, мы можем сравнить любые двузначные числа.   Физминутка З а к р е п л я й-к а! Работа по учебнику. Стр.28 №3 (рис.Гномики ) Вывод Сравнение чисел.   Стр.28 №4 (письменно) 20…30      90…50 40…10      60…80 Стр 29 №5 (рис. Редиски) Стр.29 №6(письменно) Р а с ш и ф р у й-ка ! Расшифровка    1                    2                  3               4                      5   7+2=9 я       2+4=6 о       5-4=1 е      7-4=3е           8-5=3в 3+4=7 н       4-2=2 т       6-3=3 и      5+3=8к          4+3=7р 4+4=8 а       1+6=7 а       4+4=8л      9-7=2о           6-2=4а 3+3=6 з       5-2=3 в        2+7=9ч      2+5=7л         7+2=9с                     8+1=9 с       4+3=7с       4+2=6г         4-2=2и                                                                                  4+2=6н 6 7 8  9       9 6 9 2 7 3    9 3 7 1 8  2    7 3 6 8 2     9 7 4 3 6 2 З н а я       с о с т а в      ч и с е  л  ,    л е г к о      с р  а в н и	29- двузначное, состоит из 2 дес. и 9 ед., пред.28  след.30д.,нечетное Сравнивают числа Доказывают: какое число больше, какое меньше?   Сравнение двузначных чисел Сравнивать двузначные числа, опираясь на новые знания). Дети рисуют графическую модель чисел 34 и 54 Вывод: чем меньше десятков в числе, тем меньше двузначное число Чем больше десятков,тем больше двузначное число Называем состав чисел Состав чисел:72= 7 дес. 2 ед.     76=7 дес.6 ед.     6                          7 10-2=8т           7-4=3и 9-4=5ь             8-6=2л 8-5=3в             10-4=6с 6-2=4а              3+6=9ч                          7+1=8а 3 4 8 5           9  3  6  2 8  в а т ь           ч  и  с  л а.
V. Итог урока. Цель – подвести итог проделанной работе на уроке.	И т о г о в а я VII. Итог урока. — Назовите тему урока. -Чему вы научились на уроке?                                       Расскажите по схеме:         Я запомнил …         Я знаю…         Я смог… — Как бы вы оценили свою работу? Почему? Ваша самооценка совпала с моей. Вы сегодня работали отлично. Спасибо за урок!	Ответы детей.

Сравнение двузначных чисел, представление их в виде суммы разрядных слагаемых

Конспект урока по математике в 1 классе (УМК «Гармония»)

Тема урока: «Сравнение двузначных чисел, представление их в виде суммы разрядных слагаемых»

Цель: создать дидактические условия для совершенствования умения сравнивать двузначные числа (с помощью числовой прямой и знания разрядного состава чисел), а так же формировать умение представлять двузначное число в виде суммы разрядных слагаемых.

Задачи:

— образовательная: совершенствовать навыки сложения и вычитания двузначных чисел вида 80+3, 30+8;

— развивающая: развивать в процессе вычислений познавательную активность, внимание, память, мышление, аккуратность в письме.

Ход урока:

I. Оргмомент.

– Прозвенел, друзья, звонок! Начинается урок!

 

II. Актуализация знаний. Устный счёт.

1. Числовой ряд.

— Назовите последующее число 35, 49, 78;

— Назовите предыдущее число 30, 40, 70;

— Назовите соседей числа 36, 58, 69;

2. Разрядные слагаемые

На доске запись 56, 14, 52, 54, 12, 16

— Прочитайте числа

— Сколько в каждом числе десятков и единиц?

— На какие группы можно разделить данные числа?

(на две группы по цифре, указывающей на количество десятков: 14, 12, 16, и 56, 52, 54; на три группы по цифре единиц: 12, 52 ; 14, 54 ; 16, 56)

3. Назовите числа у которых :

2 дес. 6 ед.; 5 дес.; 7 дес.2 ед.; 3 дес.9 ед, ; 6 дес.5 ед.; 9дес. ; 6 дес. 6 ед; набольшее двузначное число, наименьшее двузначное число.

 

III. Введение в тему урока.

а) На доске записаны числа 5, 10, 15

— Прочитайте числа. — Установите закономерность в данном ряду чисел. (В данном ряду числа увеличиваются на 5.)

— На какие группы можно разбить эти числа? (Однозначные и двузначные; круглые и некруглые.

Подумайте — какое число лишнее и почему? (5 т.к. оно однозначное).

— Расскажите все, что знаете об этих числах.

— Связаны ли между собой эти числа? Как? Составьте 4 числовых выражения с ними.(2 на сложение и 2 на вычитание)

— Какое из этих чисел можно представить в виде суммы разрядных слагаемых?

— Сегодня мы будем много выполнять таких заданий. Как вы думаете — чему мы будем продолжать учиться на уроке? (представлять двузначные числа в виде суммы разрядных слагаем

— Как вы думаете — для чего мы должны уметь это делать? (чтобы находить значения числовых выражений)

б) — Какие еще действия можно выполнить с двузначными числами? (сравнить их при помощи знаков > или <. Сравните числа 10 и 15. Это можно сделать 2 способами.

Способ первый: с опорой на числовую прямую (записана на доске).

Так, 10< 15 т. к. при счете 10 называем раньше и наоборот.

Способ второй: с опорой на разрядный состав чисел: сначала обращаем внимание на старший разряд- десятки, затем (если это необходимо) — на единицы.

— Таких заданий мы тоже сегодня выполним еще немало. Ребята, чему мы будем еще продолжать учиться на уроке? (сравнивать двузначные числа)

 

IV. Закрепление изученного.

а) Фронтальная работа по учебнику с.56 №138 (представление чисел в виде суммы разрядных слагаемых), частично выносится на доску.

ФИЗМИНУТКА

1, 2, 3, 4, 5 –

Все умеем мы считать.

Отдыхать умеем тоже.

Руки за спину положим,

Голову поднимем выше и легко-легко подышим!

б) Работа в парах— сравнение двузначных чисел с. 56 №139

Время ограничивается, с последующей проверкой (выносится на доску, обговариваются разные варианты). Самооценка.

в) Групповая дифференцированная работа (разбиение на группы осуществляется учителем предварительно согласно уровню подготовки обучающихся).

Каждой группе предлагается карточка – на которой 3 вида заданий на сравнение:    

— двузначных чисел ( 80…82 , 73…37, 64….46 и др.),

— двузначного числа и выражения (67- 7…60 , 46…48-1 и др.),

— числовых выражений (70+ 5…80-10 , 46-6…46-40 и др.).

Результат заранее вынесен на доску, скрыт до проверки. Проверка, оценка работы групп в целом и степени участия каждого участника.

г) Нахождение значений числовых выражений, основанных на умении представлять число в виде суммы двух слагаемых с. 56 № 143. Работа проводится устно или письменно в зависимости от оставшегося времени с взаимопроверкой или фронтально с последующей самооценкой.

 

V. Итог урока.

— Наш урок подходит к концу. Чему продолжали учиться на уроке?

 

VI. Рефлексия.

— Все ли у вас получилось? Возникали ли затруднения в процессе работы? Оцените свою работу на уроке, выбрав звездочку соответствующего цвета (принцип светофора)

Опубликовано 17. 03.16 в 13:58 в группе «Учителя начальных классов, работающих по УМК «Гармония»»

Сравнение чисел с использованием разрядности (определение, типы и примеры)

Пример 1: Сравните 25 490 и 25 671.

 

Решение:

Оба числа пятизначные.

Составьте диаграмму разрядности,

 

 

Начните слева. Сравнивайте цифры в каждом разряде, пока цифры не различаются,

 

Сравните десять тысяч,

2 5,490

2 5,671 Можно увидеть, 2 десять тысяч = 2 десять тысяч

Сравните тысячи,

2 5 , 490

2 5 , 671 Мы можем видеть, 5 тысяч = 5. тысячи

 

Сравните сотни,

25, 4 90 

25, 6 71    Мы видим, что 4 сотни < 6 сотен

Поэтому мы используем цифры для сравнения чисел.

Итак, 25,490 < 25 671

 

Пример 2. Сравните 6709 и 569.

 

Решение:

5-значное число 3, 6,709 — четырехзначное число. SO,

6,709> 569

Пример 3: Сравните 29 650 и 20000 + 9000 + 600 + 60 + 9.

Решение:

Измените номера на стандартную форму,

. номер, 29 650 

Второй номер, 20000 + 9000 + 600 + 60 + 9

 

 

Второе число имеет стандартную форму: 29669

Оба числа пятизначные.

Составьте диаграмму разрядности,

 

 

Начните слева. Сравните цифры в каждом разряде, пока цифры не станут разными,

 

Сравните крайние левые цифры, т. е. цифры в разряде десятков тысяч,

2 9,650

2 9,669   

Мы видим, что цифры равны 2 для чисел

2 десять тысяч = 2 десяти тысячам

 

Сравните вторую слева цифру, т. ,650 

2 9 ,669    

Мы видим, что цифры 9 для чисел

9 тысяч = 9 тысяч

 

цифра слева, третья цифра

. ,

29, 6 50

29, 6 69

Можно видеть, что цифры составляют 6 для чисел

6 Сотни = 6 сотен

Сравните четвертую левую, т.е. цифра на The Tens Place,

29,6 5 0

29,6 6 9

Можно видеть, что цифры 5 и 6,

5 TENS <6 TENS

SO, 29 650 < 239 669

 

Пример 4. Поставьте соответствующий символ <, > или =.

500 225 Пятьсот тысяч двести двадцать пять

 

Решение:

Преобразовать числа в стандартную форму,

Первое число в стандартной форме: 500 225 двести тысяч,

2 тысяч двадцать пять.

Стандартная форма: 500 225

Теперь мы видим, что все цифры обоих чисел одинаковы. Это дает результат, что оба числа равны.

500 225 = пятьсот тысяч двести двадцать пять  

 

Пример 5. Две разные игрушечные машинки стоят 1500 и 1551 доллар. Какая цена меньше?

 

Решение:

Цена первой машинки 1500 долларов.

Цена первой машинки 1551$.

Оба номера четырехзначные.

Составьте диаграмму разрядности,

 

 

Начните слева. Сравните цифры в каждом месте, пока цифры не различаются,

Сравните тысячи,

1 , 500

1 , 551, мы можем увидеть, 1 тысяча = тысяча

Сравните сотни, сотни, 1 тысяча = тысяча

.

1, 5 00

1, 5 51      Мы видим, 5 сотен = 5 сотен0005

1,5 5 1      Мы видим, что 0 десятков < 5 десятков

 

Итак, мы используем разряд десятков для сравнения чисел.

1500 $ < 1551 $

Следовательно, цена первой игрушечной машинки меньше.

Числа до 2 цифр — определение, разрядное значение

В двузначных числах есть только два разряда — разряд единиц и разряд десятков. Каждое число, состоящее более чем из 1 цифры, имеет разные цифры, описываемые их разрядными значениями. Двузначные числа начинаются с 10 и заканчиваются на 99. Другими словами, наименьшее двузначное число равно 10, а наибольшее двузначное число равно 99.

1.	Что такое двузначные числа?
2.	Как записывать числа до 2 цифр?
3.	Общие ошибки чисел до 2 цифр
4.	Часто задаваемые вопросы о номерах до 2 цифр

Что такое двузначные числа?

Двузначные числа — это числа, состоящие из двух цифр, которые начинаются с цифры 10 и заканчиваются цифрой 99. Они не могут начинаться с нуля, потому что в этом случае они будут считаться однозначной цифрой. Цифра в разряде десятков может быть любым числом от 1 до 9. Например, 45, 78, 12 — двузначные числа.

Разрядное значение в двузначных числах

Разрядное значение — это положение каждой цифры в числе. Когда мы говорим об однозначных числах, есть только одно разрядное значение, которое является разрядом единиц. Когда мы подходим к двузначным числам, есть два разряда — единицы и десятки. Обратите внимание на следующий рисунок, на котором показано двузначное число 23, написанное вместе с его разрядными значениями. Цифра 2 стоит на месте десятков и означает 20, а цифра 3 стоит на месте единиц и означает 3.

Присвоение разрядных значений

Мы знаем, что разрядное значение числа говорит о позиции цифры. В двузначных числах единственными разрядами являются десятки и единицы.

Давайте посмотрим на следующий набор чисел, чтобы понять сочетание единиц и десятков:

а.) 33 ⇒ 3 десятка + 3 единицы = (3 × 10) + (3 × 1) = 30 + 3 = 33

б.) 18 ⇒ 1 десяток + 8 единиц = (1 × 10) + (8 × 1) = 10 + 8 = 18

в.) 27 ⇒ 2 десятка + 7 единиц = (2 × 10) + ( 7 × 1) = 20 + 7 = 27

Как записывать числа до 2 цифр?

Двузначные числа можно записывать в виде цифр, прописью и в расширенной форме.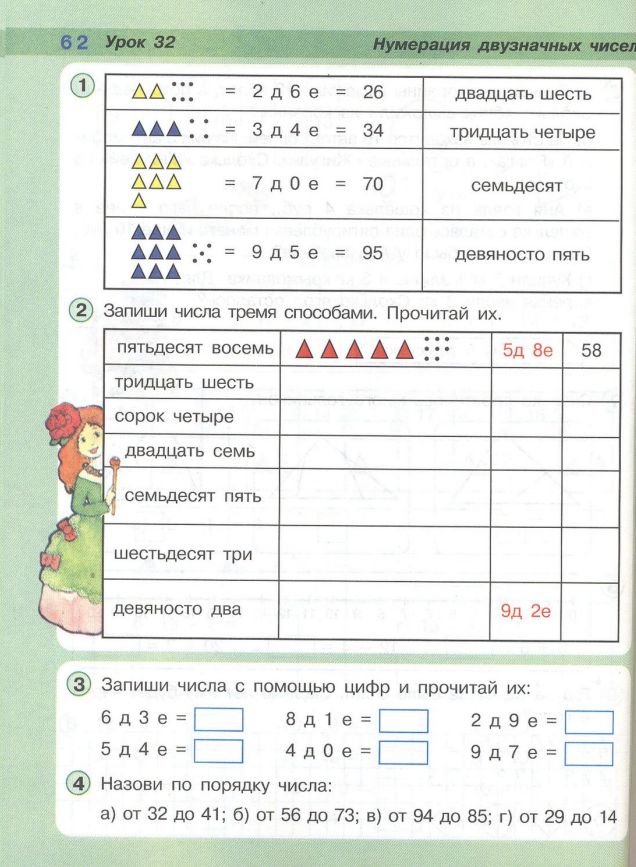 Например, 45 — это двузначное число. Давайте посмотрим, как это можно записать тремя способами.

• В цифровой форме: 45
• Прописью: сорок пять
• В развернутом виде: 40+5

Двузначные числа в словах

Когда числа записываются словами с помощью разрядных значений, это помогает нам писать их по буквам. Самое маленькое двузначное число — 10, которое записывается как десять. После этого числа от 11 до 20 записываются как 11 – одиннадцать, 12 – двенадцать, 13 – тринадцать, 14 – четырнадцать, 15 – пятнадцать, 16 – шестнадцать, 17 – семнадцать, 18 – восемнадцать, 19.- девятнадцать, а 20 — двадцать. После этого они записываются как 21 — двадцать один, 22 — двадцать два, 23 — двадцать три и так далее, пока не дойдет до 30 — тридцать, и тот же образец следует после тридцати, сорока и так далее.

Двузначные числа в расширенной форме

Расширенная форма числа помогает узнать о его составляющих. Развернутую форму двузначного числа можно показать по-разному. Рассмотрим двузначное число 57.

• Число 57 можно записать в одной форме как 57 = (5 × десятков) + (7 × единиц)
• По-другому это можно записать как 57 = (5 × 10) + (7 × 1)
• Третий способ записать 57 в расширенной форме: 57 = 50 + 7.

Общие ошибки чисел до 2 цифр

• Дети часто могут назвать все числа до 99 (или 100), но могут ошибаться, когда их просят найти большее число между двумя числами. Они повторяют числа от 1 до 100 так, как будто выучили буквы алфавита. Если это произойдет, то найти большее число между 14 и 15 так же сложно, как найти большую букву между С и D. Дети должны понимать, что, в отличие от букв, числа связаны друг с другом. 15 ровно на единицу больше, чем 14. Для этого можно использовать числовые линии и цветные счетчики, чтобы связать звук с количеством.
• Дети склонны ошибаться при работе с числами при изменении разряда десятков. Например, при переходе от 19 к 20, от 29 к 30, от 39 к 40 и т. д. Часто двузначные числа вводятся без привязки к разрядным значениям. Хотя это облегчает запоминание чисел, это может быть не лучшей стратегией, поскольку дети не видят числа, составленные из общего набора цифр от 0 до 9. В этом случае можно использовать счеты для моделирования чисел и основания. -10 блоков могут быть использованы, чтобы помочь им визуализировать числа.
• Дети делают ошибки при написании или чтении цифр словами, особенно от одиннадцати до девятнадцати. Нет никакой замены практике. Дети должны практиковаться в написании названий чисел. Как правило, при небольшой преднамеренной и целенаправленной практике эту ошибку можно легко исправить.

Советы по числам до 2 цифр

Ниже приведены некоторые советы и рекомендации по числам до 2 цифр.

• При умножении любого однозначного числа (от 1 до 9) на 10 получается двузначное число. Например, 4 × 10 = 40
• Наименьшее двузначное число, состоящее только из одной цифры, равно 11.
• Наименьшее двузначное число, состоящее из двух разных цифр, равно 10. (10 также является наименьшим двузначным числом)
• Наибольшее двузначное число, использующее только одну цифру, равно 99. (99 также является наибольшим двузначным числом).
• Наибольшее двузначное число, использующее все разные цифры, равно 98.
• В двузначных числах только два разряда: десятки и единицы.
• Есть девяносто «двухзначных чисел», начиная с 10-99.

Вот список всех чисел до 2 цифр от 10 до 99.

Наименьшее двузначное число

Наименьшее двузначное число — 10, поскольку предыдущее число — 9, которое является однозначным числом.

Наибольшее двузначное число

Наибольшее двузначное число — 99, поскольку следующее число — 100, которое является трехзначным числом.

Важные примечания

Ниже приведены некоторые важные примечания, связанные с числами до 2 цифр, которые мы изучали в этой статье.

• Наименьшее двузначное число — 10, а наибольшее двузначное число — 99.
• Всего девяносто двузначных чисел.
• Двузначное число не может начинаться с 0, так как в этом случае оно будет рассматриваться как однозначное число.

☛ Статьи по теме

• Номера до 3 цифр
• Номера до 4 цифр
• Номера до 5 цифр
• Номера до 6 цифр
• Номера до 7 цифр
• Номера до 8 цифр
• Номера до 9 цифр
• Номера до 10 цифр

 

Примеры двузначных чисел

1. Пример 1: В чем разница между самым большим двузначным числом и числом 20?

   Решение: Наибольшее двузначное число = 99
   Разница между 99 и 20 составляет 99 — 20 = 79

   .

2. Пример 2: Создайте двузначное число, в котором 7 соответствует разряду десятков, а 5 — разряду единиц. Запишите номер в развернутой форме и напишите его номерное название.

   Решение: Если 7 в разряде десятков и 5 в разряде единиц, число равно 75.
   Расширенная форма 75 = 70 + 5. Это также можно записать как (7 десятков) + (5 единиц) или (7 × 10) + (5 × 1) 9.0479 Имя числа 75 — это семьдесят пять.

3. Пример 3: Напишите первые четыре «двузначных числа» и последние четыре «двузначных числа».

   Решение: Первые четыре двузначных числа: 10, 11, 12, 13.

   Последние четыре двузначных числа: 96, 97, 98, 99.

перейти к слайдуперейти к слайдуперейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по числам до 2 цифр

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о номерах до 2 цифр

Что такое двузначные числа в математике?

Число называется двузначным, если оно состоит из двух цифр, в котором цифра десятков должна быть от 1 до 9, оно не может начинаться с нуля, потому что в этом случае оно станет однозначным числом. Например, 35, 45, 60, 11 и так далее — двузначные числа.

Сколько существует двузначных чисел?

Всего существует девяносто двузначных чисел, начиная с 10 и заканчивая 99. Это означает, что наименьшее двузначное число равно 10, а самое большое двузначное число равно 99.

Какое самое большое 2- Цифровой номер?

Самое большое двузначное число — 99, а следующее число — 100, которое является трехзначным числом.

Какое самое маленькое двузначное число?

Наименьшее двузначное число — 10, потому что предыдущее число — 9, т. е. однозначное число.

Какое наибольшее двузначное число делится на 10?

Самое большое двузначное число, которое делится на 10, — это 90. Хотя самое большое двузначное число — 99, оно не делится на 10.

Какое наибольшее двузначное число можно составить из 8 и 6?

Наибольшее двузначное число, которое можно составить из 8 и 6, — это 86. Поскольку 8 больше 6, поэтому мы оставляем 8 на разряде десятков, а 6 — на разряде единиц. Следовательно, 86 — это самое большое двузначное число, состоящее из цифр 8 и 6.

Запишите расширенную форму данного двузначного числа 65.

Расширенную форму числа 65 можно представить как 60 + 5. Это также можно записать как 6 десятков + 5 единиц или (6 × 10) + (5 × 1).

Сколько десятков в двузначном числе 20?

В данном числе 20 цифра 2 стоит на месте десятков. Следовательно, в числе 20 2 десятка. Это можно записать как 20 = 2 десятка + 0 единиц.

Могут ли двузначные числа начинаться с 0?

Нет, двузначные числа не могут начинаться с 0. Разряд десятков в двузначном числе не может быть нулем, это может быть любое число от 1 до 9, в противном случае оно будет считаться однозначным числом. Например, 05, 06, 07 — все однозначные числа, а 56, 78, 79 — двузначные числа.

Каковы разрядные значения в числах до 2 цифр?

Значение разряда помогает определить положение цифр. В двузначных числах всего два разряда — десятки и единицы.