Программа для построения разверток геометрических тел: ПРОГРАММА 3D МОДЕЛИРОВАНИЯ ПРИ ПОСТРОЕНИИ РАЗВЕРТОК ПОВЕРХНОСТЕЙ

alexxlab / / Разное

Чертежи и развертки геометрических тел | План-конспект урока по технологии (7 класс) по теме:

ЧЕРТЕЖИ И РАЗВЕРТКИ ГЕОМЕТРИЧЕСКИХ ТЕЛ. УРОК 2.

ЦЕЛИ:

— закрепить понятие геометрические  тела;

— читать  и  строить  их чертежи геометрических тел;

—  способствовать  самостоятельному  изучению построению разверток геометрических тел;

— развивать  пространственные представления и  мышление, умение работать с  информационными источниками;

— воспитывать чувство времени, ответственности в  коллективе.

 ТИП  УРОКА: урок  изучения  нового  материала

МАТЕРИАЛЬНОЕ  ОБЕСПЕЧЕНИЕ:  модели геометрических тел, таблицы- задания, учебники, чертежные принадлежности, ножницы, чертежная бумага.

МЕТОДЫ  ПРОВЕДЕНИЯ:    беседа, выполнение  чертежей геометрических тел и разверток,  моделирование.

ЛИТЕРАТУРА: « Черчение»  Ботвинников А.Д.,Виноградов В.Н., Вышнепольский И.С.

ХОД  УРОКА

1.Организационная  часть. ( 0,5  мин.)

Очень правильно, очень мудро,

Да  не будет помехой лень,

Утром  говорить всем: «Доброе … ( утро)»,

Ну а  днем говорить: «Добрый. .( день)».

Просмотр готовности учащихся  к  уроку.

2. Сообщение темы урока ( 0,5 мин.)

ТЕМА  УРОКА: «ЧЕРТЕЖИ И РАЗВЕРТКИ ГЕОМЕТРИЧЕСКИХ ТЕЛ»

(Слайд 1)

На прошлом уроке мы рассмотрели некоторые геометрические тела, научились строить их чертежи и развертки. Давайте вспомним, что такое геометрическое тело? Какие геометрические тела бывают?

(Слайд 2)

3. Изучение  нового  материала (15 мин)

Сегодня на уроке мы познакомимся с телами вращения и закрепим старый материал.

  1. Цилиндр – это геометрическое тело, образованное вращением прямоугольника вокруг одной из его сторон.

(Слайды 3, 4)

Рассмотрим  проекции цилиндра. Главный вид имеет форму прямоугольника  с размерами высоты и диаметра основания, вид сверху имеет форму окружности с  размером диаметра, вид слева имеет форму прямоугольника с размерами высоты и диаметра основания.

(Слайд 5)

Рассмотрим развертку цилиндра. Она состоит из трех частей – боковой поверхности и верхнего и нижнего оснований. Боковая поверхность – прямоугольник с размерами высоты и длины, которая высчитывается по формуле  С=πd. Нижнее и верхнее основания – окружности с размерами диаметра d.

(Слайд 6)

  1. Конус – это геометрическое тело, образованное вращением прямоугольного треугольника вокруг своей оси, проходящей через один из его катетов.

(Слайды 7, 8)

Рассмотрим  проекции конуса. Главный вид имеет форму треугольника с размерами высоты и диаметра основания, вид сверху имеет форму окружности с  размером диаметра, вид слева имеет форму треугольника с размерами высоты и диаметра основания.

(Слайд 9)

Рассмотрим развертку конуса. Она состоит из боковой поверхности – сектор R+ образующей конуса,  угол α подсчитывается по формуле α =360º*d/2R

(Слайд 10)

  1. Сфера (шар) – геометрическое тело, образованное вращением половины окружности вокруг оси, проходящей через его диаметр.

(Слайды 11, 12)

Рассмотрим проекции сферы. Главный вид имеет форму окружности с размером диаметра, вид сверху имеет форму окружности с размером диаметра, вид слева имеет форму окружности с размером диаметра. Используя условный знак диаметра можно сократить количество изображений до одного с надписью сфера.

(Слайд 13)

Рассмотрим развертку сферы. Если сферу разрезать на одинаковые части и затем их склеить, то получится развертка сферы. В школьном курсе черчения мы не изучаем развертку сферы.

  1. Практическая работа. (18 мин)

Сейчас вам предстоит выполнить развертки различных геометрических тел. Вы разделены на 4 группы. В каждой группе к концу урока должно быть – куб, четырехугольная призма, треугольная призма, четырехугольная пирамида, цилиндр, конус. На ваших столах лежат схемы выполнения разверток и размеры геометрических тел. Приступайте к работе.

  1. Подведение итогов. (3 мин)

Что вам понравилось на сегодняшнем уроке?

Добились ли вы поставленных целей? Все ли успели выполнить работу?

  1. Домашнее задание.

§16.

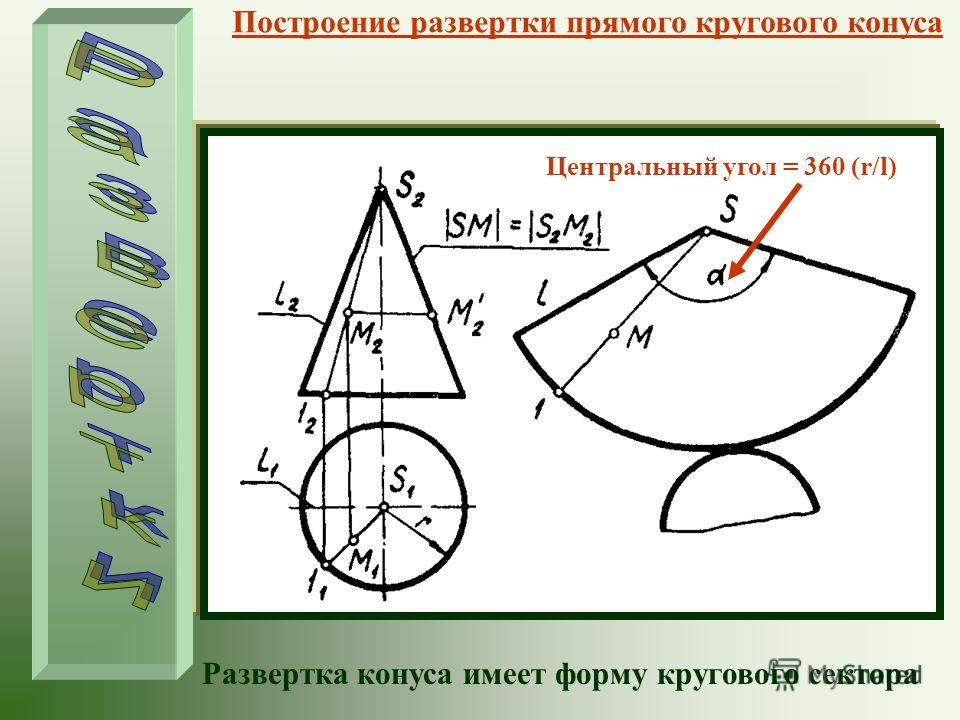
Построение разверток поверхностей геометрических тел

Разверткой поверхности многогранника называют плоскую фигуру, полученную в результате последовательного совмеще­ния с плоскостью чертежа всех граней многогранника.

Рассмотрим построение разверток неко­торых простейших тел.

Начнем с наиболее характерного объема — куба (рис. 4). У куба все ребра и грани равны, боковая поверхность состоит из четырех равных квад­ратов, основания куба — два квадрата, тождественные квадратам боковой поверхности. Построим на листе развертку боковой поверхно­сти и граней основания. Затем по металлической линейке делаем над­резы глубиной примерно на 1/3 листа ватмана или тонкого картона. Затем развертку вырезаем. Для того чтобы собрать полученную раз­вертку при достаточной плотности бумаги, грани можно склеить встык друг с другом.

Рис. 4

Рис. 5.

Построение разверток поверхностей призмы и цилиндра

Однако при недостаточном опыте в макетировании лучше исполь­зовать следующий прием. На развертке у каждой грани куба делают отвороты краев, т.е. откладывают от каждой стороны полоски шири­ной 3—5 мм. Затем делают с наружной стороны надрезы макетным ножом по металлической линейке по линиям сгиба ребер. После этого вырезают развертку вместе с отворотами, осторожно сги­бают по ребрам и надрезанным отворотам, аккуратно смазывают от­гибы клеем ПВА и прижимают их к противоположенным граням. При достаточной аккуратности выполнения и точности вычерчивания раз­вертки макет получится качественным.

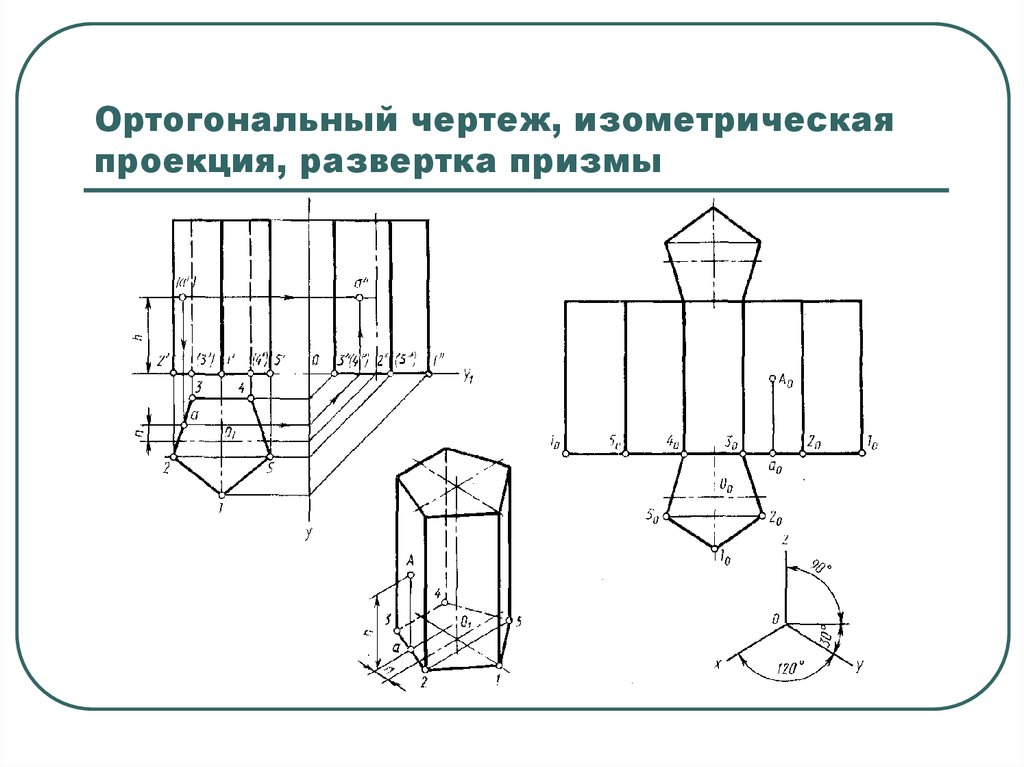
Развертка поверхности прямой призмы представляет собой плоскую фигуру, со­ставленную из боковых граней — прямо­угольников и двух равных между собой многоугольников оснований. Для примера взята правильная шестиугольная призма (рис. 5, а). Боковые грани призмы представляют собой равные между собой прямоугольники шириной

а и высотой Н, а основания — правильные шестиугольни­ки со стороной, равной а. Так как разме­ры граней известны, построение развертки нетрудно выполнить. Для этого на гори­зонтальной прямой последовательно от­кладывают шесть отрезков, равных сторо­не основания а шестиугольника, т. е. 5а. Из полученных точек восстанавливают перпен­дикуляры длиной, равной высоте при­змы Н. Соединяя полученные отрезки, проводят вторую горизонтальную прямую. Полученный прямоугольник (Н/6а) яв­ляется разверткой боковой поверхности призмы. Затем на одной оси пристраивают фигуру оснований — два шестиугольника со сторонами, равными а. Контур обводят сплошной основной линией, а линии сги­ба — штрихпунктирной тонкой с двумя точками.

С помощью подобного построения мож­но вычертить развертки прямых призм с любой фигурой в основании. Разница будет лишь в количестве и ширине граней боковой поверхности.

Аналогично строится и развертка повер­хности цилиндра (рис. 5, б). Только ши­рина ее равняется d (длине окружности основания).

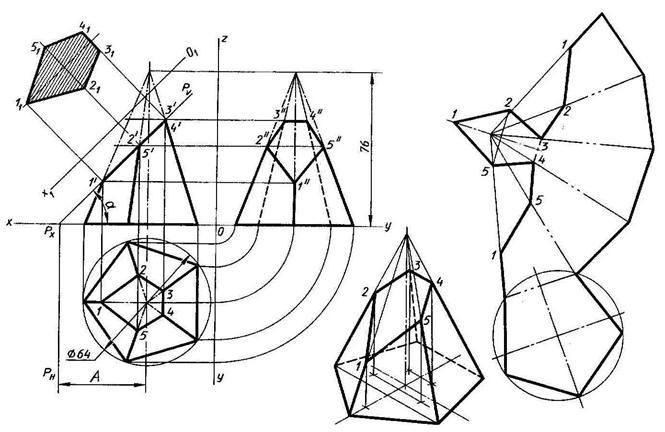
Развертка поверхности правильной пи­рамиды представляет собой плоскую фигу­ру, составленную из боковых граней — равнобедренных или равносторонних треу­гольников и правильного многоугольника основания. Для примера взята правильная четырехугольная пирамида (рис. 6, а). Решение задачи осложняется тем, что не­известна величина боковых граней пира­миды, так как их ребра не параллельны ни одной из плоскостей проекций. Поэтому начинают построение с определения вели­чины ребра SA способом вращения (см. рис. 6, в). Определив длину на­клонного ребра SA

, равную s‘a1, проводят из произвольной точки s, как из центра, дугу окружности радиусом s‘a1. По этой дуге откладывают четыре отрезка, равных стороне основания пирамиды, которое на чертеже спроецировалось в истинную ве­личину. Найденные точки соединяют пря­мыми с точкой s.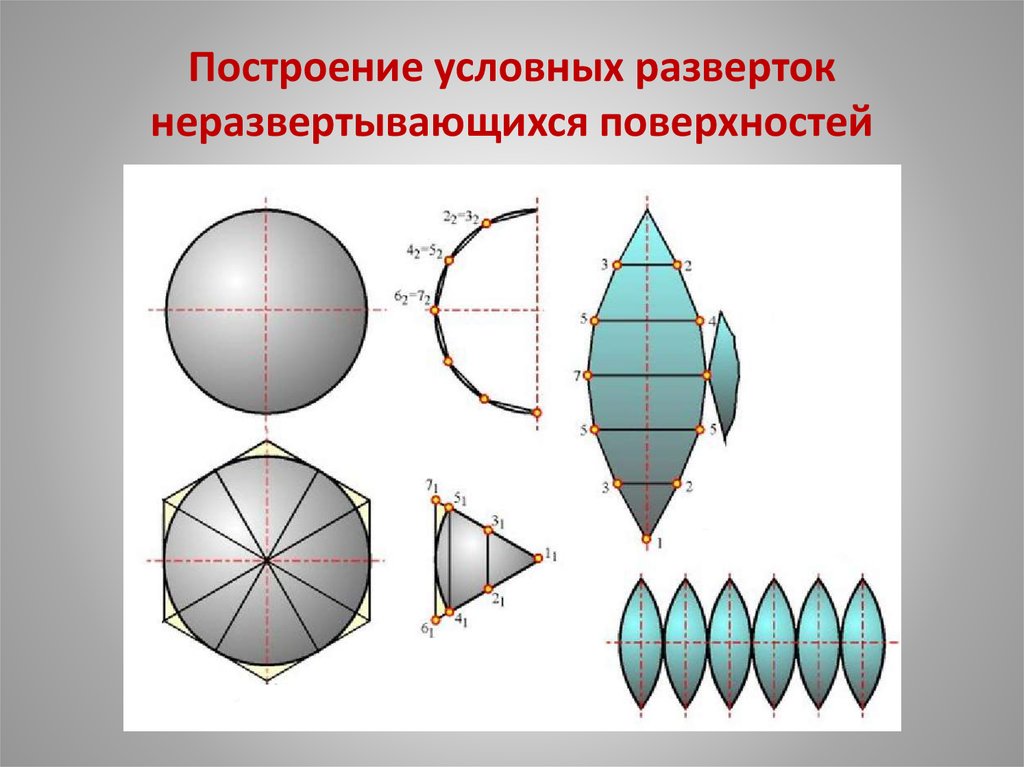 Получив, таким образом, развертку боковой поверхности, пристраи­вают к основанию одного из треугольников квадрат, равный основанию пирамиды.

Развертка поверхности прямого круго­вого конуса представляет собой плоскую фигуру, состоящую из кругового сектора и круга (рис. 6, б).

Построение выполняют следующим об­разом. Проводят осевую линию и из точки, взятой на ней, как из центра, очерчивают радиусом

R1, равным обра­зующей конуса s‘a‘, дугу окружности. Затем подсчитывают угол сектора по формуле  = 360°  R/L, где R — радиус окружности основания конуса; Lдлина образующей боковой поверхности конуса. В примере  = 360° 15/38 = 142,2°.

Этот угол строят симметрично относи­тельно осевой линии с вершиной в точке S. К полученному сектору пристраивают круг с центром на осевой линии и диа­метром, равным диаметру основания конуса.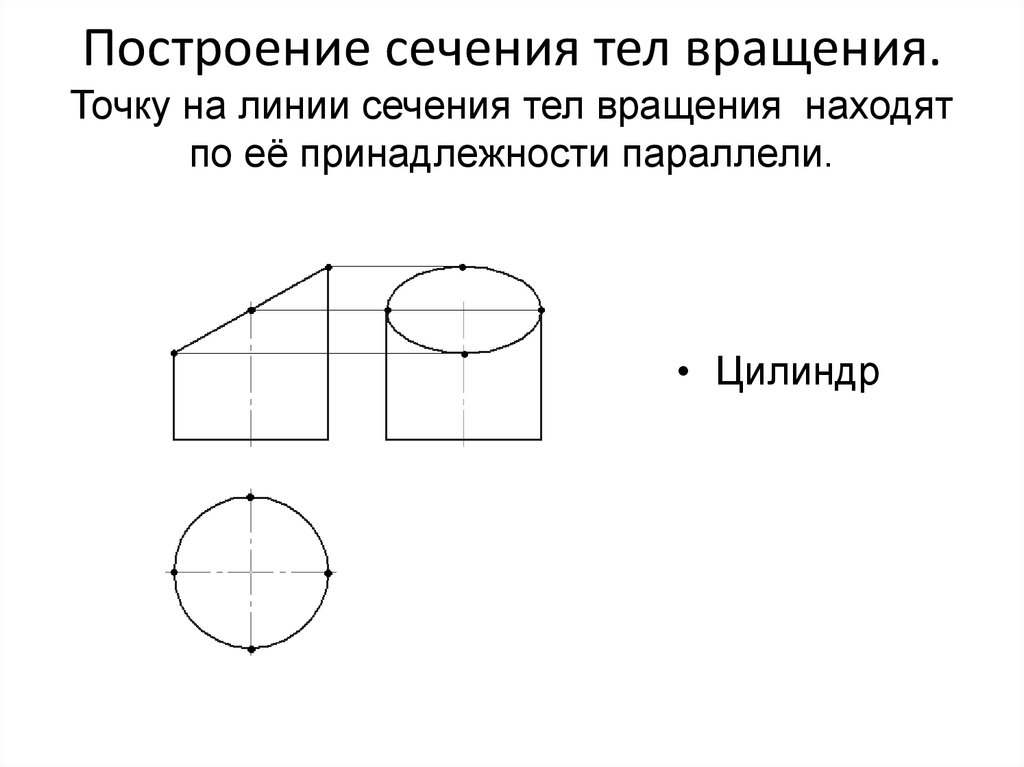

Рис. 6. Построение разверток поверхно­стей пирамиды и конуса

BUILD3D

BUILD3D — это революционный программный инструмент для построения готовых к трехмерному анализу геометрий.

Мощный дизайн, основанный на функциях, позволяет быстро создавать трехмерные геотехнические модели со сложной топографией или геологией, туннелями или реками и трехмерной геометрией из файлов САПР.

Бесшовная интеграция

BUILD3D включает возможность импорта поверхностных сеток непосредственно из геологической модели Leapfrog через подключение Central. Геометрию поверхности, созданную в программе САПР, также можно импортировать в виде сетки фоновой поверхности для упрощения создания геометрии. BUILD3D поддерживает импорт нескольких 2D-сечений из Leapfrog через Central или через исходные файлы САПР.

 

Дизайн на основе элементов

BUILD3D — это инструмент для создания геометрии на основе элементов, который позволяет изменять модель в любой момент истории проектирования.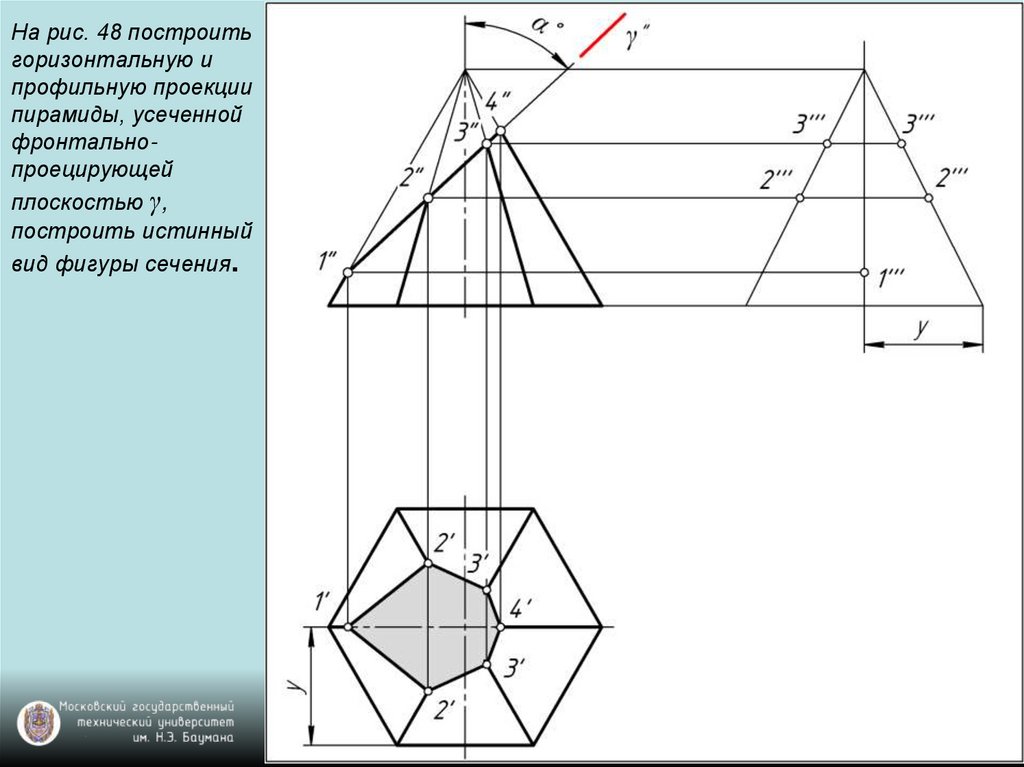 Изменения быстро и автоматически распространяются на всю геометрию модели, обеспечивая огромную экономию времени.

Мощные операции

В BUILD3D доступен набор мощных логических операций, включая пересечение, вырезание, слияние и впечатывание. Эти операции предоставляют необходимые инструменты для создания 3D-геометрии с нуля или изменения геометрии, импортированной из файлов STEP.

Генерация сетки

Генерация конечно-элементной сетки во всей трехмерной области одним нажатием кнопки. BUILD3D автоматически создает чистую сетку, избавляя от необходимости тратить часы на ручную настройку сетки и назначение материалов и граничных условий.

Плотины и дамбы

Импорт сложной топографии поверхности или стратиграфических границ из файлов САПР и использование импортированных поверхностей для создания областей. Импортируйте геометрию плотины или используйте инструменты плоскости и эскиза для создания плотины в BUILD3D. Используйте функцию «Сдвиг», чтобы сместить поперечное сечение дамбы вдоль естественного течения реки.

Дороги, мосты и насыпи

Используйте элементы плоскости и эскиза в BUILD3D для создания геометрии дорог и насыпей или импортируйте их из файлов САПР. Проведите дорогу и поперечное сечение насыпи по заданному пути.

Карьеры

Импорт поверхностей карьера и геологических формаций из файлов САПР. Используйте элементы выреза для удаления материала в карьере и настройте несколько анализов для моделирования выемки котлована. Эти анализы могут быть использованы для оценки просачивания и стабильности подземных вод с течением времени.

Подземные раскопки

Используйте инструмент Sweep для создания тела, представляющего собой туннель, прорезающий участки почвы или породы. Используйте операции вырезания для удаления материала из туннеля. Включите несколько геометрий в один файл проекта, представляющий строительство туннеля с течением времени.

  • Создание геометрии на основе элементов обеспечивает значительную экономию времени
  • Геометрия на основе NURBS для большей гибкости и точности
  • Импорт расчетов 2D GeoStudio с материалами и граничными условиями
  • Импорт тел (SETP/STP, IGES), профилей (STP, IGES) или фоновой сетки (STL, DWG/DXF)
  • Интуитивно понятные инструменты эскиза, включая эскиз, плоскость, развертку, выдавливание
  • Простые логические операции: пересечение, вырезание, слияние и отпечаток
  • Материалы, граничные условия, применяемые к геометрическим объектам
  • Генерация чистой сетки с тетраэдрической или шестигранной сеткой
  • Подставка для больших моделей
  • Мощная визуализация результатов, включая контуры и изоповерхности
  • Экспорт сетки поверхности, тела или результатов из выбранных узлов или поверхностей

Как создавать развертки с открытыми траекториями в Creo

Написано: Аарон Шоу

  • 22. 12.2016

Создание элемента постоянного поперечного сечения, который следует открытой траектории, с помощью функции сдвига в Creo Parametric

Наряду с вытягиванием, смешиванием, вращением и т. д. смещение является одной из основных возможностей надежного приложения 3D CAD, такого как Creo Parametric . При создании сдвига вы можете создать твердотельный элемент или элемент поверхности. Добавляйте или удаляйте материал при протягивании секции по одной или нескольким выбранным траекториям, управляя ориентацией, вращением и геометрией секции.

 

 

Вверху: элемент, созданный путем сдвига Т-образного профиля вдоль пути траектории. Внизу: материал был удален путем протягивания кругового профиля по слегка измененной траектории, создав канал.

Траектория — это путь, по которому пронесется ваш участок. Траектория должна быть выбранным эскизом, кривой или кромкой. Траектория развертки не может быть создана с помощью внутреннего эскиза.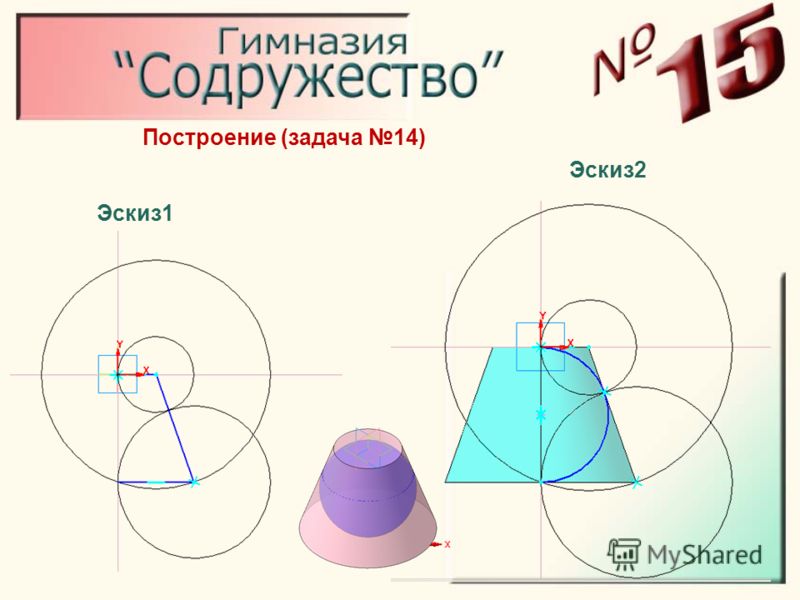

Вот как создать развертку:

  1. В ленточном меню модели откройте инструмент Sweep
    .
  2. Выберите траекторию.
  3. Нарисуйте секцию для развертки или выберите предварительно определенную секцию из палитры Sketcher . Напоминание: сечение — это форма профиля, которая будет перемещаться по траектории. На изображении выше сечение имеет Т-образную форму.
  4. Если вы выбрали предустановленное сечение, отредактируйте размеры и опорную точку.
  5. Перетащите контрольную точку в центр траектории.
  6. Предварительный просмотр геометрии и завершение элемента.

Оттуда вы можете добавлять скругления и дуги, а также скруглять окружности, прямоугольники и т. д. Посмотрите это видео Learning Exchange, чтобы узнать больше.

Не отставайте от Creo!

Подписавшись на PTC Express, наш электронный информационный бюллетень для всех, кто интересуется 3D САПР и проектированием, вы можете получить гораздо больше советов и идей, а также новости PTC Creo, истории клиентов и советы экспертов.

PTC Express бесплатен и ежемесячно приходит прямо в ваш почтовый ящик.

[ Ред. Эта Эта статья была опубликована ранее. Некоторый контент был обновлен. ]

Теги:

  • Канадский доллар
  • Розничная торговля и потребительские товары
  • Подключенные устройства

об авторе

Аарон Шоу

Аарон Шоу присоединился к PTC в 2013 году, в настоящее время он является старшим менеджером по формированию спроса на САПР. Он отвечает за маркетинговую стратегию САПР и ее реализацию по всему миру. Ему нравится играть в гольф, есть острую пищу, читать, путешествовать и болеть за все бостонские команды. Аарон — выпускник Университета штата Пенсильвания, вы можете следить за ним в Твиттере @AaronEShaw.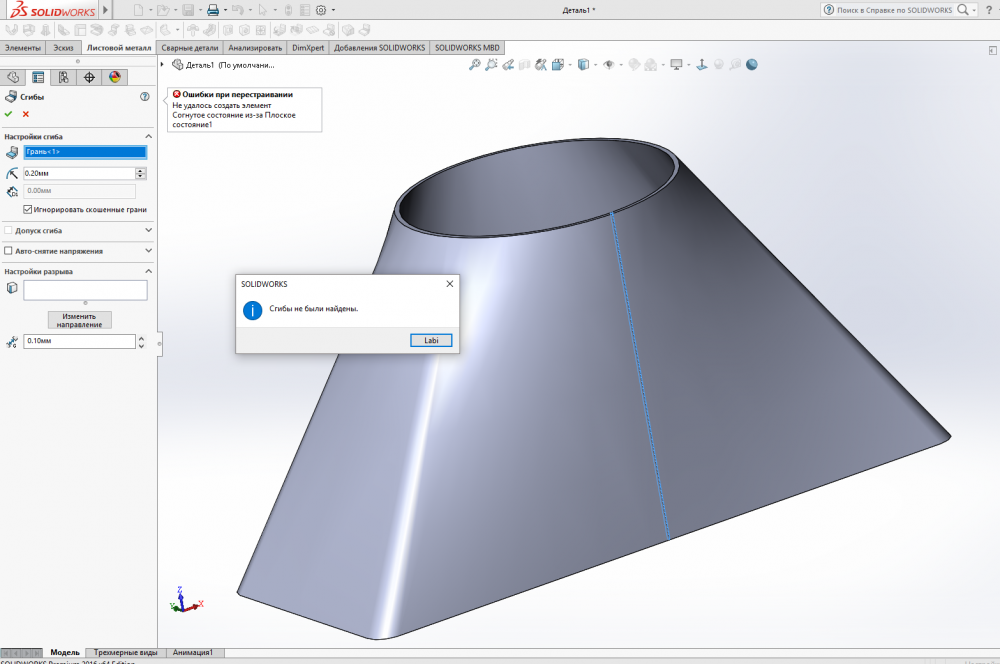


Вас также может заинтересовать:

Крео

6 новых технологий САПР (и когда их использовать)

Узнайте о 6 новых технологиях САПР и их влиянии на разработку продуктов…

САПР Подключенные устройства

Крео, Виндчилл

Прорыв в технологии Fusion Ignition: разработка идеального источника экологически чистой энергии…

Генеральный директор PTC Джим Хеппельманн пишет о важности National Igniti…

САПР PLM

Крео

Возрастающая роль искусственного интеллекта в инженерии: часть 2

Изучите реальный пример того, как искусственный интеллект (ИИ) в.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *