Прогрессия геометрическая график: Геометрическая прогрессия | ЮКлэва

9 класс. Алгебра. Геометрическая прогрессия. — Геометрическая прогрессия.

Комментарии преподавателя

Посмотрев этот видеоурок, пользователи смогут получить представление о теме «Определение и свойства геометрической прогрессии, формула n-го члена». В ходе занятия учитель познакомит с понятием геометрической прогрессии, расскажет о ее свойствах. Кроме того, на уроке будет дана формула n-го члена и будет показано, как правильно применять ее на практике.

 

 

 

Тема: Гео­мет­ри­че­ская про­грес­сия

Урок: Опре­де­ле­ние и свой­ства гео­мет­ри­че­ской про­грес­сии, фор­му­ла n–го члена

На уроке да­ет­ся опре­де­ле­ние гео­мет­ри­че­ской про­грес­сии, вы­во­дит­ся фор­му­ла об­ще­го члена, ре­ша­ют­ся ти­по­вые за­да­чи.

Чис­ло­вую по­сле­до­ва­тель­ность, все члены ко­то­рой от­лич­ны от нуля и каж­дый член ко­то­рой, на­чи­ная со вто­ро­го, по­лу­ча­ет­ся из преды­ду­ще­го члена умно­же­ни­ем его на одно и то же число q, на­зы­ва­ют гео­мет­ри­че­ской про­грес­си­ей.

При этом число q на­зы­ва­ют зна­ме­на­те­лем про­грес­сии.

Ма­те­ма­ти­че­ская за­пись.

гео­мет­ри­че­ская про­грес­сия, ее члены , при этом:

Иная за­пись:, т.е. .

Рас­смот­рим при­ме­ры гео­мет­ри­че­ских про­грес­сий:

 здесь каж­дый сле­ду­ю­щий член по­лу­ча­ет­ся из преды­ду­ще­го умно­же­ни­ем на 2; по­лу­чен­ная по­сле­до­ва­тель­ность при этом воз­рас­та­ет (

2.  здесь каж­дый сле­ду­ю­щий член по­лу­ча­ет­ся из преды­ду­ще­го умно­же­ни­ем на ; по­лу­чен­ная по­сле­до­ва­тель­ность при этом убы­ва­ет (

Те­перь вы­ве­дем фор­му­лу n–го члена гео­мет­ри­че­ской про­грес­сии.

Рас­смот­рим гео­мет­ри­че­скую про­грес­сию , при этом

.

Тогда,

. . . . . . . . . . .

n=1,2,3,…

До­ка­жем по­лу­чен­ную фор­му­лу ме­то­дом пол­ной ма­те­ма­ти­че­ской ин­дук­ции.

Дано:гео­мет­ри­че­ская про­грес­сия,

.

До­ка­зать:.

До­ка­за­тель­ство.

1. Про­ве­рим спра­вед­ли­вость фор­му­лы дляn =1: 

2. Пред­по­ло­жим, что фор­му­ла спра­вед­ли­ва для n=k: 

3. До­ка­жем, что из спра­вед­ли­во­сти фор­му­лы для n=k сле­ду­ет спра­вед­ли­вость фор­му­лы для n=k+1: 

Вывод:  фор­му­ла верна для всех 

Рас­смот­рим гео­мет­ри­че­скую про­грес­сию как функ­цию на­ту­раль­но­го ар­гу­мен­та и по­стро­им ее гра­фик.

Обо­зна­чим, тогда 

,  это по­ка­за­тель­ная функ­ция на­ту­раль­но­го ар­гу­мен­та.

Рас­смот­рим при­ме­ры.

1.  

.

Пе­рей­дя к функ­ции, имеем

Со­ста­вим таб­ли­цу зна­че­ний функ­ции.

n	1	2	3	4
	1	2	4	8

И по­стро­им ее гра­фик.

Рис. 1.

, по­это­му гра­фик – это толь­ко от­дель­ные точки, ко­то­рые лежат на по­ка­за­тель­ной кри­вой.

2.  ;

.

Пе­рей­дя к функ­ции, имеем

Со­ста­вим таб­ли­цу зна­че­ний функ­ции.

n	1	2	3	4
	1

И по­стро­им ее гра­фик.

Рис. 2

Снова гра­фик – это от­дель­ные точки, ле­жа­щие на по­ка­за­тель­ной кри­вой.

Из гра­фи­ков видно, что если гео­мет­ри­че­ская про­грес­сия воз­рас­та­ет, то воз­рас­та­ет очень быст­ро, а если убы­ва­ет, то убы­ва­ет тоже быст­ро (как по­ка­за­тель­ная функ­ция).

Далее рас­смот­рим ти­по­вые за­да­чи, для ре­ше­ния ко­то­рых по­на­до­бит­ся фор­му­ла об­ще­го члена гео­мет­ри­че­ской про­грес­сии:

1. Дано:гео­мет­ри­че­ская про­грес­сия, . Найти: . Ре­ше­ние:  Ответ: 

2. Дано:гео­мет­ри­че­ская про­грес­сия,. Про­ве­рить, яв­ля­ет­ся ли число 1536 чле­ном этой про­грес­сии, если да, найти его номер. Ре­ше­ние:  Ответ: 

3. Дано:гео­мет­ри­че­ская про­грес­сия, .  Найти:  Ре­ше­ние:  Ответ: 

4. Дано:гео­мет­ри­че­ская про­грес­сия, .   Найти:  Ре­ше­ние:  Ответ: 

Если из­вест­ны два члена гео­мет­ри­че­ской про­грес­сии то спра­вед­ли­ва фор­му­ла:

.

Дей­стви­тель­но,  Рас­смот­рим еще одну за­да­чу.

5. Дано:гео­мет­ри­че­ская про­грес­сия, .  Найти:  Ре­ше­ние:  Ответ: 

н­та.

Вы­ве­дем далее фор­му­лу суммы ко­неч­но­го числа чле­нов гео­мет­ри­че­ской про­грес­сии.

Дано: гео­мет­ри­че­ская про­грес­сия.

Найти:

Ре­ше­ние:.

Умно­жим обе части этого ра­вен­ства на q:

.

И вы­чтем из пер­во­го ра­вен­ства вто­рое:

,

 ,

.

В по­лу­чен­ной фор­му­ле , рас­смот­рим част­ный слу­чай

Гео­мет­ри­че­ская про­грес­сия  имеет nрав­ных чле­нов, по­это­му ее сумма

Итак, , при ;   при .

Далее рас­смот­рим  ти­по­вые за­да­чи, для ре­ше­ния ко­то­рых по­на­до­бит­ся фор­му­ла суммы чле­нов гео­мет­ри­че­ской про­грес­сии:

1. Дано:гео­мет­ри­че­ская про­грес­сия, . Найти:  Ре­ше­ние: . Ответ: 

2. Дано:гео­мет­ри­че­ская про­грес­сия, .

Найти: . Ре­ше­ние:  Ответ: 

3.  «Ле­ген­да об изоб­ре­та­те­ле шах­мат». Дано:гео­мет­ри­че­ская про­грес­сия,  .  Найти:  Ре­ше­ние:  Ответ:  А те­перь ле­ген­да. Во­сточ­ный пра­ви­тель за­хо­тел на­гра­дить муд­ре­ца за то, что он на­учил пра­ви­те­ля иг­рать в шах­ма­ты. Муд­рец по­про­сил на первую клет­ку шах­мат­ной доски по­ло­жить одно зер­ныш­ко пше­ни­цы, а на каж­дую сле­ду­ю­щую в 2 раза боль­ше зерен, чем на преды­ду­щую. Шах­мат­ная доска имеет 64 клет­ки, по­это­му общее ко­ли­че­ство зерен на доске – это сумма 64 чле­нов гео­мет­ри­че­ской про­грес­сии, у ко­то­рой . Мы толь­ко что нашли, что Ока­за­лось, что это число на­столь­ко огром­но, что у пра­ви­те­ля не на­шлось столь­ко пше­ни­цы. Воз­рас­та­ю­щая гео­мет­ри­че­ская про­грес­сия воз­рас­та­ет очень быст­ро и сумма даже не очень боль­шо­го числа чле­нов – огром­ное число.

1. Дано:гео­мет­ри­че­ская про­грес­сия,  .  Найти:  Ре­ше­ние:  Ответ: 

2. Най­ди­те сумму Ре­ше­ние:Дан­ная сумма яв­ля­ет­ся сум­мой гео­мет­ри­че­ской про­грес­сии, дей­стви­тель­но, ,от­но­ше­ние не за­ви­сит от n, т. е. это гео­мет­ри­че­ская про­грес­сия. В этой про­грес­сии , тогда . Ответ:.

3. До­ка­жи­те тож­де­ство До­ка­за­тель­ство: Притож­де­ство спра­вед­ли­во. При имеем гео­мет­ри­че­скую про­грес­сию  (). В преды­ду­щей за­да­че мы вы­чис­ли­ли , тогда Тож­де­ство до­ка­за­но.

Источник конспекта: http://interneturok.ru/ru/school/algebra/9-klass/progressii/opredelenie-i-svoystva-geometricheskoy-progressii-formula-n-go-chlena?konspekt&chapter_id=38

 

Источник видео: http://www.youtube.com/watch?v=vl47O6_MPtY

Урок алгебры по теме «Геометрическая прогрессия». 9-й класс

Цели урока:

• образовательная – воспроизведение и коррекция опорных знаний по теме; формирование навыков решения экзаменационных задач на геометрическую прогрессию;
• развивающая — развитие логического мышления, навыков самоконтроля в подготовке к ГИА;
• воспитательная – воспитание культуры умственного труда, познавательного интереса к предмету; коммуникативности.

Тип урока: урок обобщения и систематизации знаний.

Оборудование: комплекты для устного счета, раздаточный дидактический материал – тесты, сборники экзаменационных заданий, компьютер, видеопроектор, листки самоконтроля.

Структура урока:

№	Этап урока	Вид работы	Содержание (цель) этапа	Время (мин)
I	Оргмомент.	Фронтально.	Постановка цели урока. Знакомство с планом работы на уроке.	1
II	Устный счет.	Фронтально, в парах.	Отработка устных вычислительных навыков.	3
III	Диктант по формулам.	Взаимопроверка.	Проверка и коррекция знаний формул геометрической прогрессии.	5
IV	Работа с тестом.	Работа в парах. Самопроверка.	Формирование умений применять формулы для установления истинности или ложности утверждений. Развитие навыков самоконтроля.	7
V	Решение задач из сборника экзаменационных заданий.	Работа в группах. Проверка и коррекция решения через видеопроектор.	Совершенствование навыков решения задач на геометрическую прогрессию. Воспитание коммуникативности.	15
VI	Решение познавательных задач.	Построение графика.	Развитие навыков применения знаний по теме для решения познавательных задач.	6
VII	Задание на дом.	Запись в дневниках, чтение задания по учебнику.	Комментирование содержания домашнего задания.	1
VIII	Итог урока.	Проверка листов самоконтроля.	Обобщение полученных результатов работы через листы самоконтроля. Предварительное выявление проблем.	2

Ход урока

I. Оргмомент.

Объявить тему урока, дидактическую цель, сообщить план работы.

II. Устный счет.

Раздаточный материал для устного счета находится на столах учащихся. Каждый сидящий на 1 варианте отвечает по одному примеру, сосед по парте проверяет ответ.

Задания для устного счета.

Вычислите:

1) 5³; 2) 2⁴; 3) (-2)⁷; 4) (0,2)²; 5) (-0,2)³; 6) (-1)²; 7) (-1)⁵; 8) (-0,3)²; 9) 1,3²; 10) 16⁰;

16) 2¹⁰ : 2⁸; 17) 3² : 3; 18) 3^{2n + 2} : 3²ⁿ; 19) 2⁴ * 2³; 20) 0,5 * 2³.

III. Диктант по формулам.

Класс пишет под диктовку учителя, один учащийся работает на обороте доски. Затем ответы открываются, учащиеся за партой меняются тетрадями, и проводится взаимопроверка.

Задание 1. Запишите рекуррентную формулу n-го члена геометрической прогрессии и выразите из нее знаменатель прогрессии.

Задание 2. Запишите формулу n-го члена геометрической прогрессии.

Задание 3. Запишите формулу суммы n первых членов геометрической прогрессии.

Задание 4. Запишите формулу суммы бесконечно убывающей геометрической прогрессии.

Задание 5. Запишите характеристическое свойство геометрической прогрессии.

Ответы:

Дополнительный вопрос: Дать определение геометрической прогрессии и привести пример.

Выставление оценок в листы самоконтроля по количеству верных ответов по 5-бальной шкале.

IV. Работа с тестом.

Тест “Установите, истинны или ложны следующие утверждения”:

Задание 1. Последовательность, заданная формулой b_n = 3²ⁿ, — геометрическая прогрессия.

Решение:

Ответ: да.

Задание 2. Третий член геометрической прогрессии, у которой равен -18.

Решение:

Ответ: нет.

Задание 3. Сумма семи первых членов геометрической прогрессии, у которой b₁ = 3, q_{= 2, равна 384.}

Решение:

Ответ: нет.

Задание 4. Геометрическая прогрессия, заданная формулой , является бесконечно убывающей.

Решение:

Ответ: нет.

Задание 5. Сумма бесконечно убывающей геометрической прогрессии равна , если

Решение:

Ответ: да.

Проверка через видеопроектор и выставление оценок в листы самоконтроля по количеству верных ответов по 5-бальной шкале.

V. Решение задач из сборника экзаменационных заданий ГИА.

Задача 1. Сумма первых трех членов геометрической прогрессии равна 9, а сумма следующих трех ее членов равна -72. Найдите восьмой член этой прогрессии.

Решение:

Ответ: -384.

Задача 2. Существует ли геометрическая прогрессия, в которой

Решение:

Ответ: да.

Задача 3. Является ли число 64 членом геометрической прогрессии 0,5; 1; …?

Решение:

Ответ: да.

Задача 4. Найдите сумму бесконечно убывающей геометрической прогрессии b_n, если b₂ —_{b4 = 3 и b1 — b3 = 6.}

Решение:

Ответ: 16.

Задача 5. При каком целом значении х последовательность х, х + 2, 5х – 2 является геометрической прогрессией?

Решение:

Согласно характеристическому свойству геометрической прогрессии имеем: (х + 2)² = х(5х – 2).

Откуда х = — 0,5 – число не целое и х = 2 – число целое.

Ответ: 2.

Выставление оценок в листы самоконтроля по количеству верных ответов по 5-балльной шкале.

VI. Решение познавательных задач.

Задача 1. Один биолог “открыл” удивительную разновидность амеб. Каждая из них через минуту делится на две. В пробирку биолог кладет одну амебу, и ровно через час вся пробирка оказывается заполненной амебами. Сколько потребовалось бы времени, чтобы вся пробирка заполнилась амебами, если бы в нее положили вначале не одну, а две?

Решение:

Запишем две геометрические прогрессии одна под другой:

1; 2; 4; 8; 16; 32; … и

2; 4; 8; 16; 32;…

Тогда очевидно, что задача решается с конца. Минуту назад колба с одной амебой была заполнена наполовину. Следовательно, нужно 59 минут, чтобы вся пробирка заполнилась амебами, если бы в нее положили вначале не одну, а две.

Ответ: 59 минут.

Задача 2. Построить график геометрической прогрессии 1; 2; 4; 8; 16;… .

Решение:

b₁ = 1; q = 2; b_n = b₁* q^{n – 1} = (b₁ : q) * qⁿ = 0,5 * qⁿ .

Заполним таблицу и нанесем точки на систему координат.

n	1	2	3	4	5
bn= 0,5 * 2n	1	2	4	8	16

Получаем точечный график. Точки графика лежат на кривой, которую в 10-м классе при изучении показательной функции назовем экспонентой.

VII. Задание на дом.

Задачи из учебника и сборника ГИА по теме “Геометрическая прогрессия”.

VIII. Итог урока.

Учащиеся оценивают свою работу как среднее арифметическое трех оценок, выставленных в листках самоконтроля.

Называются самые трудные задания, которые вызвали затруднения для дальнейшей коррекции на следующем уроке.

Примечание. Учащиеся обучаются по учебнику для общеобразовательных учреждений: Алгебра. 9 класс: учеб. для общеобразоват. учреждений / [Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова]; под ред. С.А. Теляковского. – 18-е изд. — М.: Просвещение, 2011.

Математические визуализации | Геометрическая последовательность

Геометрические последовательности или геометрические прогрессии
Геометрия Реальный анализ Комплексный анализ Вероятность История Помощь Контакт Ссылки Карта сайта Обновления Испания	Последовательность — это упорядоченный список чисел. Некоторые последовательности следуют шаблону. Каждое число в последовательности называется срок . Если мы рассматриваем последовательность как функцию, ее областью определения являются натуральные числа. Геометрическая последовательность (или геометрическая прогрессия) — это последовательность чисел, в которой каждый член после первого задается путем умножения предыдущий на фиксированное ненулевое число, константу, называемую обыкновенным отношением . Любой член геометрической прогрессии можно выразить формулой для общего члена: При соотношении r больше 1 имеем возрастающую последовательность (экспоненциальный рост). Даже если отношение очень мало, последовательность начинает медленно увеличиваться, но после достаточного количества шагов рост становится все больше и больше. Например, это это результат после 300 шагов, если соотношение равно 1,01: Если отношение r положительно и меньше 1, то последовательность убывающая и общий член стремится к 0. Когда отношение r отрицательно, последовательность чередуется. Если отношение r находится в диапазоне от -1 до 0, переменная последовательность имеет общий член, стремящийся к 0. Если отношение r меньше -1, переменная последовательность по модулю стремится к бесконечности (без знака, если рассматривать значение из-за переменного знака). Мы можем рассмотреть сумму n членов геометрической прогрессии. Мы можем вывести формулу: В следующем приложении мы можем поиграть с разными случаями с положительным знаменателем: Вы можете увидеть поведение, если общее отношение больше 1 (сумма растет и растет): Если общее отношение меньше 1, сумма приближается к числу: Серия — это сумма бесконечных членов последовательности. Если положительное r меньше 1, вы можете суммировать эти бесконечные числа, и результатом будет число. Можно сказать, что ряд сходится (оно приближается к некоторому пределу). Если положительный r больше или равно 1, то ряд не приближается к некоторому числу, потому что он становится все больше и больше. Тогда можно сказать, что ряд расходится. В следующем приложении мы можем поиграть с общим случаем. Теперь общий рацион может быть положительным или отрицательным: Расходящийся чередующийся ряд: Сходящийся альтернативный ряд: Условие сходимости геометрического ряда с ненулевым знаменателем r : И формула такова: БОЛЬШЕ ССЫЛОК

Создание геометрической последовательности

Последнее обновление 1 неделю назад

Мне часто приходится генерировать геометрическую последовательность, поэтому я создал эту простую онлайн-утилиту, которая делает это за меня. Он позволяет вам генерировать столько чисел геометрического ряда, сколько вам нужно в любой базе. Он работает в браузере и основан на инопланетных технологиях из будущего.

Параметры генератора геометрической прогрессии

Примеры генератора геометрической прогрессии (нажмите, чтобы попробовать!)

Геометрическая последовательность кубов

В этом примере мы начинаем геометрическую последовательность с 1 и вычисляем 50 ее элементов. Общий коэффициент для этого ряда установлен равным 3, а это значит, что каждое последующее значение в ряду утраивается и мы получаем список кубов.

 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683, 59049, 177147, 531441, 1594323, 4782969, 14348907, 43046721, 129140163, 387420489, 1162261467, 3486784401, 10460353203, 31381059609, 94143178827, 282429536481, 847288609443, 2541865828329, 7625597484987, 22876792454961, 68630377364883, 205891132094649, 617673396283947, 1853020188851841, 5559060566555523, 16677181699666569, 50031545098999707, 150094635296999121, 450283905890997363, 1350851717672992089, 4052555153018976267, 12157665459056928801, 36472996377170786403, 109418989131512359209, 328256967394537077627, 9847703611232881, 295431873065058643, 8862938119652501095929, 26588814358957503287787, 79766443076872509863361, 2392993292306175295
 

Десятичная база

Рациональное обыкновенное отношение

В этом примере мы используем дробное обыкновенное отношение -0,2 для геометрической прогрессии. Поскольку отношение отрицательное и меньше единицы, мы получаем чередующуюся (меняющую знак с минуса на плюс) и затухающую геометрическую прогрессию.

 -1
0,2
-0,04
0,008
-0,0016
0,00032
-0,000064
0,0000128
-0,00000256
0,000000512 

Десятичная база

Шестнадцатеричная геометрическая последовательность

В этом примере мы создаем забавную геометрическую последовательность в шестнадцатеричной системе счисления.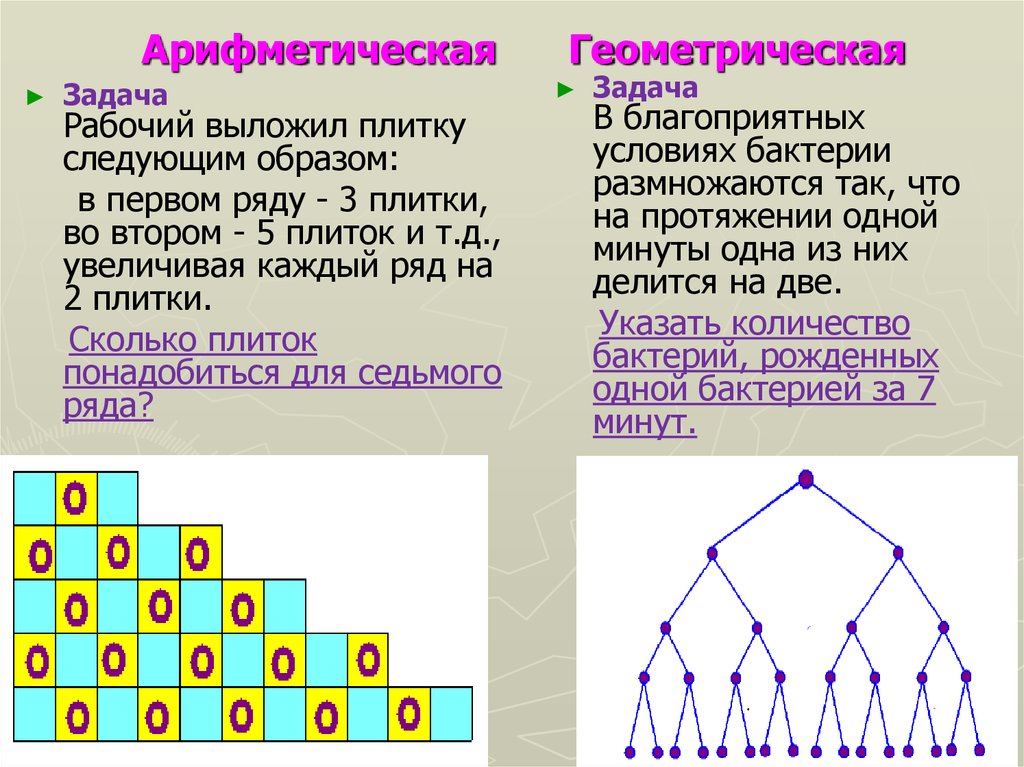 Мы начинаем с 10 (что равно «а» по основанию 16) и вычисляем первые 20 членов последовательности. Поскольку отношение установлено равным -1, абсолютное значение членов остается неизменным, однако каждый раз меняется знак.

 а; -а; а; -а; а; -а; а; -а; а; -а; а; -а; а; -а; а; -а; а; -а; а; -а 

Шестнадцатеричная база

Как работает этот генератор геометрической прогрессии?

Этот генератор геометрических рядов полностью работает в вашем браузере и написан на JavaScript. Чтобы выполнить работу, он использует один массив и цикл для . Во-первых, он инициализирует массив начальным значением , которое указано в опциях. Затем он создает цикл для с условием остановки, когда массив достигает числа элементов (длина серии; указывается в параметрах). В цикле он отслеживает последний элемент массива , умножает его на коэффициент (общий коэффициент; указывается в параметрах) и добавляет новый член в конец массива с помощью функции array.push() . Для работы с большими числами используется библиотека bignumber.js , а все операции умножения выполняются функцией bignumber times() . Когда цикл заканчивается, он array.map() s функция bignumber toString(base) для преобразования членов ряда в база (указывается в опциях). После этого он array.