Произведение матриц онлайн: Онлайн калькулятор. Умножение матриц.

Умножить матрицу на вектор онлайн

Результат умножения вектора-строки на матрицу с*A

Результат умножения матрицы на вектор-столбец A*b

Каждый вектор можно рассматривать как одностолбцовую или однострочную матрицу. Одностолбцовую матрицу будем называть вектор-столбцом, а однострочную матрицу — вектор-строкой.

Если A-матрица размера m*n, то вектор столбец b имеет размер n, а вектор строка b имеет размер m.

Таким образом, что бы умножить матрицу на вектор, надо рассматривать вектор как вектор-столбец. При умножении вектора на матрицу, его нужно рассматривать как вектор -строку.

Пример.

Умножить матрицу

\(\begin{pmatrix} 1+2i & 2+i & 1+3i \\ 2 & 4+2i & 2+5i \end{pmatrix}\)

на комплексный вектор

\(\begin{pmatrix} 2+2i  \\ 1+4i \\ 2+2i \end{pmatrix}\)

Получаем результат

Результат умножения матрицы на вектор A*b

Результат умножения вектора на матрицу b*A

 

Как видите при неизменной размерности вектора, у нас могут существовать два решения.

Хотелось бы обратить Ваше внимание на то что матрица в первом и втором варианте, несмотря на одинаковые значения, совершенно разные (имеют различную размерность)

 

В первом случае вектор считается как столбец и тогда необходимо  умножать матрицу на вектор, а во втором случае у нас вектор-строка и тогда у нас произведение вектора на матрицу.

 

 

Свойства умножения матрицы на вектор

 — матрица   — вектор столбец   — вектор-строка  — произвольное число

1. Произведение матрицы на сумму векторов-столбцов равна сумме произведений матрицы на каждый из векторов

2. Произведение суммы векторов-строк на матрицу  равна сумме произведений векторов на матрицу

3. Общий множитель вектора  можно вынести за пределы произведения матрицы на вектор/вектора на матрицу

4.Произведение вектора-строки на произведение матрицы и вектора столбца, равноценно произведению произведения вектора-строки на матрицу и вектора-столбца.

 

Удачных расчетов!!

 

Умножение матриц

Расчет умножения матриц онлайн. Умножьте матрицы порядка 2×3, 1×3, 3×3, 2×2 с 3×2, 3×1, 3×3, 2×2. Динамические расчеты, нахождения произведения матриц.

Умножение матриц возможно когда число столбцов первой матрицы равно числу строк второй матрицы.

Матрица 1

X

Матрица 2

3x33x22x33x11x32x2

X

3x33x22x33x11x32x2

В первой части мы рассмотрим умножение квадратных матриц. В следующей части Вы узнаете, как умножить разные матрицы (например, 2х3 до 3х3).

Здесь мы будем умножать матрицу 3х3 (3 ряда, 3 колонки) на другую матрицу 3х3 (3 ряда, 3 колонки).

Матрица A		Матрица B
a11 a12 a13 a21 a22 a23 a31 a32 a33	x	b11 b12 b13 b21 b22 b23 b31 b32 b33

В результате мы получим матрицу 3х3. Нам придется рассчитать каждую клетку результатов матрицы отдельно. Результат выразим через X.

Шаг 1:Рассчитаем x11
Для того, чтобы вычислить результат  x11 мы будем использовать первую строку матрицы А и первый столбец матрицы В.

Результат X		Матрица A		Матрица B
x11 x12 x13 x21 x22 x23 x31 x32 x33	=	a11 a12 a13 a21 a22 a23 a31 a32 a33	x	b11 b12 b13 b21 b22 b23 b31 b32 b33

Мы можем представить результат  x11 = a11 x b11 + a12 x b21 + a13 x b31

Шаг 2: Рассчитаем x12
Для того, чтобы вычислить результат x12 мы будем использовать первую строку матрицы А и втором столбце матрицы В.

Результат X		Матрица A		Матрица B
x11 x12 x13 x21 x22 x23 x31 x32 x33	=	a11 a12 a13 a21 a22 a23 a31 a32 a33	x	b11 b12 b13 b21 b22 b23 b31 b32 b33

Мы можем представить резальтат x12 = a11 x b12 + a12 x b22 + a13 x b32

По той же методике мы вычислим значения для всех ячеек.

Результат Матрица

a11xb11 + a12xb21 + a13xb31 a11xb12 + a12xb22 + a13xb32 a11xb13 + a12xb23 + a13xb33 a21xb11 + a22xb21 + a23xb31 a21xb12 + a22xb22 + a23xb32 a21xb13 + a22xb23 + a23xb33 a31xb11 + a32xb21 + a33xb31 a31xb12 + a32xb22 + a33xb32 a31xb13 + a32xb23 + a33xb33

вектор умножить на матрицу онлайн

Вы искали вектор умножить на матрицу онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить произведение матриц, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вектор умножить на матрицу онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вектор умножить на матрицу онлайн,вычислить произведение матриц,вычислить произведение матриц онлайн с решением,дробь умножить на матрицу онлайн,как дробь умножить на матрицу,как умножить матрицу на матрицу 3х3,как умножить обратную матрицу на матрицу,калькулятор матриц онлайн с решением умножение,калькулятор матриц онлайн умножение матриц,калькулятор матриц перемножение,калькулятор матриц произведение,калькулятор матриц умножение,калькулятор матриц умножение матриц онлайн,калькулятор матрицы онлайн умножение,калькулятор матрицы умножение,калькулятор матрицы умножение онлайн,калькулятор онлайн матрицы умножение,калькулятор онлайн умножение матрицы,калькулятор перемножения матриц,калькулятор произведение матриц,калькулятор произведения матриц,калькулятор произведения матриц онлайн,калькулятор умножение матриц,калькулятор умножение матрицу на матрицу,калькулятор умножение матрицы,калькулятор умножение матрицы на матрицу,калькулятор умножение матрицы на матрицу онлайн,калькулятор умножение матрицы онлайн,калькулятор умножения матриц,калькулятор умножения матриц онлайн,матрица на матрицу умножение,матрица на матрицу умножение онлайн,матрица онлайн умножение,матрица умножение на матрицу онлайн,матрица умножение онлайн,матрица умножить на матрицу,матрицу умножить на вектор онлайн,матрицу умножить на матрицу онлайн,матрицу умножить на обратную матрицу,матрицы калькулятор умножение,матрицы найти произведение,матрицы онлайн калькулятор умножение,матрицы перемножение,матрицы умножение калькулятор,матрицы умножение онлайн,матрицы умножение онлайн калькулятор,матрицы умножения,матрицы умножить,множення матриць,найдите произведение матриц,найти произведение матриц,найти произведение матриц калькулятор онлайн,найти произведение матриц онлайн,найти произведение матриц онлайн калькулятор,найти произведение матриц онлайн с решением,найти произведение матрицы,найти произведения матриц,обратную матрицу умножить на матрицу,онлайн калькулятор матриц умножение матриц,онлайн калькулятор матриц умножения,онлайн калькулятор матрицы умножение,онлайн калькулятор найти произведение матриц,онлайн калькулятор перемножение матриц,онлайн калькулятор произведение матриц,онлайн калькулятор произведения матриц,онлайн калькулятор умножение матриц,онлайн калькулятор умножение матриц с подробным решением,онлайн калькулятор умножение матриц с решением,онлайн калькулятор умножение матриц с решением онлайн,онлайн калькулятор умножение матрицы,онлайн калькулятор умножение матрицы на матрицу,онлайн калькулятор умножения матриц,онлайн матрица умножение,онлайн перемножение матриц,онлайн умножение двух матриц,онлайн умножение матриц на матрицу,онлайн умножение матрица,онлайн умножение матрицы,онлайн умножение матрицы на матрицу,онлайн умножение трех матриц,онлайн умножения матриц,онлайн умножить матрицу на матрицу,перемножение матриц,перемножение матриц 3 на 3,перемножение матриц калькулятор,перемножение матриц онлайн,перемножение матриц онлайн калькулятор,перемножение матрицы,перемножить матрицы,перемножить матрицы онлайн,произведение матриц онлайн,произведение матриц онлайн калькулятор,произведения матриц калькулятор,произведения матриц калькулятор онлайн,произведения матриц онлайн калькулятор,решение матриц умножение матриц,умножение двух матриц онлайн,умножение матриц,умножение матриц 2 на 2,умножение матриц калькулятор,умножение матриц калькулятор онлайн,умножение матриц на матрицу онлайн,умножение матриц онлайн,умножение матриц онлайн калькулятор,умножение матриц онлайн калькулятор с подробным решением,умножение матриц онлайн калькулятор с решением,умножение матриц онлайн с решением,умножение матриц с,умножение матриц трех онлайн,умножение матрица,умножение матрица на матрица,умножение матрица на матрица онлайн,умножение матрица на матрицу онлайн,умножение матрица онлайн,умножение матрицу на матрицу калькулятор,умножение матрицы 3х3 на матрицу 3х3,умножение матрицы калькулятор,умножение матрицы калькулятор онлайн,умножение матрицы на вектор онлайн,умножение матрицы на матрицу 3х3,умножение матрицы на матрицу калькулятор,умножение матрицы на матрицу калькулятор онлайн,умножение матрицы на матрицу онлайн,умножение матрицы на матрицу онлайн калькулятор,умножение матрицы на матрицу онлайн с решением,умножение матрицы на матрицы калькулятор,умножение матрицы онлайн,умножение матрицы онлайн калькулятор,умножение обратной матрицы на матрицу,умножение онлайн матрица,умножение трех матриц,умножение число на матриц онлайн,умножения матриц онлайн,умножения матриц онлайн калькулятор,умножения матрицу на матрицу,умножения матрицы,умножить вектор на матрицу онлайн,умножить дробь на матрицу онлайн,умножить матрицу а на матрицу в,умножить матрицу на вектор онлайн,умножить матрицу на дробь онлайн,умножить матрицу на матрицу,умножить матрицу на матрицу онлайн,умножить матрицу на матрицу онлайн с решением,умножить матрицы,умножить матрицы онлайн,умножить матрицы онлайн с решением.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вектор умножить на матрицу онлайн. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычислить произведение матриц онлайн с решением).

Где можно решить любую задачу по математике, а так же вектор умножить на матрицу онлайн Онлайн?

Решить задачу вектор умножить на матрицу онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Умножение матриц в EXCEL. Примеры и описание

В этой статье рассмотрены операции умножения матриц с помощью функции МУМНОЖ() или англ. MMULT и с помощью других формул, а также свойства ассоциативности и дистрибутивности операции умножения матриц. Примеры решены в MS EXCEL.

Операция умножения двух матриц А и В определена только для случаев, когда число столбцов матрицы А равно числу строк матрицы В.

Произведение матрицы А порядка P x N и матрицы В порядка N x Q — это такая матрица С порядка P x Q, у которой каждый элемент равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В , то есть:

Для умножения матриц в MS EXCEL существует специальная функция МУМНОЖ() , которую нужно вводить как формулу массива .

Рассмотрим сначала умножение квадратных матриц 2 х 2.

Разместим матрицы в диапазонах А8:В9 и D8:E9 (см. файл примера ).

Результат, также матрицу 2 х 2, будем вводить в диапазон H8:I9 .

Для этого:

• выделите указанный диапазон H8:I9
• поставьте курсор в Строку формул (или нажмите клавишу F2 )
• введите формулу =МУМНОЖ(A8:B9;D8:E9)
• нажмите CTRL+SHIFT+ENTER

Выделенный диапазон заполнится элементами матрицы. В принципе можно выделить заведомо б о льший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.

Удалить отдельный элемент матрицы А*В не удастся — только все элементы сразу (выделите весь диапазон и нажмите клавишу DEL ).

Чтобы изменить значения аргументов функции (например, поменять матрицы местами), выделите любую ячейку матрицы, нажмите F2 , исправьте формулу и нажмите CTRL+SHIFT+ENTER .

Альтернативной формулой для перемножения матриц является формула массива =СУММПРОИЗВ($A8:$B8;ТРАНСП(D$8:D$9)) . Введите формулу в верхнюю левую ячейку диапазона и нажмите CTRL+SHIFT+ENTER . Затем скопируйте ее вниз и вправо на нужное количество ячеек.

Если попытаться перемножить матрицы неподходящей размерности (когда число столбцов матрицы А НЕ равно числу строк матрицы В), то функция МУМНОЖ() вернет ошибку #ЗНАЧ!

В файле примера также продемонстрированы свойства ассоциативности и дистрибутивности операции умножения матриц.

Решение матриц онлайн

Решение матриц онлайн является одним из самых востребованных запросов в интернете среди студентов, при этом сервисов, где можно решить онлайн матрицу, практически нет. И снова на помощь придет многофункциональный математический калькулятор. В его арсенал входит решение матриц онлайн, в нашем калькуляторе можно выполнить все основные операции над матрицами!

Матрица — это совокупность значений, записанных в прямоугольную таблицу. Каждый элемент матрицы имеет двойной порядковый номер в этой таблице, а именно номер столбца и номер строки. Размер матрицы определяется количеством строк и столбцов в таблице. Например, размер матрицы 3 на 5 значит, что она состоит из трех строк и пяти столбцов.

Обратите внимание, 5 x 5 — это максимальный размер матрицы, которую может решить бесплатный калькулятор, предлагаемый на нашем сайте.

Как решать матрицы в онлайн калькуляторе?

Чтобы вызвать калькулятор матриц, нажмите кнопку Matrix.

Кнопка, открывающая калькулятор матриц:

Панель управления дополнится инструментами, с помощью которых выполняется решение матриц онлайн. Калькулятор позволяет выполнять следующие онлайн действия над матрицами: вычитание, сложение и умножение матриц, векторное произведение, решение матричных уравнений, транспонирование, нахождение обратной матрицы и вычисление определителя матрицы.

Кнопки калькулятора, выполняющие основные действия над матрицами:

Помимо панели с кнопками онлайн калькулятор матриц содержит удобную форму для быстрого ввода выражения. В левой и правой частях задаются матрицы, их размер выбирается из выпадающего списка. В середине выпадающее меню для выбора операции, которую нужно выполнить калькулятору с заданными матрицами.

Вычисление матриц онлайн с помощью формы быстрого ввода:

Если элемент матрицы не указан, онлайн калькулятор подставляет значение «0».

Обратите внимание, при вызове меню решения матриц вся панель калькулятора смещается вверх, закрывая часть дисплея. Заполните необходимые поля и нажмите клавишу «I», чтобы увидеть дисплей в полный размер.

Вектор столбец

Матрица, состоящая только из одной строки или одного столбца, называется вектор-строкой или вектор-столбцом соответственно. В калькуляторе предусмотрены отдельные кнопки для ввода матрицы, число столбцов которой равно 1. Используйте эти клавиши, чтобы записать вектор-столбец из 3, 4 или 5 строк соответственно.

Кнопки калькулятора для ввода вектора:

Вектор-столбец из 3-х строк:

(2, 6, 8)

Квадратная матрица

Матрица называется квадратной, если число ее строк равно числу столбцов. Следует отметить, что только у квадратной матрицы может быть главная диагональ матрицы — линия, проходящая через элементы матрицы с одинаковыми индексами, начиная с ячейки первой строки первого столбца и заканчивая элементом, стоящем в последнем столбце последней строки.

Для быстрой записи квадратных матриц 2, 3 или 4-го порядка используйте специальные кнопки калькулятора.

Кнопки калькулятора для ввода квадратных матриц:

Пример квадратной матрицы 4 порядка:

[[8, 4, 1, 8][7, 1, 8, 8][8, 4, 1, 6][4, 8, 3, 1]]

Квадратные матрицы, у которых все элементы, исключая элементы главной диагонали, равны нулю, называются диагональные матрицы. Симметричная матрица чисел представляет собой таблицу, в которой все элементы, симметричные относительно главной диагонали, равны.

Пример симметричной матрицы:

[[1, 2, 8, 11][2, 3, 24, 5][8, 24, 6, 4][11, 5, 4, 9]]

Есть еще такие виды матриц в математике.

Единичная матрица чисел — это таблица, в которой элементы главной диагонали равны единице, а все остальные элементы являются нулевыми.

Пример единичной матрицы:

[[1, 0, 0, 0][0, 1, 0, 0][0, 0, 1, 0][0, 0, 0, 1]]

Таблица, у которой значение всех элементов равно 0, называется нулевая матрица.

Пример нулевой матрицы:

[[0, 0, 0, 0][0, 0, 0, 0][0, 0, 0, 0][0, 0, 0, 0]]

Сложение и вычитание матриц онлайн

С помощью калькулятора можно произвести сложение матриц онлайн, а также найти разность матриц онлайн. Чтобы вычислить сумму матриц или найти их разность, выполняются соответствующие операции над их элементами. Например, найти сумму матриц значит определить такую матрицу, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц.

Найти сумму элементов матриц или их разность можно только в том случае, если исходные матрицы одинакового размера, то-есть число их строк и столбцов соответственно равно. Вычитание и сложение матриц разного размера невозможно.

Для выполнения этих операций в калькуляторе используйте форму быстрого ввода или запишите выражение вручную.

Сложение матриц примеры

Сложение двух матриц:

[[1, 2, 3][3, 1, 2][5, 0, 6]]+[[1, 2, 5][6, 3, 2][9, 9, 9]]

Сумма двух матриц:

[[2, 7][4, 5]]+[[2, 10][6, 8]]

Векторное произведение матриц

Для выполнения этой операции используйте клавишу Cross Product.

Пример произведения векторов:

(2, 6, 4)#(8, 2, 5)

Умножение матриц

Умножение матриц онлайн калькулятор производит с помощью клавиши Vector/Matrice-Multiplication.

Перемножение матриц возможно только в том случае, если количество столбцов одной матрицы равняется количеству строк другой. Чтобы матрицу умножить на число, нужно каждый элемент матрицы умножить на это число.

Умножение матриц пример:

[[2, 8][4, 2]]*[[8, 8][7, 1]]

Умножение матрицы на число онлайн:

[[5, 6][7, 8]]*9

Решение матричных уравнений

Эта функция калькулятора позволяет находить неизвестные матрицы, которые описаны уравнением зависимости одной матрицы от другой. -1

Нахождение определителя матрицы

В калькуляторе матриц нет специальной кнопки для того, чтобы найти определитель матрицы. Но вычислить его можно, написав в поле ввода специальную функцию — оператор det(Determinant).

Пример, как найти определитель матрицы онлайн:

det(,,[2, 0, -1]])

Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>

Произведение матриц, агрегация и другие базовіе операции NumPy

Вы уже знаете, как создавать массив NumPy и как определять его элементы. Теперь пришло время разобраться с тем, как применять к ним различные операции.

Арифметические операторы

Арифметические операторы — первые, которые предстоит использовать. К числу наиболее очевидных относятся прибавление и умножение на скаляр.

>>> a = np.arange(4)
>>> a
array([0, 1, 2, 3])
>>> a+4
array([4, 5, 6, 7])
>>> a*2
array([0, 2, 4, 6])

Их можно использовать для двух массивов. В NumPy эти операции поэлементные, то есть, они применяются только к соответствующим друг другу элементам. Это должны быть объекты, которые занимают одно и то же положение, так что результатом станет новый массив, содержащий итоговые величины в тех же местах, что и операнды.

>>> b = np.arange(4,8)
>>> b
array([4, 5, 6, 7])
>>> a + b
array([ 4, 6, 8, 10])
>>> a – b
array([–4, –4, –4, –4])
>>> a * b
array([ 0, 5, 12, 21])

Более того, эти операторы доступны и для функций, если те возвращают массив NumPy. Например, можно перемножить массив на синус или квадратный корень элементов массива b.

>>> a * np.sin(b)
array([–0. , –0.95892427, –0.558831 , 1.9709598 ])
>>> a * np.sqrt(b)
array([ 0. , 2.23606798, 4.89897949, 7.93725393]) 

И даже в случае с многомерными массивами можно применять арифметические операторы поэлементно.

>>> A = np.arange(0, 9).reshape(3, 3)
>>> A
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])
>>> B = np.ones((3, 3))
>>> B
array([[ 1., 1., 1.],
       [ 1., 1., 1.],
       [ 1., 1., 1.]])
>>> A * B
array([[ 0., 1., 2.],
       [ 3., 4., 5.],
       [ 6., 7., 8.]])

Произведение матриц

Выбор оператора для поэлементного применения — это странный аспект работы с библиотекой NumPy. В большинстве инструментов для анализа данных оператор * обозначает произведение матриц. Он применяется к обоим массивам. В NumPy же подобное произведение обозначается функцией dot(). Эта операция не поэлементная.

>>> np.dot(A,B)
array([[ 3., 3., 3.],
       [ 12., 12., 12.],
       [ 21., 21., 21.]])

Каждый элемент результирующей матрицы — сумма произведений каждого элемента соответствующей строки в первой матрице с соответствующим элементом из колонки второй. Рисунок ниже показывает процесс произведения матриц (для двух элементов).

Еще один вариант записи произведения матриц — использование одной из двух матриц в качестве объекта функции dot().

>>> A.dot(B)
array([[ 3., 3., 3.],
       [ 12., 12., 12.],
       [ 21., 21., 21.]])

Но поскольку произведение матриц — это не коммутативная операция, порядок операндов имеет значение. В данном случае A*B не равняется B*A.

>>> np.dot(B,A)
array([[ 9., 12., 15.],
       [ 9., 12., 15.],
       [ 9., 12., 15.]])

Операторы инкремента и декремента

На самом деле, в Python таких операторов нет, поскольку нет операторов ++ или --. Для увеличения или уменьшения значения используются += и -=. Они не отличаются от предыдущих, но вместо создания нового массива с результатами присваивают новое значение тому же массиву.

>>> a = np.arange(4)
>>> a
array([0, 1, 2, 3])
>>> a += 1
>>> a
array([1, 2, 3, 4])
>>> a –= 1
>>> a
array([0, 1, 2, 3])

Таким образом использование этих операторов дает возможность получать более масштабные результаты, чем в случае с обычными операторами инкремента, увеличивающими значения на один. Их можно использовать в самых разных ситуациях. Например, они подходят для изменения значений без создания нового массива.

array([0, 1, 2, 3])
>>> a += 4
>>> a
array([4, 5, 6, 7])
>>> a *= 2
>>> a
array([ 8, 10, 12, 14])

Универсальные функции (ufunc)

Универсальная функция, известная также как ufunc, — это функция, которая применяется в массиве к каждому элементу. Это значит, что она воздействует на каждый элемент массива ввода, генерируя соответствующий результат в массив вывода. Финальный массив соответствует по размеру массиву ввода.

Под это определение подпадает множество математических и тригонометрических операций; например, вычисление квадратного корня с помощью sqrt(), логарифма с log() или синуса с sin().

>>> a = np.arange(1, 5)
>>> a
array([1, 2, 3, 4])
>>> np.sqrt(a)
array([ 1. , 1.41421356, 1.73205081, 2. ])
>>> np.log(a)
array([ 0. , 0.69314718, 1.09861229, 1.38629436])
>>> np.sin(a)
array([ 0.84147098, 0.90929743, 0.14112001, –0.7568025 ])

Многие функции уже реализованы в библиотеке NumPy.

Функции агрегации

Функции агрегации выполняют операцию на наборе значений, например, на массиве, и выдают один результат. Таким образом, сумма всех элементов массива — это результат работы функции агрегации. Многие из таких функций реализованы в классе ndarray.

>>> a = np. array([3.3, 4.5, 1.2, 5.7, 0.3])
>>> a.sum()
15.0
>>> a.min()
0.29999999999999999
>>> a.max()
5.7000000000000002
>>> a.mean()
3.0
>>> a.std()
2.0079840636817816

Оптимальное умножение матриц — 2 — Задачи

Имея две матрицы A и B, мы можем вычислить C = AB используя стандартные правила умножения матриц:

Число колонок в матрице A должно совпадать с числом строк матрицы B. Пусть матрица A имеет размер m × n, матрица B имеет размер n × p. Тогда матрица С будет иметь размер m × p, а для ее вычисления следует совершить m * n * p умножений.

Например, если A имеет размер 10 × 20, B имеет размер 20 × 15, то необходимо совершить 10 × 20 × 15 = 3000 умножений для вычисления матрицы C.

Перемножать несколько матриц можно несколькими способами. Например, если у нас имеются матрицы X, Y и Z, то вычислить XYZ можно либо как (XY)Z, либо как X(YZ). Пусть X имеет размер 5 × 10, Y имеет размер 10 × 20, Z имеет размер 20 × 35.

Подсчитаем количество умножений, необходимых для перемножения трех матриц в каждом из этих двух случаях:

(XY)Z

• 5 × 20 × 10 = 1000 умножений для определения матрицы (XY), имеющей размер 5 × 20.
• Потом 5 × 35 × 20 = 3500 умножений для нахождения конечного результата.
• Общее количество умножений: 4500.

X(YZ)

• 10 × 35 × 20 = 7000 умножений для определения матрицы (YZ), имеющей размер 10 × 35.
• Потом 5 × 35 × 10 умножений для нахождения конечного результата.
• Общее количество умножений: 8750.

Очевидно, что при вычислении (XY)Z требуется меньшее количество умножений.

По заданной последовательности перемножаемых матриц следует найти оптимальный порядок их умножения. Оптимальным называется такой порядок умножения матриц, при котором количество элементарных умножений минимально.

Входные данные

Состоит из нескольких тестов. Первая строка каждого теста содержит количество n (n ≤ 10) перемножаемых матриц. Далее следуют n пар целых чисел, описывающих количество строк и столбцов в матрице, размеры матриц задаются в порядке их перемножения. Последний тест содержит n = 0 и не обрабатывается.

Выходные данные

Пусть матрицы пронумерованы A1, A2,…, An. Для каждого теста в отдельной строке следует вывести его номер и скобочное выражение, содержащее оптимальный порядок умножения матриц. Тесты нумеруются начиная с 1. Вывод должен строго соответствовать формату, приведнному в примере. Если существует несколько оптимальных порядков перемножения матриц, выведите любой из них.

Калькулятор продукта Кронекера

⊗ — Онлайн-матрица

Поиск инструмента

Продукт Кронекера

Инструмент для вычисления матричного произведения Кронекера в компьютерной алгебре. Произведение Кронекера — это частный случай тензорного умножения на матрицах.

Результаты

Продукт Кронекера — dCode

Метка (и): Матрица

Поделиться

dCode и другие

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Рекламные объявления

Продукт Кронекера

Матрица М1

Нагрузка…
(если это сообщение не исчезает, попробуйте обновить страницу)

Матрица M2

Загрузка …
(если это сообщение не исчезает, попробуйте обновить страницу)

Вычислить M1⊗M2 Вычислить M2⊗M1

Ответы на вопросы (FAQ)

Как умножить 2 матрицы с помощью Кронекера?

Для $ M_1 = [a_ {ij}] $ матрица / тензор с $ m $ строками и $ n $ столбцами и $ M_2 = [b_ {ij}] $ матрица с $ p $ строками и $ q $ столбцами. Изделие Kronecker отмечено символом: крест в кружке ⊗.$ M_1 \ otimes M_2 = [c_ {ij}] $ — это большая матрица из $ m \ times p $ строк и $ n \ times q $ столбцов, с: $$ \ forall i, j: c_ {ij} = a_ {ij} .B $$

Пример: $$ M = \ begin {bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \ end {bmatrix} \ otimes \ begin {bmatrix} 7 & 8 \\ 9 & 10 \ end { bmatrix} = \ begin {bmatrix} 7 & 8 & 14 & 16 & 21 & 24 \\ 9 & 10 & 18 & 20 & 27 & 30 \\ 28 & 32 & 35 & 40 & 42 & 48 \\ 36 & 40 & 45 & 50 & 54 & 60 \ end {bmatrix} $$

Это произведение не эквивалентно классическому умножению «> матричного произведения, $ M_1 \ otimes M_2 \ neq M_1 \ dot M_2 $

Каковы свойства умножения матрицы Кронекера?

Продукт Kronecker поддерживает ассоциативность:

$$ A \ otimes (B + \ lambda \ \ cdot C) = (A \ otimes B) + \ lambda (A \ otimes C) \\ (A + \ lambda \ \ cdot B) \ otimes C = (A \ otimes C) + \ lambda (B \ otimes C) \\ A \ otimes (B \ otimes C) = (A \ otimes B) \ otimes C \\ (A \ otimes B) (C \ otimes D) = ( AC) \ otimes (BD) $$

Но произведение Кронекера некоммутативно

$$ A \ otimes B \ neq B \ otimes A $$

Продукт Кронекера также обладает некоторыми свойствами распределенности:

— Дистрибутивность при транспонировании матрицы: $ (A \ otimes B) ^ T = A ^ T \ otimes B ^ T $

— Распределимость по трассам матрицы: $ \ operatorname {Tr} (A \ otimes B) = \ operatorname {Tr} (A) \ operatorname {Tr} (B) $

— Дистрибутивность по определителям матрицы: $ \ operatorname {det} (A \ otimes B) = \ operatorname {det} (A) ^ {m} \ operatorname {det} (B) ^ {n} $

Почему это умножение называется Кронекером?

Название дань немецкому математику Леопольду Кронекеру.

Задайте новый вопрос

Исходный код

dCode сохраняет право собственности на исходный код онлайн-инструмента «Продукт Кронекера». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любой алгоритм, апплет или фрагмент «продукта Кронекера» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой «продукт Кронекера» ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанная на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.)), и никакая загрузка данных, скрипт, копирование и доступ к API для «продукта Kronecker» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.

Нужна помощь?

Пожалуйста, посетите наше сообщество dCode Discord для получения помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!

Вопросы / комментарии

Сводка

Похожие страницы

Поддержка

Форум / Справка

Ключевые слова

кронекер, произведение, умножение, матрица, тензор

Ссылки

Источник: https: // www. dcode.fr/kronecker-product

© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF. Калькулятор умножения матриц

— eMathHelp

1. Дом
2. Калькуляторы
3. Калькуляторы линейной алгебры
4. Решение математических задач (все калькуляторы)

Калькулятор найдет произведение двух матриц (если возможно) с указанными шагами.Он перемножает матрицы любого размера до 10х10 (2х2, 3х3, 4х4 и т. Д.).

Ваш ввод

Вычислить $$$ \ left [\ begin {array} {ccc} 4 & 5 & 7 \\ 2 & 1 & 0 \ end {array} \ right] \ cdot \ left [\ begin {array} {cc} 2 & 3 \\ 8 & 9 \\ 1 & 1 \ end {array} \ right]. $$$

Решение

$$$ \ left [\ begin {array} {ccc} \ color {Шоколад} {4} & \ color {Magenta} {5} & \ color {Crimson} {7} \\\ color {Зеленый} {2} & \ color {Синий} {1} & \ color {Purple} {0} \ end {array} \ right] \ cdot \ left [\ begin {array} {cc} \ color {DarkCyan} {2} & \ color {Violet} {3} \\\ color {Green} {8} & \ color {DarkBlue} {9} \\\ color {Blue} {1} & \ color {Purple} {1} \ end {array} \ right] = \ left [\ begin {array} {cc} \ color {шоколад} {\ left (4 \ right)} \ cdot \ color {DarkCyan} {\ left (2 \ right)} + \ color {Magenta} {\ left (5 \ right)} \ cdot \ color {Green} {\ left (8 \ right)} + \ color {Crimson} {\ left (7 \ right)} \ cdot \ color {Синий} {\ left (1 \ right)} & \ color {Шоколад} {\ left (4 \ right)} \ cdot \ color {Violet} {\ left (3 \ right)} + \ color {Magenta} { \ left (5 \ right)} \ cdot \ color {DarkBlue} {\ left (9 \ right)} + \ color {Crimson} {\ left (7 \ right)} \ cdot \ color {Purple} {\ left ( 1 \ right)} \\\ color {Green} {\ left (2 \ right)} \ cdot \ color {DarkCyan} {\ left (2 \ right)} + \ color {Blue} {\ left (1 \ right )} \ cdot \ color {Green} {\ left (8 \ right)} + \ color {Purple} {\ left (0 \ right)} \ cdot \ color {Blu e} {\ left (1 \ right)} & \ color {Green} {\ left (2 \ right)} \ cdot \ color {Violet} {\ left (3 \ right)} + \ color {Blue} {\ left (1 \ right)} \ cdot \ color {DarkBlue} {\ left (9 \ right)} + \ color {Purple} {\ left (0 \ right)} \ cdot \ color {Purple} {\ left (1 \ right)} \ end {array} \ right] = \ left [\ begin {array} {cc} 55 & 64 \\ 12 & 15 \ end {array} \ right] $$$

Ответ

$$$ \ left [\ begin {array} {ccc} 4 & 5 & 7 \\ 2 & 1 & 0 \ end {array} \ right] \ cdot \ left [\ begin {array } {cc} 2 & 3 \\ 8 & 9 \\ 1 & 1 \ end {array} \ right] = \ left [\ begin {array} {cc} 55 & 64 \\ 12 & 15 \ end {array} \ right] $$$ A

Калькулятор умножения матриц

Добро пожаловать в калькулятор умножения матриц , где мы рассмотрим предмет умножения матриц вместе и увидим , что это хорошо для . К сожалению, матричное произведение на несколько сложнее, чем обычное умножение. Но не волнуйтесь, это не ракетостроение, и обучение умножению матриц действительно оказывается полезным в таких областях, как алгебра, анализ и, хотите верьте, хотите нет, в реальной жизни .

Не теряйте времени, давайте научимся умножать матрицы !

Что такое

матрица и чем она хороша?

Ответ на поставленный вопрос, к сожалению, не совсем ничего.Прежде чем мы начнем с калькулятора матричного умножения , давайте представим число . Не волнуйтесь, это не начало фокусов. Мы оставляем их, когда хотим произвести впечатление на свидание. В любом случае, число , которое пришло вам в голову, может означать все, что угодно, , от количества книг, которые вы прочитали за последние несколько месяцев, до количества калорий, которые вы собираетесь сжечь, прочитав этот текст. Бесконечно много возможностей, правда?

Матрица является обобщением этого.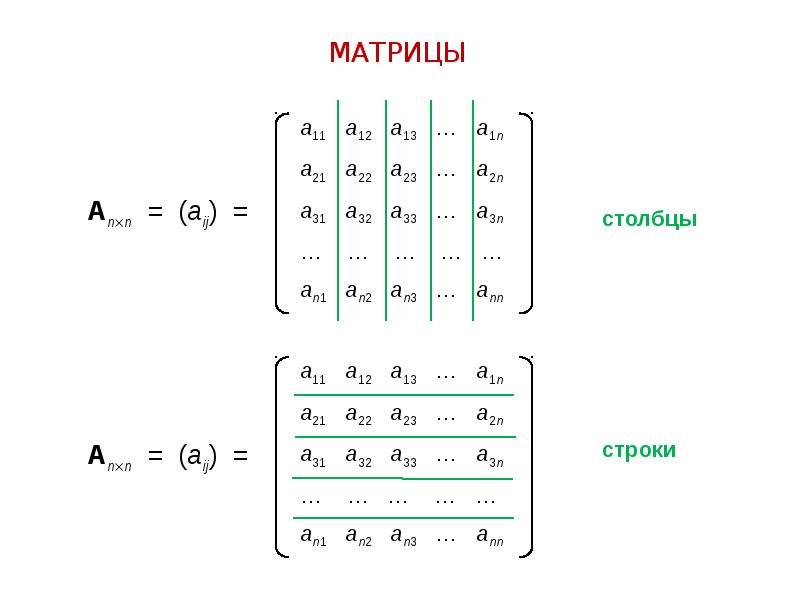 Это массив элементов (обычно чисел) с заданным количеством строк и столбцов. В частности, матрица с одной строкой и одним столбцом содержит только один элемент, поэтому мы можем рассматривать такой массив как одно число. В общем, однако, он может хранить больше информации, чем одно значение, так как … ну, , вы можете иметь столько строк и столбцов, сколько хотите . Цифры, которые они содержат, могут быть вашим рабочим временем и вашей заработной платой или временем финиша первых трех марафонцев на каждой из последних десяти Олимпийских игр.

И если вам нужен пример , какие математики используют матрицы для , то позвольте нам попробовать, сказав, что каждое линейное преобразование, то есть перемещение или вращение элемента , может быть описано матрицей . Другими словами, каждое лето, когда вы отправляетесь в путешествие, и каждое субботнее утро, когда вы смешиваете ингредиенты для блинов, вы фактически использовали матрицы. Или, если быть точным, движение может быть преобразовано в матрицу .Это похоже на то, что вы можете сказать на вечеринке после пары пива. Мы уверены, что ваши друзья будут достаточно впечатлены .

Другие научные области, которые сильно зависят от матриц , включают:

Как умножать матрицы?

Как мы уже говорили в предыдущем разделе, матрицы являются обобщением простых чисел , поэтому имеет смысл их умножать. Однако есть несколько правил умножения матриц , которым мы должны следовать, и, к сожалению, матричное произведение может быть не таким интуитивным, как обычное числовое произведение.

Во-первых, мы не можем перемножить никакую пару матриц . Еще хуже, если у нас есть матрица A и матрица B , то в целом матричное произведение A * B отличается от B * A (мы говорим, что матрицы умножения не коммутативны ) . Давайте посмотрим на формулу умножения массивов, чтобы понять, почему это так.

Предположим, что A имеет записи a _{n, m} , где n обозначает номер строки, а m обозначает столбец.Это означает, что запись _2,4 будет относиться к числу во второй строке четвертого столбца. Аналогично, пусть B имеет записи b _{n, m} . Если продукт A * B представляет собой матрицу с элементами c _{n, m} , то мы имеем

c n, m = a n, 1 * b 1, m + a n, 2 * b 2, m + a n, 3 * b 3, m + ...

Другими словами, , чтобы получить запись в строке n и столбце m матричного произведения, нам нужно взять n -ю строку первой матрицы и m -й столбец второй матрицы и умножаем их элементы попарно один на один, а затем все это просуммируем. Что ж, мы предупреждали вас, что умножение массивов не так интуитивно понятно, как обычное. Но не волнуйтесь, , мы увидим хороший пример умножения матриц в следующем разделе.

Однако, прежде чем мы попытаемся перемножить матрицы, давайте обратим внимание на несколько упомянутых нами правил умножения матриц .

1. Мы не можем перемножить никакую пару матриц. Из приведенной выше формулы мы видим, что каждый элемент матричного произведения получается путем объединения строки первой матрицы со столбцом второй матрицы и умножения их элементов один за другим.Это означает, что каждая строка массива A должна иметь столько же записей, сколько каждый столбец массива B . Это, в свою очередь, преобразуется в , первая матрица имеет столько же столбцов, сколько вторая матрица имеет строк . Обратите внимание, что наш калькулятор умножения матриц не будет работать, если не будут выполнены эти критерии.

2. Как правило, матричный продукт имеет другую форму, чем факторы. Если первая матрица имеет r строк и s столбцов, а вторая — r строк (помните, что это число должно быть таким же, как количество столбцов в первом массиве) и t столбцов, тогда результат умножения этих матриц будет иметь r строк и t столбцов.

3. Умножение массивов не коммутативно. Мы уже упоминали об этом, но теперь, когда мы узнали, как умножать матрицы, мы понимаем, почему это так. Выше мы сказали, что произведение r -строки и s -строка A с s -строк и t -столбец матрицы B является r — ряд и t — массив столбцов A * B . С другой стороны, если мы хотим найти B * A , то для начала нам потребуется s = t . В противном случае умножение этих матриц невозможно даже . Во-вторых, продукт B * A будет иметь строк и столбцов , поэтому он явно будет отличаться от A * B .

4. Это действительно обобщение обычных чисел. В качестве последнего из правил умножения матриц отметим, что все работает хорошо и красиво в самых основных случаях — когда оба фактора являются матрицами с одной записью.Тогда матричное произведение представляет собой матрицу с одним элементом, которую мы получаем путем умножения чисел из двух массивов. Эта операция коммутативна и ведет себя так же, как и обычное умножение чисел.

Пример: поиск матричного произведения

Наконец-то пришло время увидеть, как работает калькулятор умножения матриц . Возьмем

А

=

⌈ 3 -1 ⌉ | 0 2 ｜ ⌊ 1 -1 ⌋

а также

и попробуем перемножить эти матрицы на .

Прежде всего, обратите внимание, что A имеет три строки и два столбца, а B имеет две строки и два столбца. Следовательно, согласно правилам умножения матриц, мы можем безопасно найти A * B , но матричное произведение B * A не существует .

Если вам нужен простой выход, не стесняйтесь использовать калькулятор матричного умножения, чтобы найти ответ . Для этого мы начинаем с ввода количества строк и столбцов для обеих матриц.Это покажет нам символическое изображение над калькулятором с обозначениями, которые мы используем . Первый (тот, что слева) будет нашим A , а второй (правый) будет B . Сравните изображение с имеющимися у нас массивами и введите числа в калькулятор умножения матриц под правильными метками . Для первой матрицы имеем:

a₁ = 3 , a₂ = -1 ,

b₁ = 0 , b₂ = 2 ,

c₁ = 1 , c₂ = -1 ,

и для второго:

x₁ = 1 , x₂ = 0 ,

y₁ = -1 , лет = 4 .

Тем не менее, давайте также посмотрим , как калькулятор умножения матриц находит ответ . Мы начнем с представления полезного трюка , который поможет нам с умножением массива. Запишем две матрицы особым образом, разделив их парой пунктирных перпендикулярных линий:

				⁞	⌈	1	0	⌉
				⁞	⌊	-1	4	⌋
…	…	…	…	·	…	…	…	…
⌈	3	-1	⌉	⁞
|	0	2	｜	⁞
⌊	1	-1	⌋	⁞

Произведение двух матриц должно иметь три строки и два столбца, поэтому мы запишем его в правом нижнем углу таблицы выше. Обратите внимание, что запись в первой строке и первом столбце будет соответствовать умножению первого столбца первой строки A на первую строку первого столбца B , умножению второго столбца первой строки A на вторую строку первого столбца B и суммируя результаты. Это дает:

3 * 1 + (-1) * (-1) = 3 + 1 = 4 .

Следовательно, если мы запишем его в правильную ячейку нашей таблицы, как это

				⁞	⌈	1	0	⌉
				⁞	⌊	-1	4	⌋
…	…	…	…	·	…	…	…	…
⌈	3	-1	⌉	⁞	⌈	4		⌉
|	0	2	｜	⁞	|			｜
⌊	1	-1	⌋	⁞	⌊			⌋

Мы помещаем это новое число туда, где столбец и строка, которые мы использовали для его вычисления, пересекаются, поэтому мы знаем, что мы использовали, чтобы найти его. Если продолжить эту процедуру, получим

				⁞	⌈	1	0	⌉
				⁞	⌊	-1	4	⌋
…	…	…	…	·	…	…	…	…
⌈	3	-1	⌉	⁞	⌈	4	-4	⌉
|	0	2	｜	⁞	|	-2	8	｜
⌊	1	-1	⌋	⁞	⌊	2	-4	⌋

В итоге результат умножения нашего массива равен

A * B

=

⌈ 4 -4 ⌉ | -2 8 ｜ ⌊ 2 -4 ⌋

Простой онлайн-калькулятор матриц

Этот калькулятор матриц позволяет вам вводить ваши собственные матрицы 2 × 2, складывать и вычитать их, находить умножение матриц (в обоих направлениях) и обратное за вас.

Здесь показаны шаги для получения ответов.

В ячейки матрицы можно ввести любое число (не буквы) от –99 до 99.

Выход

Вот результаты с использованием заданных чисел.

Наши две матрицы:

и B =		5	−6
		1	−4

Добавление матрицы

А + В

Вычитание матрицы

А — В

Умножение матриц

В общем, если

, то произведение матриц X и Y равно:

XY

=		( a × e + b × g )	( a × f + b × h )
		( c × e + d × g )	( c × f + d × h )

Используя этот процесс, мы умножаем наши 2 данные матрицы A и B следующим образом:

AB

=		(1 × 5 + 0 × 1)	(1 × −6 + 0 × −4)
		(2 × 5 + 4 × 1)	(2 × −6 + 4 × −4)

Теперь перемножим матрицы в обратном порядке:

BA

=		(5 × 1 + −6 × 2)	(5 × 0 + −6 × 4)
		(1 × 1 + −4 × 2)	(1 × 0 + −4 × 4)

=		−7	−24
		−7	−16

Умножение матриц некоммутативно

В общем, когда мы умножаем матрицы, AB не равно BA . -1 млрд = [(0,2857, -0,4286), (0,0714, -0,3571)] [(5, -6), (1, -4)] `

`= [(1,0), (0,1)]`

Попробовать другой?

Онлайн-матричное умножение, сложение и вычитание

Список справки по математике — — Математическая справка Быстрый переход — Научный онлайн-калькулятор — Общая математика — Калькулятор фракцийКалькулятор процентовКалькулятор квадратного корняКалькулятор факторингаУпрощение выраженийКалькулятор делителейКалькулятор факторингаКалькулятор наибольшего общего множителя (GCF) Калькулятор последнего общего множителя (LCM) Калькулятор простых чисел и средство проверкиПроверка идеального числа Валидатор квадратов — Алгебра и комбинаторики -уравнения SolverQuadratic Уравнение SolverSystem уравнений SolverCombinatoricsPermutationsPolynomialsPolynomials — Сложение и SubtractionPolynomials — Умножение и DivisionPolynomials — Дифференциация и IntegrationPolynomials — Паритет калькулятор (нечетный, четный, нет) Полиномы — Корень FinderPolynomials — Сформировать из RootsMatricesMatrix Calculator- определителя, обратная матрица CalculatorMatrix — Сложение, вычитание, умножение, исчисление, интегральный калькулятор, калькулятор определенного интеграла, калькулятор производной, числовая производная КалькуляторКалькулятор пределов Отклонение CalculatorVariance CalculatorKurtosis CalculatorSkewness Calculator- Описательная статистика Калькуляторы -Матрица Центральный момент CalculatorCorrelation Матрица CalculatorCovariance Матрица CalculatorMatrix Среднее геометрическое CalculatorMatrix гармоническое среднее CalculatorMatrix межквартильный Диапазон CalculatorMatrix Эксцесс CalculatorMatrix нецентральные Момент CalculatorMatrix Среднее CalculatorMatrix Максимальная CalculatorMatrix Минимальная CalculatorMatrix Медиана CalculatorMatrix Среднее отклонение CalculatorMatrix Среднее отклонение CalculatorMatrix Quantile Калькулятор Калькулятор асимметрии квартиля матрицы Калькуляторы Калькуляторы распределения Вейбулла — Калькуляторы дискретных распределений — Калькуляторы биномиального распределения Калькуляторы геометрического распределения Калькуляторы распределения Пуассона Калькуляторы равномерного (дискретного) распределения

Умножение матриц с помощью калькулятора TI83 или TI84

Графические калькуляторы, такие как TI83 и TI84, могут выполнять множество различных операций с матрицами, включая умножение. {- 1} \ right] \).

Нажмите кнопку со стрелкой вправо, чтобы перейти в меню ПРАВКА.

Нажмите [2] или выделите 2. [B] и нажмите [ENTER].

Введите размер матрицы и значения, набирая каждое число и нажимая [ENTER]. Обратите внимание, что вторая матрица из нашего примера представляет собой матрицу 3 x 2 (строки за столбцами).

\ (\ left [\ begin {array} {cc} 4 & 0 \\ 1 & 1 \\ 3 & 9 \ end {array} \ right] \)

Шаг 3: Нажмите [2ND] и [MODE], чтобы выйти из экрана матрицы.

Откроется пустой экран.{-1} \ right] \).

Нажмите [2] или выделите 2. [B] и нажмите [ENTER].

Нажмите [ENTER], чтобы умножить матрицы.

Отсюда у вас есть окончательный ответ. Теперь мы можем написать:

\ (\ begin {align} AB & = \ left [\ begin {array} {ccc} -1 & 5 & -2 \\ 3 & 7 & 7 \\\ end {array} \ right] \ left [\ begin {массив} {cc} 4 & 0 \\ 1 & 1 \\ 3 & 9 \ end {array} \ right]
\\ & = \ boxed {\ left [\ begin {array} {cc} -5 & — 13 \\ 40 и 70 \\\ end {array} \ right]} \ end {align} \)

Распространенная ошибка: DIM MISMATCH

Предположим, что вы выполнили эти шаги и в итоге получили следующий экран.

В этом случае вы должны проверить две вещи:

1. Вы ввели правильную информацию о матрице и выбрали ли правильные матрицы для умножения?
2. Продукт определен?

Если вы правильно ввели матрицы, то эта ошибка означает, что продукт не определен. В частности, если вы выписываете размеры матриц, внутренние числа должны совпадать. В приведенном выше примере у нас были 2 x 3 и 3 x 2. Обратите внимание, что числа на внутренней стороне совпадают, поэтому продукт был определен, и мы смогли найти ответ.

Однако произведение 2 x 2 и 3 x 2 будет неопределенным, поскольку внутренние числа не совпадают. Вы бы просто написали «Не определено» в качестве ответа, если бы решали такую ​​задачу на экзамене или викторине.

Чтобы узнать больше о том, когда матричное умножение определено или не определено, перейдите по следующей ссылке.

Когда определяется умножение матриц?

объявление

Продолжайте изучение матриц и калькулятора TI83 / 84

В следующих статьях есть дополнительная информация об использовании калькулятора с матрицами:

Подпишитесь на нашу рассылку новостей!

Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.

Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!

Связанные

Калькулятор умножения матриц

— Онлайн-калькулятор умножения матриц

Калькулятор умножения матриц

вычисляет произведение двух заданных матриц. Матрица — это сеточная функция, которая имеет упорядоченный прямоугольный массив чисел. Числа расположены в ряды и столбцы.Вертикальное расположение называется столбцами, а горизонтальное расположение чисел называется строками,

.

Что такое калькулятор умножения матриц?

Калькулятор умножения матриц

— это онлайн-инструмент, который помогает выполнять различные операции умножения матриц, то есть умножения. Это поможет вам рассчитать окончательную матрицу за несколько секунд. Чтобы использовать этот калькулятор умножения матриц, введите число до 3 цифр.

Как пользоваться калькулятором умножения матриц?

Чтобы найти продукт с помощью онлайн-калькулятора умножения матриц, выполните следующие действия:

• Шаг 1: Зайдите в онлайн-калькулятор умножения матриц Cuemath.
• Шаг 2: Выберите раскрывающийся список для матриц 2×2 и 3×3, чтобы найти продукт.
• Шаг 3: Введите значение матриц в указанные поля ввода калькулятора умножения матриц.
• Шаг 4: Нажмите кнопку «Рассчитать» , чтобы найти результирующую матрицу.
• Шаг 5: Нажмите кнопку «Сброс» , чтобы найти результирующую матрицу с разными матрицами.

Как работает калькулятор умножения матриц?

Матрица определяется как математическая функция для представления набора данных, обычно используемая матрица представляет собой двумерную матрицу и используется для целей сложения векторов, умножения векторов и т. Д. Выполняемые операции с матрицей:

Умножение = \ (\ begin {matrix} a & b & c \\ d & e & f \\ g & h & i \ end {matrix} \) x \ (\ begin {matrix} j & k & l \ \ m & n & o \\ p & q & r \ end {matrix} \) \ (= \ begin {matrix} aj + bm + cp & ak + bn + cq & al + bo + cr \\ dj + em + fp & dk + en + fq & dl + eo + fr \\ gj + hm + jp & gk + hn + iq & gl + ho + ir \ end {matrix} \)

Хотите найти сложные математические решения за секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.Cuemath находит решения простым и легким способом.

Забронируйте бесплатную пробную версию Класс

Решенный пример умножения матриц

Найдите результирующую матрицу после применения операции умножения к матрице \ (\ begin {matrix} 1 & 2 \\ 3 & 4 \ end {matrix} \) & \ (\ begin {matrix} 2 & 1 \\ 4 & 2 \ end {matrix} \) и проверьте его с помощью калькулятора матричного умножения

Решение:

Дано: матрица 1 & 2 = \ (\ begin {matrix} 1 & 2 \\ 3 & 4 \ end {matrix} \) & \ (\ begin {matrix} 2 & 1 \\ 4 & 2 \ end {matrix} \ )

Умножение = \ (\ begin {matrix} a & b & c \\ d & e & f \\ g & h & i \ end {matrix} \) x \ (\ begin {matrix} j & k & l \ \ m & n & o \\ p & q & r \ end {matrix} \) \ (= \ begin {matrix} aj + bm + cp & ak + bn + cq & al + bo + cr \\ dj + em + fp & dk + en + fq & dl + eo + fr \\ gj + hm + jp & gk + hn + iq & gl + ho + ir \ end {matrix} \)

Умножение = \ (\ begin {matrix} 1 & 2 \\ 3 & 4 \ end {matrix} \) × \ (\ begin {matrix} 2 & 1 \\ 4 & 2 \ end {matrix} \) = \ (\ begin {matrix} (1 × 2) + (2 × 4) & (1 × 1) + (2 × 2) \\ (3 × 2) + (4 × 4) & (3 × 1) + (2 × 4) \ end {matrix} = \ begin {matrix} 10 & 5 \\ 22 & 11 \ end {matrix} \)

Аналогичным образом вы можете попробовать калькулятор умножения матриц и найти результирующую матрицу для следующего:

• Матрицы = \ (\ begin {matrix} 2 & 1 \\ 4 & 2 \ end {matrix} \), \ (\ begin {matrix} 3 & 3 \\ 7 & 6 \ end {matrix} \)
• Матрицы = \ (\ begin {matrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \ end {matrix} \), \ (\ begin {matrix} 2 & 1 \\ 4 & 2 \\ 5 & 4 \ конец {матрица} \)

☛ Статьи по теме: .

No related posts.