Разложение перестановок, циклы, транспозиции
Выясним, как “ведет себя” перестановка в области определения. Рассмотрим произвольную перестановку
.
Эта перестановка переводит единицу в четверку, четверку в единицу, двойка переходит в тройку, а тройка в двойку.
Если все перечисленные замены записать в той последовательности, в которой мы их производили, то рассматриваемая перестановка примет вид:
.
Нетрудно заметить, что перестановка оказалась, по существу, разложенной на две части.
.
Это означает, что наша перестановка состоит из двух независимых частей, каждая из которых перемещает элементы, принадлежащие её собственной области определения (рис. 1).
Рис. 1 – Разложение перестановки .
Именно потому, что обе части перестановки независимы, совершенно безразлично, какую из перестановок
выполнять первой,
а какую второй. Если перестановки
Если перестановки
выполнять последовательно одну за другой, то такие действия можно рассматривать, как умножение перестановок. Однако до сих пор мы говорили об умножении перестановок в тех случаях, когда области определения перестановок совпадали. Здесь же области определения перестановок различны.
Преодолеть возникшую проблему не составляет труда: условимся считать, что наши перестановки переводят каждый “недостающий” элемент в самого себя.
Таким образом, перестановка допускает следующее разложение в произведение двух независимых перестановок:
.
Легко заметить, что в данном разложении нижние строки совершенно излишни. Действительно, верхние строки состоят из тех же элементов, что и нижние, причем каждый элемент под действием перестановки переходит в следующий. Это позволяет представить нашу перестановку в виде
.
Перестановки, стоящие в правой части, называются независимыми циклами, а представление перестановки
в виде
называется
разложением перестановки
в произведение независимых циклов.
Определение. Длиной цикла называется количество входящих в него элементов (в данном случае циклы имеют длину, равную двум).
Перестановка
допускает разложение только в один цикл
длиной 4.
Разложение перестановки в произведение независимых циклов эквивалентно разбиению множества на непересекающиеся классы
, где ,.
Известно, что разбиение множества на непересекающиеся классы эквивалентно введению некоторого отношения эквивалентности. Элементы, входящие в один из циклов, являются эквивалентными между собой, а сами циклы представляют собой классы эквивалентности.
Если некоторая перестановка, определенная на множестве, которую можно представить в виде произведения независимых циклов
,
то элементы множества можно представить в виде объединения р попарно непересекающихся подмножеств
.
Таких, что
.
Множества называются-орбитами. Название это вполне обоснованно. Каждая точка принадлежит в точности одному классу эквивалентности, напримерили– орбите.
Если , тосостоит из образов точки i при действии степеней элемента
,
где – длина k-го цикла орбиты. Очевидно, чтои, причем– наименьшее число, обладающее этим свойством.
Цикл можно представить в виде:
. (4)
Цикл k оставляет на месте все точки из множества , а для любой точки
(5)
Это свойство дает нам основание называть циклы независимыми или непересекающимися циклами.
Теорема. Каждая перестановка может быть представлена в виде произведениянезависимых циклов длины. Это разложение определено однозначно с точностью до порядка следования циклов.
. (6)
Замечание. Длина
каждого k-го цикла –
,больше
или равна двум. Если циклимеет длину равную единице, то он
действует как единичная перестановка
и его в произведении (5) естественно
опускать.
Длина
каждого k-го цикла –
,больше
или равна двум. Если циклимеет длину равную единице, то он
действует как единичная перестановка
и его в произведении (5) естественно
опускать.
Например, перестановку
можно представить в виде
.
Запись перестановки в виде произведения независимых циклов (5) позволяет легко найти порядок перестановки
.
Следствие 1. Порядок перестановки(порядок циклической подгруппы) равен наименьшему общему кратному (НОК) длин независимых циклов, входящих в разложение.
Доказательство. Представим перестановку в виде произведения независимых циклов
. (7)
Тогда
Так как циклы независимы (они действуют на различных множествах), и если q – порядок циклической подгруппы,
,
то
,
где
.
Следовательно, q – общее кратное порядков циклов k, которые совпадают с их длинами .
Если q – наименьшее положительное число, для которого
,то
и
. (8)
Замечание. Два любых целых числа m и n можно записать в виде произведений одних и тех же простых чисел
.
Например
,
тогда
,
где
Множество простых чисел
.
Пример. Определить порядок перестановки вида
.
Решение. Представим перестановку в виде произведения независимых циклов, т.е.
Длины независимых цикловравны
Следовательно,
порядок рассматриваемой перестановки
равен 28.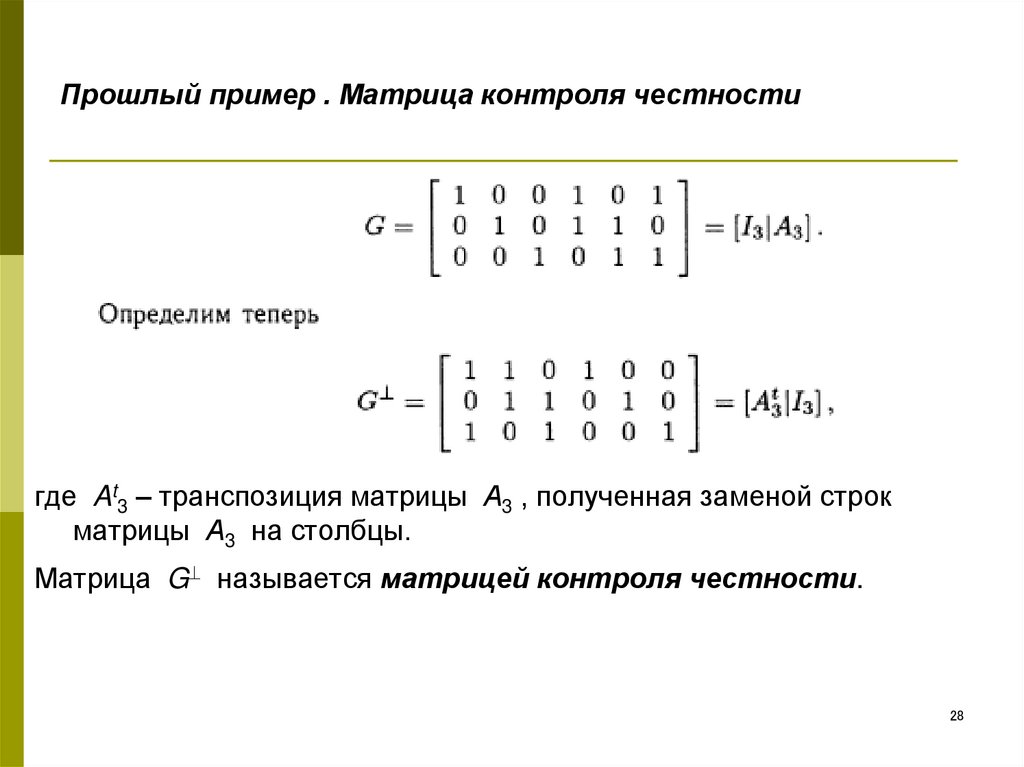
Определение. Цикл длиной два называется транспозицией. Любая транспозиция имеет вид и оставляет на местах все символы за исключением.
Теорема. Каждая перестановка может быть представлена в виде произведения транспозиции.
Доказательство. Теорема будет доказана, если мы сможем представить в виде произведений транспозиций каждый из циклов k, входящих в разложения перестановки: .
Рассмотрим произвольный цикл , напримери произведем его разложение в произведение транспозиций.
Алгоритм разложения цикла в произведение транспозиций представлен на рисунке 2.
Цикл транспозиции
Рис 2. – Разложение цикла в произведение транспозиций.
После
завершения всех операций на месте
каждого элемента цикла
оказался следующий за ним элемент, а
первый элемент перешел на последнее
место.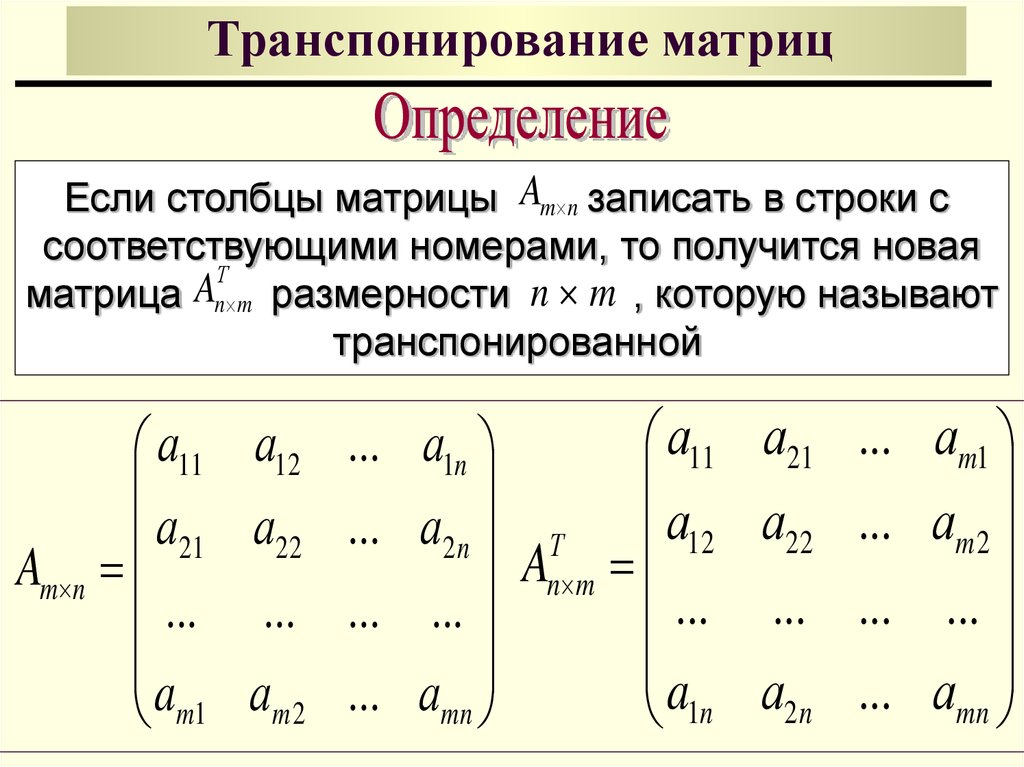 Таким образом, циклоказался разложенным в произведение
транспозиций:
Таким образом, циклоказался разложенным в произведение
транспозиций:
Естественно, это разложение не единственно. Например
.
Важно другое – и в первом и во втором его разложении имеется равное количество транспозиций – четыре. Если , то количество транспозиций равно. Раскладывая аналогичным образом каждый циклперестановкив произведение транспозиции, мы получим разложение всей перестановкив произведение транспозиций.
Замечание. Количество транспозиций в цикле может быть и больше четырех! Возьмем произвольную транспозицию из разложения этого цикла, например,. Тогда произведениесовпадает с тождественной перестановкой и циклможно представить в виде
или
,
или
.
Легко
заметить, что во всех этих случаях число
транспозиций четно и равно 4,6,8. Ясно,
что способ, «удлиняющий» разложение,
не изменяет четности исходного разложения.
Теорема. Пусть – перестановка из , а
. (9)
какое-либо разложение в произведении транспозиций. Тогда число
(10)
называется четностью (сигнатурой или знаком) перестановки и полностью определяется , т.е. не зависит от способа разложения перестановки в произведение транспозиций. Кроме того, если , то
. (11)
Данную теорему приводим без доказательства. Доказательство теоремы приведено в [1].
Определение. Перестановка называется четной, если, и нечетной, если.
Из определения четности перестановки вытекает, что все транспозиции – нечетные перестановки. Действительно, если – транспозиция, то, тогда
Следствие 1. Все
четные перестановки степени n образуют
подгруппу
порядка(она называется знакопеременной группой
степени n).
Следствие 2. Пусть перестановка разложена в произведение независимых цикловдлин, где,, …,, …,– длины независимых циклов.
Тогда
Доказательство. Действительно, по предыдущей теореме имеем
.
Кроме того, поскольку каждыйцикл записывается в виде произведениятранспозиций, то
.
Произведение — транспозиция — Большая Энциклопедия Нефти и Газа, статья, страница 2
Cтраница 2
Теорема 7.6.3. Каждая подстановка я е Sm разлагается в произведение транспозиций не единственным образом, однако четность числа транспозиций постоянна и совпадает с четностью самой подстановки. [16]
Из этого примера видно, что в разложении перестановки в произведение транспозиций порядок множителей является существен ным. [17]
Из этого примера видно, что в разложении перестановки в произведение транспозиций порядок множителей является существенным. [18]
[18]
Pi P2o — — eP / — — разложения перестановки в произведение транспозиций, то числа s и t имеют одинаковую четность. [19]
Покажем теперь, что либо каждое представление заданной подстановки в виде произведения транспозиций содержит четное число транспозиций, либо каждое такое представление содержит нечетное число транспозиций. [20]
Главный момент состоит в доказательстве того, что любая перестановка разлагается в произведение транспозиций. [21]
В самом деле, в силу теоремы 1 достаточно записать в виде произведения транспозиций каждый из циклов. [22]
Отсюда, согласно теореме 5.1.1, любая конечная подстановка представима в виде произведения транспозиций. Произведение черного числа транспозиций — четная подстановка, нечетного числа — — нечетная. Итак, хотя представление подстановки в виде произведения транспозиций и неоднозначно, число транспозиций, участвующих в произведении, всегда имеет одну и ту же четность. [23]
[23]
В самом деле, в силу теоремы 1 достаточно записать в виде произведения транспозиций каждый из циклов. [24]
Из выражений (1.26) и (1.26) видно, что циклы могут быть записаны как произведения транспозиций, и оказывается, что любая перестановка может быть представлена в виде произведения последовательности транспозиций. [25]
Очевидно, что y ( ipt ia) y; разложение у в произведение транспозиций содержит на одну транспозицию больше, чем разложение 71 отсюда sgny — sgn у и справедливость формулы ( 25) установлена. [26]
Учитывая, что транспозиции являются очень простыми подстановками, было бы полезно научиться все прочие подстановки представлять в виде произведения транспозиций. [27]
Поскольку любую подстановку можно представить в виде произведения ( независимых) циклов, то достаточно доказать, что циклы допускают разложение в произведение транспозиций. [28]
[28]
В работе Эдена и Шютцеиберже [103] доказывается, что число деревьев с п занумерованными вершинами равно числу разложений цикла степени п — 1 в произведение транспозиций. [29]
В Sn имеется ровно п ( п — 1) / 2 транспозиций. Любая подстановка у из SF ( X) представима в виде произведения транспозиций. Sn есть произведение транспозиций. [30]
Страницы: 1 2 3
абстрактная алгебра — Как записать перестановки как произведение непересекающихся циклов и транспозиций
спросил
Изменено 2 года, 1 месяц назад
Просмотрено 92к раз
$\begingroup$
$$\sigma=\begin{pmatrix} 1 и 2 &3 & 4& 5& 6&7 &8 &9&10 & 11 \\ 4&2&9&10&6&5&11&7&8&1&3 \end{pmatrix}$$
(1) Меня попросили записать эту перестановку в $S_{11}$ как произведение непересекающихся циклов, а также как произведение транспозиций.
(2) Также найдите порядок элемента. Эта перестановка четная или нечетная?
Думаю, это непересекающиеся циклы
$E_{1}=(1,4,10)$, $\;\operatorname{order}E_1 =3$
$E_{2}= (3,9 ,8,7,11),\;$ $\operatorname{order}E_{2} =5$
$E_{3}=(5,6),\;$ $\operatorname{order}E_{3} =2$
$S_{11}$= $E_{1} \cdot E_{2} \cdot E_{3}$
Порядок $\operatorname{order}E_{3}$ четный, поэтому порядок перестановки четный. Почему они спрашивают это? И какое значение имеет четность или нечетность?
Транспозиции — я читал это пару раз, но один пример в моем учебнике довольно неясен, я не уверен, что это значит?
Я думаю, что транспозиция для $E_{1}$ равна $(1,4)(1,10)$, но я не уверен, что это значит.
- абстрактная алгебра
- перестановки
$\endgroup$
6
$\begingroup$
Я буду использовать более длинный цикл, чтобы помочь описать два метода записи непересекающихся циклов как произведения транспозиций:
Допустим, $\tau = (1, 3, 4, 6, 7, 9) \in S_9$
Затем обратите внимание на шаблоны:
Метод 1: $\tau = (1, 3, 4, 6, 7, 9) = (1, 9)(1, 7)(1, 6)(1, 4)(1, 3)$
Метод 2: $\tau = (1, 3, 4, 6, 7, 9) = (1, 3)(3, 4)(4, 6)(6, 7)(7, 9)$
Оба произведения транспозиций, метод $1$ или метод $2$, представляют одну и ту же перестановку, $ \тау$. Заметим, что порядок непересекающегося цикла $\tau$ равен $6$, но в обоих выражениях $\tau$ как произведения транспозиций $\tau$ имеет $5$ (нечетное число) транспозиций. Следовательно, $\tau$ — нечетных перестановок.
Заметим, что порядок непересекающегося цикла $\tau$ равен $6$, но в обоих выражениях $\tau$ как произведения транспозиций $\tau$ имеет $5$ (нечетное число) транспозиций. Следовательно, $\tau$ — нечетных перестановок.
Теперь не забудьте перемножить транспозиции, полученные для каждого непересекающегося цикла, чтобы получить выражение перестановки $S_{11}$ как произведение произведения транспозиций, и определить, является ли она нечетной или четное:
$\сигма = (1, 4, 10)(3, 9, 8, 7, 11)(5, 6)$.
$\endgroup$
3
$\begingroup$
Если вы пропустили занятие по циклам, вы можете использовать следующий механизированный подход для записи $\sigma$ как произведения транспозиций:
$(1 \; 4) \circ \begin{pmatrix} 1 & 2 &3 & 4& 5& 6&7 &8 &9 &10 & 11 \\ 4&2&9&10&6&5&11&7&8&1&3 \end{pmatrix} =$ $\quad \quad \quad \begin{pmatrix} 1 и 2 &3 & 4& 5& 6&7 &8 &9&10 & 11 \\ 1 & 2&9&10&6&5&11&7&8&4&3 \end{pmatrix}$
$(3 \; 9) \circ \begin{pmatrix} 1 & 2 &3 & 4& 5& 6&7 &8 &9 &10 & 11 \\ 1 & 2&9&10&6&5&11&7&8&4 \end {pматрица} =$ $\quad \quad \quad \begin{pmatrix} 1 & 2 &3 & 4& 5& 6&7 &8 &9 &10 & 11 \\ 1 & 2&3&10&6&5&11&7&8&4&9 \end{pmatrix}$
$(4 \; 10) \circ \begin{pmatrix} 1 & 2 &3 & 4& 5& 6&7 &8 &9 &10 & 11 \\ 1 & 2&3&10&6&5&11&7&8&4&9 \end{pmatrix} =$ $\quad \quad \quad\; \, \begin{pmatrix} 1 & 2 &3 & 4& 5& 6&7 &8 &9 &10 & 11 \\ 1 & 2&3&4&6&5&11&7&8&10&9 \end{pmatrix}$
$(5 \; 6) \circ \begin{pmatrix} 1 & 2 &3 и 4& 5& 6&7 &8 &9&10 & 11 \\ 1 & 2&3&4&6&5&11&7&8&10&9 \end{pmatrix} = $ $\quad \quad \quad \begin{pmatrix} 1 & 2 &3 & 4& 5& 6&7 &8 &9 &10 & 11 \\ 1 & 2&3&4&5&6&11&7&8&10&9 \end{pmatrix}$
$(7 \; 11) \circ \begin{ pmatrix} 1 и 2 &3 & 4& 5& 6&7 &8 &9 &10 & 11 \\ 1 & 2&3&4&5&6&11&7&8&10&9 \end{pmatrix} = $ $\quad \quad \quad\; \, \begin{pmatrix} 1 и 2 &3 & 4& 5& 6&7 &8 &9&10 & 11 \\ 1 & 2&3&4&5&6&7&11&8&10&9 \end{pmatrix}$
$(8 \; 11) \circ \begin{pmatrix} 1 & 2 &3 & 4& 5& 6&7 &8 &9 &10 & 11 \\ 1 & 2&3&4&5&6&7&11&9&10 \end {pматрица} = $ $\quad \quad \quad \; \, \begin{pmatrix} 1 & 2 &3 & 4& 5& 6&7 &8 &9 &10 & 11 \\ 1 & 2&3&4&5&6&7&8&11&10&9 \end{pmatrix}$
$(9 \; 11) \circ\begin{pmatrix} 1 & 2 &3 & 4& 5& 6&7 &8 &9 &10 & 11 \\ 1 & 2&3&4&5&6&7&8&11&10&9 \end{pmatrix} = $ $\quad \quad \quad \; \, \begin{pmatrix} 1 & 2 &3 & 4& 5& 6&7 &8 &9 &10 & 11 \\ 1 & 2&3&4&5&6&7&8&9&10&11 \end{pmatrix}$
$ $
$\tag{ANS} \sigma = (1 \ ;4)\,(3\;9)\,(4\;10)\,(5\;6)\,(7\;11)\,(8\;11)\,(9\; 11)$
$\endgroup$
абстрактная алгебра.
 Запись перестановки как произведения транспозиций
Запись перестановки как произведения транспозицийспросил
Изменено 6 лет, 7 месяцев назад
Просмотрено 2к раз
$\begingroup$
У меня проблема с записью перестановок как произведения непересекающихся циклов. Например, в книге есть следующие циклы:
$(132)=(13)(12)$,
$(1243)(243)=(23)(34)(14)$
Может кто-нибудь объяснить эти два? Кроме того, почему умножение транспозиции само по себе дает перестановку тождества?
Заранее спасибо!
- абстрактная алгебра
- теория групп
- перестановки
$\endgroup$
$\begingroup$
В обозначении продукта перестановки обычно применяются справа налево.
