12. Производная функции
§12. ПРОИЗВОДНАЯ ФУНКЦИИ. ЭКСТРЕМУМЫ ФУНКЦИИ.
Пусть – приращение функции в точке , соответствующее приращению аргумента . Производной функции в точке называется предел
.
Геометрический смысл производной: , т.е. значе- ние производной функции в точке равно угловому коэффициенту касательной, проведенной к графику функции в точке .
Уравнение касательной , проведенной к графику функции в точке с абсциссой :
. Производная функции , рассматриваемая на множестве тех точек, где она существует, сама является функцией
113
и
обозначается .
Процесс нахождения производной называют
также дифференцированием.
Таблица производных основных элементарных функций
1.. 2..
3. . 4. .
5. . 6. . 7. .
8. . 9. .
10. .
11. .
Правила дифференцирования функций
. Пусть – постоянная, – дифференцируемые функции. Тогда:
1. .
2. .
3. .
4. .
5. , .
. (правило дифференцирования сложной функции: .
114
Физический смысл производной
Если –
функция, описывающая закон движения
материальной точки, то первая производная есть
скорость, а вторая производная – ускорение этой точки в момент времени .
Интервалы возрастания и убывания функции Если функция дифференцируема на интервале и ( ) для всех , то функция воз- растает (убывает) на интервале . Экстремумы функции Точка называется точкой максимума (минимума) функции , если существует такая окрестность точки , что для всех точек из этой окрестности выполняется неравенство ( ). Точки, в которых производная функции равна нулю или не существует, называются критическими. Точки экстремума функции находятся среди критических точек.
Достаточное
условие экстремума. Пусть функция
дифференцируема
в некоторой окрестности критической
точки ,
за исключением, быть может, самой этой
точки. Тогда:
1) если при переходе
через точку
меняет знак с плюса на минус, то
– точка максимума функции
;
2)
если при переходе через точку
меняет знак с минуса на плюс, то
– точка минимума функции
.
115
образом значений выбрать наибольшее и наименьшее.
Пример 1. Сколько существует точек на графике функции , в которых касательная параллельна прямой ? Решение. .
Угловой коэффициент касательной, проведенной к графику функции в точке с абсциссой , равен . Прямая параллельна тем касательным, у которых угловой коэффициент равен . Поэтому: ; , откуда находим: , . Ответ: .
Пример 2. Найти
площадь треугольника, образованного
осями координат и касательной к графику
функции в точке с абсциссой Решение. ; ; .
Найти
площадь треугольника, образованного
осями координат и касательной к графику
функции в точке с абсциссой Решение. ; ; .
Уравнение касательной: , т.е. .
Эта прямая пересекает координатные оси в точках и . . Ответ: .
116
Пример 3. Найти середину интервала убывания функции Решение. Функция определена и имеет производную на всей числовой прямой. Она убывает в интервале, где .
.
Итак, функция убывает в интервале . Середина этого интервала: . Ответ: 1.
Пример 4. Найти наибольшее значение функции
на отрезке . Решение. Найдем производную функции :
.
.
Наибольшее значение функции на отрезке равно наибольшему из чисел , , . Имеем: ;
; . Поэтому .
Ответ: .
Пример 5. Найти число точек экстремума функции . Решение. =
117
. . Исследуя знак производной
при переходе через эти критические точки, получаем, что – точка максимума, – точка минимума, а не является точкой экстремума. Ответ: 2. Пример 6. Найти высоту цилиндра наибольшего объема, вписанного в шар радиуса .
Решение. Пусть – радиус основания цилиндра, – высо-та цилиндра. Проведем осевое сечение цилиндра.
.
Из
прямоугольного треугольника ,
т. е. .
е. .
Объем цилиндра: . Нужно найти значение , при котором функция принимает наибольшее значение. . . При переходе через точку производная меня- ет знак с плюса на минус, поэтому – точка максимума
118
функции .
Так как функция
в промежутке
имеет единственную точку экстремума и
это – точка максимума, то при
функция
принимает наибольшее значение в
промежутке
.
Пример 7. Найти все значения параметра , при которых наименьшее значение функции на отрезке отрицательно. Решение. Так как , то .
Обозначим . Тогда искомыми значениями параметра будут те, при которых наименьшее значение функции на отрезке отрицательно.
График
функции
– парабола, ветви которой направлены
вверх; абсцисса вершины параболы: (рис.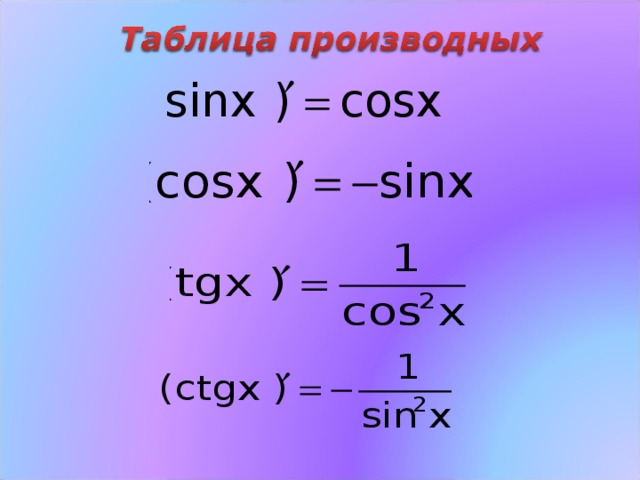 1). (В данной задаче знак дискриминанта
не имеет значения.)
1). (В данной задаче знак дискриминанта
не имеет значения.)
а) б) в)
Рис. 1
Наименьшее значение функции на отрезке в случаях а), б), в) достигается соответственно в точках
119
. Поэтому условию задачи удовлетворяют те значения параметра , которые являются решением совокупности следующих трех систем:
Имеем: ; ; . Следовательно, . Ответ: .
120
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Найти производную функции в точке : а) , ; (Ответ: )
б) , ; (Ответ: )
в) , ; (Ответ: )
г) , ; (Ответ: )
д) , .
2. Угловой коэффициент касательной к графику функции равен значению функции в точке касания.
Найти сумму абсцисс точек касания. (Ответ: 10)
3. Прямая касается параболы в точке
с абсциссой . Найти сумму . (Ответ: 2)
4. Материальная точка движется по оси по закону
( – координата в метрах, – время в
секундах). Через сколько секунд после начала движения
точка остановится? (Ответ: 5)
5. Найти длину отрезка, отсекаемого осями координат на ка-
сательной к кривой , проведенной в точке с
абсциссой . (Ответ: 25)
6. Найти площадь треугольника, образованного координат-
ными осями и касательной к кривой в точке
. (Ответ: )
(Ответ: )
121
7. К графику функции в точке
проведена касательная. Найти расстояние от начала коор-
динат до этой касательной. (Ответ: 0,6)
8. Найдите точки максимума функции . (Ответ: 2)
9. Сколько точек экстремума имеет функция ? (Ответ: 2)
10. Найти длину интервала, на котором функция
убывает. (
11. Найти количество целых чисел, принадлежащих проме-
жутку убывания функции . (Ответ: 4)
12. При каком значении максимум функции равен 2? (Ответ: – 1)
При каком значении максимум функции равен 2? (Ответ: – 1)
13. Найти модуль разности экстремумов функции . (Ответ: 13,5) 14. Найти значение функции в точке ее
минимума. (Ответ: 5)
15. Найти наименьшее значение функции на
отрезке . (Ответ: – 1)
16. Найти наибольшее значение функции
на отрезке . (Ответ: 3)
122
17. Найти наименьшее значение функции на отрезке . (Ответ: 1)
18. Найти наибольшее значение функции ,
если график этой функции проходит через точку .
(Ответ: )
19. Найти сумму
наибольшего и наименьшего целых значений
Найти сумму
наибольшего и наименьшего целых значений
функции
а) ; (Ответ: 10)
б) . (Ответ: 51)
20. Найти максимально возможную площадь прямоугольника
с периметром, равным 72. (Ответ: 324) 21. Найти высоту конуса наибольшего объема, образующая
которого имеет длину . (Ответ: 1) 22. Какую наименьшую площадь может иметь прямоугольный треугольник, на гипотенузе которого лежит точка , а катетами служат отрезки координатных осей? (Ответ: 4)
23.Из трех досок одинаковой ширины сколачивается желоб
для подачи воды. При каком угле наклона боковых сте- нок к днищу желоба площадь поперечного сечения желоба будет наибольшей? (Ответ: )
24. {2}-4ac}}{2a}.
{2}-4ac}}{2a}.
x=\frac{-\left(-23\right)±\sqrt{529-4\times 12\left(-24\right)}}{2\times 12}
Возведите -23 в квадрат.
x=\frac{-\left(-23\right)±\sqrt{529-48\left(-24\right)}}{2\times 12}
Умножьте -4 на 12.
x=\frac{-\left(-23\right)±\sqrt{529+1152}}{2\times 12}
Умножьте -48 на -24.
x=\frac{-\left(-23\right)±\sqrt{1681}}{2\times 12}
Прибавьте 529 к 1152.
x=\frac{-\left(-23\right)±41}{2\times 12}
Извлеките квадратный корень из 1681.
x=\frac{23±41}{2\times 12}
Число, противоположное -23, равно 23.
x=\frac{23±41}{24}
Умножьте 2 на 12.
x=\frac{64}{24}
Решите уравнение x=\frac{23±41}{24} при условии, что ± — плюс. Прибавьте 23 к 41.
x=\frac{8}{3}
Привести дробь \frac{64}{24} к несократимому виду, разделив числитель и знаменатель на 8.
x=\frac{-18}{24}
Решите уравнение x=\frac{23±41}{24} при условии, что ± — минус. Вычтите 41 из 23.
x=-\frac{3}{4}
Привести дробь \frac{-18}{24} к несократимому виду, разделив числитель и знаменатель на 6. {2}}=\sqrt{\frac{1681}{576}}
{2}}=\sqrt{\frac{1681}{576}}
Извлеките квадратный корень из обеих частей уравнения.
x-\frac{23}{24}=\frac{41}{24} x-\frac{23}{24}=-\frac{41}{24}
Упростите.
x=\frac{8}{3} x=-\frac{3}{4}
Прибавьте \frac{23}{24} к обеим частям уравнения.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Цепное правило
Цепное правило
Цепное правило
Наша цель — дифференцировать такие функции, как
y = (3x + 1) 10
Цепное правило Если является функцией u, и ты = u(x) является функцией x затем dy dy
дю |
В нашем примере у нас есть
y =
и 10
и
у =
3x + 1
так что
dy/dx = (dy/du)(du/dx)
= (10u 9 )
(3) = 30u 9 = 30 (3x+1) 9
Доказательство цепного правила
Вспомните альтернативное определение производной:
Примеры
Найти f'(x), если
f(x) = (x 3 — x + 1) 20
f(x) = (x 4 — 3x 3 + х) 5
f(x) = (1 — x) 9 (1-x 2 ) 4
(х 3 + 4х — 3) 7
f(x) =
(2x — 1) 3
Решение:
Здесь
f(u) = u 20
иu(x) = x 3 — х + 1
Так что производная равна[20u 19 ] [3x 2 — 1] = [20(x 3 — x + 1) 19 ] [3x 2 — 1]
Здесь
f(u) = u 5
иu(x) = x 4 — 3x 3 + x
Так что производная равна[5u 4 ] [4x 3 — 9x 2 + 1] = [5(x 4 — 3x 3 ) + х) 4 ] [4x 3 — 9x 2 + 1]
Здесь нам нужны и произведение, и цепное правило.

f'(x) = [(1 — х) 9 ] [(1 — х 2 ) 4 ]’ + [(1 — х) 9 ] ‘ [(1 — x 2 ) 4 ]
Сначала мы вычисляем[(1 — x 2 ) 4 ] ‘ = [4(1 — х 2 ) 3 ] [-2x]
и[(1 — x) 9 ] ‘ = [9(1 — x) 8 ] [-1]
Собрав все это вместе, мы получимf'(x) = [(1 — х) 9 ] [4(1 — х 2 ) 3 ] [-2x] — [9(1 — x) 8 ] [(1 — x 2 ) 4 ]
Здесь нам нужны и частное, и цепное правило.
(2x — 1) 3 [(х 3 + 4х — 3) 7 ] ‘ — (x 3 + 4x — 3) 7 [(2x — 1) 3 ]
f ‘(x) =
(2x — 1) 6
Сначала мы вычисляем[(x 3 + 4x — 3) 7 ] ‘ = [7(x 3 + 4x — 3) 6 ] [3x 2 + 4]
и[(2x — 1) 3 ] ‘ = [3(2x — 1) 2 ] [2]
Все это вместе дает.
 7(2x — 1) 3 (x 3 + 4x — 3) 6 (3x 2 +
4) + 6(x 3 + 4x — 3) 7 (2x — 1) 2
7(2x — 1) 3 (x 3 + 4x — 3) 6 (3x 2 +
4) + 6(x 3 + 4x — 3) 7 (2x — 1) 2
f ‘(x) =
(2x — 1) 6
Упражнение
Найдите производную отх 2 (5 — х 3 ) 4
f(x) =
3 — х
Заявка
Предположим, вы положили в банк 1000 долларов под процентную ставку. r начисляется ежемесячно в течение 3 лет. Тогда сумма А, которая будет на счету в конце из трех лет будет
А = 1000(1 + г/12) 36
Найдите скорость, с которой растет А по отношению к увеличению процентной ставки.


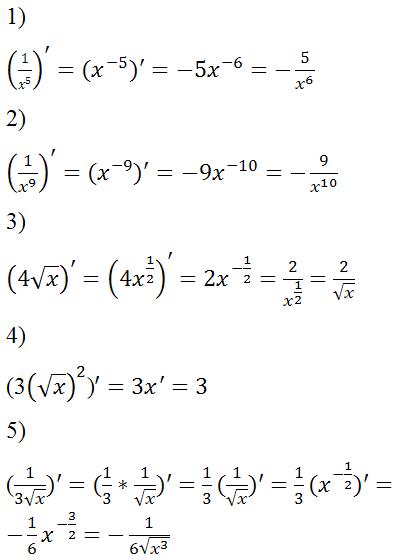 7(2x — 1) 3 (x 3 + 4x — 3) 6 (3x 2 +
4) + 6(x 3 + 4x — 3) 7 (2x — 1) 2
7(2x — 1) 3 (x 3 + 4x — 3) 6 (3x 2 +
4) + 6(x 3 + 4x — 3) 7 (2x — 1) 2