Производная.Таблица производных. Найти производную функции.
- Альфашкола
- Статьи
- Производная
Дифференциальное исчисление было изобретено Ньютоном и Лейбницем в конце \(17\) века. Это дало мощный толчок в развитии математических исследований. Дифференциальное исчисление радикально изменило математику, как в практических, так и в теоретических вопросах. Операция нахождения производной функции называется дифференцированием.
В учебной программе по естественным наукам и технике дифференциальное исчисление образует мост между элементарной математикой, такой как геометрия, алгебра и тригонометрия, векторный анализ и сложные переменные.
Дифференциальное исчисление использует определение производной и свободно использует такие понятия, как дифференциал \(dx\), который отличается от конечной разности Δx. Производная может быть записана \(\frac{dy}{dx}\). Символ \(\frac{dy}{dx}\) используется двояко – как цельный символ производной и как частное дифференциалов.
В самом определении производной в точке подставим на \(x:\)
\(f'(x_0)=\lim\limits_{Δx\to 0} \frac{f(x_o+Δx)-f(x_0)}{Δx}=\lim\limits_{Δx\to 0} \frac{Δy}{Δx};\)
\(f'(x)=\lim\limits_{Δx\to 0} \frac{f(x+Δx)-f(x)}{Δx}=\lim\limits_{Δx\to 0} \frac{Δy}{Δx};\)
Итого функция определяется \(y=f(x)\) по закону:
\(\lim\limits_{Δx\to 0} \frac{f(x+Δx)}{Δx}\)
в соответствии другой функции \(y’=f'(x)\) , которая называется производной функцией или просто производной.
\frac{5}{3}\).
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Kateryna Toprak
Репетитор по математике
Стаж (лет)
Образование:
Erciyes üniversitesi
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
6 yıldır Türkiye’ de yaşamaktayım.
Rusça ve Ukraynaca dillerine ana dilim olması sebebiyle ve de Rus Dili Edebiyatı mezunu olmam sebebiyle hem teorik hem pratikte hakimim.
2018’ den bu yana Türklere Rusça öğretmenliği yapmaktayım. Derslerimizi hedeflerinize ve seviyenize göre hazırlamaktayım, (konuşma, dinleme ve okuma aktiviteleri uyguluyorum). Ana dilimi anlatmaktan çok keyif alıyorum ve eminim ki siz de alırsınız.
2019′ den bu yana yabancilara (Rusça bilenlere) Türkçe öğretmenliği yapmaktayım.
Анастасия Сергеевна Черная
Репетитор по математике
Стаж (лет)
Образование:
Кубанский Государственный Университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5-11 классов.
Подготовка к ОГЭ, ЕГЭ (базовый и профильный). Люблю математику за то, что она развивает аналитическое и критическое мышление
Системно-деятельностный подход
Информационно-развивающий и репродуктивный методы
Подробное и доступное объяснение, уважительное отношение, индивидуальный подход
Умею находить подход к ученикам любого уровня подготовки.
Андрей Алексеевич Тарасов
Репетитор по математике
Стаж (лет)
Образование:
Новосибирский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-11 классов, ВПР/ОГЭ/ЕГЭ, и по физике 6-9 классы ВПР/ОГЭ.
Убежден, что математику может понять каждый человек.
Со мной вы получите заряд уверенности в себе, поймете, что математика — это не скучно, а безумно интересно!
С нетерпением жду всех на занятиях!
Похожие статьи
- Периметр параллелограмма
- Объем прямоугольной призмы
- Конус
- ОГЭ по математике, базовый уровень. Простейшие уравнения
- Решаем текстовые задачи
- Комплексы из-за внешности: учимся любить себя на примере звезд
- Традиции и приметы на Хэллоуин: празднуем «страшный» праздник по всем правилам
- Как организовать режим школьника на каникулах, чтобы потом было легче снова идти в школу
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Производная функции
Исторически математический анализ произошёл из задач механики, из необходимости
описывать движение физических тел, их скорости и ускорения.
15.1Определение производной
15.1.1Функции как динамические процессы
Рассмотрим функцию y=f(x) и пусть x — это время, а y — результат измерения какой-то величины в момент времени x. Это может быть артериальное давление у пациента, или популяция некоторого вида, или количество людей, зараженных вирусом — что угодно. Но проще всего про это думать так: есть точка, которая может двигаться вверх и вниз, f(x) — это вертикальная координата (то есть просто высота) этой точки в момент времени x. Тогда про эту функцию можно думать в динамических терминах. Например, рассмотрим функцию, заданную графиком на рис. 15.1.
Рис. 15.1: График функции
Этот график можно интерпретировать следующим образом. В момент времени x=−4
точка находилась на высоте y=−1.
Рис. 15.2: График функции и движение точки
Именно такую интерпретацию функций мы будем использовать в дальнейшем в этой лекции.
15.1.2Производная как мгновенная скорость
Рассмотрим функцию, заданную графиком на рис. 15.3. Пусть нас интересует скорость движения точки в какой-то момент времени x0.
Рис. 15.3: Вычисление средней скорости движения на интервале времени от x0 до x0+Δx.
В школе нас учат, что чтобы найти скорость, нужно поделить расстояние на время.
Рассмотрим период от момента x0 до момента x0+Δx, где
Δx — какое-то небольшое число. (Выражение Δx нужно воспринимать
как неделимый символ, читается «дельта-икс».) В начале периода точка имела
высоту f(x0), а в конце — f(x0+Δx). Пройденное расстояние между
двумя моментами равно разности этих двух значений:
расстояние=f(x0+Δx)−f(x0)
Тут нужно иметь в виду, что нас интересует «чистое расстояние», вычисляемое с учётом знака — не «сколько мы проехали», а «на сколько поднялись». Например, если в течение этого промежутка точка в какой-то момент двигалась вниз, в это время «пройденное расстояние» уменьшалось, а не увеличивалось. Также «расстояние» может быть отрицательным, если новое значение высоты f(x0+Δx) окажется меньше исходного (то есть в итоге точка опустилась ниже, чем была).
Вернёмся к вычислению скорости. Время движения равно просто Δx. Значит, скорость движения — вернее, средняя скорость движения на интервале от x0 до x0+Δx находится по формуле:
средняя скорость=f(x0+Δx)−f(x0)Δx
Однако, нужно иметь в виду, что на промежутке от x0 до x0+Δx
движение не обязано быть равномерным — в какие-то моменты точка могла двигаться
быстрее, в какие-то медленнее.
Нас же интересует, что происходит в сам момент
времени x0, интересует мгновенная скорость в этот момент. Чтобы
изменение скорости на промежутке длиной Δx не влияло на оценку скорости
в момент x0, нужно сделать длину этого промежутка как можно меньше. Иными
словами, перейти к пределу при Δx→0. Так мы и получим производную.
Определение 1.Производная функции f в точке x0 равна мгновенной скорости изменения функции в этой точке. Она обозначается через f′(x0) и определяется следующим образом:
f′(x0)=limΔx→0f(x0+Δx)−f(x0)Δx.(15.1)
f′(x0)==limΔx→0f(x0+Δx)−f(x0)Δx.(15.1)
Также можно обозначить x:=x0+Δx и записать тот же предел следующим образом:
f′(x0)=limx→x0f(x)−f(x0)x−x0.(15.2)
15.2Интерпретация производной
15.2.1Линейная функция и равномерное движение
Рассмотрим функцию f(x)=kx+b. Это хорошо известная линейная функция (по
крайней мере, в матанализе её называют именно так, хотя специалисты по линейной
алгебре с этим могли бы и поспорить).
Возьмём произвольный начальный момент
x0, произвольный промежуток длины Δx и посчитаем среднюю скорость за этот
промежуток:
ср. скорость=f(x0+Δx)−f(x0)Δx=k(x0+Δx)+b−(kx0+b)Δx==kx0+kΔx+b−kx0−bΔx=kΔxΔx=k.
ср. скорость=f(x0+Δx)−f(x0)Δx==k(x0+Δx)+b−(kx0+b)Δx==kx0+kΔx+b−kx0−bΔx==kΔxΔx=k.
Итак, каким бы ни был начальный момент и какой бы промежуток мы ни взяли, средняя скорость будет всегда одинаковой и равной k. Таким образом, линейная функция задаёт движение с постоянной скоростью. Производная линейной функции, как следует из определения, во всех точках одинакова и равна k.
Коэффициент k называется угловым коэффициентом линейной функции f(x)=kx+b (или угловым коэффициентом прямой, которая является графиком этой функции). Он показывает, на сколько позиций мы сдвинемся вверх, если подождём одну единицу времени (то есть сдвинемся на одну единицу по горизонтали), см. рис. 15.4.
Рис. 15.4: Линейная функция y=kx+b, её график и смысл коэффициентов.
Коэффициент
b задаёт смещение по вертикали, а k — наклон прямой.
Геометрически, угловой коэффициент — это тангенс угла наклона прямой, заданной как график линейной функции, к горизонтальной оси.
15.2.2Секущие и касательные
Рассмотрим теперь какую-нибудь нелинейную функцию, например, такую, график
которой изображён на рис. 15.5. Пусть нас интересует производная в
точке x0. Рассмотрим выражение под знаком предела в определении производной
(15.1) и возьмём какое-то конкретное значение Δx.
Проведём прямую через точки (x0,f(x0)) и (x+Δx,f(x+Δx)). Она
называется секущей для графика функции y=f(x). Поскольку секущая — это
прямая, она является графиком линейной функции. Угловой коэффициент этой прямой
как раз и равен средней скорости. Иными словами, если мы хотим двигаться
равномерно (с постоянной скоростью) на промежутке времени от x0 до x0+Δx и при этом пройти именно то расстояние, которое мы прошли: от f(x0) до
f(x0+Δx), то нужно двигаться как раз со средней скоростью на этом
промежутке.
Рис. 15.5: Секущая к графику функции
Будем теперь уменьшать Δx. В этом случае одна точка на графике будет неподвижной, а другая будет к ней приближаться, см. анимацию на рис. 15.6. Секущая при этом может поворачиваться вокруг точки (x0,f(x0)). Однако если существует предел в определении производной, то у секущей будет существовать предельный угловой коэффициент, и значит предельное положение — она будет «стремиться» (в кавычках — потому что мы не определяли, что может значить «стремиться» для прямых) к прямой, проходящей через точку (x0,f(x0)) с угловым коэффициентом k=f′(x0). У этой прямой есть специальное название: касательная.
Определение 2. Касательная к графику функции y=f(x) в точке x0 — это прямая, проходящая через точку (x0,f(x0)) и имеющая угловой коэффициент k=f′(x0).
Рис. 15.6: Секущая стремится к касательной
Про касательную можно думать так. Представьте себе, что график на
рис.
15.5 вблизи точки (x0,f(x0)) вырезан из фанеры —
вернее, то, что находится над графиком — это кусок фанеры, а то, что под
графиком, мы отрезали лобзиком (ровно по графику). Теперь можно взять недлинную
линейку и приложить её к графику в точке (x0,f(x0)) как можно плотнее.
Тогда линейка пройдёт ровно вдоль касательной, см. рис. 15.7.
Рис. 15.7: Нахождение касательной с помощью линейки.
Рис. 15.8: В отличие от касательной к окружности, касательная к графику функции может иметь больше одной точки пересечения с графиком
15.2.3Производная как функция
Выбирая разные точки в качестве x0 в определении производной, мы будем получать разное значение предела (15.1). Таким образом, производная функции — это новая функция.
Полезно представлять себе визуально, как связан график функции и график её
производной. По определению, производная — это мгновенная скорость возрастания
функции в точке. Таким образом, если по графику видно, что где-то функция
возрастает, то её производная там положительна.
Если возрастает быстро, производная
большая. Если убывает, производная отрицательна, и так далее. (Аккуратные
формулировки для этих утверждений мы приведём позже, а потом их докажем.) Можно
мысленно прикладывать касательные в разных точках, прикидывать их угловые
коэффициенты и находить таким образом точки на графике производной.
Рассмотрим, например, график, изображенный на рис. 15.9 сверху, и прикинем, чему равна производная в отмеченных точках.
Рис. 15.9: Связь графика функции с графиком касательной.
В точке x1 функция убывает, равно как и в точке x2. Но если посмотреть на
касательные в этих точках, видно, что в x1 функция убывает быстрее, чем в
x2 (в x1 касательная ближе к вертикальной, график более крутой, чем в
x2), то есть f′(x1)<f′(x2)<0. Можно отметить на графике касательной
две точки: они обе должны быть ниже горизонтальной оси, и точка, соответствующая
x1, ниже, чем та, которая соответствует x2. Теперь посмотрим на точку
x3=0.
В ней касательная горизонтальна. Выражаясь динамическим языком, это
момент разворта: левее мы двигались вниз (функция убывала), в момент времени 0
на мгновение остановились и потом стали двигаться вверх. Мгновенная скорость в
точке 0 равна нулю. Это значит, что соответствующая точка на графике
касательной будет лежать на горизонтальной оси. Наконец, можно посмотреть на
точки x4 и x5. Мы видим, что в обоих точках функция возрастает, но в x5
возрастает быстрее, чем в x4 — график со временем становится начинает расти
круче. Это означает, что производная в точке x5 больше производной в x4, и
это также нужно отразить на графике производной. Получается кривая, похожая на
изображенную на рисунке 15.9 внизу.
Весь этот анализ мы провели, исходя просто из формы графика, не обращаясь к
формулам. Конечно, наш результат носит качественный характер — чисто глазомерно
нельзя найти точных значений производной функции, которая задана графиком,
нарисованным от руки. Тем интереснее сравнить эти «глазомерные» результаты с
точно посчитанными.
График, который мы нарисовали, похож на параболу, график функции f(x)=x2. Давайте найдём её производную, пользуясь опредлением:
f′(x0)=limΔx→0(x0+Δx)2−x20Δx=limΔx→0x20+2×0Δx+Δx20−x20Δx=limΔx→0(2×0+Δx)=2×0.
f′(x0)=limΔx→0(x0+Δx)2−x20Δx==limΔx→0x20+2×0Δx+Δx20−x20Δx==limΔx→0(2×0+Δx)=2×0.
Точка x0 произвольная, можно заменить её просто на x и записать f′(x)=2x. Скорее всего, вы помните эту формулу из школьного курса. Таким образом, график производной — это прямая линия. И она ведёт себя именно так, как мы нарисовали!
15.3Существование производной
15.3.1Дифференцируемость и непрерывность
Всякий раз, когда мы видим определение, заданное с помощью предела, мы должны задать вопрос: а всегда ли существует этот предел? Как правило, ответ: «не всегда». Это относится и к производной.
Определение 3. Если у функции f существует производная в точке x0, функция назыается дифференцируемой в этой точке.
Что может помешать функции быть дифференцируемой? Много что.
Во-первых, чтобы предел (15.1) в принципе имел бы смысл, функция f должна быть определена в точке x0 (иначе нельзя посчитать f(x0)) и некоторой её окрестности (иначе нельзя посчитать f(x0+Δx)). Но этого, конечно, мало.
Необходимым условием дифференцируемости является непрерывность. Если функция не является непрерывной в точке, то она точно не является дифференцируемой в этой точке. Это можно сформулировать в виде следующей теоремы.
Теорема 1. Если функция f дифференцируема в точке x0, то она непрерывна в этой точке.
Доказательство. Пусть мы знаем, что производная существует, то есть существует предел
limΔx→0f(x0+Δx)−f(x0)Δx=f′(x0).
Чтобы доказать непрерывность функции f в точке x0, нужно изучить предел limx→x0f(x), или, что то же самое,
limΔx→0f(x0+Δx).
Преобразуем выражение под знаком предела.
Во-первых, вычтем и добавим
f(x0):
limΔx→0f(x0+Δx)=limΔx→0(f(x0+Δx)−f(x0)+f(x0))=….
limΔx→0f(x0+Δx)==limΔx→0(f(x0+Δx)−f(x0)+f(x0))=….
Теперь возьмём первые два слагаемые и умножим и поделим их на Δx (под знаком предела Δx не может обращаться в ноль, поэтому операция корректна):
…=limΔx→0(f(x0+Δx)−f(x0)Δx⋅Δx+f(x0)).
Теперь заметим, что выражение f(x0+Δx)−f(x0)Δx стремится к f′(x0) при Δx→0, Δx стремится к нулю, значит, их произведение стремится к f′(x0)⋅0=0. Предел второго слагаемого, числа f(x0), равен ему самому (это константа, не зависящая от Δx). Значит, предел всего выражения равен 0+f(x0), то есть f(x0). Значит
limx→x0f(x)=limΔx→0f(x0+Δx)=f(x0)
и функция f непрерывна в точке x0.∎
15.3.2Точки изломов
Итак, чтобы быть дифференцируемой в некоторой точке, функция должна быть по
меньшей мере непрерывной в этой точке.
Но достаточно ли этого? Оказывается, нет.
Пример 1. Рассмотрим функцию f(x)=|x|, см. рис. 15.10.
Рис. 15.10: График функции y=|x|.
Есть ли у неё производная в точке x0=0? Давайте найдём предел:
limΔx→0|0+Δx|−|0|Δx=limΔx→0|Δx|Δx.
Модуль раскрывается по-разному в зависимости от знака Δx. Как мы обсуждали выше (см. замечание 1), Δx не обязана быть положительной, и нужно рассмотреть два случая. Если Δx>0, выражение под знаком предела превращается в 1, то есть
limΔx→0+|Δx|Δx=limΔx→0+1=1.
Для отрицательных Δx модуль раскрывается со знаком минус, и дробь равна −1. Значит,
limΔx→0−|Δx|Δx=limΔx→0−(−1)=−1.
Таким образом, при приближении к нулю с разных сторон, функция стремится к разным значениям, и общего предела нет. Функция не дифференцируема в точке x=0.
Графически, это соответствует тому, что у неё в точке x=0 наблюдается
излом.
Если проводить секущие, то при Δx>0 они будут совпадать с
прямой y=x, а при Δx<0 — с прямой y=−x. Никакого общего
предельного положения секущей не будет, и касательной в точке x=0 тоже не
будет.
15.3.3Вертикальные касательные
Точки изломов, как у функции f(x)=|x| — один из механизмов, как непрерывная функция может быть не дифференцируемой. Но он не единственный.
Пример 2. Рассмотрим функцию f(x)=3√x−1. Попробуем построить касательную в
точке x0=1. На анимации на рис. 15.11 видно, что по
мере приближения второй точке пересечения к точке (1,0), секущая
становится всё вертикальнее и вертикальнее. Можно аккуратно доказать (вы
сделаете это на семинаре), что предел в определении производной в этом
случае равен бесконечности, то есть не существует. Касательная тоже не
существует — по крайней мере, в соответствии с нашим определением. Можно
было бы сказать, что касательная вертикальна, но вертикальная прямая не
является графиком функции y=kx+b, и это потребовало бы расширения нашего
определения касательной — чего мы делать не будем, поскольку в этом сейчас
нет никакой непосредственной необходимости.
Рис. 15.11: Вертикальная касательная
Вертикальные касательные и изломы — не единственные причины, по которым функция может не будет дифференцируемой — но, пожалуй, самые важные с практической точки зрения. С некоторыми другими способами вы встретитесь на семинаре.
15.4Касательные и линейные приближения
15.4.1Формулировка и иллюстрация
По своему смыслу, касательная — это такая прямая, которая проходит вблизи графика функции (что, собственно, и означает «касается»). Чтобы придать этому аккуратный смысл, сформулируем такое утверждение.
Утверждение 1. Функция f дифференцируема в точке x0 тогда и только тогда, когда существует такое число k∈R и такая функция α(Δx), определенная в проколотой окрестности нуля, и стремящаяся к нулю при Δx→0, что справедливо равенство
f(x0+Δx)=f(x0)+kΔx+α(Δx)⋅Δx.(15.3)
f(x0+Δx)==f(x0)+kΔx+α(Δx)⋅Δx.(15.3)
В этом случае k=f′(x0).
Прежде, чем приступить к доказательству, давайте обсудим, что всё это значит. Что означает условие (15.3)? С помощью замены x=x0+Δx, его можно переписать в таком виде:
f(x)=f(x0)+k(x−x0)+α(x−x0)⋅(x−x0).(15.4)
f(x)==f(x0)+k(x−x0)++α(x−x0)⋅(x−x0).(15.4)
Пусть f дифференцируема в точке x0 и k=f′(x0). Рассмотрим функцию l, заданную следующим образом:
l(x)=f(x0)+f′(x0)⋅(x−x0).
Это линейная функция, графиком которой является касательная к графику y=f(x) в точке x0. Действительно, во-первых, она проходит через точку (x0,f(x0)) (подставьте x=x0 и убедитесь в этом). А во-вторых, её угловой коэффициент равен значению производной в точке x0.
Таким образом, равенство (15.4) записывается в виде:
f(x)=l(x)+α(x−x0)⋅(x−x0).(15.5)
f(x)==l(x)+α(x−x0)⋅(x−x0).(15.5)
Если бы в нём не было второго слагаемого, это бы просто означало, что функция
линейна и её график совпадает с касательной.
Второе слагаемое, α(x−x0)⋅(x−x0) показывает, на сколько сильно график функции отклоняется от
касательной, см. рис. 15.12.
Рис. 15.12: Отклонение графика функции от касательной
Утверждение, которое мы сейчас рассматриваем, говорит, что это отклонение становится маленьким, если Δx маленькое — но не просто маленьким, а «маленьким по сравнению с Δx». Действительно, если вернуться к выражению (15.3), в правой части мы видим три слагаемых: f(x0), kΔx и α(Δx)Δx. Второе и третье слагаемые оба становятся маленькими при маленьких Δx. Но при этом второе слагаемое пропорционально Δx, а третье — уменьшается быстрее, чем Δx. Например, если k=1/10, выражение kΔx всегда ровно в десять раз меньше Δx, а выражение α(Δx)Δx при уменьшении Δx становится в десять, потом в сто, потом в тысячу раз меньше Δx — и так во сколько угодно раз меньше.
Почему это важно? Давайте посмотрим на график какой-нибудь функции вблизи фиксированной точки, см. рис. 15.13.
Рис.
15.13: Увеличение графика функции и касательной вблизи фиксированной точки.
На каждом графике мы выбираем область вблизи точки (x0,f(x0)) (она
нарисована зелёным) и растягиваем её на всю картинку — так получается
следующий график.
На первом графике различие между графиком нашей функции и её касательной было хорошо заметно, при каждом увеличении это различие становилось всё меньше и меньше, и на последней картинке настоящий график практически не виден — его полностью загораживает касательная, то есть две кривые почти совпадают. Почему так происходит?
Чтобы посмотреть на график под большим увеличением вблизи точки (x0,f(x0)),
нужно выбрать на исходной картинке небольшой прямоугольник вблизи этой точки и
растянуть его на всю картинку. Пусть в качестве этого прямоугольника мы взяли
квадрат со стороной 2h (то есть отступили от точки x0 вправо и влево на
h, и аналогично по вертикали отступили от f(x0) вверх и вниз на h). Если
мы теперь растянем этот квадратик на всю картинку (допустим, размера 1 на 1), то
все расстояния умножатся на 1/h.
(Когда h маленькое, 1/h
большое и произойдёт сильное увеличение.)
Посмотрим теперь на формулу (15.5). Она говорит, что разница между графиком функции и касательной равна α(Δx)Δx. Поскольку мы рисуем только часть картинки в нашем квадратике, |Δx|≤h. В новом масштабе, с учётом растяжения в 1/h раз, соответствующее расстояние между графиками окажется равно
|α(Δx)||Δx|h≤|α(Δx)|.
Но если h маленькое, то |Δx| маленький и эта величина стремится к нулю! Таким образом, результат, который мы видим на рис. 15.13, не является чем-то удивительным — в нём вся суть понятия касательной, и на самом деле вся суть идеи дифференцируемости: вблизи фиксированной точки дифференцируемая функция очень близка к линейной функции, задающей касательную в этой точке.
15.4.2Доказательство утверждения о линейном приближении
Доказательство утверждения 1. Нам нужно доказать эквивалентность двух утверждений:
- функция f дифференцируема в точке x0;
- существует представление (15.
3), которое говорит о
том, что функция f хорошо приближается некоторой линейной
функцией в окрестности точки x0.
3), которое говорит о
том, что функция f хорошо приближается некоторой линейной
функцией в окрестности точки x0.Из дифференцируемости следует линейное приближение. Пусть функция f дифференцируема в точке x0. Положим k=f′(x0) и
α(Δx):=f(x0+Δx)−f(x0)Δx−k.
В этом случае представление (15.3) соблюдается (я просто выразил α(Δx) из него), и содержательным является утверждение, что α(Δx)→0 при Δx→0. Докажем его:
limΔx→0α(Δx)=limΔx→0(f(x0+Δx)−f(x0)Δx−k)=f′(x0)−k=0.
limΔx→0α(Δx)==limΔx→0(f(x0+Δx)−f(x0)Δx−k)==f′(x0)−k=0.
Мы воспользовались определением производной, теоремой о пределе суммы и тем фактом, что мы сами выбрали k=f′(x0).
Из линейного приближения следует дифференцируемость. Наборот, пусть теперь известно, что представление (15.3) верно для какого-то k и α(Δx), причём α(Δx)→0. Докажем, что функция f дифференцируема в точке x0 и f′(x0)=k. Из (15.3) следует, что
α(Δx)=f(x0+Δx)−f(x0)Δx−k.
Перенесём k в левую часть и перейдём к пределу при Δx→0. Имеем:
limΔx→0f(x0+Δx)−f(x0)Δx=limx→Δxα(Δx)+k=k.
limΔx→0f(x0+Δx)−f(x0)Δx==limx→Δxα(Δx)+k=k.
Мы воспользовались тем фактом, что α(Δx)→0 при Δx→0 и пределом суммы. Теперь в левой части стоит определение производной функции f в точке x0, а справа k. Значит, производная существует и равна k.∎
15.5Заключение
Производная — мощный инструмент анализа функций. Мы аккуратно ввели это понятие и обсудили механическую и геометрическую интуицию, которая за ним стоит. На следующей лекции мы обсудим, как находить производные, а затем — как их применять.
← Предыдущая глава Следующая глава →
Что такое производная? Геометрический и физический смысл производной
Производная функции − это результат дифференцирования функции.
Дифференцирование в математике — это процесс, при котором функция f превращается в другую функцию f’ («производная от f»).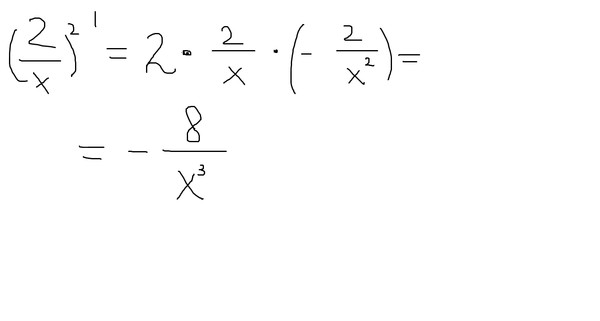
Простыми словами, производная — это средний наклон между двумя точками:
Интегрирование — это обратный процесс, т. е. восстановление функции по данной производной.
Например, функция x² (на графике выше) является одним из интегралов от 2x (пунктирная синяя линия), поскольку производная x² равна 2x.
Геометрический смысл производной функции
Производная функции f(x) в данной точке — это наклон касательной f(x) в точке a, как показано на рисунке.
Эта прямая линия образует угол, который на данном рисунке мы назвали β и он зависит от наклона касательной (она является производной в данной точке). Таким образом: tan β = f´(a).
Физический смысл производной функции
Представьте точку, которая движется по прямой с постоянно меняющейся скоростью. Её скорость постоянно меняется, поэтому она рассчитывается в момент «t0». Для этого нам нужно рассчитать короткий промежуток времени Δt, а расстояние, которое точка пройдёт за это время будет ΔS.
Таким образом её скорость будет примерно ΔS / Δt. Чем меньше промежуток времени Δt, тем точнее будет результат (скорость). Самую точную мгновенную скорость точки в момент t0 можно получить, если рассчитать предел Δt —>0. Таким образом:
Таблица производных функций
Как пользоваться этой таблицей?
Например, производная линейной функции a*x равна константе, стоящей вместе с переменной x, т. е.: (а*x)′ = а.
Или нужно найти производную функции f(x) = 2 cos x:
f’(x) = (2 cos x)’ = 2 (cos x)’ = 2 (– sin x) = –2 sin x
Как найти производную?
Пример 1
f(x) = 6x³
f′(x) = 3 * 6x²
f′(x) = 18x²
Степень от x спускается и из неё нужно вычесть 1.
Пример 2
f(x) = 3x³ – 5x² + 6x − 5
f'(x) = 3*3x² – 2*5x¹ + 6 − 0
f(x) = 9x² – 10x + 6
Пример 3
f(x) = (x−4) (2x+x²)
Нужно сначала раскрыть скобки:
f(x) = (x−4) (2x+x²)=
f(x) = 2x² − 8x + x³ − 4x²
f(x) = x³ − 2x² − 8x
Теперь можно приступать к поиску производной, как и в предыдущих примерах степень от x спускается и из неё нужно вычесть 1:
f´(x) = (x³ − 2x² − 8x)´=
f´(x) = 3x² − 2*2x¹ − 8 =
f´(x) = 3x² − 4x − 8
Пример 4
f(x) = √x
Переведём сначала корень в степень:
f(x) = x ^ (½)
Теперь можно производить вычисления производной с обычной формулой степеней:
f´(x) = ½ * x ^ (½ – 1)
f´(x) = ½ * x ^ (– ½)
f´(x) = ½ * (1/√x)
Можно остановиться здесь, но бывает, что ответ с корнем в знаменателе не считается совсем правильным, поэтому умножаем всю вторую дробь на «√x/√x».
(1/√x) * (√x/√x) = √x/x
Значит правильный и «красивый» ответ:
f´(x) = ½ * (√x/x)
Пример 5
f(x) = sin x − cos x
Из таблицы мы знаем:
(sin x)´ = cos x
(cos x)´ = − sin x
Так как это вычитание, осталось только подставить:
f´(x) = (sin x − cos x)´
f´(x) = cos x − (− sin x)
f´(x) = cos x + sin x
Сложные функции — примеры
Правило сложной функции:
(u (v))´ = u´ (v) * v´
Пример
1. Сначала нужно разобраться, что «arctg x» является нашей простой (внутренней) частью функции, это наше “v” формулы.
2. Применяем формулу корня из таблицы в левой части, получится 1/2 √arctg x, оставляя правую нерешённой.
3. Применяем формулу arctg x из таблицы (1/ (1 + x²)).
4. Совмещаем и готово
4.1. Если хотите «красивый» ответ, нужно убрать корень из знаменателя, умножая всю эту дробь на √arctgx / √arctgx.
Получится √arctgx / (2 (1 + x²) arctgx)
Как определить знак производной?
1.
Определить точки, в которых производная равна нулю (также называются критическими точками).
2. Начертить таблицу, в которую вставляются все критические точки, а между ними оставляются незаполненными по одному окошку.
3. Выбрать значения x до и после полученного интервала, подставить в производную. Если значение получилось больше нуля, то знак будет плюс, если меньше — минус.
Пример:
y = x² – 6x + 17
Её производная y’ = 2x – 6.
Расчёт критических точек:
y’ = 0
2x – 6 = 0
2x = 6
x = 3
Значит в нашей таблице будет только одна критическая точка x = 3, и оставим место на «до» и «после».
| x < 3 | x = 3 | x > 3 |
|---|---|---|
| 0 |
Далее выбираем любой x сначала меньше 3, а потом больше 3.
1. для x < 3 выбираем, например, x = 1 и подставляем в производную y’ = 2x – 6 ⇔ y’(1) = 2 * 1 – 6 = -4 <0, значит в таблицу записываем «–» (это означает, что в этой точке функция убывает).
2. для x > 3 выбираем, например, x = 4 и подставляем в производную y’ = 2x – 6 ⇔ y’(4) = 2 * 4 – 6 = 2 >0, значит в таблицу записываем «+» (это означает, что в этой точке функция возрастает).
| x < 3 | x = 3 | x > 3 |
|---|---|---|
| – | 0 | + |
Вторая производная
Можно вычислить и «производную производной», обозначается она как y’’. Если использовать предыдущий пример:
y = x² – 6x + 17
- её производная y’ = 2x – 6
- вторая производная y’’ = (2x – 6)’ = 2
Её физический смысл: это скорость изменения скорости движения точки, которая принадлежит графику функции.
Что такое композиция функций?
Иногда называется сложной функцией.
Сложная функция обычно записывается как (f o g) (x), т. е. можно «изобразить g (x) через f (x)» или наоборот.
Например, даны две функции: f (x) = 2x + 3 и g (x) = – x² + 5.
Требуется узнать (f o g) (x), это означает «f (g (x))».
Решение:
Нужно подставить в функцию f (вместо x) функцию g
(f o g) (x) = f (g (x)) = f (–x² + 5) = 2 (–x² + 5) + 3 = – 2x² + 10 + 3 = – 2x² + 13
Если нужно узнать (g o f) (x), это «g (f (x))».
Решение:
(g o f) (x) = g (f (x)) = g (2x + 3) = – (2x + 3)² + 5 = – (4х² + 12x + 9) + 5 = – 4х² – 12x – 9 + 5 = – 4х² – 12x – 4
Узнайте также про Интегралы и Логарифмы.
DMCA (Copyright) Complaint to Google :: Notices :: Lumen
sender
4book
[Private] UA Sent on COUNTRY: UA 🇺🇦recipient
Google LLC
to Google LLC in 2017, and as of August, 2022, all Google submissions are marked as from Google, LLC.»/> [Private]
Mountain View, CA, 94043, USsubmitter
Google LLC
- Notice Type:
- DMCA
Copyright claim #1
Kind of Work: Unspecified
Description Ответы к вопросам и задачам учебника по Химии 9 класс автора Ярошенко 2017 год.
Original URLs:
- 4book.org — 1 URL
Allegedly Infringing URLs:
- freegdz. com — 1 URL
Click here to request access and see full URLs.
Copyright claim #2
Kind of Work: Unspecified
Description Ответы к заданиям и тестам тетради по географии за 9 класс автора Бойко за 2017 год написанные от руки
Original URLs:
- 4book.org — 1 URL
Allegedly Infringing URLs:
- freegdz.com — 1 URL
- vshkole.com — 1 URL
Click here to request access and see full URLs.
Copyright claim #3
Kind of Work: Unspecified
Description Ответы к заданиям практических работ тетради по географии за 9 класс автора Стадник за 2017 год написанные от руки
Original URLs:
- 4book.org — 1 URL
- vshkole. com — 1 URL
Allegedly Infringing URLs:
- freegdz.com — 1 URL
Click here to request access and see full URLs.
Copyright claim #4
Kind of Work: Unspecified
Description Ответы к заданиям рабочей тетради по Биологии за 9 класс автора Андерсон 2017 года (напечатанные и написанные от руки)
Original URLs:
- 4book.org — 1 URL
Allegedly Infringing URLs:
- freegdz.com — 1 URL
Click here to request access and see full URLs.
Copyright claim #5
Kind of Work: Unspecified
Description Ответы к заданиям рабочей тетради по Основам здоровья за 9 класс автора Таглина 2017 года написанные от руки
Original URLs:
- 4book. org — 1 URL
Allegedly Infringing URLs:
- freegdz.com — 1 URL
- vshkole.com — 1 URL
Click here to request access and see full URLs.
- 4book.
Copyright claim #6
Kind of Work: Unspecified
Description Ответы к рабочей тетради (workbook) по Английскому языку за 9 класс автора Карпюк 2017 года написанные от руки
Original URLs:
- 4book.org — 1 URL
Allegedly Infringing URLs:
- vshkole.com — 1 URL
Click here to request access and see full URLs.
Copyright claim #7
Kind of Work: Unspecified
Description Ответы к упражнениям рабочей тетради (workbook) по Английскому языку за 10 класс автора Карпюк 2018 год написанные от руки
Original URLs:
- 4book. org — 1 URL
Allegedly Infringing URLs:
- vshkole.com — 1 URL
Click here to request access and see full URLs.
- 4book.
Copyright claim #8
Kind of Work: Unspecified
Description Решение задач к учебнику Физика 10 класс Баряхтар 2018 год написанные от руки.
Original URLs:
- 4book.org — 1 URL
Allegedly Infringing URLs:
- vshkole.com — 1 URL
Click here to request access and see full URLs.
Copyright claim #9
Kind of Work: Unspecified
Description Решение к задачам разделов по геометрии (§ 4. Паралельність у просторі, § 5. Перпендикулярність у просторі) к учебнику Математика 10 класс Мерзляк 2018 год написанные от руки
Original URLs:
- 4book. org — 1 URL
Allegedly Infringing URLs:
- freegdz.com — 1 URL
- vshkole.com — 1 URL
Click here to request access and see full URLs.
- 4book.
Copyright claim #10
Kind of Work: Unspecified
Description Решения к заданиям Геометрия 10 класс к учебнику Мерзляк 2018 год написанные от руки.
Original URLs:
- 4book.org — 1 URL
Allegedly Infringing URLs:
- freegdz.com — 1 URL
- vshkole.com — 1 URL
Click here to request access and see full URLs.
com — 1 URL
com — 1 URL
org — 1 URL
org — 1 URL
org — 1 URL- Jurisdictions
- UA
Topics
DMCA Notices, CopyrightTags
Производная 2x — Формула, Доказательство, Примеры
Производная 2x равна 2, поскольку формула для производной функции прямой линии f(x) = ax + b задается как f'(x) = а, где а, b — действительные числа.
Дифференциация 2x рассчитывается по формуле d(ax+b)/dx = a. Мы также можем вычислить производную от 2x, используя правило степени дифференцирования, которое имеет формулу d(x n )/dx = nx n-1 . Производную 2х можно определить и с помощью других методов дифференцирования.
Далее в этой статье мы оценим производную от 2x, используя различные методы дифференцирования и ее формулу. Мы докажем дифференцирование 2x и рассмотрим несколько решенных примеров с производной 2x для лучшего понимания концепции.
| 1. | Что такое производная от 2x? |
| 2. | Производная от 2x Formula |
| 3. | Производная от 2x Proof |
| 4. | Часто задаваемые вопросы о производной 2x |
Что такое производная от 2x?
Производная функции показывает скорость изменения этой функции по отношению к изменению переменной.
Для линейной функции f(x) = ax + b производная является постоянной функцией. Следовательно, производная 2x является константой, которая определяется как 2. Мы можем оценить производную 2x, используя различные методы дифференцирования, такие как правило степени, правило произведения, первый принцип производных и формула производной линейной функции. Кроме того, поскольку мы знаем, что производная от kx равна k, отсюда следует, что производная от 2x равна 2. Давайте теперь посмотрим на формулу дифференцирования 2x.
Производная от 2x Formula
Формула для производной 2x задается как d(2x)/dx = 2. Мы можем вычислить дифференцирование 2x, используя тот факт, что производная f(x) = kx равна f'(x) = к. Используя это, мы можем сказать, что производная 2x равна 2. На изображении ниже показана формула дифференцирования 2x:
Производная от 2x Proof
Теперь, когда мы знаем, что производная от 2x равна 2, мы выведем это, используя различные правила производных.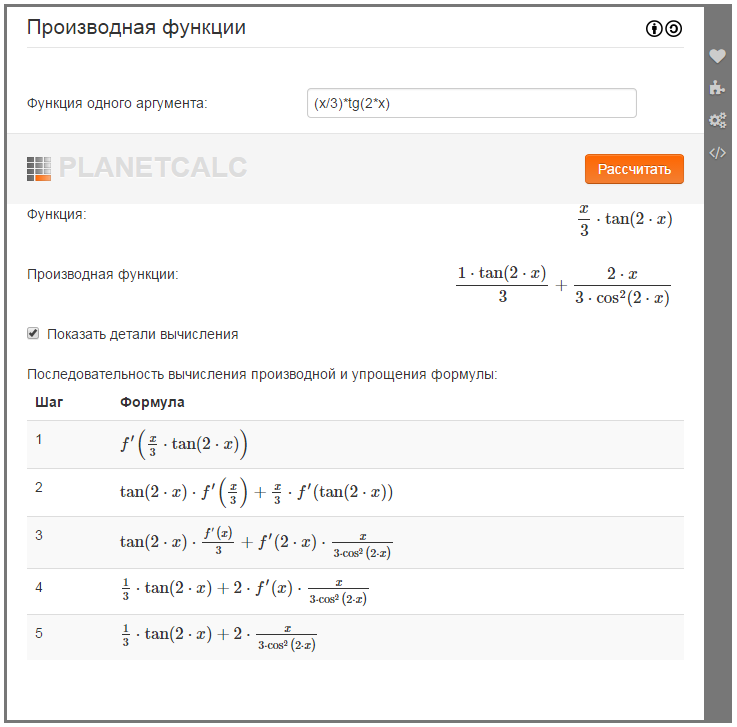
Мы можем вывести формулу, используя определение производных с использованием пределов, правила степени, правила произведения и формулы производной f (x) = ax + b.
Производная 2x с использованием ограничений
Чтобы получить производную 2x с использованием первого принципа производных, мы будем использовать следующие формулы:
- d(f(x))/dx = lim h→0 [f (х+ч) — f(х)]/ч
- lim h→0 k = k, где k — константа
d(2x)/dx = lim h→0 [2(x+h) — 2x]/h
= lim h→0 [2x + 2h — 2x]/h
= lim ч→0 [2ч]/ч
= lim ч→0 2
= 2
Следовательно, производная от 2x равна 2 по первому принципу производных.
Дифференцирование 2x с использованием степенного правила
Степенное правило дифференцирования утверждает, что производная x в степени n выражается как n умноженное на x в степени n минус 1, то есть d(x n )/dx = n x n-1 .
Мы также будем использовать производное правило скалярного кратного функции, то есть d(kf(x))/dx = kd(f(x))/dx. Следовательно, имеем d(2x)/dx = 2 dx/dx = 2. Следовательно, дифференцирование 2x равно 2,9.0009
Производная от 2x с использованием правила произведения
Правило произведения дифференцирования используется для нахождения производной произведения двух или более функций. Если у нас есть h (x) = f (x) g (x), то производная h (x) определяется как, h’ (x) = f’ (x) g (x) + f (x) g ‘(Икс). Точно так же для h(x) = 2x имеем f(x) = 2 и g(x) = x. Используя правило произведения, мы имеем
(2x)’ = (2)’ × x + 2 × (x)’
= 0 × x + 2 × 1
= 2
Следовательно, мы имеем, что производная от 2х равна 2 по правилу произведения.
Важные примечания о производной 2x
- Производная 2x равна 2, которая может быть получена с использованием различных методов дифференцирования.
- Мы можем использовать правило степени, правило произведения и первый принцип производных, мы можем получить дифференцирование 2x.
- Используя формулу [kx]’ = k, мы получаем, что производная от 2x определяется выражением [2x]’ = 2.
☛ Статьи по теме:
- Предельная формула
- Формула неявного дифференцирования
- Дифференциальные уравнения
Часто задаваемые вопросы о производной 2x
Что такое производная 2x?
Производная 2x равна 2, так как производная функции f(x) = kx определяется как f'(x) = k.
Какова формула дифференциации 2x?
Формула для дифференцирования 2x определяется выражением (2x)’ = 2, которое является постоянной функцией, так как производная линейного многочлена f(x) = ax + b является постоянной f'(x) = a.
Как найти производную от 2x?
Мы можем найти производную от 2x, используя различные правила дифференцирования, такие как правило степени, скалярное кратное функции и первый принцип производных.
Какая производная от 2x/(1 — x
2 )? Производная от 2x / (1 — x 2 ) определяется как 2(1 + x 2 )/(1 — x 2 ) 2 .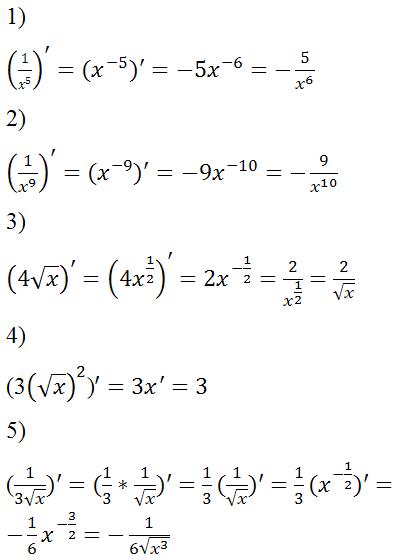
Эту производную можно вычислить с помощью частного правила дифференцирования.
Что такое вторая производная от 2x?
Вторую производную от 2x можно определить путем дифференцирования первой производной от 2x. Первая производная от 2x равна 2, которая является постоянной функцией, а производная постоянной функции равна нулю. Следовательно, вторая производная от 2x равна 0.
Какую формулу можно использовать для нахождения производной от 2x?
Мы можем использовать различные формулы дифференцирования, чтобы найти производную 2x, например:
- Первый принцип производных: d(f(x))/dx = lim h→0 [f(x+h) — f(x)]/h
- Правило произведения: h'(x) = f'(x) g(x) + f(x) g'(x), где h(x) = f(x) g(x)
- Производная kx: [kx]’ = k
Что такое производная 2х квадрата?
Производная 2x квадрат, то есть 2x 2 определяется с помощью степенной формулы производных. У нас есть (2x 2 )’ = 4x.
Следовательно, производная от 2x 2 равна 4x.
| 1 | Найти производную — d/dx | натуральное бревно х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) по x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оцените интеграл 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Производная от 2x, Доказательство, Правило произведения, Производная из первого принципа
Производная от 2x является частью Дифференциации, которая является подтемой исчисления.
В Derivative of 2x это чисто алгебраическая функция. В этой статье мы узнаем, как дифференцировать 2x, используя различные правила дифференцирования, такие как первый принцип производной, дифференцировать 2x, используя правило произведения, и дифференцировать 2x, используя правило степени.
Производная функции действительной переменной измеряет чувствительность к изменению значения функции по отношению к изменению ее аргумента. Производные являются основным инструментом исчисления. Все функции являются функциями действительных чисел (R), которые возвращают действительные значения. Они полезны для нахождения производных алгебраических функций, производных тригонометрических функций, производных логарифмических функций, определенного интеграла по частям, экспоненциальных функций, тригонометрических функций и т. д. 92[\латекс] равно 2x.
Формула для производной 2x
Формула для производной 2x: \(\){d\over{dx}}2x\) и дает нам ответ 2. Сейчас мы увидим его доказательство.
Доказательство производной 2x
Мы узнаем, как дифференцировать 2x, используя различные правила дифференцирования, такие как первый принцип производной, дифференцировать 2x, используя правило произведения, и дифференцировать 2x, используя правило степени.
Производная от 2x по степенному правилу 9{0}\\
= 2
\end{matrix}\)
Производная 2x в пределах
Нахождение доказательства любой производной с использованием пределов равносильно нахождению производной с использованием правила первого принципа. Производная по первому принципу относится к использованию алгебры для нахождения общего выражения для наклона кривой. Он также известен как дельта-метод. Производная является мерой мгновенной скорости изменения, которая равна:
Производная по первому принципу относится к использованию алгебры для нахождения общего выражения для наклона кривой. Он также известен как дельта-метод. Производная является мерой мгновенной скорости изменения, которая равна:
\(f'(x)={dy\over{dx}}=\lim _{h{\rightarrow}0}{f(x+h)–f(x)\over{h}}\)
Давайте посмотрим на доказательство того же, используя первый принцип производной.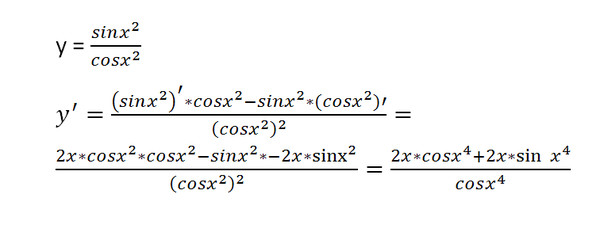
В соответствии с определением производной дифференцирование f(x) = 2x по 2x может быть записано в форме ограниченных операций.
\(\ begin{matrix}\
f'(x) = {dy\over{dx}} = \lim _{h{\rightarrow}0}{f(x+h)–f(x)\over {h}}
f(x) = 2x\\
f(x+h) = 2(x + h) = 2x + 2h\\
f(x+h)–f(x) = (2x + 2h – 2х) = 2ч\
{f(x+h)–f(x)\over{h}} = {2h\over{h}}\\
\lim _{h{\rightarrow}0}{f(x+h)– f (x) \ over {h}} = \ lim _ {h {\ rightarrow} 0} {2h \ over {h}} \\
\ lim _ {h {\ rightarrow} 0} {f (x + h) )–f(x)\over{h}}=\lim _{h{\rightarrow}0}{2}\\
f'(x)={dy\over{dx}} = 2
\end{ matrix}\)
Производная от 2x по правилу произведения
Иногда нам даются функции, которые на самом деле являются произведениями других функций. Это означает, что две функции перемножаются. Специальное правило, правило произведения, существует для дифференциации произведений двух (или более) функций.
Если y = uv, то
\({dy\over{dx}} = u{dv\over{dx}} + v{du\over{dx}}\)
Давайте посмотрим на производную 2x, используя правило продукта.
\(\begin{matrix}
\text{ Имеем: }\\
y = 2x\\
\text{ Что является произведением двух функций, поэтому мы применяем степенное правило дифференцирования: }\\
{dy\over{dx}} = u{dv\over{dx}} + v{du\over{dx}}\\
\text{ Пусть u = 2 и v = x}\\
{dy\over {dx}} = 2{d(x)\over{dx}} + x{d(2)\over{dx}}\\
\text{ Мы знаем, что } {d(x)\over{dx} } = 1 \text{ и } {d2\over{dx}} = 0\\ 9{2x}. ln(3) \)
Надеюсь, что эта статья о производной 2x была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Производная от 2x Часто задаваемые вопросы
В.1 Что такое 2x?
Ответ 1 2x — чисто алгебраическая функция. Его также можно рассматривать как составную функцию, где x — алгебраическая функция, а 2 — константа. Производные от 2x можно вычислить, используя первый принцип производной, правило произведения и правило степени. 9{0}\\
= 2\end{matrix}\)
Q.
3 Что такое вторая производная от 2x?
Ответ 3 Вторая производная или производная второго порядка функции f — это производная производной от f. Вторая производная — это скорость изменения скорости изменения точки на графике. Здесь функция xsinx. Сначала вычислим производную от xsinx. Это дает нам значение 2. Теперь, чтобы вычислить вторую производную, мы дифференцируем 2 по x. 2 — постоянная. Производная константы по любой переменной равна нулю. Пусть k — константа относительно x. Производная константы k по x записывается в следующей математической форме. \({d\over{dx}}k=0\). Следовательно, вторая производная от 2x равна 0,9.0009
Q.4 Какую формулу можно использовать для нахождения производной 2x?
Ответ 4 Мы можем вычислить производную от 2x, используя правило произведения, правило степени и первый принцип производной.
Первые принципы производной: Производная по первому принципу относится к использованию алгебры для нахождения общего выражения для наклона кривой.
Он также известен как дельта-метод. Производная является мерой мгновенной скорости изменения, которая равна: \(f'(x)={dy\over{dx}}=\lim _{h{\rightarrow}0}{f(x+ h)–f(x)\over{h}}\) 9{n-1}\)
Q.5 Что такое производная от 2x?
Ответ 5 Производная от 2x равна 2.
Скачать публикацию в формате PDF| Производная от xsinx с доказательством и формулой |
| Целые числа: изучите определения, свойства, операции и примеры здесь! |
| Рациональные числа с определением, символом, списками, свойствами, часто задаваемыми вопросами |
| Натуральные числа с определением, свойством, суммой, нечетными и четными натуральными числами |
| Декартово произведение множеств: изучите определение, свойства и способы нахождения с помощью решенных примеров |
Исчисление I. Определение производной
Онлайн-заметки Пола
Главная
/
Исчисление I
/
Производные
/ Определение производной
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-1: Определение производной
В первом разделе главы «Пределы» мы видели, что вычисление наклона касательной, мгновенной скорости изменения функции и мгновенной скорости объект в \(x = a\) требовал от нас вычислить следующий предел.
\[\ mathop {\lim }\limits_{x \to a} \frac{{f\left( x \right) — f\left( a \right)}}{{x — a}}\]
Мы также видели, что, немного изменив обозначения, этот предел можно также записать как
. \[\begin{equation}\mathop {\lim}\limits_{h \to 0} \frac{{f\left({a + h} \right) — f\left(a\right)}}{h } \label{eq:eq1}\end{уравнение}\]
Это такой важный предел, и он возникает во многих местах, что мы даем ему имя.
Мы называем это производная . Вот официальное определение производной.
Определение производной
Производная от \(f\left( x \right)\) по отношению к x является функцией \(f’\left( x \right)\) и определяется как \[\begin{equation}f’\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left({x + h} \right) — f\ слева( x \справа)}}{h} \label{eq:eq2}\end{equation}\]
Обратите внимание, что мы заменили все 92} — 16х + 35\]
Показать решение
Итак, все, что нам действительно нужно сделать, это подставить эту функцию в определение производной \(\eqref{eq:eq2}\) и выполнить некоторые алгебраические действия. Хотя, по общему признанию, алгебра временами будет несколько неприятной, но это всего лишь алгебра, так что не радуйтесь тому факту, что мы сейчас вычисляем производные.
Сначала подключите функцию к определению производной.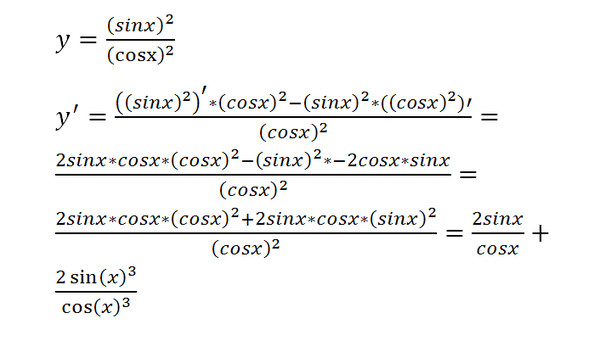
2} — 16ч}}{ч}\конец{выравнивание*}\]
Обратите внимание, что каждое слагаемое в числителе, в котором не было ч , сокращаются, и теперь мы можем вынести ч из числителя, что сократит ч в знаменателе. После этого мы можем вычислить предел.
\[\begin{align*}f’\left( x \right) & = \mathop {\lim }\limits_{h \to 0} \frac{{h\left({4x + 2h — 16} \right )}}}{ч}\\ & = \mathop {\lim}\limits_{h \to 0} 4x + 2h — 16\\ & = 4x — 16\end{align*}\]
Итак, производная
\[f’\влево( х \вправо) = 4x — 16\]
Пример 2 Найдите производную следующей функции, используя определение производной. \[g\left( t \right) = \frac{t}{{t + 1}}\]
Показать решение
Это будет немного сложнее, если говорить об алгебре.
Однако за пределами этого он будет работать точно так же, как и в предыдущих примерах. Во-первых, мы вставляем функцию в определение производной,
\[\begin{align*}g’\left( t \right) & = \mathop {\lim }\limits_{h \to 0} \frac{{g\left({t + h} \right) — g \ left( t \ right)}} {h} \\ & = \ mathop {\ lim } \ limit_ {h \ to 0} \ frac {1} {h} \ left ( {\ frac {{t + h }}{{t + h + 1}} — \frac{t}{{t + 1}}} \right)\end{align*}\]
Обратите внимание, что мы изменили все буквы в определении, чтобы они соответствовали заданной функции. Также обратите внимание, что мы написали дробь гораздо более компактно, чтобы помочь нам в работе.
Как и в случае с первой проблемой, мы не можем просто подставить \(h = 0\). Итак, нам нужно будет немного упростить ситуацию. В этом случае нам нужно будет объединить два члена в числителе в одно рациональное выражение следующим образом.
\[\ begin{align*}g’\left( t \right) & = \mathop {\lim }\limits_{h \to 0} \frac{1}{h}\left({\frac{{\ влево( {t + h} \right)\left( {t + 1} \right) — t\left( {t + h + 1} \right)}}{{\left( {t + h + 1} \right)\left( {t + 1} \right)}}} \right)\\ & = \mathop {\lim }\limits_{h \to 0} \frac{1}{h}\left( { \frac{{{t^2} + t + th + h — \left( {{t^2} + th + t} \right)}}{{\left( {t + h + 1} \right) \left( {t + 1} \right)}}} \right)\\ & = \ mathop {\lim }\limits_{h \to 0} \frac{1}{h}\left({\frac{ h}{{\left( {t + h + 1} \right)\left( {t + 1} \right)}}} \right)\end{align*}\]
Прежде чем закончить, давайте отметим пару вещей.
Во-первых, мы не умножали знаменатель. Умножение знаменателя слишком усложнит ситуацию, поэтому давайте не будем усложнять. Далее, как и в первом примере, после упрощения у нас в числителе остались только члены с ч , и теперь мы можем отменить ч на выходе.
Итак, при отмене ч мы можем вычислить предел и получить производную. 92}}}\]
Пример 3 Найдите производную следующей функции, используя определение производной. \[R\влево( z \вправо) = \sqrt {5z — 8} \]
Показать решение
Сначала подключите определение производной, как мы сделали это в двух предыдущих примерах.
\[\begin{align*}R’\left( z \right) & = \mathop {\lim }\limits_{h \to 0} \frac{{R\left({z + h} \right) — R \ влево ( z \ вправо)}} {h} \\ & = \ mathop {\ lim } \ limit_ {h \ to 0} \ frac {{\ sqrt {5 \ left ({z + h} \ right) — 8} — \sqrt {5z — 8} }}{h}\end{align*}\]
В этой задаче нам нужно рационализировать числитель.
Вы ведь помните рационализацию из класса алгебры, верно? На уроке алгебры вы, вероятно, рационализировали только знаменатель, но вы также можете рационализировать числители. Помните, что при рационализации числителя (в данном случае) мы умножаем и числитель, и знаменатель на числитель, за исключением того, что мы меняем знак между двумя членами. Вот рационализаторская работа по этой задаче,
. \[\ begin{align*}R’\left( z \right) & = \ mathop {\lim }\limits_{h \to 0} \frac{{\left({\sqrt {5\left({z + h} \right) — 8} — \sqrt {5z — 8} } \right)}}{h}\frac{{\left( {\sqrt {5\left( {z + h} \right) — 8} + \sqrt {5z — 8} } \right)}}{{\left( {\sqrt {5\left({z + h} \right) — 8} + \sqrt {5z — 8}} \ справа)}}\\ & = \mathop {\lim }\limits_{h \to 0} \frac{{5z + 5h — 8 — \left( {5z — 8} \right)}}{{h\left ( {\ sqrt {5 \ left ( {z + h} \ right) — 8} + \ sqrt {5z — 8} } \ right)}} \\ & = \ mathop {\ lim } \ limits_ {h \ to 0} \frac{{5h}}{{h\left( {\sqrt {5\left({z + h} \right) — 8} + \ sqrt {5z — 8}} \справа)}}\конец{выравнивание*}\]
Опять же, после упрощения у нас осталось только ч в числителе.
Итак, отменяем ч и оцениваем лимит.
\[\ begin{align*}R’\left( z \right) & = \mathop {\lim }\limits_{h \to 0} \frac{5}{{\sqrt {5\left({z + h} \right) — 8} + \sqrt {5z — 8} }}\\ & = \frac{5}{{\sqrt {5z — 8} + \sqrt {5z — 8} }}\\ & = \frac{5}{{2\sqrt {5z — 8} }}\end{align*}\]
Итак, мы получаем производную от
\[R’\left( z \right) = \frac{5}{{2\sqrt {5z — 8} }}\]
Давайте рассмотрим еще один пример. Этот будет немного другим, но в нем есть смысл, который нужно сделать.
Пример 4. Определить \(f’\left( 0 \right)\) для \(f\left( x \right) = \left| x \right|\).
Показать решение
Поскольку эта задача требует производной в определенной точке, мы продолжим и используем ее в нашей работе. Это сделает нашу жизнь проще, и это всегда хорошо.
Итак, вставьте определение и упростите.
\[\begin{align*}f’\left( 0 \right) & = \mathop {\lim }\limits_{h \to 0} \frac{{f\left({0 + h} \right) — f\left( 0 \right)}}{h}\\ & = \mathop {\lim}\limits_{h \to 0} \frac{{\left| {0 + ч} \право| — \влево| 0 \right|}}{h}\\ & = \mathop {\lim }\limits_{h \to 0} \frac{{\left| h \right|}}{h}\end{align*}\]
Подобную ситуацию мы уже видели, когда искали пределы в бесконечности. Так как в этом разделе мы не можем просто отменить 9+ }} 1\\ & = 1\end{align*}\]
Два односторонних предела различны, поэтому
\[\ mathop {\lim}\limits_{h \to 0} \frac{{\left| ч \справа|}}{ч}\]
не существует. Однако это предел, который дает нам производную, которая нам нужна.
Если предела не существует, то и производная не существует.
В этом примере мы, наконец, увидели функцию, для которой производная не существует в точке.
Это факт жизни, о котором мы должны знать. Производные не всегда будут существовать. Обратите также внимание, что это ничего не говорит о том, существует ли производная где-либо еще. На самом деле производная функции абсолютного значения существует в каждой точке, кроме той, которую мы только что рассмотрели, \(x = 0\).
Предыдущее обсуждение приводит к следующему определению.
Определение
Функция \(f\left( x \right)\) называется дифференцируемой в точке \(x = a\), если \(f’\left( a \right)\) существует и \( f\left( x \right)\) называется дифференцируемой на интервале, если производная существует для каждой точки этого интервала.
Следующая теорема показывает нам очень хорошую связь между непрерывными и дифференцируемыми функциями.
Теорема
Если \(f\left( x \right)\) дифференцируема в \(x = a\), то \(f\left( x \right)\) непрерывна в \(x = a\).
Доказательство этой теоремы см.
в разделе «Доказательство различных производных формул» в главе «Дополнительно».
Обратите внимание, что эта теорема не работает в обратном порядке. Рассмотрим \(f\left( x \right) = \left| x \right|\) и взглянем на
\[\ mathop {\lim}\limits_{x \to 0} f\left(x\right) = \mathop {\lim}\limits_{x \to 0} \left| х \ справа | = 0 = f\влево( 0 \вправо)\]
Таким образом, \(f\left( x \right) = \left| x \right|\) непрерывно в точке \(x = 0\), но мы только что показали выше в примере 4, что \(f\left (x \right) = \left| x \right|\) не дифференцируема в точке \(x = 0\).
Альтернативное обозначение
Далее нам нужно обсудить некоторые альтернативные обозначения производной. Типичное обозначение производной — это «штриховое» обозначение. Однако есть еще одно обозначение, которое иногда используется, поэтому давайте рассмотрим его.
Для функции \(y = f\left( x \right)\) все следующие эквиваленты эквивалентны и представляют собой производную от \(f\left( x \right)\) по х .
\[f’\left( x \right) = y’ = \frac{{df}}{{dx}} = \frac{{dy}}{{dx}} = \frac{d}{{dx} }\left( {f\left( x \right)} \right) = \frac{d}{{dx}}\left( y \right)\]
Поскольку иногда нам также необходимо вычислять производные, нам также нужна запись для вычисления производных при использовании дробной записи. Итак, если мы хотим оценить производную при \(x = a\), все следующие условия эквивалентны.
\[f’\влево( а \вправо) = {\влево. {y’} \right|_{x = a}} = {\left. {\ frac {{df}}{{dx}}} \right|_{x = a}} = {\left. {\ frac {{dy}} {{dx}}} \right|_{x = a}}\]
Также обратите внимание, что иногда мы опускаем часть \(\left( x \right)\) в функции, чтобы несколько упростить запись. В этих случаях следующие условия эквивалентны.
\[f’\влево( х \вправо) = f’\]
В качестве последнего примечания в этом разделе мы признаем, что вычисление большинства производных непосредственно из определения — довольно сложный (и иногда болезненный) процесс, полный возможностей сделать ошибки.
Через пару разделов мы начнем разрабатывать формулы и/или свойства, которые помогут нам получить производную многих распространенных функций, чтобы нам не приходилось слишком часто прибегать к определению производной.
Однако это не означает, что не важно знать определение производной! Это важное определение, которое мы всегда должны знать и помнить. Это просто то, с чем мы не собираемся так много работать.
6. Производные произведения и частные
М. Борна
ПРАВИЛО ПРОДУКТА
Если u и v являются двумя функциями x , то производная произведения ув дается…
Не пропустите…
Далее в этом разделе:
Частное правило
`(d(uv))/(dx)=u(dv)/(dx)+v(du)/dx`
На словах это можно запомнить как:
«Производная произведения двух функций равна производной второй, умноженной на первую, и производной первой, умноженной на вторую».
Откуда взялась эта формула? Как и все встречающиеся нам формулы дифференцирования, она основана на производных от первых принципов.
Пример 1
Если у нас есть продукт, подобный
y = (2 х 2 + 6 x )(2 x 3 + 5 x 2 )
мы можем найти производную без умножения выражение справа.
Ответить
Используем замены u = 2 х 2 + 6 х и v = 2 92)` (в главе Дифференциация трансцендентных функций.) Почленно умножить это выражение невозможно, поэтому нужен метод дифференцирования произведений таких функций.
Примечание
Мы можем записать правило произведения разными способами:
`(d(uv))/(dx)=uv’+vu’`
ИЛИ
`(d(fg))/(dx)` `=f(x)d/(dx)g(x)+g(x)d/(dx)f(x)`… и т.
д.ЧАСТНОЕ ПРАВИЛО
(А 92)`
Нужна помощь в решении другой задачи исчисления? Попробуйте решение проблем.
Отказ от ответственности: IntMath.com не гарантирует точность результатов. Решатель задач предоставлен Mathway.
Математическая сцена — Производные — Урок 2
Математическая сцена — Производные — Урок 2 — Дифференцирующие многочлены2009 Расмус Эф и Джанн Сак |
Урок 2
Дифференцирующие многочлены
Наклон касательной меняется в зависимости от формула функции, обычно называемая f(x), и точка, в которой касательная касается кривой.
Три разных касательных в трех разных
цвета были нарисованы на приведенной выше диаграмме. Красный тангенс, для
например, касается
график f(x) только в одной точке (0,1).
Градиент касательной равен
можно найти, вычислив среднюю скорость изменения или градиент на бесконечном
небольшой интервал вокруг точки (0, 1).
Теперь мы собираемся найти общий метод или формула для нахождения градиента в любой точке функции. Эта формула или новой функции, называется производной исходной функции. Когда мы найдем это мы говорим, что мы дифференцируем функцию. Производная f (x) равна пишется с использованием апострофа после f. Обозначается f(x) или y. также часто используется обозначение dy/dx.
Первый взгляд на константу функция, или f(x) = k, где k — постоянное значение, для пример f(x) = 2 или y = 2 График показан здесь.
В этом случае трудно говорить о касательной, так как сам график представляет собой горизонтальную линию. Градиент линии очевидно, 0, поэтому мы можем сказать, что если f(x) = 2 тогда f(x) = 0. Это верно для всех постоянных функций, их графики горизонтальные линии и градиент 0,
Правило таково: если f(x) = k тогда f(x) = 0,
На второй диаграмме показано
три прямые линии с разными градиентами.
Производная функции
градиент и поэтому мы получаем следующие результаты:
y = 2x + 1 имеет градиент 2, поэтому y = 2
год = x + 1 имеет градиент 1, поэтому у = 1
г. = х + 1 имеет градиент следовательно у =
Все функции первой степени имеют прямую линию графиков и поэтому заключаем, что если дифференцировать функции вида f(x) = ax + b мы получаем f(x) = a.
Далее мы рассмотрим квадратичная функция е (х) = х 2 .
Мы можем найти производная путем нахождения средней скорости изменения на бесконечно малом интервале как мы делали в урок 1.
Определение производной:
Рассчитываем это используя функцию f(x) = x 2 .
Кому найти f(x+h) мы подставить (x+h) в формулу функции вместо x. |
Пример 1
Дифференцировать функцию
f(x) = 2x 2 + 4x.
Обратите внимание, что если мы продифференцируем 2x 2 мы получаем 22x (выше мы обнаружили, что производная от x 2 равна 2x). Линия y = 4x имеет градиент 4, поэтому производная 4x равна 4.
Добавление этих двух результатов вместе дает нам результат, что производная от 2x 2 + 4х это 4х + 4, тот же результат, что и раньше,
Следующее правило, которое легко доказать, относится к добавлению функций:
f(x) = ах 2 + bx + c имеет производную f(x) = 2ax + b. |
Пример 2
Дифференцировать функцию .
Вместо деления на 2 можно подумать об этом
например, как умножение каждого члена на, и поэтому мы можем применить приведенное выше
правила. Обратите внимание, что они применяются только при делении на постоянное число.
Заметьте также, что константа имеет производную 0, такую же, как и любая другая
постоянный.
Отмена для упрощения получить
Пример 3
Дифференцировать f(x) = х 3 . У нас нет правил, поэтому далеко для функций третьей степени, поэтому мы должны использовать определение:
Пример 4
Дифференцировать f(x) = х 4 .
Приведенные выше примеры дают нам следующие результаты:
f(х) = х 0 имеет производную f(x) = 0
f(х) = х 1 имеет производную f(x) = 1x 0
f(х) = х 2 имеет производную f(x) = 2x 1
f(х) = х 3 имеет производную f(x) = 3x 2
f(x) = x 4 имеет производную f(x) = 4x 3
В любом случае результат может получить путем умножения на исходный показатель или степень и уменьшения мощность на одного.
Можно показать, что этот результат применим в целом, и мы можем написать следующее правило:
е (х) = х п имеет производную f(x) = nx №1 |
Пример 5
Используйте правила, которые мы нашли
различать
е (х) = х 5 2x 4 + 3x 3 4x 2 + 5x 6.
f(x) = 5x 4 24x 3 + 33x 2 42x + 5 0
= 5x 4 8x 3 + 9x 2 8x + 5
Пример 6
Найдите уравнение касательной к кривой f(x) = x 5 5x 3 + 4x в точке , где x = 1,
Начнем с поиска y значение при x = 1.
f(1) = 1 5 + 4 = 0
Касательная находится в точке (1, 0).
Далее находим формулу для градиент путем дифференцирования функции.
f(x) = 5x 4 53x 2 + 4
= 5x 4 15x 2 + 4
Мы можем найти градиент когда x = 1, путем вычисления f(1).
f(1) = 5 15 + 4 = 6
Используя формулу для уравнение прямой дает нам искомое уравнение.
у = 6(х 1) + 0
г. = 6х + 6
| Мы можем проверить нашу
результаты путем построения графика функции и тангенса. |
