Математика для безнадёжных гуманитариев. Урок 3 / Newtonew: новости сетевого образования
Вот уже больше месяца в группе Фейсбука с эмоциональным названием «Математика — великая и ужасная!» этой непростой науке учат взрослых гуманитариев.
Группу ведут профессор математики Нелли Литвак и журналист Алла Кечеджан. Нелли, как положено профессору, даёт задания и разбирает решения, помогая добраться до сути. А Алла, как и положено журналисту, задаёт вопросы и придумывает свои примеры, чтобы общение в группе развивалось и приближало всех к пониманию Великой и Ужасной Математики.
Говорят, что математику надо учить в детстве, а потом — безнадёга. Однако я считаю, что всё происходит вовремя. Когда я была маленькой, не было даже калькуляторов, не говоря уже о компьютерах, которые рисуют многомерные графики. К тому же не было никакой возможности задавать вопросы профессору математики онлайн.
Алла Кечеджан, журналист с 20-летним стажем
Здесь можно задавать вопросы «А зачем это вообще знать?» и «Почему это нужно доказывать?».
Можно и нужно делать ошибки. Но нельзя сомневаться в своих способностях к математике и категорически нельзя кого-либо критиковать.
Алла Кечеджан и Нелли Литвак бросают спасательный круг тем, кто не верит в свои математические способности.
flickr.com
Newtonew поддерживает инициативу по реабилитации запуганных школьной математикой гуманитариев. У нас на сайте Нелли каждую неделю делится пройденным материалом. На прошлых занятиях читатели Newtonew доказывали теорему Пифагора и подступили к вычислению длины кривой. Сегодня двигаемся дальше, в дремучий лес интегралов и производных…
Учёные давно доказали, что «математического гена» не существует. Математику, как и велосипед, в состоянии осилить любой человек.
Нелли Литвак, профессор прикладной математики, университет Твенте, Нидерланды
Занятие 3. Великие и ужасные интеграл и производная
Задание №1. Наконец-то интеграл
Пора разбираться, как же все-таки вычислить длину кривой.
2 (х в квадрате) и самые маленькие треугольнички, которые мне удалось нарисовать. (На формулу под рисунком пока не смотрите).
Рисунок 1
Длину каждой маленькой гипотенузы можно подсчитать по теореме Пифагора, а потом всё это сложить. Посмотрите, на рисунке 1 красная линия, состоящая из маленьких гипотенуз, практически не отличается от кривой.
Многие догадались, что делать дальше. Треугольники должны становиться всё меньше и меньше.
На рисунке 1 у одного треугольничка справа я подписала стороны. Сторону, параллельную оси х, я обозначила dx, а сторону, параллельную оси у, обозначила dy. Шажок dx по оси х мы задаем сами и можем сделать его всё меньше и меньше. На рисунке я написала, что dx уменьшается. В математике мы говорим: «Стремится к нулю». Это обозначается стрелочкой, как на рисунке: dx → 0.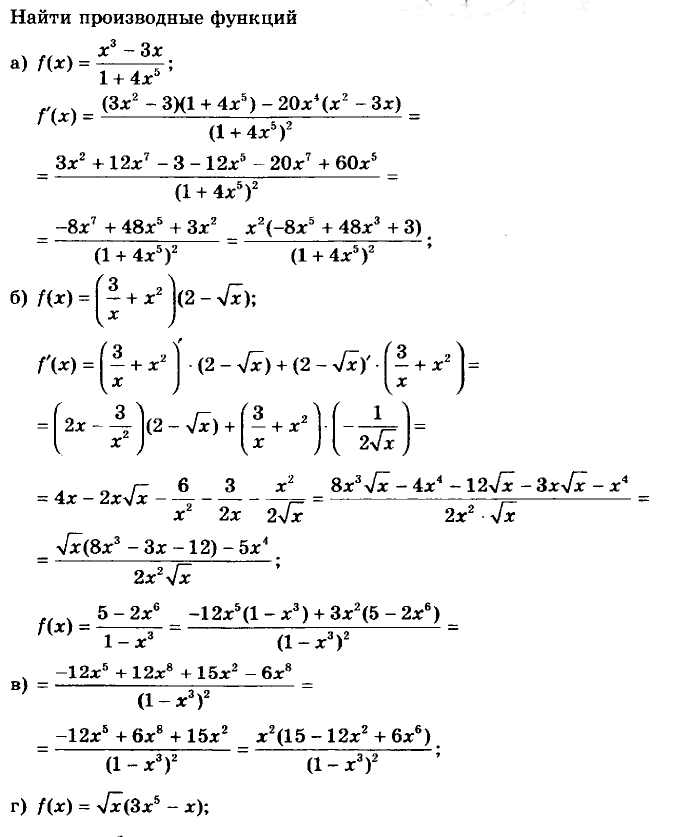
Понятно, что и dy, и гипотенуза тоже будет становиться всё меньше и меньше и стремиться к нулю.
Что будет, когда dx станет бесконечно маленьким? Если включить воображение, то понятно, что красная линия превратится в параболу!
Отлично. Осталось только понять, как сложить бесконечное количество бесконечно маленьких гипотенуз! Мда…
Люди долго не умели этого делать, и научились только в XVII веке, когда Ньютон и Лейбниц независимо разработали основы современного математического анализа — дифференциальное и интегральное исчисление. Вот до каких великих и ужасных слов нас довела теорема Пифагора!
Дорогие друзья, пришло время посмотреть на формулу под рисунком 1. Начнём с самого страшного — жуткой загогулины в самом начале. Знакомьтесь, это и есть интеграл.
Извините за громкое имя, в нашей науке есть отвратительная традиция обзывать всё подряд сложными и непонятными словами. В качестве компенсации мы всё это пишем с маленькой буквы.
Участники группы с нетерпением ждали, когда же будет интеграл, и вдохновлялись классикой.
На самом деле страшная загогулина — это вытянутая латинская буква S. Похоже? S от слова sum — «сумма».
Интеграл — это просто сумма бесконечного числа бесконечно маленьких слагаемых.
Заслуга Ньютона и Лейбница в том, что они смогли придать этому смысл, дать строгое определение и научились это считать. Мы с вами разберёмся в смысле, а считает пусть программа Wolfram, её для этого и придумали.
Итак, интеграл — это сумма бесконечного числа бесконечно маленьких слагаемых. Сразу после знака интеграла (математики говорят: «под интегралом») написано, как в данном случае выглядят слагаемые. В нашем случае слагаемые — это крошечные гипотенузы. И посмотрите, именно это и написано под интегралом: длина гипотенузы по теореме Пифагора! Узнали?
А что означают -2 и 2 под и над знаком интеграла? Вы, наверное, уже догадались: они обозначают, откуда и докуда мы хотим посчитать длину параболы.
2. Кривая-то другая, а принцип тот же. И поэтому выражение под интегралом пока такое же.
Рисунок 2
Значит, мы ещё не разобрались до конца. Нам нужно понять: каким образом форма кривой влияет на выражение под интегралом? «Собака зарыта» в dy.
Вернёмся к рисунку 1. Я отметила точку х, и от этой точки отложила dx. От чего зависит dy?
- От длины dx.
- От того, насколько «крутая» наша кривая в районе точки х. И, конечно, эта «крутизна» будет разной для разных кривых. Поэтому у параболы будет одно изменение dy, а у кривой на рисунке 2 — совсем другое.
Нам понадобится два-три задания, чтобы в этом разобраться. Для начала попробуем понять, чему равно dy на параболе.
ЗАДАНИЕ. Посмотрите на рисунок 1. Вы увидите, что dy — это разница между двумя значениями у: в точке х и в точке, «близкой к х», которая находится на расстоянии dх.
2, чтобы подсчитать dy в конкретной точке.
Например: подсчитайте dy если х=4/3 (примерно 1,33333, как на рисунке 1), а dx=0,01. Воспользуйтесь калькулятором Google (как это сделать, мы разбирались на прошлом занятии).
- Если не хотите связываться с дробями, возьмите х=1.
- Если хотите, выберете какой-то другой х или dx, только dx должен быть маленьким.
- Если хотите, подсчитайте dy для кривой на рисунке 2, когда х=4/3 или x=1.
Лирическое отступление. Как понимать бесконечные суммы
Зачем складывать бесконечное число слагаемых? И как их складывать, если слагаемые бесконечно маленькие, то есть неизвестные, и их бесконечно много, то есть неизвестно сколько?
Это хорошие вопросы. Именно из-за таких вопросов анализ в университете начинается с определения «предела». Я постараюсь ответить без математических формальностей, а вы постарайтесь понять.
Начнём с того, что «бесконечное» число не означает, что оно «неизвестное».
Мы прекрасно знаем, что такое бесконечность, и умеем обращаться с этим понятием. Например, мы с вами считаем длину параболы на отрезке между -2 и 2. То есть длина отрезка равна 4. Теперь представьте, что мы разбили этот отрезок на участки длиной 0,01. Сколько маленьких отрезков получилось? Их 400, и в сумме 400 слагаемых. Если dx станет 0,001, то отрезков станет 4000.
То есть мы точно знаем, сколько слагаемых будет для любого, самого маленького значения dx. Поэтому ничего неизвестного здесь нет: dx мы сами задаём и уменьшаем, и для любого значения dx мы точно знаем, сколько у нас слагаемых и чему равна сумма гипотенуз.
Теперь посмотрим, зачем нам уменьшать dx. Изначально мы в принципе понятия не имеем, как считать длину кривой. Люди это знали не всегда. Зато мы умеем считать гипотенузу прямоугольного треугольника. Отлично. Пририсуем к параболе треугольники и посчитаем сумму гипотенуз.
Получится примерно длина параболы. Чем меньше треугольнички, тем ближе мы подберёмся к точному значению. Да. Но только какими бы маленькими треугольнички не были, это так и останется приближением!
Чтобы получить точный ответ, нужно посмотреть, что произойдёт «в пределе», когда треугольнички станут бесконечно маленькими, и их крошечные точечные гипотенузы сольются с параболой.
А откуда мы знаем, что произойдёт «в пределе», когда dx будет всё меньше и меньше и превратится в точку? Ведь и треугольников уже не будет… Некоторые участники правильно заметили, что это нетривиальный вопрос. Поэтому нам и нужен анализ! Формальное доказательство практически невозможно понять без подготовки. Но я надеюсь, что до сути мы доберёмся за 2-3 задания.
Суть в том, что, когда мы уменьшаем dx, то мы видим, как наше приближение подбирается ближе и ближе к длине кривой. Что же будет «в пределе»? На самом деле, интеграл — это и есть запись такого предела.
И мы можем доказать интуитивно понятный факт, что этот предел есть и что он даст нам правильный ответ.
Дело в том, что в анализе мы изучили разные свойства интегралов, и мы научились их считать абсолютно точно! То есть путь такой:
1. Сначала приближаем кривую с помощью гипотенуз.
2. Уменьшаем dx, получаем интеграл.
3. Ура, интегралы мы умеем считать!
Последнему «ура» я не смогу вас научить прямо сейчас, для этого нужно понять много разных определений и решить много задач. Когда мы закончим эту тему, дам одно задание, чтобы у вас появилось представление, как мы, математики, это делаем.
Задание №2. Знакомая и незнакомая производная
Итак, когда в математике нам удалось свести что-то к интегралу, то мы очень радуемся. Потому что из математического анализа мы очень много знаем об интегралах и умеем их считать совершенно точно.
Но пока наш интеграл нас не очень устраивает. Дело в том, что с помощью математического анализа мы умеем считать интегралы, которые записаны так, как на рисунке ниже.
Видите разницу? Под знаком интеграла стоит f(x) — это какая-то формула, зависящая от х. И она умножается на dx. А наш интеграл на рисунке 1 не такой. Там ещё под корнем болтается dy.
Интеграл, каким его любят математики. Почему интегралы записываются именно так и как их считать, я объясню позже.
Как же избавиться от dy под корнем? Дорогие друзья, настало время познакомиться с понятием «производная».
Я не называю «производную» «великой и ужасной», потому что это понятие встречается и в обычной жизни. Вы можете сказать про молодого сотрудника: «Уровень у него пока так себе, но производная отличная!» Что это означает? Я думаю, понятно: человек быстро растет!
Как бы вы сформулировали, что означает производная в обычной жизни? Наверное, самое простое определение — это скорость изменения. Быстрые положительные изменения — значит, производная большая и положительная.
Стагнация — это никакой производной, можно сказать, производная равна нулю. А ухудшение означает, что производная отрицательная.
В общем и целом, производная говорит не о том, где мы сейчас, а об изменении, точнее, о скорости изменения. Что же такое производная в математике? Как всегда — в точности то же самое, что и в жизни.
Производная — это скорость изменения функции. И всё. И больше ничего! Ну, кроме немножко «великих и ужасных» обозначений.
Обозначений у производной два. Если у нас есть какая-то функция у, которая зависит от х, то производную функции y обозначают:
- либо штрихом, то есть y’,
- либо как dy, делённое на dx, то есть dy/dx.
Посмотрите внимательно: уж не те ли это самые dx и dy под интегралом? Да, они самые! Поэтому нам сейчас и понадобилась производная. В следующем задании подставим её в интеграл на рисунке 1!
Посмотрим ещё раз на рисунок 1
Запись dy/dx очень естественная.
Помните, что это скорость изменения функции? За «время» dx функция «проходит расстояние» dy. Чему равна скорость? Расстояние, делённое на время, то есть dy/dx.
Теперь давайте снова посмотрим на параболу. Понятно, что скорость изменения параболы везде разная. Если х отрицательный, то по параболе мы скатываемся вниз, к нулю. В нуле функция начинает расти, но очень медленно. А дальше растет всё быстрее и быстрее. Как же мы можем говорить о «скорости изменения»?
Мы можем это делать, когда dx и dy очень маленькие, то есть когда мы находимся в маленькой окрестности точки. Помните, в одном из заданий мы воспользовались Wolfram и нарисовали параболу от -2 до 2, а потом, в маленькой окрестности, от 1 до 1,01?
Парабола от -2 до 2
Помните, что в маленькой окрестности кривая стала похожа на прямую? То есть в маленькой окрестности точки мы можем говорить о постоянной «скорости изменения», в точности равной dy/dx.
Это и есть производная в данной точке!
Участок параболы от 1 до 1.01
В общем и целом, вы уже готовы к вычислению производных. Главное — не впадать в ступор от формул, а помнить, что мы говорим о «скорости изменения», и пользоваться здравым смыслом.
ЛАЙФХАК. ЧТО ДЕЛАТЬ, ЕСЛИ ПРИБЛИЖАЕТСЯ СТУПОР.
Во-первых, знайте: вы не одиноки. Мои студенты впадают в ступор на каждом занятии. Во-вторых, следуйте этим простым инструкциям.
Что НЕ НУЖНО делать при приближении ступора: смотреть невидящим стеклянным взглядом на формулу и говорить себе что-то типа «как это сложно», «я вообще ничего не понимаю», «какой кошмар», «это не моё» и так далее.
Что НУЖНО делать: понять, что именно вызывает сложности, и сформулировать вопрос (именно вопрос, а не утверждение). Первым вопросом нередко оказывается: «С чего начать?» Очень часто, как только вы задали себе вопрос, вы сами же найдёте ответ. Но если не нашли, то задайте вопрос в комментариях, я постараюсь ответить.
«Ах, зачем я так ревела! — подумала Алиса, плавая кругами и пытаясь понять, в какой стороне берег. — Вот глупо будет, если я утону в собственных слезах!» (Л. Кэрролл, «Алиса в Стране чудес»)
upload.wikimedia.org
Для разминки начнём с функции, которая вообще не меняется. Например, если наша функция у всегда равна 100, как температура кипения воды при атмосферном давлении — она всегда одинаковая, в какое время вы бы ни вскипятили чайник. Можете сами придумать такие функции, которые не меняются. На рисунке ниже я нарисовала в общем виде: y=с.
Функция, которая не меняется.
Чему равна производная такой функции? Функция не меняется, то есть ноль изменений. Производная равна нулю! А если посмотреть по формуле? Действительно, какую бы точку вы не взяли, изменения по оси y просто не будет. То есть dy всегда равно нулю. А тогда dy/dx=0.
2. Для этого нам понадобится раскрыть скобки. Помните, как?
Давным-давно, в самом начале занятий в группе мы этому учились.
Шаг 2. Теперь разделите dy на dx. Вы почти у цели, но у вас остался неприкаянный dx.
Шаг 3. Вспомните, что мы говорим о бесконечно маленькой окрестности, то есть dx стремится к нулю и исчезает!
Упрощаем. Правила сокращения
Когда мы считаем производную, то нам нужно что-то сократить, упростить выражение. Участники группы хотели, как всегда, разобраться до конца, и задали вопрос: какие вообще правила сокращения?
Это абсолютно фундаментальный вопрос, на котором в большой степени строится абстрактное понятие числа. Пусть и не в строгой математической формулировке.
Удивительно, что правил всего два, и они знакомы вам очень хорошо! Вот эти правила.
- Если число вычесть из самого себя, то получится 0.
Например, 5-5=0. - Если число разделить на само себя, то получится 1. Например, 5/5=1.
Например, 5-5=0.Оба эти правила вам понадобятся при выполнении задания. На рисунке примеры. А последний пример — это не просто пример, а подсказка для задания.
Правила сокращения
Идём стабильно по прямой
Приведу пример, чтобы было понятно, как записывать решение в последнем задании.
Давайте возьмём прямую, как на этом рисунке. Известное со школы уравнение y=a*x+b. Постараемся найти производную от этой функции.
Сначала здравый смысл. Что будет со скоростью изменения функции? Прямая растёт равномерно, с постоянной скоростью. Значит, производная должна быть постоянной и равной это скорости.
Теперь давайте посмотрим, как это сделать по формуле dy/dx. В ответе получается dy/dx=a. Производная постоянная. И красота: чем больше а, тем круче прямая и тем больше скорость изменения функции.
Всё правильно!
В ответе получается dy/dx = a.
Только формула прямой очень простая, у вас после деления на dx все dx сократятся. Когда вы будете считать производную для параболы, то dx останется. Тут надо учесть, что мы говорим о скорости в бесконечно маленькой окрестности точки, то есть dx стремится к нулю и исчезает.
На следующем занятии мы наконец-то «победим» длину параболы. А пока — выполняйте задания, спрашивайте в комментариях в группе, если что-то непонятно. И не давайте себе впадать в ступор!
Производная и ее применения — презентация онлайн
Производная и ее применения
Определение. Производной функции y=f(x),
заданной на некотором интервале (a;b), в точке х
этого интервала, называют предел отношения
приращения функции в этой точке к
соответствующему приращению аргумента,
когда приращение аргумента стремится к нулю.
Производную функции f(x) обозначают f ‘(x) и
говорят: «эф штрих от икс».
Следовательно,
f
f ( x) lim
x x
3. Алгоритм нахождения производной (для функции y=f(x)).
Зафиксировать значение х, найти f(x).Дать аргументу х приращение ∆х, перейти в
новую точку х+∆х, найти f(x+∆x).
Найти приращение функции: ∆у=f(x+∆x)–f(x).
у
Составим отношения
.
x
f
Вычислить lim x
x
Этот предел и есть f ‘(x).
4. Пример. Найти производную функции у=2х+3 в точке х=3
у (3) 2 3 3 9f ( x x) 2 (3 x) 3 2 x 9
y y (3 x) y (3) 2 x
y 2 x
2
x x
f
2
lim
x x
у (3) = 2
5. Физический смысл производной
Если при прямолинейном движении путь s,пройденной точкой, есть функция от времени t,
т.е. s=f(t), то скорость точки есть производная от
пути по времени, т.е. v(t)=f ‘(t), этот факт
выражает механический смысл производной.
6. пример
Тело движется по прямой так, что расстояние S (вметрах) от него до точки В этой прямой изменяется
по закону S (t ) 2t 12t 3(t – время движения в
секундах).
Через сколько секунд после началадвижения ускорение тела будет равно 36 м/ с 2 ?
Решение. Из механического смысла производной
имеем скорость – это производная пути по времени.
Скорость изменяется по закону v(t ) S (t ) 6t 24t . Так
как ускорение – это производная скорости по
времени, то ускорение изменяется по закону
a(t ) v (t ) 12t 24 , с другой стороны ускорение равно
2
с
36 м/ . Решим уравнение 12t 24 36
, t=5 c.
Ответ: через 5 секунд.
3
2
2
7. Геометрический смысл производной
Если в точке х 0 к графику функции y=f(x)проведена касательная, то число f ‘( х0) есть
тангенс угла альфа между этой касательной и
положительным направлением оси ОХ, т.е.
f ‘( х 0)=tgα. Этот угол называю углом наклона
касательной. Этот факт выражает
геометрический смысл производной.
8. Пример
На рисунке изображен график функции y=f(x)и касательная к нему в точке с абсциссой х .
Найдите значение производной функции f(x)
0
в точке х 0 .
Рис.1
9. Решение.
Значение производной f(x) в точке х 0 естьзначение тангенса угла, образованного
касательной к графику функции с
положительным направлением оси ОХ. Из
треугольника АВС (рис.1).
tga tg ( CAB)
Ответ: 1,75.
CB 7
1,75
AB 4
10. Вычисление производных
Формулами дифференцирования обычноназывают формулы для нахождения
производных конкретных функций.
11. Формулы дифференцирования
C 0x 1
( x n ) n x n 1
1
( x )
2 x
1
1
2
x
x
(sin x) cos x
(cos x) sin x
1
cos 2 x
1
(ctgx) 2
sin x
arcsin x 1 2 , x 1
1 x
1
(arccos x)
, x 1
2
1 x
1
(arctgx)
1 x2
1
(arcctgx)
1 x2
(tgx)
(ln x)
1
x
1
(log a x)
x ln a
(e x ) e x
(a x ) a x ln a
12. Формулы дифференцирования
1u
u
1
(log a u )
u
u ln a
(eu ) eu u
(ln u )
(a u ) a u ln a u
13.
Правила дифференцированияТеорема 1.Если функции y=f(x) и y=g(x) имеют
производную в точке x, то и их сумма имеет
производную в точке x, причем производная
суммы равна сумме производных:
( f ( x) g ( x)) f x g ( x)
14. Теорема 2
Если функция y=f(x) имеет производную в точкех, то и функция y=kf(x) имеет производную в
точке х, причем
kf x
kf x
15. Теорема 3
. Если функции y=f(x) и y=g(x) имеютпроизводную в точке x, то и их произведение
имеет производную в точке x, причем
( f ( x) g ( x)) f x g ( x) f ( x) g ( x)
16. Теорема 4
Если функции y=f(x) и y=g(x) имеют производнуюв точке x и в этой точке g(x) ≠0,
то функция
y
f x
g x
имеет производную в точке х, причем
f x
f x g x f x g x
g 2 ( x)
g x
17. Теорема 5
Если функция f имеет производную в точкех0
а функция g имеет производную в точке y0 f x0 ,
то сложная функция h x g f x также имеет
производную в точке х0 , причем
h x0 g f x0 f x0
Примеры.
Найтипроизводные функций
.
Решения
1.
f x x 3 x 4 ;
1.
f x 3×3 1 4 x 4 1 3x 2 4 x3 .
2.
f x 3x 3 2 x 2 ;
2.
f x 3 3×3 1 2 2 x 2 1 9 x 2 4 x.
3.
f x x 2 x 3 x ;
3.
f x
x 2x
3
1
x x 2 x3 x
2 x 3 x x 2 3x 3 1 1
2 x
2 x3 x
x 6×2 1 .
2 x
4.
2×2 4
f x
;
5x 8
4.
2x
f x
2
4 5x 8 2 x 2 4 5 x 8
5x 8
2
5x 8
2
20 x 2 32 x 10 x 2 20 10 x 2 32 x 20
.
5x 8 2
5x 8 2
5.
f x 8 x 4 ;
3
4 x 5 x 8 2 x 2 4 5
2
2
2
5. f x 3 8 x 4 8 x 4 3 8 x 4 8 24 8 x 4 .
19. Применение производной при исследовании функции
Пример 1.Функция y=f(x) определена на промежутке (-5;9). На
рисунке 2 изображен график производной этой
функции. Определите число касательных к графику
функции y=f(x), которые наклонены под углом 45 0
к положительному направлению оси абсцисс.
Рис.2
20. Решение.
Пусть α –угол касательной, проведенной кграфику функции y=f(x) в точке х 0
,и
положительным направлением оси абсцисс,
тогда tg f x0 .
У=1
Рис.3
Так как tg 450 1 , то для
решения задачи
достаточно определить
количество точек
пересечения графика
функции y f x и
прямой у=1. Таких
точек четыре.
21. Пример 2
На рисунке 2 Рис.2 изображен графикпроизводной функции y=f(x) найдите абсциссу
точки, в которой касательная к графику y=f(x)
параллельна прямой у=1 или совпадает с ней.
Решение. Так как касательная параллельна
прямой у=1, то ее угловой коэффициент равен 0
и тогда производная равна 0. По графику (рис.2)
определяем, что производная обращается в
ноль при х=-4; х=-0,5; х=3; х=7.
Рис.4
Ответ: -4; -0,5; 3; 7.
23. Пример 3.
На рисунке 5 изображен график функции y=f(x),определенной на промежутке . Определите
количество целых точек, в которых
производная функции f(x) положительна.
Рис.5
24. Решение.
Производная функцииположительна в тех целых
точках, которые
принадлежат какомунибудь промежутку
возрастания, за
исключением точек, в
которых производная равна
нулю (в этих точках
касательная к графику
функции параллельна оси
ОХ) или не существует. По
рисунку 2 определяем
абсциссы таких точек: -4; -3;
2; 3; 4. Таких точек пять.
Рис.6
25. Пример 4.
На рисунке 5изображен график
функции y=f(x), определенной на интервале (5;9). Определите количество целых точек, в
которых производная функции отрицательна.
Решение. Производная функции отрицательна в
тех целых точках, которые принадлежат
какому-нибудь промежутку убывания функции,
за исключением точек, в которых производная
равна нулю (в этих точках касательная к
графику функции параллельна оси ОХ) или не
существует. По рисунку определяем абсциссы
таких точек: -1; 0; 6; 7; 8. Таких точек пять.
Рис.
5Рис.7
Ответ:5
27. Пример 5.
На рисунке 2изображен график
производной функции y=f(x), определенной на
интервале (-5;9). Найдите промежутки
возрастания функции y=f(x). В ответе укажите
длину наибольшего из них.
Решение. Промежуткам возрастания функции
соответствуют промежутки, на которых
производная данной функции положительна.
По графику определяем, что наибольший из
этих промежутков имеет длину 4.
4
Рис.8
29. Пример 6.
На рисунке 2изображен график
производной функции y=f(x), определенной на
интервале (-5;9). Найдите промежутки
убывания функции y=f(x). В ответе укажите
длину наибольшего из них.
Решение. Промежуткам убывания функции
соответствуют промежутки, на которых
производная данной функции отрицательна. По
графику определяем, что наибольший из этих
промежутков имеет длину 3,5.
Рис.2
3,5
Рис.9
31. Пример 7.
На рисунке Рис.2 изображен графикпроизводной функции y=f(x), определенной на
интервале (-5;9).
Найдите количество точекмаксимума функции y=f(x).
Решение. Точек максимума здесь две, так как
график производной 4 раза меняет знак на
интервале (-5;9), из них два раза с плюса на
минус. Это и есть точки максимума.
Рис.10
33. Пример 8.
На рисункеизображен график
производной функции y=f(x), определенной на
интервале (-5;9). Найдите точки минимума
функции y=f(x).
Решение. На графике производной видно, что на
интервале (-5;9)производная 4 раза меняет знак
в точках х=-4; х=-0,5; х=3; х=7. Причем в точках
х=-4; х=3 он меняется с минуса на плюс. Значит,
эти точки являются точками минимума, так как
в точках х=-4 и х=3 характер монотонности
функции f(x) меняется с убывания на
возрастание.
Рис.2
-4
3
Рис.11
35. Пример 9.
На рисункеизображен график
производной функции y=f(x), определенной на
интервале (-5;9). Найдите количество точек
экстремума функции y=f(x).
Рис.
2Решение. На промежутке (-5;9) точек
экстремума функции y=f(x) ровно четыре: -4; 0,5; 3; 7.
-3
-0,5
Рис.12
3
7
37. Пример 10
На рисунке 13 изображен график производнойфункции y=f(x), определенной на интервале (5;4). Укажите абсциссы точек, в которой
касательная к графику функции y=f(x) имеет
наименьший и наибольший угловой
коэффициент.
Рис.13
38. Решение.
Угловой коэффициент касательной kкас. f x0 . Пографику определяем, что наименьшее значение
функция y f x достигает при x0 1 . А наибольшее
значение функция y f x достигает при x0 2 .
-2
Рис.14
39. Пример 11.
На рисункеизображен график
производной функции y=f(x), определенной на
интервале (-5;9). Найдите количество точек, в
которых касательная к графику функции y=f(x)
параллельна прямой у=-4х+3 или совпадает с
ней.
Касательная к графику функции y=f(x) в
некоторой точке параллельна прямой у=-4х+3,
если значение производной функции в этой
точке равно угловому коэффициенту прямой, то
есть f x 4 .
По графику (рис. 15) видно, чтопринимает значение -4 в одной точке.
Рис.2
у=-4
Рис.15
41. Пример 12.
.К графику функции y=f(x) проведена
касательная в точке с абсциссой x0 4 . На
рисунке 16 изображен график производной
этой функции. Определите градусную меру угла
наклона касательной.
Решение. Пусть
– угол наклона данной
касательной к оси абсцисс. Так как
.
,
то
f 4 1
tg 1
Отсюда получаем
.
Ответ: 1350
135 0
Рис. 16
42. Пример 14.
НаРис.5
изображен график функции y=f(x),
определенной на промежутке (-5;9). Найдите
количество точек, в которых касательная к
графику функции параллельна прямой y=-7.
Решение. Так как касательные параллельны
прямой у=-7, то они параллельны оси ОХ,
следовательно, производные функции f(x) в
точках касания должны ровняться нулю. Это
стационарные точки. На рисунке все они
являются точками экстремума (максимумами
или минимумами).
Их три.Рис.17
Ответ: 3.
Рис.5
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х9{2x}\]. |