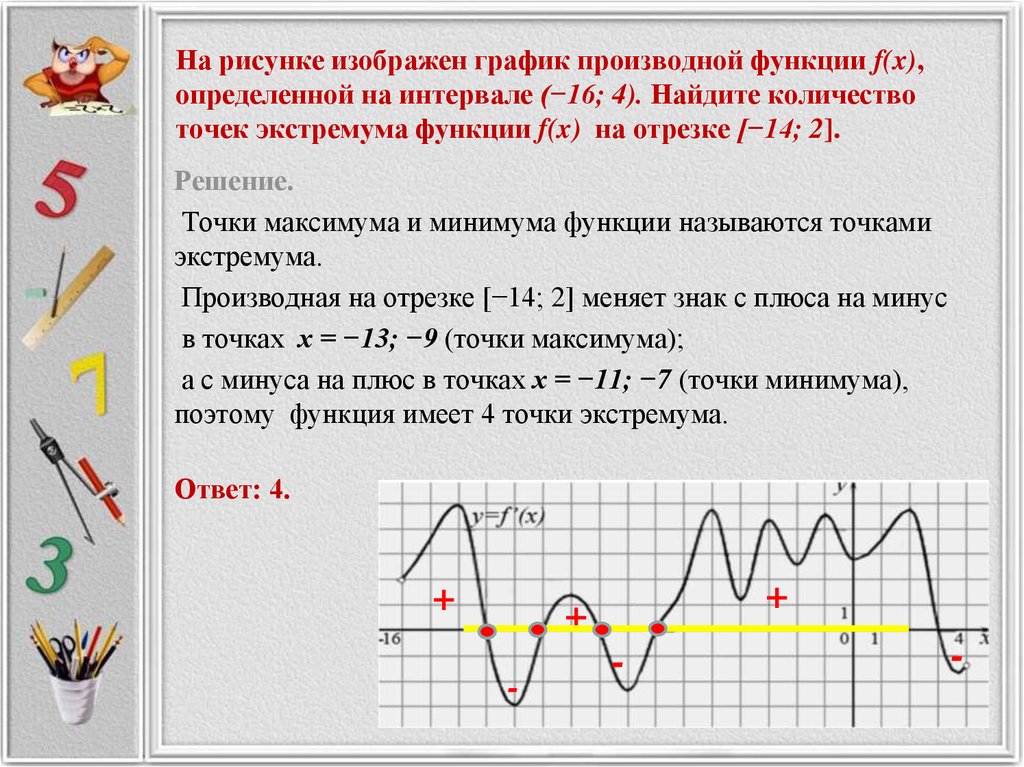
Производная fx. Производная функции
{\large\bf Производная функции}
Рассмотрим функцию y=f(x) , заданную на интервале (a, b) . Пусть x — любое фиксированная точка интервала (a, b) , а Δx — произвольное число, такое, что значение x+Δx также принадлежит интервалу (a, b) . Это число Δx называют приращением аргумента.
Определение . Приращением функции y=f(x) в точке x , соответствующим приращению аргумента Δx , назовем число
Δy = f(x+Δx) — f(x) .
Считаем, что Δx ≠ 0 . Рассмотрим в данной фиксированной точке x отношение приращения функции в этой точке к соответствующему приращению аргумента Δx
Это отношение будем называть разностным отношением. Так как значение x мы считаем фиксированным, разностное отношение представляет собой функцию аргумента Δx . Эта функция определена для всех значений аргумента Δx , принадлежащих некоторой достаточно малой окрестности точки
 Таким образом, мы имеем право рассматривать вопрос о существовании предела указанной функции при Δx → 0 .
Таким образом, мы имеем право рассматривать вопрос о существовании предела указанной функции при Δx → 0 .Определение . Производной функции y=f(x) в данной фиксированной точке x называется предел при Δx → 0 разностного отношения, то есть
При условии, что этот предел существует.
Обозначение . y′(x) или f′(x) .
Геометрический смысл производной : Производная от функции f(x) в данной точке x равна тангенсу угла между осью Ox и касательной к графику этой функции в соответствующей точке:
f′(x 0) = \tgα .
Механический смысл производной : Производная от пути по времени равна скорости прямолинейного движения точки:
Уравнение касательной к линии y=f(x) в точке M 0 (x 0 ,y 0) принимает вид
y-y 0 = f′(x 0) (x-x 0) .
Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если f′(x 0)≠ 0 , то уравнение нормали к линии y=f(x) в точке M 0 (x 0 ,y 0) записывается так:Понятие дифференцируемости функции
Пусть функция y=f(x) определена на некотором интервале (a, b) , x — некоторое фиксированное значение аргумента из этого интервала, Δx — любое приращение аргумента, такое, что значение аргумента x+Δx ∈ (a, b) .
Определение . Функция y=f(x) называется дифференцируемой в данной точке x , если приращение Δy этой функции в точке x , соответствующее приращению аргумента Δx , может быть представимо в виде
Δy = A Δx +αΔx ,
где A — некоторое число, не зависящее от Δx , а α — функция аргумента Δx , являющая бесконечно малой при Δx→ 0 .
Так как произведение двух бесконечно малых функций αΔx является бесконечно малой более высокого порядка, чем Δx (свойство 3 бесконечно малых функций), то можем записать:
Δy = A Δx +o(Δx) .
Теорема . Для того, чтобы функция y=f(x) являлась дифференцируемой в данной точке x , необходимо и достаточно, чтобы она имела в этой точке конечную производную. При этом A=f′(x) , то есть
Δy = f′(x) Δx +o(Δx) .
Операцию нахождения производной обычно называют дифференцированием.
Теорема . Если функция y=f(x) x , то она непрерывна в этой точке.
Если функция y=f(x) x , то она непрерывна в этой точке.
Замечание . Из непрерывности функции y=f(x) в данной точке x , вообще говоря, не вытекает дифференцируемость функции f(x) в этой точке. Например, функция y=|x| — непрерывна в точке x=0 , но не имеет производной.
Понятие дифференциала функции
Определение . Дифференциалом функции y=f(x) называется произведение производной этой функции на приращение независимой переменной x :
dy = y′ Δx, df(x) = f′(x) Δx .
Для функции y=x получаем dy=dx=x′Δx = 1· Δx= Δx , то есть dx=Δx — дифференциал независимой переменной равен приращению этой переменной.
Таким образом, можем записать
dy = y′ dx, df(x) = f′(x) dx
Дифференциал dy и приращение Δy функции y=f(x) в данной точке x , оба отвечающие одному и тому же приращению аргумента Δx , вообще говоря, не равны друг другу.
Геометрический смысл дифференциала : Дифференциал функции равен приращению ординаты касательной к графику данной функции, когда аргумент получает приращение Δx .
Правила дифференцирования
Рассмотрим сложную функцию y=f(φ(x))≡ F(x) , где y=f(u) , u=φ(x) . В этом случае u называют промежуточным аргументом , x — независимой переменной .
Теорема . Если y=f(u) и u=φ(x) — дифференцируемые функции своих аргументов, то производная сложной функции y=f(φ(x)) существует и равна произведению этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т. е.
е.
Замечание . Для сложной функции, являющейся суперпозицией трех функций y=F(f(φ(x))) , правило дифференцирования имеет вид
y′ x = y′ u u′ v v′ x ,
где функции v=φ(x) , u=f(v) и y=F(u) — дифференцируемые функции своих аргументов.
Теорема . Пусть функция y=f(x) возрастает (или убывает) и непрерывна в некоторой окрестности точки x 0 . Пусть, кроме того, эта функция дифференцируема в указанной точке x 0 и ее производная в этой точке f′(x 0) ≠ 0 . Тогда в некоторой окрестности соответствующей точки y 0 =f(x 0) определена обратная для y=f(x) функция x=f -1 (y) , причем указанная обратная функция дифференцируема в соответствующей точке y 0 =f(x 0) и для ее производной в этой точке y справедлива формула
Таблица производных
Инвариантность формы первого дифференциала
Рассмотрим дифференциал сложной функции. Если y=f(x) , x=φ(t) — дифференцируемы функции своих аргументов, то производная функции y=f(φ(t)) выражается формулой
y′ t = y′ x x′ t
По определению dy=y′ t dt , тогда получим
dy = y′ t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx ,
dy = y′ x dx .
Итак, доказали,
Свойство инвариантности формы первого дифференциала функции : как в случае, когда аргумент x является независимой переменной, так и в случае, когда аргумент x сам является дифференцируемой функцией новой переменной, дифференциал dy функции y=f(x) равен производной этой функции, умноженной на дифференциал аргумента dx .
Применение дифференциала в приближенных вычислениях
Мы показали, что дифференциал dy функции y=f(x) , вообще говоря, не равен приращению Δy этой функции. Тем не менее с точностью до бесконечно малой функции более высокого порядка малости, чем Δx , справедливо приближенное равенство
Δy ≈ dy .
Отношение называют относительной погрешностью равенства этого равенства. Так как Δy-dy=o(Δx) , то относительная погрешность данного равенства становится как угодно малой при уменьшении |Δх| .
Учитывая, что Δy=f(x+δ x)-f(x) , dy=f′(x)Δx , получим f(x+δ x)-f(x) ≈ f′(x)Δx или
f(x+δ x) ≈ f(x) + f′(x)Δx .
Это приближенное равенство позволяет с ошибкой o(Δx) заменить функцию f(x) в малой окрестности точки x (т.е. для малых значений Δx ) линейной функцией аргумента Δx , стоящей в правой части.
Производные высших порядков
Определение . Второй производной (или производной второго порядка) функции y=f(x) называется производная от ее первой производной.
Обозначение второй производной функции y=f(x) :
Механический смысл второй производной . Если функция y=f(x) описывает закон движения материальной точки по прямой линии, то вторая производная
Аналогично определяется третья, четвертая производная.
Определение . n -й производной (или производной n -го порядка) функции y=f(x) называется производная от ее n-1 -й производной:
y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′ .
Обозначения: y″′ , y IV , y V и т.д.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Вычисление производной — одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:
Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:
- Таблица производных экспоненциальных и логарифмических функций
Приведенные формулы используйте как справочные значения. Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена «шпаргалка» основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.
Производные простых функций
1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0
Пояснение :
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях — скорость его изменения всегда равна нулю.
2. Производная переменной равна единице
x´ = 1
Пояснение :
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение :
В данном случае, при каждом изменении аргумента функции (х ) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .
Откуда следует, что
(cx + b)» = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|» = x / |x| при условии, что х ≠ 0
Пояснение :
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.
Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)»= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)» = 2x
(x 3)» = 3x 2
Для запоминания формулы :
Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.
6. Производная дроби 1/х
(1/х)» = — 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)» = (x -1)» , тогда можно применить формулу из правила 5 таблицы производных
(x -1)» = -1x -2 = — 1 / х 2
7. Производная дроби с переменной произвольной степени в знаменателе
Производная дроби с переменной произвольной степени в знаменателе
(1 / x c)» = — c / x c+1
Пример:
(1 / x 2)» = — 2 / x 3
8. Производная корня (производная переменной под квадратным корнем)
(√x)» = 1 / (2√x) или 1/2 х -1/2
Пример:
(√x)» = (х 1/2)» значит можно применить формулу из правила 5
(х 1/2)» = 1/2 х -1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
(n √x)» = 1 / (n n √x n-1)
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше
предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться
таблицей производных и правилами дифференцирования. Для нахождения производной подходит
следующий алгоритм.
Для нахождения производной подходит
следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
11. Производная арккосинуса Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т. е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т. е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
А проверить решение задачи на производную можно на .
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение.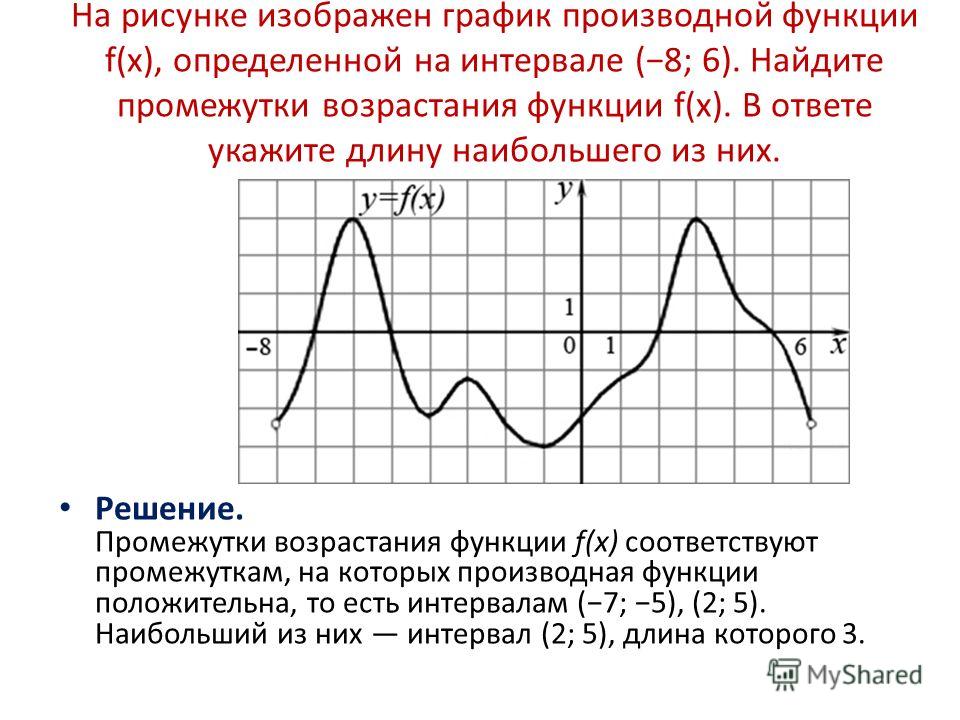 В данной функции видим произведение, один из сомножителей которых — квадратный корень
из независимой переменной, с производной которого мы ознакомились в таблице производных. По
правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
В данной функции видим произведение, один из сомножителей которых — квадратный корень
из независимой переменной, с производной которого мы ознакомились в таблице производных. По
правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Проверить решение задачи на производную можно на калькуляторе производных онлайн .
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
Примеры. Найти производные функций.
1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 .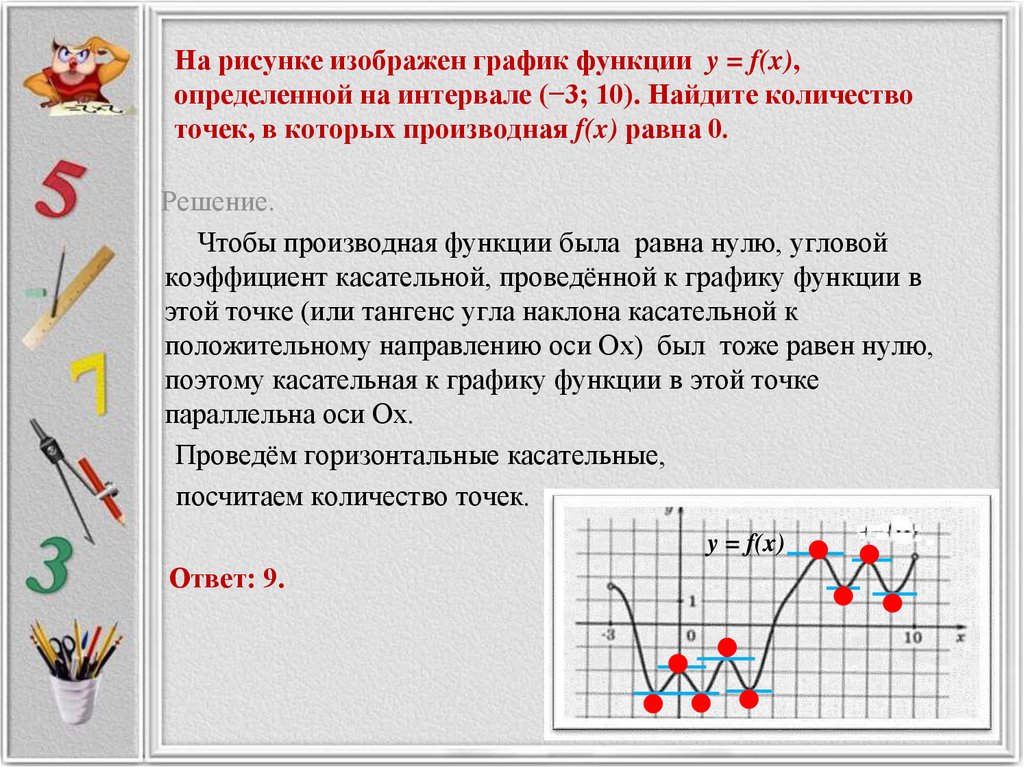 Получаем:
Получаем:
y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.
2. y=3x 6 -2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x 5 -2=18x 5 -2.
Применяем правило I , формулы 3, 5 и 6 и 1.
Применяем правило IV , формулы 5 и 1 .
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4 ), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4 . Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4 . Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
Примеры.
1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое —4,01 .
Решение.
Новое значение аргумента х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.
Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f «(х 0) = 1 .
Решение.
Значение производной в точке касания х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f «(х 0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .
3. Вывести формулу производной функции y=x n .
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)» = nx n-1 .
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования .
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых. 2
2
ПРОИЗВОДНАЯ | Энциклопедия Кругосвет
Содержание статьи- Мгновенная скорость.
- Геометрическое значение производной. Касательная к графику функции.
- Дифференцируемость функций.
- Непрерывность функции, имеющей производную. Теорема.
- Производные различных порядков.
- Дифференциалы различных порядков.
- Частная производная.
ПРОИЗВОДНАЯ – производной функции y = f(x), заданной на некотором интервале (a, b) в точке x этого интервала, называется предел, к которому стремится отношение приращения функции f в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.
Производную принято обозначать так:
.
Широко употребляются и другие обозначения:
Предел , где рассматривается только Dx > 0 или только Dx f в точке x.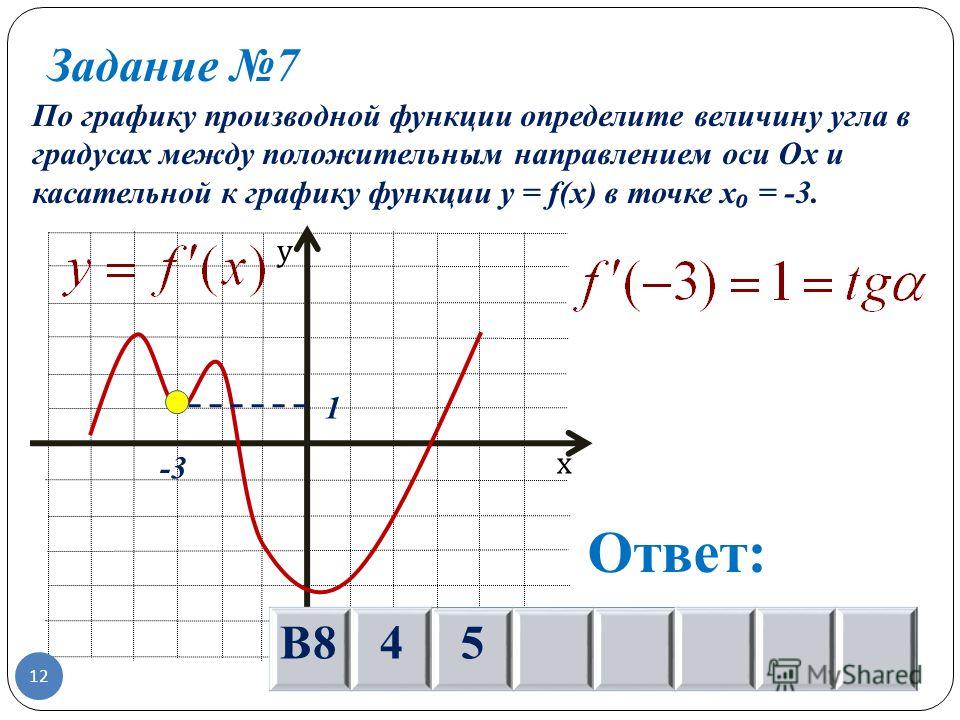 О функции f, заданной на отрезке [a, b] принято говорить, что она имеет на этом отрезке производную, если она имеет производную в любой точке интервала (a, b) и, кроме того, правую производную в точке a и левую в точке b.
О функции f, заданной на отрезке [a, b] принято говорить, что она имеет на этом отрезке производную, если она имеет производную в любой точке интервала (a, b) и, кроме того, правую производную в точке a и левую в точке b.
Понятие производной возникло как результат многовековых усилий, направленных на решение таких задач, как задача о проведении касательной к кривой, о вычислении скорости неравномерного движения, задачи о вычислении площади криволинейной фигуры. В работах Исаака Ньютона и Готфрида Вильгельма Лейбница эта деятельность получила определенное теоретическое завершение. Ньютон и Лейбниц создали общие методы дифференцирования и интегрирования функций и доказали важную теорему, носящую их имя, устанавливающую тесную связь между операциями дифференцирования и интегрирования. Однако современное изложение этих вопросов существенно отличается от того, как они излагались во времена Ньютона и Лейбница. Современный математический анализ базируется на понятии предела, которое было дано (наряду с другими важнейшими понятиями – непрерывность, интеграл и т. д.) в работах французского математика Огюстена Луи Коши.
д.) в работах французского математика Огюстена Луи Коши.
Мгновенная скорость.
Пусть точка M движется по прямой. Расстояние s движущейся точки, отсчитываемое от некоторого начального ее положения M0 , зависит от времени t , т.е. s есть функция времени t: s = f(t). Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M0, а в некоторый следующий момент t + Dt оказалась в положении M1 – на расстоянии s + Ds от начального положения (см. рис.).
Таким образом, за промежуток времени Dt расстояние s изменилось на величину Ds. В этом случае говорят, что за промежуток времени Dt величина s получила приращение Ds.
Отношение представляет собой среднюю скорость движения точки за время Dt:
.
Средняя скорость не может во всех случаях точно охарактеризовать быстроту перемещения точки M в момент времени t. Если, например, тело в начале промежутка Dt перемещалось очень быстро, а в конце очень медленно, то средняя скорость не сможет отразить указанных особенностей движения точки и дать представление об истинной скорости ее движения в момент t. Чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени Dt. Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при Dt ® 0. Этот предел называют скоростью движения в данный момент:
.
Таким образом, скоростью движения в данный момент называется предел отношения приращения пути Ds к приращению времени Dt, когда приращение времени стремится к нулю. Так как
,
то.
Геометрическое значение производной. Касательная к графику функции.

Построение касательных – одна из тех задач, которые привели к рождению дифференциального исчисления. Первый опубликованный труд, относящийся к дифференциальному исчислению и принадлежащий перу Лейбница, имел название Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления.
Пусть кривая есть график функции y = f(x) в прямоугольной системе координат (см. рис.).
При некотором значении x функция имеет значение y = f(x). Этим значениям x и y на кривой соответствует точка M0(x, y). Если аргументу x дать приращение Dx, то новому значению аргумента x + Dx соответствует новое значение функции y+Dy = f(x + Dx). Соответствующей ему точкой кривой будет точка M1(x + Dx, y + Dy). Если провести секущую M0M1 и обозначить через j угол, образованный секущей с положительным направлением оси Ox, из рисунка непосредственно видно, что .
Если провести секущую M0M1 и обозначить через j угол, образованный секущей с положительным направлением оси Ox, из рисунка непосредственно видно, что .
Если теперь Dx стремится к нулю, то точка M1 перемещается вдоль кривой, приближаясь к точке M0, и угол j изменяется с изменением Dx. При Dx ® 0 угол j стремится к некоторому пределу a и прямая, проходящая через точку M0 и составляющая с положительным направлением оси абсцисс угол a, будет искомой касательной. Ее угловой коэффициент:
.
Следовательно, f´(x) = tga
т.е. значение производной f´(x) при данном значении аргумента x равняется тангенсу угла, образованного касательной к графику функции f(x) в соответствующей точке M0(x,y) с положительным направлением оси Ox.
Дифференцируемость функций.
Определение. Если функция y = f(x) имеет производную в точке x = x0, то функция дифференцируема в этой точке.
Если функция y = f(x) имеет производную в точке x = x0, то функция дифференцируема в этой точке.
Непрерывность функции, имеющей производную. Теорема.
Если функция y = f(x) дифференцируема в некоторой точке x = x0, то она в этой точке непрерывна.
Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x0 функция y = f(x) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x| непрерывна для всех x (–Ґ х x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.
Некоторые теоремы о дифференцируемых функциях. Теорема о корнях производной (теорема Ролля). Если функция f(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка и на концах x = a и x = b обращается в нуль (f(a) = f(b) = 0), то внутри отрезка [a,b] существует, по крайней мере одна, точка x = с, a c b, в которой производная fў(x) обращается в нуль, т. е. fў(c) = 0.
е. fў(c) = 0.
Теорема о конечных приращениях (теорема Лагранжа). Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a, b] найдется по крайней мере одна точка с, a c b, что
f(b) – f(a) = f ў(c)(b – a).
Теорема об отношении приращений двух функций (теорема Коши). Если f(x) и g(x) – две функции, непрерывные на отрезке [a, b] и дифференцируемые во всех внутренних точках этого отрезка, причем gў(x) нигде внутри этого отрезка не обращается в нуль, то внутри отрезка [a, b] найдется такая точка x = с, a c b, что
.
Производные различных порядков.
Пусть функция y = f(x) дифференцируема на некотором отрезке [a, b]. Значения производной f ў(x), вообще говоря, зависят от x, т.е. производная f ў(x) представляет собой тоже функцию от x. При дифференцировании этой функции получается так называемая вторая производная от функции f(x), которая обозначается f ўў (x).
Значения производной f ў(x), вообще говоря, зависят от x, т.е. производная f ў(x) представляет собой тоже функцию от x. При дифференцировании этой функции получается так называемая вторая производная от функции f(x), которая обозначается f ўў (x).
Производной n-го порядка от функции f(x) называется производная (первого порядка) от производной n-1—го и обозначается символом y(n) = (y(n – 1))ў.
Дифференциалы различных порядков.
Дифференциал функции y = f(x), где x – независимая переменная, есть dy = f ў(x)dx, некоторая функция от x, но от x может зависеть только первый сомножитель f ў(x), второй же сомножитель (dx) является приращением независимой переменной x и от значения этой переменной не зависит. Так как dy есть функция от x, то можно определить дифференциал этой функции. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y:
Так как dy есть функция от x, то можно определить дифференциал этой функции. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y:
d(dx) = d2y = f ўў(x)(dx)2.
Дифференциалом n-го порядка называется первый дифференциал от дифференциала n-1—го порядка:
dny = d(dn–1 y) = f(n)(x)dx(n).
Частная производная.
Если функция зависит не от одного, а от нескольких аргументов xi (i изменяется от 1 до n, i = 1, 2,… n), f(x1, x2,… xn), то в дифференциальном исчислении вводится понятие частной производной, которая характеризует скорость изменения функции нескольких переменных, когда изменяется только один аргумент, например, xi .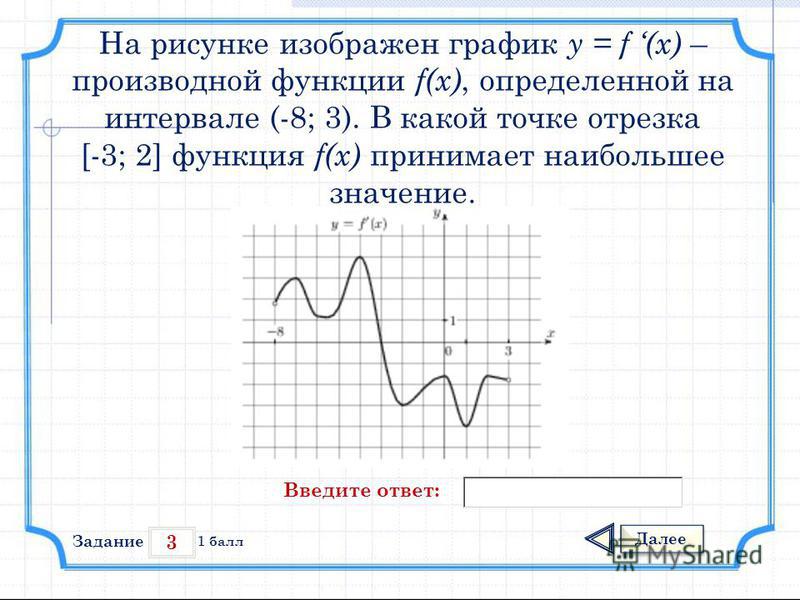 Частная производная 1-ого порядка по xi определяется как обычная производная, при этом предполагается, что все аргументы, кроме xi, сохраняют постоянные значения. Для частных производных вводятся обозначения
Частная производная 1-ого порядка по xi определяется как обычная производная, при этом предполагается, что все аргументы, кроме xi, сохраняют постоянные значения. Для частных производных вводятся обозначения
fxn, или
Определенные таким образом частные производные 1-ого порядка (как функции тех же аргументов) могут, в свою очередь, также иметь частные производные, это частные производные второго порядка и т.д. Взятые по разным аргументам такие производные называются смешанными. Непрерывные смешанные производные одного порядка не зависят от порядка дифференцирования и равны между собой.
Анна Чугайнова
Задание № 7. Производная функции. ЕГЭ . Математика. 1
ПОДГОТОВКА К ЕГЭ ПО МАТЕМАТИКЕ
1. Планиметрия
2. Стереометрия
3. Начала теории вероятностей
4. Теория вероятностей
5. Простейшие уравнения
6. Преобразование выражений
Преобразование выражений
7. Производная функции
8. Практические задачи
9. Текствые задачи
10. Графики функций
11. Исследование функций
12. Уравнения
13. Стереометрия с доказ-вом
14. Неравенства
15. Финансовая математика
16. Планиметрия с доказ-вом
17. Задачи с параметром
18. Задачи на логику
БАЗА ЗАДАНИЙ
Задание № 7. Производная функции.
1. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: 1
2. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: 0,75
3. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: -0,5
4. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: 2
5. На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0..
Ответ: -0,75
6. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: 1,4
7. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: -0,25
8. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: 0,4
9. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: -0,8
10. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: -1,25
11. На рисунке изображен график функции y=f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите значение производной в точке 8.
Ответ: 1,25
12. На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (− 5; 5). Найдите точку из отрезка [− 2; 4], в которой производная функции f(x) равна 0.
Ответ: 1
13. На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (1; 10). Найдите точку из отрезка [2; 6], в которой производная функции f(x) равна 0.
Ответ: 3
14. На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (− 11; − 2). Найдите точку из отрезка [− 10; − 4], в которой производная функции f(x) равна 0.
Найдите точку из отрезка [− 10; − 4], в которой производная функции f(x) равна 0.
Ответ: -7
15. На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (− 11; − 1). Найдите точку из отрезка [− 7; − 2], в которой производная функции f(x) равна 0.
Ответ: -4
16. На рисунке изображён график функции y=f(x), определённой на интервале (− 5; 9). Найдите количество точек, в которых производная функции f(x) равна 0.
Ответ: 6
17. На рисунке изображён график функции y=f(x), определённой на интервале (− 5; 8). Найдите количество точек, в которых производная функции f(x) равна 0.
Ответ: 8
18. На рисунке изображён график функции y=f(x), определённой на интервале (− 3; 8). Найдите количество точек, в которых производная функции f(x) равна 0.
Ответ: 7
19. На рисунке изображён график функции y=f(x), определённой на интервале (− 6; 6). Найдите количество решений уравнения f '(x)=0 на отрезке [− 4,5; 2,5].
Ответ: 4
20. На рисунке изображён график функции y=f '(x) — производной функции f(x), определённой на интервале (2; 13). Найдите точку максимума функции f(x).
Ответ: 9
21. На рисунке изображён график функции y=f '(x) — производной функции f(x), определённой на интервале (− 6; 3). Найдите точку минимума функции f(x).
Найдите точку минимума функции f(x).
Ответ: -2
22. На рисунке изображён график функции y=f '(x) — производной функции f(x), определённой на интервале (1; 10). Найдите точку минимума функции f(x).
Ответ: 9
23. На рисунке изображён график функции y=f '(x) — производной функции f(x), определённой на интервале (− 5; 5). Найдите точку максимума функции f(x).
Ответ: -1
24. На рисунке изображён график функции y=f(x), определённой на интервале (− 7; 7). Определите количество целых точек, в которых производная функции положительна.
Ответ: 8
25. На рисунке изображён график функции y=f(x), определённой на интервале (− 7; 7). Определите количество целых точек, в которых производная функции отрицательна.
Определите количество целых точек, в которых производная функции отрицательна.
Ответ: 5
1 2 3
Главная
@ 2017- 2022
База заданий сформирована из Официального Банка заданий ФИПИ,
Открытого банка заданий ЕГЭ, а также из реальных вариантов ЕГЭ прошлых лет.
Репетитор
по математике
WhatsApp: 8-913-866-07-50
| Дата: 20.11.2014 Таблица производных.Производная — одно из главных понятий высшей математики. В этом уроке мы познакомимся с этим понятием. Именно познакомимся, без строгих математических формулировок и доказательств. Это знакомство позволит: Понимать суть несложных заданий с производной; Успешно решать эти самые несложные задания; Подготовиться к более серьёзным урокам по производной. Сначала — приятный сюрприз.) Строгое определение производной основано на теории пределов и штука достаточно сложная. Это огорчает. Но практическое применение производной, как правило, не требует таких обширных и глубоких знаний! Для успешного выполнения большинства заданий в школе и ВУЗе достаточно знать всего несколько терминов — чтобы понять задание, и всего несколько правил — чтобы его решить. И всё. Это радует. Приступим к знакомству?) Термины и обозначения. В элементарной математике много всяких математических операций. Сложение, вычитание умножение, возведение в степень, логарифмирование и т.д. Если к этим операциям добавить ещё одну, элементарная математика становится высшей. Эта новая операция называется дифференцирование. Определение и смысл этой операции будут рассмотрены в отдельных уроках. Здесь же важно понять, что дифференцирование — это просто математическая операция над функцией. Берём любую функцию и, по определённым правилам, преобразовываем её. В результате получится новая функция. Вот эта новая функция и называется: производная. Дифференцирование — действие над функцией. Производная — результат этого действия. Так же, как, например, сумма — результат сложения. Или частное — результат деления. Зная термины, можно, как минимум, понимать задания.) Формулировки бывают такие: найти производную функции; взять производную; продифференцировать функцию; вычислить производную и т. Обозначается производная с помощью штришка вверху справа над функцией. Вот так: y» или f»(x) или S»(t) и так далее. Читается игрек штрих, эф штрих от икс, эс штрих от тэ, ну вы поняли…) Штрих также может обозначать производную конкретной функции, например: (2х+3)» , (x 3 )» , (sinx)» и т.д. Часто производная обозначается с помощью дифференциалов, но такое обозначение в этом уроке мы рассматривать не будем. Предположим, что понимать задания мы научились. Осталось всего ничего — научиться их решать.) Напомню ещё раз: нахождение производной — это преобразование функции по определённым правилам. Этих правил, на удивление, совсем немного. Чтобы найти производную функции, надо знать всего три вещи. Три кита, на которых стоит всё дифференцирование. 1. Таблица производных (формулы дифференцирования). 3. Производная сложной функции. Начнём по порядку. В этом уроке рассмотрим таблицу производных. Таблица производных.В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п. Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.) Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная.
Рекомендую обратить внимание на третью группу функций в этой таблице производных. Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету… Рассмотрим несколько примеров: 1. Найти производную функции y = x 3 Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат: (x 3) » = 3·x 3-1 = 3x 2 Вот и все дела. Ответ: y» = 3x 2 2. Найти значение производной функции y = sinx в точке х = 0. Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию… Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция. По табличке находим синус и соответствующую производную: y» = (sin x)» = cosx Подставляем ноль в производную: y»(0) = cos 0 = 1 Это и будет ответ. 3. Продифференцировать функцию: Что, внушает?) Такой функции в таблице производных и близко нет. Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает… Но если увидеть, что наша функция — это косинус двойного угла , то всё сразу налаживается! Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. Т.е. наша хитрая функция есть не что иное, как y = cosx . А это — табличная функция. Сразу получаем: Ответ: y» = — sin x . Пример для продвинутых выпускников и студентов: 4. Найти производную функции: Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями… То вполне можно упростить эту функцию. Вот так: А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем: Вот и всё. Это будет ответ. Надеюсь, что с первым китом дифференцирования — таблицей производных — всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования. |
Производная функции
6.1 Дифференцирование функций, заданных явно
Производной функцииy=f(x) в точкеx0называется предел отношения приращения функции в этой точке к приращению аргумента, когда последнее стремится к нулю. Производная функцииy=f(x) обозначается черезy/, илиf /(x).
Операция нахождения производной f /(x) от функцииf(x) называетсядифференцированием этой функции.
Геометрически
значение производной функции y=f(x)
в точкеx=x0равно тангенсу угла, образованного
положительным направлением осиОхи касательной, проведенной к графику
функции в точке с абсциссойx0,
то естьf /( x0)=tg (рис 6. 1).
1).
Число tg называютугловым коэффициентом касательнойи обозначаютk, то есть k =f /( x0)=tg. В прямоугольной системе координат уравнения касательной и нормали к некоторой кривой y =f (x) в точкеМ0(x0; y0) имеют вид | Рис 6.1 |
–уравнение касательной,
–уравнение нормали.
Если
функция y=f(x)
описывает какой–либо физический
процесс, то производнаяy/есть скорость протекания этого процесса.
В этом состоит физический смысл
производной.
Основные правила дифференцирования.
Пусть даны функции, имеющие производные u=u(x) и v=v(x), c=const
6.1 6.2 6.3 | 6.4 6.5 |
6.6
6.7 если дана сложная функция y=f(u), где u=u(x), то есть y=f[u(x)], где функции f(u) и u(x) имеют производные, то (правило дифференцирования сложной функции).
Основные формулы дифференцирования.
6.8 6.9 6.10 6.11 6.12 6.13 6.14 6.15 6.16 6. | 6.18 6.19 6.20 6.21 6.22 6.23 6.24 6.25 6.26 |
Пример 1. Найти производную функции .
Решение. Дифференцируем как сумму по формулам 6.4, 6.1, 6.3 правил дифференцирования и применяем формулу 6.8
Пример 2. Найти y// функции .
Решение. Дифференцируем как частное по формуле 6.5 правил дифференцирования и применяем формулы 6.2, 6.1 и 6.8
.
Пример 3. Найти y/функции .
Решение. Дифференцируем, применяя формулы производной сложной функции и формулы 6.8 и 6.12
Пример
4.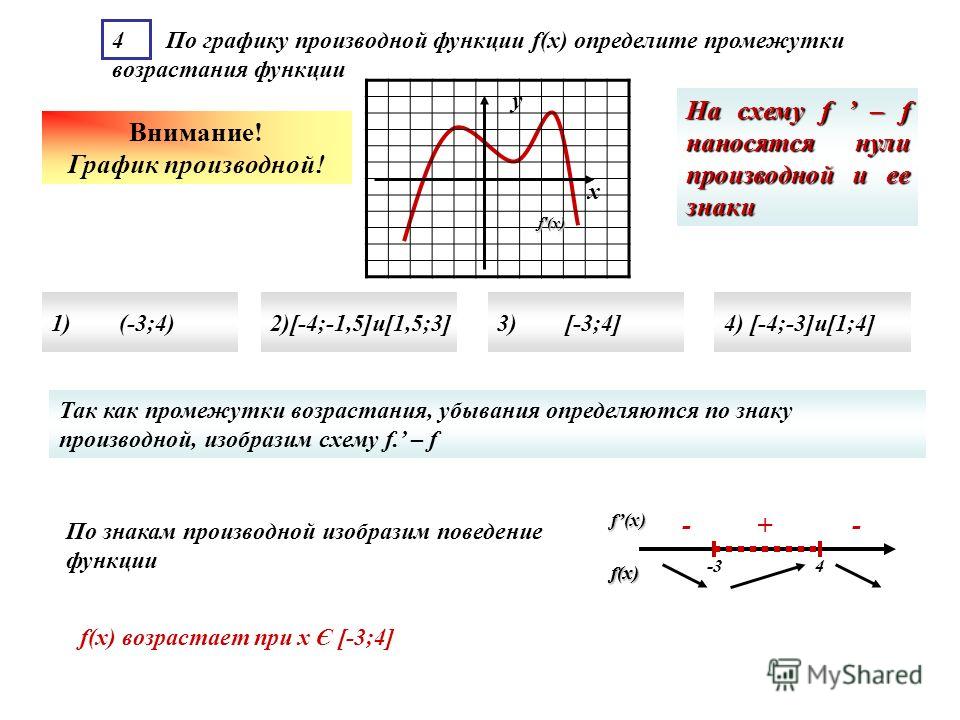 Найти y/функции
.
Найти y/функции
.
Решение. Вводим сначала дробные и отрицательные показатели, затем дифференцируем, применяя формулы 6.3, 6.2 и 6.1 и формулу 6.8
Пример 5. Найти y/функции .
Решение. Применяем сначала формулу 6.3, а для второго слагаемого формулу 6.4. Затем используем формулы 6.9, 6.14, 6.8 и 6.15
Логарифмический метод.
Иногда,
прежде чем находить производную от
заданного выражения, лучше выражение
преобразовать так, чтобы процесс
дифференцирования упрощался. Во многих
случаях оказывается выгодным, прежде
чем дифференцировать заданную функцию,
взять ее логарифм, определить затем
производную от этого логарифма и по
производной от логарифма отыскать
производную от заданной функции. Такой
прием называется способом логарифмического
дифференцирования.
Метод логарифмического дифференцирования позволяет находить производные от сложной функции вида , гдеu,v— функции аргументаx. Действительно, логарифмируя обе части исходного равенства, получаем
.
Дифференцируя последнее равенство, имеем
.
Умножая обе части равенства на y и заменяя затемy черезuv, окончательно получаем
.
Пример 6. Найтиy/, если.
Решение. Здесь основание и показатель степени зависят отx. Логарифмируя, получим
(так как).
Продифференцируем обе части последнего равенства по x. Так какyявляется функцией отx, тоlny есть сложная функцияxи. Следовательно,
или
.
Умножив последнее равенство на y, получим
.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Производные – исчисление, значение, интерпретация
Производная в исчислении – это скорость изменения величины y по отношению к другой величине x.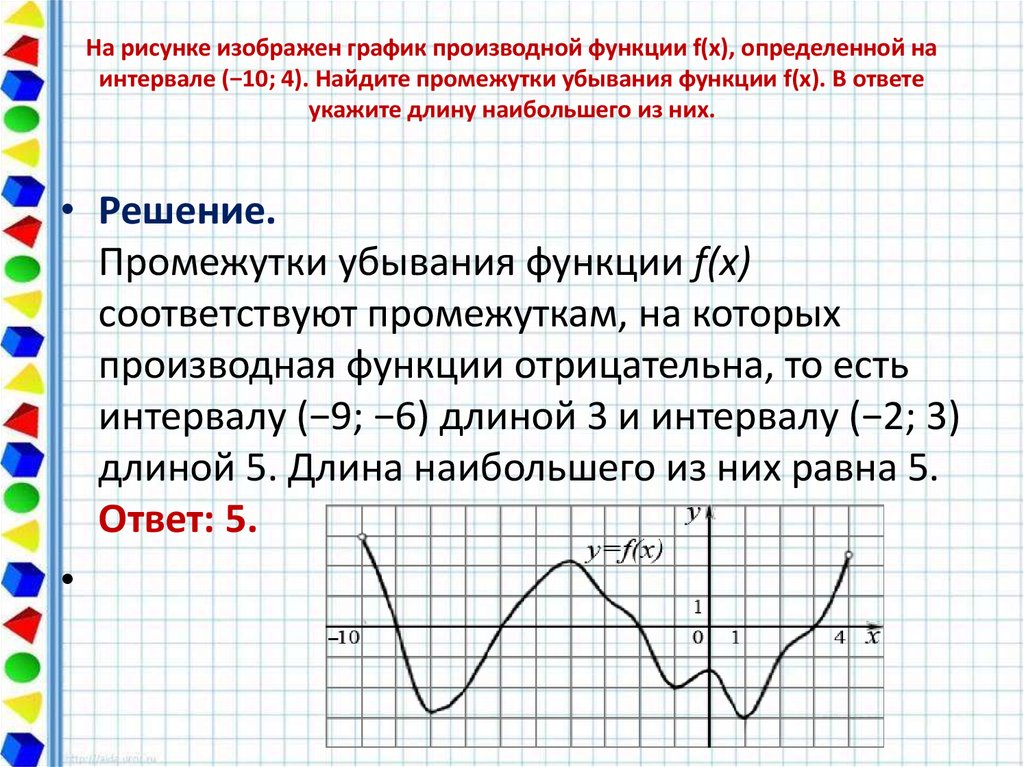 Его также называют дифференциальным коэффициентом y по отношению к x. Дифференцирование – это процесс нахождения производной функции.
Его также называют дифференциальным коэффициентом y по отношению к x. Дифференцирование – это процесс нахождения производной функции.
Давайте узнаем, что именно означает производная в исчислении и как ее найти вместе с правилами и примерами.
| 1. | Значение производных в исчислении |
| 2. | Интерпретация производных финансовых инструментов |
| 3. | Производная функции, использующая первый принцип |
| 4. | Производные формулы в исчислении |
| 5. | Основные правила деривативов |
| 6. | Производные составных функций (цепное правило) |
| 7. | Производные неявных функций |
| 8. | Параметрические производные |
| 9. | Производные высшего порядка |
| 10. | Частные производные |
11.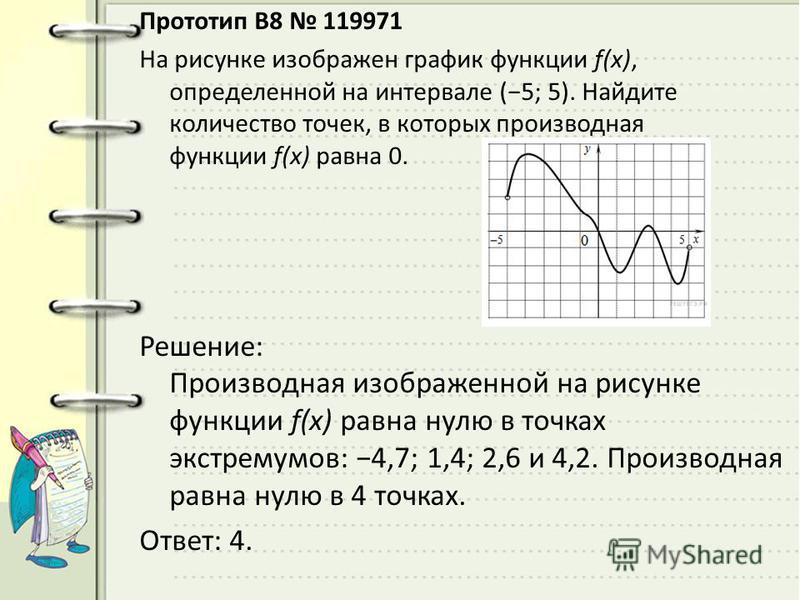 | Нахождение производной с помощью логарифмического дифференцирования |
| 12. | Максимум/минимум с использованием производных |
| 13. | Часто задаваемые вопросы о деривативах |
Значение производных в исчислении
Производная функции f(x) обычно представляется как d/dx (f(x)) (или) df/dx (или) Df(x) (или) f'(x). Давайте посмотрим, что технически означает производная. Рассмотрим кривую функции f(x) и пусть две точки на ней будут (x, f(x)) и ((x + h), f(x + h)). Тогда наклон секущей, проходящей через эти точки, равен [f(x + h) — f(x)]/(x + h — x) = [f(x + h) — f(x)/h. Посмотрите на рисунок ниже и обратите внимание, что когда расстояние между двумя точками почти равно 0 (т. е. когда h приближается к 0), вторая точка перекрывает исходную точку, а секущая становится касательной. В исчислении наклон касательной называется производной функции. то есть
- Производная функции, f ‘(x) = Наклон касательной = lim h→0 [f(x + h) — f(x) / h.

Эта формула широко известна как «предельное определение производной» (или) «производной по первому принципу».
Интерпретация деривативов
Производная функции f(x) в математике обозначается как f'(x) и может быть контекстуально интерпретирована следующим образом:
- Производная функции в точке представляет собой наклон касательной, проведенной к этой кривой в таком случае.
- Также представляет мгновенную скорость изменения в точке функции.
- Скорость частицы находится путем нахождения производной функции смещения.
- Производные используются для оптимизации (максимизации/минимизации) функции.
- Они также используются для нахождения интервалов возрастания/убывания функции, а также интервалов вогнутости функции вверх/вниз.
Таким образом, всякий раз, когда мы видим такие фразы, как «наклон/градиент», «скорость изменения», «скорость (учитывая смещение)», «максимизировать/минимизировать» и т.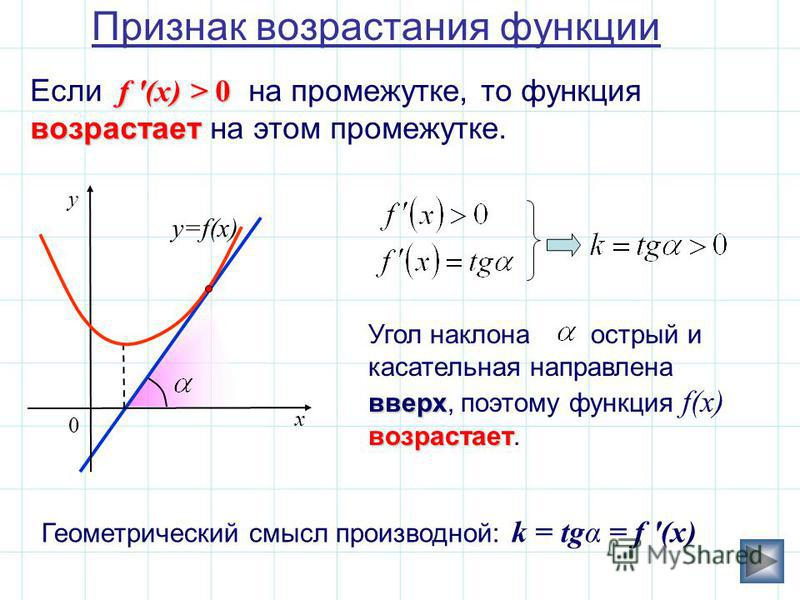 д., это означает, что используется понятие производных.
д., это означает, что используется понятие производных.
Производная функции, использующая первый принцип
Производная функции может быть получена с помощью предельного определения производной: f'(x) = lim h→0 [f(x + h) — f(x) / h. Этот процесс известен как дифференцирование по первому принципу. Пусть f(x) = x 2 , и мы найдем его производную, используя приведенную выше формулу производной. Здесь f(x + h) = (x + h) 2 , так как f(x) = x 2 . Тогда производная от f(x) равна
f ‘(x) = lim h→0 [(x + h) 2 — x 2 ] / h
= lim h→0 [ x 2 + 2xh + h 2 — x 2 ] / h
= lim ч → 0 [ 2xh + ч 2 ] / ч
= lim ч→0 [ч(2x + ч)] / ч
= lim ч→0 (2x + ч)
= 2х + 0
= 2x
Таким образом, производная x 2 равна 2x. Но может быть трудно использовать это предельное определение для нахождения производных сложных функций. Таким образом, есть некоторые производные формулы (конечно, производные от приведенного выше определения предела), которые мы можем легко использовать в процессе дифференцирования.
Таким образом, есть некоторые производные формулы (конечно, производные от приведенного выше определения предела), которые мы можем легко использовать в процессе дифференцирования.
Производные формулы в исчислении
Три основные производные алгебраической, логарифмической/экспоненциальной и тригонометрической функций выводятся из первого принципа дифференцирования и используются как стандартные формулы производных. Они следующие.
Степенное правило производных
Используя приведенный выше пример, производная x 2 равна 2x. Точно так же мы можем доказать, что производная x 3 равна 3x 2 9x is, d/dx (a x ) = a x ln a Здесь представлены производные тригонометрических функций. Здесь представлены производные обратных тригонометрических функций. Производные тригонометрических функций
Производные обратных тригонометрических функций

Основные правила деривативов
Ниже приведены основные правила производных. Давайте обсудим их подробно.
Степенное правило: Согласно этому правилу, если y = x n , то dy/dx = n x n-1 . Пример: d/dx (x 5 ) = 5x 4 .
Правило суммы/разности: Процесс производной можно распределить на сложение/вычитание.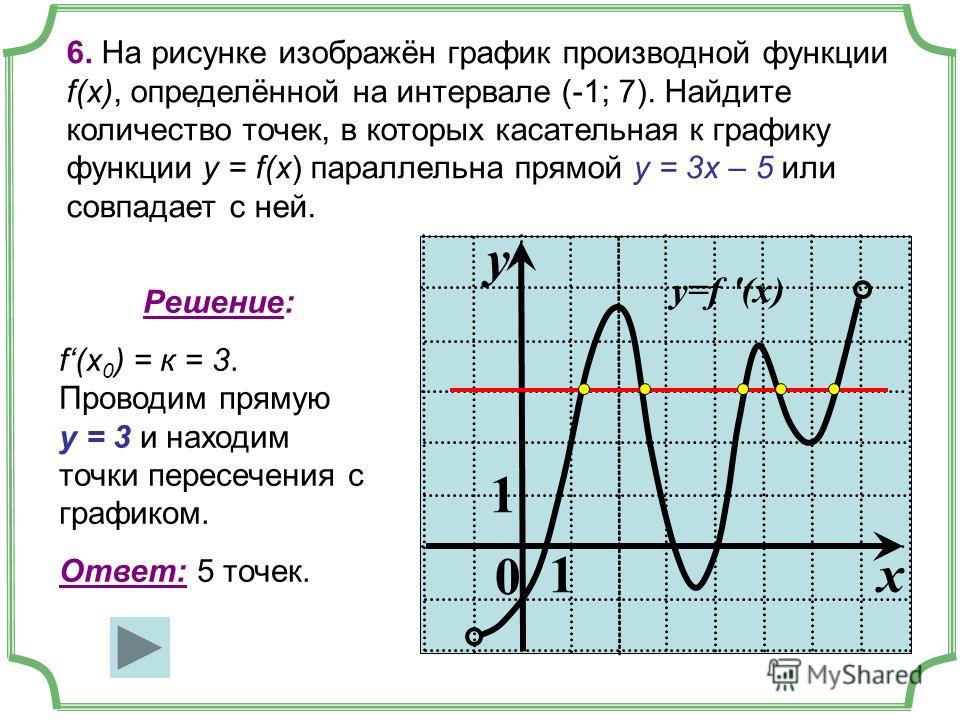 т. е. dy/dx [u ± v] = du/dx ± dv/dx.
т. е. dy/dx [u ± v] = du/dx ± dv/dx.
Правило произведения: Правило произведения производных гласит, что если функция является произведением двух функций, то ее производная есть производная второй функции, умноженная на первую функцию, прибавленная к производной первой функции, умноженной на вторая функция. dy/dx [u × v] = u · dv/dx + v · du/dx. Если у = х 5 e x , мы имеем y’ = x 5 . e x + e x . 5x 4 = e x (x 5 + 5x 4 )
Правило частных: Правило частных производных утверждает, что d/dx (u/v) = (v · du/dx — u · dv/dx)/ v 2
Постоянное кратное Правило: Постоянное кратное правило производных утверждает, что d/dx [c(f(x)] = c · d/dx f(x), т. е. , константа, которая при умножении на функцию получается в результате дифференцирования, например, d/dx (5x 2 ) = 5 д/дх (х 2 ) = 5(2х) = 10х.
Правило констант: Правило констант производных утверждает, что производная любой константы равна 0. Если y = k, где k — константа, то dy/dx = 0. Предположим, что y = 4, y’ = 0. Это правило непосредственно следует из правила мощности.
Производные составных функций (цепное правило)
Если f и g — дифференцируемые функции в своей области определения, то f(g(x)) также дифференцируема. Это известно как цепное правило дифференцирования, используемое для составных функций. (туман)'(x) = f'[(g(x)] g'(x). Это также можно записать как «если y = f(u) и u = g(x) , то dy/dx = dy/du · du/dx.
Например, рассмотрим y = tan 2 x. Это составная функция. Мы можем записать эту функцию как y = u 2 , где u = tan x. Тогда
dy/dx = 2u
du/dx = d/dx (tan x) = sec 2 x
По цепному правилу
dy/dx = dy/du · du/dx
= 2u · сек 2 x
= 2 тан x сек 2 x
Производные неявных функций
В уравнениях, где y как функция x не может быть явно определена переменными x и y, используется неявное дифференцирование. Если f(x, y) = 0, то продифференцируйте обе стороны по x и сгруппируйте члены, содержащие dy/dx, с одной стороны, а затем найдите dy/dx.
Если f(x, y) = 0, то продифференцируйте обе стороны по x и сгруппируйте члены, содержащие dy/dx, с одной стороны, а затем найдите dy/dx.
Например, 2x + y = 12
d/dx(2x + y) = d/dx(0)
2 + dy/dx = 0
dy/dx = -2
Параметрические производные
В функции у нас могут быть зависимые переменные x и y, которые зависят от третьей независимой переменной. Если x = f(t) и y = g(t), то производная вычисляется как dy/dx = f'(x)/g'(x). Предположим, что если x = 4 + t 2 и y = 4t 2 -5t 4 , то мы находим dy/dx следующим образом. 9 3
dy/dx = (dy/dt)/(dx/dt)
dy/dx = (8t -20t 3 )/ 2т
= 2т (4 — 10т 2 ) / 2т
dy/dx = 4 — 10т 2
Производные высшего порядка
Мы можем найти последовательные производные функции и получить производные более высокого порядка. Если y — функция, то ее первая производная равна dy/dx. Вторая производная d/dx (dy/dx), которую также можно записать как d 2 у/дх 2 . Третья производная d/dx (d 2 y/dx 2 ) и обозначается как d 3 y/dx 3 и так далее.
Вторая производная d/dx (dy/dx), которую также можно записать как d 2 у/дх 2 . Третья производная d/dx (d 2 y/dx 2 ) и обозначается как d 3 y/dx 3 и так далее.
В качестве альтернативы первая, вторая и третья производные f(x) могут быть записаны как f'(x), f»(x) и f»'(x). Для производных более высокого порядка мы пишем число в скобках как показатель степени. Предположим y = 4x 3 , мы получаем последовательные производные следующим образом. y’ = 12x 2 , y» = 24 x и y»’ = 24, y (4) = 0,
Частные производные
Если u = f(x,y), мы можем найти частную производную по y, оставив x константой, или мы можем найти частную производную по x, оставив y константой. Предположим, что f(x, y) = x 3 y 2 , частные производные функции равны:
- ∂f/∂y(x 3 y 2 ) = х 3 2г
Кроме того, мы можем найти частные производные второго порядка также как и ∂ 2 f/∂y ∂x.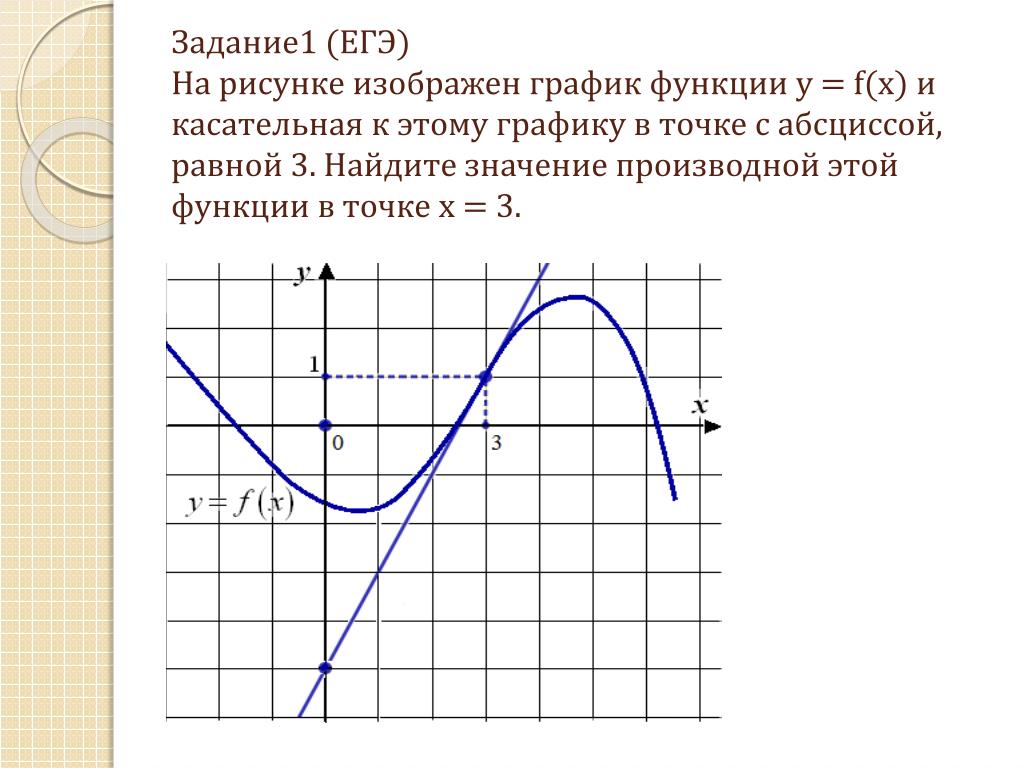
Нахождение производной с помощью логарифмического дифференцирования
Иногда функции слишком сложны, чтобы найти производные (или) одна функция может быть возведена в другую функцию, например y = f(x) g(x) . В таких случаях мы можем взять log (или) ln с обеих сторон, применить логарифмические правила, а затем дифференцировать обе стороны, чтобы получить dy/dx. Этот процесс известен как логарифмическое дифференцирование в исчислении.
Пример: Найдите производную от y = x x .
Решение:
Применив ln с обеих сторон,
ln y = ln x x
ln y = x ln x
Взяв производную с обеих сторон,7 19006 19006 (1/x) + ln x (1) (цепное правило слева и правило произведения справа)
1/y dy/dx = 1 + ln x
dy/dx = y (1 + ln x ) = х х (1 + ln х)
Максимум/минимум с использованием производных
Понятие наклона и, следовательно, производных используется для нахождения максимального или минимального значения функции. Есть два теста, которые используют производные и используются для нахождения максимумов/минимумов функции. Это
Есть два теста, которые используют производные и используются для нахождения максимумов/минимумов функции. Это
- тест первой производной
- тест второй производной
Проверка первой производной
Мы можем просто использовать первую производную для определения максимума или минимума, соблюдая следующие пункты:
- f'(x) представляет наклон касательной.
- Следовательно, если f'(x) > 0, функция возрастает, а если f'(x) < 0, функция убывает.
- Если f'(x) > 0 меняется на f'(x) < 0 в какой-то точке, то функция имеет локальный максимум в этой точке.
- Если f'(x) < 0 меняется на f'(x) > 0 в какой-то точке, то функция имеет минимум в этой точке.
- Обратите внимание, что f'(x) = 0 в локальном максимуме и локальном минимуме.
Тест второй производной
Тест второй производной использует критические точки и вторую производную для нахождения максимума/минимума. Чтобы выполнить этот тест:
- Найдите критические точки, установив f'(x) = 0.

- Подставьте каждый из них в f»(x). Если f»(x) < 0, то функция максимальна в этой точке, а если f''(x)>0, то функция в этой точке минимальна.
- Если f»(x) = 0, функция не имеет ни максимума, ни минимума в этой точке, и в этом случае она известна как точка перегиба.
Важные замечания по расчету производных:
- Производная функции — это скорость изменения одной величины по сравнению с другой.
- Производная любой непрерывной функции, дифференцируемой на отрезке [a, b], выводится с использованием первого принципа дифференцирования с использованием пределов.
- Если f(x) задано, то его производная равна f'(x) = lim h→0 [f(x + h) — f(x) / h.
- Каждая дифференцируемая функция непрерывна, но обратное может быть неверным.
☛ Статьи по теме:
- Расчетный калькулятор
- Калькулятор производных
- Калькулятор второй производной
Часто задаваемые вопросы о деривативах
Что такое производные в исчислении?
Производная в исчислении — это мгновенная скорость изменения функции по отношению к другой переменной. Дифференцирование – это процесс нахождения производной функции. Производная функции совпадает с наклоном касательной, скоростью изменения и т. д.
Дифференцирование – это процесс нахождения производной функции. Производная функции совпадает с наклоном касательной, скоростью изменения и т. д.
Определение производной.
Производная f(x) при x = a определяется как f'(x) = lim h→0 [f(x + h) — f(x)] / h. Это наклон касательной к функции f(x). В этой формуле [f(x + h) — f(x)]/h называется разностным коэффициентом.
Как найти производные?
Производные функций в математике находятся с использованием определения производной из первого фундаментального принципа дифференцирования. Если f(x) — заданная функция, ее производная получается с использованием f'(x) = lim ч → 0 [f(x + h) — f(x)] / ч. Многие правила выводятся с использованием этого определения предела, которое можно напрямую использовать для поиска производных без использования пределов.
Что такое основные производные формулы?
Формулы основных производных: d/dx (x n ) = nx n-1 , d/dx (ln x) = 1/x, d/dx (e x ) = e x , d/dx (a x ) = a x ln a, d/dx (sin x) = cos x, d/dx (cos x) = — sin x, d/dx (tan x) = сек 2 х.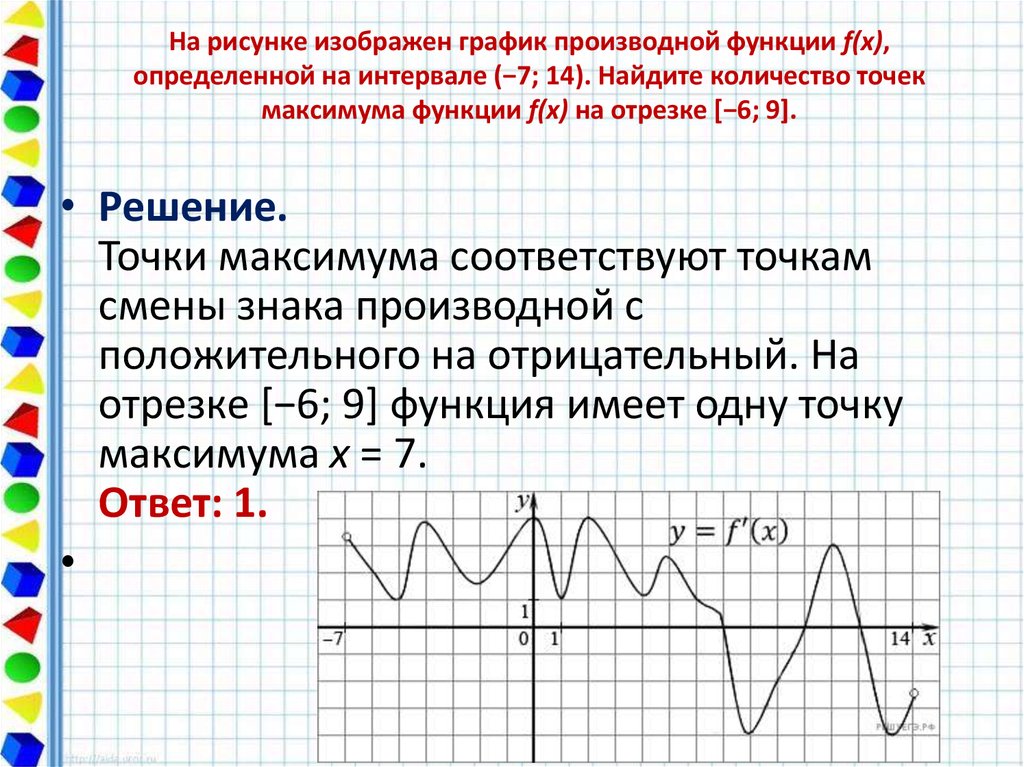
Трудно ли вычислять производные?
Процесс нахождения производных с использованием определения предела немного сложен. Чтобы сделать это проще, мы используем правила, полученные с помощью формулы. Пока мы можем помнить правила, процесс нахождения производных в исчислении очень прост, если немного попрактиковаться.
Каково применение деривативов в реальной жизни?
В реальной жизни деривативы можно использовать по-разному. Скорость изменения функции по отношению к другой величине называется производной. Чтобы проверить, является ли функция возрастающей или убывающей, чтобы найти уравнение касательной / нормали, чтобы найти максимальное и минимальное значения на графике, чтобы найти задачи смещения-движения, найти скорость при заданном смещении, найти заданное ускорение смещение и так далее.
Что такое производный пример?
Скорость — это мгновенная скорость изменения расстояния, пройденного объектом в определенное время. Первая производная от смещения объекта есть его скорость. Вторая производная смещения — это ускорение объекта. Третья производная смещения — это рывок объекта и так далее.
Вторая производная смещения — это ускорение объекта. Третья производная смещения — это рывок объекта и так далее.
В чем разница между производными и дифференцированием в исчислении?
Производная функции f(x) в точке есть не что иное, как наклон тангенса функции в этой точке и находится по пределу f'(x) = lim ч → 0 [f(x + h) — f(x)] / ч. Дифференцирование – это процесс нахождения производных.
3.2 Производная как функция
Цели обучения
- Определить производную функцию заданной функции.
- Постройте производную функцию по графику заданной функции.
- Укажите связь между производными и непрерывностью.
- Опишите три условия, при которых функция не имеет производной.
- Объясните значение производной высшего порядка.
Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке. Если мы продифференцируем функцию положения в данный момент времени, мы получим скорость в этот момент.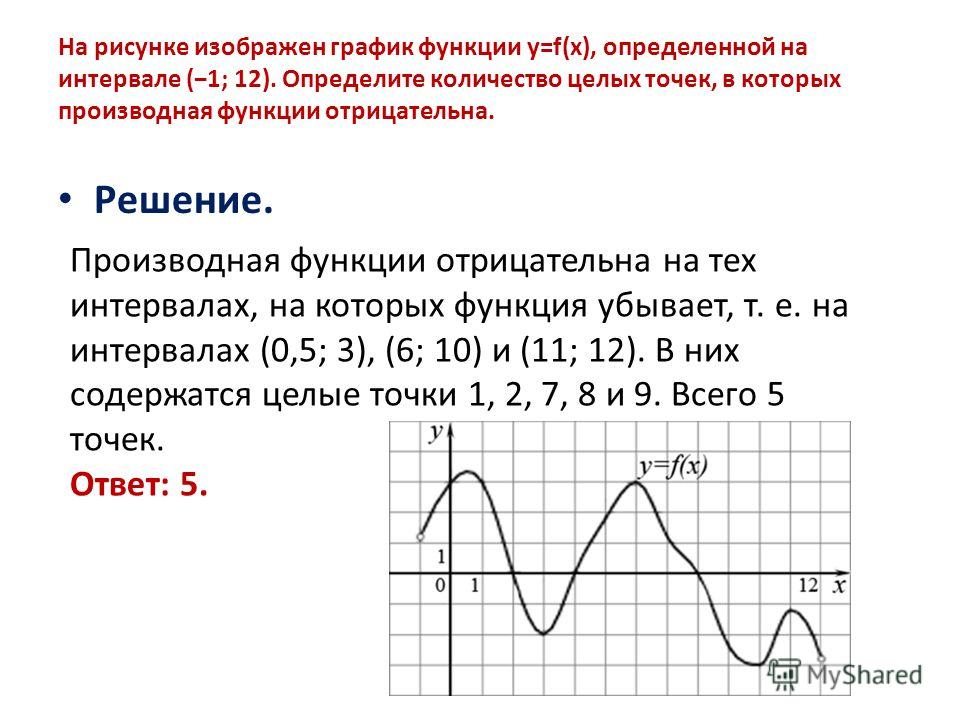 Кажется разумным заключить, что знание производной функции в каждой точке даст ценную информацию о поведении функции. Однако процесс нахождения производной даже при нескольких значениях с использованием методов из предыдущего раздела быстро стал бы довольно утомительным. В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения. 9{\prime}(a)[/latex] мы также можем использовать [latex]\frac{dy}{dx}\Big|_{x=a}[/latex] Использование [latex]\frac{dy} Нотация {dx}[/latex] (называемая нотация Лейбница) довольно распространена в технике и физике. Чтобы лучше понять эти обозначения, вспомним, что производная функции в точке — это предел наклона секущих по мере приближения секущих к касательной. Наклоны этих секущих часто выражаются в виде [латекс]\фракция{\Delta y}{\Delta x}[/latex], где [латекс]\Delta y[/латекс] — разница в [латексе] значения y[/latex], соответствующие разности значений [latex]x[/latex], которые выражаются как [latex]\Delta x[/latex] ((Рисунок)). Таким образом, производная, которую можно рассматривать как мгновенную скорость изменения [латекс]у[/латекс] по отношению к [латекс]х[/латекс], выражается как
Кажется разумным заключить, что знание производной функции в каждой точке даст ценную информацию о поведении функции. Однако процесс нахождения производной даже при нескольких значениях с использованием методов из предыдущего раздела быстро стал бы довольно утомительным. В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения. 9{\prime}(a)[/latex] мы также можем использовать [latex]\frac{dy}{dx}\Big|_{x=a}[/latex] Использование [latex]\frac{dy} Нотация {dx}[/latex] (называемая нотация Лейбница) довольно распространена в технике и физике. Чтобы лучше понять эти обозначения, вспомним, что производная функции в точке — это предел наклона секущих по мере приближения секущих к касательной. Наклоны этих секущих часто выражаются в виде [латекс]\фракция{\Delta y}{\Delta x}[/latex], где [латекс]\Delta y[/латекс] — разница в [латексе] значения y[/latex], соответствующие разности значений [latex]x[/latex], которые выражаются как [latex]\Delta x[/latex] ((Рисунок)). Таким образом, производная, которую можно рассматривать как мгновенную скорость изменения [латекс]у[/латекс] по отношению к [латекс]х[/латекс], выражается как
[латекс]\frac{dy}{dx}=\underset{\Delta x\to 0}{\lim}\frac{\Delta y}{\Delta x}[/latex]. {\prime}(x)[/latex] дает скорость изменения функции [латекс]f(x) [/latex] (или наклон касательной к [latex]f(x)[/latex]). 9{\prime}(x)[/latex] над осью [latex]x[/latex]?
{\prime}(x)[/latex] дает скорость изменения функции [латекс]f(x) [/latex] (или наклон касательной к [latex]f(x)[/latex]). 9{\prime}(x)[/latex] над осью [latex]x[/latex]?
Показать раствор
Теперь, когда мы можем построить график производной, давайте рассмотрим поведение графиков. Сначала рассмотрим связь между дифференцируемостью и непрерывностью. Мы увидим, что если функция дифференцируема в точке, она должна быть там непрерывной; однако функция, непрерывная в точке, не обязательно должна быть дифференцируемой в этой точке. На самом деле функция может быть непрерывной в точке и не быть дифференцируемой в этой точке по одной из нескольких причин. 9{\ prime} (a) = \ underset {x \ to a} {\ lim} \ frac {f (x) -f (a)} {xa} [/ латекс].
Мы хотим показать, что [латекс]f(x)[/латекс] непрерывен в [латекс]а[/латекс], показав, что [латекс]\underset{x\to a}{\lim}f(x )=f(a)[/латекс]. Таким образом,
[латекс]\begin{array}{lllll} \underset{x\to a}{\lim}f(x) & =\underset{x\to a}{\lim}(f(x) -f(a)+f(a)) & & & \\ & =\underset{x\to a}{\lim}(\frac{f(x)-f(a)}{x-a}\cdot ( x-a)+f(a)) & & & \text{Умножить и разделить} \, f(x)-f(a) \, \text{by} \, x-a.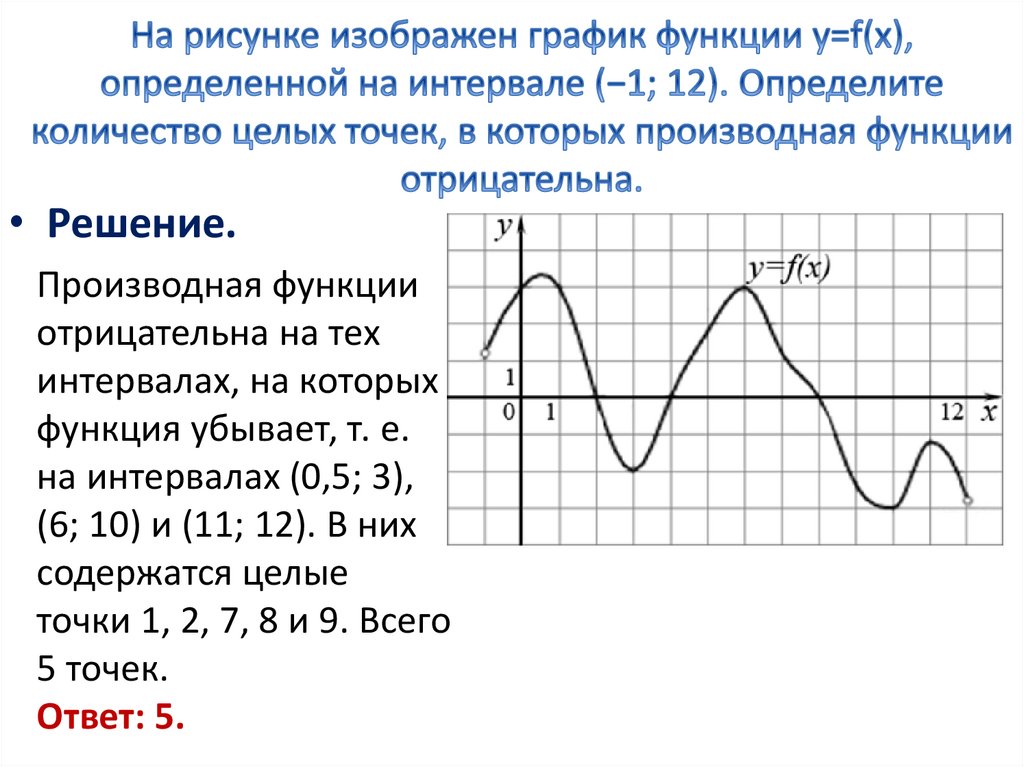 {\prime}(0)[/латекс] не определен. Это наблюдение приводит нас к мысли, что непрерывность не влечет дифференцируемости. Давайте исследовать дальше. Для [латекс]f(x)=|x|[/латекс], 9{\prime}(0)[/latex] не существует. Беглый взгляд на график [latex]f(x)=\sqrt[3]{x}[/latex] проясняет ситуацию. Функция имеет вертикальную касательную в точке 0 ((Рисунок)).
{\prime}(0)[/латекс] не определен. Это наблюдение приводит нас к мысли, что непрерывность не влечет дифференцируемости. Давайте исследовать дальше. Для [латекс]f(x)=|x|[/латекс], 9{\prime}(0)[/latex] не существует. Беглый взгляд на график [latex]f(x)=\sqrt[3]{x}[/latex] проясняет ситуацию. Функция имеет вертикальную касательную в точке 0 ((Рисунок)).
Рис. 5. Функция [latex]f(x)=\sqrt[3]{x}[/latex] имеет вертикальную касательную в точке [latex]x=0[/latex]. Она непрерывна в 0, но не дифференцируема в 0.
Функция [latex]f(x)=\begin{cases} x \sin(\frac{1}{x}) & \text{if} \, x \ne 0 \\ 0 & \text{if} \, x = 0 \end{cases}[/latex] также имеет производную, которая демонстрирует интересное поведение при 0. Мы видим, что 9{\ prime} (0) = \ underset {x \ to 0} {\ lim} \ frac {x \ sin (1 / x) -0} {x-0} = \ underset {x \ to 0} {\ lim} \sin(\frac{1}{x})[/latex].
Этого предела не существует, в основном потому, что наклоны секущих постоянно меняют направление по мере приближения к нулю ((Рисунок)).
Рис. 6. Функция [latex]f(x)=\begin{cases} x \sin(\frac{1}{x}) & \text{if} \, x \ne 0 \\ 0 & \ text{if} \, x = 0 \end{cases}[/latex] не дифференцируема в точке 0.
Итого:
- Заметим, что если функция не является непрерывной, она не может быть дифференцируемой, так как всякая дифференцируемая функция должна быть непрерывной. Однако, если функция непрерывна, она может не быть дифференцируемой.
- Мы видели, что [latex]f(x)=|x|[/latex] не может быть дифференцируемым в 0, потому что пределы наклона касательных линий слева и справа не совпадают. Визуально это вылилось в острый угол на графике функции в 0. Отсюда делаем вывод, что для того, чтобы быть дифференцируемой в точке, функция должна быть в этой точке «гладкой».
- Как мы видели на примере [latex]f(x)=\sqrt[3]{x}[/latex], функция не может быть дифференцируемой в точке, где есть вертикальная касательная.
- Как мы видели с [латексом]f(x)=\begin{cases} x \sin(\frac{1}{x}) & \text{if} \, x \ne 0 \\ 0 & \text{ if} \, x = 0 \end{cases}[/latex] функция может не быть дифференцируемой в точке и более сложными способами.
 2 + bx + c & \text{if} \, x < - 10 \\ -\frac{1}{4}x + \frac{5}{2} & \text{if} \, x \ge -10 \end{cases}[/latex], где [latex]x [/latex] и [latex]f(x)[/latex] указаны в дюймах. Чтобы вагон двигался по трассе плавно, функция [latex]f(x)[/latex] должна быть непрерывной и дифференцируемой при -10. Найдите значения [latex]b[/latex] и [latex]c[/latex], которые делают [latex]f(x)[/latex] непрерывными и дифференцируемыми. 92 & \text{if} \, x \ge 3 \end{cases}[/latex] обе непрерывны и дифференцируемы в 3.
2 + bx + c & \text{if} \, x < - 10 \\ -\frac{1}{4}x + \frac{5}{2} & \text{if} \, x \ge -10 \end{cases}[/latex], где [latex]x [/latex] и [latex]f(x)[/latex] указаны в дюймах. Чтобы вагон двигался по трассе плавно, функция [latex]f(x)[/latex] должна быть непрерывной и дифференцируемой при -10. Найдите значения [latex]b[/latex] и [latex]c[/latex], которые делают [latex]f(x)[/latex] непрерывными и дифференцируемыми. 92 & \text{if} \, x \ge 3 \end{cases}[/latex] обе непрерывны и дифференцируемы в 3.Показать решение
Производная функции сама по себе является функцией, поэтому мы можем найти производную производной. Например, производная функции положения — это скорость изменения положения или скорость. Производная скорости — это скорость изменения скорости, то есть ускорение. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать брать производные, чтобы получить третью производную, четвертую производную и так далее.
 В совокупности они обозначаются как 9{\prime}(x)=0[/латекс].
В совокупности они обозначаются как 9{\prime}(x)=0[/латекс]. - Если функция дифференцируема в точке, то она непрерывна в этой точке. Функция не является дифференцируемой в точке, если она не является непрерывной в этой точке, если она имеет в этой точке вертикальную касательную или если график имеет острый угол или точку возврата.
- Производные высшего порядка — это производные производных от второй производной до производной [latex]n\text{th}[/latex].
- Производная функция 92[/latex]
6. [latex]f(x)=\sqrt{2x}[/latex]
Показать решение
7. [латекс]f(x)=\sqrt{x-6}[/latex]
8. [латекс]f(x)=\frac{9}{x}[/latex ]
Показать решение
9. [латекс]f(x)=x+\frac{1}{x}[/latex]
10. [латекс]f(x)=\frac{1}{\sqrt{ x}}[/latex]
Показать решение
В следующих упражнениях используйте график [latex]y=f(x)[/latex] для построения графика его производной [latex]f^{\prime}(x)[/latex].
 9h-1}{h}[/latex]
9h-1}{h}[/latex]Показать решение
Для следующих функций:
- эскиз графика и
- используют определение производной, чтобы показать, что функция не дифференцируема в точке [latex]x=1[/latex].
21. [латекс]f(x)=\begin{cases} 2\sqrt{x} & \text{if} \, 0 \le x \le 1 \\ 3x-1 & \text{if } \, x>1 \end{cases}[/latex]
22. [latex]f(x)=\begin{cases} 3 & \text{if} \, x<1 \\ 3x & \text{if} \, x \ge 1 \end{cases}[/latex] 92+2 & \text{if} \, x \le 1 \\ x & \text{if} \, x>1 \end{cases}[/latex]
24. [latex]f(x )=\begin{case} 2x & \text{if} x \le 1 \\ \frac{2}{x} & \text{if} \, x>1 \end{cases}[/latex]
Показать решение
Для следующих графиков
- определите, для каких значений [latex]x=a[/latex] существует [latex]\underset{x\to a}{\lim}f(x)[/latex] но [latex]f[/latex] не является непрерывным в точке [latex]x=a[/latex], и
- определить, для каких значений [latex]x=a[/latex] функция непрерывна, но не дифференцируема при [latex]x=a[/latex].
 9{\ prime} (x) = \ underset {h \ to 0} {\ lim} \ frac {f (x + h) -f (x)} {h} [/ латекс]
9{\ prime} (x) = \ underset {h \ to 0} {\ lim} \ frac {f (x + h) -f (x)} {h} [/ латекс]
37. [latex]P(x)[/latex] обозначает население города в момент времени [latex]x[/latex] в годах.
38. [latex]C(x)[/latex] обозначает общую сумму денег (в тысячах долларов), потраченную на уступки [latex]x[/latex] клиентам в парке развлечений.
Показать раствор
39. [латекс]R(x)[/латекс] обозначает общую стоимость (в тысячах долларов) производства [латекс]х[/латекс] радиочасов.
40. [latex]g(x)[/latex] обозначает оценку (в процентах), полученную за тест с учетом [latex]x[/latex] часов обучения.
Показать раствор
41. [latex]B(x)[/latex] обозначает стоимость (в долларах) учебника по социологии в университетских книжных магазинах США в [latex]x[/latex] лет с 1990 года.
42.
 [латекс]p(x)[/латекс] обозначает атмосферное давление на высоте [латекс]х[/латекс] футов.
[латекс]p(x)[/латекс] обозначает атмосферное давление на высоте [латекс]х[/латекс] футов.{\prime}(t)[/latex] представляет и как оно ведет себя при увеличении [latex]t[/latex].
- Что эта производная говорит нам о том, как этот город пострадал от вспышки гриппа?
Показать решение
В следующих упражнениях используйте следующую таблицу, в которой показана высота [латекс]h[/латекс] ракеты Сатурн-5 для миссии Аполлон-11 [латекс]t[/латекс] через несколько секунд после запуска.
| Время (секунды) | Высота (метры) 9{\ простое число} (т) [/латекс]. Линейная, квадратичная или кубическая функция лучше всего соответствует данным? Линейная, квадратичная или кубическая функция лучше всего соответствует данным?52. Используя наилучшую линейную, квадратичную и кубическую аппроксимацию данных, определите, что [латекс]H»(t), \, G»(t)[/латекс] и [латекс]F »(t)[/latex] есть. Каков физический смысл [латекс]H»(t), \, G»(t)[/латекс] и [латекс]F»(t)[/латекс] и каковы их единицы измерения? Показать раствор Глоссарий
Исследование производной показательной функцииПроизводная показательной функции. Подробнее о видео. Уравнение \eqref{derivative_f_fprime} утверждает, что производная $f'(x)$ просто равна самой функции $f(x)$, умноженной на наше загадочное число, которое также является наклоном $f'(0) $ касательной в точке $x=0$. Это странный вывод, поэтому лучше подтвердим, что он действительно верен. Используйте следующий апплет, чтобы убедиться в правильности результата. Убедитесь, что производная $f'(x)$ действительно кратна функции $f(x)$, проверив, что отношение $f'(x)/f(x)$ не меняется при изменении $x. $. Это отношение должно быть $f'(0)$, что должно быть таинственным числом, которое вы оценили в четыре цифры, а также наклоном касательной, когда $x=0$. 9x$, где вы можете ввести значение для $b$, показано толстой синей кривой. График ее производной $f'(x)$ показан тонкой зеленой линией, а отношение $f'(x)/f(x)$ – горизонтальной серой линией. Значение функции и ее производная, оцененная при $x_0$, отображаются слева и показаны синими и зелеными точками на кривых. Во-вторых, выберите два других значения $b$, кроме $b=2$. Попробуйте одно значение $b$ меньше единицы и одно значение $b$ больше единицы, чтобы поэкспериментировать как с экспоненциальным затуханием, так и с экспоненциальным ростом. Для каждого из ваших вариантов $b$ используйте первый апплет, чтобы оценить первые четыре цифры значения таинственного предельного выражения, определяющего $g'(0)$. Затем используйте второй апплет, чтобы убедиться, что это значение является как производной $g'(0)$ в нуле, так и отношением между производной $g'(x)$ и функцией $g(x)$. 9ч-1}{ч} = 1.$$ Поскольку $e$ иррационально, мы не сможем получить точное представление этого числа с помощью этих методов. Но если бы вы были очень терпеливы и у вас был бы такой инструмент, как эти апплеты, которые могли бы оценить предел с достаточной точностью, вы могли бы оценить $e$ до 30 цифр и определить, что $$e \ приблизительно 2,71828182845 | 3 a | 3 a | 3 и имеет тот же наклон 92 133 92 134, что и кривая в этой точке. Иногда можно сказать, что касательная « только что касается » кривой или « пересекает кривую только один раз, но эти идеи иногда могут ввести нас в заблуждение. На приведенном ниже графике показаны касательные линии (выделены красным, фиолетовым и пурпурным цветом) в трех разных точках кривой y = f ( x ) (черным цветом) . Наклон и производныеКак же узнать, каким должен быть наклон касательной? Узнав о производных , вы можете использовать простую формулу m = f ‘( a ). В этой формуле дана функция f и x — значение a . Ваша задача — найти м , что представляет собой наклон касательной. Если у вас есть наклон, написать уравнение касательной линии довольно просто. Нахождение касательнойПредположим, вас попросили найти касательную для функции f ( x ) в данной точке x = a . Вот пошаговый подход:
Наклон производных мерДавайте еще раз взглянем на этот первый шаг, » Найдите производную . Помните, производная — это функция (от входной переменной x ). Путем подстановки различных входных значений, x = a , выходные значения f ‘( x ) дают вам наклоны касательных линий в каждой точке x = a . Вот что мы имеем в виду, когда говорим, что «производная измеряет наклон касательных линий». Если я хочу знать наклон f при x = 1, тогда я вычисляю f ‘(1). И если я хочу узнать наклон при x = -352/13, то я вычисляю f ‘(-352/13). Просто как тот! Пример: многочлен Теперь давайте рассмотрим пример функции: f ( x ) = x 3 + 3 x 2 + 1. Сначала найдите производную: f ‘( x ) = 3 x 2 + 6 x . (чтобы попрактиковаться в поиске деривативов, ознакомьтесь с этой статьей Magoosh о деривативах). Значение функции и значение производной в нескольких точках показаны в таблице ниже:
Для перечисленных точек мы можем легко найти уравнение касательной.
Теперь давайте посмотрим на график y = f ( x ) вместе с касательными, которые мы только что нашли. РезюмеИтак, теперь вы знаете. Производная — это не то же самое, что касательная. Вместо этого производная является инструментом для измерения наклона касательной в любой конкретной точке, точно так же, как часы измеряют время в течение дня. Имея это в виду, у вас не возникнет проблем с решением задач касательной линии на экзамене AP Calculus! Чтобы узнать больше о наклоне, касательных и производных, ознакомьтесь со следующими статьями Magoosh: Is the Derivative of a Function the Slope? и Как найти наклон линии, касательной к кривой. Гарантированно улучшите свой результат SAT или ACT. Начните свою 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep сегодня!АвторКстати, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше! Расчет AP ← Предыдущий Следующий → Мы настоятельно рекомендуем учащимся помогать друг другу и отвечать на комментарии других учащихся, если это возможно! Если вы являетесь студентом Premium Magoosh и хотели бы более персонализированного обслуживания от наших инструкторов, вы можете использовать вкладку «Справка» на панели управления Magoosh. Значение производнойПодход к C A L C U L U S Содержание | Главная 5 Скорость изменения функции Наклон прямой Наклон касательной к кривой Сеанс кривой Коэффициент разности Определение производной Производная от f ( x ) = x 2 Дифференцируемый при x Обозначения для производной Простое частное разности Раздел 2: Проблемы Производная f ( x ) = 2 x — 5 Уравнение касательной к кривой Производная от f ( x ) = x 3 ИСЧИСЛЕНИЕ ПРИМЕНЯЕТСЯ К вещам, которые не изменяются с постоянной скоростью. Скорость свободного падения, рождений и смертей в популяции, ед. Теперь, поскольку мы рассматриваем x как независимую переменную, а y как зависимую, то любое изменение Δ x значения x приведет к изменению Δ y значения у . На прямой скорость изменения — столько-то единиц и на каждую единицу x — постоянно и называется наклоном линии. Наклон прямой линии это число:
(Тема 8 предварительного исчисления.) Прямая линия имеет один и только один наклон; одна и только одна скорость изменения. Если x представляет, например, время, а y представляет расстояние, то Прямолинейный график, который их связывает, указывает на постоянную скорость. Наклон касательной к кривой Исчисление, однако, имеет дело со скоростью изменения, которая не является постоянной. Если эта кривая представляет расстояние Y в зависимости от времени X , то скорость изменения — скорость — в каждый момент времени непостоянна. Вопрос, который задает исчисление, звучит так: «Какова скорость изменения точно в точке P ?» Ответом будет наклон касательной к кривой в этой точке. И метод нахождения этого наклона — этого числа — был замечательным открытием как Исаака Ньютона (1642–1727), так и Готфрида Лейбница (1646–1716). Это метод нахождения того, что называется производной. Сеанс кривой Касательная — это прямая линия, которая касается кривой. Сеанс – это прямая линия, пересекающая кривую. Следовательно, рассмотрим секущую, которая пересекает кривую в точках P и Q . Тогда наклон этой секущей равен .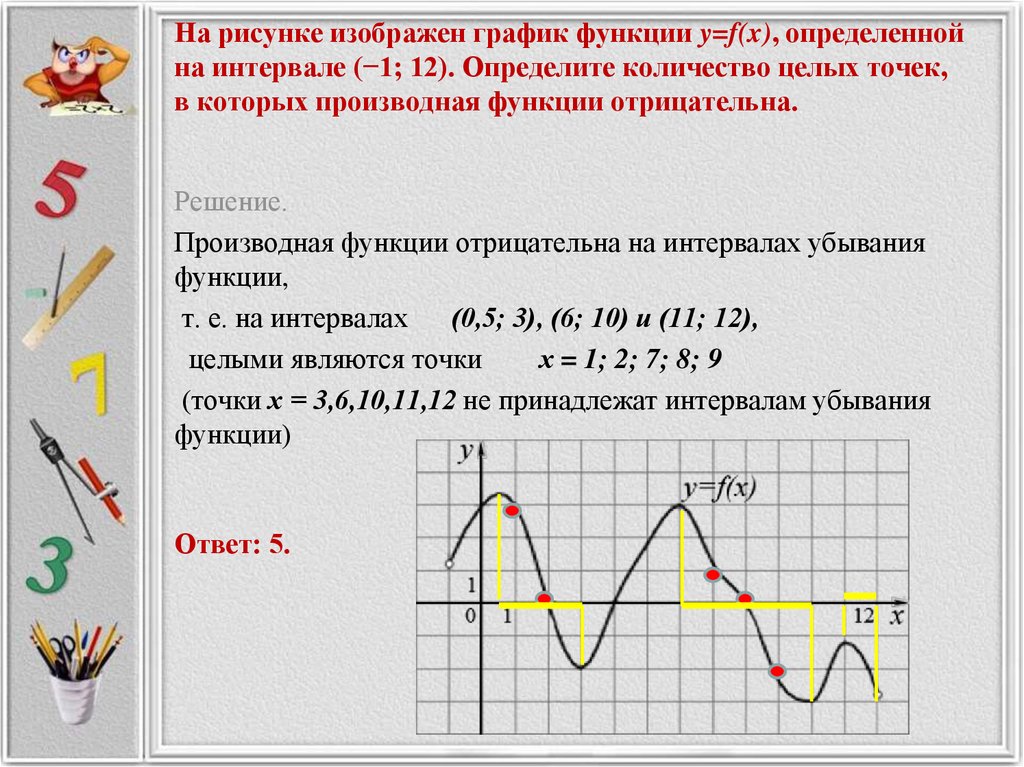
Но исчисление снова задает вопрос: Как функция изменяется точно при x 1 ? Каков наклон касательной к кривой в точке P ? Однако мы не можем оценить точно как в P , потому что Δ y и Δ x тогда были бы равны 0, а значение было бы совершенно неоднозначным. Поэтому мы будем рассматривать все более короткие расстояния Δ x , что приведет к последовательности секущих — — последовательность склонов. И мы определим касательную в точке P как предел этой последовательности наклонов. Этот наклон, этот предел и будет значением того, что мы назовем производной. Коэффициент разности Пусть y = f ( x ) — непрерывная функция, и координаты фиксированной точки P на графике равны ( x , f ( x 92)). Но когда значение x изменяется, в результате происходит изменение Δ y Затем Вот определение наклона касательной в точке Р : Наклон касательной в точке P Поскольку Δ x , а не x , является переменной, приближающейся к 0, x остается постоянной, и этот предел будет функцией x . Это частное — — называется фактором Ньютона или разностным фактором. Его вычисление и упрощение — фундаментальная задача дифференциального исчисления. Опять же, коэффициент разности является функцией Δ x . Но для упрощения письменных вычислений вместо Δ x будем писать ч .
Тогда частное разности становится: Теперь выразим определение производной следующим образом.
ОПРЕДЕЛЕНИЕ 5. Производной функции f ( x ) называется следующий предел, если он существует: Назовем этот предел функцией f ‘ ( x ) — « f — простое число x » — и когда этот предел существует, мы говорим, что f само по себе дифференцируемо в x , и что f имеет производная.
Итак, мы берем предел разностного отношения, когда ч приближается к 0. Когда этот предел существует, это означает, что разностное частное можно сделать максимально близким к этому пределу — « f ‘ ( x )» — как нам угодно. (Урок 2.) Что касается x , мы должны считать его фиксированным. Это конкретное значение, при котором мы оцениваем f ‘ ( x ). На практике мы должны упростить частное разности, прежде чем приблизить h к 0. Мы должны выразить числитель — f ( x + ч ) − f ( x ) — таким образом, что мы можем разделить его на ч . Подводя итог: производная — это функция — правило, — которое присваивает каждому значению x наклон касательной в точке ( x , f ( x )) на график f ( x ). Это скорость изменения f ( x ) в этой точке. В качестве примера применим определение, чтобы доказать, что наклон касательной к функции f ( x ) = x 2 , в точке ( x , x 2 ) будет 2 x .
Доказательство. Вот коэффициент разности, который мы будем упрощать:
Переходя от строки 1) к строке 2, мы возвели в квадрат бином x + h . (Урок 18 алгебры.) Переходя к строке 3), мы вычли x 2 с. То есть мы вычли из ( x ). Переходя к строке 4), мы разделили числитель на ч . (Урок 20 из Алгебра.) Мы можем это сделать, потому что h никогда не равно равному 0, даже когда мы берем предел (Урок 2). Завершим определение производной и возьмем предел:
Это то, что мы хотели доказать.
Всякий раз, когда мы применяем определение, мы должны алгебраически манипулировать разностным коэффициентом, чтобы мы могли просто заменить h на 0. На самом деле, вся теория пределов со всеми ее сложностями и тонкостями была изобретена именно для того, чтобы оправдать это. (Бедных Ньютона и Лейбница критиковали за оправдания того, что 19изобретатели пределов 20-го века не любили.) Мы можем положить ч = 0 здесь, потому что частное разности уменьшается до 2 x + ч и, следовательно, является полиномом от ч . Проблема. Пусть f ( х ) = х 2 , и вычислим наклон касательной к графику — а) при x = 5, С ф ‘ ( x ) = 2 x , тогда при x = 5 наклон касательной равен 10. б) при x = −3. −6. в) при x = 0, 0, Дифференцируемый при x Согласно определению, функция будет дифференцируемой при разрешении x , если там существует определенный предел. Там, где нет касательной Выше приведены два примера. Функция слева не имеет производной в точке x = 0, потому что там функция разрывна. При x = 0 касательной явно нет. Что касается графика справа, это функция абсолютного значения, г = | х |. (Тема 5 Precalculus.) И невозможно определить касательную в точке x = 0, потому что график образует там острый угол. На самом деле, наклон касательной при приближении x к 0 слева равен −1. Однако наклон, приближающийся справа, равен +1. Наклон касательной в точке 0 — которая была бы производной в точке x = 0 — следовательно , не существует . (Определение 2.2.) Функция абсолютного значения, тем не менее, непрерывна при x = 0. Поскольку левый предел самой функции, когда x приближается к 0, равен правому пределу, а именно 0. (Однако, наоборот, если функция дифференцируема в точке — если есть касательная — она также будет непрерывна и там. График будет гладким и не будет иметь разрывов.) Поскольку дифференциальное исчисление является изучением производных, оно в основном связано с функциями, которые дифференцируемы при всех значениях их областей определения. Такие функции называются дифференцируемыми функциями. Можете ли вы назвать элементарный класс дифференцируемых функций? Чтобы увидеть ответ, наведите указатель мыши на цветную область. Полиномы. Обозначения для производной Поскольку производная является этим пределом: тогда символ для самого предела (Читайте: «dee- y , dee- x «) Например, если
«Dee- y , dee- х — производная от y по отношению к х — равно 2 х .» Мы также пишем y’ ( х ) = 2 х . « у — простое число x равно 2 x ».
дифференцирующий оператор . Мы должны взять производную от того, что следует за ним. Например,
| ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|

 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
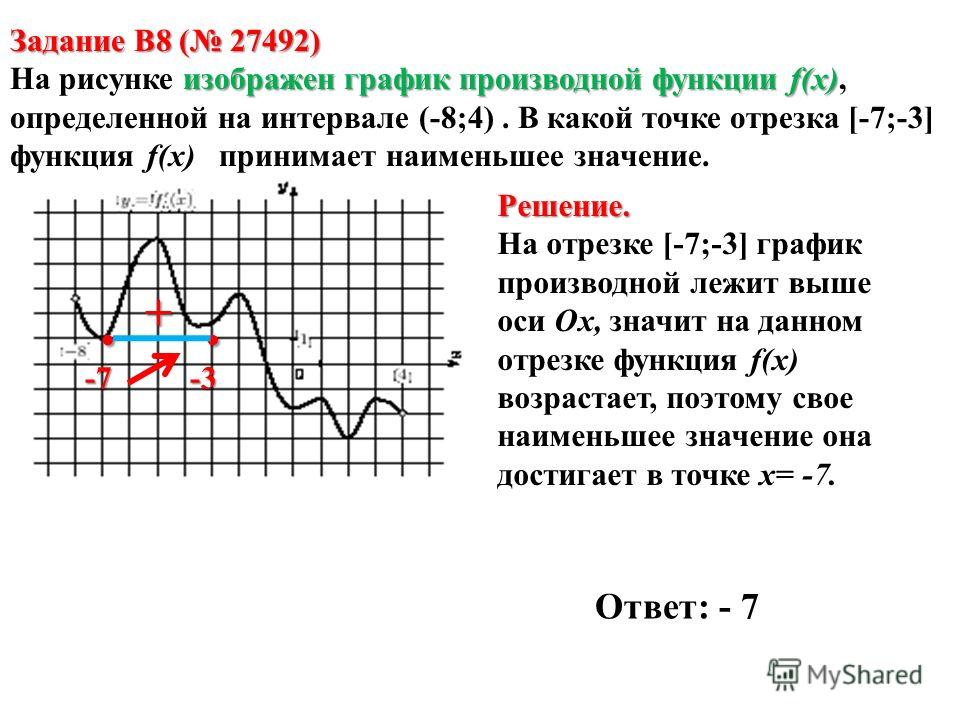 Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.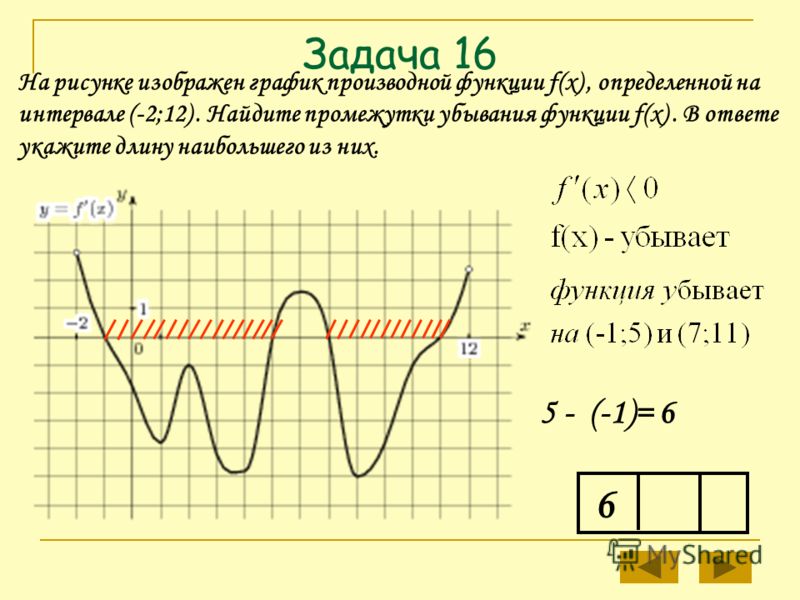
 Для начала определимся с терминологией:
Для начала определимся с терминологией:
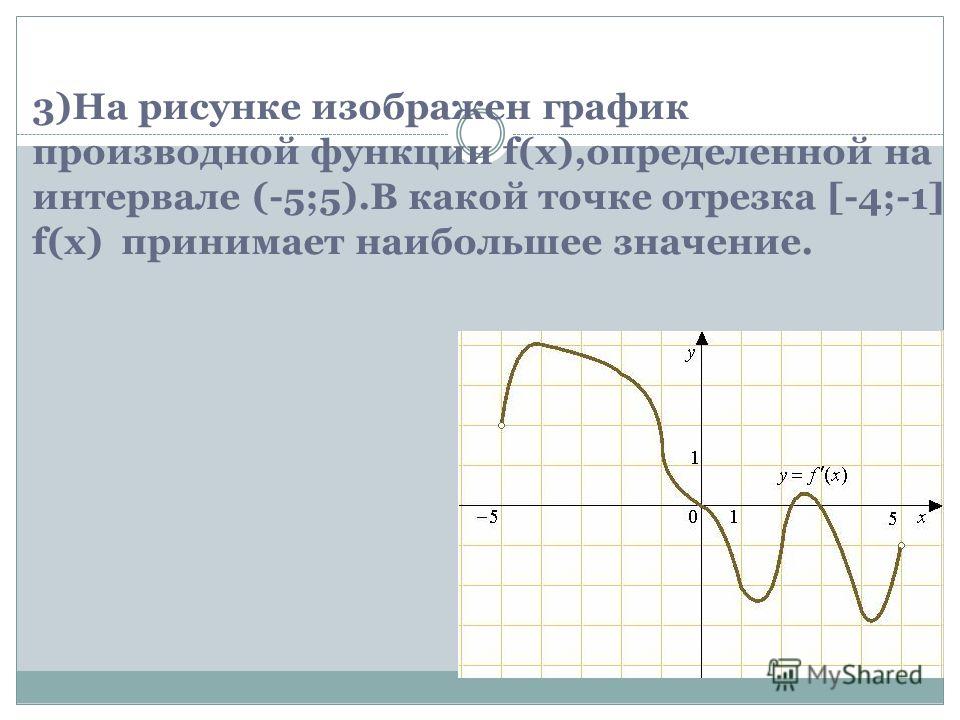 Отметим на полученном графике знаки производной. Имеем:
Отметим на полученном графике знаки производной. Имеем: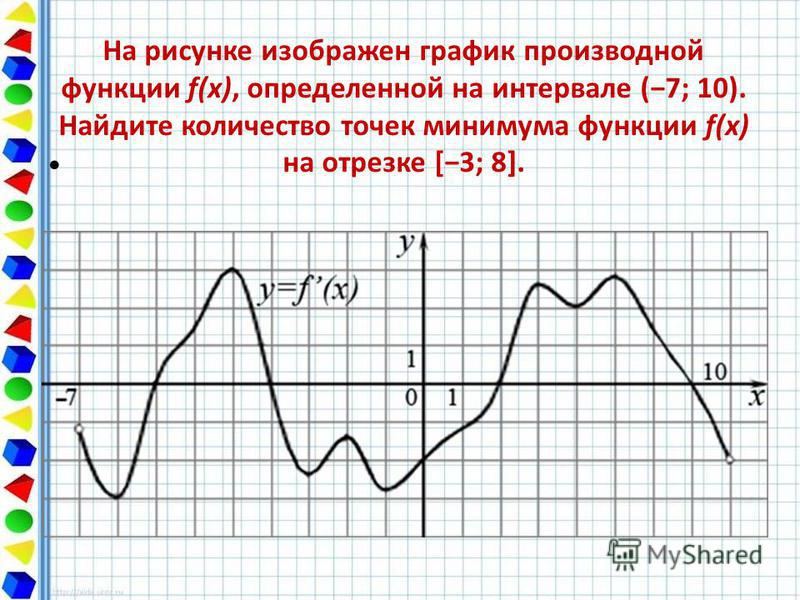 Разумеется, с целочисленными точками такой фокус не пройдет.
Разумеется, с целочисленными точками такой фокус не пройдет. е. f’(x) ≥ 0.
е. f’(x) ≥ 0.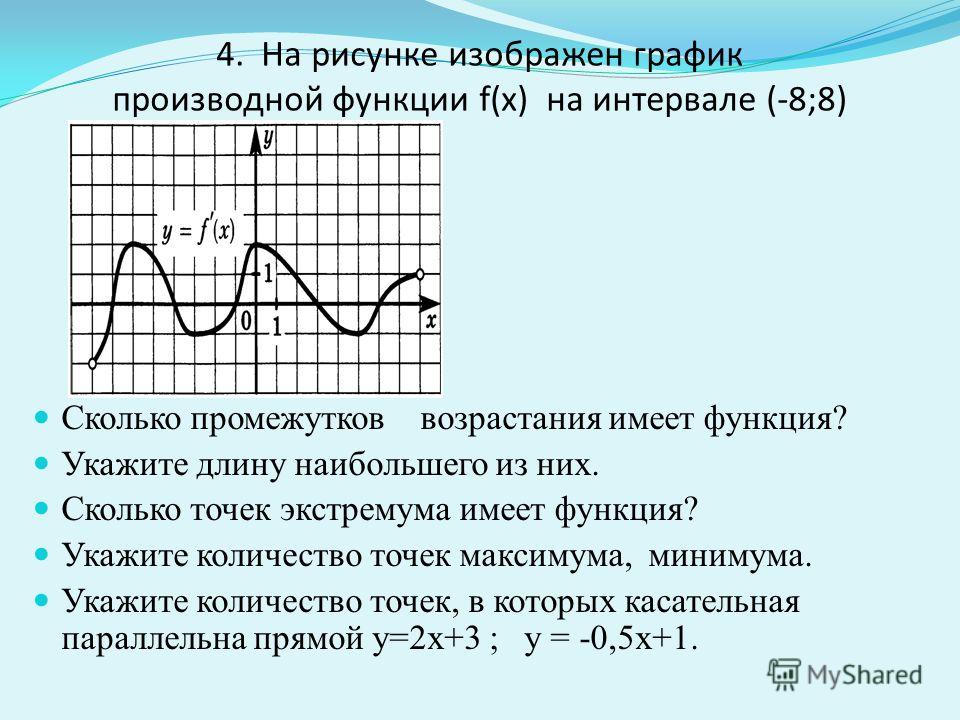 В ответе укажите сумму целых чисел, входящих в эти промежутки.
В ответе укажите сумму целых чисел, входящих в эти промежутки. nx. Формулы производных высших порядков.
nx. Формулы производных высших порядков. Для этого нам понадобятся следующие факты:
Для этого нам понадобятся следующие факты:
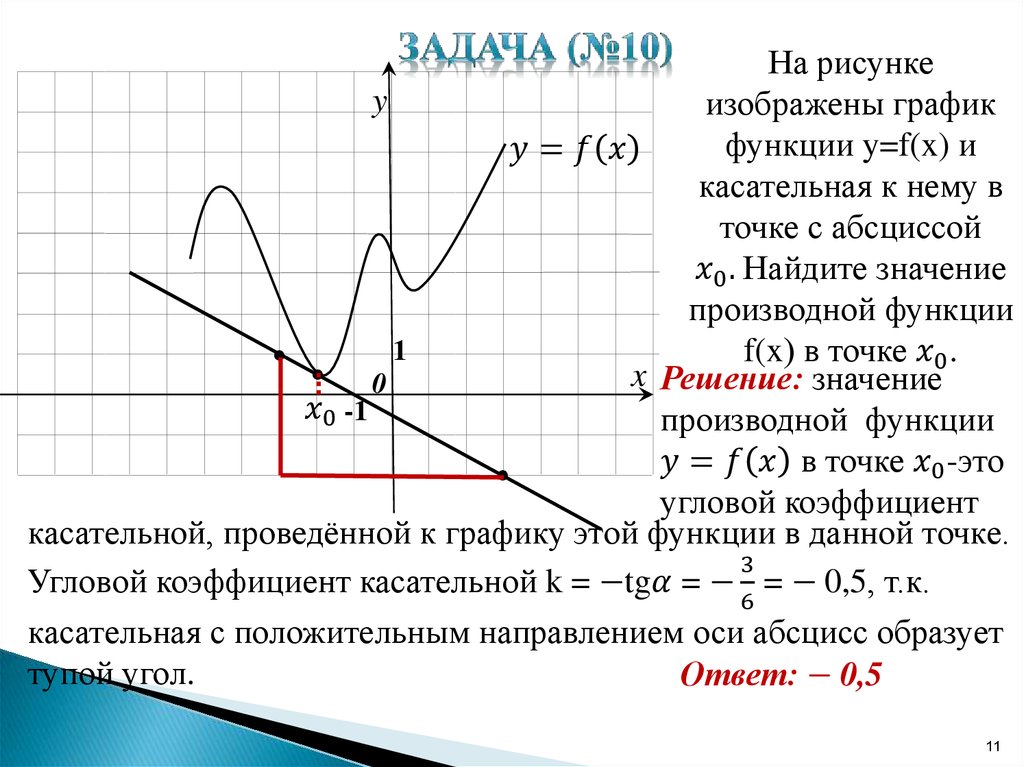
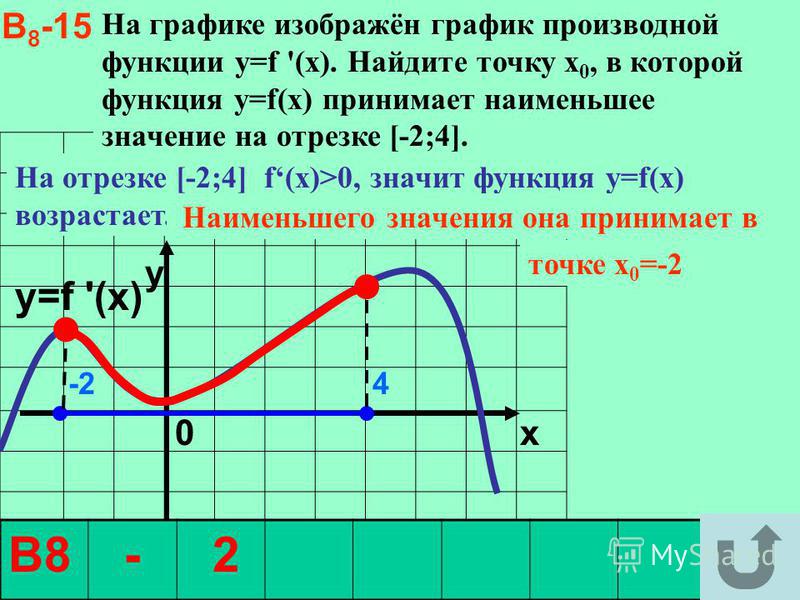 Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M 0, а в некоторый следующий момент t + Dt оказалась в положении M 1 – на расстоянии s + Ds от начального положения (см. рис .).
Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M 0, а в некоторый следующий момент t + Dt оказалась в положении M 1 – на расстоянии s + Ds от начального положения (см. рис .).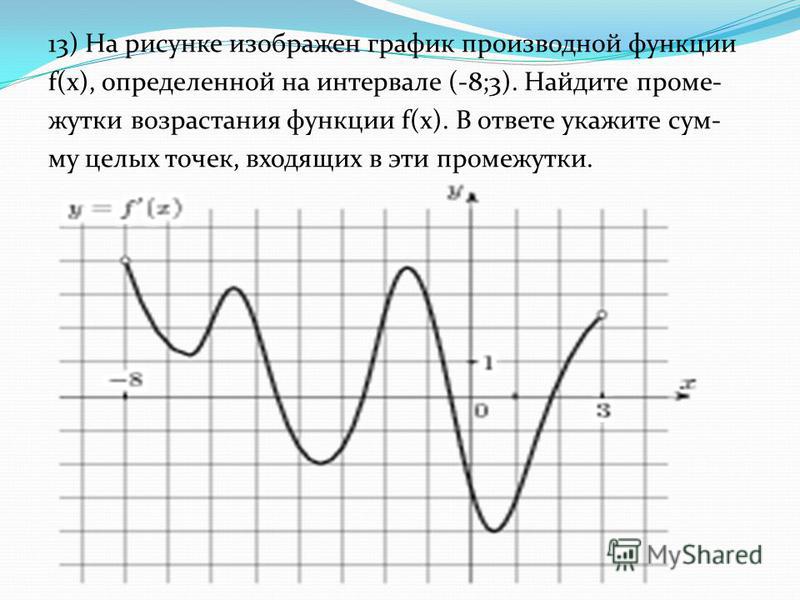 Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при Dt ® 0. Этот предел называют скоростью движения в данный момент:
Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при Dt ® 0. Этот предел называют скоростью движения в данный момент: Этим значениям x и y на кривой соответствует точка M 0(x , y ). Если аргументу x дать приращение Dx , то новому значению аргумента x + Dx соответствует новое значение функции y+ Dy = f (x + Dx ). Соответствующей ему точкой кривой будет точка M 1(x + Dx , y + Dy ). Если провести секущую M 0M 1 и обозначить через j угол, образованный секущей с положительным направлением оси Ox , из рисунка непосредственно видно, что .
Этим значениям x и y на кривой соответствует точка M 0(x , y ). Если аргументу x дать приращение Dx , то новому значению аргумента x + Dx соответствует новое значение функции y+ Dy = f (x + Dx ). Соответствующей ему точкой кривой будет точка M 1(x + Dx , y + Dy ). Если провести секущую M 0M 1 и обозначить через j угол, образованный секущей с положительным направлением оси Ox , из рисунка непосредственно видно, что . е. значение производной f ´(x ) при данном значении аргумента x равняется тангенсу угла, образованного касательной к графику функции f (x ) в соответствующей точке M 0(x ,y ) с положительным направлением оси Ox .
е. значение производной f ´(x ) при данном значении аргумента x равняется тангенсу угла, образованного касательной к графику функции f (x ) в соответствующей точке M 0(x ,y ) с положительным направлением оси Ox . В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.
В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.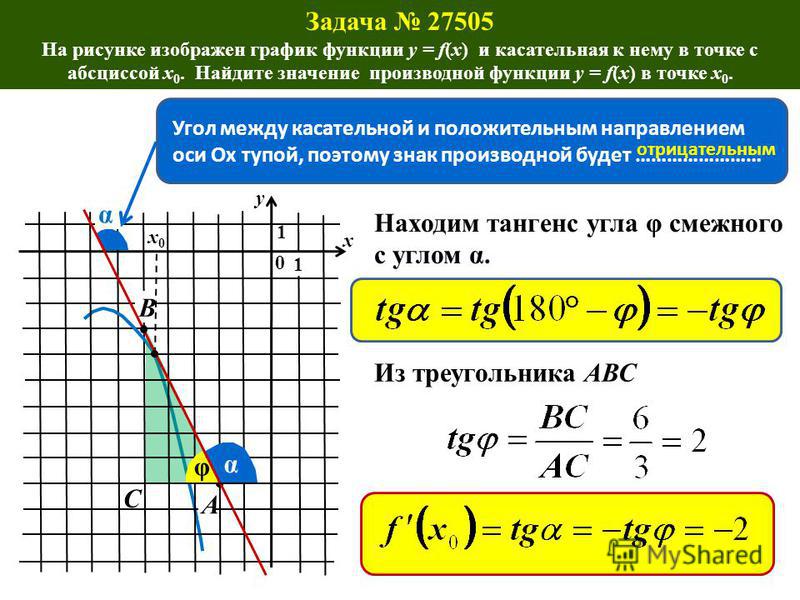

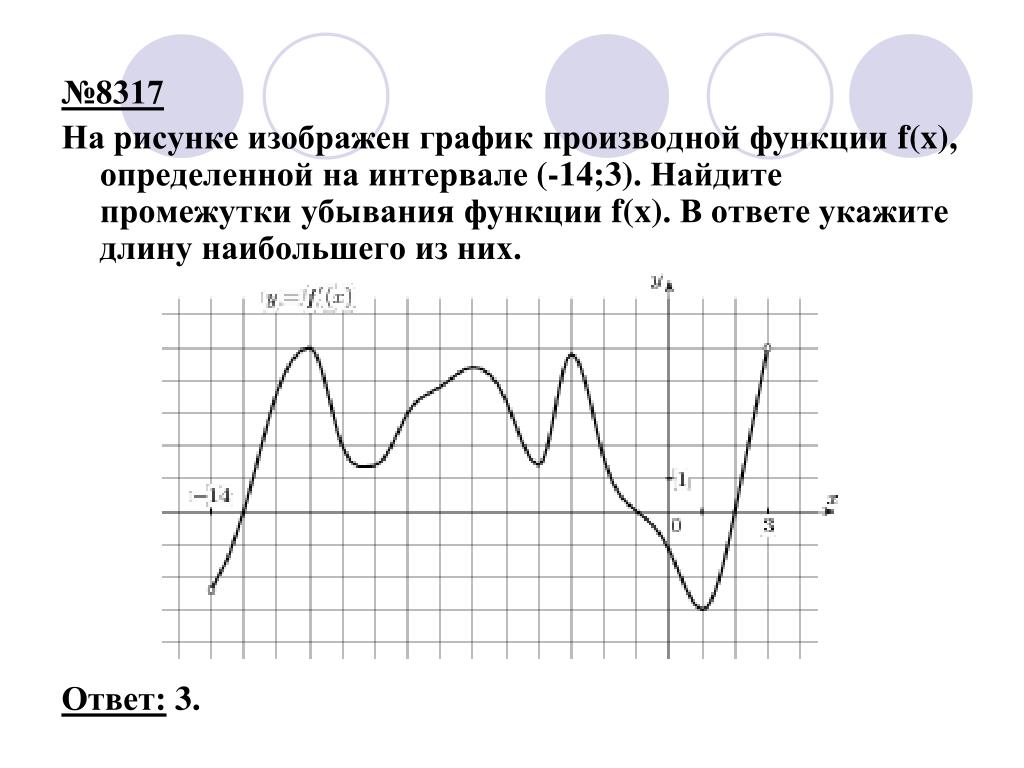

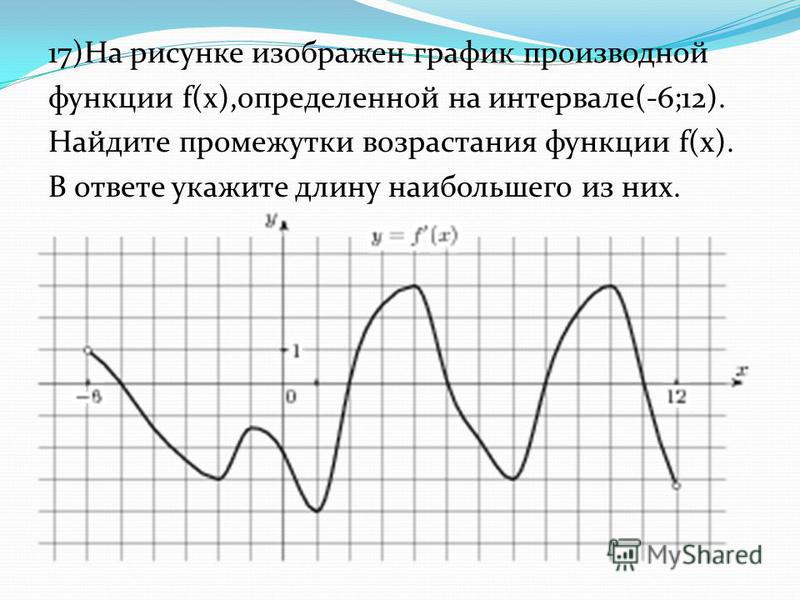 п. Это всё одно и то же. Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания.
п. Это всё одно и то же. Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания.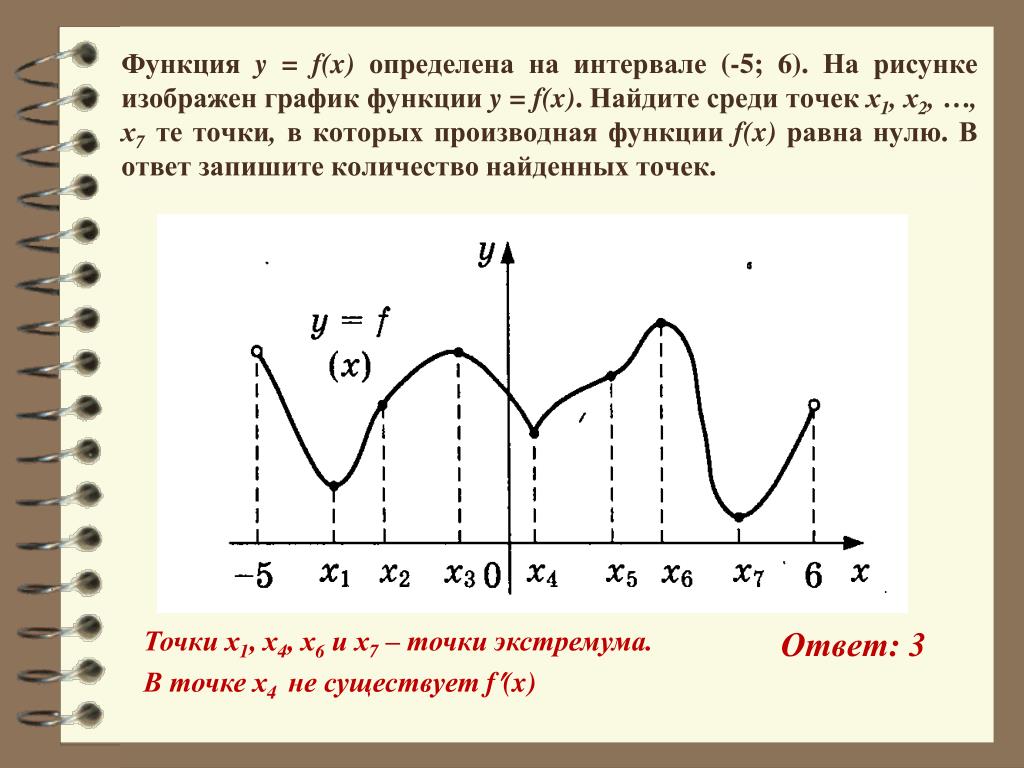 Вот они эти три кита:
Вот они эти три кита: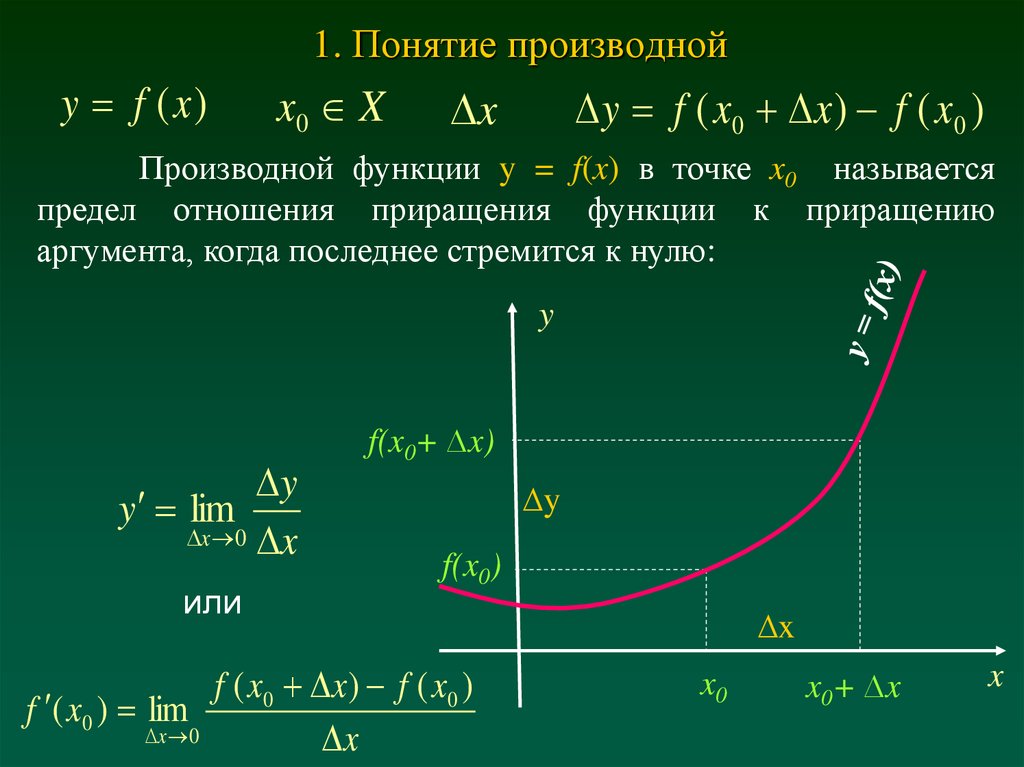
 Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)
Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)
 По формуле косинуса двойного угла:
По формуле косинуса двойного угла: Поэтому настало время набраться решимости и раскрыть тайну появления на светтаблицы производных и правил дифференцирования
. Начало положено в статьео смысле производной
, которую я настоятельно рекомендую к изучению, поскольку там мы как раз рассмотрели понятие производной и начали щёлкать задачи по теме. Этот же урок носит ярко выраженную практическую направленность, более того,
Поэтому настало время набраться решимости и раскрыть тайну появления на светтаблицы производных и правил дифференцирования
. Начало положено в статьео смысле производной
, которую я настоятельно рекомендую к изучению, поскольку там мы как раз рассмотрели понятие производной и начали щёлкать задачи по теме. Этот же урок носит ярко выраженную практическую направленность, более того,
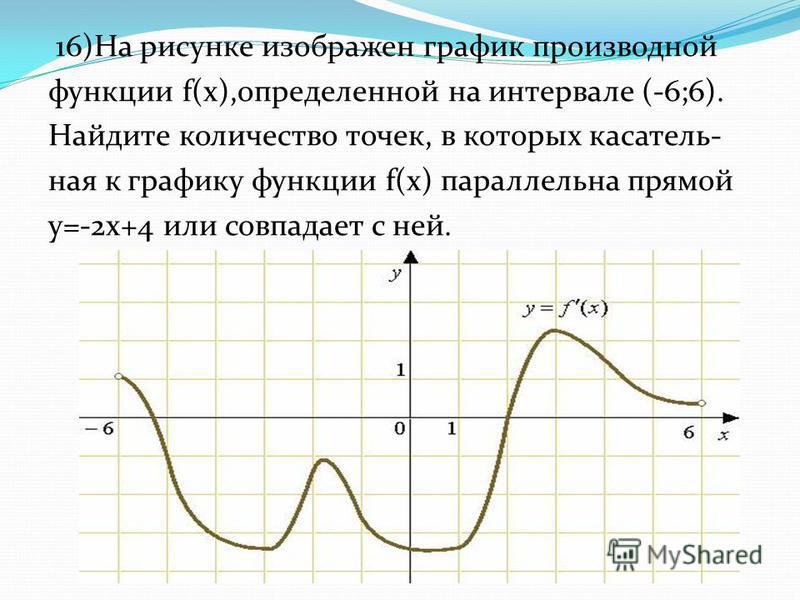
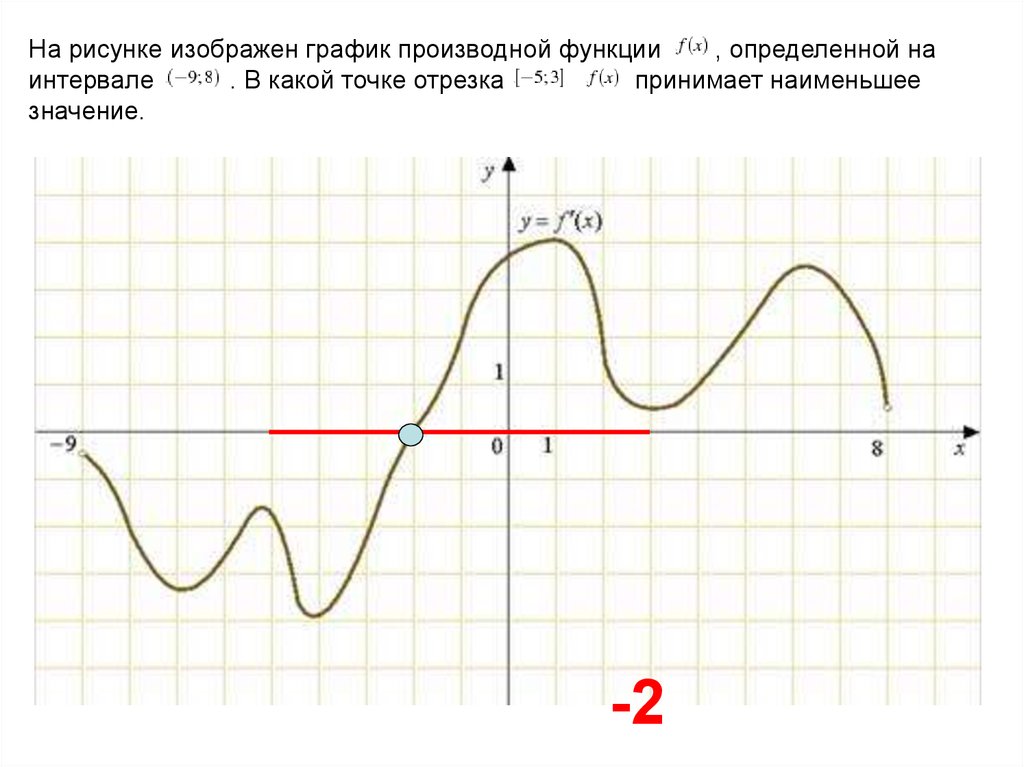
 Идея состоит в том, чтобы в начале решения избавиться от
Идея состоит в том, чтобы в начале решения избавиться от
 Тогда соответствующее приращение функции:
Тогда соответствующее приращение функции: Результат лежит на поверхности:
Результат лежит на поверхности: Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым».
Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым». В этом случае, понятно, получится не число, а производная функция.
В этом случае, понятно, получится не число, а производная функция.
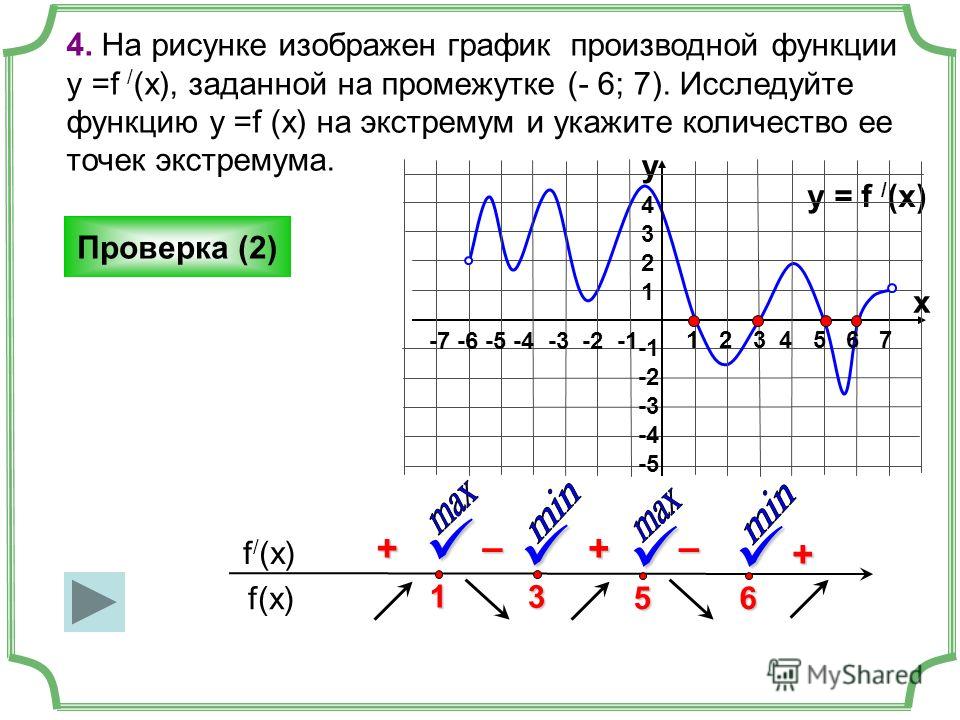 17
17
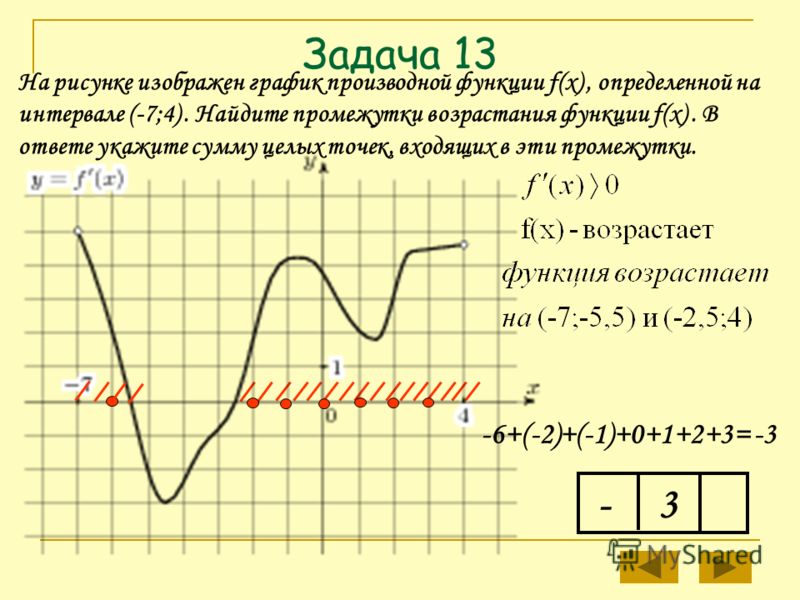
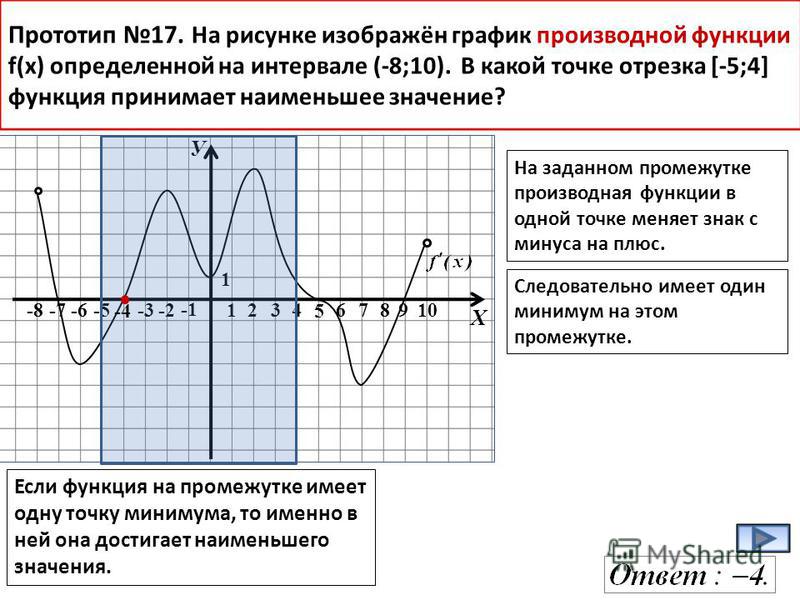 2 + bx + c & \text{if} \, x < - 10 \\ -\frac{1}{4}x + \frac{5}{2} & \text{if} \, x \ge -10 \end{cases}[/latex], где [latex]x [/latex] и [latex]f(x)[/latex] указаны в дюймах. Чтобы вагон двигался по трассе плавно, функция [latex]f(x)[/latex] должна быть непрерывной и дифференцируемой при -10. Найдите значения [latex]b[/latex] и [latex]c[/latex], которые делают [latex]f(x)[/latex] непрерывными и дифференцируемыми. 92 & \text{if} \, x \ge 3 \end{cases}[/latex] обе непрерывны и дифференцируемы в 3.
2 + bx + c & \text{if} \, x < - 10 \\ -\frac{1}{4}x + \frac{5}{2} & \text{if} \, x \ge -10 \end{cases}[/latex], где [latex]x [/latex] и [latex]f(x)[/latex] указаны в дюймах. Чтобы вагон двигался по трассе плавно, функция [latex]f(x)[/latex] должна быть непрерывной и дифференцируемой при -10. Найдите значения [latex]b[/latex] и [latex]c[/latex], которые делают [latex]f(x)[/latex] непрерывными и дифференцируемыми. 92 & \text{if} \, x \ge 3 \end{cases}[/latex] обе непрерывны и дифференцируемы в 3. В совокупности они обозначаются как 9{\prime}(x)=0[/латекс].
В совокупности они обозначаются как 9{\prime}(x)=0[/латекс]. 9h-1}{h}[/latex]
9h-1}{h}[/latex] 9{\ prime} (x) = \ underset {h \ to 0} {\ lim} \ frac {f (x + h) -f (x)} {h} [/ латекс]
9{\ prime} (x) = \ underset {h \ to 0} {\ lim} \ frac {f (x + h) -f (x)} {h} [/ латекс] [латекс]p(x)[/латекс] обозначает атмосферное давление на высоте [латекс]х[/латекс] футов.
[латекс]p(x)[/латекс] обозначает атмосферное давление на высоте [латекс]х[/латекс] футов. x$ как
\начать{выравнивать}
f'(x) &=f(x) f'(0).
\label{derivative_f_fprime}
\end{выравнивание}
x$ как
\начать{выравнивать}
f'(x) &=f(x) f'(0).
\label{derivative_f_fprime}
\end{выравнивание} {kx}$, и появятся два новых поля, в которых вы можете изменить значения $c$ и $k$. Вы можете использовать кнопки вверху для увеличения и уменьшения масштаба, а также панорамирования вида. 9ч-1}{ч}.
\конец{выравнивание*}
{kx}$, и появятся два новых поля, в которых вы можете изменить значения $c$ и $k$. Вы можете использовать кнопки вверху для увеличения и уменьшения масштаба, а также панорамирования вида. 9ч-1}{ч}.
\конец{выравнивание*} $$
Вышеупомянутые апплеты понимают $e$, так что вы можете ввести $e$ вместо $b$ в любом апплете и убедиться, что таинственный предел действительно один для этого случая. 9{кх},$$
у которого всего два параметра $c$ и $k$.
$$
Вышеупомянутые апплеты понимают $e$, так что вы можете ввести $e$ вместо $b$ в любом апплете и убедиться, что таинственный предел действительно один для этого случая. 9{кх},$$
у которого всего два параметра $c$ и $k$. {kx}.
\label{derivative_ekx}\tag{5}
\end{выравнивание}
9x$ для некоторого (неизвестного) числа $c$.
{kx}.
\label{derivative_ekx}\tag{5}
\end{выравнивание}
9x$ для некоторого (неизвестного) числа $c$. Часы измеряют время в любой момент дня .
Часы измеряют время в любой момент дня .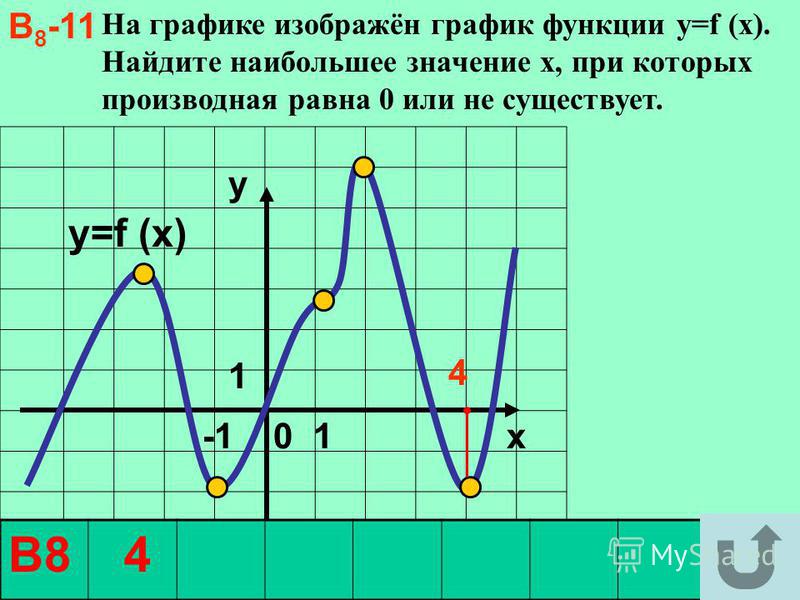
 Другими словами, подставьте ваши значения m , a и b в уравнение,
Другими словами, подставьте ваши значения m , a и b в уравнение, Мы найдем касательные в нескольких разных точках.
Мы найдем касательные в нескольких разных точках. Обратите внимание, что на экзамене AP по математическому анализу ответы с несколькими вариантами ответов могут быть упрощены. Итак, я показал вам как форму точка-наклон, так и упрощенную, или наклон-пересечение , форма касательной.
Обратите внимание, что на экзамене AP по математическому анализу ответы с несколькими вариантами ответов могут быть упрощены. Итак, я показал вам как форму точка-наклон, так и упрощенную, или наклон-пересечение , форма касательной.
 Спасибо!
Спасибо! y за каждую единицу x . Значения функции, называемой производной, будут варьироваться в зависимости от скорости изменения.
y за каждую единицу x . Значения функции, называемой производной, будут варьироваться в зависимости от скорости изменения. Скажем, 45 миль в час — в каждый момент времени.
Скажем, 45 миль в час — в каждый момент времени. (Тема 4 предварительного исчисления.) Пусть теперь x изменится на величину Δ x . Тогда новая координата x равна x + Δ x .
(Тема 4 предварительного исчисления.) Пусть теперь x изменится на величину Δ x . Тогда новая координата x равна x + Δ x .  Так как он будет производным от f ( x ), мы называем это производной функцией или производной от f ( x ). Чтобы напомнить нам, что оно было получено из f ( x ), мы обозначаем его как f’ ( x ) — « f-простое число из x «.
Так как он будет производным от f ( x ), мы называем это производной функцией или производной от f ( x ). Чтобы напомнить нам, что оно было получено из f ( x ), мы обозначаем его как f’ ( x ) — « f-простое число из x «.



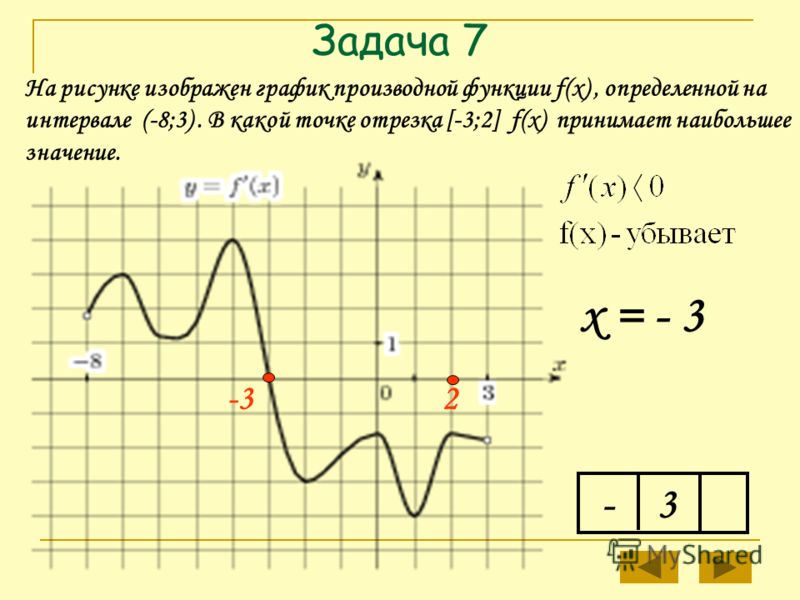 Графически это означает, что график при этом значении x будет касательная. При каких же значениях функция , а не будет дифференцируемой?
Графически это означает, что график при этом значении x будет касательная. При каких же значениях функция , а не будет дифференцируемой? Это иллюстрирует непрерывность в точке не является гарантией дифференцируемости — существования касательной — в этой точке.
Это иллюстрирует непрерывность в точке не является гарантией дифференцируемости — существования касательной — в этой точке.